Design and Optimization of High-Pressure Water Jet for Coal Breaking and Punching Nozzle Considering Structural Parameter Interaction
Abstract
:1. Introduction
2. Construction Features and Principle
3. Effect of Key Structural Parameters on Water Jet Performance
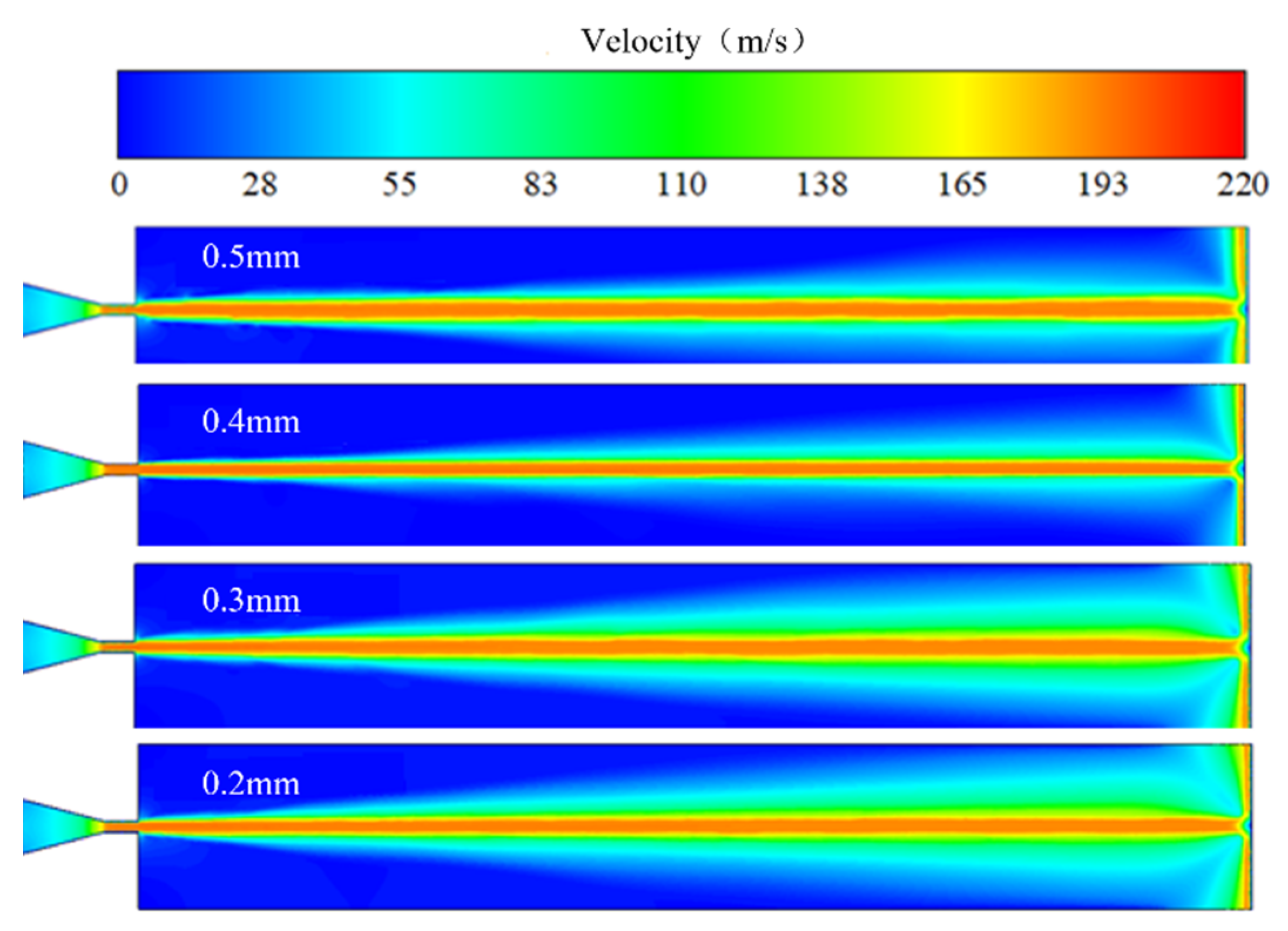
3.1. Computational Model
3.2. Numerical Simulation
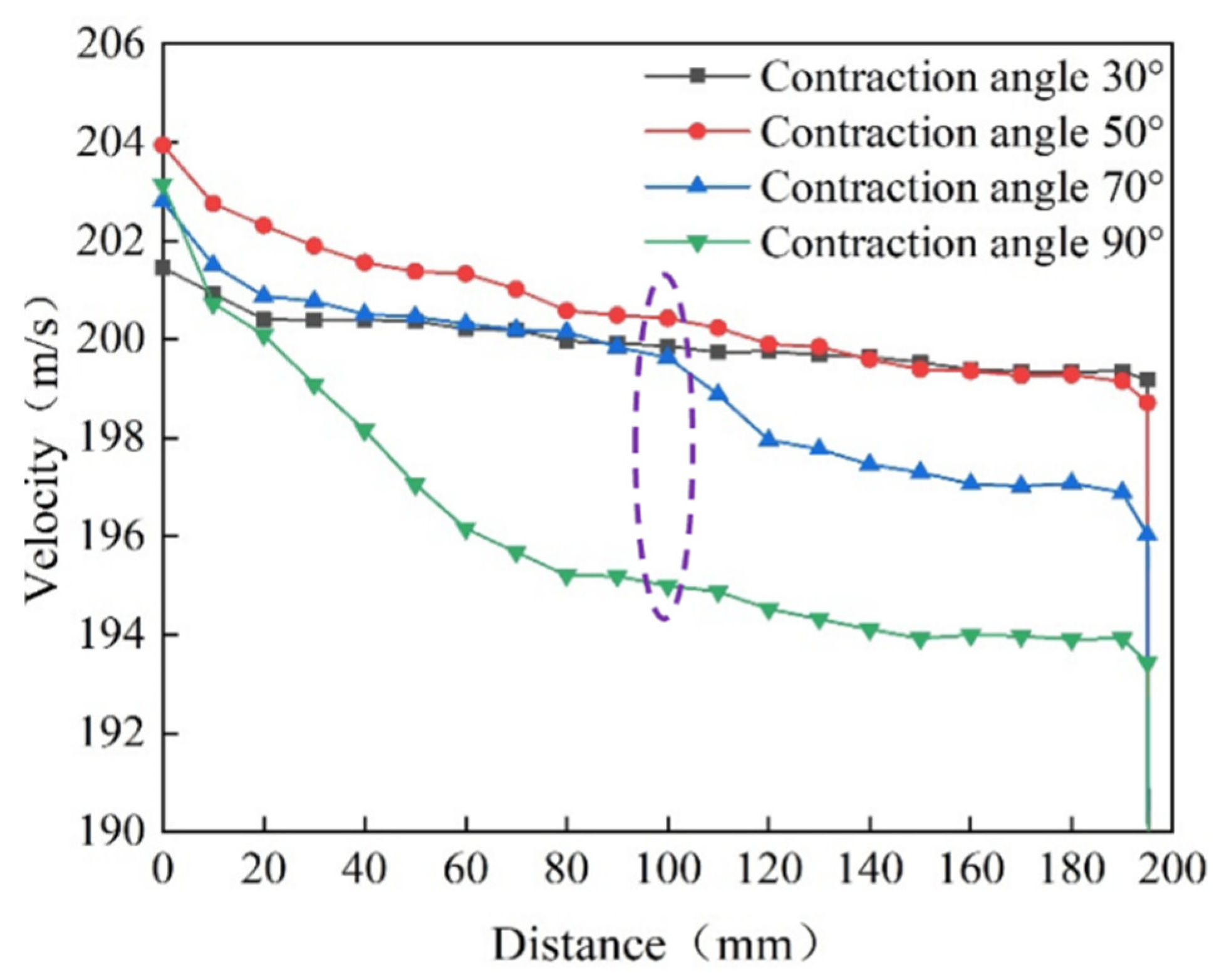
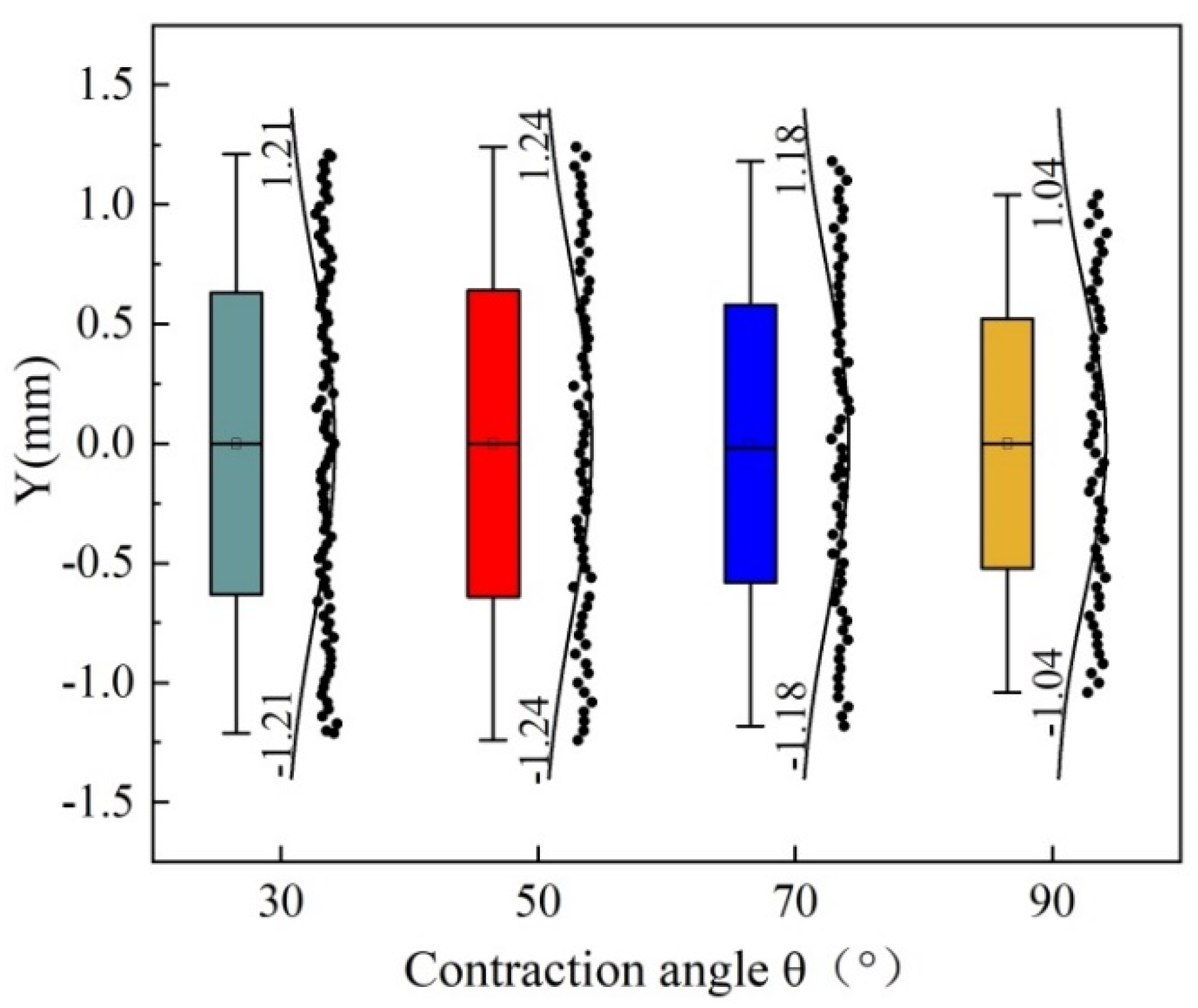
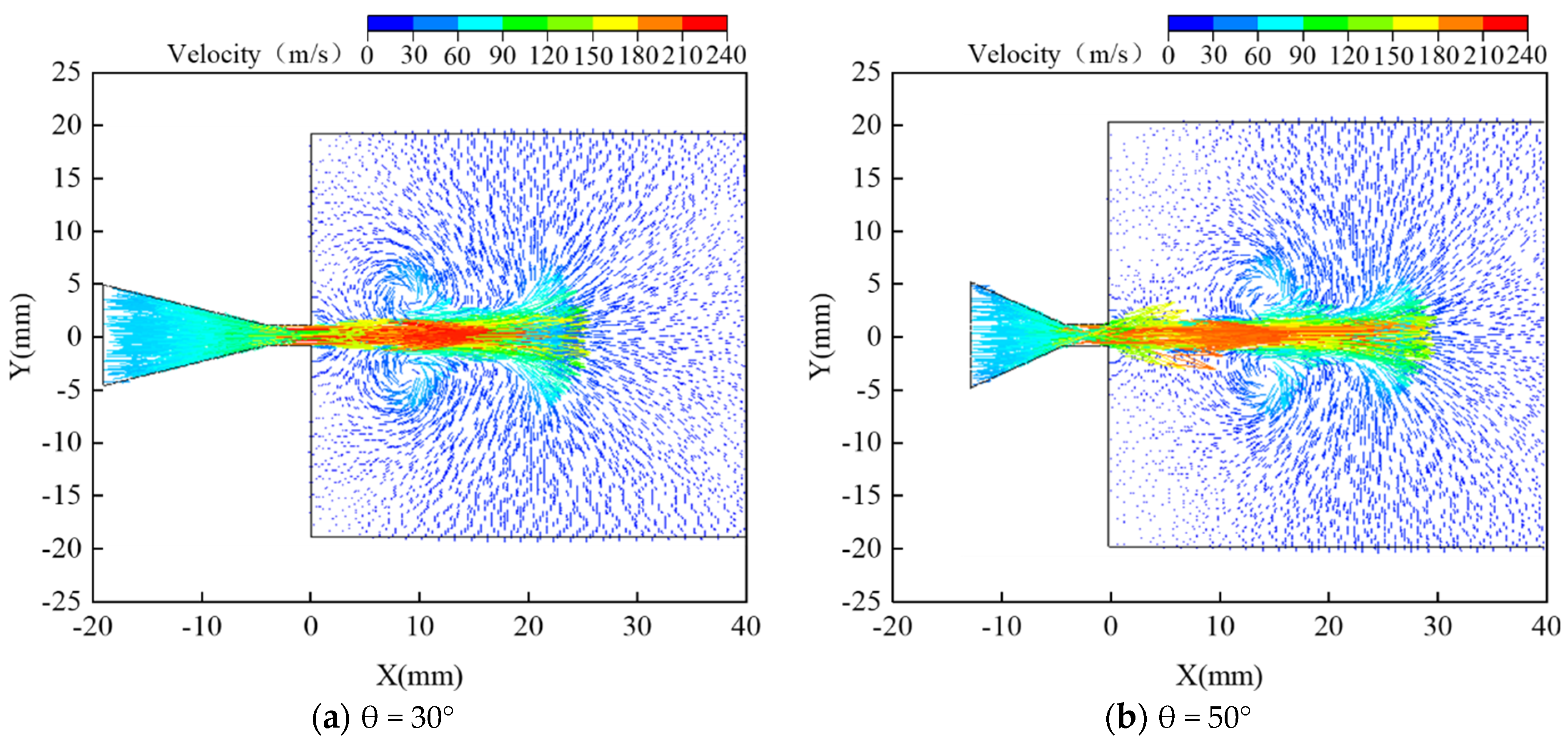
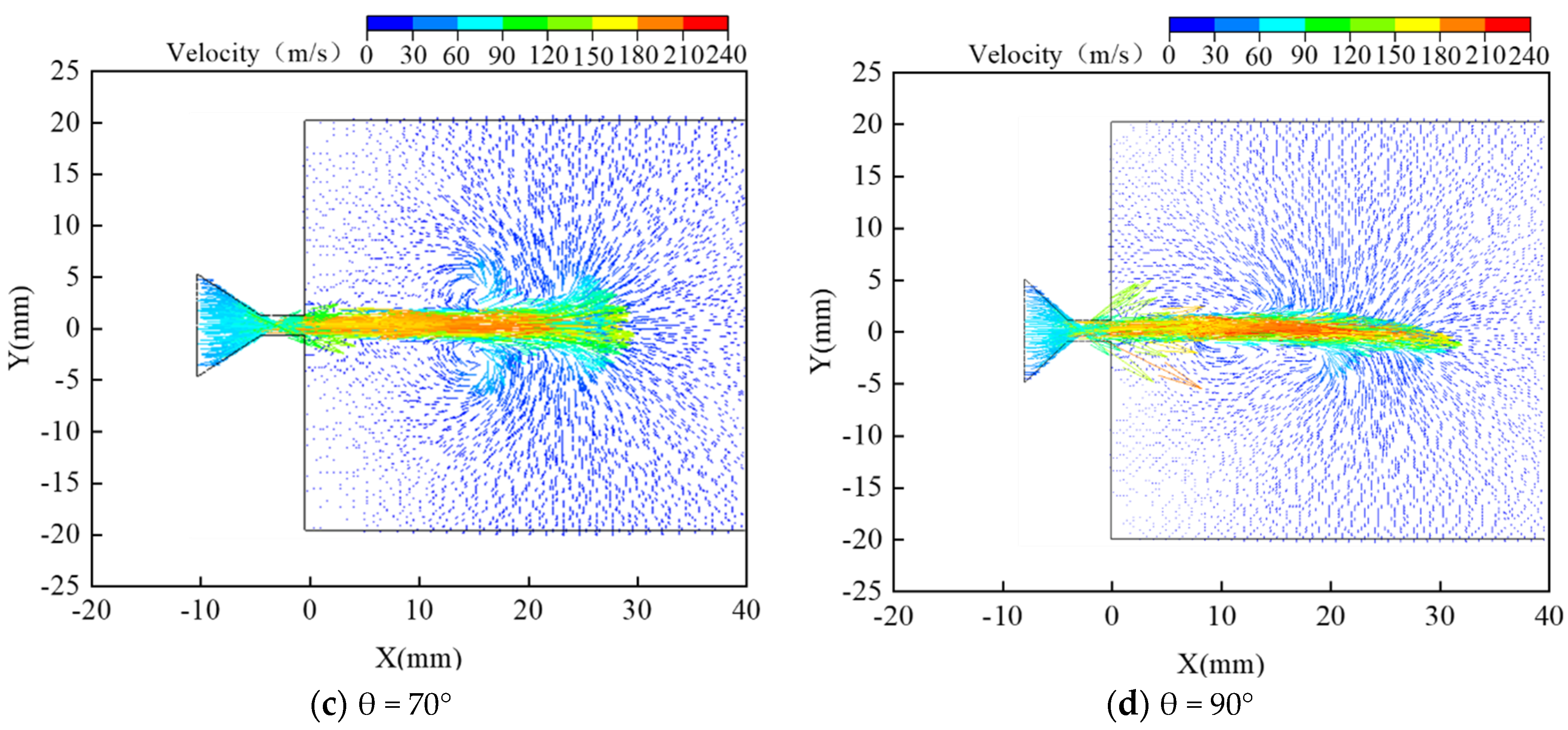
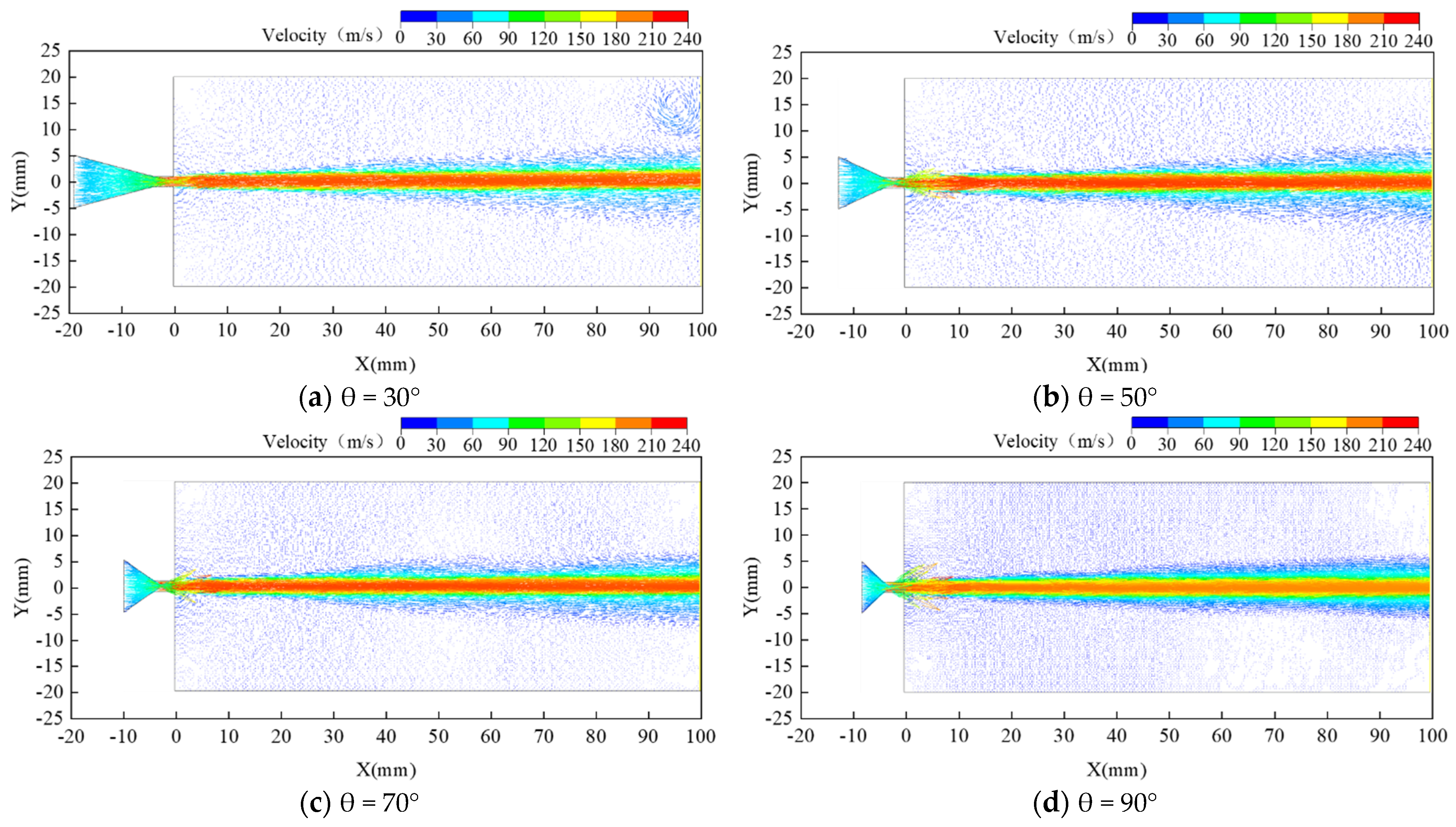
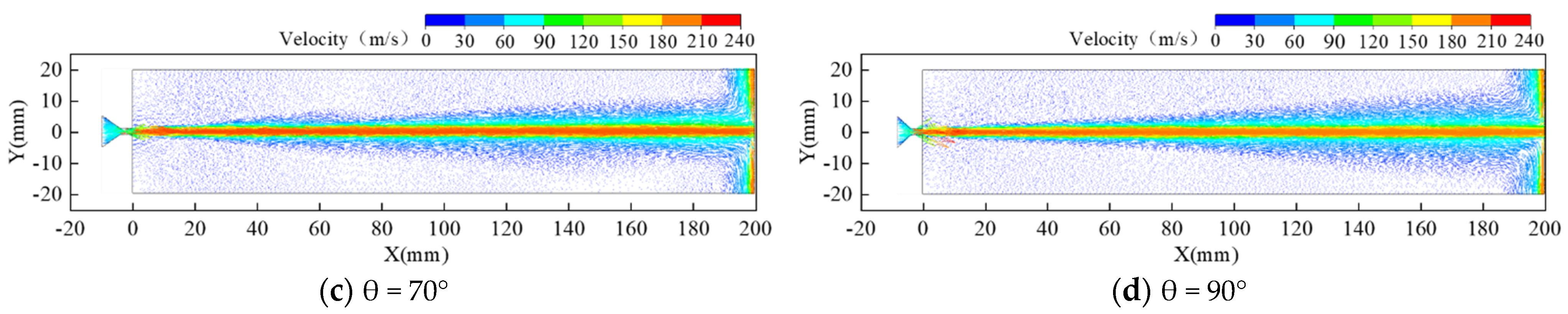
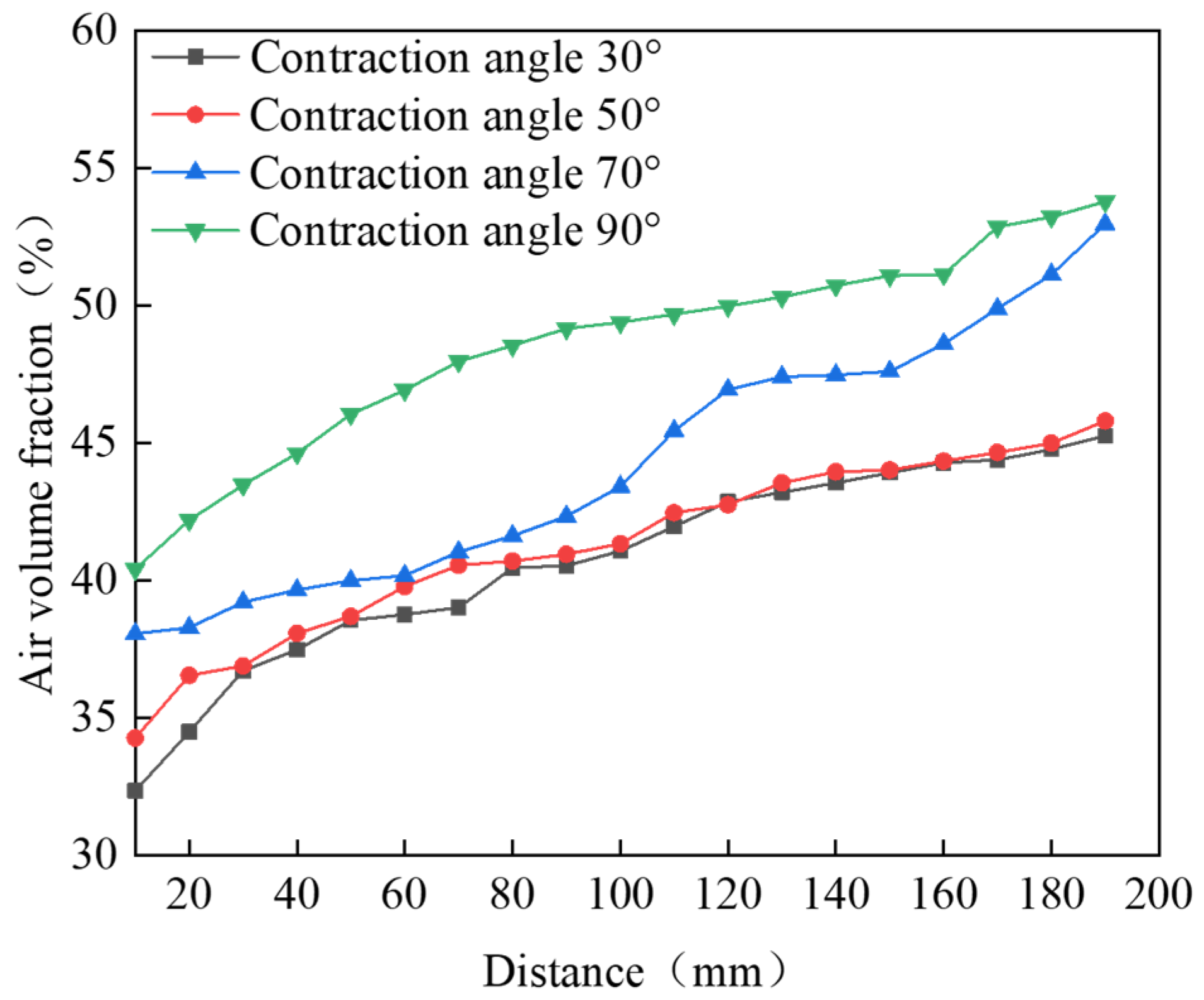
3.2.1. Effect of Contraction Angle on Water Jet Performance
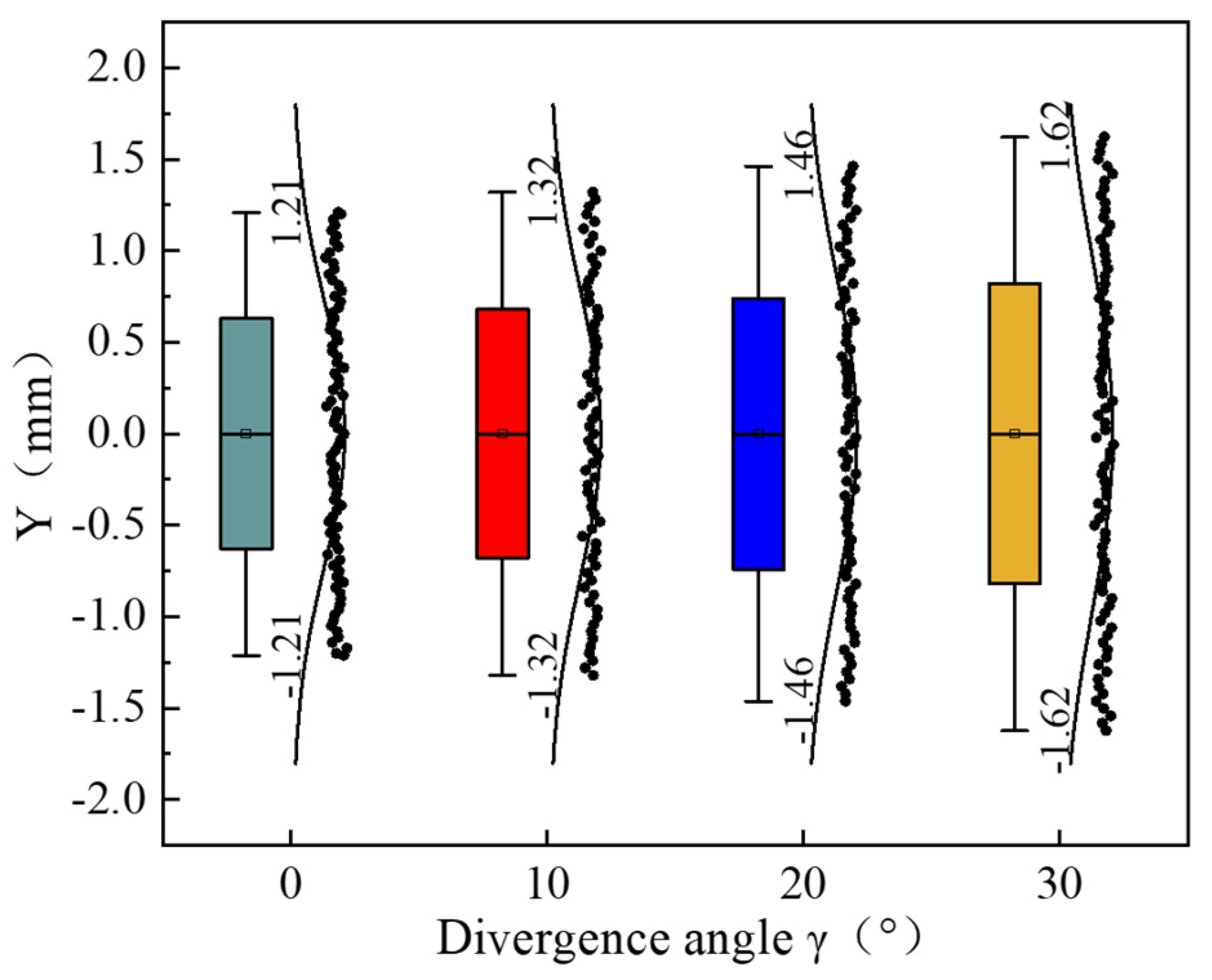
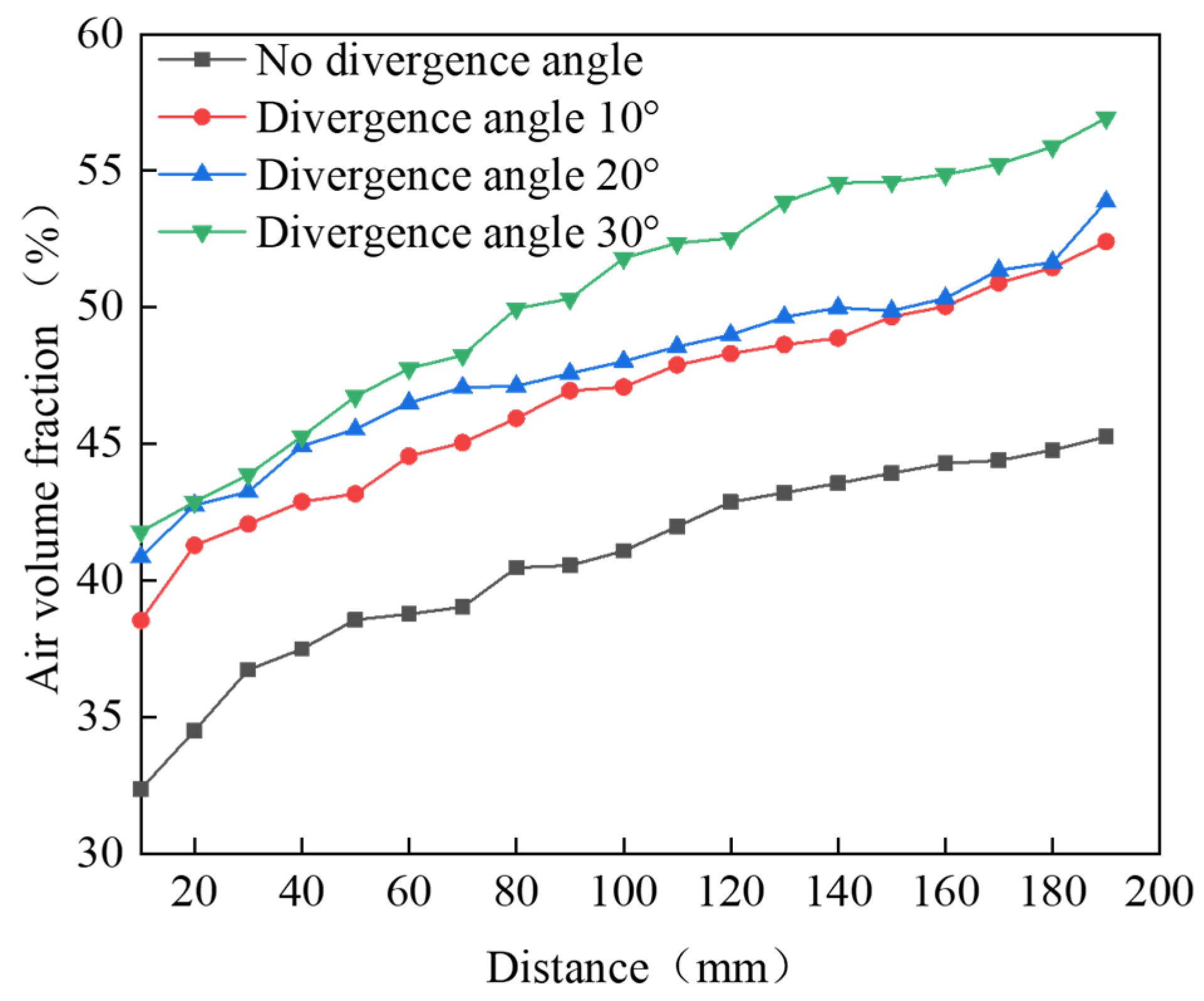
3.2.2. Effect of Outlet Divergence Angle on Water Jet Performance
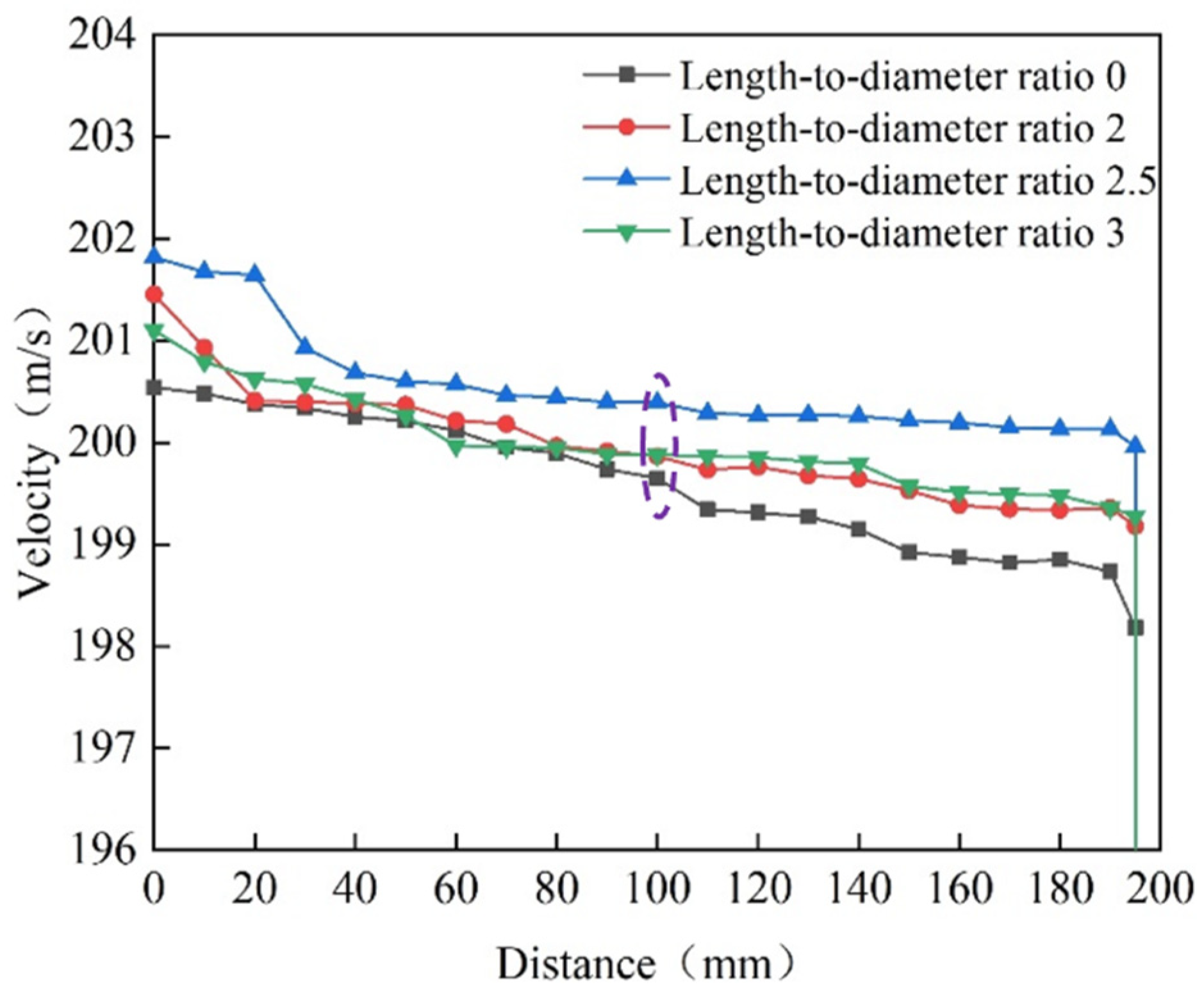
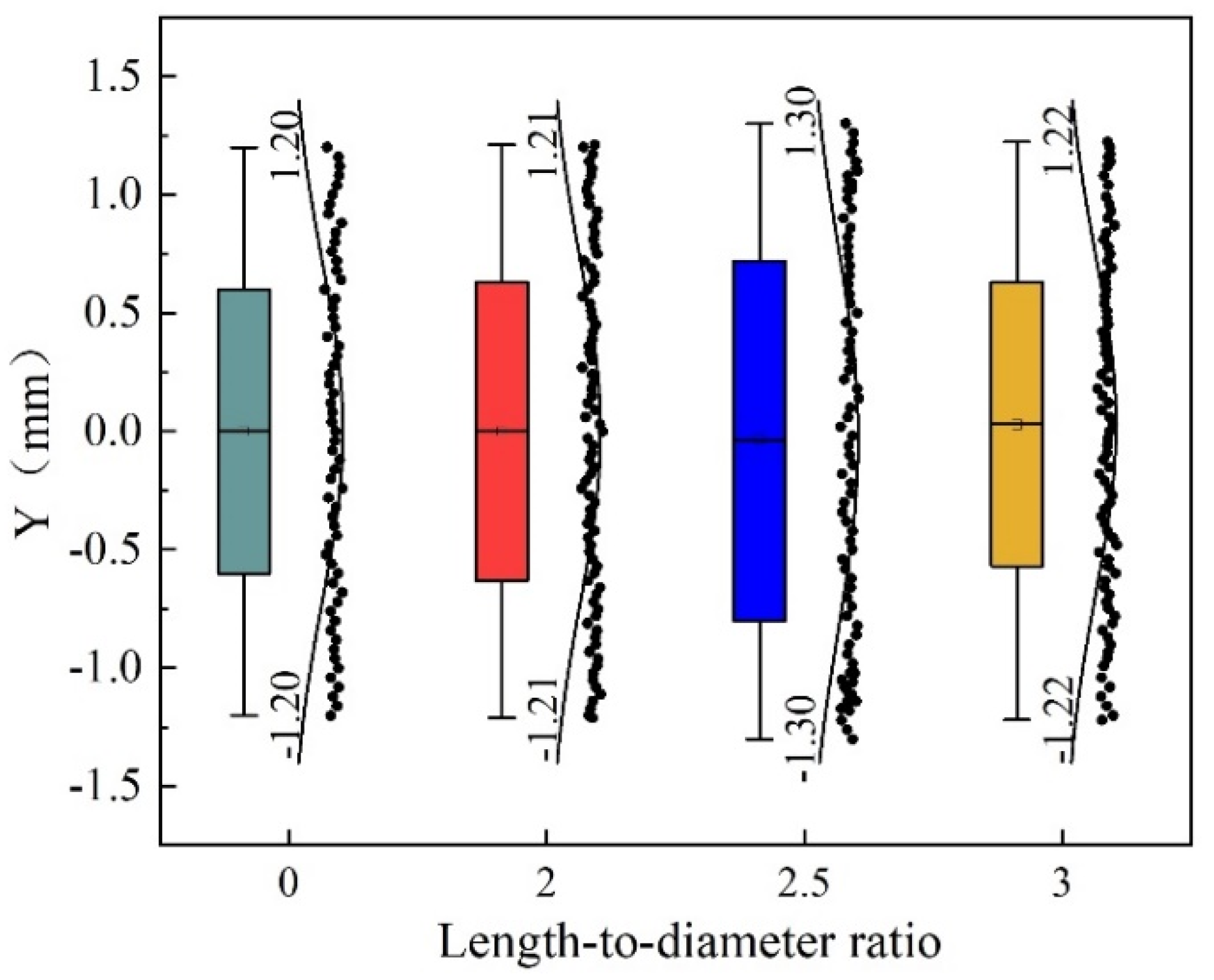
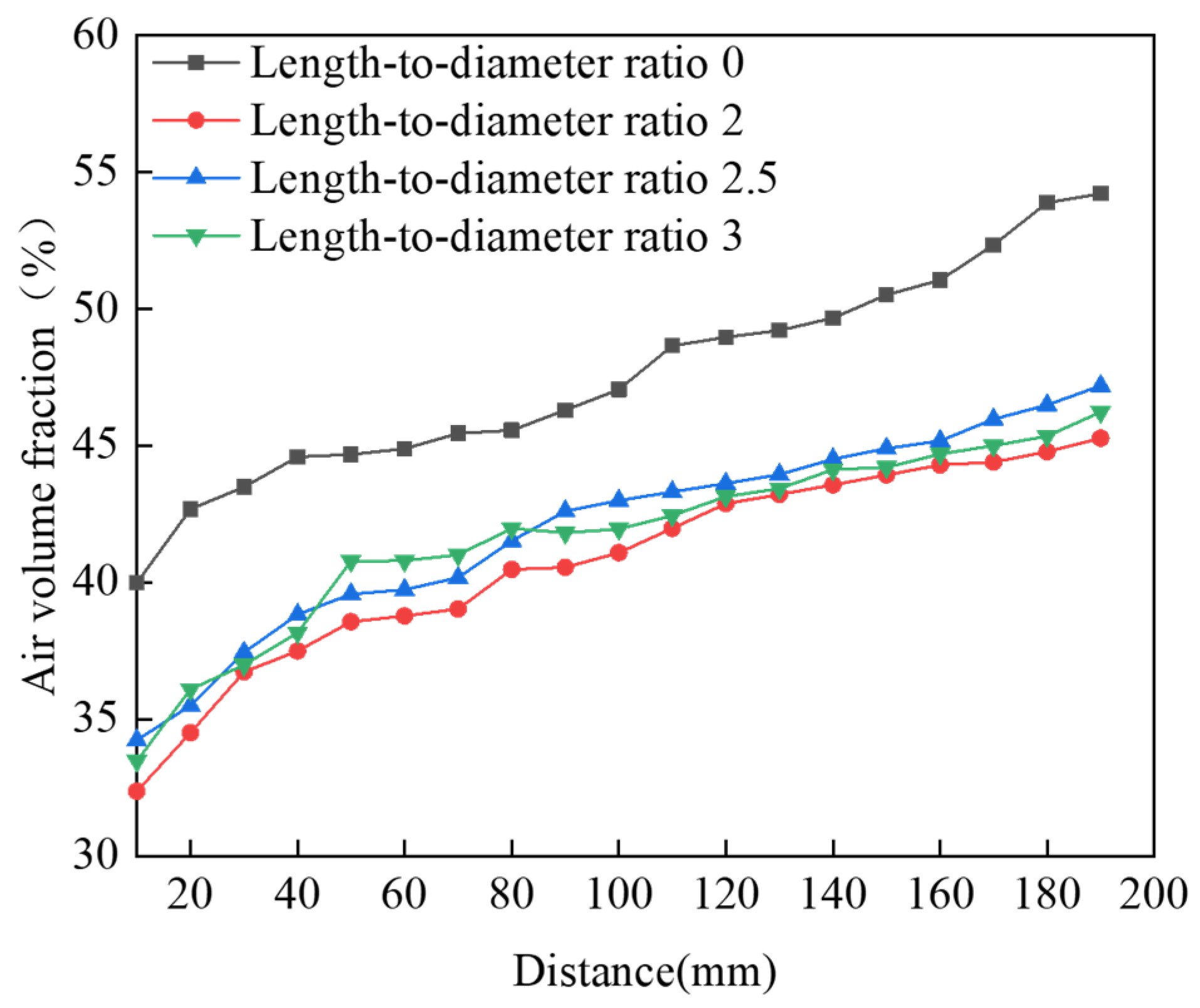
3.2.3. Effect of the Length-to-Diameter Ratio on Water Jet Performance
3.3. Analysis and Discussion
4. Orthogonal Experiment
4.1. Experiment Design
4.2. Results and Discussion
4.2.1. Range Analysis of the Orthogonal Experiment
4.2.2. Variance Analysis of the Orthogonal Experiment
4.3. Comprehensive Analysis of Experimental Data Based on Orthogonal Experiment
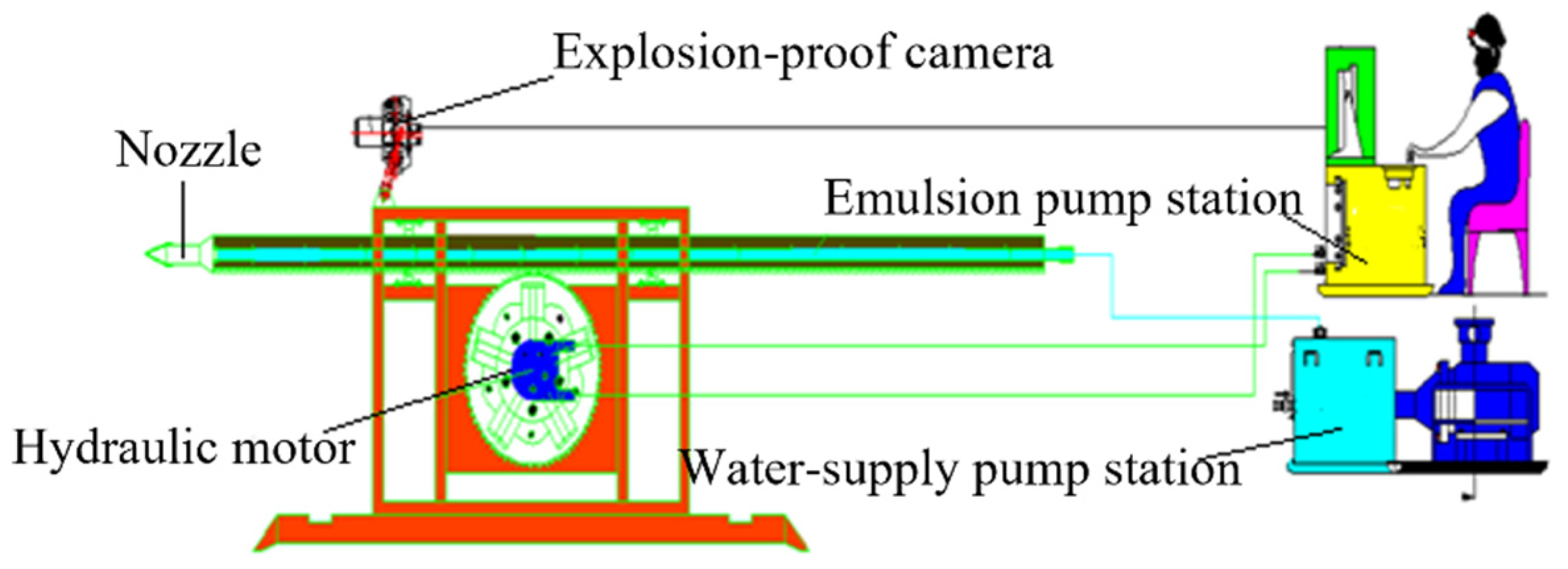
5. Field Experiments
5.1. Determination of Coal Firmness Coefficient
5.2. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, Z.H. Water Jet Theory and Technology; China University of Petroleum Press: Dongying, China, 1998. [Google Scholar]
- Chen, X.C.; Deng, S.S.; Guan, J.F.; Hua, W.X. Experiment and simulation research on abrasive water jet nozzle wear behavior and anti-wear structural improvement. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2023–2033. [Google Scholar] [CrossRef]
- Njock, P.G.A.; Chen, J.; Modoni, G.; Arulrajah, A.; Kim, Y.H. A review of jet grouting practice and development. Arab. J. Geosci. 2018, 11, 459. [Google Scholar] [CrossRef]
- Singh, D.; Premachandran, B.; Kohli, S. Effect of nozzle shape on jet impingement heat transfer from a circular cylinder. Int. J. Therm. Sci. 2015, 96, 45–69. [Google Scholar] [CrossRef]
- Vinze, R.; Chandel, S.; Limaye, M.D.; Prabhu, S.V. Influence of jet temperature and nozzle shape on the heat transfer distribution between a smooth plate and impinging air jets. Int. J. Therm. Sci. 2016, 99, 136–151. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Wiśniewski, P.; Dykas, S.; Zhang, G. Permeability enhancement properties of high-pressure abrasive water jet flushing and its application in a soft coal seam. Front. Energy Res. 2021, 9, 679623. [Google Scholar] [CrossRef]
- Chen, C.; Nie, S.L.; Wu, Z.J.; Li, Z.Y. A study of high pressure water jet characteristics by CFD simulation. Mach. Tool Hydraul. 2006, 2, 103–105. [Google Scholar]
- Wen, J.; Chen, C. Multifunctional experimental device of teaching model and its application of water jet testing and breaking rock. Sci. Technol. Eng. 2017, 17, 168–172. [Google Scholar] [CrossRef]
- Kong, L.; Wang, Y.; Lei, X.; Feng, C.; Wang, Z. Integral modeling of abrasive waterjet micro-machining process. Wear 2021, 482–483, 203987. [Google Scholar] [CrossRef]
- Nedelcu, D.; Cojocaru, V.; Avasiloaie, R.C. Numerical investigation of nozzle jet flow in a pelton microturbine. Machines 2021, 9, 158. [Google Scholar] [CrossRef]
- Wen, J.W.; Chen, C. Optimizing the structure of the straight cone nozzle and the parameters of borehole hydraulic mining for huadian oil shale based on experimental research. Energies 2017, 10, 2021. [Google Scholar] [CrossRef] [Green Version]
- Li, H.S.; Liu, S.Y.; Jia, J.G.; Wang, F.C.; Guo, C.W. Numerical simulation of rock-breaking under the impact load of self-excited oscillating pulsed water jet. Tunn. Undergr. Space Technol. 2020, 96, 179–192. [Google Scholar] [CrossRef]
- Chen, X.X.; Wang, C.; Shi, W.D.; Zhang, Y.C. Numerical simulation of submerged impinging water jet at different impact angles. J. Drain. Irrig. Mach. Eng. 2020, 38, 658–662. [Google Scholar]
- Rahman, M.S.; Tay, G.F.K.; Mark, F.T. Effects of nozzle geometry on turbulent characteristics and structure of surface attaching jets. Flow Turbul. Combust. 2019, 103, 797–825. [Google Scholar] [CrossRef]
- Huang, F.; Hu, B.; Zuo, W.Q.; Li, S.Q. Experiments on the impact pressure of high-pressure water jet under different nozzle shapes. J. Chongqing Univ. 2019, 42, 124–133. [Google Scholar]
- Liu, Y.; Cui, J.W.; Jian, P.; Liu, X.T. Effect of nozzle structure on coal breakage of SC-CO2 used for well drilling. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 67. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Zhang, Y.; Xiang, W.; He, Z.; Shi, W. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 496–508. [Google Scholar] [CrossRef]
- Yang, M.G.; Xiao, S.N.; Kang, C.; Wang, Y.L. Effect of geometrical parameters on submerged cavitation jet discharged from profiled central-body nozzle. Chin. J. Mech. Eng. 2013, 26, 476–482. [Google Scholar] [CrossRef]
- Hong, C.Y.; Yang, R.Y.; Huang, Z.W.; Liu, W.; Chen, J.X.; Cong, R.C. Experimental investigation on coal-breakage performances by abrasive nitrogen-gas jet with a conical nozzle. Int. J. Rock Mech. Min. Sci. 2021, 142, 104781. [Google Scholar] [CrossRef]
- Qiang, Z.R.; Wu, M.P.; Miao, X.J.; Rupy, S. CFD research on particle movement and nozzle wear in the abrasive water jet cutting head. Int. J. Adv. Manuf. Technol. 2018, 95, 4091–4100. [Google Scholar] [CrossRef]
- Wang, H.; Qian, Z.; Zhang, D.; Wang, T.; Wang, C. Numerical study of the normal impinging water jet at different impinging height, based on Wray-Agarwal turbulence model. Energies 2020, 13, 1744. [Google Scholar] [CrossRef] [Green Version]
- Peng, G.J.; Tian, L.; Hao, C.; Hong, S.M.; Ye, D.X.; You, B.J. Numerical and experimental study of hydraulic performance and wear characteristics of a slurry pump. Machines 2021, 9, 373. [Google Scholar] [CrossRef]
- Ekiciler, R.; Cetinkaya, M.S.; Arslan, K. Convective heat transfer investigation of a confined air slot-jet impingement cooling on corrugated surfaces with different wave shapes. J. Heat Transf. 2019, 141, 22202. [Google Scholar] [CrossRef]
- Liu, S.Y.; Zhou, F.Y.; Li, H.S.; Chen, Y.Q.; Wang, F.C.; Guo, C.W. Experimental investigation of hard rock breaking using a conical pick assisted by abrasive water jet. Rock Mech. Rock Eng. 2020, 53, 4221–4230. [Google Scholar] [CrossRef]
- Chen, J.; Guo, L.W.; Zhang, J.Y. Relationship between shock parameter and coal particle parameter of advanced premixed micro-soft abrasive coal-water jet. Powder Technol. 2021, 379, 393–406. [Google Scholar] [CrossRef]
- Fang, M.H.; Yu, T.; Feng, F.; Jeff, X. An experimental investigation of abrasive suspension flow machining of injector nozzle based on orthogonal test design. Int. J. Adv. Manuf. Technol. 2020, 110, 1071–1082. [Google Scholar] [CrossRef]
- Zhou, J.R.; Zhao, M.M.; Wang, C.; Gao, Z.J.; Zhu, Y. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock. Vib. 2021, 2021, 6616456. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Wang, R.; Tang, S.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump combining improved lenet-5 and PSO hyper parameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Wang, H.; Long, B.; Wang, C.; Han, C.; Li, L. Effects of the impeller blade with a slot structure on the centrifugal pump performance. Energies 2020, 13, 1628. [Google Scholar] [CrossRef]
- Shen, H.J. Structural optimization and test of nozzle for coal seam slotting. Saf. Coal Mines 2020, 51, 10–13. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Huang, F.; Liu, X.; Ao, X. On the failure pattern of sandstone impacted by high-velocity water jet. Int. J. Impact Eng. 2015, 76, 67–74. [Google Scholar] [CrossRef]
- Yu, Y.F.; Li, C.X.; Meng, H.B.; Wang, Y.F.; Wu, J.H. Flow and entrainment characteristics of jet from different shape nozzles. Chin. J. Process Eng. 2014, 14, 549–555. [Google Scholar]
- Azad, M.; Quinn, W.R.; Groulx, D. Mixing in turbulent free jets issuing from isosceles triangular orifices with different apex angles. Exp. Therm. Fluid Sci. 2012, 39, 237–251. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Tang, F.; Wang, C. Multi-Disciplinary optimization design of axial-flow pump impellers based on the approximation model. Energies 2020, 13, 779. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.W.; Qi, Z.W.; Seyed, S.B.; Pei, X.J.; Tom, I. Research on the structures and hydraulic performances of the typical direct jet nozzles for water jet technology. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 558–570. [Google Scholar] [CrossRef]
- Chen, B.; Gao, D.R.; Li, Y.B.; Chen, C.Q.; Yuan, X.M.; Wang, Z.S.; Sun, P. Investigation of the droplet characteristics and size distribution during the collaborative atomization process of a twin-fluid nozzle. Int. J. Adv. Manuf. Technol. 2020, 107, 1625–1639. [Google Scholar] [CrossRef]
- Humaira, Y.; Naveed, I.; Anum, T. Engineering applications of peristaltic fluid flow with hall current, thermal deposition and convective conditions. Mathematics 2020, 8, 1710. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Q.; Yang, Y.; Wang, C. Performance differences of electrical submersible pump under variable speed schemes. Int. J. Simul. Model. 2021, 20, 76–86. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An improved convolutional neural network with an adaptable learning rate towards multi-signal fault diagnosis of hydraulic piston pump. Adv. Eng. Inform. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Liang, B.J.; Gao, D.R. Optimization of structural parameters of fan—Shaped high-pressure nozzle. J. Drain. Irrig. Mach. Eng. 2020, 38, 69–75. [Google Scholar]
- Zhu, Y.; Li, G.; Wang, R.; Tang, S.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump based on wavelet analysis and improved Alex Net. Sensors 2021, 21, 549. [Google Scholar] [CrossRef]
- He, W.; Xue, W.D.; Tang, B. Optimization Method of Experimental Design and Data Analysis; Chemical Industry Press: Beijing, China, 2012. [Google Scholar]
- GB/T 23561.12-2010; Methods for Determining the Physical and Mechanical Properties of Coal and Rock—Part 12: Methods for Determining Coal Hardiness Coefficient. Standards Press of China: Beijing, China, 2011.
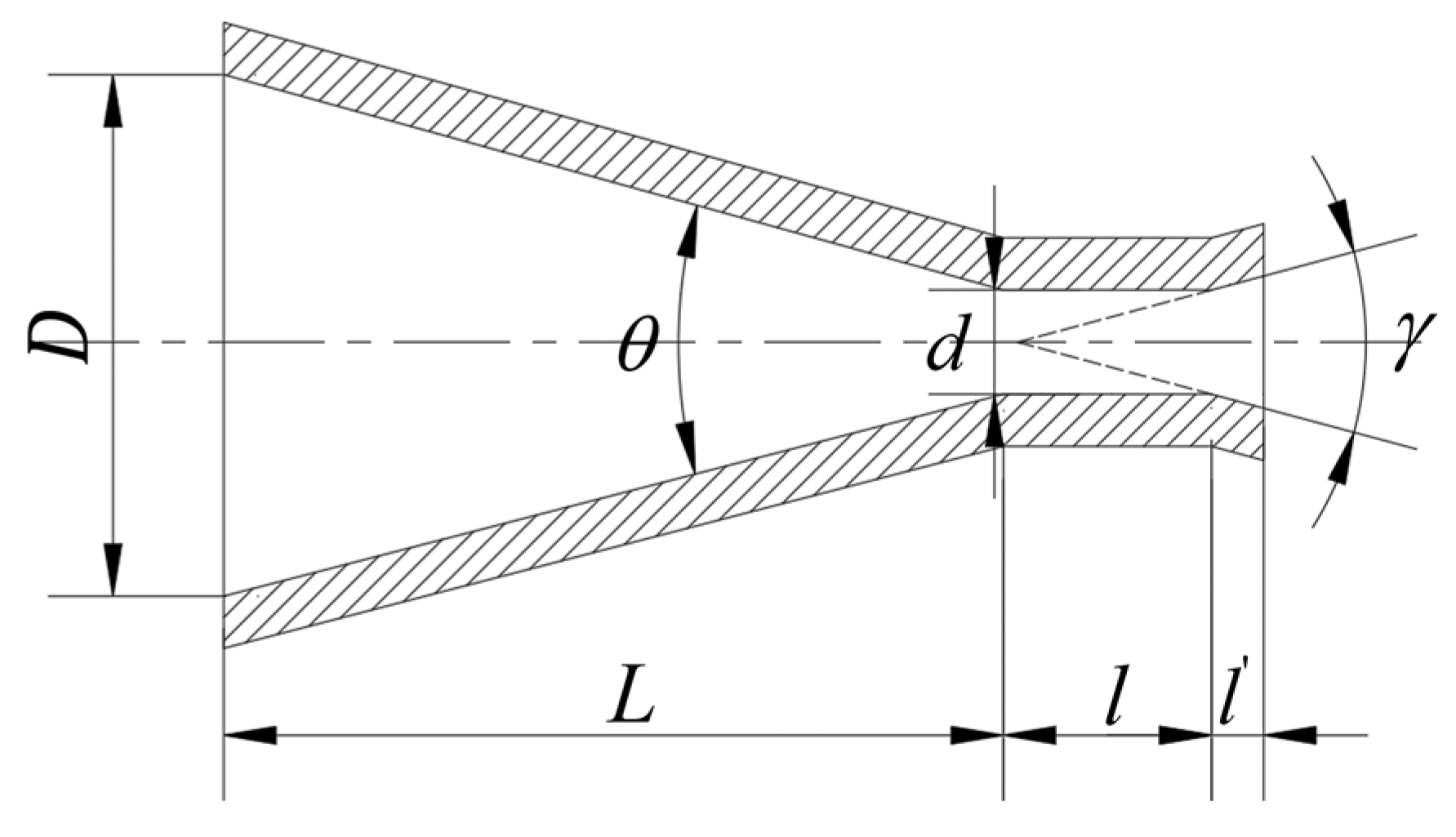





| Structure Parameter | Inlet Contraction Angle (°) | Outlet Divergence Angle (°) | Length-to-Diameter Ratio | Inlet Diameter (mm) | Outlet Diameter (mm) |
|---|---|---|---|---|---|
| Initial nozzle | 30 | 0 | 2 | 10 | 2 |
| Improved nozzle | 30, 50, 70, 90 | 0 | 2 | 10 | 2 |
| 30 | 0, 10, 20, 30 | 2 | 10 | 2 | |
| 30 | 0 | 0, 2, 2.5, 3 | 10 | 2 |
| Grid Size (mm) | Grid Quantity | Velocity Distribution (m/s) |
|---|---|---|
| 0.5 | 26,528 | 198.0234–200.9876 |
| 0.4 | 41,419 | 198.4325–201.0324 |
| 0.3 | 74,391 | 199.9132–201.4522 |
| 0.2 | 176,040 | 199.9246–201.4703 |
| Level | A | B | C |
|---|---|---|---|
| θ (°) | γ (°) | l/d | |
| 1 | 30 | 0 | 2 |
| 2 | 50 | 20 | 2.5 |
| 3 | 70 | 30 | 3 |
| Factors | A | B | AB | A2B | C | AC | A2C | BC | ABC | A2BC | B2C | AB2C | A2B2C | Maximum X-Axis Velocity (m/s) | Half of Effective Y-Axis Extension Distance (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experimental Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| 1 | 30 | 0 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 199.865 | 1.212 |
| 2 | 30 | 0 | 1 | 1 | 2.5 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 200.393 | 1.303 |
| 3 | 30 | 0 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 199.879 | 1.221 |
| 4 | 30 | 20 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 199.868 | 1.323 |
| 5 | 30 | 20 | 2 | 2 | 2.5 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 199.424 | 1.503 |
| 6 | 30 | 20 | 2 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 2 | 2 | 2 | 200.024 | 1.402 |
| 7 | 30 | 30 | 3 | 3 | 2 | 1 | 1 | 3 | 3 | 3 | 2 | 2 | 2 | 198.397 | 1.463 |
| 8 | 30 | 30 | 3 | 3 | 2.5 | 2 | 2 | 1 | 1 | 1 | 3 | 3 | 3 | 198.118 | 1.563 |
| 9 | 30 | 30 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 198.350 | 1.532 |
| 10 | 50 | 0 | 2 | 3 | 2 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 200.484 | 1.242 |
| 11 | 50 | 0 | 2 | 3 | 2.5 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 199.382 | 1.283 |
| 12 | 50 | 0 | 2 | 3 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 199.426 | 1.281 |
| 13 | 50 | 20 | 3 | 1 | 2 | 2 | 3 | 2 | 3 | 1 | 3 | 1 | 2 | 199.181 | 1.341 |
| 14 | 50 | 20 | 3 | 1 | 2.5 | 3 | 1 | 3 | 1 | 2 | 1 | 2 | 3 | 198.277 | 1.522 |
| 15 | 50 | 20 | 3 | 1 | 3 | 1 | 2 | 1 | 2 | 3 | 2 | 3 | 1 | 198.390 | 1.401 |
| 16 | 50 | 30 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 2 | 2 | 3 | 1 | 197.160 | 1.502 |
| 17 | 50 | 30 | 1 | 2 | 2.5 | 3 | 1 | 1 | 2 | 3 | 3 | 1 | 2 | 198.476 | 1.582 |
| 18 | 50 | 30 | 1 | 2 | 3 | 1 | 2 | 2 | 3 | 1 | 1 | 2 | 3 | 195.748 | 1.441 |
| 19 | 70 | 0 | 3 | 2 | 2 | 3 | 2 | 1 | 3 | 2 | 1 | 3 | 2 | 198.331 | 1.183 |
| 20 | 70 | 0 | 3 | 2 | 2.5 | 1 | 3 | 2 | 1 | 3 | 2 | 1 | 3 | 198.936 | 1.191 |
| 21 | 70 | 0 | 3 | 2 | 3 | 2 | 1 | 3 | 2 | 1 | 3 | 2 | 1 | 199.225 | 1.101 |
| 22 | 70 | 20 | 1 | 3 | 2 | 3 | 2 | 2 | 1 | 3 | 3 | 2 | 1 | 195.775 | 1.361 |
| 23 | 70 | 20 | 1 | 3 | 2.5 | 1 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 195.603 | 1.381 |
| 24 | 70 | 20 | 1 | 3 | 3 | 2 | 1 | 1 | 3 | 2 | 2 | 1 | 3 | 195.284 | 1.321 |
| 25 | 70 | 30 | 2 | 1 | 2 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 3 | 188.234 | 1.421 |
| 26 | 70 | 30 | 2 | 1 | 2.5 | 1 | 3 | 1 | 3 | 2 | 3 | 2 | 1 | 193.189 | 1.602 |
| 27 | 70 | 30 | 2 | 1 | 3 | 2 | 1 | 2 | 1 | 3 | 1 | 3 | 2 | 191.606 | 1.522 |
| Factors | A | B | C | A × B | A × C | B × C |
|---|---|---|---|---|---|---|
| Maximum X-axis velocity (m/s) | 38.135 | 36.643 | 14.603 | 18.178 | 8.967 | 6.934 |
| Half of effective Y-axis extension distance(mm) | 0.512 | 2.611 | 0.882 | 0.317 | 0.212 | 0.252 |
| Source of Variance | Deviation Sum of Squares | Degree of Freedom | Variance | Variance Ratio | Significant Level |
|---|---|---|---|---|---|
| A | 90.207 | 2 | 45.1035 | 44.22725 | * * |
| B | 75.918 | 2 | 37.959 | 37.22155 | * * |
| C | 10.32 | 2 | 5.16 | 5.059754 | * |
| A × B | 32.482 | 4 | 8.1205 | 7.962738 | * * |
| A × C | 5.765 | 4 | 1.44125 | ||
| B × C | 5.346 | 4 | 1.3365 | ||
| A × B × C | 5.206 | 8 | 0.65075 | ||
| Error | 16.317 | 16 | 1.019813 | ||
| Sum | 255.244 | 26 | |||
| Fa | F0.05(2, 16) = 3.63, F0.05(4, 16) = 3.01, F0.05(8, 16) = 2.59 F0.01(2, 16) = 6.23, F0.01(4, 16) = 4.77, F0.01(8, 16) = 3.89 | ||||
| Source of Variance | Deviation Sum of Squares | Degree of Freedom | Variance | Variance Ratio | Significant Level |
|---|---|---|---|---|---|
| A | 0.017 | 2 | 0.0085 | 20.4 | * * |
| B | 0.383 | 2 | 0.1915 | 459.6 | * * |
| C | 0.048 | 2 | 0.024 | 57.6 | * * |
| A × B | 0.011 | 4 | 0.00275 | 6.6 | * * |
| A × C | 0.003 | 4 | 0.00075 | ||
| B × C | 0.006 | 4 | 0.0015 | 3.6 | * |
| A × B × C | 0.002 | 8 | 0.00025 | ||
| Error | 0.005 | 12 | 0.000417 | ||
| Sum | 0.473 | 26 | |||
| Fa | F0.05(2, 12) = 3.88, F0.05(4, 12) = 3.26, F0.05(8, 12) = 2.85 F0.01(2, 12) = 6.93, F0.01(4, 12) = 5.41, F0.01(8, 12) = 4.5 | ||||
| Coal Wall | Sample Position | Firmness Coefficient of Group 1 | Firmness Coefficient of Group 2 | Firmness Coefficient of Group 3 | Average of Firmness Coefficient |
|---|---|---|---|---|---|
| 1 | A1 | 0.51 | 0.53 | 0.52 | 0.5222 |
| B1 | 0.52 | 0.51 | 0.53 | ||
| C1 | 0.52 | 0.52 | 0.54 | ||
| 2 | A2 | 0.53 | 0.52 | 0.52 | 0.5256 |
| B2 | 0.52 | 0.53 | 0.54 | ||
| C2 | 0.54 | 0.51 | 0.52 | ||
| 3 | A3 | 0.52 | 0.53 | 0.53 | 0.5244 |
| B3 | 0.51 | 0.53 | 0.53 | ||
| C3 | 0.52 | 0.51 | 0.54 | ||
| 4 | A4 | 0.52 | 0.52 | 0.53 | 0.5267 |
| B4 | 0.53 | 0.53 | 0.54 | ||
| C4 | 0.53 | 0.52 | 0.52 |
| Experimental Group | Structural Parameters | Punching Depth (m) | Punching Diameter (m) | ||
|---|---|---|---|---|---|
| A (°) | B (°) | C | |||
| Initial nozzle | 30 | 0 | 2 | 0.63 | 0.11 |
| Improved 1 | 50 | 0 | 2 | 0.71 | 0.15 |
| Improved 2 | 70 | 30 | 2.5 | 0.58 | 0.21 |
| Improved 3 | 50 | 20 | 2.5 | 0.74 | 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Cheng, M.; Cai, Y.; Guo, L.; Gao, D. Design and Optimization of High-Pressure Water Jet for Coal Breaking and Punching Nozzle Considering Structural Parameter Interaction. Machines 2022, 10, 60. https://doi.org/10.3390/machines10010060
Chen L, Cheng M, Cai Y, Guo L, Gao D. Design and Optimization of High-Pressure Water Jet for Coal Breaking and Punching Nozzle Considering Structural Parameter Interaction. Machines. 2022; 10(1):60. https://doi.org/10.3390/machines10010060
Chicago/Turabian StyleChen, Lihuan, Muzheng Cheng, Yi Cai, Liwen Guo, and Dianrong Gao. 2022. "Design and Optimization of High-Pressure Water Jet for Coal Breaking and Punching Nozzle Considering Structural Parameter Interaction" Machines 10, no. 1: 60. https://doi.org/10.3390/machines10010060
APA StyleChen, L., Cheng, M., Cai, Y., Guo, L., & Gao, D. (2022). Design and Optimization of High-Pressure Water Jet for Coal Breaking and Punching Nozzle Considering Structural Parameter Interaction. Machines, 10(1), 60. https://doi.org/10.3390/machines10010060





