Correlation between the Internal Flow Pattern and the Blade Load Distribution of the Centrifugal Impeller
Abstract
:1. Introduction
2. Implementation Process Based on PIV
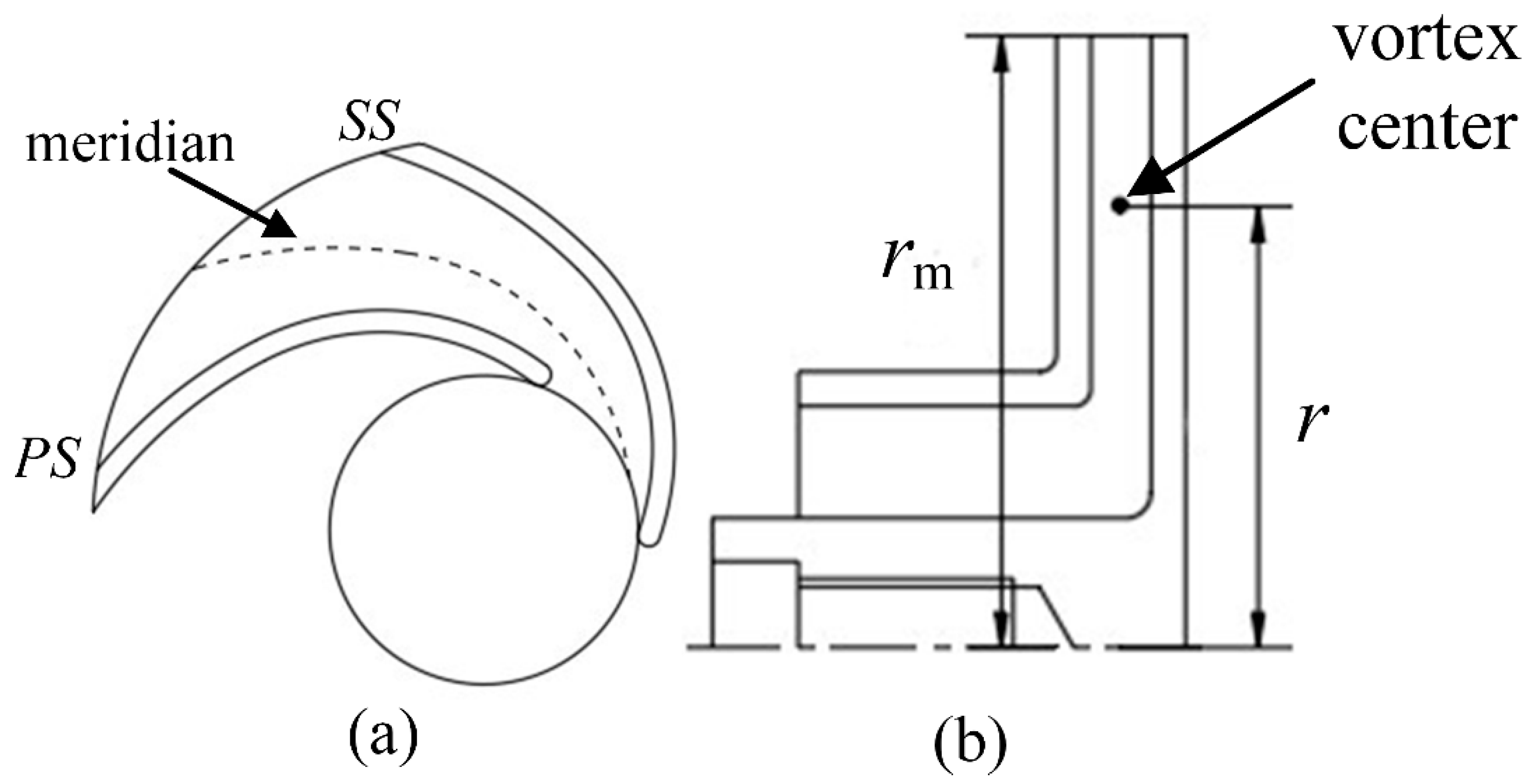
2.1. Theoretical Basis of Blade Load
2.2. Methodology
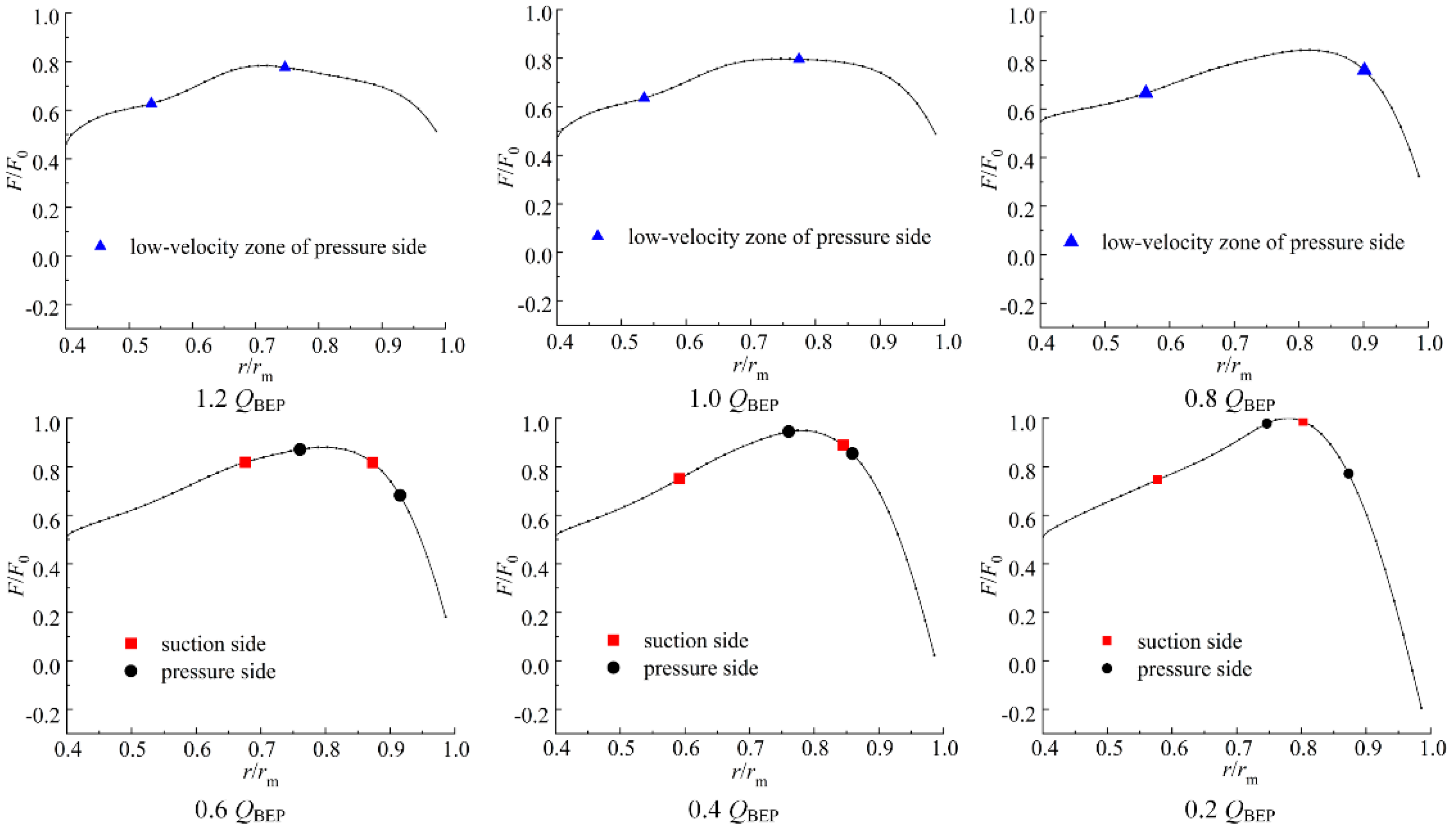
2.3. Results of Blade Load
3. Analysis of Internal Flow Patterns
3.1. Discussion on the Relative Velocity Field
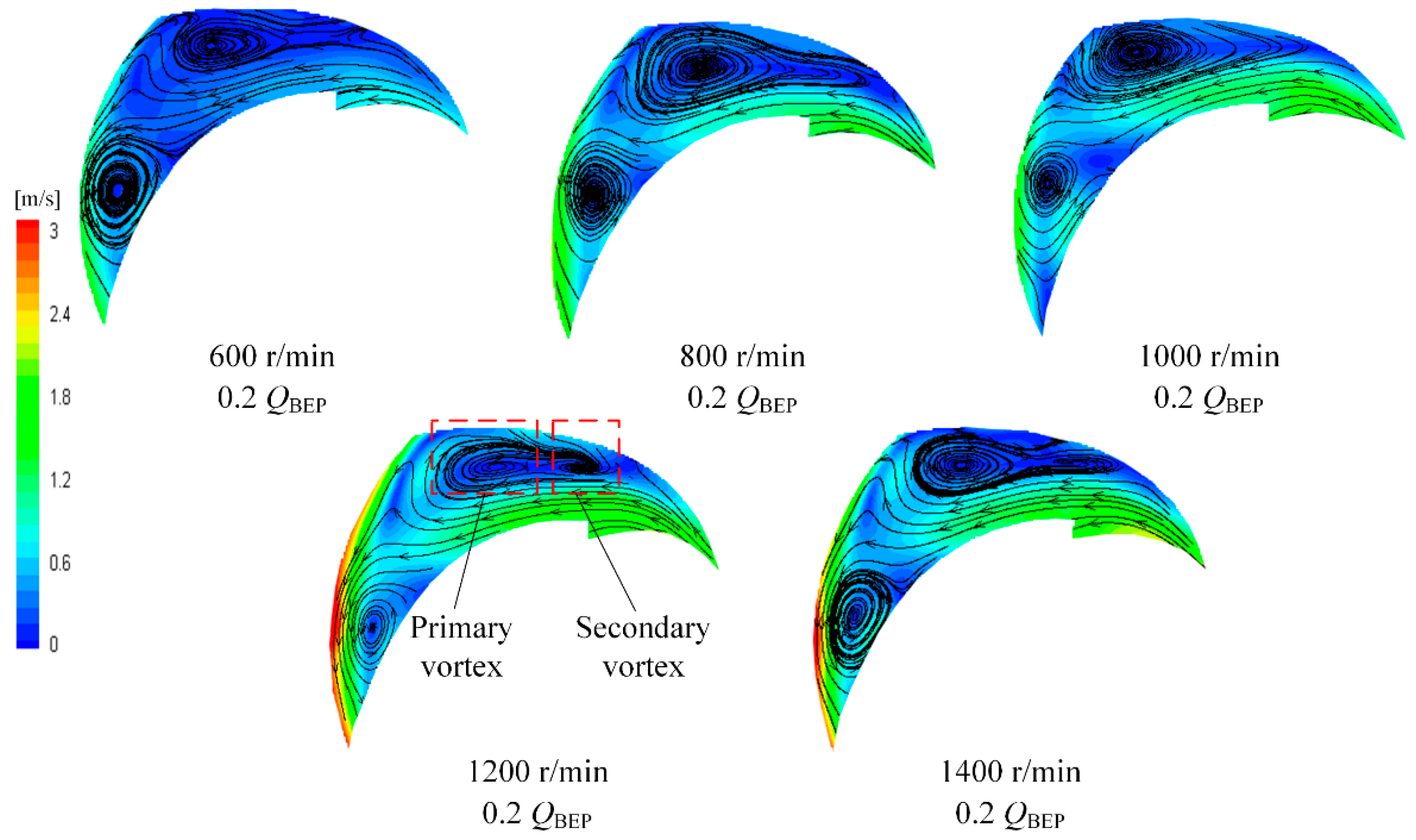
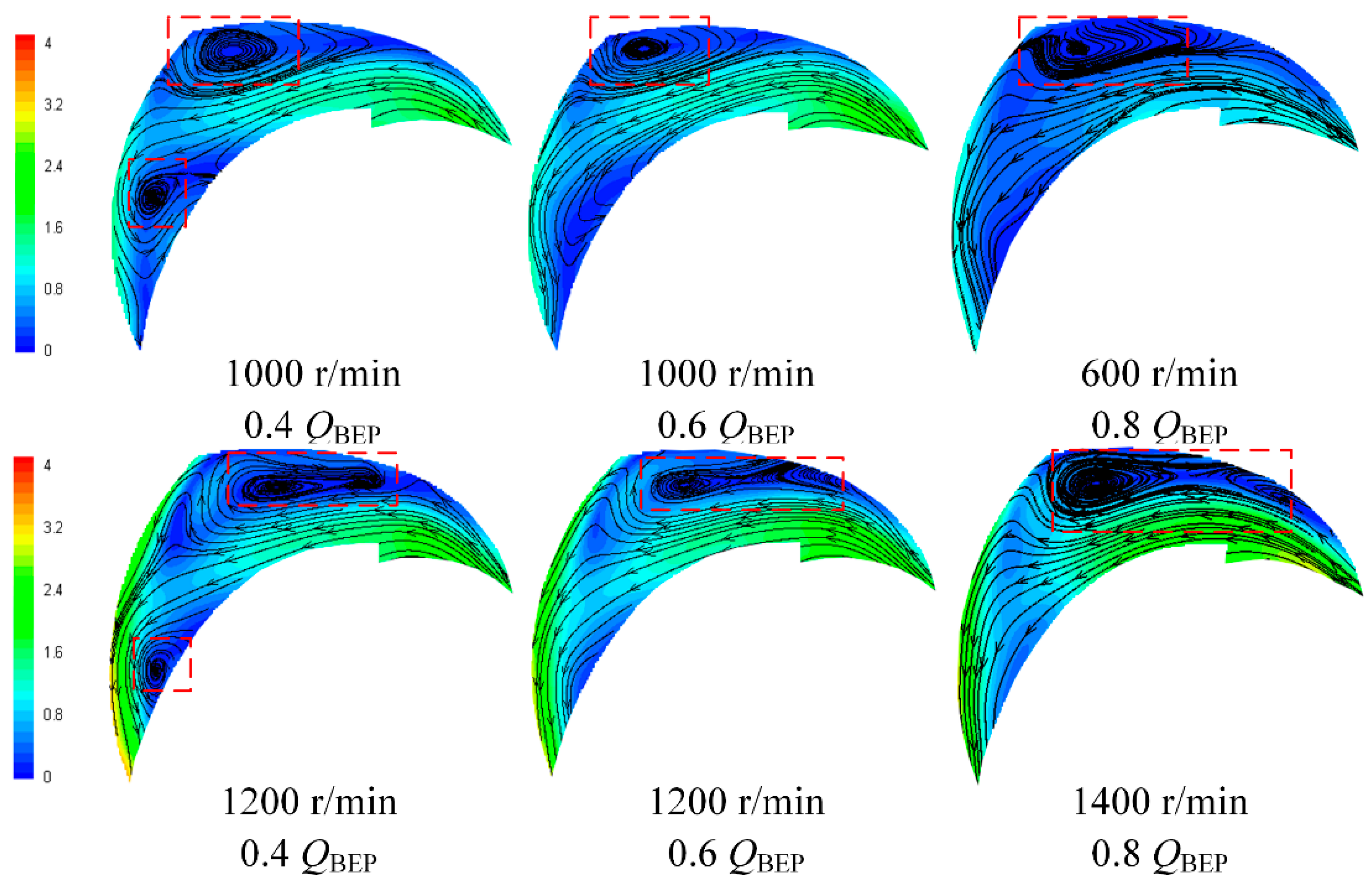
3.2. Discussion on the Vortex in the Flow Channel
4. Effect of Flow Pattern in the Flow Channel on the Blade Load Distribution
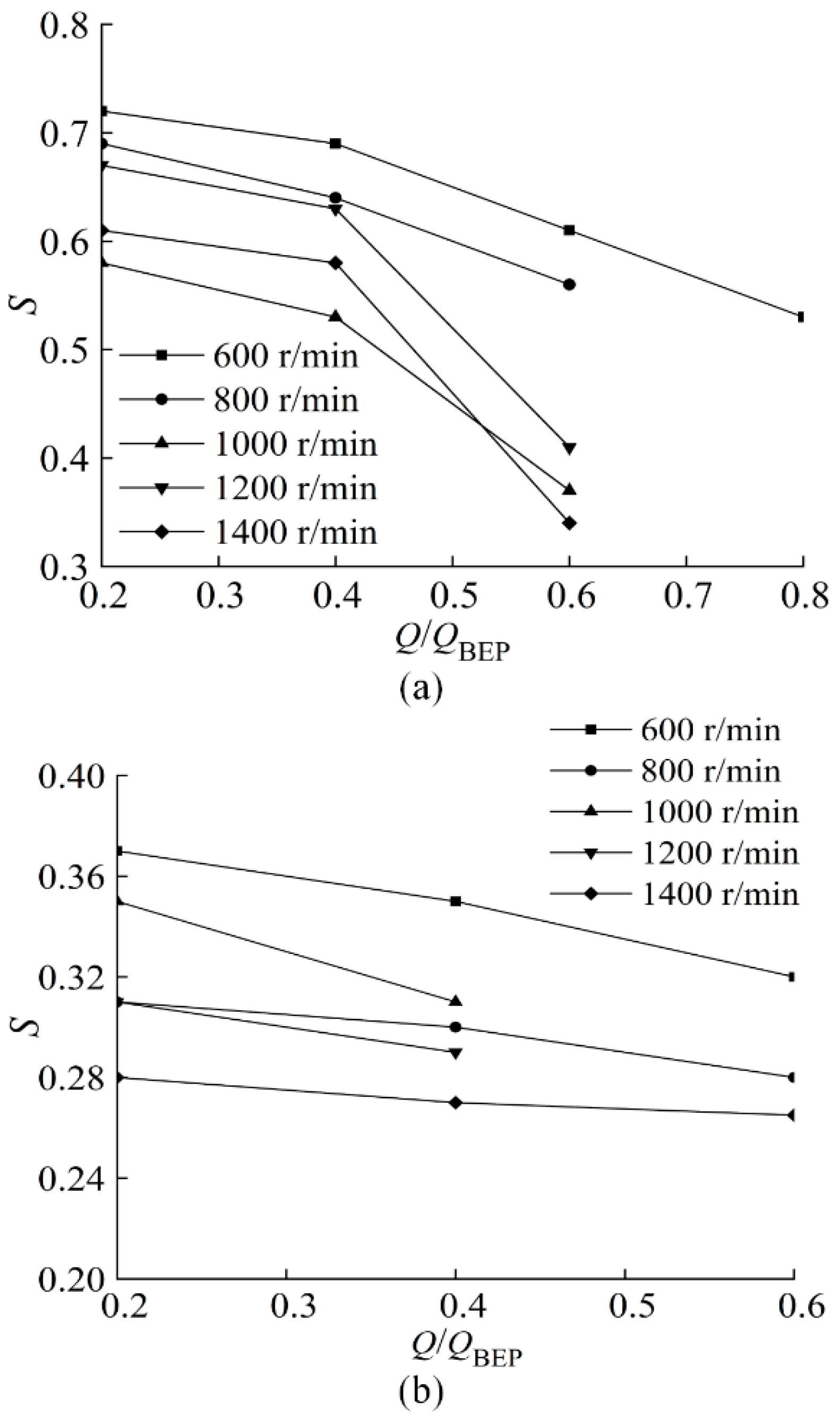
4.1. Correlation of Internal Flow Pattern and Blade Load
4.2. Reasons for the Difference in Blade Load
5. Conclusions
- (i)
- Based on the PIV method, the images taken in the test were converted into usable relative velocity field data through a series of post-processing. On this basis, the concept of the circumferential mean angular momentum was innovatively used to obtain the blade load value.
- (ii)
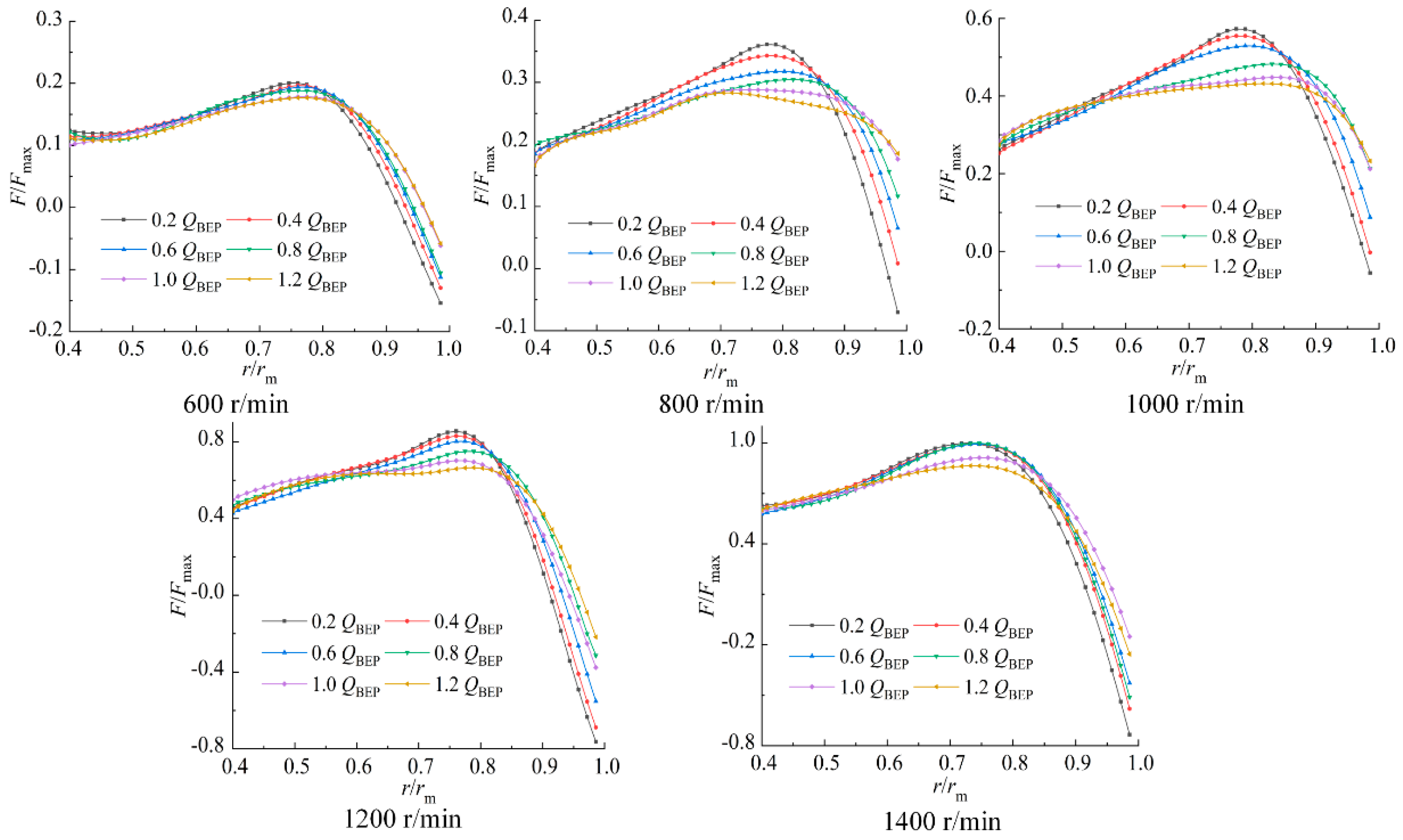
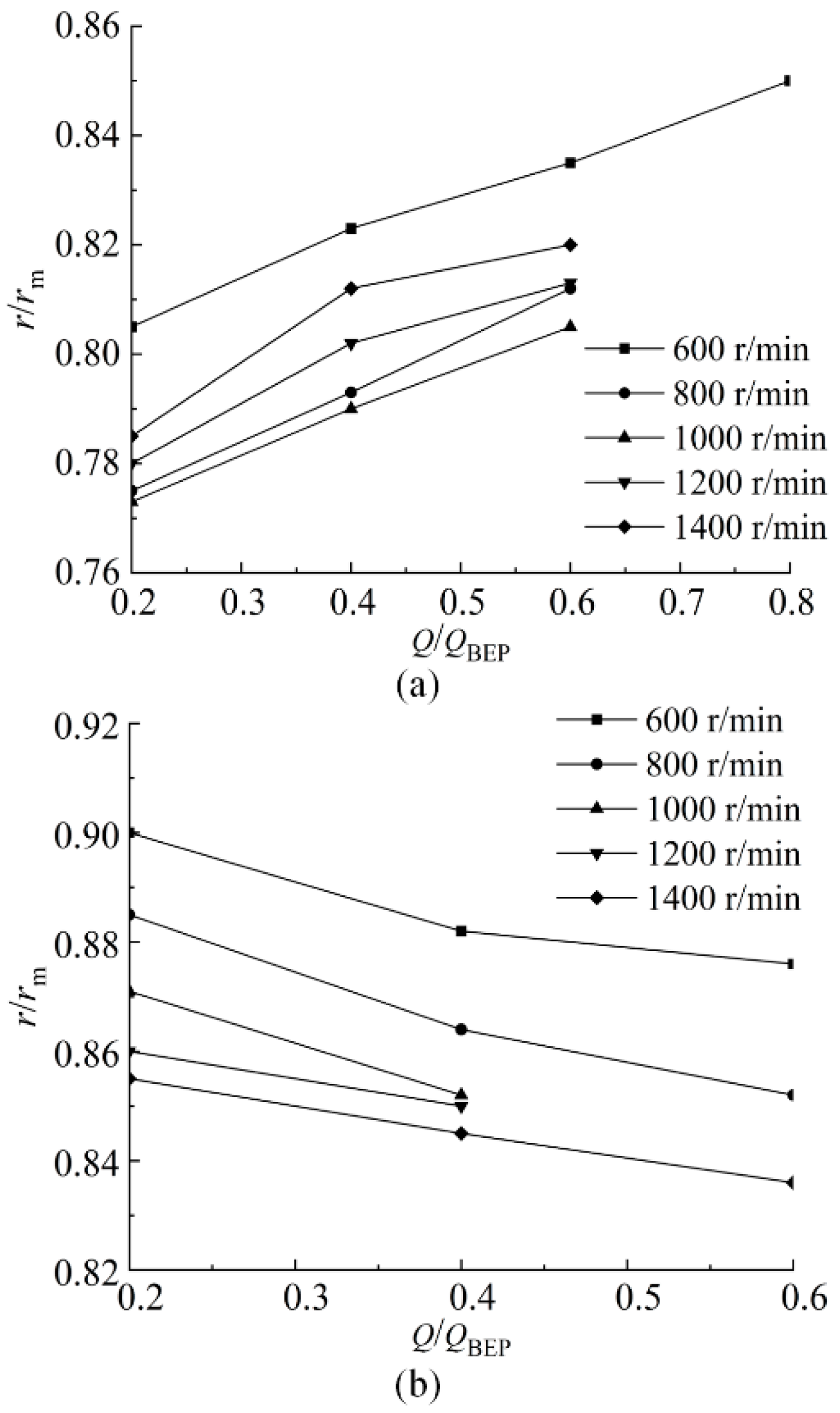
- The scale of counterclockwise vortex was smaller than that of clockwise vortex. In general, the scale of both type vortexes increased with the decrease of rotational speed. The positions of the vortex centers were distributed in the range of r/rm = 0.77–0.9, and the peak blade loads were located at the position of r/rm = 0.75–0.85.
- (iii)
- The blade load distribution along the impeller channel was interrelated with the flow pattern. The vortexes redistributed blade load by changing the absolute flow angle of the flow. Additionally, the clockwise vortex made the position of the maximum blade load closer to the outlet, while the counterclockwise vortex had the opposite effect. Additionally, the number of vortexes in the flow channel influenced the blade load distribution.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Ethical Approval
References
- Shigemitsu, T.; Ogawa, Y.Y.; Nakaishi, E. PIV Measurement of Internal Flow in Mini Centrifugal Pump. Int. J. Fluid Mach. Syst. 2019, 12, 251–260. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Zhang, Y.C.; Xiang, W.; He, Z.M.; Shi, W.D. Numerical study of coupled flow in blocking pulsed jet impinging on a rotating wall. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 508. [Google Scholar] [CrossRef]
- Zhou, J.R.; Zhao, M.M.; Wang, C.; Gao, Z.J. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock Vib. 2021, 5, 6616456. [Google Scholar] [CrossRef]
- Wang, H.L.; Hu, Q.X.; Yang, Y.; Wang, C. Performance differences of electrical submersible pump under variable speed schemes. Int. J. Simul. Model. 2021, 20, 76–86. [Google Scholar] [CrossRef]
- Shi, L.J.; Zhu, J.; Tang, F.P.; Wang, C. Multi-Disciplinary optimization design of axial-flow pump impellers based on the approximation model. Energies 2020, 13, 779. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Li, G.P.; Wang, R.; Tang, S.N.; Su, H.; Cao, K. Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization. Appl. Acoust. 2021, 183, 108336. [Google Scholar] [CrossRef]
- Wang, Y.P.; Yang, H.; Chen, B.; Gao, P.L.; Zhu, Z.C. Analysis of vortexes formed in flow channel of a five-bladed centrifugal water pump by means of PIV method. AIP Adv. 2019, 9, 075011. [Google Scholar] [CrossRef] [Green Version]
- Atkins, M.D.; Kim, T. Isotropic-planar illumination for PIV experiments. Exp. Fluids 2015, 56, 63. [Google Scholar] [CrossRef]
- Zhang, N.; Gao, B.; Li, Z.; Daisy, N. Unsteady flow structure and its evolution in a low specific speed centrifugal pump measured by PIV. Exp. Therm. Fluid Sci. 2018, 97, 133–144. [Google Scholar] [CrossRef]
- Zhang, D.; Cheng, L.; Li, Y.Y.; Jiao, W.X. The hydraulic performance of twin-screw pump. J. Hydrodyn. 2020, 32, 605–615. [Google Scholar] [CrossRef]
- Bennacer, R.; Sefiane, K. Proper orthogonal decomposition (POD) analysis of flow structure in volatile binary droplets. Int. Commun. Heat Mass Transf. 2016, 71, 172–175. [Google Scholar] [CrossRef]
- Guo, X.M.; Zhu, Z.C.; Shi, G.P.; Huang, Y. Effects of rotational speeds on the performance of a centrifugal pump with a variable-pitch inducer. J. Hydrodyn. 2017, 29, 854–862. [Google Scholar] [CrossRef]
- Si, Q.R.; Dupont, P.; Dazin, A.; Roussette, O.; Yuan, S.Q.; Bayeul, A. An Experimental Study of the Flow Field Inside the Diffuser Channel of a Laboratory Centrifugal Pump. J. Fluids Eng. 2015, 137, 061105. [Google Scholar] [CrossRef]
- Wu, Y.L.; Liu, S.H.; Yuan, H.J.; Shao, J. PIV measurement on internal instantaneous flows of a centrifugal pump. Sci. China Technol. Sci. 2011, 54, 270–276. [Google Scholar] [CrossRef]
- Li, X.J.; Chen, H.; Chen, B.; Luo, X.W.; Yang, B.F.; Zhu, Z.C. Investigation of flow pattern and hydraulic performance of a centrifugal pump impeller through the PIV method. Renew. Energ. 2020, 162, 561–574. [Google Scholar] [CrossRef]
- Westra, R.W.; Broersma, L.; Kruyt, N.P.; Van, K. PIV Measurements and CFD Computations of Secondary Flow in a Centrifugal Pump Impeller. J. Fluids Eng. 2010, 132, 061104. [Google Scholar] [CrossRef]
- Yu, S.C.M.; Chua, L.P.; Leo, H.L. The angle-resolved velocity measurements in the impeller passages of a model bio-centrifugal pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 547–568. [Google Scholar] [CrossRef]
- Liu, H.L.; Wang, K.; Kim, H.B.; Tan, M.G. Experimental investigation of the unsteady flow in a double-blade centrifugal pump impeller. Sci. China Technol. Sci. 2013, 56, 812–817. [Google Scholar] [CrossRef]
- Gaetani, P.; Boccazzi, A.; Sala, R. Low field in the vaned diffuser of a centrifugal pump at different vane setting angles. J. Fluids Eng. 2012, 134, 031101. [Google Scholar] [CrossRef]
- Wang, L.K.; Lu, J.L.; Liao, W.L.; Wang, W. Numerical analysis of the formation mechanism and suppression method of the reverse flow in a semi-open centrifugal pump. J. Mech. Sci. Technol. 2020, 34, 3667–3678. [Google Scholar] [CrossRef]
- Poujol, N.; Trébinjac, I.; Duquesne, P. Effects of inlet guide vanes on the performance and stability of an aeronautical centrifugal compressor. J. Turbomach. 2020, 143, 101010. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S.; Kanfoudi, H.; Akrout, M. The effects of the rotor-stator interaction on unsteady pressure pulsation and radial force in a centrifugal pump. J. Hydrodyn. 2018, 30, 672–681. [Google Scholar] [CrossRef]
- Zhang, R.H.; Guo, R.; Yang, J.H.; Luo, J.Q. Inverse Method of Centrifugal Pump Impeller Based on Proper Orthogonal Decomposition (POD) Method. Chin. J. Mech. Eng. 2017, 30, 1025–1031. [Google Scholar] [CrossRef]
- Li, X.J.; Gao, P.L.; Zhu, Z.C.; Li, Y. Effect of the blade loading distribution on hydrodynamic performance of a centrifugal pump with cylindrical blades. J. Mech. Sci. Technol. 2018, 32, 1161–1170. [Google Scholar] [CrossRef]
- Li, J.W.; Zhang, Y.N.; Yu, J.X. Experimental investigations of a prototype reversible pump turbine in generating mode with water head variations. Sci. China Technol. Sci. 2018, 61, 604–611. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Chen, T.; Li, J.W.; Yu, J.X. Experimental Study of Load Variations on Pressure Fluctuations in a Prototype Reversible Pump Turbine in Generating Mode. J. Fluids Eng. 2017, 139, 074501. [Google Scholar] [CrossRef]
- Sun, W.Y.; Huang, G.F. Integrated lifting line/surface panel method for optimal propeller design with consideration of hub effect. J. Hydrodyn. 2019, 31, 1218–1230. [Google Scholar] [CrossRef]
- Durante, D.; Dubbioso, G.; Testa, C. Simplified hydrodynamic models for the analysis of marine propellers in a wake-field. J. Hydrodyn. 2013, 25, 954–965. [Google Scholar] [CrossRef]
- Li, X.J.; Chen, B.; Luo, X.W.; Zhu, Z.C. Effects of flow pattern on hydraulic performance and energy conversion characterisation in a centrifugal pump. Renew. Energy 2020, 151, 475–487. [Google Scholar] [CrossRef]
- Fujiwara, K.; Sriram, R.; Kontis, K. Experimental investigations on the sharp leading-edge separation over a flat plate at zero incidence using particle image velocimetry. Exp. Fluids 2020, 61, 205. [Google Scholar] [CrossRef]




| Parameter Name | Value |
|---|---|
| Inlet diameter D1 (mm) | 56 |
| Outlet diameter D2 (mm) | 142 |
| Inlet angle of blade β1 (°) | 28 |
| Outlet angle of blade β2 (°) | 34 |
| Blade width (mm) | 7 |
| Blade thickness (mm) | 4 |
| Wrap angle of blade φ (°) | 96 |
| Specific speed ns | 23.8 |
| Blade number Z | 5 |
| Rotational Speeds (r/min) | Optimum Flow Points (m3/h) | Corresponding Heads (m) |
|---|---|---|
| 600 r/min | 1.0 | 1.0 |
| 800 r/min | 1.7 | 1.5 |
| 1000 r/min | 1.8 | 2.67 |
| 1200 r/min | 2.3 | 3.7 |
| 1400 r/min | 2.5 | 5.05 |
| Rotational Speed | Flow | Position (Suction Side) | Position (Pressure Side) | Position (Maximum Load) |
|---|---|---|---|---|
| 600 r/min | 0.2 | 0.805 | 0.9 | 0.76 |
| 0.4 | 0.823 | 0.882 | 0.775 | |
| 0.6 | 0.835 | 0.876 | 0.785 | |
| 800 r/min | 0.2 | 0.775 | 0.885 | 0.78 |
| 0.4 | 0.793 | 0.864 | 0.785 | |
| 0.6 | 0.812 | 0.852 | 0.79 | |
| 1000 r/min | 0.2 | 0.773 | 0.871 | 0.785 |
| 0.4 | 0.79 | 0.852 | 0.8 | |
| 0.6 | 0.805 | 0.81 | ||
| 1200 r/min | 0.2 | 0.782 | 0.86 | 0.785 |
| 0.4 | 0.8 | 0.85 | 0.79 | |
| 0.6 | 0.813 | 0.805 | ||
| 1400 r/min | 0.2 | 0.785 | 0.855 | 0.74 |
| 0.4 | 0.812 | 0.845 | 0.745 | |
| 0.6 | 0.82 | 0.836 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, X.; Zhu, Z.; Li, X. Correlation between the Internal Flow Pattern and the Blade Load Distribution of the Centrifugal Impeller. Machines 2022, 10, 40. https://doi.org/10.3390/machines10010040
Chen B, Chen X, Zhu Z, Li X. Correlation between the Internal Flow Pattern and the Blade Load Distribution of the Centrifugal Impeller. Machines. 2022; 10(1):40. https://doi.org/10.3390/machines10010040
Chicago/Turabian StyleChen, Bo, Xiaowu Chen, Zuchao Zhu, and Xiaojun Li. 2022. "Correlation between the Internal Flow Pattern and the Blade Load Distribution of the Centrifugal Impeller" Machines 10, no. 1: 40. https://doi.org/10.3390/machines10010040
APA StyleChen, B., Chen, X., Zhu, Z., & Li, X. (2022). Correlation between the Internal Flow Pattern and the Blade Load Distribution of the Centrifugal Impeller. Machines, 10(1), 40. https://doi.org/10.3390/machines10010040






