1. Introduction
The labyrinth seal is a significant constitutional part of rotating machinery which primarily reduces internal flow leakage and isolates high- and low-pressure regions. When fluid flows through the seal cavities, an inhomogeneous pressure distribution is formed at the outlet, and thereby a resultant force acting on the rotor, i.e., the sealing force, is generated. If the seal fails to work properly, leakage will occur and can result in accidents, threatening the safety of the equipment [
1,
2].
Many research works have been carried out to improve the rotordynamic stability of the seal-rotor system. The effects of the layout of anti-stagnation nozzles on rotordynamic characteristics are investigated for a novel anti-stagnation labyrinth seal, using a computational fluid dynamics (CFD) method [
3]. The influences of inlet preswirls on the static and dynamic stability of the labyrinth seal with different blade numbers are studied based on experimental data and numerical simulations [
4]. Swirl brakes have also received attention in the research field. Related works are concerned with the relation between rotordynamic performance and the various lengths, clearances, numbers, rotation angles, and axial arrangement of swirl brakes [
5,
6]. Operation conditions are also considered in the existing literature, including the maximum pressure loads of labyrinth seal’s teeth [
7], the rotor eccentricity [
8], the rotating speed [
9], the inlet pressure [
3], and tooth bending damage [
10].
However, due to the complexity of seal structure, the gas flow in a seal usually turns out to be turbulent but not laminar, causing difficulties when calculating sealing forces. Most of the previous studies only satisfy the ideal state assumption and ignore the uncertain factors arising from the gas flow. Furthermore, to simplify the computation process, these studies hypothesize that the orbit of the rotor center is circular or elliptic in shape. However, as the shaft spins eccentrically, the gas flow forces usually turn out to be nonuniform in the circumferential direction, and some spiral flow is formed in multiple directions in the cavities due to the friction between gas flows and the inlet preswirl [
11]. Besides, the gas flow will constantly collide with the tooth and wall, and leakage flow will inevitably disturb the main flow, causing changes in the state of the main flow [
12]. The strong impact, shear, vortex, and transient evolution all occur within the gas flow, causing random effects of sealing forces on the rotor and bringing great difficulty in estimating dynamic coefficients [
12,
13,
14]. Besides, parameters coupled with the uncertain structural model from a subjective geometric transformation (e.g., the flow coefficient and the dynamic load factor) cannot be accurately estimated, enlarging the errors between the theoretical results and the experimental ones.
Random uncertainties will interfere with the stability of the gas flow and bring random variations to the orbit of the rotor center. Thus, the orbit will become irregular, with large errors compared with the traditional one [
15,
16,
17]. To this end, researchers use some alternative methods in solving the dynamic equation to obtain a more accurate trajectory expression in the study of the characteristics of a seal-rotor system [
15,
18,
19,
20]. Nevertheless, these methods are applicable only when the model parameters are provided or can be estimated with comprehensive knowledge of the system and flow state. Moreover, most methods only consider the data uncertainties but cannot solve the natures of the model uncertainties. To overcome the shortcomings of the above methods, the nonparametric modeling technique was introduced, in which both types of uncertainties can be included in the study of structural dynamics [
21]. After that, the nonparametric modeling technique was extended to solve the rotordynamic problems of the uncertain symmetric rotor, and the effects of random uncertain factors on the dynamic performance of the rotor were investigated in detail [
22,
23].
In the following content, the aforementioned uncertain gas flow is taken as the random excitations introduced into the momentum equation, and the orbit motion is represented by combining an elliptic trajectory with the bounded noise perturbation to estimate the dynamic characteristic coefficients, from which the disturbance clearance function, cavity coefficients, and sealing forces are rederived in the case of random uncertain orbit. Finally, several numerical examples are employed to illustrate the present procedure.
2. Mathematical Models
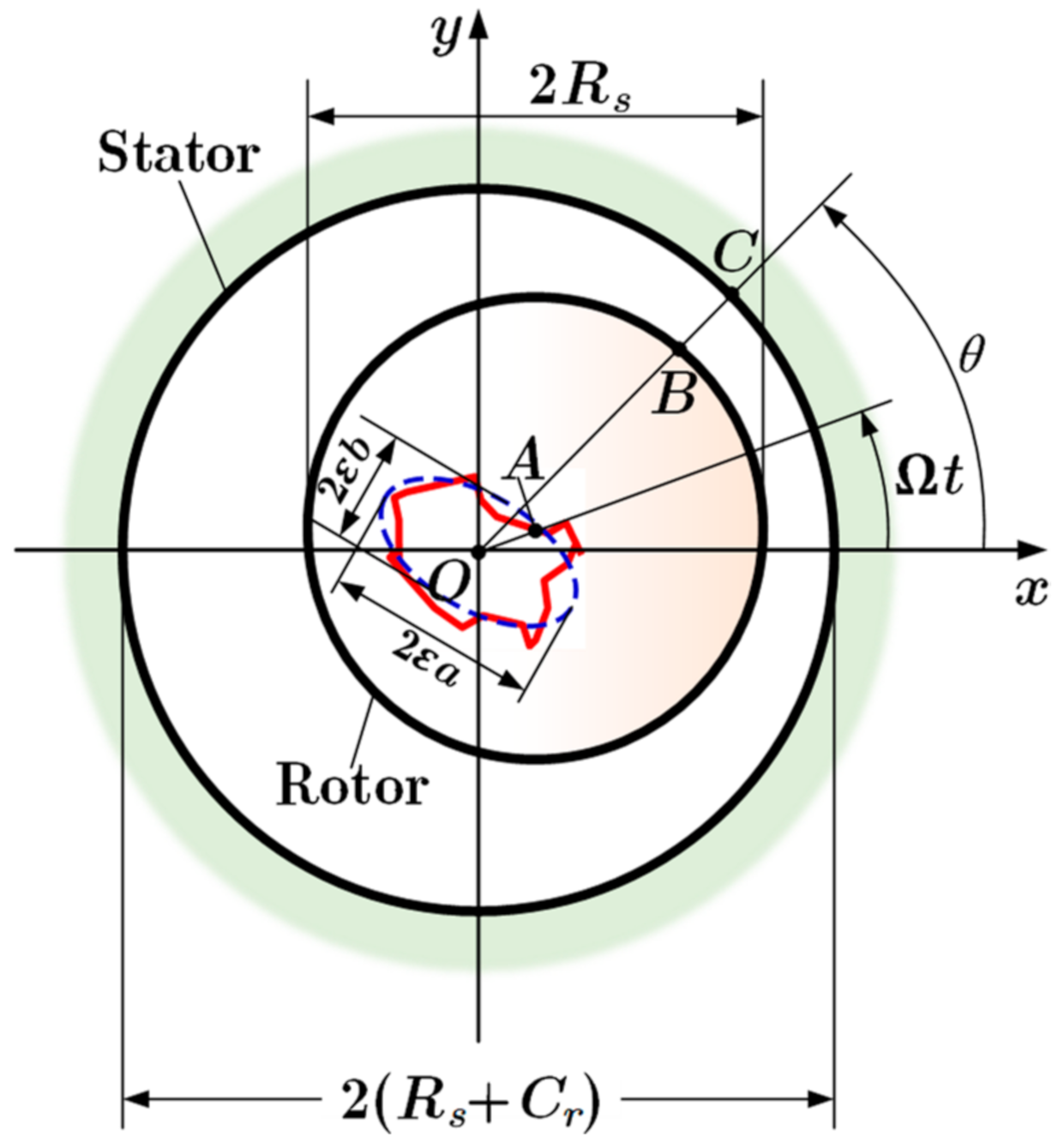
Two main types of labyrinth seals are applied in engineering practice, with one being the see-through style (including the seal teeth on the stator (TOS) and the seal teeth on the rotor (TOR)) and the other one being the interlocking style, which has its teeth both on the rotor and the stator (ILS). The ILS is considered in the present study, in which its geometry is illustrated in
Figure 1. Detailed explanations regarding its dimensions can be found in Ref. [
13].
In a typical cavity, the fluid dynamics are governed by the continuity equation and the circumferential momentum equation. When the concentric rotor rotates with a constant speed with no eccentricity, gas flow in the labyrinth seal is steady, axial-symmetric, and time-independent. Under this steady state, the continuity equation implies that the mass flow rate from one cavity to the next equals the constant
, i.e.,
where
represents the mass flow rate through the clearance of the
ith tooth. According to the generalized Neumann’s equation [
1,
13], the value of
depends on the geometry, temperature, and pressure difference between two adjacent cavities, which can be written as
In Equation (2), the orifice contraction coefficient
is determined by Chaplygin’s formula [
2,
13]:
where
represents the specific heat ratio.
The kinetic energy carry-over coefficient
equals to unity for the first cavity, while
gives its estimations for other teeth [
2,
13].
Geometric parameters in Equation (2) include the rotor radius
Rs and the radial clearance
Cr. The gas in each seal cavity is assumed to obey the ideal gas law. Thus, its pressure distribution can be written as
where
,
Rg, and
Ti are the gas density, gas constant, and gas temperature, respectively. Usually, the isenthalpic flow results in an isothermal process for gas flows, which means a constant gas temperature is preserved among all the cavities (
).
Once the parameters in Equations (1)–(5) are provided, e.g., the gas temperature T, inlet pressure , and outlet pressure , the flow rate and pressure distribution in each cavity can be calculated by coupling these equations iteratively.
The randomness of the flow may generate randomly uncertain excitations, which will affect the stability and reliability of the seal-rotor system in practice. Thus, the randomly uncertain factors should be considered in establishing the circumference momentum equation [
24], which is rewritten as
where
is the volume of each cavity and
S is the surface of the control volume. Circumferential force
within the control volume of each cavity includes the pressure component and the shear force component, with both acting along the circumferential direction, while
represents the random excitation due to the uncertainty of the gas flow.
For the system shown in
Figure 1, a specific form of Equation (6) is given by
where
represents the cross-section area of a cavity and
H is the non-asymmetric clearance. Both
A and
H vary with
. The dimensionless shear stress lengths in Equation (7) are defined as
For simplicity, we assume that the randomly uncertain perturbation is weak compared with the actions of the main gas flow, i.e.,
where
f0 is a constant and
. The bounded noise excitation is expressed as [
25]:
where
is the central frequency,
is the standard Wiener process with strength
, and
is a random phase uniformly distributed in the interval
, which renders the process correlation-stationary at all times. The mean of the bounded noise is zero and
gives the correlation function. Moreover, the two-sided spectral density of this random process can be computed as [
25]
and the shape of the power spectrum rests with
and
. In general, it has two peaks symmetrically located in the positive and negative frequency domains. When
,
becomes a narrow-band random process, which provides a good simulation for the Dryden spectrum of wind turbulence and the von Karman spectrum of vibration transmitted through the ground by changing the values of
and
[
24].
Except for the pressures and velocities, many other parameters in the continuity equation and the circumferential momentum equation need to be determined. According to work by Eser [
24], Equations (1) and (6) can be transformed by employing the perturbation method and neglecting the terms of order
and their higher-order counterparts as
and
The parameters involved in Equations (13) and (14) can refer to Ref. [
24], except that the form of
has now been changed to
where
has the same meaning as that in Ref. [
24].
A new term in Equation (15), resulting from the random uncertainties, will affect the estimations of the cavity parameters. To calculate the sealing force, most of the intermediate parameters embedded in these equations should be determined in advance, which can only be obtained with the orbit of the rotor center.
3. Estimations of the Dynamic Coefficients
In the process of solving the first-order continuity equation and circumferential momentum equation, the orbit motion should be provided, which is primarily assumed to be a standard elliptic trajectory in the existing literature. However, random excitation from the uncertainty of gas flow causes the rotor center not to rotate along the elliptic trajectory. Therefore, taking the randomly uncertain factors into account, the horizontal and vertical position function of the rotor center
A to cavity center
O (see
Figure 2) can be written as
where
Randomly uncertain perturbations in
x- and
y- directions can again be expressed by the bounded noises
and
. Assuming that the perturbations come from the same resources and have the same center frequency
but with different strengths (
and
) and random phases (
and
), their formation can be written as
According to Shinozuka’s work [
26], each physical realization of the bounded noises can be generated by a series of cosine functions with random frequencies, i.e.,
where
represents the amplitude,
is the non-negative random frequency independently distributed in the range
,
is the random phase uniformly distributed in the interval
,
N0 is a positive integer with large enough value, and
is the frequency increment. As each physical realization of the bounded noises
is approximated by the sum of
N0 harmonic functions, it can be considered a deterministic one. Physical realization from Equation (18) is almost ergodic for a large enough value of
N0 [
26].
Similarly, the physical realizations of
and
can be generated by
where
and
are the amplitudes in the
x- and
y-directions,
is the non-negative independent random frequency,
and
are the random phases, and
N1 is a positive integer with large enough value.
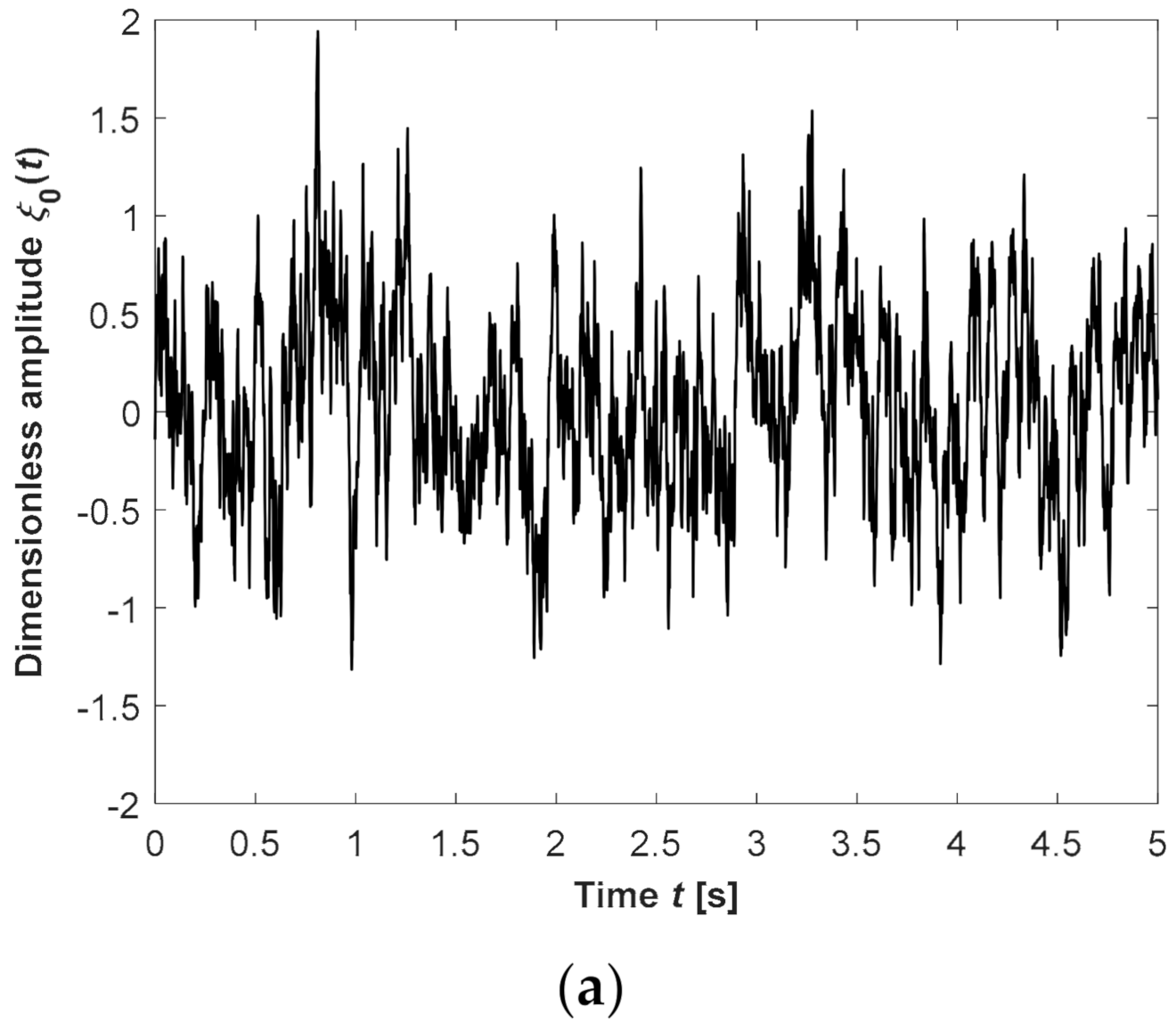
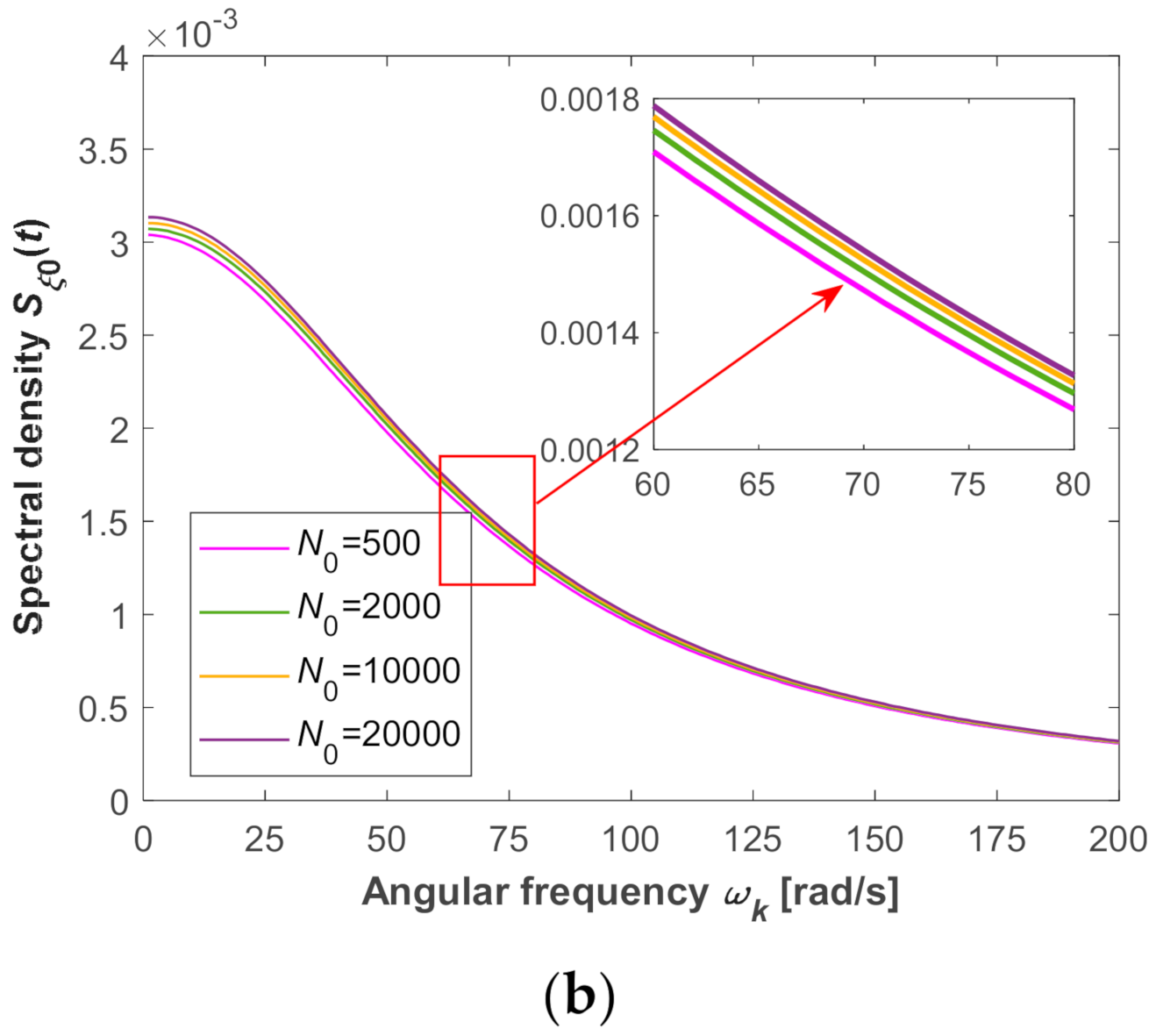
A sample function generated by Equation (18) is displayed in
Figure 3a, where
,
, and
. When
N0 approaches a large value, as shown in
Figure 3b, its spectral density is almost consistent with the theoretical one, indicating that the sample function is a good approximation of random bounded noise and can ensure the ergodicity of each physical realization.
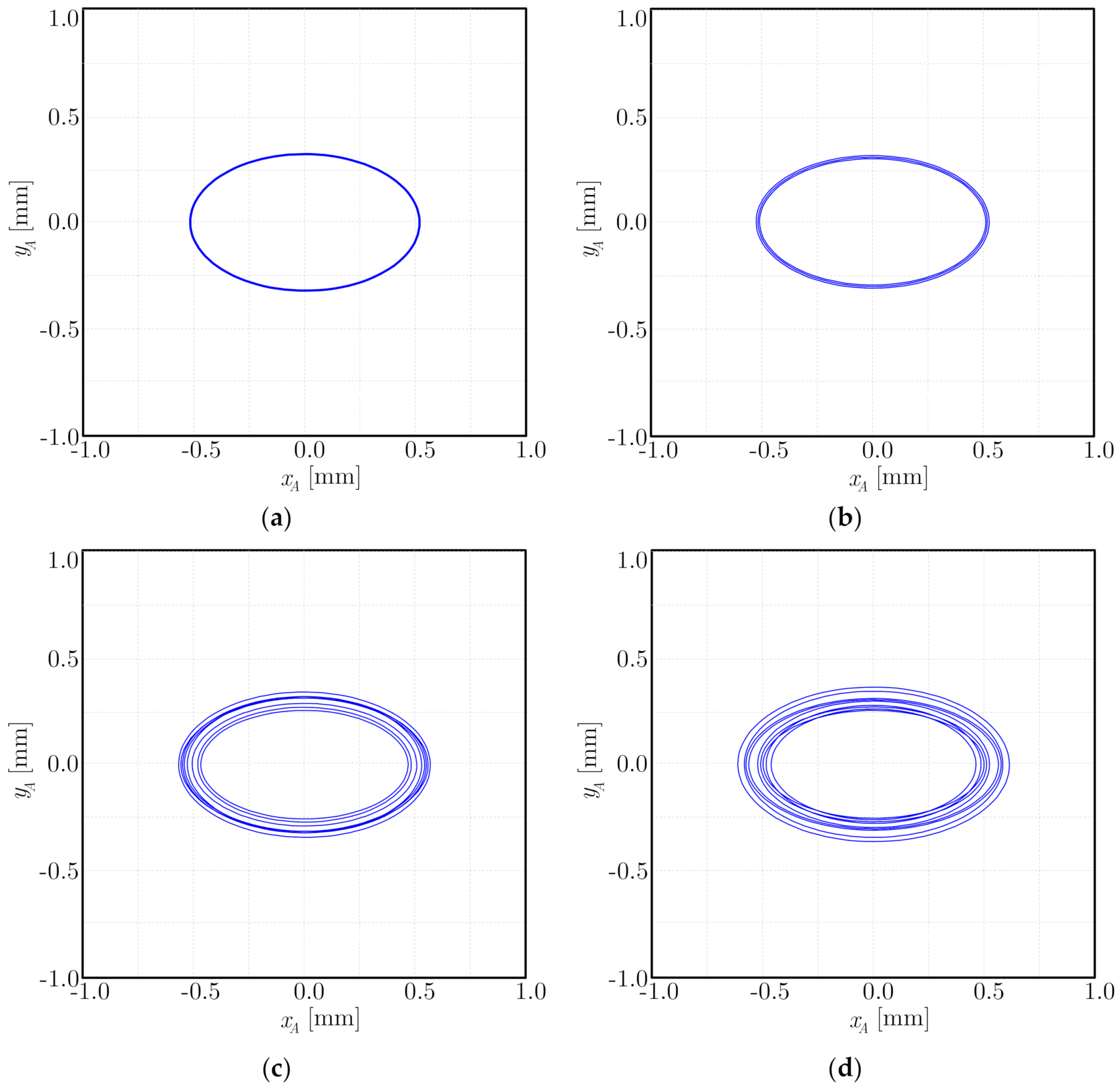
In
Figure 2, the dashed ellipse is the idealized trajectory, while the solid red orbit represents its realistic counterpart with an uncertain bounded noise perturbation. The disturbance clearance function is defined by the distance between point
B on the rotor and point
C on the stator, written as
As each sample of the bounded noise is simulated by a series of cosine functions, the perturbation analysis can be appreciably used to express the length of
OB as
When the perturbation analysis is performed, the eccentricity of the disturbed rotor is characterized by the perturbation parameter
, where
e is the deviation distance of the rotor center from the cavity center. The flow variables are then expanded as
Consequently, the coordinates of point
B are derived as
Since
A and
B are located at the center and edge of the rotor, respectively, the distance between them equals to the radius
Rs, i.e.,
Substituting Equations (16) and (22) into Equation (23), we can obtain that
where
Neglecting the terms of
and the higher-order counterparts,
can be derived as
According to Equation (19), its exponential form is
The solutions of the first-order continuity equation and momentum equation can be given by substituting Equation (26) into Equations (13) and (14) as
where the parameters
,
,
, and
with the superscript ‘+’ represent the coefficients of the terms
and
, while the parameters
,
,
, and
with the superscript ‘
’ represent the coefficients of the terms
and
.
It can be found from the expressions of , , and that the intermediate parameters are comprised of two parts under the uncertain perturbations. The former part corresponds to the ideal elliptic orbit, and the second part corresponds to the fluctuation caused by the weak bounded noise. During a certain iteration process, the fluctuations of the intermediate parameters are different from each other among the various samples.
Substituting Equations (26)–(28) into Equations (13) and (14) yields
and
where the parameters with a subscript ‘
g’ represent the fluctuation components due to the bounded noise.
In previous studies, only Equations (29) and (30) were investigated, and the additional term
in Equation (30) was not included. Equations (31) and (32) are introduced here due to the random uncertainty in the orbit motion. Obviously, compared with the traditional ellipse case, more parameters and additional equations are involved during the solution process. For the convenience of analysis, we define the vectors as follows:
and Equations (29)–(32) can be transformed into their matrix forms as
where
Equations (33)–(36) involve twelve unknown parameters, including
and
for the
ith cavity and their counterparts for the
and
cavity. Besides, an extra series of randomly uncertain parameters
is also included. Considering a labyrinth seal with
cavities, a system of four linear equations can be written for each cavity as
resulting in an
banded system with linear equations to determine the unknowns. The above equations can be solved by applying the Gaussian elimination method.
Since asymmetric forces exist during operation, rotor performances characterized by the direct and cross-coupled stiffness and damping coefficients should be changed accordingly. The equation of motion of the seal-rotor system can then be written as [
24]:
where
Fx and
Fy are the total net forces generated by the gas leakage in
x- and
y-directions, respectively. The influence coefficients in the damping and stiffness matrix satisfy
,
,
, and
. It should be noted that the coefficients in Equation (45) originate only from one sample of the randomly uncertain trials, and 32 or more samples are required to ensure ergodicity.
The total net forces can be obtained by integrating the disturbance pressure and disturbance shear stress along the rotor surface as follows:
Substituting the pressure component, the shear force component, and the intermediate parameters into Equation (46), we obtain that,
where the randomly uncertain factors caused by the gas excitation is also included. Similarly, substituting the randomly uncertain orbit expression Equation (19) into Equation (45), the total net forces can be written as.
Comparing Equation (48) with Equation (47) by defining
and
the dynamic coefficients are derived as
As previously mentioned, the external random excitation will disturb the gas flow in a labyrinth seal, and in return, the variation of the gas flow brings about an unstable sealing force acting on the rotor to cause further unpredictable variations of the rotor position. The parameters of each cavity, such as , will change with the random excitation, which can directly affect the values of and . Therefore, all the above factors are closely linked with each other during the calculation process, and the dynamic coefficients will deviate from the ideal ones, which can be seen from Equation (53).
Although each sample of a random process can be recognized as a deterministic realization once it is generated by some approximation method, even faint noisy factors may bring about obvious change and affect the stability of the rotor system. To show the impact of random uncertainty on the dynamic coefficients, several numerical examples are illustrated in the following section for a more detailed discussion of the results.
5. Conclusions
In field applications, random uncertainties (e.g., turbulent gas flow, nonuniform gas flow forces, multi-direction spiral flow, and leakage) inevitably exist when gas flows through the labyrinth seal, causing random excitations to be generated and irregular deviations of the orbit motion from an elliptic trajectory. From this point of view, the rotordynamic coefficients of a seal-rotor system are investigated in our work by adopting the random uncertainty method and are rederived sequentially by adding the corresponding stochastic terms into the solving model. The orbit of the rotor center is assumed to be made up of two parts, i.e., a regular ellipse and a bounded noise perturbation, from which the disturbance clearance function, the corresponding coefficients of each cavity, and the sealing force acting on the rotor are rederived. Through the random uncertainty modeling technique, not only can the experimental deviations of dynamic coefficients be proved by the statistical analysis results of their theoretical values, but rules can also be made to guide the field design works rather than relying on some theoretical results from the deterministic models.
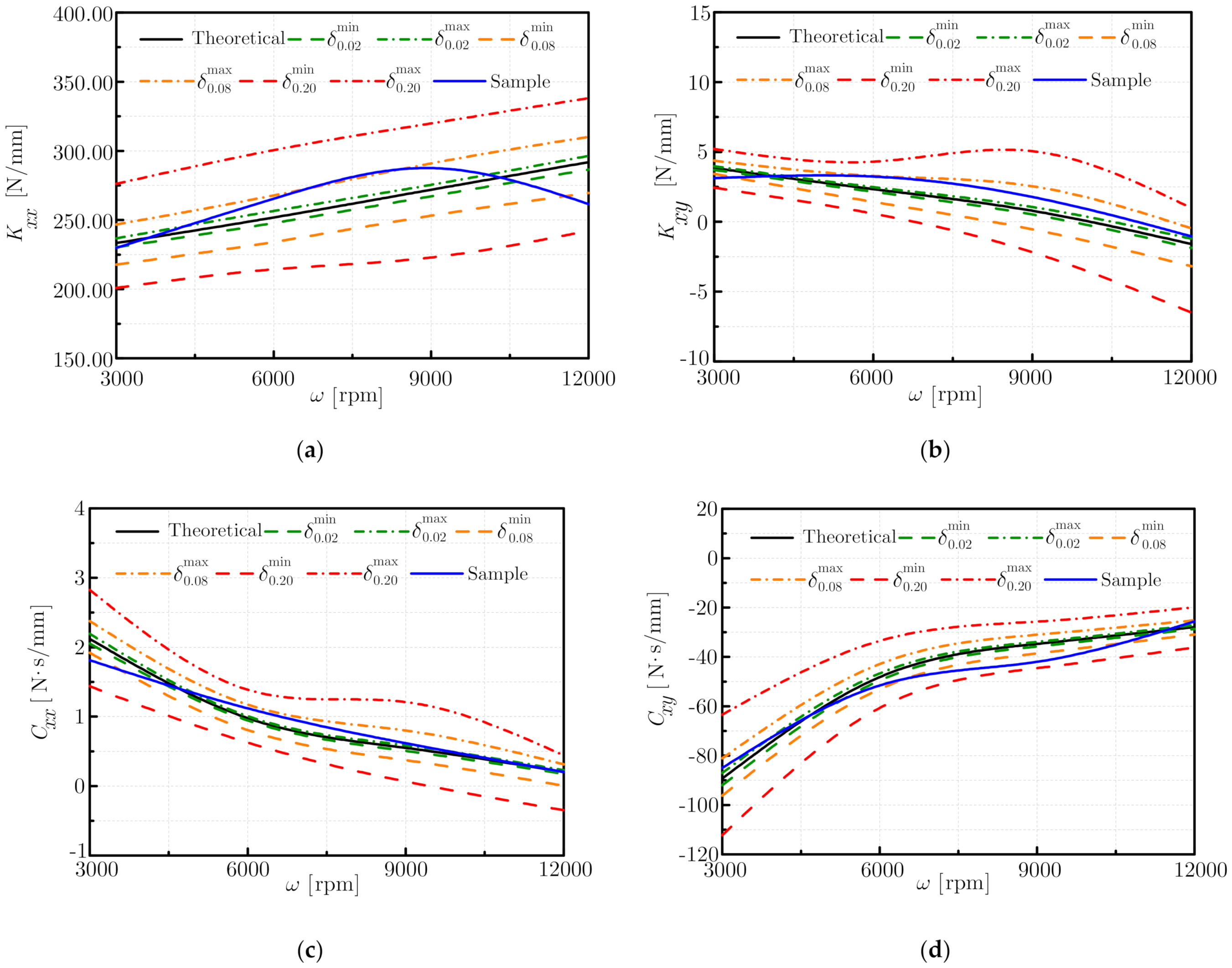
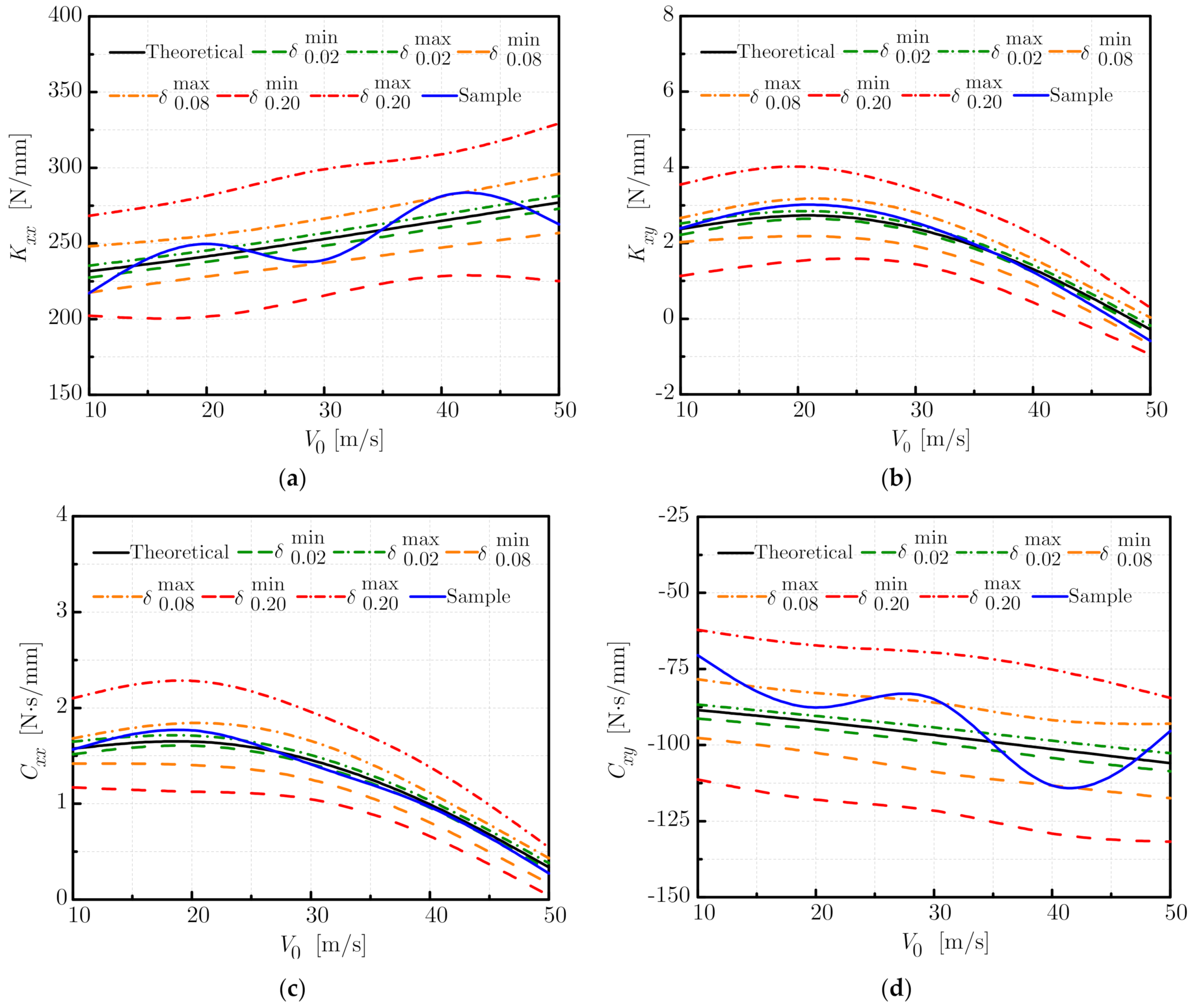
In total, 32 samples of the randomly uncertain orbit are generated for different rotating speeds, pressure differences, and inlet whirl velocities. The orbits are compared with their theoretical ones corresponding to the regular elliptic orbits. Numerical results show that differences exist among the effects of rotating speed, pressure difference, and inlet whirl velocity. Generally speaking, strong deviations in the direct stiffness and cross-coupled damping coefficients arise under the randomly uncertain factors. More specifically, Kxx monotonically increases and Kxy decreases as the rotating speed increases. The envelopes of Cxx show a downward trend, and Cxy monotonically increases against the rotating speed. Pressure difference also significantly affects the dynamic coefficients. A monotonically increased Kxx and a decreased Kxy are observed for an enlarged pressure difference. On the other hand, Cxx shows a remarkable reduction while Cxy remains almost unchanged. As for the inlet whirl velocity, a monotonically increasing Kxx and a decreasing Kxy, Cxx, and Cxy are observed for a larger inlet whirl velocity. To be noted is that Kxy and Cxx go through a short period of increase before decreasing monotonically. Deviation levels of the dynamic coefficients are directly related to randomly uncertain perturbations and are usually positively related to such perturbation strengths.
Thus, the running status of the rotor cannot be accurately revealed by the previous models under ideal conditions. It is necessary to take the uncertain factors into consideration to have an insight into the system behavior. We believe that the present work can help others to study the effects of uncertain factors on the dynamic coefficients of large rotating machinery from a practical point of view.