Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet
Abstract
:1. Introduction
2. Suspension Abrasive Water Jet Nozzle
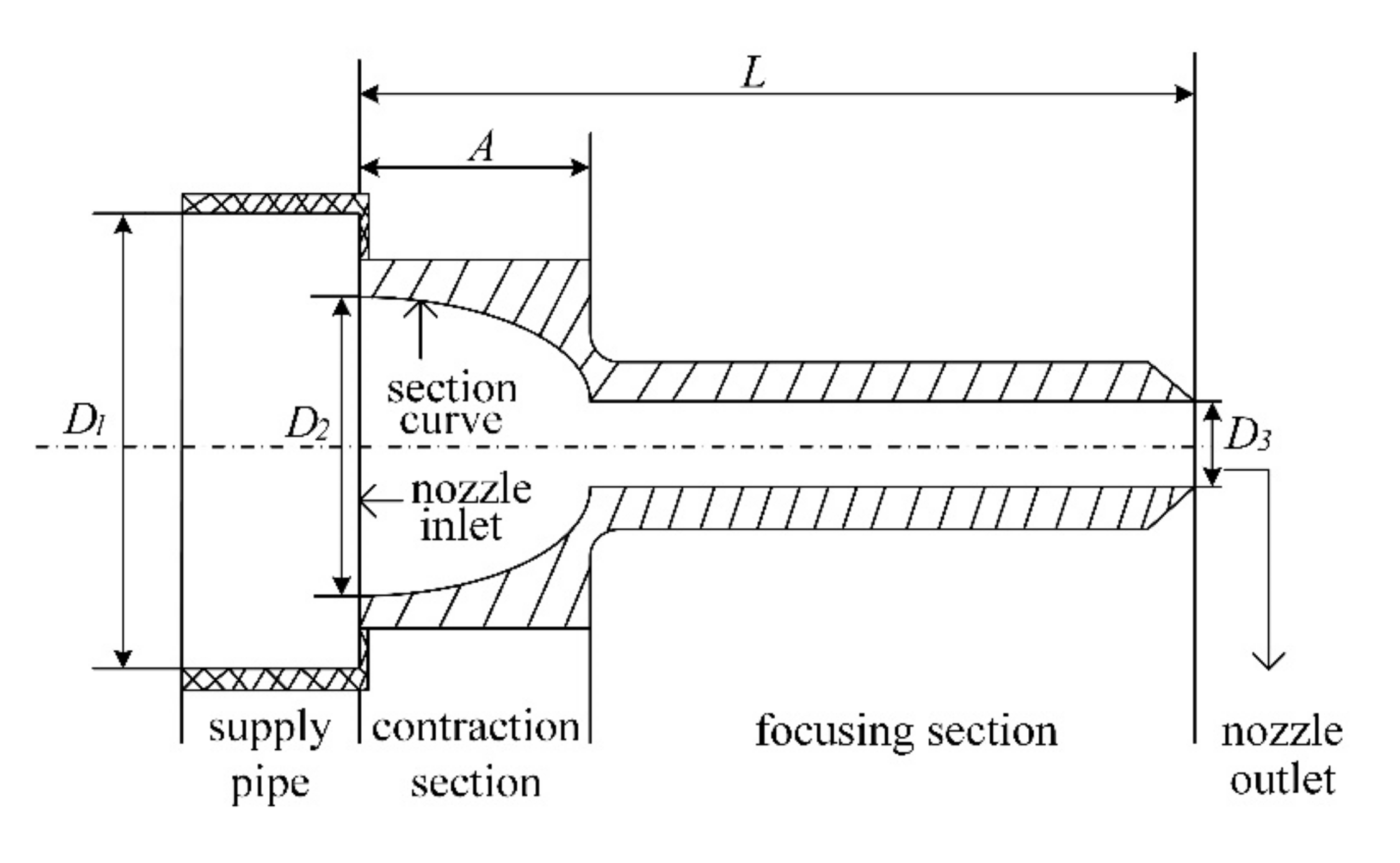
2.1. Nozzle Section Geometry
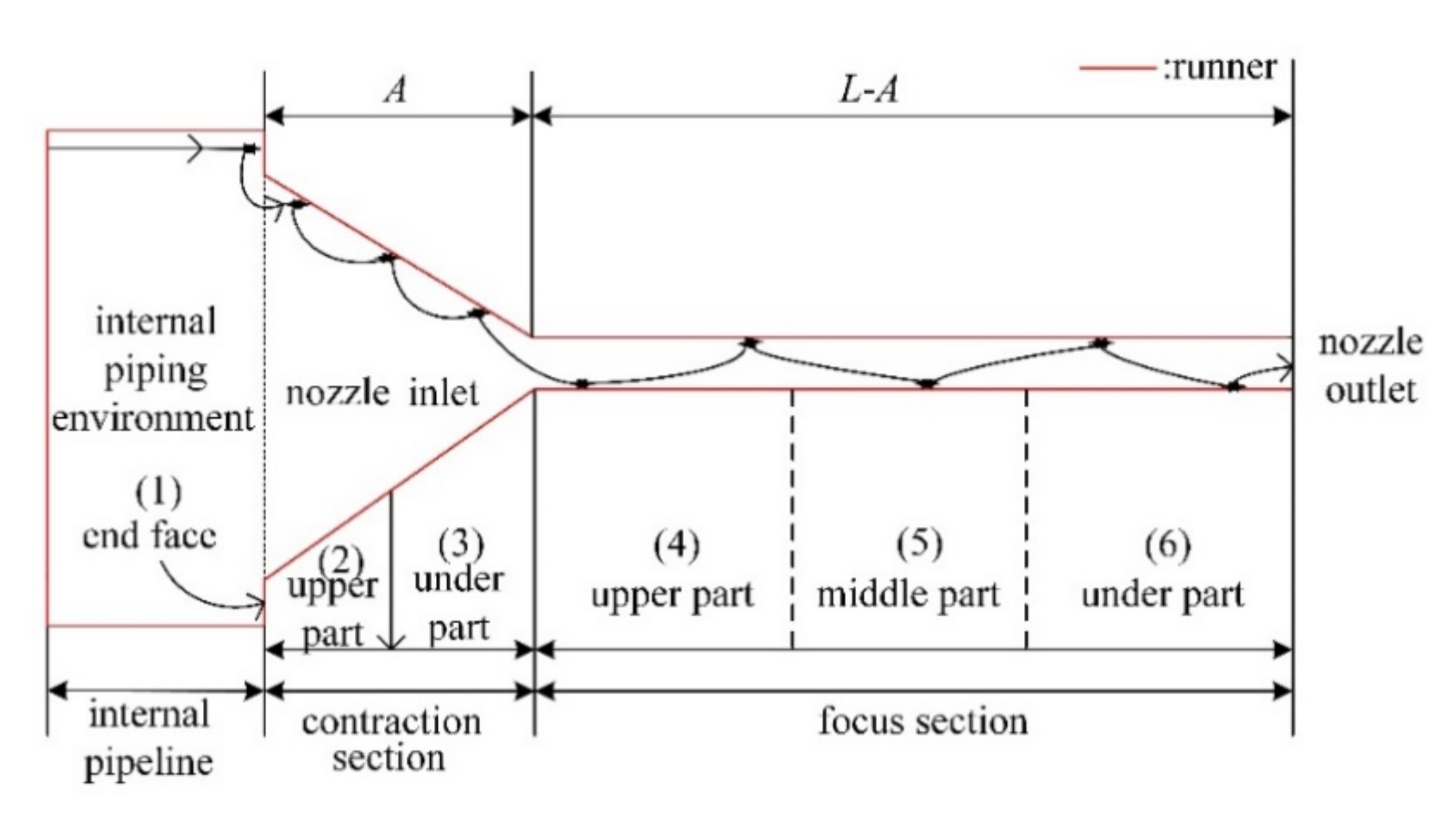
2.2. Geometry for CFD Simulation
2.3. Mesh and Independence
3. CFD Simulation Method
- Fluid flow within the nozzle is stable and the medium is incompressible.
- No heat transfer occurs between the water and the surroundings.
- The particle size of the abrasive particles is uniform with the same physical and chemical properties.
- The roughness of the runner surface is uniform and ideal.
- The effect of buoyancy can be ignored.
3.1. Governing Equations
3.2. Discrete Phase Model
3.3. Coefficient of Elastic Recovery
3.4. Erosion Rate Model
4. Optimization of the Nozzle Geometry
4.1. Parameter Planning
4.2. Nozzle Performance and Variable Effects
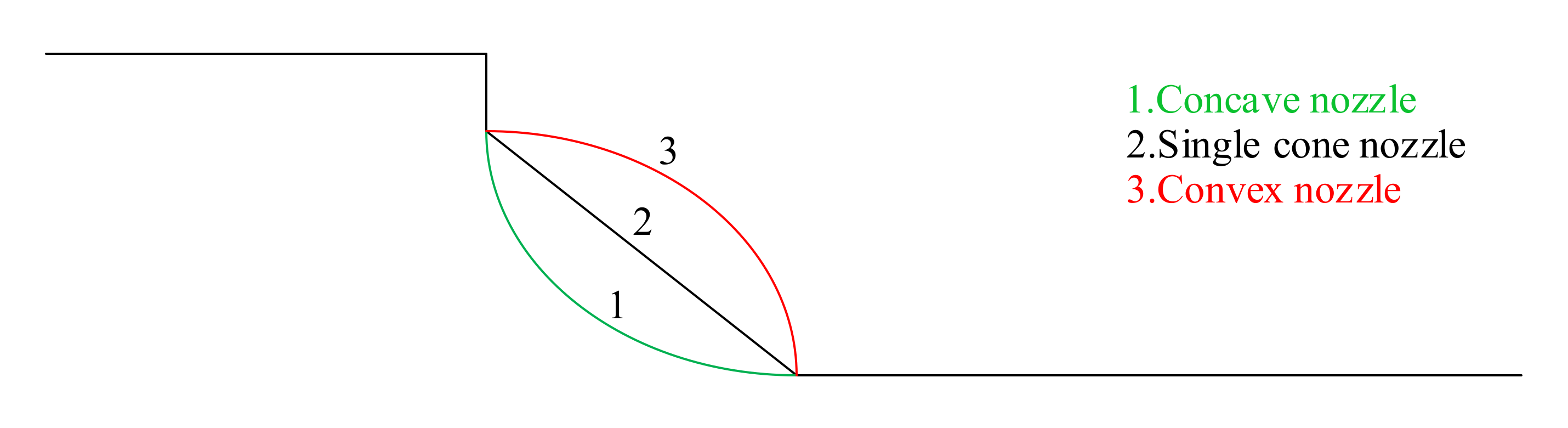
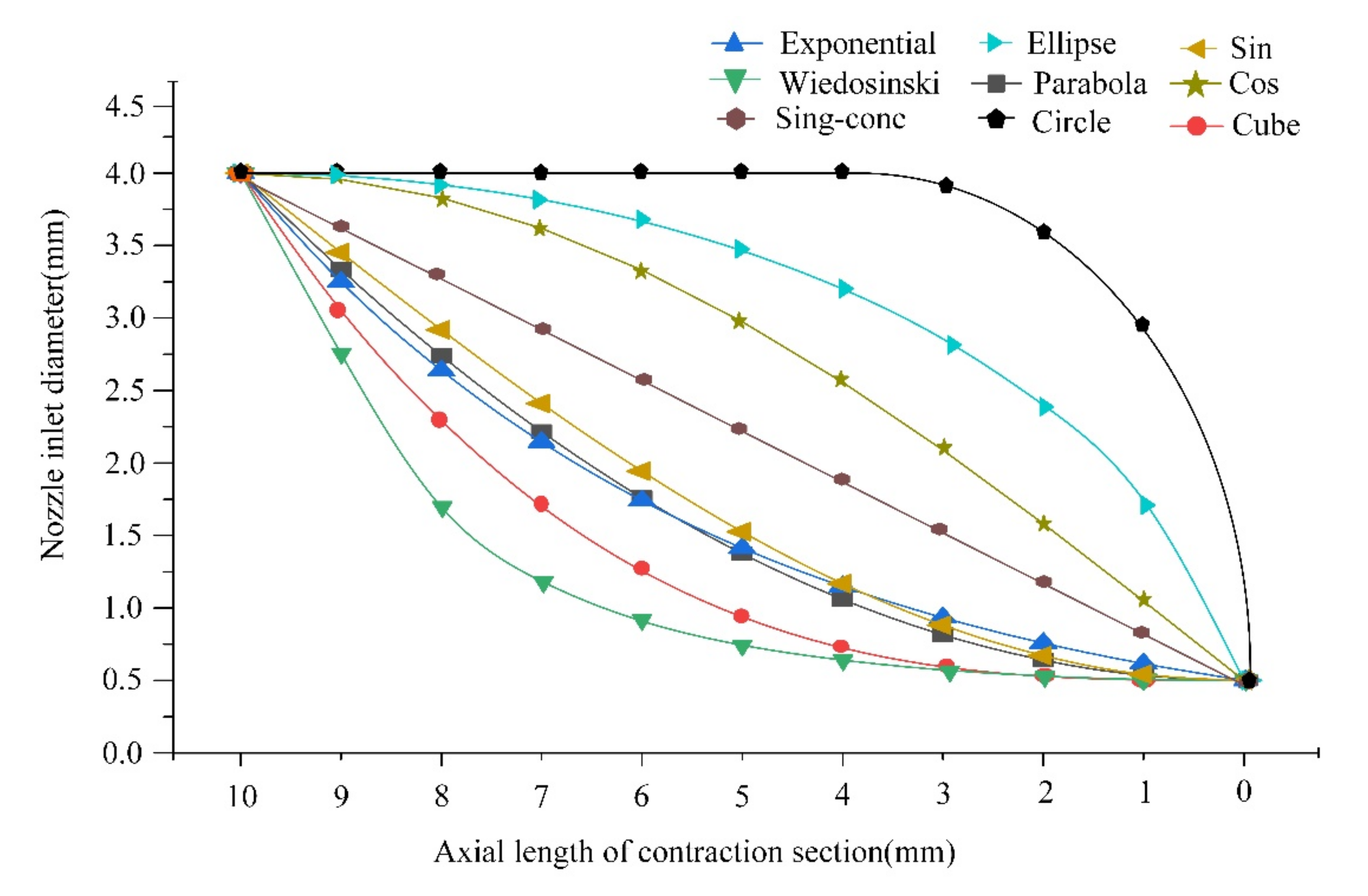
4.2.1. Influence of the Contraction Section Shape
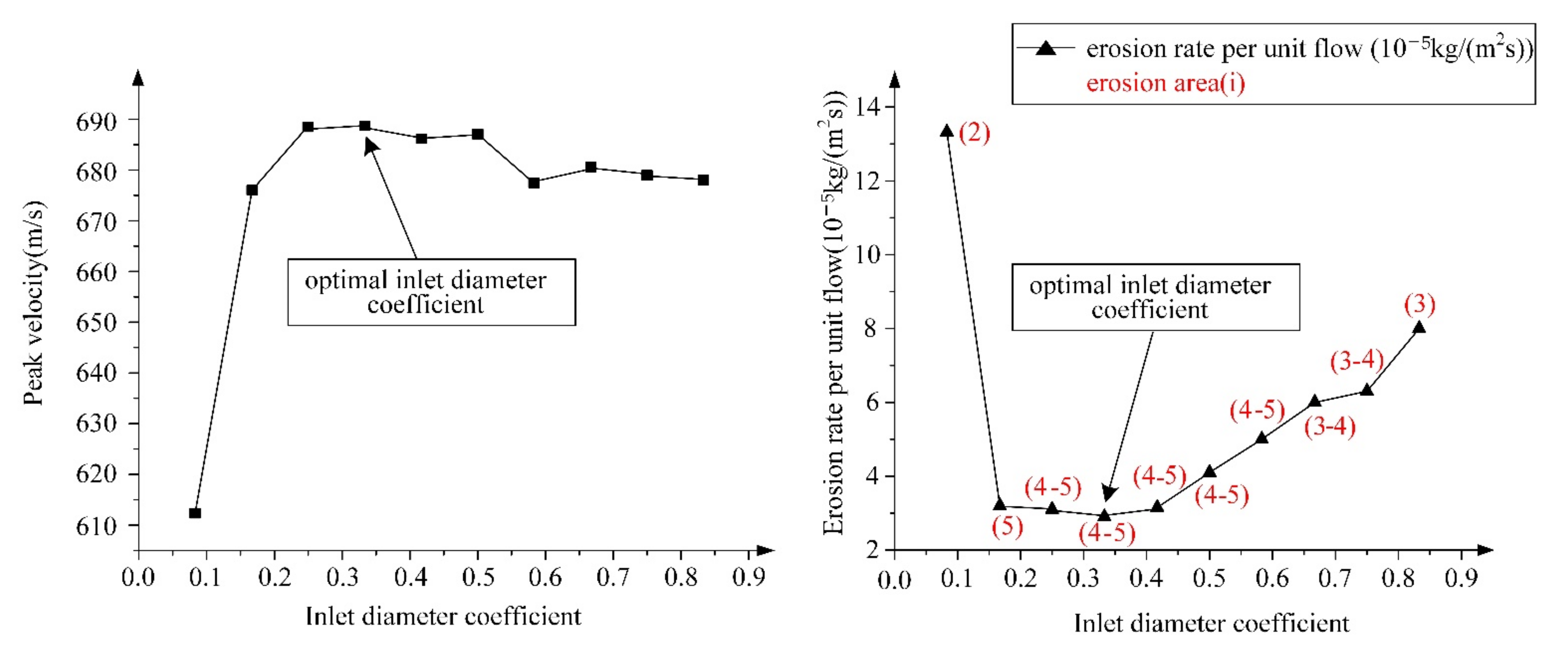
4.2.2. Effect of the Inlet Diameter Coefficient on Nozzle Performance
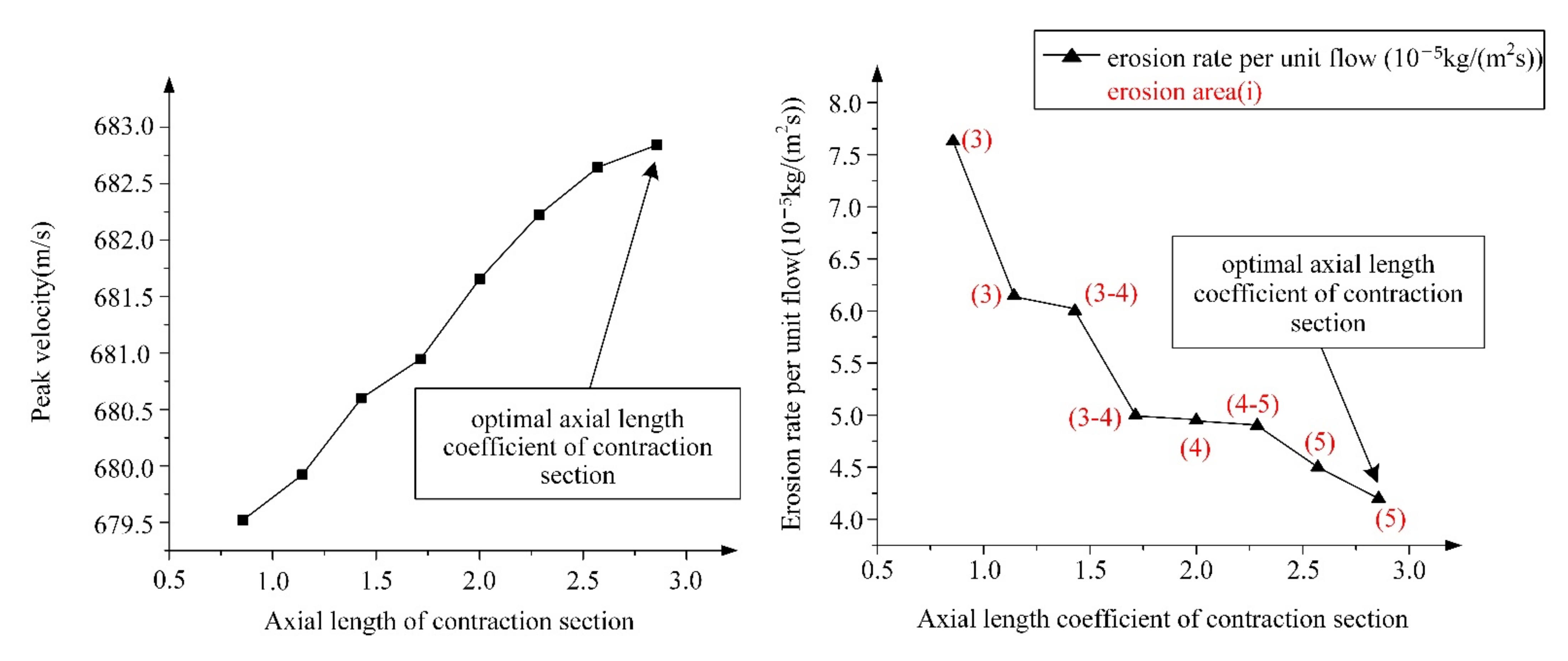
4.2.3. Effect of the Axial Length Coefficient of the Contraction Section on Nozzle Performance
4.3. Optimization Method for the Optimal Section Nozzle
4.4. The Optimal Contraction Section
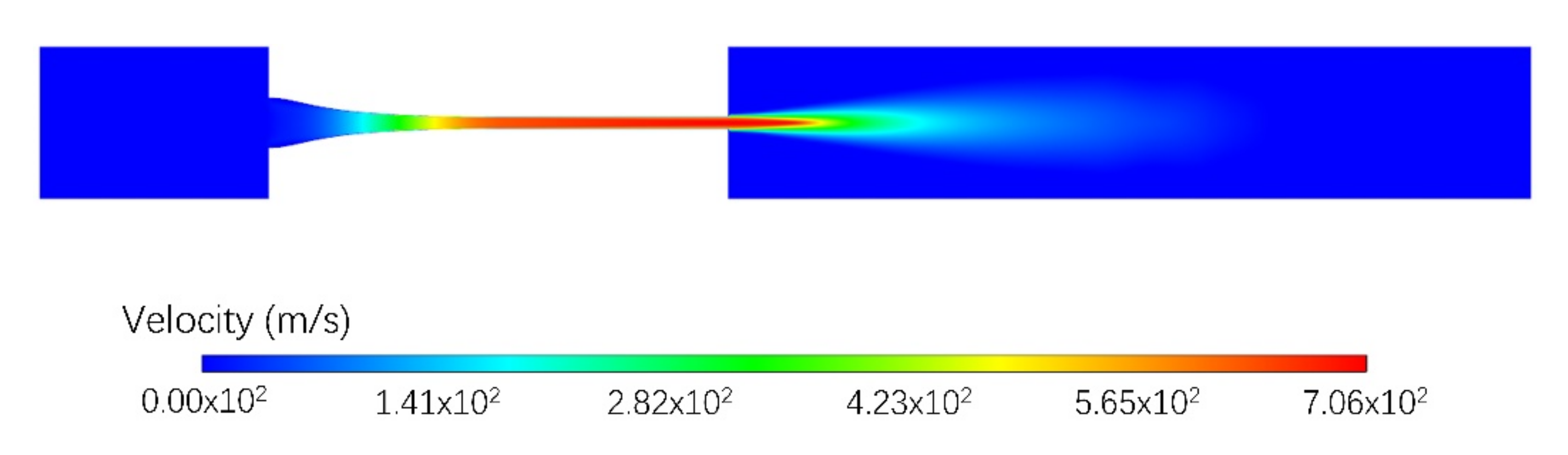
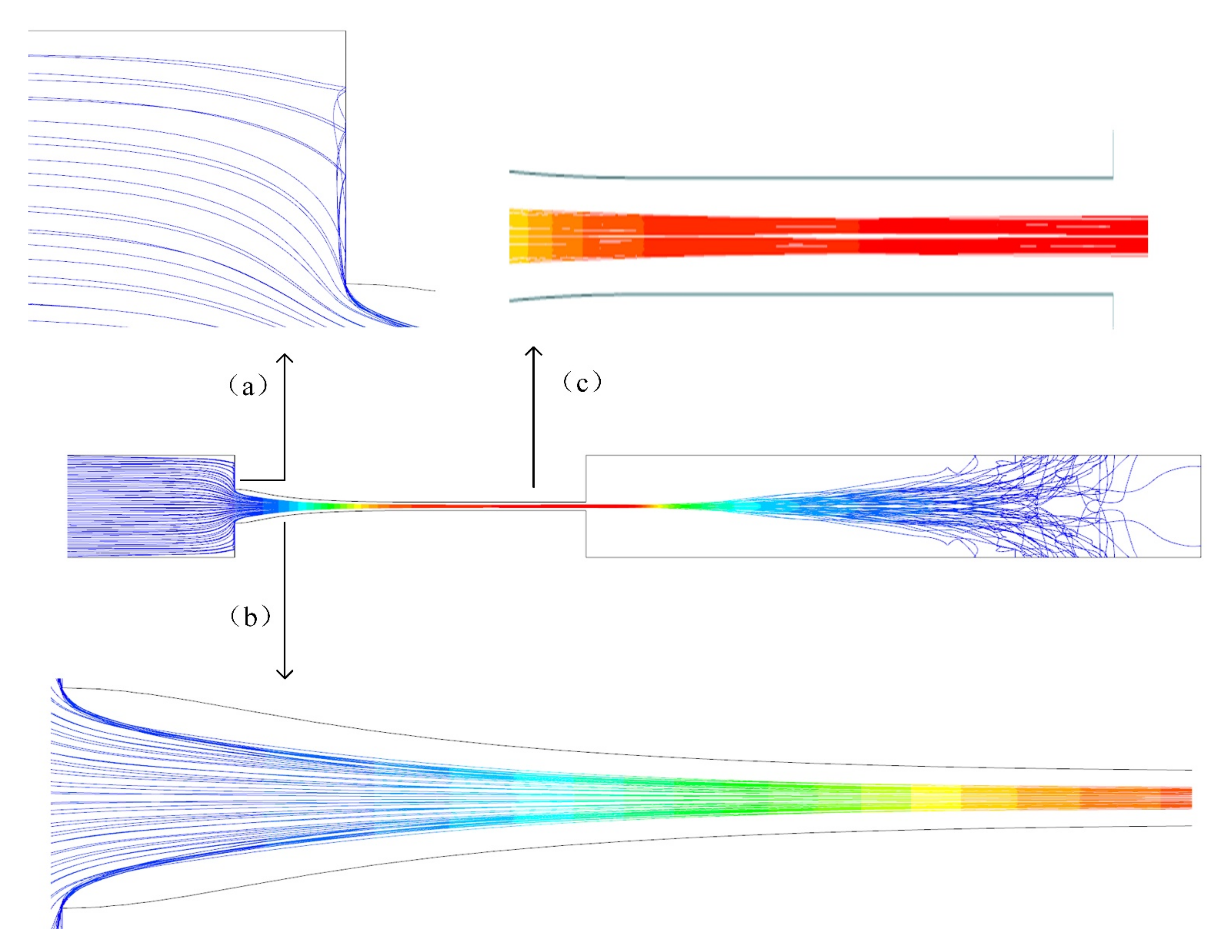
4.5. Simulation Analysis of the Optimal Nozzle
5. Analysis of the Influence of Operation Parameters
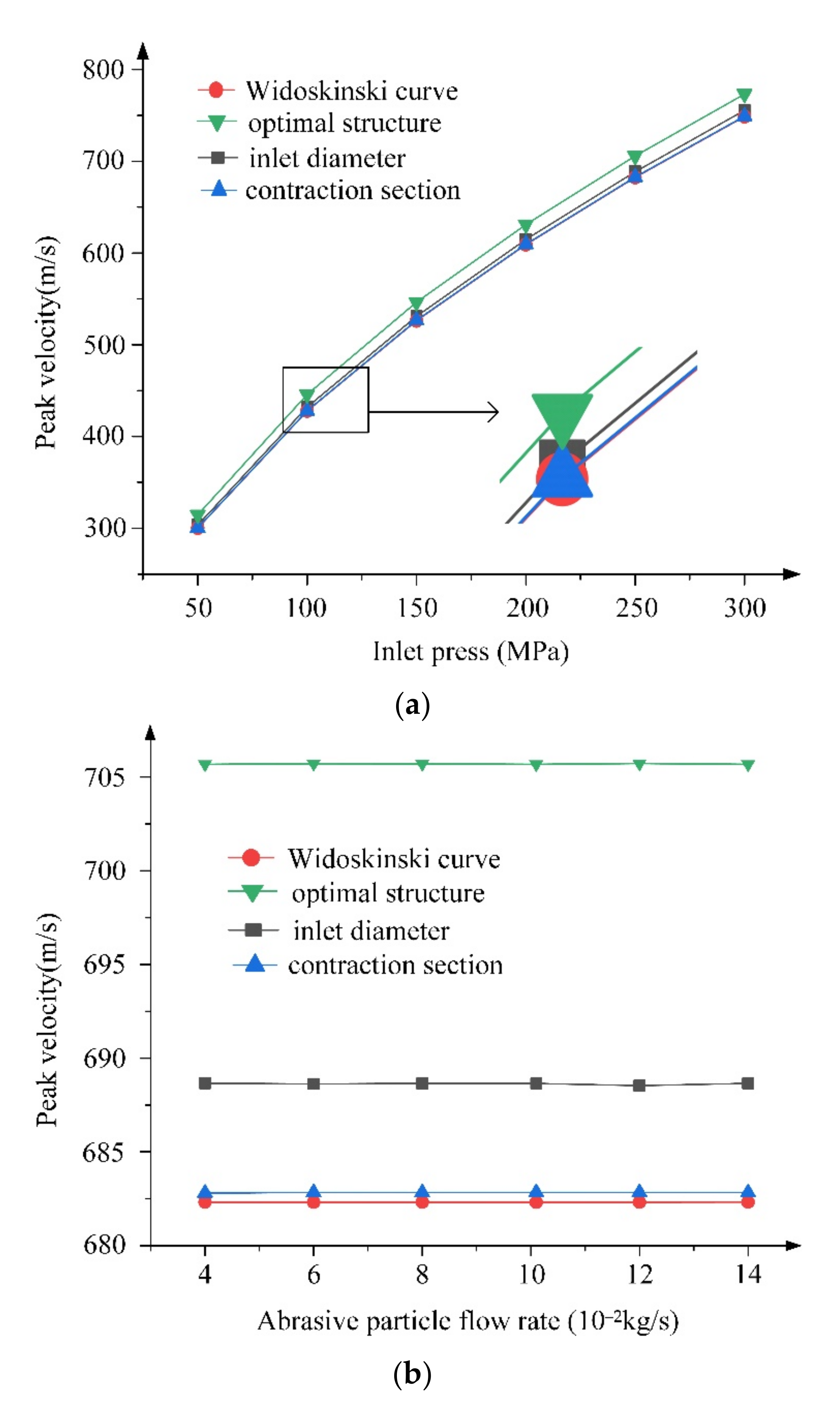
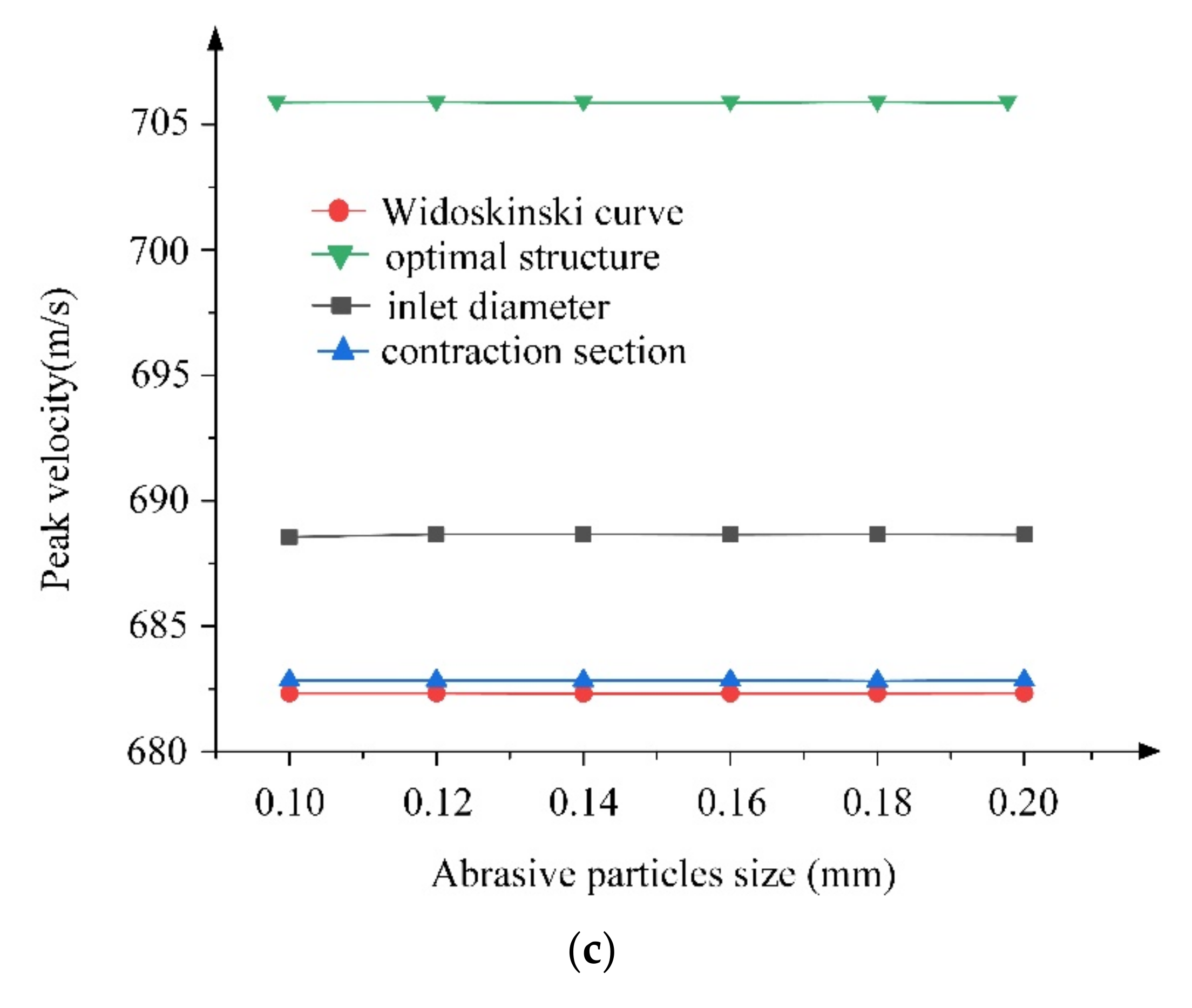
5.1. Operation Parameter Effects on the Peak Velocity
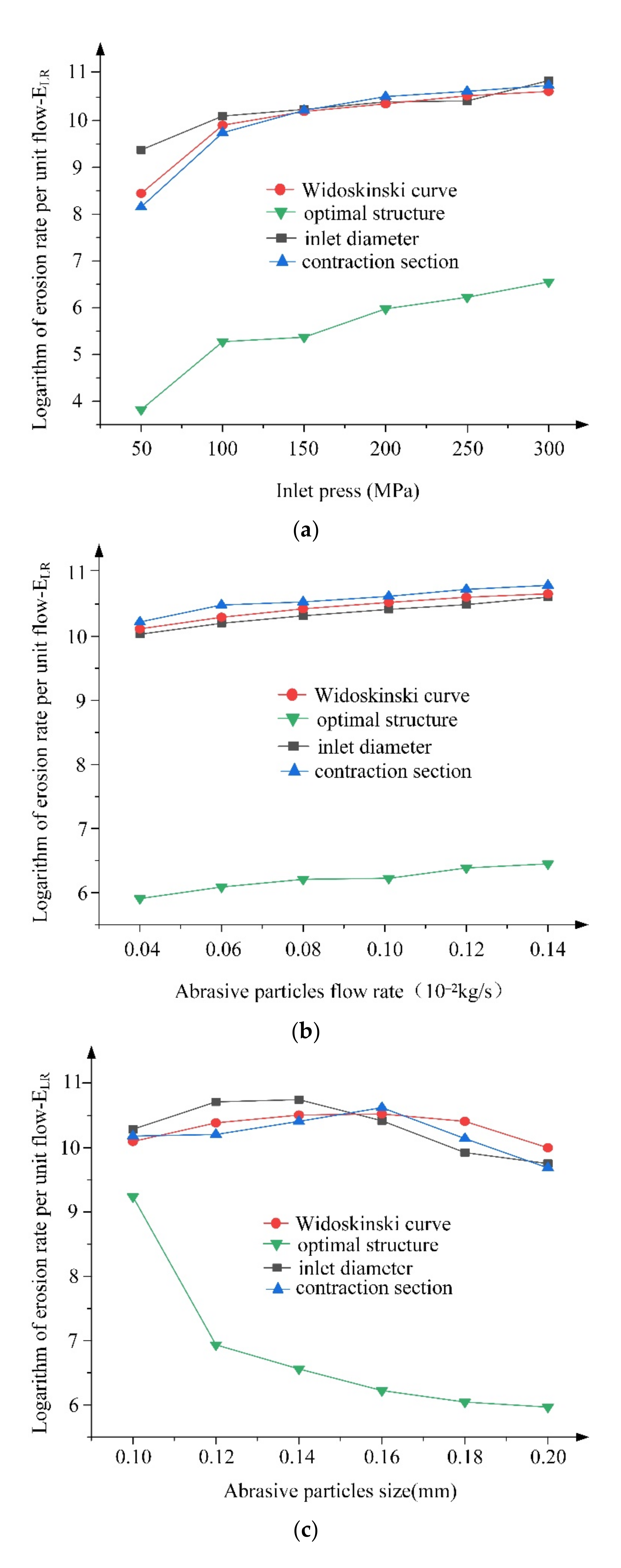
5.2. Effects of Operation Parameters on the Erosion Rate of Unit Flow
6. Conclusions
- (1)
- Regarding the life cycle and cutting ability, the axial length coefficient of the optimal nozzle contraction section is 2.857, the inlet diameter coefficient is 0.333 and the optimal contraction section curve is a Widosinski curve.
- (2)
- The inlet diameter coefficient has a low impact on the peak velocity, but has a big effect on the peak erosion rate and the main erosion position.
- (3)
- The axial length coefficient of the contraction section has a big effect on the erosion rate of the nozzle. The unit flow erosion rate can be reduced by increasing the axial length coefficient and the erosion position moves downstream.
- (4)
- The optimal nozzle produces the minimum unit flow erosion rate in all cases and the main erosion happens at the end surface of the nozzle, which has a low impact on the life cycle of the nozzle. Changing the operation parameters, including inlet pressure, abrasive particle size and abrasive particle flow rate does not affect the optimal results. The optimal nozzle has gained a significantly improved performance compared with the nozzles with single-optimized parameters, including the inlet diameter coefficient, contraction length coefficient and contraction section curve.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiong, X.S. High Pressure Waterjet Technology & Engineering; Hefei University of Technology Press: Hefei, China, 2006; pp. 30–56. [Google Scholar]
- Junlong, S.; Changxia, L.; Hongqi, L.; Bin, L. Effect of mechanical properties and impact angles on erosion behavior of B4C/TiB2 matrix ceramic nozzle materials. Ceram. Int. 2016, 42, 8826–8832. [Google Scholar] [CrossRef]
- Deng, J.X. Wear behaviors of ceramic nozzles with laminated structure at their entry. Wear 2009, 266, 30–36. [Google Scholar] [CrossRef]
- Oka, Y.; Hutchings, I.M. Dependence of Material Hardness on Erosion by Solid Particle Impact. Corros. Eng. 2009, 39, 610–616. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact—Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Tilly, G.P.; Sage, W. The interaction of particle and material behaviour in erosion processes. Wear 1970, 16, 447–465. [Google Scholar] [CrossRef]
- Oka, Y.I.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact—Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Finnie, I. The Mechanism of Erosion of Ductile Metals. In Proceedings of the 3rd U.S. National Congress of Applied Mechanics, Providence, RI, USA, 11–14 June 1958. [Google Scholar]
- Bozzini, B.; Ricotti, M.E.; Boniardi, M.; Mele, C. Evaluation of erosion-corrosion in multiphase flow via CFD and experimental analysis. Wear 2003, 255, 237–245. [Google Scholar] [CrossRef]
- Stack, M.M.; Abdelrahman, S.M.; Jana, B.D. A new methodology for modelling erosion-corrosion regimes on real surfaces: Gliding down the galvanic series for a range of metal-corrosion systems. Wear 2010, 268, 533–542. [Google Scholar] [CrossRef] [Green Version]
- Long, X.; Ruan, X.; Liu, Q.; Chen, Z.; Xue, S.; Wu, Z. Numerical investigation on the internal flow and the particle movement in the abrasive waterjet nozzle. Powder Technol. 2017, 314, 635–640. [Google Scholar] [CrossRef]
- Kartal, F. Study and evaluation of abrasive water jet turning process performance on AA5083. Materialwissenschaft und Werkstofftechnik 2020, 51, 212–220. [Google Scholar] [CrossRef]
- Ma, Q.; Lin, J.; Yang, K.; Xie, H.; Guo, C. Experimental study on abrasive recycling in cutting with abrasive suspension water jet. Int. J. Adv. Manuf. Technol. 2021, 114, 969–979. [Google Scholar] [CrossRef]
- Anand, U.; Katz, J. Prevention of nozzle wear in abrasive water suspension jets (AWSJ) using porous lubricated nozzles. J. Tribol. 2003, 125, 168–180. [Google Scholar] [CrossRef]
- Hashish, M. Observations of Wear of Abrasive-Waterjet Nozzle Materials. J. Tribol. 1994, 116, 439–444. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. The effects of system and geometric parameters on abrasive water jet nozzle wear. Int. J. Mach. Tools Manuf. 2002, 42, 615–623. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. A Study of Nozzle Wear in Abrasive Entrained Water Jetting Environment. J. Tribol. 2000, 122, 465–471. [Google Scholar] [CrossRef]
- Chen, X.C.; Deng, S.S.; Guan, J.F.; Hua, W.X. Experiment and simulation research on abrasive water jet nozzle wear behavior and anti-wear structural improvement. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2023–2033. [Google Scholar] [CrossRef]
- Zuo, W.; Huang, C.; Liu, Y.; Han, H.; Hao, F.; Zhao, F.; Huang, F. Analysis and Modeling of Particle Velocities in Premixed Abrasive Water Jets. Geofluids 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Du, M.M.; Wang, H.J.; Dong, H.Y.; Guo, Y.J.; Ke, Y.L. Numerical research on multi-particle movements and nozzle wear involved in abrasive waterjet machining. Int. J. Adv. Manuf. Technol. 2021, 117, 2845–2858. [Google Scholar] [CrossRef]
- Gavrilov, I.Y.; Popov, V.V.; Sorokin, I.Y.; Tishchenko, V.A.; Khomyakov, S.V. A contactless technique for determining the average sizes of erosion-hazardous droplets in polydisperse wet steam flow. Therm. Eng. 2014, 61, 577–584. [Google Scholar] [CrossRef]
- Mostofa, M.G.; Kil, K.Y.; Hwan, A.J. Computational fluid analysis of abrasive waterjet cutting head. J. Mech. Sci. Technol. 2010, 24, 249–252. [Google Scholar] [CrossRef]
- Wang, R.H.; Wang, M.B. A two-fluid model of abrasive waterjet. J. Mater. Process. Technol. 2010, 210, 190–196. [Google Scholar] [CrossRef]
- Kowsari, K.; Nouraei, H.; Samareh, B.; Papini, M.; Spelt, J.K. CFD-aided prediction of the shape of abrasive slurry jet micro-machined channels in sintered ceramics. Ceram. Int. 2016, 42, 7030–7042. [Google Scholar] [CrossRef]
- Kim, J.H.; Joo, H.G.; Lee, K.Y. Simulation of solid particle erosion in WC-Ni coated wall using CFD. J. Mater. Process. Technol. 2015, 224, 240–245. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications. J. Nat. Gas Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Nguyen, V.B.; Nguyen, Q.B.; Liu, Z.G.; Wan, S.; Lim, C.Y.H.; Zhang, Y.W. A combined numerical-experimental study on the effect of surface evolution on the water-sand multiphase flow characteristics and the material erosion behavior. Wear 2014, 319, 96–109. [Google Scholar] [CrossRef]
- Jafari, M.; Mansoori, Z.; Avval, M.S.; Ahmadi, G.; Ebadi, A. Modeling and numerical investigation of erosion rate for turbulent two-phase gas-solid flow in horizontal pipes. Powder Technol. 2014, 267, 362–370. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Han, Z.W.; Yin, W.; Wang, H.Y.; Ge, C.; Jiang, J.L. Numerical Experiment of the Solid Particle Erosion of Bionic Configuration Blade of Centrifugal Fan. Acta Metall. Sin. 2013, 26, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Grant, G.; Tabakoff, W. Erosion prediction in turbomachinery due to environmental solid particles. In Proceedings of the 12th Aerospace Sciences Meeting, Washington, DC, USA, 30 January–1 February 1974. [Google Scholar]
- Campos-Amezcua, A.; Gallegos-Munoz, A.; Romero, C.A.; Mazur-Czerwiec, Z.; Campos-Amezcua, R. Numerical investigation of the solid particle erosion rate in a steam turbine nozzle. Appl. Therm. Eng. 2007, 27, 2394–2403. [Google Scholar] [CrossRef]
- Haugen, K.; Kvernvold, O.; Ronold, A.; Sandberg, R. Sand erosion of wear-resistant materials: Erosion in choke valves. Wear 1995, 186, 179–188. [Google Scholar] [CrossRef]
- Safikhani, H.; Abbassi, A.; Khalkhali, A.; Kalteh, M. Multi-objective optimization of nanofluid flow in flat tubes using CFD, Artificial Neural Networks and genetic algorithms. Adv. Powder Technol. 2014, 25, 1608–1617. [Google Scholar] [CrossRef]
- Manshadi, M.D.; Aghajanian, S. Computational aerodynamic optimization of wing-design concept at supersonic conditions by means of the response surface method. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 1–15. [Google Scholar] [CrossRef]
- Uebel, K.; Rossger, P.; Prufert, U.; Richter, A.; Meyer, B. CFD-based multi-objective optimization of a quench reactor design. Fuel Process. Technol. 2016, 149, 290–304. [Google Scholar] [CrossRef]




| Mesh Configurations | Cell Numbers | Peak Velocity (m/s) | Variation (%) | Erosion Area | Peak Erosion Rate 10−5 (kg/(m2s)) | Variation (%) |
|---|---|---|---|---|---|---|
| Coarse | 13,720 | 683.69 | −0.002 | 3–4 | 1.491 | 0.13 |
| Medium | 23,450 | 682.25 | −0.212 | 3–4 | 1.507 | 1.21 |
| Fine | 42,240 | 685.16 | 0.214 | 3–4 | 1.469 | –1.34 |
| Average | - | 683.70 | - | - | 1.489 | - |
| Curve | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Type | Parabola | Exponential | Sin | Cube | Wiedosinski | Ellipse | Circle | Cos | Single cone |
| Parameter | Values Tested | Simulation Initial Value |
|---|---|---|
| Sc | S1 S2 S3 S4 S5 S6 S7 S8 S9 | S2 |
| A (mm) | 6 8 10 12 14 16 18 20 | 10 |
| λc | 0.857 1.143 1.429 1.714 2.000 2.286 2.571 2.857 | 1.429 |
| D2 (mm) | 1 2 3 4 5 6 7 8 9 10 | 8 |
| λi | 0.083 0.167 0.250 0.333 0.417 0.500 0.583 0.667 0.75 0.833 | 0.667 |
| D1 (mm) | D2 (mm) | D3 (mm) | Sc | A (mm) | L (mm) |
|---|---|---|---|---|---|
| 12 | 8 | 1 | S9 | 10 | 40 |
| Inlet Press | Abrasive Size | Total Flow Rate | D1 (mm) | D2 (mm) | D3 (mm) |
|---|---|---|---|---|---|
| 250 MPa | 0.16 mm | 0.101 kg/s | 12 | 8 | 1 |
| Section Curve | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Peak velocity (m/s) | 680 | 679 | 679 | 678 | 683 | 642 | 680 | 663 | 668 |
| Erosion rate per unit flow (10−5 kg/(m2s)) | 8.4 | 10.1 | 8.4 | 7.9 | 3.4 | 16.3 | 8.9 | 4.3 | 9.2 |
| Performance improvement (%) | 8.7 | −9.8 | 8.7 | 14.1 | 63.0 | −77.2 | 3.3 | 53.3 | - |
| Erosion area | 3–4 | 4–5 | 4 | 3–4 | 3–4 | 3–5 | 3–5 | 2–3 | 3–5 |
| Type | Peak Velocity (m/s) | Erosion Area | ELR |
|---|---|---|---|
| Optimal nozzle | 706 | 1 | 6.23 |
| Product nozzle | 668 | 3–5 | 10.96 |
| Performance Improvement (%) | 5.64 | - | 43.2 |
| Parameter | λi | λc | Sc |
|---|---|---|---|
| Optimal | 0.333 | 2.857 | Widosinski curve |
| Parameter | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Abrasive particle flow rate (kg/s) | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 |
| Abrasive particle size (mm) | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 | 0.20 |
| Inlet press (MPa) | 50 | 100 | 150 | 200 | 250 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yao, S.; Yun, F.; Wang, X.; Wang, L.; Wu, Y. Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet. Machines 2022, 10, 3. https://doi.org/10.3390/machines10010003
Li Z, Yao S, Yun F, Wang X, Wang L, Wu Y. Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet. Machines. 2022; 10(1):3. https://doi.org/10.3390/machines10010003
Chicago/Turabian StyleLi, Zhibo, Shaoming Yao, Feihong Yun, Xiangyu Wang, Liquan Wang, and Yongtao Wu. 2022. "Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet" Machines 10, no. 1: 3. https://doi.org/10.3390/machines10010003
APA StyleLi, Z., Yao, S., Yun, F., Wang, X., Wang, L., & Wu, Y. (2022). Simulation and Optimization of the Nozzle Section Geometry for a Suspension Abrasive Water Jet. Machines, 10(1), 3. https://doi.org/10.3390/machines10010003





