On the Numerical Solution of Fractional Boundary Value Problems by a Spline Quasi-Interpolant Operator
Abstract
1. Introduction
2. Materials and Methods
2.1. Fractional Boundary Value Problems
2.2. The Cardinal B-Splines through the Truncated Power Function
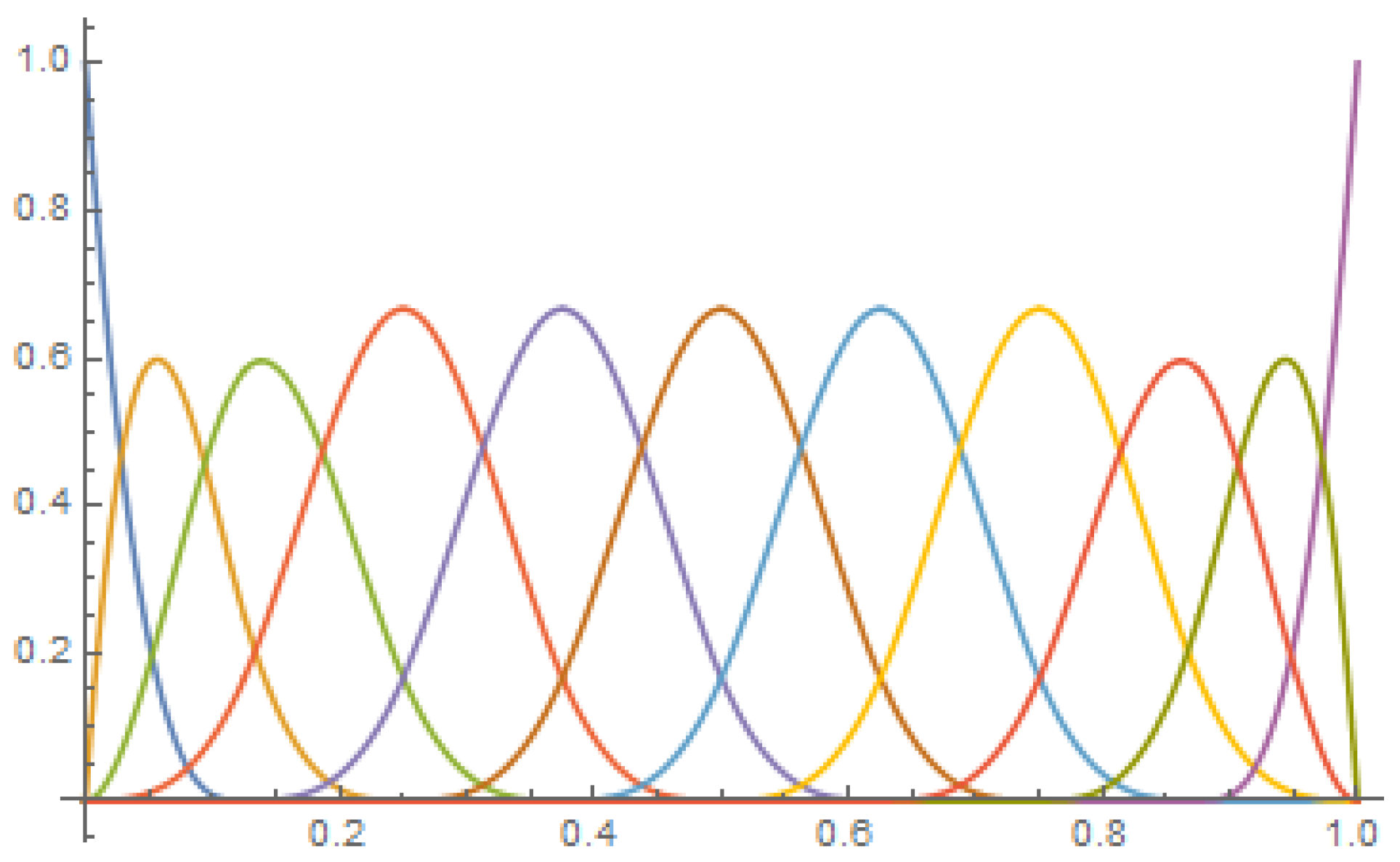
2.3. B-Spline Bases on the Finite Interval
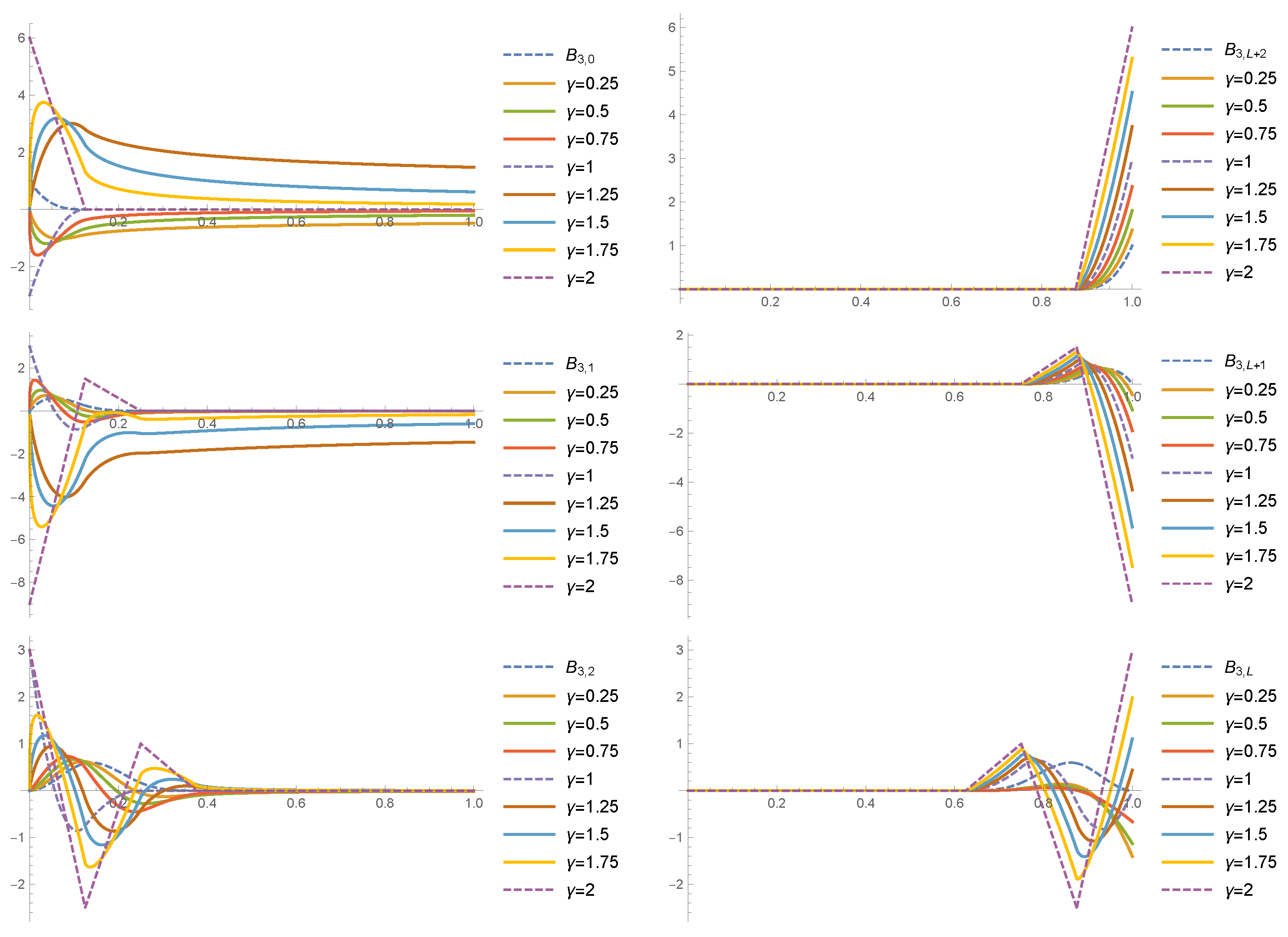
2.4. Fractional Derivatives of Cardinal B-Splines
2.5. The Schoenberg-Bernstein Operator
3. The Collocation Method
4. Numerical Results
4.1. Example 1
4.2. Example 2
5. Conclusions
Funding
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon & Breach Science Publishers: Switzerland, 1993. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics; Nonlinear Physical Science; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Diethelm, K.; Freed, A.D. On the solution of nonlinear fractional-order differential equations used in the modeling of viscoplasticity. In Scientific Computing in Chemical Engineering II; Springer: Berlin/Heidelberg, Germany, 1999; pp. 217–224. [Google Scholar]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2007, 4, 153–192. [Google Scholar]
- Agarwal, R.P.; Benchohra, M.; Hamani, S. A survey on existence results for boundary value problems of nonlinear fractional differential equations and inclusions. Acta Appl. Math. 2010, 109, 973–1033. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E. Piecewise polynomial collocation for linear boundary value problems of fractional differential equations. J. Comput. Appl. Math. 2012, 236, 3349–3359. [Google Scholar] [CrossRef]
- Acosta, G.; Borthagaray, J.P.; Bruno, O.; Maas, M. Regularity theory and high order numerical methods for the (1D)-fractional Laplacian. Math. Comput. 2018, 87, 1821–1857. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- He, J.H. A tutorial review on fractal spacetime and fractional calculus. Int. J. Theor. Phys. 2014, 53, 3698–3718. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl 2015, 1, 1–13. [Google Scholar]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H.; Wu, G.C.; Austin, F. The variational iteration method which should be followed. Nonlinear Sci. Lett. A 2010, 1, 1–30. [Google Scholar]
- Liu, H.Y.; He, J.H.; Li, Z.B. Fractional calculus for nanoscale flow and heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1227–1250. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Comparison between the homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput. Math. Appl. 2007, 54, 910–919. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. The variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl. 2009, 58, 2199–2208. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. Int. J. 2006, 22, 558–576. [Google Scholar] [CrossRef]
- Ford, N.J.; Morgado, M. Fractional boundary value problems: Analysis and numerical methods. Fract. Calc. Appl. Anal. 2011, 14, 554–567. [Google Scholar] [CrossRef]
- Chen, S.; Shen, J.; Wang, L.L. Generalized Jacobi functions and their applications to fractional differential equations. Math. Comput. 2016, 85, 1603–1638. [Google Scholar] [CrossRef]
- Mao, Z.; Karniadakis, G.E. A spectral method (of exponential convergence) for singular solutions of the diffusion equation with general two-sided fractional derivative. SIAM J. Numer. Anal. 2018, 56, 24–49. [Google Scholar] [CrossRef]
- Ismail, M.; Saeed, U.; Alzabut, J.; Rehman, M. Approximate solutions for fractional boundary value problems via green-cas wavelet method. Mathematics 2019, 7, 1164. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Pitolli, F. A fractional B-spline collocation method for the numerical solution of fractional predator-prey models. Fractal Fract. 2018, 2, 13. [Google Scholar] [CrossRef]
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]
- Diethelm, K.; Garrappa, R.; Stynes, M. Good (and not so good) practices in computational methods for fractional calculus. Mathematics 2020, 8, 324. [Google Scholar] [CrossRef]
- De Boor, C.; Fix, G.J. Spline approximation by quasiinterpolants. J. Approx. Theory 1973, 8, 19–45. [Google Scholar] [CrossRef]
- Lyche, T.; Schumaker, L.L. Local spline approximation methods. J. Approx. Theory 1975, 15, 294–325. [Google Scholar] [CrossRef]
- Goodman, T.N.T.; Sharma, A. A Modified Bernstein-Schoenberg Operator. In Constructive Theory of Functions 87; Sendov, B., Ed.; Bulgarian Academy Sciences: Sofia, Bulgaria, 1988. [Google Scholar]
- Lee, B.G.; Lyche, T.; Mørken, K. Some examples of quasi-interpolants constructed from local spline projectors. In Mathematical Methods for Curves and Surfaces. Oslo 2000; Lyche, T., Schumaker, L., Eds.; Vanderbilt University Press: Nashville, TN, USA, 2001; pp. 243–252. [Google Scholar]
- Sablonnière, P. Recent progress on univariate and multivariate polynomial and spline quasi-interpolants. In Trends and Applications in Constructive Approximation; De Bruin, M., Mache, D., Szabados, J., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; Volume 177, pp. 229–245. [Google Scholar]
- Schoenberg, I.J. On spline functions. In Inequalities; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1967; pp. 255–291. [Google Scholar]
- Pezza, L.; Pitolli, F. A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 2018, 147, 210–219. [Google Scholar] [CrossRef]
- Pellegrino, E.; Pezza, L.; Pitolli, F. A collocation method in spline spaces for the solution of linear fractional dynamical systems. Math. Comput. Simul. 2019, 176, 266–278. [Google Scholar] [CrossRef]
- Kolk, M.; Pedas, A.; Tamme, E. Smoothing transformation and spline collocation for linear fractional boundary value problems. Appl. Math. Comput. 2016, 283, 234–250. [Google Scholar] [CrossRef]
- Vainikko, G. Multidimensional Weakly Singular Integral Equations; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1993; Volume 1549. [Google Scholar]
- De Boor, C. A Practical Guide to Splines; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Schumaker, L.L. Spline Functions: Basic Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pitolli, F. Optimal B-spline bases for the numerical solution of fractional differential problems. Axioms 2018, 7, 46. [Google Scholar] [CrossRef]
- Unser, M.; Blu, T. Fractional splines and wavelets. SIAM Rev. 2000, 42, 43–67. [Google Scholar] [CrossRef]
- Marsden, M.J. An identity for spline functions with applications to variation diminishing spline approximation. J. Approx. Theory 1970, 3, 7–49. [Google Scholar] [CrossRef]
- Ascher, U. Discrete least squares approximations for ordinary differential equations. SIAM J. Numer. Anal. 1978, 15, 478–496. [Google Scholar] [CrossRef]
- Pellegrino, E.; Pezza, L.; Pitolli, F. A collocation method based on discrete quasi-interpolatory operators for the solution of time fractional differential problems. 2020; in preparation. [Google Scholar]


| 0 | 0.25 | 0.5 | 0.75 | 1 | |
|---|---|---|---|---|---|
| 6.46 × 10 | 4.21 × 10 | 1.99 × 10 | 2.10 × 10 | 1.89 × 10 |
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 |
| h | |||||
|---|---|---|---|---|---|
| 3.18 × 10 | 3.43 × 10 | 5.97 × 10 | 1.84 × 10 | 3.85 × 10 | |
| 1.75 × 10 | 2.43 × 10 | 8.12 × 10 | 3.38 × 10 | 1.06 × 10 | |
| 1.02 × 10 | 1.93 × 10 | 1.23 × 10 | 6.64 × 10 | 2.70 × 10 | |
| 6.18 × 10 | 1.94 × 10 | 1.97 × 10 | 1.34 × 10 | 6.80 × 10 | |
| 3.79 × 10 | 2.31 × 10 | 3.29 × 10 | 2.75 × 10 | 1.70 × 10 | |
| 2.36 × 10 | 3.05 × 10 | 5.63 × 10 | 5.70 × 10 | 4.26 × 10 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitolli, F. On the Numerical Solution of Fractional Boundary Value Problems by a Spline Quasi-Interpolant Operator. Axioms 2020, 9, 61. https://doi.org/10.3390/axioms9020061
Pitolli F. On the Numerical Solution of Fractional Boundary Value Problems by a Spline Quasi-Interpolant Operator. Axioms. 2020; 9(2):61. https://doi.org/10.3390/axioms9020061
Chicago/Turabian StylePitolli, Francesca. 2020. "On the Numerical Solution of Fractional Boundary Value Problems by a Spline Quasi-Interpolant Operator" Axioms 9, no. 2: 61. https://doi.org/10.3390/axioms9020061
APA StylePitolli, F. (2020). On the Numerical Solution of Fractional Boundary Value Problems by a Spline Quasi-Interpolant Operator. Axioms, 9(2), 61. https://doi.org/10.3390/axioms9020061





