Discrete and Fuzzy Models of Time Series in the Tasks of Forecasting and Diagnostics
Abstract
1. Introduction
- Collection and conversion of existing accumulated data (a priori data) into a form appropriate for analyzing the history of objects from the current subject area.
- Purposeful preservation of the dynamics of changes in the state of the studied objects.
- Length of the series. The length of the series is usually described as the number of observations of the parameter. Sometimes the length of the series may also mean the time elapsed from the initial to the final observation [4]. Kendel writes in [4] that in contrast with statistics in time series analysis the amount of information is not proportional to the number of sample members, because “… sequential quantities are not independent.”
- Discreteness and continuity. Discreteness and continuity is determined by the nature of the changes in time during which the observation is made. Discrete time series can be obtained from continuous time series in two ways [3]:
- With sampling of values from continuous time series at a specific interval;
- With the accumulation of values over a period of time.
- Determinacy. The time series is called deterministic when the future values of the time series are determined by any mathematical function. The time series is called non-deterministic, random or stochastic, if future values are described only by the probability distribution. The stochastic time series can be stationary or non-stationary. A time series is called stationary if its properties are independent of the start point of the time. In particular, it has [3]:
- Constant expected value (the average value with relation to which it varies),
- Constant variance that defines the range of its oscillations relative to the average value,
- Constant autocovariance coefficients,
- Constant autocorrelation coefficients.
The dispersion of any set of observations should not change when the observation time is shifted by any integer value for a strictly stationary discrete time series [3]. - Moment and Interval. An interval time series is a sequence in which the level of a phenomenon is related to a result accumulated over a specified time interval. The collectivity of levels produces a moment time series if the level of a series characterizes the phenomenon under study at a particular moment in time. An important difference between the moment time series and the interval time series is that the sum of the levels of the interval time series gives the total value for the interval as the real indicator [4].
- Completeness. In complete time series, the dates of registration or the end of periods follow one after another at equal intervals. In incomplete time series, the principle of equal intervals is not respected [4].
- Prediction of future values of a time series by its current and past values.
- Determination of the transfer function of the system.
- Design of simple control schemes with the direct and reverse connection.
- The construction of a mathematical system that describes the behavior of a time series in a compressed form.
- To explain the behavior of a time series using other variables as a hypothesis.
- The analysis results obtained in 1 or 2 can be used to predict the behavior of a time series.
- In the case of 2, it is possible to control the system by generating signals of upcoming changes or by investigating what might happen if some of the model parameters are changed.
- Analysis of joint development over time of several variables.
- The construction of a formalized representation of the modeled system with the definition of its significant parameters (determination of the nature of the time series).
- Prediction of future values of the time series, i.e., determination of the type of transfer function.
- Modeling and analysis of processes characterized by a high degree of uncertainty (including “non-stochastic”).
- Revealing hidden patterns and extracting new knowledge from time series.
2. Time Series Models
2.1. Time Series Exponential Smoothing Models
2.2. Fuzzy Time Series Models
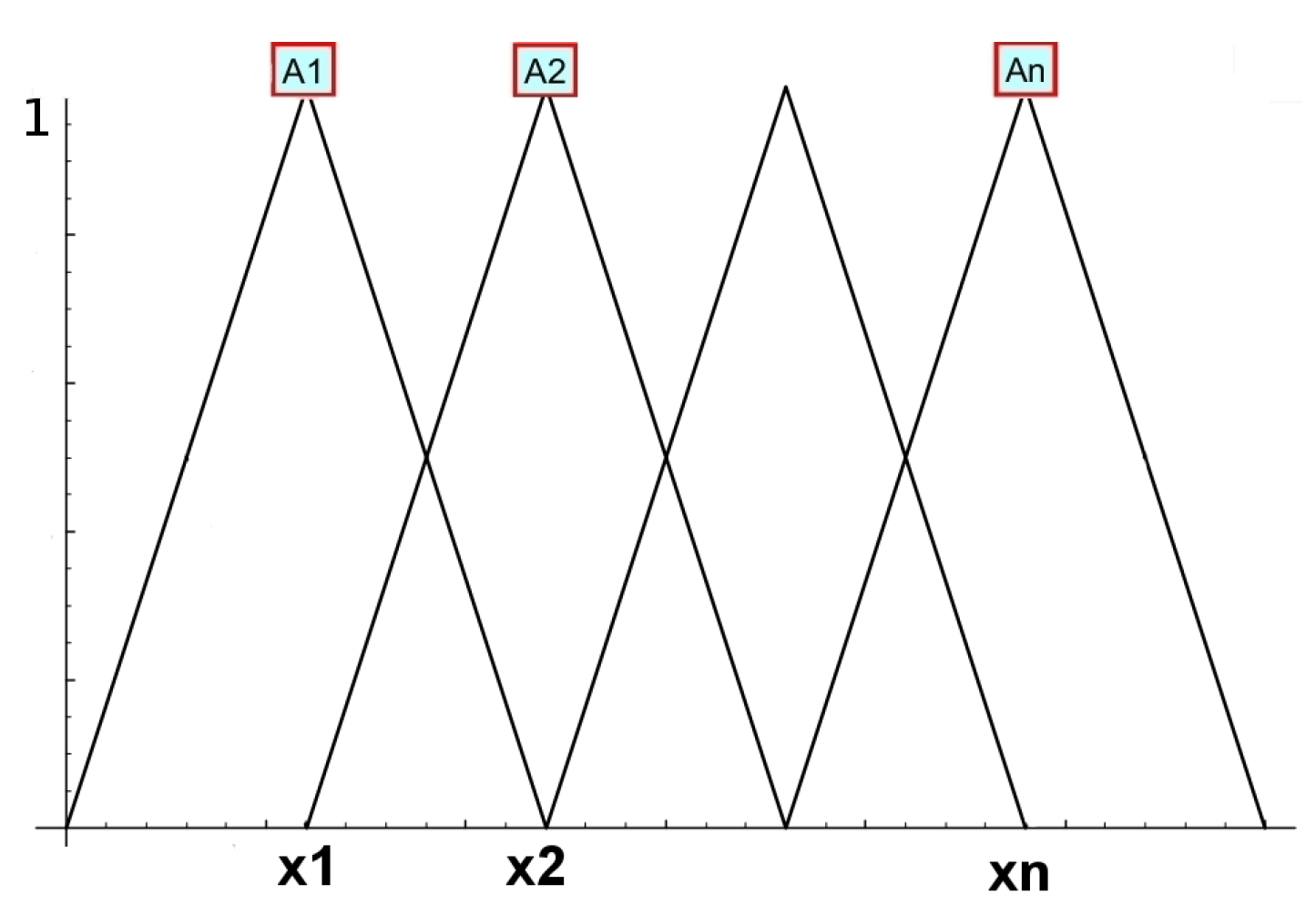
- Definition of the set of linguistic terms that specify the properties of the observed numerical characteristic.
- A partition of a set of real numbers on which a numerical characteristic is defined into subsets that characterize properties.
- Comparison of the linguistic term (word of the natural language) of semantics expressed by the membership function.
- Definition of accessories of time series values to linguistic terms.
- Modeling dependencies in the form of fuzzy implications and their implementation based on the fuzzy inference algorithm [7].
- A set of fuzzy production rules (rule base).
- A set of membership functions for the base of the fuzzy variable.
- Defuzzification block.
- Inference block.
- Set time series values: .
- Define a universal set , parameters and a set of membership functions of fuzzy sets defined on this universal set .
- Selects the representation of fuzzy objects of the time series for modeling.
- Evaluation of fuzzy objects in a time series.
- Decomposition of a time series.
- Postulate the fuzzy model class.
- Identification of a model of a systematic component of a time series (trend).
- Identification of a model of an irregular component of a time series.
- Analysis of the adequacy of the model.
- Application for forecasting and research of results.
2.2.1. Modeling of Fuzzy Tendencies
2.2.2. Integration of Fuzzy Modeling and Exponential Smoothing
- Step 1.
- The universum for the values of the time series is determined and the intervals for the fuzzy partition are set. The universum can usually be defined as , where , and the minimum and maximum values of the time series, respectively, and and are two positive integers set by an expert in the subject area. An interval is determined after the length of the partition, the universe can be divided into parts of equal length.
- Step 2.
- Fuzzy sets are determined based on the universe and historical data of the time series.
- Step 3.
- The fuzzification of historical data is performed. For example, the value of a time series belongs to a fuzzy set if the maximum degree of membership of this value belongs to a fuzzy set .
- Step 4.
- Establishment of logical relations and their grouping according to the current states of fuzzy data.
- Step 5.
- Building the forecast. Let
- Option 1: There is only one fuzzy logical relation. If then is equal to .
- Option 2: If , then is equal to .
- Step 6.
- Defuzzification. The centroid method is applied to obtain numerical results.
- Without a trend and seasonality:It is understood here that the fuzzification operation replaces smoothing.
- Without a trend with an additive seasonal component of the period p:.
- Additive trend without seasonal component:.
- Additive trend with additive seasonal component of the period p:.
2.2.3. Fuzzy Time Series Smoothing Models
- For each , if ;
- For each , is continuous on ;
- .
- The mapping such that is linear.
- If , then the components of the F-transform of the function f are equal; in addition, .
- Components F-transforms minimize the following functionwhich can be considered as weighted standard deviation criterion.
2.3. Combinations and Collectives of Time Series Models
2.3.1. The Combination of Models Based on the Information Criterion
2.3.2. The Combination of Models with Fuzzy Weights Based on the Information Criterion
2.4. Fuzzy Time Series Models of Higher Orders
A Time Series Model Based on Fuzzy Sets of Type 2
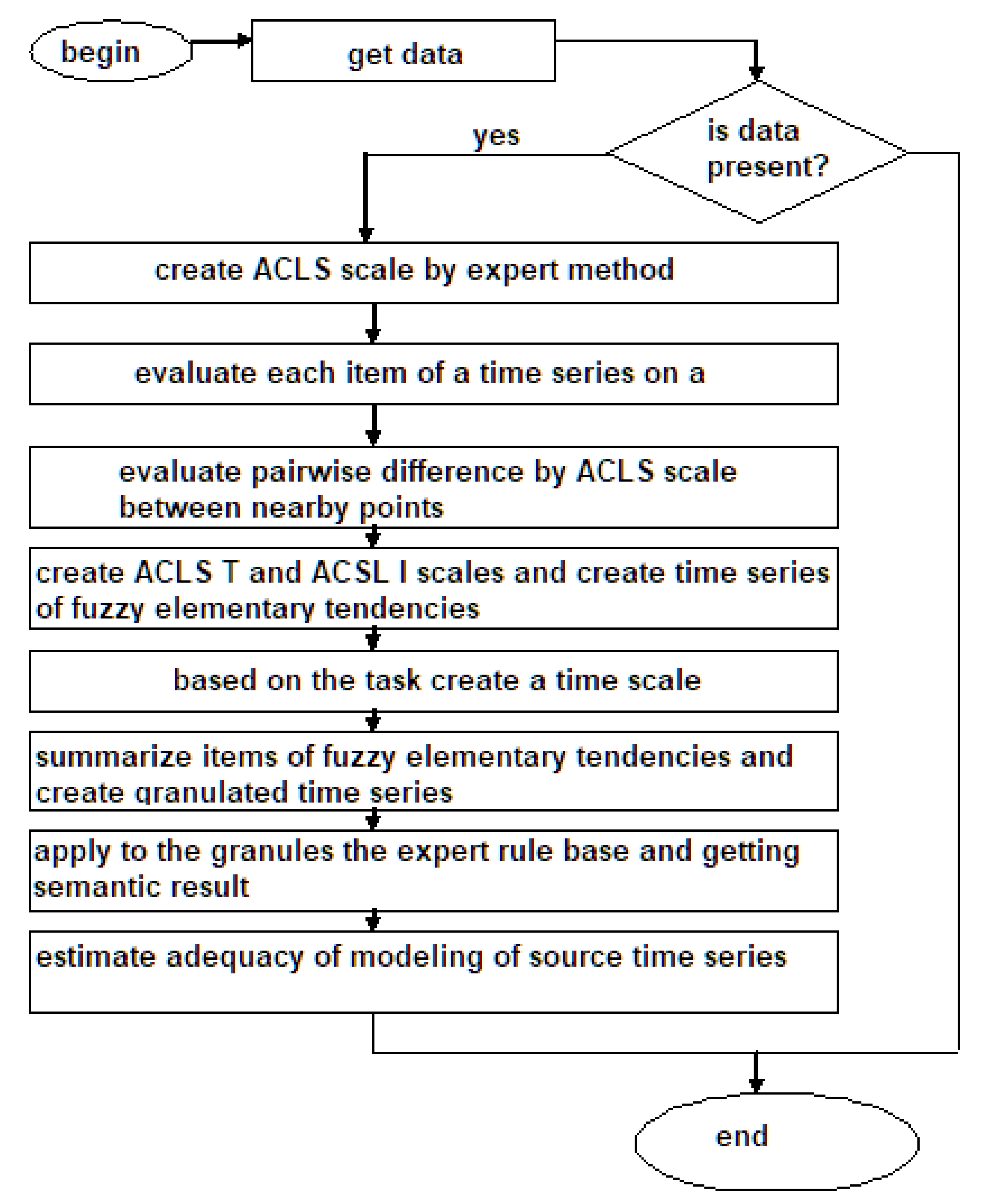
2.5. Algorithm for Smoothing and Forecasting of Time Series
- Determination of the universe of observations. , where and are minimal and maximal values of a time series respectively.
- Definition of membership functions for a time series , where l is the number of membership functions of fuzzy sets; n is the length of a time series. The number of membership functions and, accordingly, the number of fuzzy sets is chosen relatively small. The motivation for this solution is the multi-level approach to modeling a time series. It is advantageous to reduce the number of fuzzy sets at each level to decrease the dimension of the set of relations. Obviously, this approach will decrease the quality of approximation of a time series. However, creating the set of membership functions at the second and higher levels will increase the approximation accuracy with an increase in the number of levels.
- Definition of fuzzy sets for a series. In that case, the superscript defines the type of fuzzy sets. , where l is the number of type 1 fuzzy sets, m is the number of type 2 fuzzy sets.
- Fuzzification of a time series by type 1 sets.
- Fuzzification a time series by type 2 sets.
- Creation of relations. The rules for the creation of relations are represented in the form of pairs of fuzzy sets in terms of antecedents and consequents, for example: .
- Doing forecasting for the first and second levels based on a set of rules. The forecast is calculated by the centroid method, first on type 1 fuzzy sets , then on type 2 fuzzy sets.
- Evaluation of forecasting errors.
3. Applied Problems of Time Series Modeling
3.1. Problems Statement of Applied Time Series Modeling
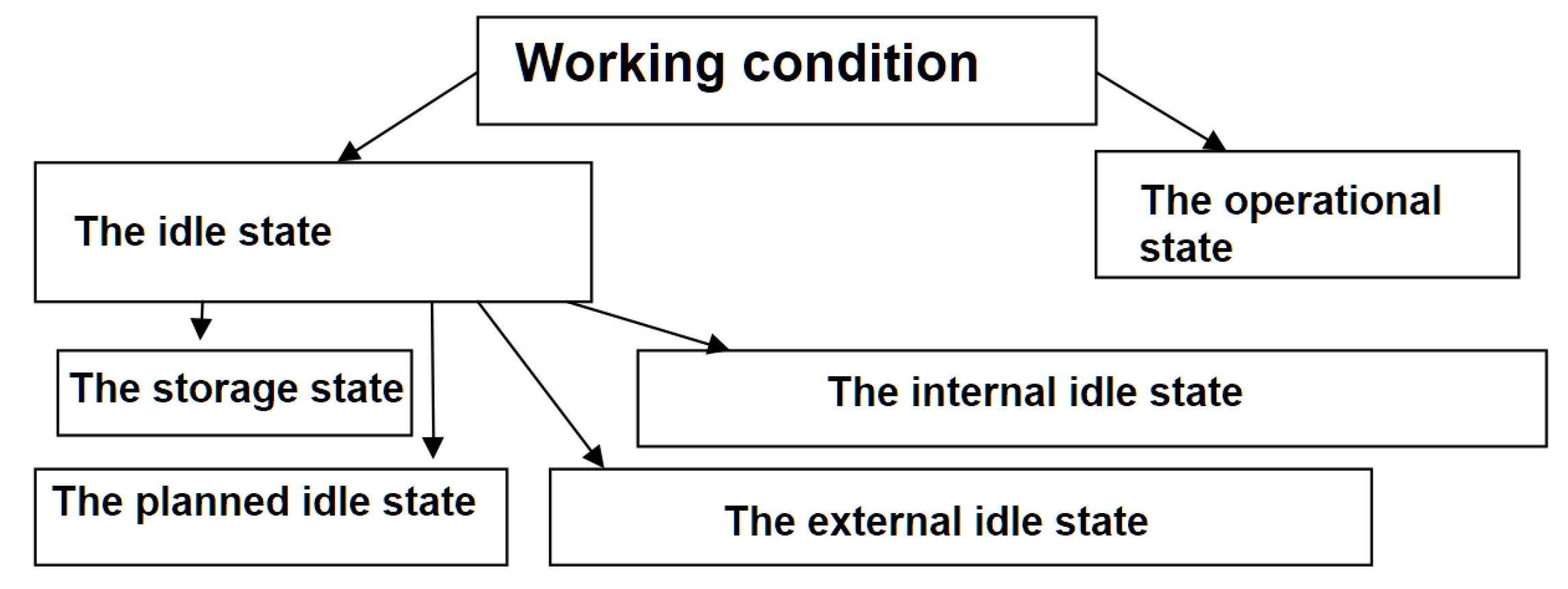
3.2. Diagnostics of the Technical System
- The storage state;
- The planned idle state;
- The internal idle state (the failure or incompleteness of the scheduled maintenance);
- The external idle state (different organizational reasons).
- Failures as a result of defects in design, operational documentation, production technology;
- Failures as a result of the dispersion of units characteristics within the established permissible values, or as a random adverse combination of operating modes.
- For reasons of occurrence of failures:
- Design failures. Design failures arise due to errors in the design of the product, inaccurate consideration of the actual operating conditions of the product, etc.;
- Production failures. Production failures arise due to deviations in the technological process of the product, improperly organized metrological support of production processes, etc.;
- Operational failures. Operational failures usually occur due to violation of the conditions of the established operating modes of products.
- By the nature of the change in the quality indicator of the helicopter [6]:
- Sudden failures. Sudden failures characterized by a sudden change in one or more properties of the helicopter;
- Gradual failures. Gradual failures are characterized by a gradual (slow) change in the values of one or more parameters of the helicopter. The causes of gradual failures of helicopter include:
- −
- The aging process of structural elements as a gradual change in the properties of materials over time;
- −
- Helicopter wear. Wear is a process of gradual change of material during friction. Wear occurs when the material particles are separated from the interaction surface of the material with their subsequent permanent deformation.
- −
- Fatigue process of structural elements. Fatigue of elements is the process of the gradual accumulation of material damage under the influence of alternating mechanical stresses. Fatigue of elements can be thermal and mechanical.
- By the nature of the stability of a failure state:
- Persistent failures;
- Glitches;
- Intermittent failures.
- By the possibility of following use of the helicopter:
- Complete failures—loss of all product features;
- Partial failures—when the product can still perform some functions declared in the functional specification.
- By the presence of external manifestations of failure:
- Overt failure;
- Hidden failure.
- By possibility and advisability of the failure elimination:
- Removable failures;
- Fatal failures.
- By mutual dependence from each other failures are divided into:
- Independent failures have their reasons for occurrence;
- Dependent failures due to failure of another unit.
- By the degree of impact on flight safety:
- Catastrophic failures;
- Emergency failures;
- Failures leading to a difficult situation;
- Failures that complicate the conditions for further flight.
- By the nature of detection using information-measuring control:
- Controlled failure;
- Uncontrolled failure.
- Main gearbox;
- Engine power plant.
- Destruction or wear of parts and components of a free turbine;
- Non-localized engine destruction;
- Starter failure;
- Engine shutdown;
- Destruction or wear of parts and units of a turbocharger;
- Destruction of the engine oil unit.
- “Low”: (0.25, 0.5, 1.9);
- “Medium”: (1.6, 2.5, 3.45);
- “High”: (3.06, 4, 5);
- “Recession”: (minZ-1, minZ, −0.45), where minZ is the minimum value of the difference obtained on the analyzed series;
- “Stability”: (−0.5, 0, 0.5);
- “Growth”: (0.45, maxZ, maxZ+1), where maxZ is the maximum value of the difference obtained on the analyzed series.
- “Short”: ();
- “Average”: ();
- “Long”: ().
- Getting information about the values of key physical indicators.
- Formation of a time series for each of these indicators.
- Formation of a granular time series.
- Evaluation of the state of the helicopter. A condition is considered correct if none of the values fell into a dangerous situation.
- If the work is recognized as not correct for less than 20% of the values, then repeated testing is necessary. Otherwise, it is necessary to conduct a technical inspection of the problem unit.
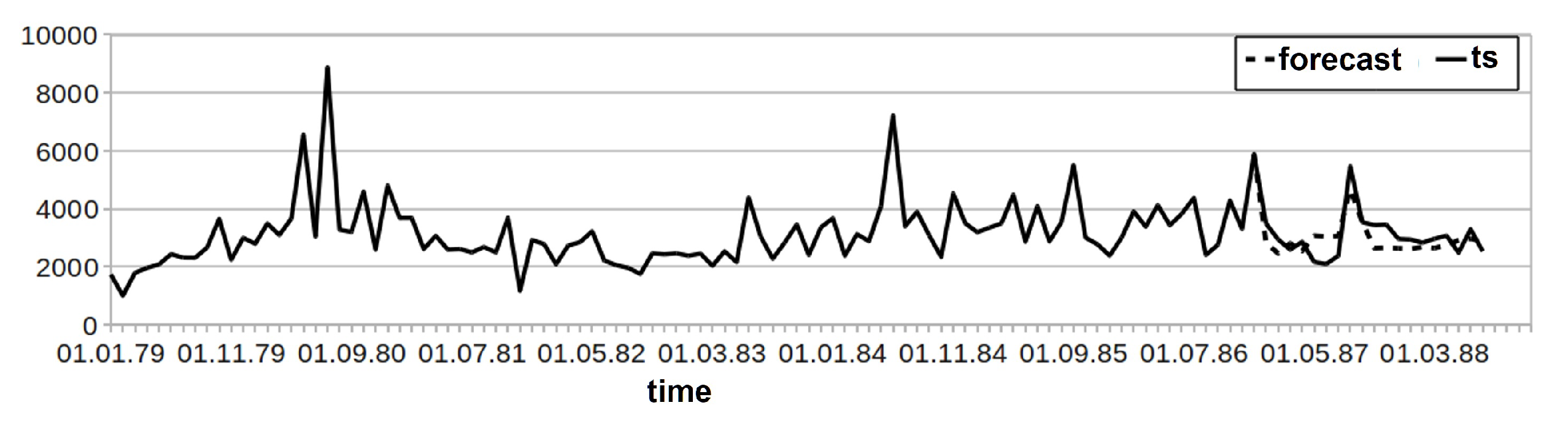
3.3. Forecasting Technical Time Series
- To detect errors not detected at the testing stages;
- To detect unauthorized access to resources from individual users;
- To optimize network configuration;
- To balance the load between its resources;
- To provide network development planning.
3.4. Forecasting Economic Time Series
- “Very Short”: (0, 3, 5);
- “Short”: (4, 6, 8);
- “Continuous”: (7, 9, 11);
- “Long”: (10, 12, 14);
- “Very Long”: (13, 15, 27).
- For current ratio:
- “If long-term growth is observed, then the favorable situation at the enterprise”;
- “If a long or medium decline is observed, then the unfavorable situation at the enterprise”;
- “If a short intense decline is observed, then the company needs to be more careful about its cash and assets”.
- For quick ratio:
- “If there is continued growth, then the favorable situation at the enterprise”.
- For the coefficient of financial independence:
- “If long-term growth is observed, then the favorable situation at the enterprise”;
- “If a long or medium decline is observed, then the unfavorable situation at the enterprise”.
- For the coefficient of financial independence in terms of working capital:
- “If long-term growth is observed, then the favorable situation at the enterprise”;
- “If a long or medium decline is observed, then the unfavorable situation at the enterprise”.
- For the financial independence ratio in terms of stocks:
- “If long-term growth is observed, then the favorable situation at the enterprise”;
- “If a long or medium decline is observed, then the unfavorable situation at the enterprise”.
- For the coefficient of attraction (ratio of own and borrowed funds):
- “If long-term growth is observed, then the favorable situation at the enterprise”;
- “If a long or medium decline is observed, then the unfavorable situation at the enterprise”.
4. Experiemts
4.1. Characterization of the Service for Technical Series Modeling
4.2. Characterization the Database for Economic Time Series Modeling
4.3. Technical Series Experiment Results
4.4. The Results of Experiments with Economic Time Series
4.5. Benchmarking Efficiency
- Trend forecasting method: neural network with absolute values;
- The degree of autoregressive by trend points: 3;
- Number of points covered by the basis function: 11.
- Trend forecasting method: neural network with absolute and relative values;
- The level of autoregressive by trend points: 1;
- The number of points covered by the basis function: 9.
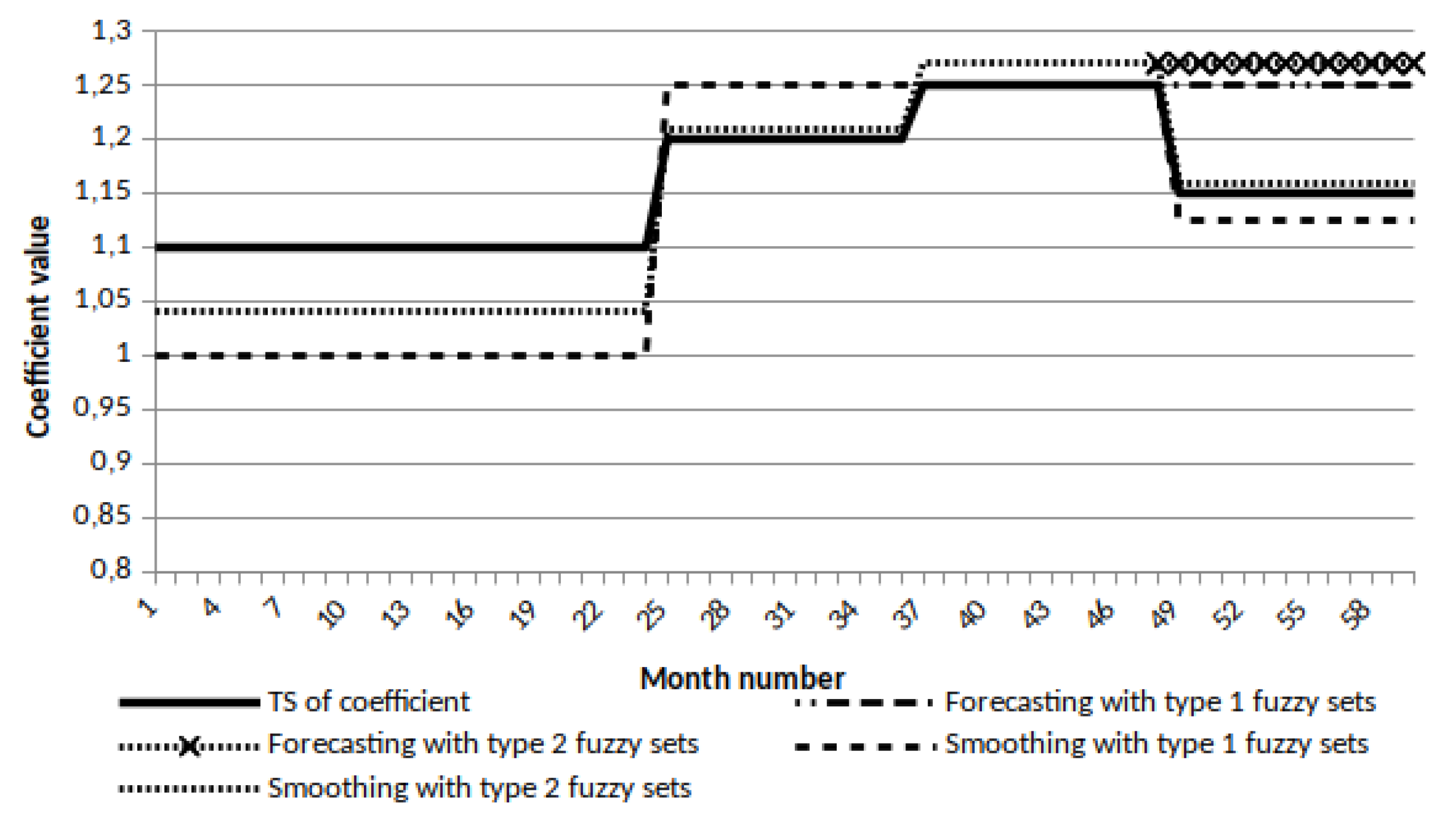
4.6. Analyzing Time Series of Economic Indicators
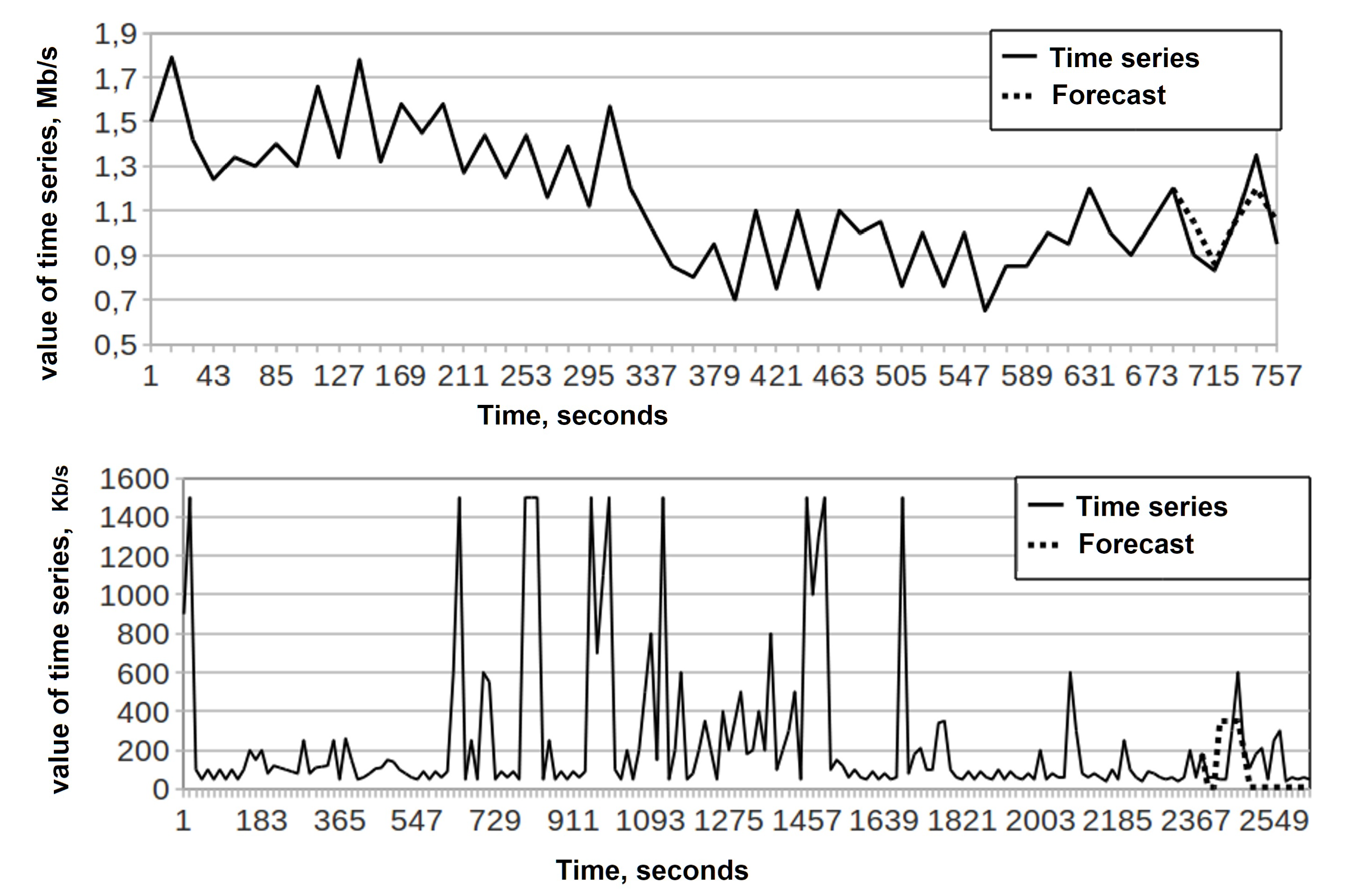
4.7. Analyzing Time Series of Computer Network Traffic
- Fuzzy models of the proposed structural-linguistic approach demonstrate a stable advantage to the compared basic fuzzy model and one neural network model. This is confirmed by the fact that models of fuzzy trends:
- (a)
- Are adequate in solving all problems (100%);
- (b)
- Surpasses the fuzzy model in the accuracy of forecasting the values of the time series in all problems (100%) and on average more than 2.5 times;
- (c)
- Is superior or not inferior to the fuzzy model in the accuracy of predicting fuzzy trends in the time series in all tasks (100%);
- (d)
- Surpass neural network models in 80% of tasks in the accuracy of forecasting the values of the time series and on average more than three times;
- (e)
- More than two times the accuracy of predicting fuzzy trends in the time series;
- (f)
- Is inferior in 20% (in three tasks) in the accuracy of forecasting the values of the time series by 1.3 times in neural network models.
- Neural network models are inadequate in solving one problem (in 6%).
- The fuzzy model in 94% of tasks is inadequate (in 14 out of 15 tasks), significantly inferior in the accuracy of forecasting the values and trends of the time series to the author’s models of fuzzy trends (more than 10 and six times, respectively).
- The fuzzy model in 47% of the tasks is inadequate (in seven out of 15 tasks), significantly inferior in the accuracy of forecasting the values and trends of the time series to the author’s models of fuzzy trends (more than 2.5 and five times, respectively).
- For short time series (25 and 55 values) the accuracy of forecasting the values of the time series according to the SMAPE criterion is acceptable and stable (from 2.5% to 6.6% and from 8.7% to 15%, respectively);
- For a smooth long time series prediction accuracy of time series values according to the SMAPE criterion is low, while it is 3 times higher for the forecast horizon from 2% to 10% and 1.4 times lower for the forecast horizon of 20% compared with the undeveloped time series.
- As the length of the time series increases, the accuracy of predicting the values of the time series decreases on average, and the error increases.
4.8. Smoothing and Predicting Time Series Based on Type 2 Fuzzy Sets
4.8.1. Time Series Smoothing
- for F-transform—2.01%,
- for model with type 2 fuzzy sets—0.65%.
- For F-transform—47.54%,
- For model with type 2 fuzzy sets—13.23%.
4.8.2. Time Series Approximation
- Fuzzification of the time series by type 1 and type 2 fuzzy sets.
- The number of fuzzy sets of each type is 3.
- The shape of fuzzy sets is isosceles triangles.
- For type 1 fuzzy sets the SMAPE is 5.06%.
- For type 2 fuzzy sets the SMAPE is 2.82%.
- For type 1 fuzzy sets the SMAPE is 18.61%.
- For type 2 fuzzy sets the SMAPE is 9.66%.
- The quality of the approximation is depended on the number of fuzzy sets. The experiment has shown that the small number of fuzzy sets possible to achieve a high approximation quality.
- The boundaries of the fuzzy sets is also important. The approximation result has a low quality at the initial segments for both time series presented in the experiment. The problem of choosing the boundaries of intervals of fuzzy sets remains relevant.
4.8.3. Time Series Forecasting
- The forecast made for the test interval that contains 10 points.
- The forecast is made based on both type 1 and type 2 fuzzy sets.
- For type 1 fuzzy sets the SMAPE is 7.69%.
- For type 2 fuzzy sets the SMAPE is 9.27%.
- For type 1 fuzzy sets the SMAPE is 39.41%.
- For type 1 fuzzy sets the SMAPE is 27.91%.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alalwan, J.; Thomas, M.; Weistroffer, H. Decision Support Capabilities of Enterprise Content Management Systems: An Empirical Investigation. Decis. Support Syst. 2014, 68, 39–48. [Google Scholar] [CrossRef]
- Anderson, T.W. The Statistical Analysis of Time Series; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis. Forecasting and Control; Series in Time Series Analysis; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Kendall, M. Time Series; Finansy I Statistica: Moscow, Russia, 1981. (In Russian) [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; Wiley Series in Probability and Statistics; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Yarushkina, N.G.; Voronina, V.V.; Egov, E.N. Application of entropy measures in the diagnosis of technical time series. Autom. Control. Process. 2015, 2, 55–63. (In Russian) [Google Scholar]
- Afanasieva, T.V.; Namestnikov, A.M.; Perfilieva, I.G.; Romanov, A.A.; Yarushkina, N.G. Time Series Forecasting: Fuzzy Models; Ulyanovsk State Technical University: Ulyanovsk, Russia, 2014; Volume 145. (In Russian) [Google Scholar]
- McCormick, G.P. Communications to the Editor—Exponential Forecasting: Some New Variations. Manag. Sci. 1969, 15, 311–320. [Google Scholar] [CrossRef]
- Makridakis, S.; Hibon, M. The M3-Competition: Results, Conclusions and Implications. Int. J. Forecast. 2000, 16, 451–476. [Google Scholar] [CrossRef]
- Small, G.; Wong, R. The Validity of Forecasting. In Proceedings of the Pacific Rim Real Estate Society International Conference, Christchurch, New Zealand, 21–23 January 2002; 2002 PRRESS. pp. 1–14. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Novák, V. Mining information from time series in the form of sentences of natural language. Int. J. Approx. Reason. 2016, 78, 192–209. [Google Scholar] [CrossRef]
- Zadeh, L. A theory of approximate reasoning. Mach. Intell. 1979, 9, 149–194. [Google Scholar]
- Yarushkina, N.G.; Afanasyeva, T.V.I.G. Perfilieva Intellectual Analysis of Time Series; Ulyanovsk State Technical University: Ulyanovsk, Russia, 2010; 320p. (In Russian) [Google Scholar]
- Yarushkina, N.; Afanaseva, T.V. Fuzzy Modeling and Trend Analysis of Time Series; Intelligent Control Systems: Ulyanovsk, Russia, 2010; pp. 301–305. (In Russian) [Google Scholar]
- Yarushkina, N.G.; Perfilieva, I.G. Tatyana Vasilievna Afanasyeva Integral method of fuzzy modeling and analysis of fuzzy trends. Autom. Control. Process. 2010, 2, 59–63. (In Russian) [Google Scholar]
- Yarushkina, N.G.; Afanasyeva, T.V. Fuzzy time series as a tool for assessing and measuring the dynamics of processes. Sensors Syst. 2007, 12, 46–50. (In Russian) [Google Scholar]
- Wang, D.; Pedrycz, W.; Li, Z. A Two-Phase Development of Fuzzy Rule-Based Model and Their Analysis. IEEE Access 2019, 7, 80328–80341. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Jiang, A.; Mei, C.; E, J.; Shi, Z. Nonlinear combined forecasting model based on fuzzy adaptive variable weight and its application. J. Cent. South Univ. Technol. 2010, 17, 863–867. [Google Scholar] [CrossRef]
- Ge, P.F.; Wang, J.; Ren, P.; Gao, H.; Luo, Y. A New Improved Forecasting Method Integrated Fuzzy Time Series With The Exponential Smoothing Method. Int. J. Environ. Pollut. 2013, 51, 206–221. [Google Scholar] [CrossRef]
- Huarng, K. Effective lengths of intervals to improve forecasting in fuzzy time series. Fuzzy Sets Syst. 2001, 123, 387–394. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy Transform: Application to the Reef Growth Problem. Fuzzy Log. Geol. 2004, 275–300. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Perfilieva, I.G.; Yarushkina, N.G.; Afanasieva, T.V. Time series analysis by discrete F-transform. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; pp. 1–4. [Google Scholar]
- Vovk, V.G. Universal forecasting algorithms. Inf. Comput. 1992, 96, 245–277. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. Combination forecasts of output growth in a seven-country data set. J. Forecast. 2004, 23, 405–430. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. (Methodological) 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Kolassa, S. Combining exponential smoothing forecasts using Akaike weights. Int. J. Forecast. 2011, 27, 238–251. [Google Scholar] [CrossRef]
- Bajestani, N.S.; Zare, A. Forecasting TAIEX using improved type 2 fuzzy time series. Expert Syst. Appl. 2011, 38, 5816–5821. [Google Scholar] [CrossRef]
- Perfilieva, I.; Yarushkina, N.; Afanasieva, T.; Romanov, A. Time series analysis using soft computing methods. Int. J. Gen. Syst. 2013, 42, 687–705. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Voronina, V. Mathematical Modeling of Diagnostic Parameters of Aircraft on the basis of Granulated Time Series; Ulyanovsk State Technical University: Ulyanovsk, Russia, 2011. [Google Scholar]
- Afanasyeva, T.V. Modeling Fuzzy Trends in Time Series; UlSTU: Ulyanovsk, Russia, 2013. [Google Scholar]
- Voronina, V.V.; Timina, I.A. Development of an analysis module for multidimensional time series for a system for assessing the financial condition of an enterprise. In Proceedings of the 1st All-Russian Scientific-Practical Conference “Applied Information Systems”, Ulyanovsk, Russia, 26–30 May 2014; pp. 4–10. (In Russian). [Google Scholar]
- Shishkina, V.V. Estimation and forecasting of the financial condition of an enterprise based on time series of fuzzy elementary trends. Acad. J. Izvestia Samara Sci. Cent. Russ. Acad. Sci. 2010, 12, 498–505. (In Russian) [Google Scholar]
- Afanasyeva, T.V. Methodology, Models and Complexes of Programs for Analyzing Time Series Based On Fuzzy Trends; Ulyanovsk State Technical University: Ulyanovsk, Russia, 2012. (In Russian) [Google Scholar]
- CIF—Computational Intelligence in Forecasting. Available online: Https://irafm.osu.cz/cif/main.php (accessed on 29 March 2020).








| Physical Indicator | Main Gearbox | Power Plant |
|---|---|---|
| Engine torque, degree | 0–128 | |
| Engine exhaust temperature, °C | 0–1000 | |
| Engine oil temperature, °C | −50–200 | |
| Engine oil pressure, kgf/cm | 0–8 | |
| Main gearbox oil temperature, °C | −50–150 | |
| Gearbox oil pressure, kgf/cm | 0–8 |
| Physical Indicator | Range Boundaries | Dang. Low | Low | Normal | High | Dang. High |
|---|---|---|---|---|---|---|
| Engine torque, | 0–128 | a < 0 | a = 65 | a = 88.5 | ||
| degree | b = 60 | b = 75 | b = 90 | |||
| c = 65.5 | c = 88.6 | c > 128 | ||||
| Engine exhaust | 0–1000 | a,b < 0 | a = 600 | a = 720 | ||
| temperature, °C | c = 560 | b = 700 | b = 800 | |||
| d = 600.5 | c = 720.5 | c > 1000 | ||||
| Engine oil | −50–200 | a < −60 | a = −39.9 | a = −4.9 | a = 110 | a = 120 |
| temperature, °C | b = −50 | b = −30 | b = 80 | b = 115 | b = 150 | |
| c = −40 | c = −5 | c = 110.1 | c = 120.1 | c > 200 | ||
| Engine oil | 0–8 | a < 0 | a = 1.99 | a = 2.45 | a = 4 | a = 4.5 |
| pressure, kgf/cm | b = 1 | b = 2.2 | b = 3 | b = 4.2 | b = 5 | |
| c = 2 | c = 2.5 | c = 4.05 | c = 4.55 | c > 8 | ||
| Main gearbox | −50–150 | a < −60 | a = −39.9 | a = −14.9 | a = 70 | a = 90 |
| oil temperature, °C | b = −50 | b = −30 | b = 60 | b = 80 | b = 100 | |
| c = −40 | c = −15 | c = 70.1 | c = 90.1 | c > 150 | ||
| Gearbox oil | 0–8 | a < 0 | a = 1.99 | a = 3.45 | a = 4.55 | a = 7.5 |
| pressure, kgf/cm | b = 1 | b = 2.2 | b = 4 | b = 5 | b = 7.8 | |
| c = 2 | c = 3.5 | c = 4.55 | c = 7.55 | c > 8 |
| Indicator Name |
|---|
| Current ratio |
| Product profitability |
| Working capital turnover ratio |
| Financial independence ratio |
| General solvency rate |
| Debt to equity ratio (attraction ratio) |
| Maneuverability ratio of own circulating assets |
| Row Number | Board Number | Run Time, Seconds | Defect in the Engine | Defect in the Main Gearbox |
|---|---|---|---|---|
| 1 | 210111 | 3614 | No | No |
| 2 | 240111 | 4199 | No | No |
| 3 | 250111 | 1061 | No | No |
| 4 | 000 | 3614 | Yes | No |
| 5 | 000 | 4199 | No | Yes |
| 6 | 000 | 1061 | Yes | Yes |
| 7 | 000 | 3614 | Yes | No |
| 8 | 000 | 4199 | No | Yes |
| 9 | 000 | 1061 | Yes | Yes |
| 10 | 000 | 3614 | Yes | No |
| 11 | 000 | 4199 | No | Yes |
| 12 | 000 | 1061 | Yes | Yes |
| Series Number | Codename for a Series | Number of Points | Interpretation | Character | Origin |
|---|---|---|---|---|---|
| in the Database | |||||
| 1 | 2–6_F | 14 | Long | - | Real |
| 2 | 2–8_F | 22 | Long | - | Real |
| 3 | 2–9_F | 15 | Long | - | Real |
| 4 | 2–10_F | 46 | Long | Stationary | Artificial |
| 5 | 2–11_F | 29 | Long | Stationary | Artificial |
| 6 | 2–12_F | 51 | Long | Growth with noise | Artificial |
| 7 | 3–15_F | 7 | Short | - | Real |
| 8 | 3–16_F | 8 | Short | - | Real |
| 9 | 3–17_F | 7 | Short | - | Real |
| 10 | 3–24_F | 7 | Short | - | Real |
| 11 | 3–25_F | 7 | Short | - | Real |
| Row Number | Board Number | Run Time, | Engine Defect | Defect in the | Conclusion of |
|---|---|---|---|---|---|
| Seconds | Main Gear | the System | |||
| 1 | 210111 | 3614 | No | No | Norm |
| 2 | 240111 | 4199 | No | No | Norm |
| 3 | 250111 | 1061 | No | No | Norm |
| 4 | 000 | 3614 | Yes | No | Possibly dangerous |
| 5 | 000 | 4199 | No | Yes | Possibly dangerous |
| 6 | 000 | 1061 | Yes | Yes | Dangerously |
| 7 | 000 | 3614 | Yes | No | Possibly dangerous |
| 8 | 000 | 4199 | Yes | Yes | Dangerously |
| 9 | 000 | 1061 | No | Yes | Possibly dangerous |
| 10 | 000 | 3614 | Yes | No | Possibly dangerous |
| 11 | 000 | 4199 | No | Yes | Possibly dangerous |
| 12 | 000 | 1061 | Yes | Yes | Dangerously |
| Coded Time Series | Time Series | FT SMAPE, | F-Transform SMAPE, | Comparison of |
|---|---|---|---|---|
| Name in DB | Length | % | % | SMAPE,% |
| 2-6_F | Long | 27.16 | 5.050 | 22.11 |
| 2-8_F | Long | 1.19 | 3.145 | −1.955 |
| 2-9_F | Long | 9.63 | 1.264 | 8.366 |
| 2-10_F | Long | 7.16345 × 10 | 4.155 | −4.15499 |
| 2-11_F | Long | 40.73 | 0.567 | 40.163 |
| 2-12_F | Long | 1.56 | 0.705 | 0.855 |
| 3-15_F | Short | 10.81 | 27.684 | −16.874 |
| 3-16_F | Short | 1.19 | 20.702 | −19.512 |
| 3-17_F | Short | 3.55 | 53.017 | −49.467 |
| 3-24_F | Short | 32.30 | 18.988 | 13.312 |
| 3-25_F | Short | 25.28 | 88.682 | −63.402 |
| Avg. SMAPE | 13.95 | 20.36 | −6.41 |
| Time Series | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Length | 14 | 15 | 46 | 51 | 13 | 7 | 7 | 7 | 7 | 7 |
| Average SMAPE,% | 12.7 | 0.9 | 17.4 | 1.1 | 6.7 | 27.6 | 2.6 | 3.5 | 1.3 | 14.7 |
| Exp. 1 | 18.64 | 4.7 | 17.41 | 1.12 | 9.74 | 27.62 | 6.61 | 0.004 | 1.3 | 1.7 |
| Exp. 2 | 3.04 | 0.007 | 17.41 | 1.12 | 4.66 | 27.62 | 0.007 | 5.9 | 1.3 | 1.7 |
| Exp. 3 | 20.11 | 4.7 | 17.41 | 1.12 | 4.66 | 27.62 | 6.61 | 0.004 | 1.3 | 34.24 |
| Exp. 4 | 18.64 | 4.7 | 17.41 | 1.12 | 4.66 | 27.62 | 0.007 | 5.9 | 1.3 | 1.7 |
| Exp. 5 | 3.04 | 4.7 | 17.41 | 1.12 | 9.74 | 27.62 | 0.007 | 5.9 | 1.3 | 34.24 |
| Time Series No. | Smape Time Series Forecast For Test Part | ||||
|---|---|---|---|---|---|
| Proposed Method | 33 Phienthrakul, Kijsirikul 25.69% | 35 Pucheta, Patino, Kuchen 27.39% | 44 Kuremoto, Obayashi, Kobayashi 38.45% | Statistica | |
| 102 | 18.88 | 35.28 | 18.61 | 41.9 | 5.52 |
| 104 | 23.25 | 39.09 | 22.909 | 107.4 | 7.62 |
| 108 | 15.008 | 23.34 | 106.4 | 11.13 | |
| Average | Models of ForecastPro | Proposed Model of Fuzzy Tendencies | Fuzzy Model | Neural Network Model |
|---|---|---|---|---|
| SMAPE% | 83.1 | 45.9 | 103.8 | 63.5 |
| ARIMA Model | Proposed Model of Fuzzy Tendencies | Fuzzy Model | Neural Network Model | |
|---|---|---|---|---|
| Average by 65% TS | 25.35 | 6.16 | 16.3 | 16.2 |
| Average by 100% TS | - | 11.34 | 23.58 | 30.74 |
| TS (Interval) | Neural Network | Fuzzy Model | Fuzzy Tendency |
|---|---|---|---|
| Model (SMAPE,%) | (SMAPE,%) | Model (SMAPE,%) | |
| Port14 (5%) | 2.6 | 49.8 | 2.5 |
| Port14 (10%) | 9.8 | 12.7 | 6.6 |
| 14 (20%) | 9.8 | 30 | 4.17 |
| Port 1 _4 (2%) | 2.1 | 38 | 8.7 |
| Port 1_4 (5%) | 10 | 19.4 | 15 |
| Port 1_4 (10%) | 13 | 50.6 | 8.8 |
| Port 1_4 (20%) | 16 | 43.5 | 10.9 |
| F-load (2%) | 121 | 151 | 25.8 |
| F-load (5%) | 154 | 417 | 41 |
| F-load (10%) | 58.9 | 315 | 43 |
| F-load (20%) | 73 | 2677 | 87 |
| load (2%) | 625 | 3220 | 91.8 |
| load (5%) | 215 | 4121 | 147 |
| load (10%) | 362 | 5076 | 83.7 |
| load (20%) | 440 | 9204 | 62 |
| Average | 140.9 | 1695 | 42.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanov, A.; Voronina, V.; Guskov, G.; Moshkina, I.; Yarushkina, N. Discrete and Fuzzy Models of Time Series in the Tasks of Forecasting and Diagnostics. Axioms 2020, 9, 49. https://doi.org/10.3390/axioms9020049
Romanov A, Voronina V, Guskov G, Moshkina I, Yarushkina N. Discrete and Fuzzy Models of Time Series in the Tasks of Forecasting and Diagnostics. Axioms. 2020; 9(2):49. https://doi.org/10.3390/axioms9020049
Chicago/Turabian StyleRomanov, Anton, Valeria Voronina, Gleb Guskov, Irina Moshkina, and Nadezhda Yarushkina. 2020. "Discrete and Fuzzy Models of Time Series in the Tasks of Forecasting and Diagnostics" Axioms 9, no. 2: 49. https://doi.org/10.3390/axioms9020049
APA StyleRomanov, A., Voronina, V., Guskov, G., Moshkina, I., & Yarushkina, N. (2020). Discrete and Fuzzy Models of Time Series in the Tasks of Forecasting and Diagnostics. Axioms, 9(2), 49. https://doi.org/10.3390/axioms9020049





