Generalized Briot-Bouquet Differential Equation Based on New Differential Operator with Complex Connections

Abstract

A class of Briot–Bouquet differential equations is a magnificent part of investigating the geometric behaviors of analytic functions, using the subordination and superordination concepts. In this work, we aim to formulate a new differential operator with complex connections (coefficients) in the open unit disk and generalize a class of Briot–Bouquet differential equations (BBDEs). We study and generalize new classes of analytic functions based on the new differential operator. Consequently, we define a linear operator with applications.

1. Introduction

Inequalities in a complex domain play a massive role in function theory. They have been employed to introduce the geometric interpolation of analytic functions in the open unit disk. Moreover, they have been utilized to formulate generalized classes of analytic functions. Recently, Lupas [1] suggested a combination of two famous differential operators given by Ruscheweyh [2] and Sàlàgean [3] to present a set of inequalities and inclusions by using the concept of subordination.

In this study, we shall define a new differential operator of complex coefficients and study its behaviors based on the properties of the theory of geometric functions. The new operator will be formulated in generalized sub-classes of starlike functions. Subordination inequalities include the generalized operator, and some well-known functions are discussed. Sharp results are indicated in the sequel. As an application, we introduce a generalization of a class of Briot–Bouquet differential equations (BBDEs) in the complex domain. Consequently, examples are illustrated utilizing the time-space BBDEs. A comparison with recent works is shown in the sequel.

2. Differential Operators

The theory of special functions in one variable has a long and ironic past; the rising importance in special functions of several variables is moderately contemporary. Currently, there has been quick progress specifically in the area of special functions with the consideration of symmetries and harmonic analysis connected with root systems. The drive for this work comes from some generalizations of the theory of symmetric spaces, whose functions can be written as special functions depending on definite sets of parameters. A key implementation in the study of special functions with reflection symmetries is Dunkl operators, which are known as a class of differential-difference operators. In this effort, we present a Dunkl differential-difference operator of the first type in a complex domain, under a special class of analytic functions, called a class of normalized analytic functions. This class plays an important role in the field of geometric function theory. Based on this connection between the Dunkl operator and geometric function theory, we impose a major class of geometric presentations called the starlike class of analytic functions. A significant motivation to study Dunkl operators is created by their application in the analysis of quantum many-body systems of a special type. These operators describe integrated systems in one dimension and have seen considerable increased attention in mathematical physics, especially in conformal field theory (see [4,5] for recent works).

Let ⋀ be the class of the analytic functions taking the expansion:

$$⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{⋎}_n{\xi }^n,\xi \in \cup =\{\xi :|\xi |<1\}.$$

(1)

For a function $⋎\in \bigwedge ,$ the Ruscheweyh formulation of the derivative is given by the following expansion formula:

$$R^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{C}_{m+n-1}^m{⋎}_n{\xi }^n,$$

where the term $C_{m+n-1}^m$ is the combination of coefficients. Moreover, the Sàlàgean derivation expansion is defined by:

$$S^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{n}^m{⋎}_n{\xi }^n.$$

Consequently, Lupas combined the above operators to get a linear operator as follows [1]:

$$L_{\alpha }^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }[\alpha n^m+(1-\alpha )C_{m+n-1}^m]{⋎}_n{\xi }^n,\xi \in \cup ,\alpha \in [0,1].$$

Here, we introduce a differential operator taking the following expansion:

$$\begin{array}{cc}\hfill & D_{\lambda }^0⋎\left(\xi \right)=⋎\left(\xi \right)\hfill \\ \hfill & D_{\lambda }^1⋎\left(\xi \right)=\xi {⋎}^{\prime }\left(\xi \right)+\lambda \left(\left(⋎\left(\xi \right)-\xi \right)-\left(⋎(-\xi )+\xi )\right)\right),\lambda \in \mathbb{C}\hfill \\ \hfill & ⋮\hfill \\ \hfill & D_{\lambda }^m⋎\left(\xi \right)=D_{\lambda }(D_{\lambda }^{m-1}⋎\left(\xi \right))\hfill \\ \hfill & =\xi +\sum _{n=2}^{\infty }{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^n.\hfill \end{array}$$

(2)

For $\lambda =0,$ the operator reduces to the Sàlàgean differential operator. Moreover, the operator $D_{\lambda }^m$ imposes a modification of the Dunkl operator of the first type [6,7], where $\lambda$ is the Dunkl parameter, which indicates the balance between the differential and difference part in Equation (2). One of its applications is recognizing the harmonic and oscillation behaviors of the solution, and $⋎(-\xi )$ is the reflection of the function $⋎\left(\xi \right)$, which plays a significant role in the symmetry problem. Moreover, when $m=2$, the operator reduces to the generalized Dunkl-Coulomb operator [8].

Remark 1.

We note that the original Dunkl operator admits the formula (see [9]):

$$D⋎\left(\xi \right)={⋎}^{\prime }\left(\xi \right)+\frac{\lambda }{2}\left(⋎\left(\xi \right)-⋎(-\xi )\right),$$

which implies that $D⋎\left(\xi \right)\notin \bigwedge .$ Therefore, (2) is a modification that gives $D⋎\left(\xi \right)\in \bigwedge$ (the class of normalized functions in the geometric function theory).

We proceed with discussing the behavior of the term $\lambda (1+{(-1)}^{n+1})$. Obviously, when:

$$\lambda :=\frac{1}{1-e^{2i\pi }}=\underset{n\to \infty }{lim}\frac{1}{(1+{(-1)}^{n+1})},$$

we get the shifted Sàlàgean differential operator:

$$D^m⋎\left(\xi \right)=\xi +\sum _{n=2}^{\infty }{[n+1]}^m{⋎}_n{\xi }^n.$$

(3)

Furthermore, we have:

$$\underset{n\to \infty }{lim}(1+{(-1)}^{n+1})=1+e^{2i\pi },$$

which implies that for $\lambda :=\frac{1}{1+e^{2i\pi }},$ we get (3). The term $(1+{(-1)}^{n+1})$ plays an important role in the oscillation problem, which was discussed in [8] (see Figure 1):

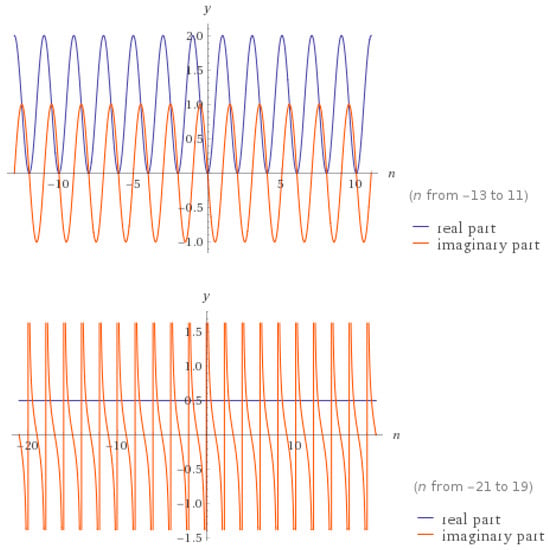
Figure 1. The first graph is $(1+{(-1)}^{n+1})$, and the second is $1/(1+{(-1)}^{n+1})$.

For functions ⋎ and ⋏ in ⋀, we say that ⋎ is subordinated to ⋏, denoted by $⋎\prec ⋏$, if there occurs a Schwarz function $\top \in \cup$ with $\top \left(0\right)=0$ and $|\top (\xi \left)\right|<1,\xi \in \cup$ so that $⋎\left(\xi \right)=⋏(\top (\xi \left)\right)$ for all $\xi \in \cup$ (see [10]). Basically, $⋎\left(\xi \right)\prec ⋏\left(\xi \right)$ is equivalent to $⋎\left(0\right)=⋏\left(0\right)$ and $⋎(\cup )\subset ⋏(\cup ).$

3. Briot–Bouquet Differential Equation

The investigation of the complex Briot–Bouquet differential equations (BBDEs) is the study of a special class of differential equations whose consequences are designed in a complex domain (such as the open unit disk). The chief formula of BBDE is:

$$\frac{\xi {(⋎\left(\xi \right))}^{\prime }}{⋎\left(\xi \right)}=\mathsf{\Lambda }\left(\xi \right),⋎\in \bigwedge ,\xi \in \cup .$$

One can find different applications of these equations in dynamic and control systems (see [11,12,13]). The operator (2) can be used to generalize BBDE as follows:

$${\displaystyle \frac{\xi {(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}=\mathsf{\Lambda }\left(\xi \right),\xi \in \cup ,⋎\in \bigwedge ,$$

(4)

where $\mathsf{\Lambda }\left(\xi \right)$ is univalent convex in $\cup .$ Our aim is to study the upper outcome of (4) by using subordination inequalities.

Theorem 1.

Let $⋎\in \bigwedge$ and $\mathsf{\Lambda }\left(\xi \right)$ be univalent convex in ∪ fulfilling the subordination formula:

$${\displaystyle \frac{\xi {(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}\prec \mathsf{\Lambda }\left(\xi \right).$$

(5)

Then, the upper bound of the solution of (5) is:

$$D_{\lambda }^m⋎\left(\xi \right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right),$$

where $\mathsf{\Psi }\left(\xi \right)$ is analytic in $\cup ,$ with $\mathsf{\Psi }\left(0\right)=0$ and $\left|\mathsf{\Psi }\right(\xi \left)\right|<1$. In addition, for $\left|\xi \right|=\iota$, $D_{\lambda }^m⋎\left(\xi \right)$ achieves the inequality:

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(-\iota \left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{D_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right).$$

Proof. 

By the definition of the subordination, Inequality (5) satisfies that there exists a Schwarz function with $\mathsf{\Psi }\left(0\right)=0$ and $\left|\mathsf{\Psi }\right(\xi \left)\right|<1$ such that:

$${\displaystyle \frac{\xi {(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}=\mathsf{\Lambda }\left(\mathsf{\Psi }\left(\xi \right)\right),\xi \in \cup .$$

This leads to the equation:

$${\displaystyle \frac{{(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}-{\displaystyle \frac{1}{\xi }}={\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\xi \left)\right)-1}{\xi }}.$$

By integrating both sides, we obtain:

$$log{D}_{\lambda }^m⋎\left(\xi \right)-log\xi ={\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota .$$

A computation yields:

$$log\left({\displaystyle \frac{D_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right)={\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota ,$$

(6)

which is equivalent to the fact:

$$D_{\lambda }^m⋎\left(\xi \right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right).$$

Further, the function $\mathsf{\Lambda }$ designs the disk $0<\left|\xi \right|<\iota <1$ on a territory, which is symmetric convex, agreeing with the real axis, that is:

$$\mathsf{\Lambda }(-\iota |\xi \left|\right)\le \mathsf{\Re }\left(\mathsf{\Lambda }\right(\mathsf{\Psi }\left(\iota \xi \right)\left)\right)\le \mathsf{\Lambda }\left(\iota \right|\xi \left|\right),\iota \in (0,1);$$

thus, we attain the following inequalities:

$$\mathsf{\Lambda }(-\iota )\le \mathsf{\Lambda }(-\iota |\xi \left|\right),\mathsf{\Lambda }\left(\iota \right|\xi \left|\right)\le \mathsf{\Lambda }\left(\iota \right).$$

By employing the above inequalities, we obtain the integral inequalities:

$${\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \le \mathsf{\Re }\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right)\le {\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota ,$$

which leads to the next inequalities:

$${\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \le log\left|{\displaystyle \frac{D_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le {\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota ,$$

and:

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(-\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{D_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left|\xi \right|\left)\right)-1}{\iota }}d\iota \right).$$

We conclude that:

$$exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(-\iota \left)\right)-1}{\iota }}d\iota \right)\le \left|{\displaystyle \frac{D_{\lambda }^m⋎\left(\xi \right)}{\xi }}\right|\le exp\left({\int }_0^1{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right).$$

 □

Theorem 2.

Suppose that $⋎\in \bigwedge$ with non-negative connections. If $\mathsf{\Re }\left(\lambda \right)>0$ and $\mathsf{\Lambda },$ in Equation (4), is univalent convex in $\cup ,$ then there occurs a solution fulfilling upper bound inequality:

$$D_{\lambda }^m⋎\left(\xi \right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right),$$

(7)

where $\mathsf{\Psi }\left(\xi \right)$ is analytic in $\cup ,$ with $\mathsf{\Psi }\left(0\right)=0$ and $\left|\mathsf{\Psi }\right(\xi \left)\right|<1$.

Proof. 

In view of the assumptions, we attain:

$$\begin{array}{cc}\hfill & \mathsf{\Re }\left({\displaystyle \frac{\xi {(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}\right)>0\hfill \\ \hfill & \iff \mathsf{\Re }\left(\frac{\xi +{\sum }_{n=2}^{\infty }n{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^n}{\xi +{\sum }_{n=2}^{\infty }{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^n}\right)>0\hfill \\ \hfill & \iff \mathsf{\Re }\left(\frac{1+{\sum }_{n=2}^{\infty }n{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^{n-1}}{1+{\sum }_{n=2}^{\infty }{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n{\xi }^{n-1}}\right)>0\hfill \\ \hfill & \iff \left(\frac{1+{\sum }_{n=2}^{\infty }n{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n}{1+{\sum }_{n=2}^{\infty }{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n}\right)>0,\xi \to 1^{+}\hfill \\ \hfill & \iff \left(1+\sum _{n=2}^{\infty }n{[n+\lambda (1+{(-1)}^{n+1})]}^m{⋎}_n\right)>0.\hfill \end{array}$$

In addition, we confirm that $(D_{\lambda }^m⋎)\left(0\right)=0$, which implies that:

$${\displaystyle \frac{\xi {(D_{\lambda }^m⋎\left(\xi \right))}^{\prime }}{D_{\lambda }^m⋎\left(\xi \right)}}\in \mathcal{P}.$$

Hence, according to Theorem 1, we arrive at (7). □

Numerical Examples

We deal with the following examples.

Example 1.

Suppose the parametric BB-control system (time-space equation):

$${\displaystyle \frac{\xi {\left(D_{\lambda }^m{⋎}_{\tau }\left(\xi \right)\right)}^{\prime }}{D_{\lambda }^m{⋎}_{\tau }\left(\xi \right)}}=\frac{1+\xi }{1-\xi },$$

(8)

where $0<\tau <1,\left|\xi \right|<1$ and:

$${⋎}_{\tau }\left(\xi \right)=\frac{\xi }{{(1-\tau \xi )}^2}$$

$$=\xi +2\tau {\xi }^2+3{\tau }^2{\xi }^3+4{\tau }^3{\xi }^4+5{\tau }^4{\xi }^5+6{\tau }^5{\xi }^6+O\left({\xi }^7\right).$$

Our aim is to apply Theorem 2. By operating the formula of (2) for different values of $\lambda >0$, we have:

$$D_{0.1}^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)=\xi +4\tau {\xi }^2+9.6{\tau }^2{\xi }^3+16{\tau }^3{\xi }^4+26{\tau }^4{\xi }^5+O\left({\xi }^6\right),$$

$$D_{0.5}^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)=\xi +4\tau {\xi }^2+12{\tau }^2{\xi }^3+16{\tau }^3{\xi }^4+30{\tau }^4{\xi }^5+O\left({\xi }^6\right),$$

$$D_1^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)=\xi +4\tau {\xi }^2+15{\tau }^2{\xi }^3+16{\tau }^3{\xi }^4+35{\tau }^4{\xi }^5+O\left({\xi }^6\right)$$

$$D_2^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)=\xi +4\tau {\xi }^2+21{\tau }^2{\xi }^3+16{\tau }^3{\xi }^4+45{\tau }^4{\xi }^5+O\left({\xi }^6\right).$$

Now, a computation implies that:

$$\begin{array}{cc}\hfill \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\mathsf{\Lambda }\left(\mathsf{\Psi }\right(\iota \left)\right)-1}{\iota }}d\iota \right)& =\xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\frac{1+\iota }{1-\iota }-1}{\iota }}d\iota \right)\hfill \\ \hfill & \approx \xi exp(-2log(\xi -1\left)\right),\mathsf{\Re }\left(\xi \right)<1\hfill \\ \hfill & =\xi +2{\xi }^2+3{\xi }^3+4{\xi }^4+5{\xi }^5+O\left({\xi }^6\right).\hfill \end{array}$$

(9)

Comparing the connection values of $D_{\lambda }^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)$ and (9), we conclude that $\tau \in [0.5,1)$ implies that:

$$D_{\lambda }^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)\prec \xi exp\left({\int }_0^{\xi }{\displaystyle \frac{\frac{1+\iota }{1-\iota }-1}{\iota }}d\iota \right).$$

Therefore, $D_{\lambda }^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)$ is a solution of Equation (8).

Example 2.

In this example, we consider a wave equation taking the formula:

$${\displaystyle \frac{\xi {\left(D_{\lambda }^m{⋎}_{\tau }\left(\xi \right)\right)}^{\prime }}{D_{\lambda }^m{⋎}_{\tau }\left(\xi \right)}}=1+sin\left(\xi \right),$$

(10)

where $0<\tau <1,\left|\xi \right|<1$ and ${⋎}_{\tau }\left(\xi \right)=\frac{\xi }{{(1-\tau \xi )}^2}.$

It is clear that:

$${\int }_0^{\xi }(sin\left(\iota \right)/\iota )d\iota =Si\left(\xi \right)=\xi -{\xi }^3/18+{\xi }^5/600+O\left({\xi }^6\right),$$

where $Si$ is the sin integral function. Consequently, we have:

$$\xi exp\left({\int }_0^{\xi }{\displaystyle \frac{(1+sin(\iota \left)\right)-1}{\iota }}d\iota \right)=\xi -{\xi }^3/18+{\xi }^5/600+O\left({\xi }^6\right).$$

By compering the connection values, we indicate that $\tau \in [0,14.7]$, and Equation (10) has an upper univalent solution for all λ satisfying:

$$D_{\lambda }^1\left(\frac{\xi }{{(1-\tau \xi )}^2}\right)\prec \xi exp\left(Si\left(\xi \right)\right).$$

Remark 2.

Theorem 2 admits the following facts:

• The nonlinear model that we studied has no computational complexity cost. It is, fairly enough, not high speed because we have one variable and one parameter.
• It focuses on a starlike formula, which corresponds to the diffusion of the natural system of differential equations. Therefore, we reformulated the Dunkl operator to be suitable for this study.
• Theorem 2 gives the upper analytic solution in the open unit disk. Moreover, the upper bound solution is convex univalent; thus, all the trajectories approximate slightly the solution of Equation (7).

4. Linear Combination Operator

This work deals with a new operator combining $R^m$ and $D_{\lambda }^m$ as follows:

$$\begin{array}{cc}\hfill J_{\alpha ,\lambda }^m⋎\left(\xi \right)& =(1-\alpha )R^m⋎\left(\xi \right)+\alpha D_{\lambda }^m⋎\left(\xi \right)\hfill \\ \hfill & =\xi +\sum _{n=2}^{\infty }\mathsf{[}(1-\alpha )C_{m+n-1}^m+\alpha {\left(n+\lambda \mathsf{(}1+{(-1)}^{n+1}\mathsf{)}\right)}^m\mathsf{]}{⋎}_n{\xi }^n.\hfill \end{array}$$

(11)

Remark 3.

• $m=0⟹J_{\alpha ,\lambda }^0⋎\left(\xi \right)=⋎\left(\xi \right);$
• $\lambda =0⟹J_{\alpha ,0}^m⋎\left(\xi \right)=L_{\alpha }^m⋎\left(\xi \right);$
• $\alpha =0⟹J_{0,\lambda }^m⋎\left(\xi \right)=R^m⋎\left(\xi \right);$
• $\alpha =1⟹J_{1,\lambda }^m⋎\left(\xi \right)=D_{\lambda }^m⋎\left(\xi \right);$
• $\lambda =0,\alpha =1⟹J_{1,0}^m⋎\left(\xi \right)=S^m⋎\left(\xi \right).$

Definition 1.

Let $\alpha \ge 0,\lambda \in \mathbb{C},$ and $m\in \mathbb{N}.$ A function $⋎\in \bigwedge$ belongs to ${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$ if and only if:

$${\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\prec \sigma \left(\xi \right),\xi \in \cup ,$$

where σ is a univalent function with a positive real part in ∪ satisfying $\sigma \left(0\right)=1,\mathsf{\Re }\left({\sigma }^{\prime }\left(\xi \right)\right)>0.$

Note that the class ${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$ is a generalization of some classes of analytic functions. Moreover, this class is a specialist of the Ma and Minda class [14] given as follows (${\mathfrak{S}}^{*}\left(\sigma \right)$):

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec \sigma \left(\xi \right).$$

Moreover, when $\sigma \left(\xi \right)=1+sin\left(\xi \right)$ and $m=0,$ the class:

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec 1+sin\left(\xi \right)$$

was studied by Cho et al. [15]. Our class is a generalization of two classes given by Khatter et al. [16] as follows:

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec \beta +(1-\beta )\sqrt{1+\xi }$$

and

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec \beta +(1-\beta )e^{\xi },$$

where $\beta =0$ introduces the class [17]:

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec e^{\xi }.$$

Kumar et al. [18] defined the class by using Bell numbers as follows:

$${\displaystyle \frac{\xi {⋎}^{\prime }\left(\xi \right)}{⋎\left(\xi \right)}}\prec e^{e^{\xi }-1}.$$

Theorem 3.

If $\beta \in [0,1],\xi \in \cup$, then each function of the form:

• $\sigma \left(\xi \right)=\beta +(1-\beta )\sqrt{1+\xi },$
• $\sigma \left(\xi \right)=\beta +(1-\beta )e^{\xi },$
• $\sigma \left(\xi \right)=\beta +(1-\beta )(1+sin(\xi \left)\right),$
• $\sigma \left(\xi \right)=\beta +(1-\beta )e^{e^{\xi }-1},$

has the upper and lower bound for all $r\in (0,1),\theta \in [0,2\pi )$ as follows:

$$\underset{\left|\xi \right|=r}{min}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=\sigma (-r)=\underset{\left|\xi \right|=r}{min}\left|\sigma \left(\xi \right)\right|$$

and

$$\underset{\left|\xi \right|=r}{max}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=\sigma \left(r\right)=\underset{\left|\xi \right|=r}{max}\left|\sigma \left(\xi \right)\right|.$$

Proof. 

The first and second type can be located in [16]. We only need to prove the third type. For $\beta =0,$ we have the function $\sigma \left(\xi \right)=1+sin\left(\xi \right)$ (see [15]). It is clear that:

$$sin\left(\xi \right)=sin\left(r{e}^{i\theta }\right)=sin(rcos\left(\theta \right))cosh(rsin\left(\theta \right))+icos(rcos\left(\theta \right))sinh(rsin\left(\theta \right))$$

therefore, we have

$$\mathsf{\Re }\left(\sigma \right(\xi \left)\right)=1+sin(rcos(\theta \left)\right)cosh(rsin(\theta \left)\right).$$

Consequently, by taking $r\to 0,$ we obtain:

$$\underset{\left|\xi \right|=r}{min}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=1-sin\left(r\right)=\underset{\left|\xi \right|=r}{min}\left|\sigma \left(\xi \right)\right|=1.$$

Moreover, we have:

$$|sin\left(r{e}^{i\theta }\right){|}^2={cos}^2(rcos\theta )sinh2(rsin\theta )+{sin}^{2}2(rcos\theta )cosh2(rsinr)\le {sinh}^2\left(r\right);$$

thus, this yields:

$$\underset{\left|\xi \right|=r}{max}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=1+sin\left(r\right)=\underset{\left|\xi \right|=r}{max}\left|\sigma \left(\xi \right)\right|\le 1+{sinh}^2\left(r\right).$$

Extending the above result, for $\beta >0,$ we have:

$$\underset{\left|\xi \right|=r}{min}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=\beta +(1-\beta )(1-sin\left(r\right))=\underset{\left|z\right|=r}{min}\left|\sigma \left(\xi \right)\right|=1,$$

and

$$\underset{\left|\xi \right|=r}{max}\mathsf{\Re }\left(\sigma \left(\xi \right)\right)=\beta +(1-\beta )(1+sin\left(r\right))=\underset{\left|\xi \right|=r}{max}\left|\sigma \left(\xi \right)\right|\le \beta +(1-\beta )(1+{sinh}^2\left(r\right)).$$

This is similar for the last assertion. ☐

The next result can be found in [10].

Lemma 1.

If $\tau >0$ and $\sigma \in \mathfrak{H}[1,n]$, then there are constants $\wp >0$ and $\nu >0$ with $\nu =\nu (\wp ,\tau ,n)$, so that:

$$\sigma \left(\xi \right)+\tau \xi {\sigma }^{\prime }\left(\xi \right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\nu }\Rightarrow \sigma \left(\xi \right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\wp }.$$

Lemma 2.

Let $\phi \left(\xi \right)$ be a convex function in ∪, $h\left(\xi \right)=\phi \left(\xi \right)+n\nu \left(\xi {\phi }^{\prime }\left(\xi \right)\right)$ for $\nu >0$, and n be a positive integer. If $\varrho \in \mathfrak{H}\left[\phi \right(0),n],$ and:

$$\varrho \left(\xi \right)+\nu \xi {\varrho }^{\prime }\left(\xi \right)\prec h\left(\xi \right),\xi \in \cup ,$$

then

$$\varrho \left(\xi \right)\prec \phi \left(\xi \right),$$

and this result is sharp.

5. Subordination Inequalities

Here, we are concerned with the class ${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$ for special types of $\sigma \left(\xi \right)$ that are given in Theorem 3.

Theorem 4.

The class ${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$ achieves the following inclusion:

$${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )\subset {\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\gamma )\subset {\mathfrak{S}}_m^{*}(\alpha ,\lambda ),$$

where σ is one of the types in Theorem 3 and:

$${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\gamma ):=\{⋎\in \bigwedge \mathsf{\Re }({\displaystyle \frac{\xi (J_{\alpha ,\lambda }^m⋎\left(\xi \right)){)}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}})>\gamma \};$$

$${\mathfrak{S}}_m^{*}(\alpha ,\lambda ):=\{⋎\in \bigwedge \mathsf{\Re }({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}})>0\}.$$

Proof. 

Let $⋎\in {\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$, and let $\sigma \left(\xi \right)=\beta +(1-\beta )\sqrt{1+\xi },$ then we have the inequality:

$${\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\prec \beta +(1-\beta )\sqrt{1+\xi },\xi \in \cup .$$

In view of Theorem 3, we obtain:

$$\underset{\left|\xi \right|=1^{-}}{min}\mathsf{\Re }(\beta +(1-\beta )\sqrt{1+\xi })<\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\underset{\left|\xi \right|=1^{+}}{max}\mathsf{\Re }(\beta +(1-\beta )\sqrt{1+\xi }),$$

which yields:

$$\beta <\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\beta +(1-\beta )\sqrt{2}.$$

Hence, we have:

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\kappa }^m⋎\left(\xi \right)}}\right)>\beta :=\gamma \ge 0,$$

and consequently, we get the requested result. Consider $\sigma \left(\xi \right)=\beta +(1-\beta )e^{\xi };$ we have:

$$\underset{\left|\xi \right|=1}{min}\mathsf{\Re }(\beta +(1-\beta )e^{\xi })<\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\underset{\left|\xi \right|=1}{max}\mathsf{\Re }(\beta +(1-\beta )e^{\xi }),$$

which implies:

$$(\beta +(1-\beta ){\displaystyle \frac{1}{e}})<\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<(\beta +(1-\beta )e),$$

that is:

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)>(\beta +(1-\beta ){\displaystyle \frac{1}{e}}):=\gamma \ge 0.$$

Similarly, by letting $\sigma \left(\xi \right)=\beta +(1-\beta )(1+sin(\xi \left)\right)$, then we have:

$$\underset{\left|\xi \right|=1}{min}\mathsf{\Re }(\beta +(1-\beta )(1+sin\left(\xi \right)))<\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\underset{\left|\xi \right|=1}{max}\mathsf{\Re }(\beta +(1-\beta )(1+sin\left(\xi \right))),$$

which leads to:

$$(\beta +0.158(1-\beta ))<\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<(\beta +1.841(1-\beta )),$$

and this brings the inequality:

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)>(\beta +0.158(1-\beta )):=\gamma \ge 0.$$

☐

Remark 4.

In Theorem 4,

• $m=0,\beta =0,\sigma \left(\xi \right)=1+sin\xi ⟹$ [15];
• $m=0⟹$ [16];
• $m=0,\beta =0,\sigma \left(\xi \right)=e^{\xi }⟹$ [19];
• $m=0,\beta =0,\sigma \left(\xi \right)=\sqrt{1+\xi }⟹$ [19].

Theorem 5.

The class ${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )$ achieves the following inclusion:

$${\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma )\subset {\mathfrak{M}}_m(\alpha ,\lambda ,\gamma ):=\{⋎\in \bigwedge \mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\gamma ,\gamma >1\}.$$

where σ is given in Theorem 3.

The set ${\mathfrak{M}}_m(\alpha ,\lambda ,\gamma )$ is a generalization of the set:

$$\mathfrak{M}\left(\gamma \right):=\{⋎\in \bigwedge \mathsf{\Re }\left({\displaystyle \frac{\xi {(⋎\left(\xi \right))}^{\prime }}{⋎\left(\xi \right)}}\right)<\gamma ,\gamma >1\}$$

given by Uralegaddi et al. [20].

Proof. 

Let $⋎\in {\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma ),$ where $\sigma$ is given in Theorem 3. By the proof of Theorem 4, we have:

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\beta +(1-\beta )\sqrt{2}:=\gamma ,$$

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<\beta +(1-\beta )e:=\gamma$$

and:

$$\mathsf{\Re }\left({\displaystyle \frac{\xi {(J_{\alpha ,\kappa }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)<(\beta +1.841(1-\beta )):=\gamma ,$$

Hence, $⋎\in {\mathfrak{M}}_m(\alpha ,⋎\left(\xi \right),\gamma ),$ where the value of $\gamma$ is based on the function $\sigma ,$ which completes the proof. ☐

Remark 5.

In Theorem 5,

• $m=0,\beta =0,\sigma \left(\xi \right)=1+sin\xi ⟹$ [15];
• $m=0,\sigma \left(\xi \right)=\beta +(1-\beta )e^{\xi }⟹$ [16], Theorem 2.5;
• $m=0,\sigma \left(\xi \right)=\beta +(1-\beta )\left(\sqrt{1+\xi }\right)⟹$ [16], Theorem 2.6;
• $m=0,\beta =0,\sigma \left(\xi \right)=\left(\sqrt{1+\xi }\right)⟹$ [16], Corollary 2.7.

Theorem 6.

If $⋎\in \bigwedge$ satisfies the subordination:

$$\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)\left(2+{\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{″}}{{(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}}-{\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,⋎\left(\xi \right)}^m⋎\left(\xi \right)}}\right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\tau }$$

then $⋎\in {\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma ),$ where $\sigma \left(\xi \right)={\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\wp }$ for $\wp >0,\tau >0.$

Proof. 

To employ Lemma 1, a calculation implies that:

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)+\xi {\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)}^{\prime }\hfill \\ \hfill & =\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)\left(2+{\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{″}}{{(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}}-{\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)\hfill \\ \hfill & \prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\tau }.\hfill \end{array}$$

Thus, in view of Lemma 1, we have:

$$\left({\displaystyle \frac{\xi {(J_{\alpha ,\lambda }^m⋎\left(\xi \right))}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)\prec {\left[{\displaystyle \frac{1+\xi }{1-\xi }}\right]}^{\wp }:=\sigma \left(\xi \right),$$

which implies that $⋎\in {\mathfrak{S}}_m^{*}(\alpha ,\lambda ,\sigma ).$ ☐

Theorem 7.

Let φ be a convex function such that $\phi \left(0\right)=0$, and let ℏ be the function:

$$\hslash \left(\xi \right)=\phi \left(\xi \right)+{\displaystyle \frac{\xi }{1-\ell }}{\phi }^{\prime }\left(\xi \right),\xi \in \cup ,\ell \in (0,1).$$

If for a function, $⋎\in \bigwedge$ satisfies the subordination:

$${\left({\displaystyle \frac{\xi }{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }{\displaystyle \frac{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}{1-\ell }}\left({\displaystyle \frac{{\left(J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)\right)}^{\prime }}{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}-\ell {\displaystyle \frac{{\left(J_{\alpha ,\lambda }^m⋎\left(\xi \right)\right)}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)\prec \hslash \left(\xi \right)$$

then:

$$\left({\displaystyle \frac{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}\right){\left({\displaystyle \frac{\xi }{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }\prec \phi \left(\xi \right),\xi \in \cup .$$

The outcome is sharp.

Proof. 

We aim to apply Lemma 2. Let:

$$\varrho \left(\xi \right)=\left({\displaystyle \frac{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}\right){\left({\displaystyle \frac{\xi }{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }.$$

A differentiation implies that:

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\xi }{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}\right)}^{\ell }{\displaystyle \frac{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}{1-\ell }}\left({\displaystyle \frac{{\left(J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)\right)}^{\prime }}{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}}-\ell {\displaystyle \frac{{\left(J_{\alpha ,\lambda }^m)⋎\left(\xi \right)\right)}^{\prime }}{J_{\alpha ,\lambda }^m⋎\left(\xi \right)}}\right)=\varrho \left(\xi \right)+\left({\displaystyle \frac{1}{1-\ell }}\right)\xi {\varrho }^{\prime }\left(\xi \right)\end{array}$$

Thus, by the assumption, we have:

$$\varrho \left(\xi \right)+\left({\displaystyle \frac{1}{1-\ell }}\right)\xi {\varrho }^{\prime }\left(\xi \right)\prec \hslash \left(\xi \right)=\phi \left(\xi \right)+{\displaystyle \frac{\xi }{1-\ell }}{\phi }^{\prime }\left(\xi \right),\xi \in \cup .$$

Employing Lemma 2 yields $\varrho \left(\xi \right)\prec \hslash \left(\xi \right),$ which means:

$$({\displaystyle \frac{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}{\xi }}){({\displaystyle \frac{\xi }{J_{\alpha ,\lambda }^{m+1}⋎\left(\xi \right)}})}^{\ell }\prec \phi \left(\xi \right),\xi \in \cup .$$

This result is sharp. ☐

Remark 6.

In Theorem 6, $\lambda =0⟹$ [21] Theorem 2.14.

6. Conclusions

This study was concerned with a class of Briot–Bouquet differential equations utilizing a new differential operator of complex connections. Some inequalities involving the subordination concept were investigated. For future work, the idea of [22] will be used to present a harmonic class of Briot–Bouquet differential equations.