Distribution Tableaux, Distribution Models
Abstract
:1. Introduction
2. Preliminaries
2.1. Syllogistic
2.2. Distribution
- is distributed in p if and only if p entails a proposition of the form “every is …”
- is not distributed in p if and only if is distributed in the contradictory of p.
2.3. Term Functor Logic
2.4. TFL Tableaux
3. Distribution Models
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Geach, P.T. Reference and Generality: An Examination of Some Medieval and Modern Theories; Contemporary Philosophy/Cornell University, Cornell University Press: Ithaca, NY, USA, 1962. [Google Scholar]
- Williamson, C. Traditional Logic as a Logic Distribution-values. Log. Et Anal. 1971, 14, 729–746. [Google Scholar]
- Sommers, F. Distribution Matters. Mind 1975, LXXXIV, 27–46. [Google Scholar] [CrossRef]
- Sommers, F. The Logic of Natural Language; Clarendon Library of Logic and Philosophy, Clarendon Press: New York, NY, USA; Oxford University Press: Oxford, UK, 1982. [Google Scholar]
- Wilson, F. The distribution of terms: A defense of the traditional doctrine. Notre Dame J. Form. Log. 1987, 28, 439–454. [Google Scholar] [CrossRef]
- Englebretsen, G. Something to Reckon with: The Logic of Terms; Canadian Electronic Library, Books Collection; University of Ottawa Press: Ottawa, ON, Canada, 1996. [Google Scholar]
- Sommers, F.; Englebretsen, G. An Invitation to Formal Reasoning: The Logic of Terms; Ashgate: Farnham, UK, 2000. [Google Scholar]
- Englebretsen, G. Bare Facts and Naked Truths: A New Correspondence Theory of Truth; Ashgate Pub. Limited: Farnham, UK, 2006. [Google Scholar]
- Castro-Manzano, J.M.; Reyes-Cárdenas, P.O. Term Functor Logic Tableaux. South Am. J. Log. 2018, 4, 1–22. [Google Scholar]
- de Rijk, L. Peter of Spain (Petrus Hispanus Portugalensis): Tractatus: Called Afterwards Summule Logicales. First Critical ed. from the Manuscripts; van Gorcum & Co.: Assen, The Netherlands, 1972. [Google Scholar]
- Arnauld, A.; Nicole, P.; Buroker, J. Antoine Arnauld and Pierre Nicole: Logic Or the Art of Thinking; Cambridge Texts in the History of Philosophy; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Keynes, J. Studies and Exercises in Formal Logic: Including a Generalisation of Logical Processes in Their Application to Complex Inferences; Macmillan: London, UK, 1887. [Google Scholar]
- Sommers, F. On a Fregean Dogma. In Problems in the Philosophy of Mathematics; Lakatos, I., Ed.; Studies in Logic and the Foundations of Mathematics; Elsevier: Amsterdam, The Netherlands, 1967; Volume 47, pp. 47–81. [Google Scholar] [CrossRef]
- Englebretsen, G. The New Syllogistic; Peter Lang: Bern, Switzerland, 1987. [Google Scholar]
- Englebretsen, G.; Sayward, C. Philosophical Logic: An Introduction to Advanced Topics; Bloomsbury Academic: London, UK, 2011. [Google Scholar]
- Quine, W.V.O. Predicate Functor Logic. In Proceedings of the Second Scandinavian Logic Symposium; Fenstad, J.E., Ed.; North-Holland: Amsterdam, The Netherlands, 1971. [Google Scholar]
- Noah, A. Predicate-functors and the limits of decidability in logic. Notre Dame J. Form. Log. 1980, 21, 701–707. [Google Scholar] [CrossRef]
- Kuhn, S.T. An axiomatization of predicate functor logic. Notre Dame J. Form. Log. 1983, 24, 233–241. [Google Scholar] [CrossRef]
- Sommers, F. Intelectual Autobiography. In The Old New Logic: Essays on the Philosophy of Fred Sommers; Oderberg, D.S., Ed.; Bradford Book: Cambridge, MA, USA, 2005; pp. 1–24. [Google Scholar]
- Bastit, M. Jan Łukasiewicz contre le dictum de omni et de nullo. Philos. Sci. 2011, 15, 55–68. [Google Scholar] [CrossRef]
- D’Agostino, M.; Gabbay, D.M.; Hähnle, R.; Posegga, J. Handbook of Tableau Methods; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Priest, G. An Introduction to Non-Classical Logic: From If to Is; Cambridge Introductions to Philosophy; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Hähnle, R. Tableaux and Related Methods. In Handbook of Automated Reasoning (in 2 volumes); Robinson, J.A., Voronkov, A., Eds.; Elsevier: Amsterdam, The Netherlands; MIT Press: Cambridge, MA, USA, 2001; pp. 100–178. [Google Scholar] [CrossRef]
- Carnap, R. Die alte und die neue Logik. Erkenntnis 1930, 1, 12–26. [Google Scholar] [CrossRef]
- Geach, P.T. Logic Matters; University of California Press: Berkeley, CA, USA, 1980. [Google Scholar]

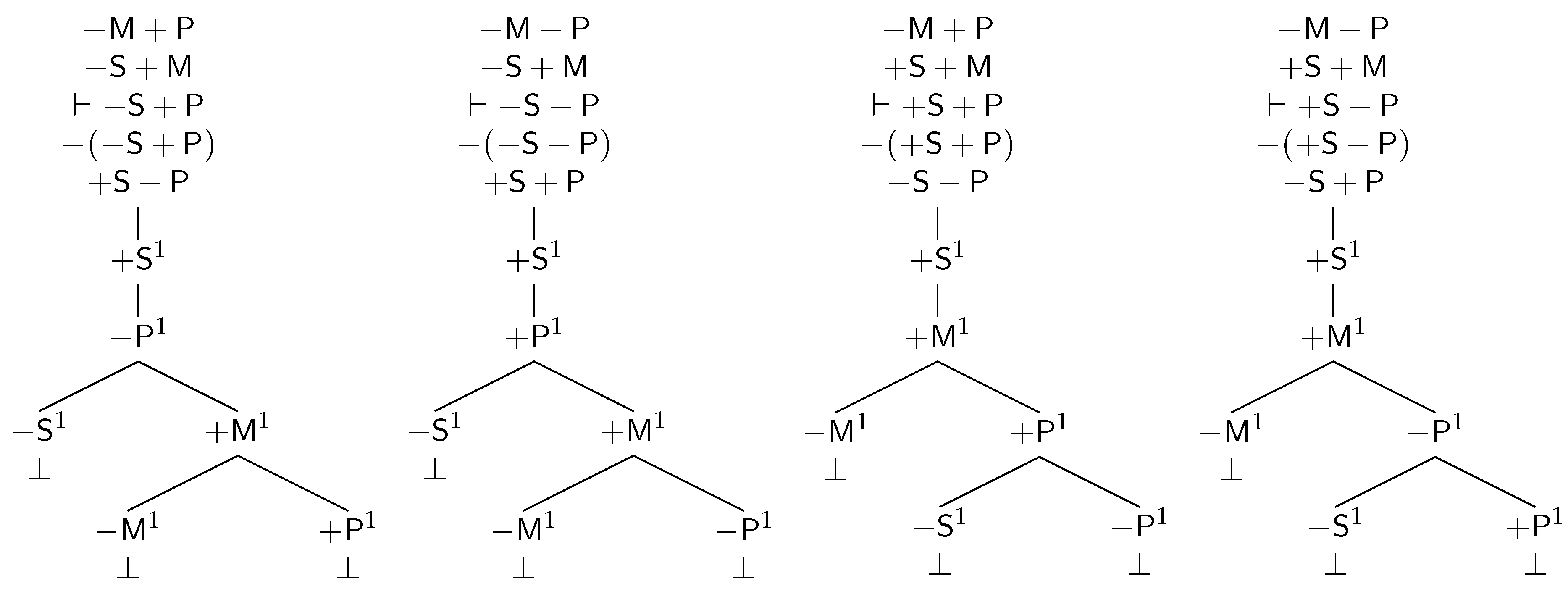
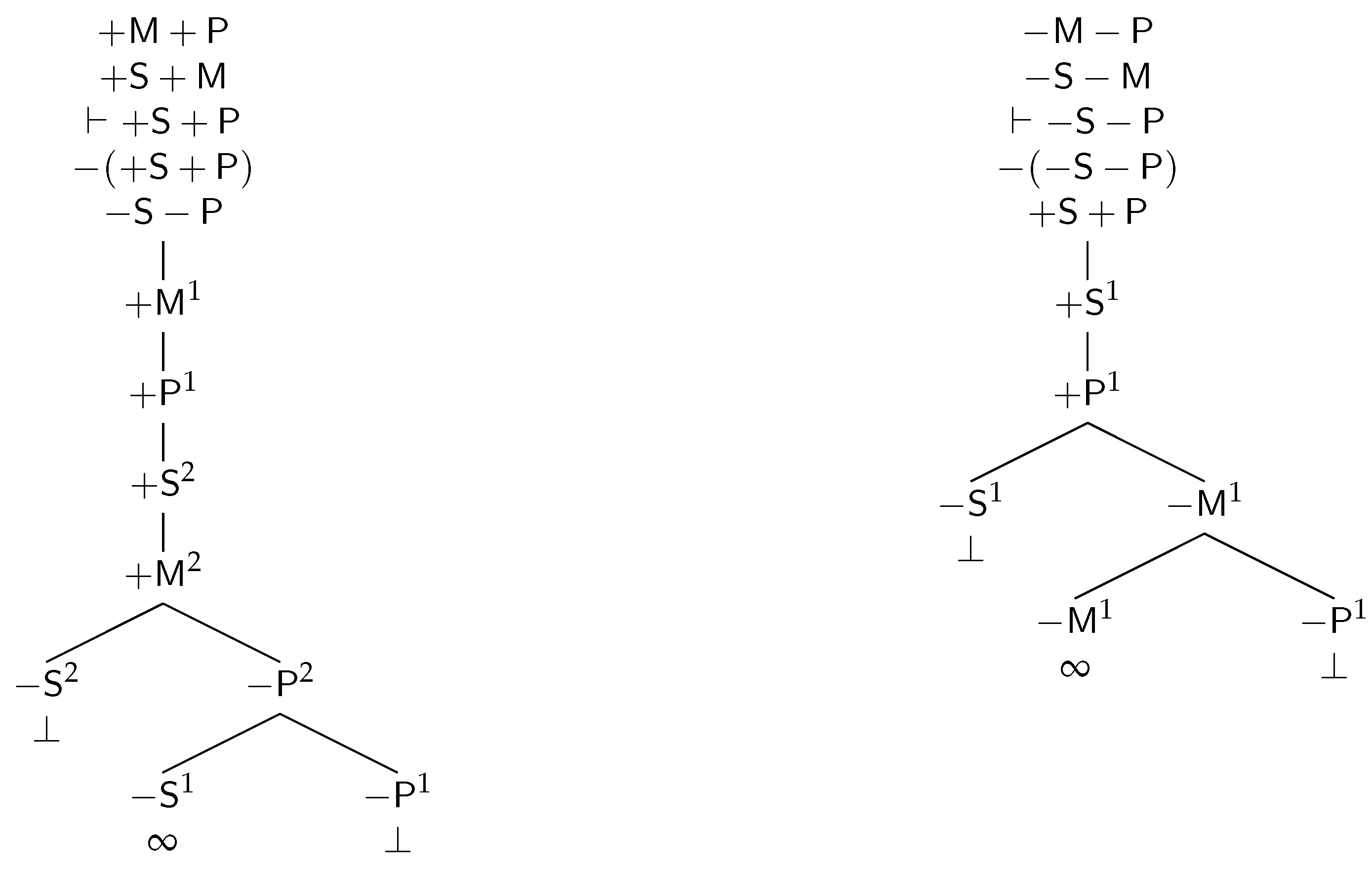

| First | Second | Third | Fourth |
|---|---|---|---|
| Figure | Figure | Figure | Figure |
| Proposition | |
|---|---|
| 1. | All mammals are animals. |
| 2. | All dogs are mammals. |
| ⊢ | All dogs are animals. |
| Proposition | TFL | |
|---|---|---|
| 1. | All mammals are animals. | |
| 2. | All dogs are mammals. | |
| ⊢ | All dogs are animals. |
| Proposition | Arithmetic Sum | |
|---|---|---|
| 1. | ||
| 2. | ||
| ⊢ |
| Proposition | Arithmetic Sum | |
|---|---|---|
| 1. | ||
| 2. | ||
| ⊢ |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Manzano, J.-M. Distribution Tableaux, Distribution Models. Axioms 2020, 9, 41. https://doi.org/10.3390/axioms9020041
Castro-Manzano J-M. Distribution Tableaux, Distribution Models. Axioms. 2020; 9(2):41. https://doi.org/10.3390/axioms9020041
Chicago/Turabian StyleCastro-Manzano, J.-Martín. 2020. "Distribution Tableaux, Distribution Models" Axioms 9, no. 2: 41. https://doi.org/10.3390/axioms9020041
APA StyleCastro-Manzano, J.-M. (2020). Distribution Tableaux, Distribution Models. Axioms, 9(2), 41. https://doi.org/10.3390/axioms9020041





