Dynamics of HIV-TB Co-Infection Model
Abstract
1. Introduction
2. Mathematical Model
2.1. HIV-TB Co-infection Model
2.2. Equilibrium Solutions
- Endemic Equilibrium pointwhere, .
2.3. Reproduction Number
2.4. Persistence of Disease
2.5. Stability Analysis
- P.1 For , is globally asymptotically stable.
- P.2 for .
- P.3 For , is globally asymptotically stable.
- P.4 for .
- P.5 For , is globally asymptotically stable.
- P.6 for
3. Backward Bifurcation
3.1. Sensitivity Analysis of
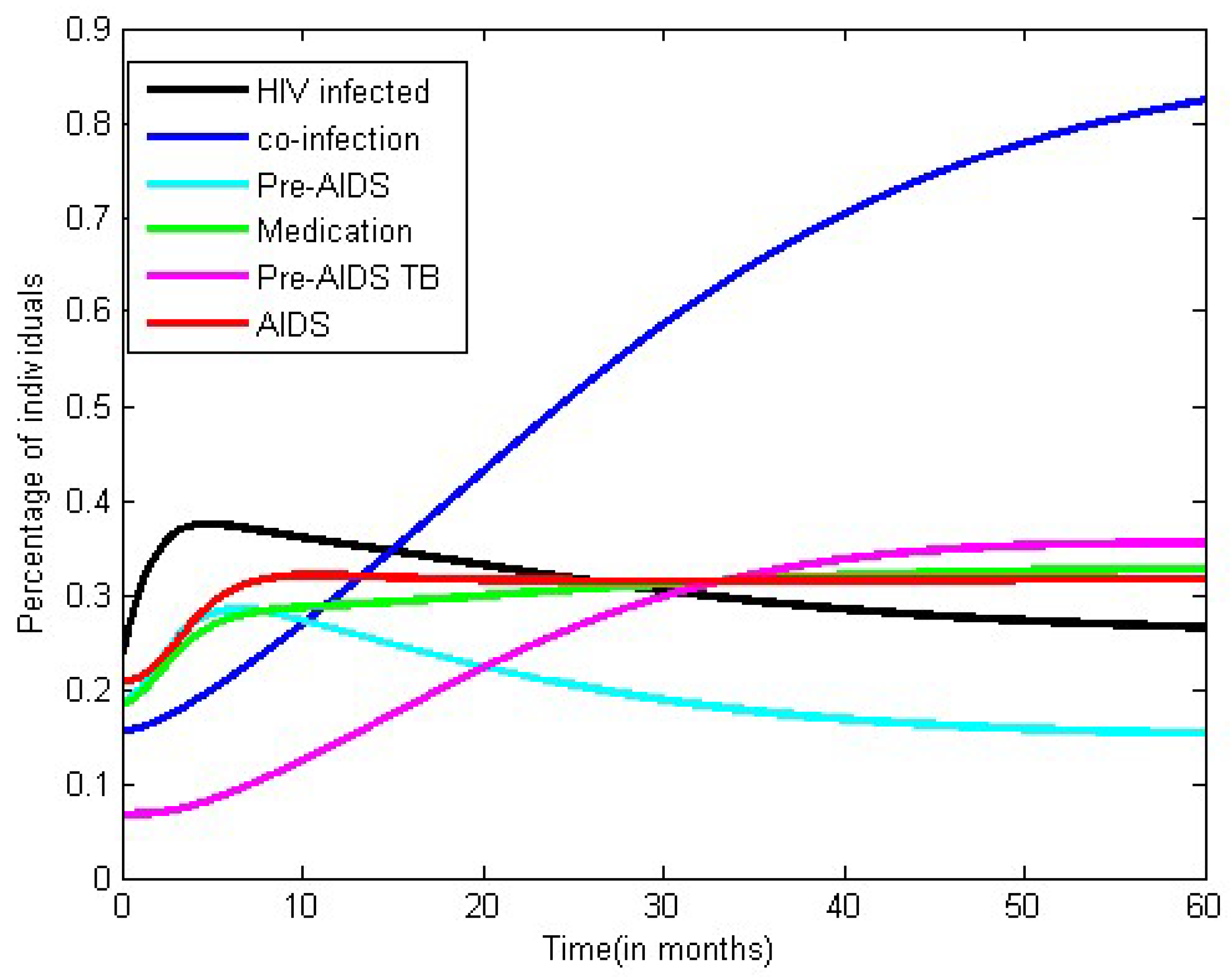
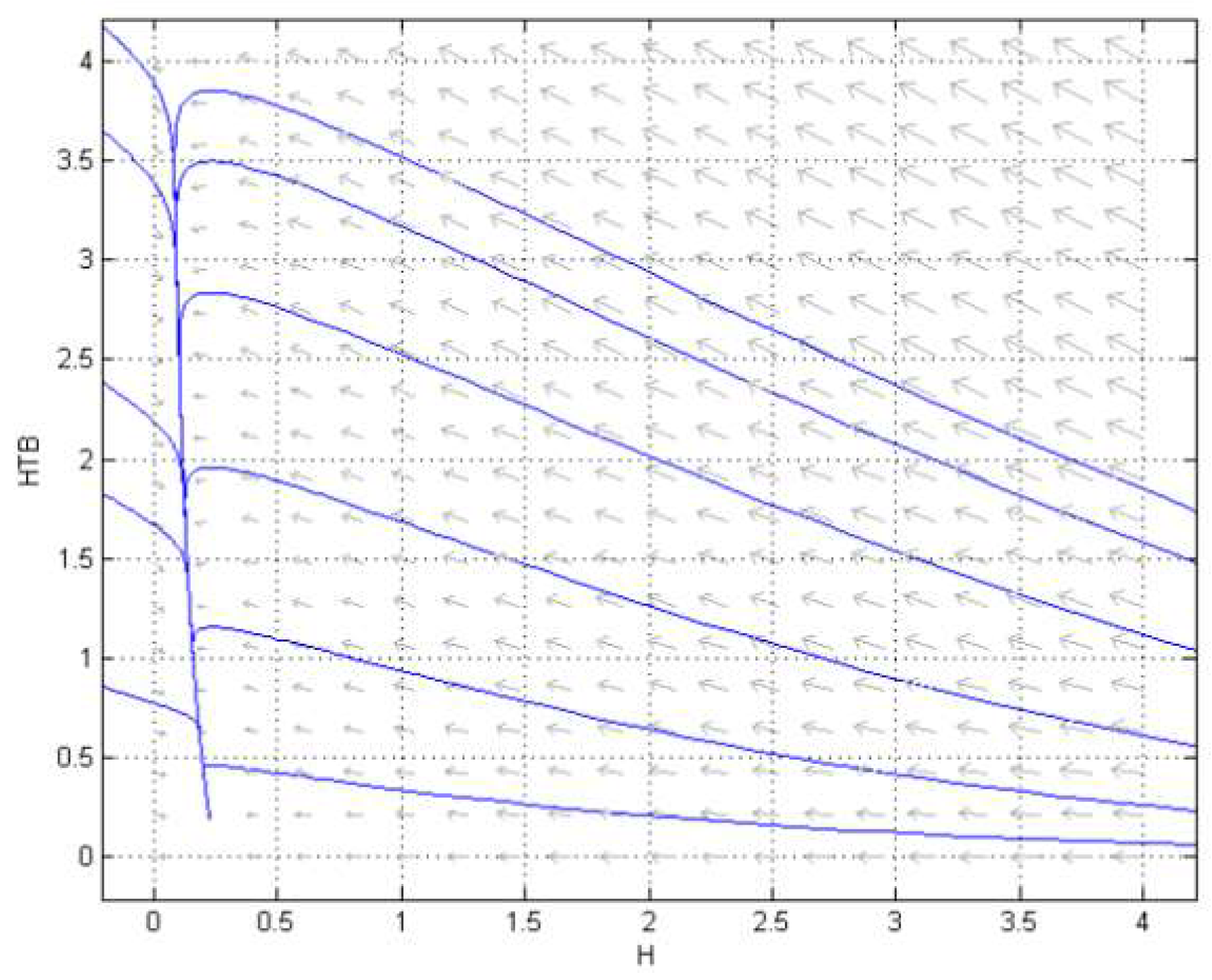
3.2. Numerical Simulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Available online: https://www.who.int/news-room/fact-sheets/detail/hiv-aids (accessed on 3 January 2020).
- Available online: https://www.who.int/tb/areas-of-work/tb-hiv/en/ (accessed on 3 January 2020).
- Kwan, C.K.; Ernst, J.D. HIV and tuberculosis: A deadly human syndemic. Clin. Microbiol. Rev. 2011, 24, 351–376. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.avert.org/professionals/hiv-programming/hiv-tb-coinfection (accessed on 3 January 2020).
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A Math. Phys. Char. 1927, 115, 700–721. [Google Scholar]
- Cattani, C.; Ciancio, A. Qualitative analysis of second-order models of tumor—Immune system competition. Math. Comput. Model. 2008, 47, 1339–1355. [Google Scholar] [CrossRef]
- Cattani, C.; Ciancio, A. Hybrid two scales mathematical tools for active particles modelling complex systems with learning hiding dynamics. Math. Models Methods Appl. Sci. 2007, 17, 171–187. [Google Scholar] [CrossRef]
- Kirschner, D. Dynamics of Co-infection with M. tuberculosis and HIV-1. Theor. Popul. Biol. 1999, 55, 94–109. [Google Scholar] [CrossRef] [PubMed]
- Naresh, R.; Tripathi, A. Modelling and analysis of HIV-TB co-infection in a variable size population. Math. Model. Anal. 2005, 10, 275–286. [Google Scholar] [CrossRef][Green Version]
- Huo, H.F.; Chen, R.; Wang, X.Y. Modelling and stability of HIV/AIDS epidemic model with treatment. Appl. Math. Model. 2016, 40, 6550–6559. [Google Scholar] [CrossRef]
- Bhunu, C.P.; Garira, W.; Mukandavire, Z. Modeling HIV/AIDS and tuberculosis coinfection. Bull. Math. Biol. 2009, 71, 1745–1780. [Google Scholar] [CrossRef] [PubMed]
- Roeger, L.I.W.; Feng, Z.; Castillo-Chavez, C. Modeling TB and HIV co-infections. Math. Biosci. Eng. 2009, 6, 815–837. [Google Scholar] [PubMed]
- Singh, R.; Ali, S.; Jain, M. Epidemic model of HIV/AIDS transmission dynamics with different latent stages based on treatment. Am. J. Appl. Math. 2016, 4, 222–234. [Google Scholar] [CrossRef][Green Version]
- Silva, C.J.; Torres, D.F. Modeling TB-HIV syndemic and treatment. J. Appl. Math. 2014, 248407. [Google Scholar] [CrossRef]
- Available online: https://aidsinfo.nih.gov/understanding-hiv-aids/fact-sheets/26/90/hiv-and-tuberculosis--tb- (accessed on 3 January 2020).
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Freedman, H.I.; Ruan, S.; Tang, M. Uniform persistence and flows near a closed positively invariant set. J. Dyn. Differ. Equ. 1994, 6, 583–600. [Google Scholar] [CrossRef]
- Thieme, H.R. Epidemic and demographic interaction in the spread of potentially fatal diseases in growing populations. Math. Biosci. 1992, 111, 99–130. [Google Scholar] [CrossRef]
- Feng, Z.; Castillo-Chavez, C.; Capurro, A.F. A model for tuberculosis with exogenous reinfection. Theor. Popul. Biol. 2000, 57, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Chavez, C.; Blower, S.; van den Driessche, P.; Kirschner, D.; Yakubu, A.A. (Eds.) Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Dntroduction; Springer Science & Business Media: Berlin, Germany.
- LaSalle, J.P. The stability of dynamical systems. Soc. Ind. Appl. Math. 1976, 25. [Google Scholar] [CrossRef]
- Khan, M.A.; Islam, S.; Khan, S.A. Mathematical modeling towards the dynamical interaction of leptospirosis. Appl. Math. Inf. Sci. 2014, 8, 1049–1056. [Google Scholar] [CrossRef]







| Notations | Description | Parametric Values |
|---|---|---|
| Number of individuals at any instant of time | 100 | |
| Birth rate | 0.2 | |
| Rate at which co-infection occurs | 0.45 | |
| Rate at which HIV-infected individuals reaches pre-AIDS stage | 0.48 | |
| Rate at which HIV-infected individualsopt for medication | 0.31 | |
| Rate at which co-infected individual goes for medication | 0.1 | |
| Rate at which co-infection (HIV-TB) individual joins pre-AIDS TB stage | 0.037 | |
| Rate at which pre-AIDS infectives opt for medication | 0.25 | |
| Rate at which pre-AIDS TB infectives undergo medication | 0.15 | |
| Rate at which pre-AIDS infected individuals join pre-AIDS TB class | 0.8 | |
| Rate at which pre-AIDS suffer from full-blown AIDS | 0.3 | |
| Rate at which Pre-AIDS TB infectives joins full-blown AIDS TB class | 0.001 | |
| Rate at which treated infectives move to AIDS class | 0.78 | |
| Rate at which individuals with full-blown AIDS suffer from TB | 0.35 | |
| Natural death rate | 0.002 | |
| Death rate due to AIDS | 0.6 | |
| Death rate due to co-infection | 0.52 |
| Parameter | Value | Observation |
|---|---|---|
| 1 | The transmission rate of HIV is directly proportional to birth rate. | |
| 0.4925 | The transmission rate of co-infection occurs at 49%. | |
| 0.9013 | Among HIV infectives, around 90% of them join the pre-AIDS stage. | |
| 0.6084 | Individuals moving toward medication can be increased further by creating awareness programs. | |
| 0.5172 | ||
| 0.77 | 77% of individuals in pre-AIDS class opt for medication. | |
| 0.5022 | From the pre-AIDS, class 50% of individuals undergo medication for TB disease. | |
| 0.5075 | Transmission occurs at the rate of 50% from the pre-AIDS class to pre-AIDS TB. | |
| 0.724 | The number of individuals in pre-AIDS class suffering from AIDS can be reduced if they take treatment while in pre-AIDS class. | |
| 0.9967 | The transmission rate of individuals from pre-AIDS TB stage to AIDS TB stage highly effects the sensitivity of . | |
| 0.9793 | Natural death rate cannot be removed completely even if the treatment is opted for in initial stage. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, N.H.; Sheoran, N.; Shah, Y. Dynamics of HIV-TB Co-Infection Model. Axioms 2020, 9, 29. https://doi.org/10.3390/axioms9010029
Shah NH, Sheoran N, Shah Y. Dynamics of HIV-TB Co-Infection Model. Axioms. 2020; 9(1):29. https://doi.org/10.3390/axioms9010029
Chicago/Turabian StyleShah, Nita H, Nisha Sheoran, and Yash Shah. 2020. "Dynamics of HIV-TB Co-Infection Model" Axioms 9, no. 1: 29. https://doi.org/10.3390/axioms9010029
APA StyleShah, N. H., Sheoran, N., & Shah, Y. (2020). Dynamics of HIV-TB Co-Infection Model. Axioms, 9(1), 29. https://doi.org/10.3390/axioms9010029




