Stability of Equilibria of Rumor Spreading Model under Stochastic Perturbations
Abstract
:1. Introduction
2. Equilibria of the Model
3. Stochastic Perturbations, Centralization, and Linearization
4. Stability of the Equilibria
- -
- mean square stable if for each there exists a such that , , provided that ;
- -
- asymptotically mean square stable if it is mean square stable and the solution of Equation (9) satisfies the condition provided that .
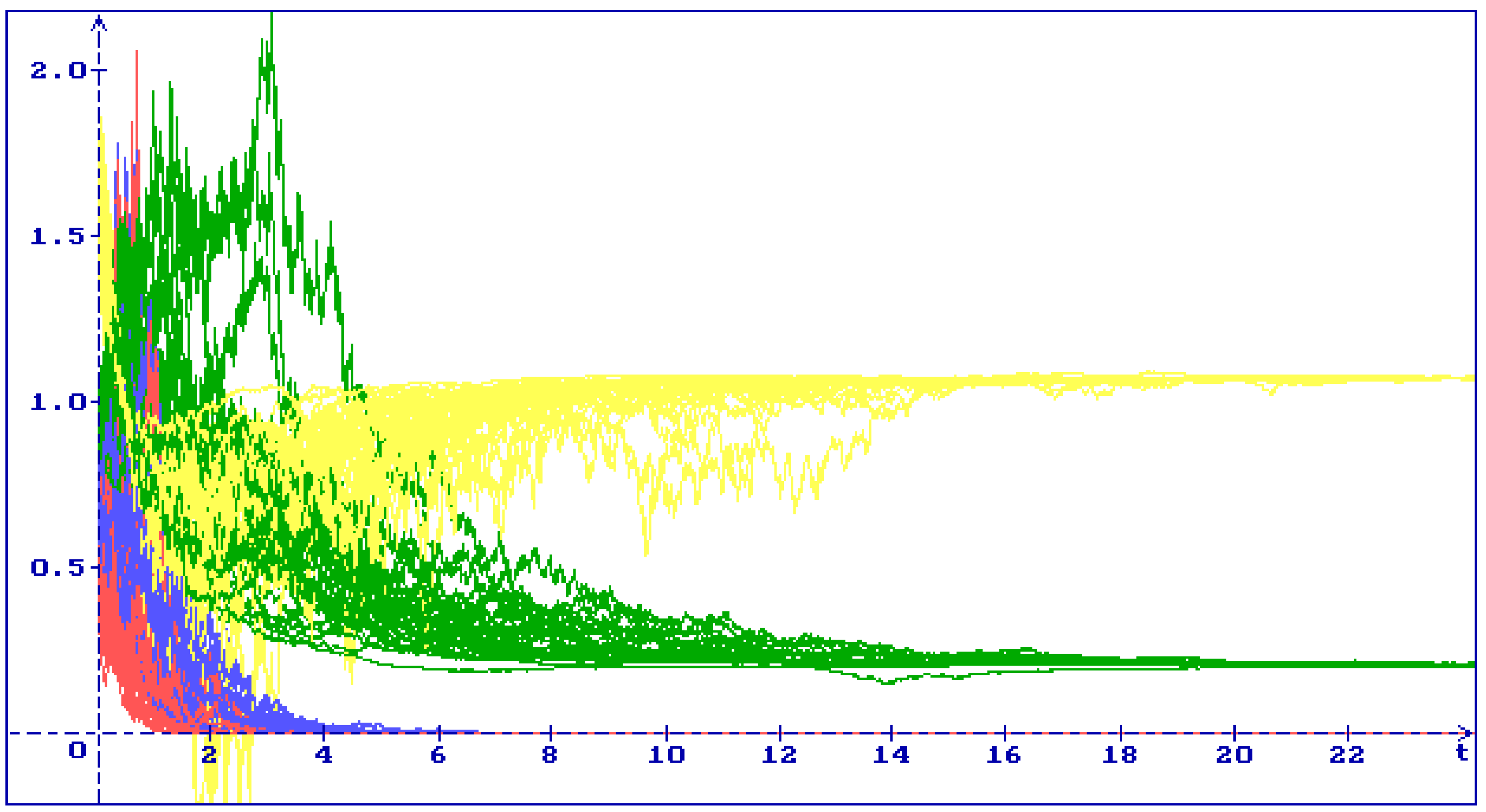
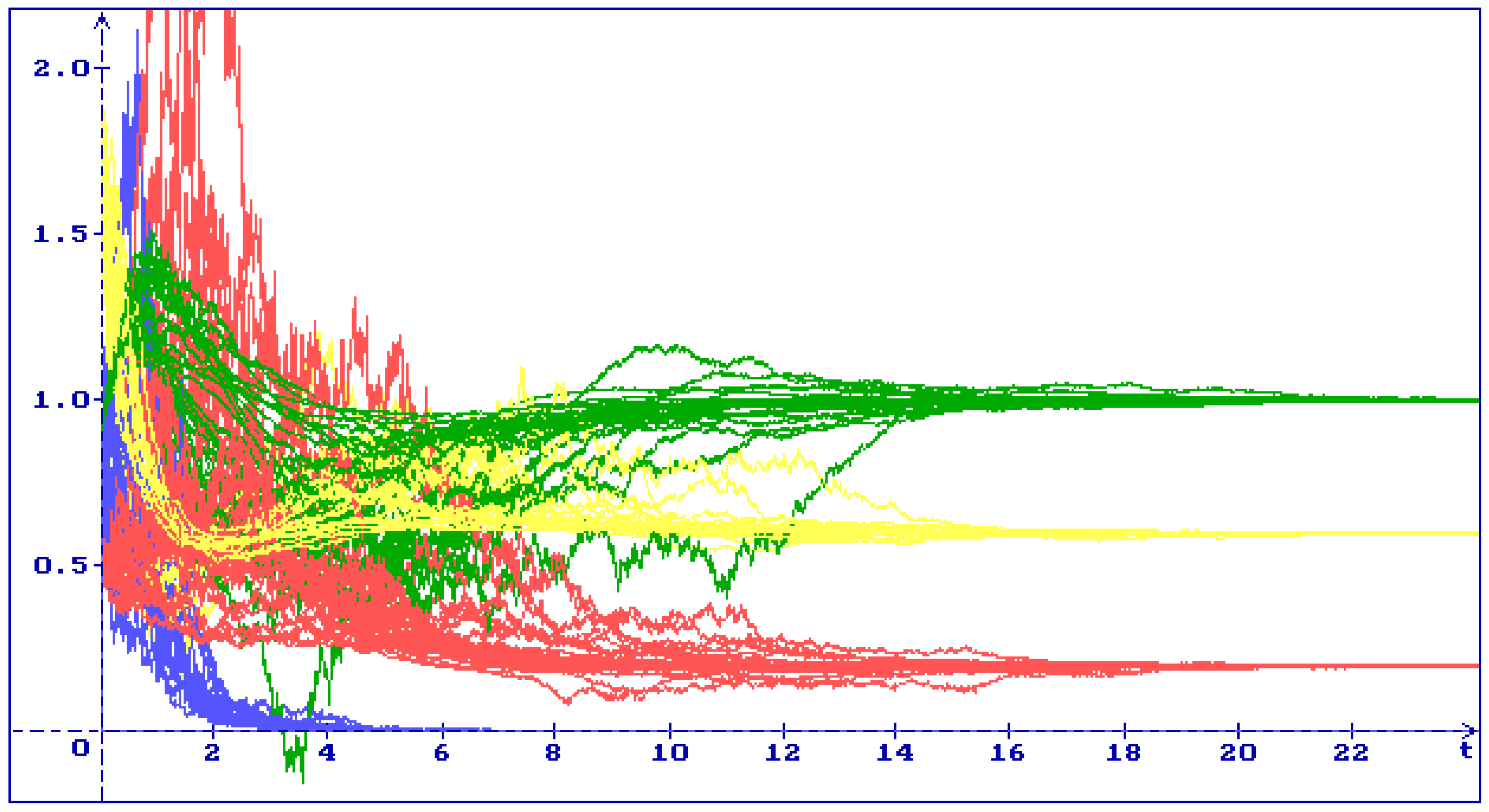
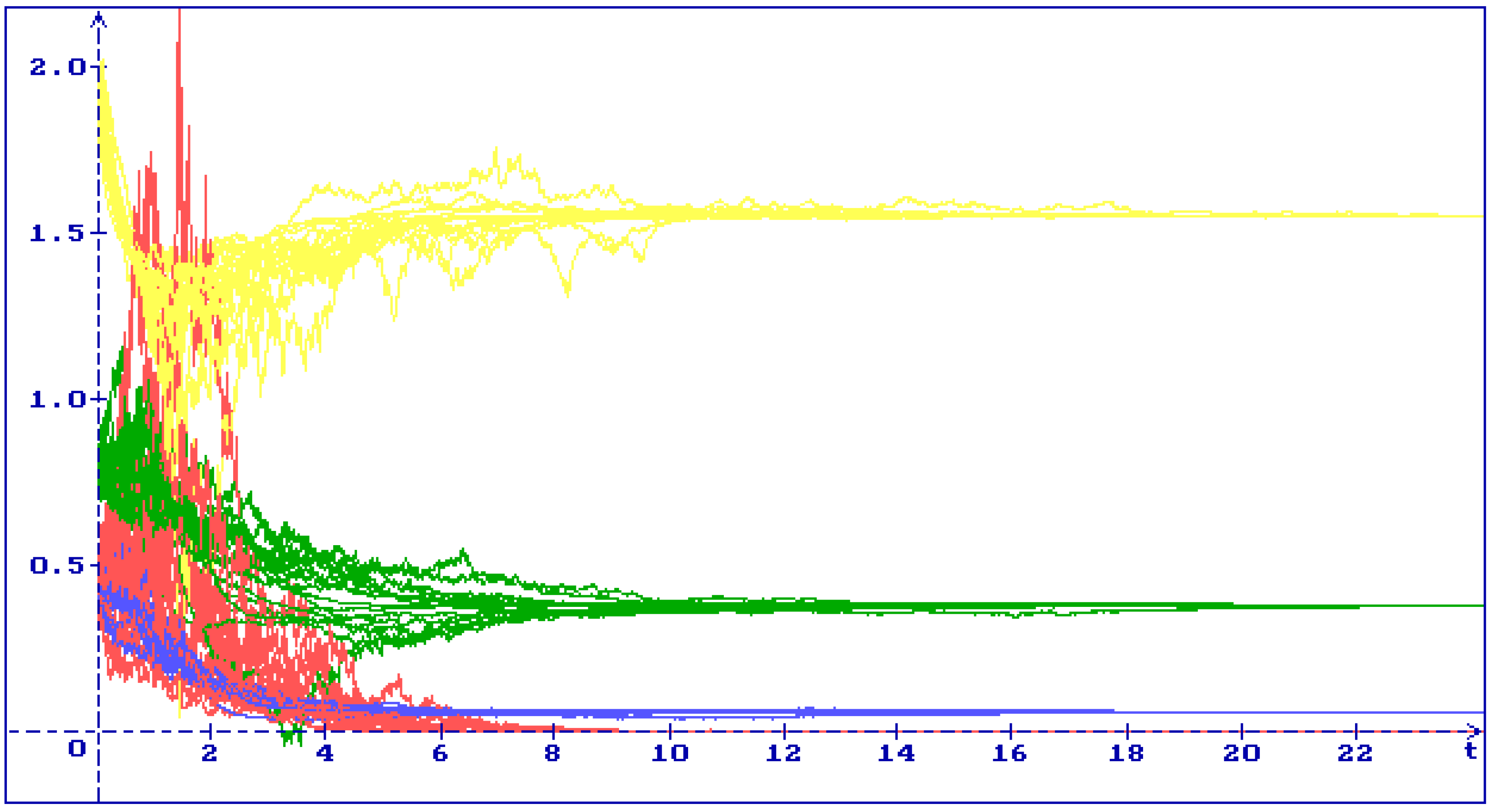
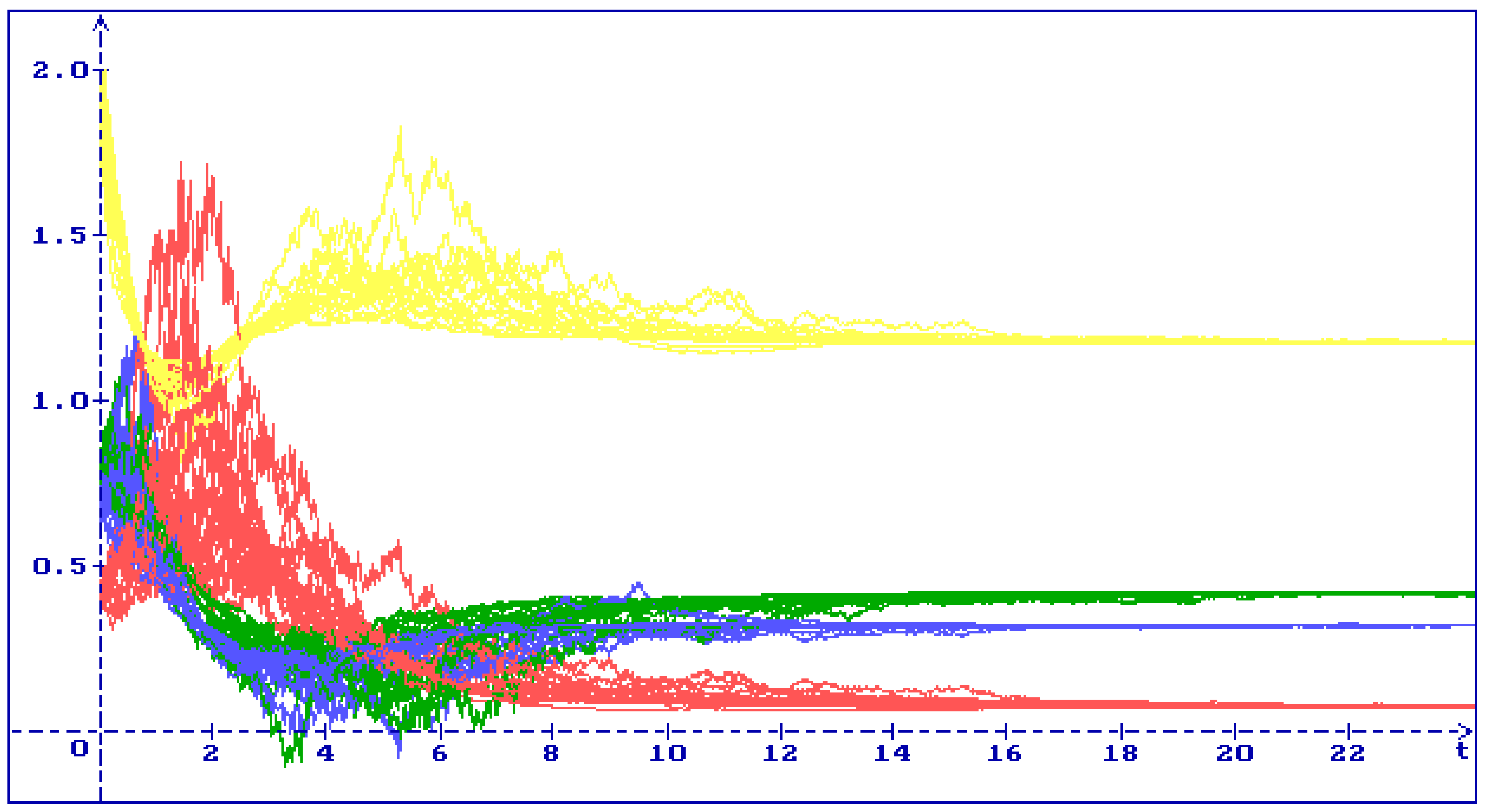
4.1. Stability of the Equilibrium
4.2. Stability of the Equilibrium
4.3. Stability of the Equilibrium
4.4. Stability of the Equilibrium
4.5. Stability of the Equilibrium
5. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Equilibria of the System (1)
Appendix A.2. Stability of the System of Two Stochastic Differential Equations
References
- Beretta, E.; Kolmanovskii, V.; Shaikhet, L. Stability of epidemic model with time delays influenced by stochastic perturbations. Math. Comput. Simul. 1998, 45, 269–277. [Google Scholar] [CrossRef]
- Magal, P.; Webb, G. The parameter identification problem for SIR epidemic models: Identifying unreported cases. J. Math. Biol. 2018, 77, 1629–1648. [Google Scholar] [CrossRef] [PubMed]
- Kiouach, D.; Sabbar, Y. Stability and Threshold of a Stochastic SIRS Epidemic Model with Vertical Transmission and Transfer from Infectious to Susceptible Individuals. Discret. Dyn. Nat. Soc. 2018, 2018, 7570296. [Google Scholar] [CrossRef] [Green Version]
- Santonja, F.-J.; Shaikhet, L. Analysing social epidemics by delayed stochastic models. Discret. Dyn. Nat. Soc. 2012, 2012, 530472. [Google Scholar] [CrossRef] [Green Version]
- Santonja, F.-J.; Shaikhet, L. Probabilistic stability analysis of social obesity epidemic by a delayed stochastic model. Nonlinear Anal. Real World Appl. 2014, 17, 114–125. [Google Scholar] [CrossRef]
- Dietz, K. Epidemics and Rumours: A Survey. J. R. Stat. Soc. Ser. A Gener. 1967, 130, 505–528. [Google Scholar] [CrossRef] [Green Version]
- Zanette, D.H. Dynamics of rumor propagation on small-world networks. Phys. Rev. E 2002, 65, 041908. [Google Scholar] [CrossRef] [Green Version]
- Galam, S. Modelling rumors: The no plane pentagon french hoax case. Physica A 2003, 320, 571–580. [Google Scholar] [CrossRef] [Green Version]
- Moreno, Y.; Nekovee, M.; Pacheco, A.F. Dynamics of rumor spreading in complex networks. Phys. Rev. E 2004, 69, 066130. [Google Scholar] [CrossRef] [Green Version]
- Nekovee, M.; Moreno, Y.; Bianconi, G.; Marsili, M. Theory of rumour spreading in complex social networks. Physica A 2007, 374, 457–470. [Google Scholar] [CrossRef] [Green Version]
- Kawachi, K. Deterministic models for rumor transmission. Nonlinear Anal. Real World Appl. 2008, 9, 1989–2028. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z. An interplay model for rumour spreading and emergency development. Physica A 2009, 388, 4159–4166. [Google Scholar] [CrossRef]
- Roshani, F.; Naimi, Y. Effects of degree-biased transmission rate and nonlinear infectivity on rumor spreading in complex social networks. Phys. Rev. E 2012, 85, 036109. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.J.; Wang, J.J.; Chen, Y.C.; Wang, Q.; Cheng, J.J.; Cui, H.X. SIHR rumor spreading model in social networks. Physica A 2012, 391, 2444–2453. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Han, Y.; Wang, X. Rumor spreading model with trust mechanism in complex social networks. Commun. Theor. Phys. 2013, 59, 510–516. [Google Scholar] [CrossRef]
- Zhao, L.; Qiu, X.; Wang, X.; Wang, J. Rumor spreading model considering forgetting and remembering mechanisms in homogeneous networks. Physica A 2013, 392, 987–994. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Huang, R. SIRaRu rumor spreading model in complex networks. Physica A 2014, 398, 43–55. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Huang, R. 2SI2R rumor spreading model in homogeneous networks. Physica A 2014, 413, 153–161. [Google Scholar] [CrossRef]
- Zan, Y.; Wu, J.; Li, P.; Yu, Q. SICR rumor spreading model in complex networks: Counterattack and self-resistance. Physica A 2014, 405, 159–170. [Google Scholar] [CrossRef]
- Ji, K.; Liu, J.; Xiang, G. Anti-rumor dynamics and emergence of the timing threshold on complex network. Physica A 2014, 411, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Afassinou, K. Analysis of the impact of education rate on the rumor spreading mechanism. Physica A 2014, 414, 43–52. [Google Scholar] [CrossRef]
- Xia, L.L.; Jiang, G.P.; Song, B.; Song, Y.R. Rumor spreading model considering hesitating mechanism in complex social networks. Physica A 2015, 437, 295–303. [Google Scholar] [CrossRef]
- Zhang, N.; Huang, H.; Duarte, M.; Zhang, J. Risk analysis for rumor propagation in metropolises based on improved 8-state ICSAR model and dynamic personal activity trajectories. Physica A 2016, 451, 403–419. [Google Scholar] [CrossRef]
- Wan, C.; Li, T.; Wang, Y.; Liu, X. Rumor Spreading of a SICS Model on complex social networks with counter mechanism. Open Access Libr. J. 2016, 3, 1–11. [Google Scholar] [CrossRef]
- Jie, R.; Qiao, J.; Xu, G.; Meng, Y. A study on the interaction between two rumors in homogeneous complex networks under symmetric conditions. Physica A 2016, 454, 129–142. [Google Scholar] [CrossRef]
- Huo, L.; Wang, L.; Song, N.; Ma, C.; He, B. Rumor spreading model considering the activity of spreaders in the homogeneous network. Physica A 2017, 468, 855–865. [Google Scholar] [CrossRef]
- Liu, Q.M.; Li, T.; Su, M.C. The analysis of an SEIR rumor propagation model on heterogeneous network. Physica A 2017, 469, 372–380. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Y.G. Rumor spreading model with noise interference in complex social networks. Physica A 2017, 469, 750–760. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, Y.; Li, W.; Liu, H. Rumor and authoritative information propagation model considering super spreading in complex social networks. Physica A 2018, 506, 395–411. [Google Scholar] [CrossRef]
- Shaikhet, L. Lyapunov Functionals and Stability of Stochastic Functional Differential Equations; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Shaikhet, L.; Bunimovich-Mendrazitsky, S. Stability Analysis of Delayed Immune Response BCG Infection in Bladder Cancer Treatment Model by Stochastic Perturbations. Comput. Math. Methods Med. 2018, 2018, 9653873. [Google Scholar] [CrossRef] [PubMed]
- Fridman, E.; Shaikhet, L. Simple LMIs for stability of stochastic systems with delay term given by Stieltjes integral or with stabilizing delay. Syst. Control Lett. 2019, 124, 83–91. [Google Scholar] [CrossRef]
- Gikhman, I.I.; Skorokhod, A.V. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Shaikhet, L. Stability of the zero and positive equilibria of two connected neoclassical growth models under stochastic perturbations. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 86–93. [Google Scholar] [CrossRef]
- Shaikhet, L. Stability of the neoclassical growth model under perturbations of the type of Poisson’s jumps: Analytical and numerical analysis. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 78–87. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaikhet, L. Stability of Equilibria of Rumor Spreading Model under Stochastic Perturbations. Axioms 2020, 9, 24. https://doi.org/10.3390/axioms9010024
Shaikhet L. Stability of Equilibria of Rumor Spreading Model under Stochastic Perturbations. Axioms. 2020; 9(1):24. https://doi.org/10.3390/axioms9010024
Chicago/Turabian StyleShaikhet, Leonid. 2020. "Stability of Equilibria of Rumor Spreading Model under Stochastic Perturbations" Axioms 9, no. 1: 24. https://doi.org/10.3390/axioms9010024
APA StyleShaikhet, L. (2020). Stability of Equilibria of Rumor Spreading Model under Stochastic Perturbations. Axioms, 9(1), 24. https://doi.org/10.3390/axioms9010024



