Interval Analysis and Calculus for Interval-Valued Functions of a Single Variable—Part II: Extremal Points, Convexity, Periodicity

Abstract

We continue the presentation of new results in the calculus for interval-valued functions of a single real variable. We start here with the results presented in part I of this paper, namely, a general setting of partial orders in the space of compact intervals (in midpoint-radius representation) and basic results on convergence and limits, continuity, gH-differentiability, and monotonicity. We define different types of (local) minimal and maximal points and develop the basic theory for their characterization. We then consider some interesting connections with applied geometry of curves and the convexity of interval-valued functions is introduced and analyzed in detail. Further, the periodicity of interval-valued functions is described and analyzed. Several examples and pictures accompany the presentation.

1. Introduction

Interval arithmetic and interval analysis initiated with [1,2,3], in relation with the algebraic aspects of how arithmetical operations can be defined for intervals and how to solve problems like algebraic, differential, integral equations or others when intervals are involved. Recently, the interest for this topic increased significantly, in particular after the implementation of specific tools and classes in the C++ and Julia (among others) programming languages, or in computational systems like MATLAB or Mathematica. The research activity in the calculus for interval-valued or set-valued functions (of one or more variables) is now very extended, particularly in connection with the more general calculus for fuzzy-valued functions with applications to almost all fields of applied mathematics. One of the first contributions in the interval-valued calculus is [4] (1979). Similar ideas, in the more general setting of fuzzy valued functions (see, e.g., [5,6]), were developed in [7,8,9]. Contributions in this area are contained, among others, in the papers on gH-differentiability (see, e.g., [10,11,12,13,14,15]; see also [16,17]) and in papers on interval and fuzzy optimization and decision making (e.g, [11,18,19,20,21,22,23,24,25,26]). The multidimensional convex case is analyzed in [27].

This paper is part II of our work on the calculus for interval-valued functions. In part I, we have presented a discussion of partial orders in the space ${\mathcal{K}}_C$ of real intervals, with properties on limits, continuity, gH-differentiability and monotonicity for functions $F:[a,b]⟶{\mathcal{K}}_C$.

In this part, we present a discussion on extremal points (Section 3), concavity and convexity (Section 4) with the use of gH-derivative for its complete analysis; an illustrative example is given in Section 5. Periodicity of interval valued functions is outlined in Section 6 and illustrated with the help of some famous plane curves; conclusions and hints for further work are given in Section 7.

2. Basic Results on Interval Valued Functions

We denote by ${\mathcal{K}}_C$ the family of all bounded closed intervals in $\mathbb{R}$, i.e.,

$${\mathcal{K}}_C=\left\{\left[a^{-},a^{+}\right]|a^{-},a^{+}\in \mathbb{R}\mathrm{and}{a}^{-}\le a^{+}\right\}.$$

The well-known midpoint-radius representation is very useful: for $A=\left[a^{-},a^{+}\right]$, define the midpoint $\widehat{a}$ and radius $\tilde{a}$, respectively, by

$$\widehat{a}=\frac{a^{+}+a^{-}}{2}\mathrm{and}\tilde{a}=\frac{a^{+}-a^{-}}{2},$$

so that $a^{-}=\widehat{a}-\tilde{a}$ and $a^{+}=\widehat{a}+\tilde{a}$. We will denote an interval by $A=[a^{-},a^{+}]$ or, in midpoint notation, by $A=(\widehat{a};\tilde{a})$; so

$${\mathcal{K}}_C=\left\{(\widehat{a};\tilde{a})|\widehat{a},\tilde{a}\in \mathbb{R}\mathrm{and}\tilde{a}\ge 0\right\}.$$

Using midpoint notation, the Minkowski-type operations, for $A=(\widehat{a};\tilde{a}),B=(\widehat{b};\tilde{b})$ and $\tau \in \mathbb{R}$ are:

• $A{\oplus }_{M}B=(\widehat{a}+\widehat{b};\tilde{a}+\tilde{b})$,
• $\tau A=(\tau \widehat{a};|\tau |\tilde{a})$,
• $-A=(-\widehat{a};\tilde{a})$,
• $A{\ominus }_{M}B=(\widehat{a}-\widehat{b};\tilde{a}+\tilde{b})$.

The $gH$-difference of two intervals always exists and, in midpoint notation, is given by

$$\begin{array}{cc}\hfill A{\ominus }_{gH}B& =(\widehat{a}-\widehat{b};|\tilde{a}-\tilde{b}|)\subseteq A{\ominus }_{M}B;\hfill \end{array}$$

the $gH$-addition for intervals is defined by

$$\begin{array}{cc}\hfill A{\oplus }_{gH}B& =A{\ominus }_{gH}(-B)\hfill \\ \hfill & =(\widehat{a}+\widehat{b};|\tilde{a}-\tilde{b}|)\subseteq A{\oplus }_{M}B.\hfill \end{array}$$

Endowed with Pompeiu–Hausdorff distance $d_H:{\mathcal{K}}_C\times {\mathcal{K}}_C\to {\mathbb{R}}_{+}\cup \left\{0\right\}$, defined by

$$d_H(A,B)=\max \left\{{\displaystyle \underset{a\in A}{\max }}d(a,B),{\displaystyle \underset{b\in B}{\max }}d(b,A)\right\}$$

with $d(a,B)={\min }_{b\in B}|a-b|$ and given also as $d_H(A,B)=∥A{\ominus }_{gH}B∥$ (here, for $C\in {\mathcal{K}}_C$, $∥C∥=\max \{\left|c\right|;c\in C\}=d_H(C,\left\{0\right\})$), the metric space $({\mathcal{K}}_C,d_H)$ is complete.

In part I we have introduced a family of general partial order relations, in terms of the gH-comparison index, as follows:

Definition 1.

Given two intervals $A=\left[a^{-},a^{+}\right]=\left(\widehat{a};\overline{a}\right)$ and $B=\left[b^{-},b^{+}\right]=(\widehat{b};\tilde{b})$ and ${\gamma }^{-}\le 0$, ${\gamma }^{+}\ge 0$ (eventually ${\gamma }^{-}=-\infty$ and/or ${\gamma }^{+}=+\infty$) we define the following order relation, denoted ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$,

$$A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B⟺\left\{\begin{array}{c}\widehat{a}\le \widehat{b}\\ \tilde{a}\ge \tilde{b}+{\gamma }^{+}\left(\widehat{a}-\widehat{b}\right)\\ \tilde{a}\le \tilde{b}+{\gamma }^{-}\left(\widehat{a}-\widehat{b}\right)\end{array}\right.$$

(1)

The space $({\mathcal{K}}_C,{⪷}_{{\gamma }^{-},{\gamma }^{+}})$ is a lattice [28,29]. A strict partial order ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$ and a strong partial order ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$ (asymmetric and transitive) are defined as follows:

Definition 2.

Given $A=\left[a^{-},a^{+}\right]=\left(\widehat{a};\overline{a}\right)$ and $B=\left[b^{-},b^{+}\right]=(\widehat{b};\tilde{b})$ and ${\gamma }^{-}\le 0$, ${\gamma }^{+}\ge 0$ (eventually ${\gamma }^{-}=-\infty$ and/or ${\gamma }^{+}=+\infty$ ) we define the following (strict) order relation, denoted ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$,

$$A{⪯}_{{\gamma }^{-},{\gamma }^{+}}B⟺\left\{\begin{array}{c}\widehat{a}<\widehat{b}\\ \tilde{a}\ge \tilde{b}+{\gamma }^{+}\left(\widehat{a}-\widehat{b}\right)\\ \tilde{a}\le \tilde{b}+{\gamma }^{-}\left(\widehat{a}-\widehat{b}\right)\end{array}\right.$$

(2)

and the following (strong) order relation, denoted ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$,

$$A{\prec }_{{\gamma }^{-},{\gamma }^{+}}B⟺\left\{\begin{array}{c}\widehat{a}<\widehat{b}\\ \tilde{a}>\tilde{b}+{\gamma }^{+}\left(\widehat{a}-\widehat{b}\right)\\ \tilde{a}<\tilde{b}+{\gamma }^{-}\left(\widehat{a}-\widehat{b}\right)\end{array}\right.$$

(3)

We have seen in part I that, by varying the two parameters $-\infty \le {\gamma }^{-}\le 0$ and $0\le {\gamma }^{+}\le +\infty$, we can obtain a continuum of partial order relations for intervals and, in particular, we have the following equivalences [29]:

• (Part I, Proposition 6): If A and B are two intervals, then it holds that

  (1)

  $A{⪷}_{LU}B⟺A{⪷}_{-1,1}B$,

  (2)

  $A{⪷}_{C{W}_M}B⟺A{⪷}_{-\infty ,0}B$,

  (3)

  $A{⪷}_{C{W}_m}B⟺A{⪷}_{0,+\infty }B$,

  (4)

  $A{⪷}_{LC}B⟺A{⪷}_{-\infty ,1}B$,

  (5)

  $A{⪷}_{UC}B⟺A{⪷}_{-1,+\infty }B$.

• (Part I, Remark 2)

  $$A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B\iff (A{⪯}_{{\gamma }^{-},{\gamma }^{+}}B\mathrm{or}A=B)$$

  .
• (Part I, Proposition 7-e)

  $${\mathcal{K}}_C=\mathbb{I}(A;{\gamma }^{-},{\gamma }^{+})\bigcup {\mathbb{D}}_{<}(A;{\gamma }^{-},{\gamma }^{+})\bigcup {\mathbb{D}}_{>}(A;{\gamma }^{-},{\gamma }^{+}) \mathrm{where}$$

  $${\mathbb{D}}_{<}(A;{\gamma }^{-},{\gamma }^{+})=\{X\in {\mathcal{K}}_C|A{⪷}_{{\gamma }^{-},{\gamma }^{+}}X\},$$

  $${\mathbb{D}}_{>}(A;{\gamma }^{-},{\gamma }^{+})=\{X\in {\mathcal{K}}_C|X{⪷}_{{\gamma }^{-},{\gamma }^{+}}A\},$$

  $$\mathbb{I}(A;{\gamma }^{-},{\gamma }^{+})=\{X\in {\mathcal{K}}_C|X\notin {\mathbb{D}}_{<}(A;{\gamma }^{-},{\gamma }^{+}),X\notin {\mathbb{D}}_{>}(A;{\gamma }^{-},{\gamma }^{+})\}.$$

  are the sets of intervals dominated by A, dominating A and incomparable with A, respectively.
• (Part I, Proposition 8) for all $A\in {\mathcal{K}}_C$,

  $$A=\inf ({\mathbb{D}}_{<}(A;{\gamma }^{-},{\gamma }^{+}))\mathit{and}A=\sup ({\mathbb{D}}_{>}(A;{\gamma }^{-},{\gamma }^{+})).$$
• (Part I, Proposition 9) For ${\gamma }^{-}\le 0$, ${\gamma }^{+}\ge 0$ and all $A,B\in {\mathcal{K}}_C$,

  $$A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B\iff (-B){⪷}_{-{\gamma }^{+},-{\gamma }^{-}}(-A),$$

  where $-A$ and $-B$ are the opposite intervals of A and B.
• (Part I, Lemma 1) For the lattice $({\mathcal{K}}_C,{⪷}_{{\gamma }^{-},{\gamma }^{+}})$ with ${\gamma }^{-}<0$, ${\gamma }^{+}>0$ and for any $A,B\in {\mathcal{K}}_C$ it is
  (1a) $A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B$⟹$A{\ominus }_{gH}B{⪷}_{{\gamma }^{-},{\gamma }^{+}}0$ (in the right part of implication, ${\gamma }^{+}$ is not involved);
  (1b) $A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B$⟹ $0{⪷}_{{\gamma }^{-},{\gamma }^{+}}B{\ominus }_{gH}A$ (in the right part of implication, ${\gamma }^{-}$ is not involved);
  (2) $A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B⟺\left(A{\ominus }_{gH}B{⪷}_{{\gamma }^{-},{\gamma }^{+}}0\mathrm{and}B{\ominus }_{gH}A{⪸}_{-{\gamma }^{+},-{\gamma }^{-}}0\right)$;
  (3) assuming $-{\gamma }^{-}={\gamma }^{+}=\gamma >0$, then $A{⪷}_{\gamma }B⟺(A{\ominus }_{gH}B{⪷}_{\gamma }0)⟺(B{\ominus }_{gH}A{⪸}_{\gamma }0)$.

Recall that, from

$$A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B\iff (A{⪯}_{{\gamma }^{-},{\gamma }^{+}}B\mathrm{or}A=B),$$

the reverse order is defined by $A{⪸}_{{\gamma }^{-},{\gamma }^{+}}B\iff B{⪷}_{{\gamma }^{-},{\gamma }^{+}}A$, i.e.,

$$A{⪸}_{{\gamma }^{-},{\gamma }^{+}}B⟺\left\{\begin{array}{c}\widehat{a}\ge \widehat{b}\\ \tilde{a}\le \tilde{b}+{\gamma }^{+}\left(\widehat{a}-\widehat{b}\right)\\ \tilde{a}\ge \tilde{b}+{\gamma }^{-}\left(\widehat{a}-\widehat{b}\right).\end{array}\right.$$

(4)

An interval-valued function is defined to be any $F:[a,b]⟶{\mathcal{K}}_C$ with $F(x)=[f^{-}(x),f^{+}(x)]\in {\mathcal{K}}_C$ and $f^{-}(x)\le f^{+}(x)$ for all $x\in [a,b]$. In midpoint representation, we write $F(x)=\left(\widehat{f}(x);\tilde{f}(x)\right)$ where $\widehat{f}(x)\in \mathbb{R}$ is the midpoint value of interval $F(x)$ and $\tilde{f}(x)\in {\mathbb{R}}^{+}\cup \left\{0\right\}$ is the nonnegative half-length of $F(x)$:

$$\widehat{f}(x)=\frac{f^{+}(x)+f^{-}(x)}{2}\mathrm{and}\tilde{f}(x)=\frac{f^{+}(x)-f^{-}(x)}{2}\ge 0$$

so that

$$f^{-}(x)=\widehat{f}(x)-\tilde{f}(x)\mathrm{and}{f}^{+}(x)=\widehat{f}(x)+\tilde{f}(x).$$

In the half-plane $(\widehat{z};\tilde{z})$, $\tilde{z}\ge 0$, each interval $F(x)$ is identified with the point $(\widehat{f}(x);\tilde{f}(x))$.

We will consider the same example functions adopted in part I:

Example 1.

Let $[a,b]=[-1.25,2.5]$, $F:[a,b]\to {\mathcal{K}}_C$, $F(x)=\left(-x^3+2x^2+x-1;1+\sin (\frac{\pi }{2}x)\right)$ in midpoint notation, i.e., $\widehat{f}(x)=-x^3+2x^2+x-1$, $\tilde{f}(x)=1+\sin (\frac{\pi }{2}x)$. For $x=-1.25$ we have $F(-1.25)=(2.828;1.854)=[0.974,4.682]$ and for $x=2.5$ it is $F(2.5)=(-1.625;1.5)=[-3.125,-0.125]$; the values of $x\in [-1.25,2.5]$ where the midpoint function $\widehat{f}(x)$ is minimal or maximal are, approximately, $x_m=-0.215$ with interval value $F(x_m)=(-1.113;1.110)$ and $x_M=1.549$ with interval value $F(x_M)=(1.631;1.424)$.

Example 2.

Let $[a,b]=[-2,4]$, $F:[a,b]\to {\mathcal{K}}_C$, $F(x)=\left(-x^3+4x^2+3x-1;\left|x^2-x-2\right|\right)$. Function $\widehat{f}(x)$ is differentiable on $]a,b[$ with ${\widehat{f}}^{\prime }(x)=-3x^2+8x+3$ and $\tilde{f}(x)$ is differentiable with $\tilde{f}{(x)}^{\prime }=(2x-1)sign(x^2-x-2)$ for $x\ne -1$ and $x\ne 2$; at these two points the left and right derivatives exist: ${\tilde{f}}_l^{\prime }(-1)=-3$, ${\tilde{f}}_r^{\prime }(-1)=3$, ${\tilde{f}}_l^{\prime }(2)=-3$, ${\tilde{f}}_r^{\prime }(2)=3$. Function $F(x)$ is gH-differentiable on $]a,b[$ (including the points $x=-1$ and $x=2$) and $F_{gH}^{\prime }(x)=\left(-3x^2+8x+3;\left|2x-1\right|\right)$; right and left gH-derivatives exist at $a=-2$ and $b=4$, respectively. At the points $a_1=-0.527525$, $a_2=-0.189255$, $a_3=2.527525$ and $a_4=3.522588$, the gH-derivatives are (approximately) $F_{gH}^{\prime }(a_1)=[-4.11,0]$, $F_{gH}^{\prime }(a_2)=[0,2.757]$, $F_{gH}^{\prime }(a_3)=[0,8.11]$, $F_{gH}^{\prime }(a_1)=[-12.09,0]$.

Limits and continuity can be characterized, in the Pompeiu–Hausdorff metric $d_H$ for intervals, by the $gH$-difference. Recalling Proposition 10 in part I, we have that, for a function $F:K⟶{\mathcal{K}}_C$ $K\subseteq \mathbb{R}$, an interval $L=[l^{-},l^{+}]\in {\mathcal{K}}_C$ and an accumulation point $x_0$, we have

$${\displaystyle \underset{x\to x_0}{\lim }}F(x)=L\iff {\displaystyle \underset{x\to x_0}{\lim }}(F(x){\ominus }_{gH}L)=0$$

where the limits are in the metric $d_H$. If, in addition, $x_0\in K$, we have

$${\displaystyle \underset{x\to x_0}{\lim }}F(x)=F(x_0)\iff {\displaystyle \underset{x\to x_0}{\lim }}(F(x){\ominus }_{gH}F(x_0))=0.$$

In midpoint notation, let $F(x)=(\widehat{f}(x);\tilde{f}(x))$ and $L=(\widehat{l};\tilde{l})$. Then the limits and continuity can be expressed, respectively, as

$${\displaystyle \underset{x\to x_0}{\lim }}F(x)=L\iff {\displaystyle \underset{x\to x_0}{\lim }}\widehat{f}(x)=\widehat{l}\mathrm{and}{\displaystyle \underset{x\to x_0}{\lim }}\tilde{f}(x)=\tilde{l}$$

(5)

and

$${\displaystyle \underset{x\to x_0}{\lim }}F(x)=F(x_0)\iff {\displaystyle \underset{x\to x_0}{\lim }}\widehat{f}(x)=\widehat{f}(x_0)\mathrm{and}{\displaystyle \underset{x\to x_0}{\lim }}\tilde{f}(x)=\tilde{f}(x_0).$$

The gH-derivative for an interval-valued function, expressed in terms of the difference quotient by gH-difference, is defined as follows:

Definition 3.

Let $x_0\in ]a,b[$ and h be such that $x_0+h\in ]a,b[$. Then the gH-derivative of a function $F:]a,b[\to {\mathcal{K}}_C$ at $x_0$ is defined as

$$F_{gH}^{\prime }(x_0)={\displaystyle \underset{h\to 0}{\lim }}\frac{1}{h}[F(x_0+h){\ominus }_{gH}F(x_0)]$$

(6)

if the limit exists. The interval $F_{gH}^{\prime }(x_0)\in {\mathcal{K}}_C$ satisfying (6) is called the generalized Hukuhara derivative of F (gH-derivative for short) at $x_0$.

Recall that if $\tilde{f}$ is not differentiable or if its left and right derivatives do not have the same absolute value, then $F_{gH}^{\prime }(x)$ does not exist, but possibly the left and right gH-derivatives $F_{(l)gH}^{\prime }$, $F_{(r)gH}^{\prime }$ exist and we have $F_{(l)gH}^{\prime }(x)=({\widehat{f}}_l^{\prime }(x);|{\tilde{f}}_l^{\prime }(x)|)$, $F_{(r)gH}^{\prime }(x)=({\widehat{f}}_r^{\prime }(x);|{\tilde{f}}_r^{\prime }(x)|)$, where ${(·)}_l^{\prime }$ and ${(·)}_r^{\prime }$ are the notations for left and right derivatives.

The right gH-derivative of F at $x_0$ is $F_{(r)gH}^{\prime }(x_0)={\displaystyle \underset{h\searrow 0}{\lim }}\frac{1}{h}[F(x_0+h){\ominus }_{gH}F(x_0)]$ while, to the left, it is defined as $F_{(l)gH}^{\prime }(x_0)={\displaystyle \underset{h\nearrow 0}{\lim }}\frac{1}{h}[F(x_0+h){\ominus }_{gH}F(x_0)]$. The gH-derivative exists at $x_0$ if and only if the left and right derivatives at $x_0$ exist and are the same interval. In terms of midpoint representation $F(x)=\left(\widehat{f}(x);\tilde{f}(x)\right)$, the existence of the left and right derivatives ${\tilde{f}}_l^{\prime }(x)$ and ${\tilde{f}}_r^{\prime }(x)$ is required with $\left|{\tilde{f}}_l^{\prime }(x)\right|=\left|{\tilde{f}}_r^{\prime }(x)\right|={\tilde{w}}_F(x)\ge 0$ (in particular ${\tilde{w}}_F(x)=\left|{\tilde{f}}^{\prime }(x)\right|$ if ${\tilde{f}}^{\prime }(x)$ exists) so that

$$F_{gH}^{\prime }(x)=\left({\widehat{f}}^{\prime }(x);{\tilde{w}}_F(x)\right).$$

(7)

For a gH-differentiable function, higher-order gH-derivatives are defined analogously to the ordinary case, using the gH-differences applied to the gH-derivatives of previous order:

Definition 4.

Let $F:]a,b[\to {\mathcal{K}}_C$ be gH-differentiable on $]a,b[$ and $x_0\in ]a,b[$ and h be such that $x_0+h\in ]a,b[$. The second order gH-derivative of $F(x)$ at $x_0$ is defined as

$$F_{gH}^{″}(x_0)={\displaystyle \underset{h\to 0}{\lim }}\frac{1}{h}[F_{gH}^{\prime }(x_0+h){\ominus }_{gH}{F}_{gH}^{\prime }(x_0)]$$

(8)

if the limit exists.

The interval $F_{gH}^{″}(x_0)\in {\mathcal{K}}_C$ satisfying (8) is called the second order gH-derivative of F at $x_0$.

Inductively, if the gH-derivatives of orders $1,2,\dots ,k-1$ of $F(x)$ exist on $]a,b[$, denoted respectively by $F_{gH}^{(1)}(x),F_{gH}^{(2)}(x),\dots ,F_{gH}^{(k-1)}(x)$, the gH-derivative of order k is defined as

$$F_{gH}^{(k)}(x_0)={\displaystyle \underset{h\to 0}{\lim }}\frac{1}{h}[F_{gH}^{(k-1)}(x_0+h){\ominus }_{gH}{F}_{gH}^{(k-1)}(x_0)]$$

(9)

if the limit exists.

The interval $F_{gH}^{(k)}(x_0)\in {\mathcal{K}}_C$ satisfying (9) is called the k-order gH-derivative of F at $x_0$.

In terms of notation, we will denote $F(x)$ also by $F_{gH}^{(0)}(x)$. The class of functions $F:]a,b[\to {\mathcal{K}}_C$ with continuous gH-derivatives of orders $1,2,\dots ,k$ at all points $x\in ]a,b[$ for $k\ge 1$, will be denoted by ${\mathcal{C}}_{gH}^{(k)}(]a,b[)$; in particular, ${\mathcal{C}}_{gH}^{(0)}([a,b])$ will denote the class of continuous functions on $[a,b]$ (with right and left continuity at the extremal points).

Remark 1.

In the case of an interval-valued function in the form $F(x)=\left(\widehat{f}(x);\tilde{f}(x)\right)$, $x\in [a,b]$, with $\tilde{f}(x)=\left|\phi (x)\right|$ where $\widehat{f}(x)$ and $\phi (x)$ (assuming that $\phi (x)$ has at most a finite number of zeros in [a,b]) have derivatives ${\widehat{f}}^{(i)}(x)$, ${\phi }^{(i)}(x)$ for $i=1,\dots ,k$, we have that $F(x)$ has all the gH-derivatives $F_{gH}^{(i)}(x)=\left({\widehat{f}}^{(i)}(x);\left|{\phi }^{(i)}(x)\right|\right)$, i=1,…,k. Indeed, either $\phi (x)$ does not change sign or it changes sign at a finite set of points $a_1,\dots ,a_n\in ]a,b[$, we have that the absolute value function $\left|\phi (x)\right|$ has derivative at all points $x\ne a_j$ with ${\left(\left|\phi (x)\right|\right)}^{\prime }={\phi }^{\prime }(x)sign(\phi (x))$; on the other hand, considering left and right derivatives at each $a_j$, it is ${\left(\left|\phi (a_j)\right|\right)}_l^{\prime }=\pm {\left(\left|\phi (a_j)\right|\right)}_r^{\prime }$ for all $j=1,\dots ,n$; it follows that $\tilde{f}(x)=\left|\phi (x)\right|$ has always left and right derivatives with the same absolute values and this ensures that, at all points $x\in ]a,b[$, $F_{gH}^{\prime }(x)=\left({\widehat{f}}^{\prime }(x);\left|{\phi }^{\prime }(x)\right|\right)$. Considering that $F_{gH}^{\prime }(x)$ has the same form as $F(x)$, it is immediate to conclude inductively that the same form is valid for all $i=1,\dots ,k$.

3. Extrema of Interval Valued Functions

The three concepts of monotonicity defined in part I (simple, strict and strong), based on the orders ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$, ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$ and ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$, translate into different concepts of extrema. We will adopt the following terminology:

Definition 5.

If $F(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)$, we say that $F(x_0)$ dominates $F(x)$ with respect to the partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ (for short, $F(x_0)$ $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominates $F(x)$), or equivalently that $F(x)$ is $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominated by $F(x_0)$.

We say that $F(x)$ and $F(x_0)$ are incomparable with respect to ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ if both $F(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)$ and $F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_0)$ are not valid.

Analogous domination rules are defined in terms of the strict and strong order relations ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$ and ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$, respectively.

Remark 2.

Observe that if $F(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)$ and $F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_0)$, i.e., if $F(x)$ and $F(x_0)$ are $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominating each other, then $F(x)=F(x_0)$ and vice-versa, i.e., reciprocal dominance is equivalent to coincidence; the same remains true if the two orders for the dominance are obtained with different pairs $({\gamma }_1^{-},{\gamma }_1^{+})$, $({\gamma }_2^{-},{\gamma }_2^{+})$, ${\gamma }_i^{-}\le 0$ and ${\gamma }_i^{+}\ge 0$ ($i=1,2$), i.e., if $F(x_0){⪷}_{{\gamma }_1^{-},{\gamma }_1^{+}}F(x)$ and $F(x){⪷}_{{\gamma }_2^{-},{\gamma }_2^{+}}F(x_0)$, then $F(x)=F(x_0)$ and vice-versa.

Let us now define the important definitions of order-based minimum and maximum points for an interval valued function.

Definition 6.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function and $x_0\in [a,b]$. Consider the order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ with ${\gamma }^{-}\le 0$, ${\gamma }^{+}\ge 0$. We say that, with respect to ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$,

(a) 

$x_0$ is a local lattice-minimum point of F ($min$-point for short) if there exists $\delta >0$ such that $F(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)$ for all $x\in ]x_0-\delta ,x_0+\delta [\cap [a,b]$, i.e., if all $F(x)$ around $x_0$ are $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominated by $F(x_0)$;

(b) 

$x_0$ is a local lattice-maximum point of F ($max$-point for short) if there exists $\delta >0$ such that $F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_0)$ for all $x\in ]x_0-\delta ,x_0+\delta [\cap [a,b]$, i.e., if all $F(x)$ around $x_0$ $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominate $F(x_0)$.

In case (a) we say that $x_0$ is a $({\gamma }^{-},{\gamma }^{+})$-min-point for F and in case (b) we say that $x_0$ is a $({\gamma }^{-},{\gamma }^{+})$-max-point.

Conditions (a) or (b) in the definition above imply that if there exists $x^{\prime }\in [a,b]$ such that $\widehat{f}(x^{\prime })=\widehat{f}(x_0)$ and $\tilde{f}(x^{\prime })\ne \tilde{f}(x_0)$ then it is impossible to have $F(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x^{\prime })$ nor $F(x^{\prime }){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_0)$ (unless ${\gamma }^{-}=-\infty$ and ${\gamma }^{+}=+\infty$); this means that, except for trivial cases, if $\widehat{f}(x^{\prime })=\widehat{f}(x_0)$ then $F(x^{\prime })$ and $F(x_0)$ are $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-incomparable or coincident.

Remark that a lattice-type extremal value corresponds, locally, to the smallest or greatest elements in the lattice $({\mathcal{K}}_C,{⪷}_{{\gamma }^{-},{\gamma }^{+}})$; it is clear that condition (a) implies that a min-point $x_m$ of F is necessarily a local minimum of the midpoint function $\widehat{f}$, while condition (b) implies that a max-point $x_M$ of F is a local maximum of $\widehat{f}$. It follows that a min-point or a max-point of F are to be searched, respectively, among the minimum or the maximum points of the midpoint function $\widehat{f}$. But this is not sufficient; indeed, lattice-type minimality and maximality, with respect to the partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ can be recognized exactly in terms of the three function $\widehat{f}$, $\tilde{f}-{\gamma }^{+}\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$, as we will see in this section.

It will be useful to explicitly write the conditions for $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominance of a general interval $F(x)$, with respect to the intervals $F(x_m)$ and $F(x_M)$, that characterize the minimality and the maximality of a point $x_m$ (for min) or a point $x_M$ (for max). Without explicit distinction between strict or strong dominance, we have

$$F(x){⪸}_{{\gamma }^{-},{\gamma }^{+}}F(x_m)\iff \left\{\begin{array}{c}\widehat{f}(x)\ge \widehat{f}(x_m)\\ \tilde{f}(x)\le \tilde{f}(x_m)+{\gamma }^{+}\left(\widehat{f}(x)-\widehat{f}(x_m)\right)\\ \tilde{f}(x)\ge \tilde{f}(x_m)+{\gamma }^{-}\left(\widehat{f}(x)-\widehat{f}(x_m)\right),\end{array}\right.$$

(10)

and

$$F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_M)\iff \left\{\begin{array}{c}\widehat{f}(x)\le \widehat{f}(x_M)\\ \tilde{f}(x)\ge \tilde{f}(x_M)+{\gamma }^{+}\left(\widehat{f}(x)-\widehat{f}(x_M)\right)\\ \tilde{f}(x)\le \tilde{f}(x_M)+{\gamma }^{-}\left(\widehat{f}(x)-\widehat{f}(x_M)\right).\end{array}\right.$$

(11)

Proposition 1.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function. Then

(a) 

$x_m\in [a,b]$ is a min-point of F if and only if it is a minimum of $\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ and it is a maximum of $\tilde{f}-{\gamma }^{+}\widehat{f}$;

(b) 

$x_M\in [a,b]$ is a max-point of F if and only if it is a maximum of $\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ and it is a minimum of $\tilde{f}-{\gamma }^{+}\widehat{f}$.

Proof. 

For (a), from the three conditions in (10), the first $\widehat{f}(x)\ge \widehat{f}(x_m)$ says that $x_m$ is a local minimum of $\widehat{f}$, the second $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)\le \tilde{f}(x_m)-{\gamma }^{+}\widehat{f}(x_m)$ say that $x_m$ is a local maximum of $\tilde{f}-{\gamma }^{+}\widehat{f}$, the third $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)\ge \tilde{f}(x_m)-{\gamma }^{-}\widehat{f}(x_m)$ say that $x_m$ is a local minimum of $\tilde{f}-{\gamma }^{-}\widehat{f}$. The proof of (b) is analogous, using the conditions in (11). □

In particular, for the ${⪷}_{LU}$ order, obtained with ${\gamma }^{-}=-1$, ${\gamma }^{+}=1$, we have $\tilde{f}-{\gamma }^{+}\widehat{f}=-f^{-}$, $\tilde{f}-{\gamma }^{-}\widehat{f}=f^{+}$ and the conditions to have a min-point are equivalent to having simultaneously a minimum for $f^{-}$ and $f^{+}$ (and automatically for $\widehat{f}$); on the other hand, max-point conditions are equivalent to have the same maximum points for $f^{-}$ and $f^{+}$, in the ordinary sense.

The discussion above highlights the restricting notion of a lattice-extreme point, as it is not frequent that simultaneous extrema occur for the three functions $\widehat{f}$, $\tilde{f}-{\gamma }^{-}\widehat{f}$ and $\tilde{f}-{\gamma }^{+}\widehat{f}$. The following definition is more general, as it considers the possibility that intervals $F(x)$ for different x are locally incomparable with respect to the actual order relation.

Definition 7.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function and $x_m,x_M\in [a,b]$. We say that, with respect to the order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ and the corresponding strict order ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$,

(c) $x_m$ is a local best-minimum point of F (best-min for short) if:

(c.1) it is a local minimum for the midpoint function $\widehat{f}$, and

(c.2) there exists $\delta >0$ and no point $x\in ]x_m-\delta ,x_m+\delta [\cap [a,b]$ with $F(x)\ne F(x_m)$ such that $F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x_m)$;

(d) $x_M$ is a local best-maximum point of F (best-max for short) if:

(d.1) it is a local maximum for the midpoint function $\widehat{f}$, and

(d.2) there exists $\delta >0$ and no point $x\in ]x_M-\delta ,x_M+\delta [\cap [a,b]$ with $F(x)\ne F(x_M)$ such that $F(x_M){⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)$.

Remark 3.

The definitions above are clearly valid also for points $x_0\in [a,b]$ coincident with one of a or b. It is also evident that a lattice-type extremum is also a best-type extremum.

Definitions of strict and strong (local) extremal points can be given by considering the strict ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$ or the strong ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$ orders associated to the lattice order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$.

Definition 8.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function. With respect to an order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ and the associated strict order ${⪯}_{{\gamma }^{-},{\gamma }^{+}}$ or strong order ${\prec }_{{\gamma }^{-},{\gamma }^{+}}$, we say that

-

a best-min point $x_m$ is a strict (respectively strong) best-minimum point if there exists $\delta >0$ and no point $x\in ]x_m-\delta ,x_m+\delta [\cap [a,b]$ with $F(x){⪯}_{{\gamma }^{-},{\gamma }^{+}}F(x_m)$ (or $F(x){\prec }_{{\gamma }^{-},{\gamma }^{+}}F(x_m)$, respectively);

-

a best-max point $x_M$ is a strict (respectively strong) best-maximum point if there exists $\delta >0$ and no point $x\in ]x_M-\delta ,x_M+\delta [\cap [a,b]$ with $F(x_M){⪯}_{{\gamma }^{-},{\gamma }^{+}}F(x)$ (or $F(x_M){\prec }_{{\gamma }^{-},{\gamma }^{+}}F(x)$, respectively).

Remark 4.

It is clear that the definitions of lattice-type and best-type extremality do not require any assumptions on continuity of the interval-valued function F on $[a,b]$; in the case of continuity (or left/right continuity) the existence of extreme points is also related to the local left and/or right monotonicity of F (with respect to the same partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$).

In order to illustrate basic properties of the various concepts of min/max (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-extremality, we will consider a continuous function $F:[a,b]\to {\mathcal{K}}_C$ and will suppose that there exist two points $x_m,x_M\in [a,b]$ such that $x_m$ is a local minimum point and $x_M$ is a local maximum point, in one of the types defined above.

In the half plane of points $(\widehat{z};\tilde{z})$, $\tilde{z}\ge 0$, the intervals $F(x_m)$ and $F(x_M)$ have midpoint representation, respectively,

$$F(x_m)=\left(\widehat{f}(x_m);\tilde{f}(x_m)\right)\mathrm{and}F(x_M)=\left(\widehat{f}(x_M);\tilde{f}(x_M)\right).$$

(12)

It is immediate that if $x_m\in [a,b]$ is a lattice-minimum point, i.e., there exists a neighborhood of $x_m$ such that all $F(x)$ satisfy (10), then no such $F(x)$ is incomparable with $F(x_m)$; analogously, if $x_M\in [a,b]$ is a lattice-maximum point, i.e., there exists a neighborhood of $x_M$ such that all $F(x)$ satisfy (11), then no such $F(x)$ is incomparable with $F(x_M)$. We can express this fact by saying that the (local) min-efficient frontier for the $min$-point $x_m$ is concentrated into the single interval $F(x_m)$; analogously, the (local) max-efficient frontier for the max-point $x_M$ is concentrated into the single interval $F(x_M)$.

When instead $x_m$ and $x_M$ are best-type extrema and not lattice-type, then it is important to identify the intervals $F(x)$, in particular with x in a neighborhood of $x_m$ or $x_M$, that are not min-dominated by $F(x_m)$ (or do not max-dominate $F(x_M)$); clearly, these $F(x)$ are necessarily (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-incomparable with $F(x_m)$ (or with $F(x_M)$, respectively).

Corresponding to a minimum and to a maximum point of F, we are then interested in identifying the locally (min/max)-efficient intervals $F(x)$ and what we will call the local min or max efficient frontier for $F(x_m)$ and $F(x_M)$ around points $x_m$ and $x_M$, respectively.

In the half plane $(\widehat{z};\tilde{z})$ the conditions to recognize the (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-based dominance and incomparability, assuming ${\gamma }^{-}<0$ and ${\gamma }^{+}>0$, can be written by considering the two lines through $F(x_m)$ with equations

$$F(x_m):\left\{\begin{array}{c}\tilde{z}=\tilde{f}(x_m)+{\gamma }^{+}\left(\widehat{z}-\widehat{f}(x_m)\right)\\ \tilde{z}=\tilde{f}(x_m)+{\gamma }^{-}\left(\widehat{z}-\widehat{f}(x_m)\right)\end{array}\right.$$

and the two lines through $F(x_M)$ with equations

$$F(x_M):\left\{\begin{array}{c}\tilde{z}=\tilde{f}(x_M)+{\gamma }^{+}\left(\widehat{z}-\widehat{f}(x_M)\right)\\ \tilde{z}=\tilde{f}(x_M)+{\gamma }^{-}\left(\widehat{z}-\widehat{f}(x_M)\right).\end{array}\right.$$

For any $x\in [a,b]$ define the following sets of points (sets of intervals in midpoint representation)

$$\begin{array}{cc}\hfill {\mathbb{D}}^{-}(x;{\gamma }^{-},{\gamma }^{+})& =\left\{Z|F(x){⪷}_{{\gamma }^{-},{\gamma }^{+}}Z\right\},\hfill \\ \hfill {\mathbb{D}}^{+}(x;{\gamma }^{-},{\gamma }^{+})& =\left\{Z|Z{⪷}_{{\gamma }^{-},{\gamma }^{+}}F(x)\right\}.\hfill \end{array}$$

The intervals $Z=(\widehat{z};\tilde{z})$ belonging to ${\mathbb{D}}_F^{-}(x;{\gamma }^{-},{\gamma }^{+})$ are $({⪷}_{{\gamma }^{-},{\gamma }^{+}})$-dominated by interval $F(x)$ and the ones belonging to ${\mathbb{D}}_F^{+}(x;{\gamma }^{-},{\gamma }^{+})$ are $({⪸}_{{\gamma }^{-},{\gamma }^{+}})$-dominated by interval $F(x)$. If $x_m$ and $x_M$ are not lattice-type extrema of F, then there exist points $x\in [a,b]$ around $x_m$ (respectively, $x_M$) such that $F(x)\in {\mathbb{D}}_F^{-}(x_m;{\gamma }^{-},{\gamma }^{+})$ (respectively, $F(x)\in {\mathbb{D}}_F^{+}(x_M;{\gamma }^{-},{\gamma }^{+})$). The first step in finding the efficient frontier for a strict minimum and a strict maximum is the following:

Proposition 2.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function with values in the lattice $({\mathcal{K}}_C,{⪷}_{{\gamma }^{-},{\gamma }^{+}})$ endowed by a partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$, ${\gamma }^{-}\le 0,{\gamma }^{+}\ge 0$. Let $x_m,x_M\in [a,b]$ be local strict best-min and local strict best-max points of F. Then, there exist $x_m^L\le x_m$, $x_m^R\ge x_m$, $x_M^L\le x_M$ and $x_M^R\ge x_M$ (all belonging to $[a,b]$) such that, respectively,

1. 

$F(x)$ is incomparable with $F(x_m)$, for all $x\in [x_m^L,x_m^R]$, $x\ne x_m$;

2. 

$F(x)$ is incomparable with $F(x_M)$, for all $x\in [x_M^L,x_M^R]$, $x\ne x_M$.

Proof. 

The proof follows immediately from the definition of strict best-min and best-max points and from the fact that the sets ${\mathbb{D}}_F^{-}(x_m;{\gamma }^{-},{\gamma }^{+})$ and ${\mathbb{D}}_F^{+}(x_M;{\gamma }^{-},{\gamma }^{+})$ are indeed intervals (eventually singletons). □

With reference to Example 1, function $\widehat{f}(x)$ has a local minimum point $x_m=-0.215$ and a local maximum point $x_M=1.549$; with the partial order ${⪷}_{LU}$, i.e., ${\gamma }^m=-1$ and ${\gamma }^{+}=1$, the locally non-dominated points corresponding to $[x_m^L,x_m^R]$ and $[x_M^L,x_M^R]$ are black colored in the top picture of Figure 1; we have $[x_m^L,x_m^R]=[-0.672,-0.003]$ and $[x_M^L,x_M^R]=[1.029,1.916]$, marked with vertical red colored lines around $x_m=-0.215$ and $x_M=1.549$ in the bottom picture.

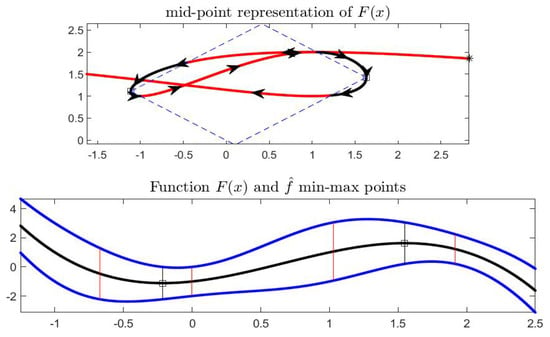
Figure 1. Local min and max points of $F(x)$ in Example 1; function $\widehat{f}(x)$ has a minimum point at $x_m=-0.215$ and a maximum at $x_M=1.549$. Black colored intervals in midpoint representation (top picture) are not dominated by $F(x_m)=(-1.113;1.110)$ for the local min and are not dominated by $F(x_M)=(1.631;1.424)$ for the local max. They correspond to the domain subintervals $[-0.672,-0.003]$ and $[1.029,1.916]$ delimited by vertical red lines in the bottom picture.

The intervals $[x_m^L,x_m^R]$ for a minimum, or $[x_M^L,x_M^R]$ for a maximum, are not difficult to determine; for example, for a minimum point $x_m$, a simple algorithm is to move on left and right of $x_m$ by small steps of length $h>0$ at points $x_m-kh$, $k=1,2,\dots$ until $F(x_m-kh)$ is not dominated by $F(x_m)$ and at points $x_m+kh$, $k=1,2,\dots$ until $F(x_m+kh)$ is not dominated by $F(x_m)$; if $F(x_m-k_m^{L}h)$ is the first dominated value on left and $F(x_m+k_m^{R}h)$ is the first dominated value on right, the extremes $x_m^L$ and $x_m^R$ are found by appropriate bisection iterations to refine the search up to a prescribed precision. An analogous procedure can be designed for a maximum point $x_M$, by moving on the left and right until points $x_M-k_M^{L}h$ and $x_M+k_M^{R}h$ with $F(x_M-k_M^{L}h)$ and $F(x_M+k_M^{R}h)$ dominated by $F(x_M)$; in this case the extremes $x_M^L$ and $x_M^R$ are found by bisections up to a prescribed precision.

A first consequence of Proposition 2 is a sufficient condition for a lattice-type extremal point.

Proposition 3.

Let $F:[a,b]\to {\mathcal{K}}_C$; if $x_m$ (respectively, $x_M$) is a minimum point (a maximum point) of function $\widehat{f}(x)$ and $x_m^L=x_m=x_m^R$ (or $x_M^L=x_M=x_M^R$) then $x_m$ is a lattice min-point (respectively $x_M$ is a lattice max-point) of $F(x)$ and vice versa.

Proof. 

Indeed, in this cases, we have ${\mathbb{D}}_F^{-}(x_m;{\gamma }^{-},{\gamma }^{+})=\left\{F(x_m)\right\}$ and ${\mathbb{D}}_F^{+}(x_M;{\gamma }^{-},{\gamma }^{+})=\left\{F(x_M)\right\}$. □

A second consequence of the last proposition is that the efficient intervals $F(x)$, relative to the best-min point $x_m$ or to the best-max point $x_M$, in the case where they are not lattice extrema, are to be searched among the points $x\in [x_m^L,x_m^R]$ and $x\in [x_M^L,x_M^R]$, respectively.

The final step is now to characterize the points of $[x_m^L,x_m^R]$ and $[x_M^L,x_M^R]$ that contain, respectively, $x_m$, $x_M$ and are such that all the corresponding $F(x)$ define the local efficient frontier of F around $F(x_m)$ and $F(x_M)$, respectively.

We start with a formal definition of the min/max efficient frontier:

Definition 9.

Let $F:[a,b]\to {\mathcal{K}}_C$ be an interval-valued function and let $x_m,x_M\in [a,b]$ be local strict best-min and local strict best-max points of F with respect to the partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$, ${\gamma }^{-}\le 0,{\gamma }^{+}\ge 0$.

(a) 

The (local) min-efficient frontier of function F associated to the best-min point $x_m$ (or to the best-min interval-value $F(x_m)$) is the set $E_{\min }(F,x_m)$ of interval-values $F(x)$ such that:

(a.1) 

$F(x_m)\in E_{\min }(F,x_m)$,

(a.2) 

if $x^{\prime },x^{″}\in [a,b]$ and $F(x^{\prime }),F(x^{″})\in E_{\min }(F,x_m)$ then $F(x^{\prime })$ and $F(x^{″})$ are (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-incomparable,

(a.3) 

no other set $E^{\prime }$ containing $E_{\min }(F,x_m)$ has property (a.2).

The set of points $x\in [x_m^L,x_m^R]$ such that $F(x)\in E_{\min }(F,x_m)$ are the local min-efficient points corresponding to $x_m$ and is denoted by $ef{f}_{\min }(F;x_m)$.

(b) 

The (local) max-efficient frontier of function F associated to the best-max point $x_M$ (or to the best-max interval-value $F(x_M)$) is the set $E_{\max }(F,x_M)$ of interval-values $F(x)$ such that:

(b.1) 

$F(x_M)\in E_{\max }(F,x_M)$,

(b.2) 

if $x^{\prime },x^{″}\in [a,b]$ and $F(x^{\prime }),F(x^{″})\in E_{\max }(F,x_M)$ then $F(x^{\prime })$ and $F(x^{″})$ are (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-incomparable,

(b.3) 

no other set $E^{\prime }$ containing $E_{\max }(F,x_m)$ has property (b.2).

The set of points $x\in [x_M^L,x_M^R]$ such that $F(x)\in E_{\max }(F,x_M)$ are the local max-efficient points corresponding to $x_M$ and is denoted by $ef{f}_{\max }(F;x_M)$.

Clearly, the efficient frontiers $ef{f}_{\min }(F;x_m)$ or $ef{f}_{\max }(F;x_M)$ are subsets of the interval in Proposition 2; but their characterization is not easy, as we can imagine in cases where the function $F(x)$ has possible inflexion or angular points, tangency of high order, multiple nodes, fractal-like or complex pathological patterns (see, e.g., [30]). In those cases it is not immediate to determine which points are not dominated by others of the same interval, or possibly the efficient frontiers may not be intervals.

In the case where function $F(x)$ represents locally a convex plane curve, standard results in elementary differential geometry (see, e.g., [31], chapter 2) are of help in our context. We recall briefly some facts.

Let $C_F$ be the curve, in the half-plane $(\widehat{z};\tilde{z})$ with parametric equations $\widehat{z}=\widehat{f}(x)$, $\tilde{z}=\tilde{f}(x)$ and parameter $x\in [a,b]$ and assume that the curve is simple (no multiple points) and differentiable (i.e., both $\widehat{f}(x)$ and $\tilde{f}(x)$ are differentiable at internal points); one says that the curve $C_F$ has the convexity property if each of its points is such that the curve lies on one side of the tangent line to this point. In our setting, the convexity of $C_F$ is required only locally, by considering the restriction of $F(x)$ to points around $x_m$ (or $x_M$). More precisely, let’s fix the notion of local convexity of $C_F$ by distinguishing the case of a minimum to the case of a maximum point.

Assumption 1.

For a min point $x_m$ (not a lattice min) we will assume that there exist ${\delta }_m^{{}^{\prime }},{\delta }_m^{{}^{″}}\ge 0$ (not both equal to zero) such that the curve corresponding to the restriction of $F(x)$ to the interval $\left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]$ is simple and convex; this happens if the portion of plane on right of the curve, i.e., the set

$${\mathit{P}}_{min}(x_m)={\displaystyle \bigcup _{x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]}}\left\{\left(\widehat{z};\tilde{f}(x)\right)|\widehat{z}\ge \widehat{f}(x)\right\},$$

(13)

is convex; in this case, the following portion of the half plane is convex and bounded

$${\mathit{S}}_{min}(x_m)={\mathit{P}}_{min}(x_m)\bigcap \left\{\left(\widehat{z};\tilde{z}\right)|{\widehat{z}}_{min}\le \widehat{z}\le {\widehat{z}}_{max}\mathrm{and}{\tilde{z}}_{min}\le \tilde{z}\le {\tilde{z}}_{max}\right\}$$

(14)

where ${\widehat{z}}_{min}=\min \left\{\widehat{f}(x)|x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]\right\}$, ${\widehat{z}}_{max}=\max \left\{\widehat{f}(x)|x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]\right\}$ and ${\tilde{z}}_{min}=\min \left\{\tilde{f}(x)|x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]\right\}$, ${\tilde{z}}_{max}=\max \left\{\tilde{f}(x)|x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]\right\}$.

It is not restrictive to assume that interval $\left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]$ is the biggest subinterval of $[x_m^L,x_m^R]$ where the curve $F(x)$ is locally convex.

Assumption 2.

For a max point $x_M$ (not a lattice max), assuming the existence of ${\delta }_M^{{}^{\prime }},{\delta }_M^{{}^{″}}\ge 0$ such that the curve $F(x)$ on interval $\left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]$ is simple and convex, we obtain that the portion of plane on left of the curve, i.e.,

$${\mathit{P}}_{max}(x_M)={\displaystyle \bigcup _{x\in \left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]}}\left\{\left(\widehat{z};\tilde{f}(x)\right)|\widehat{z}\le \widehat{f}(x)\right\},$$

(15)

is convex; in this case, the following set is convex and bounded

$${\mathit{S}}_{max}(x_M)={\mathit{P}}_{max}(x_M)\bigcap \left\{\left(\widehat{z};\tilde{z}\right)|{\widehat{z}}_{min}\le \widehat{z}\le {\widehat{z}}_{max}\mathrm{and}{\tilde{z}}_{min}\le \tilde{z}\le {\tilde{z}}_{max}\right\}$$

(16)

where, this time,

${\widehat{z}}_{min}=\min \left\{\widehat{f}(x)|x\in \left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]\right\}$, ${\widehat{z}}_{max}=\max \left\{\widehat{f}(x)|x\in \left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]\right\}$

and similarly for ${\tilde{z}}_{min}$ and ${\tilde{z}}_{max}$ in terms of $\tilde{f}(x)$.

It is not restrictive to assume that interval $\left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]$ is the biggest subinterval of $[x_M^L,x_M^R]$ where the curve $F(x)$ is locally convex.

Under Assumptions 1 or 2 (using the same notation) we can prove the following results:

Proposition 4.

Let ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order on ${\mathcal{K}}_C$ and let $F:[a,b]\to {\mathcal{K}}_C$ be such that $x_m\in ]a,b[$ is a local min point of $\widehat{f}(x)$ and Assumption (A) is satisfied. Then there exist two points $x_m^{\prime },x_m^{″}\in [x_m^L,x_m^R]$ with $x_m^{\prime }\le x_m\le x_m^{″}$ and such that, for $x\in \left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]$,

(1) 

either $x_m^{\prime }$ maximizes $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and $x_m^{″}$ minimizes $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$,

(2) 

or $x_m^{\prime }$ minimizes $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$ and $x_m^{″}$ maximizes $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$.

Furthermore, interval $[x_m^{\prime },x_m^{″}]$ is the local efficient frontier $ef{f}_{min}(F;x_m)$ of Definition 9.

In particular, if $x_m^{\prime }$ and $x_m^{″}$ are internal to the local convexity region and $\widehat{f}(x)$, $\tilde{f}(x)$ are differentiable, then

$$\left\{\begin{array}{c}{\tilde{f}}^{\prime }(x_m^{\prime })={\gamma }^{+}{\widehat{f}}^{\prime }(x_m^{\prime })\\ {\tilde{f}}^{\prime }(x_m^{″})={\gamma }^{-}{\widehat{f}}^{\prime }(x_m^{″})\end{array}\right.or\left\{\begin{array}{c}{\tilde{f}}^{\prime }(x_m^{″})={\gamma }^{+}{\widehat{f}}^{\prime }(x_m^{″})\\ {\tilde{f}}^{\prime }(x_m^{\prime })={\gamma }^{-}{\widehat{f}}^{\prime }(x_m^{\prime })\end{array}\right..$$

(17)

Proof. 

Consider the two lines with equations $\tilde{z}=q^{+}+{\gamma }^{+}\widehat{z}$ and $\tilde{z}=q^{-}+{\gamma }^{-}\widehat{z}$; points of the curve $F(x)$ in common with one of the two lines will satisfy the equations ${\phi }^{+}(x)=\tilde{f}(x)-q^{+}-{\gamma }^{+}\widehat{f}(x)=0$ and ${\phi }^{-}(x)=\tilde{f}(x)-q^{-}-{\gamma }^{-}\widehat{f}(x)=0$. Solving for $q^{+}$ and $q^{-}$ one obtains $q^{+}=\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and $q^{-}=\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$ and at such common points the two lines have equations: $\tilde{z}=\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)+{\gamma }^{+}\widehat{z}$ and $\tilde{z}=\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)+{\gamma }^{-}\widehat{z}$. Now, by condition (A), the intercepts $q^{+}$ and $q^{-}$, as functions of x, are monotonic around $x_m$; then the maximum value $q_{\ast }^{+}$ of the $q^{+}(x)$ is attained at a point $x_m^{+}$ and the $q^{-}(x)$ has a minimum value $q_{\ast }^{-}$ attained at a point $x_m^{-}$.

By taking $x_m^{\prime }=\min \left\{x_m^{-},x_m^{+}\right\}$ and $x_m^{″}=\max \left\{x_m^{-},x_m^{+}\right\}$, it is clear that conclusions (1) or (2) are satisfied.

If the points $x_m^{+}$ and $x_m^{-}$ are internal to the convexity region $\left[x_m-{\delta }_m^{{}^{\prime }},x_m+{\delta }_m^{{}^{″}}\right]$, then the derivatives of $q^{+}$ and $q^{-}$ at the attained max and min points (respectively) will be zero; this proves conditions (17). They mean that the line of equation $\tilde{z}=q_{\ast }^{+}+{\gamma }^{+}\widehat{z}$ is tangent to the curve $F(x)$ at point $F(x_m^{+})$ and the line $\tilde{z}=q_{\ast }^{-}+{\gamma }^{-}\widehat{z}$ is tangent to $F(x)$ at point $F(x_m^{-})$.

The proof concludes by observing that the efficient region is exactly the interval $x\in [x_m^{\prime },x_m^{″}]$; indeed, by local convexity,

(a)

no points $F(x)$ with $x\in [x_m^{\prime },x_m^{″}]$ are dominated (or dominate) other points in the same interval, and

(b)

points $F(x)$ with $x<x_m^{\prime }$ and $x>x_m^{″}$ (if any) are dominated by $F(x_m^{\prime })$ and by $F(x_m^{″})$, respectively.

 □

Proposition 5.

Let ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order on ${\mathcal{K}}_C$ and let $F:[a,b]\to {\mathcal{K}}_C$ be such that $x_M\in ]a,b[$ is a local max point of $\widehat{f}(x)$ and Assumption (B) is satisfied. Then there exist two points $x_M^{\prime },x_M^{″}\in [x_M^L,x_M^R]$ with $x_M^{\prime }\le x_M\le x_M^{″}$ and such that, for $x\in \left[x_M-{\delta }_M^{{}^{\prime }},x_M+{\delta }_M^{{}^{″}}\right]$,

(1) 

either $x_M^{\prime }$ minimizes $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and $x_M^{″}$ maximizes $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$,

(2) 

or $x_M^{\prime }$ maximizes $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$ and $x_M^{″}$ minimizes $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$.

Furthermore, interval $[x_M^{\prime },x_M^{″}]$ is the local efficient frontier $ef{f}_{max}(F;x_M)$ of Definition 9.

In particular, if $x_M^{\prime }$ and $x_M^{″}$ are internal to the local convexity region and $\widehat{f}(x)$, $\tilde{f}(x)$ are differentiable, then

$$\left\{\begin{array}{c}{\tilde{f}}^{\prime }(x_M^{\prime })={\gamma }^{+}{\widehat{f}}^{\prime }(x_M^{\prime })\\ {\tilde{f}}^{\prime }(x_M^{″})={\gamma }^{-}{\widehat{f}}^{\prime }(x_M^{″})\end{array}\right.or\left\{\begin{array}{c}{\tilde{f}}^{\prime }(x_M^{″})={\gamma }^{+}{\widehat{f}}^{\prime }(x_M^{″})\\ {\tilde{f}}^{\prime }(x_M^{\prime })={\gamma }^{-}{\widehat{f}}^{\prime }(x_M^{\prime })\end{array}\right..$$

(18)

Proof. 

We can proceed analogously to the proof of Proposition 4; in this case, under condition (B), two points $x_M^{-}$ and $x_M^{+}$ are obtained by minimizing the intercept $q^{+}=\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and by maximizing $q^{-}=\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$, respectively. Taking $x_M^{\prime }=\min \{x_M^{-},x_M^{+}\}$ and $x_M^{″}=\max \{x_M^{-},x_M^{+}\}$, the tangency conditions with the curve $F(x)$ are exactly the ones in (18). □

A procedure for the efficient frontiers corresponding to a minimum or maximum point can be obtained in a similar way as for determining the intervals $[x_m^L,x_m^R]$, or $[x_M^L,x_M^R]$; e.g., for a minimum, we move on left and right of $x_m$ by small steps $x_m-kh$ and $x_m+kh$, $k=1,2,\dots$ until the monotonicity of intercepts $q^{+}$ or $q^{-}$ is interrupted in two consecutive points or, equivalently, until a point is found which dominates the next one. Also in this case, we can refine the search by appropriate bisections.

A complete example with several possible situations is presented in Section 5.

With reference to Example 1, the efficient frontiers are $ef{f}_{min}(F;-0.215)=[-0.473,-0.109]$ and $ef{f}_{max}(F;1.549)=[1.279,1.742]$ (see Figure 2).

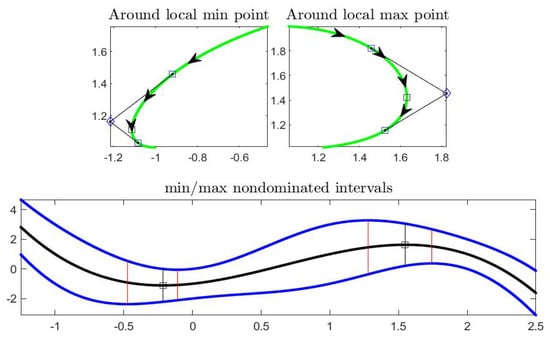
Figure 2. Efficient frontiers for min and max points of $F(x)$ in Example 1. The top pictures show the efficient frontier for $x_m$ (left) and for $x_M$ (right) with the tangent lines to the curve F. In the bottom picture, the efficient frontiers are delimited by vertical red segments containing the min and the max points.

In the next Figure 3, the first derivatives of the three functions $\widehat{f}(x)$, $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$ are visualized (the second is changed in sign with respect to the notation in conditions (A) and (B)); by checking appropriate monotonicity of the three derivatives, we see that condition (A) is satisfied in a neighborhood of $x_m$ and condition (B) is valid around $x_M$. Corresponding to the relevant points, the three derivatives are zero, according to Propositions 4 and 5 (picture on top).

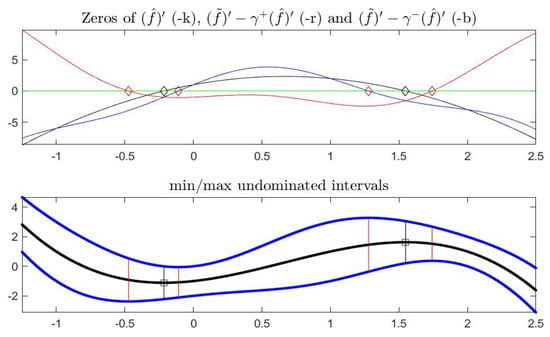
Figure 3. Efficient frontier for min and max points of $F(x)$ in Example 1. The top picture reproduces the derivatives of the three relevant functions $\widehat{f}(x)$, $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ and $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$.

Consider the function $F(x)=\left(\cos (2\pi x);1+\left|x\right|{\sin }^2(\pi x)\right)$ (midpoint notation) of Example 2 with $x\in [-\frac{1}{2},1]$. Figure 4 contains the graph of $F(x)=\left[f^{-}(x),f^{+}(x)\right]$ in interval form (top picture) and in midpoint form $F(x)=\left(\widehat{f}(x);\tilde{f}(x)\right)$ (bottom).

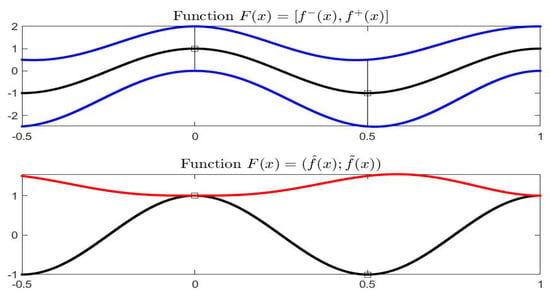
Figure 4. Interval (top) and midpoint (bottom) representations of function $F(x)$ in Example 2.

The point $x_M=0$ with $F(x_M)=(1;1)=[0,2]$ is a local maximum of function $\widehat{f}$ and the point $x_m=\frac{1}{2}$ with $F(x_m)=(-1;\frac{3}{2})=[-\frac{5}{2},\frac{1}{2}]$ is a local minimum of $\widehat{f}$.

Let us chose, e.g., ${\gamma }^{-}=-1$ and ${\gamma }^{+}=\frac{1}{2}$; Figure 5 shows the (${⪷}_{-1,\frac{1}{2}}$)-dominance for the interval-values $F(x)$ with x around $x_m$ and $x_M$. In midpoint representation, $F(x_m)$ appears on the left portion of the top picture and $F(x_M)$ on the right portion; the parallelogram contains the intervals $F(x)$ (in red color) of the graph of F that are (${⪷}_{-1,\frac{1}{2}}$)-dominated by $F(x_m)$ and (${⪸}_{-1,\frac{1}{2}}$)-dominated by $F(x_M)$. The bottom picture marks the intervals $F(x_m)$ and $F(x_M)$ and shows the intervals $[x_m^L,x_m^R]$ and $[x_M^L,x_M^R]$ corresponding to the points around $x_m$ and $x_M$ with dominated interval-values. Clearly, $x_M$ results in a local (and global on the considered domain $[-\frac{1}{2},1]$ of F) lattice-maximum point of F, while $x_m$ is a local (and global) best-minimum point. Indeed, we have that $[x_M^L,x_M^R]$ reduces to the single point $x_M$ while $[x_m^L,x_m^R]$ is the interval $[0.4670,0.5329]$, approximated numerically as it is depending on the actual values of ${\gamma }^{-}$ and ${\gamma }^{+}$.

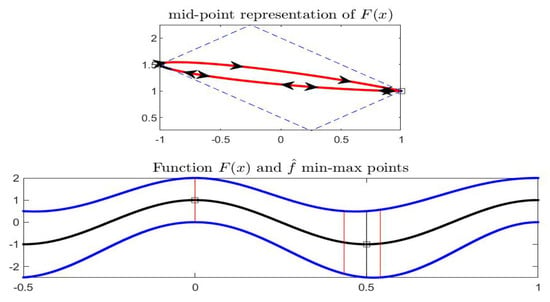
Figure 5. Local min and max points of F(x) in Example 2; function $\widehat{f}(x)$ has a minimum point at $x_m={\displaystyle \frac{1}{2}}$ and a maximum at $x_M=0$. Black colored intervals in midpoint representation (top picture) are not dominated by $F(x_m)=(-{\displaystyle \frac{5}{2}};{\displaystyle \frac{1}{2}})$ for the local min and are not dominated by $F(x_M)=(1;1)$ for the local max. They correspond to the domain subintervals delimited by vertical red lines in the bottom picture.

The local min-efficient frontier corresponding to the best-min point $x_m$, i.e., the points in $ef{f}_{\min }(F;x_m)$, can be easily computed (see below) and are pictured in Figure 6. In the top picture, the green points are the ones min-dominated by $x_m$, corresponding to the points in $[x_m^L,x_m^R]$; the efficient frontier $E_{\min }(F;x_m)$ is identified in the mid-point graph of $F(x)$ by the green points intercepted by the lines with angular coefficients ${\gamma }^{+}>0$, ${\gamma }^{-}<0$ and “tangent” to the graph of F (see below for the details). In the bottom part of the same Figure, the min-efficient frontier is evidenced by vertical lines around $x_m$, corresponding to the points $x\in ef{f}_{\min }(F;x_m)$.

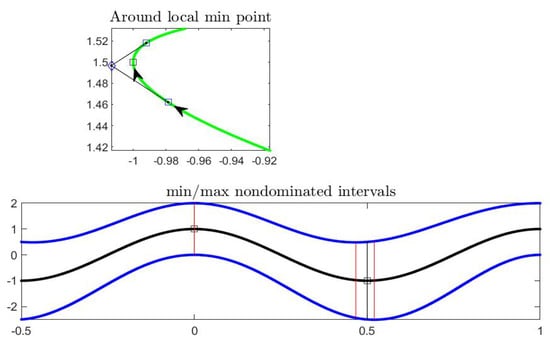
Figure 6. Efficient frontiers for min and max points of $F(x)$ in Example 2. The top picture shows the efficient frontier for $x_m$ with the tangent lines to the curve F. In the bottom picture, the efficient frontiers are delimited by vertical red segments containing the min and max points (the max point is lattice type maximum).

We conclude this section to see how local extremality of a point $x_m$ (minimum) or $x_M$ (maximum) is connected to the left and/or right gH-derivatives $F_{(l)gH}^{\prime }(x_0)=\left({\widehat{f}}_l^{\prime }(x_0);\left|{\tilde{f}}_l^{\prime }(x_0)\right|\right)$, $F_{(r)gH}^{\prime }(x_0)=\left({\widehat{f}}_r^{\prime }(x_0);\left|{\tilde{f}}_r^{\prime }(x_0)\right|\right)$ or to the gH-derivative $F_{gH}^{\prime }(x_0)$ if the two are equal.

Let $F:[a,b]\to {\mathcal{K}}_C$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order. Suppose first that $x_0\in ]a,b[$, $F_{gH}^{\prime }(x_0)=\left({\widehat{f}}^{\prime }(x_0);{\tilde{w}}_F(x_0)\right)$ exists (here ${\tilde{w}}_F(x_0)=\left|{\tilde{f}}_l^{\prime }(x_0)\right|=\left|{\tilde{f}}_r^{\prime }(x_0)\right|$). We have seen that if $x_0$ is a local minimum or maximum point, then ${\widehat{f}}^{\prime }(x_0)=0$ so that $F_{gH}^{\prime }(x_0)=\left(0;{\tilde{w}}_F(x_0)\right)$; as a consequence, a necessary condition for a local min or max at a point of differentiability is that $0\in F_{gH}^{\prime }(x_0)$. If also ${\tilde{w}}_F(x_0)=0$ (i.e., if ${\tilde{f}}^{\prime }(x_0)=0$), then $F_{gH}^{\prime }(x_0)=\left(0;0\right)=0$. Otherwise, if ${\tilde{w}}_F(x_0)>0$, by the continuity of $\tilde{f}$, there exists a neighborhood of $x_0$ where $F(x)$ is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-incomparable with $F(x_0)$. So, we have the following Fermat-like property:

Proposition 6.

Let $F:]a,b[\to {\mathcal{K}}_C$, $x_0\in ]a,b[$, F gH-differentiable at $x_0$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order on ${\mathcal{K}}_C$.

(1) 

If $x_0$ is a lattice extremum for F (a lattice-min or a lattice-max point), then $F_{gH}^{\prime }(x_0)=0$;

(2) 

If $x_0$ is a best-extremum for F (a best-min or a best-max point), then $0\in$ $F_{gH}^{\prime }(x_0)$.

Also contrapositive versions of the statements are evident: if $0\notin$ $F_{gH}^{\prime }(x_0)$, then $x_0$ is not a local extremum for F.

In the cases where F has left or right gH-derivatives at $x_0$ (or they are not equal), necessary conditions for a lattice-min or a best-min (respectively, a lattice-max or a best-max) can be easily deduced according to Proposition 14 in part I.

Proposition 7.

Let $F:[a,b]\to {\mathcal{K}}_C$, $x_0\in [a,b]$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order on ${\mathcal{K}}_C$. Suppose that F has left and right gH-derivatives at $x_0$ (if $x_0=a$ or $x_0=b$ we consider only the right or the left gH-derivatives, respectively)

(1.a) 

If $x_0$ is a lattice minimum point for F, then $F_{(l)gH}^{\prime }(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}0$ and $F_{(r)gH}^{\prime }(x_0){⪸}_{{\gamma }^{-},{\gamma }^{+}}0$;

(1.b) 

If $x_0$ is a lattice maximum point for F, then $F_{(l)gH}^{\prime }(x_0){⪸}_{{\gamma }^{-},{\gamma }^{+}}0$ and $F_{(r)gH}^{\prime }(x_0){⪷}_{{\gamma }^{-},{\gamma }^{+}}0$;

(2.a) 

If $x_0$ is a best-minimum point for F, then $0\in$ $F_{gH}^{\prime }(x_0)$.

(2.b) 

If $x_0$ is a best-maximum point for F, then $0\in$ $F_{gH}^{\prime }(x_0)$.

The following are sufficient conditions based on the “sign” of left and right gH-derivatives, analogous to the well known situation for single-valued functions.

Proposition 8.

Let $F:[a,b]\to {\mathcal{K}}_C$, $x_0\in [a,b]$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a partial order on ${\mathcal{K}}_C$. Suppose that F has left and right gH-derivatives at $x_0$ (if $x_0=a$ or $x_0=b$ we consider only the right or the left gH-derivatives, respectively)

(a) 

If $F_{(l)gH}^{\prime }(x_0){\prec }_{{\gamma }^{-},{\gamma }^{+}}0$ and $F_{(r)gH}^{\prime }(x_0){\succ }_{{\gamma }^{-},{\gamma }^{+}}0$, then $x_0$ is a best minimum point for F;

(b) 

If $F_{(l)gH}^{\prime }(x_0){\succ }_{{\gamma }^{-},{\gamma }^{+}}0$ and $F_{(r)gH}^{\prime }(x_0){\prec }_{{\gamma }^{-},{\gamma }^{+}}0$, then $x_0$ is a best maximum point for F.

4. Concavity and Convexity of Interval-Valued Functions

We have three types of convexity, similar to the monotonicity and local extremum concepts.

Definition 10.

Let $F:[a,b]\to {\mathcal{K}}_C$ be a function and let ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$, ${\gamma }^{-}\le 0,{\gamma }^{+}\ge 0$ be a partial order for intervals. We say that

(a-i) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){⪷}_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in [0,1]$;

(a-ii) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){⪸}_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in [0,1]$.

(b-i) 

$F$ is strictly (${⪯}_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){⪯}_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in ]0,1[$;

(b-i) 

F is strictly (${⪯}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){\succsim }_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in ]0,1[$.

(c-i) 

F is strongly (${\prec }_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){\prec }_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in ]0,1[$;

(c-iii) 

F is strongly (${\prec }_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $[a,b]$ if and only if $F((1-\lambda )x_1+\lambda x_2){\succ }_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2),$ $\forall x_1,x_2\in [a,b]$ and all $\lambda \in ]0,1[$.

The convexity of a function $F=\left(\widehat{f};\tilde{f}\right)$ is related to the concavity of function $-F=\left(-\widehat{f};\tilde{f}\right)$, as follows:

Proposition 9.

Let $F:[a,b]\to {\mathcal{K}}_C$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a given partial order with ${\gamma }^{-}<0$, ${\gamma }^{+}>0$. Consider also the partial order ${⪷}_{-{\gamma }^{+},-{\gamma }^{-}}$. Then $F=\left(\widehat{f};\tilde{f}\right)$ is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex if and only if $-F=\left(-\widehat{f};\tilde{f}\right)$ is (${⪷}_{-{\gamma }^{+},-{\gamma }^{-}}$)-concave. In particular, if ${\gamma }^{+}=-{\gamma }^{-}=\gamma >0$, then F is (${⪷}_{\gamma }$)-convex if and only if $-F$ is (${⪷}_{\gamma }$)-concave.

Proof. 

We know (part I, Proposition 9) that, for intervals $A,B\in {\mathcal{K}}_C$, it is $A{⪷}_{{\gamma }^{-},{\gamma }^{+}}B$ if and only if $(-B){⪷}_{-{\gamma }^{+},-{\gamma }^{-}}(-A)$; in the last partial order, the roles of ${\gamma }^{-}$ and ${\gamma }^{+}$ are interchanged by changing their sign so that $-{\gamma }^{+}<0$ and $-{\gamma }^{-}>0$. The proof follows immediately. □

The following result expresses the (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convexity of F in terms of the convexity of functions $\widehat{f}$, $\tilde{f}-{\gamma }^{+}\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$:

Proposition 10.

Let $F=\left(\widehat{f};\tilde{f}\right):[a,b]\to {\mathcal{K}}_C$ and ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ be a given partial order; then

1. 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex if and only if $\widehat{f}$ is convex, $\tilde{f}-{\gamma }^{+}\widehat{f}$ is concave and $\tilde{f}-{\gamma }^{-}\widehat{f}$ is convex;

2. 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave if and only if $\widehat{f}$ is concave, $\tilde{f}-{\gamma }^{+}\widehat{f}$ is convex and $\tilde{f}-{\gamma }^{-}\widehat{f}$ is concave.

Proof. 

For 1., let $x_1,x_2\in [a,b]$ and $\lambda \in [0,1]$ and denote $x_{\lambda }=(1-\lambda )x_1+\lambda x_2$. Condition $F(x_{\lambda }){⪷}_{{\gamma }^{-},{\gamma }^{+}}(1-\lambda )F(x_1)+\lambda F(x_2)$ means

$$\left\{\begin{array}{c}\widehat{f}(x_{\lambda })\le (1-\lambda )\widehat{f}(x_1)+\lambda \widehat{f}(x_2)\\ \tilde{f}(x_{\lambda })\ge (1-\lambda )\tilde{f}(x_1)+\lambda \tilde{f}(x_2)+{\gamma }^{+}\left(\widehat{f}(x_{\lambda })-(1-\lambda )\widehat{f}(x_1)-\lambda \widehat{f}(x_2)\right)\\ \tilde{f}(x_{\lambda })\le (1-\lambda )\tilde{f}(x_1)+\lambda \tilde{f}(x_2)+{\gamma }^{-}\left(\widehat{f}(x_{\lambda })-(1-\lambda )\widehat{f}(x_1)-\lambda \widehat{f}(x_2)\right)\end{array}\right.;$$

From the first inequality, $\widehat{f}$ is convex; the second inequality becomes

$$\tilde{f}(x_{\lambda })-{\gamma }^{+}\widehat{f}(x_{\lambda })\ge (1-\lambda )\left(\tilde{f}(x_1)-{\gamma }^{+}\widehat{f}(x_1)\right)+\lambda \left(\tilde{f}(x_2)-{\gamma }^{+}\lambda \widehat{f}(x_2)\right)$$

i.e., $\tilde{f}(x)-{\gamma }^{+}\widehat{f}(x)$ is concave. The third inequality is

$$\tilde{f}(x_{\lambda })+{\gamma }^{-}\widehat{f}(x_{\lambda })\le (1-\lambda )\left(\tilde{f}(x_1)+{\gamma }^{-}\widehat{f}(x_1)\right)+\lambda \left(\tilde{f}(x_2)+{\gamma }^{-}\lambda \widehat{f}(x_2)\right),$$

i.e., $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$ is convex. To prove 2., we can proceed in a similar way. □

Strict (${⪯}_{{\gamma }^{-},{\gamma }^{+}}$)-convexity (respectively, concavity) of F in terms of functions $\widehat{f}$, $\tilde{f}-{\gamma }^{+}\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ can be easily deduced: in this case, the midpoint function $\widehat{f}$ is strictly convex (respectively, concave), $\tilde{f}-{\gamma }^{+}\widehat{f}$ is concave (respectively, convex) and $\tilde{f}-{\gamma }^{-}\widehat{f}$ is convex (respectively, concave). Strong convexity of F corresponds to strict convexity and/or concavity of $\widehat{f}$, $\tilde{f}-{\gamma }^{+}\widehat{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ (in the right way).

It is interesting to remark that an interval-valued function $F=(\widehat{f};\tilde{f})$ which is both (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex and (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $[a,b]$ exhibits a strong linearity, in the sense that both $\widehat{f}$ and $\tilde{f}$ are linear on $[a,b]$; indeed, from $F((1-\lambda )x_1+\lambda x_2)=(1-\lambda )F(x_1)+\lambda F(x_2)$ one obtains

$$\begin{array}{cc}\hfill \widehat{f}((1-\lambda )x_1+\lambda x_2)& =(1-\lambda )\widehat{f}(x_1)+\lambda \widehat{f}(x_2)\hfill \\ \hfill \tilde{f}((1-\lambda )x_1+\lambda x_2)& =(1-\lambda )\tilde{f}(x_1)+\lambda \tilde{f}(x_2).\hfill \end{array}$$

Proposition 11.

Let $F=\left(\widehat{f};\tilde{f}\right):[a,b]\to {\mathcal{K}}_C$ be (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex or (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave; then F is continuous on $]a,b[$.

Proof. 

From Proposition 10, the three functions $\widehat{f}$, $g^{+}=\tilde{f}-{\gamma }^{+}\widehat{f}$ and $g^{-}=\tilde{f}-{\gamma }^{-}\widehat{f}$ are convex or concave, hence they are continuous on the internal points of $[a,b]$. As $\tilde{f}=g^{+}+{\gamma }^{+}\widehat{f}$ and both $g^{+}$ and $\widehat{f}$ are continuous, we have that $\widehat{f}$ and $\tilde{f}$ are continuous and F is continuous. □

From Proposition 10, several ways to analyze (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convexity (or concavity) in terms of the first or second derivatives of functions $\widehat{f}$, ${\gamma }^{+}\widehat{f}-\tilde{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ can be easily deduced.

Proposition 12.

Let $F=\left(\widehat{f};\tilde{f}\right):]a,b[\to {\mathcal{K}}_C$ with differentiable $\widehat{f}$ and $\tilde{f}$;

1. 

If the first order detivatives ${\widehat{f}}^{\prime }$ and ${\tilde{f}}^{\prime }$ exist, then:

(1-a) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $]a,b[$ if and only if ${\widehat{f}}^{\prime }$, ${\gamma }^{+}{\widehat{f}}^{\prime }-{\tilde{f}}^{\prime }$ and ${\tilde{f}}^{\prime }-{\gamma }^{-}{\widehat{f}}^{\prime }$ are increasing (nondecreasing) on $]a,b[$;

(1-b) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $]a,b[$ if and only if ${\widehat{f}}^{\prime }$, ${\gamma }^{+}{\widehat{f}}^{\prime }-{\tilde{f}}^{\prime }$ and ${\tilde{f}}^{\prime }-{\gamma }^{-}{\widehat{f}}^{\prime }$ are decreasing (nonincreasing) on $]a,b[$;

2. 

If the second order derivatives ${\widehat{f}}^{″}$ and ${\tilde{f}}^{″}$ exist and are continuous, then:

(2-a) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $]a,b[$ if and only if ${\widehat{f}}^{″}\ge 0$, ${\gamma }^{+}{\widehat{f}}^{″}-{\tilde{f}}^{″}\ge 0$ and ${\tilde{f}}^{″}-{\gamma }^{-}{\widehat{f}}^{″}\ge 0$ on $]a,b[$;

(2-b) 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $]a,b[$ if and only if ${\widehat{f}}^{″}\le 0$, ${\gamma }^{+}{\widehat{f}}^{″}-{\tilde{f}}^{″}\le 0$ and ${\tilde{f}}^{″}-{\gamma }^{-}{\widehat{f}}^{″}\le 0$ on $]a,b[$.

Proof. 

The proof follows from well-known results in elementary calculus. □

In order to connect concavity and convexity with the monotonicity of the gH-derivative and, for a partial order ${⪷}_{\gamma }$ with $\gamma >0$, with the “sign” of the second-order gH-derivative, we need the following well known result on real convex functions:

Lemma 1.

For a function $g:]a,b[\to \mathbb{R}$ to be convex on $]a,b[$, a necessary and sufficient condition is that for all $x_0\in ]a,b[$ the incremental function $g_{x_0}:]a,b[\setminus \left\{x_0\right\}\to \mathbb{R}$, defined by $g_{x_0}(x)=\frac{g(x)-g(x_0)}{x-x_0}$ is nondecreasing for $x\in ]a,b[\setminus \left\{x_0\right\}$. Furthermore, g admits left and right derivatives at any $x_0\in ]a,b[$ and $g_l^{\prime }(x_0)\le g_r^{\prime }(x_0)$.

Proof. 

Consider $x_1<x_2$ (both different from $x_0$); after simple manipulations, we have

$$\begin{array}{cc}\hfill \frac{g_{x_0}(x_1)-g_{x_0}(x_2)}{x_1-x_2}& =\frac{(x_1-x_0)\left(g(x_2)-g(x_0)\right)-(x_2-x_0)\left(g(x_1)-g(x_0)\right)}{(x_2-x_1)(x_2-x_0)(x_1-x_0)}\hfill \\ \hfill & =\frac{(x_1-x_2)g(x_0)+(x_2-x_0)g(x_1)+(x_0-x_1)g(x_2)}{(x_1-x_2)(x_2-x_0)(x_0-x_1)}.\hfill \end{array}$$

(19)

On the other hand, from the convexity of g, we have $g(x)\le g(x_1)+\frac{g(x_2)-g(x_1)}{x_2-x_1}(x-x_1)$ for all $x\in [x_1,x_2]$ and, taking $x_1<x_0<x_2$ (this is not restrictive because the right-hand side in (19) is symmetric with respect to $x_0$, $x_1$ and $x_2$) we obtain $(x_2-x_1)g(x_0)\le (x_2-x_0)g(x_1)+g(x_2)(x_0-x_1)$ and, combining with the second line in (19),

$$\frac{g_{x_0}(x_1)-g_{x_0}(x_2)}{x_1-x_2}=\frac{-\left((x_2-x_1)g(x_0)-(x_0-x_1)g(x_2)-(x_2-x_0)g(x_1)\right)}{(x_2-x_1)(x_2-x_0)(x_0-x_1)}\ge 0.$$

To prove the last part, the incremental function $x\to g_{x_0}(x)$ is nondecreasing and admits left and right limits at $x_0$, with $G_l={\displaystyle \underset{x\nearrow x_0}{\lim }}{g}_{x_0}(x)\le {\displaystyle \underset{x\searrow x_0}{\lim }}{g}_{x_0}(x)=G_r$; on the other hand, clearly, $G_l=g_l^{\prime }(x_0)$ and $G_r=g_r^{\prime }(x_0)$ and this completes the proof. □

Proposition 13.

Let $F:[a,b]\to {\mathcal{K}}_C$ for all $x_0\in ]a,b[$. Consider the incremental functions of $\widehat{f}$ and $\tilde{f}$, defined for $x\in ]a,b[$, $x\ne x_0$ by

$$\widehat{h}(x;x_0)=\frac{\widehat{f}(x)-\widehat{f}(x_0)}{x-x_0},\tilde{h}(x;x_0)=\frac{\tilde{f}(x)-\tilde{f}(x_0)}{x-x_0}$$

and let ${\tilde{h}}^{+}(x;x_0)$ and ${\tilde{h}}^{-}(x;x_0)$ be the incremental functions of ${\gamma }^{+}\widehat{f}-\tilde{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ respectively, given by

$${\tilde{h}}^{+}(x;x_0)={\gamma }^{+}\widehat{h}(x;x_0)-\tilde{h}(x;x_0),{\tilde{h}}^{-}(x;x_0)=\tilde{h}(x;x_0)-{\gamma }^{-}\widehat{h}(x;x_0).$$

Then

1. 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex on $[a,b]$ if and only if $\widehat{h}(x;x_0)$, ${\tilde{h}}^{+}(x;x_0)$ and ${\tilde{h}}^{-}(x;x_0)$ are nondecreasing in $]a,b[\setminus \left\{x_0\right\}$.

2. 

F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $[a,b]$ if and only if $\widehat{h}(x;x_0)$, ${\tilde{h}}^{+}(x;x_0)$ and ${\tilde{h}}^{-}(x;x_0)$ are nonincreasing in $]a,b[\setminus \left\{x_0\right\}$.

Proof. 

From Proposition 10, the three functions $\widehat{f}$, ${\gamma }^{+}\widehat{f}-\tilde{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ are convex (in case 1.) or concave (in case 2.); by virtue of Lemma 1 their incremental functions $\widehat{h}(x;x_0)$, ${\tilde{h}}^{+}(x;x_0)$ and ${\tilde{h}}^{-}(x;x_0)$ are either non decreasing (in case 1.) or non increasing (in case 2.) and the conclusion follows. □

Proposition 14.

Let $F=\left(\widehat{f};\tilde{f}\right):]a,b[\to {\mathcal{K}}_C$ and let ${\gamma }^{-}\le 0$, ${\gamma }^{+}\ge 0$. If F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex or (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-concave on $]a,b[$, then $F_{(l)gH}^{\prime }$ and $F_{(r)gH}^{\prime }$ both exist on $]a,b[$. If ${\widehat{f}}_l^{\prime }={\widehat{f}}_r^{\prime }$ then also ${\tilde{f}}_l^{\prime }={\tilde{f}}_r^{\prime }$ and $F_{(l)gH}^{\prime }=F_{(r)gH}^{\prime }=F_{gH}^{\prime }$.

Proof. 

We know that F is (${⪷}_{{\gamma }^{-},{\gamma }^{+}}$)-convex if and only if $\widehat{f}$, ${\gamma }^{+}\widehat{f}-\tilde{f}$ and $\tilde{f}-{\gamma }^{-}\widehat{f}$ are convex; from the second part of Lemma 1, their left and right derivatives exist so that also ${\tilde{f}}_l^{\prime }$ and ${\tilde{f}}_r^{\prime }$ exist. It follows that $F_{(l)gH}^{\prime }=\left({\widehat{f}}_l^{\prime };\left|{\tilde{f}}_l^{\prime }\right|\right)$ and $F_{(r)gH}^{\prime }=\left({\widehat{f}}_r^{\prime };\left|{\tilde{f}}_r^{\prime }\right|\right)$ with ${\widehat{f}}_l^{\prime }\le {\widehat{f}}_r^{\prime }$, ${\gamma }^{+}{\widehat{f}}_l^{\prime }-{\tilde{f}}_l^{\prime }\le {\gamma }^{+}{\widehat{f}}_r^{\prime }-{\tilde{f}}_r^{\prime }$, ${\tilde{f}}_l^{\prime }-{\gamma }^{-}{\widehat{f}}_l^{\prime }\le {\tilde{f}}_r^{\prime }-{\gamma }^{-}{\widehat{f}}_r^{\prime }$. If ${\widehat{f}}_l^{\prime }={\widehat{f}}_r^{\prime }$ then $-{\tilde{f}}_l^{\prime }\le -{\tilde{f}}_r^{\prime }$, ${\tilde{f}}_l^{\prime }\le {\tilde{f}}_r^{\prime }$ and ${\tilde{f}}_l^{\prime }={\tilde{f}}_r^{\prime }={\tilde{f}}^{\prime }$, so ${\tilde{f}}^{\prime }$ exists. □

Remark 5.

Analogously to the relationship between the sign of second derivative and convexity for ordinary functions, we can establish conditions for convexity of interval functions and the sign of the second order gH-derivative $F_{gH}^{″}(x)$; for example, a sufficient condition for strong ${\prec }_{LU}$-convexity (i.e., with respect to the partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$ with ${\gamma }^{+}=-{\gamma }^{-}=1$) is the following (compare with Proposition 12):

1. 

If $F_{gH}^{″}(x_0){\prec }_{LU}0$ then $F(x)$ is strongly concave at $x_0$.

2. 

If $F_{gH}^{″}(x_0){\succ }_{LU}0$ then $F(x)$ is strongly convex at $x_0$.

A simple case is the function $F(x)$ of Example 2, for which the second-order gH-derivative exist for all $x\in [-2,4]$ with $F_{gH}^{″}(x)=\left(-6x+8;2\right)=[-6x+6,-6x+10]$. $F(x)$ is strongly convex for $x\in ]-2,1[$ and strongly concave for $x\in ]{\displaystyle \frac{5}{3}},4[$; if $x\in ]1,{\displaystyle \frac{5}{3}}[$ we have $0\in [-6x+6,-6x+10]$ so that $F(x)$ cannot be strongly convex nor concave.

5. Complete Discussion of an Example

We conclude the presentation of our results with a complete discussion of the following example.

Complete Example: function $F:\mathbb{R}\to {\mathcal{K}}_C$ is defined by $\widehat{f}(x)=\cos (x)+2\cos ({\displaystyle \frac{x}{2}})$ and $\tilde{f}(x)=1.2+\sin (x)$ for $x\in [a,b]=[-{\displaystyle \frac{3}{4}},{\displaystyle \frac{3}{4}}]$. In this example, we have chosen ${\gamma }^{-}=-1.2$, ${\gamma }^{+}=0.8$. Remark that both $\widehat{f}(x)$ and $\tilde{f}(x)$ are differentiable so that, in midpoint notation, the first order gH-derivative is $F_{gH}^{\prime }(x)=({\widehat{f}}^{\prime }(x);|{\tilde{f}}^{\prime }(x)|)$ and the second order gH-derivative is $F_{gH}^{″}(x)=({\widehat{f}}^{″}(x);|{\tilde{f}}^{″}(x)|)$ (see [12,14]).

All computations are performed with a precision of at least five decimal digits.

Internally to $[a,b]$, we consider eleven points where $\widehat{f}(x)$ is locally minimal or maximal (we will ignore the first and last ones as too near to boundaries a, b). They are marked in Figure 7 by a blue diamond symbol. They are denoted $x_i,i=1,2,\dots ,11$ corresponding to the rows in Table 1.

Figure 7. Interval-valued function $F(x)$ (top) of the Complete Example. Bottom picture gives functions $\widehat{f}(x)$ (black color) and $\tilde{f}(x)$ (red).

Table 1. Relevant points of $F(x)$ in the Complete Example.

i	${\mathit{x}}_{\mathit{i}}$	$\mathit{F}({\mathit{x}}_{\mathit{i}})$	${\mathit{F}}_{\mathit{gH}}^{\prime }({\mathit{x}}_{\mathit{i}})$	${\mathit{F}}_{\mathit{gH}}^{″}({\mathit{x}}_{\mathit{i}})$	Type	Efficient Region
1	−0.637302	$(0.549;1.506)$	$(0.0;0.735)$	$(-73.71;35.18)$	max	$[-0.6433,-0.6078]$
2	−0.490592	$(0.184;1.089)$	$(0.0;3.842)$	$(78.26;7.600)$	min	$[-0.5619,-0.4425]$
3	−0.382304	$(0.358;0.807)$	$(0.0;0.726)$	$(-76.13;41.61)$	max	$[-0.3987,-0.3753]$
4	−0.245329	$(0.046;1.029)$	$(0.0;2.956)$	$(79.91;0.844)$	min	$[-0.2755,-0.1930]$
5	−0.127422	$(0.262;1.252)$	$(0.0;0.0)$	$(-77.31;38.70)$	max	$\{-0.127422\}$
6	0.0	(0.0;1.0)	(0.0;3.142)	(80.46;0.0)	min $x_m$	[-0.0523,0.0334]
7	0.127422	$(0.262;0.748)$	$(0.0;0.0)$	$(-77.31;38.70)$	max	$\left\{0.127422\right\}$
8	0.245329	$(0.046;0.971)$	$(0.0;2.956)$	$(79.91;0.844)$	min	$[0.2125,0.2905]$
9	0.382304	$(0.358;1.193)$	$(0.0;0.726)$	$(-76.13;41.61)$	max $x_M$	$[0.3769,0.4174]$
10	0.490592	$(0.184;0.911)$	$(0.0;3.842)$	$(78.26;7.600)$	min	$[0.4176,0.5328]$
11	0.637302	$(0.549;0.494)$	$(0.0;0.735)$	$(-73.71;35.18)$	max	$[0.6241,0.6453]$

The two points $x_m=0$ and $x_M=0.3823$, corresponding to a local minimum and maximum of $\widehat{f}(x)$ and marked, in the $(x,y)$-plane, with a square symbol, will be analyzed in detail. The vertical segments in top of Figure 7 represent intervals $F(x_m)=[-1,1]$ and $F(x_M)=[-0.8356,1.5506]$.

Figure 8 gives the first order gH-derivative of $F(x)$; remark that, according to fourth column in Table 1, we always have $0\in F_{gH}^{\prime }(x_i)$ and $F_{gH}^{\prime }(x_5)=F_{gH}^{\prime }(x_7)=0$.

Figure 8. Complete Example: first order gH-derivative $F_{gH}^{\prime }(x)$ in interval form; black curve is ${\widehat{f}}^{\prime }(x)$.

In Figure 9 the gH-derivative is pictured in midpoint half plane $\left(\widehat{z};\tilde{z}\right)$; the points where ${\widehat{f}}^{\prime }(x)=0$ are marked in correspondence with the value $\widehat{z}$ on the abscissa (compare also with Table 1).

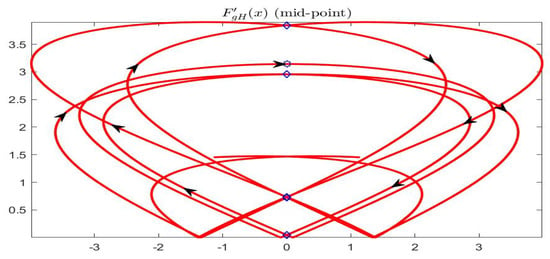
Figure 9. Complete Example: first order gH-derivative $F_{gH}^{\prime }(x)=\left({\widehat{f}}^{\prime }(x);\left|{\tilde{f}}^{\prime }(x)\right|\right)$ in midpoint form.

The second order gH-derivative, represented in Figure 10, shows that the intervals $F_{gH}^{″}(x)$, as expected, are entirely positive at the minima and negative at the maxima. Remark that in no points the first and second derivatives of $\widehat{f}(x)$ are simultaneously zero.

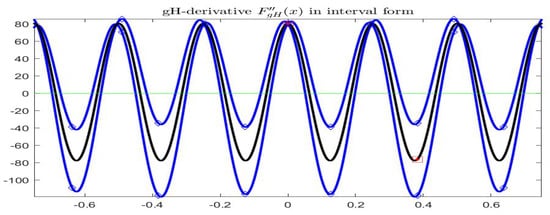
Figure 10. Complete Example: second order gH-derivative $F_{gH}^{″}(x)$ in interval form; the black curve is ${\widehat{f}}^{″}(x)$.

In this example, where both $\widehat{f}(x)$ and $\tilde{f}(x)$ have continuous second order derivative, the convexity region is particularly simple to identify, due to a well known Theorem based on the sign of the curvature of curve $C_F$ associated to $F(x)$. We consider the following function $\kappa (x)={\widehat{f}}^{\prime }(x){\tilde{f}}^{″}(x)-{\widehat{f}}^{″}(x){\tilde{f}}^{\prime }(x)$ (its sign coincides with the sign of the curvature of $C_F$ at x). We then search for the points, on the left and right of $x_m$, at which the sign of $\kappa (x)$ has the same sign of $\kappa (x_m)$. Analogous result is valid for $x_M$ (see Chapter 6 in [32] for the general result). In our example we find the interval $[-0.14535,0.07545]$ around $x_m$ and the interval $[0.37170,0.41745]$ around $x_M$ (see Figure 11).

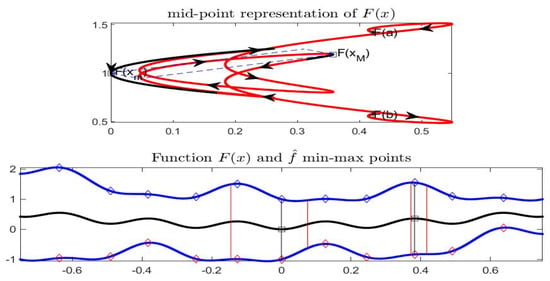
Figure 11. Complete Example: local convexity of curve $C_F$ corresponding to $x_m$ and $x_M$ (top picture). In the bottom picture, the values of x corresponding to local convex portion of $F(x)$ are delimited by red vertical lines.

From the local convexity of the curve $C_F$, the efficient regions corresponding to $x_m$ and $x_M$ are computed under Assumption 1 for min and Assumption 2 for max; the resulting intervals, illustrated in Figure 12, are, respectively, $[-0.05235,0.03345]$ around $x_m$ and the interval $[0.37695,0.41745]$ for $x_M$.

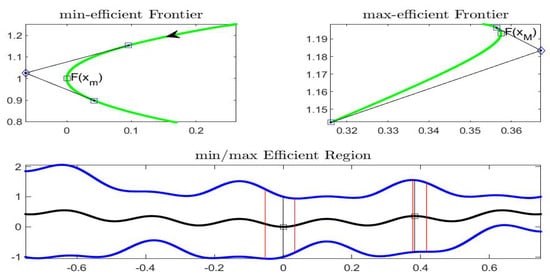
Figure 12. Complete Example: (top) efficient regions corresponding to $x_m$ and $x_M$ (top picture), obtained by tangency conditions. (Bottom) the efficient regions around the min and max points are delimited by vertical red lines.

The next Figure 13 gives the three functions $\widehat{f}(x)$, ${\gamma }^{+}\widehat{f}(x)-\tilde{f}(x)$, $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$; as we have seen in part I, their sign gives information on the monotonicity of $F(x)$. In particular, if all three functions (observe that the second function is changed in sign with respect to the properties in part I) have the same sign (hence are also not zero) at a point x, then $F(x)$ is strictly increasing or decreasing with respect to the partial order ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$. The same information can be eventually deduced from the sigh of the tree derivatives ${\widehat{f}}^{\prime }(x)$, ${\gamma }^{+}{\widehat{f}}^{\prime }(x)-{\tilde{f}}^{\prime }(x)$, ${\tilde{f}}^{\prime }(x)-{\gamma }^{-}{\widehat{f}}^{\prime }(x)$, given in Figure 14; at points where the three derivatives have different signs, then function $F(x)$ is not ${⪷}_{{\gamma }^{-},{\gamma }^{+}}$-monotonic.

Figure 13. Complete Example: functions $\widehat{f}(x)$, ${\gamma }^{+}\widehat{f}(x)-\tilde{f}(x)$, $\tilde{f}(x)-{\gamma }^{-}\widehat{f}(x)$.

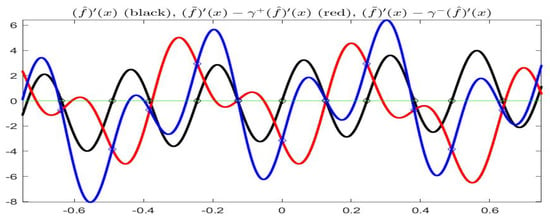
Figure 14. Complete Example: functions ${\widehat{f}}^{\prime }(x)$, ${\gamma }^{+}{\widehat{f}}^{\prime }(x)-{\tilde{f}}^{\prime }(x)$, ${\tilde{f}}^{\prime }(x)-{\gamma }^{-}{\widehat{f}}^{\prime }(x)$.

The results of our analysis, as described for the min and max points $x_m$ and $x_M$, are visualized in Figure 15, giving the midpoint representation of $F(x)$. Here, we see the position of point $F(x_m)$, with the delimiters $F(x_m^{\prime })$, $F(x_m^{″})$ of the efficient region $E_{min}(F;x_m)$ (in green color); analogously, the position of the max point $F(x_M)$ is evidenced, with the delimiters $F(x_M^{\prime })$, $F(x_M^{″})$ of the efficient region $E_{max}(F;x_M)$. Clearly, the two points correspond to local best-min and best-max points (not of lattice type).

Figure 15. Complete Example: function $F(x)$ is represented in midpoint form, together with the efficient points corresponding to $x_m$ and $x_M$.

The last three Figures summarize, respectively, the computations for all the local minima and maxima considered in Table 1. The first Figure 16 reproduces $F(x)$ in interval form, with the visualization of the six local maxima and the five local minima, classified according to the computations. The points $x_i$, $i=1,2,\dots ,11$ in the first column of Table 1, together with corresponding interval values $F(x_i)$ (as in the second column) are marked with a vertical segment in black color. Correspondingly, the efficient regions are delimited by vertical lines (cyan-colored for max points and magenta for min points). There are two local maxima, corresponding to $x_5=-0.127422$ with $F(x_5)=(0.262;1.252)=[-0.99,1.514]$ and $x_7=0.127422$ with $F(x_7)=(0.262;0.748)=[-0.486,1.01]$ which are lattice max-points: the efficient frontier coincides with the point itself and the two maximal intervals dominate locally all the near intervals $F(x)$ (in the figure, the black and cyan vertical lines are coincident). This is also visible in Figure 17 in terms of the values of the three derivatives ${\widehat{f}}^{\prime }(x)$, ${\gamma }^{+}{\widehat{f}}^{\prime }(x)-{\tilde{f}}^{\prime }(x)$ and ${\tilde{f}}^{\prime }(x)-{\gamma }^{-}{\widehat{f}}^{\prime }(x)$ evaluated at $x_i$ and at the points defining the efficient regions: for the two lattice maxima, the three derivative are zero, while in the other minima or maxima only ${\widehat{f}}^{\prime }(x_i)$ is zero and the other two derivatives do not have (at least generally) the same sign (but one or both may possibly be zero).

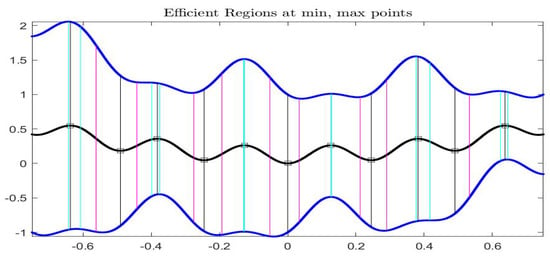
Figure 16. Complete Example: function $F(x)$ is represented in interval form, and all the zeros $x_i$ of $\widehat{f}(x)$ are classified as min or max points; all the efficient regions are delimited by vertical lines (cyan-colored for six max points and magenta for five min points). The black vertical lines are the intervals $F(x_i)$, $i=1,2,\dots ,11$.

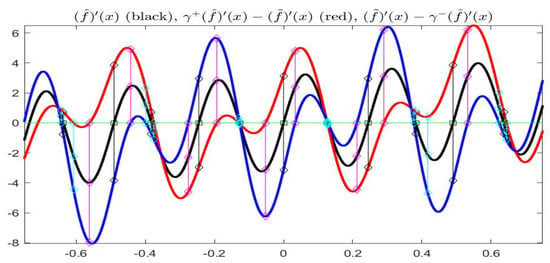
Figure 17. Complete Example: functions ${\widehat{f}}^{\prime }(x)$, ${\gamma }^{+}{\widehat{f}}^{\prime }(x)-{\tilde{f}}^{\prime }(x)$ and ${\tilde{f}}^{\prime }(x)-{\gamma }^{-}{\widehat{f}}^{\prime }(x)$ are evaluated at classified min and max points and the corresponding efficient frontiers are delimited by vertical lines (cyan-colored for max and magenta for min points).

Finally, Figure 18 summarizes all the computations by the midpoint visualization of our function $F(x)$, with all the points $F(x_i)$ and the corresponding efficient regions.

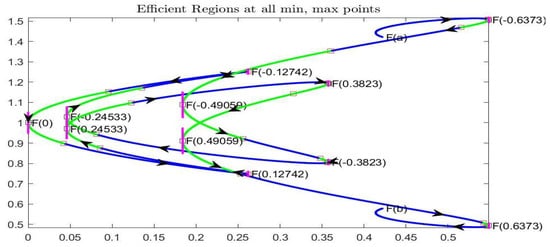
Figure 18. Complete Example: function $F(x)$ is represented in midpoint form, and all local minima (five points) and maxima (six points) are marked together with corresponding efficient regions.

6. An Outline of Periodic Interval-Valued Functions (and Famous Plane Curves)

Considering points where the trajectory of an interval-valued function $F(x)=(\widehat{f}(x);\tilde{f}(x))$ crosses itself, i.e., $x_1$, $x_2$ exist with $F(x_1)=F(x_2)$ (equivalently $\widehat{f}(x_1)=\widehat{f}(x_2)$ and $\tilde{f}(x_1)=\tilde{f}(x_2))$, it follows that periodicity of F is also easy to describe.

Definition 11.

A function $F:[a,b]\to {\mathcal{K}}_C$ is said to be periodic if, for some nonzero constant $T\in ]0,b-a[$, it occurs that $F(x+T)=F(x)$ for all $x\in [a,b]$ with $x+T\in [a,b]$ (i.e., for all $x\in [a,b-T]$). A nonzero constant T for which this is verified, is called a period of the function and if there exists a least positive constant T with this property, it is called the fundamental period.

Obviously, if F has a period T, then this also implies that: $(\widehat{f}(x+T);\tilde{f}(x+T))=(\widehat{f}(x);\tilde{f}(x))$, so that $\widehat{f}(x+T)=\widehat{f}(x)$ and $\tilde{f}(x+T)=\tilde{f}(x)$, for all $x\in [a,b-T]$, i.e., $\widehat{f}$ and $\tilde{f}$ are periodic with period T; remark that if T is the fundamental period of F, this does not necessarily imply that T is fundamental period for both $\widehat{f}$ and $\tilde{f}$. On the other hand, the periodicity of $\widehat{f}$ and $\tilde{f}$ does not necessarily imply the periodicity of F.

Proposition 15.

Let $F:[a,b]\to {\mathcal{K}}_C$ be a continuous function such that $F(x)=(\widehat{f}(x);\tilde{f}(x))$ with $\widehat{f}$ periodic of period $\widehat{T}$ and $\tilde{f}$ of period $\tilde{T}$. Then it holds that:

(1) 

if the periods $\widehat{T}$ and $\tilde{T}$ are commensurable, i.e., $\frac{\widehat{T}}{\tilde{T}}\in \mathbb{Q}$ ($\frac{\widehat{T}}{\tilde{T}}=\frac{p}{q}$, such that p and q are coprime) then the function F is periodic of period $T=lcm(\widehat{T},\tilde{T})$, i.e,. T is the least common multiple between $\widehat{T}$ and $\tilde{T}$ (i.e., $T=p\tilde{T}=q\widehat{T}$);

(2) 

if the periods $\widehat{T}$ and $\tilde{T}$ are not commensurable, i.e., $\frac{\widehat{T}}{\tilde{T}}\notin \mathbb{Q}$, then function F is not periodic.

Periodic Example 1: consider the function $F:\mathbb{R}\to {\mathcal{K}}_C$ defined by periodic functions $\widehat{f}(x)=5\sin \left(-3x+{\displaystyle \frac{\pi }{3}}\right)$ and $\tilde{f}(x)=\left|cos({\displaystyle \frac{9}{4}}x)\right|$. Figure 19 and Figure 20 picture $F(x)$ for $x\in [a,b]=[0,{\displaystyle \frac{4}{3}}\pi ]$. On this interval, function $\widehat{f}(x)$ has two minimal and two maximal points (see bottom picture in Figure 19). We have chosen $x_m=0.8726$ with $F(x_m)=(-5;0.3825)$ and $x_M=4.014$ with $F(x_M)=(5;0.9238)$, located in Figure 20, where also the points corresponding to efficient regions $ef{f}_{min}(F;x_m)=[0.8243,0.9169]$ and $ef{f}_{max}(F,x_M)=[3.993,4.032]$ are given in green color. Here ${\gamma }^{-}=-1$ and ${\gamma }^{+}=1$ giving the $({⪷}_{LU})$-order.

Figure 19. Periodic Example 1: Function $F(x)$ is pictured on top and functions $\widehat{f}(x)$, $\tilde{f}(x)$ on bottom. Marked points correspond to $x_m$ and $x_M$, where the two functions are differentiable.

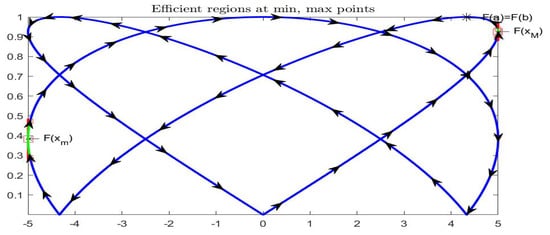
Figure 20. Periodic Example 1: midpoint representation of function $F(x)$; marked points are $F(x_m)$ and $F(x_M)$ and the efficient $E_{\min }(F;x_m)$ and $E_{\max }(F,x_M)$ points are marked in green color.

Periodic Example 2 (Siamese fishes): function $F:\mathbb{R}\to {\mathcal{K}}_C$ is defined by periodic functions $\widehat{f}(x)=5\cos (x)-(\sqrt{2}-1)\cos (5x)$ and $\tilde{f}(x)=1.5+\sin (4x)$. Figure 21 and Figure 22 picture $F(x)$ for $x\in [a,b]=[0,2\pi ]$. Internal to this interval, function $\widehat{f}(x)$ has two minimal and three maximal points (see bottom picture in Figure 21); we have chosen $x_m=2.7489$ with $F(x_m)=(-4.7779;0.5)$ and $x_M=0.3911$ with $F(x_M)=(4.7779;2.5)$, located in Figure 22, where also the points corresponding to efficient regions $ef{f}_{min}(F;x_m)=[2.1828,2.7489]$ and $ef{f}_{max}(F,x_M)=[0,0.3927]$ are given in green color. Here ${\gamma }^{-}=-1$ and ${\gamma }^{+}=0.5$.

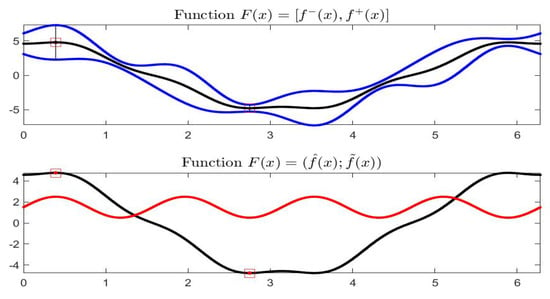
Figure 21. Periodic Example 2 (Siamese fishes): function $F(x)$ is pictured on top and functions $\widehat{f}(x)$, $\tilde{f}(x)$ on bottom. Marked points correspond to $x_m$ and $x_M$, where the two functions are differentiable.

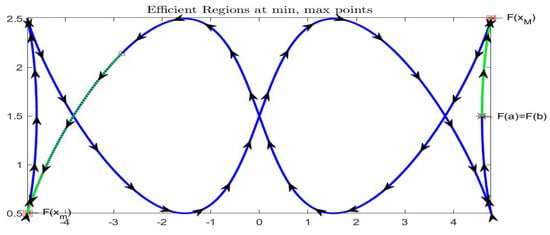
Figure 22. Periodic Example 2 (Siamese fishes): midpoint representation of function $F(x)$; marked points are $F(x_m)$ and $F(x_M)$ and the efficient $E_{\min }(F;x_m)$ and $E_{\max }(F,x_M)$ points are marked in green color.

Periodic Example 3 (big fish): function $F:\mathbb{R}\to {\mathcal{K}}_C$ is defined by periodic functions $\widehat{f}(x)=\cos (x)+2\cos ({\displaystyle \frac{x}{2}})$ and $\tilde{f}(x)=1.2+\sin (x)$. Figure 23 and Figure 24 picture $F(x)$ for $x\in [a,b]=[0,4\pi ]$. Internal to this interval, function $\widehat{f}(x)$ has two minimal and one maximal points (see bottom picture in Figure 23); we have chosen $x_m=8.378$ with $F(x_m)=(-1.5;2.066)$ and $x_M=2\pi$ with $F(x_M)=(-1,1.2)$, located in Figure 24, where also the points corresponding to efficient regions $ef{f}_{min}(F;x_m)=[8.1568,8.8555]$ and $ef{f}_{max}(F,x_M)=[5.4488,7.1176]$ are given in green color. Here ${\gamma }^{-}=-2$ and ${\gamma }^{+}=2$.

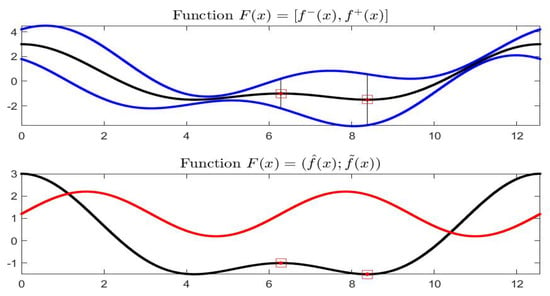
Figure 23. Periodic Example 3 (big fish): function $F(x)$ is pictured on top and functions $\widehat{f}(x)$, $\tilde{f}(x)$ on bottom. Marked points correspond to $x_m$ and $x_M$, where the two functions are differentiable.

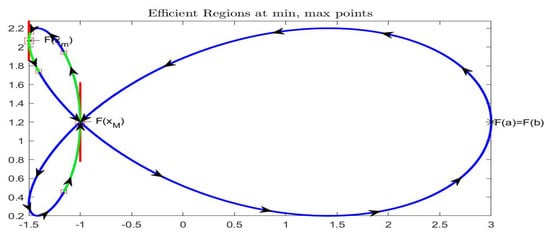
Figure 24. Periodic Example 3 (big fish): midpoint representation of function $F(x)$; marked points are $F(x_m)$ and $F(x_M)$ and the efficient $E_{\min }(F;x_m)$ and $E_{\max }(F,x_M)$ sets of points are marked in green color.

7. Conclusions and Further Work

In the first part of this work (part I, see [33]) we have introduced a general framework for ordering intervals, using a comparison index based on gH-difference; the suggested approach includes most of the partial orders proposed in the literature and preserves important desired properties, including that the space of real intervals is a lattice with the bounded property (all bounded sets of intervals have a supremum and an infimum interval).

The monotonicity properties are then defined and analyzed in [33] in terms of the suggested partial orders; the relevant connections with gH-derivative are also established.

In this paper (part II), we define concepts related to extremal points (local/global minimum or maximum), using the same general partial orders described in part I, and we analyze the important concepts of concavity and convexity; furthermore, we establish the connections between extremality, convexity, and concavity with first-order and second-order gH-derivatives.

Interesting connections with differential geometry and with periodic curves (as in [30,31,32]) are sketched and briefly analyzed.

We consider these notes as a first step in the mathematical analysis for interval functions of a single variable. Appropriate extensions to study the case of interval functions of more variables (initiated with a recent paper [14]) have been considered and will be the subject of future research.

As we have said in the introduction to part I, the scope of this paper is not to discuss problems in the arithmetic with intervals, extended intervals (Kautcher arithmetic), modal intervals, directed intervals (these are some of the terms and approaches proposed in the very extended literature related to interval analysis) or in the structure of spaces of intervals (semi-linearity, quasi-linearity).

Our setting here is the standard interval analysis, based on Minkowski-type operations (also said to be based on the extension principle), with the supplement of gH-difference and gH-addition (not to be substitutes of standard difference and addition). Surely, a well-documented survey to describe and compare the different approaches raised since the origins of intervals in various fields of mathematics should be of great interest and importance, in particular, to reconstruct the (seemingly different) motivations and to describe the (in most cases equivalent) proposals presented in the literature. A specifically dedicated paper in this sense is one of our future research interests.

Several additional properties and applications can be possibly established, in particular with reference to specific problems and questions such as, e.g., the study of almost-periodicity for interval-valued functions in constructive mathematics (see [34,35,36]) or the solution of interval differential equations (IDE), including the extension of ordinary and partial differential equations to the interval-valued case using gH-derivatives (examples of reflected and advanced differential equations of special type are described, e.g., in [37]).