2. the Space of Real Intervals
We denote by
the family of all bounded closed intervals in
, i.e.,
To describe and represent basic concepts and operations for real intervals, the well-known
midpoint-radius representation is very useful: for a given interval
, define the midpoint
and radius
, respectively, by
so that
and
. We denote an interval by
or, in midpoint notation, by
; so
Notation: The symbols and notation , with , (and similarly ,…, , …, ), using low-case characters, will refer to real intervals denoted in upper-case characters; when we refer to an interval , its elements are denoted as , with , and the interval by in extreme-point representation or, equivalently, by , in midpoint notation.
Given and , we have the following classical (Minkowski-type) addition, scalar multiplication and difference:
,
,
,
.
Using midpoint notation, the previous operations, for and are:
,
,
,
.
We refer to [
5,
6,
7] for further details on interval arithmetic.
Generally, the subscript in the notation of Minkowski-type operations will be removed, and classical addition and subtraction will be denoted by ⊕ and ⊖, respectively, but we will insert the subscript in cases where these operations are used in combination with other operations.
We denote the generalized Hukuhara difference (
-difference in short) of two intervals
A and
B as:
It is easy to show that
and
are both valid if and only if
C is a singleton. The
-difference of two intervals always exists and is equal to
the
-addition for intervals is defined by
The Minkowski addition ⊕ is associative and commutative and with neutral element ; hereafter 0 will also denote the singleton . In general, , i.e., the opposite of A is not the inverse of A in Minkowski addition (unless is a singleton). A first implication of this fact is that in general, additive simplification is not valid, i.e., . Instead, we always have and , (and other properties that will be given in the following, when needed).
If , we will denote by the length of interval A. Remark that only if (except for trivial cases) and that or only if A or B are singletons.
Remark 1. The introduction of two additions , and two differences , for intervals is not motivated here as an attempt to define a “true" arithmetic in ; for example, and are both commutative with neutral element 0, but only is associative. As we will see extensively, the four operations are each-other strongly related and their properties motivate the (appropriate) use of them in the context of interval analysis and calculus.
For two intervals
the Pompeiu–Hausdorff distance
is defined by
with
. The following properties are well known:
It is known ([
14,
36]) that
where for
, the quantity
is called the
magnitude of
C and an immediate property of the
-difference for
is
It is also well known that is a complete metric space. The concepts of a convergent sequence of intervals , is considered in the metric space , endowed with the distance:
Definition 1. We say that if and only if for any real there exists an such that for all .
The following equivalence is always true, as it is a trivial application of (
2):
3. Orders for Intervals
The following partial order for intervals is well known and extensively used ( stands for Lower-Upper):
Definition 2. Given , , we say that
- (i)
if and only if and ,
- (ii)
if and only if and ( or ),
- (iii)
if and only if and .
The corresponding reverse orders are, respectively, , and .
Using midpoint notation
,
, the partial orders
and
above can be expressed as
the partial order
can be expressed in terms of
with the additional requirement that at least one of the inequalities is strict.
Proposition 1. Let with . We have
- (i.a)
if and only if ;
- (ii,a)
if and only if and ;
- (iii,a)
if and only if ;
- (i,b)
if and only if ;
- (ii,b)
if and only if and ;
- (iii,b)
if and only if .
Proof. If , then so that is equivalent to . Analogously, is equivalent to . □
Proposition 2. Let with , . We have
- (i.a)
if and only if ;
- (ii.a)
if and only if ;
- (iii.a)
if and only if ;
- (i.b)
if and only if ;
- (ii.b)
if and only if ;
- (iii.b)
if and only if .
Proof. For case (i.a) we have that implies and so ; the other cases are analogous. □
Definition 3. Given , we clearly have that We say that A and B are LU-incomparable if neither nor .
Proposition 3. Let with , . The following are equivalent:
- (i)
and B are LU-incomparable;
- (ii)
is not a singleton and ;
- (iii)
;
- (iv)
or .
Proof. (i) ⟺ (ii): LU-incomparability means that neither nor , i.e., that neither nor and this is equivalent with both and , i.e., .
(ii)⟺(iii): validity of (ii) means and this is equivalent to or ; so, (ii) and (iii) are equivalent.
(ii)⟺(iv): observe that ; then is equivalent to or . But is equivalent to and i.e., ; and is equivalent to and , i.e., . □
Proposition 4. If , then
- (i)
if and only if ;
- (ii)
If then ;
- (iii)
If then
Proof. It is easy to check that and (i) follows.
For (ii), if then and we get and . Then, , and from we have . On the other hand, and we conclude that .
For (iii), if then and we get and . Then, , and from we have ; on the other hand, and we conclude that . □
The problem of ordering intervals has been a topic of intense research in several areas. We consider the ordering induced by the -difference and the natural order on the real numbers.
Given an interval , we define the 2-norm of C by such that , , .
The gH-difference in midpoint notation is
where
is its midpoint and
is its radius.
The following comparison index, based on the gH-difference and the 2-norm, has been introduced in [
58,
59]. We recall here the definition and the basic properties.
Definition 4. Given two distinct intervals , the gH-comparison index is defined asit has the following properties: - ○
, , ,
- ○
, ( and ),
- ○
, .
We can write
and, assuming the condition
, we define the following
gH-comparison ratioThe comparison ratio is very useful in the characterization of different order relations for intervals; let us consider two distinct intervals and search for (partial) order relations to decide if A is less than B, or if A is greater than B, or if A and B are incomparable.
If the comparison is easy as indeed, being , either or and the decision can be based simply on the comparison of the midpoint values.
If and , then A and B are incomparable with respect to any order relation; indeed, in that case, the intervals are equally centered and one of them is strictly included in the other (we can eventually have a preference for the bigger or the smaller one, but there is no simple way to quantify how much one is better or worse than the other).
The interesting and more complex case to analyze is when . Consider first the comparison “A is less than B”, formally “decide if or not”. If and A and B do not overlap with internal points, i.e., when , it is reasonable to accept , as no element in A is greater than any elements in B; instead, some indecision is justified if the two intervals overlap internally.
We can analyze this situation using the comparison ratio ; we distinguish two cases, (I) , and (II) , .
- Case (I):
( and so that ); it is immediate to see that . If , i.e., if , then no element in B is smaller than all elements in A. But if , i.e., if , then elements of B exist on the left of A and the ratio measures how much elements of B are better than all elements of A, with respect to how much the central value of A is better that the central value of B. In some sense, gives a relative measure of a possible “loss” if we chose A against B based on central values (expecting a mid-value “gain” ).
- Case (II):
( and so that ); it is immediate to see that . If , i.e., if , then no element in A is greater than all elements in B. But if , i.e., if , then elements of A exist on the right of B and the ratio measures how many elements of A are worse than all elements of B, with respect to how much the central value of A is better than the central value of B. In some sense, gives a relative measure of a possible “loss” if we chose A against B based on the central values (expecting a mid-value “gain” ).
Summarizing, we can say that in accepting on the basis of the comparison of the midpoint values, a possibly positive (worst-case) loss appears when or when ; we then have the following interpretation of the comparison ratio :
If and , no possible worst-case loss appears in accepting .
If and , a possible worst-case loss in accepting appears because some values of B (on the left side) are less than all values of A; the quantity gives a relative measure of the possible loss with respect to the possible midpoint gain.
If and , a possible worst-case loss in accepting appears because some values of A (on the right side) are greater than all values of B; the quantity gives a relative measure of the possible loss with respect to the midpoint gain.
The gH-comparison index will be used extensively in the rest of this paper. In a similar way we can define a comparison index based on M-difference and 2-norm.
Definition 5. Given two intervals A, B, the M-comparison index is defined aswhere is the M-difference. Given two distinct intervals , it has the following properties: - ○
, , ,
- ○
, ( and ),
- ○
, .
Assuming
, we can define the M-comparison ratio
The reciprocal of the ratio
, called acceptability index
has been introduced in [
60,
61]: it always exists when
(i.e., when at least one of
A and
B is a proper interval). Given two distinct intervals
and
it has the following basic properties:
- (1)
if , we obtain (i.e., all values of A are less than or equal to all values of B)
- (2)
if , we have (i.e., all values of A are greater than or equal to all values of B)
As discussed extensively in [
60], if the index
is positive, then it gives a measure of acceptability of the inequality
: if
then
is accepted with degree
.
The two ratios and are not related each-other in a simple way; e.g., let’s compare with for the following intersecting intervals and in particular if
- 1a.
, : , ,
- 2a.
, : , ,
Or if
- 1b.
, : , ,
- 2b.
, : , .
In the four cases, the acceptability index has the same value while the gH-comparison ratio has significantly different values; it is then clear that the two indices will not produce comparable results.
The three order relations , and in Definition 2 can be generalized in terms of the gH-comparison index as follows:
Definition 6. Given two intervals and and , (eventually and/or ) we define the following order relation, denoted , It is immediate to see that the relation
with
,
is reflexive (i.e.,
), antisymmetric (i.e., if
and
then
) and transitive (i.e., if
and
then
). It follows that
is a partial order and
is a lattice [
59].
Definition 7. Given two intervals and and , (eventually and/or ) we define the following (strict) order relation, denoted , The relation with , is asymmetric (i.e., only one of or can be valid) and transitive.
Definition 8. Given two intervals and and , (eventually and/or ) we define the following (strong) order relation, denoted , The relation with , is asymmetric and transitive.
There are specific values of
and
which make the order relation
equivalent to
-order and other orders suggested in the literature (see [
59] for details).
Proposition 5. Let A and B be two intervals; then it holds that
- (1)
, i.e., (9) with and , - (2)
, , i.e., (9) with and , - (3)
, , i.e., (9) with and , - (4)
, , , i.e., (9) with and , - (5)
, , , i.e., (9) with and .
By varying the two parameters
,
, we obtain a continuum of partial order relations for intervals and we have the following equivalences [
59]:
Proposition 6. If A and B are two intervals then it holds that
- (1)
,
- (2)
,
- (3)
,
- (4)
,
- (5)
.
Remark 2. To have we need and . It follows that for the order relation with in , we have the equivalence Definition 9. For a given interval , we define the following sets of intervals X which are
- (a)
-dominated by A: - (b)
-dominating A: - (c)
-incomparable with A:
Proposition 7. For any , and any intervals , we have
- a.
if and only if ;
- b.
if and only if ;
- c.
;
- d.
;
- e.
.
Proof. The proof of all the properties can be easily obtained by direct manipulation of involved definitions; we omit the details. □
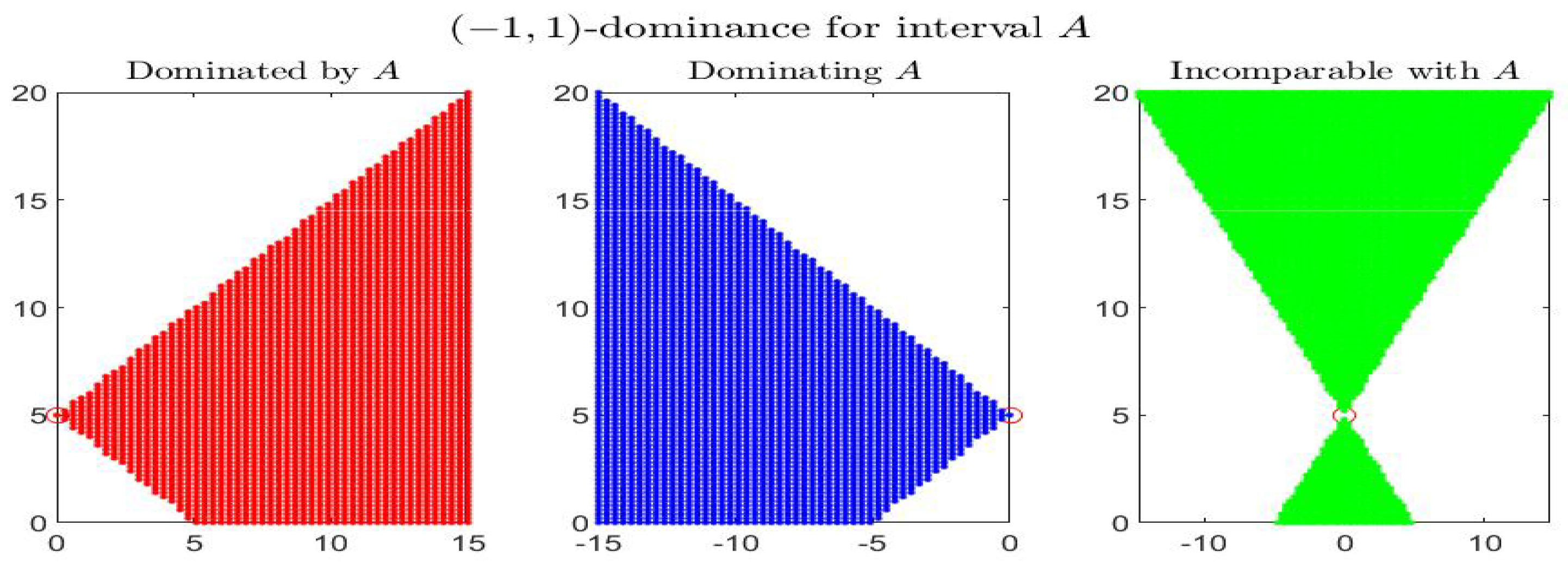
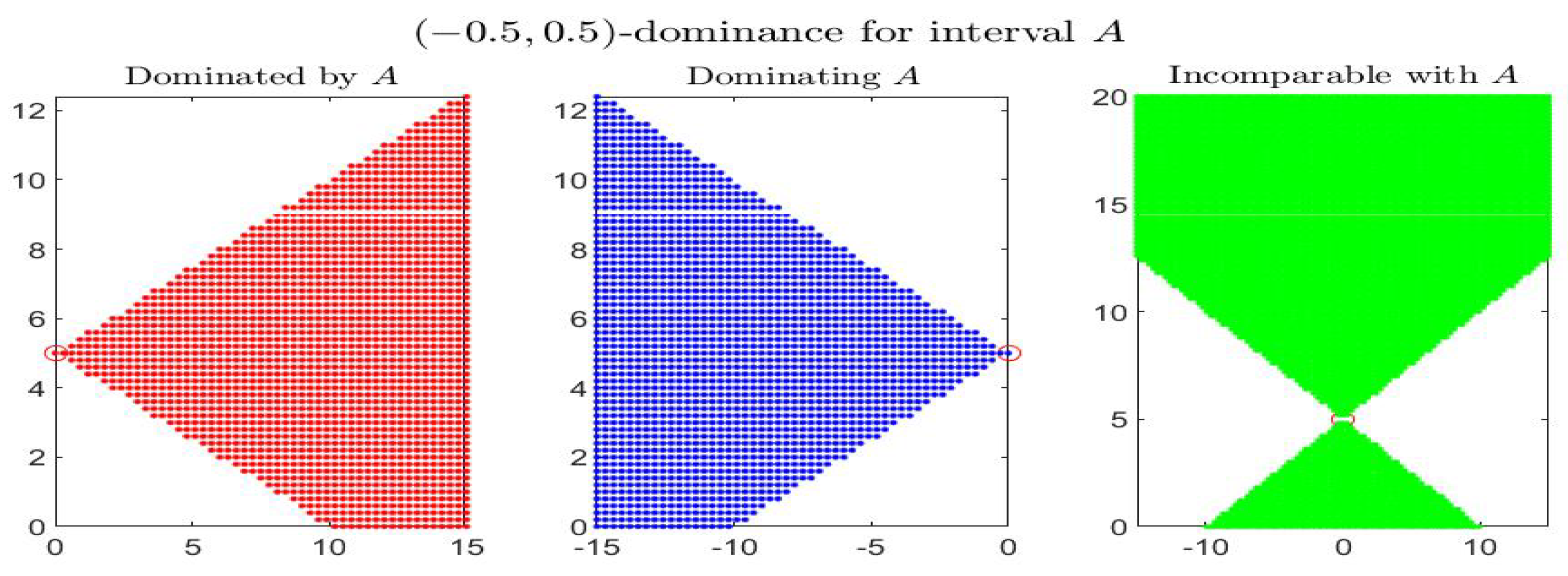
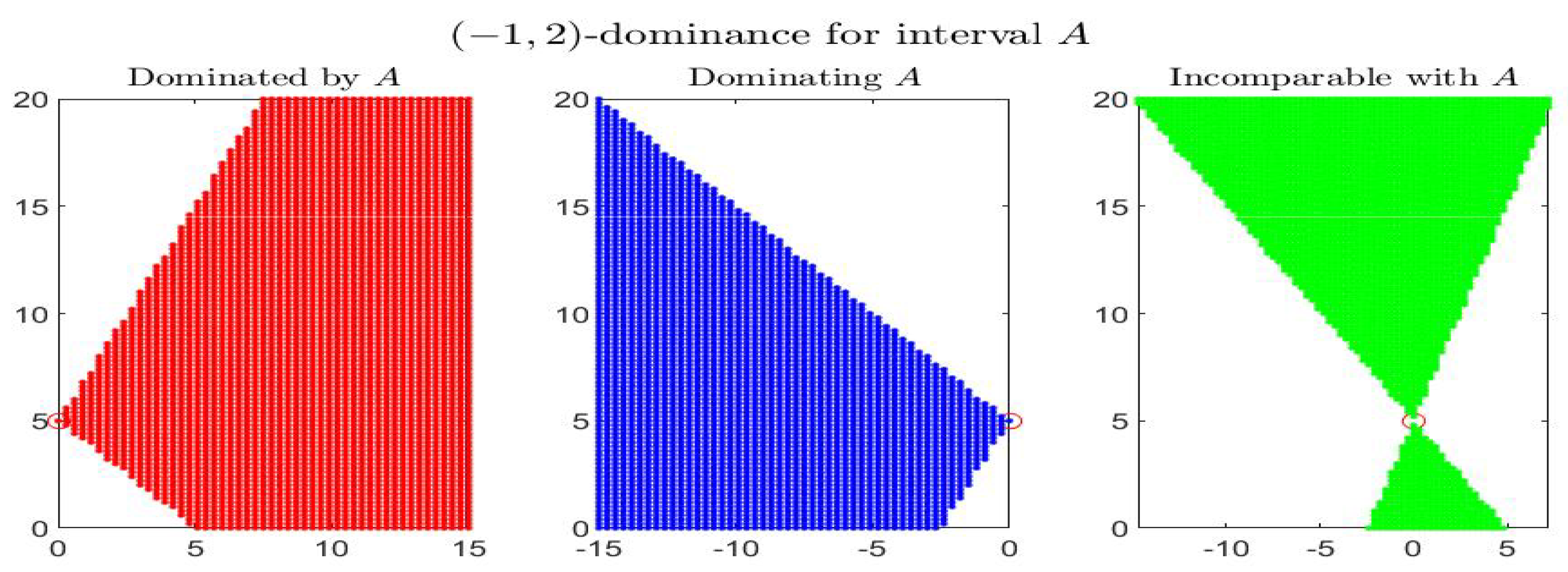
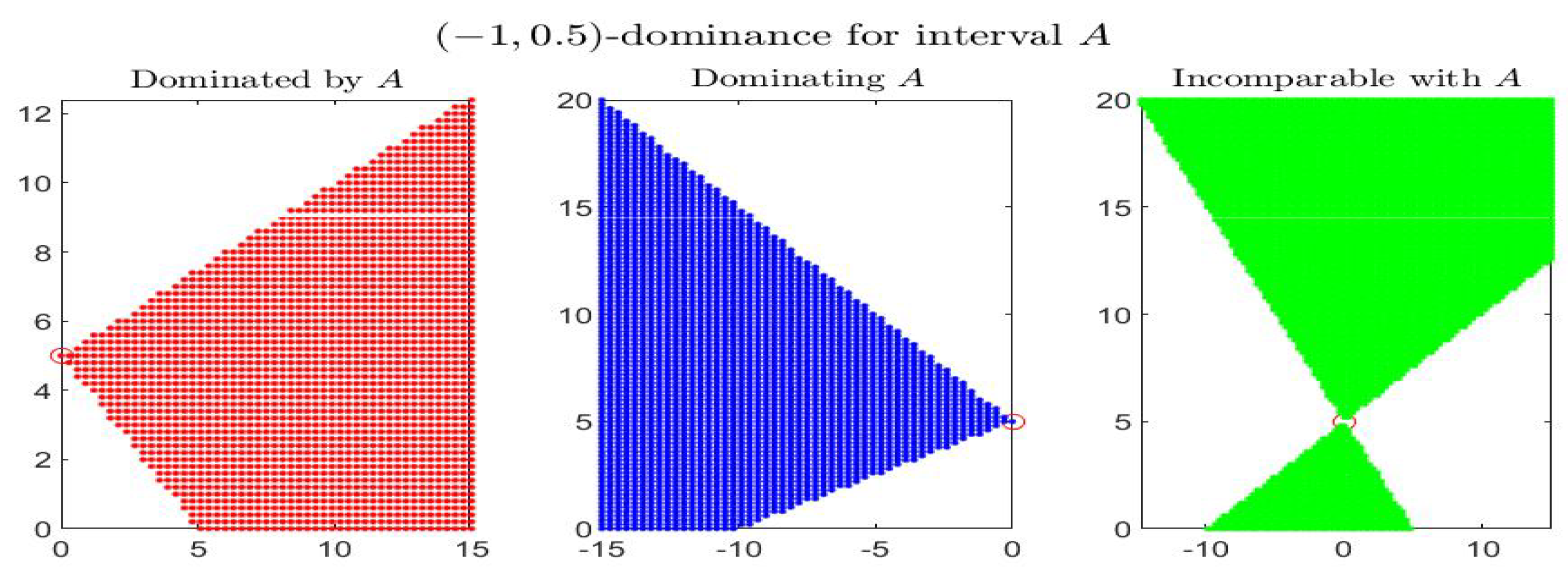
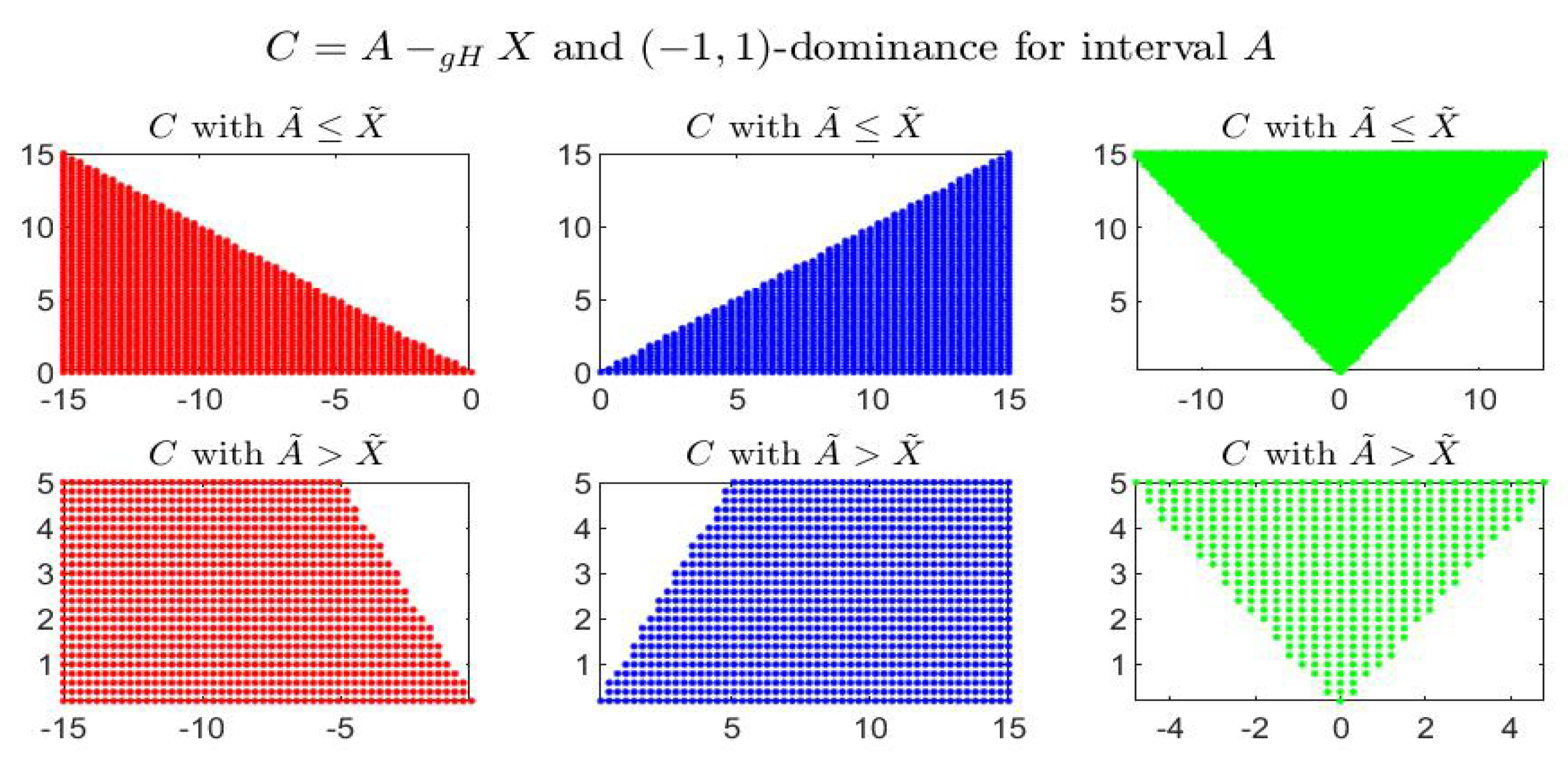
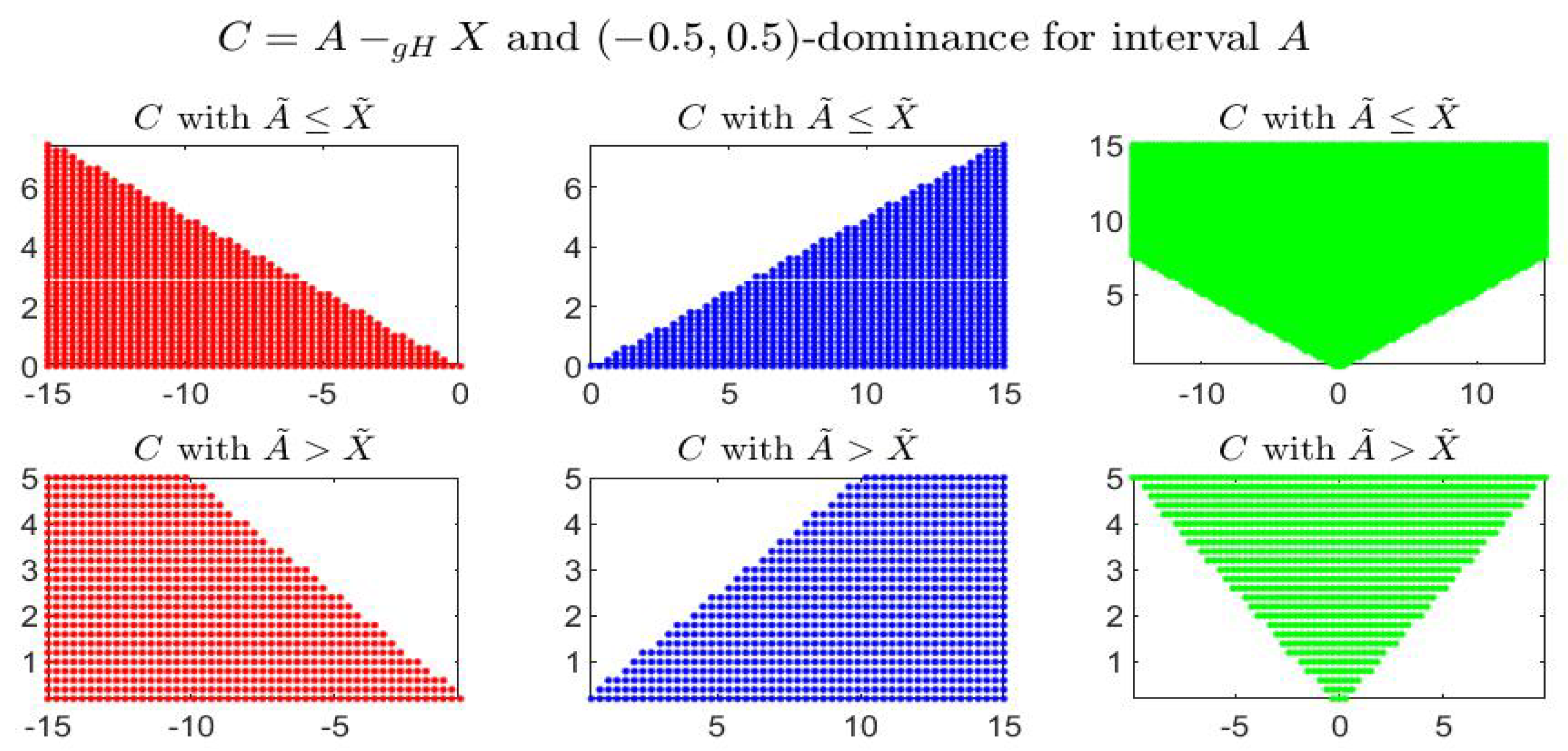
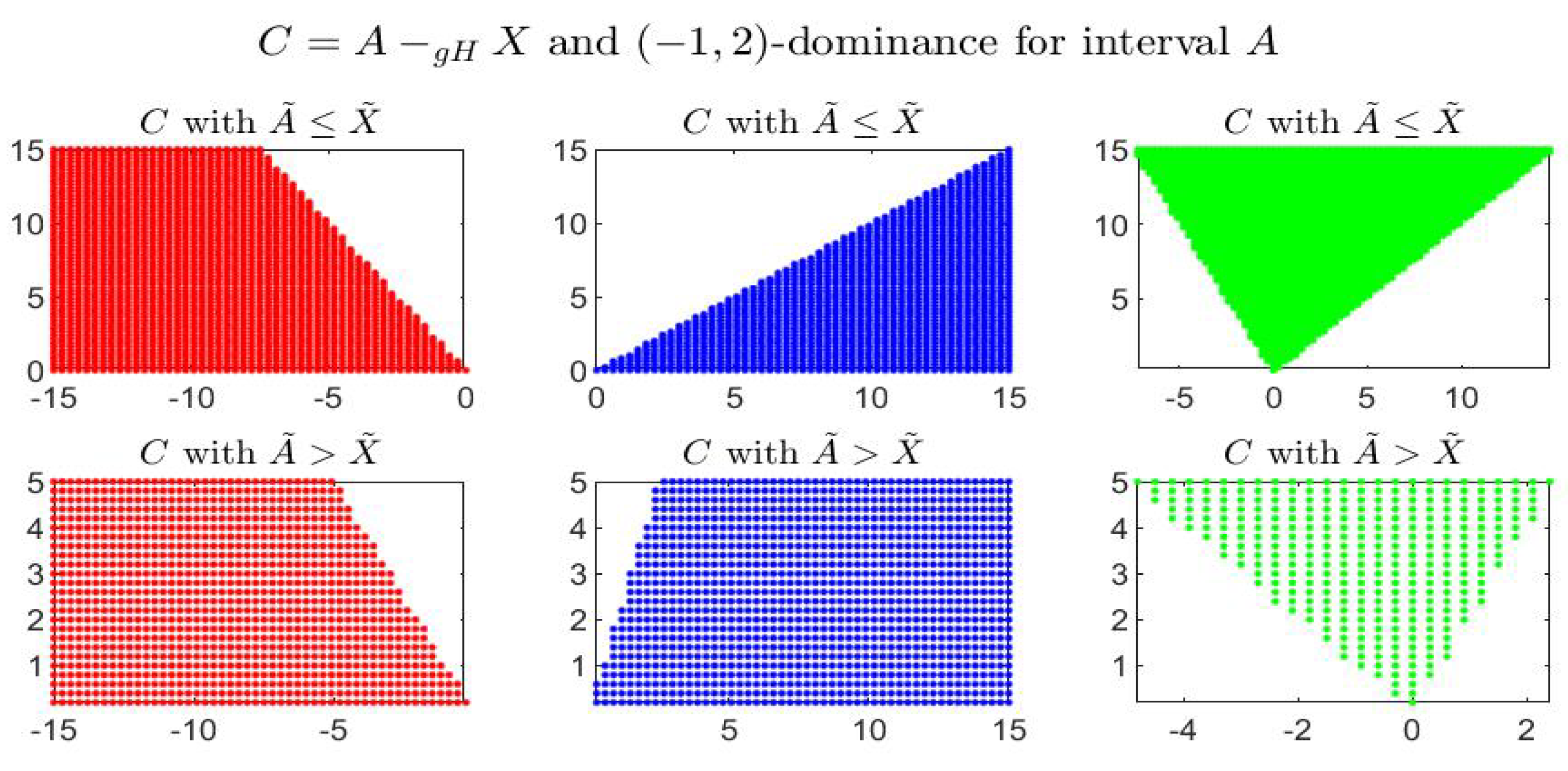
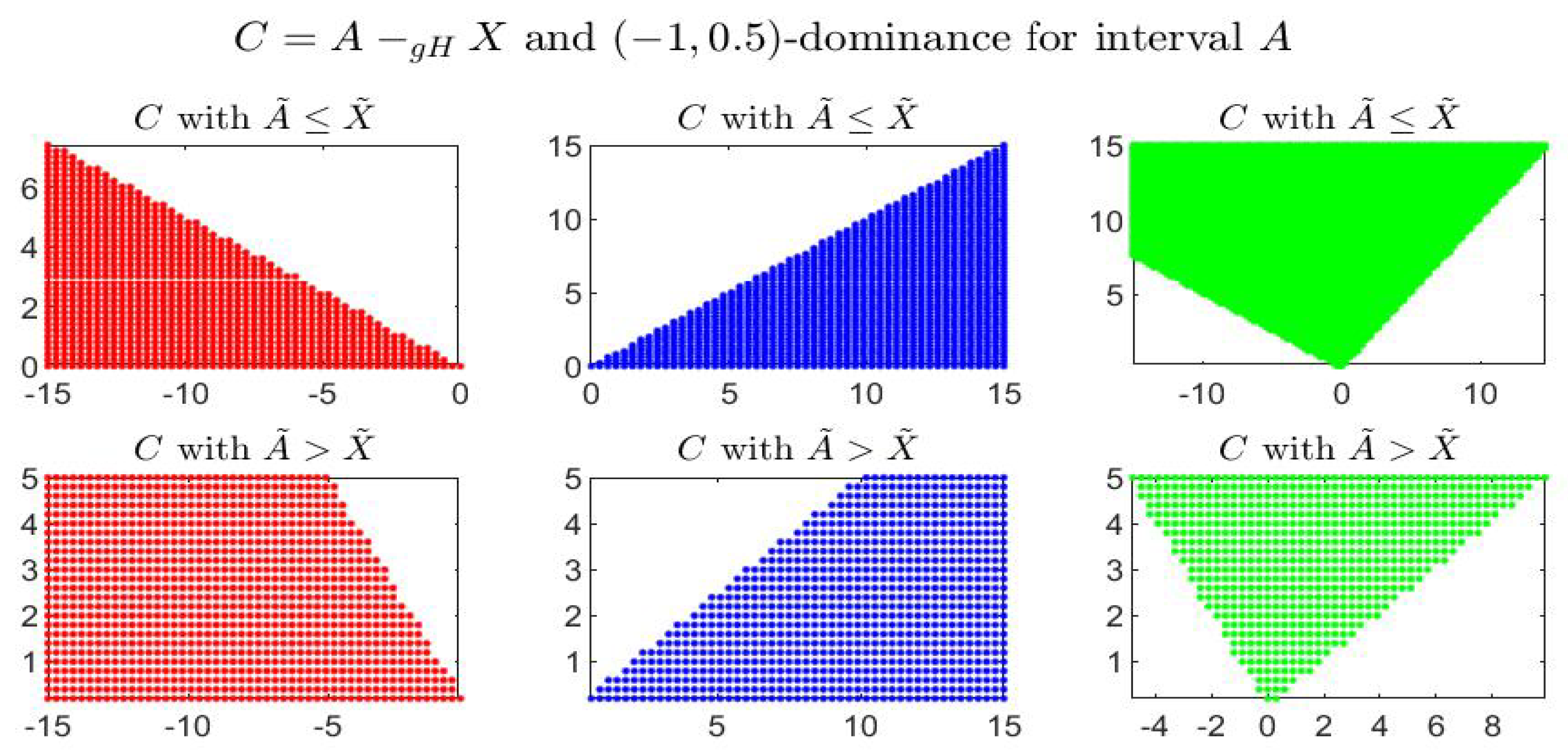
Consider the following example: the four figures show, for the given interval
, the corresponding set of dominated, dominating and incomparable intervals, respectively the sets
(red colored pictures),
(blue-colored regions) and
(in green color), for partial orders (
) with four different pairs
. In particular it is shown:
-dominance (i.e.,
-dominance) in
Figure 1,
-dominance in
Figure 2,
-dominance in
Figure 3 and
-dominance in
Figure 4. All the figures consider intervals
in the range
and
.
By inspecting the four figures, we see that with respect to the
-order (
Figure 1, with
) or an order with
(
Figure 2, with
), the set of incomparable intervals is symmetric with respect to the vertical line
; when
(
Figure 3) the right part of the incomparable region, determined by an increase of
, tends to become more vertical and reduces in favor of the dominated region (red colored) and the dominating region (blue-colored). The opposite effect appears if
decreases (
Figure 4).
The lattice structure of , endowed with the partial order , can be further analyzed by considering the basic concepts of least upper bound (lub or sup) and greatest lower bound (glb or inf). For two intervals , a (common) upper bound is an interval such that and . A (common) lower bound is an interval such that and .
The
least upper bound for
, denoted
or
, is a common upper bound
Z such that every other upper bound
is such that
; analogously, the
greatest lower bound for
, denoted
or
, is a common lower bound
Z such that every other lower bound
is such that
. It is immediate to see that
and
always exist (and are unique) for any
(see [
59] for details).
If is any subset of intervals, we say that is bounded from below (lower bounded) with respect to if and only if there exists such that for all and we say that is bounded from above (upper bounded) with respect to if and only if there exists such that for all . If is both lower and upper bounded, we say it is bounded.
Every bounded subset of admits inf and sup.
Proposition 8. Consider a partial order on and let be any nonempty bounded subset of intervals. Then, there exist both such that for all We also have, for all , Proof. We will prove only Equation (
15) by a constructive procedure; the proof of equations in (
16) is immediate. Let
be any lower bound and
any upper bound for
and consider the four lines, in the half-plane
, with equations
They intersect the vertical axis
with intercepts, respectively,
,
and
,
. Considering an arbitrary element
, the two lines trough
S with angular coefficients
and
, with equations
and
, respectively, have intercepts
,
and their sets
and
are both bounded with
and
for all
. Consequently, there exist the four real numbers
,
,
,
with
and
. Finally, the intersection point of the two lines
and
corresponds to the interval
; analogously, the intersection point of the two lines
and
corresponds to the interval
. More precisely, we have
and
This completes the proof. □
If, for a nonempty bounded subset we have that or are elements of , then there exist the intervals or, respectively, .
Interesting bounded subsets in
are the “segment” with extremes
and the “interval” with extremes
, defined, respectively, by
and, assuming
(here, the dominance is essential),
If is a bounded subset of , we clearly have , with equality if and only if with .
We conclude this section with an interesting property.
Proposition 9. For a given partial order with , , consider the partial order ; then, for all ,where and are the opposite intervals of A and B. Proof. Starting with inequalities (
8) that define
and recalling that
the conclusion follows after a few simple algebraic manipulations. □
In particular, if
, i.e.,
so that
, we have that for any bounded subset
,
where the (bounded) subset
is defined by
5. Interval-Valued Functions
An interval-valued function is defined to be any
with
and
for all
. In midpoint representation, we write
where
is the midpoint value of interval
and
is the nonnegative half-length of
:
so that
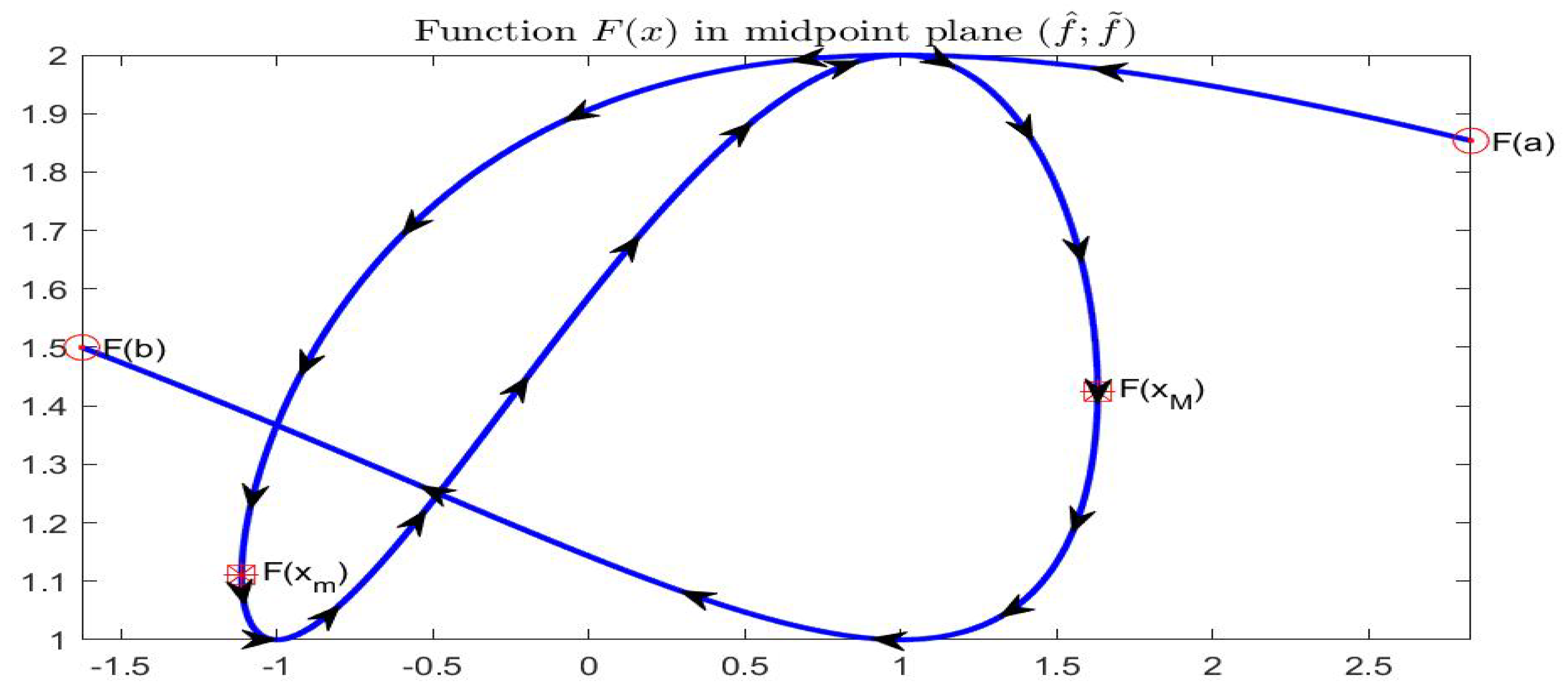
We will frequently use a second graphical representation of F, obtained in the half-plane , , where each interval is identified with the point and the arrows give the direction of moving the intervals for increasing .
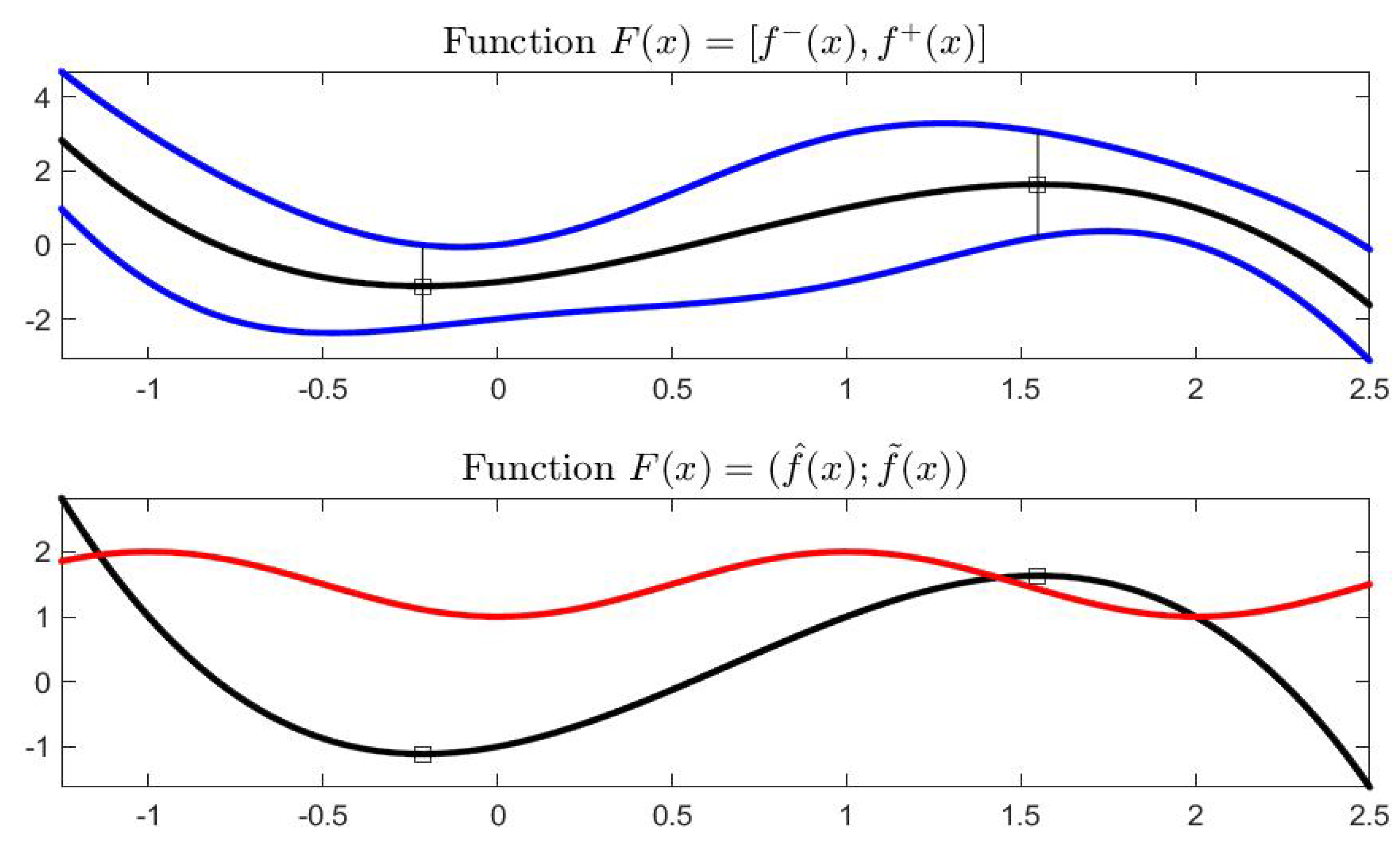
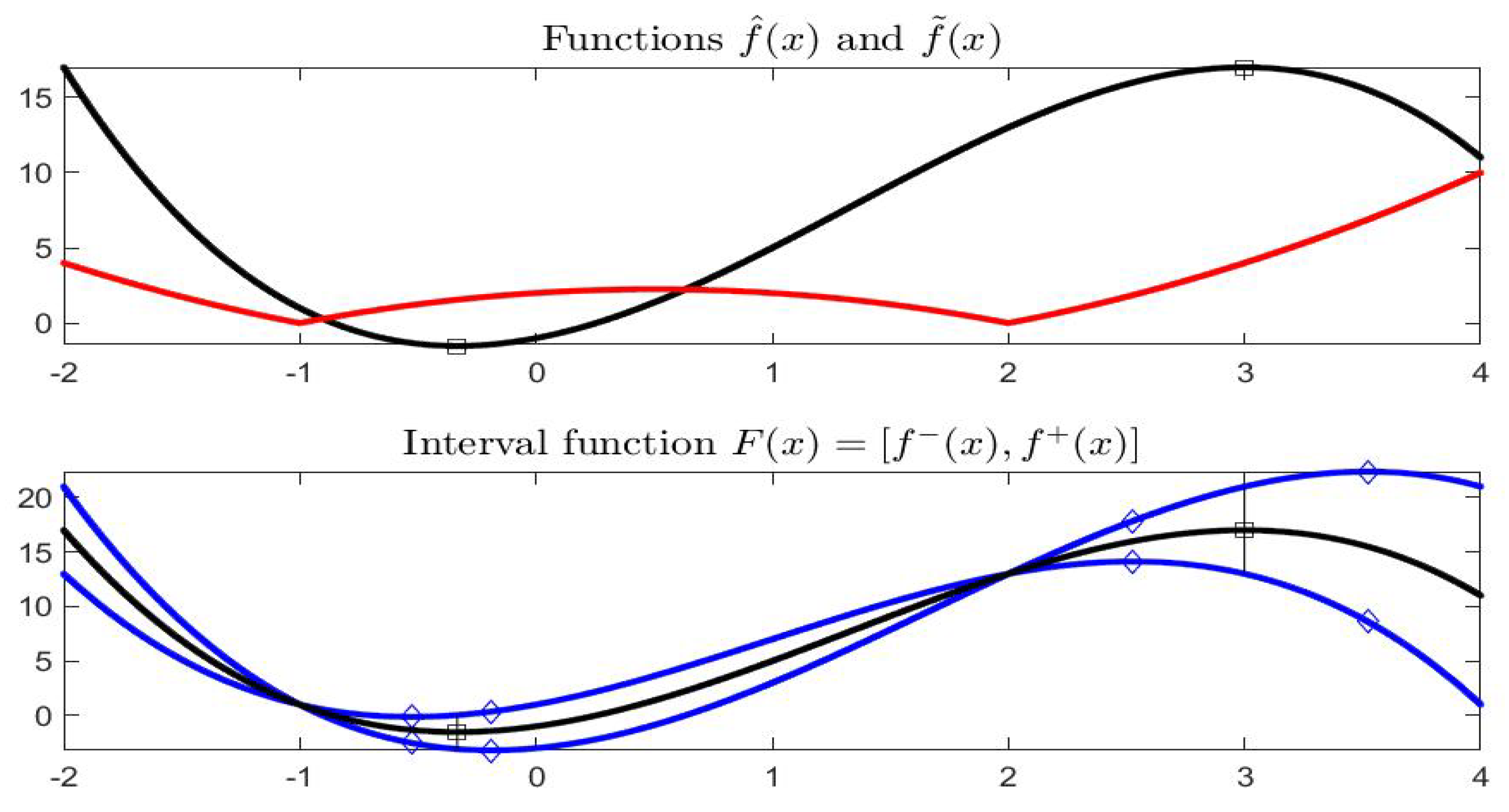
Example 1. Let , in midpoint notation, i.e., , . Using the corresponding endpoint functions, the graphical representation of in the plane is given in Figure 9. For we have and for it is ; by lucking at the midpoint representation in in Figure 10, the arrows start at point and terminate at point . The values of where the midpoint function is minimal or maximal are, approximately, with interval value and with interval value . Limits and continuity can be characterized, in the Pompeiu–Hausdorff metric
for intervals, by the
-difference. The following result is well known [
15]; the second equivalence defines the continuity at an accumulation point.
Proposition 10. Let , , be such that and let . Let be an accumulation point of K. Then we havewhere the limits are in the metric . If, in addition, , we have Proof. Follows immediately from the property . □
In midpoint notation, let
and
; then the limits and continuity can be expressed, respectively, as
and
The following proposition connects limits to the order of intervals; we will consider the lattice with partial order defined for any fixed values of and . Analogous results can be obtained for the reverse partial order .
Proposition 11. Let be interval-valued functions and an accumulation point for K.
- (i)
if for all in a neighborhood of and , , then ;
- (ii)
If for all in a neighborhood of and , then .
Proof. We will use the midpoint notation for intervals. For the proof of
i), we have
if and only if
and
; from (
24) we have at the limit that
and
and this means that
. For the proof of
ii) we have
,
and
,
; from
,
we have that
exists; on the other hand,
and from
, we also have
and
so that
; the conclusion follows from (
24) applied to
G. □
Remark 5. Similar results as in Propositions 10 and 11 are valid for the left limit with , ( for short) and for the right limit , ( for short); the condition that if and only if is obvious.
The gH-derivative for an interval-valued function, expressed in terms of the difference quotient by gH-difference, has been first introduced in 1979 by S. Markov (see [
12]). In the fuzzy context it has been introduced in [
13,
62]; the interval case has been analyzed in [
15] and the fuzzy case again reconsidered (level wise) in [
30]. Several authors have then proposed alternative equivalent definitions and studied its properties and applications; actually, it is of interest for an increasing number of researchers. A very recent and complete description of the algebraic properties of gH-derivative can be found in [
63].
Definition 10. Let and h be such that , then the gH-derivative of a function at is defined asif the limit exists. The interval satisfying (25) is called the generalized Hukuhara derivative of F (gH-derivative for short) at . For the function in Example 1, we have that both
and
are differentiable so that
exists at all internal points (see
Figure 11 and
Figure 12).
Also, one-side derivatives can be considered. The right gH-derivative of F at is while to the left it is defined as . The gH-derivative exists at if and only if the left and right derivatives at exist and are the same interval.
The following properties are indeed immediate to prove.
Proposition 12. Let be given, . Then
- (1)
is left gH-differentiable at if and only if and are left differentiable at ; in this case,
- (2)
is right gH-differentiable at if and only if and are right differentiable at ; in this case, .
- (3)
is gH-differentiable at if and only if is differentiable and is left and right differentiable at with and in this case, ; equivalently, if and only if .
In terms of midpoint representation
we can write
and taking the limit for
, we obtain the gH-derivative of
F, if and only if the two limits
and
exist in
; remark that the midpoint function
is required to admit the ordinary derivative at
x. With respect to the existence of the second limit, the existence of the left and right derivatives
and
is required with
(in particular
if
exists) so that we have
or, in the standard interval notation,
Equation (
26) is of help in the interpretation of gH-derivative; indeed, the separation of midpoint and half-length components in
is inherited by the gH-derivative
. In particular, the correspondence
shows that the midpoint derivative
is the derivative of the midpoint
while the half-length derivative is the absolute value
of the left and right derivatives of the half-length
(with
, for details see [
33,
35]).
For a function
, we can define the gH-comparison index-function of
by
If
has gH-derivative
at
x, we can consider the gH-comparison index of
at
x, given by
and if
, the ratio
is well defined so that
(
if
,
if
,
if
). We can use the index
extensively, to valuate the order relations
and similar.
The partial order
can be appropriately introduced for the gH-derivative by the inequality
, i.e.,
; if
and
are differentiable, we have
and the inequality is equivalent to
If
is not differentiable or if its left and right derivatives do not have the same absolute value, then
does not exist, but possibly the left and right gH-derivatives
,
exist and we have
,
, where
and
are the notations for left and right derivatives. In this case, the inequalities
are equivalent to
and the inequalities
are equivalent to
Observe that if
, then the other conditions in (
29) and (
30) become
so that
; as a consequence, if
and
, then we cannot have neither
nor
, i.e.,
and 0 are incomparable.
Remark 6. As we have seen, the existence of gH-derivative is equivalent to the existence (and their equality) of both the left and right gH-derivatives, defined as followsandindeed, we have and . In many cases, the midpoint function is defined as where is differentiable; then, if also exists, we have that is gH-differentiable and .
6. Monotonicity of Functions with Values in
Monotonicity of interval-valued functions has not been much investigated and this is partially due to the lack of unique meaningful definition of an order for interval-valued functions. By definition of the lattice , endowed with the partial order ( and ) and with use of the reverse order , we can analyze monotonicity and, using the gH-difference, related characteristics of inequalities for intervals.
Definition 11. Let be given, . We say that F is
(a-i) -nondecreasing on if implies for all ;
(a-ii) -nonincreasing on if implies for all ;
(b-i) (strictly) -increasing on if implies for all ;
(b-ii) (strictly) -decreasing on if implies for all ;
(c-i) (strongly) -increasing on if implies for all ;
(c-ii) (strongly) -decreasing on if implies for all .
If one of the six conditions is satisfied, we say that F is monotonic on ; the monotonicity is strict if (b-i,b-ii) or strong if (c-i,c-ii) are satisfied.
The monotonicity of can be analyzed also locally, in a neighborhood of an internal point , by considering condition (or condition ) for and with a positive small .
Definition 12. Let be given, and . Let (for positive δ) denote a neighborhood of . We say that F is (locally)
(a-i) -nondecreasing at if implies for all and some ;
(a-ii) -nonicreasing at if implies for all and some ;
(b-i) (strictly)-increasing at if implies for all and some ;
(b-ii) (strictly)-decreasing at if implies for all and some ;
(c-i) (strongly) -increasing at if implies for all and some ;
(c-ii) (strongly) -decreasing at if implies for all and some .
We have
if and only if
,
and
, i.e., for increasing case,
so that
is
-monotonic at
according to the monotonicity of the three functions
,
and
:
Proposition 13. Let be given, and . Then
- (i)
is -nondecreasing at if and only if is nondecreasing, is nonincreasing and is nondecreasing at ;
- (ii)
is -nonincreasing at if and only if is nonincreasing, is nondecreasing and is nonincreasing at .
Analogous conditions are valid for strict and strong monotonicity.
The following scheme summarizes these results:
Remark 7. In terms of the endpoint functions and , given by , , the conditions in (32) are written asand the conditions on and , for the monotonicity of F are less intuitive than the ones on and : If we divide the three inequalities in (
32) by
we obtain, for
F to be
-nondecreasing at
,
Analogously, for
F to be
-nonincreasing at
, we obtain
Suppose now that
and
have both left and right (finite) derivatives at
; denote them by
,
,
,
. Taking the limits in (
34) and (
35) with
and
, we obtain the conditions for
-monotonicity of
F at
:
Proposition 14. Let be given, and assume that and have left and right derivatives at an internal point . The following are necessary conditions for local monotonicity:
(i-n) If F is -nondecreasing or -increasing at , then (ii-n) If F is -nonincreasing or -decreasing at , then The following are sufficient conditions for local strong monotonicity:
(i-s) Ifthen F is strongly -increasing at ; (ii-s) Ifthen F is strongly -decreasing at . If
and
exist on
, then the conditions for monotonicity can be expressed in the obvious way as for elementary calculus, in terms of the derivatives
,
and
. Therefore, the necessary conditions for nonincreasing
are
and for nondecreasing
are
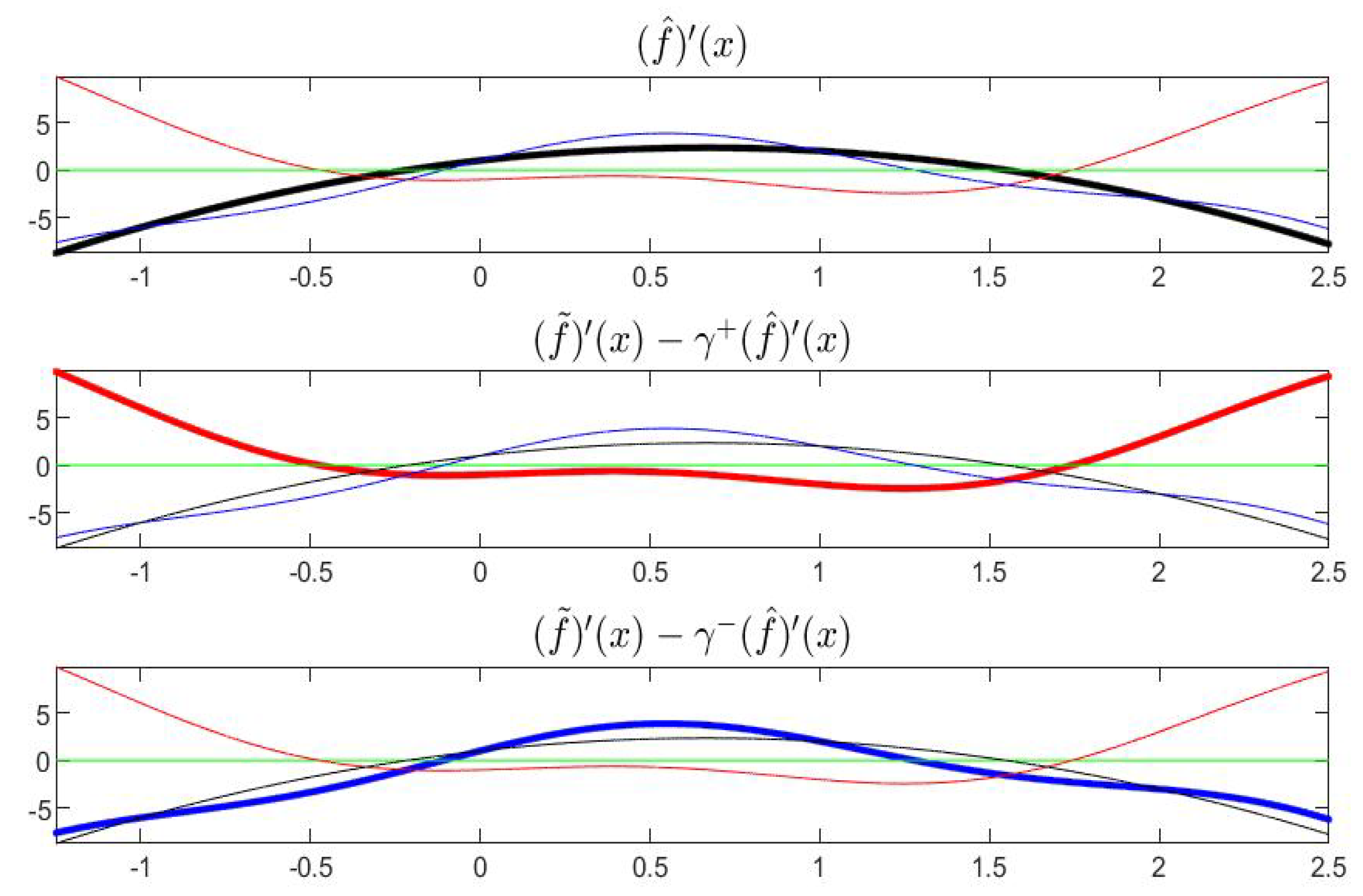
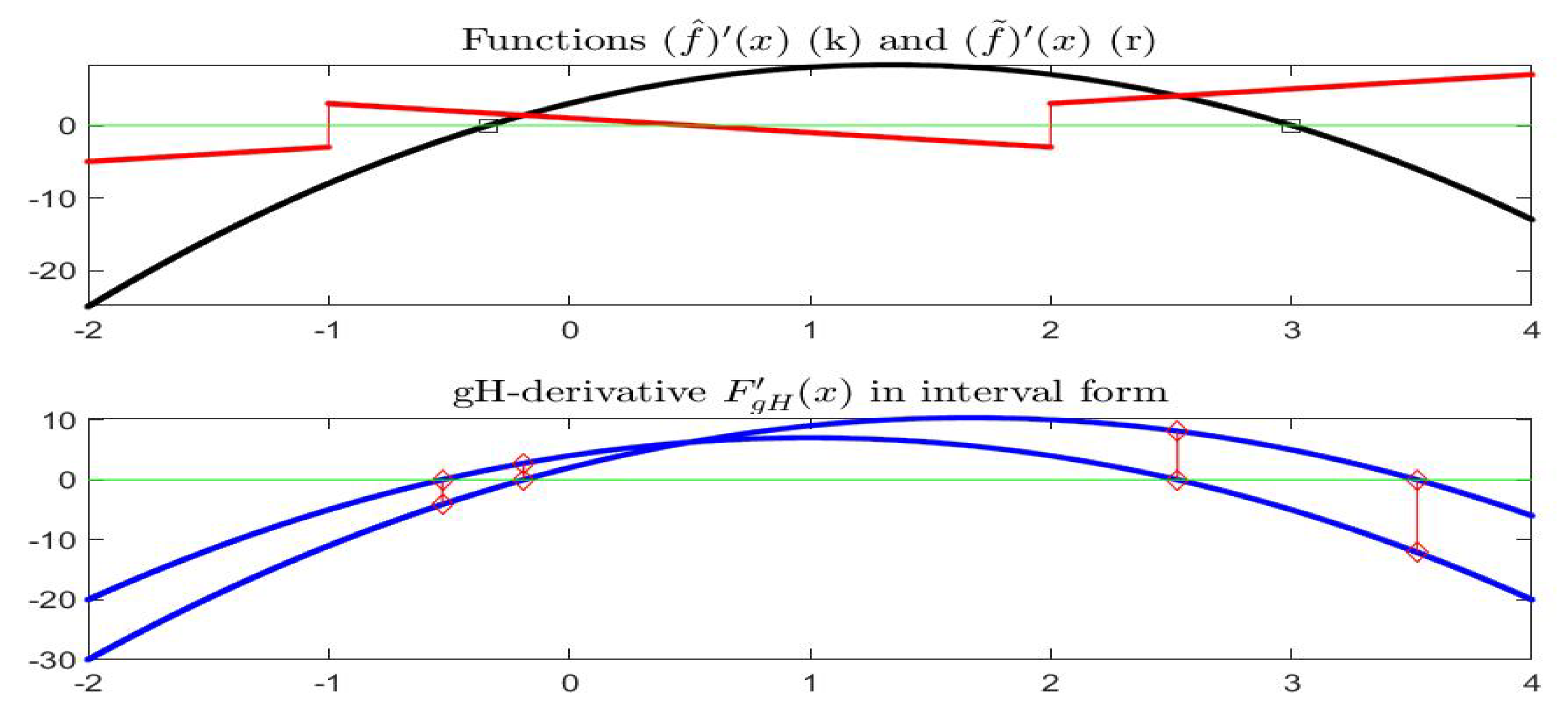
With reference to Example 1, the functions
,
and
are pictured in
Figure 13 and their derivatives are in
Figure 14; the partial order is fixed with
and
, i.e.,
.
Now, but only for the case of a partial order with the condition that , i.e., , we can establish a strong connection between the monotonicity of F and the sign of its gH-derivative . Denote the corresponding partial order simply by .
Proposition 15. Let be given, and assume F has gH-derivative at the internal points . Let be fixed. Then
- (1)
If F is -nondecreasing on , then for all x, ;
- (2)
If F is -nonincreasing on , then for all x, .
Proof. We prove only (i). By definition, and F is continuous. If F is nondecreasing, then, for sufficiently small we have and so which gives; by taking the limit for , . On the other hand, for , we have , i.e., which gives; by taking the limit for we get and, changing sign on both sides, it is . The proof of (ii) is similar. □
An analogous result is also immediate, relating strong (local) monotonicity of F to the “sign” of its left and right derivatives and ; at the extreme points of , we consider only right (at a) or left (at b) monotonicity and right or left derivatives. Again we assume the condition .
Proposition 16. Let be given, with left and/or right gH-derivatives at a point . Then
(i.a) if , then F is strongly -increasing on for some (here );
(i.b) if , then F is strongly -increasing on for some (here );
(ii.a) if , then F is strongly -decreasing on for some (here );
(ii.b) if , then F is strongly -decreasing on for some (here ).
Proof. We prove only (i.a). From
we have
and
, i.e.,
; then
,
and the conclusion follows from conditions (
38). □
We conclude this section with the following
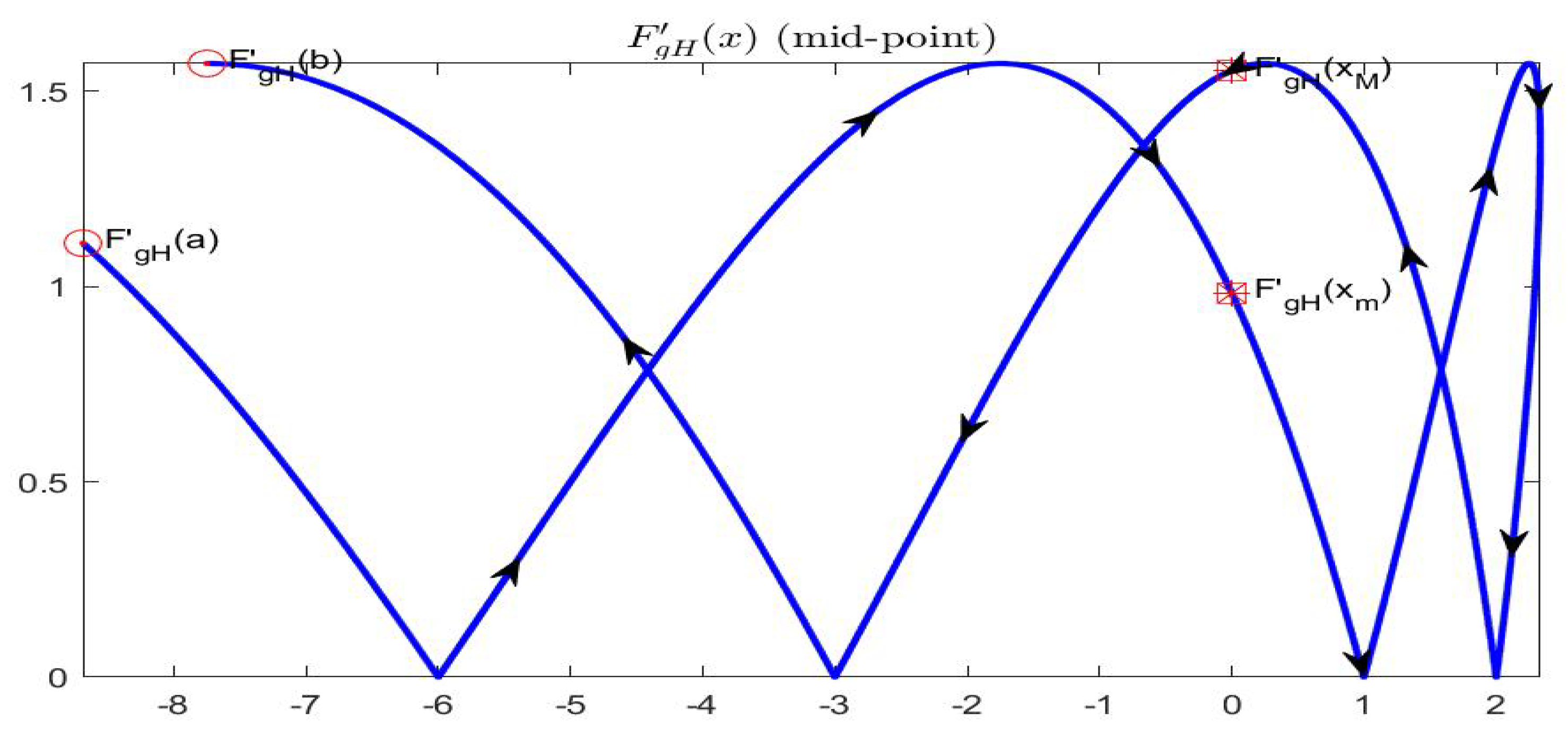
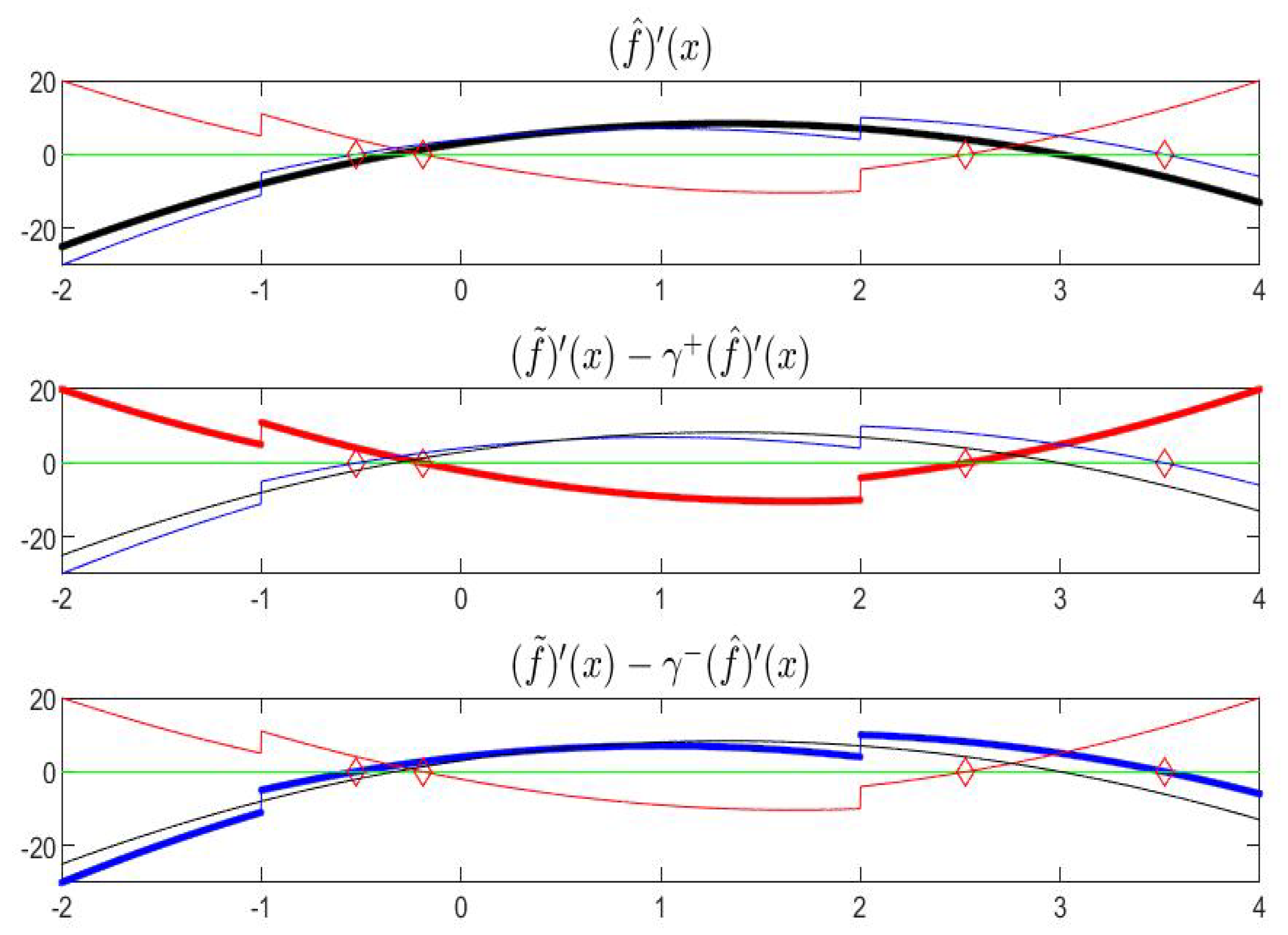
Example 2. Function , , for , is defined by and (Figure 15). Remark that function is differentiable on with and is differentiable with for and ; at these two points the left and right derivatives exist: , , , .
Function
is gH-differentiable on
(including the points
and
) and
(
Figure 16). Also right and left gH-derivatives exist at
and
, respectively. Considering the points
,
,
and
, the corresponding gH-derivatives are (approximately)
,
,
,
.
With
, i.e., with (
)-order, the functions
,
and
are pictured in
Figure 17.
According to Proposition 13, necessary conditions for decreasing
are satisfied on
and
and for increasing
are satisfied on
. Corresponding necessary conditions using the sign of the derivatives of functions
,
and
can be checked in
Figure 18; at the points
and
we can apply the conditions involving left and right derivatives of
.
Finally, according to Proposition 16, it is easy to check that the sufficient conditions for strong monotonicity are satisfied: decreasing on and , increasing on . In the remaining points and the sufficient conditions for strong monotonicity are not satisfied (the interval-valued gH-derivatives of contain zero as an interior value).