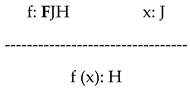Logic of Typical and Atypical Instances of a Concept—A Mathematical Model

Abstract

In this paper, we give a mathematical model of the logic of determination of objects (LDO) based on preordered sets, and a mathematical model of the logic of typical and atypical instances (LTA). We prove that LTA is an extension of LDO. It can manipulate several types of “exceptions”. Finally, we show that the structural part of LTA can be modeled by a quasi topology structure (QTS).

1. Introduction

The difference between typical instances and atypical instances in a natural categorization process has been introduced by E. Rosh and studied by cognitive psychology [1,2] and AI. A lot of the knowledge representation systems are expressed using fuzzy concepts but a degree of membership raises some problems for natural categorizations (especially for classification problems in anthropology, ethnology, archeology, and linguistics, but also in ontologies): atypical instances of a concept cannot be apprehended adequately by different degrees from a prototype. Other formal approaches, as paraconsistent logics or non-monotonic logics, often conceptualize atypical objects as exceptions. An alternative approach was developed with the logic of typical and atypical instances (LTA) [3] and logic of determination of objects (LDO) [4]. In order to give a logical approach of typicality/atypicality associated to a concept we distinguish explicitly, in LTA, a conceptual property f (“concept” or predicate in the Frege’s approach and classical logic) from a concept ^f, associated to a conceptual property and characterized by an intension and by an essence, a part of the intension. A typical instance of a concept inherits all properties of intension; an atypical instance inherits only properties of essence, but it is a full member of the category associated to a concept and not a member with a weak degree of membership. In natural categorization, there are often exceptions which do not inherit some properties of the essence; the exceptions cannot be considered as atypical instances as they belong to the boundary of the category, that is the difference between the extension of a conceptual property and the extension of the corresponding concept (the set of all instances inheriting all properties of the essence). In LDO a typical object τf is introduced, which is canonically associated to a concept ^f. Object τf is an abstract object such that it is the best representative object of the concept. From τf more or less objects are explicitly built that fall under the concept ^f, in using a functional composition of different determination operators δk associated to conceptual properties k (in general not in the intension of the concept). When a property δk is the negation of a conceptual property of the intension of a concept, the generated object becomes an atypical object. All typical and atypical objects generated from τf by determination operators belong to the expansion of the concept ^f that contains the extension of fully determinate instances of the concept. Some compositions of determination operators (incoherent compositions) can build objects that are out of the category associated to a concept.

In LTA the types of fully determined objects are extended objects to “exceptions”.

This paper is organized in six sections as follows: Introduction, the logic of determination of objects (LDO), a formal description of the logic of determination of objects (LDO) as a preordered set model, the logic of typical and atypical instances (LTA), LTA as a quasi topology structure, conclusions.

The works directly related to this work are [3,4,5,6,7].

The novelties of this paper are:

• Theorem 1 which represents a fundamental theorem for the model of the LDO. It asserts that the LDO structure can be represented by a Galois lattice;
• The quasi topology structure (QTS) of the fully determinate objects Ext f in LTA.

2. The Logic of Determination of Objects (LDO)

2.1. Informal Description

The logic of determination of objects (LDO) is a non-classical logic of concepts and objects. It contains a theory of typicality. It is due to Jean-Pierre Desclés [8] and described as a logical model in [4]. LDO is defined within the framework of combinatory logic [9] with functional types.

LDO is inspired by the semantics of natural languages. It solves some problems that classical logic cannot describe and solve:

• It supplys a solution for the mismatch between logic categories and linguistic categories (adjectives, intransitive verbs often represented by unary predicates);
• It considers the determination as a logic operator in order to represent linguistic expression as a book, a red book, a book which is on the table;
• It reconsiders the duality of extension–intension via its theory of typicality; the entension and the intension of a concept are no longer in duality.

The LDO has a structural part and an inferential part.

Its structural part is formed by a triple of:

• A network of concepts;
• A set of objects;
• A type theory.

LDO was described as an typed applicative system in the Curry′s sense [9]. A concept is an operator, an object is an operand in Curry′s sense [9] where a conceptual proprerty is an operator and an object is always an operand (on the applicative systems and combinatory logic as a logical formalism of operators composed and transformed by an intrinsic way, see the book of J.-P. Desclés, G. Guibert and B. Sauzay [10]). With every concept f, the following are canonically associated [4]:

• An object called typical object τf, which represents the concept f as an object. This object is completely (fully) indeterminate;
• A determination operator σf, constructing an object more determinate than the object to which it is applied;
• The intension of the concept f, Int f, conceived as the class of all concepts that the concept f «includes», that is, a semantic network of concepts structured by the relation «IS-A»;
• The essence of a concept f, Ess f; it is the class of concepts such that they are inherited by all objects falling under the concept f;
• The expanse of the concept f, Exp f, which contains all more or less determinate objects to whom the concept f can be applied;
• A part of the expanse is the extension Ext f of the concept f; it contains all fully (completely, totally) determinate objects such that the concept f applies to.

From the viewpoint of determination, in LDO, objects are of two kinds: fully (completely, totally) determinate objects and more or less determinate objects. From the viewpoint of some of their properties, LDO captures two kinds of objects: typical objects and atypical objects. The typical objects in Exp f inherit all concepts of Int f. The atypical objects in Exp f inherit only some concepts of Int f.

The inferential part of LDO contains axioms and rules of inferences. Some of the rules decide of the typicality of an object as regard with some concept [4]. In [11], we analysed the nature of these rules issued from the theory of typicality of LDO versus the paraconsistence. More precisely, we show that the rule establishing that an object that is an atypical object of a concept in the frame of the LDO is a particular case of the RA₁ rule of Da Costa [12]. We arrive at the following interpretation of the weakening of the principle of contradiction (¬(B ∧ ¬B)) contained by the RA₁ rule inside the LDO: an object obtained by a LDO-rule using this form of the weakening of the principle of contradiction (¬(B ∧ ¬B)) is an atypical object. From the point of view of managing negation, we can conclude that LDO is a particular case of a paraconsistent logic. For its power of description and especially for its basic notions (to emphasise the distinction between object and concept and between extention and intension), we can state that LDO is a description logic capturing at least one more cognitive feature: the typicality of objects.

2.2. Formal Description of LDO

LDO can be regarded as a formal theory of concepts and objects.

LDO = ($ℱ$, $𝒪$, T) where:

$ℱ$ is the set of concepts, $𝒪$ is the set of objects, T is a type theory. A concept is an operator, whereas an object is always an operand. Types are associated with concepts and objects.

The types theory of LDO is a theory of functional types [9] containing:

• Primitive types are: J individual entity type, H truth value (sentence) type;
• Functional type constructor: F;
• Rules.

The rules of the type theory are:

• Primitive types are types;
• If α and β are types, then Fαβ is a type;
• All types are obtained by one of the above rules.

In LDO:

• All objects are operands of type J; all propositions are of type H;
• All concepts are operators of type FJH.

An expression X of type α is specified by: X: α.

The applicative scheme that expresses the application of a concept to an object is:

If f(x) is true, that is f(x) = T one says that “the object x falls under the concept f”, if f(x) is false, that is f(x) = ⊥ one says that “the object x does not fall under the concept f”. In LDO, N₁ is the operator of negation defined as:

(N₁ f) (x) = T, if and only if (f x) = ⊥

It has the classical logic property: (N₁ (N₁g)) = g.

In LDO, N₀ is the negation of a sentence defined as:

N₀(f (x)) = T, if and only if f (x) = ⊥

LDO is an applicative language of different types of operators (on functional types, [4]) applied to operands of different types; it is composed of:

• Objects of type J and concepts of type FJH.
• Predicates defined on individual objects (concepts of type FJH) and the relators between individuals with respective types FJFJH, FJFJFJH, etc.);
• Proposition of type of H;
• Connectives between propositions are of the type FHFHH;
• Fregean quantifiers: simple quantifiers with the type FFJHH; restricted quantifiers with the type FFJHFFJHH;
• Operators of negation with the type FHH (classical negation) defined only on propositions.

2.3. Basic Operators of LDO

2.3.1. The Constructor of the “Typical Object”: the Operator τ

This operator denoted by τ and called the constructor of the typical object builds an object totally indeterminate starting from a concept. Its type is FFJHJ; it canonically associates to each concept f, an indeterminate object τf, called “typical object”. Its applicative scheme is:

The object τf, is the “best representative object of the concept f; it is totally indeterminate, typical and abstractly represents the concept f in the form of an “any typical object whatever” This expression was chosen to encode the notion captured by the word “quelconque” in French. The typical object τf associated with f is unique. For example, if we take as concept f, the concept “to-be-a-man” then, the typical object associated is “a-man”. For the concept f, “to-be-a-computer”, τf is “a-computer”:

2.3.2. The Operator of Determination: the Operator δ

The operator δ, called the constructor of determination operators, builds a determination operator, starting from a given concept.

The operator δ canonically associates a determination operator of the type FJJ to each concept f.

The type of operator δ is FFJHFJJ. Its applicative scheme is:

A determination operator δ is an operator which being applied to an object x constructs another object y: y = ((δf) x) (We use the prefixed notation of a function, that is (f x) for f(x)). The object y is more determinate than the object x, by means of the determination added by δ. For example, if the concept f is “to-be-red”, then δf is “red”; if f is “to-be-on-the-table, then δf is “which-is-on-the-table”. The determination δf, “to-be-red” applied to the object “a-book” gives the more determinate object “a-red-book”.

Determinations can be composed of each other. A chain of determination Δ is a finite string of the form Δ = δg₁ o δg₂, …, o δg_n. The composition of determinations is associative and supposed to be commutative.

2.3.3. Objects in LDO

More or Less Determinate Objects

A more or less determinate object is an object recursively obtained starting from the object τf by:

• τf is a more or less determinate object;
• If δf is a chain of determinations, then y = ((δg₁ o δg₂, …, o δg_n) x) = (δg₁ (δg₂ (…, δg_n(x), …)) is a more or less determinate object;
• Each more or less determinate object is obtained by the above rules.

Fully Determinate Objects

An object x is fully (totally) determinate if and only if for each determination δg we have:

(δg x) = x

In LDO, objects are of two kinds from the point of view of their “determination”:

• More or less determinate objects;
• Fully determinate objects.

Nevertheless, all of them are of type J.

2.3.4. Concepts and Objects

Classes of Concepts Associated with a Concept f

In LDO we postulate the existence of two classes of concepts corresponding to a given concept f:

The intension of a concept f, Int f being the class of all concepts subsumed (included) by concept f; for example, the concepts “to-have-two-legs” and “to-have-a-mind” are both in the intension of the concept “to-be-a-man”; if f is “to-be-a-bird”, then in its intension there is the concept “to-fly”.

The essence of a concept f, Ess f is the class of all concepts necessarily included by f.

The class Ess f is included in Int f. The concept “to-be-a-man” has the concept “to-have-two-legs” in its intension but not in its essence. As for the concept “to-have-a-mind” it is right in the essence of the concept “to-be-a-man”. In other words, the essence of a concept f is the set of concepts necessarily comprised in f. If we remove a concept g from the essence of f, we “destroy” the concept f; it remains not the same. If a concept g is in the essence of a concept f, then the negation of g cannot belong to this essence. For the concept “to-be-a-bird”, the concept “to-fly” is in its intension but not in its essence.

Classes of Objects Associated with a Concept f

The LDO has two classes of objects associated with a concept:

Expansion (etendue in French (the Port Royal logic talks about “etendue”)). The expansion of f, denoted by Exp f is the set of all objects of (more or less determinate or fully determinate) to which f can be applied:

Exp(f) = {x/f(x) = T}

Extension. The extension of f, denoted by Ext f is the set of all objects fully determinate) to which f can be applied:

Ext(f) = {x/f(x) = T}

2.3.5. Theory of Typicality in LDO

Let us take a concept f. From the point of view of inheritance of concepts in their intension, the objects falling under it are of two kinds: typical objects of f and atypical objects of f.

Typical Object of f

An object x falling under f is a typical object of f if and only if:

For each chain of determination Δ constructs x starting from τf and for each determination along the chain we have:

• Either each determination concept is in the intension of f and its negation is not in the intension of f;
• Or if there is a determination concept such that itself and its negation are in the intension of f, then this determination concept belongs to the characteristic intension of x;
• Roughly speaking, a typical object of f is an object that inherits all the concepts of the intension of f, Int f.

Atypical Object of f

An object x falling under f is an atypical object of f if and only if:

There is a chain of determination Δ construct x starting from τf such that:

• Either there is a determination concept that it is not in the intension of f, but its negation belongs to this intension;
• Or if all determination concepts are in the intension of f, then x has an atypical “ascendant” as object.

Roughly speaking, an atypical object of f is an object that does not inherit all the concepts of the intension of f, Int f.

The typicality in LDO is based on the notion of determination.

2.3.6. The Logic of Determination of Objects (LDO) as a Deductive System

The contributions of the LDO to logic consist more in its structural part than in its deductive part. As system of deduction LDO is a natural deduction system in Gentzen sense with types associated to objects. It contains two types of inferences: typicality inferences inside the typical objects field and inferences inside the atypical objects field.

3. A Formal Description of the Logic of Determination of Objects (LDO) as a Preordered Set Model

In the LDO such as it is presented above, the set $ℱ$ can be seen as a collection of properties. From the functional point of view, the concept f, as element f ∈ $ℱ$ is an operator. From the structural point of view, it is a couple (Ess f, Int f), with Ess f and Int f being subsets of $ℱ$. We can organize $ℱ$ as a preordered set by the relation (→) between two concepts. Between the concepts f and g one can consider that g is more primary than f. It is defined by:

g→f  if g is one of the properties of f

(1)

Objects as elements of $𝒪$ are ranked by the relation --->. It is defined by:

For any objects o₁, o₂ ∈ $𝒪$, o₁ ---> o₂ iff the object o₂ is more determinate than the object o₁

(2)

The set O is organized in this way as a preordered set.

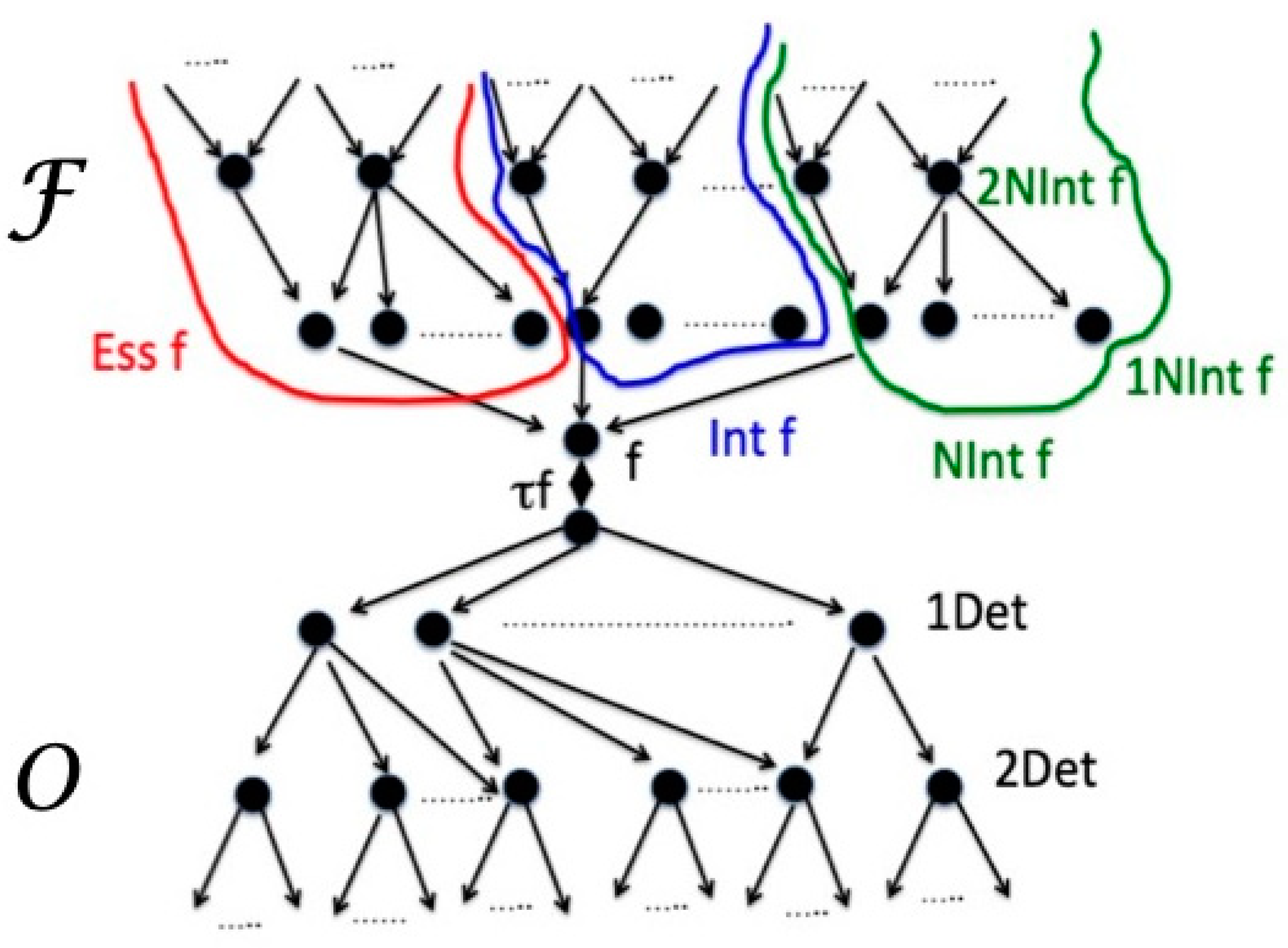
In Figure 1, the couple ($ℱ$, $𝒪$) corresponding to a concept f and to the object τf is represented by a graph. The vertices of this graph are properties in the upper side, the objects in the lower side. The arrows correspond to the two order relations above. In the upper side the subsets Ess f (in red) and Int f (in blue) are shown. The set NInt f (in green) is the set of negations of some properties of f concerning, eventually, atypical objects corresponding to τf.

One can remark that vertices both in the concept (properties) side and in the objects side are organized on levels. In the upper side the properties on the same level are supposed to be independent. The length of a chain g →ⁿf can be interpreted as the number of properties in depth subsumed by the concept f.

In the lower side a level corresponds to the number of determinations between τf and the objects of the level. This is 1Det τf are the objects obtained from τf by a single determination, 2Det τf are the objects obtained from τf by two determinations, etc. These objects are more or less determinate objects. The last level of objects is the level of completely determinate objects i.e. the level of Ext f.

One can remark that the entire model of Figure 1 is a special network formed by two preordered sets. The difference between this model and the approach in [4] consists in the fact that the structural part of LDO is described now in terms of filters and ideals [13], not only in terms of sets.

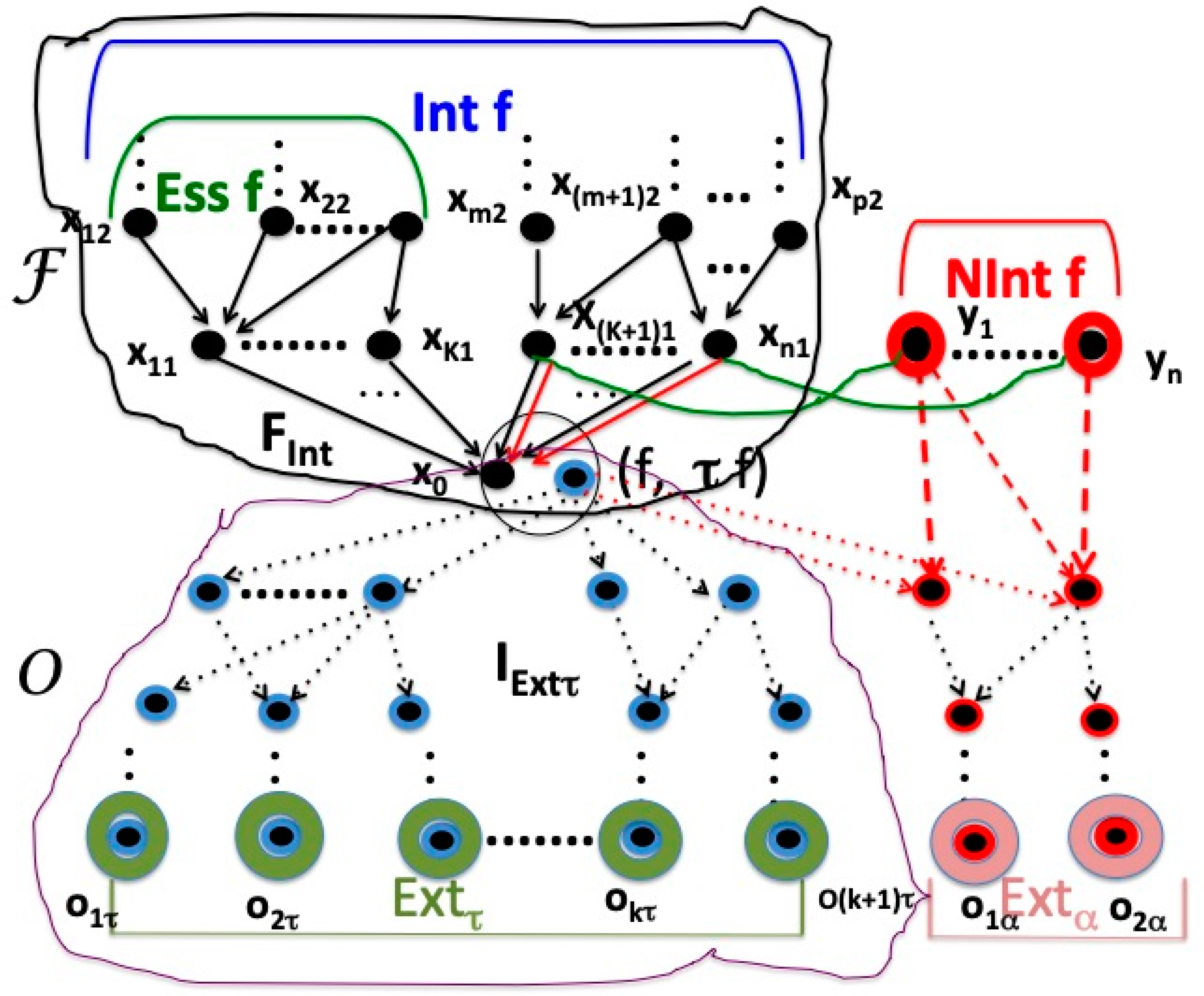
Figure 2 represents the network corresponding to a concept f and its typical indeterminate object τf of LDO. This network is composed by two parts the sub-network of concepts in the upper side F and the sub-network of objects in the lower side (O). In the whole network, the vertex f corresponding to the concept f in the upper side and the vertex τf corresponding to the fully indeterminate object are identified as a single and same vertex (f, τf).

We remark that we can build a pair of a filter and an ideal (F,I) [13], the filter being in the upper side $ℱ$, the ideal in the lower side $𝒪$. Such a pair is the subset of the whole network and it represents the mathematical modeling of the relation between a concept and some of its underlying objects. Roughly speaking, a route of the network in Figure 2 is structured top-down by two sub-networks: the concepts sub-network corresponding to $ℱ$, and the objects sub-network corresponding to $𝒪$.

A route from left to right of the sub-network $ℱ$ brings out the intension of a concept f and the essence of the concept f. The intension of a concept f, Int f (in blue) is formed by the sub-network in the upper side up to the concept f included it. The essence of a concept f Ess f (in green) is a sub-network of Int f included f. The arrows correspond to the order relation from Equation (1). We can remark the sub-network NInt f (in red) which is the part corresponding to negation of concept in intension. Because of the LDO theory of typicality, a negation of a concept is described explicitly in NInt f. The vertices corresponding to negation are linked to their positive (not negated) counterparts by a green line. The arrow related with a negation is dotted in red.

Typical objects are represented in the sub-network $𝒪$ by black-green double circles. Atypical objects are represented by red-rose double circles in $𝒪$. The last level is the level of fully determinate typical objects Ext τ and of fully determinate atypical objects Ext α. Dotted arrows correspond to relation in Equation (2).

The Galois Connexion and the Galois Lattice of LDO

The analysis of Figure 2 carried out above leads us to define a Galois connection on the couple ($ℱ$, $𝒪$).

Definition 1 [14].

A Galois connection between two preordered sets (P ≤ _P) and (Q ≤ _Q) is a couple of functions m₁ and m₂ such that:

m₁: (P ≤ _P) → (Q ≤ _Q), m₂: (Q ≤ _Q) → (P ≤ _P) with
For all p ∈ P, p ≤ _P m₂(m₁(p)) and for all q ∈ Q, q ≤ _P m₁(m₂(q)).

(3)

Definition 2 [13].

A couple (($𝒫$(P), ⊆), ($𝒫$(Q, ⊆))) is called a Galois lattice.

In the case of LDO formal model, one supposes both networks O and F to be finite.

Let us denote by Fil the set of all filters in $ℱ$ and by $𝒫$(Fil) the power set of Fil. In the same way, we denote by Id all the ideals in $𝒪$ and $𝒫$(Id) the power set of Id. We take $𝒫$(Fil) as P from Definition 1. The role of Q from Definition 1 is played by $𝒫$(Id).

Remark 1.

In the double network ($ℱ$, $𝒪$) there are several types of filters and ideals:

• A single filter corresponding to the intension Int f denoted by F_Int (in Figure 2, in black);
• A single ideal corresponding to all typical objects denoted by I_Extτ (in Figure 2, in magenta);
• Several filters containing concepts from the intension Int f and, in the counterpart NInt f (see Figure 2) negations of concepts in Int f. Such a filter is denoted by F_Int-NInt;
• Several ideals containing some typical and some atypical objects. Such an ideal is denoted by I_typ-atyp.

Definition 3.

Let us define m₁: ($𝒫$(Fil), ⊆) → ($𝒫$(Id), ⊆) and) by:

m₁(F_Int-NInt) = Extτ   if F_Int-NInt; = F_Int
m₁(F_Int-NInt) = I_typ-atyp   otherwise

(4)

and m₂: ($𝒫$(Id), ⊆) → ($𝒫$(Fil), ⊆) by:

m₂(I_typ-atyp) = F_Int   if I_typ-atyp = Extτ
m₂(I_typ-atyp) = F_Int-NInt   otherwise

(5)

Theorem 1.

The couple (m₁, m₂) is a Galois connection on the double network (($𝒫$(Fil) ⊆), ($𝒫$(Id) ⊆))).

Corollary 1.

The double network (($𝒫$(Fil), ⊆), ($𝒫$(Id), ⊆))) is the Galois lattice associated to the LDO model.

4. The Logic of Typical and Atypical Instances (LTA)

The logic of typical and atypical instances (LTA) is a logic that distinguishes the concept f from the property f. The property is an element of F, and the concept is the quadruple:

^f = < f, Ess f, Int f, NInt f >

(6)

A concept ^f is the quadruple formed by the property, the intension, the essence and, eventually, the set of negations of some concepts from intension. This logic extends the logic of determination of objects.

LTA allows us to make the whole problem slightly more complex by taking into account objects which being no longer atypical, are nevertheless on the external outer edges of the category, so apprehended as being related to the category but no longer belonging to it. Otherwise, ontologies of domains are structured networks of concepts and of classes of objects. Generally, in these ontologies, the problem of typical/atypical is not considered. Inside these ontologies only some objects are treated as exceptions without doing a deep “logical” analysis (especially the analysis of intensions) establishing that an object must be considered as an atypical object internal to the category or as an object on the edges of the category, and so “almost belonging” to it but not “belonging entirely”.

We start with an example that is the analysis of a concept with the resulting categorization when one takes into account some properties of this concept and its typical objects. This example is about the typical and atypical objects of the class of inhabitants of a city.

Example.

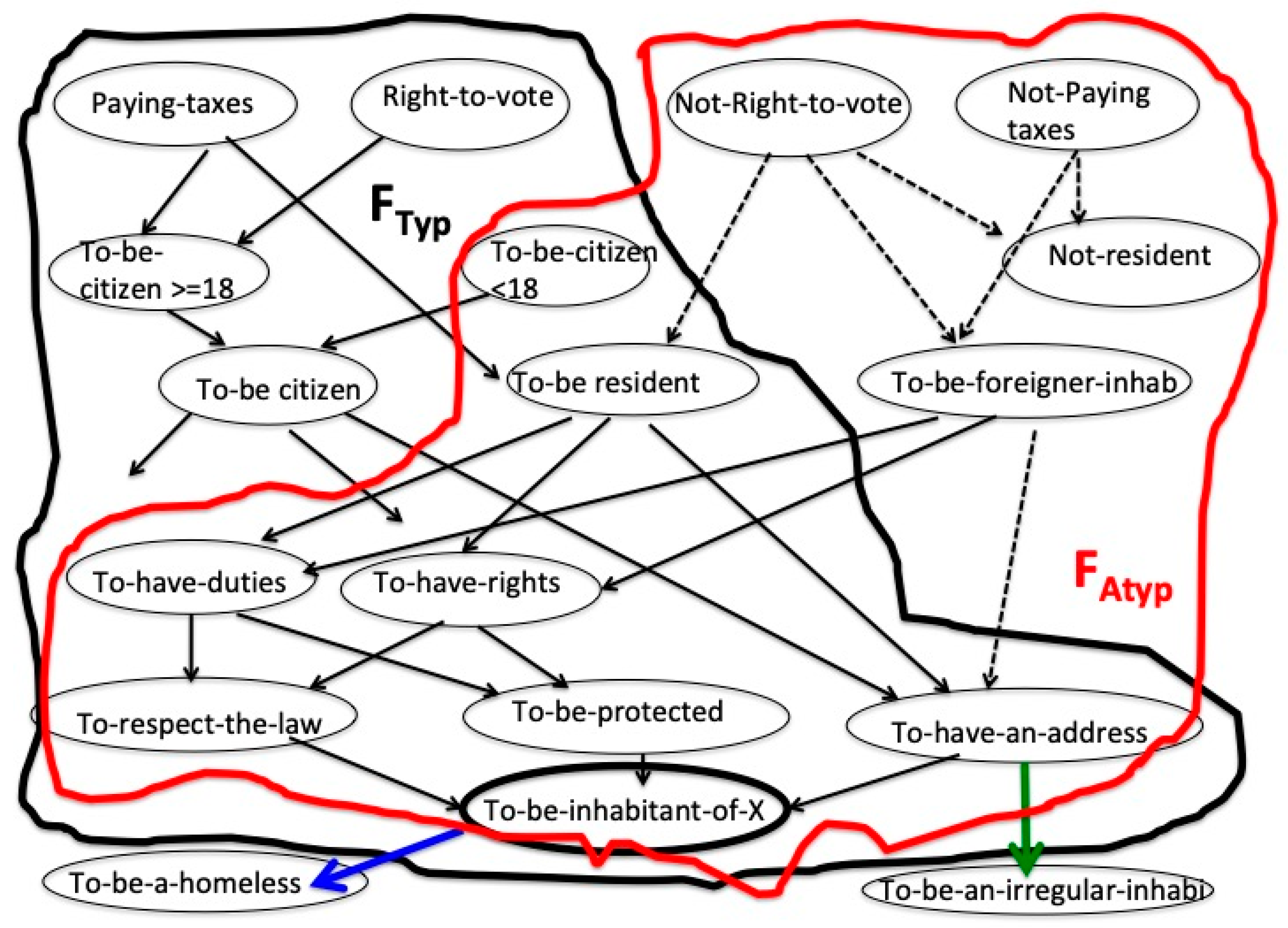
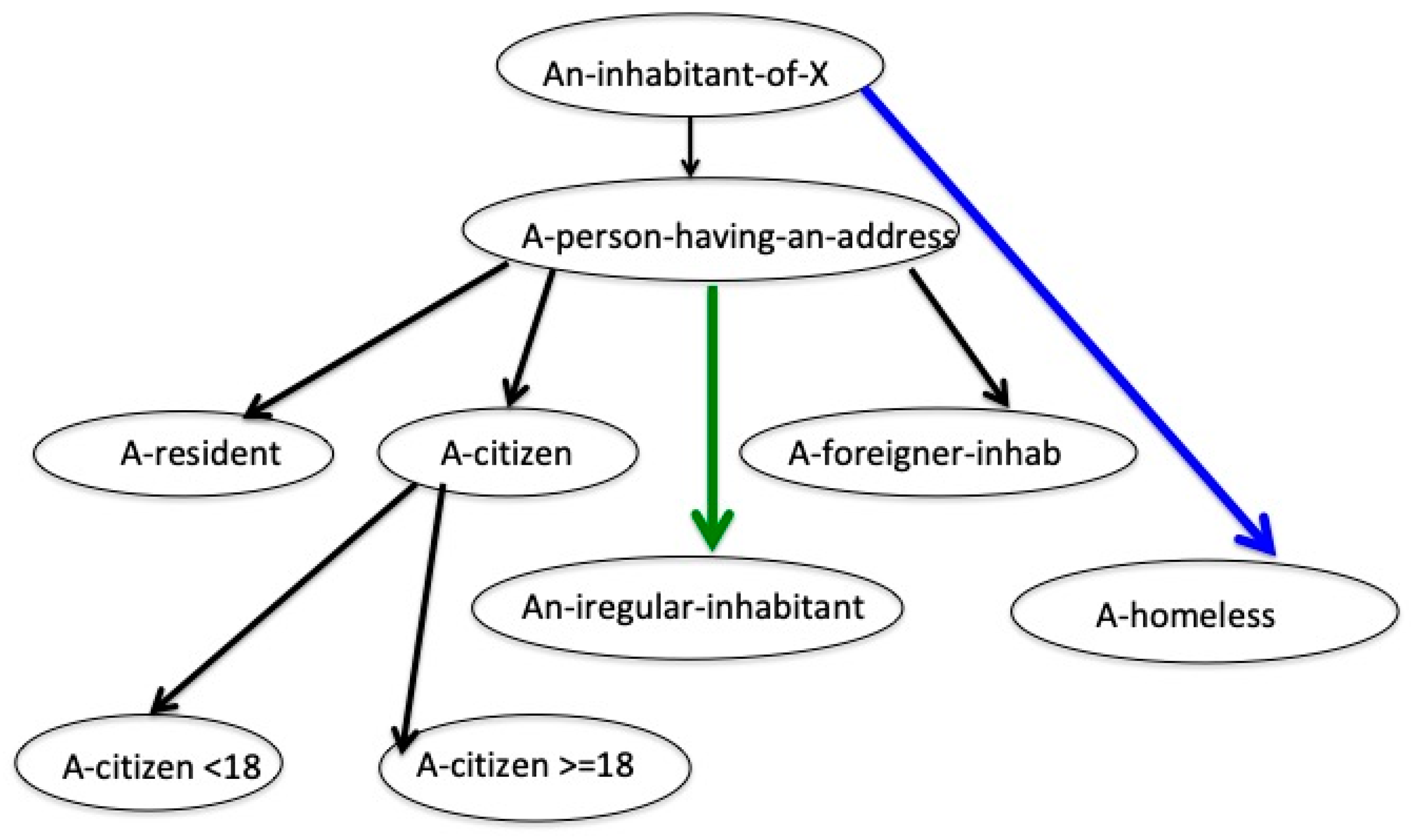
The concept “living-in-X (inhabitant-of-X)” contains the property “to-be-inhabitant-of-X”. This concept has an intension containing properties “to-have-rights” and “to-have-duties”. These properties imply “to-be-protected-by-law” and “to-respect-the-law”, respectively. All inhabitants of the city are not substitutable for one another. Some of them, the citizens, have the citizenship of the country, the others (e.g., the foreigners residing in the city) do not. All citizens must pay taxes and after age of 18 they have the right to vote. The foreigners pay taxes but, generally, they do not have the right to vote, though in some countries some foreigner residents who are not citizens also have the right to vote providing that, however, they are residents and have paid taxes for five years. One must consider also inhabitants without fixed residence (homeless) being not irregular residents (“sans papiers”). They lose (at least in some categorizations) some of their rights (such as the access to health care) and they are not considered constrained to certain duties (e.g., to pay taxes). The lattice of the concepts F corresponding to the concept f inhabitant-of-X is presented in Figure 3. The lattice of objects of the same concept f is presented in Figure 4.

We can see from Figure 3, for example that the property to-be-a-citizen-under-18 years generates an atypical object “a-citizen-under-18-years” because it is related to the property “not-right-to-vote” represented in Figure 4.

In Figure 4, we can see two particular objects “an-irregular-inhabitant” and “a-homeless”. The first one is determined only by two properties “to-have-an-address” and “to-be-an inhabitant-of-X”, both belonging to the intension of “to-be-an inhabitant-of-X” (green arrow). The second one is determined only by “to-be-an inhabitant-of-X” (blue arrow). So, they both are “exceptions” but with a status different from the status of typical objects or atypical objects of the concept “to-be-an inhabitant-of-X”. The object “an-irregular-inhabitant” has the property “to-be-an inhabitant of the city” and the property “to-have-an-address” both belonging to the intension of “to-be-an inhabitant-of-X”. The object “a-homeless” just falls under the property “to-be-an inhabitant-of-X”.

Informal Description of LTA Versus LDO

• In LTA the vertices of $ℱ$ are properties, a concept is represented by entire lattice $ℱ$. That is because it is based by the difference between property and concept.
• In LTA in the part of objects $𝒪$, there are at least two categories of objects unless typical objects and atypical objects:
  • Strong exceptions (the “homeless”, in Example);
  • Weak exceptions (the “irregular inhabitant” in Example).

The difference between LDO and LTA is the following:

• The LDO describes the structure of a concept f;

The LTA structure, by integrating several type of objects, considers a network having several networks ($ℱ$, $𝒪$) (Figure 2) interrelated corresponding to concepts f, g, …, h that is {(f, τf), (g, τg), …, (h,τh)}.

5. LTA as a Quasi Topology Structure

5.1. Quasi Topology Structure (QTS) Definition

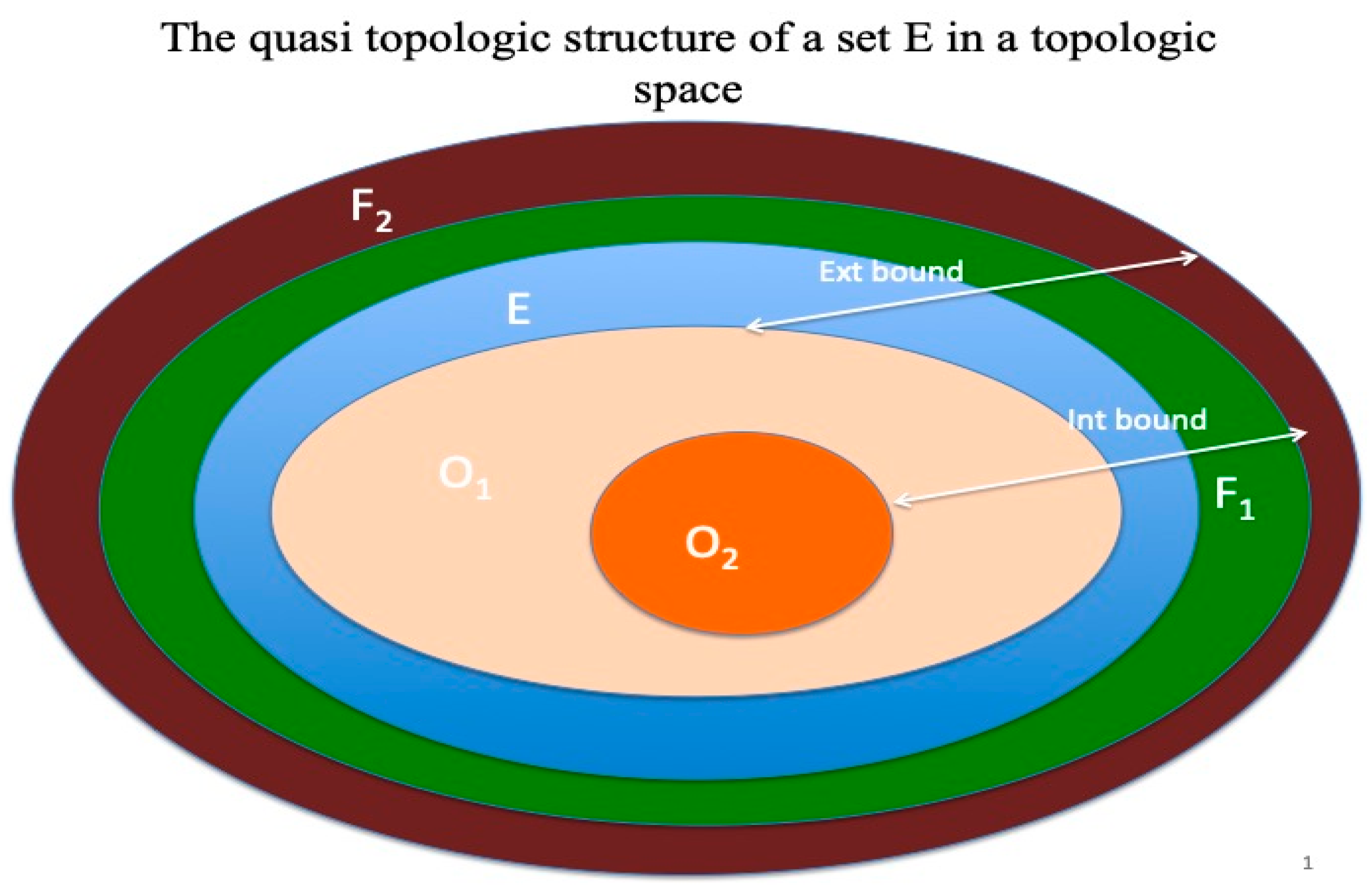
Definition 4 [5].

Let <X, O> be a topological space where X denotes the space and O denotes the topology. We say that a set E from this space is structured by a quasi topology or it has a quasi topology structure (QTS) if there exists two open sets O₁ and O₂ of O, and two closed sets F₁ and F₂ such that:

O₂ ⊂ O₁ ⊆ E ⊆ F₁ ⊂ F₂

(7)

with:

O₁ is the biggest open set contained in E, that is O₁ = Int (E),

(8)

F₁ is the smallest closed set containing E, that is F₁ = Cl(E),

(9)

O₂ is the biggest open set strictly contained in O₁,

(10)

F₂ is the smallest closed set strictly containing F₁.

(11)

The set O₂ is said to be the strict interior of E; the set O₁ is the large interior of E. The set F₂ is said to be the large closure of E and the set F₁ the strict closure of E.

The internal boundary, the external boundary, the strict boundary and the large boundary of E are defined by:

Int-bound(E) = F₁ − O₂,

(12)

Ext-bound(E) = F₂ − O₁,

(13)

Large-bound(E) = Int-bound(E) ∪ Ext-bound(E),

(14)

Bound(E) = Cl(E) – Int(E) = F₁ – O₁.

(15)

The above definition is presented in an intuitive way in Figure 5.

Remark 2.

In this definition, the structure of quasi topology (QTS) is limited to topological space X being a topological space. In [15], we extended the QTS to some types of approximation spaces (rough sets spaces) by replacing the notions of openness and closure by the corresponding notions of rough sets.

5.2. The QTS of the LTA

The background framework is the systems of two networks of type from Figure 2, one associated to a network F_f, corresponding to the concept ^f = <f, Ess f, Int f, NInt f>, the other F_g, corresponding to concept ^g = < g, Ess g, Int g, NInt g >.

The space X from Definition 4 is the entire set of fully determinate objects of O_f and O_g, namely Ext f ∪ Ext g. We define a QTS on the fully determinate objects related to the concept ^f.

There are four relations between fully determinate objects related to ^f. These relations are defined based on the structure of F_f.

• The objects verifying all the properties from Ess f and Int f. These objects are typical objects. They form the set O₂;
• The objects verifying all the properties from Ess f and at least one property of NInt f. These objects are atypical objects. They form the set O′₂;
• The objects verifying some properties from Ess f and some properties of Int. These objects are weak exceptions. They form the set F₁;
• The objects verifying only the property f as property. These objects are strong exceptions. They form the set F₂.

Definition 5.

Let us define the following relations on the approximation space X = Ext f ∪ Ext g:

• typ f (o₁,o₂) defined by:

  for all o₁, o₂, typ (o₁,o₂) iff o₁,o₂ are typical objects.
  It is an equivalent relation. All typical objects form an equivalent class;
• atyp ^kf (o₁,o₂) defined by:

  for all o₁, o₂, typ (o₁,o₂) iff o₁, o₂ are atypical objects with k their degree of atypicality.
  There are n relations atyp_k, f for k = 1, …, n, where n is the degree of atypicality. The degree of typicality of an object o is the number of properties of NInt verifying by this object. All the atypical objects having the same degree of atypicality are considered to be equivalent;
• wex_i f (weak exception) defined by:

  For all o₁, o₂, wex_i f (o₁, o₂) iff o₁, o₂ are both objects falling under the same number of properties of Ess f.
  There are m relations wex_i, f for i = 1, …. m if Ess f has m properties. All the objects falling under the same number of properties of Ess f are considered to be equivalent;
• strongex f (strong exception) defined by:

  strongex f (o) iff o in an object verifying only the property f.
  The relation strongex f is an unary (function prototype length 1);

Remark 3.

All the relations above are defined as relations between objects but as regarding of the LDO structure (interrelated) related to the concept ^f. For this reason, their names are followed by f.

In LTA, a set E of objects belonging to Ext f ∪ Ext g but analyzed regarding to concept ^f contains objects that are directly related to concept ^f as the typical objects of f and the atypical objects of f, and other objects which are related to the property f but belong to the structure corresponding to another concept g.

Theorem 2.

Let us denote by (atyp f)* = ∪_k=1,…n (atyp_k f)* and by (wex f)* = ∪_i=1,…m wex_i f. A subset, set E of the approximation space (Ext f ∪ Ext g, typ f ∪ (atyp f)*, (wex f) *∪ strongex f) has the following QTS structure:

O₂ = Ext_typ f

O₁ = (Ext_typ f ∪ (Ext_atyp f)*)

F₁ = Ext_wex f

F₂ = Ext_strongex f

We can easily prove that O₂ is the lower approximation of E as regarding to the relation typ f, O₁ is the lower approximation of E as regarding to the relation typ f ∪ (atyp f)*, F₁is the upper approximation of E as regarding to the relation (wex f)* and F₂ is the upper approximation of E as regarding to the relation strongex f.

It is obvious that O₂ ⊂ O₁ ⊆ E ⊆ F₁ ⊂ F₂.

Remark 4.

This QTS structure in an approximation space is a hybridization built up with four relations and the lower and the upper approximation of a set regarding to them.

We call this structure the QTS structure associated to a set of fully determinate objects in LTA.

6. Conclusions

In this paper a mathematical model of the logic of determination of objects (LDO) introduced in [4] is presented. The novelty of this model is the fact that it describes the structural level of LDO by notions of preordered sets and lattices. To represent the conceptual structure of LDO as a network allows us to extend the main theorem of formal concept analysis [13] stating that the lattice of concepts is a Galois lattice to LDO by establishing a Galois lattice associated to LDO network by Theorem 1.

A mathematical model of the logic of typical and atypical Instances (LTA) [3] is also described as an extension of LDO model. In the case of LTA we give a quasi topology structure (QTS) [6,7] to a set of objects related to a concept.

The LDO and its associated Galois lattice theorem allows a computer software for analysis and categorization inside ontologies to be built.

The QTS structure in LTA represents a type of approximation different from those existing until now. It can be also useful as a model in a computer-based tool of categorization.