A New Generalized Projection and Its Application to Acceleration of Audio Declipping
Abstract
1. Introduction
2. Methods
2.1. Proximal Algorithms
2.2. Proximal Operators
2.3. The New Relation of Projections
3. Discussion on the New Result
4. Experiment
4.1. Problem Formulation
4.2. The Gabor Operators
4.3. Problem Solution
4.4. Condat Algorithm
| Algorithm 1: Condat algorithm (CA) adapted to solving Equation (26). |
 |
4.5. Douglas–Rachford Algorithm
| Algorithm 2: Douglas–Rachford algorithm (DR) solving Equation (29) |
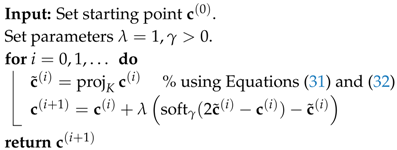 |
4.6. Comparison of the Algorithms
- Sparsifying step: one soft thresholding, which is performed elementwise, and thus it is , and one analysis , which is
- Reliable part: one synthesis G and one analysis , both
- Each of the clipped parts: one synthesis, , and one elementwise projection, .
- Sparsifying step: one soft thresholding, which is
- Projection onto K: one synthesis G and one pseudoinverse , which is in the order of , i.e., in our particular setup; projection that is performed elementwise, .
4.7. Redundancy of the Real-Part Operator
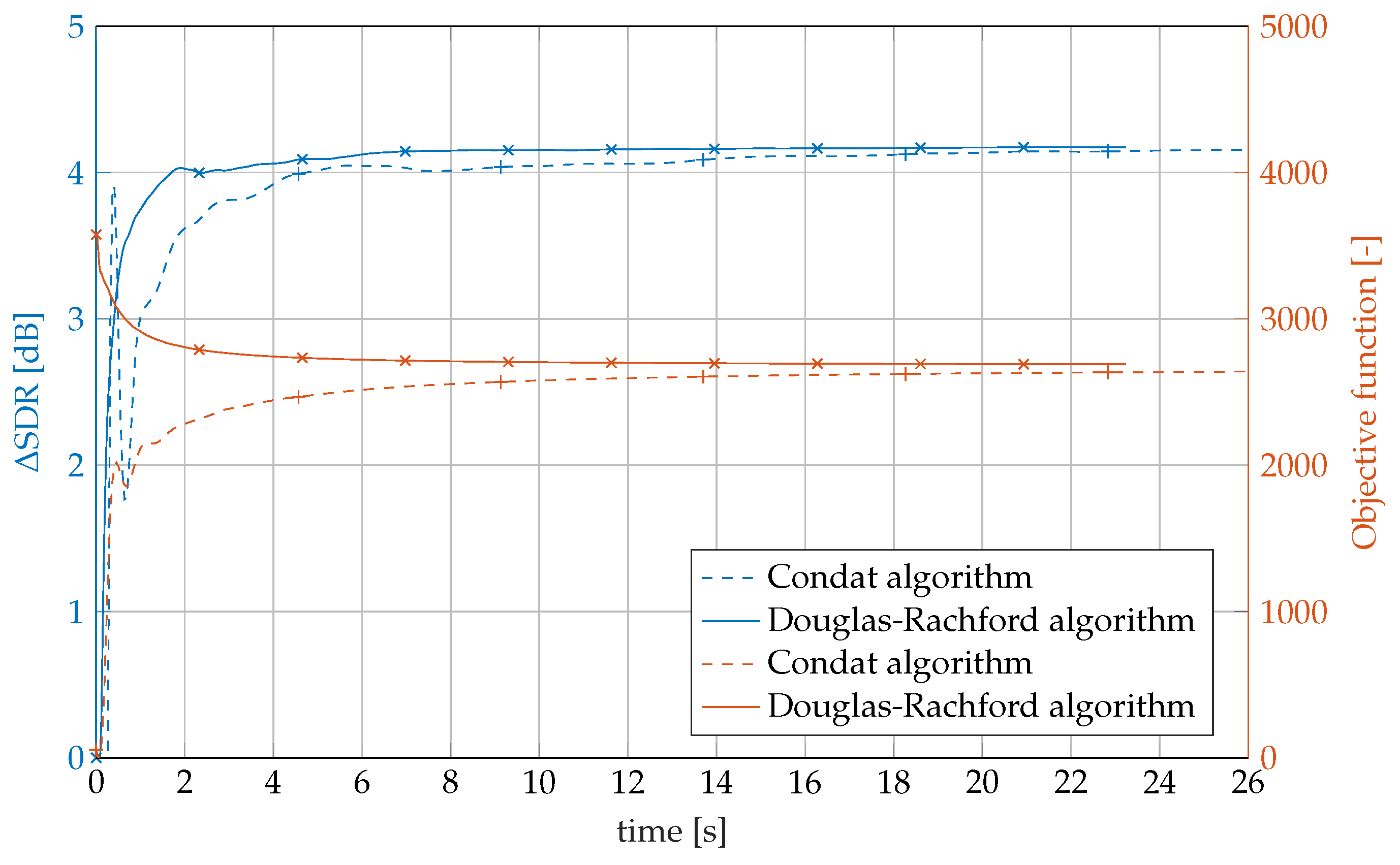
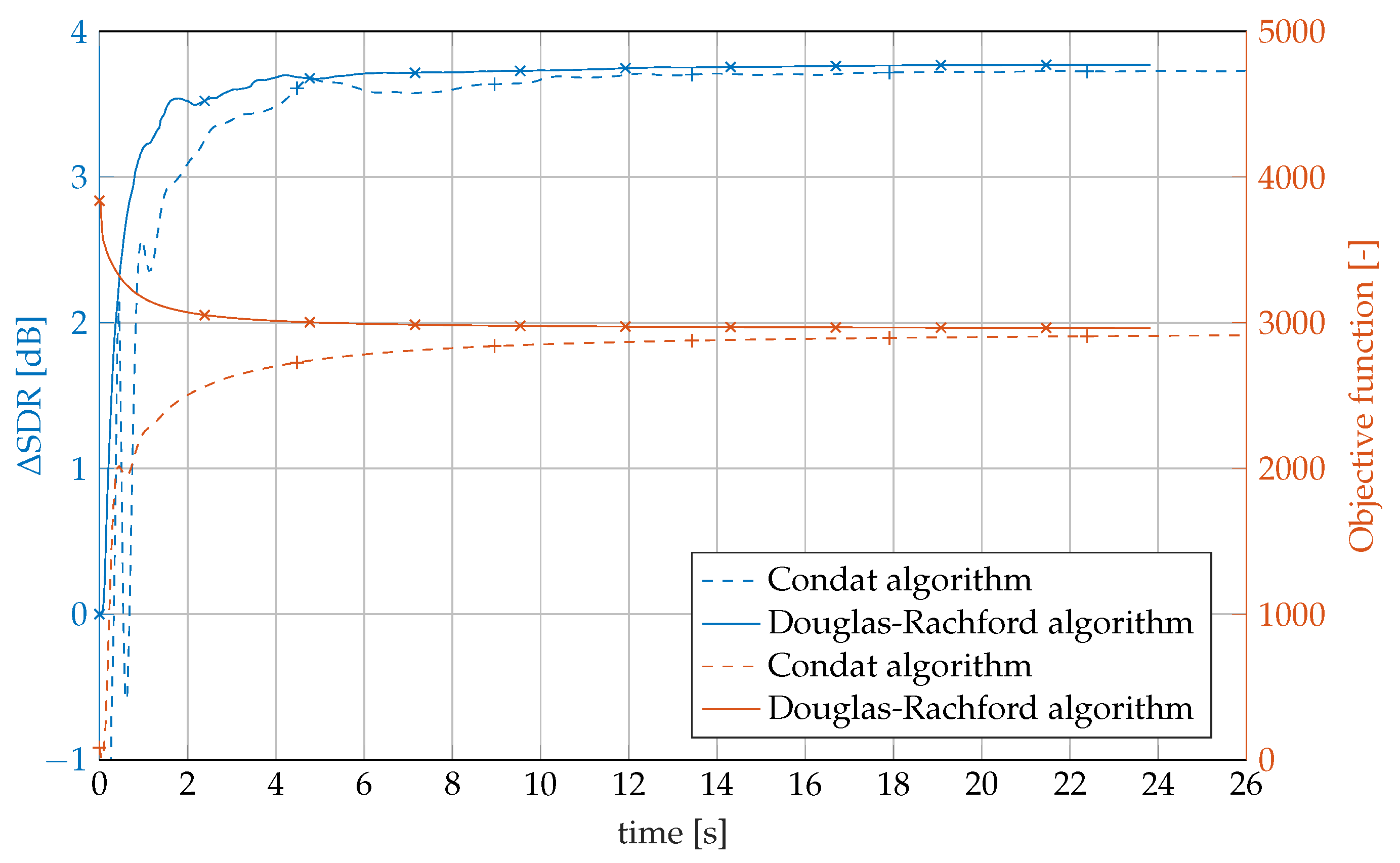
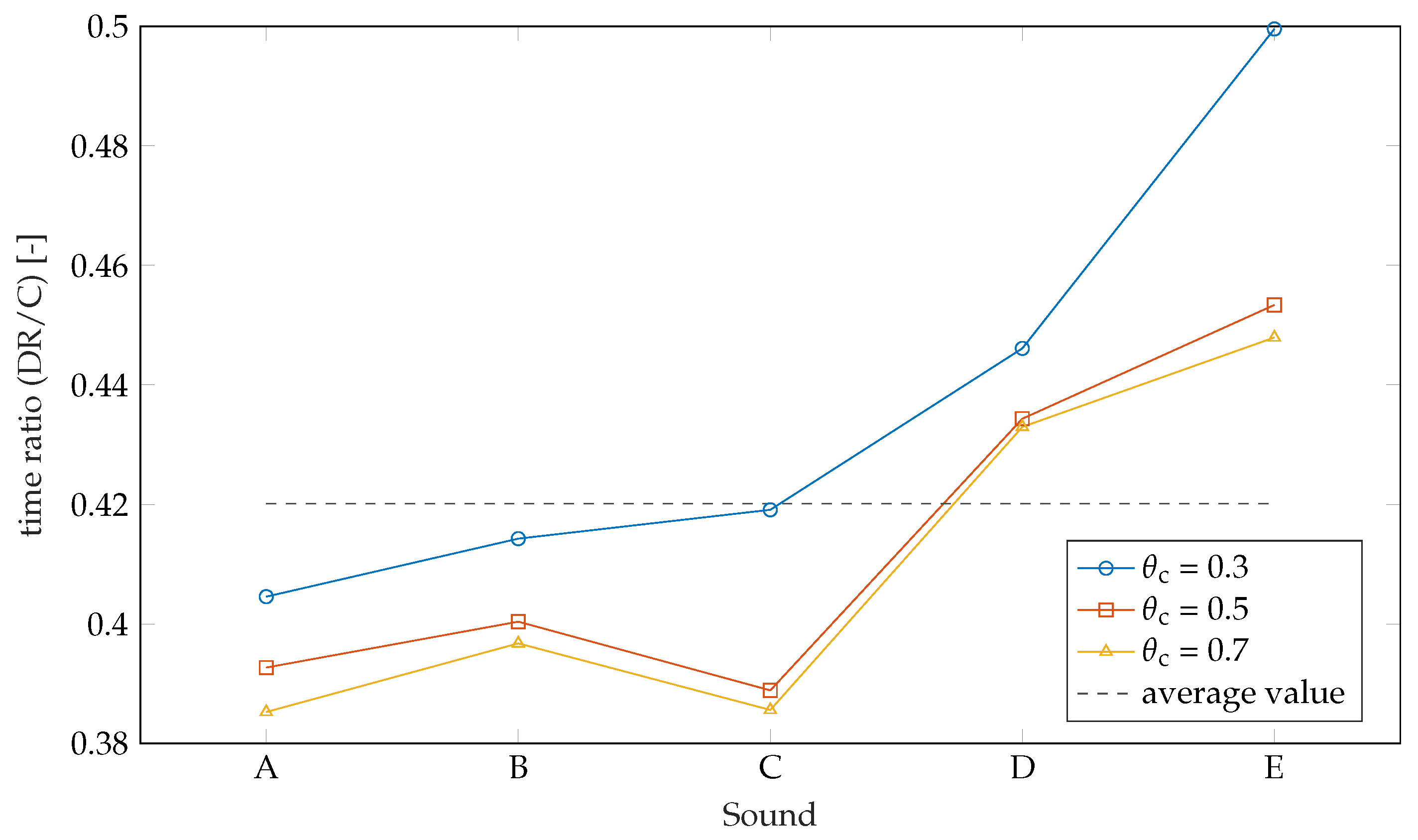
4.8. Results
4.9. Other Applications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CA | Condat Algorithm |
| DCT | Discrete Cosine Transform |
| DFT | Discrete Fourier Transform |
| DGT | Discrete Gabor Transform |
| DR | Douglas–Rachford (algorithm) |
| FBB-PD | Forward–Backward-Based Primal–Dual (algorithm) |
| FFT | Fast Fourier Transform |
| MDCT | Modified Discrete Cosine Transform |
| PA | Proximal Algorithm |
| SDR | Signal-to-Distortion Ratio |
| STFT | Short-Time Fourier Transform |
References
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Combettes, P.; Pesquet, J. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering; Springer: New York, NY, USA, 2011; pp. 185–212. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd ed.; Springer: Cham, Switzerland, 2011. [Google Scholar]
- Bayram, I. On the convergence of the iterative shrinkage/thresholding algorithm with a weakly convex penalty. IEEE Trans. Signal Process. 2016, 64, 1597–1608. [Google Scholar] [CrossRef]
- Chambolle, A.; Pock, T. A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 2011, 40, 120–145. [Google Scholar] [CrossRef]
- Komodakis, N.; Pesquet, J. Playing with duality: An overview of recent primal-dual approaches for solving large-scale optimization problems. IEEE Signal Process. Mag. 2015, 32, 31–54. [Google Scholar] [CrossRef]
- Condat, L. A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 2013, 158, 460–479. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Parekh, A.; Bayram, I. Convex 1-D total variation denoising with non-convex regularization. IEEE Signal Process. Lett. 2015, 22, 141–144. [Google Scholar] [CrossRef]
- Boyd, S.P.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Daňková, M.; Rajmic, P.; Jiřík, R. Acceleration of perfusion MRI using locally low-rank plus sparse model. In Latent Variable Analysis and Signal Separation; Springer: Liberec, Czech Republic, 2015; pp. 514–521. [Google Scholar]
- Condat, L. A generic proximal algorithm for convex optimization—Application to total variation minimization. Signal Process. Lett. IEEE 2014, 21, 985–989. [Google Scholar] [CrossRef]
- Fadili, M.; Starck, J.L. Monotone operator splitting for optimization problems in sparse recovery. In Proceedings of the 2009 16th IEEE International Conference on Image Processing, Piscataway, NJ, USA, 7–10 November 2009; pp. 1461–1464. [Google Scholar]
- Combettes, P.; Pesquet, J. A Douglas–Rachford splitting approach to nonsmooth convex variational signal recovery. IEEE J. Sel. Top. Signal Process. 2007, 1, 564–574. [Google Scholar] [CrossRef]
- Šorel, M.; Bartoš, M. Efficient JPEG decompression by the alternating direction method of multipliers. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 271–276. [Google Scholar] [CrossRef]
- Combettes, P.; Wajs, V. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- Moreau, J.J. Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. Fr. 1965, 93, 273–299. [Google Scholar] [CrossRef]
- Christensen, O. Frames and Bases, an Introductory Course; Birkhäuser: Boston, MA, USA, 2008. [Google Scholar]
- Christensen, O. An Introduction to Frames and Riesz Bases; Birkhäuser: Boston, MA, USA; Basel, Switzerland; Berlin, Germany, 2003. [Google Scholar]
- Gröchenig, K. Foundations of Time-Frequency Analysis; Birkhäuser: Basel, Switzerland, 2001. [Google Scholar]
- Balazs, P.; Dörfler, M.; Jaillet, F.; Holighaus, N.; Velasco, G. Theory, implementation and applications of nonstationary Gabor frames. J. Comput. Appl. Math. 2011, 236, 1481–1496. [Google Scholar] [CrossRef] [PubMed]
- Necciari, T.; Balazs, P.; Holighaus, N.; Søndergaard, P.L. The ERBlet transform: An auditory-based time-frequency representation with perfect reconstruction. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–30 May 2013; pp. 498–502. [Google Scholar] [CrossRef]
- Meyer, C.D. Matrix Analysis and Aplied Linear Algebra; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Gröchenig, K. Non-uniform sampling in higher dimensions: From trigonometric polynomials to bandlimited functions. In Modern Sampling Theory: Mathematics and Applications; Benedetto, J.J., Ferreira, P.J.S.G., Eds.; Birkhäuser Boston: Boston, MA, USA, 2001; pp. 155–171. [Google Scholar] [CrossRef]
- Bogdanova, I.; Vandergheynst, P.; Antoine, J.P.; Jacques, L.; Morvidone, M. Stereographic wavelet frames on the sphere. Appl. Comput. Harmon. Anal. 2005, 19, 223–252. [Google Scholar] [CrossRef]
- Adcock, B.; Gataric, M.; Hansen, A.C. Weighted frames of exponentials and stable recovery of multidimensional functions from nonuniform Fourier samples. Appl. Comput. Harmon. Anal. 2017, 42, 508–535. [Google Scholar] [CrossRef]
- Daubechies, I.; Grossmann, A.; Meyer, Y. Painless nonorthogonal expansions. J. Math. Phys. 1986, 27, 1271–1283. [Google Scholar] [CrossRef]
- Wickerhauser, M.V. Mathematics for Multimedia; Birkhäuser: Boston, MA, USA, 2009. [Google Scholar]
- Vetterli, M.; Kovačević, J.; Goyal, V. Foundations of Signal Processing; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zölzer, U. DAFX: Digital Audio Effects, 2nd ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Etter, W. Restoration of a discrete-time signal segment by interpolation based on the left-sided and right-sided autoregressive parameters. IEEE Trans. Signal Process. 1996, 44, 1124–1135. [Google Scholar] [CrossRef]
- Abel, J.; Smith, J. Restoring a clipped signal. In Proceedings of the 1991 ICASSP-91 International Conference on Acoustics, Speech, and Signal Processing, Toronto, ON, Canada, 14–17 May 1991; Volume 3, pp. 1745–1748. [Google Scholar] [CrossRef]
- Dahimene, A.; Noureddine, M.; Azrar, A. A simple algorithm for the restoration of clipped speech signal. Informatica 2008, 32, 183–188. [Google Scholar]
- Selesnick, I. Least squares with examples in signal processing. OpenStax CNX. 2013. Available online: https://cnx.org/contents/XRPKcVgh@1/Least-Squares-with-Examples-in-Signal-Processing (accessed on 14 September 2019).
- Bilen, Ç.; Ozerov, A.; Pérez, P. Audio declipping via nonnegative matrix factorization. In Proceedings of the 2015 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 18–21 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Adler, A.; Emiya, V.; Jafari, M.; Elad, M.; Gribonval, R.; Plumbley, M. Audio Inpainting. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 922–932. [Google Scholar] [CrossRef]
- Adler, A.; Emiya, V.; Jafari, M.; Elad, M.; Gribonval, R.; Plumbley, M. A constrained matching pursuit approach to audio declipping. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 329–332. [Google Scholar] [CrossRef]
- Defraene, B.; Mansour, N.; Hertogh, S.D.; van Waterschoot, T.; Diehl, M.; Moonen, M. Declipping of audio signals using perceptual compressed sensing. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 2627–2637. [Google Scholar] [CrossRef]
- Siedenburg, K.; Kowalski, M.; Dorfler, M. Audio declipping with social sparsity. In Proceedings of the 2014 IEEE International Conference on IEEE Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 1577–1581. [Google Scholar]
- Kitić, S.; Jacques, L.; Madhu, N.; Hopwood, M.; Spriet, A.; De Vleeschouwer, C. Consistent iterative hard thresholding for signal declipping. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–30 May 2013; pp. 5939–5943. [Google Scholar] [CrossRef]
- Kitić, S.; Bertin, N.; Gribonval, R. Audio declipping by cosparse hard thresholding. In Proceedings of the 2nd Traveling Workshop on Interactions between Sparse models and Technology, Namur, Belgium, 27–29 August 2014. [Google Scholar]
- Kitić, S.; Bertin, N.; Gribonval, R. Sparsity and cosparsity for audio declipping: A flexible non-convex approach. In LVA/ICA 2015—The 12th International Conference on Latent Variable Analysis and Signal Separation; Springer: Liberec, Czech Republic, 2015. [Google Scholar]
- Záviška, P.; Rajmic, P.; Průša, Z.; Veselý, V. Revisiting synthesis model in sparse audio declipper. In LVA/ICA 2018—The 14th International Conference on Latent Variable Analysis and Signal Separation; Springer: Guildford, UK, 2018; pp. 429–445. [Google Scholar] [CrossRef]
- Záviška, P.; Rajmic, P.; Mokrý, O.; Průša, Z. A proper version of synthesis-based sparse audio declipper. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 591–595. [Google Scholar] [CrossRef]
- Weinstein, A.J.; Wakin, M.B. Recovering a clipped signal in sparseland. Sampl. Theory Signal Image Process. 2013, 12, 55–69. [Google Scholar]
- Siedenburg, K.; Dörfler, M. Structured sparsity for audio signals. In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx-11), Paris, France, 19–23 September 2011; pp. 23–26. [Google Scholar]
- Kowalski, M.; Siedenburg, K.; Dörfler, M. Social sparsity! Neighborhood systems enrich structured shrinkage operators. IEEE Trans. Signal Process. 2013, 61, 2498–2511. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Bayram, I.; Kamasak, M. A simple prior for audio signals. IEEE Trans. Acoust. Speech Signal Process. 2013, 21, 1190–1200. [Google Scholar] [CrossRef]
- Bayram, I.; Akykıldız, D. Primal-dual algorithms for audio decomposition using mixed norms. Signal Image Video Process. 2014, 8, 95–110. [Google Scholar] [CrossRef]
- Rajmic, P.; Bartlová, H.; Průša, Z.; Holighaus, N. Acceleration of audio inpainting by support restriction. In Proceedings of the 7th International Congress on Ultra Modern Telecommunications and Control Systems, Brno, Czech Republic, 6–8 October 2015. [Google Scholar]
- Søndergaard, P.L.; Torrésani, B.; Balazs, P. The linear time frequency analysis toolbox. Int. J. Wavelets Multiresolution Anal. Inf. Process. 2012, 10. [Google Scholar] [CrossRef]
- Holighaus, N.; Wiesmeyr, C. A class of warped filter bank frames tailored to non-linear frequency scales. arXiv 2016, arXiv:1409.7203. [Google Scholar]
- Donoho, D. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Bruckstein, A.M.; Donoho, D.L.; Elad, M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev. 2009, 51, 34–81. [Google Scholar] [CrossRef]
- Rajmic, P. Exact risk analysis of wavelet spectrum thresholding rules. In Proceedings of the 2003 10th IEEE International Conference on Electronics, Circuits and Systems, Sharjah, United Arab Emirates, 14–17 December 2003; Volume 2, pp. 455–458. [Google Scholar] [CrossRef]
- Hiriart-Urruty, J.B.; Lemaréchal, C. Fundamentals of Convex Analysis; Springer: New York, NY, USA, 2001. [Google Scholar]
- Průša, Z.; Søndergaard, P.L.; Holighaus, N.; Wiesmeyr, C.; Balazs, P. The large time-frequency analysis toolbox 2.0. In Sound, Music, and Motion; Aramaki, M., Derrien, O., Kronland-Martinet, R., Ystad, S., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014; pp. 419–442. [Google Scholar]
- Rencker, L.; Bach, F.; Wang, W.; Plumbley, M.D. Fast iterative shrinkage for signal declipping and dequantization. In Proceedings of the iTWIST’18—International Traveling Workshop on Interactions between Low-Complexity Data Models and Sensing Techniques, Marseille, France, 21–23 November 2018. [Google Scholar]
- Mokrý, O.; Záviška, P.; Rajmic, P.; Veselý, V. Introducing SPAIN (SParse Audio INpainter). In Proceedings of the 27th European Signal Processing Conference (EUSIPCO), A Coruña, Spain, 2–6 September 2019. [Google Scholar]
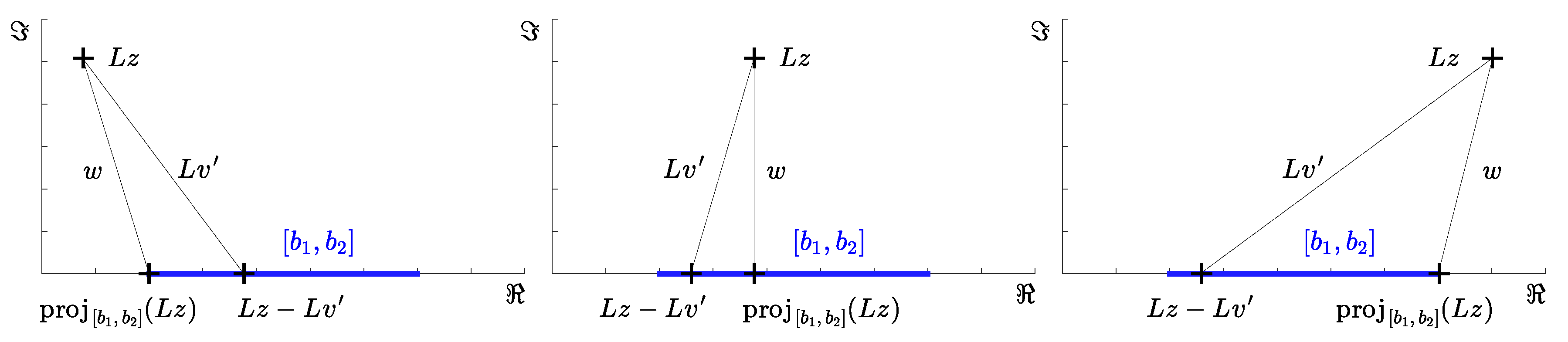

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajmic, P.; Záviška, P.; Veselý, V.; Mokrý, O. A New Generalized Projection and Its Application to Acceleration of Audio Declipping. Axioms 2019, 8, 105. https://doi.org/10.3390/axioms8030105
Rajmic P, Záviška P, Veselý V, Mokrý O. A New Generalized Projection and Its Application to Acceleration of Audio Declipping. Axioms. 2019; 8(3):105. https://doi.org/10.3390/axioms8030105
Chicago/Turabian StyleRajmic, Pavel, Pavel Záviška, Vítězslav Veselý, and Ondřej Mokrý. 2019. "A New Generalized Projection and Its Application to Acceleration of Audio Declipping" Axioms 8, no. 3: 105. https://doi.org/10.3390/axioms8030105
APA StyleRajmic, P., Záviška, P., Veselý, V., & Mokrý, O. (2019). A New Generalized Projection and Its Application to Acceleration of Audio Declipping. Axioms, 8(3), 105. https://doi.org/10.3390/axioms8030105




