Correction to “On a Class of Hermite-Obreshkov One-Step Methods with Continuous Spline Extension” [Axioms 7(3), 58, 2018]

Francesca Mazzia; Alessandra Sestini

doi:10.3390/axioms8020059

and

¹

Dipartimento di Informatica, Università degli Studi di Bari Aldo Moro, 70125 Bari, Italy

²

Dipartimento di Matematica e Informatica U. Dini, Università di Firenze, 50134 Firenze, Italy

^*

Author to whom correspondence should be addressed.

^†

Member of the INdAM Research group GNCS.

Axioms2019, 8(2), 59;https://doi.org/10.3390/axioms8020059

This article belongs to the Special Issue Advanced Numerical Methods in Applied Sciences

Version Notes

Order Reprints

Abstract

The authors of the above mentioned paper specify that the considered class of one-step symmetric Hermite-Obreshkov methods satisfies the property of conjugate-symplecticity up to order

p + r,

where

r = 2

and p is the order of the method. This generalization of conjugate-symplecticity states that the methods conserve quadratic first integrals and the Hamiltonian function over time intervals of length

O (h^{- r})

. Theorem 1 of the above mentioned paper is then replaced by a new one. All the other results in the paper do not change. Two new figures related to the already considered Kepler problem are also added.

Keywords:

initial value problems; one-step methods; Hermite–Obreshkov methods; symplecticity; B-splines; BS methods

Introduction

In paper [1] we analyzed the numerical solution of the first order Ordinary Differential Equation (ODE),

y^{'} (t) = f (y (t)), t \in [t_{0}, t_{0} + T],

(1)

associated with the initial condition:

y (t_{0}) = y_{0},

(2)

where

f : {I R}^{m} \to {I R}^{m}, m \geq 1,

is a

C^{R - 1}, R \geq 1,

function on its domain and

y_{0} \in {I R}^{m}

is assigned. In particular, we considered the numerical solution of Hamiltonian problems which in canonical form can be written as follows:

y^{'} = J \nabla H (y), y (t_{0}) = y_{0} \in {I R}^{2 ℓ},

(3)

with

y = (\begin{matrix} q \\ p \end{matrix}), q, p \in {I R}^{ℓ}, J = (\begin{matrix} O & I_{ℓ} \\ - I_{ℓ} & O \end{matrix}),

(4)

where

q

and

p

are the generalized coordinates and momenta,

H : {I R}^{2 ℓ} \to I R

is the Hamiltonian function and

I_{ℓ}

stands for the identity matrix of dimension ℓ. Note that the flow

φ_{t} : y_{0} \to y (t)

associated with the dynamical system (3) is symplectic; this means that its Jacobian satisfies:

\frac{\partial φ_{t} {(y)}^{⊤}}{\partial y} J \frac{\partial φ_{t} (y)}{\partial y} = J, \forall y \in {I R}^{2 ℓ} .

(5)

We recall that a one-step numerical method

Φ_{h} : {I R}^{2 ℓ} \to {I R}^{2 ℓ}

with stepsize h is symplectic if the discrete flow

y_{n + 1} = Φ_{h} (y_{n}), n \geq 0,

satisfies:

\frac{\partial Φ_{h} {(y)}^{⊤}}{\partial y} J \frac{\partial Φ_{h} (y)}{\partial y} = J, \forall y \in {I R}^{2 ℓ} .

(6)

Two numerical methods

Φ_{h}, Ψ_{h}

are conjugate to each other if there exists a global change of coordinates

χ_{h}

, such that:

Ψ_{h} = χ_{h} \circ Φ_{h} \circ χ_{h}^{- 1}

with

χ_{h} (y) = y + O (h)

uniformly for

y

varying in a compact set and ∘ denoting a composition operator [2]. A method which is conjugate to a symplectic method is said to be conjugate symplectic, this is a less strong requirement than symplecticity, which allows the numerical solution to have the same long-time behavior of a symplectic method. A more relaxed property, shared by a wider class of numerical schemes, is a generalization of the conjugate-symplecticity property, introduced in [3]. A method

y_{1} = Ψ_{h} (y_{0})

of order p is conjugate-symplectic up to order

p + r

, with

r \geq 0

, if a global change of coordinates

χ_{h} (y) = y + O (h^{p})

exists such that

Ψ_{h} = χ_{h} \circ Φ_{h} \circ χ_{h}^{- 1}

, with the map

Ψ_{h}

satisfying

\frac{\partial Ψ_{h} {(y)}^{⊤}}{\partial y} J \frac{\partial Ψ_{h} (y)}{\partial y} = J + O (h^{p + r + 1}) .

(7)

A consequence of property (7) is that the method

Ψ_{h} (y)

nearly conserves all quadratic first integrals and the Hamiltonian function over time intervals of length

O (h^{- r})

(see [3]).

Recently, the class of Euler–Maclaurin Hermite–Obreshkov (EMHO) methods for the solution of Hamiltonian problems has been analyzed in [4] where the conjugate symplecticity up to order

p + 2

of the p-th order methods was proven. In this paper, we fix Theorem 1 of [1] related to symmetric one-step BS Hermite–Obreshkov (BSHO) methods, proving that the conjugate-symplecticity property is satisfied by the R-th one-step symmetric Hermite–Obreshkov method up to order

2 R + 2

.

Let

t_{i}, i = 0, \dots, N,

be an assigned partition of the integration interval

[t_{0}, t_{0} + T]

, and let us denote by

u_{i}

an approximation of

y (t_{i})

. We consider one-step symmetric BSHO method as follows, setting

u_{0} : = y_{0},

u_{n + 1} = u_{n} + \sum_{j = 1}^{R} h_{n}^{j} β_{j}^{(R)} (u_{n}^{(j)} - {(- 1)}^{j} u_{n + 1}^{(j)}), n = 0, \dots, N - 1,

(8)

where

h_{n} : = t_{n + 1} - t_{n}

,

β_{j}^{(R)} : = \frac{1}{j!} \frac{R (R - 1) \dots (R - j + 1)}{(2 R) (2 R - 1) \dots (2 R - j + 1)}

, and

u_{i}^{(j)}

, for

j \geq 1,

denotes the

(j - 1)

-th Lie derivative of

f

computed at

u_{i}

,

u_{i}^{(j)} : = D_{j - 1} f (u_{i}), j = 1, \dots, R,

(9)

where

D_{0} = I

is the identity operator and

D_{k} f (z)

is defined as the k-th total derivative of

f (y (t))

computed at

y (t) = z,

where for the computation of the total derivative it is assumed that

y

satisfies the differential equation in (1). Thus for example

D_{1} f (z) = \frac{\partial f}{\partial y} (z) f (z),

where

\frac{\partial f}{\partial y}

is the

m \times m

Jacobian matrix of

f .

Note that we use the subscript to define the Lie operator to avoid confusion with the same order classical derivative operator in the following denoted as

D^{k} .

With this clarification on the definition of

u_{i}^{(j)},

following the lines of the proof given in [4], we can actually prove that the R-th one-step symmetric BSHO method is conjugate symplectic up to order

2 R + 2

.

We show that the map

y_{1} = Ψ_{h} (y_{0})

associated with the BSHO method is such that

Ψ_{h} (y) = Φ_{h} (y) + O (h^{2 R + 3})

, where

y_{1} = Φ_{h} (y_{0})

is a suitable conjugate symplectic B-series integrator.

Theorem 1.

The map

u_{1} = Ψ_{h} (u_{0})

associated with the one-step method (8) admits a B-series expansion and is conjugate to a symplectic B-series integrator up to order

2 R + 2

.

Proof.

The existence of a B-series expansion for

y_{1} = Ψ_{h} (y_{0})

is directly deduced from [5], where a B-series representation of a generic multi-derivative Runge-Kutta method has been obtained. By defining the two characteristic polynomials of the trapezoidal rule:

ρ (z) : = z - 1, σ (z) : = \frac{1}{2} (z + 1)

and the shift operator

E (u_{n}) : = u_{n + 1},

the R-th method described in (8) reads,

ρ (E) u_{n} = \sum_{k = 1}^{⌈ R / 2 ⌉} 2 β_{2 k - 1}^{(R)} h^{2 k - 1} σ (E) u_{n}^{(2 k - 1)} - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} ρ (E) u_{n}^{(2 k)} .

(10)

We now consider a function

v (t)

, a stepsize h and the shift operator

E_{h} (v (t)) : = v (t + h)

, and we look for a continuous function

v (t)

that satisfies (10) in the sense of formal series (a series where the number of terms is allowed to be infinite), using the relation

E_{h} = \sum_{j = 0}^{\infty} \frac{h^{j}}{j!} D^{j} \equiv e^{h D}

where

D = D^{1}

is the classical derivative operator,

ρ (e^{h D}) v (t) = \sum_{k = 1}^{⌈ R / 2 ⌉} 2 β_{2 k - 1}^{(R)} h^{2 k - 1} σ (e^{h D}) D_{2 k - 2} f (v (t)) - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} ρ (e^{h D}) D_{2 k - 1} f (v (t)) .

By multiplying both sides of the previous equation by

D ρ {(e^{h D})}^{- 1}

, we obtain:

D v (t) = h D ρ {(e^{h D})}^{- 1} σ (e^{h D}) \sum_{k = 0}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} D_{2 k} f (v (t)) - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D D_{2 k - 1} f (v (t)) .

(11)

Now, since Bernoulli numbers define the Taylor expansion of the function

z / (e^{z} - 1)

and

b_{0} = 1, b_{1} = - 1 / 2

and

b_{j} = 0

for the other odd

j,

we have:

\frac{z σ (e^{z})}{ρ (e^{z})} = \frac{1}{2} \frac{z (e^{z} + 1)}{e^{z} - 1} = \frac{z}{e^{z} - 1} + \frac{z}{2} = 1 + \sum_{j = 1}^{\infty} \frac{b_{2 j}}{(2 j)!} z^{2 j} .

Thus, we can write (11) as

\dot{v} (t) = ((I + \sum_{j = 1}^{\infty} \frac{b_{2 j}}{(2 j)!} h^{2 j} D^{2 j}) (I + \sum_{k = 1}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} D_{2 k}) - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D D_{2 k - 1}) f (v (t)) .

Adding and subtracting terms involving the classical derivative operator

D^{2 k}, D^{2 k - 1}

, we get

\begin{matrix} \dot{v} (t) = & ((I + \sum_{j = 1}^{\infty} \frac{b_{2 j}}{(2 j)!} h^{2 j} D^{2 j}) \\ (I + \sum_{k = 1}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} D^{2 k} + \sum_{k = 1}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} (D_{2 k} - D^{2 k})) \\ - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D D^{2 k - 1} - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D (D_{2 k - 1} - D^{2 k - 1})) f (v (t)) . \end{matrix}

that we recast as

\begin{matrix} \dot{v} (t) = & ((I + \sum_{j = 1}^{\infty} \frac{b_{2 j}}{(2 j)!} h^{2 j} D^{2 j}) (I + \sum_{k = 1}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} D^{2 k}) \\ - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D^{2 k}) f (v (t)) \\ + ((I + \sum_{j = 1}^{\infty} \frac{b_{2 j}}{(2 j)!} h^{2 j} D^{2 j}) (\sum_{k = 1}^{⌈ R / 2 ⌉ - 1} 2 β_{2 k + 1}^{(R)} h^{2 k} (D_{2 k} - D^{2 k})) \\ - \sum_{k = 1}^{⌊ R / 2 ⌋} β_{2 k}^{(R)} h^{2 k} D (D_{2 k - 1} - D^{2 k - 1})) f (v (t)) . \end{matrix}

(12)

Since

v (t) = y (t) + O (h^{2 R})

, due to the regularity conditions on the function

f

, we see that

(D^{i} - D_{i}) f (v (t)) = O (h^{2 R}), i = 1, \dots, R - 1

and hence the solution

v (t)

of (12) is

O (h^{2 R + 2})

-close to the solution of the following initial value problem

\dot{w} (t) = f (w (t)) + \sum_{j = R}^{\infty} δ_{j} h^{2 j} D^{2 j} f (w (t)),

(13)

with:

δ_{j} : = \sum_{k = 0}^{⌈ R / 2 ⌉ - 1} \frac{b_{2 (j - k)}}{(2 (j - k))!} 2 β_{2 k + 1}^{(R)}, j \geq R .

that has been derived from (12) by neglecting the sums containing the derivatives

D_{2 k}, D_{2 k - 1}

. Observe that

δ_{j} = 0

for

j = 1, \dots, R - 1,

since the method is of order

2 R

(see [2], Theorem 3.1, page 340). We may interpret (13) as the modified equation of a one-step method

y_{1} = Φ_{h} (y_{0})

, where

Φ_{h}

is evidently the time-h flow associated with (13). Expanding the solution of (13) in Taylor series, we get the modified initial value differential equation associated with the numerical scheme by coupling (13) with the initial condition

w (t_{0}) = y_{0}

. Thus,

Φ_{h}

is a B-series integrators. The proof of the conjugated symplecticity of

Φ_{h}

follows exactly the same steps of the analogous proof in Theorem 1 of [4]. Since

Ψ_{h} (y) = Φ_{h} (y) + O (h^{2 R + 3})

and

Φ_{h}

is conjugate-symplectic, the result follows using the same global change of coordinates

χ_{h} (y)

associated to

Φ_{h}

. □

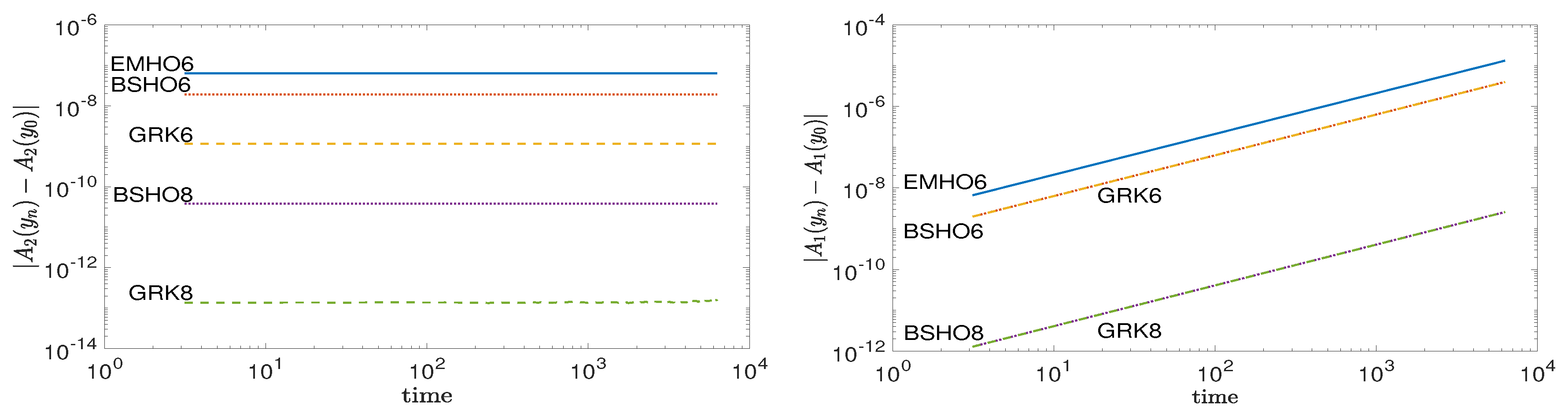
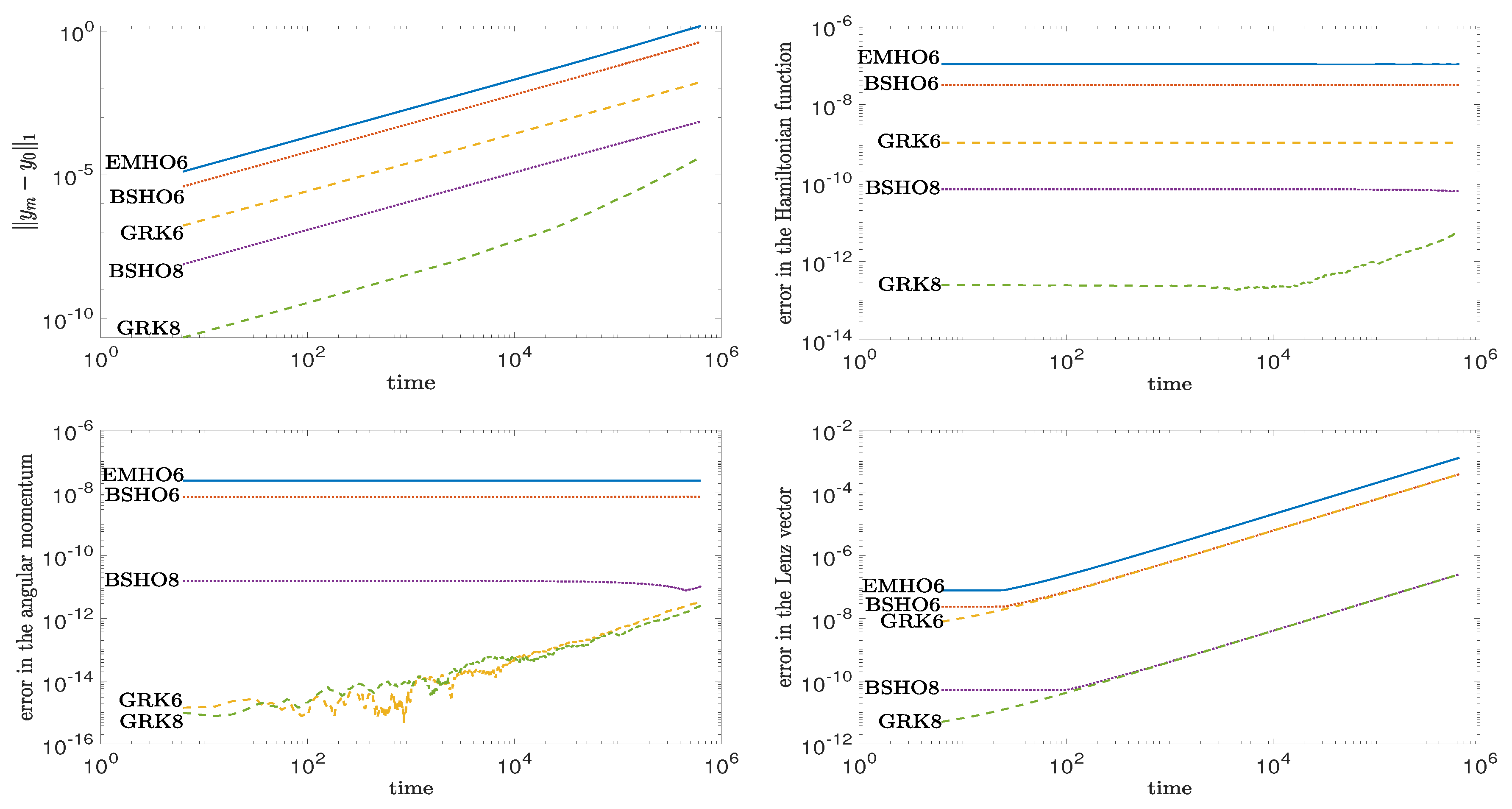
We report in Figure 1 the bottom-rigth picture of Figure 2 of [1], related to the Kepler problem, where we noticed that the error in the second component of the Lenz vector was not correctly computed, for completness Figure 1 also reports the error in the first component of the Lenz vector. To stress that the methods show a good long time behavior for Hamiltonian problems, we report also, in Figure 2 the results using a longer integration interval of

10^{5}

periods and all the other parameters unchanged. In the pictures we report the maximum error in each period for the Hamiltonian function, the angular mument and the Lenz vector. The results remain consistent, showing a linear grows in the error and in the Lenz vector and a near conservation of the Hamiltonian and of the angular moment.

Figure 1. Kepler problem: results for the sixth (BSHO6, red dotted line) and eighth (BSHO8, purple dotted line) order BSHO methods, sixth order Euler–Maclaurin method (EMHO6, blue solid line) and sixth (Gauss–Runge–Kutta (GRK6), yellow dashed line) and eighth (GRK8-green dashed line) order Gauss methods. (Left) error in the second component of the Lenz vector; (Right) error in the first component of the Lenz vector.

Figure 2. Kepler problem: results for the sixth (BSHO6, red dotted line) and eighth (BSHO8, purple dotted line) order BSHO methods, sixth order Euler–Maclaurin method (EMHO6, blue solid line) and sixth (Gauss–Runge–Kutta (GRK6), yellow dashed line) and eighth (GRK8-green dashed line) order Gauss methods. (Top-left) Absolute error of the numerical solution; (Top-right) error in the Hamiltonian function; (Bottom-left) error in the angular momentum; (Bottom-right) error in the first component of the Lenz vector.

All the other results in the paper do not change.

Author Contributions

Conceptualization, F.M. and A.S. Formal analysis, F.M. and A.S. Investigation, F.M. and A.S. Methodology, F.M. and A.S. Writing, original draft, F.M. and A.S. Writing, review and editing, F.M. and A.S.

Funding

Supported by INdAM through GNCS 2018 research projects.

Acknowledgments

We thank Felice Iavernaro for helpful discussions related to this research. We are also grateful to Ernst Hairer for helping us in fixing the results in Theorem 1.

Conflicts of Interest

The authors declare no conflict of interest.

References

Mazzia, F.; Sestini, A. On a class of conjugate symplectic Hermite-Obreshkov one-step methods with continuous spline extension. Axioms 2018, 7, 58. [Google Scholar] [CrossRef]
Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
Hairer, E.; Zbinden, C.J. On conjugate symplecticity of B-series integrators. IMA J. Numer. Anal. 2013, 33, 57–79. [Google Scholar] [CrossRef]
Iavernaro, F.; Mazzia, F.; Mukhametzhanov, M.; Sergeyev, Y. Conjugate symplecticity properties of Euler–Maclaurin methods and their implementation on the Infinity Computer. arXiv 2018, arXiv:1807.10952. [Google Scholar]
Hairer, E.; Murua, A.; Sanz-Serna, J. The non-existence of symplectic multi-derivative Runge–Kutta methods. BIT 1994, 34, 80–87. [Google Scholar] [CrossRef]

Figure 1. Kepler problem: results for the sixth (BSHO6, red dotted line) and eighth (BSHO8, purple dotted line) order BSHO methods, sixth order Euler–Maclaurin method (EMHO6, blue solid line) and sixth (Gauss–Runge–Kutta (GRK6), yellow dashed line) and eighth (GRK8-green dashed line) order Gauss methods. (Left) error in the second component of the Lenz vector; (Right) error in the first component of the Lenz vector.

Figure 2. Kepler problem: results for the sixth (BSHO6, red dotted line) and eighth (BSHO8, purple dotted line) order BSHO methods, sixth order Euler–Maclaurin method (EMHO6, blue solid line) and sixth (Gauss–Runge–Kutta (GRK6), yellow dashed line) and eighth (GRK8-green dashed line) order Gauss methods. (Top-left) Absolute error of the numerical solution; (Top-right) error in the Hamiltonian function; (Bottom-left) error in the angular momentum; (Bottom-right) error in the first component of the Lenz vector.

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Correction to “On a Class of Hermite-Obreshkov One-Step Methods with Continuous Spline Extension” [Axioms 7(3), 58, 2018]

Abstract

Introduction

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics