1. Introduction
The main goal of the optimization methods is to find the best solution of a set of possible solutions to a problem; for some cases, the search space is very extensive, which leads to a computational cost that is too high. To solve this problem there are different computational intelligence techniques that provide tools to solve these optimization problems [
1].
Nowadays, control is one of the most important applications of fuzzy logic because it provides a greater robustness in the design of fuzzy controllers and a higher performance than classically used control tools [
2].
Due to this, fuzzy controllers are used to deal with complex plants; however, the advantages offered by fuzzy logic and fuzzy sets, along with the appearance of the type-2 fuzzy logic, amplifies the probability of designing better fuzzy controllers [
3,
4].
Fuzzy control helps us combine expert knowledge with measurements and processes based on mathematical models. Fuzzy systems convert a knowledge base into a mathematical model that has been shown to be effective in many applications in industry and real life [
5,
6].
Fuzzy logic can adapt to the real world, it can work and it can understand everyday expressions like “it’s very cold”, “it’s very low”, etc. The key lies in its adaptation to natural language, each fuzzy set having a membership function associated with each element that represents the fact that both elements are part of the set [
7].
A fuzzy set is an extension of the traditional sets; its main difference is that in the traditional one an element may or may not belong to that set, while in the fuzzy sets each element may belong to more than one set with a certain membership degree [
8].
Fuzzy logic tries to imitate human thought in the computer, whereas classical computation can only handle dual values like false or true, or yes or no. Fuzzy logic uses mathematical models to represent subjective notions such as “big, small” or “hot, cold” for values that can be manipulated by the computer [
9].
In recent years, there has been an increase in research on type-1 and type-2 fuzzy logic; published works can been found on parameters adjustment in metaheuristic algorithms, and control that is based on fuzzy logic has been investigated in order to improve performance, as is shown in the following works:
In an improved evolutionary method with fuzzy logic for combining particle swarm optimization and genetic algorithms [
10], a hybrid approach is described for the optimization of particle swarm optimization (PSO) and ant colony optimization (ACO) using fuzzy logic for the dynamic adjustment of the parameters of both algorithms.
In the gravitational search algorithm-based design of fuzzy control systems with a reduced parametric sensitivity [
11], the design of the fuzzy control systems is proposed using the Gravitational Search Algorithm; the Takagi-Sugeno fuzzy controller, characterized by linear models of the second order with an integral component, are obtained.
Also in model-free sliding mode fuzzy controllers for reverse osmosis desalination plants [
12]. In this case, Takagi-Sugeno fuzzy controllers are proposed for flow control and conductivity in desalination plants. The controllers are designed in view of the inequalities of the linear matrix as constraints using the gray wolf algorithm for their optimization.
Muthiah-Nakarajan and Noel proposed the galactic swarm optimization (GSO) as an algorithm that has proven to have a good performance dealing with multimodal problems or with a high number of dimensions; because it presents multiple exploration and exploitation cycles, it offers us the possibility of finding the best solutions without getting stuck [
13,
14].
This paper presents a modification to the GSO metaheuristic with the use of type-1 fuzzy systems for the adjustment of the c
3 and c
4 parameters in the GSO algorithm [
15]. In addition to a type-1 fuzzy system extension, we are also using type-2 fuzzy logic to give rise to an interval type-2 fuzzy system (IT2), and this proposal was used for the optimization of the membership functions of the controller of the autonomous mobile robot [
16]. Experiments were carried out optimizing the fuzzy controller for the aforementioned study case, and the optimization was initially carried out with the original galactic swarm optimization, after which the T1 and IT2 fuzzy systems were used to perform the fuzzy controller optimization, in the same way that the original GSO algorithm was experimented with by adding noise to the plant and without noise in order to compare the proposed approach.
The organization of this paper is as follows:
Section 2 explains the operation and equations present in the original GSO algorithm. In
Section 3 the development of the proposed approach for the fuzzy controller optimization of the autonomous mobile robot is presented. In
Section 4 the case study of the autonomous mobile robot is presented.
Section 5 shows the results obtained from the experiments developed with the proposed approach and the autonomous mobile robot plant, and finally in
Section 6 the conclusions are presented.
2. Galactic Swarm Optimization
The original galactic swarm optimization algorithm mimics the motion of stars and galaxies in the universe. The stars are not evenly distributed in the cosmos, and they are concentrated in galaxies that in turn are not evenly distributed. The attraction of the stars and galaxies in the GSO algorithm is emulated in the following way [
13,
15].
First, the initial population is divided into subpopulations which will be called sub-swarms; all the individuals of the sub-swarms begin their movement according to the PSO algorithm by a determined number of iterations, and all the individuals in each subpopulation will be attracted towards the individual with better fitness; at the end of the iterations each of the subpopulations will be represented by the best individual of each of the subpopulations.
The best individuals of all the subpopulations will pass into a second phase, where they will form a new super swarm, and (in the same way they will move according to the PSO algorithm at the end of the iterations) the GSO algorithm will return us the best individual of the super swarm which will represent the best solution found in the entire initial population.
All the necessary steps to perform the operation of the GSO algorithm are summarized in the following pseudocode, where the two necessary phases of the GSO algorithm are presented [
13]:
Given that the PSO algorithm is used as a basis in galactic swarm optimization, the algorithm consists of exploration and exploitation phases for which it uses parameters in the calculation of the velocity that reduces or increases as time passes to control the exploration phase and move on to the exploitation phase.
By linearly decreasing, the PSO algorithm tends to have a global search capability when starting the execution and a local search when approaching the end of the execution.
These parameters are the constants of acceleration that make the solutions approach the best local and global solutions, and for this they initially take fixed values and change their values on a mathematical form.
Dynamic optimization problems, where the environment changes dynamically, require that the search algorithm has the ability to search non-linearly to follow the changing environment. Therefore, it must be changed dynamically for a better balance between the local and global search.
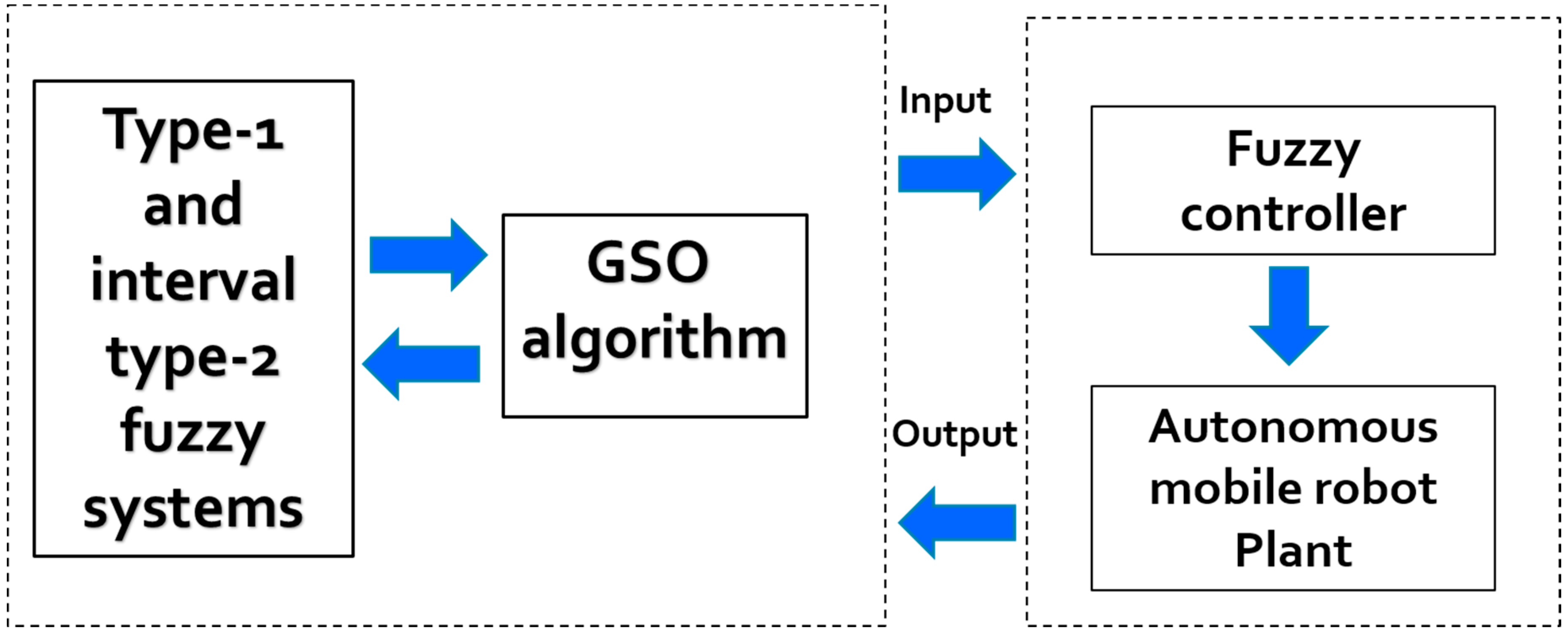
3. Proposed Approach (FGSO)
This paper presents a modification to the GSO metaheuristic with the use of type-1 (T1) and interval type-2 (IT2) fuzzy logic for the parameter adjustment of the GSO algorithm.
The use of parameter adjustment in metaheuristic algorithms has become a widely used strategy in recent years. The results published by some authors show significant improvements when the dynamic adjustment of parameters in metaheuristic algorithms is used. The use of fuzzy logic in metaheuristic algorithms is a technique that allows algorithms to perform an automatic search for the optimal values of the parameters that play an important role in the performance of metaheuristic algorithms.
The use of non-linear plants for fuzzy control can turn out to be a complex task because the exact knowledge of each of the components or characteristics that make up the plant is very rarely obtained, so fuzzy sets and fuzzy logic principles are used to model the operation of the plant.
The main contribution of this document is the use of T1 and IT2 fuzzy systems for the dynamic adjustment of the c
3 and c
4 parameters as the iterations pass, which will be used for the optimization of the membership functions of the controller of the autonomous mobile robot. The proposed method can be found in
Figure 1.
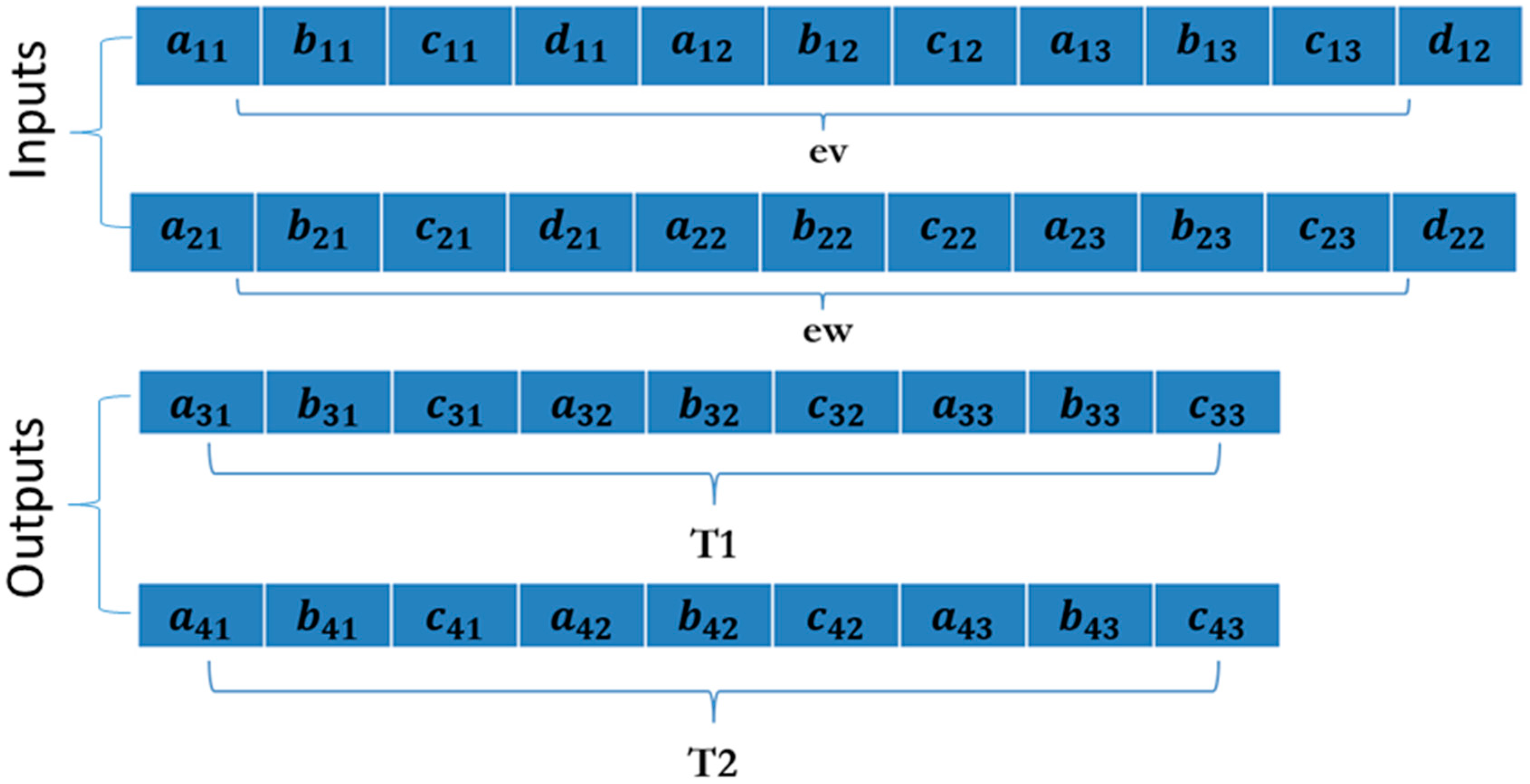
The optimization of the fuzzy controller of the autonomous mobile robot (AMR) consists in finding the appropriate parameters for the membership functions of the fuzzy controller. Here, each individual used in our proposal will contain the necessary parameters to generate a fuzzy controller, which will be tested in the hopes of obtaining better results than those that can be obtained so far by establishing the parameters of the membership functions based on experience. In
Figure 2 we can find the composition of the individuals used in our proposed methodology [
10,
17,
18].
The type-1 fuzzy set is characterized by having a membership function that can take values between 0 and 1, and is represented as a set of ordered pairs of a certain element; its degree of belonging to said set is defined by the following expression [
19,
20]:
where
is the membership degree of each element.
T1 fuzzy logic was proposed as an imprecision of human language, where the degree of belonging in a range of 0 to 1 is considered.
The appearance of IT2 fuzzy logic provides a more complete model that considers the vagueness and uncertainty, which increases the robustness and improves the performance of your applications [
21,
22,
23].
An IT2 fuzzy set is represented by two membership functions, a lower and an upper; the area that lies between these membership functions is called a footprint of uncertainty. The mathematical expression is as follows [
24,
25]:
where
represents the membership degree of each element,
X is the primary domain and
is the secondary domain.
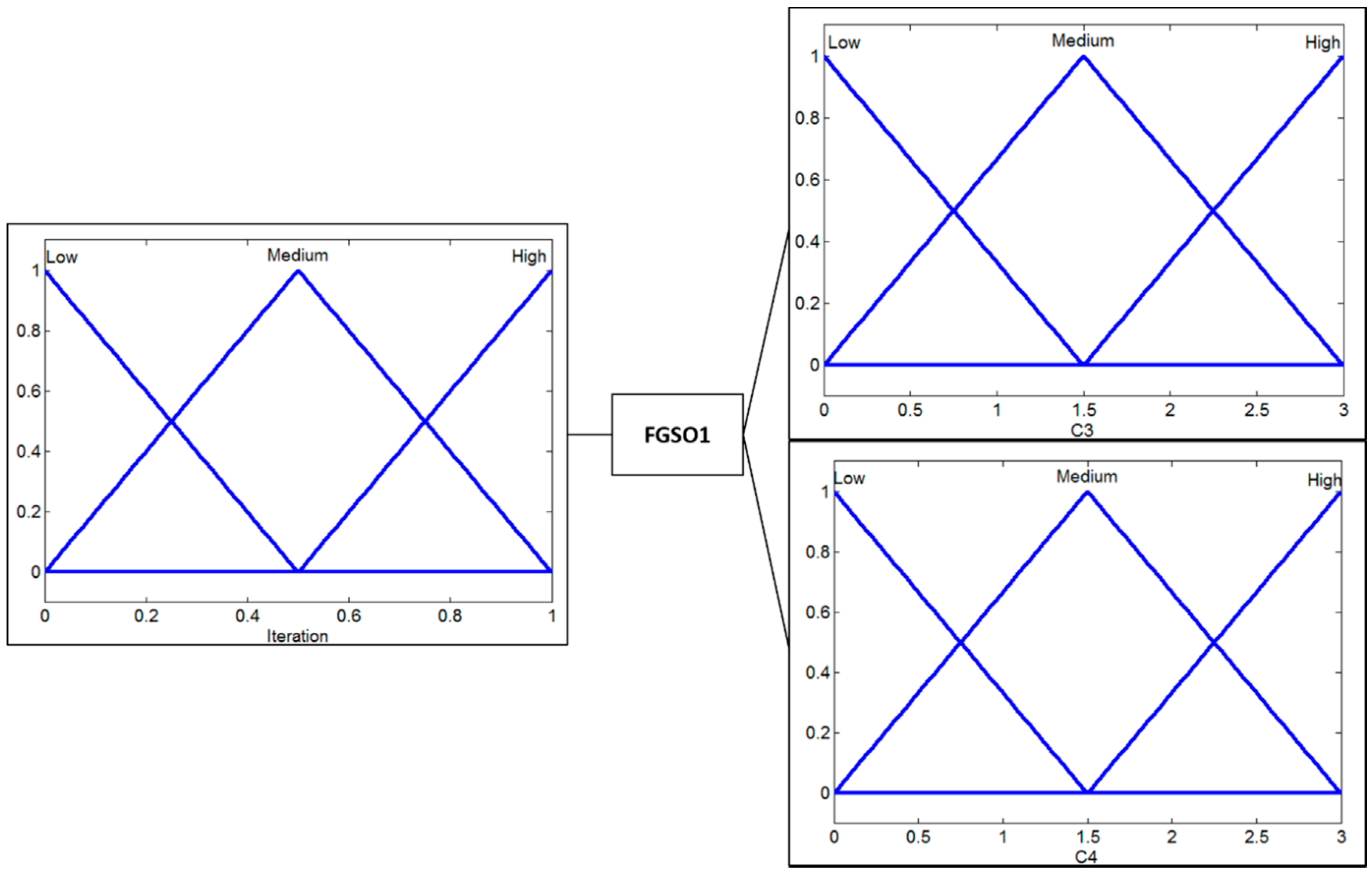
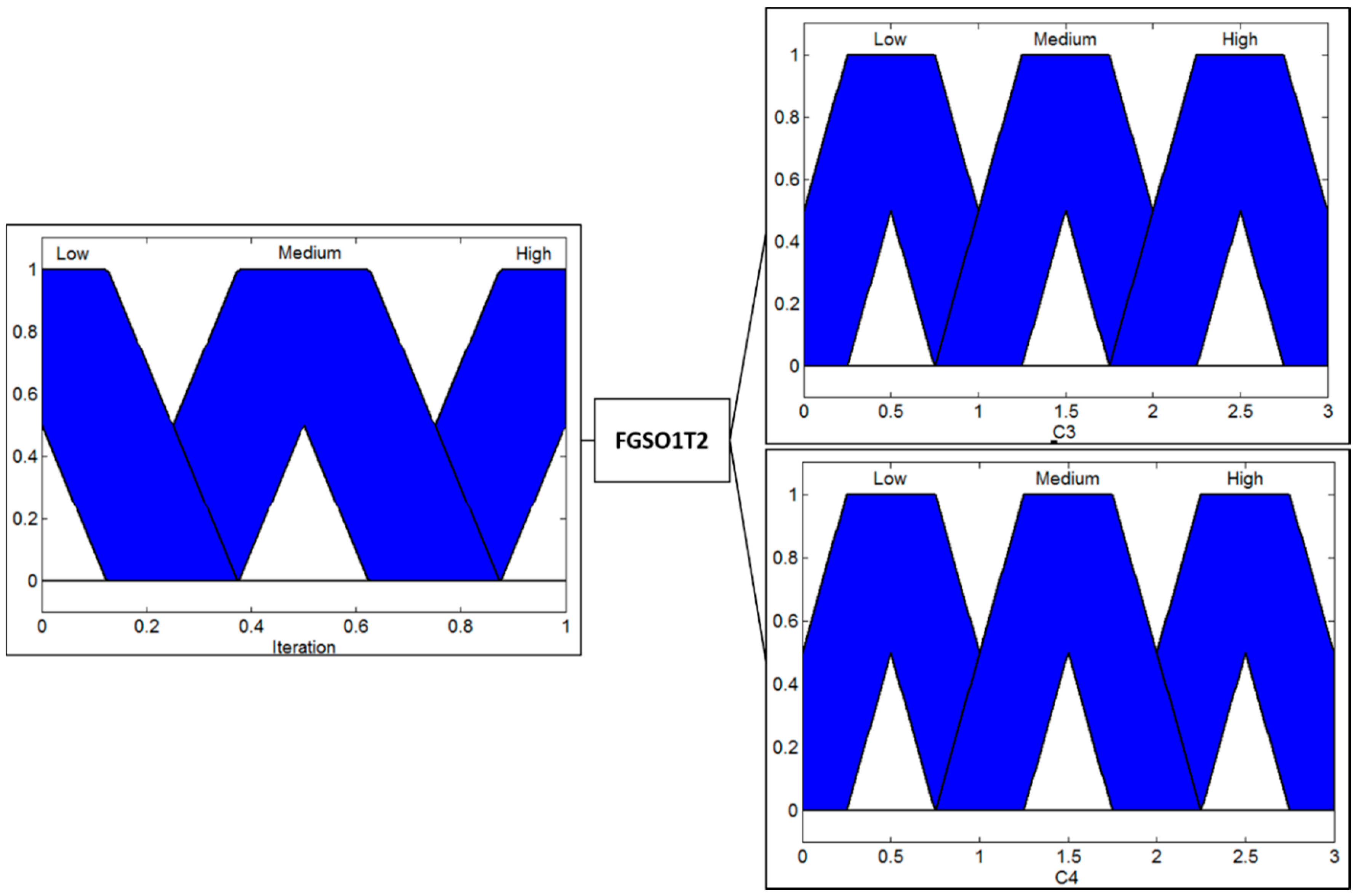
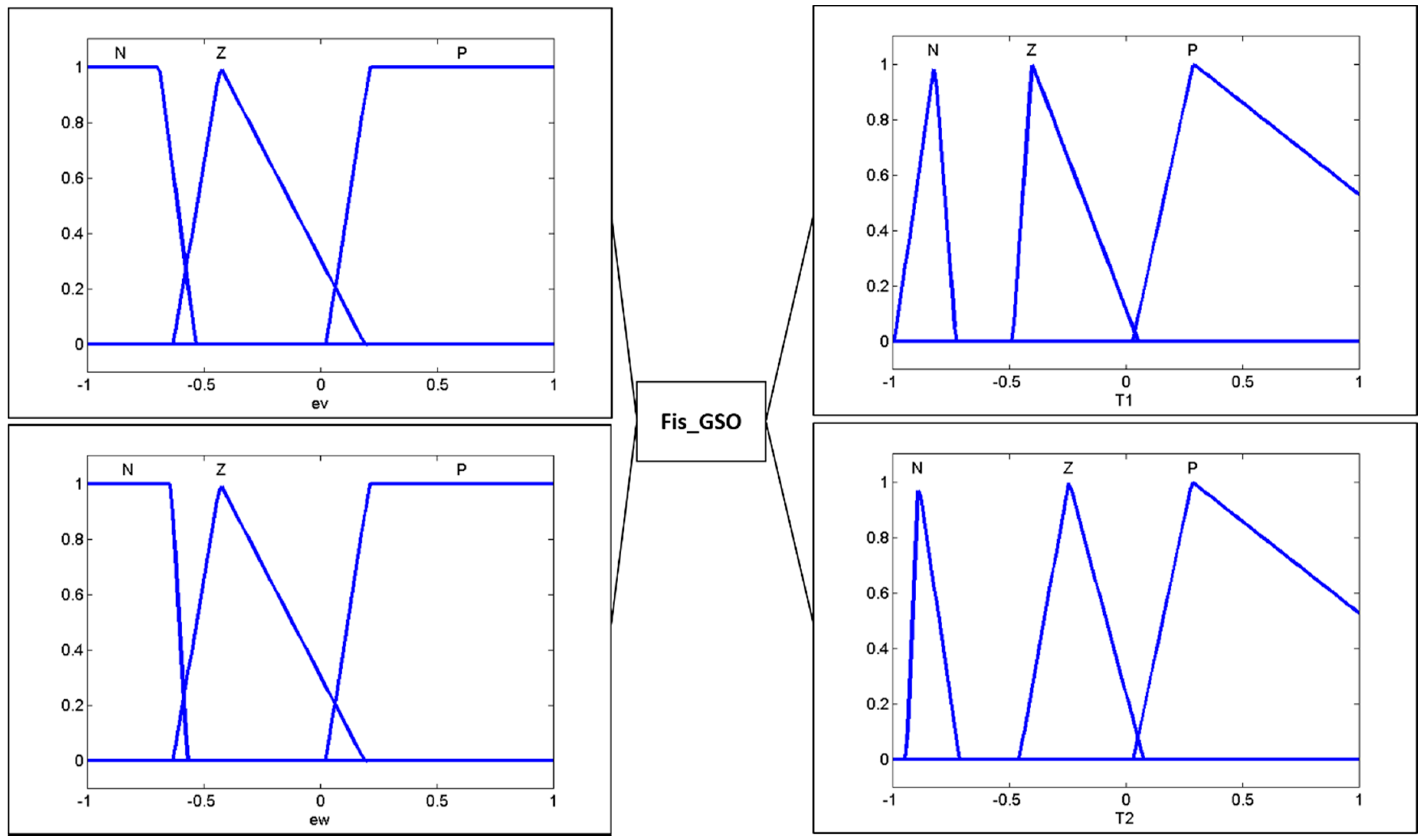
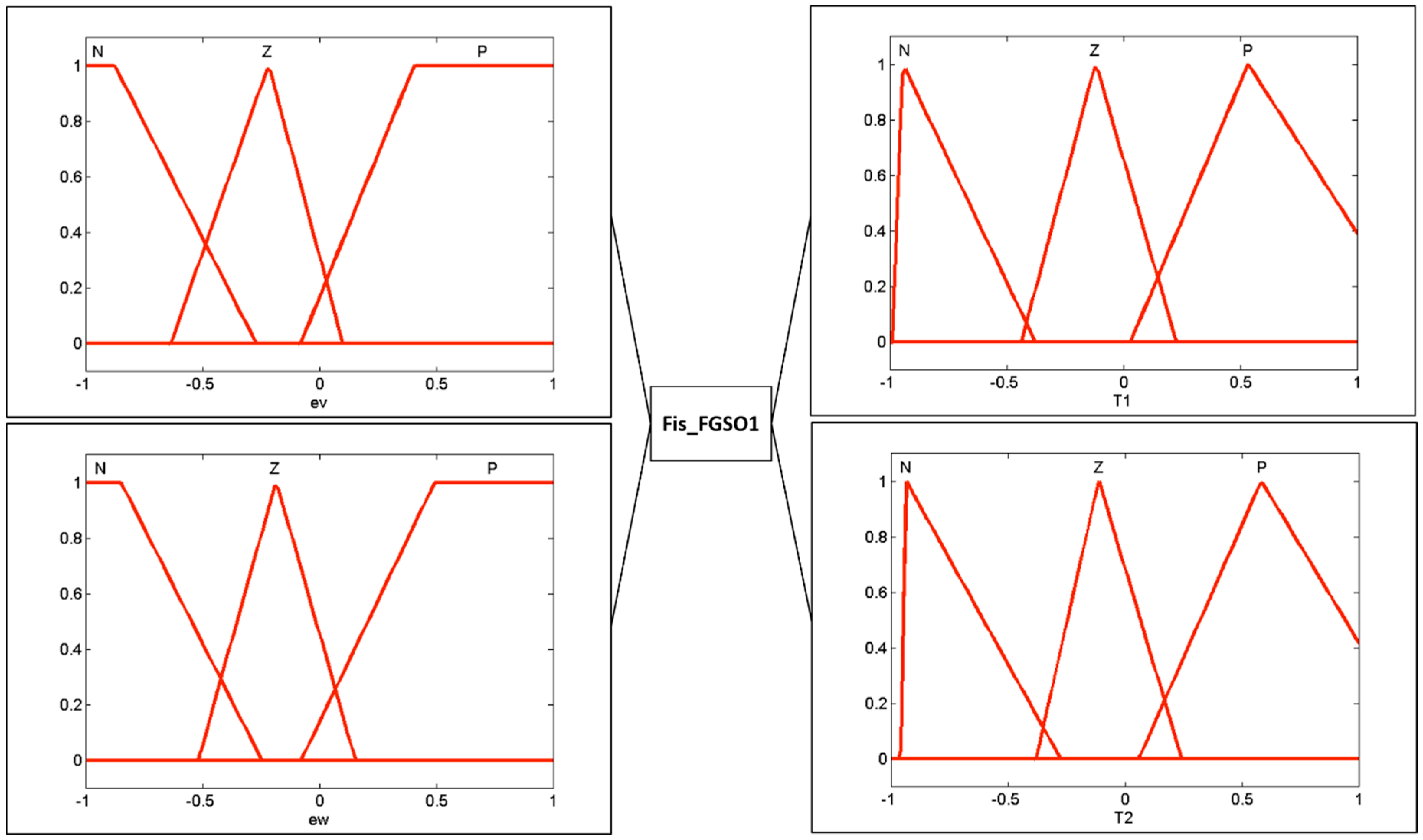
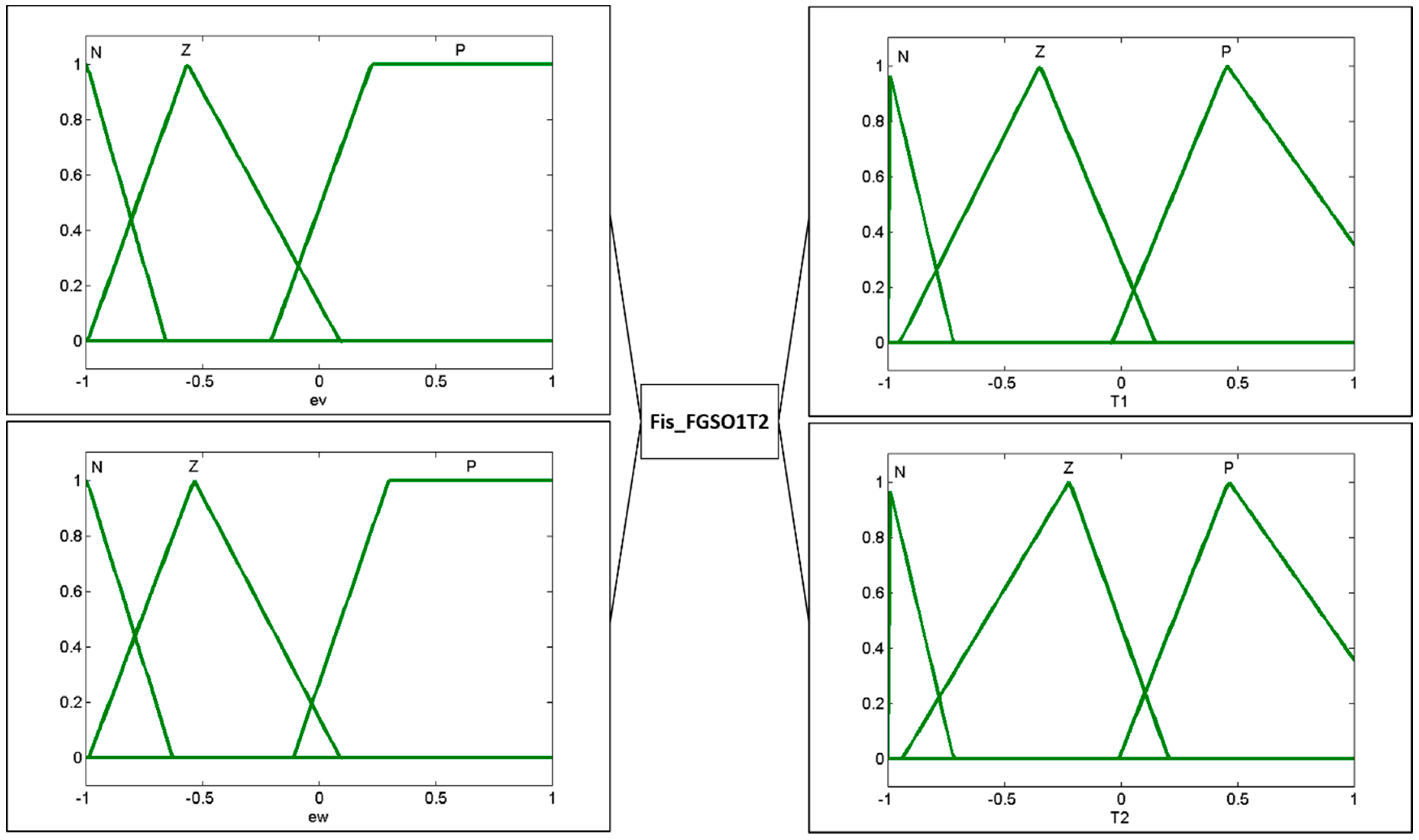
The design of the IT2 fuzzy system is based on a T1 fuzzy system previously used [
15], these fuzzy systems have an iteration as an input variable that is formed by three triangular membership functions; the c
3 and c
4 parameters represent the output variables that likewise have 3 triangular membership functions. The design of these fuzzy systems is shown in
Figure 3 and
Figure 4.
The variable iteration is obtained by means of a percentage of the current iterations and the total of the iterations with which the algorithm works; the expression used for the calculation is presented below [
26,
27]:
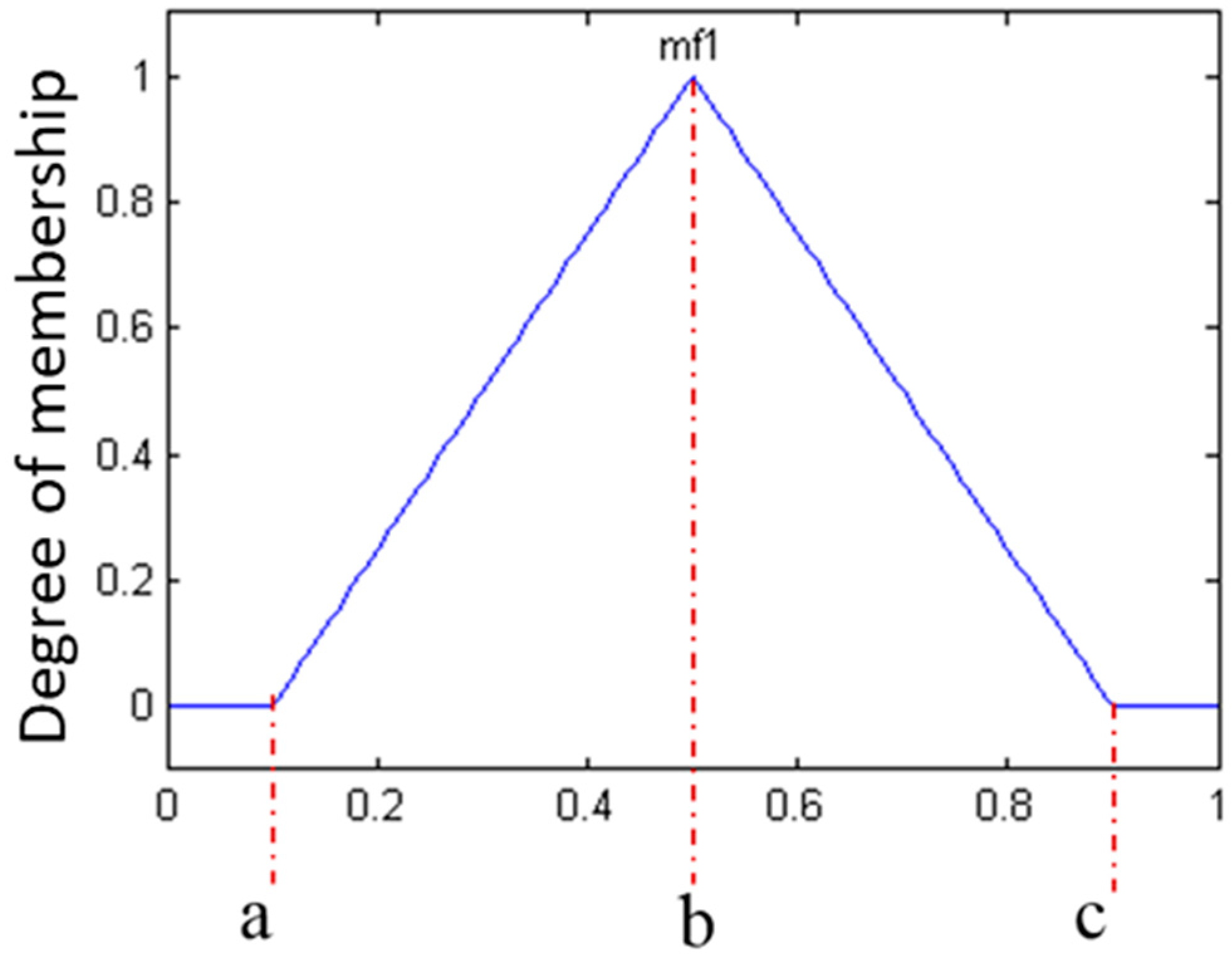
The representation of the triangular membership functions of the T1 fuzzy system consists of 3 parameters
a,
b and
c, where
a <
b <
c is shown as follows [
20]:
where
a and
c are the parameters that represent the edges of the triangle, and the parameter
b is the center for forming the triangular membership function, as shown in
Figure 5.
In the design of the T1 fuzzy system, input and output variables are used: in this case, one input and two outputs. The variables as mentioned above are the iterations representing the input variables, and the c
3 and c
4 parameters are the iterations representing the output variables. The knowledge representation of the variables is shown in the following equations [
28]:
The representation of the triangular membership functions of the IT2 fuzzy system consists of 6 parameters
a1,
b1,
c1,
a2,
b2 and
c2, where
a1 <
a2,
b1 <
b2 and
c1 <
c2 is shown as follows [
29]:
where
a1,
a2,
c1 and
c2 are the parameters that represent the edges of the triangle, and the parameters
b1 and
b2 are the center for forming the IT2 triangular membership function, as shown in
Figure 6 [
30,
31].
For the design of the IT2 fuzzy system, the T1 fuzzy system presented above is used as a base, where the iteration represents the input variable and the c
3 and c
4 parameters the output variables. The knowledge representation of the IT2 fuzzy system variables is presented in the following equations:
The design of the fuzzy rules is the same, given that the IT2 fuzzy system is an extension of the T1 fuzzy system; both are of the Mamdani type, the first using the T1 fuzzy logic and the second using the T2 fuzzy logic. These fuzzy systems have 3 fuzzy rules, where the idea is that, as the algorithm begins to work, they explore; and as the iterations pass, they explore, as shown in
Figure 7 [
15].
4. Autonomous Mobile Robot
To test the proposed methodology with the dynamic adjustment of the parameters using the T1 and IT2 fuzzy systems, we consider the case of an autonomous mobile robot. For this particular case the fuzzy controller design is optimized to control an autonomous mobile robot, and the main function of the fuzzy controller is to provide a control of the motors to minimize the error in a pre-established trajectory [
5,
32].
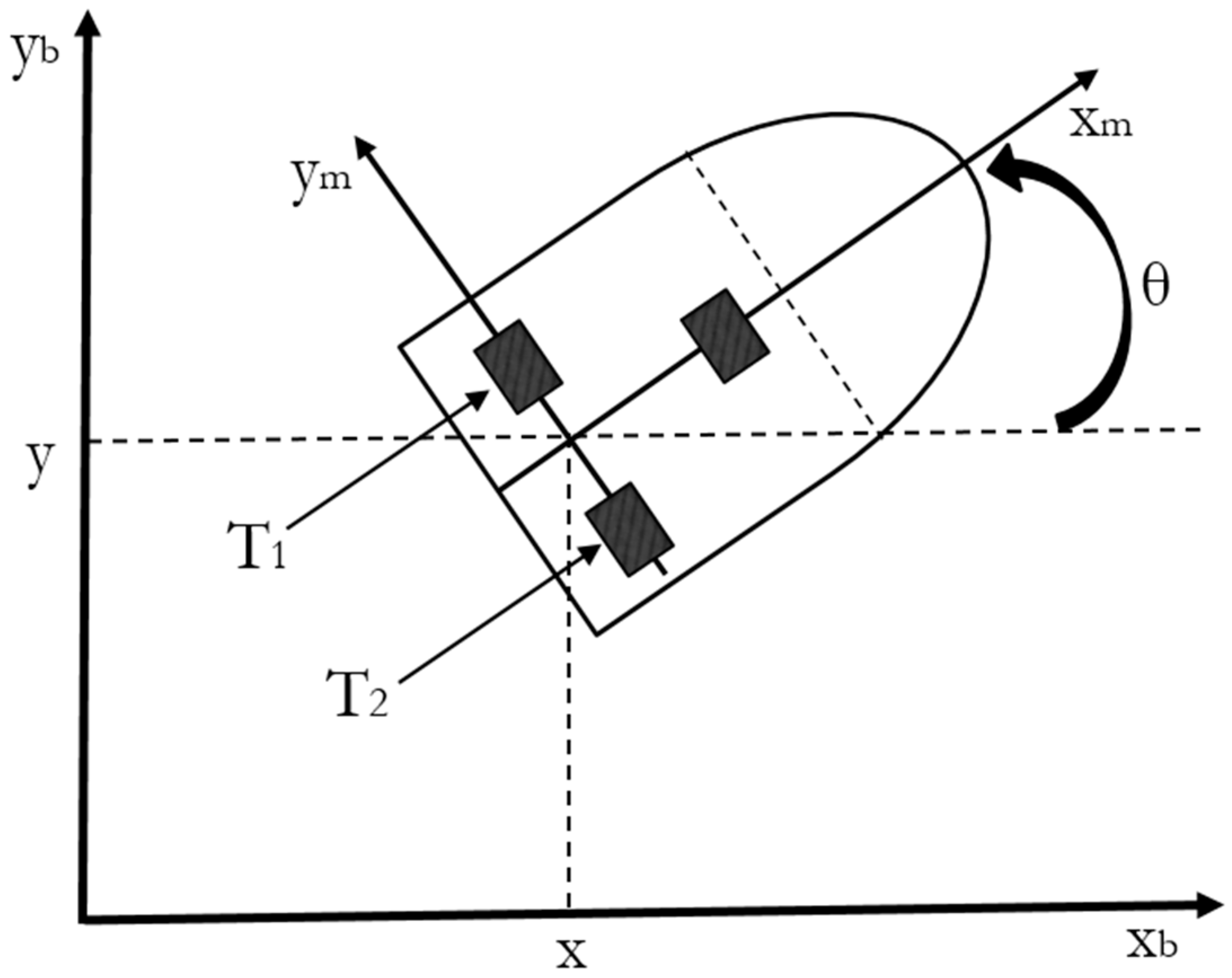
The design of the robot is presented in
Figure 8, which has 2 wheels with motors and a passive wheel for the stabilization of the same. The operation of the autonomous mobile robot model is determined by the following equations [
33,
34,
35]:
where
q = (
x,
y,
θ)
T is the coordinate vector, which describes the position of the robot, (
v,
w)
T represents the linear and angular velocity vector,
τ = (
τ1,
τ2) is the torque vector applied to the wheels of the robot,
τ1 and
τ2 represent the right and left wheels,
is the uniform disturbance vector,
is a symmetric and positive inertial matrix,
is the vector of the centripetal and Coriolis forces, and
is a diagonal positive defined damping matrix [
36,
37].
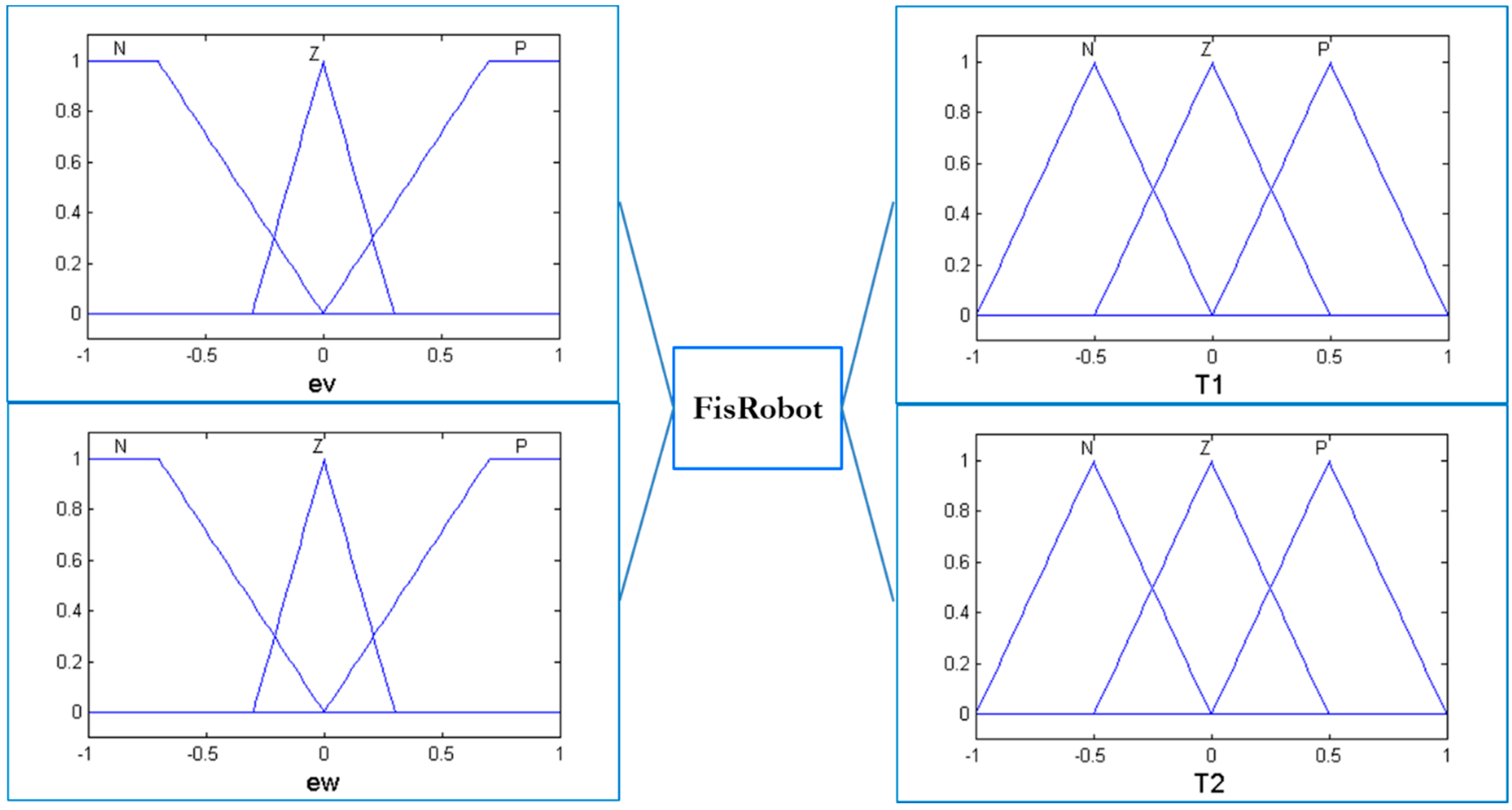
Fuzzy Controller
The fuzzy system of the mobile robot controller consists of two input variables and two output variables; the first input variable is ev (error in linear velocity), the second input variable is ew (error in angular velocity), and both input variables have two trapezoidal membership functions at the ends and a triangle at the center labeled N (negative), Z (zero) and P (positive) [
1,
38].
The first output variable is
τ1 (torque 1), the second output variable is
τ2 (torque 2); for the output variables, three triangular membership functions labeled N, Z and P are used. The design of the fuzzy controller of the autonomous mobile robot can be found in
Figure 9 [
4,
33].
The fuzzy controller rules used to control the dynamics of the plant, in this case the autonomous mobile robot, are shown in
Figure 10.
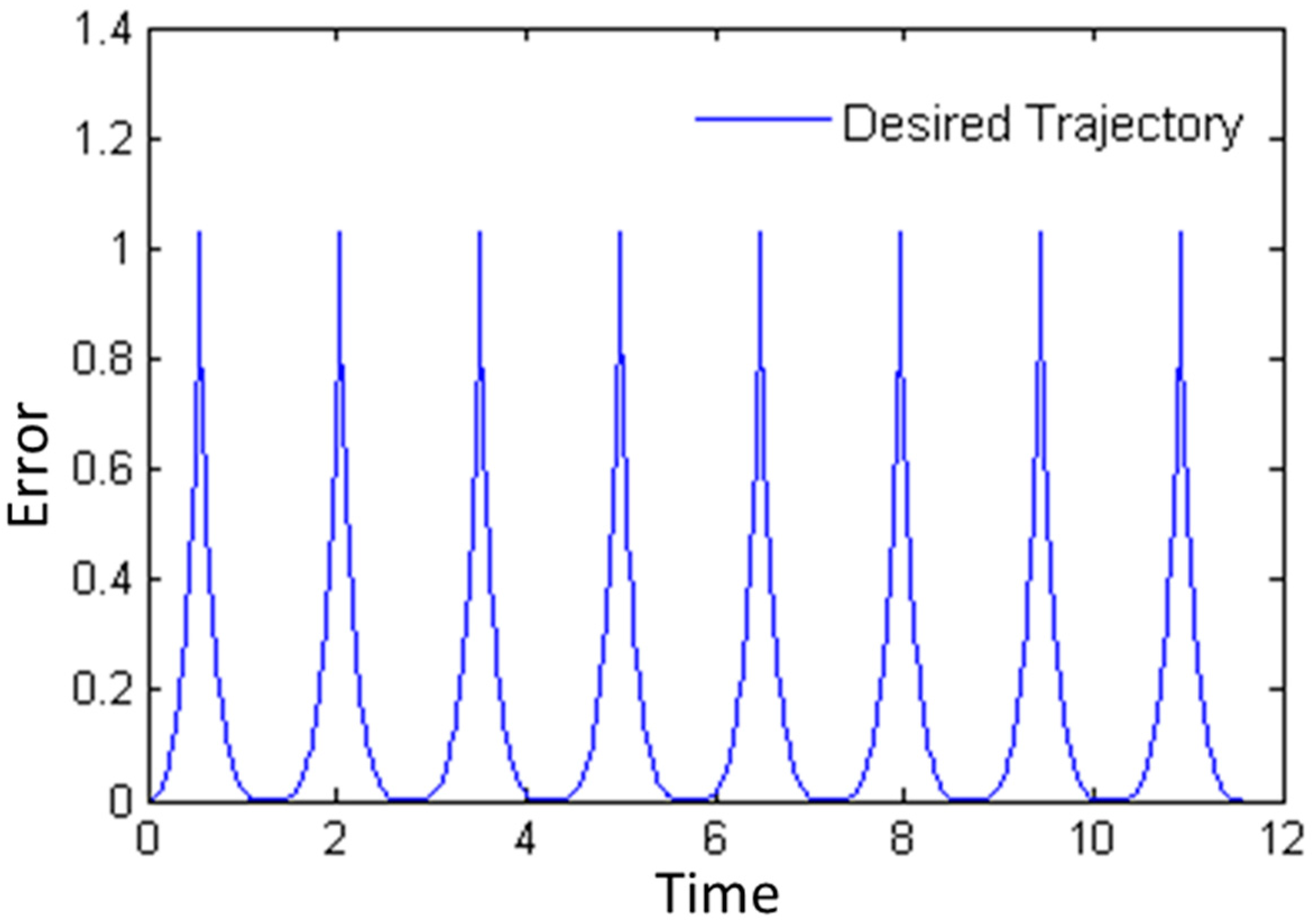
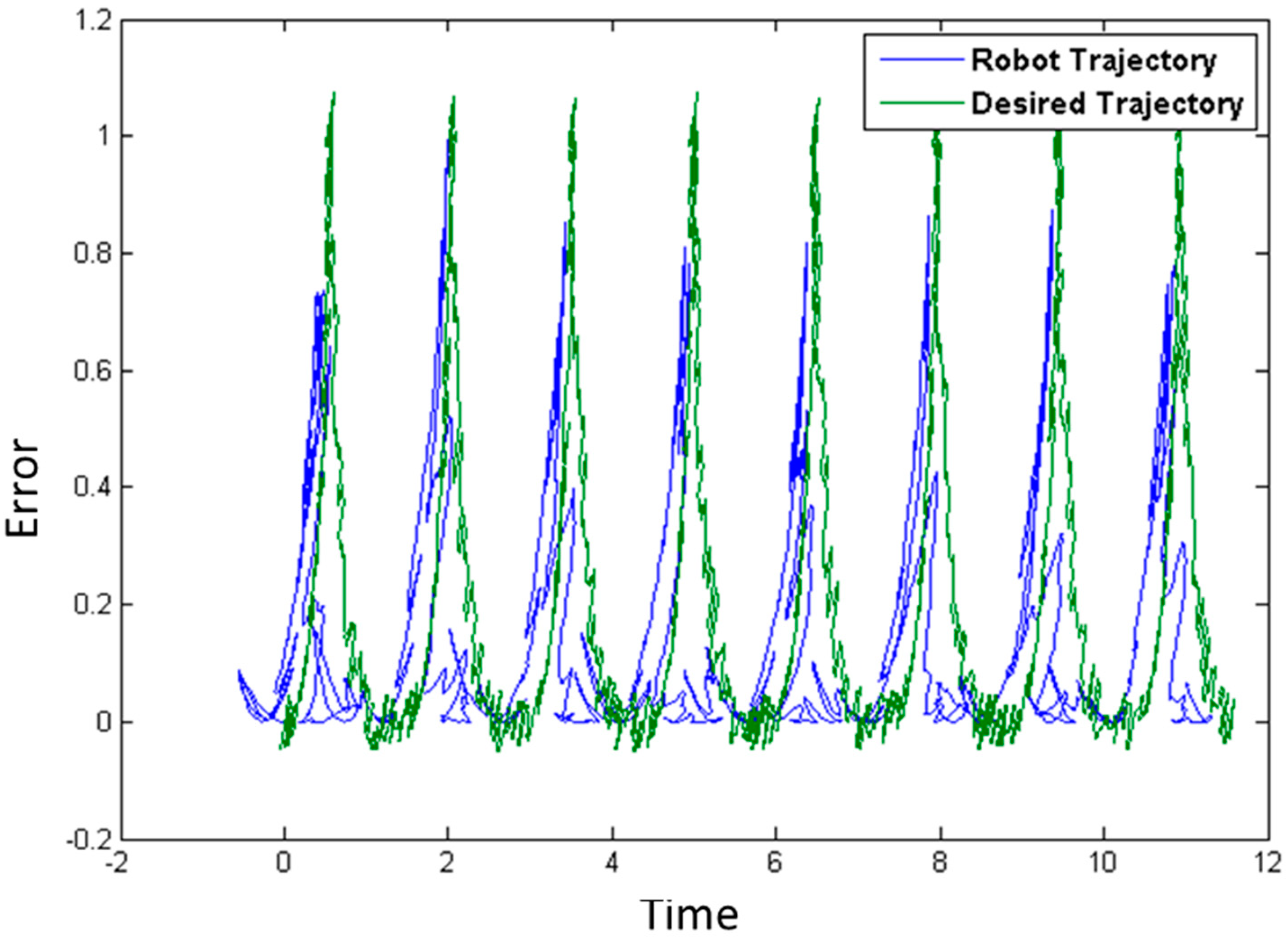
The desired trajectory for the robot to follow begins at the point (0, 0) and turns in order to generate a “U” shaped trajectory; furthermore, to create a more complex problem, the trajectory is repeated on several occasions, as shown in
Figure 11.
With the intention of providing better comparison tools between type-1 and interval type-2 fuzzy systems, a modification is made to the autonomous mobile robot, where random number generators are added to simulate the noise in the plant with a level of 5% [
40].
After adding noise to the plant, the trajectory of the desired reference varies slightly with respect to the original, as can be seen in
Figure 12.
5. Experimental Results
The study case of the autonomous mobile robot is used to test the proposal described in
Section 3, where the T1 and IT2 fuzzy systems are used for the dynamic adjustment of the c
3 and c
4 parameters used in the galactic swarm optimization.
The galactic swarm optimization was applied to the optimization of the parameter values of the membership functions of the autonomous mobile robot controller, and the GSO parameters used to perform the optimization are shown in
Table 1.
To evaluate the performance of our proposal and the original galactic swarm optimization, a series of performance indices are used, such as the mean square error (MSE), which is described in the below equation [
32,
41]:
where
is the reference value at time
i,
is the value produced by the system at time
i and
N is the number of samples considered.
In order to perform a comparison with the GSO algorithm some variants of the original GSO algorithm were used: the first is the fuzzy galactic swarm optimization (FGSO1) using the T1 fuzzy systems, the second is the FGSO1T2 using the IT2 fuzzy systems. The results obtained with the variants and the original GSO algorithm are presented in
Table 2 and
Table 3.
In
Table 2 we find the average, the best, the worst and the standard deviation of the results obtained after 30 simulations of the mobile autonomous robot plant without adding noise or disturbances. The results show that our proposal FGSO1, using the T1 fuzzy systems, is where better results are obtained on average, followed by the GSO algorithm and finally the proposed FGSO1T2 using the IT2 fuzzy systems. The averages of the results for each of the proposed methods are illustrated in
Figure 13.
In
Table 3 we find the mean, the best, the worst and the standard deviation of the results obtained after 30 simulations of the mobile autonomous robot plant adding a noise level of 5%. The results show that our proposal FGSO1T2 using the IT2 fuzzy systems is where we obtain better results on average, followed by the proposal FGSO1 using the T1 fuzzy and finally the GSO algorithm. The averages of the results for each of the proposed methods are illustrated in
Figure 14.
The figures shown below represent the best trajectories found after performing the simulations of the autonomous mobile robot plant.
Figure 15 shows the best simulation obtained with the proposed method FGSO1 in the experiments carried out without noise. In
Figure 16, we find the best simulation with noise in the autonomous mobile robot plant with the proposed method FGSO1T2.
The best controllers found with our proposed approach and the original GSO algorithm are shown below, where we can note the arrangement of the points of the membership functions after having performed the optimization of the fuzzy controller with each one of the proposals presented in the previous section. The first controller is shown in
Figure 17, obtained by performing the optimization with the original GSO algorithm; the second controller is shown in
Figure 18, found using our proposal FGSO1 using the T1 fuzzy systems, and finally the controller shown in
Figure 19 is obtained after performing the optimization of the controller with the proposal FGSO1T2 using the IT2 fuzzy systems.
Statistical Comparison
In order to validate the performance of our proposed method using the T1 and IT2 fuzzy systems for the optimization of the membership functions of the autonomous mobile robot, a statistical comparison is made to find evidence that our proposed method yields competitive results for the case study of the autonomous mobile robot plant.
First, the statistical comparison is made between the original GSO and our proposed method that uses the T1 and IT2 fuzzy systems for the adjustment of the c3 and c4 parameters. Then a comparison is made with the PSO algorithm. All comparisons are made by experimenting with the autonomous mobile robot plant without adding noise or disturbances to the simulations and adding 5% noise in the simulations of the autonomous mobile robot plant.
The statistical test used to perform the statistical comparison between the methods mentioned above is the
z test. In
Table 4, we can find the parameters used [
17,
28].
H0 is the null hypothesis; it establishes that the average of the proposals FGSO1 and FGSO1T2 (μ1) is greater than or equal to the average of the original GSO algorithm (μ2); furthermore, Ha is the alternative hypothesis (claim) that establishes that the average of the proposals FGSO1 and FGSO1T2 (μ1) is less than the average of the original GSO algorithm (μ2).
In
Table 5, the results with a 95% level of significance and a rejection zone for values lower than −1.645 are presented. The results of the statistical test for the experiments of the simulations without adding noise to the plant of the autonomous mobile robot give values of −2.4936 for the first comparison, rejecting
H0 and accepting
Ha; there is therefore enough evidence to affirm that the average of the proposal FGSO1 is lower than the average of the original GSO algorithm; there is a
z value of 1.3656 for the second comparison, accepting
H0, so that the average of the proposal FGSO1T2 is greater than or equal to the average of the original GSO algorithm.
Table 6 show the results with a 95% level of significance and a rejection zone for values lower than −1.645. The results of the statistical test for the experiments of the simulations with a 5% noise level in the signal of the plant of the autonomous mobile robot give values of −4.7511 and −4.2023. As a result, the
H0 is rejected and the
Ha is accepted; there is significant evidence to affirm that the average of the proposals FGSO1 and FGSO1T2 is lower than the average of the original GSO algorithm.
The H0 null hypothesis establishes that the average of the original GSO algorithm and the proposals FGSO1 and FGSO1T2 (μ1) is greater than or equal to the average of the original PSO algorithm, and the variants PSO + T1FS and PSO + IT2FS (μ2); furthermore, the Ha alternative hypothesis (claim) establishes that the average of the original GSO algorithm and the proposals FGSO1 and FGSO1T2 (μ1) is less than the average of the original PSO algorithm, and the variants PSO + T1FS and PSO + IT2FS (μ2).
Table 7 shows the results with a 95% level of significance and a rejection zone for values lower than −1.645. The results of the statistical test for the experiments of the simulations without adding noise to the plant of the autonomous mobile robot give values of −4.4229 and −5.1972, rejecting
H0 and accepting
Ha. There is therefore enough evidence to affirm that the average of the original GSO algorithm and the proposal FGSO1 is lower than the average of the original PSO algorithm and the variant PSO + T1FS. Finally, with a
z value of −0.7116 for the comparison between the proposal FGSO1T2 and the variant PSO + IT2FS,
H0 is accepted; so the average of the proposal FGSO1T2 is greater than or equal to the average of the variant PSO + IT2FS.
Table 8 shows the results with a 95% level of significance and a rejection zone for values lower than −1.645. The results of the statistical test for the experiments of the simulations with a 5% noise level in the signal of the plant of the autonomous mobile robot give values of −11.3293, −29.3360 and −26.0009, so
H0 is rejected and the
Ha is accepted; there is significant evidence to affirm the average of the original.
The GSO algorithm and the proposals FGSO1 and FGSO1T2 are lower than the average of the original PSO algorithm, and of the variants PSO + T1FS and PSO + IT2FS.
6. Conclusions
The main contribution in this paper is the study of the original galactic swarm optimization: of the variants FGSO1 using type-1 fuzzy systems and the variants FGSO1T2 using type-2 fuzzy systems, applied in the optimization controller of the mobile robot. Type-1 and interval type-2 fuzzy logic show a good management of the uncertainty in complex problems where disturbances or noise are present in the plant, and fuzzy controllers maintain stability in the simulation results.
For the results obtained without using noise or disturbances, the variant using type-1 fuzzy logic FGSO1 was the one with better results, thus obtaining a better controller than the original GSO. With the use of noise in the plant signal, the variants FGSO1 and FGSO1T2 manage to improve the obtained results with respect to the original GSO algorithm. The best overall fuzzy controller design was found with FGSO1T2, even if on average it could not show a statistical advantage.
In order to compare the performance of our proposal against other metaheuristics, a comparison was made with respect to the PSO algorithm. For the simulations carried out without adding noise to the mobile autonomous robot plant; our variants GSO, FGSO1 and FGSO1T2 managed to overcome the results obtained by the PSO algorithm, as well as its variants PSO + T1FS and PSO + IT2FS.
In the comparison made by adding noise to the plant in the same way, our proposal offered more competitive results than those obtained with PSO and its variants, and all this is based on the results presented in
Section 5.
We can conclude that the GSO algorithm and the proposed variants fuzzy galactic swarm optimization (FGSO1) and FGSO1T2 using the IT2 fuzzy systems show competitive results when applied to the optimization of the membership functions from the study case of the autonomous robot mobile. As a result, we will continue to investigate this area to even further explore the behavior of the GSO algorithm and the use of the type-1 and type-2 fuzzy logic, since good results have been presented in control problems and in the optimization of the benchmark mathematical functions according to the current study and previous publications.