Complex Soliton Solutions to the Gilson–Pickering Model
Abstract
:1. Introduction
2. General Properties of BSEFM
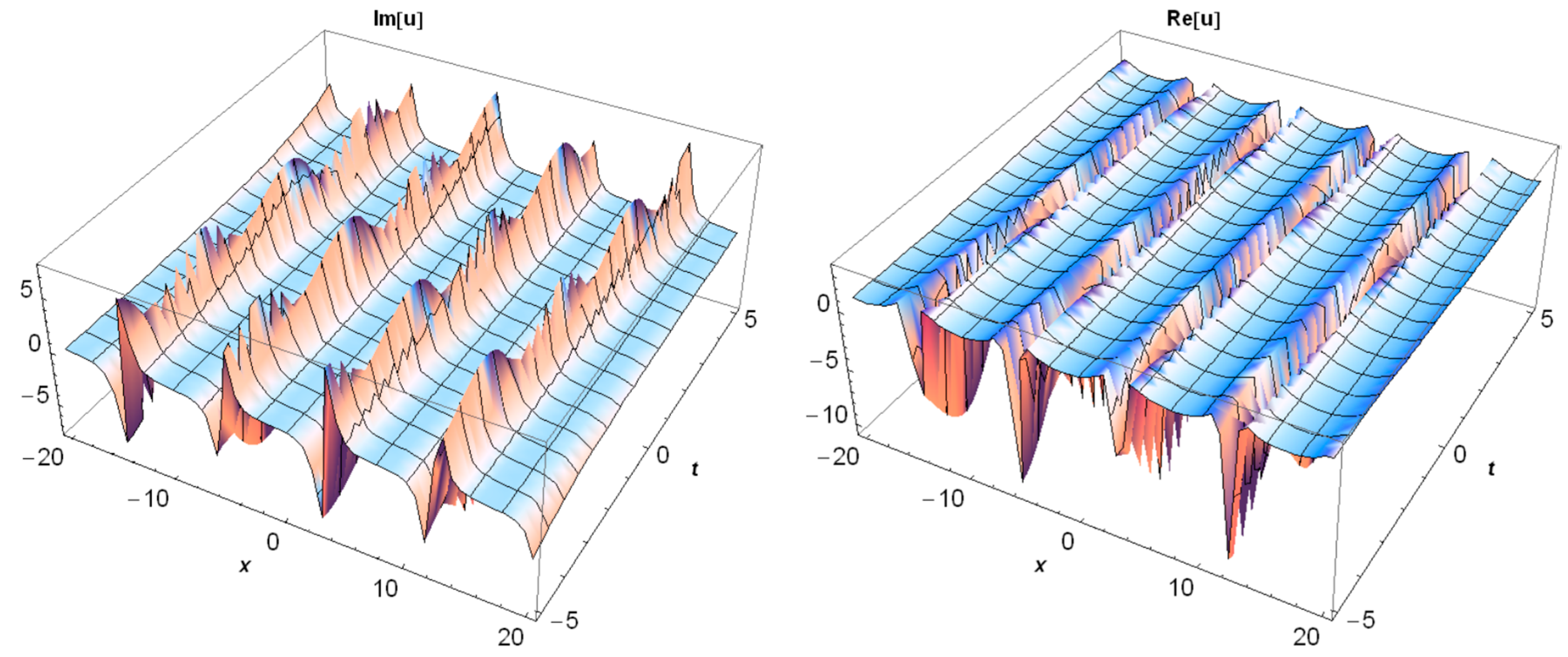
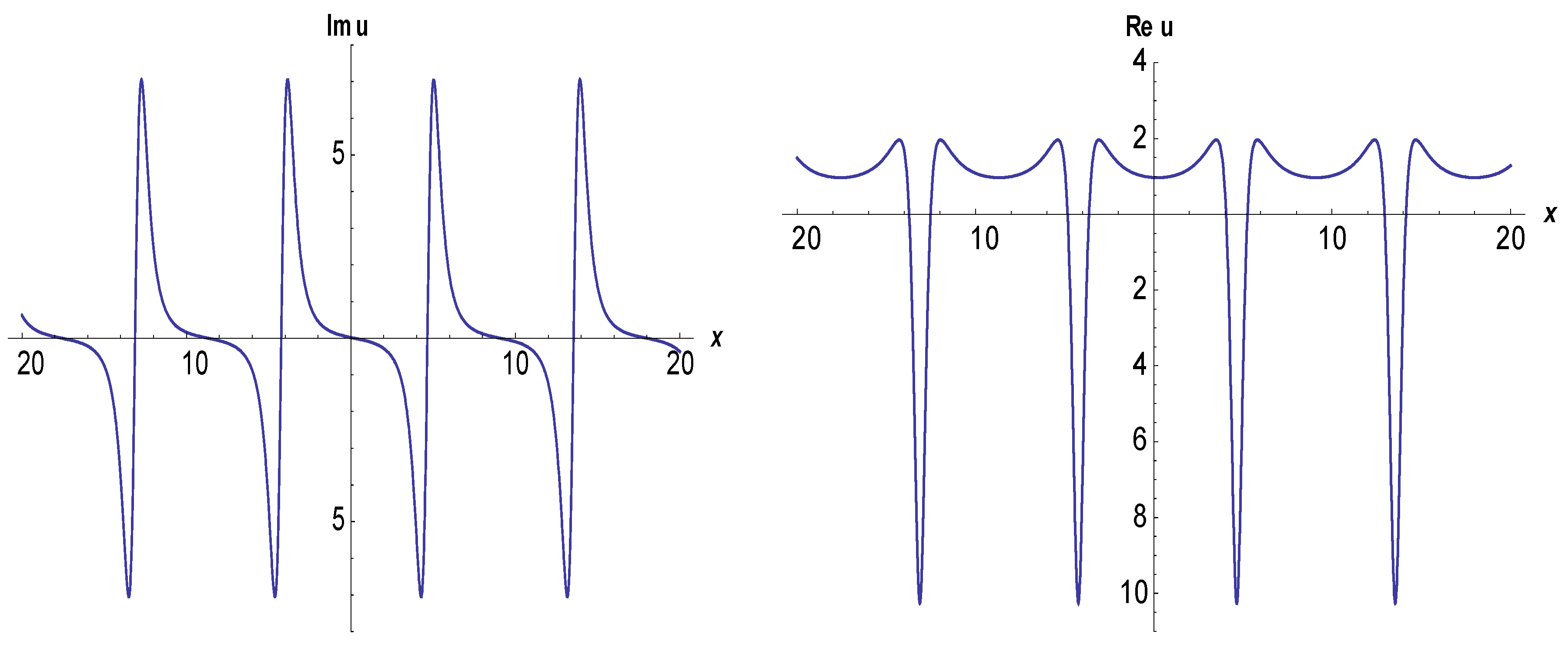
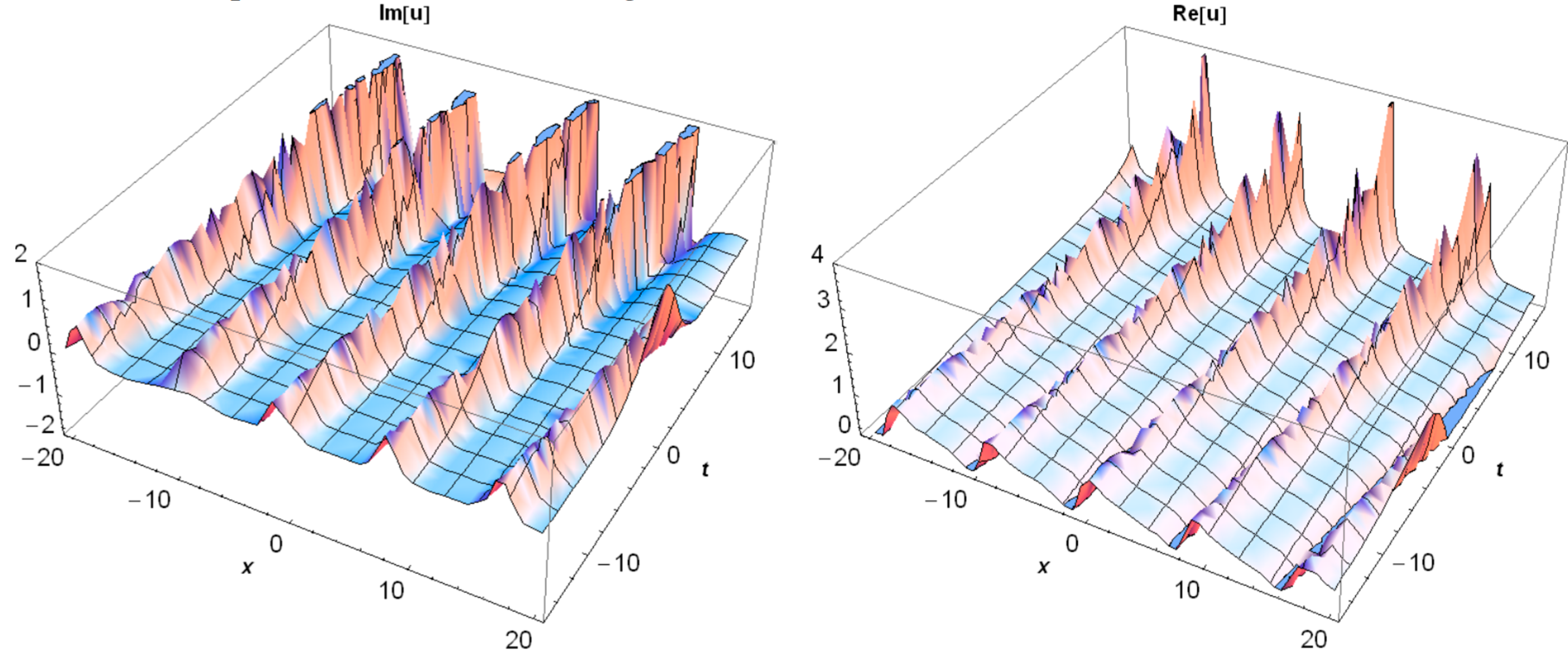
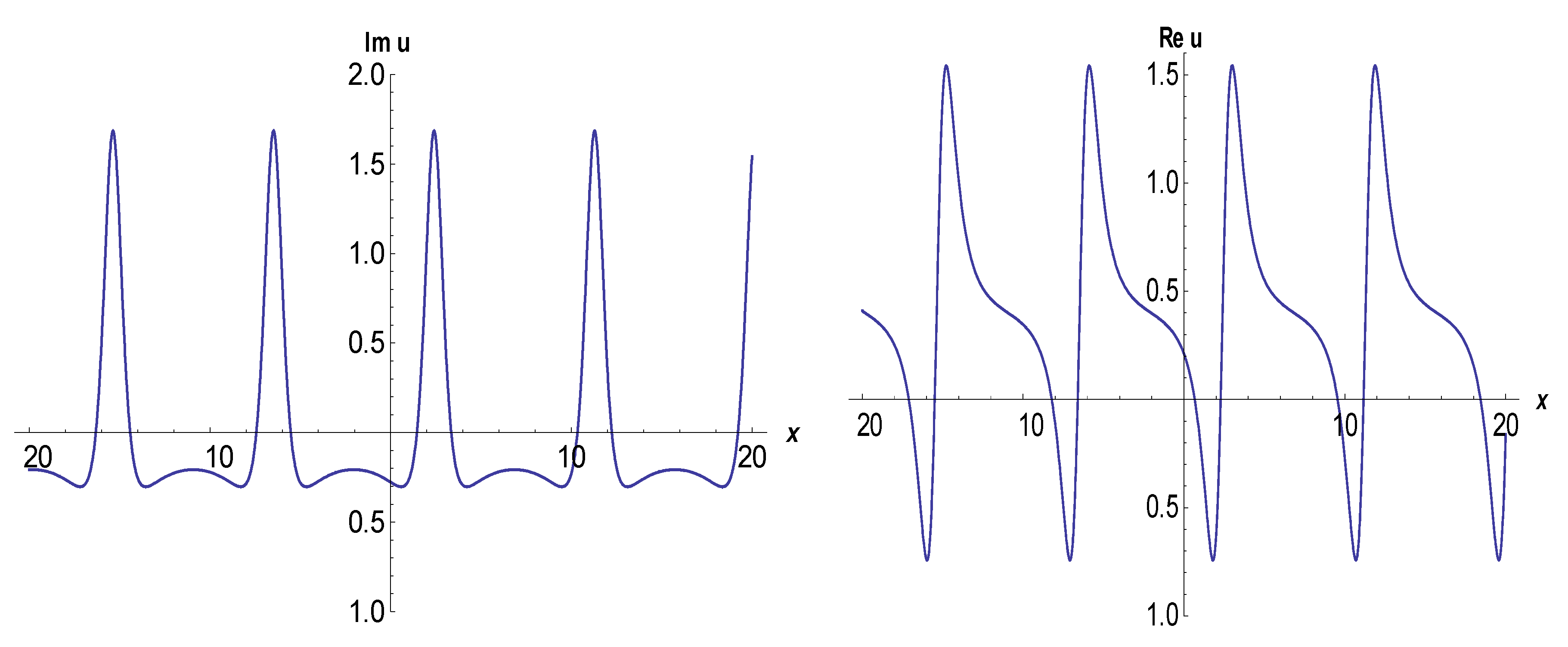
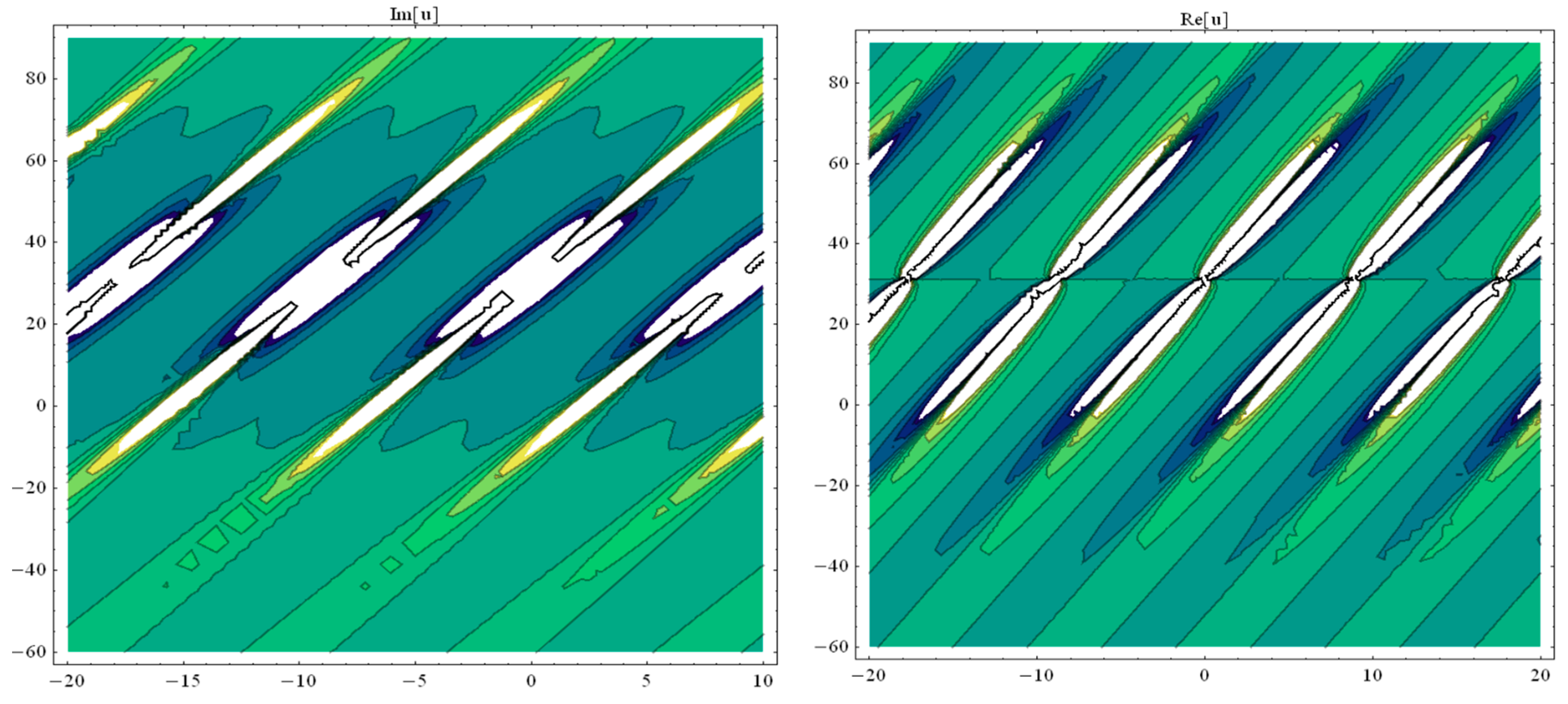
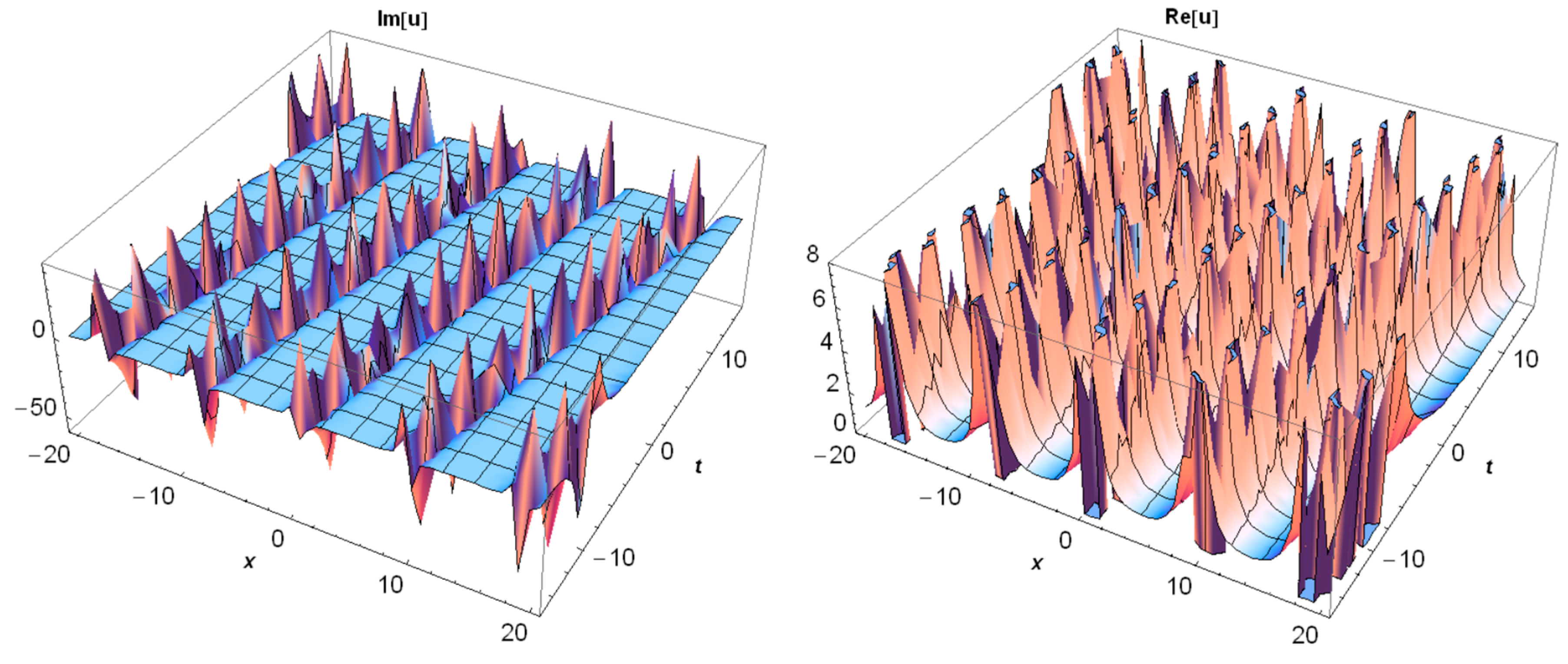
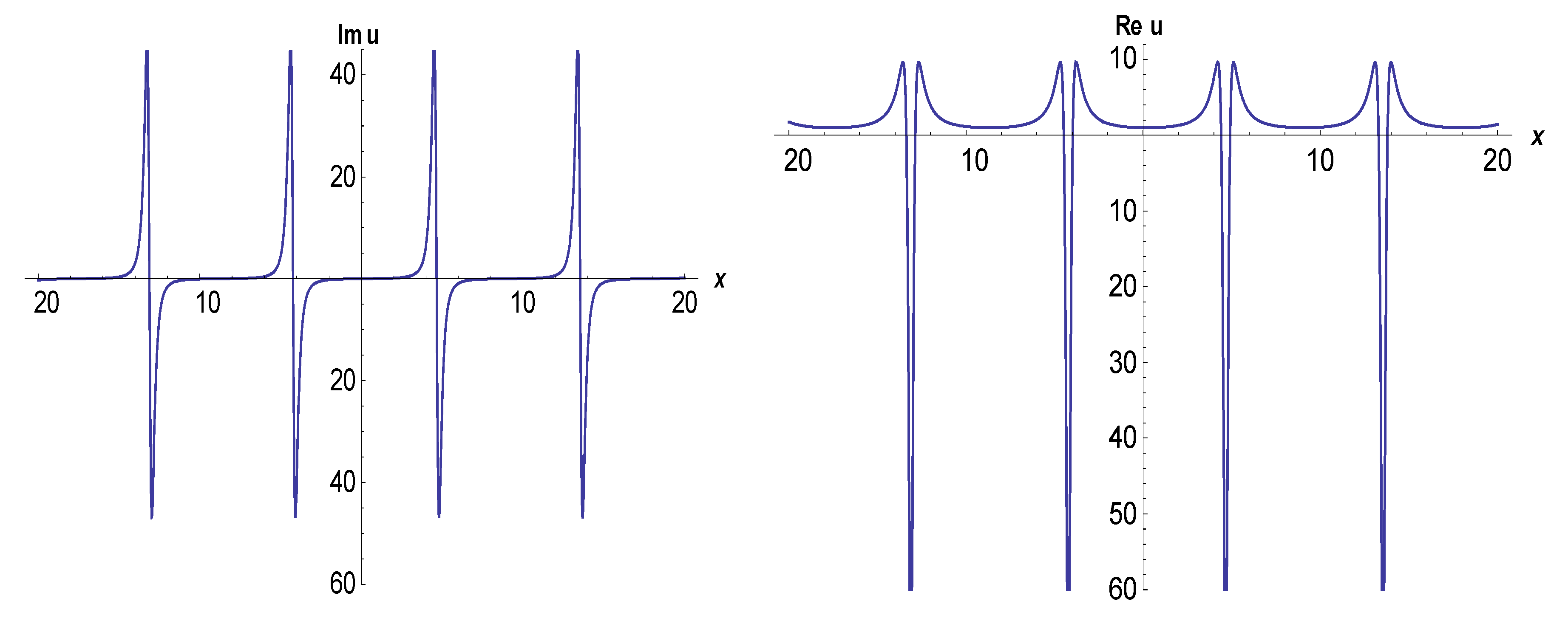
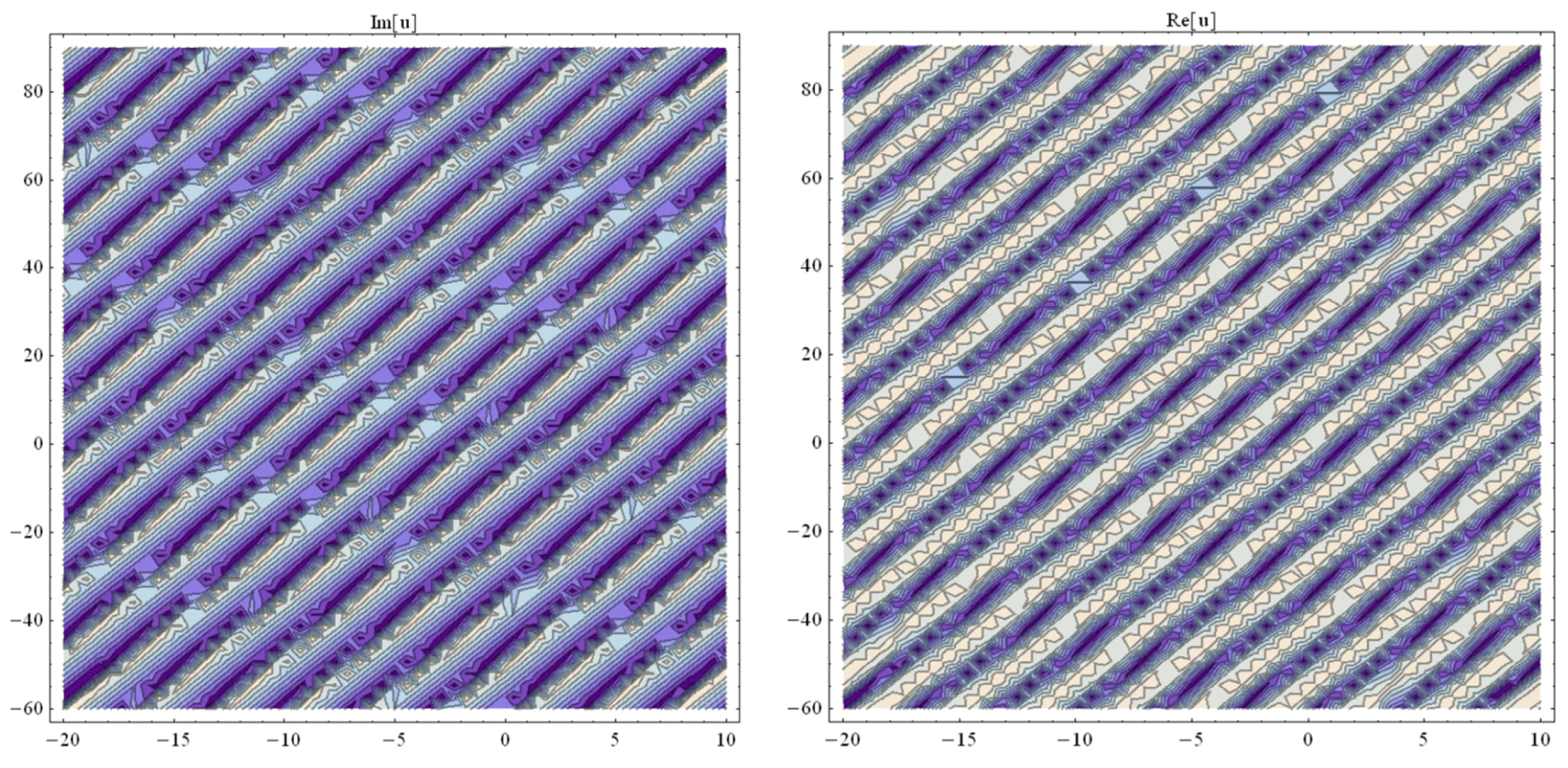
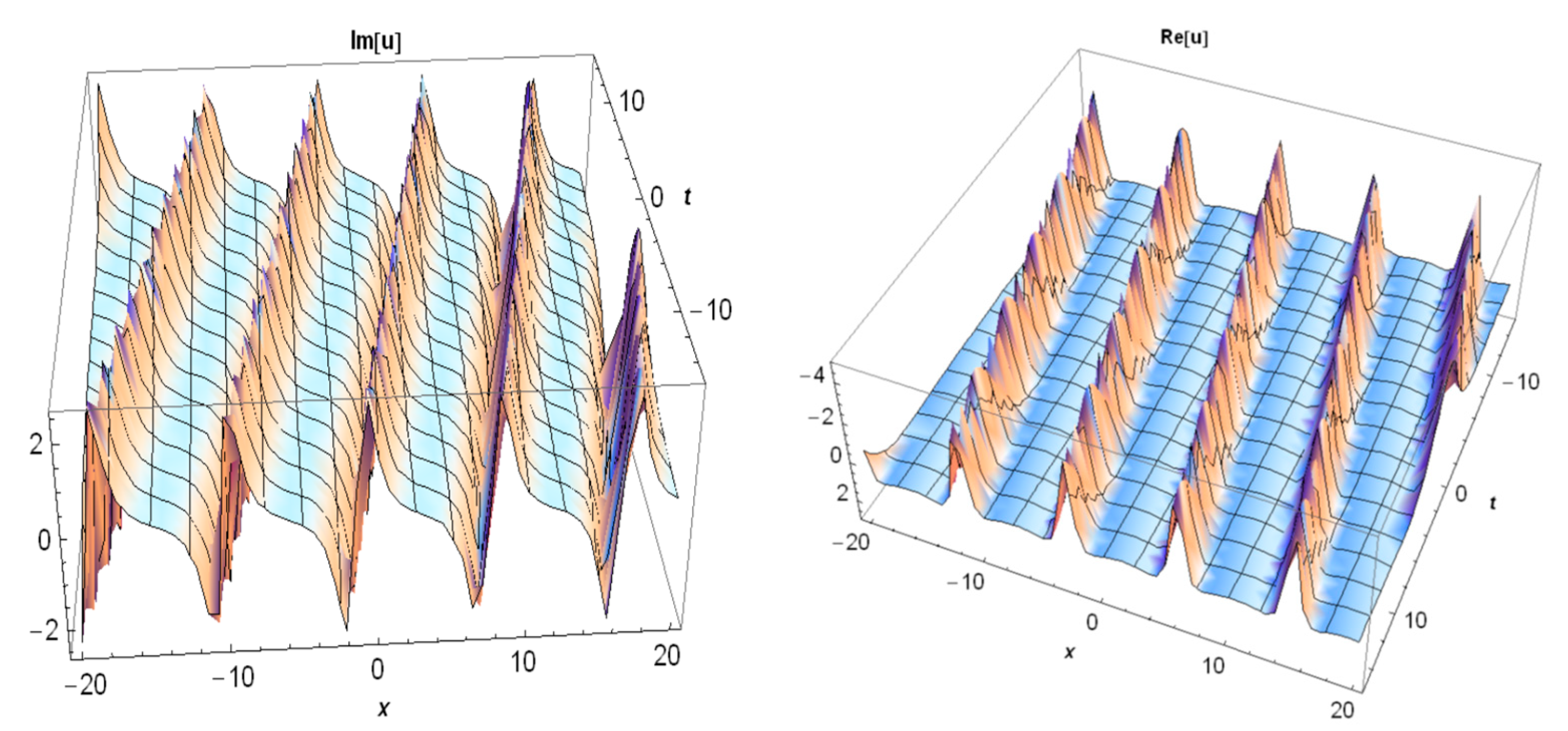
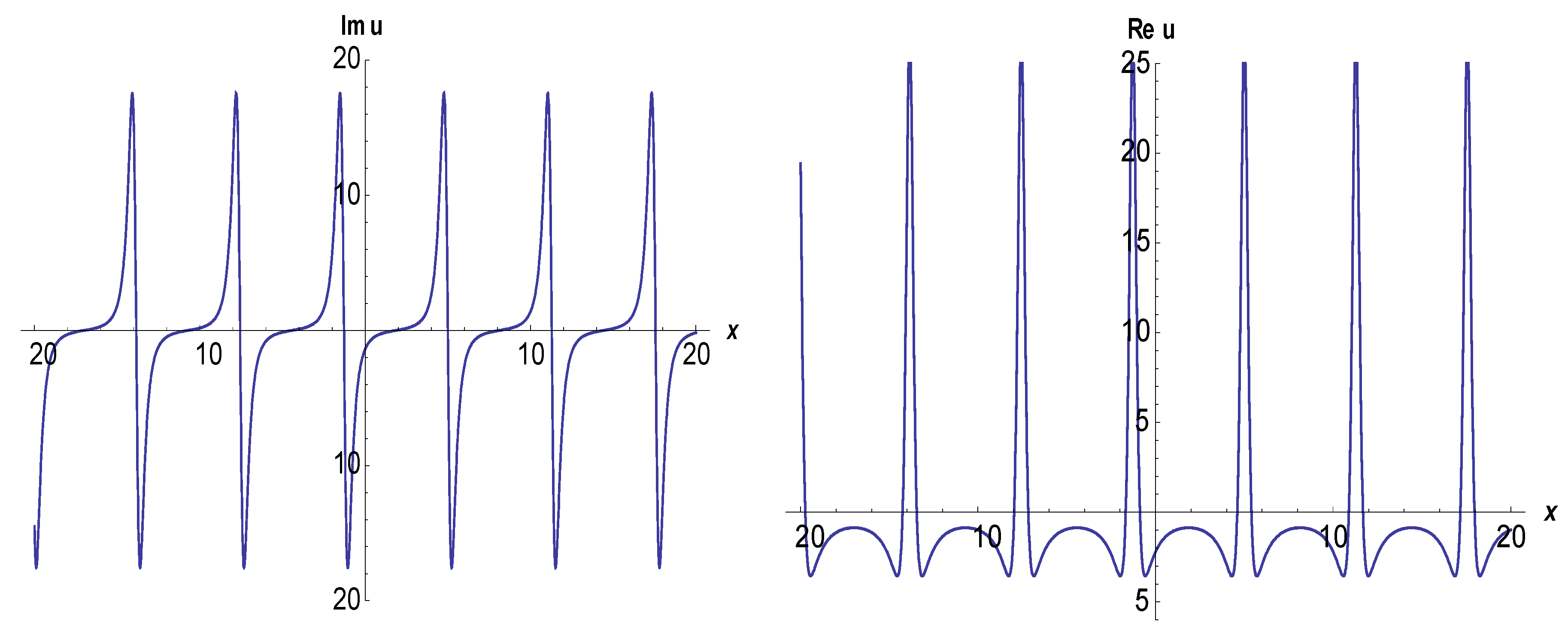
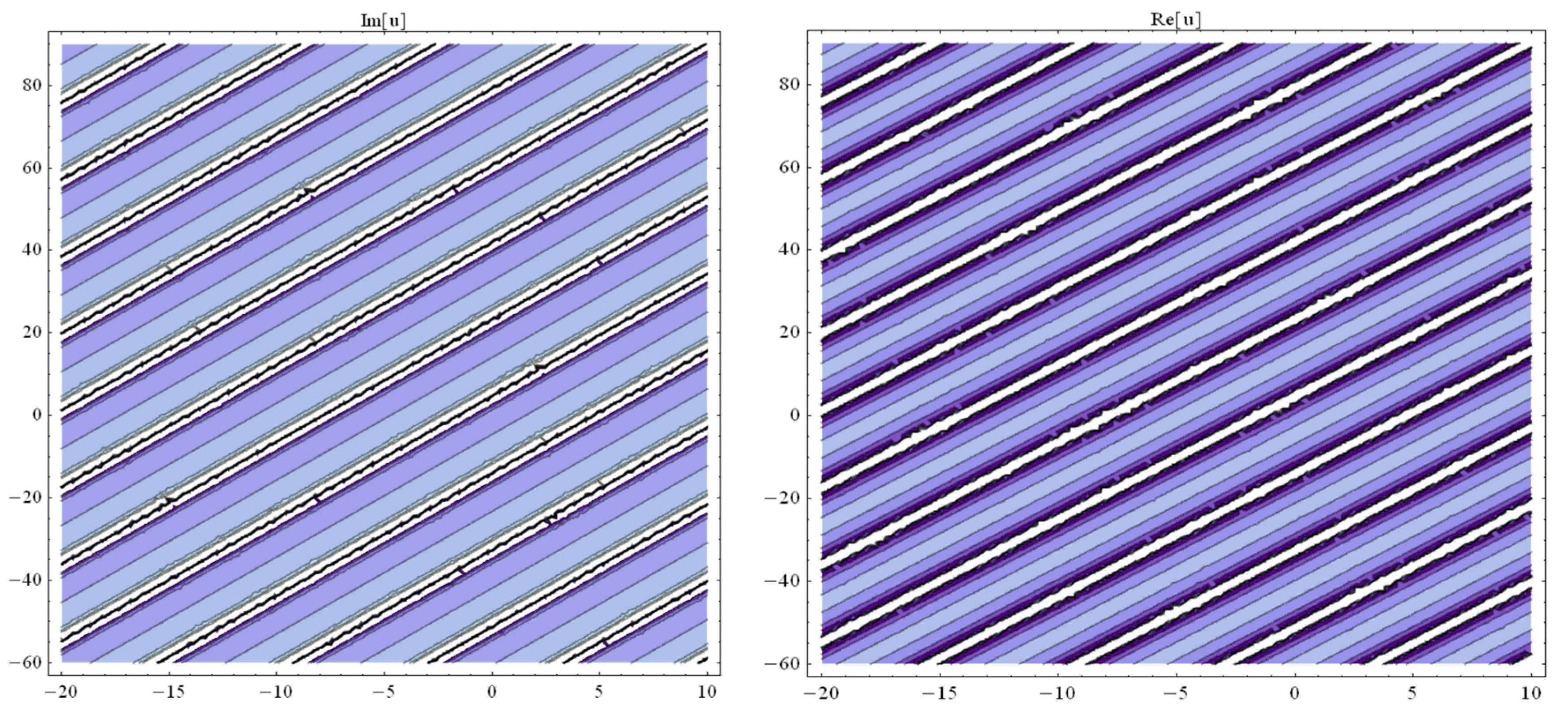
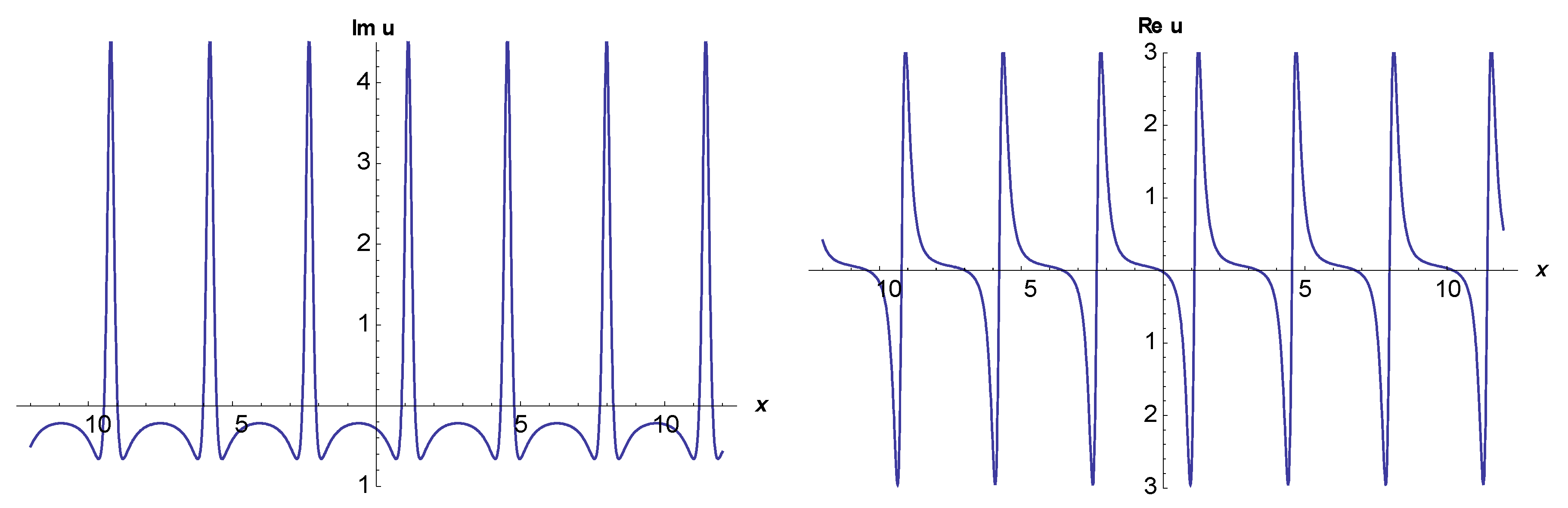
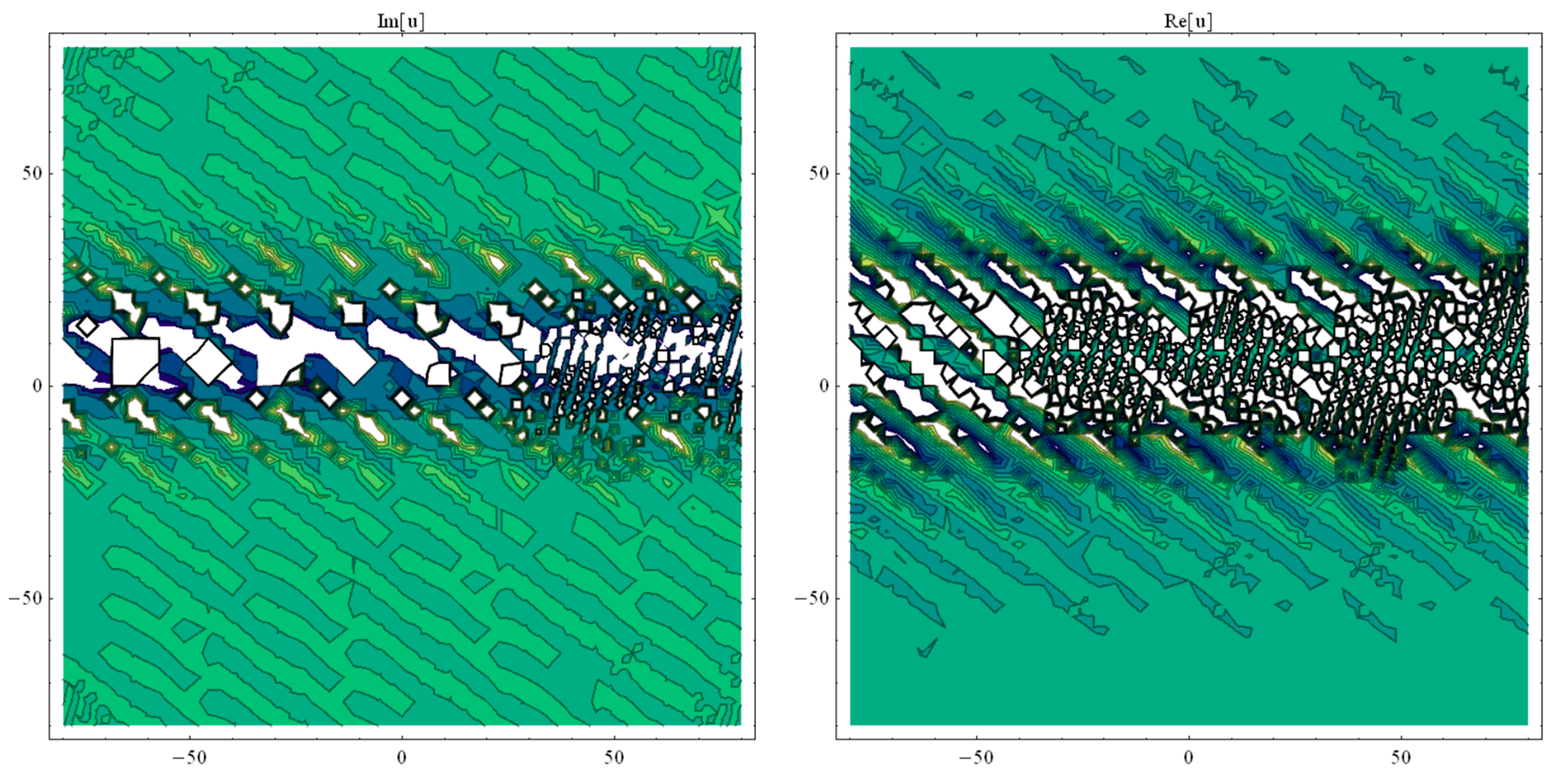
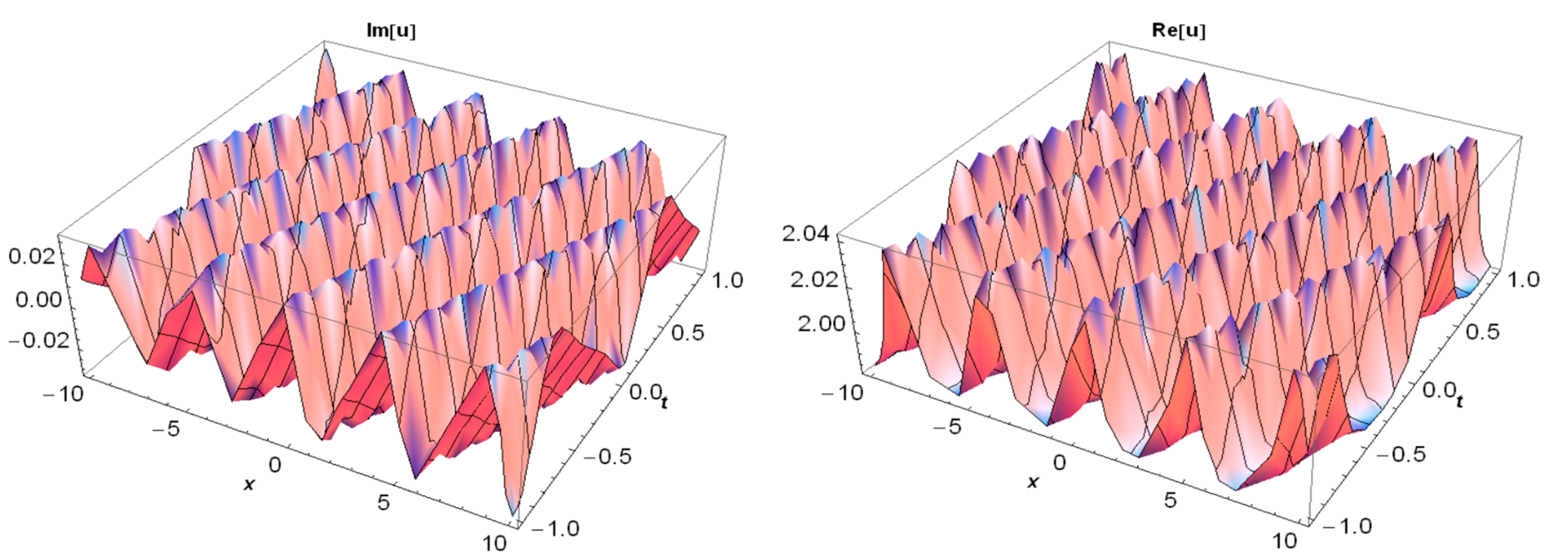
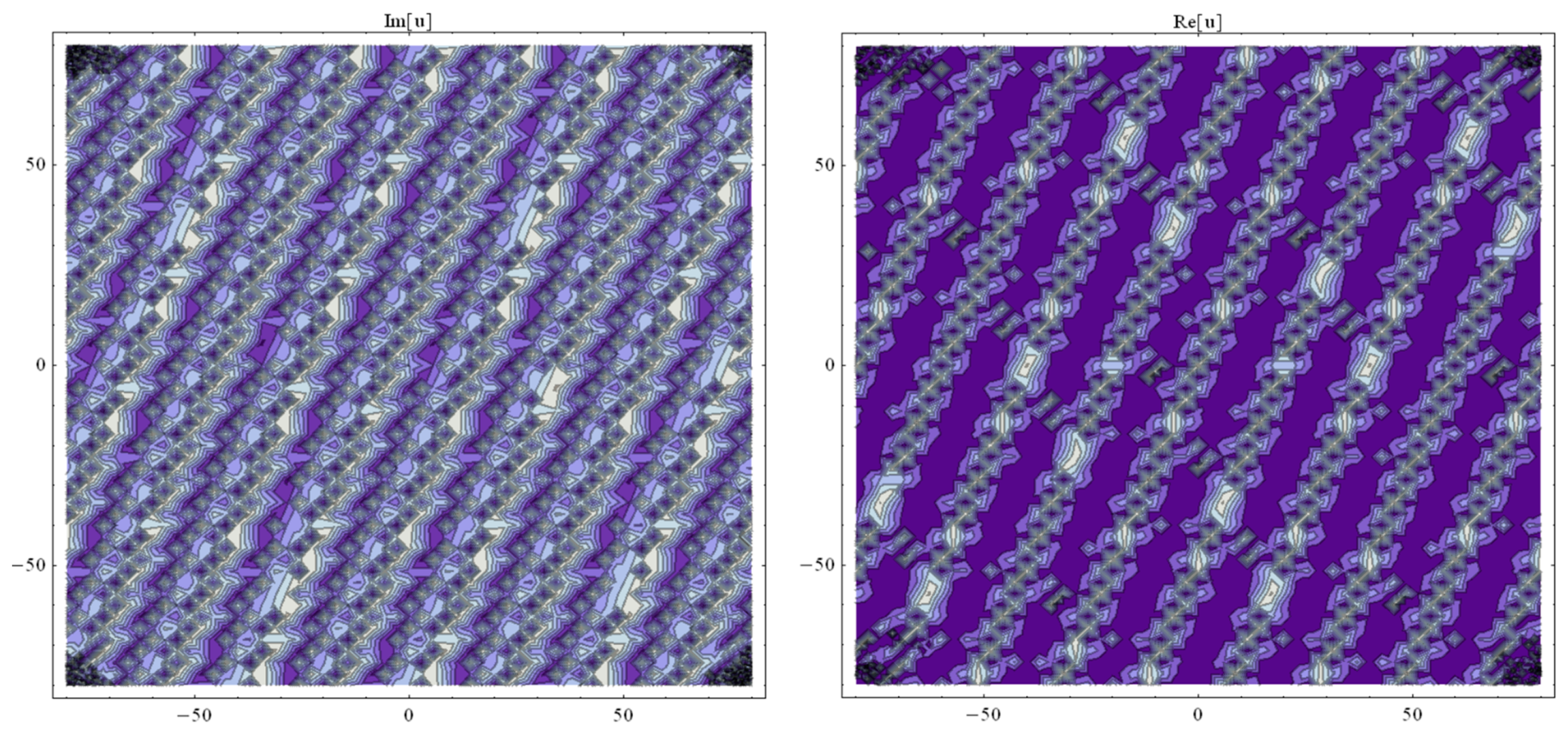
3. Application of the BSEFM
4. Conclusions
Funding
Conflicts of Interest
References
- Gilson, C.; Pickering, A. Factorization and Painleve analysis of a class of nonlinear third-order partial differential equations. J. Phys. A Math. Gen. 1995, 28, 2871–2888. [Google Scholar] [CrossRef]
- Irshad, A.; Mohyud-Din, S.T. Tanh-Coth Method for Nonlinear Differential Equations. Stud. Nonlinear Sci. 2012, 3, 24–48. [Google Scholar]
- Fan, X.; Yang, S.; Zhao, D. Travelling wave solutions for the Gilson–Pickering equation by using the simplified G’/G-expansion method. Int. J. Nonlinear Sci. 2009, 8, 368–373. [Google Scholar]
- Ebadia, G.; Karab, A.H.; Petkovic, M.D.; Biswas, A. Soliton solutions and conservation laws of the Gilson–Pickering equation. Waves Random Complex Media 2011, 21, 378–385. [Google Scholar] [CrossRef]
- Chen, A.; Huang, W.; Tang, S. Bifurcations of travelling wave solutions for the Gilson–Pickering equation. Nonlinear Anal. Real World Appl. 2009, 10, 2659–2665. [Google Scholar] [CrossRef]
- Ebadi, G.; Biswas, A. Application of the G’/G—Expansion method for nonlinear diffusion equations with nonlinear source. J. Frankl. Inst. 2010, 347, 1391–1398. [Google Scholar] [CrossRef]
- Li, C.; Tang, S.; Huang, W.; Chen, A. Peakons, Solitary Patterns and Periodic Solutions for Generalized Gilson-Pickering Equations. Far East J. Appl. Math. 2009, 35, 301–307. [Google Scholar]
- Zabihi, F.; Saffarian, M. A Meshless Method Using the Radial Basis Functions for Numerical Solution of the Gilson-Pickering Equation. In Proceedings of the 46th Annual Iranian Mathematics Conference, Yazd, Iran, 25–28 August 2015; pp. 1–4. [Google Scholar]
- Aslan, I. Exact and explicit solutions to nonlinear evolution equations using the division theorem. Appl. Math. Comput. 2011, 217, 8134–8139. [Google Scholar] [CrossRef]
- Araci, S.; Ozer, O. Extended q-Dedekind-type Daehee-Changhee sums associated with extended q-Euler polynomials. Adv. Differ. Equ. 2015, 2015, 272–276. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Opt. Quantum Electron. 2018, 50, 138. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. Solitons in an inhomogeneous Murnaghan’s rod. Eur. Phys. J. Plus 2018, 133, 228. [Google Scholar] [CrossRef]
- Cattani, C.; Ciancio, A. On the fractal distribution of primes and prime-indexed primes by the binary image analysis. Phys. A 2016, 460, 222–229. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Yokus, A.; Baskonus, H.M. On the exact and numerical solutions to the coupled Boussinesq equation arising in ocean engineering. Indian J. Phys. 2018, 1–10, Accepted. [Google Scholar] [CrossRef]
- Ciancio, A.; Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. New structural dynamics of isolated waves via the coupled nonlinear Maccari’s system with complex structure. Indian J. Phys. 2018, 92, 1281–1290. [Google Scholar] [CrossRef]
- Baskonus, H.M. New complex and hyperbolic function solutions to the generalized double combined Sinh-Cosh-Gordon equation. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2017; Volume 1798, p. 020018. [Google Scholar]
- Ciancio, A.; Quartarone, A. A Hybrid Model for Tumor-Immune Competition. U.P.B. Sci. Bull. Series A 2013, 75, 125–136. [Google Scholar]
- Baskonus, H.M. New acoustic wave behaviors to the Davey–Stewartson equation with power-law nonlinearity arising in fluid dynamics. Nonlinear Dyn. 2016, 86, 177–183. [Google Scholar] [CrossRef]
- Seadawy, A. Three-dimensional nonlinear modified Zakharov–Kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comput. Math. Appl. 2016, 71, 201–206. [Google Scholar] [CrossRef]
- Ünlükal, C.; Şenel, M.; Şenel, B. Risk Assessment with Failure Mode and Effect Analysis and Gray Relational Analysis Method in Plastic Enjection Prosess. In Proceedings of the ITM Web of Conference, Girne, Cyprus, 4–6 May 2018; Volume 22, pp. 1–10. [Google Scholar]
- Bulut, H.; Sulaiman, T.A.; Baskonus, H.M.; Yazgan, T. Novel Hyperbolic Behaviors to Some Important Models Arising in Quantum Science. Opt. Quantrum. Electron. 2017, 49, 349. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yokus, A.; Gulluoglu, N.; Baskonus, H.M.; Bulut, H. Regarding the Numerical and Stability Analysis of the Sharma-Tosso-Olver Equation. In Proceedings of the ITM Web of Conference, Girne, Cyprus, 4–6 May 2018; Volume 22, pp. 1–9. [Google Scholar]
- Ilhan, O.A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. On the new wave Solutions to a Nonlinear Model Arising in Plasma Physics. Eur. Phys. J. Plus. 2018, 133, 27. [Google Scholar] [CrossRef]
- Ozer, O. A Note on Structure of Certain Real Quadratic Number Fields. Iran. J. Sci. Technol. 2017, 41, 759–769. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H.; Akturk, T. Investigations of dark, bright, combined dark-bright optical and other soliton solutions in the complex cubic nonlinear Schrödinger equation with-potential. Superlattices Microstruct. 2018, 115, 19–29. [Google Scholar] [CrossRef]
- Yokus, A.; Sulaiman, T.A.; Gulluoglu, M.T.; Bulut, H. Stability Analysis, Numerical and Exact Solutions of the (1+1)-Dimensional NDMBBM Equation. In Proceedings of the ITM Web of Conference, Girne, Cyprus, 4–6 May 2018; Volume 22, pp. 1–10. [Google Scholar]
- Yokus, A.; Sulaiman, T.A.; Baskonus, H.M.; Atmaca, S.P. On the exact and numerical solutions to a nonlinear model arising in mathematical biology. In Proceedings of the ITM Web of Conference, Girne, Cyprus, 4–6 May 2018; Volume 22, pp. 1–10. [Google Scholar]
- Baskonus, H.M.; Askin, M. Travelling Wave Simulations to the Modified Zakharov-Kuznetsov Model Arising in Plasma Physics. In Proceedings of the 6th International Youth Science Forum LITTERIS ET ARTIBUS, Computer Science and Engineering, Lviv, Ukraine, 24–26 November 2016. [Google Scholar]
- Cilingir, I.; Demir, H. Application of the Hybrid Differential Transform Method to the nonlinear equations. Appl. Math. 2012, 3, 1–10. [Google Scholar]
- Cattani, C. A review on Harmonic Wavelets and their fractional extension. J. Adv. Eng. Comput. 2018, 2, 224–238. [Google Scholar] [CrossRef]
- Cilingir, I.; Demir, H. New Algorithm for the Lid-driven Cavity Flow Problem with Boussinesq-Stokes Suspension. Karaelmas J. Sci. Eng. 2018, 8, 462–472. [Google Scholar]
- Arshad, M.; Seadawy, A.R.; Lu, D. Bright-dark solitary wave solutions of generalized higher-order nonlinear Schrödinger equation and its applications in optics. J. Electromagn. Waves Appl. 2017, 31, 1711–1721. [Google Scholar] [CrossRef]
- Demir, H. Temporal differential transform and spatial finite difference methods for unsteady heat conduction equations with anisotropic diffusivity. Gazi Univ. J. Sci. 2014, 27, 1063–1076. [Google Scholar]
- Seadawy, A.R. Ionic acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev-Petviashvili-Burgers equations in quantum plasma. Math. Methods Appl. Sci. 2017, 40, 1598–1607. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Khater, M.M. Bifurcations of new multi soliton solutions of the van der Waals normal form for fluidized granular matter via six different methods. Results Phys. 2017, 7, 2028–2035. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Lu, D.; Khater, M.M. Bifurcations of traveling wave solutions for Dodd–Bullough–Mikhailov equation and coupled Higgs equation and their applications. Chin. J. Phys. 2017, 55, 1310–1318. [Google Scholar] [CrossRef]
- Ozer, O. Determination of Fundamental Units of Real Quadratic Number Fields Related with Specific Continued Fraction Expansions. Egypt. Comput. Sci. J. 2018, 42, 1–12. [Google Scholar]
- Ozer, O.; Pekin, A. An Algorithm for Explicit Form of Fundamental Units of Certain Real Quadratic Fields and Period Eight. Eur. J. Pure Appl. Math. 2015, 8, 343–356. [Google Scholar]
- Bas, E.; Panakhov, E.; Yilmazer, R. The uniqueness theorem for hydrogen atom equation. TWMS J. Pure Appl. Math. 2013, 4, 20–28. [Google Scholar]
- Duran, S.; Askin, M.; Sulaiman, T.A. New soliton properties to the ill-posed Boussinesq equation arising in nonlinear physical science. Int. J. Optim. Control Theor. Appl. 2017, 7, 240–247. [Google Scholar] [CrossRef]
- Askin, M. Effect of the Transition Metal Elements on the Relaxation Times in the Agar Solutions. Asian J. Chem. 2007, 19, 3191–3196. [Google Scholar]
- Baskonus, H.M.; Koc, D.A.; Bulut, H. New travelling wave prototypes to the nonlinear Zakharov-Kuznetsov equation with power law nonlinearity. Nonlinear Sci. Lett. A Math. Phys. Mech. 2016, 7, 67–76. [Google Scholar]
- Bulut, H.; Atas, S.S.; Baskonus, H.M. Some novel exponential function structures to the Cahn–Allen equation. Cogent Phys. 2016, 3, 1–8. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Erdogan, F.; Ozkul, A.; Asmouh, I. Novel Behaviors to the Nonlinear Evolution Equation Describing the Dynamics of Ionic Currents along Microtubules. In Proceedings of the ITM Web of Conference, Istanbul, Turkey, 20–22 May 2017; Volume 13, pp. 1–5. [Google Scholar]
- Zheng, B. Application of a Generalized Bernoulli SubODE Method for Finding Traveling Solutions of Some Nonlinear Equations. WSEAS Trans. Math. 2012, 7, 618–626. [Google Scholar]
- Baskonus, H.M.; Bulut, H.; Emir, D.G. Regarding New Complex Analytical Solutions for the Nonlinear Partial Vakhnenko-Parkes Differential Equation via Bernoulli Sub-Equation Function Method. Math. Lett. 2015, 1, 1–9. [Google Scholar]
- Ma, W.X.; Fuchssteiner, B. Explicit and Exact Solutions to a Kolmogorov-Petrovskii-Piskunov Equation. Int. J. Non-Linear Mech. 1996, 31, 329–338. [Google Scholar] [CrossRef]
- Ma, W.X.; Li, J.; Khalique, C.M. A Study on Lump Solutions to a Generalized Hirota-Satsuma-Ito Equation in (2+1)-Dimensions. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X.; Qin, Z. Abundant Mixed Lump-Soliton Solutions to the BKP Equation. East Asian J. Appl. Math. 2018, 8, 224–232. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X.; Qin, Z. Lump and lump-soliton solutions to the (2+1)—Dimensional Ito equation. Anal. Math. Phys. 2018, 8, 427–436. [Google Scholar] [CrossRef]



© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baskonus, H.M. Complex Soliton Solutions to the Gilson–Pickering Model. Axioms 2019, 8, 18. https://doi.org/10.3390/axioms8010018
Baskonus HM. Complex Soliton Solutions to the Gilson–Pickering Model. Axioms. 2019; 8(1):18. https://doi.org/10.3390/axioms8010018
Chicago/Turabian StyleBaskonus, Haci Mehmet. 2019. "Complex Soliton Solutions to the Gilson–Pickering Model" Axioms 8, no. 1: 18. https://doi.org/10.3390/axioms8010018
APA StyleBaskonus, H. M. (2019). Complex Soliton Solutions to the Gilson–Pickering Model. Axioms, 8(1), 18. https://doi.org/10.3390/axioms8010018




