Best Proximity Point Theorems on Rectangular Metric Spaces Endowed with a Graph

Abstract

In this paper, we ensure the existence and uniqueness of a best proximity point in rectangular metric spaces endowed with a graph structure.

1. Introduction

Over the last decades, many researchers have focused on fixed point theory since it plays a very important role in the resolution of several mathematical models in various fields, see References [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. One of the tools used is the well-known Banach contraction principle, which states that if $(X,d)$ is a complete metric space and $f:X⟶X$ is a contraction self-mapping, then f has a unique fixed point in X. On the other hand, if f is a non-self mapping, that is, $f:A⟶B$, where A and B are two subsets of X, then f might not necessary have a fixed point, which leads one to think of an approximate solution x of $fx=x$ such that x is closet to $fx$: thereby, best proximity point theory appeared. We recall the definition of a best proximity point.

Definition 1.

Let $(X,d)$ be a metric space, A and B two subsets of X and a mapping $f:A⟶B$. We denote by $d(A,B)$ the distance between A and B as follows

$$d(A,B)=min\left\{d\right(x,y):x\in A,b\in B\}.$$

An element $u\in A$ is called a best proximity point of the mapping f if

$$d(u,fu)=d(A,B).$$

(1)

There are many variants and extensions of results for the existence of a best proximity point. For more details, we refer to References [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].

One of the generalized metric spaces is the rectangular metric space introduced first by Branciari [30]. Metric spaces endowed with a graph were introduced by Jachymski [31], which is an extension of metric spaces with partial order structures. In this paper, we consider rectangular metric spaces with the additional structure of a graph. Our contribution is that of proving the existence of a unique best proximity point for mappings satisfying different contractive conditions.

2. Preliminaries

In this section, we present some useful preliminary definitions and results related to our study. First, we remind the reader of the definition of rectangular metric spaces along with the topology.

Definition 2.

[30] Let X be a nonempty set. If the function $d:X^2⟶[0,\infty )$ satisfies the following conditions for all $x,y,z\in X$:

(r₁) 

$x=y$ if and only if $d(x,y)=0$;

(r₂) 

$d(x,y)=d(y,x)$;

(r₃) 

$d(x,y)\le d(x,u)+d(u,v)+d(v,y)$ for all different $u,v\in X\backslash \{x,y\}$,

then the pair $(X,d)$ is called a rectangular metric space.

Definition 3.

[30] Let $(X,d)$ be a rectangular metric space. Then,

1. 

a sequence $\left\{x_n\right\}$ in X converges to a point x if and only if ${\displaystyle \underset{n\to \infty }{lim}d(x_n,x)=0}$.

2. 

a sequence $\left\{x_n\right\}$ in X is called Cauchy if ${\displaystyle \underset{n,m\to \infty }{lim}d(x_n,x_m)=0}$.

3. 

$(X,d)$ is said to be complete if every Cauchy sequence $\left\{x_n\right\}$ in X converges to a point $x\in X$.

4. 

Let $B_r(x_0,\delta )=\{y\in Xsuchthatd(x_0,y)<\delta \}$ be an open ball in $(X,d)$. A mapping $f:X⟶X$ is continuous at $x_0\in X$ if for each $ϵ>0$, there exists $\delta >0$ so that $f\left(B_r(x_0,\delta )\right)\subset B_r(f{x}_0,ϵ)$.

Now, we present the definition of a best proximity point in the rectangular metric spaces $(X,d)$.

Definition 4.

Let $A,B$ be nonempty subsets of $(X,d)$ and $f:A⟶B$ be a given mapping. We denote by $d(A,B)=inf\left\{d\right(a,b):a\in A,b\in B\}$. An element $u\in A$ is called a best proximity point for the mapping f if $d(u,fu)=d(A,B)$. We denote by $A_0$ and $B_0$ the following sets:

$$\begin{array}{c}\hfill A_0=\{x\in A:d(x,y)=d(A,B)forsomey\in B\}\end{array}$$

(2)

$$\begin{array}{c}\hfill B_0=\{y\in B:d(x,y)=d(A,B)forsomex\in A\}.\end{array}$$

(3)

The concept of P-property was defined by Raj in Reference [32].

Definition 5.

[32] Let $(A,B)$ be a pair of non-empty subsets of $(X,d)$ such that $A_0\ne \varnothing$. We say that the pair $(A,B)$ has the P-property if and only if for $x_1,x_2\in A_0$ and $y_1,y_2\in B_0$ $\left.\begin{array}{cc}d(x_1,y_1)\hfill & =d(A,B)\hfill \\ d(x_2,y_2)\hfill & =d(A,B)\hfill \end{array}\right\}⟹d(x_1,x_2)=d(y_1,y_2)$.

Here, let us recall some preliminaries from graph theory. Let X be a nonempty set and $\Delta =\left\{\right(x,x)\in X\times X,x\in X\}$. A graph G is a pair $(V,E)$ where $V=V\left(G\right)$ is a set of vertices coinciding with X and $E=E\left(G\right)$ the set of its edges such that $\Delta \subset E\left(G\right)$. Furthermore, throughout this paper, we assume that the graph G has no parallel edges, that is, we do not allow it to get two or more edges that are incident to the same two vertices. By reversing the direction of edges in G, we get the graph denoted $G^{-1}$ where its set of edges and vertices are defined as follows:

$$E\left(G^{-1}\right)=\{(x,y)\in X^2:(y,x)\in E\left(G\right)\}\mathrm{and}V\left(G^{-1}\right)=V\left(G\right).$$

Consider the graph $\tilde{G}$ consisting of all vertices and edges of G and $G^{-1}$, that is,

$$E(\tilde{G})=E\left(G\right)\cup E\left(G^{-1}\right).$$

(4)

We denote by $\tilde{G}$ the undirected graph obtained by ignoring the direction of edges of G.

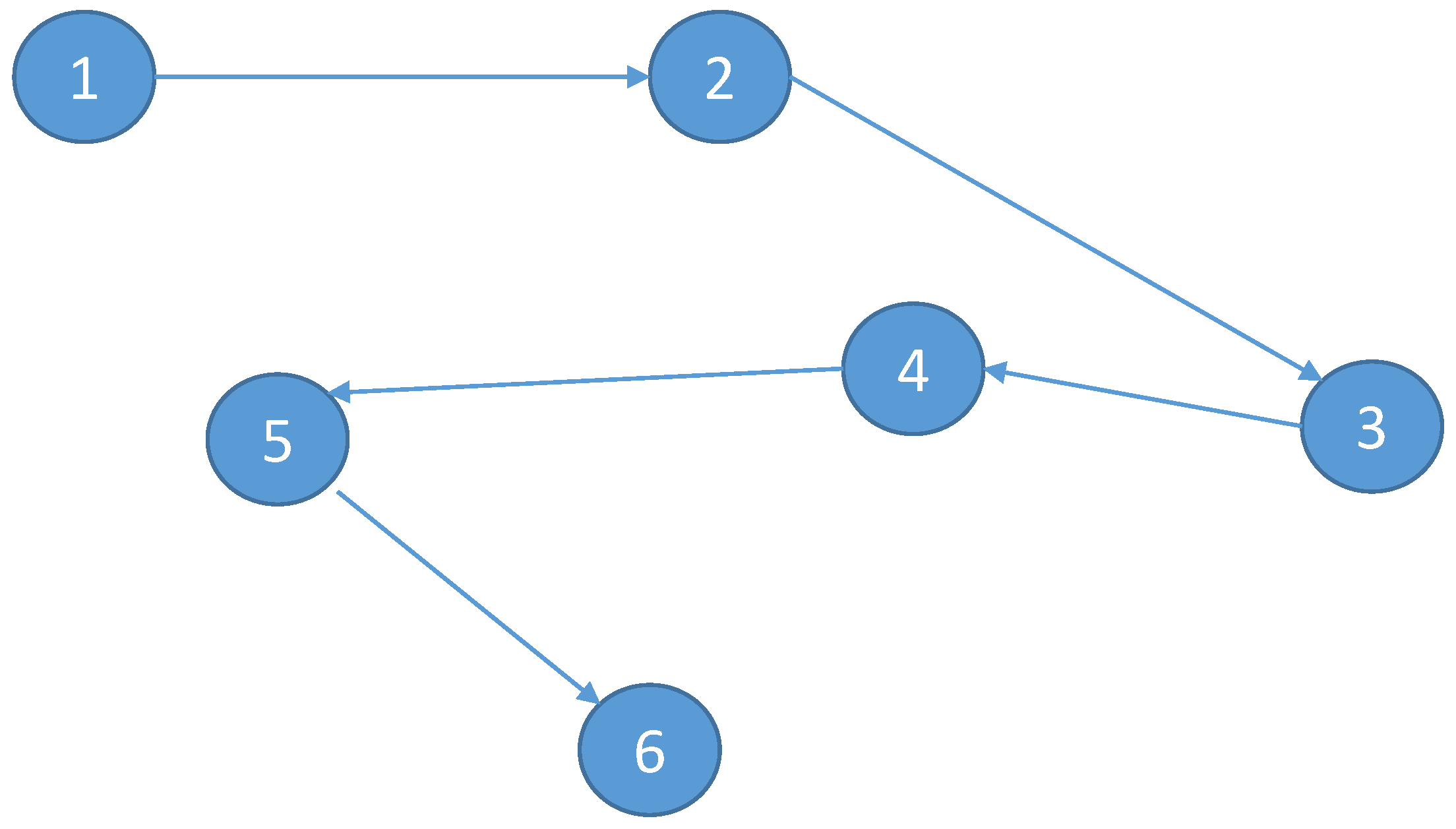
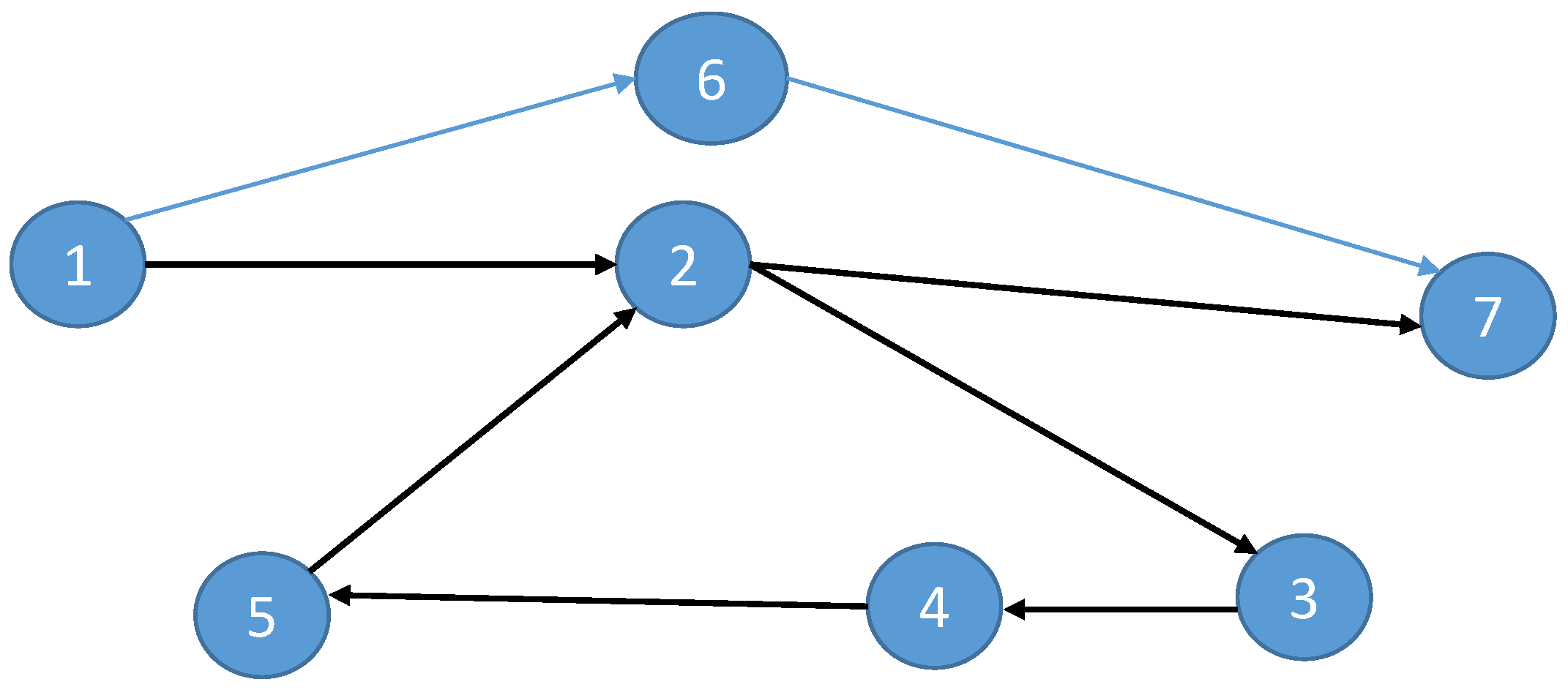
Definition 6.

[31] A subgraph is a graph which consists of a subset of a graph’s edges and associated vertices.

Definition 7.

[31] Let x and y be two vertices in a graph G. A path in G from x to y of length n ($n\in \mathbb{N}\cup \left\{0\right\}$) is a sequence ${\left(x_i\right)}_{i=0}^n$ of $n+1$ distinct vertices such that $x_0=x$, $x_n=y$ and $(x_i,x_{i+1})\in E\left(G\right)$ for $i=1,2,\dots ,n$.

Definition 8.

[31] A graph G is said to be connected if there is a path between any two vertices of G and it is weakly connected if $\tilde{G}$ is connected.

Definition 9.

[31] A path is called elementary if no vertices appear more than once in it. For more details see Figure 1 and Figure 2.

Figure 1. Elementary path.

Figure 2. Non Elementary path.

Let $(X,d)$ be a rectangular metric space. The graph G may be converted to a weighted graph by assigning to each edge the distance given by the rectangular metric between its vertices. In order to later apply the rectangular inequality to the vertices of the graph, we need to consider a graph of length bigger than 2, which means that between two vertices, we can find a path through at least two other vertices.

3. Main Results

First, let $(X,d)$ be a rectangular metric space and G be a directed graph without parallel edges such that $V\left(G\right)=X$.

Definition 10.

Let A and B be two nonempty subsets of $(X,d)$. A mapping $f:A⟶B$ is said to be a G- contraction mapping if for all $x,y\in A$, $x\ne y$ with $(x,y)\in E\left(G\right)$:

(i) 

$d(fx,fy)\le \alpha d(x,y)$, for some $\alpha \in [0,1)$,

(ii) 

$\left.\begin{array}{cc}d(x_1,fx)\hfill & =d(A,B)\hfill \\ d(y_1,fy)\hfill & =d(A,B)\hfill \end{array}\right\}⟹(x_1,y_1)\in E\left(G\right),\forall x_1,y_1\in A.$

Our first main result is as follows:

Theorem 1.

Let $(X,d)$ be a complete rectangular metric space, A and B be two nonempty closed subsets of $(X,d)$ such that $(A,B)$ has the P-property. Let $f:A⟶B$ be a continuous G-contractive mapping such that $f\left(A_0\right)\subseteq B_0$ and $A_0\ne \varnothing$. Assume that d is continuous and the following condition $\left(C_1\right)$ holds: there exist $x_0$ and $x_1$ in $A_0$ such that there is an elementary path in $A_0$ between them and $d(x_1,f{x}_0)=d(A,B)$.

Then, there exists a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ with $d(x_{n+1},f{x}_n)=d(A,B)$ for $n\in \mathbb{N}$. Moreover, if there exists a path ${\left(y^i\right)}_{i=0}^s\subseteq A_0$ in G between any two elements x and y, then f has a unique best proximity point.

Proof. 

From the condition $\left(C_1\right)$, there exist two points $x_0$ and $x_1$ in $A_0$ such that $d(x_1,f{x}_0)=d(A,B)$ and a path ${\left(t_0^i\right)}_{i=0}^N$ in G between them such that the sequence ${\left\{t_0^i\right\}}_{i=0}^N$ containing points of $A_0$. Consequently, $t_0^0=x_0$, $t_0^N=x_1$ and $(t_0^i,t_0^{i+1})\in E\left(G\right)$ $\forall 0\le i\le N$.

Given that $t_0^1\in A_0$, $f\left(A_0\right)\subseteq B_0$ and from the definition of $A_0$, there exists $t_1^1\in A_0$ such that $d(t_1^1,f{t}_0^1)=d(A,B)$. Similarly, for $i=2,\dots ,N$, there exists $t_1^i\in A_0$ such that $d(t_1^i,f{t}_0^i)=d(A,B)$.

As ${\left(t_0^i\right)}_{i=0}^N$ is a path in G then $(t_0^0,t_0^1)=(x_0,t_0^1)\in E\left(G\right)$. From the above, we have $d(x_1,f{x}_0)=d(A,B)$ and $d(t_1^1,f{t}_0^1)=d(A,B)$. Therefore, as f is a G-contraction, it follows that $(x_1,t_1^1)\in E\left(G\right)$. In a similar manner, it follows that

$$(t_1^{i-1},t_1^i)\in E\left(G\right)\mathrm{for}i=2,\dots ,N.$$

(5)

Let $x_2=t_1^N$. Then, ${\left(t_1^i\right)}_{i=0}^N$ is a path from $x_1=t_1^0$ to $x_2=t_1^N$. For each $i=2,\dots ,N$, as $t_1^i\in A_0$ and $f{t}_1^i\in f\left(A_0\right)\subseteq B_0$, then by the definition of $B_0$, there exists $t_2^i\in A_0$ such that $d(t_2^i,f{t}_1^i)=d(A,B)$. In addition, we have $d(x_2,f{x}_1)=d(A,B)$. As above mentioned, we obtain

$$(x_2,t_2^1)\in E\left(G\right)\mathrm{and}(t_2^{i-1},t_2^i)\in E\left(G\right)\forall i=1,2,\dots ,N.$$

(6)

Let $x_3=t_2^N$. Then, ${\left(t_2^i\right)}_{i=0}^N$ is a path from $t_2^0=x_2$ and $t_2^N=x_3$.

Continuing in this process, for all $n\in \mathbb{N}$, we generate a path ${\left(t_n^i\right)}_{i=0}^N$ from $x_n=t_n^0$ and $x_{n+1}=t_n^N$. As a consequence, we build a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ where $x_{n+1}\in {\left[x_n\right]}_G^N$ and $d(x_{n+1},f{x}_n)=d(A,B)$ such that

$$d(t_{n+1}^i,f{t}_n^i)=d(A,B)\forall i=0,\dots ,N.$$

(7)

From the P-property of $(A,B)$ and (7), it follows for each $n\in \mathbb{N}$,

$$d(t_n^{i-1},t_n^i)=d(f{t}_{n-1}^{i-1},f{t}_{n-1}^i)\forall i=1,\dots ,N.$$

(8)

Next, we claim that $d(x_n,x_{n+1})\le {\alpha }^{n}C$, where C is a constant. To prove the claim, we need to consider the following two cases where ${\left(t_n^i\right)}_{i=0,\dots ,N}$ is a path from $x_n$ to $x_{n+1}$.

Note that for all $i=0,\dots ,N$, ${\left(t_n^i\right)}_{i=0,\dots ,N}$ are different owing to the fact that the considered path $\left(t_n^i\right)$ is elementary. Then, we can apply the triangular inequality $\left(r_3\right)$.

Case 1:$N=2k+1$ (N is odd).

For any positive integer n, we get

$$\begin{array}{ccc}\hfill d(x_n,x_{n+1})& =& d(t_n^0,t_n^N)=d(t_n^0,t_n^{2k+1})\hfill \\ & \le & d(t_n^0,t_n^1)+d(t_n^1,t_n^2)+d(t_n^2,t_n^{2k+1})\hfill \\ & \le & d(t_n^0,t_n^1)+d(t_n^1,t_n^2)+\dots +d(t_n^{2k},t_n^{2k+1})\hfill \\ & \le & {\displaystyle \sum _{i=1}^{2k+1}d(t_n^{i-1},t_n^i)}\hfill \\ & =& {\displaystyle \sum _{i=1}^{N}d(f{t}_{n-1}^{i-1},f{t}_{n-1}^i).}\hfill \end{array}$$

(9)

Knowing that $(t_{n-1}^{i-1},t_{n-1}^i)\in E\left(G\right)$ for all $n\in \mathbb{N},$ and f is a G-contraction, we obtain from (9)

$${\displaystyle d(x_n,x_{n+1})\le \alpha \sum _{i=1}^{N}d(t_{n-1}^{i-1},t_{n-1}^i)\forall n\in \mathbb{N}.}$$

(10)

By induction, it follows that for all $n\in \mathbb{N}$

$${\displaystyle d(x_n,x_{n+1})\le {\alpha }^n\sum _{i=1}^{N}d(t_0^{i-1},t_0^i)=C{\alpha }^n}$$

(11)

where ${\displaystyle C=\sum _{i=1}^{N}d(t_0^{i-1},t_0^i)}$.

Case 2:$N=2k$ (N is even).

$$\begin{array}{ccc}\hfill d(x_n,x_{n+1})& =& d(t_n^0,t_n^N)=d(t_n^0,t_n^{2k})\hfill \\ & \le & d(t_n^0,t_n^1)+d(t_n^1,t_n^2)+d(t_n^2,t_n^{2k})\hfill \\ & \le & d(t_n^0,t_n^1)+d(t_n^1,t_n^2)+\dots +d(t_n^{2k-3},t_n^{2k-2})+d(t_n^{2k-2},t_n^{2k})\hfill \\ & =& {\displaystyle \sum _{i=1}^{2k}d(t_n^{i-1},t_n^i)-d(t_n^{2k-2},t_n^{2k-1})-d(t_n^{2k-1},t_n^{2k})+d(t_n^{2k-2},t_n^{2k})}\hfill \\ & \le & {\displaystyle \sum _{i=1}^{2k}d(t_n^{i-1},t_n^i)+d(t_n^{2k-2},t_n^{2k})}\hfill \\ & \le & {\displaystyle \sum _{i=1}^{2k}d(f{t}_{n-1}^{i-1},f{t}_{n-1}^i)+d(t_n^{2k-2},t_n^{2k}).}\hfill \end{array}$$

By the same arguments used in Case 1, we deduce that ${\displaystyle \sum _{i=1}^{2k}d(f{t}_{n-1}^{i-1},f{t}_{n-1}^i)\le {\alpha }^n\sum _{i=1}^{N}d(t_0^{i-1},t_0^i)}$. On the other hand, $d(t_n^{2k-2},t_n^{2k})\le {\alpha }^{n}d(t_0^{2k-2},t_0^{2k})$. Indeed, from (7), we have $d(t_n^{2k-2},f{t}_{n-1}^{2k-2})=d(A,B)$ and $d(t_n^{2k},f{t}_{n-1}^{2k})=d(A,B)$ and using the P-property, we get

$$\begin{array}{ccc}\hfill d(t_n^{2k-2},t_n^{2k})& =& d(f{t}_{n-1}^{2k-2},f{t}_{n-1}^{2k})\hfill \\ & \le & \alpha d(t_{n-1}^{2k-2},t_{n-1}^{2k})\hfill \\ & \le & {\alpha }^{n}d(t_0^{2k-2},t_0^{2k}).\hfill \end{array}$$

(12)

Then, we conclude that $d(x_n,x_{n+1})\le {\alpha }^{n}C$ where ${\displaystyle C=\sum _{i=1}^{N}d(t_0^{i-1},t_0^i)+d(t_0^{2k-2},t_0^{2k})}$.

Let us prove that $\left\{x_n\right\}$ is a Cauchy sequence. Let $n,m\in \mathbb{N}$ such that $m\ge n$. We suppose w.l.o.g that m is odd ($m=2k+1$) since the case $m=2k$ is similar. Note that $x_n=t_0^n$, $x_{n+1}=t_n^N$ and $t_0^n\ne t_n^N$ for all n since the path ${\left(t_n^i\right)}_{i=0,\dots ,N}$ is elementary. Then, using the triangular inequality of the rectangular metric, we obtain

$$\begin{array}{ccc}\hfill d(x_n,x_m)& \le & d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\dots +d(x_{m-1},x_m)\hfill \\ & \le & d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\dots +d(x_{m-1},x_m)\hfill \\ & \le & C{\alpha }^n+C{\alpha }^{n+1}+\dots +C{\alpha }^{m-1}\hfill \\ & =& C{\alpha }^n(1+\alpha +\dots +{\alpha }^{m-n-1})\hfill \\ & \le & {\displaystyle C\frac{{\alpha }^n}{1-\alpha }.}\hfill \end{array}$$

As $\alpha <1$, then ${\displaystyle \underset{n,m⟶\infty }{lim}d(x_n,x_m)=0}$. Therefore, ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ is a Cauchy sequence and there exists $u\in A$ such that $x_n⟶u$ as $n⟶\infty$.

Using the continuity of f, we get $f{x}_n⟶fu$ as $n⟶\infty$. Now, using the continuity of the rectangular metric function, we obtain $d(x_{n+1},f{x}_n)$ converges to $d(u,fu)$ as $n⟶\infty$.

Since $d(x_{n+1},f{x}_n)=d(A,B)$, the sequence ${\left\{d(x_{n+1},f{x}_n)\right\}}_n$ is constant. Consequently, $d(u,fu)=d(A,B)$. Then, u is a best proximity point of f.

In order to prove the uniqueness of the best proximity point u, we assume that there exist u and $u^{\prime }$ such that

$$\begin{array}{ccc}\hfill d(u,fu)& =& d(A,B)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill d(u^{\prime },f{u}^{\prime })& =& d(A,B).\hfill \end{array}$$

(14)

Knowing that the pair $(A,B)$ has the P-property, from (13) and (14), we get $d(u,u^{\prime })=d(fu,f{u}^{\prime })$. Since f is a G-contraction, we obtain $d(u,u^{\prime })=d(fu,f{u}^{\prime })\le \alpha d(u,u^{\prime })$, which holds unless

$$d(u,u^{\prime })=0,\mathrm{then}u=u^{\prime }.$$

 □

Definition 11.

Let $f:A⟶B$ be a mapping. Define $X_f\left(G_{A_0}\right)$ as

$$X_f\left(G_{A_0}\right):=\{x\in A_0:\exists y\in A_{0}forwhichd(y,fx)=dist(A,B)and(x,y)\in E\left(G\right)\}.$$

(15)

Definition 12.

Let A and B be two non-empty subsets of $(X,d)$. A mapping $f:A⟶B$ is said to be a G-weakly contractive mapping if for all $x,y\in A$, $x\ne y$ with $(x,y)\in E\left(G\right)$:

(i) 

$d(fx,fy)\le d(x,y)-\psi \left(d\right(x,y\left)\right)$, where $\psi :[0,\infty )⟶[0,\infty )$ is a continuous and nondecreasing function such that ψ is positive on $(0,\infty )$, $\psi \left(0\right)=0$ and ${\displaystyle \underset{t\to \infty }{lim}\psi \left(t\right)=\infty }$. If A is bounded, then the infinity condition can be omitted.

(ii) 

$\left.\begin{array}{cc}d(x_1,fx)\hfill & =d(A,B)\hfill \\ d(y_1,fy)\hfill & =d(A,B)\hfill \end{array}\right\}⟹(x_1,y_1)\in E\left(G\right),\forall x_1,y_1\in A.$

Our second main result is as follows:

Theorem 2.

Let $(X,d)$ be a complete rectangular metric space endowed with a directed graph, A and B be two nonempty closed subsets of $(X,d)$ such that $(A,B)$ has the P-property. Let $f:A⟶B$ be a continuous G-weakly contractive mapping such that $f\left(A_0\right)\subseteq B_0$. Assume that d is continuous and $A_0$ is a closed nonempty set. Then, there exists a sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ in $A_0$ such that $d(x_{n+1},f{x}_n)=d(A,B)$ for $n\in \mathbb{N}$. Moreover, f has a unique best proximity point.

Proof. 

It follows from the definition of $A_0$ and $B_0$ that for every $x\in A_0$, there exists $y\in B_0$ such that $d(x,y)=dist(A,B)$. Conversely, for every $y^{\prime }\in B_0$ there exists $x^{\prime }\in A_0$ such that $d(x^{\prime },y^{\prime })=dist(A,B)$. Since $f\left(A_0\right)\subset B_0$, for every $x\in A_0$ there exists $y\in A_0$ such that $d(y,fx)=dist(A,B)$.

Let $x_0\in X_f\left(G_{A_0}\right)$, then there exists $x_1\in A_0$ such that $(x_0,x_1)\in E\left(G\right)$ and $d(x_1,f{x}_0)=dist(A,B)$. On the other hand, since $x_1\in A_0$ and $f\left(A_0\right)\subset B_0$, there exists $x_2\in A_0$ such that $d(x_2,f{x}_1)=dist(A,B)$ and because f is a G-weakly contractive mapping, we get $(x_1,x_2)\in E\left(G\right)$. We repeat this process in a similar way, we build a sequence $\left\{x_n\right\}$ in $A_0$ such that

$$\begin{array}{ccc}\hfill (x_n,x_{n+1})& \in & E\left(G\right)\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill d(x_{n+1},f{x}_n)& =& dist(A,B)\forall n\in \mathbb{N}.\hfill \end{array}$$

(17)

Since the pair $(A,B)$ has the P-property, we conclude that $d(x_n,x_{n+1})=d(f{x}_{n-1},f{x}_n)$ for all $n\in \mathbb{N}$. Then, for any positive integer n

$$\begin{array}{ccc}\hfill d(x_n,x_{n+1})& =& d(f{x}_{n-1},f{x}_n)\hfill \\ & \le & d(x_{n-1},x_n)-\psi \left(d(x_{n-1},x_n)\right)\hfill \\ & \le & d(x_{n-1},x_n).\hfill \end{array}$$

(18)

If we denote by $v_n=d(x_n,x_{n+1})$, from (18), $\left\{v_n\right\}$ is a nonnegative decreasing sequence. Hence, $\left\{v_n\right\}$ converges to some real number $v\ge 0$. Suppose that $v>0$. As $\psi$ is increasing, for any positive integer n, we have

$$\begin{array}{ccc}\hfill v_n=d(x_n,x_{n+1})& \le & d(x_{n-1},x_n)-\psi \left(d(x_{n-1},x_n)\right)\hfill \\ & =& v_{n-1}-\psi \left(v_{n-1}\right)\hfill \\ & \le & v_{n-1}-\psi \left(v\right).\hfill \end{array}$$

At the limit, $v\le v-\psi \left(v\right)<v$, which is a contradiction, so $v=0$, that is,

$$d(x_n,x_{n+1})⟶0\mathrm{as}n⟶\infty .$$

(19)

Similarly, we find that

$$d(x_n,x_{n+2})⟶0\mathrm{as}n⟶\infty .$$

(20)

Now, let us prove that $\left\{x_n\right\}$ is a Cauchy sequence.

For any $ϵ>0$, choose N such that

$$\begin{array}{ccc}\hfill d(x_N,x_{N+1})& <& min\{{\displaystyle \frac{ϵ}{8}},\psi ({\displaystyle \frac{ϵ}{8}})\}\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill d(x_N,x_{N+2})& <& min\{{\displaystyle \frac{ϵ}{8}},\psi ({\displaystyle \frac{ϵ}{8}})\}.\hfill \end{array}$$

(22)

Let $B[x_N,ϵ]:=\{x\in X:d(x_N,x)<ϵ\}$ be a closed ball with center $x_N$ and radius $ϵ$. We claim that $f\left(B[x_N,ϵ]\right)\subseteq B[f{x}_{N-1},ϵ]$.

Using the P-property, we obtain

$\left.\begin{array}{cc}d(x_N,f{x}_{N-1})\hfill & =dist(A,B)\hfill \\ d(x_{N+1},f{x}_N)\hfill & =dist(A,B)\hfill \end{array}\right\}⟹$

$$d(x_N,x_{N+1})=d(f{x}_{N-1},f{x}_N).$$

(23)

Consider $x\in B[x_N,ϵ]$, i.e., $d(x_N,x)\le ϵ$. We distinguish two cases $d(x_N,x)\le {\displaystyle \frac{ϵ}{2}}$ and $d(x_N,x)>{\displaystyle \frac{ϵ}{2}}$.

Case 1:$d(x_N,x)\le {\displaystyle \frac{ϵ}{2}}$.

Using the rectangular inequality, we distinguish the following two subcases:

• If $f{x}_{N-1}=f{x}_{N+1}$, $f{x}_{N+2}=fx$ and $f{x}_{N+1}\ne f{x}_{N+2}$, we have

$$\begin{array}{ccc}\hfill d(f{x}_{N-1},fx)& =& d(f{x}_{N+1},f{x}_{N+2})\hfill \\ & \le & d(x_{N+1},x_{N+2})-\psi \left(d(x_{N+1},x_{N+2})\right)\hfill \\ & \le & d(x_{N+1},x_{N+2})\hfill \\ & =& d(f{x}_N,f{x}_{N+1})\hfill \\ & \le & d(x_N,x_{N+1})\hfill \\ & \le & {\displaystyle \frac{ϵ}{8}}.\hfill \end{array}$$

In the case where $f{x}_{N+1}=f{x}_{N+2}$, we obtain $d(f{x}_{N-1},fx)=0$.

• If $f{x}_{N-1}\ne f{x}_{N+1}$, $f{x}_{N+2}\ne fx$ and $f{x}_{N+1}\ne f{x}_{N+2}$, we have

$$\begin{array}{ccc}\hfill d(f{x}_{N-1},fx)& \le & d(f{x}_{N-1},f{x}_{N+1})+d(f{x}_{N+1},f{x}_{N+2})+d(f{x}_{N+2},fx)\hfill \\ & =& d(x_N,x_{N+2})+d(f{x}_{N+1},f{x}_{N+2})+d(f{x}_{N+2},fx)\hfill \\ & \le & d(x_N,x_{N+2})+d(x_{N+1},x_{N+2})-\psi \left(d(x_{N+1},x_{N+2})\right)+d(x_{N+2},x)-\psi \left(d(x_{N+2},x)\right)\hfill \\ & \le & d(x_N,x_{N+2})+d(x_{N+1},x_{N+2})+d(x_{N+2},x)\hfill \\ & \le & d(x_N,x_{N+2})+d(x_{N+1},x_{N+2})+d(x_{N+2},x_{N+1})+d(x_{N+1},x_N)+d(x_N,x)\hfill \\ & \le & d(x_N,x_{N+2})+2d(x_{N+1},x_{N+2})+d(x_{N+1},x_N)+d(x_N,x)\hfill \\ & \le & d(x_N,x_{N+2})+2d(x_N,x_{N+1})-2\psi \left(d(x_N,x_{N+1})\right)+d(x_{N+1},x_N)+d(x_N,x)\hfill \\ & \le & d(x_N,x_{N+2})+3d(x_N,x_{N+1})+d(x_N,x)\hfill \\ & \le & {\displaystyle \frac{ϵ}{8}}+3\times {\displaystyle \frac{ϵ}{8}}+{\displaystyle \frac{ϵ}{2}}=ϵ\hfill \end{array}$$

which implies that $fx\in B[f{x}_{N-1},ϵ]$.

Case 2:${\displaystyle \frac{ϵ}{2}}<d(x_N,x)\le ϵ$.

• If $f{x}_{N-1}=f{x}_{N+1}$, $f{x}_N=fx$ and $f{x}_{N+1}=f{x}_N$, we get

$$\begin{array}{ccc}\hfill d(f{x}_{N-1},fx)& \le & d(f{x}_{N+1},f{x}_N)\hfill \\ & \le & d(x_{N+1},x_N)-\psi \left(d(x_{N+1},x_N)\right)\hfill \\ & \le & d(x_{N+1},x_N)\hfill \\ & \le & {\displaystyle \frac{ϵ}{8}}.\hfill \end{array}$$

• If $f{x}_{N-1}\ne f{x}_{N+1}$, $f{x}_N\ne fx$ and $f{x}_{N+1}\ne f{x}_N$, we have

$$\begin{array}{ccc}\hfill d(f{x}_{N-1},fx)& \le & d(f{x}_{N-1},f{x}_{N+1})+d(f{x}_{N+1},f{x}_N)+d(f{x}_N,fx)\hfill \\ & \le & d(x_N,x_{N+2})+d(x_{N+1},x_N)-\psi \left(d(x_{N+1},x_N)\right)+d(x_N,x)-\psi \left(d(x_N,x)\right)\hfill \\ & \le & d(x_N,x_{N+2})+d(x_{N+1},x_N)+d(x_N,x)-\psi \left(d(x_N,x)\right)\hfill \\ & \le & {\displaystyle \frac{ϵ}{8}}+{\displaystyle \frac{ϵ}{8}}+ϵ-\psi \left({\displaystyle \frac{ϵ}{2}}\right)\hfill \\ & =& {\displaystyle \frac{ϵ}{4}}+ϵ-\psi \left({\displaystyle \frac{ϵ}{2}}\right)\hfill \\ & \le & {\displaystyle \frac{ϵ}{2}}+ϵ-\psi \left({\displaystyle \frac{ϵ}{2}}\right)\hfill \\ & \le & \psi \left({\displaystyle \frac{ϵ}{2}}\right)+ϵ-\psi \left({\displaystyle \frac{ϵ}{2}}\right)=ϵ.\left(\mathrm{since}\psi \mathrm{is}\mathrm{increasing}\right).\hfill \end{array}$$

Then, $d(f{x}_{N-1},fx)\le ϵ$, which gives that $fx\in B[f{x}_{N-1},ϵ]$. Thus, we obtain that

$$f\left(B[x_N,ϵ]\right)\subseteq B[f{x}_{N-1},ϵ].$$

(24)

Claim: If $y\in B[f{x}_{N-1},ϵ]$ with $d(x,y)=dist(A,B)$ for some $x\in A_0$, then $x\in B[x_N,ϵ]$.

Let $y\in B[f{x}_{N-1},ϵ]$. Then,

$$d(f{x}_{N-1},y)\le ϵ.$$

(25)

Assume that there exists $x\in A_0$ such that $d(x,y)=dist(A,B)$. From (17), we get $d(x_N,f{x}_{N-1})=dist(A,B)$ which gives us using the P-property,

$$d(x,x_N)=d(y,f{x}_{N-1}).$$

(26)

From (25) and (26), we obtain that $d(x,x_N)\le ϵ$, i.e., $x\in B[x_N,ϵ]$ and the claim is proved.

From (21) and (23), we have $x_{N+1}\in B[x_N,ϵ]$. Then, using (24), we get $f{x}_{N+1}\in B[f{x}_{N-1},ϵ]$, i.e.,

$$d(f{x}_{N+1},f{x}_{N-1})\le ϵ.$$

(27)

Since $d(x_{N+2},f{x}_{N+1})=dist(A,B)$, by the precedent claim $d(x_{N+2},f{x}_N)\le ϵ$. Again, from (24), $d(x_{N+2},f{x}_{N-1})\le ϵ$ and from the claim $d(x_{N+3},f{x}_N)\le ϵ$. In this way, we obtain

$$d(x_{N+m},x_N)\le ϵ\forall m\in \mathbb{N}.$$

(28)

Thus, the sequence $\left\{x_n\right\}$ is Cauchy. Since A is a closed subset of the complete rectangular metric space, there exists $x^{\ast }\in A$ such that

$${\displaystyle \underset{n\to \infty }{lim}{x}_N=x^{\ast }.}$$

(29)

From the continuity of f, we obtain

$${\displaystyle \underset{n\to \infty }{lim}f{x}_N=f{x}^{\ast }.}$$

(30)

Then, using the continuity of the rectangular metric, we obtain

$$d(x_{N+1},f{x}_N)⟶d(x^{\ast },f{x}^{\ast })asN⟶\infty .$$

(31)

From (17), $d(x_{N+1},x_N)=dist(A,B)$, we conclude that ${\left\{d(x_{N+1},x_N)\right\}}_N$ is a constant sequence equal to $dist(A,B)$. Therefore, from (31), $d(x^{\ast },f{x}^{\ast })=dist(A,B)$. Thereby, $x^{\ast }$ is a best proximity point of f.

Let us prove the uniqueness of the best proximity point. Consider $x_1,x_2$ two different best proximity points. Then, $d(x_1,f{x}_1)=d(x_2,f{x}_2)=dist(A,B)$. From the P-property, we obtain $d(x_1,x_2)=d(f{x}_1,f{x}_2)$. Using that f is weakly G-contractive, we get

$$0<d(x_1,x_2)=d(f{x}_1,f{x}_2)\le d(x_1,x_2)-\psi \left(d(x_1,x_2)\right)<d(x_1,x_2),$$

(32)

which is a contradiction. Therefore, $x_1=x_2$.  □

Definition 13.

Let $(X,d)$ be a rectangular metric space and G be a directed graph. Let $A,B$ be two nonempty subsets of X. A non-self mapping $T:A⟶B$ is said to be

• a G- proximal Kannan mapping if for $x,y,u,v\in A$, there exists $b\in [0,\frac{1}{2})$ such that
  $\left.\begin{array}{cc}(x,y)\hfill & \in E\left(G\right)\hfill \\ d(u,Tx)\hfill & =d(A,B)\hfill \\ d(v,Ty)\hfill & =d(A,B)\hfill \end{array}\right\}⟹d(u,v)\le b[d(x,v)+d(y,u)].$
• proximally G-edge preserving if for each $x,y,u,v\in A$
  $\left.\begin{array}{cc}(x,y)\hfill & \in E\left(G\right)\hfill \\ d(u,Tx)\hfill & =d(A,B)\hfill \\ d(v,Ty)\hfill & =d(A,B)\hfill \end{array}\right\}⟹(u,v)\in E\left(G\right)$.

Our third main result is as follows:

Theorem 3.

Let $(X,d)$ be a rectangular metric space and G a directed graph. Let $A,B$ be two nonempty closed subsets of X. Assume that $A_0$ is nonempty and d is continuous. Let $T:A⟶B$ be a continuous non-self mapping satisfying the following properties:

• T is proximal G-edge preserving and a G-proximal Kannan mapping such that $T\left(A_0\right)\subseteq B_0$.
• There exist $x_0,x_1\in A_0$ such that

  $$d(x_1,T{x}_0)=d(A,B)and(x_0,x_1)\in E\left(G\right).$$

  (33)

  Then, T has a best proximity point $x^{\ast }$ in A. Furthermore, the sequence $\left\{x_n\right\}$ defined by $d(x_n,T{x}_{n-1})=d(A,B)$ for all $n\in \mathbb{N}$ converges to $x^{\ast }$. Moreover, if there exists a path in G between any two points of A, then the best proximity point is unique.

Proof. 

From (33), there exist $x_0,x_1\in A_0$ such that

$$d(x_1,T{x}_0)=d(A,B)\mathrm{and}(x_0,x_1)\in E\left(G\right).$$

(34)

Since $T\left(A_0\right)\subseteq B_0$, we have $T{x}_1\in B_0$ and there exists $x_2\in A_0$ such that

$$d(x_2,T{x}_1)=d(A,B).$$

(35)

Using the proximally G-edge preserving of T, (34) and (35), we get $(x_1,x_2)\in E\left(G\right)$. By continuing this process, we obtain the sequence $\left\{x_n\right\}$ in $A_0$ such that

$$d(x_n,T{x}_{n-1})=d(A,B)$$

(36)

$$\mathrm{with}(x_n,T{x}_{n-1})\in E\left(G\right)\forall n\in \mathbb{N}.$$

(37)

Now, let us prove that $\left\{x_n\right\}$ is a Cauchy sequence in A. Note that if there exists $n_0\in \mathbb{N}$ such that $x_{n_0}=x_{n_0+1}$, from (36), we get that $x_{n_0}$ is a best proximity point of T. Therefore, we may assume that $x_{n-1}\ne x_n$ for all $n\in \mathbb{N}$.

Since T is a G-proximal Kannan mapping for each $n\in \mathbb{N}$, we obtain $(x_{n-1},x_n)\in E\left(G\right)$, $d(x_n,T{x}_{n-1})=d(A,B)$ and $d(x_{n+1},T{x}_n)=d(A,B)$ which imply that

$$d(x_n,x_{n+1})\le b[d(x_{n-1},x_{n+1})+d(x_n,x_n)]\le bd(x_{n-1},x_{n+1}).$$

By induction, we obtain

$$d(x_n,x_{n+1})\le b^{n}d(x_0,x_2)=b^{n}C\forall n\in \mathbb{N}.$$

(38)

As $b<{\displaystyle \frac{1}{2}}$, then $d(x_n,x_{n+1})⟶0$ as $n⟶\infty$. Let $p\ge 1$.

Case 1:

$$\begin{array}{ccc}\hfill d(x_n,x_{n+(2p+1)})& =& d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\dots +d(x_{n+2p},x_{n+2p+1})\hfill \\ & \le & b^{n}C+b^{n+1}C+\dots +b^{n+2p}C\hfill \\ & =& (b^n+b^{n+1}+\dots +b^{n+2p})C⟶0\mathrm{as}n,p⟶\infty .\hfill \end{array}$$

(39)

Case 2:

$$\begin{array}{ccc}\hfill d(x_n,x_{n+\left(2p\right)})& =& d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\dots +d(x_{n+2p-2},x_{n+2p})\hfill \\ & \le & d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\dots +d(x_{n+2p-2},x_{n+2p-1})+d(x_{n+2p-1},x_{n+2p})\hfill \\ & +& d(x_{n+2p-2},x_{n+2p})\hfill \\ & \le & {\displaystyle \sum _{k=n}^{n+2p-1}C{b}^k+d(x_{n+2p-2},x_{n+2p}).}\hfill \end{array}$$

(40)

Knowing that ${\displaystyle \sum _{k=n}^{n+2p-1}C{b}^k⟶0}$ as $n,p⟶\infty$, we shall prove that $d(x_{n+2p-2},x_{n+2p})⟶0$ as $n,p⟶\infty$. From (36), we can conclude that

$$\begin{array}{ccc}\hfill d(x_{n+2p-2},T{x}_{n+2p-1})& =& d(A,B)\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill d(x_{n+2p},T{x}_{n+2p+1})& =& d(A,B).\hfill \end{array}$$

(42)

On the other hand, from (37) we get $(x_{n+2p-1},x_{n+2p})\in E\left(G\right)$ and $(x_{n+2p},x_{n+2p+1})\in E\left(G\right)$. Then, since G is a connected graph, there exists a path between $x_{n+2p-1}$ and $x_{n+2p+1}$ in G. Therefore,

$$(x_{n+2p-1},x_{n+2p+1})\in E\left(G\right).$$

(43)

Knowing that T is a G-proximal Kannan mapping and from (41)–(43), we obtain

$$\begin{array}{ccc}\hfill d(x_{n+2p-2},x_{n+2p})& \le & b[d(x_{n+2p-1},x_{n+2p})+d(x_{n+2p+1},x_{n+2p-2})]\hfill \\ & \le & b[d(x_{n+2p-1},x_{n+2p})+d(x_{n+2p-2},x_{n+2p-1})+d(x_{n+2p-1},x_{n+2p})+d(x_{n+2p},x_{n+2p+1})]\hfill \\ & =& b[2d(x_{n+2p-1},x_{n+2p})+d(x_{n+2p-2},x_{n+2p-1})+d(x_{n+2p},x_{n+2p+1})]\hfill \\ & \le & b[2C{b}^{n+2p-1}+C{b}^{n+2p-2}+C{b}^{n+2p}]⟶0\mathrm{as}n,p\to \infty .\hfill \end{array}$$

(44)

Therefore, from (40), we conclude that $d(x_n,x_{n+2p})⟶0$ as $n,p⟶\infty$. It follows that $\left\{x_n\right\}$ is a Cauchy sequence in A. Since A is closed, there exists $x^{\ast }\in A$ such that $x_n⟶x^{\ast }$ as $n⟶\infty$. By the continuity of T, we obtain $T{x}_n⟶T{x}^{\ast }$ as $n⟶\infty$. Since d is assumed to be continuous, we get $d(x_{n+1},T{x}_n)⟶d(x^{\ast },T{x}^{\ast })$ as $n⟶\infty$. By (36), we conclude that

$$d(x^{\ast },T{x}^{\ast })=d(A,B).$$

Thus, $x^{\ast }$ is a best proximity point of T and the sequence $\left\{x_n\right\}$ defined by $d(x_{n+1},T{x}_n)=d(A,B)$ converges to $x^{\ast }$ for all $n\in \mathbb{N}$.

Let us prove the uniqueness of the best proximity point $x^{\ast }$. Suppose that $x_1^{\ast }$ and $x_2^{\ast }$ are two best proximity points. Then, we obtain $d(x_1^{\ast },T{x}_1^{\ast })=d(A,B)$, $d(x_2^{\ast },T{x}_2^{\ast })=d(A,B)$ and $(x_1^{\ast },x_2^{\ast })\in E\left(G\right)$, which gives $d(x_1^{\ast },x_2^{\ast })\le b[d(x_1^{\ast },x_2^{\ast })+d(x_1^{\ast },x_2^{\ast })]=2bd(x_1^{\ast },x_2^{\ast })$. Therefore, we get $(1-2b)d(x_1^{\ast },x_2^{\ast })\le 0$, which implies that $1-2b\le 0$$⟹b\ge {\displaystyle \frac{1}{2}}$. It is a contradiction with respect to $b<{\displaystyle \frac{1}{2}}$. Then, $d(x_1^{\ast },x_2^{\ast })=0$, that is, $x_1^{\ast }=x_2^{\ast }$ and so the uniqueness of the best proximity point follows. □

4. Conclusions and Perspectives

In Theorems 1–3, we assumed that the rectangular metric space is continuous, which is a strong hypothesis and does not hold in general. To our knowledge, our work is the first attempt to prove best proximity point results not only in the setting of rectangular metric spaces, but with the addition of a graph theory structure. Finally, an open question, how does one prove the above three theorems when omitting the continuity of the rectangular metric?