All topological spaces considered in this paper are assumed to be Tychonoff and all topological groups are assumed to be Hausdorff (and thus Tychonoff as well).
As usual, denotes the set of natural numbers, and denotes the first infinite cardinal. We freely identify with . The symbol denotes the Stone-Čech compactification of . Recall that can be identified with the set of all free ultrafilters on . For sets X and Y, the symbol denotes the set of all functions from X to Y.
A group, of which each element has order 2, is called a Boolean group. Every Boolean group is abelian, so holds for each element x of a Boolean group. We use to denote the unique (Boolean) group with two elements.
1. Definitions
Let
p be a free ultrafilter on
. Recall that a point
x of a topological space
X is a
p-limit of a sequence
of points of
X provided that
for every neighbourhood
V of
x in
X [
1].
The next notion is due to Angoa, Ortiz-Castillo, and Tamariz-Mascarúa [
2,
3].
Definition 1. Let p be a free ultrafilter on . A space X is strongly p-pseudocompact if it has the following property: For every sequence of non-empty open subsets of X, one can choose a point for all in such a way that the resulting sequence has a p-limit in X.
We shall also consider a weaker property.
Definition 2. A space X is selectively pseudocompact (called also strongly pseudocompact) provided that, for every sequence of non-empty open subsets of X, one can choose a point for all in such a way that the resulting sequence has a p-limit in X for some free ultrafilter p on (depending on the sequence in question).
This notion was introduced by García-Ferreira and Ortiz-Castillo [
4] under the name “strongly pseudocompact.” Dorantes-Aldama and the first listed author gave a list of equivalent descriptions of this property in ([
5], Theorem 2.1) and proposed an alternative name for it, calling a space with this property “selectively pseudocompact” ([
5], Definition 2.2). This terminology was later adopted in [
6].
Clearly, strongly p-pseudocompact spaces are selectively pseudocompact (strongly pseudocompact).
The following notion is due to Dorantes-Aldama and the first listed author ([
5], Definition 2.3).
Definition 3. A space X is selectively sequentially pseudocompact provided that, for every sequence of non-empty open subsets of X, one can choose a point for all in such a way that the resulting sequence has a convergent subsequence.
Selectively sequentially pseudocompact spaces are selectively pseudocompact (strongly pseudocompact), while the converse does not hold in general [
5].
When considering the property from Definition 1 for multiple ultrafilters p simultaneously, one could obtain two natural versions as follows:
Definition 4. Let P be a non-empty subset of . A space X is
- (i)
strongly P-bounded provided that, for every sequence of non-empty open subsets of X, one can choose a point for all in such a way that the resulting sequence has a p-limit in X for every ;
- (ii)
strongly P-pseudocompact provided that X is strongly p-pseudocompact for each .
The notion of strong
P-boundedness is due to Angoa, Ortiz-Castillo, and Tamariz-Mascarúa [
2,
3]. To the best of our knowledge, the notion from Item (ii) of Definition 4 appears to be new.
For every non-empty subset
P of
, the implication
trivially holds. It is also clear that the larger the subset
P of
is, the stronger the corresponding property of strong
P-boundedness and strong
P-pseudocompactness is.
Remark 1. (i) A sequence in a topological space X has a p-limit in X for every if and only if its closure in X is compact [1]. Therefore, strong -boundedness of a space X is easily seen to be equivalent to the following property: For every sequence of non-empty open subsets of X, there exists a compact subset K of X which has a non-empty intersection with each . The spaces having this property are called pseudo-
-bounded
in [2,3]. (ii) Infinite strongly -bounded spaces contain infinite compact subsets. Indeed, an infinite space X contains a sequence of pairwise disjoint non-empty open subsets. If X is strongly -bounded, then the compact subspace K of X as in Item (i) must be infinite.
Recall that a space X is ω-bounded if every countable subset of X has compact closure in X. A space is pseudocompact if every real-valued continuous function on it is bounded.
2. Introduction
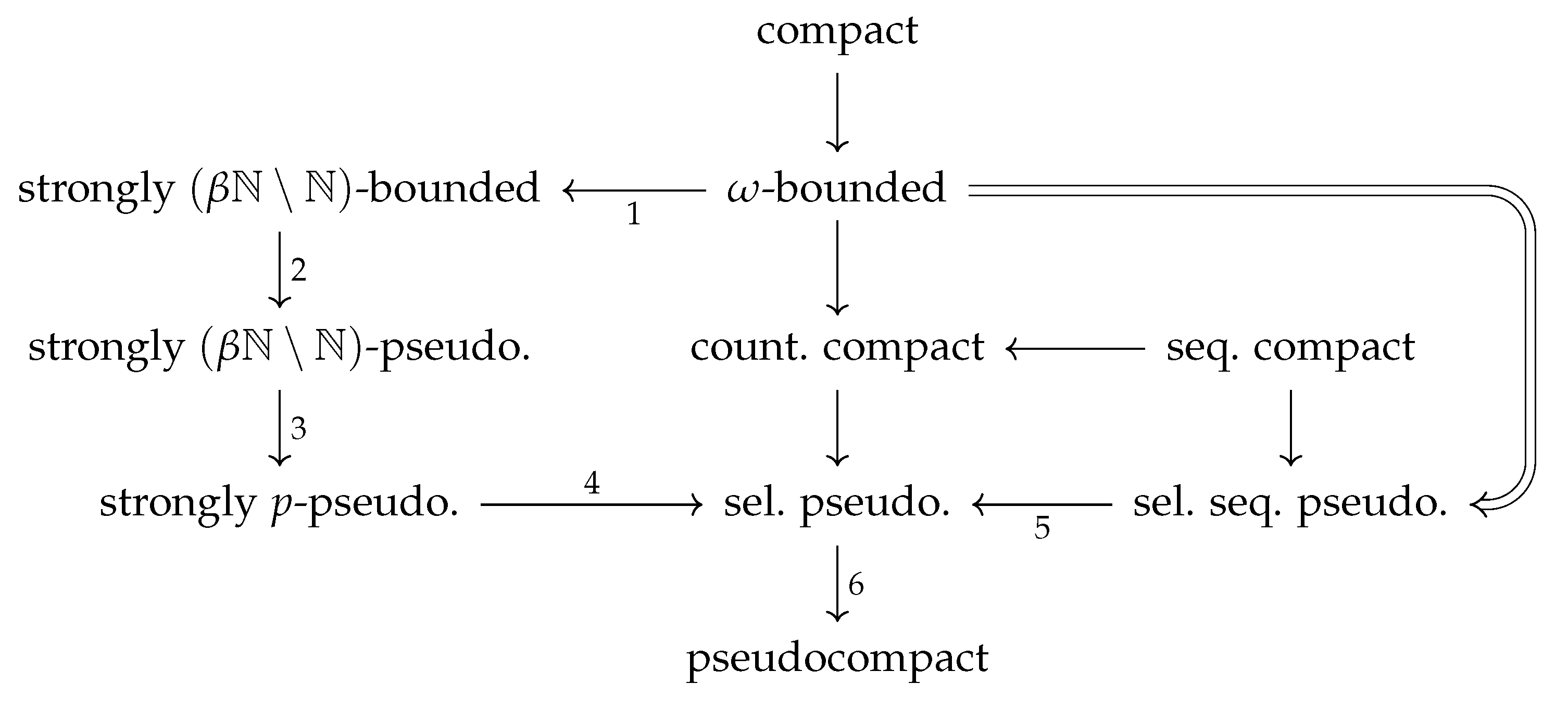
The diagram in
Figure 1 summarizes implications between notions introduced in
Section 1.
The double arrow in
Figure 1 denotes the implication which holds only in the class of topological groups and fails for general topological spaces, as has been shown in [
5].
Now we shall discuss the reversibility of arrows in
Figure 1 in the class of topological groups. In Example 1, we show that Arrow 1 is not reversible. Our Corollary 2 shows that Arrow 2 is not reversible. In the text following ([
7], Question 2.6), García-Ferreira and Tomita mention that there exist two free ultrafilters
p and
q on
and a topological group
G which is strongly
p-pseudocompact but not strongly
q-pseudocompact; in particular,
G is not strongly
-pseudocompact. This shows that Arrow 3 is not reversible.
Assuming Continuum Hypothesis CH, García-Ferreira and Tomita gave an example of a selectively pseudocompact group
G whose square
is not selectively pseudocompact [
6]. Since strong
p-pseudocompactness is preserved by products [
3] and implies selective pseudocompactness,
G cannot be strongly
p-pseudocompact for
any free ultrafilter
p on
. This shows that Arrow 4 is not reversible under CH. The reversibility of this arrow in ZFC alone remains unclear; see Question 6.
Next, we turn our attention to Arrows 5 and 6.
García-Ferreira and Tomita in [
7] gave an example demonstrating that Arrow 6 is not reversible in the class of topological groups. The authors later showed in [
8] that many examples of pseudocompact groups known in the literature fail to be selectively pseudocompact, thereby establishing relative abundance of examples witnessing non-reversibility of Arrow 6 for topological groups.
Dorantes-Aldama and the first listed author gave a consistent example of a countably compact (thus, selectively pseudocompact) topological group which is not selectively sequentially pseudocompact ([
5], Example 5.7), and they asked whether such an example exists in ZFC alone ([
5], Question 8.3):
Question 1. - (i)
Is there a ZFC example of a selectively pseudocompact (abelian) group which is not selectively sequentially pseudocompact?
- (ii)
Is there a ZFC example of a countably compact (abelian) group which is not selectively sequentially pseudocompact?
We shall answer Item (i) of this question positively in Corollary 5, thereby showing that Arrow 5 of
Figure 1 is not reversible in the class of topological groups. Moreover, an example we construct has much stronger property than mere selective pseudocompactness; see Corollary 4 (i).
Item (ii) of Question 1 remains open.
We refer the reader to [
5] for examples witnessing the non-reversibility of arrows in
Figure 1 without numbers assigned to them in the class of topological groups.
The paper is organized as follows.
Section 3 contains our results related to Question 1. The main result here is Theorem 1. Corollary 2 in this section shows that the implication in Equation (
1) is not reversible for
, even in the class of topological groups.
Section 4 collects definitions of and background material on free Boolean groups over a set and free precompact Boolean groups of a topological space. In
Section 5, we define a notion of a coherent map
f and introduce a topology on its domain so that the continuity of
f with respect to this topology becomes equivalent to
f being coherent. Splitting maps are defined in
Section 6. The notion of a coherent splitting map is used in the proof of Theorem 1. The main result in this section is Theorem 2 and its Corollary 7. In
Section 7, we apply the latter to show that for every infinite subset
A of the free precompact Boolean group
G of an arbitrary topological sum
, where each space
is either discrete or maximal, one can find a continuous group homomorphism
such that the set
is infinite for every
(Theorem 3). This result is applied to deduce that all separable pseudocompact subsets of
G as above are finite (Theorem 4). In
Section 8, we discuss some connections of our results to known results in the literature. Theorem 2 is proved in
Section 9, and
Section 10 is devoted to the proof of Theorem 1. Open questions are listed in
Section 11.
3. Results
The main goal of the paper is to prove the following theorem.
Theorem 1. Let κ be an infinite cardinal such that and P be a non-empty subset of satisfying . There exists a dense strongly P-pseudocompact subgroup of without infinite separable pseudocompact subsets.
The proof of this theorem is postponed until
Section 10.
Let denote the cardinality of the continuum. Applying Theorem 1 to and , we obtain the following:
Corollary 1. There exists a dense strongly -pseudocompact subgroup G of without infinite separable pseudocompact subsets.
The group
G in this corollary is clearly infinite. By Remark 1 (ii), infinite strongly
-bounded spaces contain infinite compact subsets (and thus, also infinite separable pseudocompact subsets). Therefore, “strong
-pseudocompactness” of
G in Corollary 1 cannot be strengthened to its “strong
-boundedness.” By the same reason, the topological group
G from Corollary 1 witnesses the validity of the following corollary, showing that Arrow 2 in
Figure 1 is not reversible, even for topological groups.
Corollary 2. A strongly -pseudocompact Boolean group need not be strongly -bounded.
This corollary shows that the implication in Equation (
1) is not reversible when
, even in the class of topological groups.
Given a free ultrafilter p on , we can apply Theorem 1 to and to obtain the following:
Corollary 3. For every free ultrafilter p on , there exists a dense strongly p-pseudocompact subgroup of without infinite separable pseudocompact subsets.
If
is an infinite cardinal, then every dense subset of
must be infinite. Since infinite selectively sequentially pseudocompact spaces contain non-trivial convergent sequences by ([
5], Proposition 3.1) and convergent sequences are separable and pseudocompact, the topological groups from Theorem 1 and its Corollaries 1 and 3 are not selectively sequentially pseudocompact. In particular, we have the following corollary.
Corollary 4. - (i)
There exists a dense strongly -pseudocompact subgroup of which is not selectively sequentially pseudocompact.
- (ii)
For every free ultrafilter p on , there exists a dense strongly p-pseudocompact subgroup of which is not selectively sequentially pseudocompact.
As can be seen from
Figure 1, the topological groups from Corollary 4 are selectively pseudocompact. Therefore, the following particular version of Corollary 4 (ii) provides a positive answer to Question 1 (i).
Corollary 5. There exists a selectively pseudocompact Boolean group (of weight ) which is not selectively sequentially pseudocompact.
Our next remark clarifies the strength of the condition “without infinite separable pseudocompact subsets” appearing in Theorem 1 and its Corollaries 1 and 3. Indeed, this remark shows that the topological groups in these results contain no infinite subsets which belong to any of the following classes of spaces:
countably pseudocompact;
countably pracompact;
countably compact;
compact.
Remark 2. - (i)
Hernández and Macario [9] say that a space X is countably pseudocompact
if, for every countable subset A of X, there exists a countable subset B of X such that and is pseudocompact. (Here denotes the closure of B in X.) It is immediately obvious from this definition that every infinite countably pseudocompact space contains an infinite separable pseudocompact subset. - (ii)
A space X is said to be countably pracompact
if X contains a dense set Y such that every infinite subset of Y has an accumulation point in X; see ([10], Ch. III, Sec. 4). Let X be an infinite countably pracompact space, and let Y be its dense subspace such that every infinite subset of Y has an accumulation point in X. Since X is infinite and Y is dense in X, the set Y must be infinite. Fix a countably infinite subset S of Y. Then is a separable space. Note that every infinite subset of S has an accumulation point in C. Since S is dense in C, it easily follows that C is pseudocompact. We proved that an infinite countably pracompact space contains an infinite separable pseudocompact subset. - (iii)
Since countably compact spaces are countably pracompact, it follows from (ii) that every infinite countably compact space contains an infinite separable pseudocompact subset.
- (iv)
Since compact spaces are countably compact, it follows from (iii) that every infinite compact space contains an infinite separable pseudocompact subset.
Remark 3. The topological groups from Theorem 1 and all its corollaries above are (Pontryagin) reflexive. Indeed, the topological group G from Theorem 1 has no infinite separable pseudocompact subsets, so all compact subsets of G are finite by Remark 2 (iv). Since G is pseudocompact, it is reflexive by ([11], Theorem 2.8) (this also follows from ([12], Lemma 2.3 and Theorem 6.1)). Finally, the topological groups from all corollaries of Theorem 1 are obtained by application of this theorem, so they inherit their reflexivity from it. Corollaries 1 and 3 and
Figure 1 suggest the following natural question:
Question 2. Does there exist an infinite abelian (or even Boolean) strongly -bounded group G satisfying one of the following conditions:
- (i)
G is not selectively sequentially pseudocompact;
- (ii)
G does not have non-trivial convergent sequences?
Since infinite selectively sequentially pseudocompact spaces contain non-trivial convergent sequences by ([
5], Proposition 3.1), Item (ii) of this question is stronger than Item (i). By Remark 1 (ii), Item (ii) of the question cannot be further strengthened by requiring all compact subsets of
G to be finite.
According to the double arrow in
Figure 1, a positive answer to Question 2 (i) would provide an example of a strongly
-bounded (abelian) group which is not
-bounded. However, a topological group with these properties can be easily constructed.
Example 1. Strongly -bounded abelian groups need not be ω-bounded. Indeed, let κ be an uncountable cardinal, and let H be a countably infinite subgroup of the torus group . For every , let be the constant function from κ to defined by for all . Define . Let be the Σ-product in , and let G be the smallest subgroup of containing . Note that C is a closed subgroup of G which is not compact. Indeed, if C were compact, its projection H on a fixed coordinate would be compact as well, and as H would be an infinite compact subgroup of , we would find that , in contradiction to our assumption that H is countable. Since C is a countably infinite non-compact closed subgroup of G, this shows that G is not ω-bounded. Since G has a dense ω-bounded subgroup D, it is strongly -bounded.
Example 1 shows that Arrow 1 in
Figure 1 is not reversible, even for topological groups.
The next remark shows that the assumption in Theorem 1 that the cardinal satisfies is essential and cannot be omitted, at least in ZFC.
Remark 4. Under the Generalized Continuum Hypothesis (GCH), if , then every dense pseudocompact subgroup G of contains a non-trivial convergent sequence [13]. Further results in this direction can be found in [14]. 4. Free Boolean Groups and Free Precompact Boolean Groups
Let X be a set. The set of all finite subsets of X becomes an abelian group with the symmetric difference as its group operation + and the empty set as its zero element. Clearly, if are disjoint, then . Each element E of has order 2, as , so is a Boolean group.
If one abuses notation by identifying an element with the singleton , then each element of the group admits a unique decomposition , so the set X can be naturally considered as the set of generators of . (Here we agree that .)
Every map
has a unique extension
to a homomorphism of
to
defined by
where the sum is taken in the group
. Since the variety
of all Boolean groups is generated by the single group
, the group
coincides with the free group in the variety
over a set
X [
15]. Thus,
is the
free Boolean group over
X. (Note that the trivial group is the free Boolean group over the empty set.)
Recall that a topological group is
precompact if it is a subgroup of some compact group, or equivalently, if its completion is compact. The class of all precompact Boolean groups forms a variety
of topological groups [
16,
17]. Therefore, given a topological space
X, there exists the free object
of
X in
[
18,
19] which we shall call the free precompact Boolean group of
X.
Definition 5. Let be the variety of all precompact Boolean groups. For a topological space X, a topological group is said to be the free precompact Boolean group of X provided it satisfies two properties:
- (i)
,
- (ii)
there exists a continuous map such that
- (a)
is algebraically generated by , and
- (b)
for every continuous map with , there exists a continuous homomorphism such that .
A description of
as the reflection of the free (abelian) topological group of a space
X in the class
of precompact Boolean groups can be found in ([
20],
Section 9). Another description for zero-dimensional spaces
X is given in Lemma 2 below. The reason why zero-dimensionality of a space
X plays such an important role can be seen from the following lemma.
Lemma 1. For a topological space X, the following conditions are equivalent:
- (i)
The map from Item (ii) of Definition 5 is a homeomorphic embedding;
- (ii)
X is zero-dimensional.
Proof. (i) → (ii) Since by Definition 5 (i), is a precompact Boolean group. Then the completion K of is a compact Boolean group, so K is zero-dimensional. Since , the subspace of K is zero-dimensional as well. Finally, since is homeomorphic to X by our assumption, it follows that X is zero-dimensional.
(ii) → (i) Since X is zero-dimensional, there exists a homeomorphic embedding , where for a suitable cardinal . Let and be as in Definition 5 (ii). Since is an injection, so is . Therefore, is a bijection, so it has its inverse map . Similarly, since is a bijection, it has its inverse . Now, by Definition 5 (ii) (b), so . Since is a homeomorphic embedding, its inverse is continuous. Since is continuous as well, so is the composition . Since is continuous by Definition 5 (ii), we conclude that is a homeomorphism. We have proved that is a homeomorphic embedding. □
Lemma 2. Let X be a zero-dimensional topological space and let be the family of all continuous maps from X to the group endowed with the discrete topology. Consider the initial topology on with respect to the family of homomorphisms; that is, the family forms a subbase for the topology . Then the topological group coincides with the free precompact Boolean group of X, as witnessed by the natural inclusion map of X into (sending each to ) taken as . Furthermore, induces on X the original topology of X.
Proof. First, we check Items (i) and (ii) of Definition 5.
(i) Since is the initial topology with respect to the family consisting of homomorphisms into the compact group , it is precompact. Since is a Boolean group, we have .
(ii) Item (a) is clear, as algebraically generates . To check Item (b), suppose that and is a continuous map. It follows from that G is a precompact Boolean group, so its completion K is a compact Boolean group. The standard facts of the duality theory imply that K is topologically isomorphic to the Cartesian product for some cardinal . Therefore, we can identify G with a subgroup of .
Let be arbitrary. Consider the projection on the th coordinate. Then the composition map is continuous, so . Now by our definition of . Since the topology has the family as its subbase, it follows that the homomorphism is continuous.
Let be the continuous homomorphism defined by for . Note that for , as each extends . This shows that . Since is a homomorphism, X algebraically generates , and G is a subgroup of , it follows that . We have defined a continuous homomorphism . Since is the natural inclusion map, from we conclude that .
It follows from (i) and (ii) that coincides with the free precompact Boolean group of X, as witnessed by the natural inclusion map of X into taken as . Since X is zero-dimensional, from Lemma 1 we conclude that is a homeomorphic embedding, which implies that induces the original topology on X. □
Definition 6. We shall say that a subspace Y of a topological space X is-embedded in X provided that every continuous map can be extended to a continuous map .
Remark 5. A clopen subset of a topological space is -embedded in it.
We finish this section with the lemma which will be needed in the future proofs.
Lemma 3. Let X be a zero-dimensional space.
- (i)
If Y is a zero-dimensional space and is a continuous injection, then the continuous homomorphism extending φ is an injection as well.
- (ii)
If a closed subset Y of X is -embedded in X, then is a closed subgroup of .
Proof. (i) It follows from Lemma 2 that, algebraically, and . Since is an injection, so is .
(ii) By Lemma 2, we can identify and with and , respectively. Since , it suffices to show that
- (a)
induces the topology on , and
- (b)
is -closed in .
In the proof below, we freely use notations from Lemma 2.
(a) Since Y is a subspace of X, one has . Since Y is -embedded in X, from Definition 6 we obtain the inverse inclusion . This establishes the equality , which implies (a) by definition of and .
(b) Suppose that
. There then exists
. Since
E is a finite subset of
X and
Y is
-closed in
X, the set
is
-closed in
X as well. Since
X is zero-dimensional, we can find a clopen subset
W of
X such that
and
. Define the function
by
and
. Since
W is clopen in
X, we have
, which implies
. Therefore,
by our definition of
. Since
and
, we have
by Equation (
2), so
. Since
,
Y algebraically generates
and
is a homomorphism, we obtain
. This shows that
. □
We refer the reader to ([
21],
Section 2) for properties of free precompact (abelian) groups and [
22] for those of free precompact Boolean groups.
5. Coherent Maps
Definition 7. Given sets and K, define and .
Definition 8. Let X be a set as in Definition 7. We shall say that a map is coherent
provided that Note that the map is coherent if and only if is a p-limit of the sequence whenever and .
Definition 9. We introduce the topology on a set X as in Definition 7 by declaring each point of to be isolated and a basic open neighbourhood of a point to be of the form for a given element .
Remark 6. Let X be a topological space from Definition 9.
- (i)
Note that for is a clopen subset of X, so is a topological sum of .
- (ii)
Since each for is a space with a single non-isolated point, it is zero-dimensional. It follows from this and (i) that X is zero-dimensional as well.
The straightforward verification of the following lemma is left to the reader.
Lemma 4. Let X be a set as in Definition 7. Then a map is coherent in the sense of Definition 8 if and only if it is continuous with respect to the topology on X described in Definition 9 and the discrete topology on .
We finish this section with two technical lemmas which will be needed in future proofs. The reader can safely skip them during the first pass.
Lemma 5. Let X and be sets as in Definition 7. Then every map admits a unique coherent extension over X.
Proof. For fixed
and
, we have
Since
p is an ultrafilter on
, there exists a unique
such that
Define
for every
and
. Finally, let
for all
. It follows from this definition and Equation (
4) that Equation (
3) holds; that is,
f is coherent by Definition 8. □
Lemma 6. Let X be a set as in Definition 7. If , and , then there exists a coherent map such that and .
Proof. Fix a finite set
such that
. It follows from
that
, so we can fix
Since
F is finite, there exists
such that
for all
with
. Define
by
Let
and
be arbitrary. If either
or
, then
for every
by Equation (
6), so
. Suppose now that
and
. Then
by Equation (
6). Since
p is a free ultrafilter on
, we have
. This implies that
, and therefore,
f is coherent by Definition 8.
If
, then either
or
by Equation (
5), so
by Equation (
6). Therefore,
. Since
is a homomorphism extending
f, it easily follows that
.
From the choice of
m and Equation (
6), we conclude that
for all
. Furthermore,
by Equation (
6).
Since
is a homomorphism extending
f, we obtain
This finishes the proof of our lemma. □
6. Coherent Splitting Maps and Their Continuity
Definition 10. Let X be a set. We shall say that a map splits
a subset A of provided that the set is infinite for each , where is the homomorphism defined in Equation (
2).
Clearly, a subset split by some map must be infinite. The converse also holds:
Lemma 7. For an arbitrary set X, every infinite subset of can be split by some map .
This lemma is part of folklore and can be proved by a straightforward induction. It can also be derived from ([
23], Lemma 4.1).
The secondary goal of this paper is to prove the following theorem strengthening Lemma 7 by additionally requiring the splitting map to be coherent.
Theorem 2. If X is a set as in Definition 7, then every infinite subset of can be split by some coherent map .
This theorem constitutes the main technical tool in the proof of Theorem 1 in
Section 10. The proof of Theorem 2 is postponed until
Section 9.
The next corollary provides a topological reformulation of Theorem 2.
Corollary 6. Let X be a set as in Definition 7 equipped with the topology described in Definition 9. Then for every infinite subset A of the free precompact Boolean group of X, there exists a continuous homomorphism such that the set is infinite for each .
Proof. In this proof, we use notations from Lemma 2. The space X is zero-dimensional by Remark 6 (ii). By Lemma 2, we can identify with . After this identification, we can think of A as being an infinite subset of . By Theorem 2, A is split by some coherent map . By Lemma 4, f is continuous, and so , which implies that . Since is the initial topology with respect to the family , the map is -continuous. Recalling our identification of with , we conclude that the homomorphism is continuous. Since A is split by f, it follows from this and Definition 10 that satisfies the conclusion of our corollary. □
Definition 11. For simplicity, we shall say that a topological space is elementary if it is homeomorphic to a subspace of of the form , where .
Corollary 7. Let K be a non-empty set. For every , let be either an at most countable discrete space or an elementary space. Let be the topological sum of the family . Then for every infinite subset A of , there exists a continuous homomorphism such that the set is infinite for each .
Proof. Let and let be the set as in Definition 7. We equip X with the topology described in Definition 9. In this proof, we use notations from Remark 6 (i).
Fix a free ultrafilter q on . Let . If is an at most countable discrete space, then we can fix an injection which will obviously be continuous. If is an elementary space, then Definition 11 allows us to identify the space with the subspace of , for a suitable . Now we can fix an injection which sends each point to the point and the point to . Clearly, is a homeomorphism between and .
Let be the map such that for every . Since each is an injection, so is . Since each is continuous, it follows from our definition of and Remark 6 (i) that is continuous as well.
Clearly, Y is zero-dimensional, and X is zero-dimensional by Remark 6 (ii). Since is a continuous injection, is a continuous monomorphism by Lemma 3 (i).
Let A be an infinite subset of . Then is an infinite subset of . By Corollary 6, we can find a continuous homomorphism such that the set is infinite for each . Now the composition is the desired homomorphism, as is a one-to-one map. □
7. Applications to Free Precompact Boolean Groups of Topological Sums of Maximal Spaces
Definition 12. Recall that a space is maximal if it is non-discrete, yet any strictly stronger topology on it is discrete.
One easily sees that every maximal space X has exactly one non-isolated point p such that the trace of the filter of neighbourhoods of p on the set of isolated points of X is an ultrafilter on D. In particular, X is zero-dimensional.
Clearly, elementary spaces from Definition 11 are precisely the countably infinite maximal spaces.
Lemma 8. Let X be either a discrete or a maximal topological space, and let Y be an at most countable closed subspace of X. Then
- (i)
Y is either elementary or discrete, and
- (ii)
Y is -embedded in X.
Proof. The conclusion of our lemma is trivial when X is a discrete space. Therefore, from now on we shall assume that X is a maximal space. Let p be the non-isolated point of X. We consider two cases.
Case 1. . If p is a non-isolated point in Y, then every neighbourhood of p intersects the set . By the maximality of X, we conclude that Y is a neighbourhood of p in X. This means that Y is clopen in X, and therefore -embedded in X by Remark 5. Applying maximality of X once again, we conclude that Y is an elementary space.
Suppose now that
p is an isolated point of
Y. Then
Y is discrete and there exists an open subset
U of
X such that
. If
is a continuous map, then the map
defined by
is continuous and extends
g. This shows that
Y is
-embedded in
X.
Case 2. . Since p is the only non-isolated point of X, all points of Y are isolated in X, so Y is discrete and open in X. Since Y is also closed in X, it is clopen in X, and so -embedded in X by Remark 5. □
Lemma 9. Let be the topological sum of a family , where each space is either discrete or maximal. Let A be an at most countable subset of . Then there exist an at most countable set and an at most countable closed subspace of for each such that the topological sum satisfies the following conditions:
- (i)
each is either elementary or discrete;
- (ii)
is an at most countable closed subgroup of ;
- (iii)
every continuous homomorphism can be extended to a continuous homomorphism ;
- (iv)
.
Proof. Since X is zero-dimensional, Lemma 2 allows us to identify with , so we can view A as a subset of . Since A is countable, there exists an at most countable set such that . Since , we can find an at most countable set , and for every we can fix an at most countable subset of such that , where . Without loss of generality, we may assume that each contains the unique non-isolated point of whenever is a maximal space. This assumption means that is closed in for each .
(i) By Lemma 8, each space is either elementary or discrete, and is -embedded in .
(ii) Since is a closed -embedded subspace of for every , we conclude that Y is a closed -embedded subspace of X. Therefore, is a closed subgroup of by Lemma 3 (ii). Since Y is zero-dimensional, Lemma 2 allows us to identify with . Since Y is at most countable, so is and thus .
(iii) Let be an arbitrary continuous homomorphism. Since the topology of induces the original topology of Y by Lemma 2, the restriction of h to Y is continuous. Since Y is -embedded in X, we can find a continuous map extending g. Since coincides with and coincides with , it follows that is a continuous homomorphism from to whose restriction to coincides with .
(iv) Since and , we have . Therefore, we can view A as a subset of . □
Theorem 3. Let be the topological sum of a family , where each space is either discrete or maximal. Then for every infinite subset A of , there exists a continuous homomorphism such that the set is infinite for each .
Proof. Without loss of generality, we may assume that A is countably infinite. Applying Lemma 9 to this A, we can obtain a subspace Y of X as in the conclusion of Lemma 9. By Item (i) of this lemma, we can apply Corollary 7 to find a continuous homomorphism such that the set is infinite for each . Applying Item (iii) of Lemma 9, we can find a continuous homomorphism extending h. Since by Item (iv) of Lemma 9, we have for each . □
Lemma 10. Let X be a topological space such that the closure of each at most countable subset of X is at most countable. Then every separable pseudocompact subspace K of X is compact and metrizable. Moreover, if K is infinite, then K contains a non-trivial convergent sequence.
Proof. Let
K be a separable pseudocompact subset of
X. Let
S be an at most countable dense subset of
K. Then its closure
C in
X is at most countable by the assumption of our lemma. Since
S is dense in
K, we have
. Thus,
K is an at most countable pseudocompact space, so it must be compact. An at most countable compact space is metrizable [
24], so
K is a metrizable compact space. The last sentence of our lemma follows from the fact that every infinite compact metrizable space has a non-trivial convergent sequence. □
Theorem 4. Let be the topological sum of a family , where each space is either discrete or maximal. Let be the free precompact Boolean group of X. Then all separable pseudocompact subsets of G are finite.
Proof. First, we check that each at most countable subset A of has at most countable closure in G. If A is finite, then it is closed in G. Suppose now that A is infinite. Applying Lemma 9 to this A, we can obtain a subspace Y of X as in the conclusion of Lemma 9. By Item (ii) of this lemma, is an at most countable closed subgroup of . Note that by Item (iv) of Lemma 9. Therefore, the closure of A in G is contained in the (at most countable) set H.
Let A be a countably infinite subset of G. Applying Theorem 3, we can find a continuous homomorphism such that the set is infinite for each . Since is continuous, is a closed subset of A for . Since is a partition of A into two disjoint infinite closed sets, A cannot be a convergent sequence. We have proved that G does not contain non-trivial convergent sequences. By Lemma 10, all separable pseudocompact subsets of G are finite. □
The group in Theorem 4 is precompact, so its completion H is a compact group. Being compact, the group H contains many non-trivial convergent sequences. Since these non-trivial convergent sequences in H might appear already in its subgroup G, this demonstrates that Theorem 4 is not completely trivial.
8. Discussion
The topic of this paper is related to a long-standing open problem of van Douwen about the existence in ZFC alone of a countably compact group without non-trivial convergent sequences. (The existence of such a group in some additional set-theoretic axioms, such as Continuum Hypothesis (CH) or Martin’s Axiom (MA), is well-known.) Indeed, it was noted in ([
5], Example 5.7) that a solution to this problem would bring a positive solution to Question 1 (ii) and thus to the weaker Question 1 (i).
The question of the existence of pseudocompact groups without infinite compact subsets (and its weaker version which only prohibits non-trivial convergent sequences) has been studied extensively [
12,
13,
14,
25,
26]. For example, Galindo and Macario proved that, under a mild additional set-theoretic assumption beyond ZFC, every pseudocompact abelian group admits a pseudocompact group topology without infinite compact subsets [
12]. Corollary 1 contributes to this topic by constructing an abelian topological group without infinite compact subsets (in fact, even without infinite separable pseudocompact subsets) which has a much stronger property than mere pseudocompactness.
Topological groups without infinite compact subsets play a prominent role in Pontryagin duality theory [
27] due to the fact that pseudocompact abelian groups without infinite compact subsets are (Pontryagin) reflexive ([
11], Theorem 2.8) (this also follows from ([
12], Lemma 2.3 and Theorem 6.1)). All topological groups we construct in this paper are reflexive by Remark 3.
The strongest precompact group topology on an abelian group is called its
Bohr topology. It is a classical result of Glicksberg that the Bohr topology on any abelian group does not have infinite compact subsets [
28]; see also ([
29],
Section 6) for an alternative proof. Since the free precompact Boolean group
of a topological space
X is precompact, its topology
is weaker than the corresponding Bohr topology, so
can have more compact subsets than the Bohr topology (in which all compact subsets are finite). Note that, when
X is discrete, then
coincides with the Bohr topology on
, so it does not have infinite compact subsets by Glicksberg’s result. Our Theorem 4 can be viewed as an extension of Glicksberg’s theorem over free precompact Boolean groups
of spaces
X very close to being discrete (indeed, maximal spaces are one step from being discrete by Definition 12).
The idea of splitting of a given infinite subset
A of a discrete abelian group
G via a homomorphism
from
G to some target topological group
H (usually
or the torus group
) is a classical technique for producing a group topology on
G without non-trivial convergent sequences. Such a splitting is always possible, modulo natural algebraic restrictions on
H and
A; see [
23,
29,
30]. However, if
G is equipped with a non-discrete group topology
, finding a
-continuous homomorphism
which splits
A is a much more difficult task, and the authors are not aware of any known results in this direction. Therefore, our Theorem 3 can be viewed as a first, albeit somewhat modest, contribution to what is undoubtedly quite an interesting topic.
9. Proof of Theorem 2
In this section, we fix a non-empty set
, a non-empty set
K and consider sets
from Definition 7. We also fix an infinite subset
A of
.
Lemma 11. If is finite, then some coherent map splits A.
Proof. Since
is finite and
A is infinite, there exists
such that the set
is infinite. Then
is an infinite subset of
. By Lemma 7, there exists a map
which splits
B. Let
be the unique coherent map extending
g given by Lemma 5. Clearly,
. Since
and
g splits
B, the map
f splits
B as well. It follows from this, Equation (
8), and Definition 10 that
Define
. Clearly,
. It follows from Equations (
7) and (
8) that
for every
, so
holds in
; therefore,
as
is a homomorphism. Combining Equations (
9) and (
10), we conclude that
is infinite for every
. Since
, the same conclusion holds when
is replaced by
A. According to Definition 10, this means that
f splits
A. □
Definition 13. We denote by the set of all triples , where , and is a coherent map. For , we let provided that , , and extends .
One easily sees that is a poset. Clearly, , so .
Recall that a set is said to be dense in provided that for every there exists such that .
Lemma 12. (i) For every , the set is dense in .
(ii) For every , the set is dense in .
Proof. (i) Suppose that . Then . Note that the extension of , obtained by letting for all and , is coherent. Then . Clearly, and .
(ii) Suppose that . Then . Define and . Note that the extension of , obtained by letting for all and , is coherent. Then . Clearly, and . □
Lemma 13. If is infinite, then for every and each , the set is dense in .
Proof. Let , , and be arbitrary. We need to find and such that , , and .
Since
B is finite, the intersection
is also finite. Furthermore, since both
and
are finite sets, so is the set
. Therefore,
is a finite subset of
. By our hypothesis,
is infinite, so there exists
such that
. Fix
,
, and
such that
. It follows from this and Equation (
12) that
.
Since a is a finite subset of , there exist finite sets and such that . By Lemma 12, without loss of generality, we may also assume that and .
Let
. Then
is well-defined. There exists a unique
such that
. Note that
so we can define a map
by
for all
.
Claim 1. and .
Proof. Since
and
by our construction, we only need to check that the map
is coherent. Let
and
be arbitrary. If
, then
by Equation (
13) and coherency of
. Suppose now that
. If
, then
for all
by Equation (
13), so
. Finally, if
, then the second line of Equation (
13) implies that
and
for all but finitely many
, as the set
a is finite. Therefore,
is a cofinite subset of
, so it belongs to
p, as
p is a free ultrafilter on
. This finishes the check of the inclusion
.
Finally, note that
extends
by the first line of Equation (
13). It follows from this,
,
, and Definition 13 that
. □
Claim 2. .
Proof. Since
, we have
, so Equation (
13) implies that
and
for all
. Since
is a homomorphism and
by our choice, this implies
This establishes our claim. □
Proof. The only condition in Equation (
11) that remains to be checked is the equality
. Since
, we have
. Note that
, so
. Since
is a homomorphism,
by Claim 2. □
Since was chosen arbitrarily, the conclusion of our lemma follows from Claims 1 and 3.
We shall need the following folklore lemma.
Lemma 14. If is an at most countable family of dense subsets of a non-empty poset , then there exists an at most countable subset of such that is a linearly ordered set and for every .
Proof. Since the family is at most countable, we can fix an enumeration of elements of . Since , there exists . By induction on , we can choose such that ; this is possible because is dense in . Now is the desired subset of . □
Lemma 15. If P and K are at most countable sets and is infinite, then some coherent map splits A.
Proof. By Lemmas 12 and 13, the family
consists of dense subsets of
. Since
P,
K, and
A are at most countable, so is
. By Lemma 14, there exists a set
such that
and
for every
.
We claim that is a coherent map from X to splitting A. Since intersects each and every , the domain of f coincides with . Since each is coherent and f extends all , it easily follows that f is coherent as well.
Suppose that
f does not split
A. Then the set
must be finite for some
, so
and thus
. Therefore,
for some
. Applying Equation (
11), we can find
such that
and
. Since
, this implies
. Therefore,
by the definition of the set
B, in contradiction with
. □
Proof of Theorem 2. Let A be an infinite subset of . Choose a countably infinite subset of A. Since , there exist at most countable sets and such that , where . Combining Lemmas 11 and 15, we can find a coherent map splitting . Let be the extension of over X obtained by letting f take 0 everywhere on . Clearly, f is a coherent map which splits . Since , f splits A as well. □
10. Proof of Theorem 1
The following lemma is part of set-theoretic folklore. We include its proof only for convenience of the reader.
Lemma 16. Let S and T be sets such that and T is infinite. Then there exists an enumeration such that for every .
Proof. Since , we can fix a surjection . Since T is infinite, we have , so we can fix a bijection . Let be the projection on the first coordinate. Define for every . We claim that is the desired enumeration. Indeed, let be arbitrary. Since f is a surjection, for some . Since and is a bijection, the set satisfies . Finally, for every , we have , so . □
Fix a cardinal such that and a set K such that . Let be a partition of K into pairwise disjoint sets such that for .
Let
P be a non-empty subset of
satisfying
. Consider the set
as in Definition 7. Note that
by Equation (
14) and our assumption on
K,
P, and
.
For a set S, we denote by the family of at most countable subsets of S and by the family of all countably infinite subsets of X.
Claim 4. - (i)
There exists an enumeration such that for every .
- (ii)
There exists an enumeration such that whenever , and .
Proof. (i) Note that and by our assumption on and , so we can apply Lemma 16 (with and ) to fix the desired enumeration .
(ii) Since and , we have , so the existence of the desired enumeration follows from Lemma 16 applied with and . □
For every , we define a coherent map differently depending on whether or .
Case 1. . In this case, we use a Theorem 2 to fix a coherent map splitting .
Case 2. . If , then we use Lemma 6 to fix a coherent map such that and ; otherwise, we let to be the constant map sending X to (this map is clearly coherent).
Claim 5. There exist an enumeration and a sequence for every such that whenever and , one can find with and for all .
Proof. Let . (We recall that denotes the set of all functions from to ; each such function s can be considered as a sequence of points of .)
Since for every , we have by our assumption on . Therefore, we can apply Lemma 16 with to fix an enumeration such that has cardinality for every .
Let . Then , so for a unique ; that is, is a function from to . We define and for all .
Let and be arbitrary. Then the function , defined by for , belongs to S. By the choice of our enumeration, the set has cardinality . In particular, there exists such that . Now and for every . □
For each , the sequence of points of the compact space has a p-limit .
For each
, define
by
Claim 6. For every and each sequence of non-empty open subsets of , there exists such that
- (i)
for all , and
- (ii)
is a p-limit of the sequence .
Proof. Fix
and a sequence
of non-empty open subsets of
. Without loss of generality, we may assume that each
is a basic open subset of
; that is,
, where each
is a non-empty (open) subset of
and
is a finite subset of
K. Then the set
is at most countable, so we can fix a countably infinite subset
I of
K containing
J. For every
,
is a non-empty subset of
, so we can select
. By Equation (
15) and Claim 5, there exists
such that
and
for all
.
(i) Fix
. By Equation (
16), we have
Since , this implies .
(ii) It suffices to check that is a p-limit of the sequence for every . We consider two cases.
Case 1.
. Since the sequence
has a
p-limit
, it follows that
is a
p-limit of the sequence
. Since
, we have
by Equation (
16). Combining this with Equation (
17), we obtain the desired conclusion.
Case 2.
. In this case, it follows from Equation (
16) that
for every
, and the conclusion follows from the fact that
is coherent. □
Claim 7. The setis dense in . Proof. Consider an arbitrary non-empty open subset
U of
. Let
for every
. Since
P is non-empty, we can choose
. Let
be as in the conclusion of Claim 6 applied to this
p and the sequence
. Then
. Since
by Equation (
14), we obtain
by Equation (
18), so
. □
Claim 8. Z is strongly P-pseudocompact.
Proof. By Definition 4 (ii), we need to check that
Z is strongly
p-pseudocompact for every
. Fix
. Let
be a sequence of non-empty open subsets of
Z. Since
Z is a subspace of
, for every
, there exists an open subset
of
such that
; in particular,
is non-empty. Let
be as in the conclusion of Claim 6 applied to
p and the sequence
. By Item (i) of this claim, we have
for every
. Since
by Equation (
14),
by Equation (
18), so
for every
. By Item (ii) of Claim 6,
is a
p-limit of the sequence
. Since
by Equation (
14), we obtain
by Equation (
18). According to Definition 1, this shows that
Z is strongly
p-pseudocompact. □
Let
G be the subgroup of
generated by
Z. Let
be the map defined by
Since G is a Boolean group, there exists a unique homomorphism extending f. Since and the latter set algebraically generates G, the homomorphism is surjective.
Claim 9. For every at most countable set , there exists an at most countable set such thatwhere is the projection on β’th coordinate. Proof. For every
, there exists a finite set
such that
Since
A is at most countable, so is the set
Therefore, is an at most countable subset of K.
Let
and
be arbitrary. Suppose that
. Then
by Equation (
22). Therefore,
by our choice of
I. Since
, we conclude that
; thus,
by Equation (
16). Since this holds for every
and
is a homomorphism, from Equations (
19) and (
21) we conclude that
This proves Equation (
20). □
Claim 10. G contains no non-trivial convergent sequences.
Proof. Consider an arbitrary countably infinite set . Since is a surjection, we can fix a countably infinite set such that and is a bijection. Let be the set as in the conclusion of Claim 9 (applied to our A). Since , we can apply Claim 4 (i) to conclude that the set has cardinality . Since , there exists . Then splits the set by our choice of . This means that the set is infinite for both .
Let
be arbitrary. Since
is a bijection, the set
is infinite. It follows from Equation (
20) that
for
, so
for
. Since the map
is continuous, it follows that
is a closed subset of
S.
Since is a bijection and is a partition of A into disjoint sets , it follows that is a partition of S into disjoint sets . Since each is infinite and closed in S, this implies that S cannot be a convergent sequence in G. □
Claim 11. If and , then the subgroup of G generated by the setis closed in G. Proof. Fix
and
. Note that
by Equations (
19) and (
23).
Let
be arbitrary. Since
is surjective,
for some
. Clearly,
. Apply Claim 9 to at most countable subset
of
to obtain at most countable set
as in the conclusion of this claim. Since
, we can apply Claim 4 (ii) to conclude that the set
has cardinality
. Since
, there exists
. Then
and
. Since
by our assumption, it follows from
and our choice of
that
and
. From this,
, Equations (
20) and (
24), we conclude that
and
Since
and
, we get
and
. Since
is continuous,
is an open neighbourhood of
g in
G disjoint from
.
For every , we found an open neighbourhood of G such that . Therefore, is closed in G. □
Claim 12. The closure of each at most countable subset of G is at most countable.
Proof. Let
S be an at most countable subset of
G. Since
Z algebraically generates
G, from Equations (
18) and (
23) we conclude that there exist
and
such that
. (Recall that
is algebraically generated by
.) Since
is closed in
G by Claim 11, the closure of
S is contained in
. Since
and
are at most countable, so is
and thus
as well. □
Claim 13. All separable pseudocompact subsets of G are finite.
Proof. This follows from Claims 10 and 12 and Lemma 10. □
Since , and Z is dense in by Claim 7, Z is dense in G. Since Z is strongly P-pseudocompact by Claim 8, so is G. By Claim 13, G does not contain infinite separable pseudocompact subsets. Finally, since , the topological groups and are topologically isomorphic.
11. Further Open Questions
In this section we list natural open questions (besides Question 2) inspired by our results.
As was mentioned in
Section 8, Galindo and Macario proved that, under a mild additional set-theoretic assumption beyond ZFC, every pseudocompact abelian group admits a pseudocompact group topology without infinite compact subsets [
12]. Question 4 below asks for an analogue of their result for other compactness-like properties listed on the left side of
Figure 1, while Question 3 is a version of Question 4 restricted to non-trivial convergent sequences. Item (iv) was excluded in Question 4 due to Remark 1 (ii).
Question 3. Let be one of the following properties:
- (i)
selectively pseudocompact;
- (ii)
strongly p-pseudocompact for some ;
- (iii)
strongly -pseudocompact;
- (iv)
strongly -bounded.
If an infinite abelian group admits a group topology with property , must it also admit a group topology with property having no non-trivial convergent sequences?
Question 4. Let be one of the properties (i)–(iii) from Question 3. If an infinite abelian group admits a group topology with property , must it also admit a group topology with property having no infinite compact subsets (or even without infinite separable pseudocompact subsets)?
It makes no sense to ask Questions 3 and 4 for properties on the right side of
Figure 1, because infinite selectively sequentially pseudocompact spaces contain non-trivial convergent sequences ([
5], Proposition 3.1).
Question 5. If an abelian group admits a pseudocompact group topology, must it also admit a group topology having one of the stronger properties (i)–(iv) listed in Question 3?
The version of Question 5 for “selective pseudocompactness” is due to García-Ferreira and Tomita ([
7], Question 2.7).
Our last question is related to the reversibility of Arrow 4 in
Figure 1 in the class of topological groups.
Question 6. Does there exist a ZFC example of a selectively pseudocompact (abelian) group which is not strongly p-pseudocompact for any free ultrafilter p on ?
An example under CH is mentioned in the text after
Figure 1.