Optimal B-Spline Bases for the Numerical Solution of Fractional Differential Problems
Abstract
1. Introduction
2. Materials and Methods
2.1. The Divided Difference Operator
2.2. The Cardinal B-Splines
2.3. Optimal B-Spline Bases
2.4. Analytical Expression of the Optimal B-Spline Bases
2.5. Fractional Derivatives of the Optimal B-Spline Bases
2.6. The Collocation-Galerkin Method
3. Results
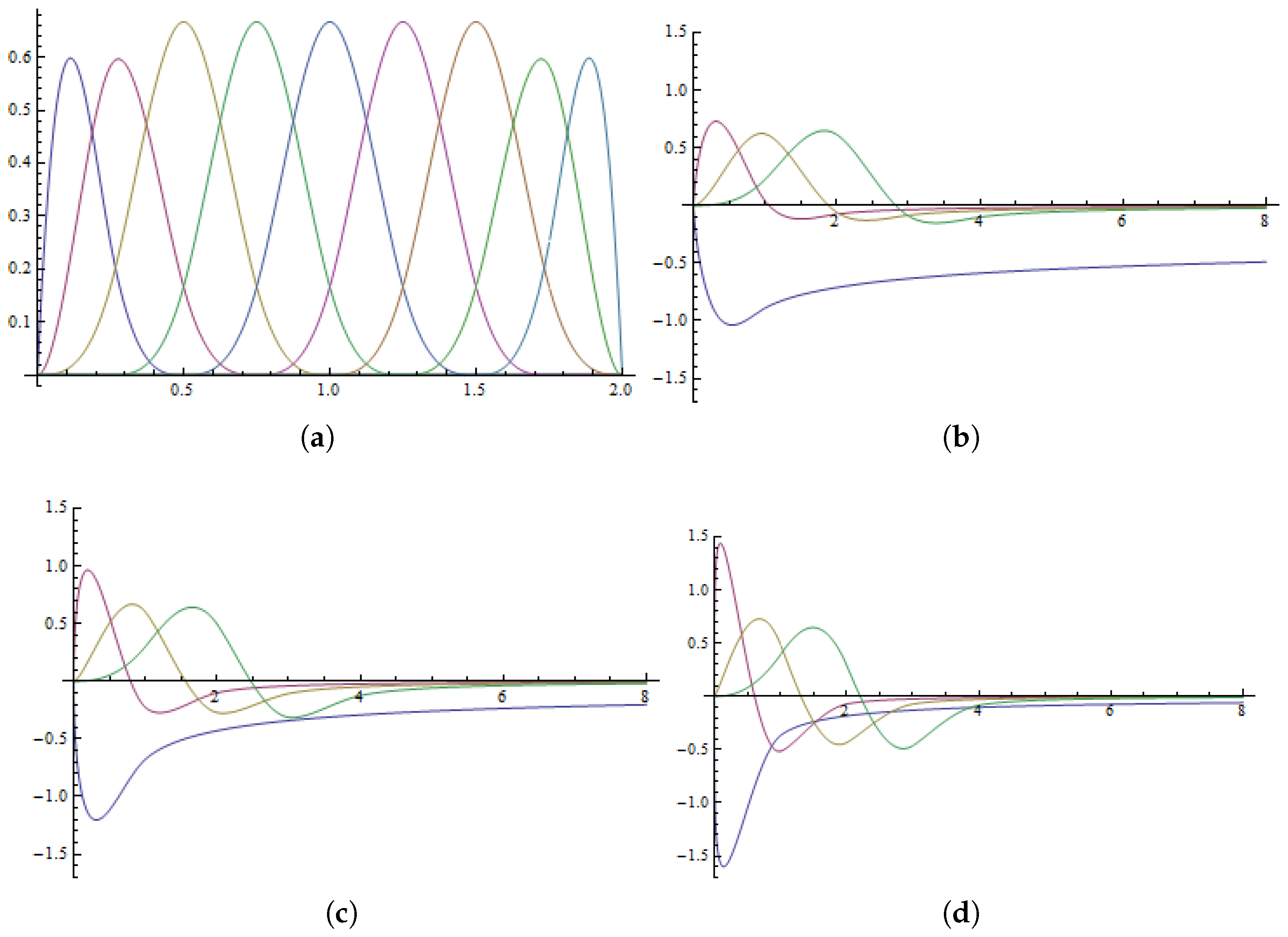
3.1. The Optimal B-Spline Basis of Degree
3.2. Numerical Tests
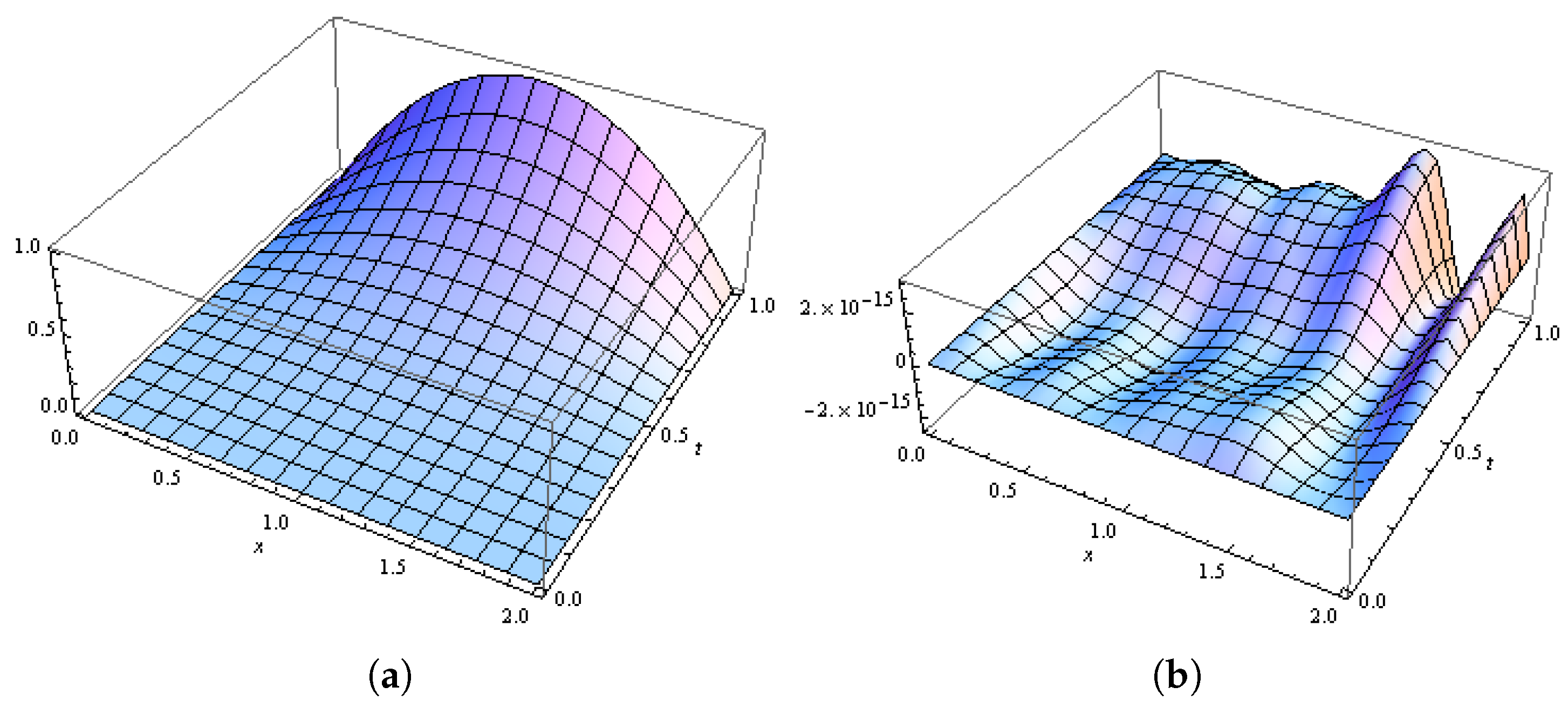
3.2.1. Test 1
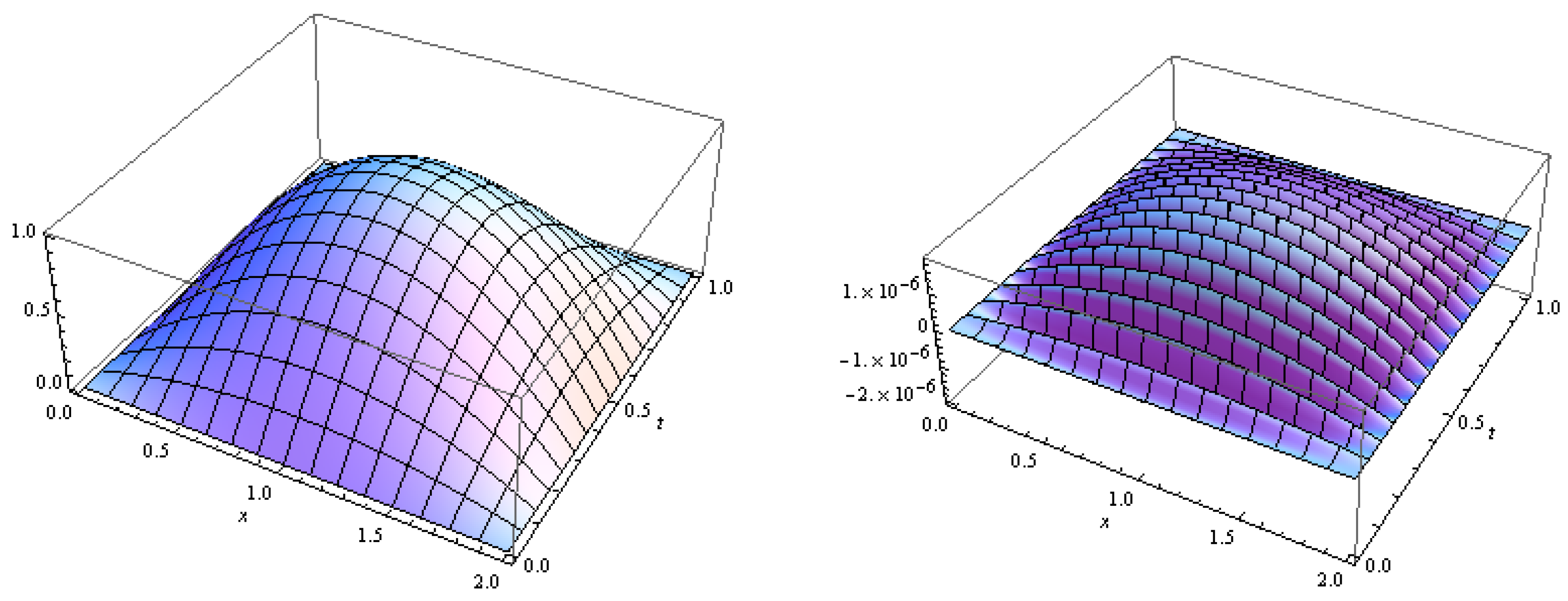
3.2.2. Test 2
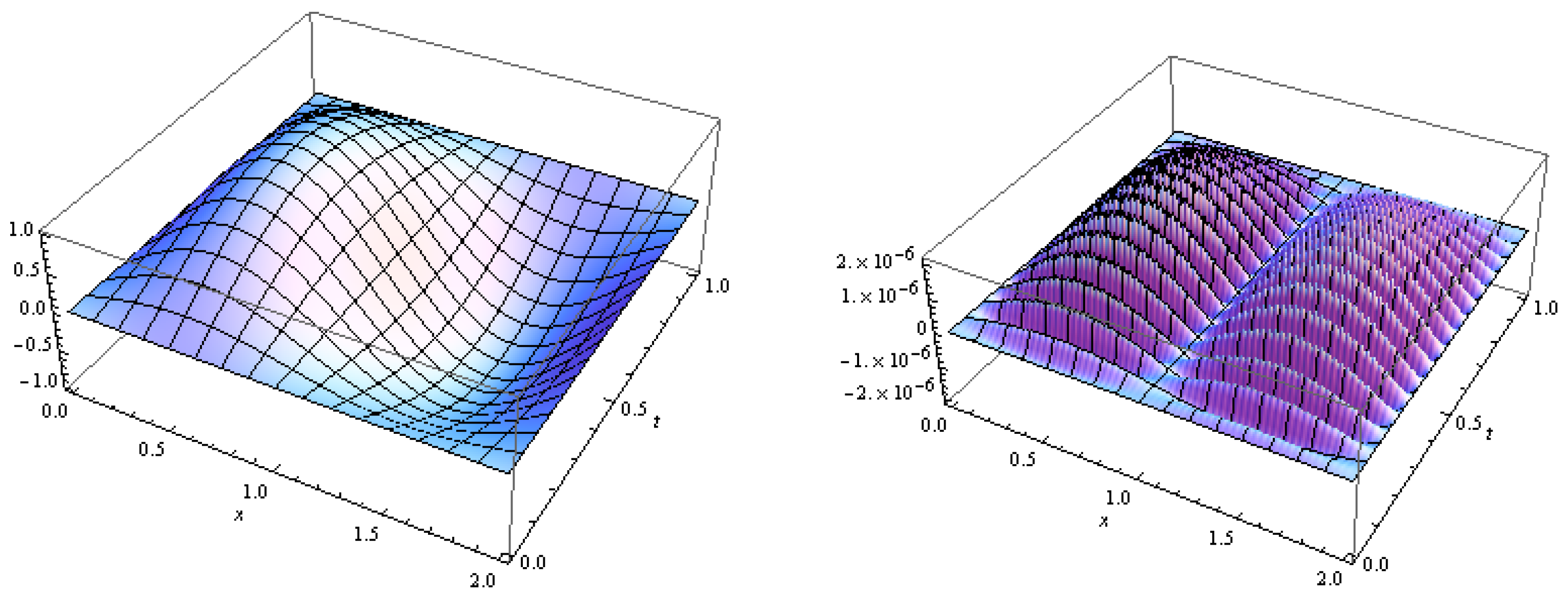
3.2.3. Test 3
4. Discussion
Funding
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: North-Holland, The Netherlands, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.; Tenreiro Machado, J.A. Advances in Fractional Calculus; Springer: Berlin, Germany, 2007. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics; Nonlinear Physical Science; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon & Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin, Germany, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Li, C.; Chen, A.; Ye, J. Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 2011, 230, 3352–3368. [Google Scholar] [CrossRef]
- Podlubny, I.; Skovranek, T.; Datsko, B. Recent advances in numerical methods for partial fractional differential equations. In Proceedings of the 2014 15th International Carpathian Control Conference (ICCC), Velke Karlovice, Czech Republic, 28–30 May 2014; pp. 454–457. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Li, C.; Chen, A. Numerical Methods for Fractional Partial Differential Equations. Int. J. Comput. Math. 2018, 95, 1048–1099. [Google Scholar] [CrossRef]
- Pitolli, F. A fractional B-spline collocation method for the numerical solution of fractional predator-prey models. Fractal Fractional 2018, 2, 13. [Google Scholar] [CrossRef]
- lHöllig, K. Finite Element Methods with B-Splines; SIAM: Philadelphia, PA, USA, 2003; Volume 26. [Google Scholar]
- Buffa, A.; Sangalli, G.; Vázquez, R. Isogeometric analysis in electromagnetics: B-splines approximation. Comput. Methods Appl. Mech. Eng. 2010, 199, 1143–1152. [Google Scholar] [CrossRef]
- Garoni, C.; Manni, C.; Serra-Capizzano, S.; Sesana, D.; Speleers, H. Spectral analysis and spectral symbol of matrices in isogeometric Galerkin methods. Math. Comput. 2017, 86, 1343–1373. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M.; Irandoust-Pakchin, S. The construction of operational matrix of fractional derivatives using B-spline functions. Communi. Nonlinear Sci. Numer. Simul. 2012, 17, 1149–1162. [Google Scholar] [CrossRef]
- Li, X. Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method. Communi. Nonlinear Sci. Numer. Simul. 2012, 17, 3934–3946. [Google Scholar] [CrossRef]
- Schumaker, L.L. Spline Functions: Basic Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Carnicer, J.M.; Peña, J.M. Totally positive bases for shape preserving curve design and optimality of B-splines. Computer Aided Geometric Design 1994, 11, 633–654. [Google Scholar] [CrossRef]
- Carnicer, J.M.; Peña, J.M. Total positivity and optimal bases. In Total Positivity and its Applications; Springer: Berlin, Germany, 1996; pp. 133–155. [Google Scholar]
- Unser, M.; Blu, T. Fractional splines and wavelets. SIAM Rev. 2000, 42, 43–67. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products: Corrected and Enlarged Edition; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Ford, N.J.; Xiao, J.; Yan, Y. A finite element method for time fractional partial differential equations. Fractional Calculus Appl. Anal. 2011, 14, 454–474. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A fractional spline collocation-Galerkin method for the time-fractional diffusion equation. Commun. Appl. Ind. Math. 2018, 9, 104–120. [Google Scholar] [CrossRef]
- Calabrò, F.; Manni, C.; Pitolli, F. Computation of quadrature rules for integration with respect to refinable functions on assigned nodes. Appl. Numer. Math. 2015, 90, 168–189. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 2018, 147, 210–219. [Google Scholar] [CrossRef]
- Forster, B.; Massopust, P. Interpolation with fundamental splines of fractional order. In Proceedings of the 9th International Conference on Sampling Theory and Applications (SampTa), Singapore, 2–6 May 2011. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 8.0.4.0; Wolfram Research, Inc.: Champaign, IL, USA, 2011. [Google Scholar]
- Calvetti, D.; Pitolli, F.; Somersalo, E.; Vantaggi, B. Bayes meets Krylov: Statistically inspired preconditioners for CGLS. SIAM Rev. 2018, 60, 429–461. [Google Scholar] [CrossRef]
- Strang, G.; Fix, G. A Fourier analysis of the finite element variational method. In Constructive Aspects of Functional Analysis; Edizioni Cremonese: Naples, Italy, 1971; pp. 796–830. [Google Scholar]
- Gori, L.; Pitolli, F. Refinable functions and positive operators. Appl. Numer. Math. 2004, 49, 381–393. [Google Scholar] [CrossRef]
- Gori, L.; Pezza, L.; Pitolli, F. Recent results on wavelet bases on the interval generated by GP refinable functions. Appl. Numer. Math. 2004, 51, 549–563. [Google Scholar] [CrossRef]
| 0.25 | 143 | 36×36 | 125 | 72×54 | 119 | 144×90 | 110 | 288×162 |
| 0.125 | 543 | 68×68 | 472 | 136×102 | 450 | 272×170 | 415 | 544×306 |
| 0.0625 | 2144 | 132×132 | 1864 | 264×198 | 1776 | 528×330 | 1639 | 1056×594 |
| 0.03125 | 8550 | 260×260 | 7434 | 520×390 | 7083 | 1040×650 | 6535 | 2080×1170 |
| 0.25 | 102 | 36×36 | 77 | 72×54 | 66 | 144×90 | 66 | 288×162 |
| 0.125 | 386 | 68×68 | 291 | 136×102 | 234 | 272×170 | 179 | 544×306 |
| 0.0625 | 1525 | 132×132 | 1148 | 264×198 | 923 | 528×330 | 706 | 1056×594 |
| 0.03125 | 6084 | 260×260 | 4579 | 520×390 | 3681 | 1040×650 | 2817 | 2080×1170 |
| 0.25 | 69 | 36×36 | 62 | 72×54 | 63 | 144×90 | 60 | 288×162 |
| 0.125 | 253 | 68×68 | 154 | 136×102 | 100 | 272×170 | 67 | 544×306 |
| 0.0625 | 1001 | 132×132 | 610 | 264×198 | 394 | 528×330 | 244 | 1056×594 |
| 0.03125 | 3991 | 260×260 | 2434 | 520×390 | 1573 | 1040×650 | 972 | 2080×1170 |
| 0.25 | ||||||
| 0.125 | 3.71 | 3.97 | 4.19 | |||
| 0.0625 | 4.23 | 4.23 | 4.16 | |||
| 0.03125 | 4.09 | 3.95 | 3.98 |
| 0.25 | ||||||
| 0.125 | 3.62 | 3.72 | 3.89 | |||
| 0.0625 | 4.28 | 4.28 | 4.19 | |||
| 0.03125 | 4.03 | 4.01 | 4.09 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitolli, F. Optimal B-Spline Bases for the Numerical Solution of Fractional Differential Problems. Axioms 2018, 7, 46. https://doi.org/10.3390/axioms7030046
Pitolli F. Optimal B-Spline Bases for the Numerical Solution of Fractional Differential Problems. Axioms. 2018; 7(3):46. https://doi.org/10.3390/axioms7030046
Chicago/Turabian StylePitolli, Francesca. 2018. "Optimal B-Spline Bases for the Numerical Solution of Fractional Differential Problems" Axioms 7, no. 3: 46. https://doi.org/10.3390/axioms7030046
APA StylePitolli, F. (2018). Optimal B-Spline Bases for the Numerical Solution of Fractional Differential Problems. Axioms, 7(3), 46. https://doi.org/10.3390/axioms7030046





