Multi-Attribute Decision-Making Method Based on Neutrosophic Soft Rough Information

Abstract

Soft sets (SSs), neutrosophic sets (NSs), and rough sets (RSs) are different mathematical models for handling uncertainties, but they are mutually related. In this research paper, we introduce the notions of soft rough neutrosophic sets (SRNSs) and neutrosophic soft rough sets (NSRSs) as hybrid models for soft computing. We describe a mathematical approach to handle decision-making problems in view of NSRSs. We also present an efficient algorithm of our proposed hybrid model to solve decision-making problems.

1. Introduction

Smarandache [1] initiated the concept of neutrosophic set (NS). Smarandache’s NS is characterized by three parts: truth, indeterminacy, and falsity. Truth, indeterminacy and falsity membership values behave independently and deal with the problems of having uncertain, indeterminant and imprecise data. Wang et al. [2] gave a new concept of single valued neutrosophic set (SVNS) and defined the set of theoretic operators in an instance of NS called SVNS. Ye [3,4,5] studied the correlation coefficient and improved correlation coefficient of NSs, and also determined that, in NSs, the cosine similarity measure is a special case of the correlation coefficient. Peng et al. [6] discussed the operations of simplified neutrosophic numbers and introduced an outranking idea of simplified neutrosophic numbers.

Molodtsov [7] introduced the notion of soft set as a novel mathematical approach for handling uncertainties. Molodtsov’s soft sets give us new technique for dealing with uncertainty from the viewpoint of parameters. Maji et al. [8,9,10] introduced neutrosophic soft sets (NSSs), intuitionistic fuzzy soft sets (IFSSs) and fuzzy soft sets (FSSs). Babitha and Sunil gave the idea of soft set relations [11]. In [12], Sahin and Kucuk presented NSS in the form of neutrosophic relation.

Rough set theory was initiated by Pawlak [13] in 1982. Rough set theory is used to study the intelligence systems containing incomplete, uncertain or inexact information. The lower and upper approximation operators of RSs are used for managing hidden information in a system. Therefore, many hybrid models have been built such as soft rough sets (SRSs), rough fuzzy sets (RFSs), fuzzy rough sets (FRSs), soft fuzzy rough sets (SFRSs), soft rough fuzzy sets (SRFSs), intuitionistic fuzzy soft rough sets (IFSRS), neutrosophic rough sets (NRSs), and rough neutrosophic sets (RNSs) for handling uncertainty and incomplete information effectively. Soft set theory and RS theory are two different mathematical tools to deal with uncertainty. Evidently, there is no direct relationship between these two mathematical tools, but efforts have been made to define some kind of relation [14,15]. Feng et al. [15] took a significant step to introduce parametrization tools in RSs. They introduced SRSs, in which parameterized subsets of universal sets are elementary building blocks for approximation operators of a subset. Shabir et al. [16] introduced another approach to study roughness through SSs, and this approach is known as modified SRSs (MSR-sets). In MSR-sets, some results proved to be valid that failed to hold in SRSs. Feng et al. [17] introduced a modification of Pawlak approximation space known as soft approximation space (SAS) in which SAS SRSs were proposed. Moreover, they introduced soft rough fuzzy approximation operators in SAS and initiated a idea of SRFSs, which is an extension of RFSs introduced by Dubois and Prade [18] . Meng et al. [19] provide further discussion of the combination of SSs, RSs and FSs. In various decision-making problems, RSs have been used. The existing results of RSs and other extended RSs such as RFSs, generalized RFSs, SFRSs and IFRSs based decision-making models have their advantages and limitations [20,21]. In a different way, RS approximations have been constructed into the IF environment and are known as IFRSs, RIFSs and generalized IFRSs [22,23,24]. Zhang et al. [25,26] presented the notions of SRSs, SRIFSs, and IFSRSs, its application in decision-making, and also introduced generalized IFSRSs. Broumi et al. [27,28] developed a hybrid structure by combining RSs and NSs, called RNSs. They also presented interval valued neutrosophic soft rough sets by combining interval valued neutrosophic soft sets and RSs. Yang et al. [29] proposed single valued neutrosophic rough sets (SVNRSs) by combining SVNSs and RSs, and established an algorithm for decision-making problems based on SVNRSs in two universes. For some papers related to NSs and multi-criteria decision-making (MCDM), the readers are referred to [30,31,32,33,34,35,36,37,38]. The notion of SRNSs is a extension of SRSs, SRIFSs, IFSRSs, introduced by Zhang et al. motivated by the idea of single valued neutrosophic rough sets (SVNRSs) introduced, we extend the single valued neutrosophic rough sets’ lower and upper approximations to the case of a neutrosophic soft rough set. The concept of a neutrosophic soft rough set is introduced by coupling both the neutrosophic soft sets and rough sets. In this research paper, we introduce the notions of SRNSs and NSRSs as hybrid models for soft computing. Approximation operators of SRNSs and NSRSs are described and their relevant properties are investigated in detail. We describe a mathematical approach to handle decision-making problems in view of NSRSs. We also present an efficient algorithm of our proposed hybrid model to solve decision-making problems.

2. Construction of Soft Rough Neutrosophic Sets

In this section, we introduce the notions of SRNSs by combining soft sets with RNSs and soft rough neutrosophic relations (SRNRs). Soft rough neutrosophic sets consist of two basic components, namely neutrosophic sets and soft relations, which are the mathematical basis of SRNSs. The basic idea of soft rough neutrosophic sets is based on the approximation of sets by a couple of sets known as the lower soft rough neutrosophic approximation and the upper soft rough neutrosophic approximation of a set. Here, the lower and upper approximation operators are based on an arbitrary soft relation. The concept of soft rough neutrosophic sets is an extension of the crisp set, rough set for the study of intelligent systems characterized by inexact, uncertain or insufficient information. It is a useful tool for dealing with uncertainty or imprecision information. The concept of neutrosophic soft sets is powerful logic to handle indeterminate and inconsistent situations, and the theory of rough neutrosophic sets is also powerful mathematical logic to handle incompleteness. We introduce the notions of soft rough neutrosophic sets (SRNSs) and neutrosophic soft rough sets (NSRSs) as hybrid models for soft computing. The rating of all alternatives is expressed with the upper soft rough neutrosophic approximation and lower soft rough neutrosophic approximation operator and the pair of neutrosophic sets that are characterized by truth-membership degree, indeterminacy-membership degree, and falsity-membership degree from the view point of parameters.

Definition 1.

Let Y be an initial universal set and M a universal set of parameters. For an arbitrary soft relation P over $Y\times M$, let $P_s:Y\to \mathcal{N}(M)$ be a set-valued function defined as $P_s(u)=\{k\in M|(u,k)\in P\},u\in Y.$

Let $(Y,M,P)$ be an SAS. For any NS $C=\{(k,T_C(k),I_C(k),F_C(k))|k\in M\}\in \mathcal{N}(M)$, where $\mathcal{N}(M)$ is a neutrosophic power set of parameter set $M,$ the lower soft rough neutrosophic approximation (LSRNA) and the upper soft rough neutrosophic approximation (USRNA) operators of C w.r.t $(Y,M,P)$ denoted by $\underline{P}(C)$ and $\overline{P}(C),$ are, respectively, defined as follows:

$$\overline{P}(C)=\{(u,T_{\overline{P}(C)}(u),I_{\overline{P}(C)}(u),F_{\overline{P}(C)}(u))|u\in Y\},$$

$$\underline{P}(C)=\{(u,T_{\underline{P}(C)}(u),I_{\underline{P}(C)}(u),F_{\underline{P}(C)}(u))|u\in Y\},$$

where

$$T_{\overline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigvee }{T}_C(k),I_{\overline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigwedge }{I}_C(k),F_{\overline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigwedge }{F}_C(k),$$

$$T_{\underline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigwedge }{T}_C(k),I_{\underline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigvee }{I}_C(k),F_{\underline{P}(C)}(u)=\underset{k\in P_s(u)}{\bigvee }{F}_C(k).$$

It is observed that $\overline{P}(C)$ and $\underline{P}(C)$ are two NSs on Y, $\underline{P}(C),\overline{P}(C):\mathcal{N}(M)\to \mathcal{P}(Y)$ are referred to as the LSRNA and the USRNA operators, respectively. The pair $(\underline{P}(C),\overline{P}(C))$ is called SRNS of C w.r.t $(Y,M,P)$.

Remark 1.

Let $(Y,M,P)$ be an SAS. If $C\in IF(M)$ and $C\in \mathcal{P}(M)$, where $IF(M)$ and $\mathcal{P}(M)$ are intuitionistic fuzzy power set and crisp power set of M, respectively. Then, the above SRNA operators $\underline{P}(C)$ and $\overline{P}(C)$ degenerate to SRIFA and SRA operators, respectively. Hence, SRNA operators are an extension of SRIFA and SRA operators.

Example 1.

Suppose that $Y=\{w_1,w_2,w_3,w_4,w_5\}$ is the set of five careers under observation, and Mr. X wants to select best suitable career. Let $M=\{k_1,k_2,k_3,k_4\}$ be a set of decision parameters. The parameters $k_1,k_2,k_3$ and $k_4$ stand for “aptitude”, “work value”, “skill” and “recent advancement”, respectively. Mr. X describes the “most suitable career” by defining a soft relation P from Y to M, which is a crisp soft set as shown in

Table 1. Crisp soft relation P.

P	${\mathit{w}}_{\mathbf{1}}$	${\mathit{w}}_{\mathbf{2}}$	${\mathit{w}}_{\mathbf{3}}$	${\mathit{w}}_{\mathbf{4}}$	${\mathit{w}}_{\mathbf{5}}$
$k_1$	$1$	$1$	$0$	$1$	$0$
$k_2$	$0$	$1$	$1$	$0$	$1$
$k_3$	$0$	$1$	$0$	$0$	$0$
$k_4$	$1$	$1$	$1$	$0$	$1$

.

$P_s:Y\to \mathcal{N}(M)$ is a set valued function, and we have $P_s(w_1)=\{k_1,k_4\},P_s(w_2)=\{k_1,k_2,k_3,k_4\},P_s(w_3)=\{k_2,k_4\},P_s(w_4)=\left\{k_1\right\}$ and $P_s(w_5)=\{k_2,k_4\}.$ Mr. X gives most the favorable parameter object C, which is an NS defined as follows:

$$C=\{(k_1,0.2,0.5,0.6),(k_2,0.4,0.3,0.2),(k_3,0.2,0.4,0.5),(k_4,0.6,0.2,0.1)\}.$$

From the Definition 1, we have

$$\begin{array}{ccc}\hfill T_{\overline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigvee }{T}_C(k)=\bigvee \{0.2,0.6\}=0.6,\hfill \\ \hfill I_{\overline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigwedge }{I}_C(k)=\bigwedge \{0.5,0.2\}=0.2,\hfill \\ \hfill F_{\overline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigwedge }{F}_C(k)=\bigwedge \{0.6,0.1\}=0.1,\hfill \end{array}$$

$$T_{\overline{P}(C)}(w_2)=0.6,I_{\overline{P}(C)}(w_2)=0.2,F_{\overline{P}(C)}(w_2)=0.1,$$

$$T_{\overline{P}(C)}(w_3)=0.6,I_{\overline{P}(C)}(w_3)=0.2,F_{\overline{P}(C)}(w_3)=0.1,$$

$$T_{\overline{P}(C)}(w_4)=0.2,I_{\overline{P}(C)}(w_4)=0.5,F_{\overline{P}(C)}(w_4)=0.6,$$

$$T_{\overline{P}(C)}(w_5)=0.6,I_{\overline{P}(C)}(w_5)=0.2,F_{\overline{P}(C)}(w_5)=0.1.$$

Similarly,

$$\begin{array}{ccc}\hfill T_{\underline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigwedge }{T}_C(k)=\bigwedge \{0.2,0.6\}=0.2,\hfill \\ \hfill I_{\underline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigvee }{I}_C(k)=\bigvee \{0.5,0.2\}=0.5,\hfill \\ \hfill F_{\underline{P}(C)}(w_1)& =& \underset{k\in P_s(w_1)}{\bigvee }{F}_C(k)=\bigvee \{0.6,0.1\}=0.6,\hfill \end{array}$$

$$T_{\underline{P}(C)}(w_2)=0.2,I_{\underline{P}(C)}(w_2)=0.5,F_{\underline{P}(C)}(w_2)=0.6,$$

$$T_{\underline{P}(C)}(w_3)=0.4,I_{\underline{P}(C)}(w_3)=0.3,F_{\underline{P}(C)}(w_3)=0.2,$$

$$T_{\underline{P}(C)}(w_4)=0.2,I_{\underline{P}(C)}(w_4)=0.5,F_{\underline{P}(C)}(w_4)=0.6,$$

$$T_{\underline{P}(C)}(w_5)=0.4,I_{\underline{P}(C)}(w_5)=0.3,F_{\underline{P}(C)}(w_5)=0.2.$$

Thus, we obtain

$$\begin{array}{ccc}\hfill \overline{P}(C)& =& \{(w_1,0.6,0.2,0.1),(w_2,0.6,0.2,0.1),(w_3,0.6,0.2,0.1),(w_4,0.2,0.5,0.6),(w_5,0.6,0.2,0.1)\},\hfill \\ \hfill \underline{P}(C)& =& \{(w_1,0.2,0.5,0.6),(w_2,0.2,0.5,0.6),(w_3,0.4,0.3,0.2),(w_4,0.2,0.5,0.6),(w_5,0.4,0.3,0.2)\}.\hfill \end{array}$$

Hence, $(\underline{P}(C),\overline{P}(C))$ is an SRNS of C.

Theorem 1.

Let $(Y,M,P)$ be an SAS. Then, the LSRNA and the USRNA operators $\underline{P}(C)$ and $\overline{P}(C)$ satisfy the following properties for all $C,D\in \mathcal{N}(M)$:

(i)

$\overline{P}(C)=\sim \underline{P}(\sim C),$

(ii)

$\underline{P}(C\cap D)=\underline{P}(C)\cap \underline{P}(D),$

(iii)

$C\subseteq D\Rightarrow \underline{P}(C)\subseteq \underline{P}(D),$

(iv)

$\underline{P}(C\cup D)\supseteq \underline{P}(C)\cup \underline{P}(D),$

(v)

$\underline{P}(C)=\sim \overline{P}(\sim C),$

(vi)

$\overline{P}(C\cup D)=\overline{P}(C)\cup \overline{P}(D),$

(vii)

$C\subseteq D\Rightarrow \overline{P}(C)\subseteq \overline{P}(D),$

(viii)

$\overline{P}(C\cap D)\subseteq \overline{P}(C)\cap \overline{P}(D),$

where $\sim C$ is the complement of C.

Proof. 

(i)

By definition of SRNS, we have

$$\begin{array}{ccc}\hfill \sim C& =& \left\{(k,F_C(k),1-I_C(k),T_C(k))\right\},\hfill \\ \hfill \underline{P}(\sim C)& =& \{(u,T_{\underline{P}(\sim C)}(u),I_{\underline{P}(\sim C)}(u),F_{\underline{P}(\sim C)}(u))|u\in Y\},\hfill \\ \hfill \sim \underline{P}(\sim C)& =& \{(u,F_{\underline{P}(\sim C)}(u),1-I_{\underline{P}(\sim C)}(u),T_{\underline{P}(\sim C)}(u))|u\in Y\},\hfill \end{array}$$

where

$$F_{\underline{P}(\sim C)}(u)=\underset{k\in P_s(u)}{\bigvee }{T}_C(k),I_{\underline{P}(\sim C)}(u)=\underset{k\in P_s(u)}{\bigvee }(1-I_C(k)),T_{\underline{P}(\sim C)}(u)=\underset{k\in P_s(u)}{\bigwedge }{F}_C(k).$$

Hence, $\sim \underline{P}(\sim C)=\overline{P}(C)$.

(ii)

$$\begin{array}{ccc}\hfill \underline{P}(C\cap D)& =& \{(u,T_{\underline{P}(C\cap D)}(u),I_{\underline{P}(C\cap D)}(u),F_{\underline{P}(C\cap D)}(u))|u\in Y\}\hfill \\ \hfill & =& \{(u,\underset{k\in P_s(u)}{\bigwedge }{T}_{(C\cap D)}(k),\underset{k\in P_s(u)}{\bigvee }{I}_{(C\cap D)}(k),\underset{k\in P_s(u)}{\bigvee }{F}_{(C\cap D)}(k))|u\in Y\}\hfill \\ \hfill & =& \{(u,\underset{k\in P_s(u)}{\bigwedge }(T_C(k)\wedge T_D(k)),\underset{k\in P_s(u)}{\bigvee }(I_C(k)\vee I_D(k)),\hfill \\ \hfill & & \underset{k\in P_s(u)}{\bigvee }(F_C(k)\vee F_D(k))|u\in Y\}\hfill \\ \hfill & =& \{(u,T_{\underline{P}(C)}(u)\wedge T_{\underline{P}(D)}(u),I_{\underline{P}(C)}(u)\vee I_{\underline{P}(D)}(u),F_{\underline{P}(C)}(u)\vee F_{\underline{P}(D)}(u))|u\in Y\}\hfill \\ \hfill & =& \underline{P}(C)\cap \underline{P}(D).\hfill \end{array}$$

(iii)

It can be easily proved by Definition 1.

(iv)

$$\begin{array}{ccc}\hfill T_{\underline{P}(C\cup D)}(u)& =& \underset{k\in P_s(u)}{\bigwedge }{T}_{C\cup D}(k)\hfill \\ \hfill & =& \underset{k\in P_s(u)}{\bigwedge }(T_C(k)\vee T_D(k))\hfill \\ \hfill & \ge & (\underset{k\in P_s(u)}{\bigwedge }{T}_C(k)\vee \underset{k\in P_s(u)}{\bigwedge }{T}_D(k))\hfill \\ \hfill & \ge & (T_{\underline{P}(C)}(u)\vee T_{\underline{P}(D)}(u)),\hfill \\ \hfill T_{\underline{P}(C\cup D)}(u)& \ge & T_{\underline{P}(C)}(u)\cup T_{\underline{P}(D)}(u).\hfill \end{array}$$

Similarly, we can prove that

$$\begin{array}{ccc}\hfill I_{\underline{P}(C\cup D)}(u)& \le & I_{\underline{P}(C)}(u)\cup I_{\underline{P}(D)}(u),\hfill \\ \hfill F_{\underline{P}(C\cup D)}(u)& \le & F_{\underline{P}(C)}(u)\cup F_{\underline{P}(D)}(u).\hfill \end{array}$$

Thus, $\underline{P}(C\cup D)\supseteq \underline{P}(C)\cup \underline{P}(D)$.

The properties (v)–(viii) of the USRNA $\overline{P}(C)$ can be easily proved similarly. ☐

Example 2.

Considering Example 1, we have

$$\begin{array}{ccc}\hfill \sim C& =& \{(k_1,0.6,0.5,0.2),(k_2,0.2,0.7,0.4),(k_3,0.5,0.6,0.2),(k_4,0.1,0.8,0.6)\},\hfill \\ \hfill \overline{P}(\sim C)& =& \{(w_1,0.6,0.5,0.2),(w_2,0.6,0.5,0.2),(w_3,0.2,0.7,0.4),(w_4,0.6,0.5,0.2),\hfill \\ \hfill & & (w_5,0.2,0.7,0.4)\},\hfill \\ \hfill \sim \overline{P}(\sim C)& =& \{(w_1,0.2,0.5,0.6),(w_2,0.2,0.5,0.6),(w_3,0.4,0.3,0.2),(w_4,0.2,0.5,0.6),\hfill \\ \hfill & & (w_5,0.4,0.3,0.2)\},\hfill \\ \hfill & =& \underline{P}(C).\hfill \\ \hfill LetD& =& \{(k_1,0.4,0.2,0.6),(k_2,0.5,0.3,0.2),(k_3,0.5,0.5,0.1),(k_4,0.6,0.4,0.7)\},\hfill \\ \hfill \underline{P}(D)& =& \{(w_1,0.4,0.4,0.7),(w_2,0.4,0.5,0.6),(w_3,0.5,0.4,0.7),(w_4,0.4,0.2,0.6),\hfill \\ \hfill & & (w_5,0.5,0.4,0.7)\},\hfill \\ \hfill C\cap D& =& \{(k_1,0.2,0.5,0.6),(k_2,0.4,0.3,0.2),(k_3,0.2,0.5,0.5),(k_4,0.6,0.4,0.7)\},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \underline{P}(C\cap D)& =& \{(w_1,0.2,0.5,0.7),(w_2,0.2,0.5,0.6),(w_3,0.4,0.4,0.7),(w_4,0.2,0.5,0.6),\hfill \\ \hfill & & (w_5,0.4,0.4,0.7)\},\hfill \\ \hfill \underline{P}(C)\cap \underline{P}(D)& =& \{(w_1,0.2,0.5,0.7),(w_2,0.2,0.5,0.6),(w_3,0.4,0.4,0.7),(w_4,0.2,0.5,0.6),\hfill \\ \hfill & & (w_5,0.4,0.4,0.7)\},\hfill \\ \hfill \underline{P}(C\cap D)& =& \underline{P}(C)\cap \underline{P}(D),\hfill \\ \hfill C\cup D& =& \{(k_1,0.4,0.2,0.6),(k_2,0.5,0.3,0.2),(k_3,0.5,0.4,0.1),(k_4,0.6,0.2,0.1)\},\hfill \\ \hfill \underline{P}(C\cup D)& =& \{(w_1,0.4,0.2,0.6),(w_2,0.4,0.4,0.6),(w_3,0.5,0.3,0.2),(w_4,0.4,0.2,0.6),\hfill \\ \hfill & & (w_5,0.5,0.3,0.2)\},\hfill \\ \hfill \underline{P}(C)\cup \underline{P}(D)& =& \{(w_1,0.4,0.4,0.6),(w_2,0.4,0.5,0.6),(w_3,0.5,0.3,0.2),(w_4,0.4,0.2,0.6),\hfill \\ \hfill & & (w_5,0.5,0.3,0.2)\}.\hfill \end{array}$$

Clearly, $\underline{P}(C\cup D)\supseteq \underline{P}(C)\cup \underline{P}(D)$. Hence, properties of the LSRNA operator hold, and we can easily verify the properties of the USRNA operator.

The conventional soft set is a mapping from a parameter to the subset of universe and let $(P,M)$ be a crisp soft set. In [11], Babitha and Sunil introduced the concept of soft set relation. Now, we present the constructive definition of SRNR by using a soft relation R from $M\times M=\acute{M}$ to $\mathcal{P}(Y\times Y=\acute{Y})$, where Y is a universal set and M is a set of parameter.

Definition 2.

A SRNR $(\underline{R}(D),\overline{R}(D))$ on Y is a SRNS, $R:\acute{M}\to \mathcal{P}(\acute{Y})$ is a soft relation on Y defined by

$$R(k_i{k}_j)=\{u_i{u}_j|\exists u_i\in P(k_i),u_j\in P(k_j)\},u_i{u}_j\in \acute{Y}.$$

Let $R_s:\acute{Y}\to \mathcal{P}(\acute{M})$ be a set-valued function by

$$R_s(u_i{u}_j)=\{k_i{k}_j\in \acute{M}|(u_i{u}_j,k_i{k}_j)\in R\},u_i{u}_j\in \acute{Y}.$$

For any $D\in \mathcal{N}(\acute{M}),$ the USRNA and the LSRNA operators of D w.r.t $(\acute{Y},\acute{M},R)$ defined as follows:

$$\overline{R}(D)=\{(u_i{u}_j,T_{\overline{R}(D)}(u_i{u}_j),I_{\overline{R}(D)}(u_i{u}_j),F_{\overline{R}(D)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

$$\underline{R}(D)=\{(u_i{u}_j,T_{\underline{R}(D)}(u_i{u}_j),I_{\underline{R}(D)}(u_i{u}_j),F_{\underline{R}(D)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

where

$$\begin{array}{ccc}\hfill T_{\overline{R}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigvee }{T}_D(k_i{k}_j),I_{\overline{R}(D)}(u_i{u}_j)=\underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigwedge }{I}_D(k_i{k}_j),\hfill \\ \hfill F_{\overline{R}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigwedge }{F}_D(k_i{k}_j),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\underline{R}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigwedge }{T}_D(k_i{k}_j),I_{\underline{R}(D)}(u_i{u}_j)=\underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigvee }{I}_D(k_i{k}_j),\hfill \\ \hfill F_{\underline{R}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in R_s(u_i{u}_j)}{\bigvee }{F}_D(k_i{k}_j).\hfill \end{array}$$

The pair $(\underline{R}(D),\overline{R}(D))$ is called SRNR and $\underline{R},\overline{R}:\mathcal{N}(\acute{M})\to \mathcal{P}(\acute{Y})$ are called the LSRNA and the USRNA operators, respectively.

Remark 2.

For an NS D on $\acute{M}$ and an NS C on M,

$$\begin{array}{ccc}\hfill T_D(k_i{k}_j)& \le & \underset{k_i\in M}{min}\left\{T_C(k_i)\right\},\hfill \\ \hfill I_D(k_i{k}_j)& \le & \underset{k_i\in M}{min}\left\{I_C(k_i)\right\},\hfill \\ \hfill F_D(k_i{k}_j)& \le & \underset{k_i\in M}{min}\left\{F_C(k_i)\right\}.\hfill \end{array}$$

According to the definition of SRNR, we get

$$\begin{array}{ccc}\hfill T_{\overline{R}(D)}(u_i{u}_j)& \le & min\{T_{\overline{R}(C)}(u_i),T_{\overline{R}(C)}(u_j)\},\hfill \\ \hfill I_{\overline{R}(D)}(u_i{u}_j)& \le & max\{I_{\overline{R}(C)}(u_i),I_{\overline{R}(C)}(u_j)\},\hfill \\ \hfill F_{\overline{R}(D)}(u_i{u}_j)& \le & max\{F_{\overline{R}(C)}(u_i),F_{\overline{R}(C)}(u_j)\}.\hfill \end{array}$$

Similarly, for the LSRNA operator $\underline{R}(D)$,

$$\begin{array}{ccc}\hfill T_{\underline{R}(D)}(u_i{u}_j)& \le & min\{T_{\underline{R}(C)}(u_i),T_{\underline{R}(C)}(u_j)\},\hfill \\ \hfill I_{\underline{R}(D)}(u_i{u}_j)& \le & max\{I_{\underline{R}(C)}(u_i),I_{\underline{R}(C)}(u_j)\},\hfill \\ \hfill F_{\underline{R}(D)}(u_i{u}_j)& \le & max\{F_{\underline{R}(C)}(u_i),F_{\underline{R}(C)}(u_j)\}.\hfill \end{array}$$

Example 3.

Let $Y=\{u_1,u_2,u_3\}$ be a universal set and $M=\{k_1,k_2,k_3\}$ be a set of parameters. A soft set $(P,M)$ on Y can be defined in tabular form (see

Table 2. Soft set $(P,M)$.

P	${\mathit{u}}_{\mathbf{1}}$	${\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}$
$k_1$	$1$	$1$	$0$
$k_2$	$0$	$0$	$1$
$k_3$	$1$	$1$	$1$

) as follows:

Let $E=\{u_1{u}_2,u_2{u}_3,u_2{u}_2,u_3{u}_2\}\subseteq \acute{Y}$ and $L=\{k_1{k}_3,k_2{k}_1,k_3{k}_2\}\subseteq \acute{M}$. Then, a soft relation R on E (from L to E) can be defined in tabular form (see

Table 3. Soft relation R.

R	${\mathit{u}}_{\mathbf{1}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}{\mathit{u}}_{\mathbf{2}}$
$k_1{k}_3$	$1$	$1$	$1$	$0$
$k_2{k}_1$	$0$	$0$	$0$	$1$
$k_3{k}_2$	$0$	$1$	$0$	$0$

) as follows:

Now, we can define set-valued function $R_s$ such that

$$\begin{array}{ccc}\hfill R_s(u_1{u}_2)& =& \left\{k_1{k}_3\right\},R_s(u_2{u}_3)=\{k_1{k}_3,k_3{k}_2\},R_s(u_2{u}_2)=\left\{k_1{k}_3\right\},R_s(u_3{u}_2)=\left\{k_2{k}_1\right\}.\hfill \end{array}$$

• Let $C=\{(k_1,0.2,0.4,0.6),(k_2,0.4,0.5,0.2),(k_3,0.1,0.2,0.4)\}$ be an NS on M, then
• $\overline{R}(C)=\{(u_1,0.2,0.2,0.4),(u_2,0.2,0.4,0.4),(u_3,0.4,0.2,0.2)\},$
• $\underline{R}(C)=\{(u_1,0.1,0.4,0.6),(u_2,0.1,0.4,0.6),(u_3,0.1,0.5,0.4)\},$
• Let $D=\{(k_1{k}_3,0.1,0.2,0.2),(k_2{k}_1,0.1,0.1,0.2),(k_3{k}_2,0.1,0.2,0.1)\}$ be an NS on $L,$ then
• $\overline{R}(D)=\{(u_1{u}_2,0.1,0.2,0.2),(u_2{u}_3,0.1,0.2,0.1),(u_2{u}_2,0.1,0.2,0.2),(u_3{u}_2,0.1,0.1,0.2)\},$
• $\underline{R}(D)=\{(u_1{u}_2,0.1,0.2,0.2),(u_2{u}_3,0.1,0.2,0.1),(u_2{u}_2,0.1,0.2,0.2),(u_3{u}_2,0.1,0.1,0.2)\}.$

Hence, $R(D)=(\underline{R}(D),\overline{R}(D))$ is SRNR.

3. Construction of Neutrosophic Soft Rough Sets

In this section, we will introduce the notions of NSRSs, neutrosophic soft rough relations (NSRRs).

Definition 3.

Let Y be an initial universal set and M a universal set of parameters. For an arbitrary neutrosophic soft relation $\tilde{P}$ from Y to M, $(Y,M,\tilde{P})$ is called neutrosophic soft approximation space (NSAS). For any NS $C\in \mathcal{N}(M),$ we define the upper neutrosophic soft approximation (UNSA) and the lower neutrosophic soft approximation (LNSA) operators of C with respect to $(Y,M,\tilde{P})$ denoted by $\overline{\tilde{P}}(C)$ and $\underline{\tilde{P}}(C),$ respectively as follows:

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(C)& =& \{(u,T_{\overline{\tilde{P}}(C)}(u),I_{\overline{\tilde{P}}(C)}(u),F_{\overline{\tilde{P}}(C)}(u))|u\in Y\},\hfill \\ \hfill \underline{\tilde{P}}(C)& =& \{(u,T_{\underline{\tilde{P}}(C)}(u),I_{\underline{\tilde{P}}(C)}(u),F_{\underline{\tilde{P}}(C)}(u))|u\in Y\},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}(C)}(u,k)\wedge T_C(k)\right),I_{\overline{\tilde{P}}(C)}(u)=\underset{k\in M}{\bigwedge }\left(I_{\tilde{P}(C)}(u,k)\vee I_C(k)\right),\hfill \\ \hfill F_{\overline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}(C)}(u,k)\vee F_C(k)\right),\hfill \\ \hfill T_{\underline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}(C)}(u,k)\vee T_C(k)\right),I_{\underline{\tilde{P}}(C)}(u)=\underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}(C)}(u,k))\wedge I_C(k)\right),\hfill \\ \hfill F_{\underline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}(C)}(u,k)\wedge F_C(k)\right).\hfill \end{array}$$

The pair $(\underline{\tilde{P}}(C),\overline{\tilde{P}}(C))$ is called NSRS of C w.r.t $(Y,M,\tilde{P}),and\underline{\tilde{P}}$ and $\overline{\tilde{P}}$ are referred to as the LNSRA and the UNSRA operators, respectively.

Remark 3.

A neutrosophic soft relation over $Y\times M$ is actually a neutrosophic soft set on Y. The NSRA operators are defined over two distinct universes Y and M. As we know, universal set Y and parameter set M are two different universes of discourse but have solid relations. These universes can not be considered as identical universes; therefore, the reflexive, symmetric and transitive properties of neutrosophic soft relations from Y to M do not exist.

Let $\tilde{P}$ be a neutrosophic soft relation from Y to M, if, for each $u\in Y$, there exists $k\in M$ such that $T_{\tilde{P}}(u,k)=1,I_{\tilde{P}}(u,k)=0,F_{\tilde{P}}(u,k)=0$. Then, $\tilde{P}$ is referred to as a serial neutrosophic soft relation from Y to parameter set M.

Example 4.

Suppose that $Y=\{w_1,w_2,w_3,w_4\}$ is the set of careers under consideration, and Mr. X wants to select the most suitable career. $M=\{k_1,k_2,k_3\}$ is a set of decision parameters. Mr. X describes the “most suitable career” by defining a neutrosophic soft set $(\tilde{P},M)$ on Y that is a neutrosophic relation from Y to M as shown in

Table 4. Neutrosophic soft relation $\tilde{P}$.

$\tilde{\mathit{P}}$	${\mathit{w}}_{\mathbf{1}}$	${\mathit{w}}_{\mathbf{2}}$	${\mathit{w}}_{\mathbf{3}}$	${\mathit{w}}_{\mathbf{4}}$
$k_1$	$(0.3,0.4,0.5)$	$(0.4,0.2,0.3)$	$(0.1,0.5,0.4)$	$(0.2,0.3,0.4)$
$k_2$	$(0.1,0.5,0.4)$	$(0.3,0.4,0.6)$	$(0.4,0.4,0.3)$	$(0.5,0.3,0.8)$
$k_3$	$(0.3,0.4,0.4)$	$(0.4,0.6,0.7)$	$(0.3,0.5,0.4)$	$(0.5,0.4,0.6)$

.

Now, Mr. X gives the most favorable decision object C, which is an NS on M defined as follows: $C=\{(k_1,0.5,0.2,0.4),(k_2,0.2,0.3,0.1),(k_3,0.2,0.4,0.6)\}$. By Definition 3, we have

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}(C)}(w_1,k)\wedge T_C(k)\right)=\bigvee \{0.3,0.1,0.2\}=0.3,\hfill \\ \hfill I_{\overline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigwedge }\left(I_{\tilde{P}(C)}(w_1,k)\vee I_C(k)\right)=\bigwedge \{0.4,0.5,0.4\}=0.4,\hfill \\ \hfill F_{\overline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}(C)}(w_1,k)\vee F_C(k)\right)=\bigwedge \{0.5,0.4,0.6\}=0.4,\hfill \end{array}$$

$$T_{\overline{\tilde{P}}(C)}(w_2)=0.4,I_{\overline{\tilde{P}}(C)}(w_2)=0.2,F_{\overline{\tilde{P}}(C)}(w_2)=0.4,$$

$$T_{\overline{\tilde{P}}(C)}(w_3)=0.2,I_{\overline{\tilde{P}}(C)}(w_3)=0.4,F_{\overline{\tilde{P}}(C)}(w_3)=0.3,$$

$$T_{\overline{\tilde{P}}(C)}(w_4)=0.2,I_{\overline{\tilde{P}}(C)}(w_4)=0.3,F_{\overline{\tilde{P}}(C)}(w_4)=0.4.$$

Similarly,

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}(C)}(w_1,k)\vee T_C(k)\right)=\bigwedge \{0.5,0.4,0.4\}=0.4,\hfill \\ \hfill I_{\underline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}(C)}(w_1,k))\wedge I_C(k)\right)=\bigvee \{0.2,0.3,0.4\}=0.4,\hfill \\ \hfill F_{\underline{\tilde{P}}(C)}(w_1)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}(C)}(w_1,k)\wedge F_C(k)\right)=\bigvee \{0.3,0.1,0.3\}=0.3,\hfill \end{array}$$

$$T_{\underline{\tilde{P}}(C)}(w_2)=0.5,I_{\underline{\tilde{P}}(C)}(w_2)=0.4,F_{\underline{\tilde{P}}(C)}(w_2)=0.4,$$

$$T_{\underline{\tilde{P}}(C)}(w_3)=0.4,I_{\underline{\tilde{P}}(C)}(w_3)=0.4,F_{\underline{\tilde{P}}(C)}(w_3)=0.3,$$

$$T_{\underline{\tilde{P}}(C)}(w_4)=0.5,I_{\underline{\tilde{P}}(C)}(w_4)=0.4,F_{\underline{\tilde{P}}(C)}(w_4)=0.5.$$

Thus, we obtain

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(C)& =& \{(w_1,0.3,0.4,0.4),(w_2,0.4,0.2,0.4),(w_3,0.2,0.4,0.3),(w_4,0.2,0.3,0.4)\},\hfill \\ \hfill \underline{\tilde{P}}(C)& =& \{(w_1,0.4,0.4,0.3),(w_2,0.5,0.4,0.4),(w_3,0.4,0.4,0.3),(w_4,0.5,0.4,0.5)\}.\hfill \end{array}$$

Hence, $(\underline{\tilde{P}}(C),\overline{\tilde{P}}(C))$ is an NSRS of C.

Theorem 2.

Let $(Y,M,\tilde{P})$ be an NSAS. Then, the UNSRA and the LNSRA operators $\overline{\tilde{P}}(C)$ and $\underline{\tilde{P}}(C)$ satisfy the following properties for all $C,D\in \mathcal{N}(M)$:

(i)

$\underline{\tilde{P}}(C)=\sim \overline{\tilde{P}}(\sim A),$

(ii)

$\underline{\tilde{P}}(C\cap D)=\underline{\tilde{P}}(C)\cap \underline{\tilde{P}}(D),$

(iii)

$C\subseteq D\Rightarrow \underline{\tilde{P}}(C)\subseteq \underline{\tilde{P}}(D),$

(iv)

$\underline{\tilde{P}}(C\cup D)\supseteq \underline{\tilde{P}}(C)\cup \underline{\tilde{P}}(D),$

(v)

$\overline{\tilde{P}}(C)=\sim \underline{\tilde{P}}(\sim C),$

(vi)

$\overline{\tilde{P}}(C\cup D)=\overline{\tilde{P}}(C)\cup \overline{\tilde{P}}(D),$

(vii)

$C\subseteq D\Rightarrow \overline{\tilde{P}}(C)\subseteq \overline{\tilde{P}}(D),$

(viii)

$\overline{\tilde{P}}(C\cap D)\subseteq \overline{\tilde{P}}(C)\cap \overline{\tilde{P}}(D).$

Proof. 

(i)

$$\begin{array}{ccc}\hfill \sim C& =& \{(k,F_C(k),1-I_C(k),T_C(k))|k\in M\}.\hfill \\ \hfill \mathrm{By}\mathrm{definition}\mathrm{of}\mathrm{NSRS},\mathrm{we}\mathrm{have}& & \hfill \\ \hfill \tilde{P}(\sim C)& =& \{\left(u,T_{\overline{\tilde{P}}(\sim C)}(u),I_{\overline{\tilde{P}}(\sim C)}(u),F_{\overline{\tilde{P}}(\sim C)}(u)\right)|u\in Y\},\hfill \\ \hfill \sim \tilde{P}(\sim C)& =& \{\left(u,F_{\overline{\tilde{P}}(\sim C)}(u),1-I_{\overline{\tilde{P}}(\sim C)}(u),T_{\overline{\tilde{P}}(\sim C)}(u)\right)|u\in Y\},\hfill \\ \hfill F_{\overline{\tilde{P}}(\sim C)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_C(k)\right)\hfill \\ \hfill & =& T_{\underline{\tilde{P}}(C)}(u),\hfill \\ \hfill 1-I_{\overline{\tilde{P}}(\sim C)}(u)& =& 1-\left(\underset{k\in M}{\bigwedge }[I_{\tilde{P}}(u,k)\vee I_{\sim C}(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge (1-I_{\sim C}(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge \left(1-(1-I_C(k))\right)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_C(k)\right)\hfill \\ \hfill & =& I_{\underline{\tilde{P}}(C)}(u),\hfill \\ \hfill T_{\overline{\tilde{P}}(\sim C)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_{\sim C}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge F_C(k)\right)\hfill \\ \hfill & =& F_{\underline{\tilde{P}}(C)}(u).\hfill \\ \hfill \mathrm{Thus},\underline{\tilde{P}}(C)& =& \sim \overline{\tilde{P}}(\sim C).\hfill \end{array}$$

(ii)

$$\begin{array}{ccc}\hfill \underline{\tilde{P}}(C\cap D)& =& \left\{\left(u,T_{\underline{\tilde{P}}(C\cap D)}(u),I_{\underline{\tilde{P}}(C\cap D)}(u),F_{\underline{\tilde{P}}(C\cap D)}(u)\right)\right\},\hfill \\ \hfill \underline{\tilde{P}}(C)\cap \underline{\tilde{P}}(D)& =& \left\{\left(u,T_{\underline{\tilde{P}}(C)}(u)\wedge T_{\underline{\tilde{P}}(D)}(u),I_{\underline{\tilde{P}}(C)}(u)\vee I_{\underline{\tilde{P}}(D)}(u),F_{\underline{\tilde{P}}(C)}(u)\vee F_{\underline{\tilde{P}}(D)}(u)\right)\right\}.\hfill \end{array}$$

Now, consider

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\underline{\tilde{P}}}(u,k)\vee T_{C\cap D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\underline{\tilde{P}}}(u,k)\vee (T_C(k)\wedge T_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\underline{\tilde{P}}}(u,k)\vee T_C(k)\right)\wedge \underset{k\in M}{\bigwedge }\left(F_{\underline{\tilde{P}}}(u,k)\vee T_D(k)\right)\hfill \\ \hfill & =& T_{\underline{\tilde{P}}(C)}(u)\wedge T_{\underline{\tilde{P}}(D)}(u),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_{\underline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge I_{C\cap D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge (I_C(k)\vee I_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k)))\wedge I_C(k)\right)\vee \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\vee I_D(k)\right)\hfill \\ \hfill & =& I_{\underline{\tilde{P}}(C)}(u)\vee I_{\underline{\tilde{P}}(D)}(u),\hfill \\ \hfill F_{\underline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_{C\cap D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge (F_C(k)\vee F_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_C(k)\right)\vee \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_D(k)\right)\hfill \\ \hfill & =& F_{\underline{\tilde{P}}(C)}(u)\vee F_{\underline{\tilde{P}}(D)}(u).\hfill \\ \hfill \mathrm{Thus},\underline{\tilde{P}}(C\cap D)& =& \underline{\tilde{P}}(C)\cap \underline{\tilde{P}}(D).\hfill \end{array}$$

(iii)

It can be easily proven by Definition 3.

(iv)

$$\begin{array}{ccc}\hfill \underline{\tilde{P}}(C\cup D)& =& \left\{\left(u,T_{\underline{\tilde{P}}(C\cup D)}(u),I_{\underline{\tilde{P}}(C\cup D)}(u),F_{\underline{\tilde{P}}(C\cup D)}(u)\right)\right\},\hfill \\ \hfill \underline{\tilde{P}}(C)\cup \underline{\tilde{P}}(D)& =& \left\{\left(u,T_{\underline{\tilde{P}}(C)}(u)\vee T_{\underline{\tilde{P}}(D)}(u),I_{\underline{\tilde{P}}(C)}(u)\wedge I_{\underline{\tilde{P}}(D)}(u),F_{\underline{\tilde{P}}(C)}(u)\wedge F_{\underline{\tilde{P}}(D)}(u)\right)\right\},\hfill \\ \hfill T_{\underline{\tilde{P}}(C\cup D)}(u)& =& \underset{k\in M}{\bigwedge }(F_{\tilde{P}}(u,k)\vee T_{C\cup D}(k))\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee [T_C(k)\vee T_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([F_{\tilde{P}}(u,k)\vee T_C(k)]\vee [F_{\tilde{P}}(u,k)\vee T_D(k)]\right)\hfill \\ \hfill & \ge & \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_C(k)\right)\vee \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_D(k)\right)\hfill \\ \hfill & =& T_{\underline{\tilde{P}}(C)}(u)\vee T_{\underline{\tilde{P}}(D)}(u),\hfill \\ \hfill I_{\underline{\tilde{P}}(C\cup D)}(u)& =& \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge I_{C\cup D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge [I_C(k)\wedge I_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([1-I_{\underline{\tilde{P}}}(u,k))\wedge I_C(k)]\wedge [(1-I_{\underline{\tilde{P}}}(u,k))\wedge I_D(k)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge I_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left((1-I_{\underline{\tilde{P}}}(u,k))\wedge I_D(k)\right)\hfill \\ \hfill & =& I_{\underline{\tilde{P}}(C)}(u)\wedge I_{\underline{\tilde{P}}(D)}(u),\hfill \\ \hfill F_{\underline{\tilde{P}}(C\cup D)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_{C\cup D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge [F_C(k)\wedge F_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([T_{\underline{\tilde{P}}}(u,k)\wedge F_C(k)]\wedge [T_{\underline{\tilde{P}}}(u,k)\wedge F_D(k)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left(T_{\underline{\tilde{P}}}(u,k)\wedge F_D(k)\right)\hfill \\ \hfill & =& F_{\underline{\tilde{P}}(C)}(u)\wedge F_{\underline{\tilde{P}}(D)}(u).\hfill \end{array}$$

(vii)

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(C\cap D)& =& \left\{\left(u,T_{\overline{\tilde{P}}(C\cap D)}(u),I_{\overline{\tilde{P}}(C\cap D)}(u),F_{\overline{\tilde{P}}(C\cap D)}(u)\right)\right\},\hfill \\ \hfill \overline{\tilde{P}}(C)\cap \overline{\tilde{P}}(D)& =& \left\{\left(u,T_{\overline{\tilde{P}}(C)}(u)\wedge T_{\overline{\tilde{P}}(D)}(u),I_{\overline{\tilde{P}}(C)}(u)\vee I_{\overline{\tilde{P}}(D)}(u),F_{\overline{\tilde{P}}(C)}(u)\vee F_{\overline{\tilde{P}}(D)}(u)\right)\right\},\hfill \\ \hfill T_{\overline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigvee }(T_{\tilde{P}}(u,k)\wedge T_{C\cap D}(k))\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge [T_C(k)\wedge T_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([T_{\tilde{P}}(u,k)\wedge T_C(k)]\wedge [T_{\tilde{P}}(u,k)\wedge T_D(k)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_D(k)\right)\hfill \\ \hfill & =& T_{\overline{\tilde{P}}(C)}(u)\wedge T_{\overline{\tilde{P}}(D)}(u),\hfill \\ \hfill I_{\overline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigwedge }\left(I_{\overline{\tilde{P}}}(u,k)\vee I_{C\cap D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(I_{\overline{\tilde{P}}}(u,k)\vee [I_C(k)\vee I_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([I_{\overline{\tilde{P}}}(u,k)\vee I_C(k)]\vee [I_{\overline{\tilde{P}}}(u,k)\vee I_D(k)]\right)\hfill \\ \hfill & \ge & \underset{k\in M}{\bigwedge }\left((I_{\overline{\tilde{P}}}(u,k))\vee I_C(k)\right)\vee \underset{k\in M}{\bigwedge }\left((I_{\overline{\tilde{P}}}(u,k))\vee I_D(k)\right)\hfill \\ \hfill & =& I_{\overline{\tilde{P}}(C)}(u)\vee I_{\overline{\tilde{P}}(D)}(u),\hfill \\ \hfill F_{\overline{\tilde{P}}(C\cap D)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\overline{\tilde{P}}}(u,k)\vee F_{C\cap D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\overline{\tilde{P}}}(u,k)\vee [F_C(k)\vee F_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([F_{\overline{\tilde{P}}}(u,k)\vee F_C(k)]\vee [F_{\overline{\tilde{P}}}(u,k)\vee F_D(k)]\right)\hfill \\ \hfill & \ge & \underset{k\in M}{\bigwedge }\left(F_{\overline{\tilde{P}}}(u,k)\vee F_C(k)\right)\vee \underset{k\in M}{\bigwedge }\left(F_{\overline{\tilde{P}}}(u,k)\vee F_D(k)\right)\hfill \\ \hfill & =& F_{\overline{\tilde{P}}(C)}(u)\vee F_{\overline{\tilde{P}}(D)}(u).\hfill \\ \hfill \mathrm{Thus},\overline{\tilde{P}}(C\cap D)& \subseteq & \overline{\tilde{P}}(C)\cap \overline{\tilde{P}}(D).\hfill \end{array}$$

The properties (v)–(vii) of the UNSRA operator $\overline{\tilde{P}}(C)$ can be easily proved similarly. ☐

Theorem 3.

Let $(Y,M,\tilde{P})$ be an NSAS. The UNSRA and the LNSRA operators $\overline{\tilde{P}}$ and $\underline{\tilde{P}}$ satisfy the following properties for all $C,D\in \mathcal{N}(M)$:

(i)

$\underline{\tilde{P}}(C-D)\supseteq \underline{\tilde{P}}(C)-\overline{\tilde{P}}(D)$,

(ii)

$\overline{\tilde{P}}(C-D)\subseteq \overline{\tilde{P}}(C)-\underline{\tilde{P}}(D).$

Proof. 

(i)

By Definition 3 and definition of difference of two NSs, for all $u\in Y,$

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee (T_C(k)\wedge F_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([F_{\tilde{P}}(u,k)\vee T_C(k)]\wedge [F_{\tilde{P}}(u,k)\vee F_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_C(k)\right)\wedge \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee F_D(k)\right)\hfill \\ \hfill & =& T_{\underline{\tilde{P}}(C)}(u)\wedge F_{\overline{\tilde{P}}(D)}(u)\hfill \\ \hfill & =& T_{\underline{\tilde{P}}(C)-\overline{\tilde{P}}(D)}(u),\hfill \\ \hfill I_{\underline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge (I_C(k)\wedge (1-I_D(k)))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([(1-I_{\tilde{P}}(u,k))\wedge I_C(k)]\wedge [(1-I_{\tilde{P}}(u,k))\wedge (1-I_D(k))]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([(1-I_{\tilde{P}}(u,k))\wedge I_C(k)]\wedge [1-\left(I_{\tilde{P}}(u,k)\vee I_D(k)\right)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left(1-\left(I_{\tilde{P}}(u,k)\vee I_D(k)\right)\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_C(k)\right)\wedge \left(1-\underset{k\in M}{\bigwedge }\left(I_{\tilde{P}}(u,k)\vee I_D(k)\right)\right)\hfill \\ \hfill & =& I_{\underline{\tilde{P}}(C)}(u)\wedge (1-I_{\overline{\tilde{P}}(D)}(u))\hfill \\ \hfill & =& I_{\underline{\tilde{P}}(C)-\overline{\tilde{P}}(D)}(u),\hfill \\ \hfill F_{\underline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge F_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge (F_C(k)\wedge T_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([T_{\tilde{P}}(u,k)\wedge F_C(k)]\wedge [T_{\tilde{P}}(u,k)\wedge T_D(k)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge F_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_D(k)\right)\hfill \\ \hfill & =& F_{\underline{\tilde{P}}(C)}(u)\wedge T_{\overline{\tilde{P}}(D)}(u)\hfill \\ \hfill & =& F_{\underline{\tilde{P}}(C)-\overline{\tilde{P}}(D)}(u).\hfill \\ \hfill \mathrm{Thus},\underline{\tilde{P}}(C-D)& \subseteq & \underline{\tilde{P}}(C)-\overline{\tilde{P}}(D).\hfill \end{array}$$

(ii)

By Definition 3 and definition of difference of two NSs, for all $u\in Y,$

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge (T_C(k)\wedge F_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigvee }\left([T_{\tilde{P}}(u,k)\wedge T_C(k)]\wedge [T_{\tilde{P}}(u,k)\wedge F_D(k)]\right)\hfill \\ \hfill & \le & \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_C(k)\right)\wedge \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge F_D(k)\right)\hfill \\ \hfill & =& T_{\overline{\tilde{P}}(C)}(u)\wedge F_{\underline{\tilde{P}}(D)}(u)\hfill \\ \hfill & =& T_{\overline{\tilde{P}}(C)-\underline{\tilde{P}}(D)}(u),\hfill \\ \hfill I_{\overline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigwedge }\left(I_{\tilde{P}}(u,k)\vee I_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(I_{\tilde{P}}(u,k)\vee (I_C(k)\wedge (1-I_D(k)))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([I_{\tilde{P}}(u,k)\vee I_C(k)]\wedge [I_{\tilde{P}}(u,k)\vee (1-I_D(k))]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([I_{\tilde{P}}(u,k)\vee I_C(k)]\wedge [1-(1-I_{\tilde{P}}(u,k))\vee (1-I_D(k))]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }(I_{\tilde{P}}(u,k)\vee I_C(k))\wedge \left(1-\underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_D(k)\right)\right)\hfill \\ \hfill & =& I_{\overline{\tilde{P}}(C)}(u)\wedge (1-I_{\underline{\tilde{P}}(D)}(u))\hfill \\ \hfill & =& I_{\overline{\tilde{P}}(C)-\underline{\tilde{P}}(D)}(u),\hfill \\ \hfill F_{\overline{\tilde{P}}(C-D)}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee F_{C-D}(k)\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee (F_C(k)\wedge T_D(k))\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left([F_{\tilde{P}}(u,k)\vee F_C(k)]\wedge [F_{\tilde{P}}(u,k)\vee T_D(k)]\right)\hfill \\ \hfill & =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee F_C(k)\right)\wedge \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_D(k)\right)\hfill \\ \hfill & =& F_{\overline{\tilde{P}}(C)}(u)\wedge T_{\underline{\tilde{P}}(D)}(u)\hfill \\ \hfill & =& F_{\overline{\tilde{P}}(C)-\underline{\tilde{P}}(D)}(u).\hfill \\ \hfill \mathrm{Thus},\overline{\tilde{P}}(C-D)& \subseteq & \overline{\tilde{P}}(C)-\underline{\tilde{P}}(D).\hfill \end{array}$$

 ☐

Theorem 4.

Let $(Y,M,\tilde{P})$ be an NSAS. If $\tilde{P}$ is serial, then the UNSA and the LNSA operators $\overline{\tilde{P}}$ and $\underline{\tilde{P}}$ satisfy the following properties for all $\varnothing ,\mathbb{M},C\in \mathcal{N}(M)$:

(i)

$\overline{\tilde{P}}(\varnothing )=\varnothing ,\underline{\tilde{P}}(\mathbb{M})=\mathbb{Y},$

(ii)

$\underline{\tilde{P}}(C)\subseteq \overline{\tilde{P}}(C).$

Proof. 

(i)

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(\varnothing )& =& \{(u,T_{\overline{\tilde{P}}(\varnothing )}(u),I_{\overline{\tilde{P}}(\varnothing )}(u),F_{\overline{\tilde{P}}(\varnothing )}(u))|u\in Y\},\hfill \\ \hfill T_{\overline{\tilde{P}}(\varnothing )}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge T_{\varnothing }(k)\right),\hfill \\ \hfill I_{\overline{\tilde{P}}(\varnothing )}(u)& =& \underset{k\in M}{\bigwedge }\left(I_{\tilde{P}}(u,k)\vee I_{\varnothing }(k)\right),\hfill \\ \hfill F_{\overline{\tilde{P}}(\varnothing )}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee F_{\varnothing }(k)\right).\hfill \end{array}$$

Since ∅ is a null NS on M, $T_{\varnothing }(k)=0,I_{\varnothing }(k)=1,F_{\varnothing }(k)=1,\mathrm{and}\mathrm{this}\mathrm{implies}{T}_{\overline{\tilde{P}}(\varnothing )}(u)=0,I_{\overline{\tilde{P}}}(u)=1,F_{\overline{\tilde{P}}}(u)=1.\mathrm{Thus},\overline{\tilde{P}}(\varnothing )=\varnothing .$

Now,

$$\begin{array}{ccc}\hfill \underline{\tilde{P}}(\mathbb{M})& =& \{(u,T_{\underline{\tilde{P}}(\mathbb{M})}(u),I_{\underline{\tilde{P}}(\mathbb{M})}(u),F_{\underline{\tilde{P}}(\mathbb{M})}(u))|u\in Y\},\hfill \\ \hfill T_{\underline{\tilde{P}}(\mathbb{M})}(u)& =& \underset{k\in M}{\bigwedge }\left(F_{\tilde{P}}(u,k)\vee T_{\mathbb{M}}(k)\right),I_{\underline{\tilde{P}}(\mathbb{M})}(u)=\underset{k\in M}{\bigvee }\left((1-I_{\tilde{P}}(u,k))\wedge I_{\mathbb{M}}(k)\right),\hfill \\ \hfill F_{\underline{\tilde{P}}(\mathbb{M})}(u)& =& \underset{k\in M}{\bigvee }\left(T_{\tilde{P}}(u,k)\wedge F_{\mathbb{M}}(k)\right).\hfill \end{array}$$

Since $\mathbb{M}$ is full NS on $M,$$T_{\mathbb{M}}(k)=1,I_{\mathbb{M}}(k)=0,F_{\mathbb{M}}(k)=0$, for all $k\in M$, and this implies $T_{\underline{\tilde{P}}(\mathbb{M})}(u)=1,I_{\underline{\tilde{P}}(\mathbb{M})}(u)=0,F_{\underline{\tilde{P}}(\mathbb{M})}(u)=0.$ Thus, $\underline{\tilde{P}}(\mathbb{M})=\mathbb{Y}.$

(ii)

Since $(Y,M,\tilde{P})$ is an NSAS and $\tilde{P}$ is a serial neutrosophic soft relation, then, for each $u\in Y$, there exists $k\in M$, such that $T_{\tilde{P}}(u,k)=1,I_{\tilde{P}}(u,k)=0,$ and $F_{\tilde{P}}(u,k)=0$. The UNSRA and LNSRA operators $\overline{\tilde{P}}(C)$, and $\underline{\tilde{P}}(C)$ of an NS C can be defined as:

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigvee }{T}_C(k),I_{\overline{\tilde{P}}(C)}(u)=\underset{k\in M}{\bigwedge }{I}_C(k),\hfill \\ \hfill F_{\overline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigwedge }{F}_C(k),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigwedge }{T}_C(k),I_{\underline{\tilde{P}}(C)}(u)=\underset{k\in M}{\bigvee }{I}_C(k),\hfill \\ \hfill F_{\underline{\tilde{P}}(C)}(u)& =& \underset{k\in M}{\bigvee }{F}_C(k).\hfill \end{array}$$

Clearly, $T_{\underline{\tilde{P}}(C)}(u)\le T_{\overline{\tilde{P}}(C)}(u),I_{\underline{\tilde{P}}(C)}(u)\ge T_{\overline{\tilde{P}}(C)}(u),F_{\underline{\tilde{P}}(C)}(u)\ge F_{\overline{\tilde{P}}(C)}(u)$ for all $u\in Y.$ Thus, $\underline{\tilde{P}}(C)\subseteq \overline{\tilde{P}}(C)$.

 ☐

The conventional NSS is a mapping from a parameter to the neutrosophic subset of universe and let $(\tilde{P},M)$ be NSS. Now, we present the constructive definition of neutrosophic soft rough relation by using a neutrosophic soft relation $\tilde{R}$ from $M\times M=\acute{M}$ to $\mathcal{N}(Y\times Y=\acute{Y})$, where Y is a universal set and M is a set of parameters.

Definition 4.

A neutrosophic soft rough relation $(\underline{\tilde{R}}(D),\overline{\tilde{R}}(D))$ on Y is an NSRS, $\tilde{R}:\acute{M}\to \mathcal{N}(\acute{Y})$ is a neutrosophic soft relation on Y defined by

$$\tilde{R}(k_i{k}_j)=\{u_i{u}_j|\exists u_i\in \tilde{P}(k_i),u_j\in \tilde{P}(k_j)\},u_i{u}_j\in \acute{Y},$$

such that

$$\begin{array}{cc}\hfill T_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\le & min\{T_{\tilde{P}}(u_i,k_i),T_{\tilde{P}}(u_j,k_j)\},\\ \hfill I_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\le & max\{I_{\tilde{P}}(u_i,k_i),I_{\tilde{P}}(u_j,k_j)\},\\ \hfill F_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\le & max\{F_{\tilde{P}}(u_i,k_i),F_{\tilde{P}}(u_j,k_j)\}.\end{array}$$

For any $D\in \mathcal{N}(\acute{M}),$ the UNSA and the LNSA of B w.r.t $(\acute{Y},\acute{M},\tilde{R})$ are defined as follows:

$$\overline{\tilde{R}}(D)=\{(u_i{u}_j,T_{\overline{\tilde{R}}(D)}(u_i{u}_j),I_{\overline{\tilde{R}}(D)}(u_i{u}_j),F_{\overline{\tilde{R}}(D)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

$$\underline{\tilde{R}}(D)=\{(u_i{u}_j,T_{\underline{\tilde{R}}(D)}(u_i{u}_j),I_{\underline{\tilde{R}}(D)}(u_i{u}_j),F_{\underline{\tilde{R}}(D)}(u_i{u}_j))|u_i{u}_j\in \acute{Y}\},$$

where

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \acute{M}}{\bigvee }\left(T_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\wedge T_D(k_i{k}_j)\right),\hfill \\ \hfill I_{\overline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \tilde{M}}{\bigwedge }\left(I_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\vee I_D(k_i{k}_j)\right),\hfill \\ \hfill F_{\overline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \tilde{M}}{\bigwedge }\left(F_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\vee F_D(k_i{k}_j)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \acute{M}}{\bigwedge }\left(F_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\vee T_D(k_i{k}_j)\right),\hfill \\ \hfill I_{\underline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \tilde{M}}{\bigvee }\left((1-I_{\tilde{R}}(u_i{u}_j,k_i{k}_j))\wedge I_D(k_i{k}_j)\right),\hfill \\ \hfill F_{\underline{\tilde{R}}(D)}(u_i{u}_j)& =& \underset{k_i{k}_j\in \tilde{M}}{\bigvee }\left(T_{\tilde{R}}(u_i{u}_j,k_i{k}_j)\wedge F_D(k_i{k}_j)\right).\hfill \end{array}$$

The pair $(\underline{\tilde{R}}(D),\overline{\tilde{R}}(D))$ is called NSRR and $\underline{\tilde{R}},\overline{\tilde{R}}:\mathcal{N}(\acute{M})\to \mathcal{N}(\acute{Y})$ are called the LNSRA and the UNSRA operators, respectively.

Remark 4.

Consideer an NS D on $\acute{M}$ and an NS C on M,

$$\begin{array}{ccc}\hfill T_D(k_i{k}_j)& \le & min\{T_C(k_i),T_C(k_j)\},\hfill \\ \hfill I_D(k_i{k}_j)& \le & max\{I_C(k_i),I_C(k_j)\},\hfill \\ \hfill F_D(k_i{k}_j)& \le & max\{F_C(k_i),F_C(k_j)\}.\hfill \end{array}$$

According to the definition of NSRR, we get

$$\begin{array}{ccc}\hfill T_{\overline{\tilde{R}}(D)}(u_i{u}_j)& \le & min\{T_{\overline{\tilde{R}}(C)}(u_i),T_{\overline{\tilde{R}}(C)}(u_j)\},\hfill \\ \hfill I_{\overline{\tilde{R}}(D)}(u_i{u}_j)& \le & max\{I_{\overline{\tilde{R}}(C)}(u_i),I_{\overline{\tilde{R}}(C)}(u_j)\},\hfill \\ \hfill F_{\overline{\tilde{R}}(D)}(u_i{u}_j)& \le & max\{F_{\overline{\tilde{R}}(C)}(u_i).F_{\overline{\tilde{R}}(C)}(u_j)\}.\hfill \end{array}$$

Similarly, for LNSRA operator $\underline{\tilde{R}}(D)$,

$$\begin{array}{ccc}\hfill T_{\underline{\tilde{R}}(D)}(u_i{u}_j)& \le & min\{T_{\underline{\tilde{R}}(C)}(u_i),T_{\underline{\tilde{R}}(C)}(u_j)\},\hfill \\ \hfill I_{\underline{\tilde{R}}(D)}(u_i{u}_j)& \le & max\{I_{\underline{\tilde{R}}(C)}(u_i),I_{\underline{\tilde{R}}(C)}(u_j)\},\hfill \\ \hfill F_{\underline{\tilde{R}}(D)}(u_i{u}_j)& \le & max\{F_{\underline{\tilde{R}}(C)}(u_i).F_{\underline{\tilde{R}}(C)}(u_j)\}.\hfill \end{array}$$

Example 5.

Let $Y=\{u_1,u_2,u_3\}$ be a universal set and $M=\{k_1,k_2,k_3\}$ a set of parameters. A neutrosophic soft set $(\tilde{P},M)$ on Y can be defined in tabular form (see

Table 5. Neutrosophic soft set $(\tilde{P},M)$.

$\tilde{\mathit{P}}$	${\mathit{u}}_{\mathbf{1}}$	${\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}$
$k_1$	$(0.4,0.5,0.6)$	$(0.7,0.3,0.2)$	$(0.6,0.3,0.4)$
$k_2$	$(0.5,0.3,0.6)$	$(0.3,0.4,0.3)$	$(0.7,0.2,0.3)$
$k_3$	$(0.7,0.2,0.3)$	$(0.6,0.5,0.4)$	$(0.7,0.2,0.4)$

) as follows:

Let $E=\{u_1{u}_2,u_2{u}_3,u_2{u}_2,u_3{u}_2\}\subseteq \acute{Y}$ and $L=\{k_1{k}_3,k_2{k}_1,k_3{k}_2\}\subseteq \acute{M}$.

Then, a soft relation $\tilde{R}$ on E (from L to E) can be defined in tabular form (see

Table 6. Neutrosophic soft relation $\tilde{R}$.

$\tilde{\mathit{R}}$	${\mathit{u}}_{\mathbf{1}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{3}}$	${\mathit{u}}_{\mathbf{2}}{\mathit{u}}_{\mathbf{2}}$	${\mathit{u}}_{\mathbf{3}}{\mathit{u}}_{\mathbf{2}}$
$k_1{k}_3$	$(0.4,0.4,0.5)$	$(0.6,0.3,0.4)$	$(0.5,0.4,0.2)$	$(0.5,0.4,0.3)$
$k_2{k}_1$	$(0.3,0.3,0.4)$	$(0.3,0.2,0.3)$	$(0.2,0.3,0.3)$	$(0.7,0.2,0.2)$
$k_3{k}_2$	$(0.3,0.3,0.2)$	$(0.5,0.3,0.2)$	$(0.2,0.4,0.4)$	$(0.3,0.4,0.4)$

) as follows:

• Let $C=\{(k_1,0.2,0.4,0.6),(k_2,0.4,0.5,0.2),(k_3,0.1,0.2,0.4)\}$ be an NS on M, then
• $\overline{\tilde{R}}(C)=\{(u_1,0.4,0.2,0.4),(u_2,0.3,0.4,0.3),(u_3,0.4,0.2,0.3)\},$
• $\underline{\tilde{R}}(C)=\{(u_1,0.3,0.5,0.4),(u_2,0.2,0.5,0.6),(u_3,0.4,0.5,0.6)\},$
• Let $B=\{(k_1{k}_3,0.1,0.3,0.5),(k_2{k}_1,0.2,0.4,0.3),(k_3{k}_2,0.1,0.2,0.3)\}$ be an NS on $L,$ then
• $\overline{\tilde{R}}(D)=\{(u_1{u}_2,0.2,0.3,0.3),(u_2{u}_3,0.2,0.3,0.3),(u_2{u}_2,0.2,0.4,0.3),(u_3{u}_2,0.2,0.4,0.3)\},$
• $\underline{\tilde{R}}(D)=\{(u_1{u}_2,0.2,0.4,0.4),(u_2{u}_3,0.2,0.4,0.5),(u_2{u}_2,0.3,0.4,0.5),(u_3{u}_2,0.2,0.4,0.5)\}.$
• Hence, $\tilde{R}(D)=(\overline{\tilde{R}}(D),\underline{\tilde{R}}(D))$ is NSRR.

Theorem 5.

Let ${\tilde{P}}_1,{\tilde{P}}_2$ be two NSRRs from universal Y to a parameter set M; for all $C\in \mathcal{N}(M),$ we have

(i)

$\underline{{\tilde{P}}_1\cup {\tilde{P}}_2}(C)=\underline{{\tilde{P}}_1}(C)\cap \underline{{\tilde{P}}_2}(C),$

(ii)

$\overline{{\tilde{P}}_1\cup {\tilde{P}}_2}(C)=\overline{{\tilde{P}}_1}(C)\cup \overline{{\tilde{P}}_2}(C).$

Theorem 6.

Let ${\tilde{P}}_1,{\tilde{P}}_2$ be two neutrosophic soft relations from universal Y to a parameter set M; for all $C\in \mathcal{N}(M),$ we have

(i)

$\underline{{\tilde{P}}_1\cap {\tilde{P}}_2}(C)\supseteq \underline{{\tilde{P}}_1}(C)\cup \underline{{\tilde{P}}_2}(C)\supseteq \underline{{\tilde{P}}_1}(C)\cap \underline{{\tilde{P}}_2}(C),$

(ii)

$\overline{{\tilde{P}}_1\cap {\tilde{P}}_2}(C)\subseteq \overline{{\tilde{P}}_1}(C)\cap \overline{{\tilde{P}}_2}(C).$

4. Application

In this section, we apply the concept of NSRSs to a decision-making problem. In recent times, the object recognition problem has gained considerable importance. The object recognition problem can be considered as a decision-making problem, in which final identification of object is founded on a given amount of information. A detailed description of the algorithm for the selection of the most suitable object based on an available set of alternatives is given, and the proposed decision-making method can be used to calculate lower and upper approximation operators to address deep concerns of the problem. The presented algorithms can be applied to avoid lengthy calculations when dealing with a large number of objects. This method can be applied in various domains for multi-criteria selection of objects. A multicriteria decision making (MCDM) can be modeled using neutrosophic soft rough sets and is ideally suited for solving problems.

In the pharmaceutical industry, different pharmaceutical companies develop, produce and discover pharmaceutical medicines (drugs) for use as medication. These pharmaceutical companies deal with “brand name medicine” and “generic medicine”. Brand name medicine and generic medicine are bioequivalent, have a generic medicine rate and element of absorption. Brand name medicine and generic medicine have the same active ingredients, but the inactive ingredients may differ. The most important difference is cost. Generic medicine is less expensive as compared to brand names in comparison. Usually, generic drug manufacturers have competition to produce products that cost less. The product may possibly be slightly dissimilar in color, shape, or markings. The major difference is cost. We consider a brand name drug “$u=\mathrm{Claritin}(\mathrm{loratadink})"$ with an ideal neutrosophic value number $n_u=(1,0,0)$ used for seasonal allergy medication. Consider

$$\begin{array}{ccc}\hfill Y& =& \{u_1=\mathrm{Nasacort}\mathrm{Aq}(\mathrm{Triamcinolone}),u_2=\mathrm{Zyrtec}\mathrm{D}(\mathrm{Cetirizine}/\mathrm{Pseudoephedrine}),\hfill \\ \hfill & & u_3=\mathrm{Sudafed}(\mathrm{Pseudoephedrine}),u_4=\mathrm{Claritin}-\mathrm{D}(\mathrm{loratadine}/\mathrm{pseudoephedrine}),\hfill \\ \hfill & & u_5=\mathrm{Flonase}(\mathrm{Fluticasone})\}\hfill \end{array}$$

is a set of generic versions of “Clarition”. We want to select the most suitable generic version of Claritin on the basis of parameters $e_1=$ Highly soluble, $e_2=$ Highly permeable, $e_3=$ Rapidly dissolving. $M=\{e_1,e_2,e_3\}$ be a set of paraments. Let $\tilde{P}$ be a neutrosophic soft relation from Y to parameter set M as shown in

Table 7. Neutrosophic soft set $(\tilde{P},M)$.

$\tilde{\mathit{P}}$	${\mathit{e}}_{\mathbf{1}}$	${\mathit{e}}_{\mathbf{2}}$	${\mathit{e}}_{\mathbf{3}}$
$u_1$	$(0.4,0.5,0.6)$	$(0.7,0.3,0.2)$	$(0.6,0.3,0.4)$
$u_2$	$(0.5,0.3,0.6)$	$(0.3,0.4,0.3)$	$(0.7,0.2,0.3)$
$u_3$	$(0.7,0.2,0.3)$	$(0.6,0.5,0.4)$	$(0.7,0.2,0.4)$
$u_4$	$(0.5,0.7,0.5)$	$(0.8,0.4,0.6)$	$(0.8,0.7,0.6)$
$u_5$	$(0.6,0.5,0.4)$	$(0.7,0.8,0.5)$	$(0.7,0.3,0.5)$

.

Suppose $C=\{(e_1,0.2,0.4,0.5),(e_2,0.5,0.6,0.4),(e_3,0.7,0.5,0.4)\}$ is the most favorable object that is an NS on the parameter set M under consideration. Then, $(\underline{\tilde{P}}(C),\overline{\tilde{P}}(C))$ is an NSRS in NSAS $(Y,M,\tilde{P}),$ where

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(C)& =& \{(u_1,0.6,0.5,0.4),(u_2,0.7,0.4,0.4),(u_3,0.7,0.4,0.4),(u_4,0.7,0.6,0.5),(u_5,0.7,0.5,0.5)\},\hfill \\ \hfill \underline{\tilde{P}}(C)& =& \{(u_1,0.5,0.6,0.4),(u_2,0.5,0.6,0.5),(u_3,0.3,0.3,0.5),(u_4,0.5,0.6,0.5),(u_5,0.4,0.5,0.5)\}.\hfill \end{array}$$

In [6], the sum of two neutrosophic numbers is defined. The sum of LNSRA and the UNSRA operators $\overline{\tilde{P}}(C)$ and $\underline{\tilde{P}}(C)$ is an NS $\overline{\tilde{P}}(C)\oplus \underline{\tilde{P}}(C)$ defined by

$$\begin{array}{ccc}\hfill \overline{\tilde{P}}(C)\oplus \underline{\tilde{P}}(C)& =& \{(u_1,0.8,0.3,0.16),(u_2,0.85,0.24,0.2),(u_3,0.79,0.2,0.2),(u_4,0.85,0.36,0.25),\hfill \\ \hfill & & (u_5,0.82,0.25,0.25)\}.\hfill \end{array}$$

Let $n_{u_i}=(T_{n_{u_i}},I_{n_{u_i}},F_{n_{u_i}})$ be a neutrosophic value number of generic versions medicine $u_i$. We can calculate the cosine similarity measure $S(n_{u_i},n_u)$ between each neutrosophic value number $n_{u_i}$ of generic version $u_i$ and ideal value number $n_u$ of brand name drug u, and the grading of all generic version medicines of Y can be determined. The cosine similarity measure is calculated as the inner product of two vectors divided by the product of their lengths. It is the cosine of the angle between the vector representations of two neutrosophic soft rough sets. The cosine similarity measure is a fundamental measure used in information technology. In [3], the cosine similarity is measured between neutrosophic numbers and demonstrates that the cosine similarity measure is a special case of the correlation coefficient in SVNS. Then, a decision-making method is proposed by the use of the cosine similarity measure of SVNSs, in which the evaluation information for alternatives with respect to criteria is carried out by truth-membership degree, indeterminacy-membership degree, and falsity-membership degree under single-valued neutrosophic environment. It defined as follows:

$$S(n_u,n_{u_i})=\frac{T_{n_u}·T_{n_{u_i}}+I_{n_u}·I_{n_{u_i}}+F_{n_u}·F_{n_{u_i}}}{\sqrt{T_{n_u}^2+T_{n_u^2}+F_{n_u}^2}+\sqrt{T_{n_{u_i}}^2+T_{n_{u_i}^2}+F_{n_{u_i}}^2}}.$$

(1)

Through the cosine similarity measure between each object and the ideal object, the ranking order of all objects can be determined and the best object can be easily identified as well. The advantage is that the proposed MCDM approach has some simple tools and concepts in the neutrosophic similarity measure approach among the existing ones. An illustrative application shows that the proposed method is simple and effective.

The generic version medicine $u_i$ with the larger similarity measure $S(n_{u_i},n_u)$ is the most suitable version $u_i$ because it is close to the brand name drug u. By comparing the cosine similarity measure values, the grading of all generic medicines can be determined, and we can find the most suitable generic medicine after selection of suitable NS of parameters. By Equation (1), we can calculate the cosine similarity measure between neutrosophic value numbers $n_u$ of u and $n_{u_i}$ of $u_i$ as follows:

$$\begin{array}{ccc}\hfill S(n_u,n_{u_1})& =& 0.9203,S(n_u,n_{u_2})=0.9386,S(n_u,n_{u_3})=0.9415,\hfill \\ \hfill S(n_u,n_{u_4})& =& 0.8888S(n_u,n_{u_5})=0.9183.\hfill \end{array}$$

We get $S(n_u,n_{u_3})>S(n_u,n_{u_2})>S(n_u,n_{u_1})>S(n_u,n_{u_5})>S(n_u,n_{u_4}).$ Thus, the optimal decision is $u_3$, and the most suitable generic version of Claritin is Sudafed (Pseudoephedrine). We have used software MATLAB (version 7, MathWorks, Natick, MA, USA) for calculations in the application. The flow chart of the algorithm is general for any number of objects with respect to certain parameters. The flow chart of our proposed method is given in Figure 1. The method is presented as an algorithm in Algorithm 1.

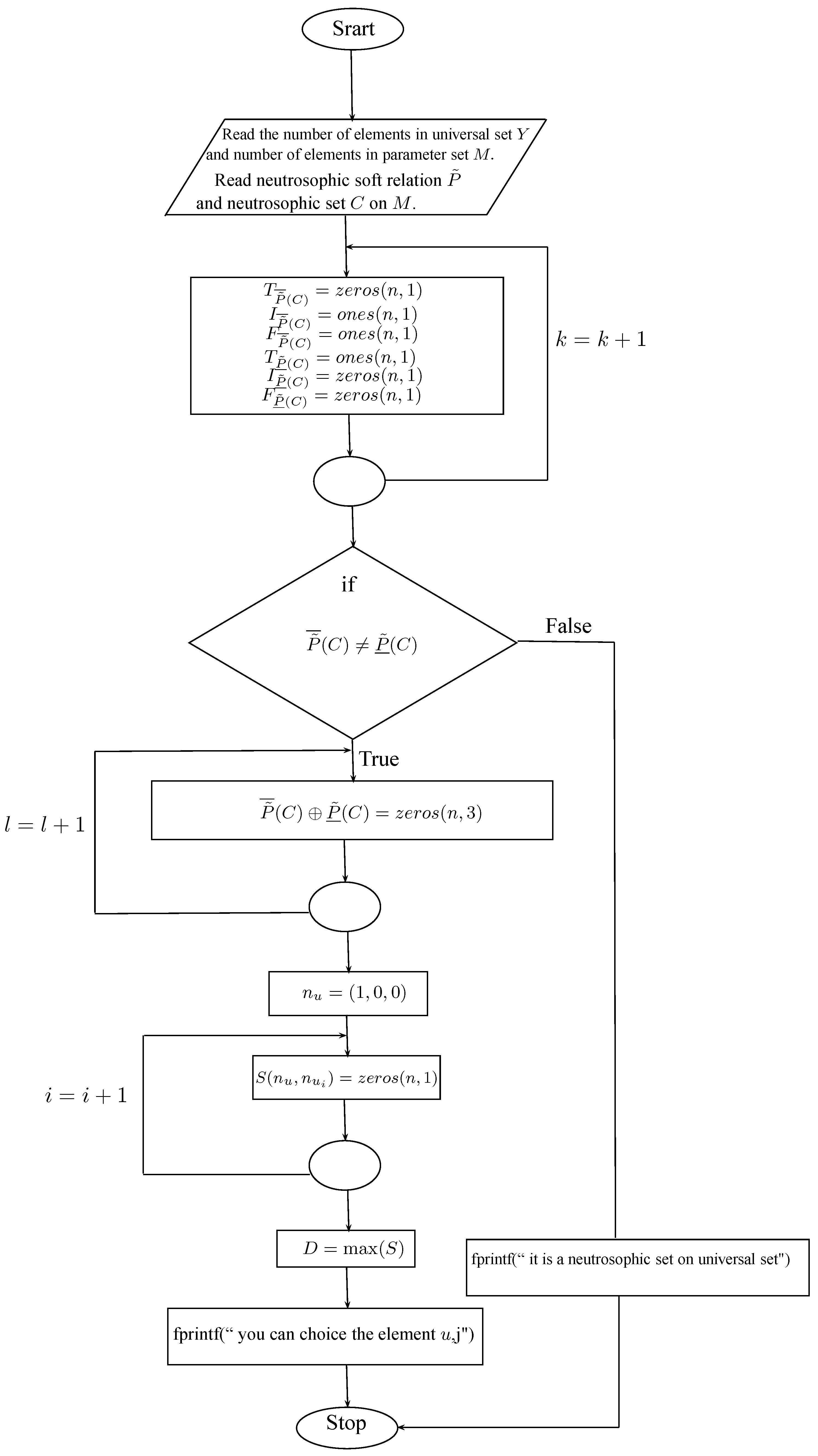
Algorithm 1: Algorithm for selection of the most suitable objects

1. Begin

2.   Input the number of elements in universal set $Y=\{u_1,u_2,\dots ,u_n\}$.

3.   Input the number of elements in parameter set $M=\{e_1,e_2,\dots ,e_m\}$.

4.   Input a neutrosophic soft relation $\tilde{P}$ from Y to M.

5.   Input an NS C on M.

6.    if $size(\tilde{P})\ne [n,3\ast m]$

7.      fprintf(‛ size of neutrosophic soft relation from universal set to parameter

set is not correct, it should be of order $\%d$x$\%d;{}^{\prime },n,3\ast m$)

8.       error(‛ Dimemsion of neutrosophic soft relation on vertex set is not correct. ’)

9.    end

10.   if $size(C)\ne [m,3]$

11.     fprintf(‛ size of NS on parameter set is not correct,

it should be of order %dx3; ’,m)

12.     error(’Dimemsion of NS on parameter set is not correct.’)

13.   end

14.  $T_{\overline{\tilde{P}}(C)}=zeros(n,1)$;

15.  $I_{\overline{\tilde{P}}(C)}=ones(n,1)$;

16.  $F_{\overline{\tilde{P}}(C)}=ones(n,1)$;

17.  $T_{\underline{\tilde{P}}(C)}=ones(n,1)$;

18.  $I_{\underline{\tilde{P}}(C)}=zeros(n,1)$;

19.  $F_{\underline{\tilde{P}}(C)}=zeros(n,1)$;

20.       if $size(\tilde{P})==[n,3\ast m]$

21.           if $size(C)==[m,3]$

22.               if $\tilde{P}>=0\&\&\tilde{P}<=1$

23.                       if $C>=0\&\&C<=1$

24.                                for $i=1:n$

25.                                         for $k=1:m$

26.                                             j=3*k-2;

27.                                             $T_{\overline{\tilde{P}}(C)}(i,1)=max(T_{\overline{\tilde{P}}(C)}(i,1),min(\tilde{P}(i,j),C(k,1)))$;

28.                                             $I_{\overline{\tilde{P}}(C)}(i,1)=min(I_{\overline{\tilde{P}}(C)}(i,1),max(\tilde{P}(i,j+1),C(k,2)))$;

29.                                             $F_{\overline{\tilde{P}}(C)}(i,1)=min(F_{\overline{\tilde{P}}(C)}(i,1),max(\tilde{P}(i,j+2),C(k,3)))$;

30.                                             $T_{\underline{\tilde{P}}(C)}(i,1)=min(T_{\underline{\tilde{P}}(C)}(i,1),max(\tilde{P}(i,j+2),C(k,1)))$;

31.                                             $I_{\underline{\tilde{P}}(C)}(i,1)=max(I_{\underline{\tilde{P}}(C)}(i,1),min((1-\tilde{P}(i,j+1)),C(k,2)))$;

32.                                             $F_{\underline{\tilde{P}}(C)}(i,1)=max(F_{\underline{\tilde{P}}(C)}(i,1),min(\tilde{P}(i,j),C(k,3)))$;

33.                                         end

34.                                  end

35.                           $\overline{\tilde{P}}(C)=(T_{\overline{\tilde{P}}(C)},I_{\overline{\tilde{P}}(C)},F_{\overline{\tilde{P}}(C)})$

36.                             $\underline{\tilde{P}}(C)=(T_{\underline{\tilde{P}}(C)},I_{\overline{\tilde{P}}(C)},F_{\underline{\tilde{P}}(C)})$

37.                            if $\overline{\tilde{P}}(C)==\underline{\tilde{P}}(C)$

38.                                  fprintf(‛ it is a neutrosophic set on universal set.${}^{\prime }$)

39.                            else

40.                                  fprintf(‛it is an NSRS on universal set.${}^{\prime }$)

41.                                  $\overline{\tilde{P}}(C)\oplus \underline{\tilde{P}}(C)=zeros(n,3)$;

42.                                          for i=1:n

43.                                                 $T_{\overline{\tilde{P}}(C)}(i)\oplus T_{\underline{\tilde{P}}(C)}(i)=T_{\overline{\tilde{P}}(C)}(i)+T_{\underline{\tilde{P}}(C)}(i)$

$-T_{\overline{\tilde{P}}(C)}(i).\ast T_{\underline{\tilde{P}}(C)}(i)$;

44.                                                 $I_{\overline{\tilde{P}}(C)}(i)\oplus I_{\underline{\tilde{P}}(C)}(i)=I_{\overline{\tilde{P}}(C)}(i).\ast I_{\underline{\tilde{P}}(C)}(i)$;

45.                                                 $F_{\overline{\tilde{P}}}(C)(i)\oplus F_{\underline{\tilde{P}}(C)}(i)=F_{\overline{\tilde{P}}(C)}(i).\ast F_{\underline{\tilde{P}}(C)}(i)$;

46.                                            end

47.                                  $n_u=(1,0,0)$;

48.                                  $S(n_u,n_{u_i})=zeros(n,1)$;

49.                                   for i=1:n

50.                                    $S(n_u,n_{u_i})={\displaystyle \frac{T_{n_u}·T_{n_{u_i}}+I_{n_u}·I_{n_{u_i}}+F_{n_u}·F_{n_{u_i}}}{\sqrt{T_{n_u}^2+T_{n_u^2}+F_{n_u}^2}+\sqrt{T_{n_{u_i}}^2+T_{n_{u_i}^2}+F_{n_{u_i}}^2}}}$;

51.                                   end

52.                              $S(n_u,n_{u_i})$

53.                              D=max(S);

54.                              l=0;

55.                              m=zeros(n,1);

56.                              D2=zeros(n,1);

57.                               for j=1:n

58.                                              if S(j,1)==D

59.                                             l=l+1;

60.                                           D2(j,1)=S(j,1);

61.                                                m(j)=j;

62.                                             end

63.                               end

64.                               for $j=1:n$

65.                                    if $m(j)=0$

66.                                   fprintf(‛ you can choice the element $u_{\%d}{}^{\prime }$,j)

67.                                    end

68.                               end

69.                      end

70.           end

71.            end

72.         end

73.     end

74. End

5. Conclusions and Future Directions

Rough set theory can be considered as an extension of classical set theory. Rough set theory is a very useful mathematical model to handle vagueness. NS theory, RS theory and SS theory are three useful distinguished approaches to deal with vagueness. NS and RS models are used to handle uncertainty, and combining these two models with another remarkable model of SSs gives more precise results for decision-making problems. In this paper, we have first presented the notion of SRNSs. Furthermore, we have introduced NSRSs and investigated some properties of NSRSs in detail. The notion of NSRS can be utilized as a mathematical tool to deal with imprecise and unspecified information. In addition, a decision-making method based on NSRSs has been proposed. This research work can be extended to (1) rough bipolar neutrosophic soft sets; (2) bipolar neutrosophic soft rough sets; (3) interval-valued bipolar neutrosophic rough sets; and (4) neutrosophic soft rough graphs.