New Order on Type 2 Fuzzy Numbers

Abstract

Since Lotfi A. Zadeh introduced the concept of fuzzy sets in 1965, many authors have devoted their efforts to the study of these new sets, both from a theoretical and applied point of view. Fuzzy sets were later extended in order to get more adequate and flexible models of inference processes, where uncertainty, imprecision or vagueness is present. Type 2 fuzzy sets comprise one of such extensions. In this paper, we introduce and study an extension of the fuzzy numbers (type 1), the type 2 generalized fuzzy numbers and type 2 fuzzy numbers. Moreover, we also define a partial order on these sets, which extends into these sets the usual order on real numbers, which undoubtedly becomes a new option to be taken into account in the existing total preorders for ranking interval type 2 fuzzy numbers, which are a subset of type 2 generalized fuzzy numbers.

1. Introduction

In the framework of fuzzy systems, in order to give a response or to make a decision, fuzzy numbers (FNs) and fuzzy quantities (FQs) need to be compared, i.e., to be ranked. In a sense, fuzzy numbers can be considered as real values with degrees of uncertainty, imprecision or vagueness. They are represented as fuzzy sets on the real line, that is, in general, they are not simply real numbers. Therefore, they cannot be compared by means of the usual total order on the set of real numbers. On the other hand, the pointwise partial order of functions, which is the standard order in the fuzzy sets, does not adequately (see Section 2.1) extend the order of real numbers. However, from the horizontal representation of the extension principle, a partial order has been established (see Equation (4)) in the FNs that extends the order of real numbers. Since Jain [1,2] and Dubois and Prade [3] introduced the concept of fuzzy numbers, many authors (see, for example, [2,4,5,6,7,8,9,10,11]) have given different methods that, although they do not produce total orders, allow one to compare the FNs and to order some of their subsets. Among these approaches are: statistical methods (see [7,10]), geometric methods (see [8]), analytical methods (e.g., in [6], the authors work with bounded variation functions), computational methods (e.g., artificial neural networks are applied in [11]) or the combination of some of these.

Bortolan et al. [12], Cheng et al. [13] and, recently, Wang et al. [14,15] reviewed a variety of existing methods for comparing FNs. Moreover, the properties that every method must satisfy to compare reasonably FNs were discussed in [14,15].

On the other hand, since the introduction of extensions of fuzzy sets, the need to define and analyze fuzzy numbers in these extensions has been pointed out. For example, intuitionist fuzzy numbers (IFNs) and generalized intuitionist fuzzy numbers (GIFNs), which are intuitionistic sets on the real line satisfying certain conditions, were defined and studied in [16,17,18]. Recently, interval type 2 fuzzy numbers (IT2FNs) have been defined in [19,20,21,22], as interval type 2 fuzzy sets (IT2FSs) on the real line fulfilling some properties. Besides, in [19,22], total preorders were given to ranking IT2FNs, but such preorders do not hold the property of antisymmetry, which is a theoretical and practical weakness. Moreover, the total preorder given in [19] does not effectively extend the order of real numbers (see Example 2).

Type 2 fuzzy sets (T2FSs) are an extension of type 1 fuzzy sets (FSs), and IT2FSs are a particular case of T2FSs. Because the membership degrees of T2FSs are fuzzy, they are better able to model uncertainty than FSs [23]. Fortunately, new methods have been introduced for the purpose of achieving a computationally-efficient and viable framework for representing T2FSs, as well as the T2FLS (type 2 fuzzy logic system) inference processes (see, for example, [24,25,26,27]). Thanks to these computational simplifications, the first applications of generalized T2FSs and not just interval type 2 fuzzy sets (IT2FSs), which is a subset of T2FSs, are now being reported, such as, for example, [24,26,27].

In this paper, we define and compare type 2 fuzzy numbers (T2FNs) and type 2 generalized fuzzy numbers (T2GFNs), which are type 2 fuzzy sets (T2FSs) on the real line, with certain conditions. These sets are more general than the ones considered in [19,20,22], so that in each application, the expert can choose the linguistic labels that best fit the specifications of the problem. We obtain a partial order in T2GFNs and in T2FNs, extending the order of real numbers, as a first step to obtain in future investigations a total order (or a preorder).

The paper is organized as follows. In Section 2, we recall some definitions, basic concepts, partial orders and properties of the FNs and generalized fuzzy numbers (GFNs) of type 1 (Section 2.1) and the T2FSs (Section 2.2). In Section 2.2, a partial order is introduced in the subset of T2FSs with convex membership degrees and with the same height. In Section 3, we define and study the T2FNs and T2GFNs. A partial order is determined on the T2GFNs extending the order of the real numbers. Furthermore, among other examples, two IT2GFNs are ordered with our partial order, and the result is compared with the one obtained applying the preorder established in [19]. Section 4 is devoted to some conclusions.

2. Preliminaries

2.1. Definitions and Properties of Fuzzy Numbers

Throughout the paper, X stands for a non-empty set that represents the universe of discourse. Additionally, ≤ denotes the usual order relation in the lattice of real numbers. The operators ∧ and ∨ are, respectively, the minimum and maximum operations on real numbers.

Definition 1.

[5,6,28] A fuzzy set (of type 1, FS) A, is characterized by a membership function $f_A$,

$$f_A:X\to [0,1],$$

where $f_A\left(x\right)$ is called the membership degree of the element $x\in X$ in the set A.

Let $F\left(X\right)$ denote the set of all fuzzy sets on X. For each $A\in F\left(\mathbb{R}\right)$, the height of A is:

$${\displaystyle w_A=\underset{\le }{sup}\left\{f_A\left(x\right):x\in \mathbb{R}\right\},}$$

and the support is:

$$supp\left(A\right)=supp\left(f_A\right)=\left\{x\in \mathbb{R}:f_A\left(x\right)>0\right\}.$$

We say that A is strongly normal if $f_A\left(x\right)=1$ for some $x\in \mathbb{R}$ and that it is normal if $w_A=1$. If A is strongly normal, then it is normal, but the opposite in general is not true. For example, the fuzzy set B on $\mathbb{R}$, with membership function:

$$f_B\left(x\right)=\left\{\begin{array}{cc}1+x\hfill & \mathrm{if}-1\le x<0;\hfill \\ 0.5-x\hfill & \mathrm{if}0\le x\le 0.5;\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

is normal, but it is not strongly normal, since there is no $x\in \mathbb{R}$ such that $f_B\left(x\right)=1$ (see Figure 1).

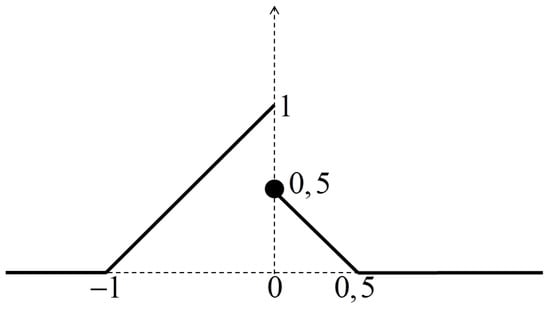
Figure 1. Normal, but non-strongly normal fuzzy set.

The $\alpha$-cut of an FS A on $\mathbb{R}$, with $0\le \alpha \le 1$, is $A_{\alpha }=\left\{x\in \mathbb{R}:f_A\left(x\right)\ge \alpha \right\}$. We say that A is convex if $f_A\left(y\right)\ge \left(f_A\left(x\right)\wedge f_A\left(z\right)\right)$, for all $x\le y\le z$ (to simplify the notation, we will also say that $f_A$ is convex). In addition, A is convex if and only if for all $\alpha$ with $0\le \alpha \le 1$, we have that $A_{\alpha }$ is a convex subset of the real line, that is an interval or the empty set.

Definition 2.

[5,6] Let X be a subset of $\mathbb{R}$, and let $f:X\to \mathbb{R}$ be a function. We say that f is upper semicontinuous at a point $x_0$ if, given $ϵ>0$, there exists a neighborhood U of $x_0$ such that $f\left(x\right)<f\left(x_0\right)+ϵ$, for all $x\in U$. We say that f is upper semicontinuous if it is upper semicontinuous at any $x\in X$.

Intuitively, a function f is upper semicontinuous at $x_0$ if, when approximating to $x_0$, $f\left(x\right)$ approximates to $f\left(x_0\right)$ or is below $f\left(x_0\right)$. That is, if ${lim}_{x\to x_0^{+}}f\left(x\right)\le f\left(x_0\right)$ and ${lim}_{x\to x_0^{-}}f\left(x\right)\le f\left(x_0\right)$. See Figure 2 and Figure 3.

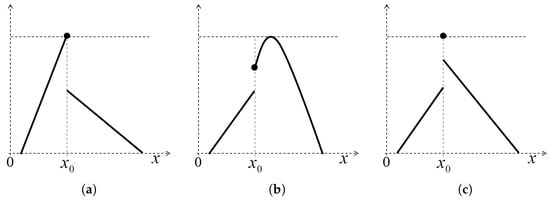
Figure 2. Upper semicontinuous functions: (a) Discontinuous from the right; (b) Discontinuous from the left; (c) Discontinuous from the right and from the left.

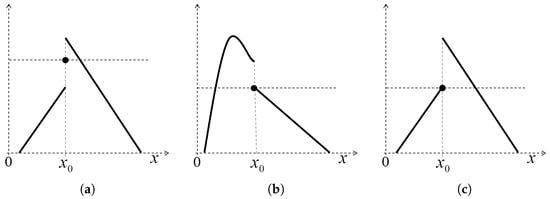
Figure 3. Non-upper semicontinuous functions: (a) Discontinuous from the right and from the left; (b) Discontinuous from the left; (c) Discontinuous from the right.

Definition 3.

[5,6] A generalized fuzzy number (GFN) A is a convex FS on $\mathbb{R}$ whose membership function $f_A$ is upper semicontinuous and with bounded support.

Any GFN A is determined by a membership function of the form [6]:

$$f_A\left(x\right)=\left\{\begin{array}{cc}{L}_A\left(x\right)\hfill & \mathrm{if}a\le x\le b;\hfill \\ w_A\hfill & \mathrm{if}b\le x\le c;\hfill \\ R_A\left(x\right)\hfill & \mathrm{if}c\le x\le d;\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $L_A:[a,b]\to [0,w_A]$ is an increasing function and $R_A:[c,d]\to [0,w_A]$ is a decreasing function. Note that the fuzzy set B of the previous example (see Figure 1) is not a GFN since its membership function is not upper semicontinuous. The functions shown in Figure 2 are GFNs, since each function is upper semicontinuous, convex and with bounded support. On the other hand, the functions shown in Figure 3 are not GFNs, because they are not upper semicontinuous functions.

A GFN A is normal if and only if its height $w_A$ equals one. In addition, if a GFN A is normal, then it is also strongly normal, because its membership function, $f_A$, is upper semicontinuous.

Definition 4.

[4,5,6] A fuzzy number (FN) A is a GFN that is strongly normal.

Because a fuzzy number A is strongly normal and convex, then $A_{\alpha }$ is an interval for all $0\le \alpha \le 1$, and since it is upper semicontinuous and with bounded support, $A_{\alpha }$ is a closed interval (see [5,6]). The function $f_B$ defined above and shown in Figure 1 is not upper semicontinuous at zero. Consequently, there exists some $\alpha$, such that $B_{\alpha }$ is not closed (for example, $B_{0.8}=[-0.2,0)$). Therefore, B is not a fuzzy number.

A real number a can be extended as a generalized fuzzy number with membership function equal to the characteristic function with height $w,{\overline{a}}_w:\mathbb{R}\to [0,1]$ where:

$${\overline{a}}_w\left(x\right)=\left\{\begin{array}{cc}w\hfill & \mathrm{if}x=a;\hfill \\ 0\hfill & \mathrm{if}x\ne a.\hfill \end{array}\right.$$

If $w=1$, the characteristic function ${\overline{a}}_1$, denoted $\overline{a}$, will be the extension of the real number a as a fuzzy number (type 1).

Similarly, a closed interval $[a,b]$ can be extended as a generalized fuzzy number with the membership function equal to the characteristic function with height $w,{\overline{[a,b]}}_w:\mathbb{R}\to [0,1]$, where:

$${\overline{[a,b]}}_w\left(x\right)=\left\{\begin{array}{cc}w\hfill & \mathrm{if}x\in [a,b];\hfill \\ 0\hfill & \mathrm{if}x\notin [a,b].\hfill \end{array}\right.$$

If $w=1$, the characteristic function ${\overline{[a,b]}}_1$ will be denoted by $\overline{[a,b]}$.

The usual partial order in the fuzzy sets, which is the partial order defined pointwise, is given by: let $A,B\in F\left(X\right)$; we say:

$$A\le B\iff f_A\le f_B,\left(f_A\left(x\right)\le f_B\left(x\right),\forall x\in X\right).$$

(1)

As is well known, this partial order is not total, and it is not the most appropriate when comparing fuzzy numbers, since it does not extend the order of real numbers. In fact, suppose we consider two different real numbers a and b, with $a<b$, as fuzzy numbers, by means of their characteristic functions $\overline{a}$ and $\overline{b}$. It is not true that $\overline{a}\le \overline{b}$, since $\overline{b}\left(a\right)=0<\overline{a}\left(a\right)=1$. Analogously, $\overline{b}\le \overline{a}$ is not true either. As a consequence, $\overline{a}$ and $\overline{b}$ are not comparable with this partial order. To summarize, the usual partial order (1) does not extend the usual order $(\le )$ of the real numbers.

By means of the Zadeh extension principle ([29]), many operations on the real numbers have been extended to the fuzzy numbers. For example, let ⚬ be a binary and surjective operation on $\mathbb{R}$, then its extension • on the fuzzy numbers is defined by any of the following equivalent expressions ([30,31,32]):

• Vertical representation:

  $$f_{A•B}\left(x\right)=\left(f_A•f_B\right)\left(x\right)=sup\left\{f_A\left(y\right)\wedge f_B\left(z\right):y\circ z=x\right\}.$$

  (2)
• Horizontal representation:

  $${\left(A•B\right)}_{\alpha }=A_{\alpha }•B_{\alpha }=\left\{a\circ b:a\in A_{\alpha },b\in B_{\alpha }\right\}.$$

  (3)

Since ⚬ is surjective, then the function $f_{A•B}$ is defined for all $x\in \mathbb{R}$ and for all fuzzy sets A and B.

From the extensions in horizontal form (3) of the operations ∨ and ∧, a new partial order ([9]) is established in the fuzzy numbers:

$$A⋞B\iff A_{\alpha }{\le }_I{B}_{\alpha },\forall \alpha \in [0,1]$$

(4)

where ${\le }_I$ is the usual partial order in the closed intervals, that is $[a,b]{\le }_I[c,d]\iff a\le c$ y $b\le d$. As (2) and (3) are equivalent on the fuzzy numbers, the partial order that is obtained from (2), denoted ⊑ (see Section 2.2), on the fuzzy numbers is equivalent to ⋞. Let us remark that the order ⋞ only is defined on fuzzy numbers, while the order ⊑ and the order given in (1) can be applied to any fuzzy sets.

The orders ⋞ and ⊑ are not total, but they are more adequate than the punctual order given in (1) to compare fuzzy numbers, since they extend the usual order of the real numbers.

2.2. About Type 2 Fuzzy Sets

From now on, we denote by $\mathbf{M}$ the set of functions from $[0,1]$ to $[0,1]$, i.e., $\mathbf{M}=Map\left([0,1],[0,1]\right)={[0,1]}^{[0,1]}$.

Definition 5.

[33,34] A type 2 fuzzy set (T2FS) A is characterized by a membership function:

$${\mu }_A:X\to \mathit{M},$$

where ${\mu }_A\left(x\right)$ is the membership degree of an element $x\in X$ in the set A and a fuzzy set in $[0,1]$. Thus,

$${\mu }_A\left(x\right)=f_x,where{f}_x:[0,1]\to [0,1].$$

Let $F_2\left(X\right)=Map\left(X,\mathbf{M}\right)$ denote the set of all type 2 fuzzy sets on X. It is worthwhile to remember that T2FSs are defined in a different way in [35]; however, both definitions are equivalent.

Example 1.

The following membership function determines a T2FS on $\mathbb{R}$:

$$\left(\mu \left(x\right)\right)\left(y\right)=f_x\left(y\right)=\left\{\begin{array}{cc}{\displaystyle -\frac{xy}{5}}& if-5\le x<0,y\in [0,1];\hfill \\ {\displaystyle \frac{xy}{7}}& if0\le x\le 7,y\in [0,1];\hfill \\ 0& ifx\notin [-5,7],y\in [0,1].\hfill \end{array}\right.$$

Definition 6.

[20,36] An interval type 2 fuzzy set (IT2FS) A is a T2FS whose membership degrees ${\mu }_A\left(x\right)$, for all $x\in X$, are characteristic functions (with height $w=1$) of closed intervals in [0,1].

Note that these sets are isomorphic to the interval-valued fuzzy sets. Moreover, the IT2FSs given in Definition 6 are a particular case of IT2FSs defined in [37]; however, here, we always use Definition 6.

Walker and Walker show in [36] that the operations on $Map(X,\mathbf{M})$ can be defined naturally from the operations on M and have the same properties. In fact, given the operation $*:\mathbf{M}\times \mathbf{M}\to \mathbf{M}$, we can define the operation $★:Map(X,\mathbf{M})\times Map(X,\mathbf{M})\to Map(X,\mathbf{M})$ such that, for each pair $f,g\in Map(X,\mathbf{M})$, we have $(f★g)\left(x\right)=f\left(x\right)\ast g\left(x\right)$, for all $x\in X$, where $f\left(x\right),g\left(x\right)\in \mathbf{M}$ (see [36]). This pointwise extension of operations also allows us to define an order in type 2 fuzzy sets from an order on their membership degrees as follows: given two T2FSs A and B with membership functions ${\mu }_A,{\mu }_B\in Map\left(X,\mathbf{M}\right)$, we have $A\preccurlyeq B$ if ${\mu }_A\left(x\right)\preccurlyeq {\mu }_B\left(x\right)$ for all $x\in X$, where ≼ is an order in $\mathbf{M}$. However, when $X=\mathbb{R}$, this way of defining an order in $Map(\mathbb{R},\mathbf{M})$ does not extend the order of $\mathbb{R}$, as happened with the usual order ≤ of the type 1 fuzzy sets. This is our motivation to define a new partial order in $Map\left(\mathbb{R},\mathbf{M}\right)$ (see Definition 15) that extends the order of real numbers (see Example 2 and Remark 6).

The following definition introduces algebraic operations on M by means of the vertical form (2) of Zadeh’s principle of extension [28,29,33,34].

Definition 7.

[36,38,39] In M, the operations ⊔ (generalized maximum), ⊓ (generalized minimum), ¬ (complementation) and the elements $\overline{0}$ and $\overline{1}$ are defined as follows:

$$\begin{array}{ccc}\hfill (f\bigsqcup g)\left(x\right)& =& sup\left\{f\left(y\right)\wedge g\left(z\right):y\vee z=x\right\};\hfill \\ \hfill (f\sqcap g)\left(x\right)& =& sup\left\{f\left(y\right)\wedge g\left(z\right):y\wedge z=x\right\};\hfill \\ \hfill \neg f\left(x\right)& =& sup\left\{f\left(y\right):1-y=x\right\}=f(1-x);\hfill \\ \hfill \overline{0}\left(x\right)& =& \left\{\begin{array}{cc}1\hfill & ifx=0;\hfill \\ 0\hfill & ifx\ne 0;\hfill \end{array}\right.\hfill \\ \hfill \overline{1}\left(x\right)& =& \left\{\begin{array}{cc}1\hfill & ifx=1;\hfill \\ 0\hfill & ifx\ne 1.\hfill \end{array}\right.\hfill \end{array}$$

The algebra $\mathbb{M}=\left(\mathbf{M},\bigsqcup ,\sqcap ,\neg ,\overline{0},\overline{1}\right)$ does not have a lattice structure, since the absorption law ([36,39]) is not fulfilled. However, both operations ⊔ and ⊓ define a partial order on M.

Definition 8.

[34,36] In M, the following two partial orders are defined:

$$f⊑g\mathrm{if}f\sqcap g=fandf⪯g\mathrm{if}f\bigsqcup g=g.$$

Generally, these two partial orders do not coincide [34,36]. The map $\overline{1}$ is the greatest element of partial order ⊑, and the map $\overline{0}$ is the least element of partial order ⪯. It is also verified that the constant function $g=0\left(g\left(x\right)=0,\mathrm{for}\mathrm{all}x\in [0,1]\right)$ is the least element of ⊑ and the greatest element of ⪯.

In order to facilitate operations on M, the following definition is given.

Definition 9.

[36,38,39] For $f\in \mathit{M}$, the functions $f^L,f^R\in \mathit{M}$ are defined as:

$$f^L\left(x\right)=\underset{\le }{sup}\left\{f\left(y\right):y\le x\right\}and{f}^R\left(x\right)=\underset{\le }{sup}\left\{f\left(y\right):x\le y\right\}.$$

$f^L$ and $f^R$ are increasing and decreasing, respectively, and ${\left(f^R\right)}^L={\left(f^L\right)}^R$ is a constant function, equal to the supremum of f.

We denote by C the set of all convex functions of M. In [36], it is shown that $f\in \mathbf{C}$ if and only if $f=f^L\wedge f^R$, and ${\mathbf{C}}_w$ will represent the set of all convex functions with given height w.

The set of all normal and convex functions of M is denoted by L. Obviously, $\mathbf{L}={\mathbf{C}}_1$. The algebra $\mathbb{L}=\left(\mathbf{L},\bigsqcup ,\sqcap ,\neg ,\overline{0},\overline{1}\right)$ is a subalgebra of $\mathbb{M}$. In L, the partial orders ⊑ and ⪯ are equivalent, and $\mathbb{L}$ is a bounded and complete lattice ($\overline{0}$ and $\overline{1}$ are the minimum and the maximum, respectively); see [34,36,39,40]. It should be noted that the characteristic functions of closed intervals in $[0,1]$, which are just the membership degrees of the IT2FSs, belong to L.

The following characterization of the partial order on L is very helpful to establish new results.

Theorem 1.

[39,40] Let $f,g\in \mathit{L}$. Then, $f⊑g$ if and only if:

$$g^L\le f^{L}and{f}^R\le g^R.$$

In [36,39], the authors did not consider ${\mathbf{C}}_w$ for any $0<w<1$; however, the study on L can be extended to ${\mathbf{C}}_w$, where the partial orders ⊑ and ⪯ are also equivalent. Thus, $\left({\mathbf{C}}_w,\bigsqcup ,\sqcap ,\neg ,{\overline{0}}_w,{\overline{1}}_w\right)$ is a bounded and complete lattice, where:

$${\overline{0}}_w\left(x\right)=\left\{\begin{array}{cc}w& \mathrm{if}x=0;\\ 0& \mathrm{if}x\ne 0;\end{array}\right.\mathrm{and}{\overline{1}}_w\left(x\right)=\left\{\begin{array}{cc}w& \mathrm{if}x=1;\\ 0& \mathrm{if}x\ne 1,\end{array}\right.$$

are the minimum and the maximum, respectively. In addition, ⊑ in ${\mathbf{C}}_w$ satisfies Theorem 1. From here on, the order ⊑ is denoted by ${⊑}_w$ when working in ${\mathbf{C}}_w$. Note, however, that we denote it by ⊑ to simplify the notation when there is no chance of confusion.

3. Type 2 Fuzzy Numbers

Haven et al. introduce in [20] an extension of the fuzzy numbers, the interval type 2 fuzzy numbers (IT2FNs).

Definition 10.

[20,22] An interval type 2 fuzzy number (IT2FN) is an IT2FS on $\mathbb{R}$, with membership function μ given by $\mu \left(x\right)=\overline{\left[a\right(x),b(x\left)\right]}$, where the functions $a,b:\mathbb{R}\to [0,1]$ are (type 1) fuzzy numbers.

The function a is the lower membership function, and b is the upper membership function.

It is worth mentioning that this definition is also given in [19] with $a,b:\mathbb{R}\to [0,1]$, where b is a (type 1) fuzzy number, and a is a (type 1) generalized fuzzy number (see Definition 3), i.e., a can be non-normal. Then, we call to these numbers given in [19] the interval type 2 generalized fuzzy numbers (IT2GFNs).

Note that the set of IT2FNs is a subset of IT2GFNs.

Next, we introduce the definitions of type 2 generalized fuzzy number (T2GFN) and type 2 fuzzy number (T2FN). These sets are new extensions of fuzzy numbers and are also extensions of interval type 2 fuzzy numbers (see Proposition 1).

Definition 11.

Given a T2FS on $\mathbb{R}$, with membership function $\mu :\mathbb{R}\to {\mathit{C}}_w$, the support of μ is defined as:

$$Supp\left(\mu \right)=\left\{x\in \mathbb{R}:\mu \left(x\right)\ne {\overline{0}}_w\right\}.$$

In addition, μ has bounded support if there exists $a,b\in \mathbb{R}$ such that

$\mu \left(x\right)={\overline{0}}_w$, for all $x\notin [a,b]$.

Remark 1.

Given two closed intervals $[a,b]$ and $[c,d]$, then ${\overline{[a,b]}}_w{⊑}_w{\overline{[c,d]}}_w$, for all w, if and only if $[a,b]{\le }_I[c,d]$.

Definition 12.

A type 2 generalized fuzzy number (T2GFN) in $\left({\mathit{C}}_w,{⊑}_w\right)$ is a T2FS on $\mathbb{R}$, such that its membership function $\mu :\left(\mathbb{R},\le \right)\to \left({\mathit{C}}_w,{⊑}_w\right)$ has bounded support, and moreover, there exists a $z_{\mu }\in \mathbb{R}$ such that μ is increasing in $(-\infty ,z_{\mu }]$ and decreasing in $[z_{\mu },\infty )$.

Example 3 shows two type 2 generalized fuzzy numbers.

Remark 2.

Given a T2GFN in ${\mathit{C}}_w$, with membership function μ, we have that:

$$\mu \left(x\right){⊑}_w\mu \left(z_{\mu }\right)forx\in (-\infty ,z_{\mu }]and\mu \left(x\right){⊑}_w\mu \left(z_{\mu }\right)forx\in [z_{\mu },\infty )$$

and therefore, for all $x\in \mathbb{R}$, $\mu \left(x\right){⊑}_w\mu \left(z_{\mu }\right)$. Consequently, ${\displaystyle \mu \left(z_{\mu }\right)=\underset{{⊑}_w}{sup}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}}$.

Besides, the set ${\displaystyle Z_{\mu }=\left\{z\in \mathbb{R}:\mu \left(z\right)=\underset{{⊑}_w}{sup}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}\right\}}$ is a point or an interval (not-empty) where μ is constant.

Remark 3.

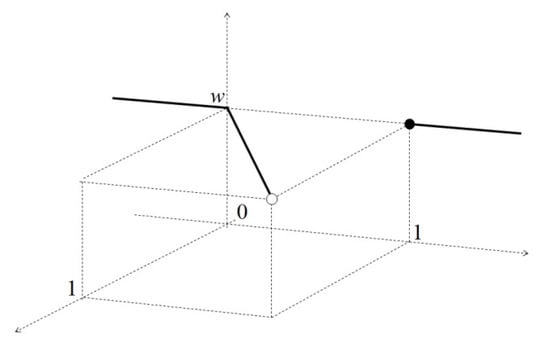
A type 2 fuzzy set on $\mathbb{R}$ with membership function,

$$\mu \left(x\right)=\left\{\begin{array}{cc}{\overline{x}}_w& ifx\in [0,1);\\ {\overline{0}}_w& otherwise,\end{array}\right.$$

(5)

is not a T2GFN, since there is no $z_{\mu }$ with the required conditions. Note that μ is increasing in $(-\infty ,1)$, but not in $(-\infty ,1]$, since, for instance, $\frac{1}{2}<1$, but $\mu \left(1\right)={\overline{0}}_w{⊑}_w{\overline{\left(\frac{1}{2}\right)}}_w=\mu \left(\frac{1}{2}\right)$ (see Figure 4; in this figure, only the image of the support of the functions corresponding to membership degrees $\mu \left(x\right)$ has been drawn).

Figure 4. Example of a type 2 fuzzy set (T2FS) that is not a type 2 generalized fuzzy number (T2GFN).

Definition 13.

A type 2 fuzzy number (T2FN) in $({\mathit{C}}_w,{⊑}_w)$ is a T2GFN, such that:

$$\underset{{⊑}_w}{sup}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}={\overline{1}}_w.$$

Remark 4.

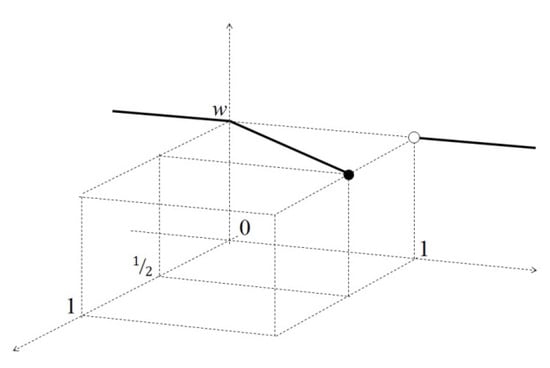
A type 2 fuzzy set on $\mathbb{R}$ with membership function,

$$\mu \left(x\right)=\left\{\begin{array}{cc}{\overline{\left(\frac{x}{2}\right)}}_w& ifx\in [0,1];\\ {\overline{0}}_w& otherwise,\end{array}\right.$$

(6)

is a type 2 generalized fuzzy number, but not a type 2 fuzzy number, since ${sup}_{{⊑}_w}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}={\overline{\left(\frac{1}{2}\right)}}_w$ (see Figure 5; in this figure, only the image of the support of the functions corresponding to the membership degrees $\mu \left(x\right)$ has been painted).

Figure 5. Example of a T2FS that is a T2GFN in ${\mathbf{C}}_w$.

Proposition 1.

An interval type 2 fuzzy number (IT2FN), defined as in Definition 10, is a T2FN in $({\mathit{C}}_1,{⊑}_1)$.

Proof. 

The membership degree $\mu \left(x\right)$ of any IT2FN is the characteristic function of an interval. That is, $\mu \left(x\right)=\overline{\left[a\right(x),b(x\left)\right]}\in {\mathbf{C}}_1=\mathbf{L}$, where $a\left(x\right)\le b\left(x\right)$ for all $x\in \mathbb{R}$. The functions a and b are fuzzy numbers of type 1 (see Definition 4). Since a is strongly normal, we have $a\left(z\right)=1$ for some $z\in \mathbb{R}$. In addition, because $a\left(z\right)\le b\left(z\right)$, then $a\left(z\right)=b\left(z\right)=1$, which implies that $\mu \left(z\right)={\overline{1}}_1=\overline{1}$.

On the other hand, because a and b are fuzzy numbers and $a\left(z\right)=b\left(z\right)=1$, we have that a and b are increasing in $(-\infty ,z]$ and decreasing in $[z,\infty )$. Thus, $a\left(x_1\right)\le a\left(x_2\right)$ and $b\left(x_1\right)\le b\left(x_2\right)$ for all $x_1\le x_2\le z$, which implies that $\overline{[a\left(x_1\right),b\left(x_1\right)]}⊑\overline{[a\left(x_2\right),b\left(x_2\right)]}$. Consequently, $\mu :\left((-\infty ,z],\le \right)\to \left({\mathbf{C}}_w,⊑\right)$ is increasing.

In a similar way, we can prove that $\mu$ is decreasing in $[z,\infty )$.

Therefore, the IT2FNs given in Definition 10 are a particular case of the T2FNs of Definition 13.  ☐

Proposition 2.

An interval type 2 generalized fuzzy number (IT2GFN) is a T2GFN in $({\mathit{C}}_1,{⊑}_1)$.

Proof. 

This is similar to the proof made for Proposition 1.  ☐

It should be noted that the set of T2GFNs is a subset of the set of T2FSs on $\mathbb{R}$, whose membership degrees are functions in ${\mathbf{C}}_w$, so the following partial order, pointwise defined, can be induced: given two T2GFNs $A,B$, we say that $A{⊑}_{w}B$ if and only if ${\mu }_A\left(x\right){⊑}_w{\mu }_B\left(x\right)$ for all $x\in \mathbb{R}$. However, this order is not convenient to compare T2GFNs, since it does not extend the natural order of real numbers, when these are represented as T2GFN, as is shown in Example 2.

Example 2.

Let A and B represent the extension of real numbers 2 and 3 to the T2FSs, respectively, with membership degrees:

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx=2;\\ \overline{0}& otherwise,\end{array}\right.and{\mu }_B\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx=3;\\ \overline{0}& otherwise.\end{array}\right.$$

Figure 6a shows the membership degrees ${\mu }_A\left(1\right)$ and ${\mu }_A\left(2\right)$ and only the image of the support of the rest of the membership degrees ${\mu }_A\left(x\right)$. Figure 6b displays the membership degrees ${\mu }_B\left(1\right),{\mu }_B\left(2\right)$ and ${\mu }_B\left(3\right)$ and only the image of the support of the rest of the membership degrees ${\mu }_B\left(x\right)$.

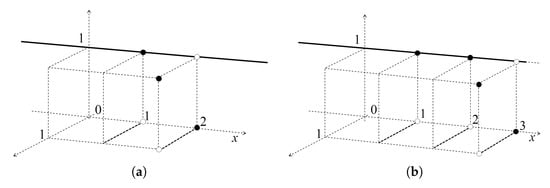
Figure 6. (a) Number 2 extended as a T2FN; (b) Number 3 extended as a T2FN.

It would be expected that $A⊑B$ as $2\le 3$, but this does not happen since ${\mu }_B\left(2\right)=\overline{0}⊑\overline{1}={\mu }_A\left(2\right)$ and ${\mu }_A\left(3\right)=\overline{0}⊑\overline{1}={\mu }_B\left(3\right)$, which implies that A and B are not comparable with that partial order.

Furthermore, the preorder given in [19] does not extend the order of $\mathbb{R}$ either. In fact, in the above paper, the authors, before comparing numbers, transform the membership function of any real number, i.e., $\overline{x}$, to the real $\overline{1}$ or $\overline{-1}$, obtaining in this example that $A=B$.

Consequently, a partial order extending the total order of $\mathbb{R}$ needs to be obtained on the T2GFNs. Before, we define two auxiliary functions.

Definition 14.

Given a T2GFN with membership degree $\mu \left(x\right)\in \left({\mathit{C}}_w,{⊑}_w\right),\forall x\in \mathbb{R}$, we define the functions ${\mu }^L,{\mu }^R:\left(\mathbb{R},\le \right)\to \left({\mathit{C}}_w,{⊑}_w\right)$ as follows:

$$\begin{array}{ccc}\hfill {\mu }^L\left(x\right)& =& \underset{{⊑}_w}{sup}\left\{\mu \left(y\right):y\le x\right\}=\underset{y\le x}{⨆}\mu \left(y\right),\hfill \\ \hfill {\mu }^R\left(x\right)& =& \underset{{⊑}_w}{sup}\left\{\mu \left(y\right):y\ge x\right\}=\underset{y\ge x}{⨆}\mu \left(y\right).\hfill \end{array}$$

Proposition 3.

Given a T2GFN in ${\mathit{C}}_w$ with membership function μ, we have ${\mu }^L\left(x\right),{\mu }^R\left(x\right)\in {\mathit{C}}_w$ for all x, and ${\mu }^L,{\mu }^R$ are increasing and decreasing functions, respectively, with respect to the partial order ${⊑}_w$.

Proof. 

Since $\mu$ is increasing in $(-\infty ,z_{\mu }]$ and decreasing in $[z_{\mu },\infty )$ for some $z_{\mu }\in \mathbb{R}$, then ${\mu }^L\left(x\right)=\mu \left(x\right)\in {\mathbf{C}}_w$, $\forall x\le z_{\mu }$ and ${\mu }^L\left(x\right)=\mu \left(z_{\mu }\right)\in {\mathbf{C}}_w$, for all $x\ge z_{\mu }$; therefore ${\mu }^L\left(x\right)\in {\mathbf{C}}_w$, for all $x\in \mathbb{R}$.

Similarly, we have ${\mu }^R\left(x\right)=\mu \left(x\right)\in {\mathbf{C}}_w$ for all $x\ge z_{\mu }$ and ${\mu }^R\left(x\right)=\mu \left(z_{\mu }\right)\in {\mathbf{C}}_w$ for all $x\le z_{\mu }$; therefore ${\mu }^R\left(x\right)\in {\mathbf{C}}_w$, for all $x\in \mathbb{R}$. In addition, it follows that ${\mu }^L$ and ${\mu }^R$ are increasing and decreasing functions, respectively, with respect to the partial order ${⊑}_w$.  ☐

Remark 5.

Given a T2GFN in ${\mathbf{C}}_w$ with membership function μ and $z_{\mu }\in \mathbb{R}$ a point where μ reaches the supremum, as ${\displaystyle \mu \left(x\right)⊑\underset{⊑}{sup}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}=\mu \left(z_{\mu }\right)}$, it is clear that:

$$\begin{array}{ccc}\hfill \underset{⊑}{sup}\left\{{\mu }^L\left(x\right):x\in \mathbb{R}\right\}& =& \underset{⊑}{sup}\left\{{\mu }^R\left(x\right):x\in \mathbb{R}\right\}=\underset{⊑}{sup}\left\{\mu \left(x\right):x\in \mathbb{R}\right\}\hfill \\ & =& {\mu }^L\left(z_{\mu }\right)={\mu }^R\left(z_{\mu }\right).\hfill \end{array}$$

Definition 15.

Let A and B be T2GFNs in ${\mathit{C}}_w$, with membership function ${\mu }_A$ and ${\mu }_B$ respectively. We define the relation $\widetilde{⊑}$ as:

$$A\widetilde{⊑}B\left(ó{\mu }_A\widetilde{⊑}{\mu }_B\right)\iff {\mu }_A^R\left(x\right){⊑}_w{\mu }_B^R\left(x\right)and{\mu }_B^L\left(x\right){⊑}_w{\mu }_A^L\left(x\right),$$

for all $x\in \mathbb{R}$.

Proposition 4.

Let A and B be T2GFNs in ${\mathit{C}}_w$, with membership functions ${\mu }_A$ and ${\mu }_B$, respectively. If A and B are comparable with $\widetilde{⊑}$, then:

$$\underset{{⊑}_w}{sup}\left\{{\mu }_A\left(x\right):x\in \mathbb{R}\right\}=\underset{{⊑}_w}{sup}\left\{{\mu }_B\left(x\right):x\in \mathbb{R}\right\}.$$

Proof. 

If $A\widetilde{⊑}B$ then ${\mu }_A^R\left(x\right)⊑{\mu }_B^R\left(x\right)$ and ${\mu }_B^L\left(x\right)⊑{\mu }_A^L\left(x\right)$ for all $x\in \mathbb{R}$. From the Remark 5, we have:

$$\underset{⊑}{sup}\left\{{\mu }_A\left(x\right):x\in \mathbb{R}\right\}=\underset{⊑}{sup}\left\{{\mu }_A^R\left(x\right):x\in \mathbb{R}\right\}⊑\underset{⊑}{sup}\left\{{\mu }_B^R\left(x\right):x\in \mathbb{R}\right\}=\underset{⊑}{sup}\left\{{\mu }_B\left(x\right):x\in \mathbb{R}\right\},$$

$$\underset{⊑}{sup}\left\{{\mu }_B\left(x\right):x\in \mathbb{R}\right\}=\underset{⊑}{sup}\left\{{\mu }_B^L\left(x\right):x\in \mathbb{R}\right\}⊑\underset{⊑}{sup}\left\{{\mu }_A^L\left(x\right):x\in \mathbb{R}\right\}=\underset{⊑}{sup}\left\{{\mu }_A\left(x\right):x\in \mathbb{R}\right\}.$$

Since ⊑ is antisymmetric, we have:

$$\underset{{⊑}_w}{sup}\left\{{\mu }_A\left(x\right):x\in \mathbb{R}\right\}=\underset{{⊑}_w}{sup}\left\{{\mu }_B\left(x\right):x\in \mathbb{R}\right\}.$$

☐

Proposition 5.

Let A and B be two T2GFNs in ${\mathit{C}}_w$, with membership functions ${\mu }_A$ and ${\mu }_B$, respectively. If $A\widetilde{⊑}B$, then $z_{{\mu }_A}\le z_{{\mu }_B}$, being $z_{{\mu }_A}={inf}_{\le }\{x\in \mathbb{R}:{\mu }_A\left(x\right)={sup}_{{⊑}_w}{\mu }_A\}$ and $z_{{\mu }_B}={inf}_{\le }\{x\in \mathbb{R}:{\mu }_B\left(x\right)={sup}_{{⊑}_w}{\mu }_B\}$.

Proof. 

If $A\widetilde{⊑}B$, then ${\mu }_B^L\left(x\right){⊑}_w{\mu }_A^L\left(x\right)$. Suppose $z_{{\mu }_B}<z_{{\mu }_A}$, then there exists $x\in \mathbb{R}$ such that $z_{{\mu }_B}<x<z_{{\mu }_A}$ and ${\mu }_B^L\left(x\right)={sup}_{{⊑}_w}{\mu }_B={sup}_{{⊑}_w}{\mu }_A$ by Proposition 4, but ${\mu }_A^L\left(x\right)⋤{sup}_{{⊑}_w}{\mu }_A$. Therefore, ${\mu }_A^L\left(x\right)⋤{\mu }_B\left(x\right)$, which is impossible.  ☐

Proposition 6.

$\widetilde{⊑}$ is a partial order in the set of T2GFNs in ${\mathbf{C}}_w$.

Proof. 

Let $A,B,C$ be three T2GFNs in ${\mathbf{C}}_w$, with membership functions ${\mu }_A,{\mu }_B$ and ${\mu }_C$, respectively.

Reflexivity: As ⊑ is a partial order in ${\mathbf{C}}_w$, it is reflexive, and thus, ${\mu }_A^R\left(x\right)⊑{\mu }_A^R\left(x\right)$ and ${\mu }_A^L\left(x\right)⊑{\mu }_A^L\left(x\right)$, for all x. Therefore, $A\widetilde{⊑}A$.

Transitivity: If $C\widetilde{⊑}A$ and $A\widetilde{⊑}B$, then, for all $x\in \mathbb{R}$, we have that:

$${\mu }_C^R\left(x\right)⊑{\mu }_A^R\left(x\right),{\mu }_A^L\left(x\right)⊑{\mu }_C^L\left(x\right),$$

$${\mu }_A^R\left(x\right)⊑{\mu }_B^R\left(x\right),{\mu }_B^L\left(x\right)⊑{\mu }_A^L\left(x\right).$$

Since ⊑ is transitive, we have that:

$${\mu }_C^R\left(x\right)⊑{\mu }_B^R\left(x\right)\mathrm{and}{\mu }_B^L\left(x\right)⊑{\mu }_C^L\left(x\right),$$

for all x. Therefore, $C\widetilde{⊑}B.$

Antisymmetry: If $A\widetilde{⊑}B$, then ${\mu }_A^R\left(x\right)⊑{\mu }_B^R\left(x\right)$ and ${\mu }_B^L\left(x\right)⊑{\mu }_A^L\left(x\right)$. Additionally, if $B\widetilde{⊑}A$, then ${\mu }_B^R\left(x\right)⊑{\mu }_A^R\left(x\right)$ and ${\mu }_A^L\left(x\right)⊑{\mu }_B^L\left(x\right)$.

Since ⊑ is antisymmetric, then:

$${\mu }_A^R\left(x\right)={\mu }_B^R\left(x\right)\mathrm{and}{\mu }_A^L\left(x\right)={\mu }_B^L\left(x\right),$$

for all x.

As A and B are T2GFNs, their membership functions are increasing in $(-\infty ,z_a]$ and $(-\infty ,z_b]$, respectively, and decreasing in $[z_a,\infty )$ and $[z_b,\infty )$, respectively, for some $z_a,z_b\in \mathbb{R}$. Therefore, ${\mu }_A^L\left(x\right)={\mu }_A\left(x\right)$, for all $x\le z_a$; ${\mu }_B^L\left(x\right)={\mu }_B\left(x\right)$, for all $x\le z_b$; ${\mu }_A^R\left(x\right)={\mu }_A\left(x\right)$, for all $x\ge z_a$; and ${\mu }_B^R\left(x\right)={\mu }_B\left(x\right)$, for all $x\ge z_b$.

Without loss of generality, we suppose $z_a\le z_b$. If $x\in (-\infty ,z_a]$, then we have ${\mu }_A\left(x\right)={\mu }_A^L\left(x\right)={\mu }_B^L\left(x\right)={\mu }_B\left(x\right)$. If $x\in [z_b,\infty )$, then we have ${\mu }_A\left(x\right)={\mu }_A^R\left(x\right)={\mu }_B^R\left(x\right)={\mu }_B\left(x\right)$.

On the other hand, if $z_a<x<z_b$, we obtain ${\mu }_B\left(x\right)⊑{\mu }_B^R\left(x\right)={\mu }_A^R\left(x\right)={\mu }_A\left(x\right)$ and ${\mu }_A\left(x\right)⊑{\mu }_A^L\left(x\right)={\mu }_B^L\left(x\right)={\mu }_B\left(x\right)$. Since ⊑ is antisymmetric, we have that ${\mu }_A\left(x\right)={\mu }_B\left(x\right)$ for all x. Therefore, $A=B$.  ☐

Remark 6.

The partial order of Definition 15 extends the order of $\mathbb{R}$. In fact, let A and B be the extensions in the T2FNs, of the real numbers a and b, respectively, such that $a\le b$, with membership functions:

$${\mu }_A\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx=a;\\ \overline{0}& otherwise,\end{array}\right.and{\mu }_B\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx=b;\\ \overline{0}& otherwise.\end{array}\right.$$

In this case, we have that:

$${\mu }_A^L\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx\ge a;\\ \overline{0}& otherwise,\end{array}\right.{\mu }_B^L\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx\ge b;\\ \overline{0}& otherwise,\end{array}\right.$$

$${\mu }_A^R\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx\le a;\\ \overline{0}& otherwise,\end{array}\right.{\mu }_B^R\left(x\right)=\left\{\begin{array}{cc}\overline{1}& ifx\le b;\\ \overline{0}& otherwise.\end{array}\right.$$

One can prove that ${\mu }_B^L\left(x\right)⊑{\mu }_A^L\left(x\right)$ and ${\mu }_A^R\left(x\right)⊑{\mu }_B^R\left(x\right)$ for all x. Then, $A\widetilde{⊑}B$, but $A\neg ⊑B$ and $B\neg ⊑A$ (see Example 2).

Note that the methods provided in [19,22] for ranking IT2FNs are total preorders; however, to the best of our knowledge, there is no previous work where a partial order is established extending the order of the real numbers to T2FNs and not just to IT2FNs or IT2GFNs. Moreover, as has already been pointed out, the preorder in [19] does not extend the order of $\mathbb{R}$; meanwhile, it can be proven that the preorder in [22] does extend it. Example 3 shows the ranking of two T2GFNs that are not IT2FNs.

Example 3.

Consider the two T2GFNs A and B given by the degrees of membership $\mu \left(x\right),\phi \left(x\right)\in {\mathit{C}}_{1/2}$, respectively, defined below. Note that A and B are not IT2FNs (see Definition 10), because $w=0.5\ne 1$, and some membership degrees of A are not characteristic functions of a point or an interval.

Let $\mu \left(x\right):[0,1]\to [0,1]$ be defined by:

• if $x\in \mathbb{R}\backslash (0,7)$, then $\mu \left(x\right)={\overline{0}}_{1/2}$;
• if $x\in (0,3)$, then $\left(\mu \left(x\right)\right)\left(y\right)=\left\{\begin{array}{cc}{\displaystyle \frac{10y}{x}-1}& \mathrm{if}y\in [\frac{x}{10},\frac{15x}{100}];\\ 2-\frac{10y}{x}& \mathrm{if}y\in [\frac{15x}{100},\frac{2x}{10}];\\ 0& \mathrm{if}y\notin [\frac{x}{10},\frac{2x}{10}];\end{array}\right.$
• if $x\in [3,5]$, then $\mu \left(x\right)={\overline{[0.7,0.9]}}_{1/2}$;
• if $x\in (5,7)$, then $\mu \left(x\right)={\overline{(2.1-0.3x)}}_{1/2}$.

In Figure 7, we only show the membership degrees of the set $A,\mu \left(x\right)$, when $x\in (0,3)$. In the other case, when $x\notin (0,3)$, the membership degrees are characteristic functions of a point or an interval with height $w=0.5$. In Figure 8, on the left, we have drawn the images of the supports of the membership degrees of the set A, as well as the projection of these values on the plane $xy$.

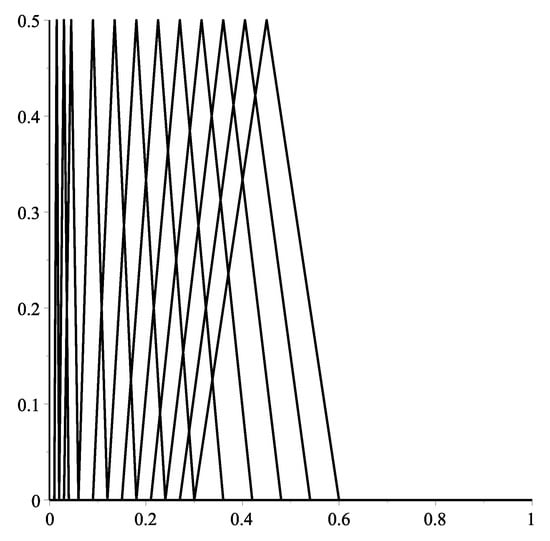
Figure 7. Membership degrees $\mu \left(x\right)$, for all $x\in (0,3)$.

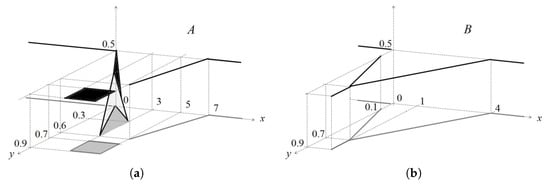
Figure 8. Membership functions of T2GFNs (a,b) given in Example 3.

Additionally, let $\phi \left(x\right):[0,1]\to [0,1]$ be defined by:

• if $x\in \mathbb{R}\backslash [0,4]$, then $\phi \left(x\right)={\overline{0}}_{1/2}$;
• if $x\in [0,1)$, then $\phi \left(x\right)={\overline{(0.6x+0.1)}}_{1/2}$;
• if $x=1$ then $\phi \left(1\right)={\overline{[0.7,0.9]}}_{1/2}$;
• if $x\in (1,4]$, then $\phi \left(x\right)={\overline{\frac{7}{30}(4-x)}}_{1/2}$.

All membership degrees of the set B are characteristic functions of a point or an interval with height $w=0.5$. On the right of Figure 8, we have drawn the image of the support of each membership degree of the set B, as well as the projection of these values on the plane $xy$.

In this example, $w=1/2,Z_{\mu }=[3,5]$ and $Z_{\phi }=\left\{1\right\}$; therefore, for all $z_{\mu }\in [3,5]$ and $z_{\phi }=1$, it is:

$$sup\left\{\mu \left(x\right):x\in \mathbb{R}\right\}=\mu \left(z_{\mu }\right)={\overline{[0.7,0.9]}}_{1/2}=\phi \left(1\right)=sup\left\{\phi \left(x\right):x\in \mathbb{R}\right\},$$

In addition, we have:

${\mu }^L:\mathbb{R}\to {[0,1]}^{[0,1]}$ is such that (see Figure 9):

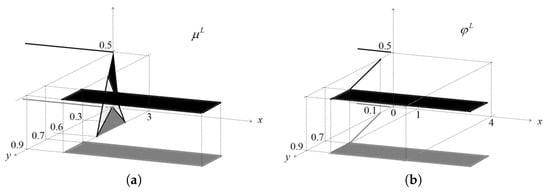
Figure 9. (a) ${\mu }^L$ and (b) ${\phi }^L$ according to Example 3.

• if $x<3$, then ${\mu }^L\left(x\right)=\mu \left(x\right)$;
• if $x\ge 3$, then ${\mu }^L\left(x\right)=\mu \left(3\right)={\overline{[0.7,0.9]}}_{1/2}$;

${\mu }^R:\mathbb{R}\to {[0,1]}^{[0,1]}$ is such that (see Figure 10):

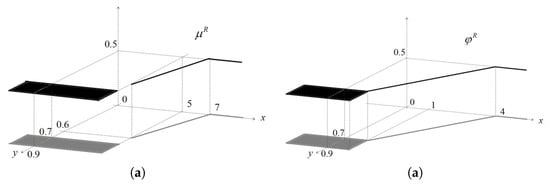
Figure 10. (a) ${\mu }^R$ and (b) ${\phi }^R$ according to Example 3.

• if $x\le 5$, then ${\mu }^R\left(x\right)=\mu \left(5\right)={\overline{[0.7,0.9]}}_{1/2}$;
• if $x>5$, then ${\mu }^R\left(x\right)=\mu \left(x\right)$.

${\phi }^L:\mathbb{R}\to {[0,1]}^{[0,1]}$ is such that (see Figure 9):

• if $x<1$, then ${\phi }^L\left(x\right)=\phi \left(x\right)$;
• if $x\ge 1$, then ${\phi }^L\left(x\right)=\phi \left(1\right)={\overline{[0.7,0.9]}}_{1/2}$;

${\phi }^R:\mathbb{R}\to {[0,1]}^{[0,1]}$ is such that (see Figure 10):

• if $x\le 1$, then $\phi \left(1\right)={\overline{[0.7,0.9]}}_{1/2}$;
• if $x>1$, then ${\phi }^R\left(x\right)=\phi \left(x\right)$.

Comparing ${\mu }^L\left(x\right)$ with ${\phi }^L\left(x\right)$ and ${\mu }^R\left(x\right)$ with ${\phi }^R\left(x\right)$ respect to the partial order ${⊑}_{1/2}$, we can prove ${\mu }^L\left(x\right){⊑}_{1/2}{\phi }^L\left(x\right)$ and ${\phi }^R\left(x\right){⊑}_{1/2}{\mu }^R\left(x\right)$ for all $x\in \mathbb{R}$. Therefore,

$$B\widetilde{⊑}A.$$

For example, from Figure 11, it follows that ${\left({\mu }^L\left(2\right)\right)}^R\left(y\right)\le {\left({\phi }^L\left(2\right)\right)}^R\left(y\right)$ and ${\left({\phi }^L\left(2\right)\right)}^L\left(y\right)\le {\left({\mu }^L\left(2\right)\right)}^L\left(y\right)$, for all $y\in [0,1]$, and then, ${\mu }^L\left(2\right){⊑}_{1/2}{\phi }^L\left(2\right)$.

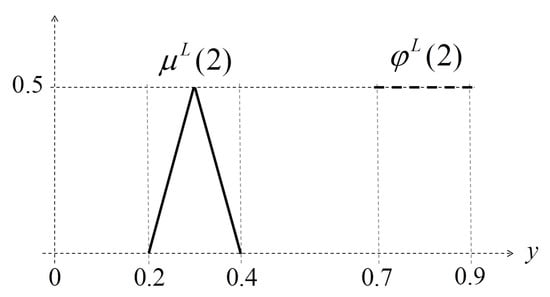
Figure 11. ${\mu }^L\left(2\right)$ and ${\phi }^L\left(2\right)$ according to Example 3.

Remark 7.

As mentioned before, in [19,22], total preorders for ranking IT2FNs were provided. One of the disadvantages of these preorders is that they do not satisfy the property of antisymmetry; therefore, two elements can be considered as equal, when they are not, which undoubtedly affects the decision making. On the other hand, from a theoretical point of view, operating or working with preorders adversely affects the consolidation of a consistent and coherent algebraic structure. A solid algebraic structure allows, among other things, the correct determination and application of operators (e.g., negations, t-norms, aggregation operators, among others). Besides, these preorders given in [19,22] reduce each IT2FN to a real value and finally compare these real values with the order of the real numbers, which implies some loss of the information (representation of the uncertainty, impression and vagueness) contained in the original form of each IT2FN. On the other hand, the partial order guarantees the algebraic properties of posets. Furthermore, with the partial order $\widetilde{⊑}$, the loss of information is minor compared to those preorders. One of the disadvantages of this partial order is that it is not total; therefore, there are elements that are non-comparable with it. Considering the above, the ideal is to have a total order, extending the order of the real numbers in the T2FNs; however, a partial order is a good starting point to obtain some total order. Anyway, it would be suitable, for ranking IT2FNs or IT2GFNs, firstly to apply the order $\widetilde{⊑}$, and if they are not comparable, then to apply the above-mentioned preorders.

It should be noted that in [19], it was established that any method to ranking IT2FNs must be consistent with the human intuition, in the sense that the more to the right an IT2FN is, the greater it will be. That is, the more to the right the centroid of an IT2FN is, the greater it will be. This property is satisfied by the order $\widetilde{⊑}$.

Example 4 shows two IT2GFNs previously ranked in [19] with the preorder CPS (centroid point and spread). We rank them with $\widetilde{⊑}$, obtaining the same decision as the one achieved with the CPS method. However, before, in the next Proposition 7, we give the characterization of $\widetilde{⊑}$, when ranking IT2GFNs exclusively.

Proposition 7.

Let A, B be two IT2GFNs, with membership degrees $\mu \left(x\right)=\overline{[a_1\left(x\right),b_1\left(x\right)]}$ and $\varphi \left(x\right)=\overline{[a_2\left(x\right),b_2\left(x\right)]}$, respectively, $\forall x\in \mathbb{R}$, then:

$$A\widetilde{⊑}B\iff a_2^L\left(x\right)\le a_1^L\left(x\right),a_1^R\left(x\right)\le a_2^R\left(x\right),b_2^L\left(x\right)\le b_1^L\left(x\right),b_1^R\left(x\right)\le b_2^R\left(x\right),\forall x\in \mathbb{R}(\iff a_1{⊑}_w{a}_2,b_1⊑b_2).$$

Proof. 

This is directly according to Definition 15, Remark 1, Proposition 5 and the usual partial order in the closed intervals, ${\le }_I$.  ☐

Example 4.

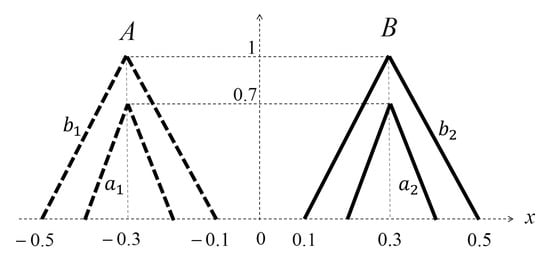
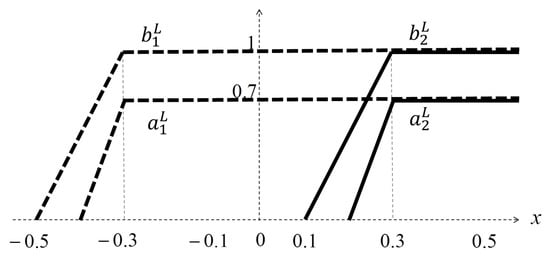
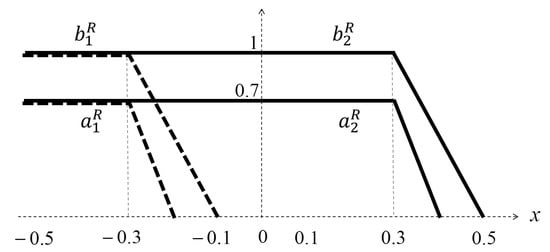
Let $A,B$ be two IT2GFNs, with membership degrees $A\left(x\right)=\overline{[a_1\left(x\right),b_1\left(x\right)]}$ and $B\left(x\right)=\overline{[a_2\left(x\right),b_2\left(x\right)]}$, $\forall x$, respectively, whose supports are shown in Figure 12. In [19], Section 4, Case 3, these IT2GFNs, $A,B$, were ranked with the CPS method, and it was obtained that B is greater than A. On the other hand, we apply the order $\widetilde{⊑}$, according to Figure 13 and Figure 14 and Proposition 7, and we obtain the same above result, i.e, $A\widetilde{⊑}B$ ($A\ne B$). In Figure 13 and Figure 14, note that $a_2^L\left(x\right)\le a_1^L\left(x\right),a_1^R\left(x\right)\le a_2^R\left(x\right),b_2^L\left(x\right)\le b_1^L\left(x\right),b_1^R\left(x\right)\le b_2^R\left(x\right),\forall x$; therefore, $A\widetilde{⊑}B$ ($A\ne B$).

Figure 12. Support of two IT2GFNs A and B, with the functions $a_1,b_1,a_2,b_2$.

Figure 13. Functions $a_1^L,b_1^L,a_2^L,b_2^L$.

Figure 14. Functions $a_1^R,b_1^R,a_2^R,b_2^R$.

Now, comparing the IT2FNs A and B in Figure 15 with the preorder given in [22] (${\prec }_{P_D}$), it results $A{\prec }_{P_D}B$ and $B{\nprec }_{P_D}A$ and also $A\widetilde{⋤}B$. Moreover, it can be proven that for any IT2FNs A and B, if $A\widetilde{⊑}B$, then $A{\prec }_{P_D}B$.

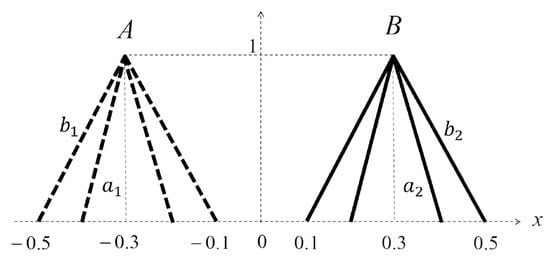
Figure 15. Support of two IT2FNs A and B.

Finally, Table 1 shows the properties fulfilled by each ranking method mentioned in this paper. Remember that:

Table 1. Comparative results for several ranking methods, “Y” = Yes, “N” = Not.

Method	Properties				Sets Can Be Compared			Extends Order of $\mathbb{R}$
	Reflex.	Antisymmetry	Trans.	Total	IT2Ns	IT2GFNs	T2GFNs-T2FNs
$\widetilde{⊑}$	Y	Y	Y	N	Y	Y	Y	Y
${⊑}_w$	Y	Y	Y	N	Y ($⊑={\le }_I$)	Y ($⊑={\le }_I$)	Y	N
${\le }_I$	Y	Y	Y	N	Y ($⊑={\le }_I$)	Y ($⊑={\le }_I$)	N	N
${\prec }_{P_D}$	Y	N	Y	Y	Y	N	N	Y
${\prec }_{CPS}$	Y	N	Y	Y	Y	Y	N	N

• $\widetilde{⊑}$ denotes the relation defined in Definition 15;
• ${⊑}_w$ denotes pointwise extension of the partial order ${⊑}_w$;
• ${\le }_I$ denotes pointwise extension of the partial order of the intervals ${\le }_I$;
• ${\prec }_{P_{CPS}}$ denotes the relation given in [19];
• ${\prec }_{P_D}$ denotes the relation given in [22].

4. Conclusions

In this work, we have defined, within the type 2 fuzzy sets (T2FSs), the fuzzy numbers (T2FNs) and the generalized fuzzy numbers (T2GFNs). It has been shown that the order on these sets naturally induced from the order on their membership degrees (pointwise extension) is not adequate, since it does not extend the usual order of real numbers. That is why a new partial order has been proposed on T2GFNs. Previously, taking into account this goal, we have generalized the partial order on L (set of convex and normal functions from $[0,1]$ to $[0,1]$) to the set of convex functions with the same height. Although, there are methods to ranking interval type 2 fuzzy numbers, the partial order obtained becomes a new option to be applied to ranking such type 2 fuzzy numbers and not only IT2FNs or IT2GFNs.

Some topics remain open for future research. Among them to study some properties of the proposed order and to obtain different ways to compare T2GFNs, allowing us to rank as many type 2 fuzzy sets as possible.