Toward Measuring Network Aesthetics Based on Symmetry
Abstract
:1. Introduction
- order O (e.g., symmetry of a polygon),
- complexity C (e.g., number of straight lines of a polygon),
2. Quantitative Methods and Network Aesthetic Measurement
3. Methods and Discussion
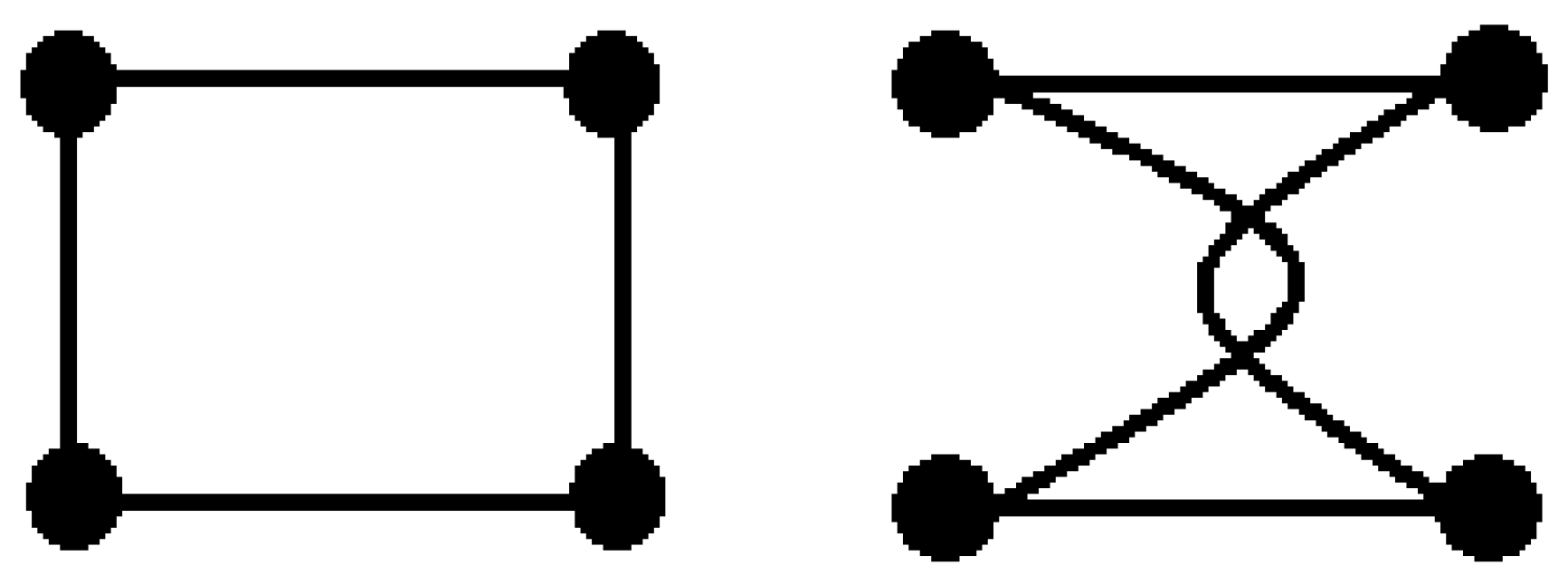
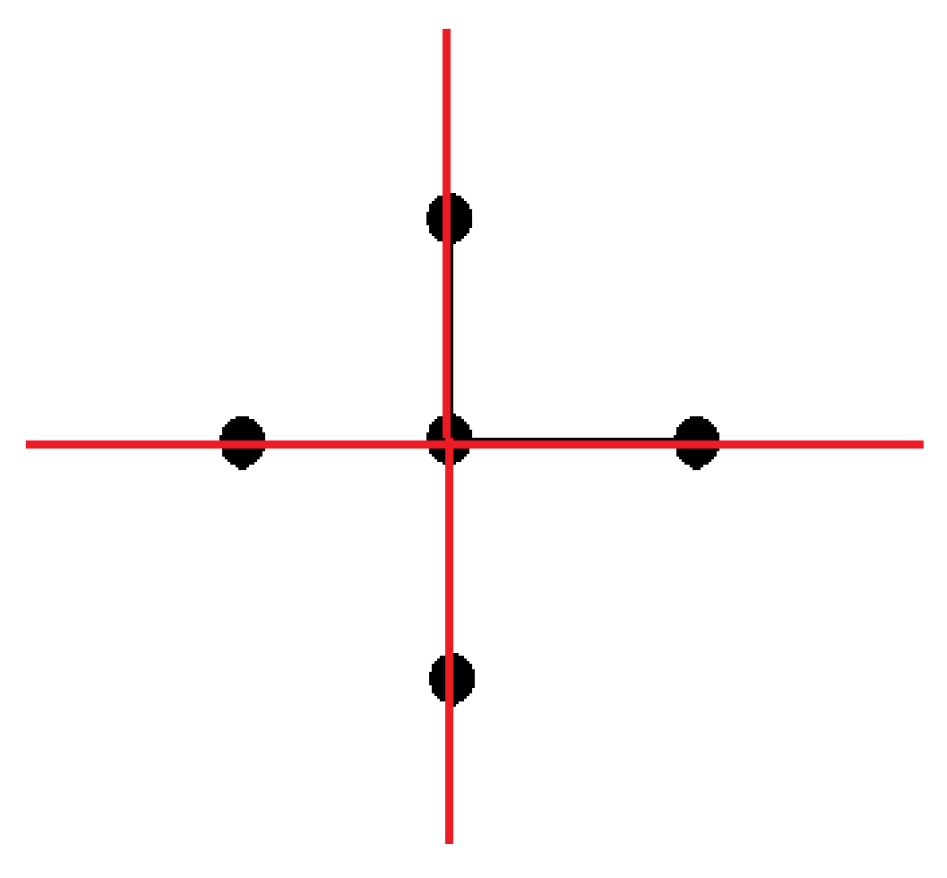
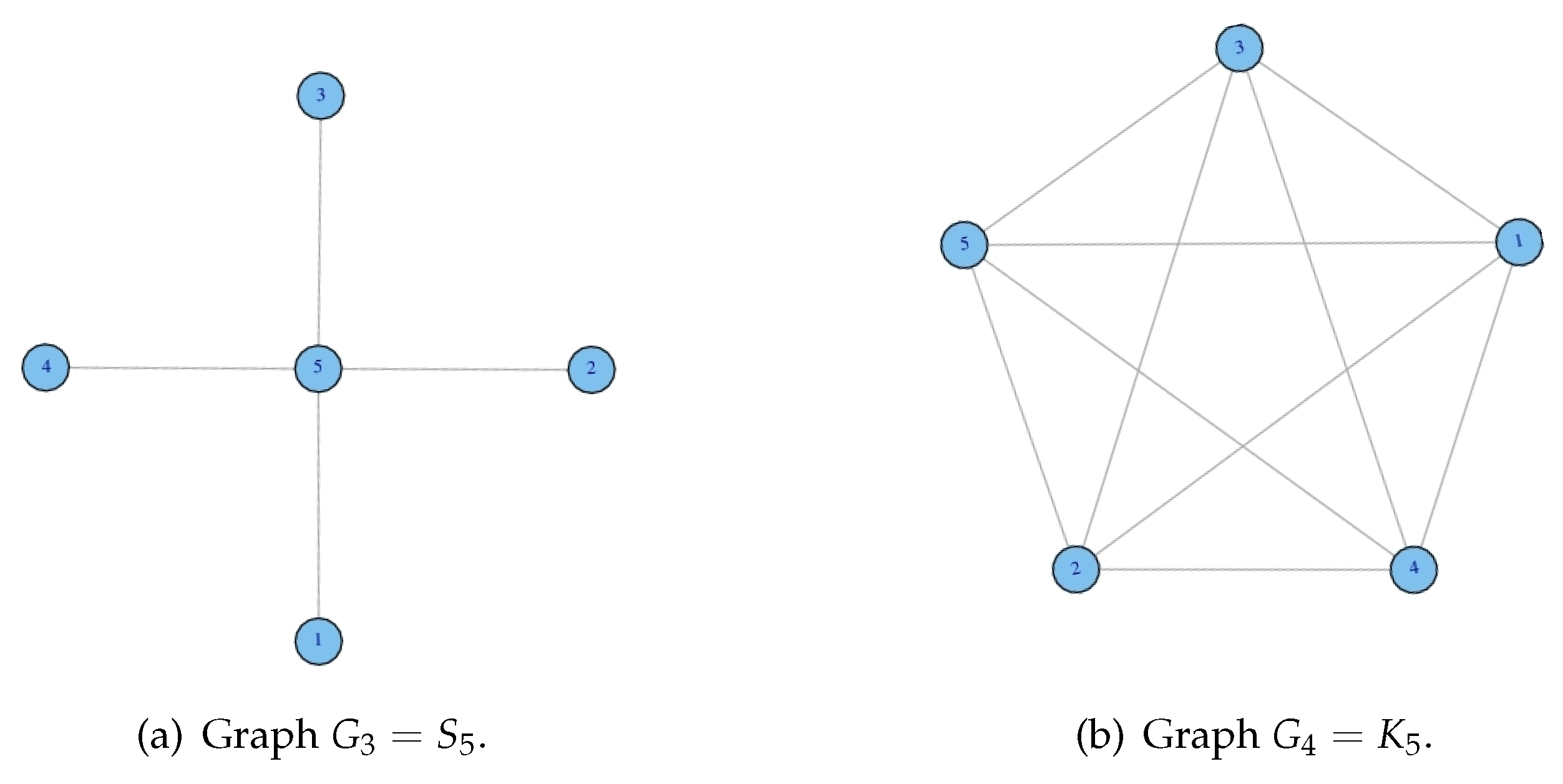
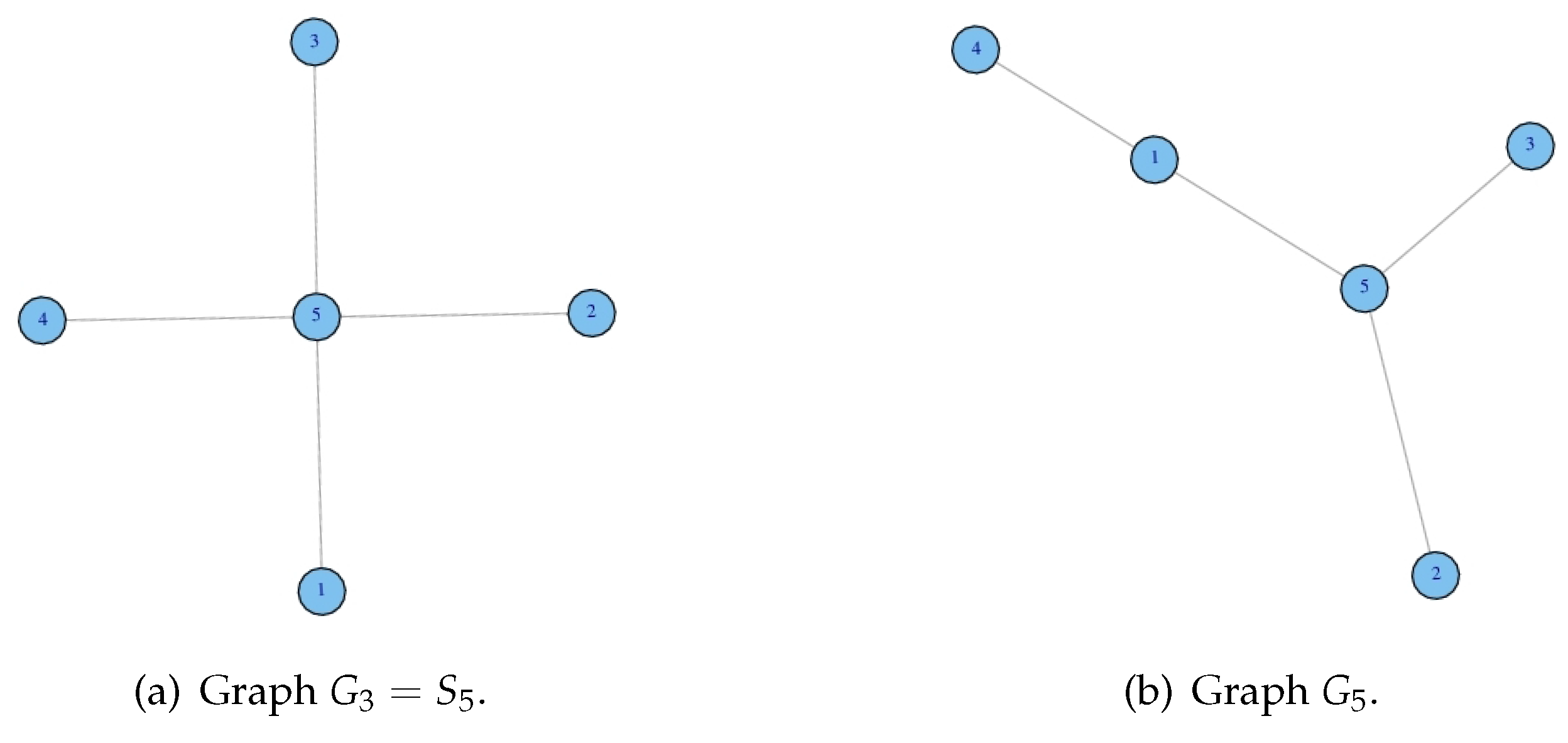
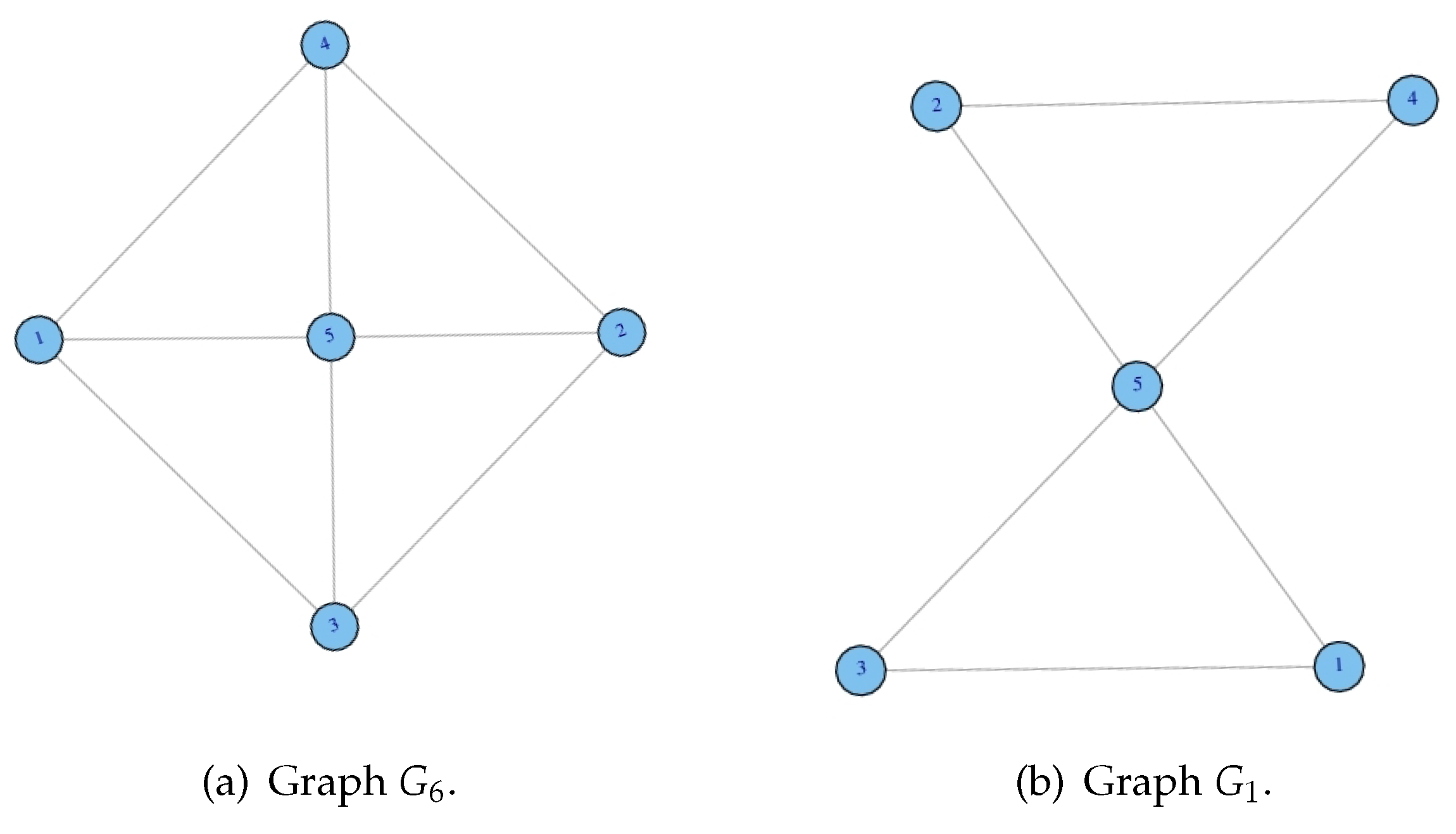
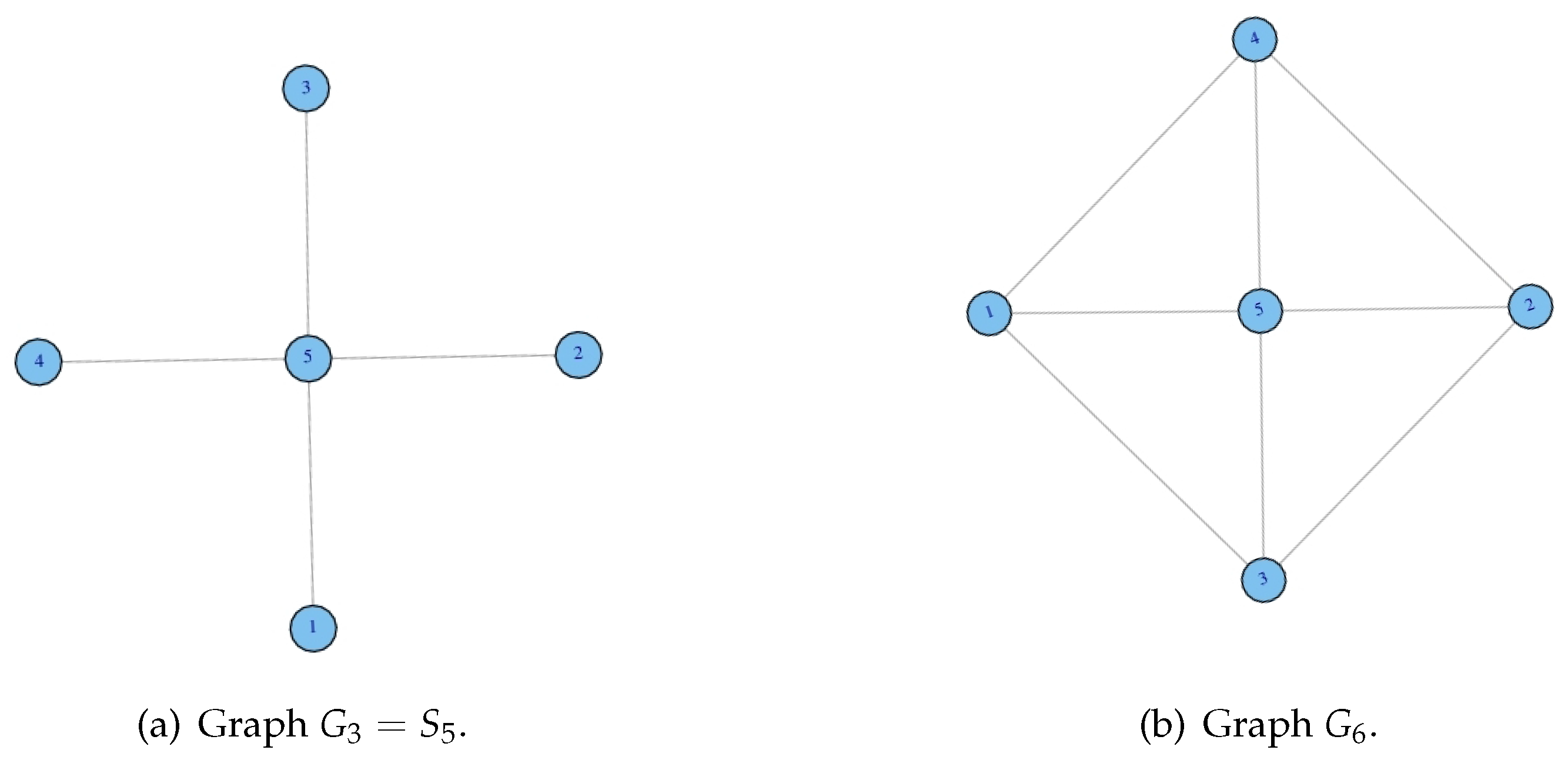
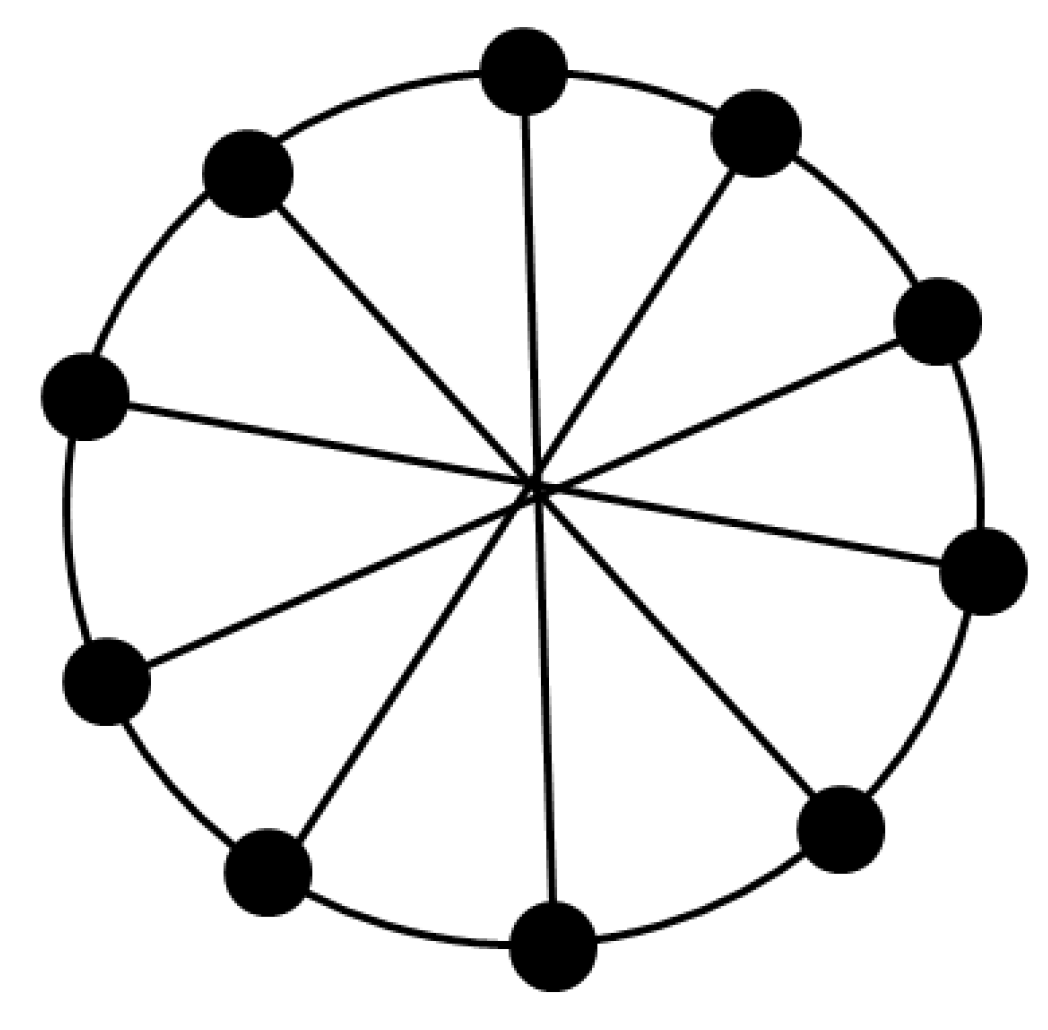
3.1. Graph-Theoretical Definitions
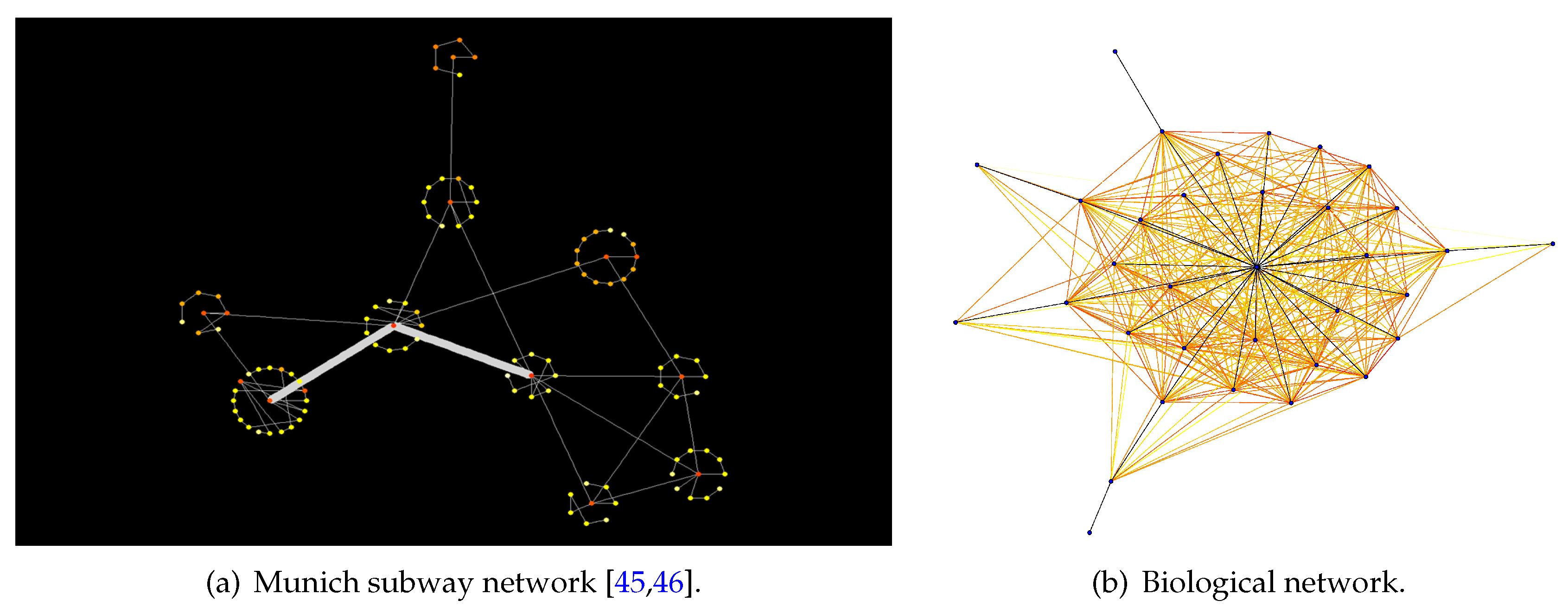
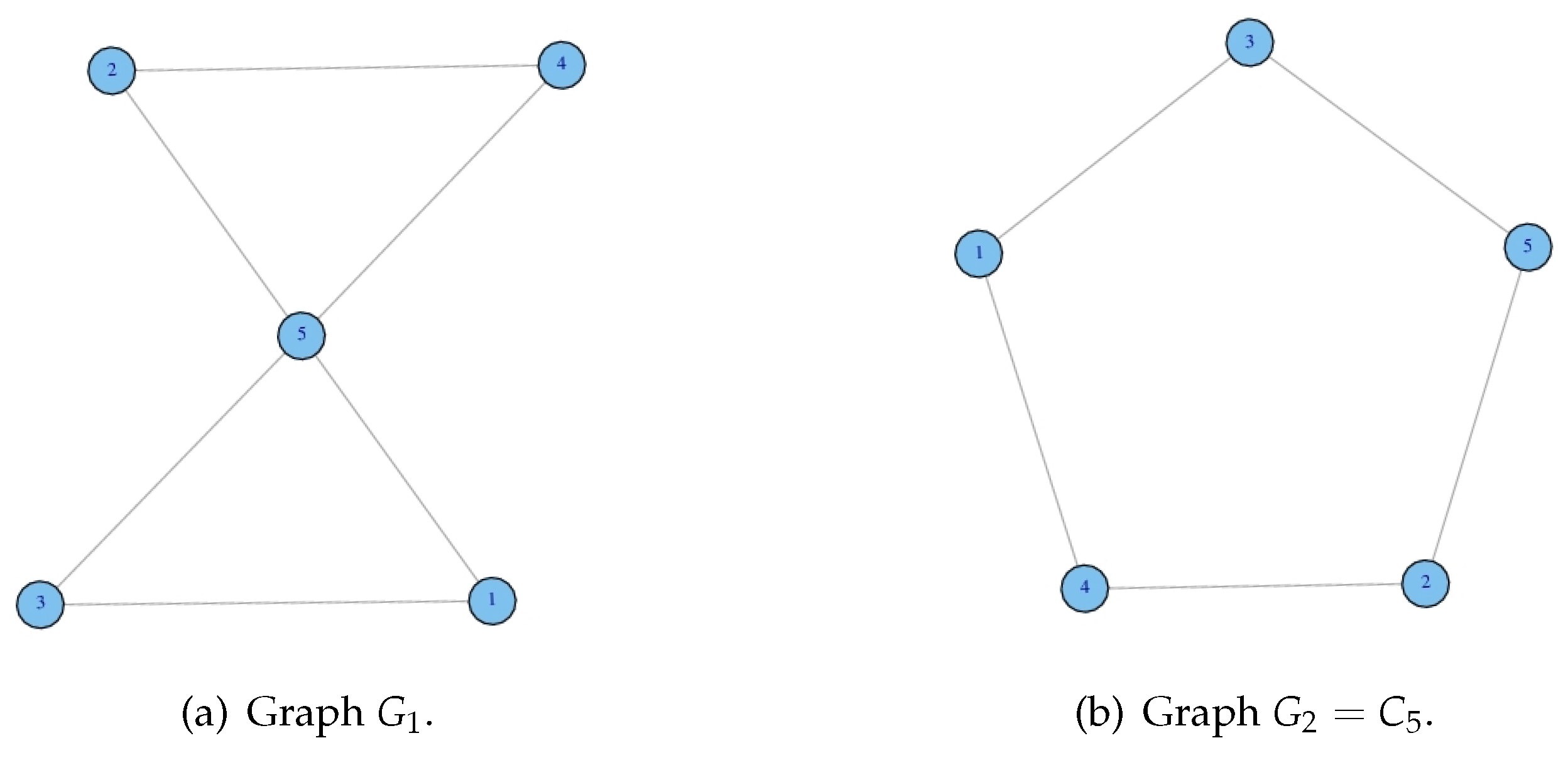
3.2. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fucks, W. Mathematische Analyse des literarischen Stils. In Studium Generale; Springer: New York, NY, USA, 1953; Volume 6. [Google Scholar]
- Ganter, B.; Mineau, G.W. Conceptual Structures: Logical, Linguistic, and Computational Issues; Lecture Notes in Artificial Intelligence; Springer: New York, NY, USA, 2000. [Google Scholar]
- Mehler, A. Textbedeutung. Zur Prozeduralen Analyse und Repräsentation Struktureller Ähnlichkeiten von Texten; Sprache, Sprechen und Computer/Computer Studies in Language and Speech; Peter Lang: Frankfurt am Main, Germany, 2001; Volume 5. [Google Scholar]
- Tuldava, J. A Statistical Method of Comparison of the Lexical Composition of Two Texts. In Methods in Quantitative Linguistics; Tuldava, J., Ed.; Wissenschaftlicher Verlag Trier: Trier, Germany, 1995. [Google Scholar]
- Birkhoff, G.D. A mathematical approach to aesthetics. Scientia (Milano) 1931, 50, 133–146. [Google Scholar]
- Boselie, F.; Leeuwenberg, E. Birkhoff Revisited: Beauty as a Function of Effect and Means. Am. J. Psychol. 1985, 98, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Bense, M. The Projects of Generative Aesthetics. In Cybernetics, Art, and Ideas; Reichardt, J., Ed.; New York Graphic Society: Greenwich, CT, USA, 1971. [Google Scholar]
- Moles, A.A. Information Theory and Esthetic Perception; University of Illinois Press: Urbana, IL, USA, 1966. [Google Scholar]
- Rigau, J.; Feixas, M.; Sbert, M. Informational Aesthetics Measures. IEEE Comput. Graph. Appl. 2008, 28, 24–34. [Google Scholar] [CrossRef] [PubMed]
- Galanter, P. Complexity, Neuroaesthetics, and Computational Aesthetic Evaluation. In Proceedings of the 13th Generative Art Conference GA2010, Milan, Italy, 15–17 December 2010; pp. 400–409. [Google Scholar]
- Purchase, H. Metrics for Graph Drawing Aesthetics. J. Vis. Lang. Comput. 2002, 13, 501–516. [Google Scholar] [CrossRef]
- Beck, F.; Burch, M.; Diehl, S. Towards an Aesthetic Dimensions Framework for Dynamic Graph Visualisations. In Proceedings of the 13-th International Conference Information Visualisation, Barcelona, Spain, 15–17 July 2009; pp. 592–597. [Google Scholar]
- Ware, C.; Purchase, H.; Colpoys, L.; McGill, M. Cognitive Measurements of Graph Aesthetics. Inf. Vis. 2002, 1, 103–110. [Google Scholar] [CrossRef]
- Battista, G.D.; Eades, P.; Tamassia, R.; Tollis, I.G. Algorithms for the Visualization of Graphs; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Dehmer, M.; Emmert-Streib, F.; Gesell, T. A comparative analysis of multidimensional features of objects resembling sets of graphs. Appl. Math. Comput. 2008, 196, 221–235. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. Entropy and the Complexity of Graphs Revisited. Entropy 2012, 14, 559–570. [Google Scholar] [CrossRef]
- Botafogo, R.A.; Rivlin, E.; Shneiderman, B. Structural Analysis of Hypertexts: Identifying Hierarchies and Useful Metrics. ACM Trans. Inf. Syst. 1992, 10, 142–180. [Google Scholar] [CrossRef]
- Schutte, M.; Dehmer, M. Large-scale analysis of structural branching measures. J. Math. Chem. 2013, 52, 805–819. [Google Scholar] [CrossRef]
- Dehmer, M.; Emmert-Streib, F. Quantitative Graph Theory. Theory and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Mowshowitz, A. Entropy and the complexity of the graphs I: An index of the relative complexity of a graph. Bull. Math. Biophys. 1968, 30, 175–204. [Google Scholar] [CrossRef] [PubMed]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Morowitz, H. Some order-disorder considerations in living systems. Bull. Math. Biophys. 1953, 17, 81–86. [Google Scholar] [CrossRef]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biol. 1956, 18, 129–135. [Google Scholar] [CrossRef]
- Rashevsky, N. Life, Information Theory, and Topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Dehmer, M. Information Theory of Networks. Symmetry 2012, 3, 767–779. [Google Scholar] [CrossRef]
- Dehmer, M.; Mowshowitz, A. A History of Graph Entropy Measures. Inf. Sci. 2011, 1, 57–78. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Gutman, I. Graph Energy; Springer: New York, NY, USA, 2012. [Google Scholar]
- Ulanowicz, R.E. Circumscribed complexity in ecological networks. In Advances in Network Complexity; Devillers, J., Balaban, A.T., Eds.; Wiley-Blackwell: Oxford, UK, 2013; pp. 249–258. [Google Scholar]
- Emmert-Streib, F.; Dehmer, M. (Eds.) Analysis of Microarray Data: A Network-Based Approach; Wiley VCH: Weinheim, Germany, 2010. [Google Scholar]
- Diudea, M.V. QSPR / QSAR Studies by Molecular Descriptors; Nova Publishing: New York, NY, USA, 2001. [Google Scholar]
- Hirata, H.; Ulanowicz, R.E. Information theoretical analysis of ecological networks. Int. J. Syst. Sci. 1984, 15, 261–270. [Google Scholar] [CrossRef]
- Ulanowicz, R.E. Quantitative methods for ecological network analysis. Comput. Biol. Chem. 2004, 28, 321–339. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Emmert-Streib, F. Mining Graph Patterns in Web-based Systems: A Conceptual View. In Genres on the Web: Computational Models and Empirical Studies; Mehler, A., Sharoff, S., Rehm, G., Santini, M., Eds.; Springer: Berlin, Germany; New York, NY, USA, 2010; pp. 237–253. [Google Scholar]
- Bunke, H.; Günter, S.; Jiang, X. Towards bridging the gap between statistical and structural pattern recognition: Two new concepts in graph matching. In Proceedings of the Advances in Pattern Recognition—ICAPR 2001, Rio de Janeiro, Brazil, 11–14 March 2001; pp. 1–11. [Google Scholar]
- Mehler, A. Textmining. In Texttechnologie. Perspektiven und Anwendungen; Lobin, H., Lemnitzer, L., Eds.; Stauffenburg: Tübingen, Germany, 2004; pp. 83–107. [Google Scholar]
- Dehmer, M.; Mehler, A. A new method of measuring similarity for a special class of directed graphs. Tatra Mt. Math. Publ. 2007, 36, 39–59. [Google Scholar]
- Emmert-Streib, F.; Dehmer, M.; Shi, Y. Fifty years of graph matching, network alignment and network comparison. Inf. Sci. 2016, 346–347, 180–197. [Google Scholar] [CrossRef]
- Mehler, A. Social Ontologies as Generalized Nearly Acyclic Directed Graphs: A Quantitative Graph Model of Social Tagging. In Towards an Information Theory of Complex Networks: Statistical Methods and Applications; Dehmer, M., Emmert-Streib, F., Mehler, A., Eds.; Birkhäuser: Boston, MA, USA; Basel, Switzerland, 2011; pp. 259–319. [Google Scholar]
- Bonchev, D. Topological order in molecules 1. Molecular branching revisited. J. Mol. Struct. THEOCHEM 1995, 336, 137–156. [Google Scholar] [CrossRef]
- Garrido, A. Analysis of asymmetry measures. Adv. Model. Optim. 2008, 2, 199–211. [Google Scholar]
- Garrido, A. Symmetry of Complex Networks. Adv. Model. Optim. 2009, 11, 615–624. [Google Scholar] [CrossRef]
- Mowshowitz, A.; Dehmer, M. A Symmetry Index for Graphs. Symmetry Cult. Sci. 2010, 21, 321–327. [Google Scholar]
- Dehmer, M.; Mehler, A.; Emmert-Streib, F. Graph-theoretical Characterizations of Generalized Trees. In Proceedings of the International Conference on Machine Learning: Models, Technologies & Applications (MLMTA’07), Las Vegas, NV, USA, 25–28 June 2007; pp. 113–117. [Google Scholar]
- Bahnhöfe des MVV. Available online: http://www.mvv-muenchen.de/de/netz-bahnhoefe/bahnhofsinformation/index.html (accessed on 12 January 2017).
- Netzpläne des MVV. Information des Münchner Verkehrs- und Tarifverbundes GmbH. Available online: http://www.mvv-muenchen.de/de/netz-bahnhoefe/netzplaene/index.html (accessed on 12 January 2017).
- Rodrigue, J.P.; Comtois, C.; Slack, B. The Geography of Transport Systems; Taylor & Francis: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tripathi, S.; Dehmer, M.; Emmert-Streib, F. NetBioV: An R package for visualizing large network data in biology and medicine. Bioinformatics 2014, 19, 2834–2836. [Google Scholar] [CrossRef] [PubMed]
- Emmert-Streib, F.; Dehmer, M. Information processing in the transcriptional regulatory network of yeast: Functional robustness. BMC Syst. Biol. 2009, 3. [Google Scholar] [CrossRef] [PubMed]
- Harary, F. Graph Theory; Addison Wesley Publishing Company: Reading, MA, USA, 1969. [Google Scholar]
- Filonik, D.; Baur, D. Measuring aesthetics for information visualization. In Proceedings of the 13th International Conference Information Visualisation, Barcelona, Spain, 15–17 July 2009; pp. 579–584. [Google Scholar]
- Frucht, R. Herstellung von Graphen mit vorgegebener abstrakter Gruppe. Compos. Math. 1939, 6, 239–250. [Google Scholar]
- Mowshowitz, A.; Mitsou, V. Entropy, orbits and spectra of graphs. In Analysis of Complex Networks: From Biology to Linguistics; Dehmer, M., Emmert-Streib, F., Eds.; Wiley-VCH: Weinheim, Germany, 2009; pp. 1–22. [Google Scholar]
- Mowshowitz, A. Entropy and the complexity of graphs II: The information content of digraphs and infinite graphs. Bull. Math. Biophys. 1968, 30, 225–240. [Google Scholar] [CrossRef] [PubMed]
- Mowshowitz, A. Entropy and the complexity of graphs III: Graphs with prescribed information content. Bull. Math. Biophys. 1968, 30, 387–414. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs IV: Entropy measures and graphical structure. Bull. Math. Biophys. 1968, 30, 533–546. [Google Scholar] [CrossRef]
- McKay, B.D.; Piperno, A. Practical Graph Isomorphism, II, 2013. Available online: http://cs.anu.edu.au/~bdm/nauty/ (accessed on 12 January 2017).
- Deza, M.M.; Deza, E. Encyclopedia of Distances, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Dehmer, M.; Emmert-Streib, F.; Mowshowitz, A.; Shi, Y. Toward Measuring Network Aesthetics Based on Symmetry. Axioms 2017, 6, 12. https://doi.org/10.3390/axioms6020012
Chen Z, Dehmer M, Emmert-Streib F, Mowshowitz A, Shi Y. Toward Measuring Network Aesthetics Based on Symmetry. Axioms. 2017; 6(2):12. https://doi.org/10.3390/axioms6020012
Chicago/Turabian StyleChen, Zengqiang, Matthias Dehmer, Frank Emmert-Streib, Abbe Mowshowitz, and Yongtang Shi. 2017. "Toward Measuring Network Aesthetics Based on Symmetry" Axioms 6, no. 2: 12. https://doi.org/10.3390/axioms6020012
APA StyleChen, Z., Dehmer, M., Emmert-Streib, F., Mowshowitz, A., & Shi, Y. (2017). Toward Measuring Network Aesthetics Based on Symmetry. Axioms, 6(2), 12. https://doi.org/10.3390/axioms6020012








