Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and Its Applications in Various Disciplines
Abstract
:1. Introduction
2. Statistical Interpretations of Fractional Integrals
3. Limiting Approach to the Generalized Gamma Bessel Model via the Pathway Operator
| Two-parameter gamma density | |
| One-parameter gamma density | |
| Exponential density | |
| Chi-square density | |
| Noncentral chi-square density |
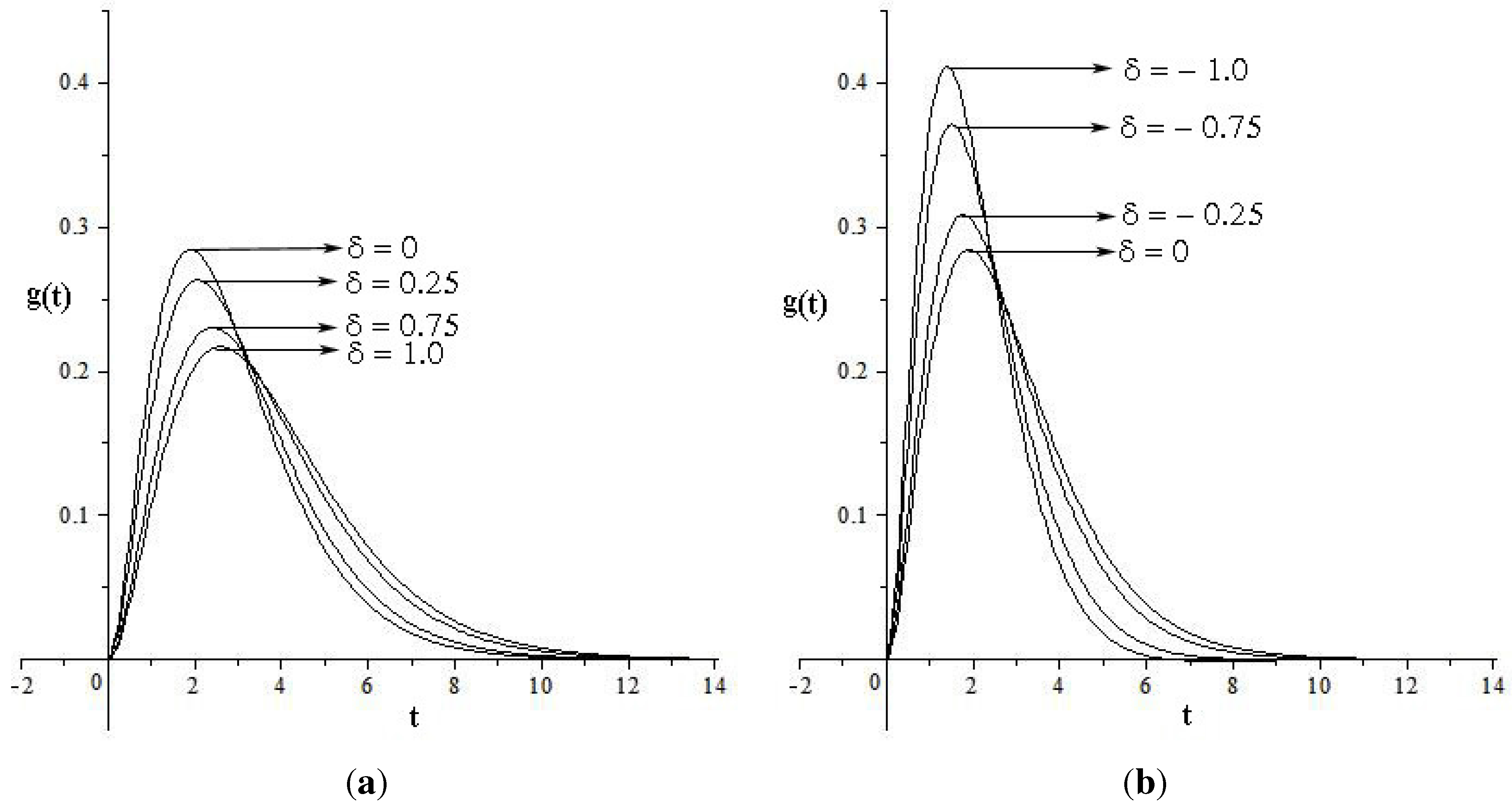
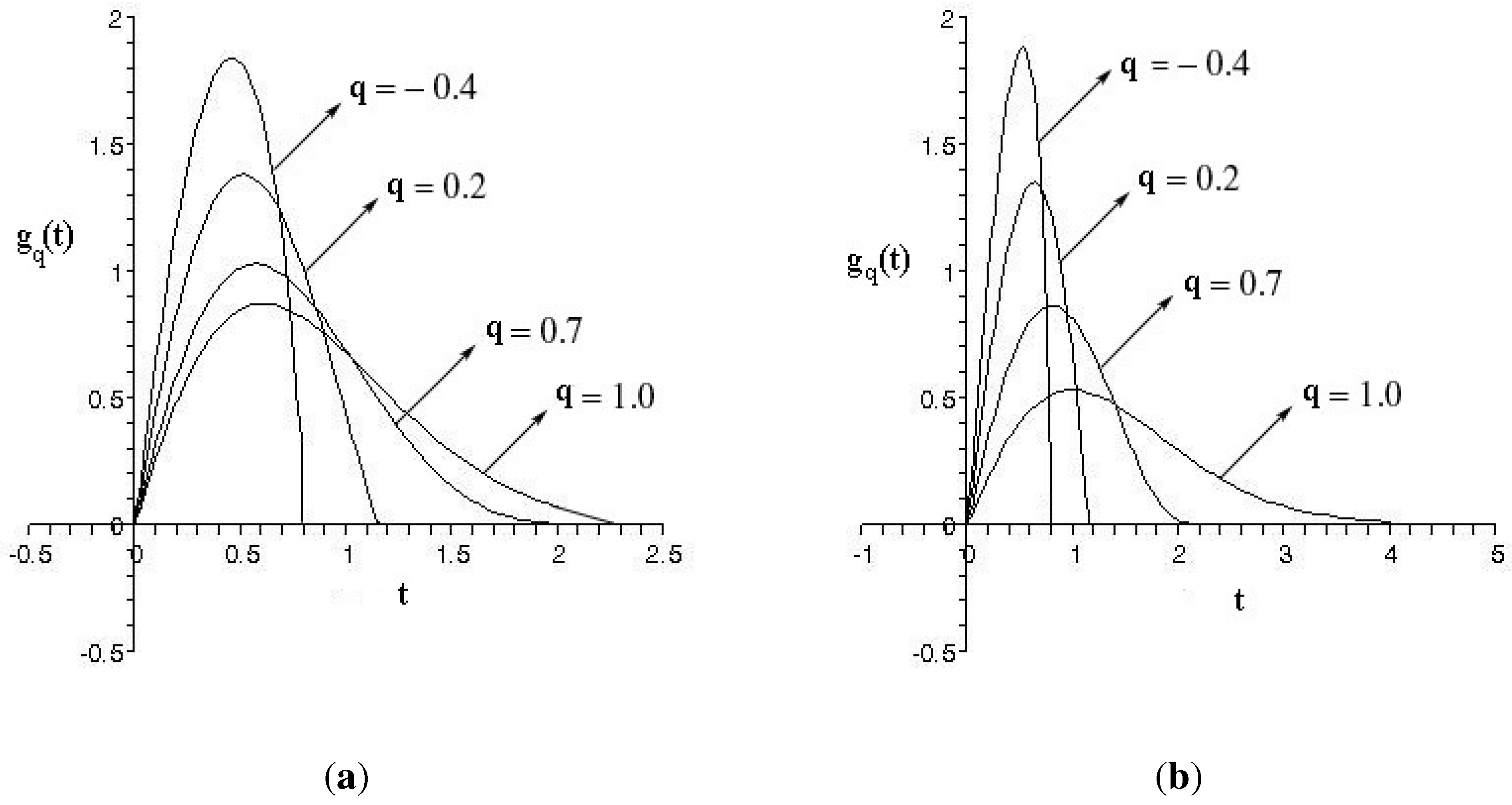
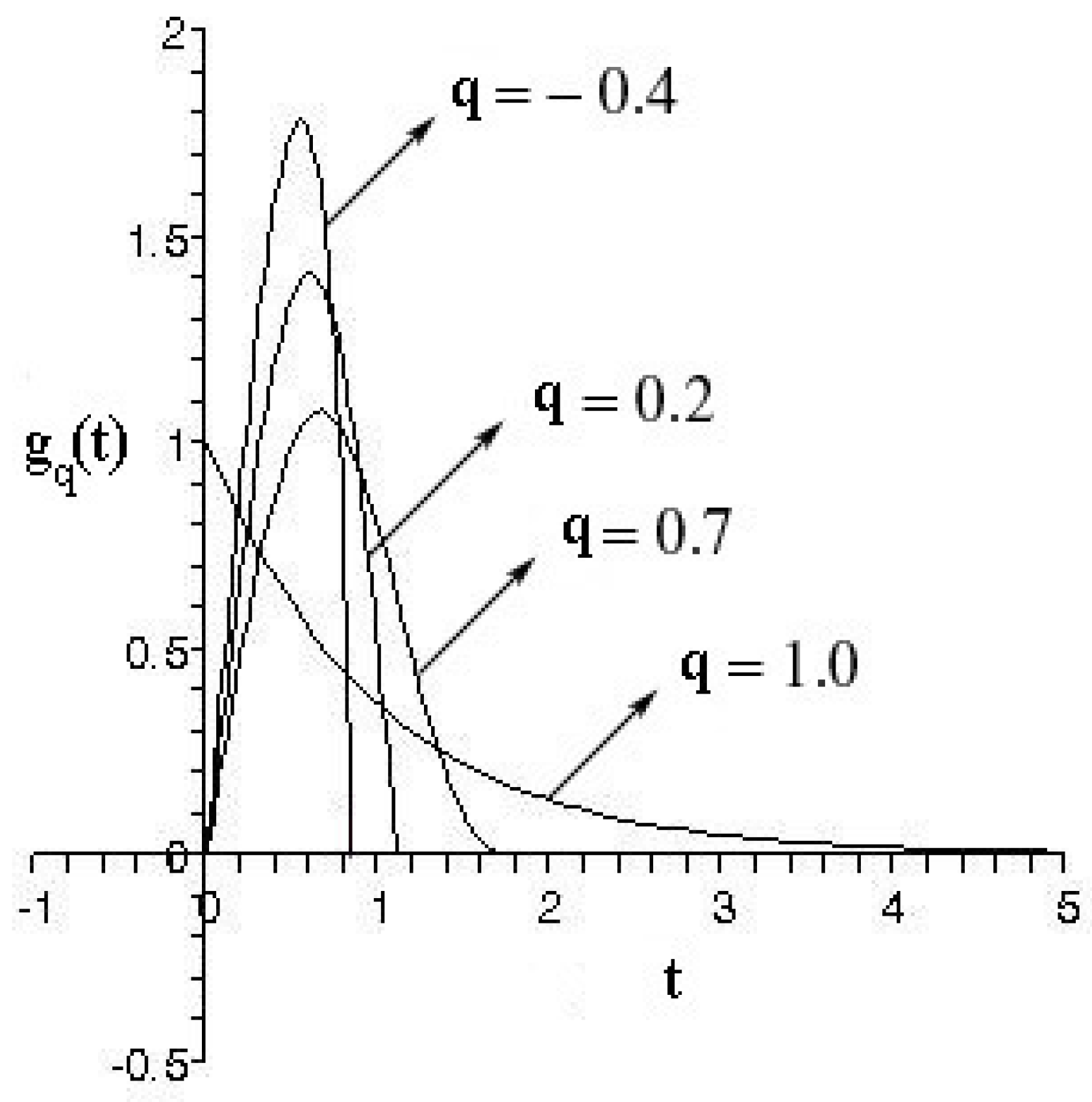
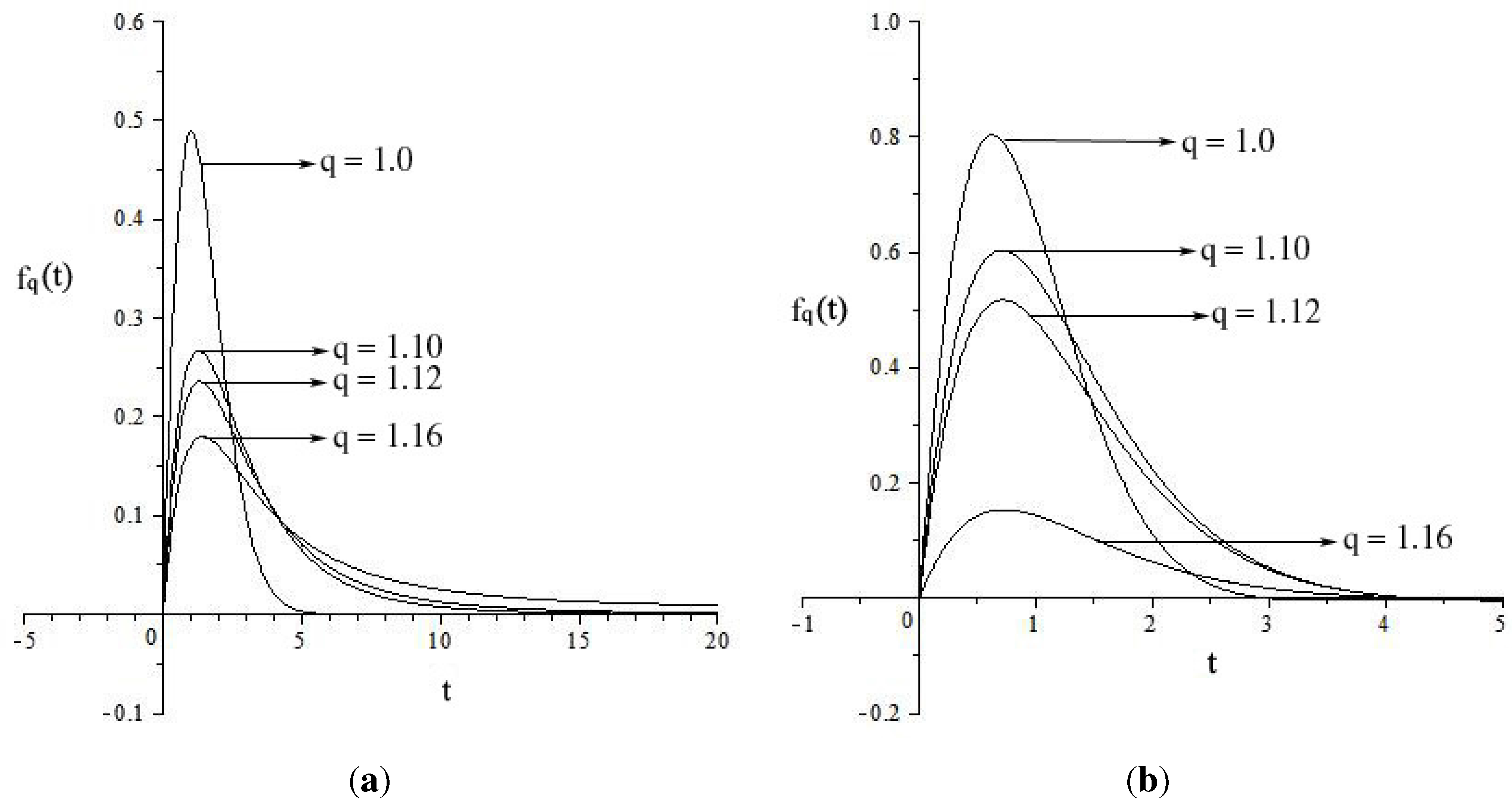
4. Applications in Statistical Mechanics
5. Applications in the Growth-Decay Mechanism
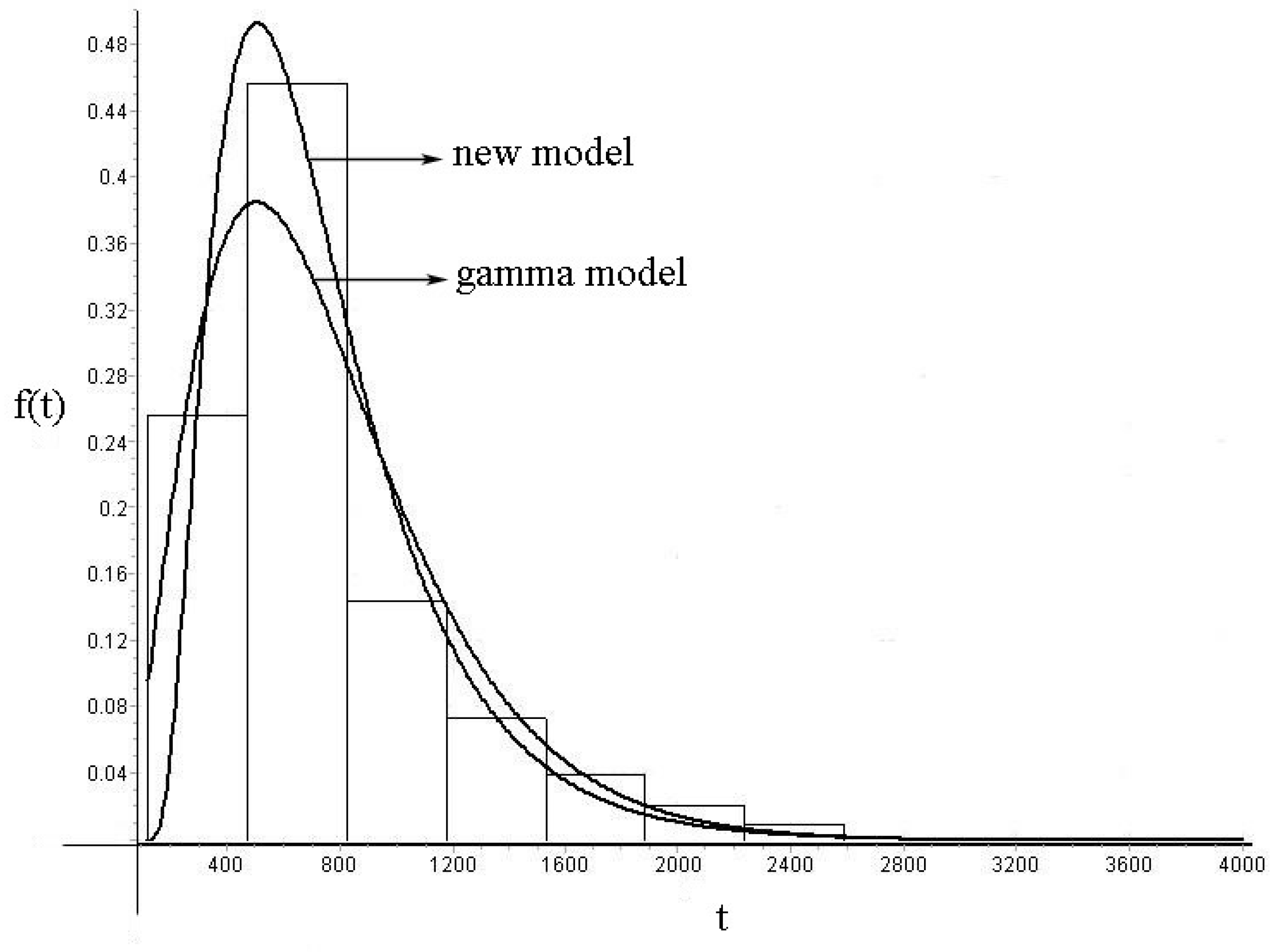
6. Applications in Solar Spectral Irradiance Modeling

Acknowledgments
Conflicts of Interest
References
- Haubold, H.J.; Mathai, A.M. The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci. 2000, 273, 53–63. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Existence of Turing instabilities in a two-species fractional reaction-diffusion system. SIAM J. Appl. Math. 2002, 62, 870–887. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Special Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Pathway model, superstatistics, Tsallis statistics and a generalized measure of entropy. Phys. A 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Fractional reaction-diffusion equations. Astrophys. Space Sci. 2006, 305, 289–296. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M. H-Transforms: Theory and Applications; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Kiryakova, V. Generalized Fractional Calculus and Applications; CRC Press: New York, NY, USA, 1994. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: New York, NY, USA, 1990. [Google Scholar]
- Mathai, A.M. A pathway to matrix-variate gamma and normal densities. Linear Algebra Its Appl. 2005, 396, 317–328. [Google Scholar] [CrossRef]
- Honerkamp, J. Stochastic Dynamical Systems: Concepts, Numerical Methods, Data Analysis; VCH Publishers: New York, NY, USA, 1994. [Google Scholar]
- Mathai, A.M. On non-central generalized Laplacianness of quadratic forms in normal variables. J. Multivar. Anal. 1993, 45, 239–246. [Google Scholar] [CrossRef]
- Nair, S.S. Pathway fractinal integration operator. Fract. Calc. Appl. Anal. 2009, 12, 237–252. [Google Scholar]
- Mathai, A.M. Fractional integrals in the matrix-variate cases and connection to statistical distributions. Integral Transform. Special Funct. 2009, 20, 871–882. [Google Scholar] [CrossRef]
- Nair, S.S. Pathway fractional integral operator and matrix-variate functions. Integral Transform. Special Funct. 2011, 22, 233–244. [Google Scholar] [CrossRef]
- Sebastian, N. Some statistical aspects of fractional calculus. J. Kerala Stat. Assoc. 2009, 20, 23–33. [Google Scholar]
- Sebastian, N. A generalized gamma model associated with Bessel function and its applications in statistical mechanics. In Proceedings of AMADE-09, Proceedings of Institute of Mathematics, Natinal Academy of Sciences, Minsk, Belarus; 2009; pp. 114–119. [Google Scholar]
- Sebastian, N. A generalized gamma model associated with a Bessel function. Integral Transform. Special Funct. 2011, 22, 631–645. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Beck, C. Stretched exponentials from superstatistics. Phys. A 2006, 365, 96–101. [Google Scholar] [CrossRef]
- Beck, C. Dynamical Foundations of Nonextensive Statistical Mechanics. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar] [CrossRef]
- Beck, C. Non-additivity of Tsallis entropies and fluctuations of temperature. Europhys. Lett. 2002, 57, 329–333. [Google Scholar] [CrossRef]
- Touchette, H. Nonextensive Entropy-Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Beck, C. Comment on critique of q-entropy for thermal statistics. Phys. Rev. E 2004, 69, 038101. [Google Scholar]
- Chavanis, P.H. Coarse-grained distributions and superstatistics. Phys. A 2006, 359, 177–212. [Google Scholar] [CrossRef]
- Joseph, D.P. Gamma distribution and extensions using pathway idea. Stat. Pap. 2011, 52, 309–325. [Google Scholar] [CrossRef]
- Krätzel, E. Integral transformations of Bessel type. 1979; 148–155. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. Mordern Problems in Nuclear and Neutrino Astrophysics; Akademie-Verlag: Berlin, Germany, 1988. [Google Scholar]
- Mathai, A.M. A Versatile Integral. CMS Project SR/S4/MS:287/05. Preprint. 2007; 9. [Google Scholar]
- Mathai, A.M.; Provost, S.B.; Hayakawa, T. Bilinear Forms and Zonal Polynomials; Lecture notes in Statistics, No. 102; Springer-Verlag: New York, MY, USA, 1995. [Google Scholar]
- Mathai, A.M. The residual effect of growth-decay mechanism and the distributions of covariance structure. Can. J. Stat. 1993, 21, 277–283. [Google Scholar] [CrossRef]
- Gueymard, C. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- Stoffel, T.; Renné, D.; Myers, D.; Wilcox, S.; Sengupta, M.; George, R.; Turchi, C. Concentrating Solar Power. Available online: http://www.nrel.gov/docs/fy10osti/47465.pdf (accessed on 13 August 2015).
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sebastian, N. Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and Its Applications in Various Disciplines. Axioms 2015, 4, 385-399. https://doi.org/10.3390/axioms4030385
Sebastian N. Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and Its Applications in Various Disciplines. Axioms. 2015; 4(3):385-399. https://doi.org/10.3390/axioms4030385
Chicago/Turabian StyleSebastian, Nicy. 2015. "Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and Its Applications in Various Disciplines" Axioms 4, no. 3: 385-399. https://doi.org/10.3390/axioms4030385
APA StyleSebastian, N. (2015). Limiting Approach to Generalized Gamma Bessel Model via Fractional Calculus and Its Applications in Various Disciplines. Axioms, 4(3), 385-399. https://doi.org/10.3390/axioms4030385





