Azumaya Monads and Comonads

Abstract

The definition of Azumaya algebras over commutative rings R requires the tensor product of modules over R and the twist map for the tensor product of any two R-modules. Similar constructions are available in braided monoidal categories, and Azumaya algebras were defined in these settings. Here, we introduce Azumaya monads on any category $\mathbb{A}$ by considering a monad $(F,m,e)$ on $\mathbb{A}$ endowed with a distributive law $\lambda :FF\to FF$ satisfying the Yang–Baxter equation (BD-law). This allows to introduce an opposite monad $(F^{\lambda },m·\lambda ,e)$ and a monad structure on $F{F}^{\lambda }$. The quadruple $(F,m,e,\lambda )$ is called an Azumaya monad, provided that the canonical comparison functor induces an equivalence between the category $\mathbb{A}$ and the category of $F{F}^{\lambda }$-modules. Properties and characterizations of these monads are studied, in particular for the case when F allows for a right adjoint functor. Dual to Azumaya monads, we define Azumaya comonads and investigate the interplay between these notions. In braided categories $(\mathcal{V},\otimes ,I,\tau )$, for any $\mathcal{V}-\mathrm{algebra}$ A, the braiding induces a BD-law ${\tau }_{A,A}:A\otimes A\to A\otimes A$, and A is called left (right) Azumaya, provided the monad $A\otimes -$(resp.$-\otimes A$) is Azumaya. If τ is a symmetry or if the category $\mathcal{V}$ admits equalizers and coequalizers, the notions of left and right Azumaya algebras coincide.

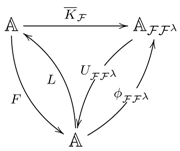
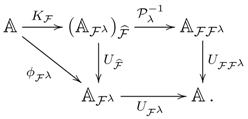
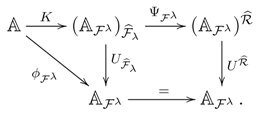
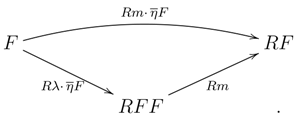
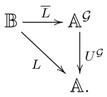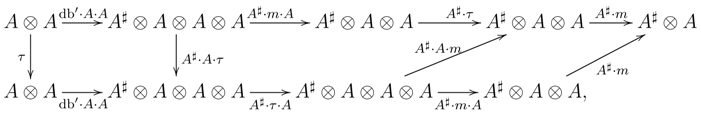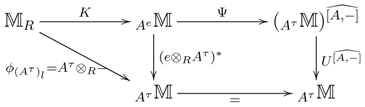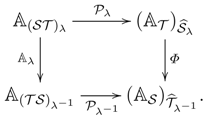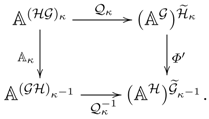1. Introduction

Azumaya algebras $\mathcal{A}=(A,m,e)$ over a commutative ring R are characterized by the fact that the functor $A{\otimes }_R-$ induces an equivalence between the category of R-modules and the category of $(A,A)$-bimodules. In this situation, Azumaya algebras are separable algebras, that is the multiplication $A{\otimes }_{R}A\to A$ splits as a $(A,A)$-bimodule map.

Braided monoidal categories allow for similar constructions as module categories over commutative rings, and so, with some care, Azumaya algebras (monoids) and Brauer groups can be defined for such categories. For finitely bicomplete categories, this was worked out by Fisher-Palmquist in [1]; for symmetric monoidal categories it was investigated by Pareigis in [2]; and for braided monoidal categories, the theory was outlined by van Oystaeyen and Zhang in [3] and Femić in [4]. It follows from the observations in [2] that, even in symmetric monoidal categories, the category equivalence requested for an Azumaya algebra A does not imply the separability of A (defined as for R-algebras).

In our approach to Azumaya (co)monads, we focus on the properties of monads and comonads on any category $\mathbb{A}$ inducing equivalences between certain related categories. Our main tools are distributive laws between monads (and comonads) as used in the investigations of Hopf monads in general categories (see [5,6]).

In Section 2, basic facts about the related theory are recalled, including Galois functors.

In Section 3, we consider monads $\mathcal{F}=(F,m,e)$ on any category $\mathbb{A}$ endowed with a distributive law $\lambda :FF\to FF$ satisfying the Yang–Baxter equation (monad BD-law). The latter enables the definition of a monad ${\mathcal{F}}^{\lambda }=(F^{\lambda },m^{\lambda },e^{\lambda })$, where $F^{\lambda }=F$, $m^{\lambda }=m·\lambda$ and $e^{\lambda }=e$. Furthermore, λ can be considered as distributive law $\lambda :F^{\lambda }F\to F{F}^{\lambda }$, and this allows one to define a monad structure on $F{F}^{\lambda }$. Then, for any object $A\in \mathbb{A}$, $F(A)$ allows for an $\mathcal{F}{\mathcal{F}}^{\lambda }$-module structure, thus inducing a comparison functor $K:\mathbb{A}\to {\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}$. We call $(\mathcal{F},\lambda )$ an Azumaya monad (in 3.3) if this functor is an equivalence of categories. The properties and characterizations of such monads are given, in particular for the case that they allow for a right adjoint functor (Theorem 3.10). Dualizing these notions leads to an intrinsic definition of Azumaya comonads (Definition 3.14). Given a monad $\mathcal{F}=(F,m,e)$ with monad BD-law $\lambda :FF\to FF$, where the functor F has a right adjoint R, a comonad $\mathcal{R}=(R,\delta ,\epsilon )$ with a comonad BD-law $\kappa :RR\to RR$ can be constructed (Proposition 3.15). The relationship between the Azumaya properties of the monad $\mathcal{F}$ and the comonad $\mathcal{R}$ is addressed in Proposition 3.16. It turns out that for a Cauchy complete category $\mathbb{A}$, $\mathcal{F}$ is an Azumaya monad and $\mathcal{F}{\mathcal{F}}^{\lambda }$ is a separable monad, if and only if $\mathcal{R}$ is an Azumaya comonad and ${\mathcal{R}}^{\kappa }\mathcal{R}$ is a separable comonad (Theorem 3.17).

In Section 4, our theory is applied to study Azumaya algebras in braided monoidal categories $(\mathcal{V},\otimes ,I,\tau )$. Then, for any $\mathcal{V}-\mathrm{algebra}$ A, the braiding induces a distributive law ${\tau }_{A,A}:A\otimes A\to A\otimes A$ and A is called left (right) Azumaya if the monad $A\otimes -:\mathcal{V}\to \mathcal{V}$ (resp. $-\otimes A:\mathcal{V}\to \mathcal{V}$) is Azumaya. In [3], $\mathcal{V}$-algebras, which are both left and right Azumaya, are used to define the Brauer group of $\mathcal{V}$. We will get various characterizations for such algebras, but will not pursue their role for the Brauer group. In braided monoidal categories with equalizers and coequalizers, the notions of left and right Azumaya algebras coincide (Theorem 4.18).

The results about Azumaya comonads provide an extensive theory of Azumaya coalgebras in braided categories $\mathcal{V}$, and the basics for this are described in Section 5. Besides the formal transfer of results known for algebras, we introduce coalgebras $\mathcal{C}$ over cocommutative coalgebras $\mathcal{D}$, and for this, Section 3 provides conditions that make them Azumaya. This extends the corresponding notions studied for coalgebras over cocommutative coalgebras in vector space categories by Torrecillas, van Oystaeyen and Zhang in [7]. Over a commutative ring $R$, Azumaya coalgebras $\mathcal{C}$ turn out to be coseparable and are characterized by the fact that the dual algebra $C^{*}=\mathrm{Hom}(C,R)$ is an Azumaya R-algebra. Notice that coalgebras with the latter property were first studied by Sugano in [8].

Let us mention that, given an endofunctor $F:\mathbb{A}\to \mathbb{A}$ with a monad and a comonad structure, a natural transformation $\lambda :FF\to FF$ is called a local prebraiding in (6.7 in [5]), provided it is a monad, as well as a comonad BD-law. For example, the Yang–Baxter operator in the definition of a weak braided Hopf algebra in Alonso Álvarez et al. (Definition 2.1 in [9]) is (among other conditions) required to be of this type. As pointed out by a referee, in Gordon et al. [10], it is suggested to generalize Azumaya algebras by considering them as weak equivalences in an appropriate tricategory.

2. Preliminaries

Throughout this section, $\mathbb{A}$ will stand for any category.

2.1. Modules and comodules.

For a monad $\mathcal{T}=(T,m,e)$ on $\mathbb{A}$, we write ${\mathbb{A}}_{\mathcal{T}}$ for the Eilenberg–Moore category of $\mathcal{T}$-modules and denote the corresponding forgetful-free adjunction by:

$${\eta }_{\mathcal{T}},{\epsilon }_{\mathcal{T}}:{\varphi }_{\mathcal{T}}⊣U_{\mathcal{T}}:{\mathbb{A}}_{\mathcal{T}}\to \mathbb{A}.$$

Dually, if $\mathcal{G}=(G,\delta ,\epsilon )$ is a comonad on $\mathbb{A}$, we write ${\mathbb{A}}^{\mathcal{G}}$ for the Eilenberg–Moore category of $\mathcal{G}$-comodules and denote the corresponding forgetful-cofree adjunction by:

$${\eta }^{\mathcal{G}},{\epsilon }^{\mathcal{G}}:U^{\mathcal{G}}⊣{\varphi }^{\mathcal{G}}:\mathbb{A}\to {\mathbb{A}}^{\mathcal{G}}.$$

For any monad $\mathcal{T}=(T,m,e)$ and an adjunction $\overline{\eta },\overline{\epsilon }:T⊣R$, there is a comonad $\mathcal{R}=(R,\delta ,\epsilon )$, where $m⊣\delta$, $\epsilon ⊣e$ (mates), and there is an isomorphism of categories (e.g., [5]):

$$\Psi :{\mathbb{A}}_{\mathcal{T}}\to {\mathbb{A}}^{\mathcal{R}},(A,h)\mapsto (A,A\stackrel{\overline{\eta }}{\to }RT(A)\stackrel{R(h)}{\to }R(A)).$$

(2.1)

Note that, for any $(A,\theta )\in {\mathbb{A}}^{\mathcal{R}}$, ${\Psi }^{-1}(A,\theta )=(A,T(A)\stackrel{F(\theta )}{\to }TR(A)\stackrel{{\overline{\epsilon }}_A}{\to }A)$.

2.2. Monad distributive laws.

Given two monads $\mathcal{T}=(T,m,e)$ and $\mathcal{S}=(S,m^{\prime },e^{\prime })$ on $\mathbb{A}$, a natural transformation $\lambda :TS\to ST$ is a (monad) distributive law of $\mathcal{T}$ over $\mathcal{S}$ if it induces the commutativity of the diagrams:

Given a distributive law $\lambda :TS\to ST$, the triple $\mathcal{S}\mathcal{T}=(ST,m^{\prime }m·S\lambda T,e^{\prime }e)$ is a monad on $\mathbb{A}$ (e.g., [11,12]). Notice that the monad structure on $\mathcal{S}\mathcal{T}$ depends on λ, and if the choice of λ needs to be specified, we write ${(\mathcal{S}\mathcal{T})}_{\lambda }$.

Furthermore, a distributive law λ corresponds to a monad ${\widehat{\mathcal{S}}}_{\lambda }=(\widehat{S},\widehat{m},\widehat{e})$ on ${\mathbb{A}}_{\mathcal{T}}$ that is a lifting of $\mathcal{S}$ to ${\mathbb{A}}_{\mathcal{T}}$ in the sense that:

$$U_{\mathcal{T}}\widehat{S}=S{U}_{\mathcal{T}}, U_{\mathcal{T}}\widehat{m}=m^{\prime }{U}_{\mathcal{T}}, U_{\mathcal{T}}\widehat{e}=e^{\prime }{U}_{\mathcal{T}}$$

.

This defines the Eilenberg–Moore category ${({\mathbb{A}}_{\mathcal{T}})}_{{\widehat{\mathcal{S}}}_{\lambda }}$ of ${\widehat{\mathcal{S}}}_{\lambda }$-modules, whose objects are triples $((A,t),s)$, with $(A,t)\in {\mathbb{A}}_{\mathcal{T}}$, $(A,s)\in {\mathbb{A}}_{\mathcal{S}}$ and a commutative diagram:

(2.2)

There is an isomorphism of categories ${\mathcal{P}}_{\lambda }:{\mathbb{A}}_{{(\mathcal{S}\mathcal{T})}_{\lambda }}\to {({\mathbb{A}}_{\mathcal{T}})}_{{\widehat{\mathcal{S}}}_{\lambda }}$ by the assignment:

$$(A,ST(A)\stackrel{\varrho }{\to }A)\mapsto ((A,T(A)\stackrel{e_{T(A)}^{\prime }}{\to }ST(A)\stackrel{\varrho }{\to }A),S(A)\stackrel{S(e_A)}{\to }ST(A)\stackrel{\varrho }{\to }A),$$

and for any $((A,t),s)\in {({\mathbb{A}}_{\mathcal{T}})}_{{\widehat{S}}_{\lambda }}$,

$${\mathcal{P}}_{\lambda }^{-1}((A,t),s)=(A,ST(A)\stackrel{S(t)}{\to }S(A)\stackrel{s}{\to }A).$$

When no confusion can occur, we shall just write $\widehat{\mathcal{S}}$ instead of ${\widehat{\mathcal{S}}}_{\lambda }$.

2.3 Proposition.

In the setting of Section 2.2, let $\lambda :TS\to ST$ be an invertible monad distributive law.

(1)

${\lambda }^{-1}:ST\to TS$ is again a monad distributive law;

(1)

$\lambda :TS\to ST$ can be seen as a monad isomorphism ${(\mathcal{T}\mathcal{S})}_{{\lambda }^{-1}}\to {(\mathcal{S}\mathcal{T})}_{\lambda }$ defining a category isomorphism:

$${\mathbb{A}}_{\lambda }:{\mathbb{A}}_{{(\mathcal{S}\mathcal{T})}_{\lambda }}\to {\mathbb{A}}_{{(\mathcal{T}\mathcal{S})}_{{\lambda }^{-1}}},(A,ST(A)\stackrel{\varrho }{\to }A)\mapsto (A,TS(A)\stackrel{\lambda }{\to }ST(A)\stackrel{\varrho }{\to }A);$$

(3)

${\lambda }^{-1}$ induces a lifting ${\widehat{\mathcal{T}}}_{{\lambda }^{-1}}:{\mathbb{A}}_{\mathcal{S}}\to {\mathbb{A}}_{\mathcal{S}}$ of $\mathcal{T}$ to ${\mathbb{A}}_{\mathcal{S}}$ and an isomorphism of categories:

$$\Phi :{({\mathbb{A}}_{\mathcal{T}})}_{{\widehat{\mathcal{S}}}_{\lambda }}\to {({\mathbb{A}}_{\mathcal{S}})}_{{\widehat{\mathcal{T}}}_{{\lambda }^{-1}}},((A,t),s)\mapsto ((A,s),t),$$

leading to the commutative diagram:

Proof. (1) and (2) followed by Lemma 4.2 in [13]; (3) is outlined in Remark 3.4 in [14].    ☐

2.4. Comonad distributive laws.

Given comonads $\mathcal{G}=(G,\delta ,\epsilon )$ and $\mathcal{H}=(H,{\delta }^{\prime },{\epsilon }^{\prime })$ on $\mathbb{A}$, a natural transformation $\kappa :HG\to GH$ is a (comonad) distributive law of $\mathcal{G}$ over $\mathcal{H}$ if it induces commutativity of the diagrams:

Given this, the triple ${(\mathcal{H}\mathcal{G})}_{\kappa }=(HG,H\kappa G·{\delta }^{\prime }\delta ,{\epsilon }^{\prime }\epsilon )$ is a comonad on $\mathbb{A}$ (e.g., [11,12]).

Also, the distributive law κ corresponds to a lifting of the comonad $\mathcal{H}$ to a comonad ${\tilde{\mathcal{H}}}_{\kappa }:{\mathbb{A}}^{\mathcal{G}}\to {\mathbb{A}}^{\mathcal{G}}$, leading to the Eilenberg–Moore category ${({\mathbb{A}}^{\mathcal{G}})}^{{\tilde{\mathcal{H}}}_{\kappa }}$ of ${\tilde{\mathcal{H}}}_{\kappa }$-comodules whose objects are triples $((A,g),h)$ with $(A,g)\in {\mathbb{A}}^{\mathcal{G}}$ and $(A,h)\in {\mathbb{A}}^{\mathcal{H}}$ with commutative diagram:

There is an isomorphism of categories ${\mathcal{Q}}_{\kappa }:{\mathbb{A}}^{{(\mathcal{H}\mathcal{G})}_{\kappa }}\to {({\mathbb{A}}^{\mathcal{G}})}^{{\tilde{\mathcal{H}}}_{\kappa }}$ given by:

$$(A,A\stackrel{\rho }{\to }HG(A))\mapsto (A,A\stackrel{\rho }{\to }HG(A)\stackrel{{\epsilon }_{G(A)}^{\prime }}{\to }G(A)),A\stackrel{\rho }{\to }HG(A)\stackrel{H({\epsilon }_A)}{\to }H(A)),$$

and for any $((A,g),h)\in {({\mathbb{A}}^{\mathcal{G}})}^{{\tilde{\mathcal{H}}}_{\kappa }}$,

$${\mathcal{Q}}_{\kappa }^{-1}((A,g),h)=(A,A\stackrel{h}{\to }H(A)\stackrel{H(g)}{\to }HG(A)).$$

The following observations are dual to 2.3.

2.5 Proposition.

In the setting of Section 2.4, let $\kappa :HG\to GH$ be an invertible comonad distributive law.

(1)

${\kappa }^{-1}:GH\to HG$ is a comonad distributive law of $\mathcal{H}$ over $\mathcal{G}$;

(2)

$GH$ allows for a comonad structure ${(\mathcal{G}\mathcal{H})}_{{\kappa }^{-1}}$ and $\kappa :HG\to GH$ is a comonad isomorphism ${(\mathcal{H}\mathcal{G})}_{\kappa }\to {(\mathcal{G}\mathcal{H})}_{{\kappa }^{-1}}$ defining a category equivalence:

$${\mathbb{A}}^{\kappa }:{\mathbb{A}}^{{(\mathcal{H}\mathcal{G})}_{\kappa }}\to {\mathbb{A}}^{{(\mathcal{G}\mathcal{H})}_{{\kappa }^{-1}}},(A,A\stackrel{\rho }{\to }HG(A))\mapsto (A,A\stackrel{\rho }{\to }HG(A)\stackrel{\kappa }{\to }GH(A);$$

(3)

${\kappa }^{-1}$ induces a lifting ${\tilde{\mathcal{G}}}_{{\kappa }^{-1}}:{\mathbb{A}}^{\mathcal{H}}\to {\mathbb{A}}^{\mathcal{H}}$ of $\mathcal{G}$ to ${\mathbb{A}}^{\mathcal{H}}$ and an equivalence of categories:

$${\Phi }^{\prime }:{({\mathbb{A}}^{\mathcal{G}})}^{{\tilde{\mathcal{H}}}_{\kappa }}\to {({\mathbb{A}}^{\mathcal{H}})}^{{\tilde{\mathcal{G}}}_{{\kappa }^{-1}}},((A,g),h)\mapsto ((A,h),g),$$

leading to the commutative diagram:

2.6. Mixed distributive laws.

Given a monad $\mathcal{T}=(T,m,e)$ and a comonad $\mathcal{G}=(G,\delta ,\epsilon )$ on $\mathbb{A}$, a mixed distributive law (or entwining) from $\mathcal{T}$ to $\mathcal{G}$ is a natural transformation $\omega :TG\to GT$ with commutative diagrams:

Given a mixed distributive law $\omega :TG\to GT$ from the monad $\mathcal{T}$ to the comonad $\mathcal{G}$, we write ${\widehat{\mathcal{G}}}_{\omega }=(\widehat{G},\widehat{\delta },\widehat{\epsilon })$ for a comonad on ${\mathbb{A}}_{\mathcal{T}}$ lifting $\mathcal{G}$ (e.g., Section 5 in [12]).

It is well-known that for any object $(A,h)$ of ${\mathbb{A}}_{\mathcal{T}}$,

$$\widehat{G}(A,h)=(G(A),G(h)·{\omega }_A), {(\widehat{\delta })}_{(A,h)}={\delta }_A, {(\widehat{\epsilon })}_{(A,h)}={\epsilon }_A$$

, and the objects of ${({\mathbb{A}}_{\mathcal{T}})}^{\widehat{\mathcal{G}}}$ are triples $(A,h,\vartheta )$, where $(A,h)\in {\mathbb{A}}_{\mathcal{T}}$ and $(A,\vartheta )\in {\mathbb{A}}^{\mathcal{G}}$ with commuting diagram:

(2.3)

2.7. Distributive laws and adjoint functors.

Let $\lambda :TS\to ST$ be a distributive law of a monad $\mathcal{T}=(T,m,e)$ over a monad $\mathcal{S}=(S,m^{\prime },e^{\prime })$ on $\mathbb{A}$. If $\mathcal{T}$ admits a right adjoint comonad $\mathcal{R}$ (with $\overline{\eta },\overline{\epsilon }:T⊣R$), then the composite:

$${\lambda }_{\diamond }:SR\stackrel{\overline{\eta }SR}{\to }RTSR\stackrel{R\lambda R}{\to }RSTR\stackrel{RS\overline{\epsilon }}{\to }RS$$

is a mixed distributive law from $\mathcal{S}$ to $\mathcal{R}$ (e.g., [5,15]) and the assignment:

$$(A,\nu :ST(A)\to A)\mapsto (A,h_{\nu }:S(A)\to A,{\vartheta }_{\nu }:A\to R(A)),\mathrm{with}$$

$$h_{\nu }:S(A)\stackrel{S(e_A)}{\to }ST(A)\stackrel{\nu }{\to }A, {\vartheta }_{\nu }:A\stackrel{{\overline{\eta }}_A}{\to }RT(A)\stackrel{R(e_{T(A)}^{\prime })}{\to }RST(A)\stackrel{R(\nu )}{\to }R(A),$$

yields an isomorphism of categories ${\mathbb{A}}_{{(\mathcal{S}\mathcal{T})}_{\lambda }}\simeq {({\mathbb{A}}_{\mathcal{S}})}^{{\widehat{\mathcal{R}}}_{{\lambda }^{\diamond }}}.$

2.8. Invertible distributive laws and adjoint functors.

Let $\lambda :TS\to ST$ be an invertible distributive law of a monad $\mathcal{T}=(T,m,e)$ over a monad $\mathcal{S}=(S,m^{\prime },e^{\prime })$ on $\mathbb{A}$. Then, ${\lambda }^{-1}:ST\to TS$ is a distributive law of the monad $\mathcal{S}$ over the monad $\mathcal{T}$ (2.3), and if $\mathcal{S}$ admits a right adjoint comonad $\mathcal{H}$ (with $\overline{\eta },\overline{\epsilon }:S⊣H$), then the previous construction can be repeated with λ replaced by ${\lambda }^{-1}$. Thus, the composite:

$${({\lambda }^{-1})}_{\diamond }:TH\stackrel{\overline{\eta }TH}{\to }HSTH\stackrel{H{\lambda }^{-1}H}{\to }HTSH\stackrel{HT\overline{\epsilon }}{\to }HT$$

is a mixed distributive law from the monad $\mathcal{T}$ to the comonad $\mathcal{H}$. Moreover, there is an adjunction $\alpha ,\beta :{\widehat{\mathcal{S}}}_{\lambda }⊣{\widehat{\mathcal{H}}}_{{({\lambda }^{-1})}_{\diamond }}:{\mathbb{A}}_{\mathcal{T}}\to {\mathbb{A}}_{\mathcal{T}}$, where ${\widehat{\mathcal{S}}}_{\lambda }$ is the lifting of $\mathcal{S}$ to ${\mathbb{A}}_{\mathcal{T}}$ considered in 2.2 (e.g., Theorem 4 in [16]), and the canonical isomorphism Ψ from (2.1) yields the commutative diagram:

(2.4)

Note that $U_{\mathcal{T}}(\alpha )=\overline{\eta }$ and $U_{\mathcal{T}}(\beta )=\overline{\epsilon }$.

2.9. Entwinings and adjoint functors.

For a monad $\mathcal{T}=(T,m,e)$ and a comonad $\mathcal{G}=(G,\delta ,\epsilon )$, consider an entwining $\omega :TG\to GT$. If $\mathcal{T}$ admits a right adjoint comonad $\mathcal{R}$ (with $\overline{\eta },\overline{\epsilon }:T⊣R$), then the composite:

$${\omega }^{\diamond }:GR\stackrel{\overline{\eta }GR}{\to }RTGR\stackrel{R\omega R}{\to }RGTR\stackrel{RG\overline{\epsilon }}{\to }RG$$

is a comonad distributive law of $\mathcal{G}$ over $\mathcal{R}$ (e.g., [5,15]), inducing a lifting ${\tilde{\mathcal{G}}}_{\omega }$ of $\mathcal{G}$ to ${\mathbb{A}}^{\mathcal{R}}$ and, thus, an Eilenberg–Moore category ${({\mathbb{A}}^{\mathcal{R}})}^{{\tilde{\mathcal{G}}}_{\omega }}$ of ${\tilde{\mathcal{G}}}_{\omega }$-comodules whose objects are triples $((A,d),g)$ with commutative diagram (see Section 2.4):

(2.5)

The following notions will be of use for our investigations.

2.10. Monadic and comonadic functors.

Let $\eta ,\epsilon :F⊣R:\mathbb{B}\to \mathbb{A}$ be an adjoint pair of functors. Then, the composite $RF$ allows for a monad structure $\mathcal{R}\mathcal{F}$ on $\mathbb{A}$ and the composite $FR$ for a comonad structure $\mathcal{F}\mathcal{R}$ on $\mathbb{B}$. By definition, R is monadic and F is comonadic, provided the respective comparison functors are equivalences,

$$K_R:\mathbb{B}\to {\mathbb{A}}_{\mathcal{R}\mathcal{F}},B\mapsto (R(B),R({\epsilon }_B)),$$

$$K_F:\mathbb{A}\to {\mathbb{B}}^{\mathcal{F}\mathcal{R}},A\mapsto (F(A),F({\eta }_A)).$$

For an endofunctor we have, under some conditions on the category:

2.11 Lemma.

Let $F:\mathbb{A}\to \mathbb{A}$ be a functor that allows for a left and a right adjoint functor and assume $\mathbb{A}$ to have equalizers and coequalizers. Then, the following are equivalent:

(a)

F is conservative;

(b)

F is monadic;

(c)

F is comonadic.

If $\mathcal{F}=(F,m,e)$ is a monad, then the above are also equivalent to:

(d)

the free functor ${\varphi }_{\mathcal{F}}:\mathbb{A}\to {\mathbb{A}}_{\mathcal{F}}$ is comonadic.

Proof. Since F is a left, as well as a right adjoint functor, it preserves equalizers and coequalizers. Moreover, since $\mathbb{A}$ is assumed to have both equalizers and coequalizers, it follows from Beck’s monadicity theorem (see [17]) and its dual that F is monadic or comonadic if and only if it is conservative.

(a)⇔(d) follows from Corollary 3.12 in [18].       ☐

2.12. $\mathcal{T}$-module functors.

Given a monad $\mathcal{T}=(T,m,e)$ on $\mathbb{A}$, a functor $R:\mathbb{B}\to \mathbb{A}$ is said to be a (left) $\mathcal{T}$-module if there exists a natural transformation $\alpha :TR\to R$ with $\alpha ·eR=1$ and $\alpha ·mR=\alpha ·T\alpha$.

This structure of a left $\mathcal{T}$-module on R is equivalent to the existence of a functor $\overline{R}:\mathbb{B}\to {\mathbb{A}}_{\mathcal{T}}$ with commutative diagram (see Proposition II.1.1 in [19])

If $\overline{R}$ is such a functor, then $\overline{R}(B)=(R(B),{\alpha }_B)$ for some morphism ${\alpha }_B:TR(B)\to R(B)$ and the collection $\{{\alpha }_B,B\in \mathbb{B}\}$ forms a natural transformation $\alpha :TR\to R$ making R a $\mathcal{T}$-module. Conversely, if $(R,\alpha :TR\to R)$ is a $\mathcal{T}$-module, then $\overline{R}:\mathbb{B}\to {\mathbb{A}}_{\mathcal{T}}$ is defined by $\overline{R}(B)=(R(B),{\alpha }_B)$.

For any $\mathcal{T}$-module $(R:\mathbb{B}\to \mathbb{A},\alpha )$ admitting an adjunction $F⊣R:\mathbb{B}\to \mathbb{A}$ with unit $\eta :1\to RF$, the composite:

$$t_{\overline{R}}:T\stackrel{T\eta }{\to }TRF\stackrel{\alpha F}{\to }RF$$

is a monad morphism from $\mathcal{T}$ to the monad $\mathcal{R}\mathcal{F}$ on $\mathbb{A}$ generated by the adjunction $F⊣R$. This yields a functor ${\mathbb{A}}_{t_{\overline{R}}}:{\mathbb{A}}_{\mathcal{R}\mathcal{F}}\to {\mathbb{A}}_{\mathcal{T}}$.

If $t_{\overline{R}}:T\to RF$ is an isomorphism (i.e., ${\mathbb{A}}_{t_{\overline{R}}}$ is an isomorphism), then R is called a $\mathcal{T}$-Galois module functor. Since $\overline{R}={\mathbb{A}}_{t_{\overline{R}}}·K_R$ (see 2.10), we have (dual to Theorem 4.4 in [20]):

2.13 Proposition.

The functor $\overline{R}$ is an equivalence of categories if and only if the functor R is monadic and a $\mathcal{T}$-Galois module functor.

2.14. $\mathcal{G}$-comodule functors.

Given a comonad $\mathcal{G}=(G,\delta ,\epsilon )$ on a category $\mathbb{A}$, a functor $L:\mathbb{B}\to \mathbb{A}$ is a left $\mathcal{G}$-functor if there exists a natural transformation $\alpha :L\to GL$ with $\epsilon L·\alpha =1$ and $\delta L·\alpha =G\alpha ·\alpha$. This structure on L is equivalent to the existence of a functor $\overline{L}:\mathbb{B}\to {\mathbb{A}}^{\mathcal{G}}$ with commutative diagram (dual to 2.12):

If a $\mathcal{G}$-functor $(L,\alpha )$ admits a right adjoint $S:\mathbb{A}\to \mathbb{B}$, with counit $\sigma :LS\to 1$, then (see Propositions II.1.1 and II.1.4 in [19]) the composite:

$$t_{\overline{L}}:LS\stackrel{\alpha S}{\to }GLS\stackrel{G\sigma }{\to }G$$

is a comonad morphism from the comonad generated by the adjunction $L⊣S$ to $\mathcal{G}$.

$L:\mathbb{B}\to \mathbb{A}$ is said to be a $\mathcal{G}$-Galois comodule functor provided $t_{\overline{L}}:LS\to G$ is an isomorphism.

Dual to Proposition 2.13, we have (see also [6,21]):

2.15 Proposition.

The functor $\overline{L}$ is an equivalence of categories if and only if the functor L is comonadic and a $\mathcal{G}$-Galois comodule functor.

2.16. Right adjoint for $\overline{L}$.

If the category $\mathbb{B}$ has equalizers of coreflexive pairs and $L⊣S$, the functor $\overline{L}$ (in 2.14) has a right adjoint $\overline{S}$, which can be described as follows (e.g., [19,20]), with the composite:

$$\gamma :S\stackrel{\eta S}{\to }SLS\stackrel{S{t}_{\overline{L}}}{\to }SG,$$

the value of $\overline{S}$ at $(A,\vartheta )\in {\mathbb{A}}^{\mathcal{G}}$ is given by the equalizer:

$$\overline{S}(A,\vartheta )\stackrel{i_{(A,\vartheta )}}{\to }S(A)\underset{{\gamma }_A}{\overset{S(\vartheta )}{\rightrightarrows }}SG(A).$$

If $\overline{\sigma }$ denotes the counit of the adjunction $\overline{L}⊣\overline{S}$, then for any $(A,\vartheta )\in {\mathbb{A}}^{\mathcal{G}}$,

$$U^{\mathcal{G}}({\overline{\sigma }}_{(A,\vartheta )})={\sigma }_A·L(i_{(A,\vartheta )}),$$

(2.6)

where $\sigma :LS\to 1$ is the counit of the adjunction $L⊣S$.

2.17. Separable functors.

(e.g., [22]) A functor $F:\mathbb{A}\to \mathbb{B}$ between any categories is said to be separable if the natural transformation:

$$F_{-,-}:\mathbb{A}(-,-)\to \mathbb{B}(F(-),F(-))$$

is a split monomorphism.

If $F:\mathbb{A}\to \mathbb{B}$ and $G:\mathbb{B}\to \mathbb{D}$ are functors, then:

(i)

if F and G are separable, then GF is also separable;

(ii)

if GF is separable, then F is separable.

2.18. Separable (co)monads.

(2.9 in [15]) Let $\mathbb{A}$ be any category.

(1)

For a monad $\mathcal{F}=(F,m,e)$ on $\mathbb{A}$, the following are equivalent:

(a)

m has a natural section $\omega :F\to FF$, such that $Fm·\omega F=\omega ·m=mF·F\omega$;

(b)

the forgetful functor $U_{\mathcal{F}}:{\mathbb{A}}_{\mathcal{F}}\to \mathbb{A}$ is separable.

(2)

For a comonad $\mathcal{G}=(G,\delta ,\epsilon )$ on $\mathbb{A}$, the following are equivalent:

(a)

δ has a natural retraction $\varrho :GG\to G$, such that $\varrho G·G\delta =\delta ·\varrho =G\varrho ·\delta G$;

(b)

the forgetful functor $U^{\mathcal{G}}:{\mathbb{A}}^{\mathcal{G}}\to \mathbb{A}$ is separable.

2.19. Separability of adjoints.

(2.10 in [15]) Let $G:\mathbb{A}\to \mathbb{A}$ and $F:\mathbb{A}\to \mathbb{A}$ be an adjoint pair of functors with unit $\overline{\eta }:1_{\mathbb{A}}\to FG$ and counit $\overline{\epsilon }:GF\to 1_{\mathbb{A}}$.

(1)

F is separable if and only if $\overline{\eta }:1_{\mathbb{A}}\to FG$ is a split monomorphism;

(2)

G is separable if and only if $\overline{\epsilon }:GF\to 1_{\mathbb{A}}$ is a split epimorphism.

Given a comonad structure $\mathcal{G}$ on G with corresponding monad structure $\mathcal{F}$ on F (see Section 2.1), there are pairs of adjoint functors:

$$\begin{array}{cc}\hfill \mathbb{A}\stackrel{{\varphi }_{\mathcal{F}}}{\to }{\mathbb{A}}_{\mathcal{F}},{\mathbb{A}}_{\mathcal{F}}\stackrel{U_{\mathcal{F}}}{\to }\mathbb{A},& {\mathbb{A}}^{\mathcal{G}}\stackrel{U^{\mathcal{G}}}{\to }\mathbb{A},\mathbb{A}\stackrel{{\varphi }^{\mathcal{G}}}{\to }{\mathbb{A}}^{\mathcal{G}};\hfill \end{array}$$

(1)

${\varphi }^{\mathcal{G}}$ is separable if and only if ${\varphi }_{\mathcal{F}}$ is separable;

(2)

$U^{\mathcal{G}}$ is separable if and only if $U_{\mathcal{F}}$ is separable, and then, any object of ${\mathbb{A}}^{\mathcal{G}}$ is injective relative to $U^{\mathcal{G}}$ and every object of ${\mathbb{A}}_{\mathcal{F}}$ is projective relative to $U_{\mathcal{F}}$.

The following generalizes criteria for separability given in Theorem 1.2 in [22].

2.20 Proposition.

Let $U:\mathbb{A}\to \mathbb{B}$ and $F:\mathbb{B}\to \mathbb{A}$ be a pair of functors.

(i)

If there exist natural transformations $1\stackrel{\kappa }{\to }FU\stackrel{{\kappa }^{\prime }}{\to }1$, such that ${\kappa }^{\prime }·\kappa =1$, then both $FU$ and U are separable.

(ii)

If there exist natural transformations $1\stackrel{\eta }{\to }UF\stackrel{{\eta }^{\prime }}{\to }1$, such that ${\eta }^{\prime }·\eta =1$, then both $UF$ and F are separable.

Proof. (i) Inspection shows that:

$$\mathbb{A}(-,-)\stackrel{{(FU)}_{-,-}}{\to }\mathbb{A}(FU(-),FU(-))\stackrel{\mathbb{A}(\kappa ,{\kappa }^{\prime })}{\to }\mathbb{A}(-,-)$$

is the identity, and hence, $FU$ is separable. By 2.17, this implies that U is also separable.

(ii) is shown symmetrically.         ☐

3. Azumaya Monads and Comonads

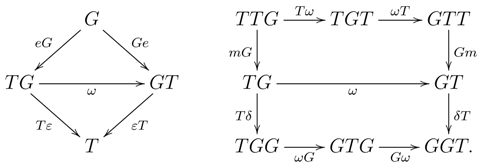
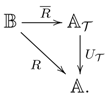
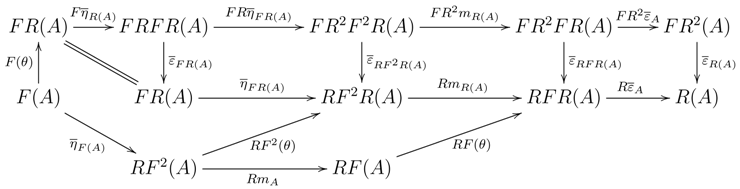
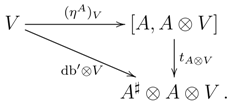
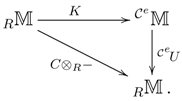
An algebra A over a commutative ring R is Azumaya provided A induces an equivalence between ${\mathbb{M}}_R$ and the category ${}_A{\mathbb{M}}_A$ of $(A,A)$-bimodules. The construction uses properties of the monad $A{\otimes }_R-$ on ${\mathbb{M}}_R$, and the purpose of this section is to trace this notion back to the categorical essentials to allow the formulation of the basic properties for monads on any category. Throughout, $\mathbb{A}$ will again denote any category.

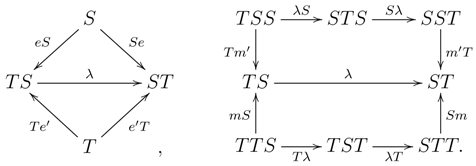
3.1 Definition.

Given an endofunctor $F:\mathbb{A}\to \mathbb{A}$ on $\mathbb{A}$, a natural transformation $\lambda :FF\to FF$ is said to satisfy the Yang–Baxter equation provided it induces the commutativity of the diagram:

For a monad $\mathcal{F}=(F,m,e)$ on $\mathbb{A}$, a monad distributive law $\lambda :FF\to FF$ satisfying the Yang–Baxter equation is called a (monad) BD-law (see Definition 2.2 in [13]).

Here, the interest in the YB-condition for distributive laws lies in the fact that it allows one to define opposite monads and comonads.

3.2 Proposition.

Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$ and $\lambda :FF\to FF$ a BD-law.

(1)

${\mathcal{F}}^{\lambda }=(F^{\lambda },m^{\lambda },e^{\lambda })$ is a monad on $\mathbb{A}$, where $F^{\lambda }=F$, $m^{\lambda }=m·\lambda$, and $e^{\lambda }=e$.

(2)

λ defines a distributive law $\lambda :F^{\lambda }F\to F{F}^{\lambda }$ making $\mathcal{F}{\mathcal{F}}^{\lambda }=(F{F}^{\lambda },\underline{m},\underline{e})$ a monad where:

$$\underline{m}=m{m}^{\lambda }·F\lambda F:FFFF\to FF,\underline{e}:=ee:1\to FF.$$

(3)

The composite $FFF\stackrel{F\lambda }{\to }FFF\stackrel{Fm}{\to }FF\stackrel{m}{\to }F$ defines a left $\mathcal{F}{\mathcal{F}}^{\lambda }$-module structure on the functor $F:\mathbb{A}\to \mathbb{A}$.

(4)

There is a comparison functor ${\overline{K}}_{\mathcal{F}}:\mathbb{A}\to {\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}$ given by:

$$A\mapsto (F(A),FFF(A)\stackrel{F({\lambda }_A)}{\to }FFF(A)\stackrel{F(m_A)}{\to }FF(A)\stackrel{m_A}{\to }F(A)).$$

Proof. (1) is easily verified (e.g., Remark 3.4 in [14], Section 6.9 in [5]).

(2) can be seen by direct computation (e.g., [5,13,14]).

(3) can be proven by a straightforward diagram chase.

(4) follows from 2.12 using the left $\mathcal{F}{\mathcal{F}}^{\lambda }$-module structure of F defined in (3).      ☐

When no confusion can occur, we shall just write $\overline{K}$ instead of ${\overline{K}}_{\mathcal{F}}$.

3.3 Definition.

A monad $\mathcal{F}=(F,m,e)$ on any category $\mathbb{A}$ with a BD-law $\lambda :FF\to FF$ is said to be Azumaya provided the comparison functor ${\overline{K}}_{\mathcal{F}}:\mathbb{A}\to {\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}$ is an equivalence of categories.

3.4 Proposition.

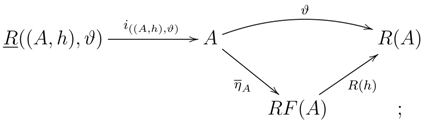
If $(\mathcal{F},\lambda )$ is an Azumaya monad on $\mathbb{A}$, then the functor F admits a left adjoint.

Proof. With our previous notation, we have the commutative diagram:

(3.1)

Since $U_{\mathcal{F}{\mathcal{F}}^{\lambda }}:{\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}\to \mathbb{A}$ always has a left adjoint and since ${\overline{K}}_{\mathcal{F}}$ is an equivalence of categories, the composite $F=U_{\mathcal{F}{\mathcal{F}}^{\lambda }}·{\overline{K}}_{\mathcal{F}}$ has a left adjoint.         ☐

This observation allows for a first characterization of Azumaya monads.

3.5 Theorem.

Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$ and $\lambda :FF\to FF$ a BD-law. The following are equivalent:

(a)

$(\mathcal{F},\lambda )$ is an Azumaya monad;

(b)

the functor $F:\mathbb{A}\to \mathbb{A}$ is monadic and the left $\mathcal{F}{\mathcal{F}}^{\lambda }$-module structure on F defined in Proposition 3.2 is Galois;

(c)

the functor $F:\mathbb{A}\to \mathbb{A}$ is monadic (with some adjunction $\eta ,\epsilon :L⊣F$), and the composite (as in 2.12):

$$t_{\overline{K}}:FF\stackrel{FF\eta }{\to }FFFL\stackrel{F\lambda L}{\to }FFFL\stackrel{FmL}{\to }FFL\stackrel{mL}{\to }FL$$

is an isomorphism of monads $\mathcal{F}{\mathcal{F}}^{\lambda }\to \mathcal{T}$, where $\mathcal{T}$ is the monad on $\mathbb{A}$ generated by this adjunction $L⊣F$.

Proof. That (a) and (b) are equivalent follows from Proposition 2.15.

(b)⇔(c) In both cases, F is monadic, and thus, F allows for an adjunction, say $L⊣F$ with unit $\eta :1\to FL$. Write $\mathcal{T}$ for the monad on $\mathbb{A}$ generated by this adjunction. Since the left $\mathcal{F}{\mathcal{F}}^{\lambda }$-module structure on the functor F is the composite:

$$FFF\stackrel{F\lambda }{\to }FFF\stackrel{Fm}{\to }FF\stackrel{m}{\to }F,$$

it follows from 2.12 that the monad morphism $t_{\overline{K}}:\mathcal{F}{\mathcal{F}}^{\lambda }\to \mathcal{T}$ induced by the diagram:

is the composite:

$$t_{\overline{K}}:FF\stackrel{FF\eta }{\to }FFFL\stackrel{F\lambda L}{\to }FFFL\stackrel{FmL}{\to }FFL\stackrel{mL}{\to }FL.$$

Thus, F is $\mathcal{F}{\mathcal{F}}^{\lambda }$-Galois if and only if $t_{\overline{K}}$ is an isomorphism.      ☐

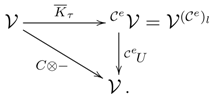
3.6. The isomorphism ${\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\mathbf{\lambda }}}\simeq {({\mathbb{A}}_{{\mathcal{F}}^{\mathbf{\lambda }}})}_{\widehat{\mathcal{F}}}$.

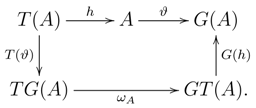
According to 2.2, for any monad BD-law $\lambda :FF\to FF$, the assignment:

$$(A,FF(A)\stackrel{\varrho }{\to }A)\mapsto ((A,F(A)\stackrel{e_{F(A)}}{\to }FF(A)\stackrel{\varrho }{\to }A),F(A)\stackrel{F{e}_A}{\to }FF(A)\stackrel{\varrho }{\to }A)$$

yields an isomorphism of categories ${\mathcal{P}}_{\lambda }:{\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}⟶{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{\widehat{\mathcal{F}}}$, where for any module $((A,h),g)\in {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{\widehat{\mathcal{F}}}$,

$${\mathcal{P}}_{\lambda }^{-1}((A,h),g)=(A,FF(A)\stackrel{Fh}{\to }F(A)\stackrel{g}{\to }A).$$

There is a functor $K_{\mathcal{F}}:\mathbb{A}\to {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{\widehat{\mathcal{F}}}$,

$$A\mapsto ((F(A),FF(A)\stackrel{{\lambda }_A}{\to }FF(A)\stackrel{m_A}{\to }F(A)),FF(A)\stackrel{m_A}{\to }F(A)),$$

with ${\overline{K}}_{\mathcal{F}}={\mathcal{P}}_{\lambda }^{-1}·K_{\mathcal{F}}$ and a commutative diagram:

Proof. Direct calculation shows that:

$${\mathcal{P}}_{\lambda }{\overline{K}}_{\mathcal{F}}(A)=((F(A),FF(A)\stackrel{{\lambda }_A}{\to }FF(A)\stackrel{m_A}{\to }F(A)),FF(A)\stackrel{m_A}{\to }F(A)),$$

for all $A\in \mathbb{A}$.         ☐

It is obvious that ${\overline{K}}_{\mathcal{F}}:\mathbb{A}\to {\mathbb{A}}_{\mathcal{F}{\mathcal{F}}^{\lambda }}$ is an equivalence (i.e., $\mathcal{F}$ is Azumaya) if and only if $K_{\mathcal{F}}:\mathbb{A}\to {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{\widehat{\mathcal{F}}}$ is an equivalence. To apply Proposition 2.13 to the functor $K_{\mathcal{F}}$, we will need a functor left adjoint to ${\varphi }_{{\mathcal{F}}^{\lambda }}$ whose existence is not a consequence of the Azumaya condition. For this, the invertibility of λ plays a crucial part.

3.7 Proposition.

Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$ with an invertible monad BD-law $\lambda :FF\to FF$.

(1)

${\lambda }^{-1}:F{F}^{\lambda }\to F^{\lambda }F$ is a distributive law inducing a monad ${({\mathcal{F}}^{\lambda }\mathcal{F})}_{{\lambda }^{-1}}=(F^{\lambda }F,\underline{\underline{m}},\underline{\underline{e}})$ where:

$$\underline{\underline{m}}=m^{\lambda }m·F{\lambda }^{-1}F:FFFF\to FF,\underline{\underline{e}}=ee:1\to FF,$$

and λ is an isomorphism of monads ${({\mathcal{F}}^{\lambda }\mathcal{F})}_{{\lambda }^{-1}}\to {(\mathcal{F}{\mathcal{F}}^{\lambda })}_{\lambda }$.

(2)

There is an isomorphism of categories:

$$\Phi :{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{{\widehat{\mathcal{F}}}_{\lambda }}\to {({\mathbb{A}}_{\mathcal{F}})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{{\lambda }^{-1}}},((A,h),g)\mapsto ((A,g),h).$$

(3)

${\lambda }^{-1}$ induces a comparison functor $K_{\mathcal{F}}^{\prime }:\mathbb{A}\to {({\mathbb{A}}_{\mathcal{F}})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{{\lambda }^{-1}}}(\simeq {\mathbb{A}}_{{({\mathcal{F}}^{\lambda }\mathcal{F})}_{{\lambda }^{-1}}})$,

$$A\mapsto ((F(A),FF(A)\stackrel{m_A}{\to }F(A)),FF(A)\stackrel{{\lambda }_A}{\to }FF(A)\stackrel{m_A}{\to }F(A)),$$

with commutative diagrams:

Proof. (1), (2) follow by Proposition 2.3; (3) is shown similarly to 3.6.      ☐

For λ invertible, it follows from the diagrams in Section 3.6, Section 3.7 that F is an Azumaya monad if and only if the functor

$$K_{\mathcal{F}}^{\prime }:\mathbb{A}\to {({\mathbb{A}}_{\mathcal{F}})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{{\lambda }^{-1}}}$$

is an equivalence of categories.

Note that if $\lambda :FF\to FF$ is a BD-law, then λ can be seen as a monad BD-law $\lambda :F^{\lambda }{F}^{\lambda }\to F^{\lambda }{F}^{\lambda }$, and it is not hard to see that the corresponding comparison functor:

$$K_{{\mathcal{F}}^{\lambda }}:\mathbb{A}\to {({\mathbb{A}}_{{({\mathcal{F}}^{\lambda })}^{\lambda }})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{\lambda }}$$

takes $A\in \mathbb{A}$ to

$$(F(A),FFF(A)\stackrel{F({\lambda }_A)}{\to }FFF(A)\stackrel{F({(m^{\lambda })}_A)}{\to }FF(A)\stackrel{{(m^{\lambda })}_A}{\to }F(A)).$$

Now, if ${\lambda }^2=1$, then $\lambda ={\lambda }^{-1}$ and ${({\mathcal{F}}^{\lambda })}^{\lambda }=\mathcal{F}$. Thus, the category ${({\mathbb{A}}_{{({\mathcal{F}}^{\lambda })}^{\lambda }})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{\lambda }}$ can be identified with the category ${({\mathbb{A}}_{\mathcal{F}})}_{{(\widehat{{\mathcal{F}}^{\lambda }})}_{{\lambda }^{-1}}}$. Modulo this identification, the functor $K_{{\mathcal{F}}^{\lambda }}^{\prime }$ corresponds to the functor $K_{{\mathcal{F}}^{\lambda }}$. It now follows from the preceding remark:

3.8 Proposition.

Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$ with a BD-law $\lambda :FF\to FF$. If ${\lambda }^2=1$, then $(\mathcal{F},\lambda )$ is an Azumaya monad if and only if $({\mathcal{F}}^{\lambda },\lambda )$ is so.

3.9. Azumaya monads with right adjoints.

Let $\mathcal{F}=(F,m,e)$ be a monad with an invertible BD-law $\lambda :FF\to FF$. Assume F to admit a right adjoint functor R, with $\overline{\eta },\overline{\epsilon }:F⊣R$, inducing a comonad $\mathcal{R}=(R,\delta ,\epsilon )$ (see 2.1). Since $\lambda :F^{\lambda }F\to F{F}^{\lambda }$ is an invertible distributive law, there is a comonad $\widehat{\mathcal{R}}={\widehat{\mathcal{R}}}_{{({\lambda }^{-1})}_{\diamond }}$ on ${\mathbb{A}}_{{\mathcal{F}}^{\lambda }}$ lifting the comonad $\mathcal{R}$ and that is right adjoint to the monad $\widehat{\mathcal{F}}$ (see 2.7), yielding a category isomorphism:

$${\Psi }_{{\mathcal{F}}^{\lambda }}:{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{{\widehat{\mathcal{F}}}_{\lambda }}\to {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}},$$

where, for any $((A,h),g)\in {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{{\widehat{\mathcal{F}}}_{\lambda }}$,

$${\Psi }_{{\mathcal{F}}^{\lambda }}((A,h),g)=((A,h),\tilde{g}) \text{with} \tilde{g}:A\stackrel{{\overline{\eta }}_A}{\to }RF(A)\stackrel{R(g)}{\to }R(A),$$

and a commutative diagram (see (2.4)):

(3.2)

For $\underline{K}:\mathbb{A}\stackrel{K}{\to }{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}_{{\widehat{\mathcal{F}}}_{\lambda }}\stackrel{{\Psi }_{{\mathcal{F}}^{\lambda }}}{\to }{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}}$, one has for any $A\in \mathbb{A}$,

$$\underline{K}(A)=((F(A),m_A·{\lambda }_A),R(m_A)·{\overline{\eta }}_{F(A)}).$$

Therefore, the A-component ${\alpha }_A$ of the induced $\widehat{\mathcal{R}}$-comodule structure $\alpha :{\varphi }_{{\mathcal{F}}^{\lambda }}\to \widehat{\mathcal{R}}{\varphi }_{{\mathcal{F}}^{\lambda }}$ on the functor ${\varphi }_{{\mathcal{F}}^{\lambda }}$ induced by the commutative diagram (3.2) (see Section 2.14), is the composite:

$${\alpha }_A:F(A)\stackrel{{\overline{\eta }}_{F(A)}}{\to }RFF(A)\stackrel{R(m_A)}{\to }RF(A).$$

It then follows that, for any $(A,h)\in {\mathbb{A}}_{{\mathcal{F}}^{\lambda }}$, the $(A,h)$-component $t_{(A,h)}$ of the corresponding comonad morphism $t:{\varphi }_{{\mathcal{F}}^{\lambda }}{U}_{{\mathcal{F}}^{\lambda }}\to \widehat{\mathcal{R}}$ is the composite:

$$t_{(A,h)}:F(A)\stackrel{{\overline{\eta }}_{F(A)}}{\to }RFF(A)\stackrel{R(m_A)}{\to }RF(A)\stackrel{R(h)}{\to }R(A).$$

(3.3)

These observations lead to the following characterizations of Azumaya monads.

3.10 Theorem.

Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$, $\lambda :FF\to FF$ an invertible monad BD-law, and $\mathcal{R}$ a comonad right adjoint to $\mathcal{F}$ (with $\overline{\eta },\overline{\epsilon }:F⊣R$). Then, the following are equivalent:

(a)

$(\mathcal{F},\lambda )$ is an Azumaya monad;

(b)

(i)

${\varphi }_{{\mathcal{F}}^{\lambda }}$ is comonadic; and

(ii)

${\varphi }_{{\mathcal{F}}^{\lambda }}$ is $\widehat{\mathcal{R}}$-Galois, that is:

$t_{(A,h)}$ in (3.3) is an isomorphism for any $(A,h)\in {\mathbb{A}}_{{\mathcal{F}}^{\lambda }}$ or

$\chi :FF\stackrel{\overline{\eta }FF}{\to }RFFF\stackrel{RmF}{\to }RFF\stackrel{R\lambda }{\to }RFF\stackrel{Rm}{\to }RF$ is an isomorphism.

Proof. Recall first that the monad ${\mathcal{F}}^{\lambda }$ is of effective descent type means that ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is comonadic.

By Proposition 2.15, the functor $\underline{K}$ making the triangle (3.2) commute is an equivalence of categories (i.e., the monad $\mathcal{F}$ is Azumaya) if and only if the monad ${\mathcal{F}}^{\lambda }$ is of an effective descent type and the comonad morphism $t:{\varphi }_{{\mathcal{F}}^{\lambda }}{U}_{{\mathcal{F}}^{\lambda }}\to \widehat{\mathcal{R}}$ is an isomorphism. Moreover, according to Theorem 2.12 in [6], t is an isomorphism if and only if for any object $A\in \mathbb{A}$, the ${\varphi }_{{\mathcal{F}}^{\lambda }}(A)$-component $t_{{\varphi }_{{\mathcal{F}}^{\lambda }}(A)}:F{\varphi }_{{\mathcal{F}}^{\lambda }}(A)\to R{\varphi }_{{\mathcal{F}}^{\lambda }}(A)$ is an isomorphism. Using now that ${\varphi }_{{\mathcal{F}}^{\lambda }}(A)=(F(A),m_A^{\lambda }=m_A·{\lambda }_A)$, it is easy to see that ${\chi }_A=t_{{\varphi }_{{\mathcal{F}}^{\lambda }}(A)}$ for all $A\in \mathbb{A}$. This completes the proof.        ☐

The existence of a right adjoint of the comparison functor $\underline{K}$ can be guaranteed by conditions on the base category.

3.11. Right adjoint for $\underline{K}$.

With the data given above, assume $\mathbb{A}$ to have equalizers of coreflexive pairs. Then:

(1)

the functor $\underline{K}:\mathbb{A}\to {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}}$ (see 3.9) admits a right adjoint $\underline{R}:{({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}}\to \mathbb{A}$ whose value at $((A,h),\vartheta )\in {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}}$ is the equalizer:

(2)

for any $A\in \mathbb{A}$, $\underline{R}\underline{K}(A)$ is the equalizer:

Proof. (1) According to 2.16, $\overline{R}((A,h),\vartheta )$ is the object part of the equalizer of:

$$A\underset{{\gamma }_{(A,h)}}{\overset{\vartheta }{\rightrightarrows }}R(A),$$

where γ is the composite $U_{{\mathcal{F}}^{\lambda }}\stackrel{U_{{\mathcal{F}}^{\lambda }}e}{\to }{U}_{{\mathcal{F}}^{\lambda }}{\varphi }_{{\mathcal{F}}^{\lambda }}{U}_{{\mathcal{F}}^{\lambda }}=U_{{\mathcal{F}}^{\lambda }}F\stackrel{U_{{\mathcal{F}}^{\lambda }}t}{\to }{U}_{{\mathcal{F}}^{\lambda }}\widehat{R}.$ It follows from the description of t that ${\gamma }_{(A,h)}$ is the composite

$$A\stackrel{e_A}{\to }F(A)\stackrel{{\overline{\eta }}_{F(A)}}{\to }RFF(A)\stackrel{R(m_A)}{\to }RF(A)\stackrel{R(h)}{\to }R(A)$$

which is just the composite $R(h)·{\overline{\eta }}_A$, since:

• ${\overline{\eta }}_{F(A)}·e_A=RF(e_A)·{\overline{\eta }}_A$ by naturality of $\overline{\eta }$ and
• $m_A·F(e_A)=1$ because e is the unit for $\mathcal{F}$.

(2) For any $A\in \mathbb{A}$, $\underline{K}(A)$ fits into the diagram (3.2).        ☐

3.12 Definition.

Write $F_F$ for the subfunctor of the functor F determined by the equalizer of the diagram:

We call the monad $\mathcal{F}$ central if $F_F$ is (isomorphic to) the identity functor.

Since $\underline{R}$ is right adjoint to the functor $\underline{K}$, $\underline{K}$ is fully faithful if and only if $\underline{R}\underline{K}\simeq 1$.

3.13 Theorem.

Assume $\mathbb{A}$ to admit equalizers of coreflexive pairs. Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$, $\lambda :FF\to FF$ an invertible BD-law and $\mathcal{R}$ a comonad right adjoint to $\mathcal{F}$. Then, the comparison functor $\underline{K}:\mathbb{A}\to {({\mathbb{A}}_{{\mathcal{F}}^{\lambda }})}^{\widehat{\mathcal{R}}}$ is:

(i)

full and faithful if and only if the monad $\mathcal{F}$ is central;

(ii)

an equivalence of categories if and only if the monad $\mathcal{F}$ is central and the functor $\underline{R}$ is conservative.

Proof. (i) follows from the preceding proposition.

(ii) Since $\mathcal{F}$ is central, the unit $\underline{\eta }:1\to \underline{R}\underline{K}$ of the adjunction $\underline{K}⊣\underline{R}$ is an isomorphism by (i). If $\underline{\epsilon }$ is the counit of the adjunction, then it follows from the triangular identity $\underline{R}\underline{\epsilon }·\underline{\eta }\underline{R}=1$ that $\underline{R}\underline{\epsilon }$ is an isomorphism. Since $\underline{R}$ is assumed to be conservative (reflects isomorphisms), this implies that $\underline{\epsilon }$ is an isomorphism, too. Thus, $\underline{K}$ is an equivalence of categories.      ☐

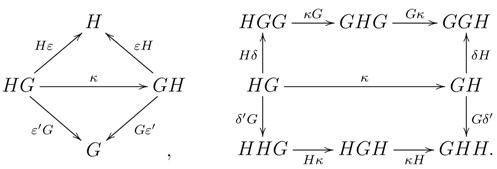
Dualizing the notion of an Azumaya monad leads to Azumaya comonads.

3.14 Definition.

For a comonad $\mathcal{G}=(G,\delta ,\epsilon )$ on $\mathbb{A}$, a comonad distributive law $\kappa :GG\to GG$ (see 2.4) satisfying the Yang–Baxter equation is called a comonad BD-law (or just a BD-law).

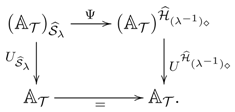
The pair $(\mathcal{G},\kappa )$ is said to be an Azumaya comonad provided that the (obvious) comparison functor ${\overline{K}}_{\kappa }:\mathbb{A}\to {\mathbb{A}}^{\mathcal{G}{\mathcal{G}}^{\kappa }}$ is an equivalence.

We leave it for the reader to dualize results about Azumaya monads to Azumaya comonads. Recall that comonad BD-laws are obtained from monad BD-laws by adjunctions (see 7.4 in [5]):

3.15 Proposition.

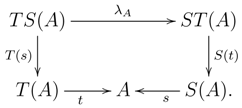
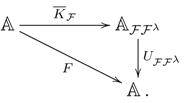
Let $\mathcal{F}=(F,m,e)$ be a monad on $\mathbb{A}$ and $\lambda :FF\to FF$ a monad BD-law. If F has a right adjoint functor R, then there is a comonad $(R,\delta ,\epsilon )$ with a comonad YB-distributive law $\kappa :RR\to RR$, where $m⊣\delta$, $\epsilon ⊣e$ and $\lambda ⊣\kappa$. Moreover, λ is invertible if and only if κ is so.

The next observation shows the transfer of the Galois property to an adjoint functor.

3.16 Proposition.

Assume $\mathcal{F}=(F,m,e)$ to be a monad on $\mathbb{A}$ with an invertible monad BD-law $\lambda :FF\to FF$ and $\overline{\eta },\overline{\epsilon }:F⊣R$ an adjunction inducing a comonad $\mathcal{R}=(R,\delta ,\epsilon )$ with invertible comonad BD-law $\kappa :RR\to RR$ (seeProposition 3.15). Then, the functor ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is $\widehat{\mathcal{R}}$-Galois if and only if the functor ${\varphi }^{{\mathcal{R}}^{\kappa }}$ is $\tilde{\mathcal{F}}$-Galois.

Proof. By Theorem 3.10 and its dual, we have to show that, for any $(A,h)\in {\mathbb{A}}_{{\mathcal{F}}^{\lambda }}$, the composite:

$$t_{(A,h)}:F(A)\stackrel{{\overline{\eta }}_{F(A)}}{\to }RFF(A)\stackrel{R(m_A)}{\to }RF(A)\stackrel{R(h)}{\to }R(A)$$

is an isomorphism if and only if, for any $(A,\theta )\in {\mathbb{A}}^{{\mathcal{R}}^{\kappa }}$, this is so for the composite:

$$t_{(A,\theta )}:F(A)\stackrel{F(\theta )}{\to }FR(A)\stackrel{F({\delta }_A)}{\to }FRR(A)\stackrel{{\overline{\epsilon }}_{R(A)}}{\to }R(A).$$

By symmetry, it suffices to prove one implication. Therefore, suppose that the functor ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is $\tilde{\mathcal{R}}$-Galois. Since $m⊣\delta$, δ is the composite:

$$R\stackrel{\overline{\eta }R}{\to }RFR\stackrel{R\overline{\eta }FR}{\to }RRFFR\stackrel{RRmR}{\to }RRFR\stackrel{RR\overline{\epsilon }}{\to }RR.$$

Considering the diagram:

in which the top left triangle commutes by one of the triangular identities for $F⊣R$ and the other partial diagrams commute by naturality, one sees that $t_{(A,\theta )}$ is the composite:

$$F(A)\stackrel{{\overline{\eta }}_{F(A)}}{\to }RFF(A)\stackrel{R{m}_A}{\to }RF(A)\stackrel{RF(\theta )}{\to }RFR(A)\stackrel{R{\overline{\epsilon }}_A}{\to }R(A).$$

Since $(A,\theta )\in {\mathbb{A}}^{{\mathcal{R}}^{\kappa }}$, the pair $(A,F(A)\stackrel{F(\theta )}{\to }FR(A)\stackrel{{\overline{\epsilon }}_A}{\to }A)$, being ${\Psi }^{-1}(A,\theta )$ (see 2.1), is an object of the category ${\mathbb{A}}_{{\mathcal{F}}^{\lambda }}$. It then follows that $t_{(A,\theta )}=t_{(A,{\overline{\epsilon }}_A·F(\theta ))}$. Since the functor ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is assumed to be $\tilde{\mathcal{R}}$-Galois, the morphism $t_{(A,{\overline{\epsilon }}_A·F(\theta ))}$, and, hence, also $t_{(A,\theta )}$, is an isomorphism, as desired.    ☐

In view of the properties of separable functors (see 2.19) and Definition 3.3, for an Azumaya monad $\mathcal{F}$, $\mathcal{F}{\mathcal{F}}^{\lambda }$ is a separable monad if and only if F is a separable functor. In this case, ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is also a separable functor, that is the unit $e:1\to F$ splits. Dually, for an Azumaya comonad $\mathcal{R}$, $\mathcal{R}{\mathcal{R}}^{\kappa }$ is separable if and only if the functor R is separable. Thus, we have:

3.17 Theorem.

Under the conditions of Proposition 3.16, suppose further that $\mathbb{A}$ is a Cauchy complete category. Then, the following are equivalent:

(a)

$(\mathcal{F},\lambda )$ is an Azumaya monad, and $\mathcal{F}{\mathcal{F}}^{\lambda }$ is a separable monad;

(b)

$(\mathcal{F},\lambda )$ is an Azumaya monad, and the unit $e:1\to F$ is a split monomorphism;

(c)

${\varphi }_{{\mathcal{F}}^{\lambda }}$ is $\widehat{\mathcal{R}}$-Galois, and $e:1\to F$ is a split monomorphism;

(d)

$(\mathcal{R},\kappa )$ is an Azumaya comonad, and the counit $\epsilon :R\to 1$ is a split epimorphism;

(e)

${\varphi }^{{\mathcal{R}}^{\kappa }}$ is $\tilde{\mathcal{F}}$-Galois, and $\epsilon :R\to 1$ is a split epimorphism;

(f)

${\varphi }^{{\mathcal{R}}^{\kappa }}$ is $\tilde{\mathcal{F}}$-Galois, and $\mathcal{R}{\mathcal{R}}^{\kappa }$ is a separable comonad.

Proof. (a)⇒(b)⇒(c) follow by the preceding remarks.

(c)⇒(a) Since $\mathbb{A}$ is assumed to be Cauchy complete, by Corollary 3.17 in [18], the splitting of e implies that the functor ${\varphi }_{{\mathcal{F}}^{\lambda }}$ is comonadic. Now, the assertion follows by Theorem 3.10.

Since ε is the mate of e, ε is a split epimorphism if and only if e is a split monomorphism (e.g., 7.4 in [5]), and the splitting of ε implies that the functor ${\varphi }^{{\mathcal{R}}^{\kappa }}$ is monadic. Applying now Theorem 3.10, its dual and Proposition 3.16 gives the desired result.        ☐

4. Azumaya Algebras in Braided Monoidal Categories

4.1. Algebras and modules in monoidal categories.

Let $(\mathcal{V},\otimes ,I,\tau )$ be a strict monoidal category ([17]). An algebra $\mathcal{A}=(A,m,e)$ in $\mathcal{V}$ (or $\mathcal{V}$-algebra, $\mathcal{V}$-monoid) consists of an object A of $\mathcal{V}$ endowed with multiplication $m:A\otimes A\to A$ and unit morphism $e:I\to A$, subject to the usual identity and associative conditions.

For a $\mathcal{V}$-algebra $\mathcal{A}$, a left $\mathcal{A}$-module is a pair $(V,{\rho }_V)$, where V is an object of $\mathcal{V}$ and ${\rho }_V:A\otimes V\to V$ is a morphism in $\mathcal{V}$, called the left action (or $\mathcal{A}$-left action) on V, such that ${\rho }_V(m\otimes V)={\rho }_V(A\otimes {\rho }_V)$ and ${\rho }_V(e\otimes V)=1$.

Left $\mathcal{A}$-modules are objects of a category ${}_{\mathcal{A}}\mathcal{V}$ whose morphisms between objects $f:(V,{\rho }_V)\to (W,{\rho }_W)$ are morphism $f:V\to W$ in $\mathcal{V}$, such that ${\rho }_W(A\otimes f)=f·{\rho }_V$. Similarly, one has the category ${\mathcal{V}}_{\mathcal{A}}$ of right $\mathcal{A}$-modules.

The forgetful functor ${}_{\mathcal{A}}U:{}_{\mathcal{A}}\mathcal{V}\to \mathcal{V}$, taking a left $\mathcal{A}$-module $(V,{\rho }_V)$ to the object V, has a left adjoint, the free $\mathcal{A}$-module functor:

$${\varphi }_A:\mathcal{V}{\to }_{\mathcal{A}}\mathcal{V},V\mapsto (A\otimes V,m_A\otimes V).$$

There is another way of seeing the category of left $\mathcal{A}$-modules involving modules over the monad associated with the $\mathcal{V}$-algebra $\mathcal{A}$.

Any $\mathcal{V}$-algebra $\mathcal{A}=(A,m,e)$ defines a monad ${\mathcal{A}}_l=(A\otimes -,\eta ,\mu )$ on $\mathcal{V}$ by putting:

• ${\eta }_V=e\otimes V:V\to A\otimes V$,
• ${\mu }_V=m\otimes V:A\otimes A\otimes V\to A\otimes V$.

The corresponding Eilenberg–Moore category ${\mathcal{V}}_{{\mathcal{A}}_l}$ of ${\mathcal{A}}_l$-modules is exactly the category ${}_{\mathcal{A}}\mathcal{V}$ of left $\mathcal{A}$-modules, and ${}_{\mathcal{A}}U⊣F$ is the familiar forgetful-free adjunction between ${\mathcal{V}}_{{\mathcal{A}}_l}$ and $\mathcal{V}$. This gives in particular that the forgetful functor ${}_{\mathcal{A}}U{:}_{\mathcal{A}}\mathcal{V}\to \mathcal{V}$ is monadic. Hence, the functor ${}_{\mathcal{A}}U$ creates those limits that exist in $\mathcal{V}$.

Symmetrically, writing ${\mathcal{A}}_r$ for the monad on $\mathcal{V}$, whose functor part is $-\otimes A$, the category ${\mathcal{V}}_{\mathcal{A}}$ is isomorphic to the Eilenberg–Moore category ${\mathcal{V}}_{{\mathcal{A}}_r}$ of ${\mathcal{A}}_r$-modules, and the forgetful functor $U_{\mathcal{A}}:{\mathcal{V}}_{\mathcal{A}}\to \mathcal{V}$ is monadic and creates those limits that exist in $\mathcal{V}$.

If $\mathcal{V}$ admits coequalizers, $\mathcal{A}$ is a $\mathcal{V}$-algebra, $(V,{\varrho }_V)\in {\mathcal{V}}_{\mathcal{A}}$ a right $\mathcal{A}$-module and $(W,{\rho }_W)\in {}_{\mathcal{A}}\mathcal{V}$ a left $\mathcal{A}$-module, then their tensor product (over $\mathcal{A}$) is the object part of the coequalizer:

$$V\otimes A\otimes W\underset{V\otimes {\rho }_W}{\overset{{\varrho }_V\otimes W}{\rightrightarrows }}V\otimes W\to V{\otimes }_{A}W.$$

4.2. Bimodules.

If $\mathcal{A}$ and $\mathcal{B}$ are $\mathcal{V}$-algebras, an object V in $\mathcal{V}$ is called an $(\mathcal{A},\mathcal{B})$-bimodule if there are morphisms ${\rho }_V:A\otimes V\to V$ and ${\varrho }_V:V\otimes B\to V$ in $\mathcal{V}$, such that $(V,{\rho }_V)\in {}_{\mathcal{A}}\mathcal{V}$, $(V,{\varrho }_V)\in {\mathcal{V}}_{\mathcal{B}}$ and ${\varrho }_V({\rho }_V\otimes B)={\rho }_V(A\otimes {\varrho }_V)$. A morphism of $(\mathcal{A},\mathcal{B})$-bimodules is a morphism in $\mathcal{V}$, which is a morphism of left $\mathcal{A}$-modules, as well as of right $\mathcal{B}$-modules. Write ${{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{B}}$ for the corresponding category.

Let $\mathcal{I}$ be the trivial $\mathcal{V}$-algebra $(I,1_I:I=I\otimes I\to I,1_I:I\to I)$. Then, ${}_{\mathcal{I}}\mathcal{V}={\mathcal{V}}_{\mathcal{I}}=\mathcal{V}$, and for any $\mathcal{V}$-algebra $\mathcal{A}$, the category ${{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{I}}$ is (isomorphic to) the category of left $\mathcal{A}$-modules ${}_A\mathcal{V}$, while the category ${{}_{\mathcal{I}}\mathcal{V}}_{\mathcal{A}}$ is (isomorphic to) the category of right $\mathcal{A}$-modules ${\mathcal{V}}_A$. In particular, ${{}_{\mathcal{I}}\mathcal{V}}_{\mathcal{I}}=\mathcal{V}$.

4.3. The monoidal category of bimodules.

Suppose now that $\mathcal{V}$ admits coequalizers and that the tensor product preserves these coequalizer in both variables (i.e., all functors $V\otimes -:\mathcal{V}\to \mathcal{V}$, as well as $-\otimes V:\mathcal{V}\to \mathcal{V}$ for $V\in \mathcal{V}$ preservedcoequalizers). The last condition guarantees that if $\mathcal{A}$, $\mathcal{B}$ and $\mathcal{C}$ are $\mathcal{V}$-algebras and if $M\in {{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{B}}$ and $N\in {{}_{\mathcal{B}}\mathcal{V}}_{\mathcal{C}}$, then $M{\otimes }_{B}N\in {{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{C}}$,

• if $\mathcal{D}$ is another $\mathcal{V}$-algebra and $P\in {{}_{\mathcal{C}}\mathcal{V}}_{\mathcal{D}}$, then the canonical morphism:

  $$(M{\otimes }_{B}N){\otimes }_{C}P\to M{\otimes }_B(N{\otimes }_{C}P)$$

  induced by the associativity of the tensor product, is an isomorphism in ${{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{D}}$,
• $({{}_{\mathcal{A}}\mathcal{V}}_{\mathcal{A}},-{\otimes }_A-,\mathcal{A})$ is a monoidal category.

Note that (co)algebras in this monoidal category are called $\mathcal{A}$-(co)rings.

4.4. Coalgebras and comodules in monoidal categories.

Associated with any monoidal category $\mathcal{V}=(\mathcal{V},\otimes ,I)$, there are three monoidal categories ${\mathcal{V}}^{\mathrm{op}}$, ${\mathcal{V}}^r$ and ${({\mathcal{V}}^{\text{op}})}^r$ obtained from $\mathcal{V}$ by reversing, respectively, the morphisms, the tensor product and both the morphisms and tensor product, i.e., ${\mathcal{V}}^{\text{op}}=({\mathcal{V}}^{\text{op}},\otimes ,I)$, ${\mathcal{V}}^r=(\mathcal{V},{\otimes }^r,I)$, where $V{\otimes }^{r}W:=W\otimes V$ and ${({\mathcal{V}}^{\text{op}})}^r=({\mathcal{V}}^{\text{op}},{\otimes }^r,I)$ (see, for example, [23]). Note that ${({\mathcal{V}}^{\text{op}})}^r={({\mathcal{V}}^r)}^{\text{op}}$.

Coalgebras and comodules in a monoidal category $\mathcal{V}=(\mathcal{V},\otimes ,I)$ are, respectively, algebras and modules in ${\mathcal{V}}^{\text{op}}=({\mathcal{V}}^{\text{op}},\otimes ,I)$. If $\mathcal{C}=(C,\delta ,\epsilon )$ is a $\mathcal{V}$-coalgebra, we write ${\mathcal{V}}^{\mathcal{C}}$ (resp. ${}^{\mathcal{C}}\mathcal{V}$) for the category of right (resp. left) $\mathcal{C}$-comodules. Thus, ${\mathcal{V}}^{\mathcal{C}}={({\mathcal{V}}^{\text{op}})}_{\mathcal{C}}$ and ${}^{\mathcal{C}}\mathcal{V}={}_{\mathcal{C}}({\mathcal{V}}^{\text{op}})$. Moreover, if ${\mathcal{C}}^{\prime }$ is another $\mathcal{V}$-coalgebra, then the category ${}^{\mathcal{C}}{\mathcal{V}}^{{\mathcal{C}}^{\prime }}$ of $(\mathcal{C},{\mathcal{C}}^{\prime })$-bicomodules is ${}_{\mathcal{C}}{({\mathcal{V}}^{\text{op}})}_{{\mathcal{C}}^{\prime }}$. Writing ${\mathcal{C}}_l$ (resp. ${\mathcal{C}}_r$) for the comonad on $\mathcal{V}$ with functor-part $C\otimes -$ (resp. $-\otimes C$), one has that ${\mathcal{V}}^{\mathcal{C}}$ (resp. ${}^{\mathcal{C}}\mathcal{V}$) is just the category of ${\mathcal{C}}_l$-comodules (resp. ${\mathcal{C}}_r$-comodules).

4.5. Duality in monoidal categories.

One says that an object V of $\mathcal{V}$ admits a left dual, or left adjoint, if there exist an object $V^{*}$ and morphisms $\mathrm{db}:I\to V\otimes V^{*}$ and $\mathrm{ev}:V^{*}\otimes V\to I$, such that the composites:

$$V\stackrel{\mathrm{db}\otimes V}{\to }V\otimes V^{*}\otimes V\stackrel{V\otimes \mathrm{ev}}{\to }V,V^{*}\stackrel{V^{*}\otimes \mathrm{db}}{\to }{V}^{*}\otimes V\otimes V^{*}\stackrel{\mathrm{ev}\otimes V^{*}}{\to }{V}^{*},$$

yield the identity morphisms. $\mathrm{db}$ is called the unit and $\mathrm{ev}$ the counit of the adjunction. We use the notation $(\mathrm{db},\mathrm{ev}:V^{*}⊣V)$ to indicate that $V^{*}$ is left adjoint to V with unit $\mathrm{db}$ and counit $\mathrm{ev}$. This terminology is justified by the fact that such an adjunction induces an adjunction of functors:

$$\mathrm{db}\otimes -,\mathrm{ev}\otimes -:V^{*}\otimes -⊣V\otimes -:\mathcal{V}\to \mathcal{V},$$

as well as an adjunction of functors:

$$-\otimes \mathrm{db},-\otimes \mathrm{ev}:-\otimes V⊣-\otimes V^{*}:\mathcal{V}\to \mathcal{V},$$

i.e., for any $X,Y\in \mathcal{V}$, there are bijections:

$$\mathcal{V}(V^{*}\otimes X,Y)\simeq \mathcal{V}(X,V\otimes Y)\text{and}\mathcal{V}(X\otimes V,Y)\simeq \mathcal{V}(X,Y\otimes V^{*}).$$

Any adjunction $(\mathrm{db},\mathrm{ev}:V^{*}⊣V)$ induces a $\mathcal{V}$-algebra and a $\mathcal{V}$-coalgebra,

$$\begin{array}{c}{\mathcal{S}}_{V,V^{*}}=(V\otimes V^{*},V\otimes V^{*}\otimes V\otimes V^{*}\stackrel{V^{*}\otimes \mathrm{ev}\otimes V}{\to }V\otimes V^{*},\mathrm{db}:I\to V\otimes V^{*}),\hfill \\ {\mathfrak{C}}_{V^{*},V}=(V\otimes V^{*},V\otimes V^{*}\stackrel{V^{*}\otimes \mathrm{db}\otimes V}{\to }V\otimes V^{*}\otimes V\otimes V^{*},\mathrm{ev}:V^{*}\otimes V\to I).\hfill \end{array}$$

Dually, one says that an object V of $\mathcal{V}$ admits a right adjoint if there exist an object $V^{♯}$ and morphisms ${\mathrm{db}}^{\prime }:I\to V^{♯}\otimes V$ and ${\mathrm{ev}}^{\prime }:V\otimes V^{♯}\to I$, such that the composites:

$$V^{♯}\stackrel{\mathrm{db}\otimes V^{♯}}{\to }{V}^{♯}\otimes V\otimes V^{♯}\stackrel{V^{♯}\otimes \mathrm{ev}}{\to }{V}^{♯},V\stackrel{V\otimes \mathrm{db}}{\to }V\otimes V^{♯}\otimes V\stackrel{\mathrm{ev}\otimes V}{\to }V,$$

yield the identity morphisms.

4.6 Proposition.

Let $V\in \mathcal{V}$ be an object with a left dual $(V^{*},\mathrm{db},\mathrm{ev})$.

(i)

For a $\mathcal{V}$-algebra $\mathcal{A}$ and a left $\mathcal{A}$-module structure ${\rho }_V:A\otimes V\to V$ on V, the morphism:

$$t_{(V,{\rho }_V)}:A\stackrel{A\otimes \mathrm{db}}{\to }A\otimes V\otimes V^{*}\stackrel{{\rho }_V\otimes V^{*}}{\to }V\otimes V^{*}$$

(the mate of ${\rho }_V$ under $\mathcal{V}(A\otimes V,V)\simeq \mathcal{V}(A,V\otimes V^{*})$) is a morphism from the $\mathcal{V}$-algebra $\mathcal{A}$ to the $\mathcal{V}$-algebra ${\mathcal{S}}_{V,V^{*}}$.

(ii)

For a $\mathcal{V}$-coalgebra $\mathcal{C}$ and a right $\mathcal{C}$-comodule structure ${\varrho }_V:V\to V\otimes C$, the morphism:

$$t_{(V,{\varrho }_V)}^c:V^{*}\otimes V\stackrel{V^{*}\otimes {\varrho }_V}{\to }{V}^{*}\otimes V\otimes C\stackrel{\mathrm{ev}\otimes C}{\to }C$$

(the mate of ${\varrho }_V$ under $\mathcal{V}(V,V\otimes C)\simeq \mathcal{V}(V^{*}\otimes V,C)$) is a morphism from the $\mathcal{V}$-coalgebra ${\mathfrak{C}}_{V,V^{*}}$ to the $\mathcal{V}$-coalgebra $\mathcal{C}$.

4.7 Definition.

Let $V\in \mathcal{V}$ be an object with a left dual $(V^{*},\mathrm{db},\mathrm{ev})$.

(i)

For a $\mathcal{V}$-algebra $\mathcal{A}$, a left $\mathcal{A}$-module $(V,{\rho }_V)$ is called Galois if the morphism $t_{(V,{\rho }_V)}:A\to V\otimes V^{*}$ is an isomorphism between the $\mathcal{V}$-algebras $\mathcal{A}$ and ${\mathcal{S}}_{V,V^{*}}$ and is said to be faithfully Galois if, in addition, the functor $V\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative.

(ii)

For a $\mathcal{V}$-coalgebra $\mathcal{C}$, a right $\mathcal{C}$-comodule $(V,{\varrho }_V)$ is called Galois if $t_{(V,{\varrho }_V)}^c:V^{*}\otimes V\to C$ is an isomorphism between the $\mathcal{V}$-coalgebras ${\mathfrak{C}}_{V,V^{*}}$ and $\mathcal{C}$ and is said to be faithfully Galois if, in addition, the functor $V\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative.

4.8. Braided monoidal categories.

A braided monoidal category is a quadruple $(\mathcal{V},\otimes ,I,\tau )$, where $(\mathcal{V},\otimes ,I)$ is a monoidal category, and τ, called the braiding, is a collection of natural isomorphisms:

$${\tau }_{V,W}:V\otimes W\to W\otimes V,V,W\in \mathcal{V},$$

subject to two hexagon coherence identities (e.g., [17]). A symmetric monoidal category is a monoidal category with a braiding τ, such that ${\tau }_{V,W}·{\tau }_{W,V}=1$ for all $V,W\in \mathcal{V}$. If $\mathcal{V}$ is a braided category with braiding τ, then the monoidal category ${\mathcal{V}}^r$ becomes a braided category with braiding given by ${\overline{\tau }}_{V,W}:={\tau }_{W,V}$. Furthermore, given $\mathcal{V}$-algebras $\mathcal{A}=(A,m_A,e_A)$ and $\mathcal{B}=(B,m_B,e_B)$, the triple:

$$\mathcal{A}\otimes \mathcal{B}=(A\otimes B,(m_A\otimes m_B)·(A\otimes {\tau }_{B,A}\otimes B),e_A\otimes e_B)$$

is again a $\mathcal{V}$-algebra, called the braided tensor product of $\mathcal{A}$ and $\mathcal{B}$.

The braiding also has the following consequence (e.g., [24]):

• If an object V in $\mathcal{V}$ admits a left dual $(V^{*},\mathrm{db}:I\to V\otimes V^{*},\mathrm{ev}:V^{*}\otimes V\to I)$, then $(V^{*},{\mathrm{db}}^{\prime },{\mathrm{ev}}^{\prime })$ is right adjoint to V with unit and counit:

  $${\mathrm{db}}^{\prime }:I\stackrel{\mathrm{db}}{\to }V\otimes V^{*}\stackrel{{\tau }_{V^{*},V}^{-1}}{\to }{V}^{*}\otimes V,{\mathrm{ev}}^{\prime }:V\otimes V^{*}\stackrel{{\tau }_{V,V^{*}}}{\to }{V}^{*}\otimes V\stackrel{\mathrm{ev}}{\to }I.$$

Thus, there are isomorphisms ${(V^{*})}^{♯}\simeq V$ and ${(V^{♯})}^{*}\simeq V$, and one uses the:

4.9 Definition.

An object V of a braided monoidal category $\mathcal{V}$ is said to be finite if V admits a left (and, hence, also a right) dual.

For the rest of this section, $\mathcal{V}=(\mathcal{V},\otimes ,I,\tau )$ will denote a braided monoidal category.

Recall that a morphism $f:V\to W$ in $\mathcal{V}$ is a copure epimorphism (monomorphism) if for any $X\in \mathcal{V}$, the morphism $f\otimes X:V\otimes X\to W\otimes X$ (and, hence, also, the morphism $X\otimes f:X\otimes V\to X\otimes W$) is a regular epimorphism (monomorphism).

4.10 Proposition.

Let $\mathcal{V}$ be a braided monoidal category admitting equalizers and coequalizers. For a finite object $V\in \mathcal{V}$ with left dual $(V^{*},\mathrm{db},\mathrm{ev})$, the following are equivalent:

(a)

$V\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative (monadic, comonadic);

(b)

$\mathrm{ev}:V^{*}\otimes V\to I$ is a copure epimorphism;

(c)

$-\otimes V:\mathcal{V}\to \mathcal{V}$ is conservative (monadic, comonadic);

(d)

$\mathrm{db}:I\to V\otimes V^{*}$ is a pure monomorphism.

Proof. Since V is assumed to admit a left dual, it admits also a right dual (see 4.8). Hence, the equivalence of the properties listed in (a) (and in (c)) follows from 2.11. It only remains to show the equivalence of (a) and (b), since the equivalence of (c) and (d) will then follow by duality.

(a)⇒(b) If $V\otimes -:\mathcal{V}\to \mathcal{V}$ is monadic, then it follows from Theorem 2.4 in [25] that each component of the counit of the adjunction $V^{*}\otimes -⊣V\otimes -$, which is the natural transformation $\mathrm{ev}\otimes -$, is a regular epimorphism. Thus, $\mathrm{ev}:V^{*}\otimes V\to I$ is a copure epimorphism.

(b)⇒(a) To say that $\mathrm{ev}:V^{*}\otimes V\to I$ is a copure epimorphism is to say that each component of the counit $\mathrm{ev}\otimes -$ of the adjunction $V^{*}\otimes -⊣V\otimes -$ is a regular epimorphism, which implies (see, e.g., [25]) that $V\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative.         ☐

4.11 Remark.

In Proposition 4.10, if the tensor product preserves regular epimorphisms, then (b) is equivalent to requiring $\mathrm{ev}:V^{*}\otimes V\to I$ to be a regular epimorphism. If the tensor product in $\mathcal{V}$ preserves regular monomorphisms, then (d) is equivalent to requiring $\mathrm{db}:I\to V\otimes V^{*}$ to be a regular monomorphism.

4.12. Opposite algebras.

For a $\mathcal{V}$-algebra $\mathcal{A}=(A,m,e)$, define the opposite algebra ${\mathcal{A}}^{\tau }=(A,m^{\tau },e^{\tau })$ in $\mathcal{V}$ with multiplication $m^{\tau }=m·{\tau }_{A,A}$ and unit $e^{\tau }=e$. Denote by ${\mathcal{A}}^e=\mathcal{A}\otimes {\mathcal{A}}^{\tau }$ and by ${}^e\mathcal{A}={\mathcal{A}}^{\tau }\otimes \mathcal{A}$ the braided tensor products. Then, A is a left ${\mathcal{A}}^e$-module, as well as a right ${}^e\mathcal{A}$-module by the structure morphisms:

$$\begin{array}{c}A\otimes A^{\tau }\otimes A\stackrel{A\otimes {\tau }_{A,A}}{\to }A\otimes A\otimes A\stackrel{A\otimes m}{\to }A\otimes A\stackrel{m}{\to }A,\hfill \\ A\otimes A^{\tau }\otimes A\stackrel{{\tau }_{A,A}\otimes A}{\to }A\otimes A\otimes A\stackrel{m\otimes A}{\to }A\otimes A\stackrel{m}{\to }A.\hfill \end{array}$$

By properties of the braiding, the morphism ${\tau }_{A,A}:A\otimes A\to A\otimes A$ induces a distributive law from the monad ${({\mathcal{A}}^{\tau })}_l$ to the monad ${\mathcal{A}}_l$ satisfying the Yang–Baxter equation, and the monad ${\mathcal{A}}_l{({\mathcal{A}}^{\tau })}_l$ is just the monad ${({\mathcal{A}}^e)}_l$. Thus, the category of ${\mathcal{A}}_l{({\mathcal{A}}^{\tau })}_l$-modules is the category ${}_{{\mathcal{A}}^e}\mathcal{V}$ of left ${\mathcal{A}}^e$-modules. Symmetrically, the category of ${\mathcal{A}}_r{({\mathcal{A}}^{\tau })}_r$-modules is the category ${\mathcal{V}}_{{}^e\mathcal{A}}$ of right ${}^e\mathcal{A}$-modules.

4.13. Azumaya algebras.

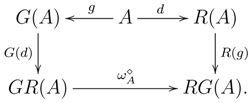
Given a $\mathcal{V}$-algebra $\mathcal{A}=(A,m,e)$, by Proposition 3.2, there are two comparison functors:

$${\overline{K}}_l:\mathcal{V}\to {\mathcal{V}}_{{\mathcal{A}}_l{({\mathcal{A}}^{\tau })}_l}={}_{{\mathcal{A}}^e}\mathcal{V},{\overline{K}}_r:\mathcal{V}\to {\mathcal{V}}_{{\mathcal{A}}_r{({\mathcal{A}}^{\tau })}_r}={\mathcal{V}}_{{}^e\mathcal{A}},$$

given by the assignments:

$${\overline{K}}_l:V⟼(A\otimes V,A\otimes A\otimes A\otimes V\stackrel{A\otimes m^{\tau }\otimes V}{\to }A\otimes A\otimes V\stackrel{m\otimes V}{\to }A\otimes V),$$

$${\overline{K}}_r:V⟼(V\otimes A,V\otimes A\otimes A\otimes A\stackrel{V\otimes m^{\tau }\otimes A}{\to }V\otimes A\otimes A\stackrel{V\otimes m}{\to }V\otimes A)$$

with commutative diagrams:

(4.1)

The $\mathcal{V}$-algebra $\mathcal{A}$ is called left (resp. right) Azumaya provided $({\mathcal{A}}_l,{\tau }_{A,A})$ (resp. $({\mathcal{A}}_r,{\tau }_{A,A})$) is an Azumaya monad.

4.14 Remark.

It follows from Proposition 3.8 that if ${\tau }_{A,A}^2=1$, the monad ${\mathcal{A}}_l$ (resp. ${\mathcal{A}}_r$) is Azumaya if and only if ${({\mathcal{A}}^{\tau })}_l$ (resp. ${({\mathcal{A}}^{\tau })}_l)$ is. Thus, in a symmetric monoidal category, a $\mathcal{V}$-algebra is left (right) Azumaya if and only if its opposite is so.

A basic property of these algebras is the following.

4.15 Proposition.

Let $\mathcal{V}$ be a braided monoidal category and $\mathcal{A}=(A,m,e)$ a $\mathcal{V}$-algebra. If $\mathcal{A}$ is left Azumaya, then A is finite in $\mathcal{V}$.

Proof. It is easy to see that when $\mathcal{V}$ and ${}_{{\mathcal{A}}^e}\mathcal{V}$ are viewed as right $\mathcal{V}$-categories (in the sense of [26]), ${\overline{K}}_l$ is a $\mathcal{V}$-functor. Hence, when ${\overline{K}}_l$ is an equivalence of categories (that is, when $\mathcal{A}$ is left Azumaya), its inverse equivalence $\overline{R}$ is also a $\mathcal{V}$-functor. Moreover, since $\overline{R}$ is left adjoint to ${\overline{K}}_l$, it preserves all colimits that exist in ${}_{{\mathcal{A}}^e}\mathcal{V}$. Obviously, the functor ${\varphi }_{{({\mathcal{A}}^e)}_l}:\mathcal{V}\to {}_{{\mathcal{A}}^e}\mathcal{V}$ is also a $\mathcal{V}$-functor, and moreover, being a left adjoint, it preserves all colimits that exist in $\mathcal{V}$. Consequently, the composite $\overline{R}·{\varphi }_{{({\mathcal{A}}^e)}_l}:\mathcal{V}\to \mathcal{V}$ is a $\mathcal{V}$-functor and preserves all colimits that exist in $\mathcal{V}$. It then follows from Theorem 4.2 in [26] that there exists an object $A^{*}$, such that $\overline{R}·{\varphi }_{{({\mathcal{A}}^e)}_l}\simeq A^{*}\otimes -$. Using now that $\overline{R}·{\varphi }_{{({\mathcal{A}}^e)}_l}$ is left adjoint to the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$, it is not hard to see that $A^{*}$ is a left dual to A.       ☐

4.16. Left Azumaya algebras.

Let $(\mathcal{V},\otimes ,I,\tau )$ be a braided monoidal category and $\mathcal{A}=(A,m,e)$ a $\mathcal{V}$-algebra. The following are equivalent:

(a)

$\mathcal{A}$ is a left Azumaya algebra;

(b)

the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is monadic, and the left ${({\mathcal{A}}^e)}_l$-module structure on it induced by the left diagram in (4.1) is Galois;

(c)

(i) A is finite with left dual $(A^{*},\mathrm{db}:I\to A\otimes A^{*},\mathrm{ev}:A^{*}\otimes A\to I)$, and the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is monadic; and

(ii) the composite ${\overline{\chi }}_0:$

$$A\otimes A\stackrel{A\otimes A\otimes \mathrm{db}}{\to }A\otimes A\otimes A\otimes A^{*}\stackrel{A\otimes {\tau }_{A,A}\otimes A^{*}}{\to }A\otimes A\otimes A\otimes A^{*}\stackrel{m\otimes A\otimes A^{*}}{\to }A\otimes A\otimes A^{*}\stackrel{m\otimes A^{*}}{\to }A\otimes A^{*}$$

is an isomorphism (between the $\mathcal{V}$-algebras ${\mathcal{A}}^e$ and ${\mathcal{S}}_{A,A^{*}})$;

(d)

(i) A is finite with right dual $(A^{♯},{\mathrm{db}}^{\prime }:I\to A^{♯}\otimes A,{\mathrm{ev}}^{\prime }:A\otimes A^{♯}\to I)$, and the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {\mathcal{V}}_{{({\mathcal{A}}^{\tau })}_l}{=}_{{\mathcal{A}}^{\tau }}\mathcal{V}$ is comonadic; and

(ii) the composite $\overline{\chi }:$

$$A\otimes A\stackrel{{\mathrm{db}}^{\prime }\otimes A\otimes A}{\to }{A}^{♯}\otimes A\otimes A\otimes A\stackrel{A^{♯}\otimes m\otimes A}{\to }{A}^{♯}\otimes A\otimes A\stackrel{A^{♯}\otimes {\tau }_{A,A}}{\to }{A}^{♯}\otimes A\otimes A\stackrel{A^{♯}\otimes m}{\to }{A}^{♯}\otimes A$$

is an isomorphism.

Proof. (a)⇔(b) follows by Proposition 2.13.

(a)⇔(c) If $\mathcal{A}$ is a left Azumaya algebra, then A has a left dual by Proposition 4.15. Thus, in both cases, A is finite, i.e., there is an adjunction $(\mathrm{db},\mathrm{ev}:A^{*}⊣A)$. Then, the functor $A^{*}\otimes -:\mathcal{V}\to \mathcal{V}$ is left adjoint to the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$, and the monad on $\mathcal{V}$ generated by this adjunction is ${({\mathcal{S}}_{A,A^{*}})}_l$. It is then easy to see that the monad morphism $t_{{\overline{K}}_l}:{({\mathcal{A}}^e)}_l\to {({\mathcal{S}}_{A,A^{*}})}_l$ corresponding to the left commutative diagram in (4.1), is just ${\overline{\chi }}_0\otimes -$. Thus, $t_{{\overline{K}}_l}$ is an isomorphism if and only if ${\overline{\chi }}_0$ is so. It now follows from Theorem 3.5 that (a) and (c) are equivalent.

(a)⇔(d) Any left Azumaya algebra has a left (and a right) dual by Proposition 4.15. Moreover, if A has a right dual $A^{♯}$, then the functor $A^{♯}\otimes -$ is right adjoint to the functor $A\otimes -$. The desired equivalence now follows by applying Theorem 3.10 to the monad ${\mathcal{A}}_l$ and using that the natural transformation χ is just $\overline{\chi }\otimes -$.         ☐

4.17 Proposition.

In any braided monoidal category, an algebra is left (resp. right) Azumaya if and only if its opposite algebra is right (resp. left) Azumaya.

Proof. We just note that if $(\mathcal{V},\otimes ,I,\tau )$ is a braided monoidal category and $\mathcal{A}$ is a $\mathcal{V}$-algebra, then ${({\tau }_{-,A})}^{-1}:A\otimes -\to -\otimes A^{\tau }$ is an isomorphism of monads ${\mathcal{A}}_l\to {({\mathcal{A}}^{\tau })}_r$, while the symmetric ${({\tau }_{A,-})}^{-1}:-\otimes A\to A^{\tau }\otimes -$ is an isomorphism of monads ${\mathcal{A}}_r\to {({\mathcal{A}}^{\tau })}_l$.      ☐

Under some conditions on $\mathcal{V}$, left Azumaya algebras are also right Azumaya and vice versa:

4.18 Theorem.

Let $\mathcal{A}=(A,m,e)$ be a $\mathcal{V}$-algebra in a braided monoidal category $(\mathcal{V},\otimes ,I,\tau )$ with equalizers and coequalizers. Then, the following are equivalent:

(a)

$\mathcal{A}$ is a left Azumaya algebra;

(b)

the left ${\mathcal{A}}^e$-module $(A,m·(A\otimes m^{\tau }))$ is faithfully Galois;

(c)

A is finite with right dual $(A^{♯},{\mathrm{db}}^{\prime }:I\to A^{♯}\otimes A,{\mathrm{ev}}^{\prime }:A\otimes A^{♯}\to I)$; the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {\mathcal{V}}_{{({\mathcal{A}}^{\tau })}_l}{=}_{{\mathcal{A}}^{\tau }}\mathcal{V}$ is comonadic; and the composite $\overline{\chi }$ in 4.16 (d) is an isomorphism;

(d)

A is finite with right dual $(A^{♯},{\mathrm{db}}^{\prime }:I\to A^{♯}\otimes A,{\mathrm{ev}}^{\prime }:A\otimes A^{♯}\to I)$; the functor $-\otimes A:\mathcal{V}\to \mathcal{V}$ is monadic; and the composite ${\overline{\chi }}_1$:

$$A\otimes A\stackrel{{\mathrm{db}}^{\prime }\otimes A\otimes A}{\to }{A}^{♯}\otimes A\otimes A\otimes A\stackrel{A^{♯}\otimes {\tau }_{A,A}\otimes A}{\to }{A}^{♯}\otimes A\otimes A\otimes A\stackrel{A^{♯}\otimes m\otimes A}{\to }{A}^{♯}\otimes A\otimes A\stackrel{A^{♯}\otimes m}{\to }{A}^{♯}\otimes A$$

is an isomorphism (between the $\mathcal{V}$-algebras ${}^e\mathcal{A}$ and ${\mathfrak{S}}_{A^{♯},A})$;

(e)

the right ${}^e\mathcal{A}$-module $(A,m·(m^{\tau }\otimes A))$ is faithfully Galois;

(f)

$\mathcal{A}$ is a right Azumaya algebra.

Proof. In view of Proposition 4.10 and Remark 4.11, (a), (b) and (c) are equivalent by 4.16.

Each statement about a general braided monoidal category $\mathcal{V}$ has a counterpart statement obtained by interpreting it in ${\mathcal{V}}^r$. Doing this for Theorem 4.16, we obtain that (d), (e) and (f) are equivalent.

(c)⇔(d) The composite $\overline{\chi }$ is the upper path and ${\overline{\chi }}_1$ is the lower path in the diagram

where $\tau ={\tau }_{A,A}$ and $·=\otimes$. The left square is commutative by naturality, the pentagon is commutative since τ is a braiding and the parallelogram commutes by the associativity of m. Therefore, the diagram is commutative, and hence, $\overline{\chi }={\overline{\chi }}_1·{\tau }_{A,A}$, that is $\overline{\chi }$ is an isomorphism if and only if ${\overline{\chi }}_1$ is so. Thus, in order to show that (c) and (d) are equivalent, it is enough to show that the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {}_{{\mathcal{A}}^{\tau }}\mathcal{V}$ is comonadic if and only if the functor $-\otimes A:\mathcal{V}\to \mathcal{V}$ is monadic. Since $\mathcal{V}$ is assumed to have equalizers and coequalizers, this follows from Lemma 2.11 and Proposition 4.10.      ☐

4.19 Remark.

A closer examination of the proof of the preceding theorem shows that if a braided monoidal category $\mathcal{V}$ admits:

• coequalizers, then any left Azumaya $\mathcal{V}$-algebra is right Azumaya,
• equalizers, then any right Azumaya $\mathcal{V}$-algebra is left Azumaya.

In the setting of 4.12, by Proposition 3.2, the assignment:

$$V⟼((A\otimes V,A\otimes A\otimes V\stackrel{m^{\tau }\otimes V}{\to }A\otimes V),A\otimes A\otimes V\stackrel{m\otimes V}{\to }A\otimes V)$$

yields the comparison functor $K:\mathcal{V}\to {({\mathcal{V}}_{{({\mathcal{A}}^{\tau })}_l})}_{\widehat{{\mathcal{A}}_l}}={{(}_{{\mathcal{A}}^{\tau }}\mathcal{V})}_{\widehat{{\mathcal{A}}_l}}$.

Now, assume the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ to have a right adjoint functor $[A,-]:\mathcal{V}\to \mathcal{V}$ with unit ${\eta }^A:1\to [A,A\otimes -]$. Then, there is a unique comonad structure $\widehat{[A,-]}$ on $[A,-]$ (right adjoint to ${\mathcal{A}}_l$; see Section 2.1), leading to the commutative diagram:

(4.2)

where $\Psi ={\Psi }_{{({\mathcal{A}}^{\tau })}_l}$. This is just the diagram (3.2), and Theorem 3.10 provides characterizations of left Azumaya algebras.

4.20 Theorem.

Let $\mathcal{A}=(A,m,e)$ be an algebra in a braided monoidal category $(\mathcal{V},\otimes ,I,\tau )$, and assume $A\otimes -$ to have a right adjoint $[A,-]$ (see above). Then, the following are equivalent:

(a)

$\mathcal{A}$ is left Azumaya;

(b)

the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {}_{{\mathcal{A}}^{\tau }}\mathcal{V}$ is comonadic, and for any $V\in \mathcal{V}$, the composite:

$$\begin{array}{cc}\hfill {\chi }_V:A\otimes A\otimes V\stackrel{{({\eta }^A)}_{A\otimes A\otimes V}}{\to }& \hfill [A,A\otimes A\otimes A\otimes V]\stackrel{[A,m\otimes A\otimes V]}{\to }[A,A\otimes A\otimes A]\\ & \hfill \stackrel{[A,{\tau }_{A,A}\otimes V]}{\to }[A,A\otimes A\otimes V]\stackrel{[A,m\otimes V]}{\to }[A,A\otimes V]\end{array}$$

is an isomorphism;

(c)

A is finite; the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {}_{A^{\tau }}\mathcal{V}$ is comonadic; and the composite:

$${\chi }_I:A\otimes A\stackrel{{({\eta }^A)}_{A\otimes A}}{\to }[A,A\otimes A\otimes A]\stackrel{[A,m\otimes A]}{\to }[A,A\otimes A]\stackrel{[A,m^{\tau }]}{\to }[A,A]$$

is an isomorphism.

Proof. (a)⇔(b) follows by Theorem 3.10.

(a)⇔(c) Since A turns out to be finite, there is a right dual $(A^{♯},{\mathrm{db}}^{\prime },{\mathrm{ev}}^{\prime })$ of A. Then, $A^{♯}\otimes -:\mathcal{V}\to \mathcal{V}$ and $[A,-]:\mathcal{V}\to \mathcal{V}$ are both right adjoint to $A\otimes -:\mathcal{V}\to \mathcal{V}$, and thus, there is an isomorphism of functors $t:[A,-]\to A^{♯}\otimes -$ inducing the commutative diagram:

(4.3)

Rewriting the morphism $\overline{\chi }$ from 4.16(d) yields the morphism ${\chi }_I$ in (c).       ☐

A symmetric characterization is obtained for right Azumaya algebras provided the functor $-\otimes A$ has a right adjoint $\{A,-\}$.

4.21 Remark.

In [3], van Oystaeyen and Zhang defined Azumaya algebras $\mathcal{A}=(A,m,e)$ in $\mathcal{V}$ by requiring $\mathcal{A}$ to be left and right Azumaya in our sense (see 4.13). The preceding Theorem 4.20 together with its right-hand version correspond to the characterization of these algebras in Theorem 3.1 in [3]. As shown in Theorem 4.18, if $\mathcal{V}$ admits equalizers and coequalizers, it is sufficient to require the Azumaya property on one side.

Given an adjunction $(\mathrm{db},\epsilon :V^{*}⊣V)$ in $\mathcal{V}$, we know from 4.5 that ${\mathcal{S}}_{V,V^{*}}=V\otimes V^{*}$ is a $\mathcal{V}$-algebra. Moreover, it is easy to see that the morphism $V^{*}\otimes V\otimes V^{*}\stackrel{\mathrm{ev}\otimes V^{*}}{\to }{V}^{*}$ defines a left ${\mathcal{S}}_{V,V^{*}}$-module structure on $V^{*}$, while the composite $V\otimes V^{*}\otimes V\stackrel{V\otimes \mathrm{ev}}{\to }V$ defines a right ${\mathcal{S}}_{V,V^{*}}$-module structure on V.

Recall from [3] that an object $V\in \mathcal{V}$ with a left dual $(V^{*},\mathrm{db},\mathrm{ev})$ is right faithfully projective if the morphism $\overline{\mathrm{ev}}:V^{*}{\otimes }_{{\mathcal{S}}_{V,V^{*}}}V\to I$ induced by $\mathrm{ev}:V^{*}\otimes V\to I$ is an isomorphism. Dually, an object $V\in \mathcal{V}$ with a right dual $(V^{♯},{\mathrm{db}}^{\prime },{\mathrm{ev}}^{\prime })$ is left faithfully projective if the morphism $\overline{{\mathrm{ev}}^{\prime }}:V{\otimes }_{{\mathcal{S}}_{V^{♯},V}}{V}^{♯}\to I$ induced by ${\mathrm{ev}}^{\prime }:V\otimes V^{♯}\to I$ is an isomorphism.

Since, in a braided monoidal category, an object is left faithfully projective if and only if it is right faithfully projective (e.g., Theorem 3.1 in [4]), we do not have to distinguish between left and right faithfully projective objects, and we shall call them just faithfully projective.

4.22 Theorem.

Let $(\mathcal{V},\otimes ,I,\tau )$ be a braided closed monoidal category with equalizers and coequalizers. Let $\mathcal{A}=(A,m,e)$ be a $\mathcal{V}$-algebra, such that the functor $A\otimes -$ admits a right adjoint $[A,-]$ (hence, $-\otimes A$ also admits a right adjoint $\{A,-\}$). Then, the following are equivalent:

(a)

$\mathcal{A}$ is left Azumaya;

(b)

$\mathcal{A}$ is right Azumaya;

(c)

A is faithfully projective, and the composite:

$$A\otimes A\stackrel{{({\eta }^A)}_{A\otimes A}}{\to }[A,A\otimes A\otimes A]\stackrel{[A,m\otimes A]}{\to }[A,A\otimes A]\stackrel{[A,m^{\tau }]}{\to }[A,A],$$

where ${\eta }^A$ is the unit of the adjunction $A\otimes -⊣[A,-]$, is an isomorphism;

(d)

A is faithfully projective, and the composite:

$$A\otimes A\stackrel{{({\eta }_A)}_{A\otimes A}}{\to }\{A,A\otimes A\otimes A\}\stackrel{\{A,m\otimes A\}}{\to }\{A,A\otimes A\}\stackrel{\{A,m^{\tau }\}}{\to }\{A,A\},$$

where ${\eta }_A$ is the unit of the adjunction $-\otimes A⊣\{A,-\}$, is an isomorphism.

Proof. That (a) and (b) are equivalent follows from Theorem 4.18.

(a)⇔(c) Since in both cases, A is finite and, thus, the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ has both left and right adjoints, in view of Proposition 4.10, we get from Lemma 2.11 that the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {}_{{\mathcal{A}}^{\tau }}\mathcal{V}$ is comonadic if and only if the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative. According to 2.5.1, 2.5.2 in [27], A is faithfully projective if and only if A is finite and the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative, and hence, the equivalence of (a) and (c) follows by Theorem 4.20.

Similarly, one proves that (b) and (d) are equivalent.        ☐

4.23. Braided closed monoidal categories.

A braided monoidal category $\mathcal{V}$ is said to be left closed if each functor $V\otimes -:\mathcal{V}\to \mathcal{V}$ has a right adjoint $[V,-]:\mathcal{V}\to \mathcal{V}$; we write ${\eta }^V,{\mathrm{ev}}^V:V\otimes -⊣[V,-]$. $\mathcal{V}$ is called right closed if each functor $-\otimes V:\mathcal{V}\to \mathcal{V}$ has a right adjoint $\{V,-\}:\mathcal{V}\to \mathcal{V}$; we write ${\eta }_V,{\mathrm{ev}}_V:-\otimes V⊣\{V,-\}$. $\mathcal{V}$ being braided left closed implies that $\mathcal{V}$ is also right closed. Therefore, assume $\mathcal{V}$ to be closed.

If $\mathcal{A}$ is a $\mathcal{V}$-algebra and $(V,{\rho }_V)\in {}_{\mathcal{A}}\mathcal{V}$, then for any $X\in \mathcal{V}$,

$$(V\otimes X,A\otimes V\otimes X\stackrel{{\rho }_V\otimes X}{\to }V\otimes X)\in {}_{\mathcal{A}}\mathcal{V},$$

and the assignment $X\to (V\otimes X,{\rho }_V\otimes X)$ defines a functor $V\otimes -:\mathcal{V}\to {}_{\mathcal{A}}\mathcal{V}$. When $\mathcal{V}$ admits equalizers, this functor has a right adjoint ${}_{\mathcal{A}}[V,-]:{}_{\mathcal{A}}\mathcal{V}\to \mathcal{V}$, where, for any $(W,{\rho }_W)\in {}_{\mathcal{A}}\mathcal{V}$, ${}_{\mathcal{A}}[V,W]$ is defined to be the equalizer in $\mathcal{V}$ of:

$$[V,W]\rightrightarrows [A\otimes V,W],$$

where one of the morphisms is $[{\varrho }_V,W]$ and the other one is the composition:

$$[V,W]\stackrel{{(A\otimes -)}_{V,W}}{\to }[A\otimes V,A\otimes W]\stackrel{[A\otimes V,{\rho }_W]}{\to }[A\otimes V,W].$$

Symmetrically, for $V,W\in {\mathcal{V}}_{\mathcal{A}}$, one defines ${\{V,W\}}_{\mathcal{A}}$.

The functor $\overline{K}=\Psi ·K:\mathcal{V}\to {{(}_{{\mathcal{A}}^{\tau }}\mathcal{V})}^{\widehat{[A,-]}}$ (in diagram (4.2)) has as right adjoint $\overline{R}:{{(}_{{\mathcal{A}}^{\tau }}\mathcal{V})}^{\widehat{[A,-]}}\to \mathcal{V}$ (see 2.16), and since Ψ is an isomorphism of categories, the composition $\overline{R}·\Psi$ is right adjoint to the functor $K:\mathcal{V}\to {{(}_{{\mathcal{A}}^{\tau }}\mathcal{V})}_{\widehat{{\mathcal{A}}_l}}$. Using now that $\mathcal{P}$ (see 3.6) is an isomorphism of categories, we conclude that $\overline{R}·\Psi ·\mathcal{P}$ is right adjoint to the functor ${\mathcal{P}}^{-1}·K:\mathcal{V}\to {}_{{\mathcal{A}}^e}\mathcal{V}$. For any $(V,h)\in {}_{{\mathcal{A}}^e}\mathcal{V}$, we put:

$${}^{\mathcal{A}}V:=\overline{R}·\Psi ·\mathcal{P}(V,h).$$

Taking into account the description of the functors $\mathcal{P}$, Ψ and $\overline{R}$, one gets that ${}^{\mathcal{A}}V$ can be obtained as the equalizer of the diagram:

$$V\stackrel{{({\eta }^A)}_V}{\to }[A,A\otimes V]\underset{[A,A\otimes e\otimes V]}{\overset{[A,e\otimes A\otimes V]}{\rightrightarrows }}[A,A\otimes A\otimes V]\underset{[A,h]}{\overset{[A,h]}{\rightrightarrows }}[A,V].$$

Symmetrically, for any $(V,h)\in {\mathcal{V}}_{{}^e\mathcal{A}}$, we define $V^{\mathcal{A}}$ as the equalizer of the diagram:

$$V\stackrel{{({\eta }^A)}_V}{\to }[A,V\otimes A]\underset{[A,V\otimes e\otimes A]}{\overset{[A,V\otimes A\otimes e]}{\rightrightarrows }}[A,V\otimes A\otimes A]\underset{[A,h]}{\overset{[A,h]}{\rightrightarrows }}[A,V].$$

The functor ${\mathcal{P}}^{-1}·K:\mathcal{V}\to {}_{{\mathcal{A}}^e}\mathcal{V}$ is just the functor $A\otimes -:\mathcal{V}\to {}_{{\mathcal{A}}^e}\mathcal{V}$ and admits as a right adjoint the functor ${}_{{\mathcal{A}}^e}[A,-]:{}_{{\mathcal{A}}^e}\mathcal{V}\to \mathcal{V}$ (see 4.23). As right adjoints are unique up to isomorphism, we get an alternative proof for Femić’s Proposition 3.3 in [4]:

4.24 Proposition.

Let $\mathcal{V}$ be a braided closed monoidal category with equalizers. For any $\mathcal{V}$-algebra $\mathcal{A}$,

the functors:	${}^{\mathcal{A}}(-),{}_{{\mathcal{A}}^e}[A,-]:{}_{{\mathcal{A}}^e}\mathcal{V}\to \mathcal{V}$
and the functors:	${(-)}^{\mathcal{A}},{\{A,-\}}_{{}^e\mathcal{A}}:{\mathcal{V}}_{{}^e\mathcal{A}}\to \mathcal{V}$

are isomorphic.

These isomorphisms allow for further characterizations of Azumaya algebras.

4.25 Theorem.

Let $\mathcal{V}$ be a braided closed monoidal category with equalizers. Then, any $\mathcal{V}$-algebra $\mathcal{A}=(A,m,e)$ is left (resp. right) Azumaya if and only if:

(i)

the morphism $e:I\to A$ is a pure monomorphism, and

(ii)

for any $(V,h)\in {}_{{\mathcal{A}}^e}\mathcal{V}$, with the inclusion $i_V:{}^{\mathcal{A}}V\to V$, we have an isomorphism:

$$A\otimes {}^{\mathcal{A}}V\stackrel{A\otimes i_V}{\to }A\otimes V\stackrel{A\otimes e\otimes V}{\to }A\otimes A\otimes V\stackrel{h}{\to }V;$$

(resp. for any $(V,h)\in {\mathcal{V}}_{{}^e\mathcal{A}}$, with the inclusion $i_V:V^{\mathcal{A}}\to V$, we have an isomorphism:

$$V^{\mathcal{A}}\otimes V\stackrel{i_V\otimes A}{\to }V\otimes A\stackrel{V\otimes e\otimes A}{\to }V\otimes A\otimes A\stackrel{h}{\to }V.)$$

Proof. The $\mathcal{V}$-algebra $\mathcal{A}$ is left Azumaya provided the functor ${\overline{K}}_l:\mathcal{V}\to {}_{{\mathcal{A}}^e}\mathcal{V}$ is an equivalence of categories. It follows from Equation (2.6) that the composite:

$$h·(A\otimes e\otimes V)·(A\otimes i_V):A\otimes {}^{\mathcal{A}}V\to V$$

is just the $\Psi ·\mathcal{P}(V,h)$-component of the counit of ${\overline{K}}_l⊣\overline{R}$ and, hence, is an isomorphism. Moreover, by Proposition 2.15, the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}:\mathcal{V}\to {}_{\mathcal{A}}\mathcal{V}$ is comonadic, whence the morphism $e:I\to A$ is a pure monomorphism (e.g., Theorem 2.1 in [18]). This proves one direction.

For the other direction, we note that, under Conditions (i) and (ii), the counit of the adjunction ${\mathcal{P}}^{-1}·{\overline{K}}_l⊣\overline{R}·\Psi ·\mathcal{P}$ (and hence, also, of the adjunction ${\overline{K}}_l=\Psi ·K⊣\overline{R}$) is an isomorphism and the functor ${\varphi }_{{({\mathcal{A}}^{\tau })}_l}$ (and hence, also, ${\overline{K}}_l$) is conservative (e.g., Theorem 2.1 in [18]), implying (as in the proof of Theorem 3.13 (ii)) that ${\overline{K}}_l$ is an equivalence of categories.

The right version of the theorem follows by duality.       ☐

4.26 Definition.

A $\mathcal{V}$-algebra $\mathcal{A}$ is called left (resp. right) central if there is an isomorphism $I\simeq {}_{{\mathcal{A}}^e}[A,-]$ (resp. $I\simeq {\{A,-\}}_{{}^e\mathcal{A}}$). $\mathcal{A}$ is called central if it is both left and right central.

4.27 Proposition.

Let $\mathcal{V}$ be a braided closed monoidal category with equalizers. Then:

(i)

any left (resp. right) Azumaya algebra is left (resp. right) central;

(ii)

if, in addition, $\mathcal{V}$ admits also coequalizers, then any $\mathcal{V}$ algebra that is Azumaya on either side is central.

Proof. (i) follows by Theorem 4.25, while (ii) follows from (i) and Theorem 4.18.    ☐

Recall that for any $\mathcal{V}$-algebra $\mathcal{A}$, an ${\mathcal{A}}^e$-module M is $U_{{\mathcal{A}}^e}$-projective provided for morphisms $g:N\to L$ and $f:M\to L$ in ${}_{{\mathcal{A}}^e}\mathcal{V}$ with $U_{{\mathcal{A}}^e}(g)$ a split epimorphism, there exists an $h:M\to N$ in ${}_{{\mathcal{A}}^e}\mathcal{V}$ with $gh=f$. This is the case if and only if M is a retract of a (free) ${\mathcal{A}}^e$-module ${\mathcal{A}}^e\otimes X$ with some $X\in \mathcal{V}$ (e.g., [28]). We apply this in the characterization of separable algebras.

4.28 Proposition.

The following are equivalent for a $\mathcal{V}$-algebra $\mathcal{A}=(A,m,e)$:

(a)

$\mathcal{A}$ is a separable algebra;

(b)

$m:A\otimes A\to A$ has a section $\xi :A\to A\otimes A$ in $\mathcal{V}$, such that:

$$(A\otimes m)·(\xi \otimes A)=\xi ·m=(m\otimes A)·(A\otimes \xi );$$

(c)

the left ${\mathcal{A}}^e$-module $(A,m·(A\otimes m^{\tau }))$ is ${}_{{\mathcal{A}}^e}U$-projective;

(d)

the functor ${}_{{\mathcal{A}}^e}U:{}_{{\mathcal{A}}^e}\mathcal{V}\to \mathcal{V}$ is separable.

4.29 Proposition.

Consider $\mathcal{V}$-algebras $\mathcal{A}$ and $\mathcal{B}$, such that the unit $e:I\to B$ of $\mathcal{B}$ is a split monomorphism. If $\mathcal{A}\otimes \mathcal{B}$ is separable in $\mathcal{V}$, then $\mathcal{A}$ is also separable in $\mathcal{V}$.

Proof. Since I is a retract of B in $\mathcal{V}$, A is a retract of $A\otimes B$ in ${}_{{\mathcal{A}}^e}\mathcal{V}$. Since $A\otimes B$ is assumed to be separable in $\mathcal{V}$, $A\otimes B$ is a retract of ${(A\otimes B)}^e$ in ${}_{{(A\otimes B)}^e}\mathcal{V}$ and, hence, also in ${}_{A^e}\mathcal{V}$. Thus, A is a retract of $A^e\otimes B^e\simeq {(A\otimes B)}^e$ in ${}_{A^e}\mathcal{V}$. Since $A^e\otimes B^e={\varphi }_{{\mathcal{A}}^e}(B^e)$, it follows that $A^e\otimes B^e$ is ${}_{A^e}U$-projective, and since retracts of a ${}_{A^e}U$-projectives are ${}_{A^e}U$-projective, A is ${}_{A^e}U$-projective, and $\mathcal{A}$ is separable by Proposition 4.28.         ☐

Following [2], a finite object V in $\mathcal{V}$ is said to be a progenerator if the counit morphism $\mathrm{ev}:V^{*}\otimes V\to I$ is a split epimorphism. The following list describes some of its properties.

4.30 Proposition.

Assume $\mathcal{V}$ to admit equalizers and coequalizers. For an algebra $\mathcal{A}=(A,m,e)$ in $\mathcal{V}$ with A admitting a left adjoint $(A^{*},\mathrm{db},\mathrm{ev})$ (see 4.5), consider the following statements:

(1)

A is a progenerator;

(2)

the morphism $\mathrm{db}:I\to A\otimes A^{*}$ is a split monomorphism;

(3)

the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is separable;

(4)

the unit morphism $e:I\to A$ is a split monomorphism;

(5)

the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is conservative (monadic, comonadic);

(6)

$A\otimes A^{*}$ is a separable $\mathcal{V}$-algebra.

One always has $(1)\iff (2)\iff (3)\iff (4)\Rightarrow (5)$ and $(1)\Rightarrow (6)$.

If I is projective (w.r.t. regular epimorphisms) in $\mathcal{V}$, then $(5)\Rightarrow (1)$.

Proof. Since A admits a left adjoint $(A^{*},\mathrm{db},\mathrm{ev})$, the functor $A^{*}\otimes -:\mathcal{V}\to \mathcal{V}$ is left, as well as right adjoint to the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$. For any $V\in \mathcal{V}$, the composite:

$$V\stackrel{\mathrm{db}\otimes V}{\to }A\otimes A^{*}\otimes V\stackrel{{\tau }_{A^{*},A}^{-1}\otimes V}{\to }{A}^{*}\otimes A\otimes V$$

is the V-component of the unit of the adjunction $A\otimes -⊣A^{*}\otimes -:\mathcal{V}\to \mathcal{V}$, while the morphism $A^{*}\otimes A\otimes V\stackrel{\mathrm{ev}\otimes V}{\to }V$ is the V-component of the counit of the adjunction $A^{*}\otimes -⊣A\otimes -:\mathcal{V}\to \mathcal{V}$. To say that $\mathrm{db}:I\to A\otimes A^{*}$ (resp. $\mathrm{ev}:A^{*}\otimes A\to I$) is a split monomorphism (resp. epimorphism) is to say that the unit (resp. counit) of the adjunction $A\otimes -⊣A^{*}\otimes -$ (resp. $A^{*}\otimes -⊣A\otimes -$) is a split monomorphism (resp. epimorphism). From the observations in 2.17, one gets (1)⇔(2)⇔(3).

By Proposition 4.10, the properties listed in (5) are equivalent. Since $\mathcal{V}$ admits equalizers, it is Cauchy complete, and (3)⇒(5) follows from Proposition 3.16 in [18].

If $e:I\to A$ is a split monomorphism, then the natural transformation $e\otimes -:1_{\mathcal{V}}\to A\otimes -$ is a split monomorphism; applying Proposition 2.20 to the pair of functors $(A\otimes -,1_{\mathcal{V}})$ gives that the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is separable, proving (4)⇒(3).

If A is a progenerator, then $\mathrm{ev}:A^{*}\otimes A\to I$ has a splitting $\zeta :I\to A^{*}\otimes A$. Consider the composite:

$$\varphi :A\stackrel{\zeta \otimes A}{\to }{A}^{*}\otimes A\otimes A\stackrel{A^{*}\otimes m}{\to }{A}^{*}\otimes A\stackrel{\mathrm{ev}}{\to }I.$$

We claim that $\varphi ·e=1$. Indeed, we have:

$$\begin{array}{cc}\hfill \mathrm{ev}·A^{*}\otimes m·\zeta \otimes A·e& =\mathrm{ev}·A^{*}\otimes m·A^{*}\otimes A\otimes e·\zeta =\mathrm{ev}·\zeta =1.\hfill \end{array}$$

The first equality holds by naturality, the second one, since e is the unit for the $\mathcal{V}$-algebra $\mathcal{A}$, and the third one since, ζ is a splitting for $\mathrm{ev}:A^{*}\otimes A\to I$. Thus, $(2)$ implies $(4)$.

Now, if A is again a progenerator, then the morphism $\mathrm{ev}:A^{*}\otimes A\to I$ has a splitting $\zeta :I\to A^{*}\otimes A$, and direct inspection shows that the morphism:

$$\xi =A\otimes \zeta \otimes A^{*}:A\otimes A^{*}\to A\otimes A^{*}\otimes A\otimes A^{*}$$

is a splitting for the multiplication $A\otimes \mathrm{ev}\otimes A^{*}$ of the $\mathcal{V}$-algebra $\mathcal{A}\otimes {\mathcal{A}}^{*}$ satisfying condition (b) of Proposition 4.28. Thus, $\mathcal{A}\otimes {\mathcal{A}}^{*}$ is a separable $\mathcal{V}$-algebra, proving the implication (2)⇒(6).

Finally, suppose that I is projective (w.r.t. regular epimorphisms) in $\mathcal{V}$ and that the functor $A\otimes -:\mathcal{V}\to \mathcal{V}$ is monadic. Then, by Theorem 2.4 in [25], each component of the counit of the adjunction $A^{*}\otimes -⊣A\otimes -$ is a regular epimorphism. Since $\mathrm{ev}:A^{*}\otimes A\to I$ is the I-component of the counit, $\mathrm{ev}$ is a regular epimorphism and, hence, splits, since I is assumed to be projective w.r.t. regular epimorphisms. Thus, A is a progenerator. This proves the implication (5)⇒(1).      ☐

4.31 Theorem.

Let $\mathcal{V}$ be a braided monoidal category with equalizers and coequalizers. For an algebra $\mathcal{A}=(A,m,e)$ in $\mathcal{V}$, the following are equivalent:

(a)

$\mathcal{A}$ is a separable left Azumaya $\mathcal{V}$-algebra;

(b)

A is a progenerator, and the morphism ${\overline{\chi }}_0:A\otimes A\to A\otimes A^{*}$ in 4.16 (c) is an isomorphism between the $\mathcal{V}$-algebras ${\mathcal{A}}^e$ and ${\mathcal{S}}_{A,A^{*}}$;

(c)

$e:I\to A$ is a split monomorphism, and $(A,m·(A\otimes m^{\tau })){\in }_{{\mathcal{A}}^e}\mathcal{V}$ is a Galois module.

Proof. (a)⇔(c) In view of Proposition 4.28, this is a special case of 3.17.

(b)⇔(c) is an easy consequence of Proposition 4.30 and Theorem 4.16.      ☐

To bring back our general theory to the starting point, let R be a commutative ring with identity and ${\mathbb{M}}_R$ the category of R-modules. Then, for any $M,N\in {\mathbb{M}}_R$, there is the canonical twist map ${\tau }_{M,N}:M{\otimes }_{R}N\to N{\otimes }_{R}M$. Putting $[M,N]:={\mathrm{Hom}}_R(M,N)$, then $({\mathbb{M}}_R,-{\otimes }_R-,R,[-,-],\tau )$ is a symmetric monoidal closed category. We have the canonical adjunction ${\eta }^M,{\epsilon }^M:M{\otimes }_R-⊣[M,-]$.

4.32. Algebras in ${\mathbb{M}}_{\mathbf{R}}$.

For any R-algebra $\mathcal{A}=(A,m,e)$, ${\tau }_{A,A}:A{\otimes }_{R}A\to A{\otimes }_{R}A$ is an invertible (involutive) BD-law allowing for the definition of the (opposite) algebra ${\mathcal{A}}^{\tau }=(A,m·\tau ,e)$. The monad $A{\otimes }_R-$ is Azumaya provided the functor $K:{\mathbb{M}}_R\to {}_{A^e}\mathbb{M}$,

$$M⟼((A{\otimes }_{R}M,A{\otimes }_{R}A{\otimes }_{R}A{\otimes }_{R}M\stackrel{A{\otimes }_R{m}^{\tau }{\otimes }_{R}M}{\to }A{\otimes }_{R}A{\otimes }_{R}M\stackrel{m{\otimes }_{R}M}{\to }A{\otimes }_{R}M),$$

is an equivalence of categories. Obviously, this holds if and only if A is an Azumaya R-algebra in the usual sense. We have the commutative diagram:

(4.4)

where ${(e{\otimes }_R{A}^{\tau })}^{*}$ is the restriction of scalars functor induced by the ring morphism $e{\otimes }_R{A}^{\tau }:A^{\tau }\to A{\otimes }_R{A}^{\tau }$.

As is easily seen, for $(M,h)\in {}_{A^{\tau }}\mathbb{M}$, the $(M,h)$-component $t_{(M,h)}:A{\otimes }_{R}M\to [A,M]$ of the comonad morphism $t:{\varphi }_{{(A^{\tau })}_l}{U}_{{(A^{\tau })}_l}\to \widehat{[A,-]}$ corresponding to the functor $\overline{K}=\Psi ·K$, takes any element $a{\otimes }_{R}m$ to the map $b\mapsto h((ba){\otimes }_{R}m)$. Thus, writing $a·m$ for $h(a{\otimes }_{R}m)$, one has for $a,b\in A$ and $m\in M$,

$$t_{(M,h)}(a{\otimes }_{R}m)=(b\mapsto (ba)·m).$$

In particular, for any $N\in {\mathbb{M}}_R$, $t_{{\varphi }_{{(A^{\tau })}_l}(N)}(a{\otimes }_{R}b{\otimes }_{R}n)=(c\mapsto (bca)·n).$

Since the canonical morphism $i:R\to A$ factors through the center of A, it follows from Theorem 8.11 in [18] that the functor $A{\otimes }_R-:{\mathbb{M}}_R\to {}_A\mathbb{M}$ (and hence, also, $A^{\tau }{\otimes }_R-:{\mathbb{M}}_R\to {}_{A^{\tau }}\mathbb{M}$) is comonadic if and only if i is a pure morphism of R-modules. Applying Theorem 4.20 and using that K is an equivalence of categories if and only if $\overline{K}=\Psi ·K$ is so, we get several characterizations of Azumaya R-algebra.

4.33 Theorem.

An R-algebra A is an Azumaya R-algebra if and only if the canonical morphism $i:R\to A$ is a pure morphism of R-modules and one of the following holds:

(a)

for any $M\in {}_{A^{\tau }}\mathbb{M}$, there is an isomorphism:

$$A{\otimes }_{R}M\to [A,M],a{\otimes }_{R}m\mapsto [b\mapsto (ba)·m];$$

(b)

for any $N\in {\mathbb{M}}_R$, there is an isomorphism:

$$A{\otimes }_{R}A{\otimes }_{R}N\to [A,A{\otimes }_{R}N],a{\otimes }_{R}b{\otimes }_{R}n\mapsto [c\mapsto bca{\otimes }_{R}n];$$

(c)

$A_R$ is finitely generated projective, and there is an isomorphism:

$$A{\otimes }_{R}A\to [A,A],a{\otimes }_{R}b\mapsto [c\mapsto bca];$$

(d)

for any $(A,A)$-bimodule M, the evaluation map is an isomorphism:

$$A{\otimes }_R{M}^A\to M,a{\otimes }_{R}m\mapsto a·m.$$

Proof. (a) follows by Theorem 3.10; (b) and (c) are derived from Theorem 4.20.

(c) An R-module is finite in the monoidal category ${\mathbb{M}}_R$ if and only if it is finitely generated and projective over R and Theorem 4.15 applies.

(d) is a translation of Theorem 4.25 into the present context.      ☐

For a (von Neumann) regular ring R, $i:R\to A$ is always a pure R-module morphism, and hence, over such rings, (equivalent) Properties (a) to (d) are sufficient to characterize Azumaya algebras.

5. Azumaya Coalgebras in Braided Monoidal Categories

Throughout, $(\mathcal{V},\otimes ,I,\tau )$ will denote a strict monoidal braided category. The definition of coalgebras $\mathcal{C}=(C,\Delta ,\epsilon )$ in $\mathcal{V}$ is recalled in 4.4.

5.1. The coalgebra ${\mathcal{C}}^{\mathbf{e}}$.

Let $\mathcal{C}$ be a $\mathcal{V}$-coalgebra. The braiding ${\tau }_{C,C}:C\otimes C\to C\otimes C$ provides a comonad BD-law allowing for the definition of the opposite coalgebra ${\mathcal{C}}^{\tau }=(C^{\tau },{\Delta }^{\tau }={\tau }_{C,C}·\Delta ,{\epsilon }^{\tau }=\epsilon )$ and a coalgebra:

$${\mathcal{C}}^e:=(C\otimes C^{\tau },(C\otimes \tau \otimes C^{\tau })(\Delta \otimes {\Delta }^{\tau }),\epsilon \otimes \epsilon ).$$

With the induced distributive law of the comonad ${\mathcal{C}}_l$ over the comonad ${({\mathcal{C}}^{\tau })}_l$, we have an isomorphism of categories ${\mathcal{V}}^{{({\mathcal{C}}^{\tau })}_l{\mathcal{C}}_l}\simeq {\mathcal{V}}^{{({\mathcal{C}}^e)}_l}={}^{{\mathcal{C}}^e}\mathcal{V}$.

5.2 Definition.

(see 3.14) A $\mathcal{V}$-coalgebra $\mathcal{C}$ is said to be left Azumaya provided for the functor ${\mathcal{C}}_l=C\otimes -:\mathcal{V}\to \mathcal{V}$, the pair $({\mathcal{C}}_l,{\tau }_{C,C}\otimes -)$ is an Azumaya comonad, i.e., the comparison functor:

$${\overline{K}}_{\tau }:\mathcal{V}\to {}^{{\mathcal{C}}^e}\mathcal{V},V⟼(C\otimes V,C\otimes V\stackrel{\Delta \otimes V}{\to }C\otimes C\otimes V\stackrel{C\otimes {\Delta }^{\tau }\otimes V}{\to }C\otimes C\otimes C\otimes V),$$

is an equivalence of categories. It fits into the commutative diagram

(5.1)

$\mathcal{C}$ is said to be right Azumaya if the corresponding conditions for ${\mathcal{C}}_r=-\otimes C$ are satisfied.

Similar to 4.15, we have:

5.3 Proposition.

Let $\mathcal{C}=(C,\Delta ,\epsilon )$ be a coalgebra in a braided monoidal category $\mathcal{V}$. If $\mathcal{C}$ is left Azumaya, then C is finite in $\mathcal{V}$.

Proof. Suppose that a $\mathcal{V}$-coalgebra $\mathcal{C}$ is left Azumaya. Then, the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$ admits a right adjoint $[C,-]:\mathcal{V}\to \mathcal{V}$ by the dual of Proposition 3.4. Write ϑ for the composite $(C\otimes {\Delta }^{\tau })·\Delta :C\to C\otimes C\otimes C$. Then, for any $V\in \mathcal{V}$, ${\overline{K}}_{\tau }(V)=(C\otimes V,\vartheta \otimes V)$, and thus, the V-component of the left ${\mathcal{C}}^e$-comodule structure on the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$, induced by the commutative diagram (5.1), is the morphism $\vartheta \otimes V:C\otimes V\to C\otimes C\otimes C\otimes V$. From 2.14, we then see that the V-component $t_V$ of the comonad morphism induced by the above diagram is the composite:

$$C\otimes [C,V]\stackrel{\vartheta \otimes [C,V]}{\to }C\otimes C\otimes C\otimes [C,V]\stackrel{C\otimes C\otimes {({\mathrm{ev}}^C)}_V}{\to }C\otimes C\otimes V,$$

where ${\mathrm{ev}}^C$ is the counit of the adjunction $C\otimes -⊣[C,-]$.

Next, let ${\sigma }_V:[C,I]\otimes V\to [C,V]$ be the transpose of the morphism ${({\mathrm{ev}}^C)}_I\otimes V:C\otimes [C,I]\otimes V\to V$, and consider the diagram:

In this diagram the rectangle is commutative by the naturality of composition. Since ${\sigma }_V$ is the transpose of the morphism ${({\mathrm{ev}}^C)}_I\otimes V$, the transpose of ${\sigma }_V$, which is the composite $C\otimes [C,I]\otimes V\stackrel{C\otimes {\sigma }_V}{\to }C\otimes [C,V]\stackrel{{({\mathrm{ev}}^C)}_V}{\to }V$, is ${({\mathrm{ev}}^C)}_I\otimes V$. Hence, the triangle in the diagram is also commutative. Now, since:

$$(C\otimes C\otimes {({\mathrm{ev}}^C)}_I\otimes V)·(\vartheta \otimes [C,I]\otimes V)=t_I\otimes V,$$

it follows from the commutativity of the diagram that $t_I\otimes V=t_V·(C\otimes {\sigma }_V)$; since $\mathcal{C}$ is assumed to be left Azumaya, both $t_I$ and $t_V$ are isomorphisms, and one concludes that $C\otimes {\sigma }_V$ is an isomorphism. Moreover, the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$ is comonadic, hence conservative. It follows that ${\sigma }_V:[C,I]\otimes V\to [C,V]$ is an isomorphism for all $V\in \mathcal{V}$. Thus, the functor $[C,I]\otimes -:\mathcal{V}\to \mathcal{V}$ is also right adjoint to the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$. It is now easy to see that $[C,I]$ is right adjoint to C.     ☐

The dual of Theorem 3.5 provides the first characterizations of left Azumaya coalgebras.

5.4 Theorem.

For a $\mathcal{V}$-coalgebra $\mathcal{C}=(C,\Delta ,\epsilon )$, the following are equivalent:

(a)

$\mathcal{C}$ is a left Azumaya $\mathcal{V}$-coalgebra;

(b)

the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$ is comonadic, and the left ${({\mathcal{C}}^e)}_l$-comodule structure on it, induced by the commutative diagram (5.1), is Galois;

(c)

(i) C is finite with right dual $(C^{♯},{\mathrm{db}}^{\prime }:I\to C^{♯}\otimes C,{\mathrm{ev}}^{\prime }:C\otimes C^{♯}\to I)$; the functor $C\otimes -:\mathcal{V}\to \mathcal{V}$ is comonadic; and

(ii) the composite ${\overline{\chi }}_0:$

$$C\otimes C^{♯}\stackrel{\Delta \otimes C^{♯}}{\to }C\otimes C\otimes C^{♯}\stackrel{C\otimes \Delta \otimes C^{♯}}{\to }C\otimes C\otimes C\otimes C^{♯}\stackrel{C\otimes \tau \otimes C^{♯}}{\to }C\otimes C\otimes C\otimes C^{♯}\stackrel{C\otimes C\otimes {\mathrm{ev}}^{\prime }}{\to }C\otimes C$$

is an isomorphism (between the $\mathcal{V}$-coalgebras ${\mathfrak{S}}_{C,C^{♯}}$ and ${\mathcal{C}}^e$);

(d)

(i) C is finite with left dual $(C^{*},\mathrm{db}:I\to C\otimes C^{*},\mathrm{ev}:C^{*}\otimes C\to I)$, and the functor ${\varphi }_{{({\mathcal{C}}^{\tau })}_l}:\mathcal{V}\to {\mathcal{V}}^{{({\mathcal{C}}^{\tau })}_l}={}^{{\mathcal{C}}^{\tau }}\mathcal{V}$ is monadic; and

(ii) the composite $\overline{\chi }:$

$$C^{*}\otimes C\stackrel{C^{*}\otimes \Delta }{\to }{C}^{*}\otimes C\otimes C\stackrel{C^{*}\otimes \tau }{\to }{C}^{*}\otimes C\otimes C\stackrel{C^{*}\otimes \Delta \otimes C}{\to }{C}^{*}\otimes C\otimes C\otimes C\stackrel{\mathrm{ev}\otimes C\otimes C}{\to }C\otimes C$$

is an isomorphism.

Proof. (a) and (b) are equivalent by the dual of Theorem 3.5.

The equivalences (a)⇔(c) and (a)⇔(d) follow from Proposition 5.3 by dualizing the proofs of the corresponding equivalences in Theorem 4.16.        ☐

Similarly, the dual form of Theorem 4.16 yields conditions for right Azumaya coalgebras $\mathcal{C}$, that is making ${\mathcal{C}}_r=-\otimes C$ an Azumaya comonad. Dualizing Theorem 4.18 gives:

5.5 Theorem.

Let $\mathcal{C}=(C,\Delta ,\epsilon )$ be a $\mathcal{V}$-coalgebra in a braided monoidal category $\mathcal{V}$ with equalizers and coequalizers. Then, the following are equivalent:

(a)

$\mathcal{C}$ is a left Azumaya coalgebra;

(b)

the left ${\mathcal{C}}^e$-comodule $(C,(C\otimes {\Delta }^{\tau })·\Delta )$ is cofaithfully Galois;

(c)

there is an adjunction ${\mathrm{db}}^{\prime },{\mathrm{ev}}^{\prime }:C⊣C^{♯}$; the functor $-\otimes C:\mathcal{V}\to \mathcal{V}$ is comonadic; and the composite $\overline{\chi }$ in 5.4 (c) is an isomorphism;

(d)

the right ${}^e\mathcal{C}$-comodule $(C,({\Delta }^{\tau }\otimes C)·\Delta )$ is cofaithfully Galois;

(e)

$\mathcal{C}$ is a right Azumaya coalgebra.

Under suitable assumptions, the base category $\mathcal{V}$ may be replaced by a comodule category over a cocommutative coalgebra. For this, we consider the:

5.6. Cotensor product.

Suppose now that $\mathcal{V}=(\mathcal{V},\otimes ,I,\tau )$ is a braided monoidal category with equalizers and $\mathcal{D}=(D,{\Delta }_{\mathcal{D}},{\epsilon }_{\mathcal{D}})$ is a coalgebra in $\mathcal{V}$. If $(V,{\rho }^V)\in {\mathcal{V}}^{\mathcal{D}}$ and $(W,{\varrho }^W)\in {}^{\mathcal{D}}\mathcal{V}$, then their cotensor product (over $\mathcal{D}$) is the object part of the equalizer:

$$V{\otimes }^{D}W\stackrel{i_{V,W}}{\to }V\otimes W\underset{V\otimes {\varrho }^W}{\overset{{\rho }^V\otimes W}{\rightrightarrows }}V\otimes D\otimes W$$

Suppose, in addition, that either:

-

for any $V\in \mathcal{V}$, $V\otimes -:\mathcal{V}\to \mathcal{V}$ and $-\otimes V:\mathcal{V}\to \mathcal{V}$ preserve equalizers, or

-

$\mathcal{V}$ is Cauchy complete, and $\mathcal{D}$ is coseparable.

Each of these condition guarantee that for $V,W,X\in {}^{\mathcal{D}}{\mathcal{V}}^{\mathcal{D}}$,

• $V{\otimes }^{D}W\in {}^{\mathcal{D}}{\mathcal{V}}^{\mathcal{D}}$;
• the canonical morphism (induced by the associativity of the tensor product):

  $$(V{\otimes }^{D}W){\otimes }^{D}X\to V{\otimes }^D(W{\otimes }^{D}X)$$

  is an isomorphism in ${}^{\mathcal{D}}{\mathcal{V}}^{\mathcal{D}}$;
• ${(}^{\mathcal{D}}{\mathcal{V}}^{\mathcal{D}},-{\otimes }^D-,D,\tilde{\tau })$, where $\tilde{\tau }$ is the restriction of τ, is a braided monoidal category.

When $\mathcal{D}$ is cocommutative (i.e., ${\tau }_{D,D}·\Delta =\Delta$), then for any $(V,{\rho }^V)\in {}^{\mathcal{D}}\mathcal{V}$, the composite ${\rho }_1^V={\tau }_{D,V}^{-1}·{\rho }^V:V\to V\otimes D$, defines a right $\mathcal{D}$-comodule structure on V. Conversely, if $(W,{\varrho }^W)\in {\mathcal{V}}^{\mathcal{D}}$, then ${\varrho }_1^W={\tau }_{W,D}·{\varrho }^W:W\to D\otimes W$ defines a left $\mathcal{D}$-comodule structure on W. These two constructions establish an isomorphism between ${}^{\mathcal{D}}\mathcal{V}$ and ${\mathcal{V}}^{\mathcal{D}}$, and thus, we do not have to distinguish between left and right $\mathcal{D}$-comodules. In this case, the cotensor product of two $\mathcal{D}$-comodules is another $\mathcal{D}$-comodule, and cotensoring over $\mathcal{D}$ makes ${}^{\mathcal{D}}\mathcal{V}$ (as well as ${\mathcal{V}}^{\mathcal{D}}$) a braided monoidal category with unit $\mathcal{D}$.

5.7. $\mathcal{D}$-coalgebras.

Consider $\mathcal{V}$-coalgebras $\mathcal{C}=(C,{\Delta }_{\mathcal{C}},{\epsilon }_{\mathcal{C}})$ and $\mathcal{D}=(D,{\Delta }_{\mathcal{D}},{\epsilon }_{\mathcal{D}})$ with $\mathcal{D}$ cocommutative. A coalgebra morphism $\gamma :\mathcal{C}\to \mathcal{D}$ is called cocentral provided the diagram:

is commutative. When this is the case, $(\mathcal{C},\gamma )$ is called a $\mathcal{D}$-coalgebra.

To specify a ${}^{\mathcal{D}}\mathcal{V}$-coalgebra structure on an object $C\in \mathcal{V}$ is to give C a $\mathcal{D}$-coalgebra structure $(\mathcal{C}=(C,{\Delta }_{\mathcal{C}},{\epsilon }_{\mathcal{C}}),\gamma )$. Indeed, if $\gamma :\mathcal{C}\to \mathcal{D}$ is a cocentral morphism, $\mathcal{C}$ can be viewed as an object of ${}^{\mathcal{D}}\mathcal{V}$ (and ${\mathcal{V}}^{\mathcal{D}}$) via:

$$C\stackrel{{\Delta }_C}{\to }C\otimes C\stackrel{\gamma \otimes C}{\to }D\otimes C,(C\stackrel{{\Delta }_C}{\to }C\otimes C\stackrel{C\otimes \gamma }{\to }C\otimes D\stackrel{{\tau }_{C,D}}{\to }D\otimes C),$$

and ${\Delta }_C$ factors through the $i_{C,C}:C{\otimes }^{D}C\to C\otimes C$ by some (unique) morphism ${\Delta }_{\mathcal{C}}^{\prime }:C\to C{\otimes }_{D}C$, that is ${\Delta }_{\mathcal{C}}=i_{C,C}·{\Delta }_{\mathcal{C}}^{\prime }$.

The triple ${\mathcal{C}}_{\mathcal{D}}=(C,{\Delta }_{\mathcal{C}}^{\prime },\gamma )$ is a coalgebra in the braided monoidal category ${}^{\mathcal{D}}\mathcal{V}$.

Conversely, any ${}^{\mathcal{D}}\mathcal{V}$-coalgebra, $(C,{\Delta }_{\mathcal{C}}^{\prime }:C\to C{\otimes }^{D}C,{\epsilon }_{\mathcal{C}}:C\to D)$ induces a $\mathcal{V}$-coalgebra:

$$\mathcal{C}=(C,C\stackrel{{\Delta }_{\mathcal{C}}^{\prime }}{\to }C{\otimes }^{D}C\stackrel{i_{C,C}}{\to }C\otimes C,C\stackrel{{\epsilon }_{\mathcal{C}}}{\to }D\stackrel{{\epsilon }_D}{\to }I),$$

and the pair $(\mathcal{C},{\epsilon }_{\mathcal{C}})$ is a $\mathcal{D}$-coalgebra.

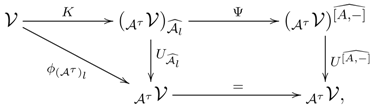
Related to any $\mathcal{V}$-coalgebra morphisms $\gamma :\mathcal{C}\to \mathcal{D}$, there is the corestriction functor:

$${(-)}_{\gamma }:{}^{\mathcal{C}}\mathcal{V}\to {}^{\mathcal{D}}\mathcal{V},(V,{\varrho }^V)\mapsto (V,(\gamma \otimes V)·{\varrho }^V),$$

and usually, one writes ${(V)}_{\gamma }=V$. If the category ${}^{\mathcal{C}}\mathcal{V}$ admits equalizers, then one has the coinduction functor:

$$C{\otimes }^D-:{}^{\mathcal{D}}\mathcal{V}\to {}^{\mathcal{C}}\mathcal{V},W\mapsto (C{\otimes }^{D}W,{\Delta }_{\mathcal{C}}{\otimes }^{D}W),$$

defining an adjunction:

$${(-)}_{\gamma }⊣C{\otimes }^D-:{}^{\mathcal{D}}\mathcal{V}\to {}^{\mathcal{C}}\mathcal{V}.$$

Considering $\mathcal{C}$ as a $(\mathcal{D},\mathcal{C})$-bicomodule by $C\stackrel{\Delta }{⟶}C{\otimes }_{R}C\stackrel{\gamma \otimes C}{⟶}D{\otimes }_{R}C$, the corestriction functor is isomorphic to $C{\otimes }^C-:{}^{\mathcal{C}}\mathcal{V}\to {}^{\mathcal{D}}\mathcal{V}$.

If $(\mathcal{C},\gamma )$ is a $\mathcal{D}$-coalgebra, then the category ${}^{{\mathcal{C}}_{\mathcal{D}}}{(}^{\mathcal{D}}\mathcal{V})$ can be identified with the category ${}^{\mathcal{C}}\mathcal{V}$, and modulo this identification, the functor

$$C_{\mathcal{D}}{\otimes }^D-:{}^{\mathcal{D}}\mathcal{V}\to {}^{{\mathcal{C}}_{\mathcal{D}}}({}^{\mathcal{D}}\mathcal{V})$$

corresponds to the coinduction functor $C{\otimes }^D-:{}^{\mathcal{D}}\mathcal{V}\to {}^{\mathcal{C}}\mathcal{V}.$

5.8. Azumaya $\mathcal{D}$-coalgebras.

Let $\mathcal{D}$ be a cocommutative $\mathcal{V}$-coalgebra. Then, a $\mathcal{D}$-coalgebra $\mathcal{C}=(C,{\Delta }_{\mathcal{C}},{\epsilon }_{\mathcal{C}})$ is said to be left Azumaya provided the comonad $({\mathcal{C}}_l,{\tilde{\tau }}_{C,C}{\otimes }^D-)$, where:

$${\mathcal{C}}_l=C{\otimes }^D-:{}^{\mathcal{D}}\mathcal{V}\to {}^{\mathcal{D}}\mathcal{V},$$

is Azumaya, i.e., (see 3.14), the comparison functor ${\overline{K}}_{\tilde{\tau }}:{}^{\mathcal{D}}\mathcal{V}\to {}^{C{\otimes }^D{C}^{\tilde{\tau }}}\mathcal{V}$ defined by:

$$V⟼(C{\otimes }^{D}V,C{\otimes }^{D}V\stackrel{{\Delta }_{\mathcal{C}}{\otimes }^{D}V}{\to }C{\otimes }^{D}C{\otimes }^{D}V\stackrel{C{\otimes }^D{\Delta }_{\mathcal{C}}^{\tilde{\tau }}{\otimes }^{D}V}{\to }C{\otimes }^{D}C{\otimes }^{D}V)$$

is an equivalence of categories. In this setting, specializing Theorem 5.4 yields various characterizations of Azumaya $\mathcal{D}$-coalgebras. For vector space categories, Azumaya $\mathcal{D}$-coalgebras $\mathcal{C}$ over a cocommutative coalgebra $\mathcal{D}$ (over a field) were defined and characterized in Theorem 3.14 in [7].

Now, let R be again a commutative ring with identity and ${\mathbb{M}}_R$ the category of R-modules. As an additional notion of interest, the dual algebra of a coalgebra comes in.

5.9. Coalgebras in ${\mathbb{M}}_{\mathbf{R}}$.

An R-coalgebra $\mathcal{C}=(C,\Delta ,\epsilon )$ consists of an R-module C with R-linear maps comultiplication $\Delta :C\to C{\otimes }_{R}C$ and counit $\epsilon :C\to R$ subject to coassociativity and counitality conditions. $C{\otimes }_R-:{\mathbb{M}}_R\to {\mathbb{M}}_R$ is a comonad, and it is customary to write ${}^{\mathcal{C}}\mathbb{M}:={\mathbb{M}}_R^{C\otimes -}$ for the category of left $\mathcal{C}$-comodules. We denote by ${\mathrm{Hom}}^C(M,N)$ the comodule morphisms between $M,N\in {}^{\mathcal{C}}\mathbb{M}$. In general, ${}^{\mathcal{C}}\mathbb{M}$ need not be a Grothendieck category, unless $C_R$ is a flat R-module (e.g., 3.14 in [29]).

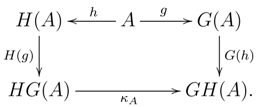
The dual module $C^{*}={\mathrm{Hom}}_R(C,R)$ has an R-algebra structure by defining for $f,g\in C^{*}$, $f*g=(g\otimes f)·\Delta$ (the definition opposite to 1.3 in [29]), yielding the monad ${\mathcal{C}}^{*}=(C^{*},*.{\epsilon }^{*})$, and there is a faithful functor:

$$\Phi :{}^{\mathcal{C}}\mathbb{M}\to {}_{{\mathcal{C}}^{*}}\mathbb{M},(M,\varrho )\mapsto C^{*}{\otimes }_{R}M\stackrel{C^{*}\otimes \varrho }{\to }{C}^{*}{\otimes }_{R}C\otimes M\stackrel{\mathrm{ev}\otimes M}{\to }M,$$

where $\mathrm{ev}$ denotes the evaluation map. The functor Φ is full if and only if for any $N\in {\mathbb{M}}_R$,

$${\alpha }_N:C{\otimes }_{R}N\to {\mathrm{Hom}}_R(C^{*},N),c\otimes n\mapsto [f\mapsto f(c)n],$$

is injective, and this is equivalent to $C_R$ being locally projective (α-condition, e.g., 4.2 in [29]). In this case, ${}^{\mathcal{C}}\mathbb{M}$ can be identified with the full subcategory $\sigma \left[{}_{{\mathcal{C}}^{*}}C\right]\subset {}_{{\mathcal{C}}^{*}}\mathbb{M}$ subgenerated by C as ${\mathcal{C}}^{*}$-module (see [29,30]).

The R-module structure of C is of considerable relevance for the related constructions, and for convenience, we recall:

5.10 Remark.

For $C_R$ the following are equivalent:

(a)

$C_R$ is finitely generated and projective;

(b)

$C{\otimes }_R-:{\mathbb{M}}_R\to {\mathbb{M}}_R$ has a left adjoint;

(c)

${\mathrm{Hom}}_R(C,-):{\mathbb{M}}_R\to {\mathbb{M}}_R$ has a right adjoint;

(d)

$C^{*}{\otimes }_R-\to {\mathrm{Hom}}_R(C,-),f{\otimes }_R-\mapsto (c\mapsto f(c)·-),$ is a (monad) isomorphism;

(e)

$C{\otimes }_R-\to {\mathrm{Hom}}_R(C^{*},-),c{\otimes }_R-\mapsto (f\mapsto f(c)·-),$ is a (comonad) isomorphism;

(f)

$\Phi :{}^{\mathcal{C}}\mathbb{M}\to {}_{{\mathcal{C}}^{*}}\mathbb{M}$ is a category isomorphism.

If this holds, there is an algebra anti-isomorphism ${\mathrm{End}}_R(C)\simeq {\mathrm{End}}_R(C^{*})$ and we denote the canonical adjunction by ${\eta }^C,{\epsilon }^C:C{\otimes }_R-⊣C^{*}{\otimes }_R-$.

5.11. The coalgebra ${\mathcal{C}}^{\mathbf{e}}$.

As in 5.1, the twist map ${\tau }_{C,C}:C{\otimes }_{R}C\to C{\otimes }_{R}C$ provides an (involutive) comonad BD-law allowing for the definition of the opposite coalgebra ${\mathcal{C}}^{\tau }=(C^{\tau },{\Delta }^{\tau },{\epsilon }^{\tau })$ and a coalgebra:

$${\mathcal{C}}^e:=(C{\otimes }_R{C}^{\tau },(C{\otimes }_R\tau {\otimes }_R{C}^{\tau })(\Delta {\otimes }_R{\Delta }^{\tau }),\epsilon {\otimes }_R\epsilon ).$$

The category ${}^{{\mathcal{C}}^e}\mathbb{M}$ of left ${\mathcal{C}}^e$-comodules is just the category of $(C,C)$-bicomodules (e.g., [31], 3.26 in [29]). A direct verification shows that the endomorphism algebra of C as a ${\mathcal{C}}^e$-comodule is just the center of $C^{*}$, that is,

$$Z(C^{*})={\mathrm{Hom}}^{{\mathcal{C}}^e}(C,C)\subset {}^{\mathcal{C}}\mathrm{Hom}(C,C)\simeq C^{*}.$$

If $C_R$ is locally projective, an easy argument shows that $C{\otimes }_{R}C$ is also locally projective as an R-module, and then, ${}^{{\mathcal{C}}^e}\mathbb{M}$ is a full subcategory of ${}_{{({\mathcal{C}}^e)}^{*}}\mathbb{M}$.

5.12 Definition.

An R-coalgebra $\mathcal{C}$ is said to be an Azumaya coalgebra provided $(C{\otimes }_R-,{\tau }_{C,C}{\otimes }_R-)$ is an Azumaya comonad (on ${\mathbb{M}}_R$), i.e., (see 3.14) the comparison functor $K:{\mathbb{M}}_R\to {}^{{\mathcal{C}}^e}\mathbb{M}$ defined by:

$$M⟼(C{\otimes }_{R}M,C{\otimes }_{R}M\stackrel{\Delta {\otimes }_{R}M}{\to }C{\otimes }_{R}C{\otimes }_{R}M\stackrel{C\otimes {\Delta }^{\tau }{\otimes }_{R}M}{\to }C\otimes C{\otimes }_{R}C{\otimes }_{R}M)$$

is an equivalence of categories. We have the commutative diagram:

By Proposition 2.15, the functor K is an equivalence provided:

(i)

the functor $C{\otimes }_R-:{}_R\mathbb{M}\to {}_R\mathbb{M}$ is comonadic, and

(ii)

the induced comonad morphism $C{\otimes }_R{\mathrm{Hom}}_R(C,-)\to {\mathcal{C}}^e{\otimes }_R-$

is an isomorphism.

If $R\simeq {\mathrm{End}}^{{\mathcal{C}}^e}(C)\simeq Z(C^{*})$, the isomorphism in (ii) characterizes C as a ${\mathcal{C}}^e$-Galois comodule as defined in 4.1 in [32], and if $C_R$ is finitely generated and projective, the condition reduces to an R-coalgebra isomorphism $C{\otimes }_R{C}^{*}\simeq C^e$.

An R-coalgebra $\mathcal{C}=(C,\Delta ,\epsilon )$ is said to be coseparable provided $C{\otimes }_R-:{\mathbb{M}}_R\to {\mathbb{M}}_R$ is a separable comonad. This is equivalent to requiring $\Delta :C\to C{\otimes }_{R}C$ to split in ${}^{{\mathcal{C}}^e}\mathbb{M}$. For more characterizations of these coalgebras, we refer to Section 3 and 3.29 in [29].

For any coseparable coalgebra $\mathcal{C}$, $Z(C^{*})$ is a direct summand of $C^{*}$.

Indeed, let $\omega :C{\otimes }_{R}C\to C$ denote the splitting morphism for Δ; we obtain the splitting sequence of $Z(C^{*})$-modules:

$$C^{*}\simeq {\mathrm{Hom}}^{{\mathcal{C}}^e}(C,C{\otimes }_{R}C)\stackrel{{\mathrm{Hom}}^{{\mathcal{C}}^e}(C,\omega )}{\to }{\mathrm{Hom}}^{{\mathcal{C}}^e}(C,C)\simeq Z(C^{*}).$$

For an Azumaya coalgebra $\mathcal{C}$, the free functor ${\varphi }_{{({\mathcal{C}}^{\tau })}_l}:{\mathbb{M}}_R\to {}^{{\mathcal{C}}^{\tau }}\mathbb{M}$ is monadic by the dual of Theorem 3.5, and hence, in particular, it is conservative. It then follows that, for each $X\in {\mathbb{M}}_R$, the morphism $\epsilon {\otimes }_{R}X:C{\otimes }_{R}X\to X$ is surjective. For $X=R$, this yields that $\epsilon :C\to R$ is surjective (hence, splitting). By Theorem 3.17, this means that $\mathcal{C}$ is also a coseparable coalgebra.

It follows from the general Hom-tensor relations that the functor $K:{\mathbb{M}}_R\to {}^{{\mathcal{C}}^e}\mathbb{M}$ has a right adjoint ${}^{{\mathcal{C}}^e}\mathrm{Hom}(C,-):{}^{{\mathcal{C}}^e}\mathbb{M}\to {\mathbb{M}}_R$ (e.g., 3.9 in [29]), and we denote the unit and counit of this adjunction by $\underline{\eta }$ and $\underline{\epsilon }$, respectively.

Besides the characterizations derived from Theorem 5.4, we have from Theorem 3.17:

5.13. Characterization of Azumaya coalgebras.

For an R-coalgebra $\mathcal{C}$, the following are equivalent:

(a)

$\mathcal{C}$ is an Azumaya coalgebra;

(b)

(i)

${\underline{\epsilon }}_X:C{\otimes }_R{}^{{\mathcal{C}}^e}\mathrm{Hom}(C,X)\to X$ is an isomorphism for any $X\in {}^{{\mathcal{C}}^e}\mathbb{M}$,

(ii)

${\underline{\eta }}_M:M\mapsto {}^{{\mathcal{C}}^e}\mathrm{Hom}(C,C{\otimes }_{R}M)$ is an isomorphism for any $M\in {\mathbb{M}}_R$.

(c)

C is a ${\mathcal{C}}^e$-Galois comodule; $C^{*}$ is a central R-algebra; and the functor $C{\otimes }_R-:{}_R\mathbb{M}\to {}_R\mathbb{M}$ is comonadic;

(d)

${\mathcal{C}}^{*}$ is an Azumaya algebra.

As shown in Proposition 5.3, an Azumaya coalgebra $\mathcal{C}$ is finite in ${\mathbb{M}}_R$, that is $C_R$ is finitely generated and projective (see Remark 5.10). Coalgebras $\mathcal{C}$ with $C_R$ finitely generated and projective for which $C^{*}$ is an Azumaya R-algebra were investigated by Sugano in [8]. As an easy consequence, he also observed that an R-algebra $\mathcal{A}$ with $A_R$ finitely generated and projective is Azumaya if and only if $A^{*}$ is an Azumaya coalgebra.