The Yang-Baxter Equation, (Quantum) Computers and Unifying Theories

Abstract

Quantum mechanics has had an important influence on building computers; nowadays, quantum mechanics principles are used for the processing and transmission of information. The Yang-Baxter equation is related to the universal gates from quantum computing and it realizes a unification of certain non-associative structures. Unifying structures could be seen as structures which comprise the information contained in other (algebraic) structures. Recently, we gave the axioms of a structure which unifies associative algebras, Lie algebras and Jordan algebras. Our paper is a review and a continuation of that approach. It also contains several geometric considerations.

1. Introduction

The importance of computers these days is so big that we could call our times the “computers era”. Quantum mechanics has had an important influence on building computers; for example, it led to the production of transistors. At present, quantum mechanics laws are used for the processing and transmission of information. The first quantum computer (which uses principles of quantum mechanics) was sold to the aerospace and security of a defense company, Lockheed Martin. The manufacturing company, D-Wave, founded in 1999 and called “a company of quantum computing”, promised to perform professional services for the computer maintenance as well. The quantum computer can address issues related to number theory and optimization, which require large computational power. An example is the Shor’s algorithm, a quantum algorithm that determines quickly and effectively the prime factors of a big number. With enough qubii, such a computer could use the Shor’s algorithm to break algorithms encryption used today.

Non-associative algebras are currently a research direction in fashion ([1], and the references therein). There are two important classes of non-associative structures: Lie structures and Jordan structures [2]. Various Jordan structures play an important role in quantum group theory and in fundamental physical theories [3]. Associative algebras and Lie algebras can be unified at the level of Yang-Baxter structures. A new unification for associative algebras, Jordan algebras and Lie algebras, was obtained recently [4], and we present further results in this paper.

Several papers published in the open access journal Axioms deal with the Yang-Baxter equation ( [5] and the references therein). The Yang-Baxter equation can be interpreted in terms of combinatorial logical circuits, and, in logic, it represents some kind of compatibility condition, when working with many logical sentences in the same time. This equation is also related to the theory of universal quantum gates and to quantum computers (for example, [6]). It has many applications in quantum groups and knot theory.

The organization of the current paper is as follows. In the next section we give the preliminaries and some interpretations of the Yang-Baxter equation in geometry. Section 3 deals with computer programs and interpretations of this equation in computer science. In Section 4, we discuss the applications of the Yang-Baxter equation in quantum groups and knot theory (with some remarks about universal gates). Section 5 is about unification theories for non-associative algebras, and their connections with the previous sections. A short conclusion section ends our paper.

2. Geometrical Interpretations of the Yang-Baxter Equation

All tensor products will be defined over the field k, and for V a k-space, we denote by τ : V ⊗ V → V ⊗ V the twist map defined by $\tau (v\otimes w)=w\otimes v$, and by $I:V\to V$ the identity map of the space V.

For $R:V\otimes V\to V\otimes V$ a k-linear map, let $R^{12}=R\otimes I,R^{23}=I\otimes R,R^{13}=(I\otimes \tau )(R\otimes I)(I\otimes \tau )$.

Definition 2.1.

A Yang-Baxter operator is k-linear map $R:V\otimes V\to V\otimes V$, which is invertible, and it satisfies the braid condition (the Yang-Baxter equation):

$$R^{12}\circ R^{23}\circ R^{12}=R^{23}\circ R^{12}\circ R^{23}$$

(1)

An important observation is that if R satisfies (1) then both $R\circ \tau$ and $\tau \circ R$ satisfy the quantum Yang-Baxter equation (QYBE):

$$R^{12}\circ R^{13}\circ R^{23}=R^{23}\circ R^{13}\circ R^{12}$$

(2)

Thus, the Equations (1) and (2) are equivalent.

There is a similar terminology for the set-theoretical Yang-Baxter equation, for which V is replaced by a set and the tensor product by the Cartesian product.

Let us now consider the interpretations of the Yang-Baxter equation in geometry.

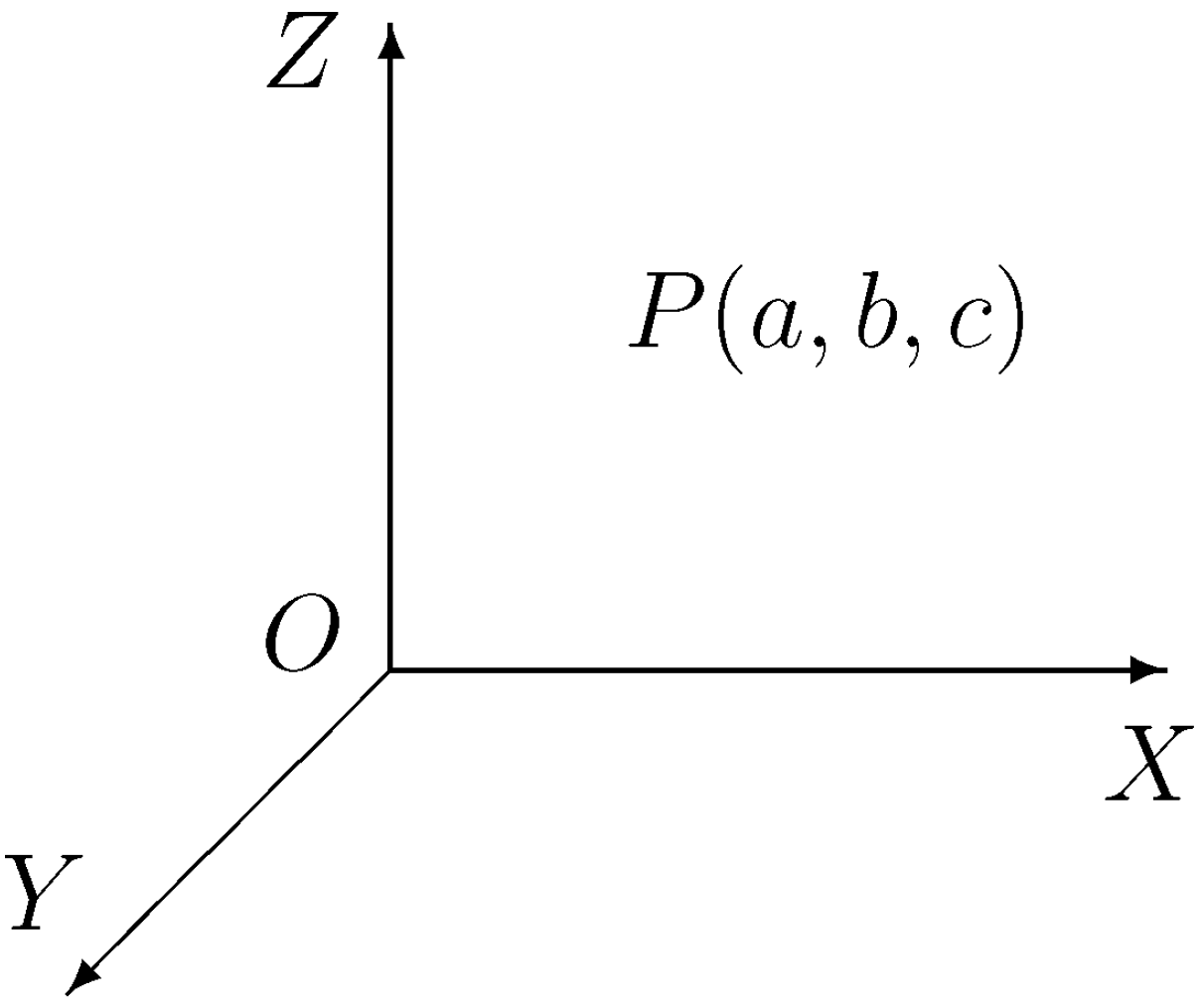
Figure 1. A three dimensional Cartesian coordinate system.

Figure 1. A three dimensional Cartesian coordinate system.

The symmetries of the point $P(a,b,c)$ (from Figure 1) about the axes $OX,OY,OZ$ are defined as follows: $S_{OX}(a,b,c)=(a,-b,-c)$, $S_{OY}(a,b,c)=(-a,b,-c)$, $S_{OZ}(a,b,c)=(-a,-b,c)$.

They form a group isomorphic with Klein’s group: $\{I,S_{OX},S_{OY},S_{OZ}\}$.

The symmetries of the point $P(a,b,c)$ about the planes $XOY,XOZ,YOZ$ are defined as follows:

$S_{XOY}(a,b,c)=(a,b,-c)$, $S_{XOZ}(a,b,c)=(a,-b,c)$, $S_{YOZ}(a,b,c)=(-a,b,c)$.

One could check the following instances of the Yang-Baxter equation:

$$S_{XOY}\circ S_{XOZ}\circ S_{YOZ}=S_{YOZ}\circ S_{XOZ}\circ S_{XOY}$$

(3)

$$S_{OX}\circ S_{OY}\circ S_{OZ}=S_{OZ}\circ S_{OY}\circ S_{OX}$$

(4)

Remark 2.2.

Let us observe that $S_{OX}\circ S_{OY}\circ S_{OZ}=I{d}_{k^3}$, and we can generalize the symmetries about the axes as follows: $S_{OX}^{\prime }(a,b,c)=(a,pb,qc)$, $S_{OY}^{\prime }(a,b,c)=(pa,b,qc)$, $S_{OZ}^{\prime }(a,b,c)=(pa,qb,c)$, for $p,q\in k$, such that $S_{OX}^{\prime }\circ S_{OY}^{\prime }\circ S_{OZ}^{\prime }=S_{OZ}^{\prime }\circ S_{OY}^{\prime }\circ S_{OX}^{\prime }$. This is a generalization for the Equation (4) as well.

It can be proved that the only rotation operators R which satisfy Equation (2) are the identity and the operator related to $S_{OX},S_{OY}$ and $S_{OZ}$.

3. The Yang-Baxter Equation in Computer Science

The Yang-Baxter equation can be interpreted in terms of combinatorial logical circuits [7]. It is also related to the theory of universal quantum gates and to the quantum computers [6,8].

In logic, it represents some kind of compatibility condition, when working with many logical sentences at the same time. Let us consider three logical sentences $p,q,r$. Let us suppose that if all of them are true, then the conclusion A could be drawn, and if $p,q,r$ are all false then the conclusion C can be drawn; in other cases, we say that the conclusion B is true. Modeling this situation by the map R, defined by $(p,q)\mapsto (p^{\prime }=p\vee q,q^{\prime }=p\wedge q)$, helps to comprise our analysis: we can apply R to the pair $(p,q)$, then to $(q^{\prime },r)$, and, finally to $(p^{\prime },q^{″})$. The Yang-Baxter equation explains that the order in which we start this analysis is not important; more explicitly, in this case, it states that $({\left(p^{\prime }\right)}^{\prime },q^{‴},r^{\prime })=(p^{\prime },q^{‴},{\left(r^{\prime }\right)}^{\prime })$.

Another interpretation of the Yang-Baxter equation is related to the algorithms and computer programs which order sequences of numbers. For example, the core of the Program 1 is related to the left hand side of Equation (2).

Program 1. Sorting by direct selection.

# include 〈iostream〉 int L,n,j,aux,i, sir[20],a,b; int main() { std::cout ≪ "You may choose how many numbers will be compared"; std::cin ≫L; int sir[L]; int sir2[L]; for (n=1;n≤L;n++) { std::cout≪"Please, give the numbers A["≪n≪"]="; std::cin≫sir[n]; std::cout≪" "≪endl; } std::cout≪"We are now ordering the given numbers!"; std::cout≪“ ”≪std::endl; for (i=1;i≤L-1;i++) for (j=i+1;j≤L;j++) if (sir[i]≥sir[j]) { aux=sir[i]; sir[i]=sir[j]; sir[j]=aux; } for (n=1;n≤L;n++) std::cout≪ “ ”≪sir[n]; std::cout≪ “ ”≪std::endl; system(“PAUSE”); return EXIT–SUCCESS; }

The Program 2 is related to the right hand side of (1).

Ordering three numbers is related to the following common solution of the Equations (1) and (2): $R(a,b)=\left(min\right(a,b),max(a,b\left)\right)$.

Program 2. The core of the “Bubble sort” program.

int m, aux; m=L; while (m) { for (int i=1; i≤L-1; i++) if (a[L-i] ≥ a[L+1-i]) { aux = a[L+1-i]; a[L+1-i] = a[L-i]; a[L-i] = aux; } m - -; }

Since R can be extended to a braiding in a certain monoidal category, we obtain an interpretation for the case when we order more numbers.

The “divide et impera” algorithm for finding the maximum of sequence of numbers could be related to Yang-Baxter systems and to the gluing procedure from [9].

4. The Yang-Baxter Equation in Quantum Groups and Knot Theory

For A be a (unitary) associative k-algebra, and $\alpha ,\beta ,\gamma \in k$, the authors of [10] defined the k-linear map:

$$R_{\alpha ,\beta ,\gamma }^A:A\otimes A\to A\otimes A,R_{\alpha ,\beta ,\gamma }^A(a\otimes b)=\alpha ab\otimes 1+\beta 1\otimes ab-\gamma a\otimes b$$

(5)

which is a Yang-Baxter operator if and only if one of the following cases holds:

(i) $\alpha =\gamma \ne 0,\beta \ne 0$; (ii) $\beta =\gamma \ne 0,\alpha \ne 0$; (iii) $\alpha =\beta =0,\gamma \ne 0$.

The link invariant associated to the operator (5) is the Alexander polynomial of knots [11,12].

For $(L,[,\left]\right)$ a Lie super-algebra over k, $z\in Z\left(L\right)=\{z\in L:[z,x]=0\forall x\in L\},\left|z\right|=0$ and $\alpha \in k$, the authors of the papers [13] and [14] defined the following Yang-Baxter operator:

$${\varphi }_{\alpha }^L:L\otimes L⟶L\otimes L,x\otimes y\mapsto \alpha [x,y]\otimes z+{(-1)}^{\left|x\right|\left|y\right|}y\otimes x$$

(6)

Remark 4.1.

In dimension two, $R_{\alpha ,\beta ,\alpha }^A\circ \tau$, can be expressed as:

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 1-q& q& 0\\ \eta & 0& 0& -q\end{array}\right)$$

(7)

where $\eta \in \{0,1\}$, and $q\in k-\left\{0\right\}$. For $\eta =0$ and $q=1$, $R_{\alpha ,\beta ,\alpha }^A$ becomes:

$$\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& -1\end{array}\right)$$

(8)

which is a universal gate (according to [8]), and it is related to the CNOT gate:

$$CNOT=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right)$$

(9)

Remark 4.2.

The matrix (8) can be interpreted as a sum of Yang-Baxter operators, using the techniques of [9].

Remark 4.3.

Using Theorem 3.1 (i) and Remark 3.3 from [15], we can construct a bialgebra structure associated to the operator $R_{\alpha ,\beta ,\gamma }^A(a\otimes b)=\alpha ab\otimes 1+\beta 1\otimes ab-\gamma a\otimes b,$ if one of the following cases holds: (i) $\alpha =\gamma \ne 0,\beta \ne 0$; (ii) $\beta =\gamma \ne 0,\alpha \ne 0$; (iii) $\alpha =\beta =0,\gamma \ne 0$.

For $\gamma =-1$ and $\alpha =\beta =0$, this is the tensor algebra $T\left(A\right)$ associated to the underlying vector space of the algebra A.

For $a,b\in T^1\left(A\right)=A$, we have: $\mu (a\otimes b)=\alpha ab\otimes 1+\beta 1\otimes ab-\gamma a\otimes b\in T^2\left(A\right).$

For $a\otimes a^{\prime }\in T^2\left(A\right)=A\otimes A$ and $b\in T^1\left(A\right)=A$, we have:

$\mu ((a\otimes a^{\prime })\otimes b)=R^{12}\circ R^{23}(a\otimes a^{\prime }\otimes b)\in T^3\left(A\right).$

For $a\in T^1\left(A\right)=A$ and $b\otimes b^{\prime }\in T^2\left(A\right)$, we have:

$\mu (a\otimes (b\otimes b^{\prime })=R^{23}\circ R^{12}(a\otimes b\otimes b^{\prime })\in T^3\left(A\right).$

In the same manner, we can compute other products.

5. Unification of Non-Associative Structures

The Equations (5) and (6) lead to the unification of associative algebras and Lie (super)algebras in the framework of Yang-Baxter structures [2,16]. On the other hand, for the invertible elements in a Jordan algebra, one can associate a symmetric space ([17], page 58), and, therefore, a Yang-Baxter operator. Thus, the Yang-Baxter equation can be thought as a unifying equation.

The first isomorfism theorem for groups (algebras) and the first isomorfism theorem for Lie algebras, can be unified as an isomorphism theorem for Yang-Baxter structures [18].

We present another way to unify non-associative structures below.

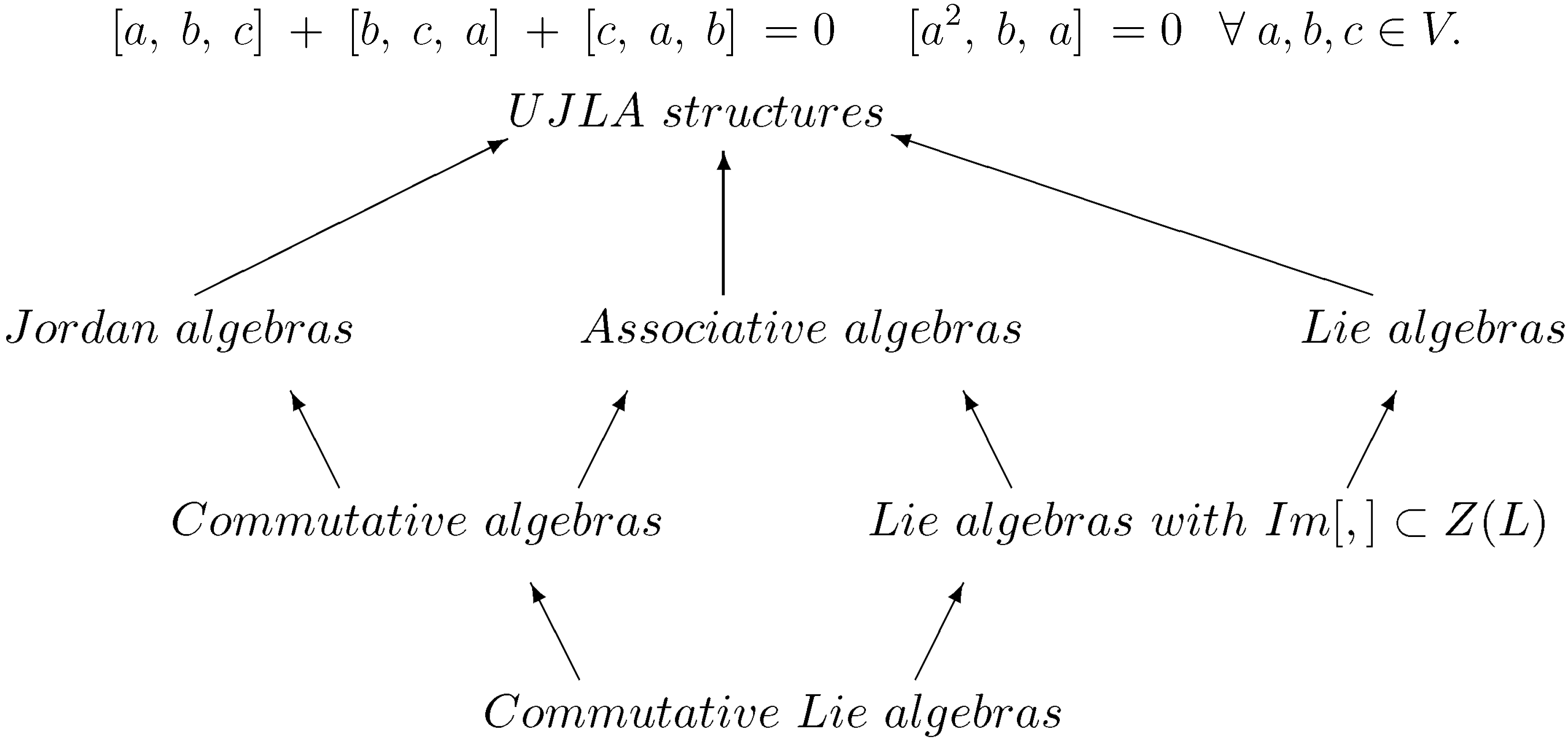
Definition 5.1.

For the vector space V, let $\eta :V\otimes V\to V,\eta (a\otimes b)=ab,$ be a linear map which satisfies:

$$\left(ab\right)c+\left(bc\right)a+\left(ca\right)b=a\left(bc\right)+b\left(ca\right)+c\left(ab\right)\forall a,b,c\in V$$

(10)

$$\left(a^{2}b\right)a=a^2\left(ba\right),\forall a,b,c\in V$$

(11)

Then, $(V,\eta )$ is called a “UJLA structure”.

Remark 5.2.

The UJLA structures unify Jordan algebras, Lie algebras and (non-unital) associative algebras [4]. Results for UJLA structures could be “decoded” in properties of Jordan algebras, Lie algebras or (non-unital) associative algebras.

Remark 5.3.

An anti-commutative UJLA structure is a Lie algebra.

Obviously, a commutative UJLA structure is a Jordan algebra.

Remark 5.4.

Let W be a vector space spanned by a and b, which are linearly independent. Let $\theta :W\otimes W\to W,\theta (x\otimes y)=xy$, be a linear map with the property: $a^2=b,b^2=a.$

If $\theta$ also satisfies the Relations (10) and (11), then $(W,\theta )$ is a (non-unital) associative algebra.

Remark 5.5.

For $(A,\theta )$, where $\theta :A\otimes A\to A,\theta (a\otimes b)=ab$, a (non-unital) associative algebra, and $\alpha ,\beta \in k$, we define a new product ${\theta }^{\prime }(a\otimes b)=\alpha ab+\beta ba$.

If $\alpha =\frac{1}{2}$ and $\beta =\frac{1}{2}$, then $(A,{\theta }^{\prime })$ is a Jordan algebra.

If $\alpha =1$ and $\beta =-1$, then $(A,{\theta }^{\prime })$ is a Lie algebra.

If $\alpha =0$ and $\beta =1$, then $(A,{\theta }^{\prime })$ is the opposite algebra of $(A,\theta )$.

Obviously, if $\alpha =1$ and $\beta =0$, then $(A,{\theta }^{\prime })$ is the algebra $(A,\theta )$.

If we put no restrictions on α and β, then $(V,\theta )$ is a UJLA structure.

The importance of the results of this section are explained in Figure 2.

Figure 2. UJLA structures in terms of associators and their interpretation.

Figure 2. UJLA structures in terms of associators and their interpretation.

6. Conclusions

The current paper is written in a transdiscipinary [19] fashion, because the Yang-Baxter equation is a transdisciplinary equation.

An explanation of the fact that the study of Jordan structures and their applications is at present a wide-ranging field of mathematical research could be the following: at the beginning, mathematics was associative and commutative, then (after the invention of matrices) it became associative and non-commutative, and now (after the invention of non-associative structures) it becomes non-associative and non-commutative [20].

Concepts as co-composition, coalgebra, coassociativity and Yang-Baxter structures play an important role in relationship with the non-associative structures. In fact, the Yang-Baxter equation can be thought as an unifying equation for dual structures [21].