Abstract
We present a general formalism for giving a measure space paired with a separable Hilbert space a quantum version based on a normalized positive operator-valued measure. The latter are built from families of density operators labeled by points of the measure space. We especially focus on various probabilistic aspects of these constructions. Simple or more elaborate examples illustrate the procedure: circle, two-sphere, plane and half-plane. Links with Positive-Operator Valued Measure (POVM) quantum measurement and quantum statistical inference are sketched.
1. Introduction
In this paper, we propose a quantum analysis, generally non-commutative, of a measure space based on a (normalized) positive-operator valued measure ((N)POVM) (in order not to spoil the text with too many acronyms, we will keep “POVM” in our paper to designate a normalized positive operator-valued measure) built from a density matrix or operator (in the quantum mechanics terminology) acting on some separable Hilbert space. One key aspect of the procedure is its probabilistic nature. Moreover, beyond the common mathematical language, our approach has or might have some deep connection with quantum measurement based on POVM [1], quantum probability (see, for instance, [2] and the references therein) or quantum statistical inference (see, for instance, [3] and the references therein). In this respect, we recommend the clear and concise introduction to the mathematics of quantum physics by Kuperberg [4].
Our work lies in the continuation of recent ones concerning what we named integral quantization [5,6,7,8,9] and leading to applications shedding new light on the still problematic question of the relation between classic and quantum worlds. The so-called coherent state (CS), or Berezin, or Klauder, or anti-Wick, or Toeplitz quantizations are particular cases of those integral quantizations of various measure sets.
Our conception of quantization rests upon a trivial observation. We notice that the formalism of classical physics rests upon highly abstract mathematical models, mainly since the invention of infinitesimal calculus, giving us the impression that improbable objects, like material phase space points, are accessible to measurements. It is true that with an excellent approximation, most of the physical phenomenon at our scale can be efficiently apprehended in that way. On the other hand, reasonably realistic scientists know that such continuous models are highly idealistic and should be viewed as such, whatever their powerful predictive qualities. Above all, we know that any attempt to maintain our “classical” models together with our classical reading of them is not experimentally sustainable over a wide range of phenomena. A quantization in a certain sense of our mathematical classical model (Bohr–Sommerfeld, canonical Dirac, Feynman path integral, geometry, deformation, CS, etc. [10]) is needed to account for observations and predictability. Usually, physicists or mathematicians have in mind as a classical structure a phase space or symplectic one that matches Hamiltonian formalism. In our mind, this represents a quite constraining restriction. With our approach, classical mathematical models with minimal structure (like a measure) might also be amenable to their quantized versions in our sense.
Now, we should answer the natural question “What is POVM quantization for?”. In quantum physics, the answer is natural and experimentally justified. Some illuminating examples are given in our previous works [5,9], where it has been shown that there is a world of quantizations leading to equivalent results from a physical point of view [11]. Starting from general models, not necessarily endowed with some physical flavor, it is interesting to provide a class of non-commutative, “fuzzy”, versions of them based on normalized POVM and resultant classical probability distributions. The method can be particularly relevant when we have to cope with geometries presenting singularities or with subset of manifolds determined by constraints [12].
In Section 2, we recall the minimal requirements that any quantization procedure should obey. A normalized positive operator-valued measure associated with the triple measure space, Hilbert space and density operator is presented in Section 3. The probabilistic content of the formalism is developed in Section 4. In Section 5, we reverse the approach by asking whether quantum formalism can be directly produced from classical probability theory. In Section 6, we examine the particular case where density operators are rank one, i.e., coherent state projectors. This allows a better understanding of the material introduced in the three previous sections. With Section 7, we enter the heart of the subject by explaining in which manner POVM quantization transforms a classical object, function or distribution into a linear operator in the companion Hilbert space. In Section 8, semi-classical aspects through lower symbols are examined. Covariant POVM quantization based on unitary irreducible representations and the relevant Schur’s lemma are described in Section 9. Then, we proceed with more or less elementary illustrations of the method: unit circle (Section 10), unit two-sphere (Section 11), plane (Section 12) and, finally, half-plane (Section 13). Some lines for future works and views about the links with quantum measurements and statistical inference are discussed in Section 14. Some necessary material is given in the two appendices.
2. Quantization: The Basics
First, on a minimal level, we understand the quantization of a set X and functions on it as a procedure fulfilling three requirements: linearity, existence of identity and self-adjointness. More precisely, quantization is:
- (1)
- A linear map:where is a vector space of complex-valued functions on a set X and is a vector space (“vector space” is in a loose sense, since the linear superposition of two operators could have a domain reduced to in infinite-dimensional Hilbert space!) of linear operators:in some complex Hilbert space , such that;
- (2)
- is mapped to the identity operator I on ;
- (3)
- A real function f is mapped to an (essentially) self-adjoint or, at least, symmetric operator in .
In a physical or a signal analysis context, one needs to add structure to X, such as a topology, a manifold structure, a closure under algebraic operations, etc. Besides, one also has the freedom to interpret the spectra of classical or quantum , so that they can be chosen as observables (in the terminology used in physics). Finally, one may add the requirement of an unambiguous classical limit of the quantum quantities, the limit operation being associated with a change of scale.
3. POVM for a Measure Space
As announced in the Introduction, we start from a minimal set of objects:
- (i)
- a measure space (or for short), where is the σ-algebra of ν-measurable subsets,
- (ii)
- a separable Hilbert space ,
- (iii)
- an X-labeled family of positive semi-definite and unit trace operators (“density matrices or operators”) on ,and resolving the identity I on ,
If X is equipped with a suitable topology, then the normalized positive operator-valued measure (POVM) on the corresponding σ-algebra of Borel sets is defined through the following map:
4. Probabilistic Density on Measure Space from POVM
There is a straightforward consequence of the identity Equation (4) in terms of probability distribution on the original measure space . Given and applying the corresponding density operator on each side of Equation (4) leads to:
Taking now the trace on each side gives:
Hence, the Hilbertian formalism combined with the original measure ν produces the X-labeled family of probability distributions:
on . The nonnegative bounded function measures in a certain sense the degree of localization of x w.r.t. , and vice versa, due to the symmetry , on the measure space . If we consider the particular case where is a rank-one projector operator:
i.e., is a “pure coherent state” (see below), then:
Thus, we could be inclined to introduce the pseudo-distance (triangular inequality is not verified in general):
Note that this quantity becomes infinite as . This limit corresponds to orthogonality of vectors and in the pure CS case.
Actually, from the fact that any density operator ρ is Hilbert–Schmidt, with norm , it is exact and could appear as more natural to introduce the associated distance:
In reality, this object forces any pair of points in X to be finitely separated, since we have:
In its general form, a density operator can be written as a statistical mixture of pure states:
Then, the corresponding probability distributions on read as:
This can be viewed as the average of the random variable with discrete probability distribution .
From the point of view of Bayesian statistical inference, we may treat X as the “parameter space of interest”, ν as a probability measure a priori on X and then as a probability density function on X, a posteriori, given an “estimated” value , where derives as a datum from some related random device with probability density function family indexed by . Then, we would be interested in an associated distance function on X to determine intervals of “distance” around the observed value . Note that for this “inferred” probability distribution on X, we have a POV measure, not an orthogonal one. From the inference point of view, the inferred probability distribution in this context, in principle, does not have a “frequency” or “ensemble” interpretation, similar to the case for a POV measure. It is the “random experiment” with the probability density function family indexed by , which, in principle, is repeatable and which would derive from a projector-valued (PV) measure. For example, see Section 6.
5. Quantum World from Classical Probabilistic Distribution?
In the previous section, we derived from the “quantum” four-tuple an X-indexed family of “classical” probability distributions . An interesting question then arises: given such a classical family, is it possible to derive a quantum ? If yes, is there uniqueness? Can we loosely think of quantum formalism as a kind of “square root” of classical probability formalism, as the quantum spin emerges from “square roots” (e.g., Dirac) of scalar wave equations (e.g., Klein–Gordon)?
Let us attempt through a simple example to explore such possibilities. Let be a finite set equipped with the measure:
A first observation has to be made concerning the existence of a family of N density matrices acting on , i.e., Hermitian -matrices with unit trace, which resolve the identity w.r.t. this measure:
Taking the trace of each side of this equation yields the constraint on the set of weights :
To simplify, we suppose that for all i. In particular, if the measure is uniform, for all i, then . Another point concerns the cardinal N of X versus the dimension n of . In its full generality, which means in the n-rank case, each density matrix is defined by real parameters. Moreover, in the present case, these N density matrices are requested to satisfy the set of equations issued from Equation (18):
Due to Equation (19), they are not independent and represent real constraints. Moreover, these constraints have to be supplemented by the (non-trivial) condition that, for all i, is a positive semi-definite matrix. This entails that we are left with a maximum of free parameters. Hence, as soon as , free parameters exist as soon as . Let us examine the minimal non-trivial case . Equation (18) assumes the matrix form:
This linear relation between two positive matrices implies that they are simultaneous diagonalizable, with respective eigenvalues , , with normalized eigenvectors , , forming an orthonormal basis of . Hence, Equation (21) is just a trivial rewriting of the resolution of the identity in :
A second observation is that if all are rank one, i.e., , , then Equation (18) reads:
which means that the set is a Parseval frame [13,14,15,16]. Such an identity is possible if ; and if , then for all i, and is an orthonormal basis.
Suppose that a family of N probability distributions is defined on the measure space , i.e., a set of non-negative numbers obeying:
Therefore, we are left with free parameters. Inspired by Equation (8), we attempt to determine a set of N density matrices from the following identities:
Now, Equation (25) leads to the set of real quadratic equations:
Actually, these are not independent, since, for each i, applying on each side gives one. Therefore, of these equations are independent. It follows the necessary condition:
for having nontrivial solutions, and uniqueness might hold with . Hence, Condition Equation (27) defines the allowed range for N with respect to n:
On the other hand, in the minimal case corresponding to rank-one density matrices , i.e., coherent states, the probabilities are given by:
Hence, these probabilities must obey the N constraints to be added to the N ones Equation (24). This means that we are left with free parameters. Let us now express the resolution of the identity Equation (23). In terms of the respective coordinates of vectors with respect to an orthonormal basis in .
Now, each projector is defined a priori by real coordinates (one constraint is for normalization, , the other one being for an arbitrary phase). There are N such projectors, so there are real parameters. From Equation (30) the latter are submitted to:
- independent real constraints issued from the diagonal ,
- real independent constraints issued from the off-diagonals .
Hence, like in Equation (27), we obtain the necessary condition:
for having nontrivial solutions, and the uniqueness (up to n phases) might hold with . This is possible for N in the range:
6. POVM from Coherent States
In this section we describe a simple method [17] for obtaining coherent states , such that . We start from another measure space and consider the Hilbert space of complex square integrable functions on X with respect to the measure μ. One then chooses in it an orthonormal set of functions (set aside the question of the evaluation map in their respective equivalence classes), satisfying the finiteness and positiveness conditions:
and in one-to-one correspondence with the elements of an orthonormal basis of the Hilbert space :
There results a family of unit vectors , the coherent states, in , which are labeled by elements of X and which resolve the identity operator in with respect to the measure:
This certainly represents the most straightforward way to build total families of states resolving the identity in . Underlying the construction, there is a Bayesian content [18], based or not on experimental evidences or on selective information choice, namely, an interplay between the set of probability distributions:
labeled by n, on the classical measure space , and the discrete set of probability distributions:
In this CS case, the probability distribution:
is expressed in terms of the reproducing kernel w.r.t. the measure :
7. POVM Integral Quantization
With the above material at hand, the integral quantization of complex-valued functions is formally defined as the linear map:
This map is properly defined if the operator is understood as the sesquilinear form:
defined on a dense subspace of . If f is real and at least semi-bounded and since is positive, the Friedrichs extension [19] of univocally defines a self-adjoint operator. If f is not semi-bounded, there is no natural choice of a self-adjoint operator associated with . In this last case, in order to construct as an observable, we need to know more about the space of states in order to examine the existence of self-adjoint extensions (e.g., boundary conditions in the case of domains defined for wave functions).
Note that the above quantization may be extended to objects that are more general than functions. We think of course of distributions if the relevant structure of X allows one to properly define them. Suppose that the measure set is also a smooth manifold of dimension n, on which is defined the space of distributions as the topological dual of the (LF)-space of compactly supported n-forms on X [20]. Here, “LF” is for “inductive limit of sequence of Frechet spaces”. Some of these distributions, e.g., or , where is the characteristic function of , express geometrical constraints. Extending the map Equation (42) yields the quantum version or of these constraints.
A different starting point for quantizing constraints, more in Dirac’s spirit [21], would consist of quantizing the function and determining the kernel of the operator . Both methods are obviously not equivalent, except for a few cases. This question of equivalence/difference gives rise to controversial opinions in fields like quantum gravity or quantum cosmology. Elementary examples illustrating this difference are worked out in [9].
8. Semi-Classical Aspects and Quantum Measurements through Lower Symbols
We arrive at the point where the probability distribution Equation (8) makes sense in regard to the objects f (functions or more singular entities) to be quantized. Indeed, some of the properties (if not all) of the operator can be grasped by examining the function defined as:
and named, within the context of Berezin quantization [22,23], lower (Lieb) or covariant (Berezin) symbols. Now, this quantity represents the local averaging of the original f with respect to the probability distribution Equation (8):
This construction is a generalization of the so-called Bargmann–Segal transform (see, for instance, [24,25]). It can also be viewed as a kind of Wigner function [5] endowed with a real probabilistic content. In addition to the functional properties of the lower symbol , one may investigate certain quantum features, such as, e.g., spectral properties of . Furthermore, the map Equation (45) represents in general a regularization of the original, possibly extremely singular, f. Another point deserves to be mentioned here. It concerns the analogy of the present formalism with quantum measurement. In a quantum physics context for which is a self-adjoint operator or observable of a system and given a density operator describing the mixed state of an ensemble, such that each of the pure states occurs with probability , the expectation value of the measurement is given by the “unsharp” representation:
Hence, it can be also viewed as the average of the original f with respect to the probability density:
Of course, this can be one element of the family of density operators from which is issued the considered quantization. Inspired by ideas developed during the two last decades by various authors, particularly Busch, Grabowski and Lahti in “Operational Quantum Physics” [26] and Holevo in “Probabilistic and Statistical Aspects of Quantum Theory” [27], we turn our attention to the classical “smeared” form, such as described in these books. If one validates the assumption that any quantum observable is issued from our POVM quantization procedure, then its measurement can be expressed as in Equation (46). This should shed new classical light on the quantum perspective, since the usual integral representation of , namely:
is issued from the spectral decomposition:
of the self-adjoint with spectral measure and is interpreted as a “sharp” measurement. In this regard, Equation (46) might be viewed as an unsharp measurement, possibly through some marginal integration [26,27].
We point out the “circular” nature of our procedure. On the one hand, we use POVM to quantize classical functions. On the other hand, we obtain a POVM quantum measurement, interpreted as an inverse transform yielding a “semi-classical object”, which, in the statistical inference context, yields an inferred probability distribution. In that sense, we treat quantization and measurement as two aspects of the same construct.
Of course, the projector-valued (PV) spectral measure corresponding to the integral representation Equation (49) might have a remote connection with the classical spectrum appearing in the integral representation Equation (42). While the POVM used for quantization, and built from a family resolving the identity with respect to the fixed measure ν, should be considered as a frame to analyze functions on X, the PV measure in Equation (49) is proper to the quantum observable and to functions of it. However, there are simple examples (consider the quantum versions of position and momentum obtained from coherent state quantization) where classical and quantum spectra can be considered as identical regardless of the difference between their respective PV and POVM. Moreover, the frame itself may be associated with a specific system to be quantized. A nice pedagogical example (the sea star) is presented in chapter 11 of [6].
9. Covariant POVM Quantizations
In explicit constructions of density operator families and related POVM quantization, the theory of Lie group representations offers a wide range of possibilities. Let G be a Lie group with left Haar measure , and let be a unitary irreducible representation (UIR) of G in a Hilbert space . Pick a density operator ρ on and let us transport it under the action of the representation operators . Its orbit is the family of density operators:
Suppose that the operator:
is defined in a weak sense. From the left invariance of we have:
and so R commutes with all operators , . Thus, from Schur’s lemma, , with:
where the density operator is chosen in order to make the integral converge. This family of operators provides the following resolution of the identity:
Let us examine in more detail the above procedure in the case of square integrable UIRs (e.g., affine group, see below). For a square-integrable UIR U for which is an admissible unit vector, i.e.,
the resolution of the identity is obeyed by the family of coherent states for the group G:
This property is easily extended to square-integrable UIR U for which ρ is an “admissible” density operator, . The resolution of the identity then is obeyed by the family: .
This allows an integral quantization of complex-valued functions on the group:
which is covariant in the sense that:
In the case when , the quantity is the regular representation. From the lower symbol, we obtain a generalization of the Berezin or heat kernel transform on G:
In the absence of square-integrability over G, there exists a definition of square-integrable covariant coherent states with respect to a left coset manifold , with H a closed subgroup of G, equipped with a quasi-invariant measure ν [6].
10. The Example of the Unit Circle
We start our series of examples with one of the most elementary ones. Actually, it is rich both in fundamental aspects and pedagogical resources. The measure set is the unit circle equipped with its uniform (Lebesgue) measure:
The Hilbert space is the Euclidean plane . The group G is the group SO(2) of rotations in the plane. As described at length in Appendix A.1, the most general form of a real density matrix can be given, as a π-periodic matrix, in terms of the polar coordinates of a point in the unit disk:
We notice that for , the density matrix is just the orthogonal projector on the unit vector with polar angle ϕ:
Due to the covariance property Equation (A16), we define the family of density operators:
where the rotation matrix is defined by Equation (A10). This family resolves the identity:
It follows the -labeled family of probability distributions on :
Such an expression reminds us of the cardioid distribution (see [28], page 51). At , we get the uniform probability on the circle, whereas at , we get the “pure state” probability distribution:
Hence, the parameter r can be thought of as the inverse of a “noise” temperature . The pseudo-distance on associated with Equation (65) is given by:
which reduces at small to:
On the other hand, the distance defined by Equation (13) reads in the present case:
which reduces at small to Equation (68) up to a constant factor.
The quantization of a function (or distribution) on the circle based on Equation (64) leads to the 2 × 2 matrix operator:
where is the average of f on the unit circle and . The symbols and are for the cosine and sine doubled angle Fourier coefficients of f:
The simplest function to be quantized is the angle function , i.e., the -periodic extension of for ,
Its eigenvalues are with corresponding eigenvectors . Its lower symbol is given by the smooth function:
11. The Example of the Unit Two-Sphere
The measure set is the unit sphere equipped with its rotationally invariant measure:
The Hilbert space is now . The group G is the group SU(2) of -unitary matrices with determinant one. We give in Appendix A.2 the essential notations and relations with quaternions.
The unit ball in parametrizes the set of complex density matrices ρ. Indeed, given a three-vector , such that , a general density matrix ρ can be written as:
We have used for convenience the quaternionic representation of the vector (see Appendix A.2 for details). If , i.e., (“Bloch sphere” in this context), with spherical coordinates , then ρ is the pure state:
Note that the above column vector has to be viewed as the spin coherent state in the Hermitian space with orthonormal basis :
Let us now transport the density matrix ρ by using the two-dimensional complex representation of rotations in space, namely the matrix SU(2) representation. For , one defines the family of density matrices labeled by ξ:
In order to get a one-to-one correspondence with the points of the two-sphere, we restrict the elements of SU(2) to those corresponding to the rotation , bringing the unit vector pointing to the North Pole to the vector with spherical coordinates , as described in Equation (A23):
with:
The value of the integral for :
shows that the resolution of the unity is achieved with , only. Then, it is clear that:
It is with this strong restriction and the simplified notation:
that we go forward to the next calculations with the resolution of the unity:
Note that the resolution of the identity with the SU(2) transport of a generic density operator Equation (75) is possible only if we integrate on the whole group, as was done in [9].
The -labeled family of probability distributions on :
At , we get the uniform probability on the sphere, whereas at , we get the probability distribution corresponding to the spin 1/2 CS Equation (77):
Like for the unit circle, the parameter r can be viewed as the inverse of a “noise” temperature .
The distance reads:
which is the usual distance on the sphere with radius r issued from the Euclidean one. The quantization of a function (or distribution) on the sphere based on Equation (84) leads to the 2 × 2 matrix operator:
where is the average of f on the unit sphere and and are Fourier coefficients of f on the sphere defined as:
Since the sphere is a phase space with canonical coordinates , and , the latter may be thought of as the simplest functions to be quantized. We find for the quantization of q:
Its eigenvalues are with corresponding eigenvectors . Its lower symbol is given by the smooth function:
The quantization of p yields the diagonal matrix:
with immediate eigenvalues and lower symbol:
Finally, we note the commutation rule:
12. The Example of the Plane
The measure set is the Euclidean plane (or complex plane) equipped with its uniform (Lebesgue) measure:
The group G is the Weyl–Heisenberg group with multiplication law:
In this group context, the plane is viewed as the coset , where C is the center in the group . Let be a separable (complex) Hilbert space with orthonormal basis . Let us suppose that the basis element is a state for n excitations of an harmonic system, e.g., a Fock number state for the quantum electromagnetic field with single-mode photons and for which is the plane of quadratures. Given an elementary quantum energy, say , and a temperature T (e.g., a noise one, like in electronics), a Boltzmann–Planck T-dependent density operator, i.e., thermal state [29], is introduced as:
We notice that at zero temperature this operator reduces to the projector on the first basis element (“ground state” or “vacuum”):
On the other hand, at a high temperature or equivalently in the classical limit , and from a classical probability point of view, one notices that we have the Rice probability density function [29]. This Rice distribution is also obtained in an analogous fashion in a classical optics context (classical, but probabilistic), “a constant phasor plus a random phasor sum”, which one may take to be the classical version of the quantum “oscillator with a coherent signal superimposed on thermal noise” (see the classical probabilistic description in [30]).
Introducing lowering and raising operators a and :
which obeys the canonical commutation rule:
We obtain the number operator, , whose spectrum is , with corresponding eigenvectors as the basis elements, . Having in hand these two operators, we build a unitary irreducible representation of the Weyl–Heisenberg group through the map:
and the composition law:
which show that the map is a projective unitary representation of the abelian group . Then, one easily derives from the Schur lemma or directly that the family of displaced operators:
where the matrix elements of the operator are given in terms of associated Laguerre polynomials [29],
with . With these properties, Equation (105) reads more explicitly as:
The resolution of the identity follows from the results given in Section 9:
More general constructions and results are given in [5]. At zero temperature, we recover the standard (Schödinger, Klauder, Glauber, Sudarshan) coherent states [31]:
Let us evaluate the probability distribution issued from . The expression of is rather elaborate:
The first term in the sum can be given a compact form [32] (warning: there are errors in Poisson generating function for Laguerre polynomials; the correct formula is found in WikiLaguerre):
where is a modified Bessel function. At , Equation (109) reduces to:
As expected, at zero temperature, this quantity is equal to one. It vanishes at infinite temperature. The pseudo-distance Equation (11) takes the form:
where the T-dependent goes to zero as It is only in the limit CS case that this quantity acquires its true Euclidean distance meaning. As for , we get:
The quantization map based on is given by:
There are translational and rotational covariances. Covariance w.r.t. complex translations reads as:
To show rotational covariance, we define in the preamble the unitary representation of the torus on the Hilbert space as the diagonal operator:
where ν is arbitrary real. Then, from the matrix elements of , one proves easily the rotational covariance property:
From the diagonal nature of , we derive the covariance of w.r.t. complex rotations in the plane,
where . In particular, for the parity operator defined by:
We have:
A covariance also holds for the conjugation operator:
The canonical commutation rule is a T-independent outcome of the above quantization:
Equivalently, with :
From this, their commutator is canonical:
We now turn our attention to the simple quadratic expressions:
where . It follows that:
where is the energy (in appropriate units) for the harmonic oscillator. The difference between the ground state energy and the minimum of the quantum potential energy is independent of the temperature, namely (experimentally verified in 1925). It has been proven in [11] (at least in the CS case) that these constant shifts in energy are inaccessible to measurement.
We now turn our attention to the quantization of the angle or phase. We write in action-angle notations for the harmonic oscillator. The quantization of a function of the action and of the angle , which is -periodic in γ, yields formally the operator:
The angular covariance property takes the form:
In particular, let us quantize the discontinuous -periodic angle function for . Since this angle function is real and bounded, its quantum counterpart is a bounded self-adjoint operator, and it is covariant according to Equation (128). In the basis , it is given by the infinite matrix:
where:
is symmetric w.r.t. the permutation of m and (from the well-known
This operator has a spectral measure with support . For a detailed study of such an operator in the CS case (), see [5].
13. The Example of the Half-Plane
The measure set is the half plane equipped with its uniform (Lebesgue) measure:
Together with the multiplication , is viewed as the affine group Aff of the real line. Aff has two non-equivalent UIRs [33,34]. Both are square integrable, and this is the rationale behind continuous wavelet analysis (see the references in [6]). The UIR is realized in the Hilbert space :
In the same Boltzmann–Planck line, as for the plane, we build the temperature-dependent density operator:
where is an orthonormal basis of . Let us choose that one which is built from Laguerre polynomials:
where is a free parameter. Then, from [32], the operator acts on as the integral transform:
where the integral kernel is given by:
Again, one derives from the Schur lemma that the transported operators:
resolve the identity:
where the constant is obtained from the integral through standard calculations in wavelet theory:
The resolution of the identity imposes the painless restriction and reads finally:
We leave the main results of the corresponding quantization to a future publication.
14. Conclusions
(1) About POVM Formalism(s)
In this first part of the Conclusions, we would like to comment with a few words about the relation between formalisms based on POVM, regardless of whether it is used in a quantization context as it is here, in quantum measurement or in statistical inference. Full developments will be the subject for a separate paper.
The inference process may briefly be described as follows. We start from a context that includes a source of data, which would be modeled by the use of a family of probability distributions indexed by some parameter(s) of theoretical interest lying in the space for the system being studied. Thus, we postulate a context that includes an experiment (actual or virtual), which requires probabilistic modeling, a so-called random experiment. The probability model refers to possible results before performing the experiment. One might conceive of the elements of X as those of primary interest upon which inference will be performed by virtue of a related secondary device, which serves as a source of data. After observing the results, one has data in hand with which to obtain an inferred probability distribution over a σ-field of sets in X, which devolve from a POV measurement.
A property to note is that the probability distribution modeling the random experiment has a so-called frequency interpretation that one can conceive of by (hypothetically) repeating the experiment in order to generate a “population” or “ensemble” consisting of realized results, but not for the POV-related inferred probability distribution.
In the inference situation, if one can obtain a probability model for the random experiment using a PV measurement and coherent states, or their generalization described in this paper, then their resolution of the identity property along with previously observed data provides us with an inferred probability distribution on the parameter(s) of interest. Examples are given in [35,36]. Furthermore, note the role played by covariant measurement as explicated in Holevo [27] and Busch, Grabowski and Lahti [26].
The POV measure is generally conceived of as an attribute of quantum physics in contrast to classical physics. In other words, the POV measure is considered to be a generalization of the PV measure, which it is, of course, mathematically, and which is necessary for quantum theory.
However, here, we see that POV measurement occurs also as an attribute of statistical inference when one has a probabilistic model, whether classical or quantum.
Note that, alternatively, if one has a deterministic model for the physics, none of the above applies. One has a direct route, provided by the theory, from data to parameter(s) of interest. No need to make much of a distinction. Let us take a simple example from medicine and biology. Small amounts of dopamine obtained from brain tissue may be measured by preparing a fluorescent derivative. In order to connect the fluorescent measurement with the amount of dopamine, one can run “standards”. This is not a problem, as long as there is a deterministic connection between the two.
The problem of inference comes up when we have probabilistic modeling rather than deterministic modeling. In that sense, one may say it is quantum rather than classical; except, as we all know, there are classical contexts in which we also need to use a probabilistic model, in which case, the inferred distribution would also involve POV measurements.
(2) About Measurement(s)
Confusion might arise because the word “measurement” is used in more than one way.
Consider a system under study which is to be described in terms of a “mathematical model”. This would include “observables”, which are associated with certain properties of the system that we “measure”. However, rarely can we measure them directly. Ordinarily, we actually measure (in the conventional sense) some related secondary system for which we can obtain experimental data. Then, the problem arises of how to relate the experimental data to the observables of the system of interest.
Further, we conceive of experiments (actual or virtual) as being repeatable, if even only hypothetically (thus enters relativity and covariant measurements).
As mentioned above, if the relationship is conceived of as being deterministic (which is usually associated with classical physics), there is usually no problem. Now, what if the model is probabilistic? Then, we have two probability models. One refers to the actual experiment in relation to some secondary system related to the one in which we are interested. That would be a family of probability distributions indexed by parameter(s) that describe the “unknown” property of interest. (Think of tossing a coin to estimate by experiment: the property p of the coin where p = chance of getting heads on one toss. It is this property in which we are interested but cannot “measure” directly. Is it a “fair” coin or not. With a probabilistic model, we cannot get a definite answer. What we can get is the odds: inferred probability distribution on the space , in this case, from data that we get by tossing the coin. The probability model for the experiment is the binomial distribution with “unknown” parameter p. The inferred probability distribution for p is the beta distribution, where the observed proportion of heads occurs in the formula.) The point is that the probabilities related to the experiment (secondary system) have a so-called “frequency interpretation”, meaning that we can generate an “ensemble” via repeats of the experiment. However, the inferred probabilities do not. There is no experiment directly related to them. We have an axiomatic definition of probability, but no frequency interpretation for it. That is the nature of probabilistic inference. That is why we have POVM in regard to inferred probability distributions and PV measures for possible experimental results of so-called “random experiments”.
Now consider theoretical models of physical systems for which there is no direct experimental background. Then, if it is classical and also probabilistic or if it is quantum and, so, necessarily probabilistic, then the consequent probabilities have no frequency interpretation and are derived from POVMs. In modeling, sometimes, it is the state that describes the system, and then, an observable gives us the probability model via expectation. In our paper, it is the POVM quantization that describes the system and, at the same time, gives a probability model via expectation.
(3) Various Uses for POVMs
In summary, we have designated three views of POVM quantization formulas. One relates to the process of quantization itself, another to theoretical modeling and another to inference.
These various uses for POVMs are inter-related, so that it is not always appropriate to separate them. In the paper, we see that these inter-relationships are revealed and discussed. Roughly speaking, we have quantization discussed in Section 2, Section 5, Section 7 and Section 8, theoretical modeling in Section 3, Section 4, Section 5, Section 8 and Section 9, inference in Section 4, Section 6, Section 8 and Section 9, and these Conclusions, along with examples. Understandably, there is much overlap between theoretical modeling and inference.
Do POVMs have a fundamental role in quantum theory? Yes. How do POVMs arise? They are used to describe a quantum system probabilistically and also in performing statistical inference. As usual, quantization is important in cases where there is a classical analogy. Examples are given.
Acknowledgments
Jean Pierre Gazeau thanks the CNPq for financial support; the World Academy of Sciences and the International Centre for Theoretical Physics (TWAS-ICTP), Trieste, and the Centro Brasileiro de Pesquisas Fìsicas—CBPF, Rio de Janeiro, for hospitality and support.
Author Contributions
The respective contributions of Jean Pierre Gazeau and Barbara Heller to the content of this article are equal in importance.
Appendix
A.1. Parametrizations of Real Density Matrices
There are various expressions for a density matrix acting on the Euclidean plane, i.e., a real positive matrix with trace equal to one. The most immediate one is the following with parameters a and b:
The above inequalities imply the following ones:
Let:
be the highest eigenvalue of ρ (the lowest one is ). The spectral decomposition of ρ reads as:
where:
is the corresponding unit eigenvector, chosen as pointing in the right half-plane. We could have also chosen the opposite pointing in the left half-plane, since . Our choice corresponds to the most immediate one in terms of the orthonormal basis of the plane issued from the canonical one through the rotation by ϕ.
Let us make explicit the decomposition Equation (A4):
We derive from this expression the polar parametrization of the parameters of ρ:
In return, we have the angle as a function of a and b:
In this way, each ρ is univocally (but not biunivocally) determined by a point in the unit disk, with polar coordinates , , .
Furthermore, note the alternative expression issued from Equation (A6):
where is the rotation matrix in the plane:
and is the diagonal Pauli matrix:
Note the important property used to get the second equality in Equation (A9):
Therefore, the expression of a matrix density to which we refer most often throughout the paper reads:
From Equation (A9) and Equation (A12), we derive the interesting multiplication formula:
and the resulting (non-closed) “algebra” of real density matrices,
A.1.1. Covariance
The expression Equation (A13) is convenient to examine the way a density matrix transforms under a rotation in the plane. We have:
A.1.2. Integrals of the Density Matrix
The computation of the three following (whose two are partial or marginal) integrals is straightforward:
where is the unit disk and .
A.2. SU(2) as Unit Quaternions Acting in
A.2.1. Rotations and Quaternions
A convenient representation is possible thanks to quaternion calculus. We recall that the quaternion field as a multiplicative group is SU(2). The correspondence between the canonical basis of , , and the Pauli matrices is , with . Hence, the matrix representation of these basis elements is the following:
Any quaternion decomposes as (resp. ) in scalar-vector notation (resp. in Euclidean metric notation). We also recall that the multiplication law explicitly reads in scalar-vector notation: . The (quaternionic) conjugate of is , the squared norm is and the inverse of a nonzero quaternion is . Unit quaternions, i.e., quaternions with norm one, the multiplicative subgroup isomorphic to SU(2), constitute the three-sphere .
On the other hand, any proper rotation in space is determined by a unit vector defining the rotation axis and a rotation angle about the axis, as is shown in Figure 1.
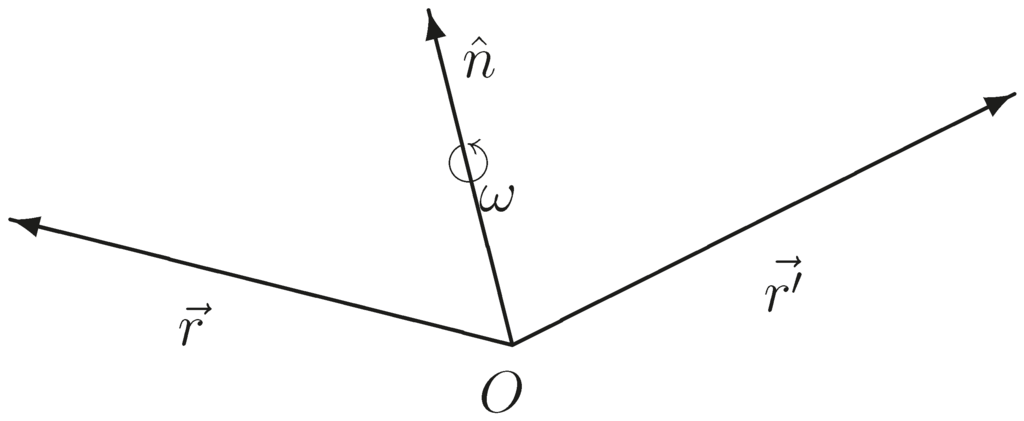
Figure 1.
Rotation in space as determined by the unit vector of the rotation axis and the rotation angle about the axis.
The action of such a rotation, , on a vector is given by:
The latter is expressed in scalar-vector quaternionic form as:
where:
or, in matrix form,
in which case, quaternionic conjugation corresponds to the transposed conjugate of the corresponding matrix.
In particular, for a given unit vector:
one considers the specific rotation that maps the unit vector pointing to the North Pole, , to , as shown in Figure 2.
with:
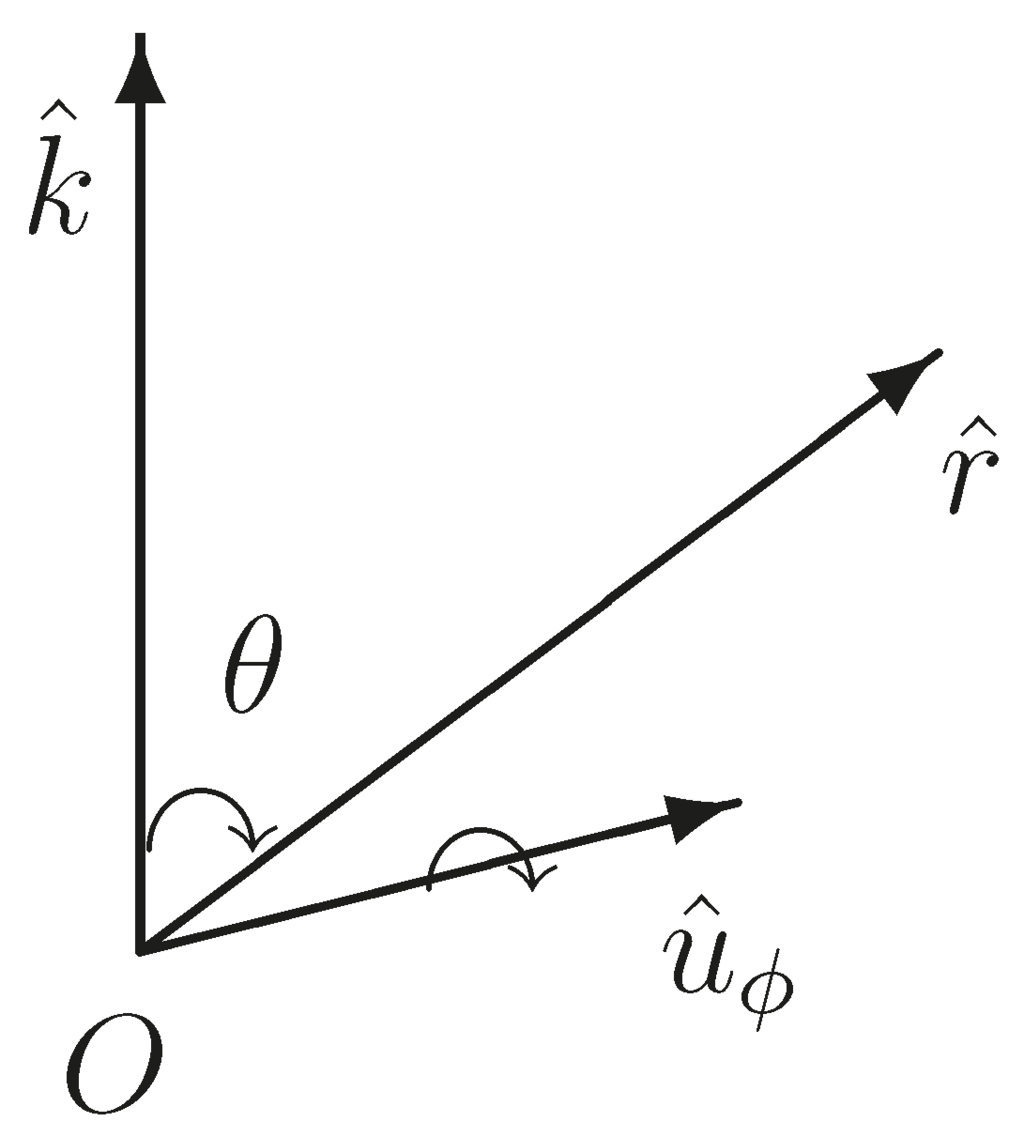
Figure 2.
Rotation mapping the unit vector pointing to the North Pole, , to .
Conflicts of Interest
The authors declare no conflict of interest.
References
- Somaraju, R.A.; Sarlette, A.; Thienpont, H. Quantum filtering using POVM measurements. In Proceedings of 2013 IEEE 52nd Annual Conference on Decision and Control (CDC), Florence, Italy, 10–13 December 2013.
- Bouten, L.; van Handel, R.; James, M.R. An introduction to quantum filtering. SIAM J. Control Optim. 2008, 46, 2199–2241. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Gill, R.D.; Jupp, P.E. On Quantum Statistical Inference. J. R. Stat. Soc. Ser. B Stat. Methodol. 2003, 65, 775–804. [Google Scholar] [CrossRef]
- Kuperberg, G. A Concise Introduction to Quantum Probability, Quantum Mechanics, and Quantum Computation. Available online: http://www.math.ucdavis.edu//intro-2005.pdf (accessed on 18 December 2014).
- Bergeron, H.; Gazeau, J.P. Integral quantizations with two basic examples. Ann. Phys. 2014, 344, 43–68. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.P. Coherent States, Wavelets and their Generalizations, 2nd ed.; Springer: New York, NY, USA, 2013; Chapter 11. [Google Scholar]
- Bergeron, H.; Curado, E.M.F.; Gazeau, J.P.; Rodrigues, Ligia M.C.S. Quantizations from (P)OVM’s. In Proceedings of the 8th Symposium on Quantum Theory and Symmetries, El Colegio Nacional, Mexico City, Mexico, 5–9 August 2013.
- Bergeron, H.; Dapor, A.; Gazeau, J.P.; Małkiewicz, P. Smooth big bounce from affine quantization. Phys. Rev. D 2014, 89. [Google Scholar] [CrossRef]
- Baldiotti, M.; Fresneda, R.; Gazeau, J.P. Three Examples of Covariant Integral Quantization. In Proceedings of 3rd International Satellite Conference on Mathematical Methods in Physics—ICMP 2013, Londrina, Brazil, 21–26 October 2013.
- Ali, S.T.; Engliš, M. Quantization methods: A guide for physicists and analysts. Rev. Math. Phys. 2005, 17. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.P.; Youssef, A. Are the Weyl and coherent state descriptions physically equivalent? Phys. Lett. A 2013, 377, 598–605. [Google Scholar] [CrossRef]
- Baldiotti, M.; Fresneda, R.; Gazeau, J.P. About Dirac & Dirac constraint quantizations. Phys. Scr. 2014, submitted. [Google Scholar]
- Benedetto, J.J.; Fickus, M. Finite normalized tight frames. Adv. Comput. Math. 2003, 18, 357–385. [Google Scholar] [CrossRef]
- Han, D.; Kornelson, K.; Weber, E. Frames for Undergraduates. Student Mathematical Library; American Mathematical Society: Providence, RI, USA, 2007; Volume 40. [Google Scholar]
- Cotfas, N.; Gazeau, J.P. Finite tight frames and some applications (topical review). J. Phys. A Math. Theor. 2010, 43. [Google Scholar] [CrossRef]
- Cotfas, N.; Gazeau, J.P.; Vourdas, A. Finite-dimensional Hilbert space and frame quantization. J. Phys. A Math. Gen. 2011, 44. [Google Scholar] [CrossRef]
- Gazeau, J.P. Coherent States in Quantum Physics; Wiley-VCH: Berlin, Germany, 2009. [Google Scholar]
- Ali, S.T.; Gazeau, J.P.; Heller, B. Coherent states and Bayesian duality. J. Phys. A Math. Theor. 2008, 41. [Google Scholar] [CrossRef]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics, II. Fourier Analysis, Self-Adjointness; Academic Press: New York, NY, USA, 1975; Volume 2. [Google Scholar]
- Grosser, M. A note on distribution spaces on manifolds. Novi Sad J. Math. 2008, 38, 121–128. [Google Scholar]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Dover: New York, NY, USA, 2001. [Google Scholar]
- Berezin, F.A. Quantization. Math. USSR Izvestija 1974, 8, 1109–1165. [Google Scholar] [CrossRef]
- Berezin, F.A. General concept of quantization. Commun. Math. Phys. 1975, 40, 153–174. [Google Scholar] [CrossRef]
- Stenzel, M.B. The Segal-Bargmann transform on a symmetric space of compact type. J. Funct. Anal. 1994, 165, 44–58. [Google Scholar] [CrossRef]
- Hall, B.C. The Segal-Bargmann “Coherent State” transform for compact Lie groups. J. Funct. Anal. 1994, 122, 103–151. [Google Scholar] [CrossRef]
- Busch, P.; Grabowski, M.; Lahti, P.J. Operational Quantum Physics; Springer-Verlag: Berlin, Germany, 1995. [Google Scholar]
- Holevo, A.S. Probabilistic and Statistical Aspects of Quantum Theory; Springerg: Berlin, Germany, 2011. [Google Scholar]
- Mardia, K.V. Statistics of Directional Data; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Goodman, J.W. Statistical Optics; Wiley Classics Library: New York, NY, USA, 2000. [Google Scholar]
- Klauder, J.R.; Sudarshan, E.C.G. Fundamentals of Quantum Optics; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer-Verlag: Berlin, Germany, 1966. [Google Scholar]
- Gel’fand, I.M.; N’aimark, M.A. Unitary representations of the group of linear transformations of the straight line. Dokl. Akad. Nauk SSSR 1947, 55, 567–570. [Google Scholar]
- Aslaksen, E.W.; Klauder, J.R. Unitary Representations of the Affine Group. J. Math. Phys. 1968, 15, 206–211. [Google Scholar] [CrossRef]
- Heller, B.; Wang, M. Group invariant inferred distributions via non-commutative probability. Inst. Math. Stat. Lect. Notes Monogr. Ser. 2006, 50, 1–19. [Google Scholar]
- Heller, B.; Wang, M. Posterior distribution for negative binomial parameter p using a group invariant prior. Stat. Probab. Lett. 2007, 77, 1542–1548. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).