Weak n-Ary Relational Products in Allegories

Abstract

Allegories are enriched categories generalizing a category of sets and binary relations. Accordingly, relational products in an allegory can be viewed as a generalization of Cartesian products. There are several definitions of relational products currently in the literature. Interestingly, definitions for binary products do not generalize easily to n-ary ones. In this paper, we provide a new definition of an n-ary relational product, and we examine its properties.

1. Introduction

Relation algebra ([1,2]) allows one to formulate first order logic (and set theory) in a quantifier-free, purely algebraic (equational) way. It has found numerous applications in mathematics and computer science (see, e.g., [3,4,5,6,7,8])., Inin particular, it is a foundation for relational databases [9]. A relation algebra without some additional structures is equivalent in expressivity to three variable fragment of first order logic [1]. A crucial ingredient that allows one to express with relation algebra all of the first order logic is the existence of Cartesian products. These can be defined equationally, as so-called relational products, within the relation algebra. In fact, the existence of relational products is strongly related to the representability of abstract relation algebras, i.e., the possibility of their realization as subalgebras of the algebra of actual binary relations.

Allegories are enriched categories generalizing a category of sets and binary relations. Accordingly, relational products in an allegory can be viewed as a more abstract version of Cartesian products. Recently allegories were used as a mathematical framework to model databases in [10,11]. There, the authors had to assume the existence of appropriate relational products in order to make the formalism applicable in other than most trivial cases, in particular, relational products allow one to define n-ary relations using binary ones.

There is a well-established definition of a binary relational product valid both for abstract relation algebras (see e.g., [3,7,12,13]) and allegories (see e.g., [14] or Definition 9 in Section 2 of this paper). In the case of the allegory of sets and binary relations, this definition characterizes, up to an isomorphism, the usual Cartesian products. For general allegories, one proves easily [14] that the relational product is a categorical product for the subcategory of maps of the given allegory, that is a subcategory consisting of those arrows (generalized relations) that behave like total functions. It should be noted that, unlike the categorical definition of the product, which involves both universal and existential quantification (for all maps, such that …there exists a unique map, such that …), the definition of a relational product involves no quantification—it is just equations, in terms of constant arrows and projection arrows, which projection arrows must satisfy. Moreover, the unique factorization, the existence of which the categorical definition asserts, is given explicitly by a simple algebraic formula in terms of projection arrows and the maps to be factorized through the product. Unfortunately, this definition of a relational product is too strong to be considered an algebraic characterization of categorical product; there are examples (see e.g., [15]) of allegories in which a categorical product in the subcategory of maps does not satisfy all of the standard axioms of a relational product. In [15] and [16], a weakening (see also Definition 10 in this paper) of the standard relational product was investigated, which still provides a categorical product in the subcategory of maps.

It is surprisingly difficult to generalize the definition of a binary relational product to an n-ary one for an arbitrary n. The most obvious one does not yield a categorical product in the subcategory of maps. A non-inductive definition (i.e., one that did not rely on the iteration of binary products) of the n-ary relational product was given in [17]. the paper (concerned with abstract relational algebra rather than with allegories) does not contain the proof that the n-ary relational product yields the n-ary categorical product for functions, though the author proves that the n-ary relational products of the same objects must be isomorphic.

In this paper, we define and investigate the weakening of an n-ary relational product from [17], which for $n=2$ is equivalent to the binary relational product defined in [15]. We prove that a weak n-ary relational product yields an n-ary categorical product in the subcategory of maps. Furthermore, we generalize to the case of weak n-ary relational products some of the results proven in [15] for weak binary relational products. Finally, we show that by composing the weak n-ary products, we again get weak n-ary products.

2. Preliminaries

We assume that the reader is familiar with basic category theory, and an excellent introduction can be found in [18]. We recall some basic categorical definitions in order to fix the clean, but somewhat idiosyncratic, notation we use. The bulk of the preliminaries is taken by introductory material on allegories, which are not widely known and for which [14] is the basic textbook.

Note that we consciously utilize the term “set” where “class” might be more appropriate in order not to clutter the presentation with the set-theoretical considerations.

2.1. Categories and Graphs

A graph $\mathcal{G}$ consists of a set of vertices $\mathrm{Obj}\left[\mathcal{G}\right]$, a set of arrows $\mathrm{Arr}\left[\mathcal{G}\right]$ and a pair of maps $\overleftarrow{(·)},\overrightarrow{(·)}:\mathrm{Arr}\left[\mathcal{G}\right]⟶\mathrm{Obj}\left[\mathcal{G}\right]$, called the source and target, respectively. We denote by ${\mathrm{Arr}}_{\mathcal{G}}(A,B)$ the set of arrows with source A and target B, where $A,B\in \mathrm{Obj}\left[\mathcal{G}\right]$.

A category $\mathcal{C}$ is a graph with associative arrow composition $f;g\in {\mathrm{Arr}}_{\mathcal{C}}(\overleftarrow{f},\overrightarrow{g})$ defined whenever $\overrightarrow{f}=\overleftarrow{g}$ (note the diagrammatic order) and identity map $\mathrm{id}:\mathrm{Obj}\left[\mathcal{C}\right]\to \mathrm{Arr}\left[\mathcal{C}\right]$, such that $\mathrm{id}(\overleftarrow{f});f=f;\mathrm{id}(\overrightarrow{f})=f$ for all $f\in \mathrm{Arr}\left[\mathcal{C}\right]$. We write ${\mathrm{id}}_A:=\mathrm{id}(A)$. When using single letter arrow names, we will often omit the semicolon composition operator abbreviating $fg:=f;g$.

We will often declare the composability of arrows using diagrams, e.g.,

$$•\stackrel{f}{\to }•\underset{h}{\overset{g}{\rightrightarrows }}•:\equiv (\overrightarrow{f}=\overleftarrow{g})\wedge (\overrightarrow{f}=\overleftarrow{h})\wedge (\overrightarrow{g}=\overrightarrow{h})$$

Note that unlike in [14], the diagrams are not considered commutative by default.

A categorical n-ary product is a family of arrows ${\{{\pi }_i\}}_{i\in \{1,\dots ,n\}}$ with a common source, such that for any other family of arrows ${\{f_i\}}_{i\in \{1,\dots ,n\}}$ with a common source and such that $\overrightarrow{f_i}=\overrightarrow{{\pi }_i}$ for all $i\in \{1,\dots ,n\}$, there exists a unique arrow h, such that $f_i=h{\pi }_i$ for all $i\in \{1,\dots ,n\}$.

2.2. Allegories

An allegory [14] $\mathcal{A}$ is a category enriched with intersection and reciprocation operators, respectively, for all $A,B\in \mathrm{Obj}\left[\mathcal{A}\right]$:

$$\begin{array}{c}·\sqcap ·:{\mathrm{Arr}}_{\mathcal{A}}(A,B)\times {\mathrm{Arr}}_{\mathcal{A}}(A,B)\to {\mathrm{Arr}}_{\mathcal{A}}(A,B),\\ {(·)}^{\circ }:{\mathrm{Arr}}_{\mathcal{A}}(A,B)\to {\mathrm{Arr}}_{\mathcal{A}}(B,A)\end{array}$$

We require these operators to satisfy the following conditions: Intersections make each hom-set a meet-semilattice (see, e.g., [19]), where we denote the associated partial order by ⊑, i.e., $R⊑S:\equiv R\sqcap S=R$, for all $R,S\in {\mathrm{Arr}}_{\mathcal{A}}(\overleftarrow{R},\overrightarrow{R})$. In addition, $·\sqcap ·$ and ${(·)}^{\circ }$ are to satisfy:

$\begin{array}{cc}\hfill R^{\circ \circ }& =R,\hfill \end{array}$	(1a)	$\begin{array}{cc}\hfill R(S\sqcap T)& ⊑RS\sqcap RT\hfill \end{array}$	(1d)
$\begin{array}{cc}\hfill {(RS)}^{\circ }& =S^{\circ }{R}^{\circ },\hfill \end{array}$	(1b)	$\begin{array}{cc}\hfill RS\sqcap T& ⊑(R\sqcap T{S}^{\circ })S\hfill \end{array}$	(1e)
$\begin{array}{cc}\hfill {(R\sqcap S)}^{\circ }& =R^{\circ }\sqcap S^{\circ },\hfill \end{array}$	(1c)

For all $R,S,T\in \mathrm{Arr}\left[\mathcal{A}\right]$, such that the above formulas are well defined. Applying the reciprocation to both sides of the Equation (1d) (right semi-distributivity) and (1e) (right modular identity), using the Equations (1a)–(1c) and redefining symbols yields easily the following right versions:

$$(S\sqcap T)R⊑SR\sqcap TR(1\text{f})RS\sqcap T⊑R(S\sqcap R^{\circ }T)$$

(1g)

Allegories generalize the allegory $\mathcal{R}$ of sets (objects) and binary relations (arrows). Because of this, we may refer to arrows in any allegory as “relations”. In $\mathcal{R}$, we write $aRb$ iff $(a,b)\in R$. The identity in $\mathcal{R}$ is $\mathrm{id}:A\mapsto \{(a,a)|a\in A\}$, and the intersection is the set intersection, i.e., $R\sqcap S:=R\cap S$, reciprocation is defined by $a{R}^{\circ }b:\equiv bRa$ and composition of relations $R,S\in \mathrm{Arr}\left[\mathcal{R}\right]$ such that $\overrightarrow{R}=\overleftarrow{S}$ is defined by:

$$a(RS)c:\equiv \exists b\in \overrightarrow{R}.aRb\wedge bSc$$

(2)

We distinguish the following classes of arrows in allegory:

• If ${\mathrm{id}}_{\overleftarrow{R}}⊑R{R}^{\circ }$, then R is called total;
• If $R^{\circ }R⊑{\mathrm{id}}_{\overrightarrow{R}}$, then R is called functional;
• If R is functional and total, it is called a map. A set of all maps in an allegory $\mathcal{A}$ is denoted by $\mathrm{Map}\left[\mathcal{A}\right]$;
• If $R{R}^{\circ }⊑{\mathrm{id}}_{\overleftarrow{R}}$, then R is called injective;
• If ${\mathrm{id}}_{\overrightarrow{R}}⊑R^{\circ }R$, then R is called surjective;
• If $\overleftarrow{R}=\overrightarrow{R}=C$ and $R⊑{\mathrm{id}}_C$, then R is called coreflexive.

If $R\in \mathrm{Arr}\left[\mathcal{A}\right]$ is an isomorphism in an allegory $\mathcal{A}$, then both R and $R^{\circ }$ are maps, and $R^{-1}=R^{\circ }$. Note that ${\mathrm{id}}_A$ for all $A\in \mathrm{Obj}\left[\mathcal{A}\right]$ is a map, and the composition of maps is a map. For any $A,B\in \mathrm{Obj}\left[\mathcal{A}\right]$, we denote by ${\top }_{A,B}$ the top element of ${\mathrm{Arr}}_{\mathcal{A}}(A,B)$, if it exists. In $\mathcal{R}$, we have ${\top }_{AB}:=A\times B$.

An arrow T is called symmetric if $T^{\circ }=T$. Some symmetric arrows might admit splittings:

Definition 1. An arrow R is called a splitting of a symmetric arrow T if and only if $R{R}^{\circ }={\mathrm{id}}_{\overleftarrow{R}}$, $R^{\circ }R=T$.

We will make frequent use of the following results (cf. [14]):

Lemma 2. $R(S\sqcap T)=RS\sqcap RT$ for all $•\stackrel{R}{\to }•\underset{T}{\overset{S}{\rightrightarrows }}•$, such that R is functional. Similarly, $(S\sqcap T)R=SR\sqcap TR$ for all $•\underset{T}{\overset{S}{\rightrightarrows }}•\stackrel{R}{\to }•$, such that $R^{\circ }$ is functional.

Lemma 3. Define $\mathfrak{Dom}(R):={\mathrm{id}}_{\overleftarrow{R}}\sqcap R{R}^{\circ }$. Then, $\mathfrak{Dom}(R\sqcap S)={\mathrm{id}}_{\overleftarrow{R}}\sqcap R{S}^{\circ }$ for all $•\underset{S}{\overset{R}{\rightrightarrows }}•$.

Lemma 4. Suppose that A is coreflexive. Then, $A=A^{\circ }$ (A is symmetric). Moreover, if B is another coreflexive arrow, such that $\overleftarrow{A}=\overleftarrow{B}$ and $\overrightarrow{A}=\overrightarrow{B}$, then $AB=A\sqcap B$. In particular, this implies that $AB=BA$, $AB$ is again coreflexive (as $A\sqcap B$ obviously is) and that A is idempotent (i.e., $AA=A$). Finally, A (and, hence, $A^{\circ }$) is functional, as $A^{\circ }A=AA=A⊑{\mathrm{id}}_{\overleftarrow{A}}$.

Lemma 5. Maps are incomparable The ordering restricted to maps is discrete, that is $f⊑g\equiv f=g$ for all $f,g\in \mathrm{Map}\left[\mathcal{A}\right]$.

Lemma 6. ([15]) Suppose that 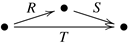and that S is functional. Then, $RS\sqcap T=(R\sqcap T{S}^{\circ })S$.

2.3. Distributive and Division Allegories

A distributive allegory is an allegory $\mathcal{A}$ in which for all hom-sets ${\mathrm{Arr}}_{\mathcal{A}}(A,B)$, there exists a bottom element ${\perp }_{AB}\in {\mathrm{Arr}}_{\mathcal{A}}(A,B)$ and a binary operation $·\bigsqcup ·:{\mathrm{Arr}}_{\mathcal{A}}(A,B)\times {\mathrm{Arr}}_{\mathcal{A}}(A,B)\to {\mathrm{Arr}}_{\mathcal{A}}(A,B)$, which together with $·\sqcap ·$ makes ${\mathrm{Arr}}_{\mathcal{A}}(A,B)$ a distributive lattice with $·\sqcap ·$ as the infimum and $·\bigsqcup ·$ as the supremum. In addition, we require that $·\bigsqcup ·$ and ${\perp }_{AB}$ satisfy:

$$R{\perp }_{\overrightarrow{R}B}={\perp }_{\overleftarrow{R}B},R(S\bigsqcup T)=RS\bigsqcup RT$$

for all $R,S,T\in \mathrm{Arr}\left[\mathcal{A}\right]$, such that the above formulae are type-correct.

A division allegory is a distributive allegory with a partial binary operation $·\backslash ·$ (called a left division), defined if and only if both arguments have the same sources, and satisfying for all

$$\begin{array}{c}\hfill \overleftarrow{R\backslash T}=\overrightarrow{R},\overrightarrow{R\backslash T}=\overrightarrow{T},S⊑R\backslash T\equiv RS⊑T\end{array}$$

Note that $\mathcal{R}$ is a division allegory with the union defined as set union, i.e., $R\bigsqcup S:=R\cup S$, bottom ${\perp }_{AB}=\varnothing$ and a left division defined by:

$$R\backslash T:=\{(x,y)\in \overrightarrow{R}\times \overrightarrow{T}|\forall z\in \overleftarrow{R}.(z,x)\in R\Rightarrow (z,y)\in T\}$$

2.4. A Functional Part of a Relation

The notion of a functional part $\mathrm{unp}(R)$ of a relation R was introduced in [3] and was later generalized to division allegories in [15]. Let $\mathcal{A}$ be a division allegory, and let $R\in \mathrm{Arr}\left[\mathcal{A}\right]$. Then, the functional part of R [3,15] is defined by:

$$\mathrm{unp}(R):=R\sqcap (R^{\circ }\backslash {\mathrm{id}}_{\overleftarrow{R}})$$

(3)

Note that in $\mathcal{R}$, we have, for any $R\in \mathrm{Arr}\left[\mathcal{R}\right]$:

$$\mathrm{unp}(R)=\{(x,y)\in R|\forall z\in \overrightarrow{R}.(x,z)\in R\Rightarrow z=y\}$$

which, together with the following lemma, justifies interpreting $\mathrm{unp}(R)$ as the functional part of R.

Lemma 7. ([3,15]) For any $R\in \mathrm{Arr}\left[\mathcal{A}\right]$, where $\mathcal{A}$ is a division allegory, we have that $\mathrm{unp}(R)$ is functional, and moreover, R is functional if and only if $R=\mathrm{unp}(R)$.

The following result, which (slightly differently phrased) was proven in [15], shows that, given relevant splittings, we can associate a map to any relation.

Lemma 8. Let $\mathcal{A}$ be a division allegory, and let $R\in \mathrm{Arr}\left[\mathcal{A}\right]$. Let also A be a coreflexive arrow, such that $A⊑\mathrm{unp}(R)\mathrm{unp}{(R)}^{\circ }$. Suppose that A has a splitting s, i.e., $s^{\circ }s=A$, $s{s}^{\circ }={\mathrm{id}}_{\overleftarrow{s}}$. Then $s;\mathrm{unp}(R)\in \mathrm{Map}\left[\mathcal{A}\right]$.

Proof. We provide the proof for completeness. Note first that s is functional as $s^{\circ }s=A⊑{\mathrm{id}}_{\overrightarrow{s}}$. Furthermore, $\mathrm{unp}(R)$ is functional by Lemma 7. Hence, $s;\mathrm{unp}(R)$ must be functional, as well, being a composition of functional arrows. The arrow $s;\mathrm{unp}(R)$ is also total as:

$$\begin{array}{cccc}\hfill s;\mathrm{unp}(R);\mathrm{unp}{(R)}^{\circ };s^{\circ }& ⊒sA{s}^{\circ }\hfill & \hfill & \{\text{as}\mathrm{unp}(R);\mathrm{unp}{(R)}^{\circ }⊒A\}\hfill \\ & =s{s}^{\circ }s{s}^{\circ }\hfill & & \{\text{as}A=s^{\circ }s\}\hfill \\ & ={\mathrm{id}}_{\overleftarrow{s}}\hfill & & \{\text{as}s{s}^{\circ }={\mathrm{id}}_{\overleftarrow{s}}\}\hfill \end{array}$$

☐

2.5. Relational Products

Here is a standard definition of a relational binary product in an allegory. Note that it is necessary to assume the existence of the top relation between objects that are supposed to be the components of the relational product.

Definition 9. ([14]) Let $\mathcal{A}$ be an allegory. A pair of arrows $•\stackrel{{\pi }_1}{\leftarrow }C\stackrel{{\pi }_2}{\to }•$ is called a relational product if and only if it satisfies the following conditions:

$$\begin{array}{c}{\pi }_1^{\circ }{\pi }_1={\mathrm{id}}_{\overrightarrow{{\pi }_1}},{\pi }_2^{\circ }{\pi }_2={\mathrm{id}}_{\overrightarrow{{\pi }_2}},\end{array}$$

(4a)

$$\begin{array}{c}{\pi }_1{\pi }_1^{\circ }\sqcap {\pi }_2{\pi }_2^{\circ }={\mathrm{id}}_C,\end{array}$$

(4b)

$$\begin{array}{c}{\pi }_1^{\circ }{\pi }_2={\top }_{\overrightarrow{{\pi }_1}\overrightarrow{{\pi }_2}}\end{array}$$

(4c)

The following is the weakening of the above definition formulated in [15]:

Definition 10. ([15]) Let $\mathcal{A}$ be an allegory. A pair of arrows $•\stackrel{{\pi }_1}{\leftarrow }C\stackrel{{\pi }_2}{\to }•$ is called a weak relational product if and only if it satisfies the following conditions:

$$\begin{array}{c}{\pi }_1^{\circ }{\pi }_1⊑{\mathrm{id}}_{\overrightarrow{{\pi }_1}},{\pi }_2^{\circ }{\pi }_2⊑{\mathrm{id}}_{\overrightarrow{{\pi }_2}},\end{array}$$

(5a)

$$\begin{array}{c}{\pi }_1{\pi }_1^{\circ }\sqcap {\pi }_2{\pi }_2^{\circ }={\mathrm{id}}_C,\end{array}$$

(5b)

(5c)

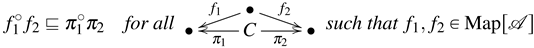
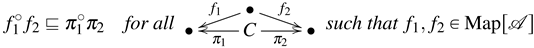
In [15], it was proven that a weak relational product is a categorical product in the subcategory of maps. Additionally, it is immediate.

3. Weak n-Ary Relational Products

The following is a generalization of the characterization of binary relational products to the characterization of n-ary products.

Definition 11. ([17]) Let $I=\{1,\dots ,n\}$. A finite family of arrows ${\{{\pi }_i\}}_{i\in I}\subseteq \mathrm{Arr}\left[\mathcal{A}\right]$ with a common source C, that is, such that $\overleftarrow{{\pi }_i}=C$ for all $i\in I$, is called an n-ary relational product if and only if it satisfies the following conditions:

$$\begin{array}{c}\forall i.{\pi }_i^{\circ }{\pi }_i={\mathrm{id}}_{\overrightarrow{{\pi }_i}},\end{array}$$

(6a)

$$\begin{array}{c}\underset{i}{\sqcap }{\pi }_i{\pi }_i^{\circ }={\mathrm{id}}_C,\end{array}$$

(6b)

$$\begin{array}{c}\forall k\in I.\left(\underset{i\in I\backslash \{k\}}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k={\top }_{\overleftarrow{{\pi }_k}\overrightarrow{{\pi }_k}}\end{array}$$

(6c)

Before we present the weakening of the above definition, we need the following piece of notation. Let $\pi :={\{{\pi }_i\}}_{i\in I}$ be a finite family of arrows in an allegory $\mathcal{A}$ with a common source. We denote:

$${\mathcal{F}}_{\pi }:=\left\{{\{f_i\}}_{i\in I}|\left(\forall i\in I.f_i\in \mathrm{Map}\left[\mathcal{A}\right]\wedge \overrightarrow{f_i}=\overrightarrow{{\pi }_i}\right)\wedge \left(\forall i,j\in I.\overleftarrow{f_i}=\overleftarrow{f_j}\right)\right\}$$

(7)

The following is the weakening of Definition 11:

Definition 12. Let $I=\{1,\dots ,n\}$. A finite family of arrows ${\{{\pi }_i\}}_{i\in I}\subseteq \mathrm{Arr}\left[\mathcal{A}\right]$ with a common source C, that is, such that $\overleftarrow{{\pi }_i}=C$ for all $i\in I$, is called a weak n-ary relational product if and only if it satisfies the following conditions:

$$\begin{array}{c}\forall i.{\pi }_i^{\circ }{\pi }_i⊑{\mathrm{id}}_{\overrightarrow{{\pi }_i}},\end{array}$$

(8a)

$$\begin{array}{c}\forall {\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi },i\in I.f_i^{\circ }{f}_i⊑{\pi }_i^{\circ }{\pi }_i,\end{array}$$

(8b)

$$\begin{array}{c}\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }={\mathrm{id}}_C,\end{array}$$

(8c)

$$\begin{array}{c}\forall J⊊I,k\in I\backslash J,{\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }.\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k⊒\left(\underset{i\in J}{\sqcap }{\pi }_i{f}_i^{\circ }\right)f_k\end{array}$$

(8d)

An immediate corollary of Equations (8a) and (8c) is that arrows ${\pi }_i$ for all i are maps. Another immediate corollary is that an n-ary relational product is also a weak n-ary relational product. The following result shows that any categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$ satisfies most of the Conditions (8):

Lemma 13. (cf. [15]). Let ${\{{\pi }_i\}}_{i\in I}$ be an n-ary categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$. Then, ${\{{\pi }_i\}}_{i\in I}$ satisfies Conditions (8a), (8b), (8d) and the “⊒” part of (8c).

Proof. Condition (8a) and the “⊒” part of Condition (8c) are satisfied, because all ${\pi }_i$’s are maps, hence, respectively, functional and total. Let now ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }$. Because ${\{{\pi }_i\}}_{i\in I}$ is a categorical n-ary product, it follows that there exists a (unique) map $h\in \mathrm{Map}\left[\mathcal{A}\right]$, such that $f_i=h{\pi }_i$ for all $i\in I$. Hence, for all $i\in I$:

$$\begin{array}{cccc}\hfill f_i^{\circ }{f}_i& ={\pi }_i^{\circ }{h}^{\circ }h{\pi }_i\hfill & \hfill & \\ & ⊑{\pi }_i^{\circ }{\pi }_i\hfill & & \{h\text{is}\text{functional}\}\hfill \end{array}$$

which proves Condition (8b). Similarly, we prove Condition (8d). Let $J⊊I$, and let $k\in I\backslash J$. Tthen:

$$\begin{array}{cccc}\hfill \left(\underset{i\in J}{\sqcap }{\pi }_i{f}_i^{\circ }\right)f_k& =\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }{h}^{\circ }\right)h{\pi }_k\hfill & \hfill & \\ & =\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right)h^{\circ }h{\pi }_k\hfill & & \{\text{by}\text{Lemma}2\}\hfill \\ & ⊑\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k\hfill & & \{h\text{is}\text{functional}\}\hfill \end{array}$$

☐

Both the binary weak relational product and n-ary relational product are axiomatized using three axioms, two of which correspond to the properties (8a) and (8c) of a weak n-ary relational product. It is therefore interesting to check if the remaining properties (8b) and (8d) are really independent or if one of them implies the other in the presence of other axioms. The following two examples prove that neither implication holds:

Example 14. Consider the allegory $\mathcal{R}$ of binary relations, and let $A\in \mathrm{Obj}\left[\mathcal{R}\right]$ be any set that is neither empty nor a singleton. It is immediate that the three maps ${\pi }_1,{\pi }_2,{\pi }_3:={\mathrm{id}}_A$ satisfy the Conditions (8a), (8b) and (8c) (for $I:=\{1,2,3\}$). They fail, however, to satisfy Condition (8d). Indeed, let $f_1,f_2,f_3:A\times A\to A$, where $f_1$ and $f_2$ are both projections on the first component of a Cartesian product $A\times A$ and $f_3$ is the projection on the second component. Then, we have that $\left({\sqcap }_{i\in \{1,2\}}{\pi }_i{\pi }_i^{\circ }\right){\pi }_3={\mathrm{id}}_A$, and $\left({\sqcap }_{i\in \{1,2\}}{\pi }_i{f}_i^{\circ }\right)f_3=f_2^{\circ }{f}_3={\top }_A$. However, as A is neither empty nor singleton, we must have ${\mathrm{id}}_A⊏{\top }_A$, contradicting Condition (8d).

Example 15. Consider the allegory $\mathcal{A}$, with two distinct objects, A and B, and with:

$$\begin{array}{c}{\mathrm{Arr}}_{\mathcal{A}}(A,A):=\{{\mathrm{id}}_A\},{\mathrm{Arr}}_{\mathcal{A}}(A,B):=\{\pi \},{\mathrm{Arr}}_{\mathcal{A}}(B,A):=\{{\pi }^{\circ }\},\mathrm{Arr}(B,B):=\{{\mathrm{id}}_B,{\pi }^{\circ }\pi \},\end{array}$$

where π satisfies:

$$\pi {\pi }^{\circ }={\mathrm{id}}_A,{\pi }^{\circ }\pi ⊏{\mathrm{id}}_B$$

This allegory can be realized in $\mathcal{R}$ by setting, e.g.,

$$A:=\{0\},B:=\{0,1\},\pi :=\{(0,0)\}$$

Let now $I:=\{1,2,3\}$, and let ${\pi }_1,{\pi }_2,{\pi }_3:=\pi$. It is immediate that both Equations (8a) and (8c) are satisfied by the ${\pi }_i$’s. To check the remaining two axioms of n-ary weak relational product, first note that ${\mathcal{F}}_{\pi }$ contains only two families of maps ${\{f_i\}}_{i\in \{1,2,3\}}$: one obtained by setting $f_1,f_2,f_3:={\mathrm{id}}_B$; the other one by setting $f_1,f_2,f_3:=\pi$. Both families satisfy property (8d); however, setting $f_1,f_2,f_3:={\mathrm{id}}_B$ provides a counterexample to Equation (8b).

The following two lemmas are crucial for proving the main result of this paper:

Lemma 16. Let $I:=\{1,\dots ,n\}$, and let ${\{{\pi }_i\}}_{i\in I}\subseteq \mathrm{Arr}\left[\mathcal{A}\right]$ be a weak n-ary relational product. Let ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }$. Define $h_J:={\sqcap }_{i\in J}{f}_i{\pi }_i^{\circ }$, for all $\varnothing \ne J\subseteq I$. Then, for all $\varnothing \ne J⊊I$ and $k\in I\backslash J$, the totality of $h_J$ implies that $h_J{\pi }_k{f}_k^{\circ }⊒{\mathrm{id}}_{\overleftarrow{h_J}}$.

Proof. Let $\varnothing \ne J⊊I$ and $k\in J\backslash I$. Assume that $h_J$ is total. Then:

$$\begin{array}{cccc}\hfill h_J{\pi }_k{f}_k^{\circ }& =\left(\underset{i\in J}{\sqcap }{f}_i{\pi }_i^{\circ }\right){\pi }_k{f}_k^{\circ }\hfill & \hfill & \{\text{definition}\text{of}{h}_k\}\hfill \\ & ⊒\left(\underset{i\in J}{\sqcap }{f}_i{\pi }_i^{\circ }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k{f}_k^{\circ }\hfill & & \{\text{by}\text{Equation}(8\text{a})\}\hfill \\ & ⊒\left(\underset{i\in J}{\sqcap }{h}_J{\pi }_i{\pi }_i^{\circ }\right){\pi }_k{f}_k^{\circ }\hfill & & \{\text{As}{h}_J⊑f_i{\pi }_i^{\circ }\text{for}\text{all}i\in J\}\hfill \\ & ⊒h_J\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k{f}_k^{\circ }\hfill & & \{\text{by}\text{Equation}(1\text{d})\}\hfill \\ & ⊒h_J{h}_J^{\circ }{f}_k{f}_k^{\circ }\hfill & & \{\text{by}\text{Equation}(8\text{d})\text{as}{h}_J^{\circ }{f}_k=\left(\underset{i\in J}{\sqcap }{\pi }_i{f}_i^{\circ }\right)f_k\}\hfill \\ & ⊒{\mathrm{id}}_{\overleftarrow{f_k}}\hfill & & \{\text{because}{h}_J\text{and}{f}_k\text{are}\text{total}\}\hfill \end{array}$$

☐

Lemma 17. Let $I:=\{1,\dots ,n\}$, and let ${\{{\pi }_i\}}_{i\in I}\subseteq \mathrm{Arr}\left[\mathcal{A}\right]$ be a weak n-ary relational product. Let ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }$. Then, $h_J:={\sqcap }_{i\in J}{f}_i{\pi }_i^{\circ }$ is total for all $\varnothing \ne J\subseteq I$.

Proof. We prove the lemma using induction on J. For the base case, note that for all $i\in I$:

$$\begin{array}{cccc}\hfill h_{\{i\}}{h}_{\{i\}}^{\circ }& =f_i{\pi }_i^{\circ }{\pi }_i{f}_i^{\circ }\hfill & \hfill & \{\text{definition}\text{of}{h}_{\{i\}}\}\hfill \\ & ⊒f_i{f}_i^{\circ }{f}_i{f}_i^{\circ }\hfill & & \{\text{by}\text{Condition}(\text{8b})\}\hfill \\ & ⊒{\mathrm{id}}_{\overleftarrow{f_1}}\hfill & & \{\text{as}{f}_i\text{is}\text{total}\}\hfill \end{array}$$

Suppose now that we have proven for some $\varnothing \ne J⊊I$ that $h_J$ is total. Note that $\mathfrak{Dom}(R)={\mathrm{id}}_{\overleftarrow{R}}$ is equivalent with R being total. We have:

$$\begin{array}{cccc}\hfill \mathfrak{Dom}(h_{J\cup \{k\}})& =\mathfrak{Dom}\left(\underset{i\in J\cup \{k\}}{\sqcap }{f}_i{\pi }_i^{\circ }\right)\hfill & \hfill & \{\text{definition}\text{of}{h}_{J\cup \{k\}}\}\hfill \\ & =\mathfrak{Dom}(h_J\sqcap f_k{\pi }_k^{\circ })\hfill & & \{\text{definition}\text{of}{h}_J\}\hfill \\ & ={\mathrm{id}}_{\overleftarrow{f_k}}\sqcap h_J{\pi }_k{f}_k^{\circ }\hfill & & \{\text{by}\text{Lemma}3\}\hfill \\ & ={\mathrm{id}}_{\overleftarrow{f_k}}\hfill & & \{\text{By}\text{Lemma}16\text{and}\text{inductive}\text{assumption}\text{that}{h}_J\text{is}\text{total.}\}\hfill \end{array}$$

☐

The following result, which is the main result of this paper, shows that an n-ary weak relational product is in fact a categorical product for maps.

Theorem 18. Suppose that ${\{{\pi }_i\}}_{i\in I}\subseteq \mathrm{Arr}\left[\mathcal{A}\right]$ is a weak n-ary relational product. Let an arrow $h\in \mathrm{Arr}\left[\mathcal{A}\right]$ and family of maps ${\{f_i\}}_{i\in I}\subseteq \mathrm{Map}\left[\mathcal{A}\right]$ be such that for all $i\in I$, we 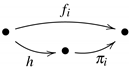have .

Then:

$$h=\underset{i}{\sqcap }{f}_i{\pi }_i^{\circ }\equiv h\in \mathrm{Map}\left[\mathcal{A}\right]\wedge \left(\forall i.h{\pi }_i=f_i\right)$$

Note that the diagram in the assumptions of the above theorem above implicitly implies that all of the maps $f_i$ have a common source.

Proof. (Theorem 18) First, assume that $h\in \mathrm{Map}\left[\mathcal{A}\right]$ and $h{\pi }_i=f_i$ for all $i\in I$. Then:

$$\begin{array}{cccc}\hfill h& =h\underset{i}{\sqcap }{\pi }_i{\pi }_i^{\circ }\hfill & \hfill & \{\text{by}\text{Equation}(\text{8c})\}\hfill \\ & =\underset{i}{\sqcap }h{\pi }_i{\pi }_i^{\circ }\hfill & \hfill & \{\text{by}\text{Lemma}2\text{as}h\in \mathrm{Map}\left[\mathcal{A}\right]\}\hfill \\ & =\underset{i}{\sqcap }{f}_i{\pi }_i^{\circ }\hfill & \hfill & \{\text{as}\forall i.h{\pi }_i=f_i\}\hfill \end{array}$$

Assume now that $h={\sqcap }_i{f}_i{\pi }_i^{\circ }$. Then:

The arrow h is functional, that is $h^{\circ }h⊑{\mathrm{id}}_{\overrightarrow{h}}$. Indeed, for all $k\in I$:

$$\begin{array}{cccc}\hfill h^{\circ }h& ={\left(\underset{i}{\sqcap }{f}_i{\pi }_i^{\circ }\right)}^{\circ }\left(\underset{j}{\sqcap }{f}_j{\pi }_j^{\circ }\right)\hfill & \hfill & \{\text{definition}\text{of}h\}\hfill \\ & ⊑{\pi }_k{f}_k^{\circ }{f}_k{\pi }_k^{\circ }\hfill & & \{\text{monotonicity}\text{of}\text{composition}\text{and}{(·)}^{\circ }\}\hfill \\ & ⊑{\pi }_k{\pi }_k^{\circ }\hfill & & \{f_k\text{is}\text{functional}\}\hfill \end{array}$$

Hence:

$$\begin{array}{cccc}\hfill h^{\circ }h& ⊑\underset{i}{\sqcap }{\pi }_i{\pi }_i^{\circ }\hfill & \hfill & \{\text{as}\forall i.h^{\circ }h⊑{\pi }_i{\pi }_i^{\circ }\}\hfill \\ & ={\mathrm{id}}_{\overrightarrow{h}}\hfill & & \{\text{by}\text{Equation}(\text{8c})\}\hfill \end{array}$$

The arrow h is total, that is $h{h}^{\circ }⊒{\mathrm{id}}_{\overleftarrow{h}}$. Indeed, this is stated in Lemma 17.

Equality $h{\pi }_i=f_i$ holds for all i. Indeed,

$$\begin{array}{cccc}\hfill h{\pi }_i& =\left(\underset{k}{\sqcap }{f}_k{\pi }_k^{\circ }\right){\pi }_i\hfill & \hfill & \{\text{substitute}\text{definition}\text{of}h\}\hfill \\ & ⊑f_i{\pi }_i^{\circ }{\pi }_i\hfill & & \{\text{meet}\text{property}\}\hfill \\ & ⊑f_i\hfill & & \{\text{by}\text{Equation}(\text{8a})\}\hfill \end{array}$$

On the other hand, we have already proven that h is a map, and so, both $h{\pi }_i$ and $f_i$ are maps; hence, by Lemma 5, $h{\pi }_i⊑f_i$ implies $h{\pi }_i=f_i$. ☐

Let us also note that our definition of a weak n-ary relational product is a generalization of a weak binary relational product, i.e., a pair of arrows ${\pi }_i$, $i=1,2$ with a common source in an allegory $\mathcal{A}$ is a weak binary relational product (Definition 10) if and only if it is a weak two-ary relational product (Definition 12). Indeed, by Theorem 18 and ([15], Theorem 2), a pair of arrows satisfying conditions of either of these two definitions is a categorical product for maps. Then, by Lemma 13 and ([15], Lemma 5) a categorical product satisfies all of the conditions of Definitions 10 and 12 apart from the “⊑” part of Equations (5b) and (8c), which in this case, are identical anyway.

An example given in [15] shows that there are indeed allegories $\mathcal{A}$ for which a categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$ does not satisfy the “⊑” part of Equation (8c); hence, one needs to assume something more about $\mathcal{A}$ to ensure that n-ary categorical products in $\mathrm{Map}\left[\mathcal{A}\right]$ satisfy all Conditions (8). The following result is a generalization of ([15], Lemma 6) to the case of weak n-ary relational products.

Lemma 19. Suppose that ${\{{\pi }_i\}}_{i\in I}$, $I=\{1,\dots ,n\}$ is an n-ary categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$. If there exists a splitting $R\in \mathrm{Arr}\left[\mathcal{A}\right]$ of ${\sqcap }_{i\in I}{\pi }_i{\pi }_i^{\circ }$, then ${\{{\pi }_i\}}_{i\in I}$ is an n-ary weak relational product.

Proof. The basic idea of the proof is the same as of the proof of ([15], Lemma 6): we first prove that ${\{R{\pi }_i\}}_{i\in I}$ is a weak n-ary relational product, and then, we use this result to prove that ${\{{\pi }_i\}}_{i\in I}$ must be a weak n-ary relational product, too. Let us denote ${\tilde{\pi }}_i:=R{\pi }_i$ for all $i\in I$. The family ${\{{\tilde{\pi }}_i\}}_{i\in I}$ satisfies Condition (8a). Indeed, we have (cf. the proof of ([15], Lemma 6)) that for all $i\in I$:

$$\begin{array}{cccc}\hfill {\tilde{\pi }}_i^{\circ }{\tilde{\pi }}_i& ={\pi }_i^{\circ }{R}^{\circ }R{\pi }_i\hfill & \hfill & \\ & ={\pi }_i^{\circ }\left({\pi }_i{\pi }_i^{\circ }\sqcap \underset{j\in I\backslash \{i\}}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i\hfill & & \{\text{as}{R}^{\circ }R=\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\}\hfill \\ & ={\mathrm{id}}_{\overrightarrow{{\pi }_i}}\sqcap {\pi }_i^{\circ }\left(\underset{j\in I\backslash \{i\}}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i\hfill & & \{\text{by}\text{Lemma}6\text{as}{\pi }_i\text{is}\text{functional}\}\hfill \\ & ⊑{\mathrm{id}}_{\overrightarrow{{\tilde{\pi }}_i}}\hfill & & \{\text{as}\overrightarrow{{\tilde{\pi }}_i}=\overrightarrow{{\pi }_i}\}\hfill \end{array}$$

Note that $R{R}^{\circ }={\mathrm{id}}_{\overleftarrow{R}}$ implies that $R^{\circ }$ is functional. Observe that for all $i\in I$:

$$\left(\underset{j\in I}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i⊑{\pi }_i$$

(9)

Indeed,

$$\begin{array}{cccc}\hfill \left(\underset{j\in I}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i& =\left({\pi }_i{\pi }_i^{\circ }\sqcap \underset{j\in I\backslash \{i\}}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i\hfill & \hfill & \\ & ={\pi }_i\sqcap \left(\underset{j\in I\backslash \{i\}}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i\hfill & \hfill & \{\text{by}\text{Lemma}6\text{as}{\pi }_i\text{is}\text{functional}\}\hfill \\ & ⊑{\pi }_i\hfill & \end{array}$$

It follows that ${\{{\tilde{\pi }}_i\}}_{i\in I}$ satisfies (cf. the proof of ([15], Lemma 6)):

$$\begin{array}{cccc}\hfill \underset{i\in I}{\sqcap }{\tilde{\pi }}_i{\tilde{\pi }}_i^{\circ }& =\underset{i\in I}{\sqcap }R{\pi }_i{\pi }_i^{\circ }{R}^{\circ }\hfill & \hfill & \\ & =R{\pi }_1{\pi }_1^{\circ }{R}^{\circ }\sqcap \underset{i\in I\backslash \{1\}}{\sqcap }R{\pi }_i{\pi }_i^{\circ }{R}^{\circ }\hfill & & \\ & =R\left({\pi }_1{\pi }_1^{\circ }\sqcap R^{\circ }(\underset{i\in I\backslash \{1\}}{\sqcap }R{\pi }_i{\pi }_i^{\circ }{R}^{\circ })R\right)R^{\circ }\hfill & & \{\text{by}\text{Lemma}6\text{as}{R}^{\circ }\text{is}\text{functional}\}\hfill \\ & ⊑R\left({\pi }_1{\pi }_1^{\circ }\sqcap \underset{i\in I\backslash \{1\}}{\sqcap }{R}^{\circ }R{\pi }_i{\pi }_i^{\circ }{R}^{\circ }R\right)R^{\circ }\hfill & & \{\text{by}\text{Equations}(\text{1g})\text{and}(\text{1d})\}\hfill \\ & =R\left({\pi }_1{\pi }_1^{\circ }\sqcap \underset{i\in I\backslash \{1\}}{\sqcap }\left((\underset{j\in I}{\sqcap }{\pi }_j{\pi }_j^{\circ }){\pi }_i{\pi }_i^{\circ }(\underset{k\in I}{\sqcap }{\pi }_k{\pi }_k^{\circ })\right)\right)R^{\circ }\hfill & & \{\text{as}{R}^{\circ }R=\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\}\hfill \\ & ⊑R\left({\pi }_1{\pi }_1^{\circ }\sqcap \underset{i\in I\backslash \{1\}}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right)R^{\circ }\hfill & & \{\text{by}\text{Equation}(9)\}\hfill \\ & =R\left(\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right)R^{\circ }\hfill & & \\ & =R{R}^{\circ }R{R}^{\circ }\hfill & & \{\text{as}{R}^{\circ }R=\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\}\hfill \\ & ={\mathrm{id}}_{\overleftarrow{R}}\hfill & \end{array}$$

On the other hand, for all $i\in I$, we have that [15] ${\tilde{\pi }}_i{\tilde{\pi }}_i^{\circ }=R{\pi }_i{\pi }_i^{\circ }{R}^{\circ }⊒R{R}^{\circ }={\mathrm{id}}_{\overleftarrow{R}}$, as ${\pi }_i$ is total, for all $i\in I$; hence, also, ${\sqcap }_{i\in I}{\tilde{\pi }}_i{\tilde{\pi }}_i^{\circ }⊒{\mathrm{id}}_{\overleftarrow{R}}$. Thus, the family ${\{{\tilde{\pi }}_i\}}_{i\in I}$ satisfies Condition (8c).

In order to see that the family ${\{{\tilde{\pi }}_i\}}_{i\in I}$ satisfies Condition (8b), note first that ${\mathcal{F}}_{\tilde{\pi }}={\mathcal{F}}_{\pi }$ and that ${\{{\pi }_i\}}_{i\in I}$ is by assumption a categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$ and, thus, by Lemma 13, satisfies all of Condition (8) but the “⊑” part of Condition (8c). Hence, for all families ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\tilde{\pi }}$, we have:

$$\begin{array}{cccc}\hfill f_i^{\circ }{f}_i& ⊑{\pi }_i^{\circ }{\pi }_i\hfill & \hfill & \{\text{by}\text{Equation}(\text{8b})\text{as}{\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }\}\hfill \\ & ⊑{\pi }_i^{\circ }\left(\underset{j\in I}{\sqcap }{\pi }_j{\pi }_j^{\circ }\right){\pi }_i\hfill & & \{\text{by}\text{the}“⊒”\text{part}\text{of}\text{Equation}(\text{8c})\}\hfill \\ & ={\pi }_i^{\circ }{R}^{\circ }R{\pi }_i\hfill & & \{\text{as}R\text{is}\text{a}\text{splitting}\text{of}\underset{j\in I}{\sqcap }{\pi }_j{\pi }_j^{\circ }\}\hfill \\ & ={\tilde{\pi }}_i^{\circ }{\tilde{\pi }}_i\hfill \end{array}$$

In order to see that the family ${\{{\tilde{\pi }}_i\}}_{i\in I}$ satisfies Condition (8d), note first that, for any ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\tilde{\pi }}={\mathcal{F}}_{\pi }$, as ${\{{\pi }_i\}}_{i\in I}$ is, by assumption, a categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$, there exists a map h, such that $f_i=h{\pi }_i$ for all $i\in I$. Furthermore, note that, as, by Lemma 13, ${\{{\pi }_i\}}_{i\in I}$ satisfies “⊒” part of Condition (8c) and R is a splitting of ${\sqcap }_{i\in I}{\pi }_i{\pi }_i^{\circ }$, we must have $R^{\circ }R={\sqcap }_{i\in I}{\pi }_i{\pi }_i^{\circ }⊒{\mathrm{id}}_{\overrightarrow{R}}$. Then, it follows that, for all $\varnothing \ne J\subseteq I$ and $k\in I\backslash J$, we have:

$$\begin{array}{cccc}\hfill \left(\underset{j\in J}{\sqcap }{\tilde{\pi }}_j{f}_j^{\circ }\right)f_k& =\left(\underset{j\in J}{\sqcap }R{\pi }_j{f}_j^{\circ }\right)f_k\hfill & \hfill & \\ & =\left(\underset{j\in J}{\sqcap }R{\pi }_j{\pi }_j^{\circ }{h}^{\circ }\right)h{\pi }_k\hfill & & \\ & =\left(\underset{j\in J}{\sqcap }R{\pi }_j{\pi }_j^{\circ }\right)h^{\circ }h{\pi }_k\hfill & & \{\text{by}\text{Lemma}2\text{as}h\text{is}\text{functional}\}\hfill \\ & ⊑\left(\underset{j\in J}{\sqcap }R{\pi }_j{\pi }_j^{\circ }\right){\pi }_k\hfill & & \{h\text{is}\text{functional}\}\hfill \\ & ⊑\left(\underset{j\in J}{\sqcap }R{\pi }_j{\pi }_j^{\circ }{R}^{\circ }R\right){\pi }_k\hfill & & \{R^{\circ }R⊒{\mathrm{id}}_{\overrightarrow{R}}\}\hfill \\ & =\left(\underset{j\in J}{\sqcap }R{\pi }_j{\pi }_j^{\circ }{R}^{\circ }\right)R{\pi }_k\hfill & & \{\text{by}\text{Lemma}2\text{as}{R}^{\circ }\text{is}\text{functional}\}\hfill \\ & =\left(\underset{j\in J}{\sqcap }{\tilde{\pi }}_j{\tilde{\pi }}_j^{\circ }\right){\tilde{\pi }}_k\hfill & \end{array}$$

By Theorem 18, we know now that ${\{{\tilde{\pi }}_i\}}_{i\in I}$ is a categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$ and that the arrow $g:={\sqcap }_{i\in I}{\pi }_i{\tilde{\pi }}_i^{\circ }$ is a map satisfying ${\pi }_i=g{\tilde{\pi }}_i$ for all $i\in I$. On the other hand, as ${\{{\pi }_i\}}_{i\in I}$ is a categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$ by assumption, the standard argument shows that g must be an isomorphism. In any allegory, the inverse of an isomorphism equals the reciprocation of this isomorphism and both the isomorphism and its inverse are maps; hence, in particular $g^{-1}=g^{\circ }$. Denote by C the common source of ${\pi }_i$’s. Putting it together, the argument being almost identical to the proof of ([15], Lemma 6) shows that the family ${\{{\pi }_i\}}_{i\in I}$ satisfies the “⊑” part of Condition (8c):

$$\begin{array}{cccc}\hfill {\mathrm{id}}_C& =g{g}^{-1}\hfill & \hfill & \\ & =\left(\underset{i\in I}{\sqcap }{\pi }_i{\tilde{\pi }}_i^{\circ }\right)g^{-1}\hfill & & \\ & =\left(\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }{(g^{-1})}^{\circ }\right)g^{-1}\hfill & & \{\text{as}{\tilde{\pi }}_i=g^{-1}{\pi }_i\text{for}\text{all}i\in I\}\hfill \\ & =\left(\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }g\right)g^{-1}\hfill & & \{\text{as}{(g^{-1})}^{\circ }={(g^{\circ })}^{\circ }=g\}\hfill \\ & =\left(\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right)g{g}^{-1}\hfill & & \{\text{by}\text{Lemma}2\text{as}{g}^{\circ }=g^{-1}\text{is}\text{functional}\}\hfill \\ & =\left(\underset{i\in I}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right)\hfill & \end{array}$$

This ends the proof, as, by Lemma 13, the family ${\{{\pi }_i\}}_{i\in I}$ satisfies all of the other conditions of Definition 12 by virtue of being the categorical product in $\mathrm{Map}\left[\mathcal{A}\right]$. ☐

In Conditions (8b) and (8d) the range of universal quantification was restricted to maps. The following result, which is the adaptation to n-ary weak relational products of ([15], Lemma 7), shows that we can modify those conditions, so that the range of quantification is restricted only by source-target considerations from the whole set of arrows in the allegory under consideration.

Lemma 20. (cf. ([15], Lemma 7)) Let $\mathcal{A}$ be a division allegory in which all partial identities split. A family ${\{{\pi }_i\}}_{i\in I}$, where $I=\{1,\dots ,n\}$, of arrows in $\mathcal{A}$ with a common source is an n-ary weak relational product if and only if it satisfies Conditions (8a) and (8c), as well as:

$$\begin{array}{c}\forall i\in I.\mathrm{unp}{(R_i)}^{\circ }\left(\underset{i\in I}{\sqcap }\mathfrak{Dom}(\mathrm{unp}(R_i))\right)\mathrm{unp}(R_i)⊑{\pi }_i^{\circ }{\pi }_i,\end{array}$$

(10a)

$$\begin{array}{c}\forall J⊊I,k\in I\backslash J.\left(\underset{i\in J}{\sqcap }{\pi }_i\mathrm{unp}{(R_i)}^{\circ }\right)\left(\underset{i\in I}{\sqcap }\mathfrak{Dom}(\mathrm{unp}(R_i))\right)\mathrm{unp}(R_k)⊑\left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k\end{array}$$

(10b)

for all families ${\{R_i\}}_{i\in I}$ of arrows in $\mathcal{A}$ with a common source and such that $\overrightarrow{R_i}=\overrightarrow{{\pi }_i}$ for all $i\in I$.

Proof. The basic idea of the proof is adapted from the proof of ([15], Lemma 7). It is immediate that if a family ${\{{\pi }_i\}}_{i\in I}$ satisfies Conditions (8a) and (8c), as well as Conditions (10), then it is a weak n-ary relational product, because for any ${\{f_i\}}_{i\in I}\in {\mathcal{F}}_{\pi }$, we have $\mathrm{unp}(f_i)=f_i$ by Lemma 7 and $\mathfrak{Dom}(\mathrm{unp}(f_i))=\mathfrak{Dom}(f_i)={\mathrm{id}}_{\overleftarrow{f_i}}$ for all $i\in I$, and thus, Conditions 10 subsume trivially Conditions (8b) and (8d). Hence, it remains to prove that Conditions (8b) and (8d) imply Conditions (10).

Assume that ${\{{\pi }_i\}}_{i\in I}$ is an n-ary weak relational product, and let ${\{R_i\}}_{i\in I}$ be a family $\mathcal{A}$ with a common source C and such that $\overrightarrow{R_i}=\overrightarrow{{\pi }_i}$ for all $i\in I$. Denote for brevity:

$$ı:=\underset{i\in I}{\sqcap }\mathfrak{Dom}(\mathrm{unp}(R_i))$$

and let s be a splitting of ı, i.e., $s{s}^{\circ }={\mathrm{id}}_{\overleftarrow{s}}$ and $s^{\circ }s=ı$. By Lemma 8, $s;\mathrm{unp}(R_i)$ is a map for all $i\in I$. Now, the families ${\{{\pi }_i\}}_{i\in I}$ and ${\{R_i\}}_{i\in I}$ satisfy Condition (10a) as, for all $i\in I$:

$$\begin{array}{cccc}\hfill \mathrm{unp}{(R_i)}^{\circ };ı;\mathrm{unp}(R_i)& =\mathrm{unp}{(R_i)}^{\circ };s^{\circ };s;\mathrm{unp}(R_i)\hfill & \hfill & \{\text{as}ı=s^{\circ }s\}\hfill \\ & ⊑{\pi }_i^{\circ };{\pi }_i\hfill & & \{\text{by}\text{Condition}(\text{8b})\text{as}s;\mathrm{unp}(R_i)\in \mathrm{Map}\left[\mathcal{A}\right]\}\hfill \end{array}$$

We prove Condition (10b) similarly. Let $\varnothing \ne J⊊I$ and $k\in I\backslash J$. Then:

$$\begin{array}{cccc}& \left(\underset{i\in J}{\sqcap }{\pi }_i;\mathrm{unp}{(R_i)}^{\circ }\right);ı;\mathrm{unp}(R_k)\hfill & \hfill & \\ \hfill =& \left(\underset{i\in J}{\sqcap }{\pi }_i;\mathrm{unp}{(R_i)}^{\circ }\right);s^{\circ };s;\mathrm{unp}(R_k)\hfill & \hfill & \{\text{as}ı=s^{\circ }s\}\hfill \\ \hfill =& \left(\underset{i\in J}{\sqcap }{\pi }_i;\mathrm{unp}{(R_i)}^{\circ };s^{\circ }\right);s;\mathrm{unp}(R_k)\hfill & \hfill & \{\text{by}\text{Lemma}2\text{as}s\text{is}\text{functional}\}\hfill \\ \hfill ⊑& \left(\underset{i\in J}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\pi }_k\hfill & & \{\text{by}\text{Condition}(\text{8d})\text{as}s;\mathrm{unp}(R_j)\text{’s}\text{are}\text{maps.}\}\hfill \end{array}$$

☐

4. Iterated Relational Products

Relational products can be iterated (see, e.g., Diagram 11). We will prove that any iterated product still satisfies the assumptions of Definition 12. It is immediate that in order to enable the trivial induction, it is enough to show that the iteration of the form depicted in the Diagram 11 is a weak $(n+m-1)$-ary relational product ( ${\pi }_i$’s are attached to $\overrightarrow{{\rho }_1}$ for notational convenience, and the proof would work the same for any other position of attachment):

(11)

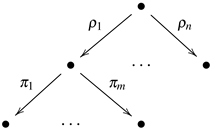
Lemma 21. Let ${\{{\rho }_k\}}_{1\le k\le n}$ and ${\{{\pi }_k\}}_{1\le k\le m}$ be weak n and m-ary relational products, respectively, such that $\overleftarrow{{\pi }_k}=\overrightarrow{{\rho }_1}$ for all $1\le k\le m$ (see Figure 1). Then, ${\{{\delta }_k\}}_{1\le k\le m+n-1}$ defined below is also a relational product:

$${\delta }_k:=\left\{\begin{array}{cc}{\rho }_1{\pi }_k\hfill & \text{if}1\le k\le m\hfill \\ {\rho }_{k-m+1}\hfill & \text{if}m<k<m+n\hfill \end{array}\right..$$

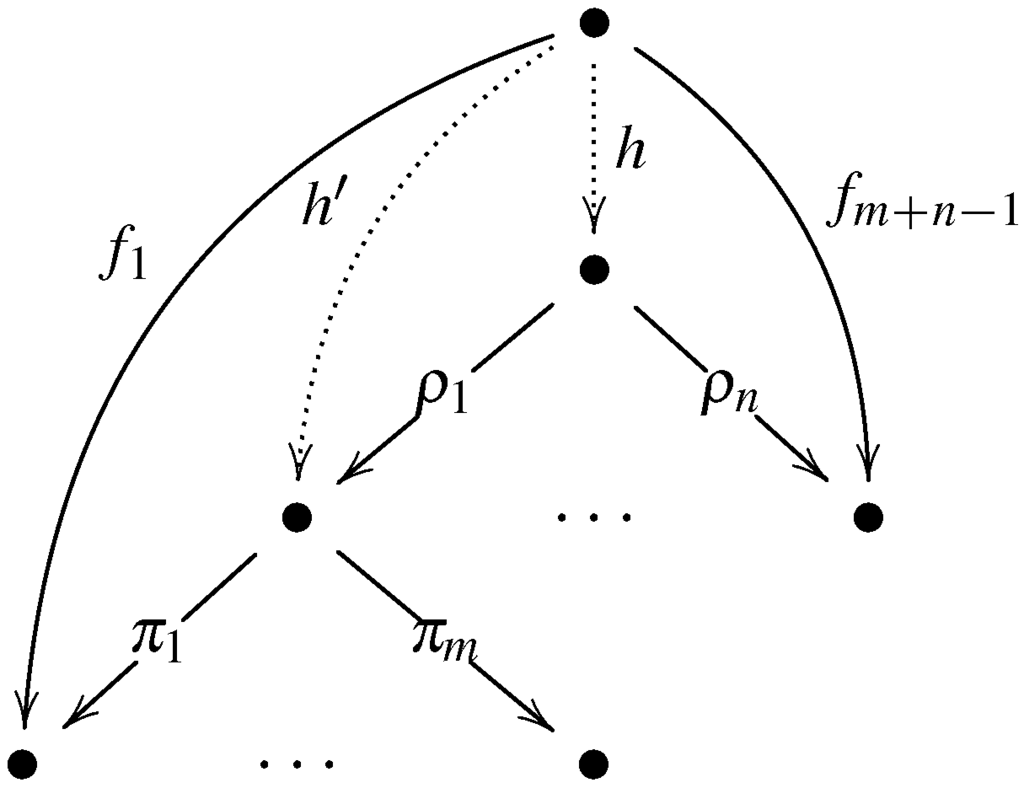
Figure 1. Construction of universal arrows.

Proof. In order to simplify the notation, we assume here that index variables i and j run through the values $\{1,\dots m\}$ and $\{2,\dots n\}$ by default. Furthermore, denote the common source of ${\rho }_i$’s by A. We will now check the satisfaction of the consecutive Conditions (8):

Identity (8a) is satisfied because ${\rho }_j^{\circ }{\rho }_j⊑{\mathrm{id}}_{\overrightarrow{{\rho }_j}}$ and ${\pi }_i^{\circ }{\rho }_1^{\circ }{\rho }_1{\pi }_i⊑{\pi }_i^{\circ }{\pi }_i⊑{\mathrm{id}}_{\overrightarrow{{\pi }_i}}$ for all i, j as π’s and ρ’s satisfy Equation (8a). Identity (8c) is satisfied as:

$$\begin{array}{cccc}\hfill \underset{k}{\sqcap }{\delta }_k{\delta }_k^{\circ }& =\left(\underset{i}{\sqcap }{\rho }_1{\pi }_i{\pi }_i^{\circ }{\rho }_1^{\circ }\right)\sqcap \left(\underset{j}{\sqcap }{\rho }_j{\rho }_j^{\circ }\right)\hfill & \hfill & \{\text{definition}\text{of}{\delta }_k\}\hfill \\ & ={\rho }_1\left(\underset{i}{\sqcap }{\pi }_i{\pi }_i^{\circ }\right){\rho }_1^{\circ }\sqcap \left(\underset{j}{\sqcap }{\rho }_j{\rho }_j^{\circ }\right)\hfill & & \{\text{by}\text{Lemma}2\}\hfill \\ & ={\rho }_1{\rho }_1^{\circ }\sqcap \left(\underset{j}{\sqcap }{\rho }_j{\rho }_j^{\circ }\right)\hfill & & \{\pi \text{’s}\text{satisfy}\text{Equation}(\text{8c})\}\hfill \\ & ={\mathrm{id}}_A\hfill & & \{\rho \text{’s}\text{satisfy}\text{Equation}(\text{8c})\}\hfill \end{array}$$

Suppose that ${\{f_i\}}_{1\le i\le m+n-1}\in {\mathcal{F}}_{\delta }$. In particular, this implies that ${\{f_i\}}_{1\le i\le m}\in {\mathcal{F}}_{\pi }$, and hence, by Theorem 18, the arrow $h^{\prime }:={\sqcap }_{1\le i\le m}{f}_i{\pi }_i^{\circ }$ (see Figure 1) is a map that satisfies $f_i=h^{\prime }{\pi }_i$ for all $1\le i\le m$. Then, $\{h^{\prime }\}\cup {\{f_k\}}_{m+1\le k\le m+n}\in {\mathcal{F}}_{\rho }$, and thus, by Theorem 18 it follows that $h:=h^{\prime }{\rho }_1^{\circ }\sqcap {\sqcap }_{2\le j\le n}{f}_{m+j-1}{\rho }_j^{\circ }$ is a map that satisfies $h^{\prime }=h{\rho }_1$, $f_{m+j-1}=h{\rho }_j$ for all $2\le j\le n$. It follows immediately that $f_i=h{\delta }_i$ for all $1\le i\le m+n-1$. Then, we can use the same methods as in the proof of Lemma 13 to verify Conditions (8b) and (8d). ☐

5. Conclusions

In the paper, we defined and investigated the weakening of an n-ary relational product from [17], which for $n=2$ is equivalent to the binary relational product defined in [15]. Our most important result is the proof that a weak n-ary relational product yields an n-ary categorical product in the subcategory of maps (Theorem 18). This result shows also that an n-ary product presented in [17] is also a categorical product for maps. Lemmas 19 and 20 generalize to the case of weak n-ary relational products the similar results proven in [15] for weak binary relational products. We also prove that by composing the weak n-ary products, we again get weak n-ary products (Lemma 21). This last result shows that the weak n-ary relational products can be constructed iteratively from the binary ones.

It should be noted that our definition of n-ary weak relational product, unlike that of usual relational product, whether binary or n-ary, does involve universal quantification. If one considers using allegories as a means of avoiding quantification when dealing with products, this is still better than a combination of universal and existential quantification (and one gets an explicit formula for a factorizing map, too). Note that the definition of a weak binary relational product in [15] involved universal quantification, as well, but this quantification could have been hidden in the definition of certain constant arrows. This is not possible with our definition.

The results presented in this paper were motivated by our work on the allegorical data model [10,11]. This model is abstract enough to model both the sharp and fuzzy relations in a uniform way, but only binary relations are modeled directly. If I is a finite set of size n and if R is an n-ary relation (in the sense of standard relational database model) with attributes $A_i$ of type $T_i$ for all $i\in I$, then, for any sets $J_1$, $J_2$ partitioning I (i.e., $I=J_1\cup J_2$, $J_1\cap J_2=\varnothing$), R can be viewed in an obvious way as a binary relation between ×${}_{i\in J_1}{T}_i$ and ×${}_{i\in J_2}{T}_i$. This simple observation shows how generalizations of n-ary relations can be represented (non-canonically) as arrows in an allegory, provided that the appropriate relational products exist.