Performance Evaluation of Shiryaev–Roberts and Cumulative Sum Schemes for Monitoring Shape and Scale Parameters in Gamma-Distributed Data Under Type I Censoring

Abstract

This paper proposes two process monitoring schemes, namely the Shiryaev–Roberts (SR) procedure and the cumulative sum (CUSUM) procedure, to detect shifts in the shape and scale parameters of Type I right-censored Gamma-distributed lifetime data. The performance of the proposed schemes is compared with that of an exponentially weighted moving average (EWMA) control chart based on deep learning networks. The performance of the proposed schemes is evaluated under various censoring rates using Monte Carlo simulations, with the average run length (ARL) as the primary metric. Furthermore, the SR and CUSUM schemes are compared for both zero-state and steady-state shifts. Simulation results indicate that the SR and CUSUM procedures exhibit superior performance, with the SR scheme showing particular advantages when the actual shift is small, while the CUSUM chart proves more effective for identifying larger shifts. The shape parameter has a significant effect on the performance of the control charts such that a reduction in the shape parameter effectively improves the ability to capture early offsets. Increased censoring rates reduce detection sensitivity. To maintain ${\mathrm{ARL}}_0$= 370, control limits h adapt differentially. The SR and CUSUM charts with different censoring rates need to recalibrate the parameter to mitigate performance losses under higher censoring conditions. The monitoring performance of the SR and CUSUM chart is enhanced by an increase in sample size. Finally, a practical example is provided to illustrate the application of the proposed monitoring schemes.

1. Introduction

Statistical process monitoring (SPM) has been widely applied in various fields, including manufacturing, healthcare, environmental monitoring, energy, transportation, supply chain management, telecommunications, education, agriculture, and more. Among the tools used for SPM, control charts are particularly prominent for detecting changes in process parameters. The concept of control charts was first introduced by Dr. Shewhart in 1931 Shewhart [1], followed by Page’s proposal of the cumulative sum (CUSUM) chart Page [2]. Over the years, extensive research on control charts has yielded significant social and economic benefits. Their user-friendly nature and simplicity have contributed to their widespread adoption across numerous industries. Traditionally, control charts are designed under the assumption that quality characteristics follow a normal distribution. However, in practice, the variables of interest often deviate from normality and may instead follow non-normal distributions. In such cases, an alternative strategy is to monitor the inter-arrival time of nonconforming events, which may exhibit a skewed distribution, such as the Gamma distribution, rather than focusing solely on the occurrence of nonconforming events.

The Gamma distribution plays a pivotal role in SPM for monitoring time-to-event data, reliability analysis, and non-negative continuous processes. Its flexibility in modeling skewed data with shape and scale parameters makes it indispensable for industrial and healthcare applications. In recent decades, significant advancements have been made in Gamma-based control chart methodologies to enhance sensitivity in detecting process shifts. Zhang et al. [3] pioneered a Gamma control chart for monitoring the time of the r-th event using a stochastic shift model. Alevizakos and Koukouvinos [4] subsequently developed a one-sided double exponential weighted moving average chart, demonstrating superior performance over conventional EWMA and Shewhart charts in detecting downward shifts. For parameter-specific scenarios, Yang et al. [5] proposed an average time to signal unbiased Gamma chart through scale parameter hypothesis testing, while also introducing an ATS-unbiased version for unknown parameter single-phase monitoring. Hybrid methodologies have further expanded the toolkit: Chakraborty et al. [6] introduced a generally weighted moving average chart, later enhanced by Alevizakos et al. [7] through a double GWMA design that outperforms DEWMA and GWMA charts in detecting moderate-to-large shifts. Shah et al. [8] innovatively employed exact probability distributions of monitoring statistics for Gamma chart design. Recent advancements include triple-smoothing techniques: Alevizakos et al. [9] proposed triple EWMA charts where bilateral and lower-unilateral schemes excel in detecting small-to-medium downward shifts, while upper-unilateral schemes show heightened sensitivity to minor upward shifts. Complementing this, Lone and Shahab [10] developed triple homogeneously weighted moving average charts with both unilateral and bilateral implementations.

With the advancement of production processes, many products now exhibit superior quality and extended lifespans. Consequently, lifetime data are often collected under censoring to reduce testing time and costs. For instance, when testing the lifetime of electronic products, practitioners may set a predetermined termination time to conclude the test, thereby minimizing resource expenditure. However, since some units may not fail by the termination time, the resulting data are incomplete; these are known as Type I right-censored data. This area has attracted significant research attention. Steiner and Mackay [11] proposed an SPM scheme based on the concept of replacing each censored observation with a conditional expected value (CEV) to detect changes in the mean of censored lifetime data. Dickinson et al. [12] developed a CUSUM scheme for monitoring censored Weibull lifetimes, while ChoiMin-jae and LeeJaeheon [13] introduced a binomial CUSUM scheme for Type I right-censored Weibull lifetimes. Xu and Jeske [14] proposed a Shewhart-type SPM scheme based on the likelihood ratio test statistic. Yu et al. [15] proposed a modified EWMA control chart for monitoring the Weibull scale parameter based on Type I censored data. Zhang et al. [16] introduced an enhanced monitoring approach, the weighted adaptive cumulative sum (WACUSUM) chart, which integrates exponential weighting with maximum likelihood estimation to effectively track reliability processes characterized by Type I censored Weibull-distributed data. Ali et al. [17] developed EWMA and CUSUM control charts for monitoring Type I censored generalized exponential distributed data. More recently, Pei-Hsi [18] combined the EWMA CEV and conditional median (CM) chart with deep learning methods to enhance efficiency for monitoring Type I right-censored Gamma-distributed data. Jiang et al. [19] proposed a new adaptive exponentially weighted moving average control chart, called the AEWMA-LR control chart, for monitoring the quality characteristics of two-parameter exponential distributions based on Type II censored data. Nadi et al. [20] introduced two Shewhart-type control charts for monitoring the relative risk rate when the lifetimes of competing risks are independent Weibull random variables. Aditi et al. [21] developed Shewhart-type control charts for monitoring the percentiles of an inverse Pareto distribution (IPD) using the complete and middle-censored data sets.

The Shiryaev–Roberts (SR) procedure is a statistical method designed for detecting changes in process parameters, particularly in scenarios where early detection of shifts is critical. Initially proposed by Shiryaev [22] for Brownian motion, the SR procedure is based on the conditional average delay time criterion, which aims to minimize the expected delay in detecting a change while controlling the rate of false alarms. Due to its robustness and efficiency, the SR procedure has been widely studied and extended to various applications. Pollak and Siegmund [23] compared the performance of the CUSUM and SR procedures in detecting shifts in the mean of a Gaussian process when the in-control (IC) value of the mean is unknown. Additionally, Kenett and Pollak [24] introduced an SR scheme for monitoring non-homogeneous Poisson distributions. Srivastava and Wu [25] conducted a comparative study of the EWMA, CUSUM, and SR procedures for detecting mean shifts. Zhang et al. [26] proposed an SR-based program for the simultaneous detection of shifts in both the process mean and variability. Furthermore, Zhang et al. [27] developed adaptive-type SR procedures designed to monitor the process mean and variance across a range of shift sizes. Moustakides et al. [28] explored integral equations for performance metrics and utilized numerical approximations to evaluate the efficiency of SR procedures. Ottenstreuer [29] investigated SR control charts for Markovian counting time series. Lastly, Yu et al. [30] investigated an SR control chart scheme for monitoring the Weibull scale parameter based on Type I censored data.

In this paper, the CUSUM and SR methods are applied to Type I right-censored Gamma-distributed data. The primary objectives of this study are threefold: (1) to systematically evaluate the adaptability of traditional control charts in censored data environments, (2) to address the performance limitations of deep learning-based monitoring approaches in practical reliability engineering scenarios, and (3) to develop simultaneous monitoring strategies for both scale and shape parameters of Gamma distributions under censoring mechanisms. The performance of the proposed methods is compared with that of an EWMA control chart based on deep learning networks, using both zero-state average run length (ARL) and steady-state average run length as performance metrics. The results demonstrate that both the CUSUM and SR control charts outperform the EWMA chart. Specifically, the SR scheme exhibits superior performance for small shifts, while for medium shifts, the SR and CUSUM schemes each show distinct advantages depending on the scenario.

We use the adaptation and application of the SR and CUSUM schemes for the joint monitoring of shape and scale parameters in Gamma-distributed processes subject to Type I censoring. This addresses a significant gap in SPM literature, where traditional control charts often assume complete data. We conduct the thorough performance evaluation that systematically compares the effectiveness of the SR and CUSUM procedures in a censored data environment. Our study moves beyond a simple comparison by evaluating their performance under a wide range of censoring rates and shift magnitudes, providing crucial insights into their relative strengths and weaknesses.

The remainder of the paper is organized as follows: Section 2 provides a review of the necessary background information, including the Gamma distribution, Type I right-censored Gamma distribution, and related work such as the EWMA CEV and CM chart combined with deep learning methods. Section 3 details the proposed CUSUM and SR methods for monitoring Type I right-censored Gamma-distributed data. Section 4 introduces the algorithm for determining the UCL and estimating ${\mathrm{ARL}}_1$. Section 5 presents a comparative analysis of the proposed methods with existing EWMA approaches. Section 6 illustrates the implementation of the CUSUM and SR charts through a real-world example. Finally, Section 7 concludes the paper with a summary of the findings.

2. Preamble and Existing Work

This section presents a systematic analysis of fundamental characteristics pertaining to the Gamma distribution, along with two existing EWMA CEV and CM schemes integrated with deep learning architectures.

2.1. The Gamma Distribution and Censoring

Let $T_1,T_2,\dots ,T_n$ denote a sequence of independent and identically distributed (i.i.d.) random variables following a Gamma distribution. The distribution is parametrized by a shape parameter $\beta >0$ and a scale parameter $\eta >0$. The probability density function (PDF) governing the lifetime measurement T is formally expressed as:

$$\begin{array}{c}\hfill f\left(t|\beta ,\eta \right)={\displaystyle \frac{{\eta }^{\beta }}{\Gamma \left(\beta \right)}}{t}^{\beta -1}exp\left(-\eta t\right),\end{array}$$

(1)

The cumulative distribution function (CDF) of the Gamma distribution is given by

$$\begin{array}{c}\hfill F(t\mid \beta ,\eta )={\int }_0^t{\displaystyle \frac{{\eta }^{\beta }}{\Gamma \left(\beta \right)}}{x}^{\beta -1}exp(-\eta x)dx,\end{array}$$

(2)

Let C represent the random variable corresponding to the censoring time. The censoring probability $P_c$, defined as the likelihood of data truncation prior to observing the terminal event, is mathematically expressed as:

$$\begin{array}{c}\hfill P_c=1-F\left(\mu =c_T\mid \beta ,\eta \right),\end{array}$$

(3)

where $c_T$ is the censoring time.

2.2. The EWMA CEV and CM Charts with Deep Learning Method

The CEV and CM metrics for the Gamma distribution are formulated as:

$$\mathrm{CEV}=\mathbb{E}\left[U\mid U\ge c_T\right]={\displaystyle \frac{\beta \eta \left[1-F\left(c_T\mid \beta +1,\eta \right)\right]}{1-F\left(c_T\mid \beta ,\eta \right)}},$$

(4)

$$\mathrm{CM}=F^{-1}\left(0.5-0.5F\left(c_T\mid \beta ,\eta \right)|\beta ,\eta \right),$$

(5)

where $F^{-1}(·\mid \beta ,\eta )$ denotes the inverse CDF of the Gamma distribution parametrized by $\beta$ and $\eta$.

Through reliability life testing, n independent observations are collected. Let $u_j$ represent the lifetime measurement of the j-th sample. The processed data $x_j$ in the sample mean $\overline{X}=n^{-1}{\sum }_{j=1}^n{x}_j$ follows:

$$x_j=\left\{\begin{array}{cc}{u}_j,\hfill & u_j\le c_T\hfill \\ \mathrm{Cd},\hfill & u_j>c_T\hfill \end{array}\right.,$$

(6)

where $\mathrm{Cd}$ corresponds to either CEV or CM values depending on the adopted estimation method. The IC process parameters are characterized by:

$$M_0=\beta \eta ,V_0=\beta {\eta }^2.$$

(7)

For decreased mean shift detection, the EWMA statistics with smoothing constant $\lambda \in (0,1]$ proposed by Pei-Hsi [18] are computed recursively as:

$$\begin{array}{cc}\hfill E_i& =min\left\{V_0,\lambda {\overline{X}}_i+(1-\lambda )E_{i-1}\right\},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill Z_i& =min\left\{M_0,\lambda {\overline{X}}_i+(1-\lambda )Z_{i-1}\right\}.\hfill \end{array}$$

(9)

A process is deemed statistically unstable if either control limit is violated:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{E}_i<h,\hfill \\ Z_i<h.\hfill \end{array}\right.\end{array}$$

(10)

Recent work by Pei-Hsi [18] has developed an innovative approach combining EWMA control charts with deep learning techniques. Their methodology integrates two variants of EWMA charts (CEV and CM) with convolutional neural networks (CNNs) and long short-term memory (LSTM) networks. The CEV and CM components provide traditional process monitoring capabilities, while the CNN layers extract spatial patterns and LSTM networks capture temporal dependencies in the data. This hybrid framework enhances detection sensitivity by leveraging both statistical process control principles and deep learning’s pattern recognition strengths. The complete implementation details, including network architectures and training procedures, are thoroughly documented in the original work Pei-Hsi [18].

3. The Proposed Control Charts

This section proposes two independent SPM frameworks for Gamma-distributed systems operating under Type I censoring conditions. The first methodology employs a CUSUM control chart designed to detect deviations in both the shape and the scale parameters. The second approach utilizes an SR control chart to monitor parameter shifts through likelihood ratio evaluation.

3.1. The CUSUM Control Chart

Let $T_{i1},T_{i2},\dots ,T_{in}$ be independent random variables following a Gamma distribution with shape parameter $\beta$ and scale parameter $\eta$, denoted as $\Gamma (\beta ,\eta )$. Here, C represents the predetermined censoring time, and $P_c$ denotes the censoring rate, as defined in Equation (3).

For statistical distributions involving right-censored data, the general form of the likelihood function can be expressed as proposed by Meeker [31]:

$$\begin{array}{c}\hfill L\left(T|\beta ,\eta \right)=\prod _{j=1}^{n}f{\left(T_{ij}|\beta ,\eta \right)}^{{\delta }_{ij}}{\left[1-F\left(T_{ij}|\beta ,\eta \right)\right]}^{1-{\delta }_{ij}},\end{array}$$

(11)

where ${\delta }_{ij}=0$ indicates a censored observation, and ${\delta }_{ij}=1$ represents an exact failure time. Here, $f(·)$ denotes the PDF of the underlying distribution, and $F(·)$ corresponds to its CDF. Under IC conditions, the lifetime variable T follows a Gamma distribution $\Gamma ({\beta }_0,{\eta }_0)$, characterized by the PDF $f_0(·)$ and CDF $F_0(·)$. Under out-of-control (OOC) conditions, the lifetime variable T follows a Gamma distribution $\Gamma ({\beta }_1,{\eta }_1)$, characterized by the PDF $f_1(·)$ and CDF $F_1(·)$. This study addresses both Phase I (retrospective analysis) and Phase II (online monitoring) scenarios under standard assumptions. Specifically, the initial parameters ${\beta }_0$ and ${\eta }_0$ are assumed to be known during the monitoring process. Then, the log-likelihood ratio statistic $Z_i$ for the i-th sample can be expressed as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill Z_i& =log\left({\displaystyle \frac{L\left(T_i|{\beta }_1,{\eta }_1\right)}{L\left(T_i|{\beta }_0,{\eta }_0\right)}}\right)\hfill \\ & =\sum _{j=1}^n{\delta }_{ij}log\left[{\displaystyle \frac{f_1\left(x_{ij}|{\beta }_1,{\eta }_1\right)}{f_0\left(x_{ij}|{\beta }_0,{\eta }_0\right)}}\right]+\sum _{j=1}^n\left(1-{\delta }_{ij}\right)log\left[{\displaystyle \frac{1-F_1\left(x_{ij}|{\beta }_1,{\eta }_1\right)}{1-F_0\left(x_{ij}|{\beta }_0,{\eta }_0\right)}}\right].\hfill \end{array}\end{array}$$

(12)

For a given random sample ${\mathbf{x}}_i=(x_{i1},x_{i2},\dots ,x_{in})$ from the Type I right-censored Gamma-distributed process, the log-likelihood ratio statistic can be derived from Equation (12) as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill Z_i& ={\delta }_i\left({\beta }_{1}log\left({\eta }_1\right)-{\beta }_{0}log\left({\eta }_0\right)+log\left[{\displaystyle \frac{\Gamma \left({\beta }_0\right)}{\Gamma \left({\beta }_1\right)}}\right]+\left({\beta }_1-{\beta }_0\right)\sum _{j=1}^{n}log{x}_{ij}-\left({\eta }_1-{\eta }_0\right)\sum _{j=1}^n{x}_{ij}\right)\hfill \\ & +\left(1-{\delta }_i\right)\sum _{j=1}^{n}log\left[{\displaystyle \frac{1-F_1\left(x_{ij}|{\beta }_1,{\eta }_1\right)}{1-F_0\left(x_{ij}|{\beta }_0,{\eta }_0\right)}}\right],\hfill \end{array}\end{array}$$

(13)

where ${\delta }_i={\sum }_{j=1}^n{\delta }_{ij}$ represents the total number of uncensored observations in the i-th batch.

Under the hypothesis of a parameter shift from the IC state $({\beta }_0,{\eta }_0)$ to the out-of-control state $({\beta }_1,{\eta }_1)$, the likelihood ratio-based CUSUM control chart can be constructed as:

$$\begin{array}{c}\hfill D_i^{-}=max\left(0,D_i^{-}+Z_i\right),D_0^{-}=0,i=1,2,3,\dots ,\end{array}$$

(14)

3.2. The SR Control Chart

Following Moustakides et al. [28], for $i\ge 1$, the instantaneous likelihood ratio ${\Lambda }_i$ between the post-change and pre-change hypotheses is defined as:

$$\begin{array}{c}\hfill {\Lambda }_i={\displaystyle \frac{f_1\left(T_{ij}\right)}{f_0\left(T_{ij}\right)}}=exp\left(Z_i\right),\end{array}$$

(15)

where $f_0\left(T_{ij}\right)$ and $f_1\left(T_{ij}\right)$ denote the probability density functions under the pre-change and post-change hypotheses, respectively. Based on this definition, the SR-type plotting statistic can be constructed as follows:

$$\begin{array}{c}\hfill R_i=\sum _{k=1}^i\prod _{j=k}^i{\Lambda }_j.\end{array}$$

(16)

The monitoring scheme triggers an OOC signal when $R_i>h$, where the control limit h is determined by setting the IC ${\mathrm{ARL}}_0$ to a predefined target value. Furthermore, the SR statistic admits the following recursive representation:

$$\begin{array}{c}\hfill R_i=\left(1+R_{i-1}\right){\Lambda }_i,\end{array}$$

(17)

where $R_0=0$. According to Equation (12), ${\Lambda }_i$ can be converted into:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\Lambda }_i=exp\left(Z_i\right)=exp\left\{\sum _{j=1}^n{\delta }_{ij}log\left[{\displaystyle \frac{f_1\left(x_{ij}|{\beta }_1,{\eta }_1\right)}{f_0\left(x_{ij}|{\beta }_0,{\eta }_0\right)}}\right]+\sum _{j=1}^n\left(1-{\delta }_{ij}\right)log\left[{\displaystyle \frac{1-F_1\left(x_{ij}|{\beta }_1,{\eta }_1\right)}{1-F_0\left(x_{ij}|{\beta }_0,{\eta }_0\right)}}\right]\right\}.\end{array}\end{array}$$

(18)

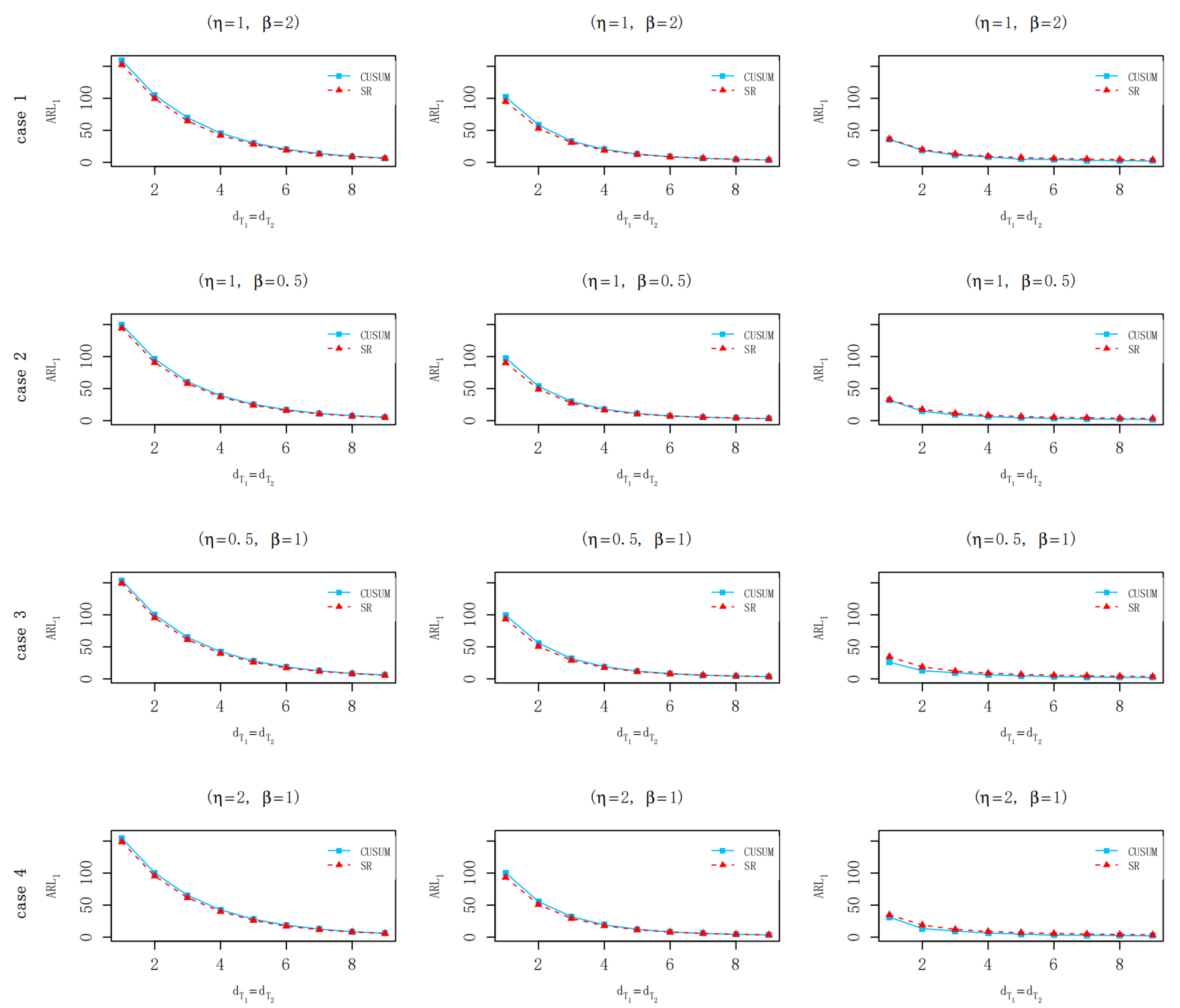
4. Simulation Studies

The ARL measures the performance of a control chart, defined as the expected number of samples before an OOC signal appears Montgomery [32]. A sufficiently large IC ARL (${\mathrm{ARL}}_0$) minimizes false alarms, while a small OOC ARL (${\mathrm{ARL}}_1$) ensures rapid shift detection. The ARL is estimated via Monte Carlo simulations using an algorithm implemented in R, assuming fixed and known IC values for the shape parameter $\beta$ and the scale parameter $\eta$.

Comprehensive evaluation of control chart efficacy necessitates dual examination of ARL metrics: zero-state (ZS-ARL) and steady-state (SS-ARL) analyses. The ZS-ARL metric assumes instantaneous process parameter deviations upon Phase II monitoring commencement, calculated as $\mathbb{E}\left[N\right|\beta ={\beta }_1,\eta ={\eta }_1]$ where N denotes the run length post-shift. Conversely, SS-ARL addresses delayed shift scenarios through ${lim}_{k\to \infty }\mathbb{E}[N-k|N>k,\beta ={\beta }_1,\eta ={\eta }_1]$, modeling processes that initially maintain IC ($\beta ={\beta }_0,\eta ={\eta }_0$) conditions before transitioning to OOC states at unknown change points. Empirical applications predominantly align with SS-ARL assumptions given the probabilistic nature of shift occurrence timing. Zwetsloot and Woodall [33] substantiate this preference through Markov chain analyses, demonstrating that control charts with headstart features exhibit ZS-ARL superiority but SS-ARL degradation ratios exceeding 40% in Monte Carlo simulations. This performance dichotomy underscores the criticality of SS-ARL incorporation for robust SPM scheme validation.

To ensure equitable performance benchmarking across monitoring schemes, all control charts were calibrated to maintain an IC zero-state ${\mathrm{ARL}}_0=370$ through parameter-specific design thresholds $d_P$. Numerical simulations employed Monte Carlo algorithms to generate 50,000 trial sequences, yielding empirical ARL estimates via $\widehat{\mathrm{ARL}}=\mathbb{E}\left[RL\right]$ where RL represents run length realizations. Steady-state ARL estimation protocol incorporated a 50-observation IC phase prior to parameter shift initiation. Figure 1 shows the algorithm for Monte Carlo simulation to determine the UCL of the SR control chart.

Taking the SR control chart as an example, the algorithm for Monte Carlo simulation to determine the UCL of the SR control chart is:

• Initialization:
  • Set the process parameters for the IC state: sample size n, censoring rate $P_C$, predetermined percent change $d_P$, shape parameter $\beta$, and scale parameter $\eta$.
  • Define the total number of simulation replications as 50,000.
  • Initialize the upper control limit with a provisional value h.
• Data Generation:
  • Draw a sample of size n from a Gamma distribution parameterized by $\beta$ and $\eta$.
• Computation of the Statistic:
  • Compute the statistic $R_i$ for the current sample.
  • If $R_i\le h$, generate a new sample (return to Step 2).
  • If $R_i>h$, note the sample index at which this first OOC event is detected, and record it as the RL.
• Iteration and Calibration:
  • Repeat Steps 2 and 3 until 50,000 run lengths are collected.
  • Calculate the mean of these run lengths to estimate the IC ${\mathrm{ARL}}_0$ corresponding to the current h.
  • Adjust h iteratively until the target ${\mathrm{ARL}}_0$ is achieved.
  • Finally, set the UCL equal to the calibrated h.

When the process experiences a shift, the OOC performance of the chart is assessed using ${\mathrm{ARL}}_1$. We assume that the occurrence of an OOC condition modifies the IC scale parameter from ${\eta }_0$ to ${\eta }_1=d_{T_1}{\eta }_0$ and ${\beta }_0$ to ${\beta }_1=d_{T_2}{\beta }_0$, where $d_{T_1}$ and $d_{T_2}$ represent the true shift magnitude. Note that $d_{T_j}$ differs from the pre-specified $d_{P_j}$, which is known prior to monitoring, while $d_{T_j}$ is unknown until the shift occurs. Figure 2 shows the algorithm to estimate ${\mathrm{ARL}}_1$.The following algorithm, implemented in R, can be used to estimate ${\mathrm{ARL}}_1$:

Step 1: Define the parameters $n,\beta ,\eta ,P_C,d_{P_j}$ and determine the corresponding control limits.

Step 2: Generate a sample of size n incorporating a shift of size $d_{T_j}$. Compute the plotting statistic $R_t$ using Equation (17).

Step 3: If the control chart signals an OOC condition, record the RL; otherwise, return to Step 2.

Step 4: After executing Steps 2 and 3 for 50,000 replications, calculate ${\mathrm{ARL}}_1$ as the average of the recorded RL values.

5. Comparison and Discussion with Existing Charts

We compare the performance of the CUSUM and SR charts with the deep learning-based EWMA chart. To ensure a fair comparison, all control charts are calibrated to achieve an IC ${\mathrm{ARL}}_0$ of approximately 370 with a sample size of $n=5,10$. The SS-ARL values, incorporating a warm-up period of 50, are estimated using Monte Carlo simulations with 50,000 iterations. The charts are evaluated under 12 parameter configurations, considering shape parameters ($\beta =0.5,1,2$), scale parameters ($\eta =0.5,1,2$), censoring rates ($P_c=0.15,0.25$), and pre-specified shift magnitudes ($d_P=0.15,0.25$).

In practical applications, the exact magnitude of a process shift is often unknown. Thus, it is crucial to evaluate the robustness of control charts designed for a specific pre-specified shift when the actual shift deviates.

Table 1. ZS-ARL comparison for $n=5,P_c=0.15,0.25,d_{T_1}=d_{T_2}$, ${\mathrm{ARL}}_0$ = 370.

${\mathit{P}}_{\mathit{c}}=0.15,\mathit{\eta }=1,\mathit{\beta }=2$							${\mathit{P}}_{\mathit{c}}=0.25,\mathit{\eta }=1,\mathit{\beta }=2$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 33.45	h = 3.28	h = 144.26	h = 3.86	h = 274.85	h = 2.80	h = 33.65	h = 3.27	h = 143.95	h = 3.81	h = 274.35	h = 2.75
	370.99	369.82	370.08	370.75	370.27	369.28	370.61	369.99	370.65	370.46	369.39	371.00
0.90	153.75	161.07	113.00	121.71	90.33	88.99	156.11	160.41	115.97	124.99	93.93	92.17
0.85	100.86	105.89	67.58	73.30	57.55	52.26	101.69	106.57	69.03	74.94	59.83	54.41
0.80	66.39	70.22	42.10	45.37	40.62	34.31	67.38	71.31	43.70	46.90	42.37	35.93
0.75	43.60	47.06	27.47	29.32	30.43	24.35	44.39	47.41	28.64	30.33	31.95	25.28
0.70	29.31	31.34	19.19	19.69	23.88	18.08	29.92	32.15	20.04	20.42	25.04	18.91
0.65	19.84	21.28	13.89	13.75	19.20	13.97	20.30	21.92	14.41	14.35	20.15	14.50
0.60	13.73	14.72	10.37	10.14	15.83	10.99	14.19	15.09	10.79	10.43	16.42	11.50
0.55	9.71	10.30	8.05	7.62	13.09	8.87	9.92	10.54	8.35	7.83	13.61	9.16
0.50	6.99	7.34	6.36	5.86	10.87	7.19	7.13	7.51	6.52	6.06	11.28	7.39
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 23.43	h = 3.03	h = 128.43	h = 3.953	h = 265.43	h = 3.00	h = 23.55	h = 3.02	h = 128.55	h = 3.94	h = 265.68	h = 2.97
	370.43	370.91	370.68	370.72	370.89	370.96	370.24	370.97	370.64	369.98	370.62	370.55
0.90	144.35	150.43	104.34	112.02	77.73	77.38	145.03	150.23	104.26	111.96	79.28	77.97
0.85	91.67	96.24	58.90	64.09	47.55	43.84	91.94	96.32	59.59	65.14	48.42	44.46
0.80	58.41	61.62	35.34	38.24	32.80	28.13	58.30	61.31	36.18	38.88	33.28	28.70
0.75	37.71	39.48	22.69	24.09	24.18	19.55	37.63	39.88	23.07	24.45	24.78	19.91
0.70	24.36	26.38	15.27	15.89	18.78	14.46	24.73	26.16	15.49	16.08	19.15	14.69
0.65	16.29	17.35	10.89	11.04	14.96	11.04	16.37	17.44	11.13	11.13	15.30	11.23
0.60	11.01	11.76	8.05	7.95	12.22	8.71	11.10	11.84	8.20	8.03	12.41	8.85
0.55	7.65	8.04	6.19	5.96	10.05	7.01	7.75	8.15	6.30	6.01	10.22	7.08
0.50	5.45	5.74	4.91	4.56	8.30	5.69	5.52	5.79	4.93	4.62	8.44	5.73
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 27.66	h = 3.15	h = 134.95	h = 3.90	h = 269.35	h = 2.90	h = 27.78	h = 3.15	h = 135.85	h = 3.87	h = 270.54	h = 2.86
	369.77	370.32	370.81	370.98	370.67	369.87	370.75	370.82	369.87	370.93	370.17	370.50
0.90	150.26	156.67	108.05	117.61	84.32	83.36	149.63	155.98	110.38	118.70	86.27	85.28
0.85	95.55	100.10	63.58	68.84	52.57	48.12	96.43	101.55	64.46	70.09	54.08	49.69
0.80	61.93	66.21	38.58	41.81	36.51	31.26	62.72	66.88	39.72	42.52	37.95	32.16
0.75	40.73	43.18	24.97	26.46	27.29	21.87	40.94	43.85	25.77	27.08	28.34	22.63
0.70	26.93	28.95	17.09	17.61	21.26	16.22	27.09	29.18	17.60	18.27	21.94	16.68
0.65	18.02	19.40	12.28	12.34	17.05	12.47	18.36	19.49	12.62	12.67	17.56	12.79
0.60	12.27	13.07	9.12	8.94	13.90	9.84	12.51	13.37	9.42	9.19	14.35	10.07
0.55	8.58	9.15	7.03	6.71	11.48	7.87	8.71	9.30	7.21	6.86	11.77	8.03
0.50	6.15	6.44	5.51	5.13	9.47	6.40	6.27	6.57	5.66	5.27	9.73	6.49
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 27.75	h = 3.15	h = 136.75	h = 3.90	h = 269.27	h = 2.90	h = 27.85	h = 3.14	h = 135.15	h = 3.88	h = 269.15	h = 2.86
	369.63	369.52	370.88	370.86	369.67	370.25	370.26	369.31	370.83	369.76	370.36	370.68
0.90	150.28	155.32	110.37	117.56	84.18	83.23	152.20	156.20	109.35	118.93	86.40	84.69
0.85	96.05	102.05	63.73	68.82	52.38	48.33	97.03	101.17	64.56	69.70	53.98	49.65
0.80	62.57	66.10	38.67	41.94	36.39	31.19	62.51	65.95	39.56	42.84	37.74	32.27
0.75	40.31	43.61	25.21	26.41	27.40	21.90	40.91	43.49	25.73	27.23	28.15	22.58
0.70	26.95	28.79	17.23	17.65	21.23	16.24	27.12	29.27	17.57	18.14	21.99	16.58
0.65	17.96	19.31	12.25	12.33	17.04	12.48	18.27	19.50	12.55	12.56	17.53	12.81
0.60	12.31	13.11	9.18	8.93	13.93	9.82	12.43	13.38	9.41	9.13	14.29	10.07
0.55	8.56	9.14	7.02	6.73	11.42	7.87	8.79	9.27	7.24	6.88	11.77	8.04
0.50	6.14	6.46	5.583	5.15	9.50	6.39	6.26	6.53	5.65	5.29	9.71	6.47

presents the ZS-ARL values for the SR and CUSUM charts under various conditions ($P_c=0.15,0.25$), assuming $n=5$ and parameter settings such as $(\beta =2,\eta =1)$, $(\beta =0.5,\eta =1)$, $(\beta =1,\eta =0.5)$, and $(\beta =1,\eta =2)$. Three pre-specified shift values ($d_P=0.2,0.5,0.8$) are examined.

Table 2. SS-ARL comparison for $n=5,P_c=0.15,0.25,d_{T_1}=d_{T_2}$, ${\mathrm{ARL}}_0$ = 370.

${\mathit{P}}_{\mathit{c}}=0.15,\mathit{\eta }=1,\mathit{\beta }=2$							${\mathit{P}}_{\mathit{c}}=0.25,\mathit{\eta }=1,\mathit{\beta }=2$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 33.71	h = 3.28	h = 158.25	h = 3.94	h = 443.85	h = 3.34	h = 33.85	h = 3.27	h = 158.55	h = 3.92	h = 445.52	h = 3.25
	370.37	369.95	369.98	370.86	369.16	369.53	369.21	369.02	370.21	369.12	369.37	371.98
0.90	152.41	159.31	94.97	101.90	36.56	35.76	153.75	159.76	96.25	102.83	37.29	33.81
0.85	99.52	104.73	53.01	58.49	19.95	18.74	101.06	105.77	53.91	58.62	20.64	17.79
0.80	64.56	69.43	30.94	33.16	13.04	11.41	66.00	70.40	31.32	34.33	13.53	12.41
0.75	42.22	45.61	18.76	20.32	9.54	8.37	43.03	45.88	19.49	21.01	9.88	7.83
0.70	28.22	30.31	12.41	12.90	7.42	4.93	28.46	30.83	12.95	13.45	7.71	4.81
0.65	18.93	20.36	8.54	8.73	6.08	4.49	19.31	20.87	8.91	9.05	6.27	4.09
0.60	12.67	13.81	6.33	6.23	5.17	2.95	13.11	14.21	6.52	6.46	5.33	2.57
0.55	8.81	9.51	4.91	4.72	4.46	2.57	9.06	9.81	5.09	4.83	4.58	2.43
0.50	6.29	6.71	3.96	3.73	3.88	2.09	6.46	6.81	4.09	3.80	3.99	1.92
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 23.58	h = 3.08	h = 137.53	h = 4.01	h = 400.43	h = 3.02	h = 23.61	h = 3.07	h = 137.83	h = 3.98	h = 403.58	h = 2.99
	370.92	370.92	370.00	370.73	369.40	370.95	369.47	370.98	370.63	369.99	369.71	370.53
0.90	144.24	149.58	90.17	97.78	32.81	32.01	144.39	148.65	90.94	97.92	33.70	31.26
0.85	90.55	96.08	48.94	53.37	17.49	14.61	91.64	94.61	48.57	53.54	17.81	16.76
0.80	57.82	60.81	27.51	30.08	11.29	9.19	57.64	60.73	27.58	30.76	11.40	9.27
0.75	36.91	39.01	16.40	17.73	8.16	6.17	37.05	39.54	16.42	18.01	8.24	6.24
0.70	23.96	25.48	10.39	11.10	6.42	4.52	24.12	25.73	10.66	11.30	6.51	4.58
0.65	15.77	17.00	7.19	7.39	5.23	3.30	15.75	16.97	7.29	7.56	5.31	3.47
0.60	10.44	11.30	5.28	5.31	4.42	2.57	10.61	11.36	5.38	5.37	4.47	2.78
0.55	7.18	7.65	4.11	4.01	3.81	2.09	7.26	7.71	4.17	4.03	3.86	2.25
0.50	5.10	5.38	3.31	3.14	3.35	1.84	5.16	5.43	3.37	3.19	3.37	1.89
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 27.73	h = 3.17	h = 145.25	h = 3.91	h = 419.35	h = 2.91	h = 27.79	h = 3.18	h = 146.15	h = 3.89	h = 423.85	h = 2.90
	369.71	370.33	370.53	370.97	369.77	369.85	370.64	370.83	369.07	370.91	369.10	370.48
0.90	149.03	153.79	93.43	99.42	34.62	25.97	148.32	154.35	93.79	101.19	35.83	27.22
0.85	95.20	99.92	50.63	55.83	18.71	12.75	95.85	99.97	51.89	56.53	19.33	16.98
0.80	61.23	64.69	28.96	31.84	12.09	9.50	62.22	65.56	29.64	32.55	12.54	11.17
0.75	39.69	42.52	17.67	19.00	8.83	6.21	40.06	43.51	18.07	19.60	9.14	6.25
0.70	25.94	27.97	11.44	11.94	6.92	4.78	26.26	28.56	11.64	12.31	7.11	5.46
0.65	17.18	18.79	7.90	8.06	5.66	3.37	17.48	19.07	8.09	8.21	5.82	3.55
0.60	11.66	12.50	5.80	5.71	4.80	2.91	11.85	12.68	5.96	5.85	4.88	3.18
0.55	8.02	8.62	4.48	4.32	4.11	2.24	8.18	8.69	4.60	4.39	4.20	2.35
0.50	5.67	6.01	3.63	3.42	3.61	2.09	5.78	6.14	3.70	3.47	3.66	2.10
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 27.85	h = 3.17	h = 145.86	h = 3.93	h = 425.57	h = 2.92	h = 28.13	h = 3.19	h = 146.75	h = 3.88	h = 426.85	h = 2.89
	370.29	370.02	369.88	370.83	369.44	370.15	370.51	370.21	370.08	370.14	370.32	369.98
0.90	148.73	154.72	93.30	100.28	34.64	31.24	149.05	152.72	93.54	101.63	35.29	30.25
0.85	95.43	100.21	50.89	55.50	18.95	13.36	95.72	100.19	51.16	56.49	19.42	22.45
0.80	61.48	65.21	29.11	32.08	12.08	9.53	61.41	65.05	29.66	32.48	12.56	8.81
0.75	40.01	42.61	17.76	19.11	8.81	6.29	40.06	42.62	18.12	19.51	9.04	6.09
0.70	26.09	27.97	11.47	12.27	6.90	4.73	26.28	28.30	11.78	12.28	7.13	5.09
0.65	17.11	18.63	7.91	8.12	5.67	3.13	17.42	18.73	8.05	8.26	5.81	2.90
0.60	11.59	12.64	5.78	5.80	4.80	2.89	11.84	12.68	5.94	5.87	4.88	2.77
0.55	8.05	8.53	4.50	4.32	4.12	2.47	8.15	8.67	4.57	4.43	4.19	2.41
0.50	5.66	6.02	3.63	3.42	3.61	2.16	5.76	6.11	3.71	3.48	3.66	1.98

presents the SS-ARL values for the SR and CUSUM charts under the same conditions as in Table 1.

Table 3. ZS-ARL comparison for $n=10,P_c=0.15,0.25,d_{T_1}=d_{T_2}$, ${\mathrm{ARL}}_0$ = 370.

${\mathit{P}}_{\mathit{c}}=0.15,\mathit{\eta }=1,\mathit{\beta }=2$							${\mathit{P}}_{\mathit{c}}=0.25,\mathit{\eta }=1,\mathit{\beta }=2$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 12.15	h = 2.44	h = 111.61	h = 4.03	h = 254.63	h = 3.27	h = 12.63	h = 2.48	h = 112.63	h = 4.01	h = 255.68	h = 3.21
	370.87	370.83	370.96	370.46	370.52	370.56	370.50	370.52	370.73	370.23	370.21	370.20
0.90	135.90	138.68	92.84	100.64	63.01	63.82	136.34	140.33	95.45	102.72	65.78	65.51
0.85	83.10	86.56	50.54	55.03	36.95	34.72	83.39	87.34	51.71	56.71	38.59	36.31
0.80	51.45	54.03	29.16	31.62	24.81	21.85	52.25	54.79	30.18	33.07	26.11	22.64
0.75	32.39	34.02	17.97	19.24	18.26	15.11	32.65	34.54	18.78	20.04	19.13	15.77
0.70	20.46	21.63	11.92	12.34	14.08	11.14	21.02	22.02	12.30	12.92	14.74	11.65
0.65	13.25	14.10	8.29	8.47	11.19	8.57	13.76	14.38	8.70	8.81	11.70	8.92
0.60	8.86	9.25	6.13	6.11	9.09	6.82	9.11	9.59	6.37	6.30	9.52	6.99
0.55	6.03	6.30	4.70	4.54	7.49	5.45	6.17	6.53	4.85	4.73	7.79	5.63
0.50	4.23	4.40	3.66	3.51	6.18	4.43	4.36	4.55	3.80	3.62	6.43	4.57
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 5.26	h = 1.63	h = 94.56	h = 4.04	h = 240.66	h = 3.45	h = 5.46	h = 1.67	h = 95.32	h = 4.03	h = 241.33	h = 3.42
	370.46	369.66	370.16	370.52	370.46	370.43	370.54	369.84	370.26	370.13	370.14	370.26
0.90	123.35	124.66	85.20	92.44	53.06	54.00	124.91	125.02	85.59	92.68	53.80	54.80
0.85	72.46	73.59	44.00	48.75	29.95	28.42	73.17	73.93	44.59	49.16	30.57	29.03
0.80	43.01	44.25	24.51	26.88	19.72	17.46	43.38	44.99	25.06	27.41	20.18	17.97
0.75	26.25	27.03	14.70	15.73	14.29	11.99	26.44	27.29	14.99	16.12	14.62	12.19
0.70	16.26	16.78	9.48	9.93	10.92	8.81	16.48	17.18	9.63	10.12	11.18	9.00
0.65	10.23	10.70	6.53	6.62	8.65	6.77	10.52	10.95	6.64	6.79	8.78	6.86
0.60	6.80	7.07	4.73	4.74	6.95	5.31	6.91	7.14	4.84	4.78	7.10	5.41
0.55	4.56	4.74	3.61	3.53	5.71	4.29	4.65	4.82	3.67	3.61	5.81	4.35
0.50	3.23	3.32	2.83	2.74	4.69	3.49	3.28	3.36	2.87	2.76	4.79	3.54
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 7.91	h = 2.03	h = 102.51	h = 4.05	h = 246.52	h = 3.35	h = 8.28	h = 2.07	h = 103.58	h = 4.02	h = 247.58	h = 3.31
	369.97	370.87	370.68	370.10	370.67	369.77	370.87	369.13	370.08	370.60	370.03	369.89
0.90	129.48	131.85	89.76	96.99	58.14	59.06	131.87	133.20	90.82	98.24	59.75	60.64
0.85	78.10	79.76	47.22	51.96	33.54	31.54	78.81	79.98	48.38	52.84	34.63	32.44
0.80	47.35	48.73	26.76	29.56	22.21	19.68	48.29	49.33	27.53	30.03	23.07	20.28
0.75	29.12	30.33	16.30	17.56	16.23	13.61	29.70	30.72	16.65	18.06	16.77	13.96
0.70	18.27	19.02	10.65	11.20	12.46	9.92	18.73	19.39	11.01	11.46	12.86	10.23
0.65	11.75	12.21	7.37	7.51	9.87	7.60	11.98	12.49	7.58	7.76	10.12	7.83
0.60	7.74	8.08	5.35	5.39	7.98	5.99	7.86	8.22	5.51	5.53	8.22	6.14
0.55	5.25	5.50	4.07	4.00	6.52	4.81	5.38	5.57	4.20	4.09	6.71	4.91
0.50	3.68	3.82	3.22	3.09	5.40	3.91	3.77	3.87	3.28	3.15	5.53	3.99
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 7.99	h = 2.04	h = 102.95	h = 4.04	h = 245.95	h = 3.36	h = 8.26	h = 2.07	h = 103.21	h = 4.03	h = 247.28	h = 3.31
	369.84	370.53	370.09	370.89	370.20	370.00	370.05	369.57	370.82	370.53	370.84	370.02
0.90	130.95	132.27	89.92	96.82	57.54	58.79	131.69	132.88	90.32	97.91	59.66	60.40
0.85	78.49	80.59	47.35	51.54	33.36	31.49	78.79	80.69	48.36	52.74	34.55	32.53
0.80	47.62	48.85	26.93	29.48	22.25	19.68	47.98	49.38	27.36	29.85	23.09	20.22
0.75	29.42	30.59	16.23	17.45	16.22	13.56	29.65	30.84	16.65	17.91	16.81	13.88
0.70	18.39	19.23	10.66	11.17	12.43	9.92	18.65	19.56	10.96	11.48	12.84	10.20
0.65	11.88	12.38	7.39	7.51	9.81	7.64	11.93	12.57	7.56	7.75	10.15	7.80
0.60	7.84	8.13	5.39	5.37	7.96	6.01	7.87	8.26	5.52	5.53	8.18	6.13
0.55	5.24	5.50	4.11	4.01	6.53	4.82	5.39	5.57	4.21	4.09	6.71	4.92
0.50	3.69	3.79	3.22	3.08	5.40	3.94	3.77	3.91	3.27	3.17	5.52	3.99

and

Table 4. SS-ARL comparison for $n=10,P_c=0.15,0.25,d_{T_1}=d_{T_2}$, ${\mathrm{ARL}}_0$ = 370.

${\mathit{P}}_{\mathit{c}}=0.15,\mathit{\eta }=1,\mathit{\beta }=2$							${\mathit{P}}_{\mathit{c}}=0.25,\mathit{\eta }=1,\mathit{\beta }=2$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 12.21	h = 2.44	h = 116.43	h = 4.08	h = 357.48	h = 3.66	h = 12.78	h = 2.47	h = 117.69	h = 4.06	h = 363.62	h = 3.61
	370.58	369.38	370.74	370.35	370.81	369.84	370.15	370.59	370.37	370.11	370.05	369.12
0.90	136.49	139.05	86.15	94.15	33.20	33.04	137.22	139.63	88.66	95.89	33.92	32.90
0.85	83.21	85.55	44.44	48.97	15.78	14.07	85.20	87.10	45.31	50.19	16.47	14.96
0.80	51.75	53.41	23.90	26.63	9.82	8.33	52.29	54.00	24.48	27.48	10.27	8.33
0.75	32.13	33.49	13.97	15.03	7.01	5.43	33.05	34.17	14.30	15.68	7.31	5.48
0.70	20.46	21.24	8.67	9.31	5.51	3.95	20.84	21.94	9.01	9.49	5.76	3.99
0.65	13.14	13.84	5.91	6.13	4.59	3.09	13.45	14.11	6.14	6.37	4.71	3.12
0.60	8.68	9.11	4.33	4.36	3.89	2.56	8.86	9.39	4.48	4.51	4.00	2.55
0.55	5.87	6.13	3.37	3.30	3.38	2.19	5.99	6.30	3.47	3.40	3.48	2.14
0.50	4.09	4.30	2.74	2.64	2.98	1.86	4.22	4.42	2.81	2.71	3.05	1.89
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{1},\mathit{\beta }=\mathbf{0.5}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 5.24	h = 1.63	h = 97.04	h = 4.07	h = 318.98	h = 3.77	h = 5.42	h = 1.66	h = 97.78	h = 4.07	h = 321.51	h = 3.75
	370.23	369.45	370.84	370.35	370.60	370.21	370.60	369.92	370.83	370.98	370.48	370.00
0.90	123.45	123.91	80.82	87.72	28.52	29.52	124.48	125.32	81.61	89.24	29.17	29.09
0.85	72.02	73.77	39.93	44.33	13.50	12.59	73.14	74.07	40.09	45.01	13.80	12.85
0.80	43.17	44.09	20.86	23.30	8.26	6.94	43.42	44.63	21.27	23.61	8.41	7.15
0.75	26.17	27.00	11.83	12.97	5.95	4.72	26.49	27.11	12.14	13.21	6.11	4.79
0.70	16.15	16.73	7.34	7.79	4.71	3.49	16.33	17.02	7.45	7.99	4.79	3.55
0.65	10.24	10.73	4.93	5.10	3.89	2.79	10.40	10.77	5.01	5.22	3.97	2.83
0.60	6.66	6.96	3.62	3.66	3.33	2.31	6.82	7.06	3.67	3.71	3.38	2.32
0.55	4.54	4.69	2.82	2.80	2.91	1.99	4.56	4.74	2.85	2.84	2.93	1.99
0.50	3.20	3.29	2.29	2.25	2.56	1.73	3.22	3.31	2.33	2.27	2.58	1.71
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{0.5},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 7.97	h = 2.04	h = 105.47	h = 4.07	h = 337.52	h = 3.70	h = 8.24	h = 2.07	h = 106.67	h = 4.06	h = 342.67	h = 3.68
	370.27	370.83	370.01	370.07	370.15	370.39	370.15	369.91	370.77	370.11	370.64	369.91
0.90	130.29	132.33	83.55	91.23	30.90	30.83	130.79	132.70	84.67	92.52	32.15	31.55
0.85	77.84	80.29	42.36	46.95	14.60	13.46	78.24	80.82	42.88	47.98	15.07	13.77
0.80	47.49	49.30	22.53	24.96	9.09	7.53	47.89	49.52	23.02	25.29	9.30	7.83
0.75	29.10	30.25	12.86	14.17	6.49	5.13	29.68	30.78	13.20	14.37	6.67	5.32
0.70	18.33	18.98	8.03	8.59	5.10	3.69	18.40	19.37	8.17	8.69	5.25	3.77
0.65	11.66	12.27	5.39	5.64	4.22	2.92	11.83	12.38	5.52	5.78	4.33	2.96
0.60	7.57	8.05	3.96	3.96	3.61	2.41	7.74	8.16	4.04	4.07	3.68	2.45
0.55	5.17	5.42	3.06	3.05	3.13	2.06	5.28	5.49	3.13	3.10	3.18	2.06
0.50	3.61	3.75	2.51	2.43	2.75	1.78	3.68	3.82	2.55	2.47	2.80	1.78
${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{15},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$							${\mathit{P}}_{\mathit{c}}=\mathbf{0}.\mathbf{25},\mathit{\eta }=\mathbf{2},\mathit{\beta }=\mathbf{1}$
${\mathit{d}}_{\mathit{T}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{1}}}={\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM	SR	CUSUM
	h = 7.96	h = 2.04	h = 106.11	h = 4.07	h = 338.31	h = 3.71	h = 8.24	h = 2.07	h = 107.23	h = 4.06	h = 341.46	h = 3.68
	370.47	370.25	370.19	369.87	370.49	369.96	370.37	370.67	370.44	370.36	370.59	369.62
0.90	129.45	133.10	83.61	90.66	30.52	30.04	130.72	131.52	84.66	92.12	31.45	31.38
0.85	78.04	80.04	41.92	47.13	14.62	13.32	78.42	80.97	43.18	48.38	15.14	14.07
0.80	47.71	48.99	22.54	25.01	9.04	7.64	48.24	49.27	23.09	25.48	9.30	7.65
0.75	29.21	30.51	12.87	14.15	6.52	5.12	29.46	30.73	13.18	14.32	6.65	5.26
0.70	18.04	18.97	8.05	8.55	5.11	3.72	18.50	19.45	8.22	8.76	5.24	3.75
0.65	11.79	12.20	5.42	5.59	4.22	2.90	11.88	12.38	5.60	5.71	4.33	2.97
0.60	7.61	7.98	3.95	3.99	3.60	2.43	7.78	8.17	4.05	4.07	3.67	2.42
0.55	5.13	5.40	3.08	3.04	3.14	2.05	5.23	5.50	3.14	3.09	3.18	2.03
0.50	3.62	3.77	2.51	2.45	2.75	1.77	3.67	3.80	2.55	2.48	2.79	1.80

present the ZS-ARL and SS-ARL values for $n=10$, under the same conditions as in Table 1 and Table 2, respectively.

For $P_c=0.15$, the SR chart exhibits superior performance in detecting small-to-moderate shifts. Specifically, when the pre-specified shift is $d_{P_1}=d_{P_2}=0.2$, the SR chart demonstrates a slightly lower ARL compared to the CUSUM chart in out-of-control scenarios. This advantage persists when $d_{P_1}=d_{P_2}=0.5$, provided that the actual shift remains small. However, as the shift magnitude increases, the CUSUM chart, designed for $d_{P_1}=d_{P_2}=0.5$, surpasses the SR chart in performance. When $d_{P_1}=d_{P_2}=0.8$, the CUSUM chart consistently outperforms the SR chart. A similar trend is observed for $P_c=0.25$ (Table 1). When the pre-specified shift is small (e.g., $d_{P_1}=d_{P_2}=0.2$), the SR chart remains marginally more effective. However, as $d_{P_1}=d_{P_2}=0.8$ and the actual shift magnitude increases, the CUSUM chart demonstrates better detection capability. Overall, the SR chart proves to be more effective in identifying small-to-moderate shifts.

In the steady-state scenario, the SR chart retains its advantage for $d_{P_1}=d_{P_2}=0.2$, irrespective of the censoring rate. However, for larger shifts ($d_{P_1}=d_{P_2}=0.8$), the CUSUM chart consistently outperforms the SR chart. When $d_{P_1}=d_{P_2}=0.5$, the relative performance of the two methods depends on the true shift magnitude: the SR chart excels for small shifts, whereas the CUSUM chart becomes more effective as the shift magnitude increases. Figure 3 displays SS-ARL comparison between the SR and CUSUM charts ($n=5$, $P_c=0.15$, ${\mathrm{ARL}}_0$ = 370. These findings align with the patterns observed in the zero-state case, reinforcing the conclusion that the SR chart is preferable for detecting small process shifts, while the CUSUM chart is better suited for larger deviations.

The shape parameter $\beta$ has a significant effect on the performance of the control charts: when $\beta$ is decreased from 2 to 0.5, the detection sensitivity increases for both the SR and CUSUM schemes, indicating that the reduction in $\beta$ effectively improves the ability to capture early offsets. The effect of the scale $\eta$ parameter on the performance of the control charts is not significant: when $\eta$ is decreased from 2 to 0.5, the performance of both the SR and CUSUM schemes is almost identical.

Comparative analysis of ZS-ARL results between censoring rates $P_c=0.15$ and $P_c=0.25$ (Table 1) under fixed $n=5$ and ${\mathrm{ARL}}_0$ = 370 reveals systematic performance variations. Increased censoring rates generally elevate ARL values across most shift magnitudes $d_{T_1}$, indicating reduced detection sensitivity. For instance, the SR chart exhibits a 1.5% ARL increase (153.75 → 156.11) at $d_{T_1}=0.90$, while the CUSUM chart shows a 2.3% degradation (7.34 → 7.51) for $d_{T_1}=0.50$, highlighting amplified impacts on small shift detection. To maintain ${\mathrm{ARL}}_0$ = 370, control limits h adapt differentially: SR limits increase slightly from 33.45 ($P_c=0.15$) to 33.65 ($P_c=0.25$), whereas CUSUM limits decrease marginally from 3.28 to 3.265, suggesting distinct compensation strategies. Notably, moderate shifts ($d_{T_1}=0.75$) demonstrate greater ARL degradation (SR: 43.60 → 44.39, +1.8%; CUSUM: 19.24 → 20.42, +6.1%), emphasizing the need for parameter recalibration to mitigate performance losses under higher censoring conditions.

A comparative analysis of ZS-ARL results between Table 1 ($n=5$) and Table 3 ($n=10$) demonstrates that increased sample size enhances control chart monitoring performance. Under identical process shift conditions ($d_{T_1}=d_{T_2}$), expanding the sample size from $n=5$ to $n=10$ yields significant reductions in ARL for both control charts. Specifically, the SR chart exhibits ARL reductions from 153.75 to 135.90 (11.6% decrease) for $d_{T_1}=0.90$ and from 6.99 to 4.23 (39.5% decrease) for $d_{T_1}=0.50$. Similarly, the CUSUM chart shows improved responsiveness with ARL decreasing from 161.07 to 138.68 (13.9% reduction) at $d_{T_1}=0.90$, and a substantial 40.1% improvement (7.34 to 4.40) for $d_{T_1}=0.50$. These results highlight the amplified detection capability of larger samples, particularly for smaller process shifts where statistical power gains are most pronounced.

To ensure a fair comparison benchmarked against Pei-Hsi [18], we evaluated the ZS-ARL performance of the proposed SR and CUSUM control charts alongside existing EWMA methods under identical operating conditions ($\eta =1$, $\beta =1$, $n=5$, ${\mathrm{ARL}}_0$ = 200). Final comparisons with existing depth-based EWMA control charts reveal that both the proposed SR and CUSUM charts demonstrate superior performance for detecting small shifts. Only for large shift detection does the CNN-based EWMA control chart outperform both SR and CUSUM control charts (see

Table 5. SS-ARL comparison for $\eta =1,\beta =1,n=5$, ${\mathrm{ARL}}_0$ = 200.

${\mathit{P}}_{\mathit{c}}=0.2$
${\mathit{d}}_{{\mathit{T}}_{\mathbf{2}}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		$\mathit{\lambda }=\mathbf{0}.\mathbf{1}$						$\mathit{\lambda }=\mathbf{0.2}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	EWMA		CNN		LSTM		EWMA		CNN		LSTM
							CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM
	h = 6.08	h = 1.76	h = 57.02	h = 3.54	h = 177.91	h = 3.29	h = 0.78	h = 0.41	h = −0.11	h = −0.03	h = −0.81	h = −0.40	h = 0.69	h = 0.36	h = −0.06	h = −0.05	h = −0.79	h = −0.40
0.80	27.36	28.75	14.87	16.29	7.08	6.29	15.52	17.85	21.59	21.86	32.63	95.62	15.50	17.21	18.01	23.91	26.72	130.62
0.70	11.52	12.10	5.97	6.47	4.21	3.20	8.78	9.73	7.38	8.80	12.53	41.08	8.08	8.57	7.30	8.87	11.48	45.06
0.60	5.42	5.67	3.29	3.34	3.10	2.22	4.99	6.78	3.71	4.88	6.51	16.26	5.27	5.50	3.01	4.39	6.30	16.46
0.50	2.87	2.99	2.21	2.17	2.44	1.70	3.64	4.16	2.36	2.75	3.72	7.92	3.90	3.92	2.25	2.06	3.88	9.34
0.20	1.07	1.07	1.09	1.07	1.28	1.05	2.38	2.55	1.19	1.17	1.29	2.44	2.07	2.26	1.13	1.00	1.23	2.52
${\mathit{P}}_{\mathit{c}}=\mathbf{0.5}$
${\mathit{d}}_{{\mathit{T}}_{\mathbf{2}}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		$\mathit{\lambda }=\mathbf{0}.\mathbf{1}$						$\mathit{\lambda }=\mathbf{0.2}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	EWMA		CNN		LSTM		EWMA		CNN		LSTM
							CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM
	h = 6.23	h = 1.77	h = 58.43	h = 3.56	h = 179.86	h = 3.27	h = 0.83	h = 0.27	h = −0.06	h = −0.02	h = −0.80	h = −0.15	h = 0.73	h = 0.25	h = −0.06	h = −0.02	h = −0.79	h = −0.15
0.80	28.22	28.86	15.21	17.45	7.30	6.19	10.96	12.37	15.82	13.60	29.42	20.26	12.28	10.34	14.71	13.20	23.71	19.39
0.70	11.81	12.24	6.15	6.61	4.26	3.24	5.48	5.19	5.32	4.31	13.53	6.95	6.54	5.26	4.75	4.03	12.07	7.68
0.60	5.44	5.74	3.36	3.41	3.14	2.20	3.49	3.55	3.04	1.86	7.03	3.60	4.09	3.36	2.58	2.01	5.87	3.58
0.50	2.96	3.09	2.24	2.18	2.46	1.68	3.73	3.61	2.05	1.26	3.70	2.08	3.14	2.48	1.42	1.27	3.78	1.97
0.20	1.07	1.08	1.10	1.08	1.28	1.05	1.68	2.21	1.26	1.00	1.27	1.04	1.84	1.39	1.00	1.00	1.30	1.02
${\mathit{P}}_{\mathit{c}}=\mathbf{0.8}$
${\mathit{d}}_{{\mathit{T}}_{\mathbf{2}}}$	${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.2}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.5}$		${\mathit{d}}_{{\mathit{P}}_{\mathbf{2}}}=\mathbf{0.8}$		$\mathit{\lambda }=\mathbf{0}.\mathbf{1}$						$\mathit{\lambda }=\mathbf{0.2}$
	SR	CUSUM	SR	CUSUM	SR	CUSUM	EWMA		CNN		LSTM		EWMA		CNN		LSTM
							CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM	CEV	CM
	h = 6.38	h = 1.80	h = 58.95	h = 3.49	h = 184.91	h = 3.17	h = 0.88	h = 0.39	h = −0.06	h = −0.03	h = −0.65	h = −0.21	h = 0.82	h = 0.37	h = −0.05	h = −0.01	h = −0.66	h = −0.22
0.80	29.32	30.49	16.17	17.34	7.95	6.73	9.78	9.23	10.03	8.88	20.20	18.41	9.49	8.21	8.83	7.80	22.51	21.44
0.70	12.12	12.90	6.62	6.96	4.55	3.55	4.78	5.99	4.46	3.61	9.51	8.11	4.85	4.49	3.69	3.15	9.23	9.22
0.60	5.81	5.95	3.56	3.59	3.31	2.17	4.48	3.96	1.98	1.51	4.39	3.39	3.09	2.92	2.43	1.68	4.71	4.10
0.50	3.06	3.19	2.34	2.26	2.54	1.60	2.11	2.70	1.38	1.14	2.45	1.90	2.27	2.23	1.58	1.31	2.71	2.35
0.20	1.08	1.08	1.10	1.07	1.28	1.02	2.58	1.28	1.00	1.00	1.06	1.01	1.25	1.31	1.00	1.01	1.05	1.00

).The SR and CUSUM schemes exhibit pronounced advantages in computational efficiency, interpretability, and unsupervised statistical process control. In contrast, machine learning methods offer a formidable capability for managing high-dimensional and complex data, as well as for identifying subtle, non-linear patterns where traditional parametric assumptions may fail.

6. Example

To validate the proposed methodology, we adopt the liquid-crystal display module (LCM) reliability test dataset from Pei-Hsi [18], comprising 30 batches of accelerated life testing data under 70 °C and 80% relative humidity conditions, with a sample size of $n=5$ per batch. Historical IC phase analysis confirms that the LCM lifetime follows a Gamma distribution with shape parameter ${\beta }_0=5.72$ and scale parameter ${\eta }_0=0.48$. To optimize testing efficiency, a Type I right-censoring scheme with censoring rate $P_c=0.8$ (equivalent to censoring time $c=1.76$ h) was implemented, where each batch test terminates at 1.76 h regardless of failure occurrences.

The monitoring procedure begins with the initialization of IC process parameters, including the sample size n, censoring rate $P_c$, predetermined percent change $d_P$, and the Gamma distribution’s shape and scale parameters $\beta$ and $\eta$. A total of 50,000 simulation replications are defined, and the UCL is initialized with a provisional value h. In the data generation step, a sample of size n is drawn from the Gamma distribution parameterized by $\beta$ and $\eta$. The monitoring statistic $R_i$ is then computed for the current sample. If $R_i$ remains below or equal to h, a new sample is generated; however, if $R_i$ exceed h, the sample index at which this first OOC signal is detected is recorded as the RL. This process is repeated iteratively until 50,000 run lengths are collected. The mean of these run lengths is calculated to estimate the IC ${\mathrm{ARL}}_0$ corresponding to the current h. The UCL h is adjusted iteratively until the target ${\mathrm{ARL}}_0$ is achieved, at which point the final UCL is set to the calibrated value of h.

The monitoring process begins by defining the necessary parameters, including the sample size n, shape parameter $\beta$, scale parameter $\eta$, censoring rate $P_c$, and the magnitude of the shift $d_{P_j}$, followed by the determination of the corresponding control limits. A sample of size n is then generated, incorporating a shift of size $d_{T_j}$, and the plotting statistic $R_t$ is computed using Equation (17). If the control chart signals an OOC condition, the RL is recorded; otherwise, the process returns to sample generation. After repeating Steps 2 and 3 for 50,000 replications, the OOC ${\mathrm{ARL}}_1$ is calculated as the average of all recorded RL values.

Following Lee and Liao’s experimental setup with smoothing constant $\lambda =0.1$ and target IC ${\mathrm{ARL}}_0$ of 200, we implemented both CUSUM and SR control charts for comparative analysis. The simulation-derived control limits were determined as $h_{SR}=20.35$ for the SR chart and $h_{CUSUM}=2.87$ for the CUSUM chart. Figure 4 presents the Phase II monitoring of all control charts for LCM data. Notably, while the CNN-based EWMA CEV chart and EWMA CEV chart triggered OOC signals at sample points 20 and 21, respectively, both our SR and CUSUM charts detected the process shift at sample point 19. This demonstrates that the detection ability of the proposed methods outperforms that of advanced CNN-enhanced methods. The proposed SR and CUSUM schemes offer two key advantages compared to CNN-based methods: simpler implementation without requiring complex deep learning architectures, and better adaptability for monitoring both shape and scale parameters in highly censored Gamma-distributed data. This makes them particularly suitable for industrial applications where computational resources are limited but reliable monitoring of multiple parameters is essential.

7. Conclusions

This study has established the effectiveness of CUSUM and SR control charts for monitoring Type I right-censored Gamma-distributed lifetime data. Through comprehensive evaluation using zero-state and steady-state ARL metrics, both control charts demonstrate superior detection capability compared to deep learning-based EWMA methods across various shift magnitudes. The results reveal an important performance characteristic: while the SR chart exhibits greater sensitivity to small process deviations, the CUSUM chart proves more effective for identifying larger shifts. This complementary performance profile provides practitioners with valuable alternatives depending on their specific monitoring requirements. Notably, the proposed methods achieve this enhanced detection performance without relying on computationally intensive deep learning architectures, offering a more practical solution for industrial implementation where both statistical reliability and operational simplicity are crucial. It should be noted that the proposed method has certain limitations. It is predicated on the assumption of known parameters, and its performance is susceptible to the accuracy of parameter estimation. Furthermore, the methodology is developed specifically for the Gamma distribution, therefore, not applicable to non-parametric scenarios. The findings contribute to the growing body of research on censored data monitoring by demonstrating how traditional statistical process control methods can be effectively adapted for modern reliability engineering applications. The proposed scheme has been validated in a manufacturing context. A promising future direction would be to explore its application in new domains such as financial risk control or medical diagnosis.The existing SR and CUSUM schemes can be extended to monitor censored data from other distributions and are also applicable to Type II censoring.