Bayesian Stochastic Inference and Statistical Reliability Modeling of Maxwell–Boltzmann Model Under Improved Progressive Censoring for Multidisciplinary Applications

Abstract

The Maxwell–Boltzmann (MB) distribution is important because it provides the statistical foundation for connecting microscopic particle motion to macroscopic gas properties by statistically describing molecular speeds and energies, making it essential for understanding and predicting the behavior of classical ideal gases. This study advances the statistical modeling of lifetime distributions by developing a comprehensive reliability analysis of the MB distribution under an improved adaptive progressive censoring framework. The proposed scheme strategically enhances experimental flexibility by dynamically adjusting censoring protocols, thereby preserving more information from test samples compared to conventional designs. Maximum likelihood estimation, interval estimation, and Bayesian inference are rigorously derived for the MB parameters, with asymptotic properties established to ensure methodological soundness. To address computational challenges, Markov chain Monte Carlo algorithms are employed for efficient Bayesian implementation. A detailed exploration of reliability measures—including hazard rate, mean residual life, and stress–strength models—demonstrates the MB distribution’s suitability for complex reliability settings. Extensive Monte Carlo simulations validate the efficiency and precision of the proposed inferential procedures, highlighting significant gains over traditional censoring approaches. Finally, the utility of the methodology is showcased through real-world applications to physics and engineering datasets, where the MB distribution coupled with such censoring yields superior predictive performance. This genuine examination is conducted through two datasets (including the failure times of aircraft windshields, capturing degradation under extreme environmental and operational stress, and mechanical component failure times) that represent recurrent challenges in industrial systems. This work contributes a unified statistical framework that broadens the applicability of the Maxwell–Boltzmann model in reliability contexts and provides practitioners with a powerful tool for decision making under censored data environments.

1. Introduction

In the latter half of the nineteenth century, James Clerk Maxwell in 1860 and Ludwig Boltzmann in 1871 formulated the probability law governing the distribution of molecular speeds in a gas at a given temperature. This formulation, now known as the Maxwell–Boltzmann (MB($\theta$)) distribution, constitutes a fundamental statistical model in classical kinetic theory, describing the distribution of molecular speeds in an ideal gas at thermal equilibrium. Recently, the MB law underpins key thermodynamic relations, such as pressure, diffusion, and thermal transport. Owing to these properties, the distribution finds extensive applications across physics, chemistry, and statistical mechanics, as well as in emerging domains such as engineering reliability analysis, where it serves as a flexible model for lifetime and degradation data (see Rowlinson [1] for details).

Let Y be a non-negative continuous random variable representing a lifetime. If $Y\sim \mathrm{MB}(\theta )$, where $\theta >0$ denotes a scale parameter, then the probability density function (PDF; $g(·)$) and cumulative distribution function (CDF; $G(·)$) of Y are given, respectively, by

$$g(y;\theta )={\displaystyle \frac{4}{\sqrt{\pi }}}{\displaystyle \frac{y^2}{\sqrt{{\theta }^3}}}{e}^{-{\displaystyle \frac{y^2}{\theta }}},y>0$$

(1)

and

$$G(y;\theta )={\Gamma }_{{\displaystyle \frac{3}{2}}}\left({\displaystyle \frac{y^2}{\theta }}\right),$$

(2)

where

$$\begin{array}{c}\hfill {\Gamma }_{\alpha }(\beta )={\displaystyle \frac{1}{\Gamma (\alpha )}}{\int }_0^{\beta }{y}^{\alpha -1}{e}^{-y}dy\mathrm{and}\Gamma (\alpha )={\int }_0^{\infty }{y}^{\alpha -1}{e}^{-y}dy\end{array}$$

denote the gamma and incomplete-gamma functions, respectively.

Function (2) admits the following equivalent form:

$$\begin{array}{cc}\hfill F(y;\theta )& =2\mathrm{erf}\left({\displaystyle \frac{y}{\sqrt{\theta }}}\right)-{\displaystyle \frac{2}{\sqrt{\pi }}}{\displaystyle \frac{y}{\sqrt{\theta }}}{e}^{-{\displaystyle \frac{y^2}{\theta }}},\hfill \\ \hfill & =1-{\displaystyle \frac{4}{\sqrt{\pi }}}{\displaystyle \frac{1}{\sqrt{{\theta }^3}}}\Im (y,2,\theta ),\hfill \end{array}$$

(3)

where $\mathrm{erf}(\alpha )={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^{\alpha }{e}^{-t^2}dt,\mathrm{and}\Im (y,\alpha ,\theta )={\int }_y^{\infty }{t}^{\alpha }{e}^{-{\displaystyle \frac{t^2}{\theta }}}dt.$

Moreover, we investigated two unknown time metrics—namely the reliability function (RF; $R(·)$) and hazard rate function (HRF; $h(·)$) of the MB($\theta$) distribution—at distinct time $x>0$, which are given, respectively, by

$$R(x;\theta )={\displaystyle \frac{4}{\sqrt{\pi }}}{\displaystyle \frac{1}{\sqrt{{\theta }^3}}}\Im (x,2,\theta )$$

(4)

and

$$h(x;\theta )={\displaystyle \frac{x^2{e}^{-\frac{x^2}{\theta }}}{\Im (x,2,\theta )}}.$$

(5)

Taking several configurations of $\theta$, Figure 1 indicates that the MB’s PDF (1) behaves like a right-skewed or unimodal density shape, while the MB’s HRF (5) is strictly increasing for $y\to +\infty$.

Figure 1. The PDF (left) and HRF (right) shapes of the MB($\theta$) distribution.

Over roughly the last decade, the MB model has evolved into a well-established tool in reliability research, attracting wide-ranging investigations under diverse censoring and sampling schemes. For example, Krishna and Malik [2,3] analyzed the model under conventional Type-II censoring (T2-C) and Type-II progressive censoring (T2-PC), respectively. Tomer and Panwar [4] considered its application in a Type-I hybrid progressive censoring (T1-HPC), while Chaudhary and Tomer [5] examined stress–strength reliability settings with T2-PC data. Pathak et al. [6] studied the distribution in the context of the T2-PC plan incorporating binomial removals under step-stress partially accelerated life testing. More recently, Elshahhat et al. [7] discussed the MB reliability metrics using samples created from a generalized T2-HPC strategy. These studies, among others, illustrate the model’s adaptability to a variety of experimental designs and reinforce its value as a versatile lifetime distribution for modern engineering reliability analysis.

The T2-PC has become a well-established tool in both reliability engineering and survival analysis, primarily because it offers greater operational flexibility than the T2-C framework. A key advantage of T2-PC is its capacity to progressively withdraw the functioning units that were investigated during the experimental design, which is particularly valuable in large-scale industrial testing or long-term clinical investigations. In a standard T2-PC arrangement, m failures are targeted from n identical experimental units, with a predetermined censoring plan $\mathbf{S}=(S_1,S_2,\dots ,S_m)$ fixed prior to commencement. Following the first observed failure $Y_{1:m:n}$, a randomly chosen set of $S_1$ surviving units is removed from the remaining $n-1$ items. Upon the second failure $Y_{2:m:n}$, a further $S_2$ units are withdrawn from the updated risk set of $n-2-S_1$ items, and this process then continues. Once the mth failure occurs, all remaining $S_m$ survivors are censored, marking the end of the experiment [8].

Within the broader class of hybrid censoring schemes, Kundu and Joarder [9] introduced the T1-HPC plan. In this setting, n test units are placed under a progressive censoring scheme $\mathbf{S}$, and the termination time is defined as $T^{★}=min(t,Y_{m:m:n})$, where t is a fixed inspection time. While this approach limits the maximum test duration, it can lead to a small number of observed failures, thereby reducing the precision of statistical inference. To address this drawback, Ng et al. [10] developed the adaptive Type-II progressive censoring (AT2-PC) strategy, where the number of failures m is fixed in advance but the censoring vector $\mathbf{S}$ can be adaptively modified during the experiment. The AT2-PC retains the sequential removal structure of T2-PC while improving estimation efficiency.

However, for test items with exceptionally long lifetimes, the AT2-PC framework may still lead to excessively prolonged experiments. To mitigate this, Yan et al. [11] recently proposed the improved AT2-PC (IAT2-PC) model. This generalization of both T1-HPC and AT2-PC incorporates two finite time thresholds—${\tau }_1$ and ${\tau }_2$, where $0<{\tau }_1<{\tau }_2<\infty$—to control the total test duration. Under IAT2-PC, m failures are planned from n starting units, with removals specified by $\mathbf{S}$. After each failure $Y_{i:m:n}$, a designated number $S_i$ of surviving units is randomly withdrawn from the remaining set. The numbers of observed failures by times ${\tau }_1$ and ${\tau }_2$ are recorded as $d_1$ and $d_2$, respectively, providing additional structure to the stopping rules while ensuring sufficient data for analysis.

Subsequently, the observed data collected by the practitioner will be one of the following censoring fashions:

• Case-1: As $Y_{m:m:n}<{\tau }_1$, stop the test at $Y_{m:m:n}$.
• Case-2: As ${\tau }_1<Y_{m:m:n}<{\tau }_2$, reset $\mathbf{S}$ as $S_{d_1+1}=\cdots =S_{m-1}=0$, stop the test at $Y_{m:m:n}$.
• Case-3: As ${\tau }_2<Y_{m:m:n}$, reset $\mathbf{S}$ as $S_{d_1+1}=\cdots =S_{d_2-1}=0$, stop the test at ${\tau }_2$.

Let $\mathbf{y}=\{(Y_1,S_1),\dots ,(Y_{d_1},S_{d_1}),(Y_{d_1+1},0),\dots ,(Y_{d_2-1},0),(Y_{d_2},S^{★})\}$ denote a sample of size $d_2$, which is obtained under an IAT2-PC from a continuous population characterized by PDF $g(·)$ and CDF $G(·)$. The joint likelihood function (LF) for this sample can be expressed as

$$L(\theta \mid \mathbf{y})\propto \prod _{i=1}^{{\Psi }_2}g\left(y_i;\theta \right)\prod _{i=1}^{{\Psi }_1}{\left[1-G\left(y_i;\theta \right)\right]}^{S_i}{\left[1-G\left(T^{★};\theta \right)\right]}^{S^{★}},$$

(6)

where $y_i\equiv Y_{i:m:n}$ for simplicity. To distinguish, Table 1 summarizes the math operators defined in the LF (6). For further clarification, a flowchart of the IAT2-PC plan is designed in Figure 2.

Table 1. Censoring levels of $T^{★},S^{★}$, ${\Psi }_i,i=1,2,$ and $(y_i,S_i)$.

Case	${\mathbf{\Psi }}_1$	${\mathbf{\Psi }}_2$	${\mathbf{S}}^{\mathbf{★}}$	${\mathbf{T}}^{\mathbf{★}}$	$\{{\mathit{y}}_{\mathit{i}},{\mathit{S}}_{\mathit{i}}\}$
1	$m-1$	m	$S_m$	$y_m$	$\{(y_1,S_1),\dots ,(y_{m-1},S_{m-1}),(y_m,S^{★})\}$
2	$d_1$	m	$n-m-{\sum }_{i=1}^{d_1}{S}_i$	$y_m$	$\{(y_1,S_1),\dots ,(y_{d_1},S_{d_1}),(y_{d_1+1},0),\dots ,(y_{m-1},0),(y_m,S^{★})\}$
3	$d_1$	$d_2$	$n-d_2-{\sum }_{i=1}^{d_1}{S}_i$	${\tau }_2$	$\{(y_1,S_1),\dots ,(y_{d_1},S_{d_1}),(y_{d_1+1},0),\dots ,(y_{d_2-1},0),(y_{d_2},0)\}$

Figure 2. Flowchart of the IAT2-PC procedure.

For clarity, we provide a simple example to illustrate the choices of ${\Psi }_1$, ${\Psi }_2$, and $\mathbf{S}$ in practice. Suppose $\mathbf{y}=(0.1,0.3,0.6,0.8,1.3,1.9,2.4,2.7,3.1,3.5)$ is a T2-PC sample with $m=10$, obtained using $\mathbf{S}=(1,1,1,1,1,1,1,1,1,1)$ from a continuous lifetime population with $n=20$. Consequently, the practitioner records one scenario for the three cases of the IAT2-PC plan based on several choices of ${\tau }_1$ and ${\tau }_2$, as summarized in Table 2.

Table 2. Censoring levels of $T^{★},S^{★}$, ${\Psi }_i,i=1,2,$ and $(y_i,S_i)$.

Case	$({\mathit{\tau }}_1,{\mathit{\tau }}_2)$	${\mathbf{\Psi }}_1$	${\mathbf{\Psi }}_2$	${\mathbf{S}}^{\mathbf{★}}$	${\mathbf{T}}^{\mathbf{★}}$	$\{{\mathit{y}}_{\mathit{i}},{\mathit{S}}_{\mathit{i}}\}$
1	(4.5, 5.5)	9	10	1	$3.5$	$\{(0.1,1),(0.3,1),(0.6,1),(0.8,1),(1.3,1),(1.9,1),(2.4,1),(2.7,1),(3.1,1),(3.5,1)\}$
2	(1.5, 4.5)	5	10	5	$3.5$	$\{(0.1,1),(0.3,1),(0.6,1),(0.8,1),(1.3,1),(1.9,0),(2.4,0),(2.7,0),(3.1,0),(3.5,0)\}$
3	(1.5, 2.5)	5	7	8	$2.5$	$\{(0.1,1),(0.3,1),(0.6,1),(0.8,1),(1.3,1),(1.9,0),(2.4,0)\}$

It should be noted here that the IAT2-PC design can be considered an extension for several common censoring schemes, including the following:

• When $t={\tau }_i$ and $i=1,2$, then the T1-HPC scheme by Kundu and Joarder [9] applies;
• When ${\tau }_2\to \infty$, then the AT2-PC scheme by Ng et al. [10] applies;
• When ${\tau }_1\to \infty$, then the T2-PC scheme by Balakrishnan and Cramer [8] applies;
• When ${\tau }_1\to 0$, $S_i=0$ for $i=1,2,\dots ,m-1$, and $S_m=n-m$, then the T2-C scheme by Bain and Engelhardt [12] applies.

Remark 1. 

The IAT2-PC scheme can be considered an extension of the T1-HPC, AT2-PC, T2-PC, and T2-C schemes.

Proof. 

See Appendix A.    □

In the IAT2-PC mechanism, the first threshold ${\tau }_1$ functions as an early warning for the elapsed experimental time, signaling that the study has reached a predefined interim stage. In contrast, the second threshold ${\tau }_2$ defines the absolute maximum duration for the experiment. Should ${\tau }_2$ be attained before the occurrence of the predetermined number of failures m, the study is forcibly terminated at time ${\tau }_2$. This refinement directly addresses the limitation of the AT2-PC design (by Ng et al. [10]), where no explicit upper bound on total test duration was guaranteed. By imposing the constraint ${\tau }_2$, the improved censoring scheme ensures that the experiment cannot exceed the designated maximum time, thereby enhancing its practical applicability. In the reliability literature, using likelihood-based (6) inference, analogous approaches have been applied to various lifetime distributions, including Weibull [13], Burr Type-III [14], Nadarajah-Haghighi [15], power half-normal [16], and inverted XLindley [17] models.

In reliability theory and lifetime analysis, the development of efficient statistical models under complex censoring schemes has become increasingly important for modern engineering applications. Classical censoring methods often fail to balance experimental cost, information retention, and statistical precision, particularly when dealing with large-scale life tests in engineering systems. The MB distribution, though originally arising in statistical physics, has recently attracted attention in reliability modeling due to its flexibility in characterizing diverse failure mechanisms with monotonic hazard structures. However, its potential remains underexplored in censored reliability contexts. On the other hand, the IAT2-PC scheme has emerged as a promising design for life-testing experiments, allowing dynamic adjustments in the number of units removed during the test, thereby enhancing efficiency while maintaining the robustness of parameter inference. Motivated by these considerations, this study aims to integrate the MB model with an IAT2-PC plan, thereby providing a more powerful and cost-effective approach to engineering failure modeling and statistical inference. However, the objectives of this study can be summarized in six outlines:

• This study is the first to investigate the MB distribution under the IAT2-PC scheme, extending its scope in reliability analysis.
• Likelihood-based inference is developed for model parameters under IAT2-PC, and the existence and uniqueness of the maximum likelihood estimator (MLE) of MB($\theta$) is established with numerical evidence.
• Bayesian estimation methods are proposed using an inverted-gamma prior and Markov chain Monte Carlo techniques, with derivations of posterior summaries and Bayes credible intervals (BCIs).
• Several interval estimation strategies were compared, including asymptotic (normal and log-normal) intervals and Bayesian (BCI and HPD) intervals, to provide robust inference tools.
• A comprehensive Monte Carlo simulation study evaluating the precision and efficiency of the proposed estimators under various censoring designs was conducted, demonstrating the advantages of the Bayesian framework.
• Two real engineering datasets were analyzed, confirming the practical applicability of the proposed modeling framework in real-world reliability experiments.

The structure of the rest of this study is organized as follows. Section 2 and Section 3 present the frequentist and Bayesian estimation methodologies, respectively. Section 5 provides Monte Carlo simulation results. Two genuine engineering applications are analyzed in Section 6. Finally, Section 7 summarizes the main conclusions and key insights derived from this work.

2. Likelihood Inference

This section is devoted to the ML estimation of the MB model parameters, namely $\theta$, $R(x)$, and $h(x)$. Under the assumption of approximate normality for the corresponding estimators, $(1-\epsilon )100\%$ ACI estimators were obtained by employing the observed Fisher information (FI) matrix in combination with the delta approach. Utilizing the expressions in (1), (2), and (6), Equation (6) can be equivalently written as follows:

$$\begin{array}{c}\hfill L(\theta |\mathbf{y})\propto {\theta }^{-{\displaystyle \frac{3n}{2}}}{e}^{-{\displaystyle \frac{1}{\theta }}{\sum }_{i=1}^{{\Psi }_2}{y}_i^2}{\Im }^{S^{★}}\left(T^{★},2,\theta \right)\prod _{i=1}^{{\Psi }_1}{\Im }^{S_i}\left(y_i,2,\theta \right).\end{array}$$

(7)

Equivalently, the log-LF of (7) becomes

$$\begin{array}{c}\hfill logL(\theta |\mathbf{y})\propto -{\displaystyle \frac{3n}{2}}log\left(\theta \right)-{\displaystyle \frac{1}{\theta }}\sum _{i=1}^{{\Psi }_2}{y}_i^2+S^{★}log\left(\Im \left(T^{★},2,\theta \right)\right)+\sum _{i=1}^{{\Psi }_1}{S}_{i}log\left(\Im \left(y_i,2,\theta \right)\right).\end{array}$$

(8)

Thereafter, the MLE of $\theta$, represented by $\widehat{\theta }$, is determined by maximizing (8), resulting in the following nonlinear expression:

$$\begin{array}{c}\hfill {\left.{\displaystyle \frac{1}{\theta }}\left[{\displaystyle \frac{1}{\theta }}\sum _{i=1}^{{\Psi }_2}{y}_i^2-{\displaystyle \frac{3n}{2}}\right]+{\displaystyle \frac{1}{{\theta }^2}}\left[S^{★}\left({\displaystyle \frac{\Im \left(T^{★},4,\theta \right)}{\Im \left(T^{★},2,\theta \right)}}\right)+\sum _{i=1}^{{\Psi }_1}{S}_i\left({\displaystyle \frac{\Im \left(y_i,4,\theta \right)}{\Im \left(y_i,2,\theta \right)}}\right)\right]\right|}_{\theta =\widehat{\theta }}=0.\end{array}$$

(9)

Remark 2. 

The MLE $\widehat{\theta }$ of θ, based on the log-LF in (8), exists and is unique for $\theta >0$.

Proof. 

See Appendix B.    □

From Equation (9), it is clear that the MLE $\widehat{\theta }$ of $\theta$ does not admit a closed-form solution. Consequently, it becomes important to assess both the existence and uniqueness of $\widehat{\theta }$. Given the complexity of the score function in (9), an analytical verification is challenging. To overcome this, we investigated these properties numerically by generating an IAT2-PC sample from the MB distribution with parameters $\theta =(0.8,1.5)$ under the configuration $n=100$, $m=50$, $({\tau }_1,{\tau }_2)=(1,2)$, and a uniform T2-PC scheme with $S_i=1$ for $i=1,2,\dots ,m$. The resulting MLE values of $\theta$ were 0.4833 and 2.4643 for the two respective cases. 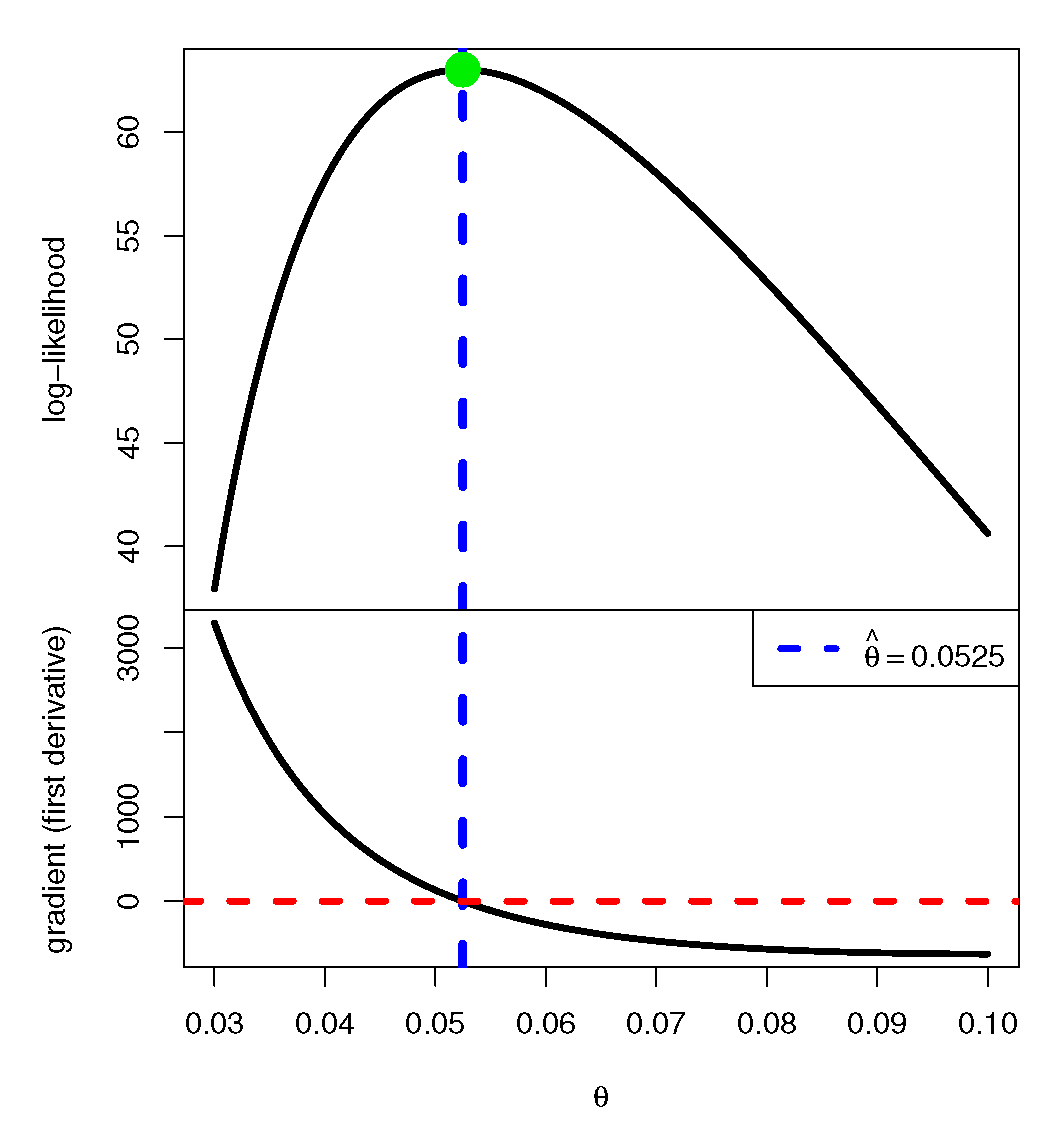Figure 3 depicts the log-LF (8) alongside the score function from (9) as functions of $\theta$ over a selected range. As shown, the vertical lines corresponding to the MLE intersect the log-likelihood curve at its maximum and cross the score function at zero. These findings confirm that the MLE of $\theta$ exists and is unique for each considered scenario.

Figure 3. Plots of the log-LF versus its gradient function.

Although providing an analytical proof of concavity is challenging due to the nonlinear structure of the likelihood, the uniqueness of the MLE can be justified under general conditions requiring the observed information matrix to be positive definite. Our numerical experiments, including eigenvalue analyses from different initial values, consistently confirm concavity in practice and thus offer strong evidence for uniqueness (see Figure 3).

After obtaining $\widehat{\theta }$, the MLEs of the RF and HRF—denoted by $\widehat{R}(x)$ and $\widehat{h}(x)$, respectively—can be readily determined from Equations (4) and (5) for $x>0$ as follows:

$$\widehat{R}(x)={\displaystyle \frac{4}{\sqrt{\pi }}}{\displaystyle \frac{1}{\sqrt{{\widehat{\theta }}^3}}}\widehat{\Im }(x,2,\widehat{\theta })$$

and

$$\widehat{h}(x)={\displaystyle \frac{x^2{e}^{-\frac{x^2}{\widehat{\theta }}}}{\widehat{\Im }(x,2,\widehat{\theta })}},$$

respectively. The Newton–Raphson (NR) algorithm, implemented through the maxLik package (by Henningsen and Toomet [18]) in the R programming environment, was employed to efficiently compute the fitted estimates $\widehat{\theta }$, $\widehat{R}(x)$, and $\widehat{h}(x)$.

3. Bayesian Inference

This section is devoted to deriving both point and credible Bayesian estimates for $\theta$, $R(x)$, and $h(x)$. Within the Bayesian framework, the specification of prior distributions and loss functions is fundamental. As highlighted by Bekker and Roux [19] and Elshahhat et al. [7], selecting an appropriate prior is often nontrivial with no universally accepted guideline. Considering that the MB parameter $\theta$ is strictly positive, the inverted-gamma $\mathrm{Inv}.\mathrm{G}(\alpha ,\beta )$ distribution offers a natural and versatile prior choice. Accordingly, we assume $\theta \sim \mathrm{Inv}.\mathrm{G}(\alpha ,\beta )$, where $\alpha ,\beta >0$ denote the hyperparameters. The Inv.G distribution (10) is a flexible prior for positive parameters, with heavier tails than the gamma and less mass near zero. Its shape varies with parameter values, and it yields simple posterior forms. Other conjugate priors, such as gamma, normal-inverse-gamma, and inverse-gamma-gamma, can also be considered.

To evaluate the sensitivity of the results to prior selection, we additionally considered a conjugate gamma prior. The posterior summaries derived under this alternative prior were nearly indistinguishable from those obtained with the proposed Inv.G prior, indicating that the Bayesian inference is robust to reasonable variations in prior specification.

Then, the prior PDF, denoted by $\vartheta (·)$, is given by

$$\vartheta \left(\theta ;\alpha ,\beta \right)={\displaystyle \frac{{\beta }^{\alpha }}{\Gamma (\alpha )}}{\theta }^{-(\alpha +1)}{e}^{-{\displaystyle \frac{\beta }{\theta }}},\theta >0,$$

(10)

where $\Gamma (·)$ denotes the gamma function, and $\alpha >0$ and $\beta >0$ are known. From (7) and (10), the posterior PDF (say $\Theta (·)$) of $\theta$ is

$$\begin{array}{c}\hfill \Theta (\theta |\mathbf{y})\propto {\theta }^{-\left({\displaystyle \frac{3n}{2}}+\alpha +1\right)}{e}^{-{\displaystyle \frac{1}{\theta }}\left(\beta +{\sum }_{i=1}^{{\Psi }_2}{y}_i^2\right)}{\Im }^{S^{★}}\left(T^{★},2,\theta \right)\prod _{i=1}^{{\Psi }_1}{\Im }^{S_i}\left(y_i,2,\theta \right),\end{array}$$

(11)

where its normalized term (say, $\Xi$) is given by

$$\begin{array}{c}\hfill \Xi ={\int }_0^{\infty }\vartheta (\theta )\times L(\theta |\mathbf{y})d\theta .\end{array}$$

We then adopted the squared-error loss (SEL) function as the primary loss criterion, owing to its widespread use and symmetric nature in Bayesian analysis. Nevertheless, the proposed approach can be readily extended to alternative loss functions. Levering the SEL, the Bayesian estimated (say $\tilde{\theta }$) of $\theta$ is acquired by the posterior-mean as follows:

$$\begin{array}{c}\hfill \tilde{\theta }={\Xi }^{-1}{\int }_0^{\infty }\theta \times \Theta (\theta |\mathbf{y})\mathrm{d}\theta .\end{array}$$

(12)

Given the posterior distribution in (11) and the nonlinear form of the LF in (7), the Bayes estimates of $\theta$, $R(x)$, and $h(x)$ under SEL are analytically intractable. Therefore, we employed the MCMC method to generate Markovian samples from (11), which were subsequently used to compute the Bayesian estimates and construct the corresponding BCI/HPD intervals for each parameter. Although the posterior density of $\theta$ in (11) does not correspond to any standard continuous distribution, using the same censoring setting provided in plotting Figure 3, Figure 4 indicates that its conditional form closely approximates a normal distribution. Consequently, following Algorithm 1, the Metropolis–Hastings (M–H) algorithm is applied to update the posterior samples of $\theta$, after which the Bayes estimates for $\theta$, $R(x)$, and $h(x)$ are obtained.

Algorithm 1 The M-H Algorithm for Sampling $\theta$, $R(x)$, and $h(x)$

1: Input: Initial estimate $\widehat{\theta }$, estimated variance $\widehat{V}(\widehat{\theta })$, total iterations ${\Re }^{•}$, burn-in ${\Re }^{\circ }$, confidence level $(1-\epsilon )$ 2: Output: Posterior mean $\tilde{\theta }$ 3: Set ${\theta }^{(0)}\leftarrow \widehat{\theta }$ 4: Set $t\leftarrow 1$ 5: while$t\le {\Re }^{•}$do 6:    Generate ${\theta }^{★}\sim N({\theta }^{(t-1)},\widehat{V}(\widehat{\theta }))$ 7:    Compute acceptance ratio: $$W\leftarrow min\left(1,{\displaystyle \frac{\Theta ({\theta }^{★}\mid \mathbf{y})}{\Theta ({\theta }^{(t-1)}\mid \mathbf{y})}}\right)$$ 8:    Generate $u\sim U(0,1)$ 9:    if $u\le W$ then 10:      Set ${\theta }^{(t)}\leftarrow {\theta }^{★}$ 11:    else 12:      Set ${\theta }^{(t)}\leftarrow {\theta }^{(t-1)}$ 13:    end if 14:    Update $R(x)$ and $h(x)$ using ${\theta }^{(t)}$ in (4) and (5) 15:    Increment $t\leftarrow t+1$ 16: end while 17: Discard the first ${\Re }^{\circ }$ samples as burn-in 18: Define ${\Re }^{★}={\Re }^{•}-{\Re }^{\circ }$ 19: Compute: $$\tilde{\theta }={\displaystyle \frac{1}{{\Re }^{★}}}\sum _{t={\Re }^{\circ }+1}^{{\Re }^{•}}{\theta }^{(t)},\tilde{R}(x)={\displaystyle \frac{1}{{\Re }^{★}}}\sum _{t={\Re }^{\circ }+1}^{{\Re }^{•}}{R}^{(t)}(x),\tilde{h}(x)={\displaystyle \frac{1}{{\Re }^{★}}}\sum _{t={\Re }^{\circ }+1}^{{\Re }^{•}}{h}^{(t)}(x)$$

Figure 4. Posterior density plots of $\theta$.

4. Interval Estimation

This section develops both asymptotic and credible interval estimates for the parameters $\theta$, $R(x)$, and $h(x)$. The asymptotic intervals—comprising the normal approximation (ACI[NA]) and normal approximation via logarithmic transformation (ACI[NL])—are constructed using the observed Fisher information. In parallel, Bayesian intervals—specifically the BCI and HPD—are obtained from the MCMC samples of the respective parameters.

4.1. Asymptotic Intervals

Beyond the point estimation, it is of considerable practical interest to construct the $100(1-\epsilon )\%$ ACI estimators for the parameters $\theta$, $R(x)$, and $h(x)$. Relying on the asymptotic properties of the MLE of $\widehat{\theta }$, these ACIs can be obtained by noting that $\widehat{\theta }$ is approximately normally distributed with the mean $\theta$ and variance–covariance (VC) matrix $V(·)$, which is typically derived from the FI matrix $I(·)$. However, due to the analytical intractability of the exact Fisher information, a more feasible approach is to approximate $V(·)$ via the observed FI matrix evaluated at $\theta =\widehat{\theta }$, which is denoted by ${I(·)|}_{\theta =\widehat{\theta }}$. Hence, the VC matrix can be estimated as follows:

$$\begin{array}{cc}\hfill V(\widehat{\theta })& =I^{-1}{(\theta )|}_{\theta =\widehat{\theta }},\hfill \end{array}$$

(13)

where

$$\begin{array}{cc}\hfill I(\theta )=& -{\displaystyle \frac{1}{{\theta }^2}}\left[{\displaystyle \frac{3n}{2}}-{\displaystyle \frac{2}{\theta }}\sum _{i=1}^{{\Psi }_2}{y}_i^2\right]\hfill \\ \hfill & +{\displaystyle \frac{2}{{\theta }^3}}\left[S^{★}\left({\displaystyle \frac{\Im \left(T^{★},2,\theta \right)\Im \left(T^{★},6,\theta \right)-{\Im }^2\left(T^{★},4,\theta \right)}{{\Im }^2\left(T^{★},2,\theta \right)}}\right)\right]\hfill \\ \hfill & +{\displaystyle \frac{2}{{\theta }^3}}\left[\sum _{i=1}^{{\Psi }_1}{S}_i\left({\displaystyle \frac{\Im \left(y_i,2,\theta \right)\Im \left(y_i,6,\theta \right)-{\Im }^2\left(y_i,4,\theta \right)}{{\Im }^2\left(y_i,2,\theta \right)}}\right)\right].\hfill \end{array}$$

For the construction of the $100(1-\epsilon )\%$ ACIs corresponding to the RF $R(x)$ and the HRF $h(x)$, it is first necessary to obtain estimates of the variances of their respective estimators, $\widehat{R}(x)$ and $\widehat{h}(x)$. A common and effective approach for this purpose is the delta method, which provides variance approximations—denoted by ${\widehat{V}}_{\widehat{R}}$ and ${\widehat{V}}_{\widehat{h}}$, respectively. Following the methodology of Greene [20], the delta method relies on the assumption that $\widehat{R}(x)$ is approximately normally distributed with mean $R(x)$ and variance ${\widehat{V}}_{\widehat{R}}$, while $\widehat{h}(x)$ follows an approximate normal distribution with mean $h(x)$ and variance ${\widehat{V}}_{\widehat{h}}$. Accordingly, the associated variances ${\widehat{V}}_{\widehat{R}}$ and ${\widehat{V}}_{\widehat{h}}$ of $R(x)$ and $R(x)$, are given by

$$\begin{array}{c}\hfill \widehat{V}(\widehat{R})\approx {\left.[A_{R}V(\theta )A_R^{\top }]\right|}_{\theta =\widehat{\theta }}\mathrm{and}\widehat{V}(\widehat{h})\approx {\left.[A_{h}V(\theta )A_h^{\top }]\right|}_{\theta =\widehat{\theta }},\end{array}$$

where

$$\begin{array}{cc}\hfill A_R& ={\displaystyle \frac{4}{\sqrt{\pi {\theta }^5}}}\left[{\displaystyle \frac{1}{\theta }}\Im (x,4,\theta )-{\displaystyle \frac{3}{2}}\Im (x,2,\theta )\right],\hfill \\ \hfill & \mathrm{and}\hfill \\ \hfill A_h& =h(x;\theta )\left[{\left({\displaystyle \frac{x}{\theta }}\right)}^2-{\displaystyle \frac{1}{2\theta }}(x+3)h(x;\theta )\right],\hfill \end{array}$$

respectively.

Thus, the respective $(1-\epsilon )100\%$ ACI[NA] estimators of $\theta$, $R(x)$, and $h(x)$ (at a significance level $\epsilon \%$) are given by

$$\left(\widehat{\theta }\mp z_{{\displaystyle \frac{\epsilon }{2}}}\sqrt{\widehat{V}(\widehat{\theta })}\right),\left(\widehat{R}(x)\mp z_{{\displaystyle \frac{\epsilon }{2}}}\sqrt{\widehat{V}(\widehat{R})}\right),\mathrm{and}\left(\widehat{h}(x)\mp z_{{\displaystyle \frac{\epsilon }{2}}}\sqrt{\widehat{V}(\widehat{h})}\right),$$

where $z_{{\displaystyle \frac{\epsilon }{2}}}$ is the upper $({\displaystyle \frac{\epsilon }{2}})$th standard Gaussian percentile point.

A notable drawback of the traditional ACI[NA] approach is that it may produce negative lower bounds for parameters that are intrinsically restricted to positive values. In such situations, it is common practice to truncate negative bounds at zero; however, this constitutes a heuristic adjustment rather than a statistically rigorous solution. To overcome this limitation and enhance the robustness of interval estimation, Meeker and Escobar [21] advocate the use of a log-transformation, leading to the ACI[NL].

Accordingly, the $(1-\epsilon )100\%$ ACI[NL] estimators of $\theta$, $R(x)$, and $h(x)$ are expressed as

$$\begin{array}{cc}\hfill & \left(\widehat{\theta }exp\left(\mp z_{{\displaystyle \frac{\epsilon }{2}}}{\widehat{\theta }}^{-1}\sqrt{\widehat{V}(\widehat{\theta })}\right)\right),\hfill \\ \hfill & \left(\widehat{R}(x)exp\left(\mp z_{{\displaystyle \frac{\epsilon }{2}}}{\widehat{R}}^{-1}(x)\sqrt{\widehat{V}(\widehat{R})}\right)\right),\hfill \\ \hfill & \mathrm{and}\hfill \\ \hfill & \left(\widehat{h}(x)exp\left(\mp z_{{\displaystyle \frac{\epsilon }{2}}}{\widehat{h}}^{-1}(x)\sqrt{\widehat{V}(\widehat{h})}\right)\right),\hfill \end{array}$$

respectively.

4.2. Bayesian Intervals

This part constructs the $(1-\epsilon )100\%$ BCI and HPD interval estimators for $\theta$, $R(x)$, and $h(x)$ based on the MCMC samples generated via Algorithm 1. The detailed steps for implementing the interval estimation procedure are outlined in Algorithm 2.

Algorithm 2 The Bayesian Interval Algorithm for $\theta$, $R(x)$, and $h(x)$

1: Input: Confidence level $(1-\epsilon )$ 2: Output: BCI and HPD intervals of $\theta$, $R(x)$, and $h(x)$ 3: Sort ${\theta }^{(t)}$ for $t={\Re }^{\circ }+1,\dots ,{\Re }^{•}$ in ascending order 4: Compute the $(1-\epsilon )100\%$ BCI of $\theta$ as: $$\left({\theta }_{\left({\displaystyle \frac{\epsilon }{2}}{\Re }^{★}\right)},{\theta }_{\left(\left(1-{\displaystyle \frac{\epsilon }{2}}\right){\Re }^{★}\right)}\right)$$ 5: Compute the $(1-\epsilon )100\%$ HPD interval of $\theta$ as: $$\left({\theta }_{(t^{⊚})},{\theta }_{(t^{⊚}+(1-\epsilon ){\Re }^{★})}\right)$$ where $t^{⊚}$ is the index that minimizes: $${\theta }_{\left(t+(1-\epsilon ){\Re }^{★}\right)}-{\theta }_{(t)}\mathrm{for}t=1,\dots ,\epsilon {\Re }^{★}$$ 6: Redo Steps 3–5 for $R(x)$ and $h(x)$

5. Monte Carlo Comparisons

To assess the accuracy and practical utility of the estimators for $\theta$, $R(x)$, and $h(x)$ derived in the preceding sections, we conducted a series of Monte Carlo simulation experiments. Following the steps outlined in Algorithm 3, the IAT2-PC procedure was executed 1000 times for each chosen value of the shape parameter $\theta$ (specifically, $\theta =0.5$ and $1.5$), enabling the computation of both point estimates and interval estimates for the parameters of interest. For a fixed $x=0.25$, the corresponding reliability and hazard function estimates, $(R(x),h(x))$, are obtained as $(0.96914,0.36327)$ for $\theta =0.5$ and $(0.99375,0.07411)$ for $\theta =1.5$. The simulations are carried out under multiple configurations defined by combinations of threshold parameters $t_i(i=1,2)$, total sample sizes n, effective sample sizes m, and censoring schemes $\mathbf{S}$. In particular, we considered ${\tau }_1\in \{1,2\}$, ${\tau }_2\in \{2,3\}$, and $n\in \{30,50,80\}$.

Table 3 lists, for each value of n, the selected values of m along with the corresponding T2–PC schemes $\mathbf{S}$. For brevity, a notation such as ‘A1[1]$\approx$($5^{[4]}$,$0^{[6]}$)’ indicates that five units are removed at each stage for the first four censoring stages. After this, the practitioner stopped the removal process for the remaining stages.

Algorithm 3 Simulate IAT2-PC Dataset from MB Lifespan Population.

1: Input: Set values for n, m, ${\tau }_i,i=1,2$, and $\mathbf{S}$ 2: Set the true value of MB($\theta$) parameter. 3: Generate m independent uniform random variables $a_1,a_2,\dots ,a_m\sim U(0,1)$ 4: for $i=1$ to m do 5:    Compute ${\displaystyle {ϵ}_i=a_i^{{\left(i+{\sum }_{j=m-i+1}^m{S}_j\right)}^{-1}}}$ 6: end for 7: for $i=1$ to m do 8:    Compute ${\displaystyle U_i=1-\prod _{j=m-i+1}^m{ϵ}_j}$ 9: end for 10: for $i=1$ to m do 11:    Compute $y_i=G^{-1}(u_i;\theta )$ 12: end for 13: Observe $d_1$ failures at time ${\tau }_1$ 14: Remove observations $y_i,i=d_1+2,\dots ,m$ 15: Set truncated sample size: $n-d_1-1-{\sum }_{i=1}^{d_1}{S}_i$ 16: Generate $m-d_1-1$ order statistics $y_{d_1+2},\dots ,y_m$ from truncated distribution: 16:     PDF: ${\displaystyle \frac{g(y)}{1-G(y_{d_1+1})}}$ 17: if $y_m<{\tau }_1$  then 18:    Case 1: End test at $y_m$ $t_1<y_m$ 19: else if $t_1<y_m$  then 20:    Case 2: End test at $y_m$ $t_2<y_m$ 21: else if $t_2<y_m$  then 22:    Case 3: End test at $t_2$ 23: end if

Table 3. Different T2-PC designs in the Monte Carlo simulations.

$({\mathit{S}}_1,{\mathit{S}}_2,\dots ,{\mathit{S}}_{\mathit{m}})$
	(30,10)		(30,20)
A1[1]	$(5^{[4]},0^{[6]})$	A1[4]	$(5^{[2]},0^{[18]})$
B1[2]	$(0^{[3]},5^{[4]},0^{[3]})$	B1[5]	$(0^{[9]},5^{[2]},0^{[9]})$
C1[3]	$(0^{[6]},5^{[4]})$	C1[6]	$(0^{[18]},5^{[2]})$
	(50,20)		(50,40)
A2[1]	$(5^{[6]},0^{[14]})$	A2[4]	$(5^{[2]},0^{[38]})$
B2[2]	$(0^{[7]},5^{[6]},0^{[7]})$	B2[5]	$(0^{[19]},5^{[2]},0^{[19]})$
C2[3]	$(0^{[14]},5^{[6]})$	C2[6]	$(0^{[38]},5^{[2]})$
	(80,30)		(80,60)
A3[1]	$(5^{[10]},0^{[20]})$	A3[4]	$(5^{[4]},0^{[56]})$
B3[2]	$(0^{[10]},5^{[10]},0^{[10]})$	B3[5]	$(0^{[28]},5^{[4]},0^{[28]})$
C3[3]	$(0^{[20]},5^{[10]})$	C3[6]	$(0^{[56]},5^{[4]})$

To further examine the sensitivity of the proposed estimation procedures within the Bayesian framework, we investigated two distinct sets of hyperparameters for each MB distribution. Adopting the prior elicitation approach outlined by Kundu [22], the hyperparameters $\alpha$ and $\beta$ in the Inv.G prior PDF are specified. Then, we adopted two prior groups (PGs) for $(\alpha ,\beta )$ for each value of MB($\theta$) as follows:

• At $\theta =0.5$: PG-1:(2.5,6) and PG-2:(5,11);
• At $\theta =1.5$: PG-1:(7.5,6) and PG-2:(15,11).

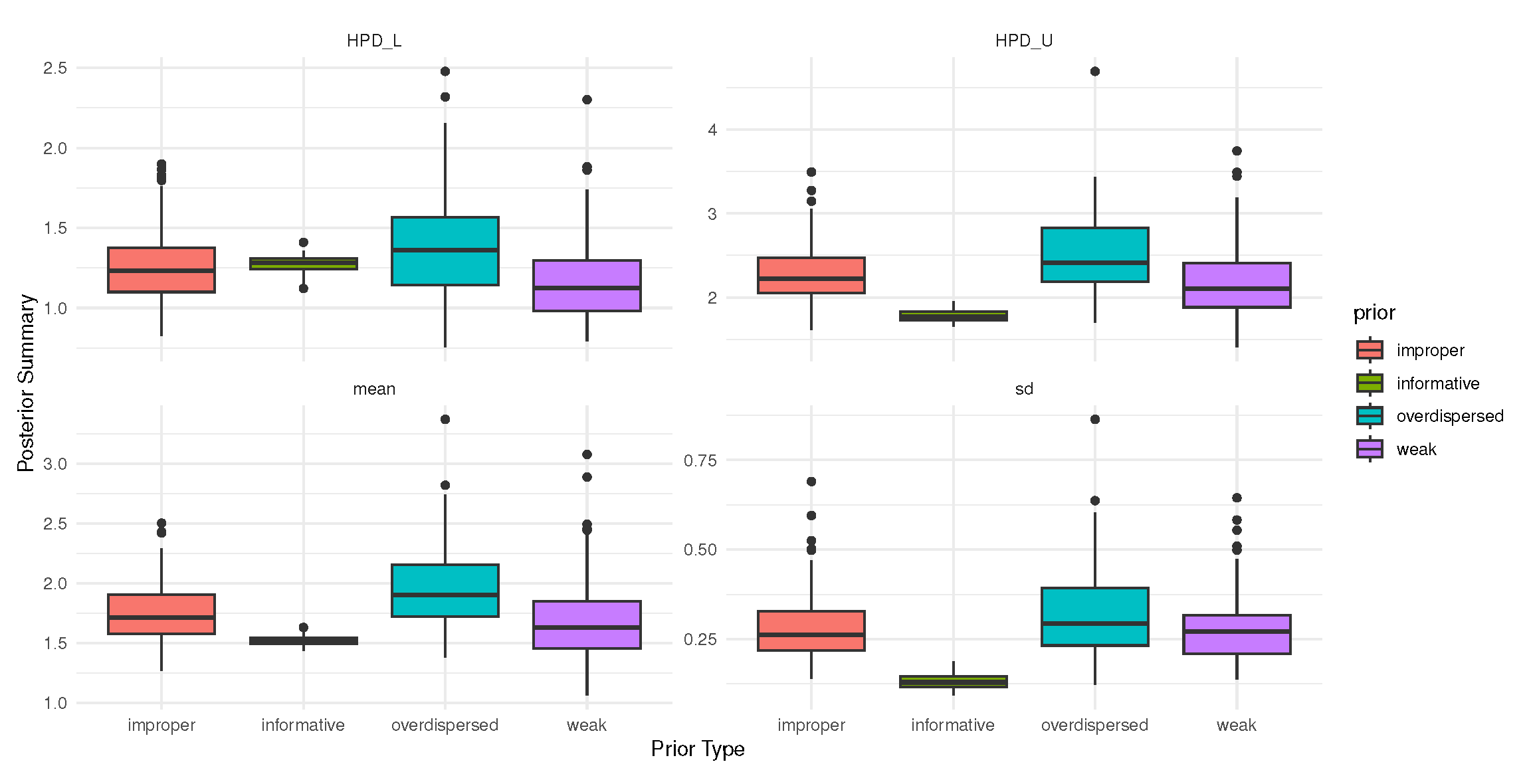
Bayesian inference always depends on the choice of prior beliefs. A sensitivity analysis checks how much the results change when different reasonable priors are used. This is especially important when prior knowledge is uncertain, partly subjective, or when guidelines require that results be shown to be reliable. To test the strength and trustworthiness of the findings, the sensitivity analysis was performed with four kinds of priors: informative (using PG-2 as a representative case), noninformative (when $\alpha =1.5,\beta =1$), weakly informative (when $\alpha =\beta =0.001$), and overdispersed (when $\alpha =15,\beta =0.01$). Figure 5 illustrates the sensitivity of posterior estimates for $\theta$ to four predefined prior types. It shows that posterior means are robust across different prior choices, while posterior uncertainty (credible interval width and standard deviation) is highly sensitive to prior informativeness. Informative priors yield the most concentrated posterior distributions, whereas improper and overdispersed priors produce wider spreads, reflecting higher uncertainty. For further details on the sensitivity analysis of posterior estimates under two (or more) different prior choices, see Alotaibi et al. [23].

Figure 5. Plot for different prior distributions of $\theta$ from MB(1.5).

Once 1000 IAT2-PC datasets were generated, the frequentist estimates and their corresponding 95% ACI[NA] and ACI[NL] estimates for $\theta$, $R(x)$, and $h(x)$ were computed using the maxLik package (Henningsen and Toomet [18]) in the R software environment (version 4.2.2).

For the Bayesian analysis, 12,000 MCMC samples were drawn, with the first 2000 iterations discarded as burn-in. The resulting Bayesian estimates, along with their 95% BCI and HPD interval estimates for $\theta$, $R(x)$, and $h(x)$, were computed using the coda package (Plummer et al. [24]) within the same R environment. For the Bayesian implementation, we employed the M–H algorithm with Gaussian proposal distributions centered at the current state. The proposal variances were tuned in preliminary runs to maintain acceptance rates between 0.80 and 0.95, ensuring good mixing properties. All parameters were restricted to the positive domain, consistent with the support of the MB distribution. Across all simulation settings, the monitored acceptance rates confirmed the stable performance of the chains.

Then, to evaluate the offered estimators obtained for the MB($\theta$) parameter, we calculated the following metrics:

• Mean Point Estimate: $\mathrm{MPE}(\check{\theta })={\displaystyle \frac{1}{1000}}{\sum }_{i=1}^{1000}{\check{\theta }}^{[i]},$
• Root Mean Squared Error: $\mathrm{RMSE}(\check{\theta })=\sqrt{{\displaystyle \frac{1}{1000}}{\sum }_{i=1}^{1000}{\left({\check{\theta }}^{[i]}-\theta \right)}^2},$
• Mean Relative Absolute Bias: $\mathrm{ARAB}(\check{\theta })={\displaystyle \frac{1}{1000}}{\sum }_{i=1}^{1000}{\check{\theta }}^{-1}\left|{\check{\theta }}^{[i]}-\theta \right|,$
• Average Interval Length: ${\mathrm{AIL}}_{95\%}(\theta )={\displaystyle \frac{1}{1000}}{\sum }_{i=1}^{1000}\left(U_{{\check{\theta }}^{[i]}}-L_{{\check{\theta }}^{[i]}}\right),$
• Coverage Percentage: ${\mathrm{CP}}_{95\%}(\theta )={\displaystyle \frac{1}{1000}}{\sum }_{i=1}^{1000}{\mathcal{O}}_{\left(L_{{\check{\theta }}^{[i]}};U_{{\check{\theta }}^{[i]}}\right)}\left(\theta \right),$

where ${\check{\theta }}^{[i]}$ denotes the estimate of $\theta$ obtained from the ith sample, $\mathcal{O}(·)$ represents the indicator function, and $(L(·),U(·))$ denotes the two-sided $(1-\epsilon )\times 100\%$ asymptotic (or credible) interval for $\theta$. The same precision measures can analogously be applied to $R(x)$ and $h(x)$.

In Table 4, Table 5 and Table 6, the point estimation results—including mean point estimates (MPEs; 1st column), root mean squared errors (RMSEs; 2nd column), and mean relative absolute biases (ARABs; 3rd column)—for $\theta$, $R(x)$, and $h(x)$ are reported. Correspondingly, Table 7, Table 8 and Table 9 present the average interval lengths (AILs; 1st column) and coverage probabilities (CPs; 2nd column) for the same parameters. In the Supplementary File, the simulation results associated with $\theta$, $R(x)$, and $h(x)$ when $\theta =1.5$ are provided. The key findings, emphasizing configurations with the lowest RMSEs, ARABs, and AILs alongside the highest CPs, are summarized as follows:

Table 4. Point estimations of $\theta$.

$({\mathit{\tau }}_1,{\mathit{\tau }}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	MLE			MCMC
Prior →						1			2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.5266	0.4929	0.4230	0.6594	0.3406	0.3167	0.7141	0.3055	0.1935
		B1[2]	0.5314	0.5111	0.5020	0.6655	0.4026	0.3259	0.7214	0.3216	0.1993
		C1[3]	0.4978	0.4520	0.3682	0.6003	0.3295	0.2723	0.6666	0.2382	0.1846
	(30,20)	A1[4]	0.5184	0.4260	0.3300	0.6262	0.2782	0.1637	0.7773	0.1440	0.1285
		B1[5]	0.5175	0.4278	0.3407	0.6185	0.2964	0.1655	0.7742	0.1462	0.1344
		C1[6]	0.4639	0.3677	0.3104	0.5879	0.2646	0.1634	0.7419	0.1426	0.1285
	(50,20)	A2[1]	0.5178	0.3439	0.2448	0.5982	0.2233	0.1509	0.7483	0.1374	0.1156
		B2[2]	0.5185	0.3666	0.2736	0.6259	0.2638	0.1583	0.7807	0.1412	0.1232
		C2[3]	0.4995	0.3180	0.2435	0.5826	0.2029	0.1429	0.7291	0.1362	0.1130
	(50,40)	A2[4]	0.5108	0.2272	0.2201	0.5799	0.1853	0.1419	0.6748	0.1107	0.1102
		B2[5]	0.5124	0.2149	0.1706	0.5811	0.1639	0.1394	0.6728	0.1095	0.1088
		C2[6]	0.3973	0.1832	0.1682	0.4645	0.1361	0.1288	0.5514	0.1055	0.1052
	(80,30)	A3[1]	0.5133	0.1381	0.1239	0.6034	0.1133	0.1131	0.6643	0.0985	0.0908
		B3[2]	0.5143	0.1669	0.1494	0.6121	0.1271	0.1170	0.6729	0.1023	0.0951
		C3[3]	0.4994	0.1341	0.1086	0.5911	0.1080	0.1007	0.6531	0.0893	0.0868
	(80,60)	A3[4]	0.5073	0.1095	0.0897	0.5777	0.0881	0.0793	0.5972	0.0775	0.0714
		B3[5]	0.5068	0.1248	0.0976	0.5685	0.0944	0.0892	0.5884	0.0830	0.0802
		C3[6]	0.4159	0.0968	0.0892	0.5105	0.0874	0.0786	0.5345	0.0762	0.0540
(2,3)	(30,10)	A1[1]	0.5005	0.2974	0.2712	0.6023	0.2007	0.1536	0.6703	0.1195	0.1183
		B1[2]	0.5012	0.3010	0.2761	0.6067	0.2063	0.1580	0.6757	0.1231	0.1217
		C1[3]	0.5000	0.2947	0.2693	0.6003	0.1616	0.1520	0.6666	0.1155	0.1133
	(30,20)	A1[4]	0.5025	0.2648	0.2623	0.5917	0.1561	0.1360	0.7470	0.0931	0.0894
		B1[5]	0.5028	0.2702	0.2648	0.5963	0.1615	0.1374	0.7544	0.1119	0.0910
		C1[6]	0.5021	0.2526	0.2526	0.5879	0.1520	0.1339	0.7419	0.0893	0.0837
	(50,20)	A2[1]	0.5021	0.2294	0.1883	0.5887	0.1365	0.1283	0.7397	0.0869	0.0829
		B2[2]	0.5024	0.2368	0.1936	0.5942	0.1457	0.1318	0.7493	0.0877	0.0833
		C2[3]	0.5016	0.1987	0.1845	0.5826	0.1364	0.1277	0.7291	0.0847	0.0814
	(50,40)	A2[4]	0.5035	0.1961	0.1821	0.5643	0.1283	0.1277	0.6572	0.0785	0.0702
		B2[5]	0.5034	0.1866	0.1805	0.5630	0.1251	0.1251	0.6556	0.0757	0.0682
		C2[6]	0.5031	0.1845	0.1772	0.5643	0.1221	0.1221	0.6519	0.0664	0.0651
	(80,30)	A3[1]	0.5020	0.1713	0.1675	0.5939	0.1078	0.0943	0.6570	0.0643	0.0632
		B3[2]	0.5023	0.1782	0.1767	0.6001	0.1082	0.0952	0.6628	0.0651	0.0650
		C3[3]	0.5017	0.1675	0.1195	0.5911	0.0999	0.0938	0.6531	0.0635	0.0563
	(80,60)	A3[4]	0.5018	0.0991	0.0950	0.5542	0.0813	0.0698	0.5749	0.0513	0.0475
		B3[5]	0.5020	0.1121	0.1024	0.5551	0.0929	0.0830	0.5770	0.0539	0.0521
		C3[6]	0.5014	0.0971	0.0791	0.5519	0.0715	0.0569	0.5722	0.0485	0.0436

Table 5. Point estimations of $R(x)$.

$({\mathit{\tau }}_1,{\mathit{\tau }}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	MLE			MCMC
Prior →						1			2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.9659	0.7158	0.6752	0.9749	0.6260	0.5918	0.9790	0.4567	0.4284
		B1[2]	0.9690	0.7249	0.7236	0.9784	0.6864	0.6626	0.9813	0.5348	0.4410
		C1[3]	0.9684	0.7201	0.6787	0.9781	0.6426	0.6247	0.9811	0.5248	0.4317
	(30,20)	A1[4]	0.9644	0.6471	0.6471	0.9745	0.4533	0.4384	0.9818	0.4284	0.3939
		B1[5]	0.9694	0.6674	0.6639	0.9767	0.5667	0.4439	0.9830	0.4397	0.3967
		C1[6]	0.9694	0.6773	0.6674	0.9762	0.5751	0.4562	0.9829	0.4476	0.4036
	(50,20)	A2[1]	0.9676	0.5458	0.5302	0.9742	0.4157	0.3990	0.9813	0.3851	0.3745
		B2[2]	0.9694	0.6316	0.5484	0.9767	0.4313	0.4173	0.9831	0.4133	0.3929
		C2[3]	0.9693	0.6190	0.5378	0.9751	0.4258	0.4027	0.9820	0.3855	0.3754
	(50,40)	A2[4]	0.9564	0.5302	0.5084	0.9648	0.3737	0.3734	0.9722	0.3111	0.3102
		B2[5]	0.9696	0.5395	0.5118	0.9745	0.3826	0.3737	0.9792	0.3586	0.3190
		C2[6]	0.9695	0.5417	0.5192	0.9744	0.3855	0.3791	0.9793	0.3649	0.3282
	(80,30)	A3[1]	0.9682	0.4984	0.3703	0.9749	0.3441	0.3094	0.9786	0.2894	0.2442
		B3[2]	0.9696	0.5221	0.5068	0.9761	0.3734	0.3133	0.9795	0.2964	0.2844
		C3[3]	0.9695	0.5007	0.4984	0.9756	0.3455	0.3116	0.9791	0.2928	0.2781
	(80,60)	A3[4]	0.9593	0.3111	0.2717	0.9694	0.2542	0.2399	0.9714	0.2310	0.1970
		B3[5]	0.9694	0.3169	0.3137	0.9744	0.3092	0.2777	0.9756	0.2534	0.2193
		C3[6]	0.9694	0.3505	0.3282	0.9738	0.3237	0.2813	0.9750	0.2769	0.2371
(2,3)	(30,10)	A1[1]	0.9770	0.7116	0.6645	0.9749	0.4670	0.4643	0.9790	0.4105	0.3691
		B1[2]	0.9773	0.7221	0.6774	0.9752	0.6613	0.4924	0.9794	0.4919	0.3835
		C1[3]	0.9771	0.7171	0.6693	0.9750	0.5086	0.4811	0.9792	0.4785	0.3732
	(30,20)	A1[4]	0.9781	0.6321	0.6321	0.9745	0.3693	0.3444	0.9818	0.3424	0.3410
		B1[5]	0.9784	0.6553	0.6521	0.9747	0.4208	0.3940	0.9820	0.3431	0.3416
		C1[6]	0.9786	0.6677	0.6553	0.9750	0.4380	0.4092	0.9822	0.3489	0.3473
	(50,20)	A2[1]	0.9778	0.5326	0.5132	0.9742	0.3486	0.3299	0.9813	0.3251	0.2930
		B2[2]	0.9785	0.6290	0.5331	0.9749	0.3691	0.3372	0.9821	0.3367	0.3223
		C2[3]	0.9782	0.6147	0.5216	0.9746	0.3503	0.3332	0.9817	0.3307	0.2935
	(50,40)	A2[4]	0.9758	0.5132	0.4864	0.9734	0.3189	0.3189	0.9782	0.2471	0.2458
		B2[5]	0.9758	0.5186	0.4955	0.9733	0.3224	0.3224	0.9784	0.2812	0.2536
		C2[6]	0.9759	0.5218	0.5086	0.9734	0.3299	0.3282	0.9785	0.2877	0.2609
	(80,30)	A3[1]	0.9767	0.4692	0.3346	0.9749	0.3021	0.2654	0.9786	0.2294	0.1977
		B3[2]	0.9772	0.5132	0.4811	0.9754	0.3071	0.2688	0.9790	0.2350	0.2296
		C3[3]	0.9769	0.4864	0.4774	0.9751	0.3042	0.2681	0.9787	0.2323	0.2258
	(80,60)	A3[4]	0.9734	0.2656	0.2301	0.9727	0.1946	0.1893	0.9740	0.1859	0.1524
		B3[5]	0.9735	0.2726	0.2715	0.9728	0.2669	0.2368	0.9742	0.1886	0.1654
		C3[6]	0.9736	0.3099	0.2938	0.9729	0.2782	0.2394	0.9743	0.1915	0.1909

Table 6. Point estimations of $h(x)$.

$({\mathit{\tau }}_1,{\mathit{\tau }}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	MLE			MCMC
Prior →						1			2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.0647	1.1911	1.1339	0.1147	1.0153	0.9384	0.1272	0.8282	0.3207
		B1[2]	0.0668	1.0427	1.0044	0.0677	0.9766	0.8858	0.0840	0.7618	0.3080
		C1[3]	0.1348	0.9074	0.8903	0.1413	0.8202	0.6919	0.1483	0.5285	0.3047
	(30,20)	A1[4]	0.0678	0.8641	0.7221	0.0911	0.4229	0.3343	0.0869	0.2582	0.2269
		B1[5]	0.0478	0.6377	0.5503	0.0549	0.4028	0.3282	0.0592	0.2443	0.2231
		C1[6]	0.0942	0.6043	0.4654	0.1378	0.3797	0.3278	0.1213	0.2443	0.2158
	(50,20)	A2[1]	0.0675	0.4634	0.3760	0.1079	0.3424	0.3140	0.0992	0.2318	0.2111
		B2[2]	0.0551	0.3754	0.3470	0.0529	0.3345	0.2744	0.0569	0.2095	0.2048
		C2[3]	0.1493	0.3466	0.3178	0.2142	0.3155	0.2595	0.1730	0.2042	0.2033
	(50,40)	A2[4]	0.0703	0.3118	0.2870	0.0856	0.2443	0.2335	0.0787	0.1987	0.1681
		B2[5]	0.0488	0.2663	0.2322	0.0603	0.2210	0.2189	0.0561	0.1962	0.1599
		C2[6]	0.0772	0.2614	0.2090	0.0894	0.2026	0.1928	0.0826	0.1907	0.1582
	(80,30)	A3[1]	0.0692	0.2434	0.2008	0.0778	0.2002	0.1832	0.0776	0.1579	0.1522
		B3[2]	0.0522	0.2161	0.1971	0.0463	0.1914	0.1506	0.0507	0.1471	0.1439
		C3[3]	0.1464	0.2076	0.1962	0.1514	0.1591	0.1436	0.1399	0.1394	0.1351
	(80,60)	A3[4]	0.0716	0.2038	0.1649	0.0871	0.1404	0.1242	0.0978	0.1235	0.1186
		B3[5]	0.0444	0.1971	0.1463	0.0506	0.1399	0.1229	0.0593	0.1166	0.0952
		C3[6]	0.0828	0.1384	0.1322	0.1084	0.1206	0.1187	0.1189	0.1114	0.0747
(2,3)	(30,10)	A1[1]	0.0826	0.4519	0.4239	0.1355	0.4142	0.3082	0.1433	0.3081	0.2400
		B1[2]	0.0788	0.4488	0.4188	0.1131	0.3185	0.3010	0.1250	0.2998	0.2335
		C1[3]	0.0820	0.4454	0.4159	0.1305	0.2926	0.2909	0.1395	0.2568	0.2309
	(30,20)	A1[4]	0.0781	0.4178	0.4101	0.0976	0.2744	0.2561	0.0926	0.2185	0.2173
		B1[5]	0.0737	0.4101	0.4081	0.0924	0.2636	0.2465	0.0873	0.2148	0.2137
		C1[6]	0.0783	0.3955	0.3955	0.0972	0.2310	0.2157	0.0914	0.2144	0.2134
	(50,20)	A2[1]	0.0780	0.3936	0.3335	0.0972	0.2309	0.2109	0.0914	0.2108	0.2018
		B2[2]	0.0743	0.3847	0.3264	0.0913	0.2192	0.2086	0.0867	0.2069	0.1837
		C2[3]	0.0778	0.3332	0.3211	0.0962	0.2181	0.2064	0.0904	0.2035	0.1834
	(50,40)	A2[4]	0.0756	0.3265	0.3182	0.0846	0.2064	0.2053	0.0782	0.1800	0.1633
		B2[5]	0.0728	0.3245	0.3100	0.0798	0.2017	0.2017	0.0743	0.1760	0.1587
		C2[6]	0.0801	0.3211	0.3043	0.0839	0.1995	0.1995	0.0777	0.1546	0.1538
	(80,30)	A3[1]	0.0763	0.3211	0.3010	0.0824	0.1923	0.1682	0.0814	0.1471	0.1437
		B3[2]	0.0737	0.3043	0.2987	0.0792	0.1903	0.1678	0.0792	0.1454	0.1413
		C3[3]	0.0762	0.2936	0.2093	0.0816	0.1890	0.1660	0.0813	0.1436	0.1237
	(80,60)	A3[4]	0.0752	0.1939	0.1838	0.0773	0.1741	0.1498	0.0871	0.1198	0.1119
		B3[5]	0.0734	0.1705	0.1699	0.0761	0.1670	0.1482	0.0857	0.1180	0.0907
		C3[6]	0.0762	0.1662	0.1440	0.0773	0.1217	0.1166	0.0867	0.1063	0.0705

Table 7. Interval estimations of $\theta$.

$({\mathit{t}}_1,{\mathit{t}}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	ACI[NA]		ACI[NL]		BCI				HPD
Prior →							1		2		1		2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.960	0.921	0.505	0.958	0.478	0.960	0.455	0.962	0.430	0.964	0.399	0.968
		B1[2]	0.966	0.921	0.522	0.957	0.491	0.959	0.458	0.962	0.433	0.964	0.414	0.968
		C1[3]	0.955	0.922	0.483	0.960	0.466	0.961	0.444	0.963	0.429	0.964	0.385	0.968
	(30,20)	A1[4]	0.390	0.967	0.384	0.968	0.376	0.968	0.366	0.969	0.362	0.970	0.352	0.970
		B1[5]	0.392	0.967	0.384	0.968	0.380	0.968	0.376	0.968	0.366	0.969	0.365	0.969
		C1[6]	0.386	0.968	0.382	0.968	0.376	0.968	0.366	0.969	0.359	0.970	0.351	0.970
	(50,20)	A2[1]	0.384	0.968	0.357	0.970	0.349	0.971	0.344	0.971	0.340	0.971	0.330	0.972
		B2[2]	0.385	0.968	0.362	0.970	0.358	0.970	0.353	0.970	0.350	0.970	0.335	0.972
		C2[3]	0.382	0.968	0.351	0.970	0.344	0.971	0.339	0.971	0.330	0.972	0.325	0.972
	(50,40)	A2[4]	0.346	0.971	0.342	0.971	0.334	0.972	0.329	0.972	0.298	0.975	0.290	0.975
		B2[5]	0.341	0.971	0.332	0.972	0.332	0.972	0.326	0.972	0.289	0.975	0.282	0.976
		C2[6]	0.337	0.972	0.328	0.972	0.326	0.972	0.295	0.975	0.276	0.976	0.273	0.977
	(80,30)	A3[1]	0.289	0.975	0.284	0.976	0.282	0.976	0.276	0.976	0.259	0.978	0.254	0.978
		B3[2]	0.295	0.975	0.291	0.975	0.286	0.976	0.284	0.976	0.261	0.978	0.257	0.978
		C3[3]	0.282	0.976	0.275	0.976	0.266	0.977	0.255	0.978	0.251	0.978	0.231	0.982
	(80,60)	A3[4]	0.260	0.978	0.252	0.978	0.248	0.979	0.243	0.979	0.225	0.982	0.210	0.982
		B3[5]	0.267	0.977	0.258	0.978	0.254	0.978	0.251	0.978	0.231	0.982	0.215	0.982
		C3[6]	0.259	0.978	0.247	0.979	0.237	0.980	0.229	0.980	0.219	0.982	0.207	0.985
(2,3)	(30,10)	A1[1]	0.524	0.956	0.497	0.959	0.467	0.961	0.444	0.963	0.399	0.967	0.383	0.968
		B1[2]	0.543	0.955	0.511	0.958	0.471	0.961	0.446	0.963	0.424	0.967	0.398	0.968
		C1[3]	0.485	0.960	0.468	0.961	0.444	0.963	0.429	0.964	0.389	0.967	0.368	0.968
	(30,20)	A1[4]	0.388	0.967	0.381	0.968	0.371	0.969	0.364	0.969	0.359	0.970	0.350	0.970
		B1[5]	0.389	0.967	0.382	0.968	0.377	0.968	0.369	0.969	0.366	0.969	0.358	0.970
		C1[6]	0.384	0.968	0.379	0.968	0.371	0.969	0.363	0.969	0.357	0.970	0.345	0.970
	(50,20)	A2[1]	0.381	0.968	0.349	0.971	0.346	0.971	0.342	0.971	0.333	0.972	0.326	0.972
		B2[2]	0.383	0.968	0.361	0.970	0.354	0.970	0.352	0.970	0.347	0.971	0.328	0.972
		C2[3]	0.379	0.968	0.346	0.971	0.341	0.971	0.335	0.972	0.328	0.972	0.322	0.973
	(50,40)	A2[4]	0.344	0.971	0.340	0.971	0.333	0.972	0.323	0.973	0.294	0.975	0.286	0.976
		B2[5]	0.337	0.972	0.332	0.972	0.327	0.972	0.321	0.973	0.285	0.976	0.279	0.976
		C2[6]	0.328	0.972	0.326	0.972	0.321	0.973	0.287	0.976	0.275	0.977	0.271	0.977
	(80,30)	A3[1]	0.288	0.975	0.284	0.976	0.281	0.976	0.266	0.977	0.256	0.978	0.245	0.978
		B3[2]	0.292	0.975	0.288	0.975	0.286	0.976	0.280	0.976	0.258	0.978	0.254	0.978
		C3[3]	0.281	0.976	0.268	0.977	0.258	0.978	0.252	0.978	0.249	0.979	0.221	0.982
	(80,60)	A3[4]	0.259	0.978	0.250	0.979	0.247	0.979	0.237	0.980	0.214	0.982	0.207	0.983
		B3[5]	0.265	0.977	0.257	0.978	0.254	0.978	0.249	0.979	0.221	0.982	0.216	0.982
		C3[6]	0.259	0.978	0.247	0.979	0.231	0.980	0.222	0.981	0.210	0.982	0.189	0.985

Table 8. Interval estimations of $R(x)$.

$({\mathit{t}}_1,{\mathit{t}}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	ACI[NA]		ACI[NL]		BCI				HPD
Prior →							1		2		1		2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.898	0.926	0.932	0.924	0.858	0.929	0.490	0.951	0.413	0.955	0.314	0.961
		B1[2]	0.946	0.923	0.953	0.923	0.902	0.926	0.512	0.949	0.486	0.951	0.318	0.961
		C1[3]	0.920	0.925	0.949	0.923	0.863	0.928	0.491	0.951	0.418	0.955	0.316	0.961
	(30,20)	A1[4]	0.617	0.943	0.643	0.941	0.415	0.955	0.389	0.957	0.310	0.961	0.303	0.962
		B1[5]	0.621	0.943	0.644	0.941	0.418	0.955	0.402	0.956	0.349	0.959	0.303	0.962
		C1[6]	0.656	0.941	0.700	0.938	0.423	0.955	0.405	0.956	0.387	0.957	0.304	0.962
	(50,20)	A2[1]	0.610	0.943	0.612	0.943	0.411	0.955	0.371	0.958	0.301	0.962	0.297	0.962
		B2[2]	0.615	0.943	0.634	0.942	0.415	0.955	0.389	0.957	0.309	0.961	0.303	0.962
		C2[3]	0.611	0.943	0.626	0.942	0.413	0.955	0.373	0.958	0.308	0.961	0.298	0.962
	(50,40)	A2[4]	0.489	0.951	0.492	0.950	0.371	0.958	0.353	0.959	0.296	0.962	0.288	0.963
		B2[5]	0.495	0.950	0.501	0.950	0.372	0.958	0.361	0.958	0.297	0.962	0.288	0.963
		C2[6]	0.514	0.949	0.597	0.944	0.381	0.957	0.363	0.958	0.299	0.962	0.293	0.962
	(80,30)	A3[1]	0.440	0.954	0.443	0.953	0.367	0.958	0.313	0.961	0.283	0.963	0.260	0.964
		B3[2]	0.452	0.953	0.484	0.951	0.370	0.958	0.350	0.959	0.293	0.962	0.266	0.964
		C3[3]	0.447	0.953	0.468	0.952	0.370	0.958	0.327	0.960	0.289	0.963	0.260	0.964
	(80,60)	A3[4]	0.355	0.959	0.358	0.958	0.322	0.961	0.277	0.963	0.238	0.966	0.232	0.966
		B3[5]	0.360	0.958	0.362	0.958	0.328	0.960	0.282	0.963	0.239	0.966	0.233	0.966
		C3[6]	0.367	0.958	0.433	0.954	0.341	0.960	0.312	0.961	0.241	0.965	0.239	0.966
(2,3)	(30,10)	A1[1]	0.858	0.929	0.898	0.926	0.617	0.943	0.482	0.951	0.411	0.955	0.306	0.962
		B1[2]	0.902	0.926	0.946	0.923	0.700	0.938	0.492	0.951	0.484	0.951	0.315	0.961
		C1[3]	0.863	0.928	0.920	0.925	0.621	0.943	0.484	0.951	0.416	0.955	0.309	0.961
	(30,20)	A1[4]	0.610	0.943	0.643	0.941	0.403	0.956	0.318	0.961	0.309	0.961	0.040	0.977
		B1[5]	0.611	0.943	0.644	0.941	0.404	0.956	0.351	0.959	0.311	0.961	0.040	0.977
		C1[6]	0.615	0.943	0.656	0.941	0.409	0.955	0.387	0.957	0.312	0.961	0.049	0.977
	(50,20)	A2[1]	0.492	0.950	0.612	0.943	0.397	0.956	0.307	0.962	0.299	0.962	0.038	0.978
		B2[2]	0.597	0.944	0.634	0.942	0.401	0.956	0.309	0.961	0.303	0.962	0.039	0.978
		C2[3]	0.495	0.950	0.626	0.942	0.398	0.956	0.309	0.961	0.302	0.962	0.039	0.978
	(50,40)	A2[4]	0.468	0.952	0.489	0.951	0.368	0.958	0.304	0.962	0.290	0.963	0.037	0.978
		B2[5]	0.484	0.951	0.501	0.950	0.369	0.958	0.305	0.962	0.296	0.962	0.037	0.978
		C2[6]	0.491	0.951	0.514	0.949	0.379	0.957	0.306	0.962	0.297	0.962	0.038	0.978
	(80,30)	A3[1]	0.422	0.955	0.443	0.953	0.354	0.959	0.295	0.962	0.273	0.964	0.034	0.978
		B3[2]	0.440	0.954	0.452	0.953	0.357	0.959	0.304	0.962	0.282	0.963	0.036	0.978
		C3[3]	0.433	0.954	0.447	0.953	0.356	0.959	0.299	0.962	0.278	0.963	0.036	0.978
	(80,60)	A3[4]	0.355	0.959	0.358	0.958	0.322	0.961	0.240	0.966	0.234	0.966	0.031	0.978
		B3[5]	0.360	0.958	0.362	0.958	0.327	0.960	0.241	0.965	0.234	0.966	0.033	0.978
		C3[6]	0.367	0.958	0.415	0.955	0.340	0.960	0.241	0.965	0.239	0.966	0.034	0.978

Table 9. Interval estimations of $h(x)$.

$({\mathit{t}}_1,{\mathit{t}}_2)$	$(\mathit{n},\mathit{m})$	T2-PC	ACI[NA]		ACI[NL]		BCI				HPD
Prior →							1		2		1		2
For $\mathit{\theta }=\mathbf{0.5}$
(1,2)	(30,10)	A1[1]	0.208	0.924	0.188	0.930	0.187	0.931	0.157	0.940	0.127	0.950	0.105	0.957
		B1[2]	0.163	0.938	0.152	0.942	0.147	0.943	0.119	0.953	0.116	0.953	0.099	0.959
		C1[3]	0.127	0.950	0.121	0.952	0.119	0.953	0.116	0.954	0.115	0.954	0.078	0.966
	(30,20)	A1[4]	0.118	0.953	0.111	0.955	0.105	0.957	0.084	0.964	0.075	0.967	0.057	0.972
		B1[5]	0.103	0.958	0.097	0.960	0.085	0.963	0.083	0.964	0.074	0.967	0.055	0.973
		C1[6]	0.101	0.958	0.081	0.965	0.078	0.966	0.075	0.967	0.073	0.967	0.053	0.974
	(50,20)	A2[1]	0.078	0.966	0.075	0.967	0.073	0.967	0.071	0.968	0.068	0.969	0.052	0.974
		B2[2]	0.078	0.966	0.075	0.967	0.070	0.968	0.064	0.970	0.062	0.971	0.052	0.974
		C2[3]	0.077	0.966	0.067	0.969	0.063	0.971	0.061	0.971	0.055	0.973	0.050	0.975
	(50,40)	A2[4]	0.065	0.970	0.062	0.971	0.059	0.972	0.058	0.972	0.055	0.973	0.050	0.975
		B2[5]	0.061	0.971	0.059	0.972	0.058	0.972	0.056	0.973	0.050	0.975	0.046	0.976
		C2[6]	0.061	0.971	0.058	0.972	0.056	0.973	0.049	0.975	0.049	0.975	0.046	0.976
	(80,30)	A3[1]	0.059	0.972	0.057	0.973	0.053	0.974	0.048	0.975	0.043	0.977	0.040	0.978
		B3[2]	0.057	0.973	0.055	0.973	0.050	0.975	0.046	0.976	0.035	0.979	0.035	0.980
		C3[3]	0.056	0.973	0.054	0.973	0.046	0.976	0.045	0.976	0.035	0.980	0.028	0.982
	(80,60)	A3[4]	0.046	0.976	0.045	0.976	0.043	0.977	0.043	0.977	0.032	0.980	0.021	0.984
		B3[5]	0.045	0.976	0.042	0.977	0.041	0.978	0.038	0.978	0.031	0.981	0.020	0.984
		C3[6]	0.044	0.977	0.040	0.978	0.040	0.978	0.028	0.982	0.025	0.983	0.012	0.987
(2,3)	(30,10)	A1[1]	0.202	0.926	0.188	0.930	0.185	0.931	0.148	0.943	0.117	0.953	0.104	0.957
		B1[2]	0.155	0.941	0.149	0.943	0.139	0.946	0.119	0.953	0.110	0.955	0.098	0.959
		C1[3]	0.122	0.952	0.121	0.952	0.118	0.953	0.116	0.954	0.109	0.956	0.075	0.967
	(30,20)	A1[4]	0.117	0.953	0.109	0.956	0.097	0.960	0.081	0.965	0.075	0.967	0.056	0.973
		B1[5]	0.103	0.958	0.096	0.960	0.083	0.964	0.079	0.965	0.073	0.967	0.054	0.973
		C1[6]	0.095	0.960	0.078	0.966	0.078	0.966	0.073	0.967	0.072	0.968	0.052	0.974
	(50,20)	A2[1]	0.078	0.966	0.075	0.967	0.071	0.968	0.069	0.968	0.065	0.970	0.051	0.974
		B2[2]	0.076	0.966	0.072	0.968	0.069	0.969	0.063	0.970	0.061	0.971	0.050	0.975
		C2[3]	0.073	0.967	0.066	0.970	0.062	0.971	0.060	0.971	0.053	0.974	0.050	0.975
	(50,40)	A2[4]	0.063	0.970	0.060	0.971	0.059	0.972	0.056	0.973	0.050	0.975	0.049	0.975
		B2[5]	0.060	0.972	0.058	0.972	0.058	0.972	0.056	0.973	0.049	0.975	0.046	0.976
		C2[6]	0.059	0.972	0.056	0.973	0.055	0.973	0.049	0.975	0.048	0.975	0.045	0.976
	(80,30)	A3[1]	0.057	0.972	0.056	0.973	0.051	0.974	0.045	0.976	0.042	0.977	0.039	0.978
		B3[2]	0.056	0.973	0.055	0.973	0.049	0.975	0.045	0.976	0.035	0.979	0.034	0.980
		C3[3]	0.054	0.973	0.053	0.974	0.046	0.976	0.043	0.977	0.034	0.980	0.027	0.982
	(80,60)	A3[4]	0.045	0.976	0.044	0.977	0.043	0.977	0.041	0.977	0.030	0.981	0.020	0.984
		B3[5]	0.044	0.976	0.041	0.978	0.041	0.978	0.037	0.979	0.028	0.982	0.019	0.984
		C3[6]	0.043	0.977	0.040	0.978	0.040	0.978	0.028	0.982	0.025	0.983	0.012	0.987

• Across all configurations, the estimation results for $\theta$, $R(x)$, and $h(x)$ exhibited satisfactory performance.
• Increasing the total sample size n (or the effective sample size m) leads to improved estimation accuracy for all parameters. A comparable improvement was observed when the total number of removals, ${\sum }_{i=1}^m{S}_i$, was reduced.
• Higher threshold values ${\tau }_i$ ($i=1,2$) enhance estimation precision, as evidenced by reductions in RMSEs, ARABs, and AILs, along with corresponding increases in CPs.
• When the value of $\theta$ increases, the following apply:

  –

  Both the RMSEs and ARABs of $\theta$ and $h(x)$ tend to increase while those of $R(x)$ tend to decrease;

  –

  The AILs of $\theta$ tend to increase while those of $R(x)$ and $h(x)$ tend to decrease;

  –

  The CPs of $R(x)$ increase while those of $\theta$ and $h(x)$ decrease.

• The Bayesian estimators obtained via MCMC, together with their credible intervals, demonstrated greater robustness compared to frequentist estimators, primarily due to the incorporation of informative Inv.G priors.
• For all considered values of $\theta$, the Bayesian estimator under PG-2 consistently outperformed other approaches. This superiority is attributable to the lower prior variance of PG-2 relative to PG-1. A similar advantage was observed when comparing credible intervals (BCI and HPD) to asymptotic intervals (ACI[NA] and ACI[NL]).
• A comparative assessment of the T2–PC designs listed in Table 3 revealed the following:

  –

  For $\theta$ and $h(x)$, configurations C$i[j]$ ($i=1,2,3$ and $j=3,6$) yielded the most accurate point and interval estimates;

  –

  For $R(x)$, configurations A$i[j]$ ($i=1,2,3$ and $j=1,4$) provided the highest estimation accuracy.

• Regarding interval estimation methods, the following apply:

  –

  The ACI[NA] method outperforms ACI[NL] for estimating $\theta$ and $h(x)$, while the ACI[NL] method performs better for $R(x)$;

  –

  The HPD method yields superior interval estimates for all parameters compared to BCI;

  –

  Overall, Bayesian interval estimators (BCI or HPD) surpass asymptotic interval estimators (ACI[NA] or ACI[NL]) in performance.

• In conclusion, for analyzing the Maxwell–Boltzmann lifetimes under the proposed sampling strategy, the Bayesian framework implemented via the MCMC methodology—particularly using the M–H algorithm with Inv.G prior knowledge—is recommended as the most effective approach.

6. Data Analysis

This section aims to illustrate the practical applicability of the proposed estimators of $\theta$, $R(x)$, and $h(x)$, as well as to verify the effectiveness of the developed estimation procedures. For this purpose, two real-world datasets, drawn from the domain of engineering, were analyzed.

6.1. Aircraft Windshield

The aircraft windshield is a critical safety component, protecting pilots and passengers from aerodynamic forces, environmental hazards, and bird strikes, while ensuring clear visibility for navigation. The windshield data reported by Murthy et al. [25] provide a valuable empirical basis for assessing and improving reliability, consisting of eighty-four recorded failure times along with additional censored observations from in-service use.

For numerical stability, in Table 10, the original failure times in the windshield data were divided by a constant factor of ten to obtain a dimensionless scale. This transformation only rescales the parameter estimates without affecting the likelihood shape or the inferential conclusions.

Table 10. The failure times of 84 aircraft windshields.

0.0040	0.0300	0.0310	0.0557	0.0943	0.0981	0.1070	0.1124	0.1248	0.1281
0.1281	0.1303	0.1432	0.1480	0.1510	0.1510	0.1568	0.1615	0.1619	0.1652
0.1652	0.1757	0.1795	0.1866	0.1876	0.1899	0.1911	0.1912	0.1914	0.2010
0.2038	0.2085	0.2089	0.2097	0.2135	0.2154	0.2190	0.2194	0.2223	0.2224
0.2230	0.2300	0.2324	0.2349	0.2385	0.2481	0.2610	0.2625	0.2632	0.2646
0.2661	0.2688	0.2823	0.2890	0.2900	0.2934	0.2962	0.2964	0.3000	0.3100
0.3114	0.3117	0.3166	0.3344	0.3376	0.3385	0.3443	0.3467	0.3478	0.3578
0.3595	0.3699	0.3779	0.3924	0.4035	0.4121	0.4167	0.4240	0.4255	0.4278
0.4305	0.4376	0.4449	0.4485	0.4570	0.4602	0.4663	0.46940

Firstly, we assessed the validity of the proposed MB$(\theta )$ model using the point and interval estimates of $\theta$, $R(x)$, and $h(x)$. To achieve this, we examined the MLE of $\theta$, along with its standard error (SEr), and the corresponding 95% ACI[NA] and ACI[NL]—including their interval lengths (Int.Ws). Additionally, we reported the Kolmogorov–Smirnov (KS) test statistic and its associated p-value for goodness-of-fit evaluation.

From Table 10, the results are as follows: MLE(SEr) of $\theta$: 0.0525(0.0046); 95% ACI[NA][Int.W]: (0.0435, 0.0614)[0.0179]; 95% ACI[NL][Int.W]: (0.0442, 0.0622)[0.0180]; and the KS statistic (p-value) is 0.0604(0.9056). These findings show that the MB model provides the best goodness of fit to the windshield data, as evidenced by the narrow confidence intervals and the large p-value in the KS distance result. Briefly, to evaluate the suitability of the MB lifetime distributions, the windshield data were fitted using the lognormal and gamma models. Model performance was assessed based on the maximized log-likelihood (LL) values, the Akaike information criterion (AIC), the Bayesian information criterion (BIC), and the corresponding p-value in the KS goodness-of-fit test. The results, summarized in Table 11, indicate that the MB distribution attained the highest LL and the lowest information criteria while also achieving the largest KS P-value, confirming its superiority among the considered candidates. As a result, the MB model provided the best fit to the observed windshield data, followed by the gamma model, whereas the lognormal model showed poor support.

Table 11. Comparison of the MB, gamma, and lognormal distributions from the windshield dataset.

Model	LL	AIC	BIC	p-Value
MB	63.02	−124.05	−121.57	0.9056
Gamma	58.68	−113.37	−108.41	0.4518
Lognormal	41.50	−79.011	−74.052	0.0552

To visually examine the numerical fitting results of the MB model, Figure 6 displays the estimated and empirical $R(y)$ curves, the estimated and empirical probability–probability (PP) plots, the estimated and empirical quantile–quantile (QQ) plots, the data histograms with the estimated PDF curve, the scaled total time on test (TTT) transform curves, and a combined boxplot-within-violin plot. As anticipated, based on the complete windshield data summarized in Table 10, the subplots in Figure 6a–d indicate a satisfactory fit of the MB model, aligning well with the numerical goodness-of-fit results; Figure 6e shows that the data exhibit a non-monotone HRF, which is consistent with the theoretical MB failure rate; lastly, Figure 6f appears relatively symmetric with a moderate spread, lacking extreme outliers or secondary peaks, which is indicative of a more uniform underlying process.

Figure 6. Six fitting diagrams of the MB model from the windshield dataset.

Plotting the profile log-likelihood against its normal equation, Figure 7 confirms both the existence and uniqueness of the MLE of $\widehat{\theta }$. Accordingly, we suggest using $\widehat{\theta }\approx 0.525$ as the initial value in subsequent estimation procedures.

Figure 7. Profile log-likelihood of the MB model from the windshield dataset.

From the complete windshield dataset, three artificial IAT2-PC samples, each with a fixed $m=44$ but different choices of $\mathbf{S}$ and threshold values ${\tau }_i(i=1,2)$, were generated and are summarized in Table 12. In the absence of prior knowledge about the MB($\theta$) model for the windshield data, an improper Inv.G prior with hyperparameters $\alpha =\beta =0.001$ was adopted for updating $\theta$. The frequentist point estimates of $\theta$ were employed as initial values for the proposed MCMC sampler. After discarding the first ${\Re }^{\circ }=5000$ iterations from a total of ${\Re }^{•}=30,000$, Bayesian point estimates and their corresponding credible interval estimates for $\theta$, $R(x)$, and $h(x)$ were obtained. For each configuration $S[i]$, $i=1,2,3$, Table 13 reports the point estimates (with standard errors) and the associated $95\%$ interval estimates (with widths) of $\theta$, $R(x)$, and $h(x)$ at $x=0.1$. The results indicate that the likelihood-based estimates of $\theta$, $R(x)$, and $h(x)$ are generally close to their Bayesian counterparts. However, Bayesian estimates consistently achieve smaller standard errors, and both the $95\%$ BCI and HPD intervals were narrower than the corresponding $95\%$ ACI[NA] and ACI[NL] intervals, reflecting higher precision.

Table 12. Different IAT2-PC samples from the windshield dataset.

Sample	S	${\mathit{\tau }}_1({\mathit{d}}_1)$	${\mathit{\tau }}_2({\mathit{d}}_2)$	${\mathit{S}}^{\mathbf{★}}$	${\mathit{T}}^{\mathbf{★}}$	Data
$S$[1]	$(4^{[10]},0^{[34]})$	0.50(44)	0.55(44)	0	0.4663	0.0040, 0.0310, 0.0943, 0.1070, 0.1124, 0.1281, 0.1303, 0.1480, 0.1510, 0.1615, 0.1795,
						0.1876, 0.1899, 0.1911, 0.1914, 0.2038, 0.2085, 0.2089, 0.2097, 0.2154, 0.2194, 0.2230,
						0.2300, 0.2324, 0.2646, 0.2661, 0.2823, 0.2962, 0.3000, 0.3100, 0.3114, 0.3385, 0.3443,
						0.3478, 0.3595, 0.3699, 0.3779, 0.4121, 0.4255, 0.4305, 0.4449, 0.4485, 0.4570, 0.4663
$S$[2]	$(0^{[17]},4^{[10]},0^{[17]})$	0.21(23)	0.47(44)	16	0.4602	0.0040, 0.0300, 0.0310, 0.0557, 0.0943, 0.0981, 0.1070, 0.1124, 0.1248, 0.1281, 0.1281,
						0.1303, 0.1432, 0.1480, 0.1510, 0.1510, 0.1568, 0.1615, 0.1795, 0.1876, 0.1899, 0.1911,
						0.2085, 0.2324, 0.2349, 0.2385, 0.2481, 0.2610, 0.2632, 0.2823, 0.2900, 0.3100, 0.3114,
						0.3467, 0.3478, 0.3578, 0.3699, 0.3924, 0.4035, 0.4305, 0.4376, 0.4485, 0.4570, 0.4602
$S$[3]	$(0^{[34]},4^{[10]})$	0.23(37)	0.29(40)	32	0.29	0.0040, 0.0300, 0.0310, 0.0557, 0.0943, 0.0981, 0.1070, 0.1124, 0.1248, 0.1281, 0.1281,
						0.1303, 0.1432, 0.1480, 0.1510, 0.1510, 0.1568, 0.1615, 0.1619, 0.1652, 0.1652, 0.1757,
						0.1795, 0.1866, 0.1876, 0.1899, 0.1911, 0.1912, 0.1914, 0.2010, 0.2038, 0.2085, 0.2089,
						0.2097, 0.2135, 0.2223, 0.2324, 0.2481, 0.2625, 0.2823

Table 13. Estimates of $\theta$, $R(x)$, and $h(x)$ from the windshield data.

Sample	Par.	MLE		MCMC		ACI[NA]			BCI
						ACI[NL]			HPD
		Est.	SEr	Est.	SEr	Low.	Upp.	Int.W	Low.	Upp.	Int.W
$S$[1]	$\theta$	0.0567	0.0069	0.0575	0.0058	0.0432	0.0702	0.0270	0.0470	0.0694	0.0224
						0.0447	0.0719	0.0273	0.0466	0.0689	0.0223
	$R(x)$	0.9593	0.0085	0.9500	0.0070	0.9426	0.9760	0.0334	0.9349	0.9622	0.0273
						0.9428	0.9761	0.0334	0.9366	0.9637	0.0270
	$h(x)$	0.4788	0.2241	1.4703	0.2056	0.0396	0.9180	0.8783	1.1105	1.9145	0.8040
						0.1913	1.1981	1.0068	1.0685	1.8640	0.7955
$S$[2]	$\theta$	0.0952	0.0112	0.0957	0.0075	0.0732	0.1172	0.0440	0.0815	0.1110	0.0295
						0.0755	0.1199	0.0444	0.0810	0.1103	0.0293
	$R(x)$	0.9593	0.0041	0.9759	0.0027	0.9513	0.9673	0.0160	0.9700	0.9807	0.0108
						0.9513	0.9673	0.0160	0.9705	0.9811	0.0106
	$h(x)$	0.4788	0.1137	0.7109	0.0804	0.2559	0.7017	0.4457	0.5685	0.8841	0.3156
						0.3006	0.7626	0.4620	0.5573	0.8690	0.3117
$S$[3]	$\theta$	0.0613	0.0074	0.0621	0.0061	0.0468	0.0759	0.0291	0.0510	0.0745	0.0235
						0.0484	0.0777	0.0294	0.0504	0.0737	0.0233
	$R(x)$	0.9593	0.0076	0.9551	0.0061	0.9443	0.9743	0.0300	0.9419	0.9659	0.0240
						0.9444	0.9744	0.0300	0.9428	0.9666	0.0238
	$h(x)$	0.4788	0.2035	1.3193	0.1805	0.0799	0.8777	0.7979	1.0042	1.7096	0.7054
						0.2081	1.1016	0.8935	0.9813	1.6812	0.6999

To examine the existence and uniqueness of the fitted MLE of $\widehat{\theta }$ for $\theta$, Figure 8 presents the log-likelihood curves together with their corresponding first derivative (score) functions for all samples $S[i]$, $i=1,2,3$, across varying values of $\theta$. In each configuration, the plots confirm that the MLE of $\widehat{\theta }$ exists and is unique, in agreement with the numerical results in Table 13, thereby justifying its use as the initial value in subsequent Bayesian inference procedures.

Figure 8. Plots of the log-likelihood/gradient functions of $\theta$ from the windshield data.

The convergence behavior of the MCMC samples for $\theta$, $R(x)$, and $h(x)$ was evaluated through trace plots and posterior density plots, as shown in Figure 9. For clarity, the posterior mean and the $95\%$ BCI bounds are indicated by red solid and red dashed lines, respectively. These plots demonstrate satisfactory convergence of the Markov chains, with posterior samples of $\theta$ being approximately symmetric, while $R(x)$ and $h(x)$ exhibit negative and positive skewness, respectively.

Figure 9. Plotting 25,000 MCMC iterations of $\theta$, $R(x)$, and $h(x)$ from the windshield dataset.

From the remaining ${\Re }^{★}=25,000$ post–burn-in MCMC iterations, several summary statistics for $\theta$, $R(x)$, and $h(x)$ were computed, including the posterior mean, mode, quartiles $Q[i]$ ($i=1,2,3$), standard deviation (SD), and skewness (Sk.) (see Table 14). These results are consistent with those in Table 13 and the visual evidence from Figure 9.

Table 14. Statistics for the 25,000 MCMC iterations of $\theta$, $R(x)$, and $h(x)$ from the windshield data.

Sample	Par.	Mean	Mode	$\mathit{Q}[1]$	$\mathit{Q}[2]$	$\mathit{Q}[3]$	SD	Sk.
$S$[1]	$\theta$	0.05750	0.05600	0.05354	0.05725	0.06124	0.00572	0.26408
	$R(x)$	0.95000	0.94895	0.94565	0.95049	0.95495	0.00698	−0.43780
	$h(x)$	1.47033	1.50095	1.32446	1.45559	1.59804	0.20553	0.44513
$S$[2]	$\theta$	0.09570	0.09028	0.09054	0.09560	0.10062	0.00748	0.13253
	$R(x)$	0.97587	0.97404	0.97415	0.97609	0.97779	0.00274	−0.43978
	$h(x)$	0.71088	0.62206	0.65467	0.70445	0.76138	0.08036	0.43934
$S$[3]	$\theta$	0.06209	0.06015	0.05794	0.06184	0.06604	0.00601	0.24489
	$R(x)$	0.95513	0.95380	0.95132	0.95557	0.95949	0.00614	−0.43738
	$h(x)$	1.31932	1.29623	1.19110	1.30639	1.43135	0.18045	0.44274

Finally, Figure 10 compares the $95\%$ ACI[NA]/ACI[NL] and BCI/HPD boundaries for the reliability indices $R(x)$ and $h(x)$ across all data points in $S[i]$, $i=1,2,3$ from the windshield dataset. The BCI and HPD methods yielded shorter Int.W findings than the corresponding ACI[NA] and ACI[NL] approaches, confirming the greater precision suggested by the results in Table 13.

Figure 10. Plots for the 95% Int.W results of $R(x)$ and $h(x)$ from the windshield data.

6.2. Mechanical Components

Mechanical components form the fundamental building blocks of machinery and engineered systems, and their reliability directly influences operational safety, performance efficiency, and maintenance costs across industrial sectors. The failure times of twenty-four mechanical components, originally reported by Murthy et al. [25], constitute a widely used benchmark dataset in reliability and lifetime analysis. The observations, ranging from 10.24 to 51.56 units of time, exhibit a positively skewed distribution with a median of approximately 19, indicating a higher frequency of early failures alongside a smaller number of prolonged lifetimes. Understanding the statistical behavior of these lifetimes enables engineers and researchers to anticipate wear-out patterns, design more durable components, and implement effective preventive maintenance strategies. To facilitate analysis, each time point in Table 15 was scaled by a factor of one hundred.

Table 15. The times to failure for 24 mechanical components.

0.1024	0.1067	0.1226	0.1410	0.1470	0.1497	0.1662	0.1712	0.1814	0.1851
0.1884	0.1908	0.1940	0.2238	0.2257	0.2285	0.2543	0.2747	0.2798	0.2993
0.3094	0.3602	0.4956	0.5156

Next, we assessed the adequacy of the MB model using the point and interval estimates of $\theta$, $R(x)$, and $h(x)$. Specifically, we considered the MLE of $\theta$, its associated Std.Er, and the corresponding 95% ACI[NA] and ACI[NL], along with their respective ILs. The KS statistic and its P-value have also been reported to evaluate the goodness-of-fit. Using Table 16, the estimates are as follows: MLE(Std.Er) of $\theta$: 0.0426(0.0071); 95% ACI[NA][Int.W]: (0.0287, 0.0565)[0.0278]; 95% ACI[NL][Int.W]: (0.0307, 0.0590)[0.0283]; and the KS statistic (p-value): 0.1637(0.4904).

Table 16. Comparison of the MB, gamma, and lognormal distributions from the mechanical dataset.

Model	LL	AIC	BIC	p-Value
MB	22.224	−42.453	−41.275	0.49
Gamma	23.560	−43.159	−40.803	0.68
Lognormal	24.494	−44.988	−42.632	0.86

Following the same comparison setup as in Table 11, the full mechanical dataset was analyzed to evaluate the fit of the MB distribution against its competitors, the gamma and lognormal distributions (see Table 16). The model comparison showed that the lognormal distribution provided the best fit, supported by the highest log-likelihood, the lowest AIC/BIC values, and the largest KS p-value. In contrast, the gamma and MB distributions yielded only a moderate fit.

Figure 11 provides a visual assessment of the MB model fit. For the complete mechanical data summarized in Table 15, panels Figure 11a–d show close agreement between the model and the observed data, corroborating the numerical goodness-of-fit results. Panel Figure 11e indicates a non-monotone HRF, consistent with the theoretical MB failure rate. Panel Figure 11f reveals a moderately skewed distribution with a primary concentration of values around 0.18 to 0.22, a secondary mode near 0.5, and a few high-value outliers, indicating possible heterogeneity or substructure in the data. The profile log-likelihood in Figure 12 further confirms the existence and uniqueness of the fitted MLE of $\widehat{\theta }$, motivating the choice of $\widehat{\theta }\approx 0.042$ as the starting value for subsequent estimation.

Figure 11. Six fitting diagrams of the MB model from the mechanical dataset.

Figure 12. Profile log-likelihood of the MB model from the mechanical dataset.

From Table 15, three artificial IAT2-PC samples were generated to evaluate the performance of the proposed inferential procedures. Each sample was constructed with a fixed sample size $m=12$ but employed distinct selections of the censoring scheme $\mathbf{S}$ and threshold values ${\tau }_i$$(i=1,2)$, as summarized in Table 17. In situations where no substantive prior information regarding the MB($\theta$) model parameters for the mechanical data is available, it is reasonable to adopt a noninformative prior to ensure minimal subjective influence. Accordingly, an improper Inv.G prior, $\mathrm{Inv}.\mathrm{G}(\alpha ,\beta )$, with hyperparameters $\alpha =\beta =0.001$ was specified for $\theta$.

Table 17. The different IAT2-PC samples from the mechanical dataset.

Sample	S	${\mathit{\tau }}_1({\mathit{d}}_1)$	${\mathit{\tau }}_2({\mathit{d}}_2)$	${\mathit{S}}^{\mathbf{★}}$	${\mathit{T}}^{\mathbf{★}}$	Data
$S$[1]	$(2^{[6]},0^{[6]})$	0.37(12)	0.40(12)	0	0.3602	0.1024, 0.1226, 0.1470, 0.1497, 0.1814, 0.1851,
						0.1884, 0.2238, 0.2257, 0.2747, 0.2798, 0.3602
$S$[2]	$(0^{[3]},2^{[6]},0^{[3]})$	0.17(6)	0.31(12)	6	0.3094	0.1024, 0.1067, 0.1226, 0.1410, 0.1497, 0.1662,
						0.1851, 0.1940, 0.2257, 0.2543, 0.2798, 0.3094
$S$[3]	$(0^{[6]},2^{[6]})$	0.20(8)	0.26(10)	10	0.26	0.1024, 0.1067, 0.1226, 0.1410, 0.1470, 0.1497,
						0.1662, 0.1908, 0.2238, 0.2543

To initiate the Bayesian analysis, the maximum likelihood estimates of $\theta$ obtained under the frequentist approach were employed as starting values for the MCMC sampler, facilitating more rapid convergence. Setting ${\Re }^{•}=30,000$ and ${\Re }^{\circ }=5000$ in the MCMC algorithm, the posterior findings, including point estimates and corresponding credible intervals, were computed for $\theta$, $R(x)$, and $h(x)$. For each experimental configuration $S[i]$, $i=1,2,3$, Table 18 reports the Bayesian posterior means together with standard errors, as well as the $95\%$ BCI and HPD bounds, alongside the analogous frequentist asymptotic confidence intervals ACI[NA] and ACI[NL]. The evaluation point was set to $x=0.05$ for both $R(x)$ and $h(x)$. A close agreement was observed between the likelihood-based and Bayesian point estimates across all parameters, suggesting robustness of the estimation framework. Nevertheless, the Bayesian approach systematically yielded smaller standard errors, and its corresponding $95\%$ BCI and HPD intervals were consistently shorter than the ACI[NA] and ACI[NL] counterparts, reflecting superior precision in parameter estimation.

Table 18. Estimates of $\theta$, $R(x)$, and $h(x)$ from the mechanical data.

Sample	Par.	MLE		MCMC		ACI[NA]			BCI
						ACI[NL]			HPD
		Est.	SEr	Est.	SEr	Low.	Upp.	Int.W	Low.	Upp.	Int.W
$S$[1]	$\theta$	0.0406	0.0093	0.0418	0.0069	0.0224	0.0588	0.0363	0.0296	0.0563	0.0267
						0.0260	0.0635	0.0376	0.0285	0.0548	0.0264
	$R(x)$	0.9593	0.0037	0.9889	0.0027	0.9520	0.9665	0.0145	0.9825	0.9931	0.0107
						0.9521	0.9666	0.0145	0.9833	0.9936	0.0103
	$h(x)$	0.4788	0.2128	0.6590	0.1613	0.0617	0.8959	0.8342	0.4066	1.0352	0.6286
						0.2004	1.1442	0.9439	0.3802	0.9882	0.6080
$S$[2]	$\theta$	0.0562	0.0126	0.0570	0.0079	0.0314	0.0809	0.0494	0.0426	0.0732	0.0307
						0.0362	0.0872	0.0510	0.0419	0.0725	0.0305
	$R(x)$	0.9593	0.0023	0.9930	0.0015	0.9548	0.9638	0.0089	0.9897	0.9954	0.0057
						0.9548	0.9638	0.0089	0.9901	0.9956	0.0055
	$h(x)$	0.4788	0.1325	0.4133	0.0863	0.2191	0.7385	0.5195	0.2763	0.6123	0.3359
						0.2783	0.8236	0.5453	0.2622	0.5856	0.3234
$S$[3]	$\theta$	0.0578	0.0139	0.0586	0.0081	0.0305	0.0851	0.0546	0.0436	0.0752	0.0316
						0.0360	0.0927	0.0566	0.0435	0.0751	0.0316
	$R(x)$	0.9593	0.0023	0.9933	0.0014	0.9547	0.9639	0.0092	0.9900	0.9955	0.0055
						0.9547	0.9639	0.0092	0.9905	0.9958	0.0053
	$h(x)$	0.4788	0.1365	0.3977	0.0844	0.2112	0.7464	0.5352	0.2657	0.5901	0.3243
						0.2738	0.8373	0.5635	0.2488	0.5620	0.3131

To verify both the existence and uniqueness of the MLE of $\widehat{\theta }$, for each sample configuration $S[i]$ with $i=1,2,3$, the curves plotted in Figure 13 reveal a single, well-defined peak of the likelihood function. This confirms that the obtained MLE exists and is unique, thereby ensuring the mathematical good posture of the estimation problem.

Figure 13. Plots of the log-likelihood/gradient functions of $\theta$ from the mechanical data.

All of the subplots in Figure 13 further support the selection of $\widehat{\theta }$ as a robust initial value in subsequent Bayesian computations. Figure 14 shows that the posterior distribution of $\theta$ appears approximately symmetric, whereas those of $R(x)$ and $h(x)$ display slight left and right skewness, respectively. Using $25,000$ post-burn-in MCMC samples, posterior summaries were computed for all three quantities of interest. These results, documented in Table 19, align closely with the earlier findings in Table 18 and are consistent with the graphical convergence diagnostics in Figure 14. Together, these numerical and graphical results confirm the reliability, stability, and internal consistency of the Bayesian estimation framework adopted in this study.

Figure 14. Plotting 25,000 MCMC iterations of $\theta$, $R(x)$, and $h(x)$ from the mechanical dataset.

Table 19. Statistics for 25,000 MCMC iterations of $\theta$, $R(x)$, and $h(x)$ from the mechanical data.

Sample	Par.	Mean	Mode	Q[1]	Q[2]	Q[13]	SD	Sk.
$S$[1]	$\theta$	0.04180	0.03893	0.03704	0.04145	0.04618	0.00681	0.34817
	$R(x)$	0.98886	0.98822	0.98733	0.98925	0.99083	0.00274	−0.86902
	$h(x)$	0.65898	0.57495	0.54348	0.63628	0.74916	0.16129	0.86412
$S$[2]	$\theta$	0.05702	0.05483	0.05156	0.05678	0.06211	0.00781	0.21507
	$R(x)$	0.99303	0.99287	0.99220	0.99323	0.99407	0.00146	−0.83720
	$h(x)$	0.41327	0.36373	0.35216	0.40171	0.46266	0.08616	0.83241
$S$[3]	$\theta$	0.05856	0.05987	0.05291	0.05835	0.06387	0.00809	0.18469
	$R(x)$	0.99330	0.99374	0.99249	0.99350	0.99431	0.00143	−0.88874
	$h(x)$	0.39767	0.37166	0.33804	0.38598	0.44551	0.08419	0.88375

Figure 15 displays the $95\%$ confidence and credible interval bounds for the reliability measures $R(x)$ and $h(x)$, which were constructed using the ACI[NA]/ACI[NL] methods, as well as the BCI/HPD approaches, for each mechanical sample configuration $S[i]$, $i=1,2,3$. Across all configurations, the Bayesian intervals, whether expressed as BCI or HPD, were consistently and substantially narrower than their classical asymptotic counterparts. This marked reduction in interval length reflects the increased estimation precision afforded by the Bayesian procedure. These graphical observations are fully consistent with the numerical results reported in Table 18, thereby reinforcing the conclusion that the Bayesian framework provides a more efficient and informative inference mechanism for $R(x)$ and $h(x)$ compared to traditional asymptotic methods.

Figure 15. Plots for the 95% Int.W results of $R(x)$ and $h(x)$ from the mechanical data.

In summary, the analyses performed on datasets derived from the improved Type-II adaptive progressive censoring scheme—encompassing both the aircraft windshield measurements and the mechanical components data—offer a thorough empirical assessment of the Maxwell–Boltzmann lifetime model. The empirical findings not only corroborate the conclusions drawn from the earlier simulation studies, but also underscore the practical utility and robustness of the proposed inferential framework for addressing real-world engineering reliability problems.

7. Concluding Remarks

In this study, we developed a comprehensive reliability analysis framework for engineering failure data under the Maxwell–Boltzmann distribution, incorporating the improved Type-II adaptive progressive censoring plan. The main contributions of this work can be summarized as follows. First, the Maxwell–Boltzmann distribution was shown to provide a flexible and analytically tractable model for characterizing engineering lifetimes, particularly in contexts where the underlying failure mechanism follows a non-monotonic hazard rate. Second, by embedding the proposed scheme, we addressed practical challenges of time and resource limitations in life-testing experiments, thereby enhancing the efficiency and adaptability of the censoring mechanism compared to traditional fixed schemes. From a methodological perspective, we derived the maximum likelihood and Bayes estimators for the unknown parameters of the Maxwell–Boltzmann model under the proposed sampling scheme and examined their asymptotic behavior. Approximate confidence intervals and Bayesian credible intervals were constructed to assess inferential accuracy, and interval estimation was further supported through estimated Fisher information and MCMC approaches, respectively. Extensive Monte Carlo simulations demonstrated the superiority of the proposed scheme in terms of parameter estimation precision and reliability assessment when compared with conventional censoring approaches. The numerical study emphasized the reduction in bias and mean squared error, as well as the improved coverage probabilities of the interval estimates. Furthermore, two real engineering datasets were analyzed to illustrate the practical relevance of the proposed methodology. While the proposed Bayesian framework exhibited strong performance, several limitations merit attention. These include its sensitivity to the specification of stress change points (${\tau }_1$, ${\tau }_2$), the computational burden associated with MCMC implementation, and increased variability in very small samples. Such limitations highlight promising directions for future research, including data-driven estimation of change points, the development of more computationally efficient algorithms, and the incorporation of small-sample corrections. Collectively, these findings position the Maxwell–Boltzmann distribution as a versatile lifetime model under complex censoring, bridging statistical physics with reliability theory. Future research may extend this framework to multivariate reliability settings, competing risks, and accelerated life-testing designs, further enhancing its role in engineering decision-making and predictive reliability analytics.