Input-to-Output Stability for Stochastic Complex Networked Control Systems
Abstract
1. Introduction
- Combining Kirchhoff’s matrix tree theorem in graph theory, Lyapunov method and stochastic analysis skills, we construct an appropriate Lyapunov function for SCNCS , which is closely related to topological structure and Lyapunov function of each node system, and propose some sufficient criteria for SCNCS to satisfy IOS.
- We apply the theoretical results to verify IOS for a class of stochastic Lurie coupled control systems on networks (SLCCSN), and the numerical test is carried out to verify the validity of our results.
2. Model Description and Preliminaries
3. Main Results
4. An Application to a Class of Stochastic Lurie Coupled Control Systems on Networks
5. Numerical Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Wang, J.; Li, P.; Luo, X.; Yang, Y. Internet of things as complex networks. IEEE Netw. 2021, 35, 238–245. [Google Scholar] [CrossRef]
- Gao, S.; Li, S.-S.; Wu, B.-Y. Periodic solutions of discrete time periodic time-varying coupled systems on networks. Chaos Solitons Fractals 2017, 103, 246–255. [Google Scholar] [CrossRef]
- Hua, Z.; Jing, X.-C.; Martínez, L. Consensus reaching for social network group decision making with ELICIT information: A perspective from the complex network. Inf. Sci. 2023, 627, 71–96. [Google Scholar] [CrossRef]
- Gao, S.; Peng, C.; Li, J.-X.; Kang, R.; Liu, X.-Q.; Zhang, C.-R. Global asymptotic stability in mean for stochastic complex networked control systems. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106162. [Google Scholar] [CrossRef]
- Radicchi, F.; Barrat, A.; Fortunato, S.; Ramasco, J. Renormalization flows in complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 026104. [Google Scholar] [CrossRef]
- Espejo, R.; Lumbreras, S.; Ramos, A. A complex-network approach to the generation of synthetic power transmission networks. IEEE Syst. J. 2019, 13, 3050–3058. [Google Scholar] [CrossRef]
- Zhang, M.-Y.; Huang, T.; Guo, Z.-X.; He, Z.-G. Complex-network-based traffic network analysis and dynamics: A comprehensive review. Phys. A Stat. Mech. Appl. 2022, 607, 128063. [Google Scholar] [CrossRef]
- Xu, X.-J.; Wang, K.; Zhu, L.-C.; Zhang, L.-J. Efficient construction of threshold networks of stock markets. Phys. A Stat. Mech. Appl. 2018, 509, 1080–1086. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yu, X.; Sun, C. Characteristic modeling approach for complex network systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1383–1388. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Y.-W.; Xiao, J.-W.; Huang, Y.-H. Robust synchronization of singular complex switched networks with parametric uncertainties and unknown coupling topologies via impulsive control. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4404–4416. [Google Scholar] [CrossRef]
- Wu, Y.-B.; Zhu, J.-L.; Li, W.-X. Intermittent discrete observation control for synchronization of stochastic neural networks. IEEE Trans. Cybern. 2020, 50, 2414–2424. [Google Scholar] [CrossRef]
- Xu, Y.; Li, W.-B.; Zhang, C.-M.; Li, W.-X. Global bipartite synchronization of fractional-order time-varying coupled signed networks with proportional delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107452. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.-X.; Feng, J.-Q. The stability of stochastic coupled systems with time-varying coupling and general topology structure. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4189–4200. [Google Scholar] [CrossRef]
- Zhang, C.-M.; Li, W.-X.; Wang, K. Graph theory-based approach for stability analysis of stochastic coupled systems with Lévy noise on networks. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1698–1709. [Google Scholar] [CrossRef]
- Rguigui, H.; Elghribi, M. Practical stabilization for a class of tempered fractional-order nonlinear fuzzy systems. Asian J. Control 2025. [Google Scholar] [CrossRef]
- Rguigui, H.; Elghribi, M. Separation principle for Caputo-Hadamard fractional-order fuzzy systems. Asian J. Control 2025. [Google Scholar] [CrossRef]
- Chen, Z.-B.; Huo, C.-X.; Zou, X.-L.; Li, W.-X. Delayed impulsive control for synchronization of complex-valued stochastic complex network with unbounded delays under cyber attacks. Chaos Solitons Fractals 2024, 180, 114526. [Google Scholar] [CrossRef]
- Sontag, E.D. Smooth stabilization implies coprime factorization. IEEE Trans. Autom. Control 1989, 34, 435–443. [Google Scholar] [CrossRef]
- Sontag, E.D.; Wang, Y. Notions of input to output stability. Syst. Control Lett. 1999, 38, 235–248. [Google Scholar] [CrossRef]
- Sontag, E.D.; Wang, Y. Lyapunov characterizations of input to output stability. Siam J. Control Optim. 2000, 39, 226–249. [Google Scholar] [CrossRef]
- Sontag, E.D.; Wang, Y. A notion of input to output stability. In Proceedings of the 1997 European Control Conference (ECC), Brussels, Belgium, 1–4 July 1997; pp. 3862–3867. [Google Scholar] [CrossRef]
- Nawarathna, R.H.H.; Lin, Y.; Wang, Y. On integral input-to-output stability properties. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; pp. 6285–6290. [Google Scholar] [CrossRef]
- Polushin, I.G.; Liu, P.-X.; Lung, C.-H. A force-reflection algorithm for improved transparency in bilateral teleoperation with communication delay. IEEE/ASME Trans. Mechatron. 2007, 12, 361–374. [Google Scholar] [CrossRef]
- Karafyllis, I.; Jiang, Z.-P. A new small-gain theorem with an application to the stabilization of the chemostat. Int. J. Robust Nonlinear 2012, 22, 1602–1630. [Google Scholar] [CrossRef]
- Mei, W.-J.; Ushirobira, R.; Efimov, D. On nonlinear robust state estimation for generalized Persidskii systems. Automatica 2022, 142, 110411. [Google Scholar] [CrossRef]
- Acikmese, B.; Hadaegh, F.Y.; Scharf, D.P.; Ploen, S.R. Formulation and analysis of stability for spacecraft formations. IET Control Theory Appl. 2007, 1, 461–474. [Google Scholar] [CrossRef]
- Zhang, C.-M.; Li, W.-X.; Su, H.; Wang, K. A graph-theoretic approach to boundedness of stochastic Cohen-Grossberg neural networks with Markovian switching. Appl. Math. Comput. 2013, 219, 9165–9173. [Google Scholar] [CrossRef]
- Zhang, C.-M.; Li, W.-X.; Wang, K. Boundedness for network of stochastic coupled van der Pol oscillators with time-varying delayed coupling. Appl. Math. Model. 2013, 37, 5394–5402. [Google Scholar] [CrossRef]
- Li, M.-Y.; Shuai, Z.-S. Global-stability problem for coupled systems of differential equations on networks. J. Differ. Equ. 2010, 248, 1–20. [Google Scholar] [CrossRef]
- Zhang, C.-M.; Chen, T.-R. Exponential stability of stochastic complex networks with multi-weights based on graph theory. Phys. A Stat. Mech. Appl. 2018, 496, 602–611. [Google Scholar] [CrossRef]
- Huo, J.-J.; Zhao, H.-Y. Dynamical analysis of a fractional SIR model with birth and death on heterogeneous complex networks. Phys. A Stat. Mech. Appl. 2016, 448, 41–56. [Google Scholar] [CrossRef]
- Su, H.; Qu, Y.-B.; Gao, S.; Song, H.-H.; Wang, K. A model of feedback control system on network and its stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1822–1831. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Q.; Wu, B.-Y. Existence and global exponential stability of periodic solutions for coupled control systems on networks with feedback and time delays. Commun. Nonlinear Sci. Numer. Simul. 2018, 63, 72–87. [Google Scholar] [CrossRef]
- Gao, S.; Guo, Y.; Cao, Z.-Q.; Feng, H. Periodic solutions for feedback control coupled systems on networks. Appl. Anal. 2021, 101, 6353–6374. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; ISBN 0-13-227828-6. [Google Scholar]
- Biggs, N.; Lloyd, E.K.; Wilson, R.J. Graph Theory; Oxford University Press: Oxford, UK, 1986; pp. 1736–1936. ISBN 0-19-853916-9. [Google Scholar]
- Mao, X. ; Stochastic Differential Equations and Applications; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 9781904275343. [Google Scholar]
- Tian, J.-K.; Zhong, S.-M.; Xiong, L.-L. Delay-dependent absolute stability of Lurie control systems with multiple time-delays. Appl. Math. Comput. 2007, 188, 379–384. [Google Scholar] [CrossRef]
- Arcak, M.; Andrew, T. Input-to-state stability for a class of lurie systems. Automatica 2002, 38, 1945–1949. [Google Scholar] [CrossRef]

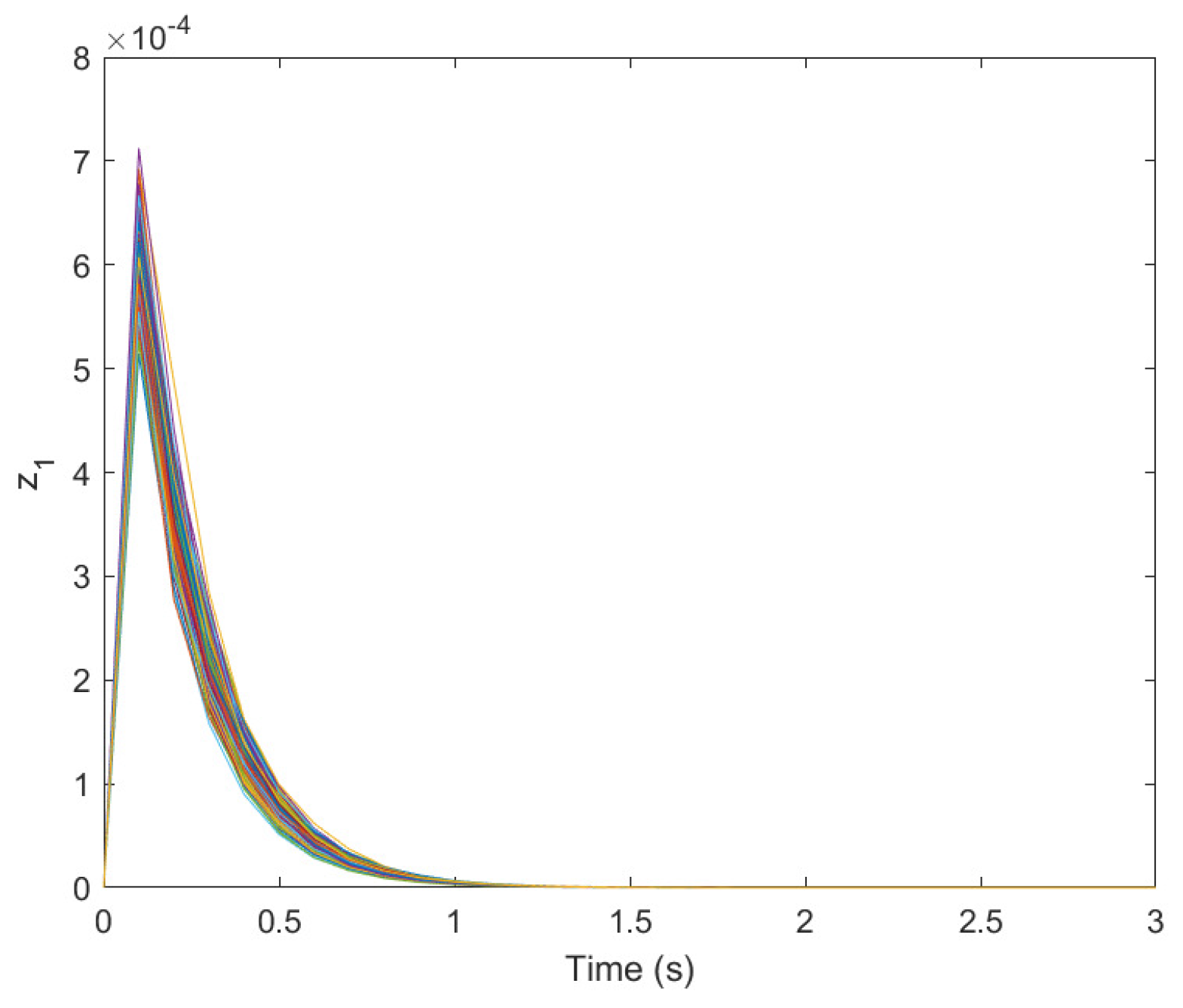


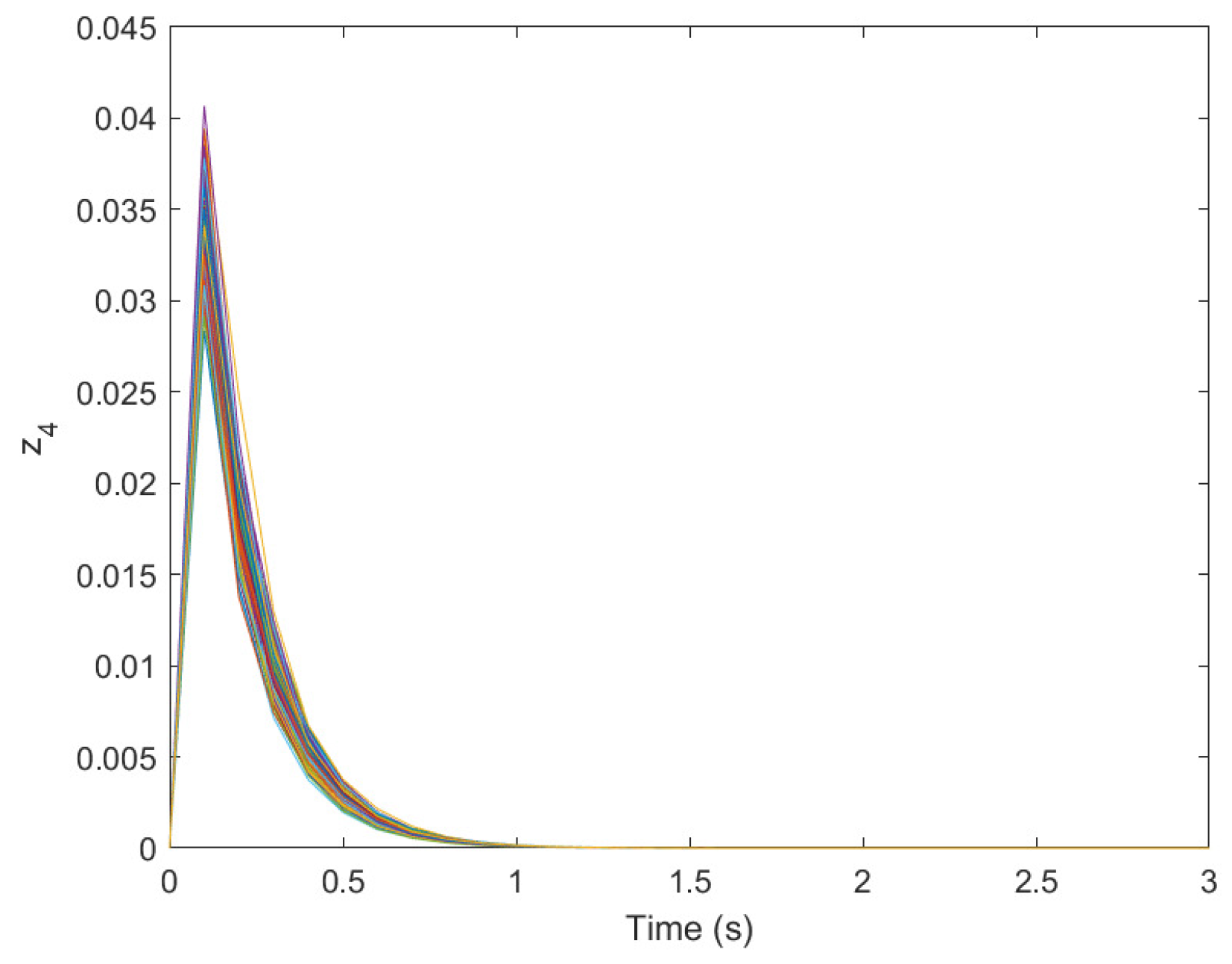
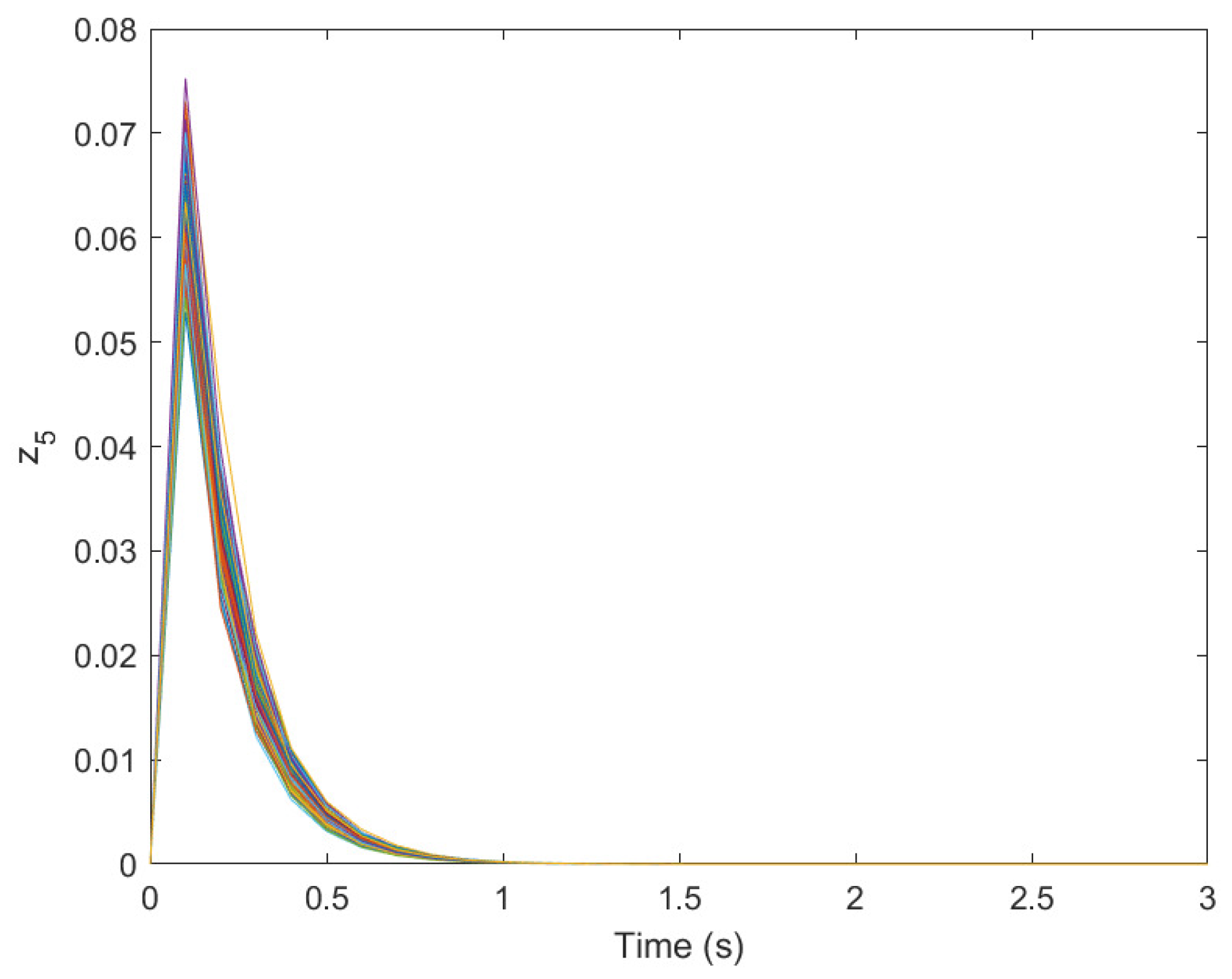
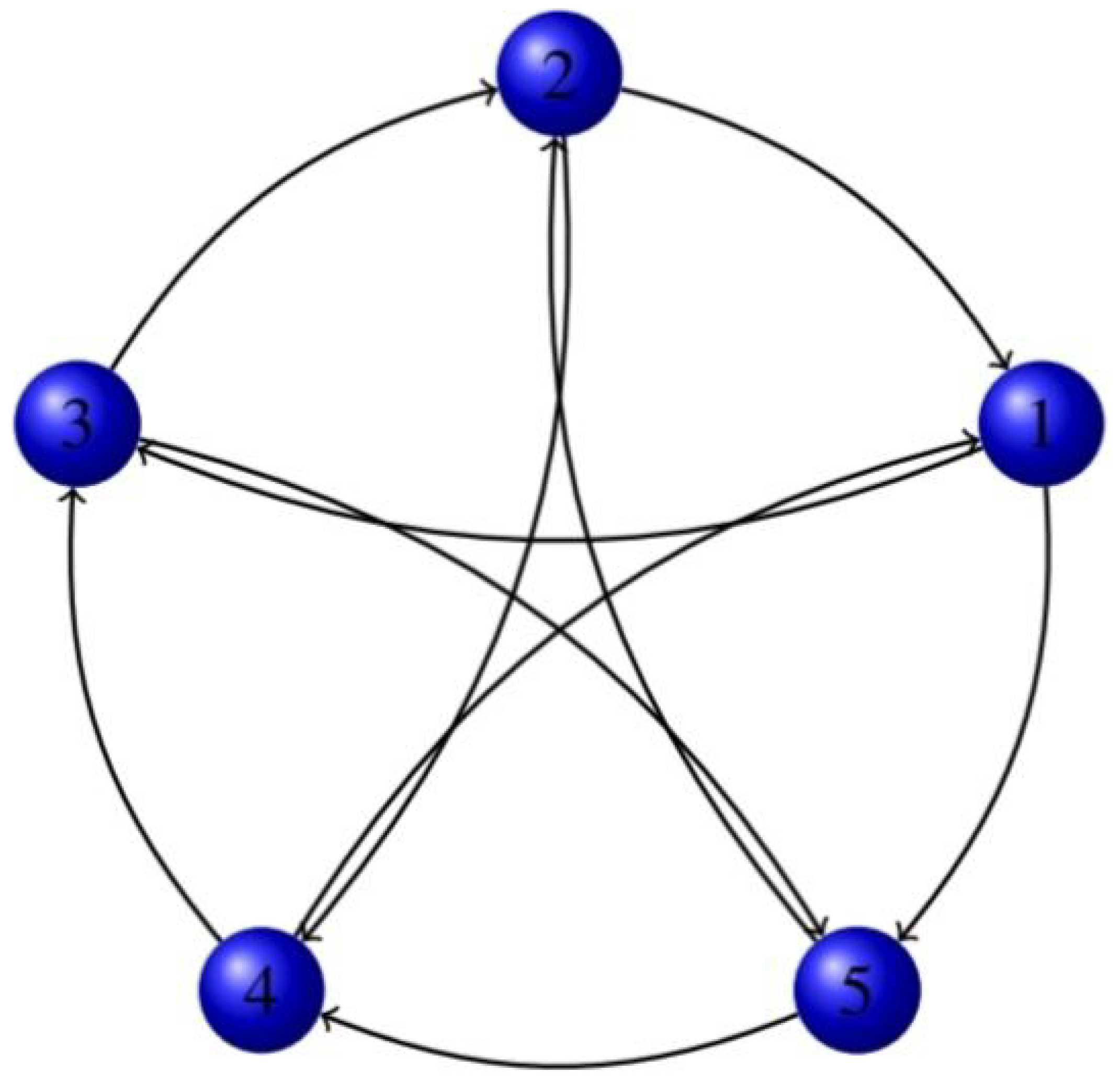
| No. | ||||||
|---|---|---|---|---|---|---|
| 1 | 2.19 | 0.01 | 0.02 | 2.15 | 1.02 | 0.01 |
| 2 | 2.21 | 0.03 | 0.02 | 2.18 | 1.03 | 0.03 |
| 3 | 2.24 | 0.05 | 0.04 | 2.22 | 1.05 | 0.04 |
| 4 | 2.28 | 0.06 | 0.05 | 2.31 | 1.07 | 0.06 |
| 5 | 2.33 | 0.08 | 0.07 | 2.43 | 1.01 | 0.07 |
| −1.65480 | −1.13495 | 1.13495 |
| −1.65455 | −1.15455 | 1.15455 |
| −1.64375 | −1.17420 | 1.17420 |
| −1.65255 | −1.25320 | 1.25320 |
| −1.74495 | −1.35255 | 1.35255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Gao, S. Input-to-Output Stability for Stochastic Complex Networked Control Systems. Axioms 2025, 14, 710. https://doi.org/10.3390/axioms14090710
Li X, Gao S. Input-to-Output Stability for Stochastic Complex Networked Control Systems. Axioms. 2025; 14(9):710. https://doi.org/10.3390/axioms14090710
Chicago/Turabian StyleLi, Xuexin, and Shang Gao. 2025. "Input-to-Output Stability for Stochastic Complex Networked Control Systems" Axioms 14, no. 9: 710. https://doi.org/10.3390/axioms14090710
APA StyleLi, X., & Gao, S. (2025). Input-to-Output Stability for Stochastic Complex Networked Control Systems. Axioms, 14(9), 710. https://doi.org/10.3390/axioms14090710






