Decompositions for Based Algebras with Bilinear Forms: A Graph Theory Connection

Abstract

We consider the category of based algebras with bilinear forms and show that any object in this category decomposes as a direct sum of irreducible orthogonal ideals. By associating an adequate graph with a based algebra with a bilinear form, this decomposition can be recovered from a graph theory viewpoint.

1. Introduction and Previous Definitions

We recall that an algebra A over a base field $\mathbb{K}$ is just a linear space A endowed with a bilinear map

$$A\times A\to A$$

$$(x,y)\mapsto xy$$

called the product of A.

A subalgebra of A is a linear subspace B of A such that $xy\in B$ for any $x,y\in B$.

A morphism of algebras is a linear map $f:A\to A^{\prime }$ such that

$$f\left(xy\right)=f\left(x\right)f\left(y\right)$$

for any $x,y\in A$.

The category of based algebras with bilinear forms, denoted by $\mathcal{B}\mathbf{Ab}$ has as objects the triplets

$$(A,\mathcal{B},\beta )$$

where A is an arbitrary $\mathbb{K}$-algebra, $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$ a fixed basis of A, and $\beta :A\times A\to \mathbb{K}$ a bilinear form.

Two objects $(A,\mathcal{B},\beta )$ and $(A^{\prime },{\mathcal{B}}^{\prime },{\beta }^{\prime })$ are fixed in $\mathcal{B}\mathbf{Ab}$. The morphisms from $(A,\mathcal{B},\beta )$ to $(A^{\prime },{\mathcal{B}}^{\prime },{\beta }^{\prime })$ are the set of algebra morphisms

$$f:A\to A^{\prime }$$

such that $f\left(\mathcal{B}\right)\subset {\mathcal{B}}^{\prime }$ and

$$\beta (x,y)={\beta }^{\prime }(f\left(x\right),f\left(y\right))$$

for any $x,y\in A$.

A subalgebra of a based algebra with a bilinear form $(A,\mathcal{B},\beta )$ is an object $(B,{\mathcal{B}}_B,{\beta }_B)$ of $\mathcal{B}\mathbf{Ab}$ such that B is a subalgebra of A, ${\mathcal{B}}_B\subset \mathcal{B}$, and ${\beta }_B{=\beta |}_{B\times B}.$ An ideal $(I,{\mathcal{B}}_I,{\beta }_I)$ of $(A,\mathcal{B},\beta )$ is a subalgebra such that $AI+IA\subset I.$ We will write only I when there is no possible confusion.

Given a based algebra with a bilinear form $(A,\mathcal{B},\beta )$, it is said that $x,y\in A$ are orthogonal if

$$\beta (x,y)=\beta (y,x)=0.$$

Two non-empty subsets $B,C\subset A$ are also called orthogonal if

$$\beta (B,C)=\beta (C,B)=0,$$

that is, if

$$\beta (x,y)=\beta (y,x)=0$$

for any $x\in B$ and $y\in C$.

The aim of this paper is to show that any based algebra with a bilinear form $(A,\mathcal{B},\beta )$ decomposes as

$$A=\underset{k\in K}{⨁}{I}_k$$

(1)

where any $I_k$ is an ideal of A; $I_j$ and $I_k$ are orthogonal for any $j,k\in K$ with $j\ne k$; any ideal in the above decomposition is irreducible, in the sense that any $I_k$ cannot be expressed as the direct sum

$$I_k=P\oplus Q$$

with P and Q as orthogonal nonzero ideals of $I_k$.

We are inspired by some ideas in [1,2,3]. Indeed, the results in these references are consequences of those in the present paper, since the classes of algebras considered in [1,2,3] are subclasses of the one considered in this work.

The above ideas follow connection techniques on the set $\mathcal{B}$. We note that these techniques were introduced in [4] for the study of the structure of split Lie algebras and have been developed and applied in many contexts (see for instance [5,6,7,8,9,10,11,12,13,14,15]).

Given a based algebra with a bilinear form $(A,\mathcal{B},\beta )$, we are going to associate it with a directed graph. We will show how it is possible to recover the decomposition given in Equation (1) by looking at this graph. Hence, the strong connection between the theory of based algebra with bilinear forms and the graph theory is shown.

An important class of based algebras is those formed by the algebras with multiplicative bases (see for instance [1,16,17]). These are algebras A admitting a linear basis $\mathcal{B}={\left\{e_i\right\}}_{i\in I}$ such that either $e_i{e}_j=0$ or $e_i{e}_j=\lambda e_k$ with $0\ne \lambda \in \mathbb{K}$ and $e_k\in \mathcal{B}.$ There are many examples of algebras with a multiplicative basis. For instance, full matrix algebras, group-algebras, quiver algebras when $\mathbb{K}$ is algebraically closed, finite-dimensional associative algebras of the finite representation type, semisimple finite-dimensional Lie algebras over algebraically closed fields of characteristic 0, semisimple locally finite split Lie algebras, and Heisenberg algebras.

If we center on the real algebras $\mathbb{R}$, $\mathbb{C}$, $\mathbb{H}$ (quaternions) and $\mathbb{O}$ (octonions), these are algebras with multiplicative bases $\mathcal{B}$ that also admit a canonical non-degenerate bilinear product $\beta :A\times A\to \mathbb{R}$, for $A\in \{\mathbb{R},\mathbb{C},\mathbb{H},\mathbb{O}\}.$ Hence, $(A,\mathcal{B},\beta )$ are examples of based algebras with bilinear forms. Here we note that these examples are fundamental in the theory of absolute valued algebras. Indeed any finite dimensional (real) absolute valued algebra can be constructed from one of these four based algebras with bilinear forms (see for instance [18,19,20]).

2. Main Results

In this section

$$(A,\mathcal{B}={\left\{e_i\right\}}_{i\in I},\beta )$$

denotes a based algebra with a bilinear form. We will call it A for short if there is not any possible confusion.

For any $i\in I$, we can consider the projection map

$$p_i:A\to \mathbb{K}$$

given by $p_i\left(x\right)={\lambda }_i$ for any $x\in A$, where

$$x=\sum _{i\in I}{\lambda }_i{e}_i$$

is the (unique) expression of x with respect to the basis $\mathcal{B}$.

We also consider a copy of $\mathcal{B}$, denoted by $\overline{\mathcal{B}},$ where its elements are denoted by $\overline{e_i}$ for any $e_i\in \mathcal{B}$. That is,

$$\overline{\mathcal{B}}=\{\overline{e_i}:e_i\in \mathcal{B}\}.$$

We will also denote $\overline{\left(\overline{e_i}\right)}:=e_i$, by $\mathcal{P}\left(\mathcal{B}\right)$, the power set of $\mathcal{B}$, and by $S_2$, the group of permutation of two elements $\{1,2\}$.

Now we define the maps $\mathfrak{p}$ and $\mathfrak{q}$ as follows:

$$\mathfrak{p}:\mathcal{B}\times (\mathcal{B}\cup \overline{\mathcal{B}})\to \mathcal{P}\left(\mathcal{B}\right)$$

as

$$\mathfrak{p}(e_{i_1},e_{i_2})=\{e_k\in \mathcal{B}:p_k\left(e_{i_{\sigma \left(1\right)}}{e}_{i_{\sigma \left(2\right)}}\right)\ne 0\mathrm{for}\mathrm{some}\sigma \in S_2\},$$

for any $e_{i_1},e_{i_2}\in \mathcal{B}$; and

$$\mathfrak{p}(e_i,\overline{e_{i_1}})=\{e_{i_2}\in \mathcal{B}:p_i\left(e_{i_{\sigma \left(1\right)}}{e}_{i_{\sigma \left(2\right)}}\right)\ne 0\mathrm{for}\mathrm{some}\sigma \in S_2\},$$

for any $e_i\in \mathcal{B}$ and $\overline{e_{i_2}}\in \overline{\mathcal{B}}.$

$$\mathfrak{q}:\mathcal{B}\times (\mathcal{B}\cup \overline{\mathcal{B}})\to \mathcal{P}\left(\mathcal{B}\right)$$

as

$$\mathfrak{q}(e_{i_1},e_{i_2})=\left\{\begin{array}{cc}\left\{e_{i_2}\right\}\hfill & \mathrm{if}\beta (e_{i_{\sigma \left(1\right)}},e_{i_{\sigma \left(2\right)}})\ne 0,\mathrm{for}\mathrm{some}\sigma \in S_2\hfill \\ \varnothing \hfill & \mathrm{if}\beta (e_{i_{\sigma \left(1\right)}},e_{i_{\sigma \left(2\right)}})=0,\mathrm{for}\mathrm{all}\sigma \in S_2,\hfill \end{array}\right.$$

for any $e_{i_1},e_{i_2}\in \mathcal{B}$; and

$$\mathfrak{q}(e_i,\overline{e_{i_1}})=\left\{\begin{array}{cc}\{e_{i_2}\in \mathcal{B}:\beta (e_{i_{\sigma \left(1\right)}},e_{i_{\sigma \left(2\right)}})\ne 0\mathrm{for}\mathrm{some}\sigma \in S_2\}\hfill & \mathrm{if}{e}_i=e_{i_1}\hfill \\ \varnothing \hfill & \mathrm{if}{e}_i\ne e_{i_1},\hfill \end{array}\right.$$

for any $e_i\in \mathcal{B}$ and $\overline{e_{i_1}}\in \overline{\mathcal{B}}.$

Now we introduce the map

$$\mathfrak{r}:\mathcal{P}\left(\mathcal{B}\right)\times (\mathcal{B}\cup \overline{\mathcal{B}})\to \mathcal{P}\left(\mathcal{B}\right),$$

as

$$\mathfrak{r}(J,a_i)=\left\{\begin{array}{cc}\varnothing \hfill & \mathrm{if}J=\varnothing \hfill \\ {\displaystyle \bigcup _{e_j\in J}}(\mathfrak{p}(e_j,a_i)\cup \mathfrak{q}(e_j,a_i))\hfill & \mathrm{if}J\ne \varnothing ,\hfill \end{array}\right.$$

for any $J\in \mathcal{P}\left(\mathcal{B}\right)$ and $a_i\in \mathcal{B}\cup \overline{\mathcal{B}}.$

Definition 1.

Let $e_i$ and $e_j$ be a couple of elements in $\mathcal{B}$. We say that $e_i$ is connected to $e_j$ if either $e_i=e_j$, or there is a sequence

$$(a_{i_1},a_{i_2},\dots ,a_{i_n}),$$

$n\ge 2$, with any $a_{i_k}\in \mathcal{B}\cup \overline{\mathcal{B}}$, $k\in \{1,\dots ,n\}$ such that

1. 

$a_{i_1}=e_i$

2. 

$$\mathfrak{r}(\left\{a_{i_1}\right\},a_{i_2}):=J_1\ne \varnothing$$

$$\mathfrak{r}(J_1,a_{i_3}):=J_2\ne \varnothing$$

$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮$

$$\mathfrak{r}(J_{n-2},a_{i_n}):=J_{n-1}\ne \varnothing .$$

3. 

$e_j\in J_{n-1}.$

The sequence $(a_{i_1},a_{i_2},\dots ,a_{i_n})$ is called a connection from $e_i$ to $e_j$.

We have introduced a relation in $\mathcal{B}$ that will be denoted by R. That is, $e_{i}R{e}_j$ if and only if $e_i$ is connected to $e_j$.

Lemma 1.

The relation R in $\mathcal{B}$ is symmetric.

Proof. 

We begin by observing that

$$e_k\in \mathfrak{p}(e_i,a_j)\mathrm{implies}{e}_i\in \mathfrak{p}(e_k,\overline{a_j})$$

(2)

for any $e_i,e_k\in \mathcal{B}$ and $a_j\in \mathcal{B}\cup \overline{\mathcal{B}}$.

To show this fact, we have to distinguish two cases:

If $a_j\in \mathcal{B}$, since $e_k\in \mathfrak{p}(e_i,a_j)$ implies $p_k\left(e_i{a}_j\right)\ne 0$ or $p_k\left(a_j{e}_i\right)\ne 0,$ we obtain in both cases that

$$e_i\in \{e_r\in \mathcal{B}:p_k\left(e_r{a}_j\right)\ne 0\}\cup \{e_s\in \mathcal{B}:p_k\left(a_j{e}_s\right)\ne 0\}=\mathfrak{p}(e_k,\overline{a_j}).$$

Where $a_j\in \overline{\mathcal{B}}$, we have $e_k\in \mathfrak{p}(e_i,a_j)$ gives us either

$$e_k\in \{e_r\in \mathcal{B}:p_i\left(e_r\overline{a_j}\right)\ne 0\}$$

or

$$e_k\in \{e_s\in \mathcal{B}:p_i\left(\overline{a_j}{e}_s\right)\ne 0\}.$$

In both possibilities we obtain $e_i\in \mathfrak{p}(e_k,\overline{a_j})$, as desired.

We also have the fact

$$e_k\in \mathfrak{q}(e_i,a_j)\mathrm{implies}{e}_i\in \mathfrak{q}(e_k,\overline{a_j}).$$

(3)

for any $e_i,e_k\in \mathcal{B}$ and $a_j\in \mathcal{B}\cup \overline{\mathcal{B}}$.

To verify it, we have (as above) to distinguish two cases:

In the first one, $a_j\in \mathcal{B}$, while in the second one, $a_j\in \overline{\mathcal{B}}:$

In the case $a_j\in \mathcal{B}$, since $e_k\in \mathfrak{q}(e_i,a_j)$, we obtain $a_j=e_k$ and $\beta (e_i,e_k)\ne 0$ or $\beta (e_k,e_i)\ne 0$. In both cases,

$$e_i\in \{e_r\in \mathcal{B}:\beta (e_k,e_r)\ne 0\}\cup \{e_s\in \mathcal{B}:\beta (e_s,e_k)\ne 0\}=\mathfrak{q}(e_k,\overline{e_k})=\mathfrak{q}(e_k,\overline{a_j}).$$

In the case $a_j\in \overline{\mathcal{B}}$, as $e_k\in \mathfrak{q}(e_i,a_j)$, we deduce $a_j=\overline{e_i}$ and

$$e_k\in \{e_r\in \mathcal{B}:\beta (e_i,e_r)\ne 0\}\cup \{e_s\in \mathcal{B}:\beta (e_s,e_i)\ne 0\}.$$

From here,

$$e_i\in \mathfrak{q}(e_k,e_i)=\mathfrak{q}(e_k,\overline{a_j}).$$

From Equations (2) and (3), we can assert that

$$e_k\in \mathfrak{r}(\left\{e_i\right\},a_j)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{e}_i\in \mathfrak{r}(\left\{e_k\right\},\overline{a_j}).$$

(4)

for any $e_i,e_k\in \mathcal{B}$ and $a_j\in \mathcal{B}\cup \overline{\mathcal{B}}$. Indeed, $e_k\in \mathfrak{r}(\left\{e_i\right\},a_j)$ gives us either $e_k\in \mathfrak{p}(e_i,a_j)$ or $e_k\in \mathfrak{q}(e_i,a_j)$. In the first case, Equation (2) shows $e_i\in \mathfrak{p}(e_k,\overline{a_j})$, while Equation (3) allows us to assert in the second case that $e_i\in \mathfrak{q}(e_k,\overline{a_j}).$ Hence, $e_i\in \mathfrak{r}(\left\{e_k\right\},\overline{a_j})$ in any case. The same argument proves the converse.

Suppose now that

$$(a_{i_1},a_{i_2},\dots ,a_{i_n})$$

is a connection from $e_i$ to $e_j$, with $e_i,e_j\in \mathcal{B}$, $e_i\ne e_j$ and $a_{i_r}\in \mathcal{B}\cup \overline{\mathcal{B}}$ for $r\in \{1,2,\dots ,n\}$.

We are going to prove that the sequence

$$(e_j,\overline{a_{i_n}},\overline{a_{i_{n-1}}},\dots ,\overline{a_{i_2}})$$

is a connection from $e_j$ to $e_i$:

There are

$$e_{k_1},e_{k_2},\dots ,e_{k_{n-2}}\in \mathcal{B}$$

such that

$$e_{k_1}\in \mathfrak{r}(\left\{e_i\right\},a_{i_2}),$$

(5)

$$e_{k_2}\in \mathfrak{r}(\left\{e_{k_1}\right\},a_{i_3}),$$

(6)

$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮$

$$e_{k_{n-2}}\in \mathfrak{r}(\left\{e_{k_{n-3}}\right\},a_{i_{n-1}}),$$

(7)

$$e_j\in \mathfrak{r}(\left\{e_{k_{n-2}}\right\},a_{i_n}).$$

(8)

By applying Equation (4) to Equations (8)–(5), in this order, we obtain

$$e_{k_{n-2}}\in \mathfrak{r}(\left\{e_j\right\},\overline{a_{i_n}}),$$

$$e_{k_{n-3}}\in \mathfrak{r}(\left\{e_{k_{n-2}}\right\},\overline{a_{i_{n-1}}}),$$

$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮$

$$e_{k_1}\in \mathfrak{r}(\left\{e_{k_2}\right\},\overline{a_{i_3}}),$$

$$e_i\in \mathfrak{r}(\left\{e_{k_1}\right\},\overline{a_{i_2}}).$$

From here we have that the sequence

$$(e_j,\overline{a_{i_n}},\overline{a_{i_{n-1}}},\dots ,\overline{a_{i_2}})$$

is a connection from $e_j$ to $e_i$, as desired. Consequently, the relation R is symmetric. □

Proposition 1.

The relation R in $\mathcal{B}$ is an equivalence relation.

Proof. 

By Definition 1, the relation R is reflexive, and by Lemma 1, R is symmetric.

From here, we just have to verify the transitivity character of R. To do that, take $e_i,e_j,e_k\in \mathcal{B}$ such that $e_{i}R{e}_j$ and $e_{j}R{e}_k$. In the case $e_i=e_j$ or $e_j=e_k$, it is clear that $e_{i}R{e}_k$. Therefore, suppose $e_i\ne e_j$ and $e_j\ne e_k$. Hence, there are

$$(a_{i_1},a_{i_2},\dots ,a_{i_n}),$$

a connection from $e_i$ to $e_j$, and

$$(b_{i_1},b_{i_2},...,b_{i_m}),$$

a connection from $e_j$ to $e_k$. It is easy to verify that the sequence

$$(a_{i_1},a_{i_2},\dots ,a_{i_n},b_{i_2},\dots ,b_{i_m})$$

is a connection from $e_i$ to $e_k.$ Hence, R is transitive. □

By the above Proposition, we can introduce the quotient set

$$\mathcal{B}/R=\{\left[e_i\right]:e_i\in \mathcal{B}\},$$

(9)

where $\left[e_i\right]$ is the set of elements in $\mathcal{B}$, which are connected to $e_i$.

Now, we can associate with any $\left[e_i\right]\in \mathcal{B}/R$ the linear subspace

$${\mathfrak{I}}_{\left[e_i\right]}:=\underset{e_j\in \left[e_i\right]}{⨁}\mathbb{K}{e}_j.$$

(10)

Observe that ${\mathfrak{I}}_{\left[e_i\right]}$ admits as a linear basis to

$${\mathcal{B}}_{{\mathfrak{I}}_{\left[e_i\right]}}:=\{e_j:e_j\in \left[e_i\right]\}\subset \mathcal{B},$$

and that we can take the bilinear form

$${\beta |}_{{\mathfrak{I}}_{\left[e_i\right]}\times {\mathfrak{I}}_{\left[e_i\right]}}:{\mathfrak{I}}_{\left[e_i\right]}\times {\mathfrak{I}}_{\left[e_i\right]}\to \mathbb{K}.$$

We will consider the triplet

$$({\mathfrak{I}}_{\left[e_i\right]},{\mathcal{B}}_{{\mathfrak{I}}_{\left[e_i\right]}},\beta {|}_{{\mathfrak{I}}_{\left[e_i\right]}\times {\mathfrak{I}}_{\left[e_i\right]}}),$$

which will be denoted, for short, as ${\mathfrak{I}}_{\left[e_i\right]}.$

Lemma 2.

Any ${\mathfrak{I}}_{\left[e_i\right]}$, $\left[e_i\right]\in \mathcal{B}/R$, is an ideal of $A.$

Proof. 

First, observe that ${\mathfrak{I}}_{\left[e_i\right]}{\mathfrak{I}}_{\left[e_j\right]}=0$ when $\left[e_i\right]\ne \left[e_j\right]$. Indeed, in the case ${\mathfrak{I}}_{\left[e_i\right]}{\mathfrak{I}}_{\left[e_j\right]}\ne 0$, there would be $e_k\in {\mathfrak{I}}_{\left[e_i\right]}$ and $e_r\in {\mathfrak{I}}_{\left[e_j\right]}$ such that $0\ne e_k{e}_r=x$. From here, there is an $e_s\in \mathcal{B}$ such that $p_s\left(e_k{e}_r\right)\ne 0$. Hence, $(e_k,e_r,\overline{e_k})$ is a connection from $e_k$ to $e_r$. Then $\left[e_i\right]=\left[e_j\right]$ is a contradiction.

Second, we have that ${\mathfrak{I}}_{\left[e_i\right]}{\mathfrak{I}}_{\left[e_i\right]}\subset {\mathfrak{I}}_{\left[e_i\right]}$ for any ${\mathfrak{I}}_{\left[e_i\right]}\in \mathcal{B}/R$. Indeed, in the case $0\ne e_k{e}_r=y$ for some $e_k,e_r\in {\mathfrak{I}}_{\left[e_i\right]}$, if we write $y={\displaystyle \sum _{s\in 1}^t}{\lambda }_s{e}_s$ with any $0\ne {\lambda }_s\in \mathbb{K}$ and any $e_s\in \mathcal{B},$ we have that ${\mathfrak{p}}_s\left(e_k{e}_r\right)\ne 0$ for any $s\in \{1,\dots ,t\}$. From here, $(e_k,e_r)$ is a connection from $e_k$ to any $e_s$ for each $s\in \{1,\dots ,t\}$. We obtain that any $e_s\in \left[e_k\right]=\left[e_i\right]$, so $y\in {\mathfrak{I}}_{\left[e_i\right]}$, as desired.

From the above, any ${\mathfrak{I}}_{\left[e_i\right]}$ is an ideal of A. □

Theorem 1.

Any based algebra with a bilinear form $(A,\mathcal{B},\beta )$ decomposes as the orthogonal direct sum of the family of irreducible ideals $\{{\mathfrak{I}}_{\left[e_i\right]}$, $\left[e_i\right]\in \mathcal{B}/R\}$. That is

$$A=\underset{\left[e_i\right]\in \mathcal{B}/R}{⨁}{\mathfrak{I}}_{\left[e_i\right]}$$

(11)

with

$$\beta ({\mathfrak{I}}_{\left[e_i\right]},{\mathfrak{I}}_{\left[e_j\right]})=0$$

when $\left[e_i\right]\ne \left[e_j\right].$

Proof. 

The fact that A is the direct sum of the family of ideals $\{{\mathfrak{I}}_{\left[e_i\right]}:\left[e_i\right]\in \mathcal{B}/R\}$ is a consequence of Equations (9) and (10) and Lemma 2.

The orthogonality of two different ideals ${\mathfrak{I}}_{\left[e_i\right]},{\mathfrak{I}}_{\left[e_j\right]}$ above can be seen as follows:

Suppose there is an $e_t\in {\mathfrak{I}}_{\left[e_i\right]}$ and $e_r\in {\mathfrak{I}}_{\left[e_j\right]}$ such that $\beta (e_t,e_r)\ne 0$. Then,

$$\mathfrak{q}(e_t,e_r)=\left\{e_r\right\},$$

so $(e_t,e_r)$ is a connection from $e_t$ to $e_r$. From here,

$${\mathfrak{I}}_{\left[e_i\right]}={\mathfrak{I}}_{\left[e_t\right]}={\mathfrak{I}}_{\left[e_r\right]}={\mathfrak{I}}_{\left[e_j\right]},$$

a contradiction.

Let us now show that any ${\mathfrak{I}}_{\left[e_i\right]}$ is irreducible. Suppose there is a decomposition ${\mathfrak{I}}_{\left[e_i\right]}=I\oplus J$ where $(I,{\mathcal{B}}_I,{\beta }_{I\times I})$ and $(J,{\mathcal{B}}_J,{\beta }_{J\times J})$ are orthogonal nonzero ideals of ${\mathfrak{I}}_{\left[e_i\right]}$. Observe that necessarily $\left[e_i\right]$ is the disjoint union

$$\left[e_i\right]={\mathcal{B}}_I\cup {\mathcal{B}}_J.$$

(12)

If we choose $e_i\in B_I$ and $e_j\in B_J$, taking into account the orthogonality of I and J, we can take a connection $(e_i,a_{i_2},\dots ,a_n)$ from $e_i$ to $e_j$ with any $a_{i_r}\in \mathcal{B}\cup \overline{\mathcal{B}}$ in such a way that we have one of the following:

(1) $a_{i_2}\in \mathcal{B}$. Then

$$0\ne e_i{a}_{i_2}=\sum _{s=1}^p{\lambda }_s{e}_{i_s}\in I,$$

$0\ne {\lambda }_s\in \mathbb{K}$ and $e_{i_s}\in \mathcal{B},$ or

$$0\ne a_{i_2}{e}_i=\sum _{t=1}^q{\delta }_t{e}_{j_t}\in I,$$

$0\ne {\delta }_t\in \mathbb{K}$ and $e_{j_t}\in \mathcal{B}$. Equation (12) means that, in the first case, any $e_{i_s}\in I$, $s\in \{1,\dots ,p\}$ and that $e_{j_t}\in I$, $t\in \{1,\dots ,q\}$ in the second case.

(2) $a_{i_2}\in \overline{\mathcal{B}}$. Then Equation (12) shows again that

$$\{e_s:p_i\left(e_s\overline{a_{i_2}}\right)\ne 0\}\cup \{e_t:p_i\left(\overline{a_{i_2}}{e}_t\right)\ne 0\}\subset I.$$

Observe that, in any case, $\mathfrak{p}(e_i,a_{i_2})\subset I.$ We also have $\mathfrak{q}(e_i,a_{i_2})\subset I$ as a consequence of the fact that, in the case $e_k\in \mathfrak{q}(e_i,a_{i_2})$, $\beta (e_i,e_k)\ne 0$ or $\beta (e_k,e_i)\ne 0$ and that $\beta (I,J)=\beta (J,I)=0$ when $I\ne J$.

By iterating this argument with the above connection

$$(e_i,a_{i_2},\dots ,a_n),$$

we conclude that $e_j\in I$, a contradiction. Hence, ${\mathfrak{I}}_{\left[e_i\right]}$ is irreducible. □

One of the most interesting facts concerning Theorem 1 is that no identity is required for the product of the algebra. That is, Theorem 1 not only holds for commutative, associative, Lie, Jordan, Leibniz, etc. algebras, but also for algebras which do not belong to any class of algebra (defined by identities, or by another property as evolution algebras).

We are going to present two examples. The first one shows an application of Theorem 1 to a totally arbitrary based algebra with a bilinear form (in the sense of the previous paragraph), while the second one is focused on the role that the bilinear form $\beta :A\times A\to \mathbb{K}$ plays in the construction developed in Theorem 1:

Example 1.

Let the 13-dimensional real algebra A with linear basis

$$\mathcal{B}=\{e_1,e_2,\dots ,e_{13}\}$$

and non-zero products among the elements of $\mathcal{B}$ given by

$$e_1{e}_5=2e_5-e_{12},$$

$$e_5{e}_1=-7e_5+4e_2-6e_3,$$

$$e_8{e}_1=7e_1+e_2-e_3+6e_8,$$

$$e_1{e}_8=9e_8,$$

$$e_5{e}_8=e_1,$$

$$e_8{e}_5=4e_2,$$

$$e_5{e}_5=e_{12}-e_3,$$

$$e_{12}{e}_{12}=e_5+e_2-e_3,$$

$$e_3{e}_3=e_2+e_5,$$

$$e_2{e}_2=e_3,$$

$$e_9{e}_9=-5e_9-5e_{13},$$

$$e_{13}{e}_9=e_9+7e_{13},$$

$$e_4{e}_4=e_7,$$

$$e_7{e}_7=e_7-e_4,$$

$$e_{10}{e}_{10}=e_6,$$

$$e_6{e}_6=5e_6+10e_{10},$$

where the remaining products among elements of $\mathcal{B}$ are zero.

The algebra A is neither commutative, nor associative, nor Lie, nor Jordan.

In A, we consider the bilinear form

$$\beta :A\times A\to \mathbb{R}$$

defined by

$$\beta (e_1,e_5)=-6,$$

$$\beta (e_5,e_8)=7,$$

$$\beta (e_8,e_8)=-3,$$

$$\beta (e_3,e_2)=1,$$

$$\beta (e_4,e_7)=9,$$

$$\beta (e_9,e_{13})=-7,$$

$$\beta (e_{12},e_{12})=16,$$

$$\beta (e_{11},e_{11})=-1,$$

the remaining products, (through β), among elements of the bases being zero.

Then $(A,\mathcal{B},\beta )$ is a based algebra with a bilinear form.

If we introduce the equivalence relation R on $\mathcal{B}$, (see Definition 1), we obtain the quotient set:

$$\mathcal{B}/R=\{\left[e_i\right]:e_i\in \mathcal{B}\}=\{\left[e_1\right],\left[e_4\right],\left[e_6\right],\left[e_9\right],\left[e_{11}\right]\},$$

where

$$\left[e_1\right]=\{e_1,e_2,e_3,e_5,e_8,e_{12}\},$$

$$\left[e_4\right]=\{e_4,e_7\},$$

$$\left[e_6\right]=\{e_6,e_{10}\},$$

$$\left[e_9\right]=\{e_9,e_{13}\}$$

and

$$\left[e_{11}\right]=\left\{e_{11}\right\}.$$

Theorem 1 allows us to assert that the based algebra with a bilinear form A decomposes as

$$A={\mathfrak{I}}_{\left[e_1\right]}\oplus {\mathfrak{I}}_{\left[e_4\right]}\oplus {\mathfrak{I}}_{\left[e_6\right]}\oplus {\mathfrak{I}}_{\left[e_9\right]}\oplus {\mathfrak{I}}_{\left[e_{11}\right]},$$

where any ${\mathfrak{I}}_{\left[e_i\right]}$, $i\in \{1,4,6,9,11\}$, is an ideal of A with basis ${\mathcal{B}}_{{\mathfrak{I}}_{\left[e_i\right]}}=\left[e_i\right]$ and where

$$\beta ({\mathfrak{I}}_{\left[e_i\right]},{\mathfrak{I}}_{\left[e_j\right]})=0$$

when $\left[e_i\right]\ne \left[e_j\right].$

Example 2.

Let the 7-dimensional real algebra A with basis

$$\mathcal{B}=\{e_1,e_2,\dots ,e_7\}$$

and non-zero products among the elements of $\mathcal{B}$ given by

$$e_1{e}_2=3e_1+e_2,$$

$$e_2{e}_2=5e_1,$$

$$e_4{e}_4=-6e_4.$$

where the remaining products among elements of $\mathcal{B}$ are zero.

In A, we consider the bilinear form

$$\beta :A\times A\to \mathbb{R}$$

defined by

$$\beta (e_1,e_2)=4,$$

$$\beta (e_2,e_3)=6,$$

$$\beta (e_4,e_4)=3,$$

$$\beta (e_5,e_4)=-3,$$

$$\beta (e_6,e_7)=1,$$

the remaining products, (through β), among elements of the bases being zero.

Then $(A,\mathcal{B},\beta )$ is a based algebra with a bilinear form.

If we introduce the equivalence relation R on $\mathcal{B}$, (see Definition 1), we obtain the quotient set:

$$\mathcal{B}/R=\{\left[e_i\right]:e_i\in \mathcal{B}\}=\{\left[e_1\right],\left[e_4\right],\left[6_6\right]\},$$

where

$$\left[e_1\right]=\{e_1,e_2,e_3\},$$

$$\left[e_4\right]=\{e_4,e_5\},$$

and

$$\left[e_6\right]=\{e_6,e_7\}.$$

By Theorem 1, we obtain that the based algebra with a bilinear form A decomposes as

$$A={\mathfrak{I}}_{\left[e_1\right]}\oplus {\mathfrak{I}}_{\left[e_4\right]}\oplus {\mathfrak{I}}_{\left[e_6\right]},$$

with each ${\mathfrak{I}}_{\left[e_i\right]}$, $i\in \{1,4,6\}$, an ideal of A with basis ${\mathcal{B}}_{{\mathfrak{I}}_{\left[e_i\right]}}=\left[e_i\right]$ and where

$$\beta ({\mathfrak{I}}_{\left[e_i\right]},{\mathfrak{I}}_{\left[e_j\right]})=0$$

when $\left[e_i\right]\ne \left[e_j\right].$

3. Interaction with Graph Theory

In this section, we are going to associate a directed graph with any based algebra with a bilinear form $(A,\mathcal{B},\beta )$, in such a way that the decomposition obtained in Theorem 1 can be easily recovered from this graph.

First, we recall that a (directed) graph is a pair $(V,E)$ where V is a (non-empty) set of vertices and $E\subset V\times V$ a set of (directed) edges connecting the vertices. In the case $(v_1,v_2)\in E$, we say that $(v_1,v_2)$ is an edge from $v_1$ to $v_2$.

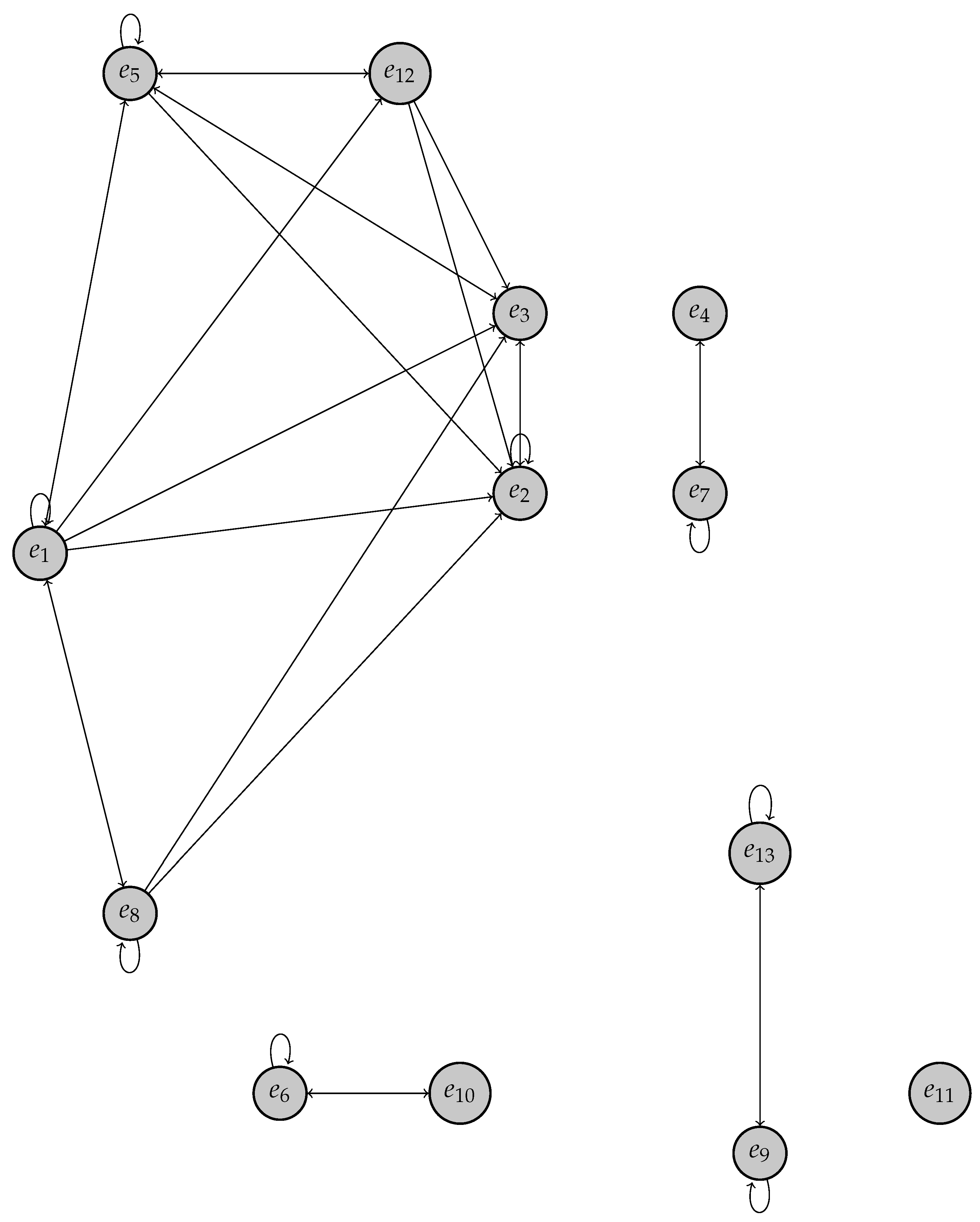
Definition 2.

Let $(A,\mathcal{B},\beta )$ be a based algebra with a bilinear form. The (directed) graph associated with $(A,\mathcal{B},\beta )$ is

$$\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right):=(V,E),$$

where $V=\mathcal{B}$ and

$$E=\{(e_i,e_r)\in V\times V:\mathrm{either}{p}_r\left(e_i{e}_j\right)\ne 0\mathrm{or}{p}_r\left(e_j{e}_i\right)\ne 0$$

$$\mathrm{for}\mathrm{some}{e}_j\in \mathcal{B}\}\cup$$

$$\{(e_i,e_r)\in V\times V:\beta (e_i,e_r)\ne 0\}.$$

Example 3.

For the based algebra with a bilinear form of Example 1, its associated graph is represented in Figure 1.

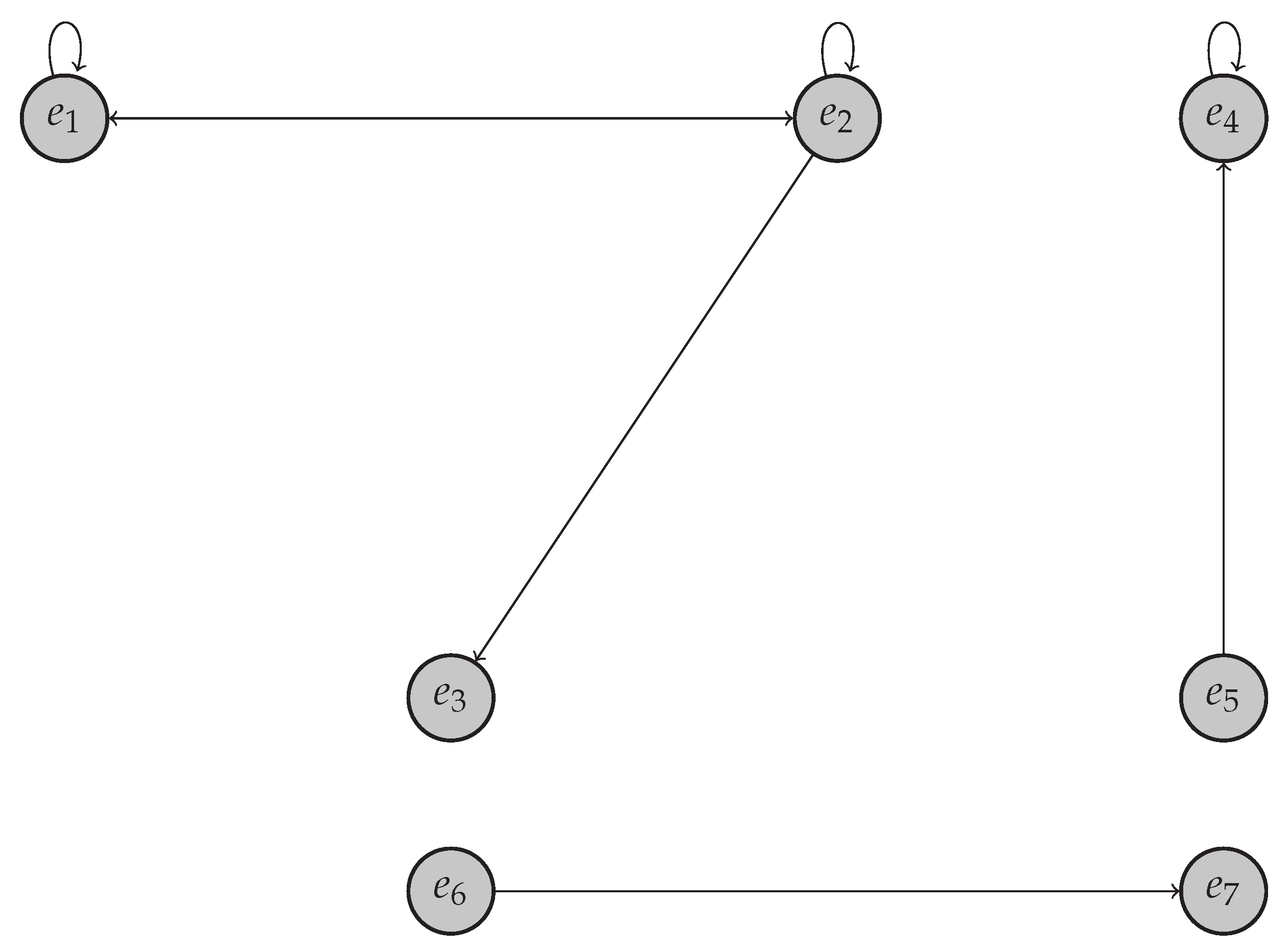
Example 4.

For the based algebra with a bilinear form of Example 2, its associated graph is represented in Figure 2.

We are going to provide an interpretation of the decomposition of a based algebra with a bilinear form $(A,\mathcal{B},\beta )$ given in Theorem 1, taking into account the above graph $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$ associated with $(A,\mathcal{B},\beta )$.

First we recall (see for instance [1]) that, given two vertices $v_i,v_j\in V$ of a directed graph $(V,E)$, an undirected path from $v_i$ to $v_j$ is an ordered family of vertices $\{v_{i_1},\dots ,v_{i_n}\}\subset V$ with $v_{i_1}=v_i$, $v_{i_n}=v_j$, and such that either $(v_{i_r},v_{i_{r+1}})\in E$ or $(v_{i_{r+1}},v_{i_r})\in E$, for $1\le r\le n-1$.

A subset of vertices $C\subset V$ is said to be connected if either C is just formed by one vertex or there is an undirected path from $v_i$ to $v_j$ for any $v_i,v_j\in C$.

A subgraph which is maximal with respect to the property of having all of its vertices connected is called a connected component of the graph.

Theorem 2.

Let $(A,\mathcal{B},\beta )$ be a based algebra with a bilinear form and consider

$$A=\underset{\left[e_i\right]\in \mathcal{B}/R}{⨁}{\mathfrak{I}}_{\left[e_i\right]}$$

(13)

its decomposition as an orthogonal direct sum of ideals given in Theorem 1. Let $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right):=(V,E)$ the associated (directed) graph corresponding to $(A,\mathcal{B},\beta )$. The following assertions hold:

1. 

For each $\left[e_i\right]\in \mathcal{B}/R$ there is only one connected component $C_{{\mathfrak{I}}_{\left[e_i\right]}}$ in $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$ such that the set of vertices in $C_{{\mathfrak{I}}_{\left[e_i\right]}}$ is $\{e_j\in \mathcal{B}:e_j\in \left[e_i\right]\}.$

2. 

For any connected component $C=(V_C,E_C)$, there is only one ideal ${\mathfrak{I}}_{\left[e_i\right]}$ in the decomposition given by Equation (13) such that $V_C=\{e_j\in \mathcal{B}:e_j\in \left[e_i\right]\}.$

Proof. 

(1). Fix some $\left[e_i\right]\in \mathcal{B}/R$. For any $e_j\in \left[e_i\right]$ with $e_j\ne e_i$, we have that $e_{i}R{e}_j$ (see Definition 1), so there is a connection

$$(e_i,a_{i_2},\dots ,a_{i_n}),$$

(14)

$n\ge 2$, from $e_i$ to $e_j$.

In the case $a_{i_2}\in \mathcal{B},$ either $e_i{a}_{i_2}\ne 0$ or $a_{i_2}{e}_i\ne 0$. Suppose $0\ne e_i{a}_{i_2}={\displaystyle \sum _{k=1}^m}{\lambda }_k{e}_k$ with ${\lambda }_k\in \mathbb{K}$, ${\lambda }_k\ne 0$ and $e_k\in \mathcal{B}$. Then there is an edge from $e_i$ to $e_k$ in $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$, for any $k\in \{1,\dots ,m\}$. In the case $a_{i_2}{e}_i\ne 0$ we can argue in a similar way.

In the case $a_{i_2}\in \overline{\mathcal{B}},$ there is an $e_k\in \mathcal{B}$ such that either $e_k\overline{a_{i_2}}={\lambda }_i{e}_i+{\displaystyle \sum _{r=1}^m}{\lambda }_r{e}_r$ with ${\lambda }_i\ne 0$ or $\overline{a_{i_2}}{e}_k={\lambda }_j{e}_i+\sum _{t=1}^s{\lambda }_t{e}_t$ with ${\lambda }_j\ne 0$. In any case, there is an edge from $e_k$ to $e_i$ in $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right).$ That is, either there is an edge $(e_i,e_k)\in \mathrm{\Gamma }\left((A,\mathcal{B},\beta )\right)$ or an edge $(e_k,e_i)\in \mathrm{\Gamma }\left((A,\mathcal{B},\beta )\right).$

Observe that, by iterating this process along the connection given by Equation (14), we obtain that $e_j$ belongs to the same connected component of $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$ as $e_i$.

Suppose now there is an $e_k\in \mathcal{B}$ that belongs to this connected component C. Since $e_i$ and $e_k$ are in C, there is an undirected path

$$\{e_{i_1},e_{i_2},e_{i_3},\dots ,e_{i_n}\}\subset V$$

(15)

with $e_{i_1}=e_i$, $e_{i_n}=e_k$, such that either $(e_{i_r},e_{i_{r+1}})\in E$ or $(e_{i_{r+1}},e_{i_r})\in E$, for $1\le r\le n-1$. Let us show that $e_i$ is connected to $e_k$ by constructing a connection form $e_i$ to $e_k$.

In the case $(e_{i_1},e_{i_2})=(e_i,e_{i_2})\in E$, we begin our connection with the pair $(e_i,e_{i_2})$, while in the case $(e_{i_2},e_{i_1})=(e_{i_2},e_i)\in E$, we will consider the pair $(e_i,\overline{e_{i_2}})$. By looking now at $e_{i_3}$ in Equation (15), we can consider as above the triplet $(e_i,e_{i_2},e_{i_3})$ or $(e_i,e_{i_2},\overline{e_{i_3}})$ or $(e_i,\overline{e_{i_2}},e_{i_3})$ or $(e_i,\overline{e_{i_2}},\overline{e_{i_3}})$. By iterating this process with Equation (15), we can construct a connection form $e_i$ to $e_k$. Hence, the connected component of $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$ containing $e_i$ has as set of vertices $\{e_j\in \mathcal{B}:e_j\in \left[e_i\right]\}$.

Finally, since the set of connected components of a graph is a partition on it. This is unique.

(2). Given any connected component $C=(V_C,E_C)$ of $\mathrm{\Gamma }\left(\right(A,\mathcal{B},\beta \left)\right)$, by taking any $e_i\in V_C$ we can apply Item (1) to obtain that ${\mathfrak{I}}_{\left[e_i\right]}$ satisfies that $V_C=\left[e_i\right]$, being also unique. □

Theorem 2 allows us to assert that we only have to look at the graph associated with a based algebra with a bilinear form to find its decomposition as a direct sum of orthogonal ideals. This decomposition will be the one given by the connected component of the graph. We illustrate this fact in the next examples:

Example 5.

If we look at the based algebra with a bilinear form in Example 1, on the one hand, we have the decomposition as a direct sum of orthogonal ideals (see Example 1):

$$A={\mathfrak{I}}_{\left[e_1\right]}\oplus {\mathfrak{I}}_{\left[e_4\right]}\oplus {\mathfrak{I}}_{\left[e_6\right]}\oplus {\mathfrak{I}}_{\left[e_9\right]}\oplus {\mathfrak{I}}_{\left[e_{11}\right]},$$

(16)

where

$$\left[e_1\right]=\{e_1,e_2,e_3,e_5,e_8,e_{12}\},$$

$$\left[e_4\right]=\{e_4,e_7\},$$

$$\left[e_6\right]=\{e_6,e_{10}\},$$

$$\left[e_9\right]=\{e_9,e_{13}\}$$

and

$$\left[e_{11}\right]=\left\{e_{11}\right\}.$$

On the other hand, the graph associated with this based algebra with a bilinear form has five connected components (see Example 3), each one corresponding with only one of the five ideals in the decomposition given by Equation (16).

Example 6.

Consider the based algebra with a bilinear form in Example 2. First, we have the decomposition as a direct sum of orthogonal ideals (see Example 2):

$$A={\mathfrak{I}}_{\left[e_1\right]}\oplus {\mathfrak{I}}_{\left[e_4\right]}\oplus {\mathfrak{I}}_{\left[e_6\right]},$$

(17)

with

$$\left[e_1\right]=\{e_1,e_2,e_3\},$$

$$\left[e_4\right]=\{e_4,e_5\},$$

and

$$\left[e_6\right]=\{e_6,e_7\}.$$

Second, the graph associated with this based algebra with a bilinear form has three connected components (see Example 4). Observe that each one is associated with only one of the three ideals in the decomposition given by Equation (17).