Max+Sum Spanning Tree Interdiction and Improvement Problems Under Weighted l_∞ Norm

Abstract

The Max+Sum Spanning Tree (MSST) problem, with applications in secure communication systems, seeks a spanning tree T minimizing ${max}_{e\in T}w\left(e\right)+{\sum }_{e\in T}c\left(e\right)$ on a given edge-weighted undirected network $G(V,E,c,w)$, where the sets V and E are the sets of vertices and edges, respectively. The functions c and w are defined on the edge set, representing transmission cost and verification delay in secure communication systems, respectively. This problem can be solved within $O\left(\right|E|log|V\left|\right)$ time. We investigate its interdiction (MSSTID) and improvement (MSSTIP) problems under the weighted $l_{\infty }$ norm. MSSTID seeks minimal edge weight adjustments (to either c or w) to degrade network performance by ensuring the optimal MSST’s weight is at least K, while MSSTIP similarly aims to enhance performance by making the optimal MSST’s weight at most K through minimal weight modifications. These problems naturally arise in adversarial and proactive performance enhancement scenarios, respectively, where network robustness or efficiency must be guaranteed through constrained resource allocation. We first establish their mathematical models. Subsequently, we analyze the properties of the optimal value to determine the relationship between the magnitude of a given number and the optimal value. Then, utilizing binary search methods and greedy techniques, we design four algorithms with time complexity $O\left(\right|E{|}^{2}log\left|V\right|)$ to solve the above problems by modifying w or c. Finally, numerical experiments are conducted to demonstrate the effectiveness of the algorithms.

1. Introduction

The Minimum Spanning Tree (MST) problem and the Bottleneck Spanning Tree (BST) problem are classical spanning tree problems in combinatorial optimization problems. Given a simple edge-weighted connected undirected graph $G(V,E,c)$, the sets V and E are the sets of vertices and edges, respectively, and $c:E\to {\mathbb{R}}^{+}$ is an edge-weight function that assigns a positive real number to each edge $e\in E$. The MST problem seeks a spanning tree $T^{*}$ such that the total edge weight is minimized, that is, $T^{*}=arg{min}_{T\in \Gamma }{\sum }_{e\in T}c\left(e\right)$, where $\Gamma$ denotes the set of all spanning trees. Conversely, the BST problem aims to find a spanning tree $T^{*}$ such that the maximum edge weight is minimized, that is, $T^{*}=arg{min}_{T\in \Gamma }{max}_{e\in T}c\left(e\right)$. Both problems optimize network structures, with MST minimizing overall cost and BST focusing on the worst-case edge in the network.

Interdiction and improvement are important optimization problems, where the objective is to minimally adjust edge weight parameters c so that the resulting network performance under modified parameters $\overline{c}$ is either no less than or no greater than a given constant on graph $G(V,E,\overline{c})$. Many scholars have conducted extensive research on these problems on MST and BST. Hsu et al. [1] first formulated the problem of deleting k edges to maximize the weight of MST on the resulting network and established fundamental theoretical foundations. Based on this, Iwano et al. [2] developed more efficient algorithms for the single-edge case through graph traversal techniques. The theoretical complexity of the generalized problem was established by Frederickson and Solis-Oba [3]. They proved that the problem is NP-hard for arbitrary k. Shen [4] subsequently enhanced this by developing more efficient approximation algorithms, while Liang [5] focused on developing polynomial-time solutions for fixed small values of k. Furthermore, Bazgan et al. [6] proposed a new efficient algorithm and adapted it to establish an implicit enumeration algorithm based on a branch and bound procedure, which can handle significantly larger instances due to a better use of memory space. Most recently, Wei et al. [7] proposed novel integer programming formulations for this problem, including a bilevel optimization framework and cutting-plane algorithms, which provided new optimization methods to disrupt network connectivity. For the interdiction problem on BST, Abdolahzadeh et al. [8] designed polynomial-time algorithms for the problems under the weighted $l_1$ norm and sum-type Hamming distance. On the improvement front, Frederickson et al. [3] designed a polynomial-time algorithm with time complexity $O(m^2{n}^{3}log{\displaystyle \frac{n^2}{m}})$ for the improvement problem on MST under the weighted $l_1$ norm, and Zenklusen [9] proposed a constant-factor approximation algorithm. Additionally, under the sum-type Hamming distance, Frederickson and Solis-Oba [3] proved the problem is NP-hard and developed an approximation algorithm.

In networks that demand both cost efficiency and robustness, such as in secure communication systems  [10], the Max+Sum Spanning Tree (MSST) problem arises as a natural generalization of both MST and BST problems. Given a graph $G(V,E,c,w)$ with two edge weight functions—$c\left(e\right)$ representing transmission costs and $w\left(e\right)$ denoting verification delays—the MSST problem seeks a spanning tree $T^{*}$ that minimizes the combined objective ${max}_{e\in T^{*}}w\left(e\right)+{\sum }_{e\in T^{*}}c\left(e\right),$ which balances both worst-case delay and total cost across all possible spanning trees. Notice that the MST and BST problems are both special cases of the more general MSST problem. The current fastest algorithm for determining the MSST of $G(V,E,c,w)$ was proposed by Punnen and Nair [11] in $O\left(\right|E|log|V\left|\right)$ time.

The study of performance enhancement in adversarial and proactive scenarios is increasingly crucial in network optimization with the rapid expansion of modern communication networks. In adversarial scenarios, the model of the interdiction problem on MSST provides a quantitative analysis tool for protecting critical information infrastructure. By identifying vulnerable points in networks, security teams can give priority to reinforce these critical connections to enhance the overall network resilience against attacks. Conversely, from a proactive optimization perspective, one can reinforce critical connections to improve overall network performance, corresponding precisely to the improvement problem on MSST. Note that network operators can adjust overall network performance under budget constraints by optimizing bandwidth allocation (adjusting weight c) and/or reducing transmission delays (adjusting weight w).

Despite its clear practical relevance, the MSST problem has received relatively little attention in the literature. Some progress has been made on the inverse MSST problem, which aims to find minimal adjustments of edge weights (to c or/and w) under specific norms to make a given spanning tree $T^0$ optimal [12]. When adjusting c under the weighted $l_{\infty }$ norm, Guan et al. [13] transformed the problem into a linear fractional combinatorial optimization problem and designed an algorithm in $O(m^{2}logn)$ time. Under the weighted $l_1$ norm, Zuo et al. [14] proposed a column generation algorithm to solve a special case of the problem, in which the minimum relative cost in each iteration can be transformed into solving a MSST problem under new parameters and can be solved in polynomial time. Further, Guan et al. [15] reformulated the problem as a linear program with an exponential number of constraints and solved it via column generation. For the weighted bottleneck Hamming distance, Guan et al. [16] proposed a $O\left(m{log}^{2}n\right)$ time algorithm based on a binary search method and showed the NP-hardness of the problem under the unit-sum Hamming distance. When adjusting w, Jia et al. [17] proposed a $O(m^{2}logn)$ time algorithm based on a binary search and the greedy technique. Interdiction and improvement problems on MSST remain significantly understudied in the existing literature, highlighting a clear research gap.

We let $G(V,E,c,w)$ be a simple edge-weighted connected undirected graph, where $V=\{v_1,v_2,\cdots ,v_n\}$ and $E=\{e_1,e_2,\cdots$, $e_m\}$ are the sets of vertices and edges, respectively. And we let $c:E\to {\mathbb{R}}^{+}$ and $w:E\to {\mathbb{R}}^{+}$ be the sum-type weight and maximum weight functions, respectively. The MSST interdiction problem (MSSTID) aims at adjusting some weights of edges (for c or/and w) to minimize the total cost under some measurement such that the weight of the optimal MSST is at least K, while the MSST improvement problem (MSSTIP) similarly aims to make the weight of the optimal MSST at most K through minimal total cost of weight modifications under some measurement. This paper mainly studies problems MSSTID and MSSTIP under the weighted $l_{\infty }$ norm by modifying w or c.

In this paper, for any $e\in E$, we let $q\left(e\right)\ge 0$ denote the cost of adjusting $w\left(e\right)$ or $c\left(e\right)$ by one unit. Note that if there is an edge $e\in E$ with $q\left(e\right)=0$, indicating zero cost, we can modify its weight directly to either its upper or lower bound to obtain a new modified graph, in which the relevant problem can then be solved. For instance, in the problem (MSSTID) under weighted $l_{\infty }$ norm by modifying w, we can set all zero-cost edges to their upper bounds and solve the problem in this modified graph. Therefore, without loss of generality, in this paper, we only consider the case when $q\left(e\right)>0$ for all $e\in E$.

For convenience, we define the following useful notations in this paper. We let $c^s\left(T\right):={\sum }_{e\in T}c\left(e\right)$ and $w\left(T\right):={max}_{e\in T}w\left(e\right)$ be the sum of weight c and the maximum weight of w on a tree T in brief. We let $f(w,c,T):=c^s\left(T\right)+w\left(T\right)$ be the combined metric denoted by $e_T^w:=argma{x}_{e\in T}w\left(e\right)$ any one edge with the maximum weight of w on a tree T.

Here is a property frequently used in this paper regarding the intersections of several piecewise linear functions.

Lemma 1

([17]). Let $Y=\{y_i=a_i+min\{{\displaystyle \frac{x}{b_i}},c_i\}|i=1,2,...,k\}$ be a set of piecewise linear functions with x as the independent variable, where $a_i,b_i,c_i$ are constants. Let $X=[X_1,X_2,...,X_N]$ be the set of x-coordinates corresponding to all intersection points of the lines in the family $Y^{\prime }=\{y=a_i+c_i,y=a_i+{\displaystyle \frac{x}{b_i}}|i=1,2,...,k\}$, sorted such that $X_j<X_{j+1},j=1,2,...,N-1$. For any interval $[X_j,X_{j+1}]$, let ${\widehat{x}}_j={\displaystyle \frac{X_j+X_{j+1}}{2}}$. If $y_{i_1}\left({\widehat{x}}_j\right)\le y_{i_2}\left({\widehat{x}}_j\right)\le \cdots \le y_{i_k}\left({\widehat{x}}_j\right)$, then $y_{i_1}\left(x_j\right)\le y_{i_2}\left(x_j\right)\le \cdots \le y_{i_k}\left(x_j\right)$ holds for all $x_j\in [X_j,X_{j+1}]$.

Note: In the line family $Y^{\prime }$, if two lines coincide, that is, they are identical, do not compute their intersection point.

The following lemma characterizes the invariance of the optimal MSST under perturbations of c or w, provided that the relative ordering of the edges remains unchanged.

Lemma 2.

Let $G(V,E,c,w)$ be a simple edge-weighted connected undirected graph. Construct an auxiliary network $G(V,E_i,c,w)$ for a given $e_i\in E$, where $E_i=\{e\in E|w\left(e\right)\le w\left(e_i\right)\}$. Suppose the network $G(V,E_i,c,w)$ is connected and the spanning tree $T_{e_i}$ is the optimal MSST with $e_i$ as its maximum weight edge.

(1) If the order of every edge is the same under c and $\overline{c}$, then the spanning tree $T_{e_i}$ remains the optimal MSST in $G(V,E_i,\overline{c},w)$ with $e_i$ as the maximum weight edge.

(2) If the order of every edge is the same under w and $\overline{w}$, then the spanning tree $T_{e_i}$ remains the optimal MSST in $G(V,E_i,c,\overline{w})$ with $e_i$ as the maximum weight edge.

Proof. 

(1) Note that $T_{e_i}$ is the optimal MSST with $e_i$ as the maximum weight edge in network $G(V,E_i,c,w)$, hence $T_{e_i}$ is the minimum spanning tree under c containing the edge $e_i$. Furthermore, $T_{e_i}$ is also the minimum spanning tree under $\overline{c}$ containing the edge $e_i$ according to the Cycle Optimality Conditions for Minimum Spanning Trees (page 519 of [18]), which implies $T_{e_i}$ remains the optimal MSST in $G(V,E_i,\overline{c},w)$ with $e_i$ as the maximum weight edge. Similarly, the proof for (1) also holds for (2).    □

The paper is organized as follows. In Section 2, we solve problem MSSTID under weighted $l_{\infty }$ norm by modifying w in $O\left(\right|E{|}^{2}log\left|V\right|)$ time by a binary search method and the greedy technique based on series of necessary analysis. Building on this approach, Section 3 solves problem MSSTIP under weighted $l_{\infty }$ norm by modifying w in $O\left(\right|E{|}^{2}log\left|V\right|)$ time. In Section 4 and Section 5, we propose two algorithms both in $O\left(\right|E{|}^{2}log\left|V\right|)$ time to solve problems MSSTID and MSSTIP under weighted $l_{\infty }$ norm by modifying c, respectively. In Section 6, numerical experiments are conducted to show the efficiency of the four algorithms. In Section 7, we draw a conclusion and put forward future research.

2. Solve Problem MSSTID_w

In this section, we study problem MSSTID under weighted $l_{\infty }$ norm by modifying w (${\mathrm{MSSTID}}_w$). For any $e\in E$, we let $q\left(e\right)>0$ denote the cost of adjusting $w\left(e\right)$ by one unit and $u\left(e\right)\ge 0$ represent the upper limit for increasing $w\left(e\right)$. The mathematical model is as follows:

$$\begin{array}{ccc}& {min}_{\overline{w}}& \underset{e\in E}{max}q\left(e\right)(\overline{w}\left(e\right)-w\left(e\right))\hfill \end{array}$$

$$\begin{array}{ccc}& s.t.& \underset{e\in T}{max}\overline{w}\left(e\right)+\sum _{e\in T}c\left(e\right)\ge K,\forall T\in \Gamma ,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & w\left(e\right)\le \overline{w}\left(e\right)\le w\left(e\right)+u\left(e\right),\forall e\in E.\hfill \end{array}$$

(2)

For any given $Q\ge 0$, we define a vector $w_Q$ as follows:

$$\begin{array}{c}\hfill w_Q\left(e\right):=w\left(e\right)+min\left\{{\displaystyle \frac{Q}{q\left(e\right)}},u\left(e\right)\right\},e\in E.\end{array}$$

(3)

Lemma 3.

The vector $w_Q$ defined as (3) is a feasible solution to problem ${MSSTID}_w$ if and only if $Q\ge Q^{*}$, where $Q^{*}$ is the optimal value of problem ${MSSTID}_w$. Moreover, if $Q=Q^{*}$, then $w_Q$ is an optimal solution of problem ${MSSTID}_w$.

Proof. 

Necessity: We let $w_Q$ defined as (3) be a feasible solution and let $w^{*}$ be an optimal solution of problem ${\mathrm{MSSTID}}_w$, that is, ${max}_{e\in E}q\left(e\right)(w^{*}\left(e\right)-w\left(e\right))=Q^{*}$. We show that $Q\ge Q^{*}$. We have

$$\begin{array}{c}\hfill \underset{e\in E}{max}q\left(e\right)\left(w_Q\left(e\right)-w\left(e\right)\right)=\underset{e\in E}{max}min\left\{Q,q\left(e\right)u\left(e\right)\right\}=min\left\{Q,\underset{e\in E}{max}q\left(e\right)u\left(e\right)\right\}.\end{array}$$

(4)

Hence, we have $Q\ge {max}_{e\in E}q\left(e\right)\left(w_Q\left(e\right)-w\left(e\right)\right)\ge {max}_{e\in E}q\left(e\right)\left(w^{*}\left(e\right)-w\left(e\right)\right)=Q^{*}$. Then $Q\ge Q^{*}$ holds.

Sufficiency: Suppose $w^{*}$ is an optimal solution to problem ${\mathrm{MSSTID}}_w$. We prove that for any $e\in E$, $w_Q\left(e\right)\ge w^{*}\left(e\right)$ holds. Suppose there exists $e_i\in E$, such that $w_Q\left(e_i\right)<w^{*}\left(e_i\right)$, that is, $w\left(e_i\right)+min\left\{{\displaystyle \frac{Q}{q\left(e_i\right)}},u\left(e_i\right)\right\}<w^{*}\left(e_i\right).$

(1) If ${\displaystyle \frac{Q}{q\left(e_i\right)}}>u\left(e_i\right)$, then $w\left(e_i\right)+u\left(e_i\right)<w^{*}\left(e_i\right)$, which contradicts with $w^{*}\left(e_i\right)\le w\left(e_i\right)+u\left(e_i\right)$.

(2) If ${\displaystyle \frac{Q}{q\left(e_i\right)}}\le u\left(e_i\right)$, then $w\left(e_i\right)+{\displaystyle \frac{Q}{q\left(e_i\right)}}<w^{*}\left(e_i\right)$, which implies $Q^{*}\ge q\left(e_i\right)\left(w^{*}\left(e_i\right)-w\left(e_i\right)\right)>Q.$ This contradicts with $Q^{*}\le Q$. Thus, Constraints (1) and (2) hold for the vector $w_Q$, confirming that $w_Q$ is indeed feasible.

We next show that ${max}_{e\in E}q\left(e\right)\left(w^{*}\left(e\right)-w\left(e\right)\right)=Q^{*}.$ Similar to the process in (4), we have ${max}_{e\in E}q\left(e\right)\left(w^{*}\left(e\right)-w\left(e\right)\right)=Q^{*}=min\{Q^{*},{max}_{e\in E}q\left(e\right)u\left(e\right)\}=Q^{*}$, where it is sufficient to show that $Q^{*}\le {max}_{e\in E}q\left(e\right)u\left(e\right)$ as for any edge $e\in E,$ we have $q\left(e\right)\left(w^{*}\left(e\right)-w\left(e\right)\right)\le q\left(e\right)u\left(e\right)$.

To sum up, the lemma holds.    □

By Conditions (1) and (2), the following lemma immediately holds.

Lemma 4.

Define $w_u:=w+u$. Let $T_w^{*}$ and $T_{w_u}^{*}$ be the optimal MSSTs under weights w and $w_u$, respectively. If $f(w,c,T_w^{*})\ge K$, then no adjustment is needed for problem ${MSSTID}_w$. If $f(w_u,c,T_{w_u}^{*})<K$, then problem ${MSSTID}_w$ is infeasible.

By Lemmas 3 and 4, we can determine the optimal value $Q^{*}$ by a binary search method, which can be proceeded as follows: First, we establish an upper bound $\overline{Q}$ and a lower bound $\underline{Q}$ for $Q^{*}$. Then, we evaluate the midpoint $Q_{mid}={\displaystyle \frac{\overline{Q}+\underline{Q}}{2}}$ to determine its relationship with $Q^{*}$ and update the bounds accordingly. This process is repeated until the interval length $|\overline{Q}-\underline{Q}|$ becomes smaller than a sufficiently small positive number $ϵ$. At this point, we consider $Q^{*}={\displaystyle \frac{\overline{Q}+\underline{Q}}{2}}$. Since the number of iterations depends on the precision $ϵ$, this algorithm is not strongly polynomial. To design a strongly polynomial-time algorithm, we present the following lemma.

Lemma 5.

Let $Q^{*}>0$ be the optimal objective value of problem ${MSSTID}_w$ and $w^{*}$ be the optimal solution constructed via (3). Then there exists a spanning tree $T^{*}$ and an edge $e_{T^{*}}^{w^{*}}\in T^{*}$ such that $f(w^{*},c,T^{*})=K$ and $q\left(e_{T^{*}}^{w^{*}}\right)(w^{*}\left(e_{T^{*}}^{w^{*}}\right)-w\left(e_{T^{*}}^{w^{*}}\right))=Q^{*}$, where $e_{T^{*}}^{w^{*}}=argma{x}_{e\in T^{*}}{w}^{*}\left(e\right)$.

Proof. 

(1) We prove that there exists $T\in \Gamma$ satisfying $f(w^{*},c,T)=K$. Suppose for $T\in \Gamma$, $f(w^{*},c,T)>K$. We define $E_1=\{e\in E|w^{*}\left(e\right)>w\left(e\right)\}$, $E_2=\{e\in E|w^{*}\left(e\right)=w\left(e\right)\}$, ${\delta }_1={min}_{e\in E_1}(w^{*}\left(e\right)-w\left(e\right))$, ${\delta }_2={min}_{T\in \Gamma }(f(w^{*},c,T)-K)$, $\delta =min\{{\delta }_1,{\delta }_2\}$. We construct $w^{\prime }\left(e\right)=\left\{\begin{array}{cc}{w}^{*}\left(e\right)-\delta ,\hfill & \forall e\in E_1\hfill \\ w^{*}\left(e\right),\hfill & \forall e\in E_2\hfill \end{array}\right.$. Clearly, $w^{\prime }$ remains feasible, but its objective value is strictly less than $Q^{*}$, contradicting the optimality of $Q^{*}$.

(2) We let ${\Gamma }^{*}=\{T\in \Gamma |f(w^{*},c,T)=K\}$ and $E_{{\Gamma }^{*}}^{w^{*}}=\left\{e_T^{w^{*}}\right|T\in {\Gamma }^{*}\}$. We prove there is $T^{*}\in {\Gamma }^{*}$ satisfying $q\left(e_{T^{*}}^{w^{*}}\right)(w^{*}\left(e_{T^{*}}^{w^{*}}\right)-w\left(e_{T^{*}}^{w^{*}}\right))=Q^{*}$. We assume for all $e\in E_{{\Gamma }^{*}}^{w^{*}}$, $q\left(e\right)(w^{*}\left(e\right)-w\left(e\right))<Q^{*}$ holds. We define $E_1=\{e\in E\setminus E_{{\Gamma }^{*}}^{w^{*}}|w^{*}\left(e\right)>w\left(e\right)\}$, $E_2=\{e\in E\setminus E_{{\Gamma }^{*}}^{w^{*}}|w^{*}\left(e\right)=w\left(e\right)\}$, ${\delta }_1={min}_{e\in E_1}(w^{*}\left(e\right)-w\left(e\right))$, ${\delta }_2={min}_{T\in \Gamma \setminus {\Gamma }^{*}}(f(w^{*},c,T)-K)$, $\delta =min\{{\delta }_1,{\delta }_2\}$. We construct $w^{\prime }\left(e\right)=\left\{\begin{array}{cc}{w}^{*}\left(e\right)-\delta ,\hfill & \forall e\in E_1\hfill \\ w^{*}\left(e\right),\hfill & \forall e\in E_2\cup E_{{\Gamma }^{*}}^{w^{*}}\hfill \end{array}\right.$. Again, $w^{\prime }$ is feasible but yields a strictly better objective value than $Q^{*}$, leading to a contradiction.    □

We now present a strongly polynomial-time algorithm to solve this problem. The main steps are as follows: (1) If the problem is feasible and requires adjustment, we compute all x-coordinates of intersection points for the line family: $\{w_Q\left(e\right)=w\left(e\right)+u\left(e\right),w_Q\left(e\right)=w\left(e\right)+{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$. We add the upper bound ${max}_{e\in E}q\left(e\right)u\left(e\right)$ and the lower bound 0 of $Q^{*}$ to this set. (2) Using a binary search method on the constructed set, we identify the interval $(Q_a,Q_b]$ containing $Q^{*}$, where $Q_a<Q^{*}\le Q_b$. We construct $w_{Q^{\prime }}$ via (3) with $Q^{\prime }:={\displaystyle \frac{Q_a+Q_b}{2}}$. (3) We compute the bottleneck value $w_0:={min}_{T\in \Gamma }{max}_{e\in T}{w}_{Q^{\prime }}\left(e\right)$ and identify the set $E_0:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\ge w_0\}$ of critical edges. By Lemmas 1 and 5, the edge $e_{T^{*}}^{w^{*}}$ defined in Lemma 5 must be in $E_0$, so we only need to verify edges in $E_0$.

Note: For Line 25 in Algorithm 1, computing the optimal MSST with $e_i$ as maximum-weight edge can be implemented as

(1) Construct a modified sum vector $\overline{c}\left(e\right)=\left\{\begin{array}{cc}c\left(e\right),\hfill & \mathrm{if}e\ne e_i\hfill \\ c\left(e_i\right)-{\sum }_{e\in E_i}(w\left(e\right)+c\left(e\right)),\hfill & \mathrm{if}e=e_i\hfill \end{array}\right..$

(2) Compute optimal MSST ${\overline{T}}_{e_i}$ on $G(V,E_i,$$\overline{c},w_{Q_a})$, that is, ${\overline{T}}_{e_i}$ is the optimal MSST with $e_i$ as maximum-weight edge on $G(V,E_i,c,w_{Q_a})$.

Algorithm 1 An algorithm to solve problem (${\mathrm{MSSTID}}_w$): $Q^{*}:=$${\mathrm{MSSTID}}_w\left(V,E,w,c,u,q,K\right)$.

Input:  Network $G=(V,E)$, four vectors $\mathit{w},\mathit{c},\mathit{u},\mathit{q}$ and a given value $\mathit{K}$.

Output:  The optimal value $Q^{*}$.

1:  Let $w_u:=w+u$. Determine the optimal MSSTs $T_w^{*}$,$T_{w_u}^{*}$ under w and $w_u$, respectively.

2:  if $f(w,c,T_w^{*})\ge K$ then

3:     return $Q^{*}:=0.$

4:  end if

5:  if $f(w_u,c,T_{w_u}^{*})<K$ then

6:     “The problem is infeasible.”

7:  end if

8:  Compute all x-coordinates of intersection points for the line family $\{w_Q\left(e\right)=w\left(e\right)+u\left(e\right),w_Q\left(e\right)=w\left(e\right)+{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$, denoted as set $Q_s$.

9:  Let $Q_{max}:={max}_{e\in E}q\left(e\right)u\left(e\right)$, $Q_s^{\prime }:=\{0\le Q_i\le Q_{max}|Q_i\in Q_s\}\cup \{0,Q_{max}\}$.

10:  Sort elements in $Q_s^{\prime }$ in ascending order.

11:  Initialization: $a:=1$, $b:=|Q_s^{\prime }|$.

12:  while $b-a>1$ do

13:     Let $k:=\lfloor {\displaystyle \frac{a+b}{2}}\rfloor$ and $Q_k:=Q_s^{\prime }\left(k\right)$. Construct $w_{Q_k}$ via (3) and determine an optimal MSST $T_{Q_k}^{*}$.

14:     if $f(w_{Q_k},c,T_{Q_k}^{*})<K$ then

15:         Update $a:=k$.

16:     else

17:         Update $b:=k$.

18:     end if

19:  end while

20:  Let $Q^{\prime }:={\displaystyle \frac{Q_a+Q_b}{2}}$. Construct $w_{Q^{\prime }}$ and $w_{Q_a}$ via (3).

21:  Let $w_0:=\underset{T\in \Gamma }{min}\underset{e\in T}{max}{w}_{Q^{\prime }}\left(e\right)$, $E_0:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\ge w_0\}$.

22:  Initialize $Q^{*}:=0$.

23:  for each $e_i\in E_0$ do

24:     Let $E_i:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\le w_{Q^{\prime }}\left(e_i\right)\}$.

25:     Compute optimal MSST $T_{e_i}$ on $G(V,E_i,c,w_{Q_a})$ with $e_i$ as the maximum-weight edge.

26:     if $f(w_{Q_a},c,T_{e_i})<K$ then

27:         Let $\delta :=K-f(w_{Q_a},c,T_{e_i})$, ${\Delta }_Q:=\delta q\left(e_i\right)$.

28:         Update $Q^{*}:=max\{{\Delta }_Q+Q_a,Q^{*}\}$.

29:     end if

30:  end for

31:  return $Q^{*}$.

Theorem 1.

Algorithm 1 correctly solves problem ${MSSTID}_w$.

Proof. 

Lines 8–19 identify the interval $(Q_a,Q_b]$ containing the optimal value $Q^{*}$. Lemma 1 guarantees that for any $Q\in [Q_a,Q_b]$, if $w_{Q^{\prime }}\left(e_{i_1}\right)\le w_{Q^{\prime }}\left(e_{i_2}\right)\cdots \le w_{Q^{\prime }}\left(e_{i_m}\right)$ holds for $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, then $w_Q\left(e_{i_1}\right)\le w_Q\left(e_{i_2}\right)\cdots \le w_Q\left(e_{i_m}\right)$ holds. This implies the maximum-weight edge for each spanning tree remains unchanged during the approximation from $Q_a$ to $Q^{*}$. As a consequence, given an edge e and a spanning tree T, if T is optimal for $w_{Q_a}$ among the trees with e as its maximum weight edge, then it remains so during the approximation process. Notice that $w_0$ is the bottleneck value under $w_{Q^{\prime }}$ in Line 21, so that we have $e_{T^{*}}^{w^{*}}\in E_0$, where $e_{T^{*}}^{w^{*}}$ is defined in Lemma 5. From Lines 23 to 30 of Algorithm 1, we sequentially determine whether each edge $e_i\in E_0$ could possibly be $e_{T^{*}}^{w^{*}}$. First, we compute the optimal MSST $T_{e_i}$ with $e_i$ as the maximum weight edge under $w_{Q_a}$. It remains the optimal MSST in $G(V,E_i,c,w_Q)$ with $e_i$ as the maximum weight edge for any $Q\in [Q_a,Q_b]$ by Lemma 2. If $f(w_{Q_a},c,T_{e_i})<K$, it implies that edge $e_i$ might be $e_{T^{*}}^{w^{*}}$. Consequently, we need to increase the weight of this edge by the minimum cost ${\Delta }_Q$ so that under the new cost $Q_a+{\Delta }_Q$, the total weight of $T_{e_i}$ is exactly K. At this point, $Q_a+{\Delta }_Q$ serves as a lower bound for $Q^{*}$, since problem ${\mathrm{MSSTID}}_w$ requires that the sum of the maximum weight and the sum-type weight in every spanning tree must be at least K. Therefore, after the for loop ends, we obtain the optimal value $Q^{*}$. □

Theorem 2.

We can solve problem ${MSSTID}_w$ by Algorithm 1 in $O(m^{2}logn)$ time.

Proof. 

Lines 1–7 require two optimal MSST computations, costing $O(mlogn)$ time. Line 8 computes intersections of $2m$ lines in $O\left(m^2\right)$ time, with $|Q_s|=O\left(m^2\right)$. Sorting (Lines 9–10) takes $O(m^{2}logm)$. The binary search method (Lines 12–19) runs $O(\log m)$ iterations, totaling $O(mlognlogm)$. Line 21 needs $O\left(m\right)$ time to calculate the bottleneck value [19]. Lines 23–30 execute $|E_0|$ iterations with one optimal MSST computation in each iteration in $O(m^{2}logn)$. Thus, the overall time complexity is $O(m^{2}logn)$. □

3. Solve Problem MSSTIP_w

This section investigates problem MSSTIP under weighted $l_{\infty }$ norm by modifying w (${\mathrm{MSSTID}}_w$). For each $e\in E$, we let $q\left(e\right)>0$ denote the unit adjustment cost for $w\left(e\right)$ and $l\left(e\right)\ge 0$ represent the downward adjustment limit with $w\left(e\right)-l\left(e\right)\ge 0$. The mathematical formulation is

$$\begin{array}{ccc}& {min}_{\overline{w}}& \underset{e\in E}{max}q\left(e\right)(w\left(e\right)-\overline{w}\left(e\right))\hfill \end{array}$$

$$\begin{array}{ccc}& s.t.& \underset{T\in \Gamma }{min}\{\underset{e\in T}{max}\overline{w}\left(e\right)+\sum _{e\in T}c\left(e\right)\}\le K,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & w\left(e\right)-l\left(e\right)\le \overline{w}\left(e\right)\le w\left(e\right),\forall e\in E.\hfill \end{array}$$

(6)

For any $Q\ge 0$, we define the weight vector $w_Q$ as follows:

$$\begin{array}{c}\hfill w_Q\left(e\right):=w\left(e\right)-min\left\{{\displaystyle \frac{Q}{q\left(e\right)}},l\left(e\right)\right\},e\in E.\end{array}$$

(7)

Similar to Lemma 3, the following lemma holds:

Lemma 6.

The vector $w_Q$ as (7) is feasible for ${MSSTID}_w$ if and only if $Q\ge Q^{*}$, where $Q^{*}$ is the optimal value. Moreover, if $Q=Q^{*}$, then $w_Q$ is an optimal solution of problem ${MSSTID}_w$.

By Conditions (5) and (6), the following lemma immediately holds.

Lemma 7.

Define $w_l:=w-l$. Let $T_w^{*}$ and $T_{w_l}^{*}$ be the optimal MSSTs under weights w and $w_l$, respectively. If $f(w,c,T_w^{*})\le K$, then no weight adjustment is required for problem ${MSSTID}_w$. If $f(w_l,c,T_{w_l}^{*})>K$, then problem ${MSSTID}_w$ is infeasible.

Building upon Lemma 6, we could employ a binary search method to determine the optimal value $Q^{*}$. However, since the number of iterations depends on the precision parameter $ϵ$, this approach does not yield a strongly polynomial-time algorithm. To develop a strongly polynomial-time algorithm, we establish the following key lemma:

Lemma 8.

Let $Q^{*}>0$ be the optimal objective value of problem ${MSSTID}_w$ and $w^{*}$ be the optimal solution constructed via (7). Then there exists a spanning tree $T^{*}$ and an edge $e_{T^{*}}^{w^{*}}\in T^{*}$ satisfying $f(w^{*},c,T^{*})=K$, and $q\left(e_{T^{*}}^{w^{*}}\right)(w\left(e_{T^{*}}^{w^{*}}\right)-w^{*}\left(e_{T^{*}}^{w^{*}}\right))=Q^{*}$.

Proof. 

(1) We first prove that $f(w^{*},c,T)\ge K$ for all $T\in \Gamma$. We suppose there is $T_0\in \Gamma$ such that $f(w^{*},c,T_0)<K$. We define $E_1=\{e\in E|w^{*}\left(e\right)<w\left(e\right)\}$, $E_2=\{e\in E|w^{*}\left(e\right)=w\left(e\right)\}$, ${\delta }_1={min}_{e\in E_1}\{w\left(e\right)-w^{*}\left(e\right)\}$, ${\delta }_2=K-f(w^{*},c,T_0)$, $\delta =min\{{\delta }_1,{\delta }_2\}$. We construct $w^{\prime }\left(e\right)=\left\{\begin{array}{cc}{w}^{*}\left(e\right)+\delta ,\hfill & e\in E_1\hfill \\ w^{*}\left(e\right),\hfill & e\in E_2\hfill \end{array}\right.,$ which remains feasible but achieves a better objective value than $Q^{*}$, contradicting with the optimality of $Q^{*}$. Thus, there is $T\in \Gamma$ with $f(w^{*},c,T)=K$.

(2) Next, we let ${\Gamma }^{*}=\{T\in \Gamma |f(w^{*},c,T)=K\}$ and $E_{{\Gamma }^{*}}^{w^{*}}=\left\{e_T^{w^{*}}\right|T\in {\Gamma }^{*}\}$. We show there is $T^{*}\in {\Gamma }^{*}$ satisfying $q\left(e_{T^{*}}^{w^{*}}\right)(w\left(e_{T^{*}}^{w^{*}}\right)-w^{*}\left(e_{T^{*}}^{w^{*}}\right))=Q^{*}$. We assume by contradiction that $(w\left(e\right)-w^{*}\left(e\right))q\left(e\right)<Q^{*}$ for all $e\in E_{{\Gamma }^{*}}^{w^{*}}$. We define $E_1=\{e\in E\setminus E_{{\Gamma }^{*}}^{w^{*}}|w^{*}\left(e\right)<w\left(e\right)\}$, $E_2=\{e\in E\setminus E_{{\Gamma }^{*}}^{w^{*}}|w^{*}\left(e\right)=w\left(e\right)\}$, ${\delta }_1={min}_{e\in E_1}\{w\left(e\right)-w^{*}\left(e\right)\}$, ${\delta }_2={min}_{T\in {\Gamma }^{*}}{min}_{e\in T\setminus \left\{e_T^{w^{*}}\right\}}(w^{*}\left(e_T^{w^{*}}\right)-w^{*}\left(e\right))$, $\delta =min\{{\delta }_1,{\delta }_2\}$. We construct $w^{\prime }\left(e\right)=\left\{\begin{array}{cc}{w}^{*}\left(e\right)+\delta ,\hfill & \forall e\in E_1\hfill \\ w^{*}\left(e\right),\hfill & \forall e\in E_2\cup E_{{\Gamma }^{*}}^{w^{*}}\hfill \end{array}\right.,$ which is feasible with better objective value, contradicting the optimality of $Q^{*}$. Therefore, the required $T^{*}$ must exist. □

We now present a strongly polynomial-time algorithm for solving problem ${\mathrm{MSSTID}}_w$ with the main steps outlined as follows. For feasible problems requiring adjustment: (1) We compute all x-coordinates of intersection points for the line family $\{w_Q\left(e\right)=w\left(e\right)-l\left(e\right),w_Q\left(e\right)=w\left(e\right)-\frac{Q}{q\left(e\right)}\mid e\in E\}$ and add the upper bound ${max}_{e\in E}q\left(e\right)l\left(e\right)$ and lower bound 0 to this set. (2) We use a binary search method on this set to determine the optimal interval $(Q_a,Q_b]$ with $Q_a<Q^{*}\le Q_b$. We construct $w_{Q^{\prime }}$ via (7) with $Q^{\prime }:=\frac{Q_a+Q_b}{2}$. (3) We compute the bottleneck value $w_0:={min}_{T\in \Gamma }{max}_{e\in T}{w}_{Q^{\prime }}\left(e\right)$ and identify critical edges $E_0:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\ge w_0\}$. By Lemmas 1 and 8, the optimal value must be attained on some edge in $E_0$, so we only need to verify edges in $E_0$.

Theorem 3.

Algorithm 2 correctly solves problem ${MSSTID}_w$.

Algorithm 2 An algorithm to solve problem ${\mathrm{MSSTID}}_w$: $Q^{*}:=$${\mathrm{MSSTID}}_w\left(V,E,w,c,l,q,K\right)$.

Input:  Network $G=(V,E)$, weight vector $\mathit{w}$, sum vector $\mathit{c}$, lower bounds $\mathit{l}$, cost vector $\mathit{q}$ and a given value K.

Output:  Optimal value $Q^{*}$.

1:  Compute $w_l:=w-l$ and optimal MSSTs $T_w^{*}$, $T_{w_l}^{*}$.

2:  if $f(w,c,T_w^{*})\le K$ then

3:     return $Q^{*}:=0.$

4:  end if

5:  if $f(w_l,c,T_{w_l}^{*})>K$ then

6:     “The problem is infeasible.”

7:  end if

8:  Compute all x-coordinates of intersection points for the line family $\{w_Q\left(e\right)=w\left(e\right)-l\left(e\right),w_Q\left(e\right)=w\left(e\right)-\frac{Q}{q\left(e\right)}\}$, denoted as $Q_s.$

9:  Let $Q_{max}:={max}_{e\in E}q\left(e\right)l\left(e\right)$, $Q_s^{\prime }:=\{0\le Q_i\le Q_{max}\mid Q_i\in Q_s\}\cup \{0,Q_{max}\}$.

10:  Sort $Q_s$ in ascending order.

11:  Initialization: $a:=1$, $b:=|Q_s^{\prime }|$.

12:  while $b-a>1$ do

13:     Let $k:=\lfloor \frac{b+a}{2}\rfloor$ and $Q_k:=Q_s^{\prime }\left(k\right)$. Construct $w_{Q_k}$ via (7). Determine the optimal MSST $T_{Q_k}^{*}$ under $w_{Q_k}$.

14:     if $f(w_{Q_k},c,T_{Q_k}^{*})\le K$ then

15:         $b:=k$.

16:     else

17:         $a:=k$.

18:     end if

19:  end while

20:  Let $Q^{\prime }:=\frac{Q_a+Q_b}{2}$. Construct $w_{Q^{\prime }}$, $w_{Q_a}$, $w_{Q_b}$ via (7).

21:  Let $w_0:=\underset{T\in \Gamma }{min}\underset{e\in T}{max}{w}_{Q^{\prime }}\left(e\right)$, $E_0:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\ge w_0\}$.

22:  Initialize $Q^{*}:=\infty$.

23:  for each $e_i\in E_0$ do

24:     Let $E_i:=\{e\in E\mid w_{Q^{\prime }}\left(e\right)\le w_{Q^{\prime }}\left(e_i\right)\}$.

25:     Compute optimal MSST $T_{e_i}$ on $G(V,E_i,c,w_{Q_a})$ with $e_i$ as the maximum-weight edge.

26:     Let $\delta :=f(w_{Q_a},c,T_{e_i})-K$, ${\Delta }_Q:=\delta q\left(e_i\right)$.

27:     if $w_{Q_a}\left(e_i\right)-\delta \ge w_{Q_b}\left(e_i\right)$ then

28:         Update $Q^{*}:=min\{{\Delta }_Q+Q_a,Q^{*}\}$.

29:     end if

30:  end for

31:  return $Q^{*}$

Proof. 

Lines 8–19 identify the interval $(Q_a,Q_b]$ containing the optimal value $Q^{*}$. Lemma 1 guarantees that for any $Q\in [Q_a,Q_b]$, if $w_{Q^{\prime }}\left(e_{i_1}\right)\le w_{Q^{\prime }}\left(e_{i_2}\right)\cdots \le w_{Q^{\prime }}\left(e_{i_m}\right)$ holds for $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, then $w_Q\left(e_{i_1}\right)\le w_Q\left(e_{i_2}\right)\cdots \le w_Q\left(e_{i_m}\right)$ holds. This implies the maximum-weight edge for each spanning tree remains unchanged during the approximation from $Q_a$ to $Q^{*}$. Notice that $w_0$ is the bottleneck value under $w_{Q^{\prime }}$ in Line 21, so that we have $e_{T^{*}}^{w^{*}}\in E_0$, where $e_{T^{*}}^{w^{*}}$ is defined in Lemma 8. From Lines 23 to 30 of Algorithm 2, we sequentially determine whether each edge $e_i\in E_0$ could possibly be $e_{T^{*}}^{w^{*}}$. We first compute the optimal MSST $T_{e_i}$ with $e_i$ as the maximum weight edge under $w_{Q_a}$ whose value $f(w_{Q_a},c,T_{e_i})>K$. It remains the optimal MSST in $G(V,E_i,c,w_Q)$ with $e_i$ as the maximum weight edge for any $Q\in [Q_a,Q_b]$ by Lemma 2. Consequently, we need to decrease the weight of this edge by the minimum cost ${\Delta }_Q$ so that under the new cost $Q_a+{\Delta }_Q$, the total weight of $T_{e_i}$ is exactly K. What is more, we consider $w_{Q_a}\left(e_{T^{*}}^{w^{*}}\right)>w_{Q^{*}}\left(e_{T^{*}}^{w^{*}}\right)\ge w_{Q_b}\left(e_{T^{*}}^{w^{*}}\right)$ at the same time, so the conditional statement in Line 27 is necessary. Notice that the case when $w_{Q_a}\left(e_i\right)-\delta <w_{Q_b}\left(e_i\right)$ means $e_i$ cannot be $e_{T^{*}}^{w^{*}}$, so we only need to consider the case $w_{Q_a}\left(e_i\right)-\delta \ge w_{Q_b}\left(e_i\right)$. Then $Q_a+{\Delta }_Q$ serves as an upper bound for $Q^{*}$, since problem ${\mathrm{MSSTID}}_w$ just requires that the sum of the maximum weight and the sum-type weight in the optimal MSST is no more than K. Therefore, after the for loop ends, we obtain the optimal value $Q^{*}$. □

Theorem 4.

We can solve problem ${MSSTID}_w$ by Algorithm 2 in $O(m^{2}logn)$ time.

Proof. 

Similar to Theorem 2, the time complexity of Lines 8–10 is $O(m^{2}logm)$. The binary search method in Lines 12–19 requires $O(\log m)$ iterations, leading to a time complexity of $O(mlognlogm)$. Line 21 computes the bottleneck value $w_0$ in $O\left(m\right)$ time. Lines 23–30 involve a loop over $|E_0|=O\left(m\right)$ edges, where each iteration requires computing an optimal MSST once, resulting in a time complexity of $O(m^{2}logn)$. Then the overall time is $O(m^{2}logn)$. □

4. Solve Problem MSSTID_c

In this section, we study problem MSSTID by modifying c under weighted $l_{\infty }$ norm (${\mathrm{MSSTID}}_c$). For any $e\in E$, we let $q\left(e\right)>0$ be the cost required to adjust one unit of $c\left(e\right)$, $u\left(e\right)\ge 0$ be the upper adjustment limit of $c\left(e\right)$. The mathematical formula is as follows:

$$\begin{array}{ccc}& {min}_{\overline{c}}& \underset{e\in E}{max}q\left(e\right)(\overline{c}\left(e\right)-c\left(e\right))\hfill \end{array}$$

$$\begin{array}{ccc}& \mathrm{s}.\mathrm{t}.& \underset{e\in T}{max}w\left(e\right)+\sum _{e\in T}\overline{c}\left(e\right)\ge K,\forall T\in \Gamma ,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & c\left(e\right)\le \overline{c}\left(e\right)\le c\left(e\right)+u\left(e\right),\forall e\in E.\hfill \end{array}$$

(9)

For any given $Q\ge 0$, we define vector $c_Q$ as

$$\begin{array}{c}\hfill c_Q\left(e\right):=c\left(e\right)+min\left\{{\displaystyle \frac{Q}{q\left(e\right)}},u\left(e\right)\right\},e\in E.\end{array}$$

(10)

Lemma 9.

The vector $c_Q$ as (10) is feasible for problem ${MSSTID}_c$ if and only if $Q\ge Q^{*}$, where $Q^{*}$ is the optimal value. Moreover, if $Q=Q^{*}$, then $c_Q$ is an optimal solution of problem ${MSSTID}_c$.

By Conditions (8) and (9), the following lemma is immediate.

Lemma 10.

Define $c_u:=c+u$. Let $T_c^{*}$ and $T_{c_u}^{*}$ be the optimal MSSTs under c and $c_u$, respectively. If $f(w,c,T_c^{*})\ge K$, then problem ${MSSTID}_c$ requires no adjustment. If $f(w,c_u,T_{c_u}^{*})<K$, then problem ${MSSTID}_c$ is infeasible.

According to Lemma 9, we can use binary search to determine the optimal value $Q^{*}$. However, the number of iterations depends on the precision $ϵ$, making it not a strongly polynomial-time algorithm. To design a strongly polynomial-time algorithm, we present the following lemma.

Lemma 11.

Let $Q^{*}>0$ be the optimal value of problem ${MSSTID}_c$, $c_{Q^{*}}$ be the optimal solution constructed by (10), $w_0={min}_{T\in \Gamma }{max}_{e\in T}w\left(e\right)$, $E_0=\{e\in E|w\left(e\right)\ge w_0\}$, $T^{*}=arg{min}_{T\in \Gamma }f(w,c_{Q^{*}},T)$. Then $f(w,c_{Q^{*}},T^{*})=K$, and $e_{T^{*}}^w\in E_0$.

Proof. 

Since $c_{Q^{*}}$ is optimal, then $f(w,c_{Q^{*}},T^{*})\ge K$. If $f(w,c_{Q^{*}},T^{*})>K$, we let $\delta ={\displaystyle \frac{f(w,c_{Q^{*}},T^{*})-K}{n-1}}$ and construct $c_{\delta }\left(e\right)=max\{c_{Q^{*}}\left(e\right)-\delta ,c\left(e\right)\}$ ( $e\in E$).

Thus, for any $T\in \Gamma$,

$$\begin{array}{ccc}\hfill f(w,c_{\delta },T)& =& w\left(T\right)+\sum _{e\in T}{c}_{\delta }\left(e\right)\hfill \\ & =& w\left(T\right)+\sum _{e\in T}max\{c_{Q^{*}}\left(e\right)-\delta ,c\left(e\right)\}\hfill \\ & \ge & w\left(T\right)+\sum _{e\in T}(c_{Q^{*}}\left(e\right)-\delta )\hfill \\ & =& w\left(T\right)+\sum _{e\in T}{c}_{Q^{*}}\left(e\right)-(n-1)\delta \hfill \\ & =& f(w,c_{Q^{*}},T)+K-f(w,c_{Q^{*}},T^{*})\ge K.\hfill \end{array}$$

Furthermore, for any $e\in E$,

$$\begin{array}{ccc}\hfill |c_{\delta }\left(e\right)-c\left(e\right)|q\left(e\right)& =& |max\{c_{Q^{*}}\left(e\right)-\delta ,c\left(e\right)\}-c\left(e\right)|q\left(e\right)\hfill \\ & =& |max\{c\left(e\right)+min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta ,c\left(e\right)\}-c\left(e\right)|q\left(e\right)\hfill \\ & =& |max\{min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta ,0\}|q\left(e\right)\hfill \end{array}$$

If $min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta \le 0$, then $|max\{min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta ,0\}|q\left(e\right)=0$.

If $min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta >0$, then

$$\begin{array}{ccc}& & |max\{min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta ,0\}|q\left(e\right)\hfill \\ & =& (min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},u\left(e\right)\}-\delta )q\left(e\right)=min\{Q^{*},q\left(e\right)u\left(e\right)\}-\delta q\left(e\right)<Q^{*}.\hfill \end{array}$$

It contradicts with the optimality of $Q^{*}$; then, $f(w,c_{Q^{*}},T^{*})=K$. Moreover, $w_0$ is the bottleneck value under weight w, so $e_{T^{*}}^w\in E_0$. □

Based on the lemmas above, we design a strongly polynomial-time algorithm to solve this problem. The main ideas are as follows: If the problem is feasible and adjustment is needed, we (1) compute all x-coordinates of intersection points for the line family $\{c_Q\left(e\right)=c\left(e\right)+u\left(e\right),c_Q\left(e\right)=c\left(e\right)+{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$ and add the upper bound ${max}_{e\in E}q\left(e\right)u\left(e\right)$ and lower bound 0 of $Q^{*}$ to this set; (2) use a binary search method on this set to determine the interval $(Q_a,Q_b]$ containing the optimal value $Q^{*}$, where $Q_a<Q^{*}\le Q_b$, compute the edge set $E_0$ from Lemma 11; (3) for each $e_i\in E_0$, construct an auxiliary network $G(V,E_i,c_{Q^{\prime }},w)$, where $E_i:=\{e\in E|w\left(e\right)\le w\left(e_i\right)\}$, $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$ and $c_{Q^{\prime }}$ is constructed by (10), find the optimal MSST $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as the maximum weight edge, determine the set $T_{e_i}^i$ of adjustable edges in $T_{e_i}$, and compute the minimum cost ${\delta }_Q$ to adjust these edges so that the total weight of $T_{e_i}$ reaches K; and finally (4) for each $e_i\in E_0$, if $T_{e_i}^i$ is non-empty, the cost $Q_a+{\delta }_Q$ gives a candidate optimal value. The maximum among all these candidates is the optimal value.

Theorem 5.

Algorithm 3 correctly solves problem ${MSSTID}_c$.

Algorithm 3 An algorithm to solve problem ${\mathrm{MSSTID}}_c$: $Q^{*}:=$${\mathrm{MSSTID}}_c\left(V,E,w,c,u,q,K\right)$.

Input:  Network $G=(V,E)$, weight vector $\mathit{w}$, sum vector $\mathit{c}$, upper bounds vector $\mathit{u}$, cost vector $\mathit{q}$ and constant $\mathit{K}$.

Output:  Optimal value $Q^{*}$.

1:  Let $c_u:=c+u$, determine the optimal MSSTs under c and $c_u$, denoted as $T_c^{*}$ and $T_{c_u}^{*}$.

2:  if $f(w,c,T_c^{*})\ge K$ then

3:     return $Q^{*}:=0.$

4:  end if

5:  if $f(w,c_l,T_{c_u}^{*})<K$ then

6:     “The problem is infeasible.”

7:  end if

8:  Compute all x-coordinates of intersection points for the line family: $\{c_Q\left(e\right)=c\left(e\right)+u\left(e\right),c_Q\left(e\right)=c\left(e\right)+{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$, denoted as set $Q_s$.

9:  Let $Q_{max}:={max}_{e\in E}q\left(e\right)u\left(e\right)$, $Q_s^{\prime }:=\{0\le Q_i\le Q_{max}|Q_i\in Q_s\}\cup \{0,Q_{max}\}$.

10:  Sort the elements in $Q_s^{\prime }$ in ascending order.

11:  Initialize $a:=1,b:=|Q_s^{\prime }|$.

12:  while $b-a>1$ do

13:     Let $k:=\lfloor {\displaystyle \frac{b+a}{2}}\rfloor$, $Q_k:=Q_s^{\prime }\left(k\right)$, construct $c_{Q_k}$ by (10), determine the optimal MSST $T_{Q_k}^{*}$ under $c_{Q_k}$.

14:     if $f(w,c_{Q_k},T_{Q_k}^{*})\ge K$ then

15:         Update $b:=k$.

16:     else

17:         Update $a:=k$.

18:     end if

19:  end while

20:  Let $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, construct $c_{Q_a},c_{Q_b},c_{Q^{\prime }}$ via (10).

21:  Let $w_0:=\underset{T\in \Gamma }{min}\underset{e\in T}{max}w\left(e\right)$, $E_0:=\{e\in E|w\left(e\right)\ge w_0\}$.

22:  Initialize $Q^{*}:=0$.

23:  for $e_i\in E_0$ do

24:     Let $E_i:=\{e\in E|w\left(e\right)\le w\left(e_i\right)\}$.

25:     Compute optimal MSST $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as the maximum weight edge.

26:     if $f(w,c_{Q_a},T_{e_i})<K$ then

27:         Compute the set $T_{e_i}^i$ of adjustable edges in $T_{e_i}$: $T_{e_i}^i:=\{e\in T_{e_i}|c_{Q_a}\left(e\right)<c_{Q_b}\left(e\right)\}$.

28:         Let ${\delta }_Q:={\displaystyle \frac{K-f(w,c_{Q_a},T_{e_i})}{{\sum }_{e_i\in T_{e_i}^i}\frac{1}{q\left(e_i\right)}}}$. Update $Q^{*}:=max\{Q^{*},{\delta }_Q+Q_a\}$.

29:     end if

30:  end for

31: return $Q^{*}$.

Proof. 

Lines 8–20 identify the interval $(Q_a,Q_b]$ containing the optimal value $Q^{*}$. By Lemma 1, for any $Q\in [Q_a,Q_b]$, if $c_{Q^{\prime }}\left(e_{i_1}\right)\le c_{Q^{\prime }}\left(e_{i_2}\right)\cdots \le c_{Q^{\prime }}\left(e_{i_m}\right)$ holds for $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, then $c_Q\left(e_{i_1}\right)\le c_Q\left(e_{i_2}\right)\cdots \le c_Q\left(e_{i_m}\right)$ holds. Line 21 computes $w_0$ and $E_0$ from Lemma 11. Notice that $w_0$ is the bottleneck value under w in Line 21, so we have $e_{T^{*}}^w\in E_0$, where $e_{T^{*}}^w$ is defined in Lemma 11. From Lines 23 to 30 of Algorithm 3, we sequentially determine whether each edge $e_i\in E_0$ could possibly be $e_{T^{*}}^w$. We first compute the optimal MSST $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as the maximum weight edge. It remains the optimal MSST in $G(V,E_i,c_Q,w)$ with $e_i$ as the maximum weight edge for any $Q\in [Q_a,Q_b]$ by Lemma 2. If $f(w,c_{Q_a},T_{e_i})<K$, then the set $T_{e_i}^i$ of adjustable edges in $T_{e_i}$ is non-empty and any edge $e\in T_{e_i}^i$ satisfies $c_{Q_a}\left(e\right)<c_{Q^{*}}\left(e\right)\le c_{Q_b}\left(e\right)\le c\left(e\right)+u\left(e\right)$ according to the construction of the line family in Line 8. Then Line 28 computes the minimal cost to increase the total weight of $T_{e_i}$ to exactly K, yielding a lower bound of the optimal value. □

Theorem 6.

We can solve problem ${MSSTID}_c$ by Algorithm 3 in $O(m^{2}logn)$ time.

Proof. 

Similar to Theorem 2, Lines 8–10 take $O(m^{2}logm)$ time. The binary search method in Lines 12–19 has $O(\log m)$ iterations, totaling $O(mlognlogm)$ time. Line 21 computes the bottleneck value $w_0$ in $O\left(m\right)$ time. Lines 23–30 loop $|E_0|=O\left(m\right)$ times, each requiring one optimal MSST computation, hence $O(m^{2}logn)$ time. Therefore, the overall time complexity is $O(m^{2}logn)$. □

5. Solve Problem MSSTIP_c

In this section, we study problem MSSTIP by modifying c under weighted $l_{\infty }$ norm (${\mathrm{MSSTID}}_c$). For any $e\in E$, we let $q\left(e\right)>0$ be the cost required to adjust one unit of $c\left(e\right)$, $l\left(e\right)\ge 0$ be the lower adjustment limit of $c\left(e\right)$ with $c\left(e\right)-l\left(e\right)\ge 0$. The mathematical model is as follows:

$$\begin{array}{ccc}& {min}_{\overline{c}}& \underset{e\in E}{max}q\left(e\right)(c\left(e\right)-\overline{c}\left(e\right))\hfill \end{array}$$

$$\begin{array}{ccc}& \mathrm{s}.\mathrm{t}.& \underset{T\in \Gamma }{min}\{\underset{e\in T}{max}w\left(e\right)+\sum _{e\in T}\overline{c}\left(e\right)\}\le K,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & c\left(e\right)-l\left(e\right)\le \overline{c}\left(e\right)\le c\left(e\right),\forall e\in E.\hfill \end{array}$$

(12)

For any given $Q\ge 0$, we define vector $c_Q$ as

$$\begin{array}{c}\hfill c_Q\left(e\right):=c\left(e\right)-min\left\{{\displaystyle \frac{Q}{q\left(e\right)}},l\left(e\right)\right\},e\in E.\end{array}$$

(13)

Lemma 12.

The vector $c_Q$ as (13) is feasible for problem ${MSSTID}_c$ if and only if $Q\ge Q^{*}$, where $Q^{*}$ is the optimal value. Moreover, if $Q=Q^{*}$, then $c_Q$ is an optimal solution of problem ${MSSTID}_c$.

By Conditions (11) and (12), the following lemma is immediate.

Lemma 13.

Define $c_l:=c-l$. Let $T_c^{*}$ and $T_{c_l}^{*}$ be the optimal MSSTs under c and $c_l$, respectively. If $f(w,c,T_c^{*})\le K$, then no adjustment is needed. If $f(w,c_l,T_{c_l}^{*})>K$, then the problem is infeasible.

By Lemma 12, we can determine $Q^{*}$ via a binary search method, but the iteration count depends on precision $ϵ$, making it not strongly polynomial. To design a strongly polynomial algorithm, we present the following lemma.

Lemma 14.

Let $Q^{*}>0$ be the optimal value of problem ${MSSTID}_c$, $c_{Q^{*}}$ be the optimal solution constructed by (13), $w_0={min}_{T\in \Gamma }{max}_{e\in T}w\left(e\right)$, $E_0=\{e\in E|w\left(e\right)\ge w_0\}$, $T^{*}=arg{min}_{T\in \Gamma }f(w,c_{Q^{*}},T)$. Then $f(w,c_{Q^{*}},T^{*})=K$, and $e_{T^{*}}^w\in E_0$.

Proof. 

Since $c_{Q^{*}}$ is optimal, then $f(w,c_{Q^{*}},T^{*})\le K$.

If $f(w,c_{Q^{*}},T^{*})<K$, let $\delta ={\displaystyle \frac{K-f(w,c_{Q^{*}},T^{*})}{n-1}}$.

We construct $c_{\delta }\left(e\right)=min\{c_{Q^{*}}\left(e\right)+\delta ,c\left(e\right)\}$ for $e\in E$. Then,

$$\begin{array}{ccc}\hfill f(w,c_{\delta },T^{*})& =& w\left(T^{*}\right)+\sum _{e\in T^{*}}{c}_{\delta }\left(e\right)\hfill \\ & =& w\left(T^{*}\right)+\sum _{e\in T^{*}}min\{c_{Q^{*}}\left(e\right)+\delta ,c\left(e\right)\}\hfill \\ & \le & w\left(T^{*}\right)+\sum _{e\in T^{*}}(c_{Q^{*}}\left(e\right)+\delta )\hfill \\ & =& w\left(T^{*}\right)+\sum _{e\in T^{*}}{c}_{Q^{*}}\left(e\right)+(n-1)\delta \hfill \\ & =& f(w,c_{Q^{*}},T^{*})+K-f(w,c_{Q^{*}},T^{*})=K.\hfill \end{array}$$

Moreover, for any $e\in E$,

$$\begin{array}{ccc}\hfill |c_{\delta }\left(e\right)-c\left(e\right)|q\left(e\right)& =& |min\{c_{Q^{*}}\left(e\right)+\delta ,c\left(e\right)\}-c\left(e\right)|q\left(e\right)\hfill \\ & =& |min\{c\left(e\right)-min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\}+\delta ,c\left(e\right)\}-c\left(e\right)|q\left(e\right)\hfill \\ & =& |min\{\delta -min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\},0\}|q\left(e\right)\hfill \end{array}$$

If $\delta -min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\}\ge 0$, then $|min\{\delta -min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\},0\}|q\left(e\right)=0$.

If $\delta -min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\}<0$, then

$$\begin{array}{ccc}& & |min\{\delta -min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\},0\}|q\left(e\right)\hfill \\ & =& (min\{{\displaystyle \frac{Q^{*}}{q\left(e\right)}},l\left(e\right)\}-\delta )q\left(e\right)=min\{Q^{*},q\left(e\right)l\left(e\right)\}-\delta q\left(e\right)<Q^{*}.\hfill \end{array}$$

It contradicts the optimality of $Q^{*}$. Hence, $f(w,c_{Q^{*}},T^{*})$$=K$. Also, $w_0$ is the bottleneck value under weight w, so $e_{T^{*}}^w\in E_0$. □

Based on lemmas above, we design a strongly polynomial-time algorithm. The main ideas are as follows. If the problem is feasible and the adjustments are needed, we (1) compute all x-coordinates of intersection points for the line family $\{c_Q\left(e\right)=c\left(e\right)-l\left(e\right),c_Q\left(e\right)=c\left(e\right)-{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$ and add ${max}_{e\in E}q\left(e\right)l\left(e\right)$ and 0 to this set; (2) use a binary search method to find the interval $(Q_a,Q_b]$ with $Q_a<Q^{*}\le Q_b$, compute $E_0$ from Lemma 14; (3) for each $e_i\in E_0$, construct auxiliary network $G(V,E_i,c_{Q^{\prime }},w)$ where $E_i:=\{e\in E|w\left(e\right)\le w\left(e_i\right)\}$, $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$ and $c_{Q^{\prime }}$ from (13), find the optimal MSST $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as maximum weight edge, determine the set $T_{e_i}^d$ of adjustable edges in $T_{e_i}$, and compute the minimum cost ${\delta }_Q$ to adjust these edges so that the total weight of $T_{e_i}$ is decreased to K; and finally (4) for each $e_i\in E_0$, if $T_{e_i}^d$ is non-empty, the cost $Q_a+{\delta }_Q$ gives a candidate optimal value. The minimum among all candidates is $Q^{*}$.

Theorem 7.

Algorithm 4 correctly solves problem ${MSSTID}_c$.

Algorithm 4 An algorithm to solve problem ${\mathrm{MSSTID}}_c$: $Q^{*}:=$${\mathrm{MSSTID}}_c\left(V,E,w,c,l,q,K\right)$.

Input:  Network $G=(V,E)$, weight vector $\mathit{w}$, sum vector $\mathit{c}$, lower bounds vector $\mathit{l}$, cost vector $\mathit{q}$, and constant $\mathit{K}$.

Output:  Optimal value $Q^{*}$.

1:  Let $c_l:=c-l$, compute optimal MSSTs $T_c^{*}$ and $T_{c_l}^{*}$.

2:  if $f(w,c,T_c^{*})\le K$ then

3:     return $Q^{*}:=0.$

4:  end if

5:  if $f(w,c_l,T_{c_l}^{*})>K$ then

6:     “The problem is infeasible.”

7:  end if

8:  Compute the set $Q_s$ of all x-coordinates of intersection points for the line family: $\{c_Q\left(e\right)=c\left(e\right)-l\left(e\right),c_Q\left(e\right)=c\left(e\right)-{\displaystyle \frac{Q}{q\left(e\right)}}|e\in E\}$.

9:  Let $Q_{max}:={max}_{e\in E}q\left(e\right)l\left(e\right)$, $Q_s^{\prime }:=\{0\le Q_i\le Q_{max}|Q_i\in Q_s\}\cup \{0,Q_{max}\}$.

10:  Sort $Q_s^{\prime }$ in ascending order.

11:   Initialize $a:=1,b:=|Q_s^{\prime }|$.

12:  while $b-a>1$ do

13:     Let $k:=\lfloor {\displaystyle \frac{b+a}{2}}\rfloor$, $Q_k:=Q_s^{\prime }\left(k\right)$, construct $c_{Q_k}$ using (13), compute optimal tree $T_{Q_k}^{*}$ under $c_{Q_k}$.

14:     if $f(w,c_{Q_k},T_{Q_k}^{*})\le K$ then

15:         Update $b:=k$.

16:     else

17:         Update $a:=k$.

18:     end if

19:  end while

20:  Let $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, construct $c_{Q_a},c_{Q_b},c_{Q^{\prime }}$ via (13).

21:  Compute $w_0:={min}_{T\in \Gamma }{max}_{e\in T}w\left(e\right)$, $E_0:=\{e\in E|w\left(e\right)\ge w_0\}$.

22:  Initialize $Q^{*}:=\infty$.

23:  for $e_i\in E_0$ do

24:     Let $E_i:=\{e\in E|w\left(e\right)\le w\left(e_i\right)\}$.

25:     Determine the optimal tree $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as maximum weight edge.

26:     Compute the set $T_{e_i}^d$ of decreasable edges in $T_{e_i}$: $T_{e_i}^d:=\{e\in T_{e_i}|c_{Q_a}\left(e\right)>c_{Q_b}\left(e\right)\}$.

27:     if $T_{e_i}^d\ne \varnothing$ then

28:         Let ${\delta }_Q:={\displaystyle \frac{f(w,c_{Q_a},T_{e_i})-K}{{\sum }_{e_i\in T_{e_i}^d}\frac{1}{q\left(e_i\right)}}}$. Update $Q^{*}:=min\{Q^{*},{\delta }_Q+Q_a\}$.

29:     end if

30:  end for

31:  return $Q^{*}$.

Proof. 

Lines 8–20 identify the interval $(Q_a,Q_b]$ containing the optimal value $Q^{*}$. By Lemma 1, for any $Q\in [Q_a,Q_b]$, if $c_{Q^{\prime }}\left(e_{i_1}\right)\le c_{Q^{\prime }}\left(e_{i_2}\right)\cdots \le c_{Q^{\prime }}\left(e_{i_m}\right)$ holds for $Q^{\prime }={\displaystyle \frac{Q_a+Q_b}{2}}$, then $c_Q\left(e_{i_1}\right)\le c_Q\left(e_{i_2}\right)\cdots \le c_Q\left(e_{i_m}\right)$ holds. Line 21 computes $w_0$ and $E_0$ from Lemma 14. Notice that $w_0$ is the bottleneck value under w in Line 21, so we have $e_{T^{*}}^w\in E_0$, where $e_{T^{*}}^w$ is defined in Lemma 14. From Lines 23 to 30 of Algorithm 4, we sequentially determine whether each edge $e_i\in E_0$ could possibly be $e_{T^{*}}^w$. We first compute the optimal MSST $T_{e_i}$ in $G(V,E_i,c_{Q^{\prime }},w)$ with $e_i$ as the maximum weight edge whose value $f(w,c_{Q_a},T_{e_i})$ must be more than K. It remains the optimal MSST in $G(V,E_i,c_Q,w)$ with $e_i$ as the maximum weight edge for any $Q\in [Q_a,Q_b]$ by Lemma 2. Then if the set $T_{e_i}^d$ of adjustable edges in $T_{e_i}$ is non-empty and any edge $e\in T_{e_i}^d$ satisfies $c_{Q_a}\left(e\right)>c_{Q^{*}}\left(e\right)\ge c_{Q_b}\left(e\right)\ge c\left(e\right)-l\left(e\right)$ according to the construction of the line family in Line 8, Line 28 computes the minimal cost to decrease the total weight of $T_{e_i}$ to exactly K, yielding an upper bound of the optimal value. □

Theorem 8.

We can solve problem ${MSSTID}_c$ by Algorithm 4 in $O(m^{2}logn)$ time.

Proof. 

Similar to Theorem 2, Lines 8–10 take $O(m^{2}logm)$ time. The binary search method in Lines 12–19 has $O(logm)$ iterations, taking $O(mlognlogm)$ time. Line 21 computes $w_0$ in $O\left(m\right)$ time. Lines 23–30 loop $|E_0|=O\left(m\right)$ times, each requiring one optimal MSST computation, hence $O(m^{2}logn)$ time. Therefore, the overall complexity is $O(m^{2}logn)$. □

6. Numerical Experiment

To evaluate the runtime performance of Algorithms 1–4, we generated seven types of random graphs with node and edge counts $(n,m)$ as (200, 500), (500, 1000), (1000, 2000), (2000, 5000), (4000, 8000), (5000, 10,000), (10,000, 15,000). For each graph size, 200 instances were randomly generated with parameters $c\sim U(1,n)$, $w\sim U(1,n^2)$, $l\sim U(0,c)$, $u\sim U(1,n)$, $q\sim U(1,m)$, and $K\sim U(f(w,c,T_c^{*})+1,f(w,c_u,T_{c_u}^{*}))$, where U stands for the uniform distribution. The algorithm was implemented in MATLAB R2020a and run on a Lenovo Legion Y7000P laptop (manufacturer: Lenovo, Beijing, China) with Windows 10, Intel(R) Core(TM) i5-8250U CPU @1.60 GHz, 8.00 GB RAM. The running times are shown in

Table 1. Computational Performance of Algorithms 1–4.

Alg.	n	m	${\mathit{T}}_{\mathbf{min}}$ (s)	${\mathit{T}}_{\mathbf{avg}}$ (s)	${\mathit{T}}_{\mathbf{max}}$ (s)
Alg. 1	200	500	0.126	0.199	0.335
	500	1000	0.196	0.385	0.617
	1000	2000	0.787	0.971	1.584
	2000	5000	3.842	6.419	11.005
	4000	8000	10.465	12.821	18.634
	5000	10,000	16.839	18.958	24.533
	10,000	15,000	55.667	62.919	78.521
Alg. 2	200	500	0.102	0.186	0.315
	500	1000	0.190	0.358	0.616
	1000	2000	0.719	0.965	1.568
	2000	5000	3.767	6.035	11.665
	4000	8000	10.686	13.391	18.363
	5000	10,000	15.936	18.614	23.490
	10,000	15,000	55.340	60.660	79.250
Alg. 3	200	500	0.065	0.251	0.593
	500	1000	0.186	0.237	0.458
	1000	2000	0.708	0.895	1.359
	2000	5000	4.215	6.561	11.748
	4000	8000	10.572	11.510	12.921
	5000	10,000	16.710	18.816	21.383
	10,000	15,000	58.867	65.429	76.413
Alg. 4	200	500	0.093	0.126	0.254
	500	1000	0.194	0.336	0.496
	1000	2000	0.689	0.935	1.443
	2000	5000	3.127	5.035	10.650
	4000	8000	11.642	14.411	19.134
	5000	10,000	16.364	19.515	23.399
	10,000	15,000	56.334	62.646	78.154

, where the running time is measured in seconds.

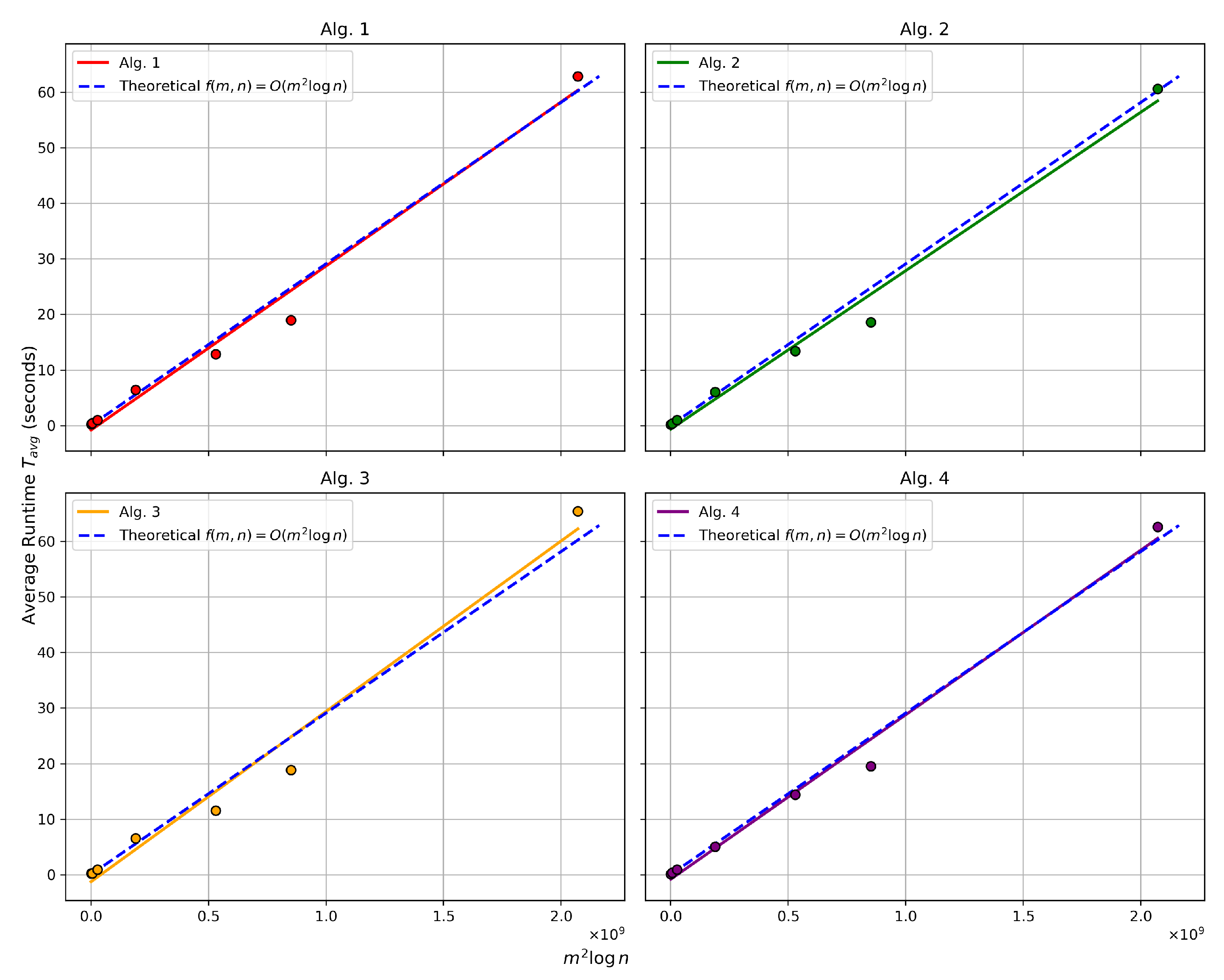
These comprehensive results confirm that all four algorithms with time complexity $O(m^{2}logn)$ maintain practical computational efficiency even for large-scale problem instances, making them suitable for real-world applications. For a better understanding of the running time complexity, we have the following Figure 1 to illustrate the comparison between the theoretical runtime complexity and the empirical average runtime of four algorithms (Algorithms 1–4).

In each sub-figure, the theoretical complexity is represented by the blue dashed line $f(m,n)=O(m^{2}logn)$, and the colored straight lines show the linear fit of the average runtime $T_{\mathrm{avg}}$ against the theoretical complexity term $O(m^{2}logn)$, with the corresponding scatter points representing the actual observed values. The results demonstrate that the empirical runtime growth aligns closely with the theoretical model, confirming the expected complexity behavior for these algorithms.

7. Conclusions and Further Research

This work presents a comprehensive study of problems MSSTID and MSSTIP under the weighted $l_{\infty }$ norm. Focusing on undirected graphs $G(V,E,c,w)$ with two edge weights c and w, we establish complete mathematical formulations for both MSSTID and MSSTIP, where the former strategically modifies edge weights c or w to degrade network performance (ensuring the weight of MSST is at least K), while the latter optimizes weight adjustments for performance enhancement (the weight of MSST is no more than K). We provide a rigorous analysis of optimal value properties and then develop four strongly polynomial-time algorithms with a time complexity of $O\left(\right|E{|}^{2}log\left|V\right|)$ through innovative combinations of binary search methods and greedy techniques. Finally, we conducted comprehensive numerical validations of the proposed methods and algorithms, demonstrating their effectiveness.

The current algorithms presented in this paper are exact algorithms, and their time complexity is confirmed and manageable. In terms of memory complexity, the primary storage requirement comes from storing the graph $G(V,E)$, which scales as $O\left(n^2\right)$, where n is the number of nodes in the graph. This memory requirement is feasible for most real-world applications, as the size of the graphs typically encountered can be handled by current computational resources.

For extremely large-scale graphs with millions of edges and nodes, further research is needed to explore more advanced methods, such as graph decomposition, which would allow us to handle larger instances efficiently. While the algorithm in this study focuses on solving problems MSSTID and MSSTIP under $l_{\infty }$ norm, it is important to note that the approach may not directly apply to similar problems under other norms. This is a common challenge in combinatorial optimization, where specialized algorithms are often required for different problem structures. Nonetheless, the methodology developed in this paper can be adapted and extended to solve related problems in other infinite models.

For future research, we can consider problems MSSTID and MSSTIP by adjusting the two edge weights (c and w) at the same time. Meanwhile we identify the weighted $l_1$ norm setting as a particularly promising direction, given its fundamental connections to inverse MSST problems and its potential to yield new theoretical insights in combinatorial optimization.