Sharp Bounds and Electromagnetic Field Applications for a Class of Meromorphic Functions Introduced by a New Operator

Abstract

In this paper, we present a new integral operator that acts on a class of meromorphic functions on the punctured unit disc ${\mathbb{U}}^{*}$. This operator enables the definition of a new subclass of meromorphic univalent functions. We obtain sharp bounds for the Fekete–Szegö inequality and the second Hankel determinant for this class. The theoretical approach is based on differential subordination. Furthermore, we link these theoretical insights to applications in 2D electromagnetic field theory by outlining a physical framework in which the operator functions as a field transformation kernel. We show that the operator’s parameters correspond to physical analogs of field regularization and spectral redistribution, and we use subordination theory to simulate the design of vortex-free fields. The findings provide new insights into the interaction between geometric function theory and physical field modeling.

1. Introduction

The study of meromorphic univalent functions is essential in complex analysis, especially in the study of geometric function classes. The class of meromorphic starlike functions was introduced and developed by Pommerenke [1], followed by significant additions from Miller [2], Mogra et al. [3], and Aouf [4]. This study makes substantial use of the concept of differential subordination, which was established by Miller and Mocanu [5], providing researchers an effective means to use majorization concepts to study analytic and meromorphic functions.

The Fekete–Szegö problem dates back to the work of Fekete and Szegö [6], who aimed to improve bounds on Taylor coefficients of normalized univalent functions. Decades of additional study into sharp coefficient inequalities, including those for meromorphic function classes, have been motivated by their findings.

Pommerenke [7] introduced the Hankel determinant, which Noonan and Thomas [8] subsequently generalized. This determinant is a useful tool for examining the relationships between coefficients and spotting extreme behavior in meromorphic and analytic functions. Further research by Ehrenborg [9] and Hayami and Owa [10] expanded its mathematical relevance.

In this paper, we expand on these foundations by presenting a novel operator that generalizes a number of well-known integral and differential operators. In order to analyze the coefficient structure of functions that are subject to the action of this operator, we derive a recurrence relation for it. Our method provides sharp bounds on the Fekete–Szegö functional as well as on the second Hankel determinant in this new meromorphic class. Also, we explain how the theoretical findings have important implications in electromagnetic field theory, particularly in the modeling of transformed singular fields.

The synergy between geometric function theory and the physical sciences is a well-known and powerful paradigm. The fundamental relationship was established by pioneers like Carathéodory [11], who connected harmonic functions to electrostatic potentials. This approach was famously used in fluid dynamics in classic works such as Milne-Thomson’s Theoretical Hydrodynamics [12], and it remains a standard tool in modern fluid mechanics engineering [13], which uses complex potentials to model fluid flow. The tradition of turning geometric function theory discoveries into physical insights remains a dynamic and diversified area of modern research. Building on this interdisciplinary legacy, which includes the application of subordination to EM cloaking [14] and the use of operator-based methods to model vortex motion and fluid dynamics [15,16], our work investigates this synergy further by employing a new operator to model the transformation and geometric control of singular fields.

The paper is structured as follows: Section 2 establishes the necessary definitions, notations, and mathematical preliminaries and lemmas. Section 3 derives sharp Fekete–Szegö inequalities for the introduced class. Section 4 obtains bounds for the second Hankel determinant. Section 5 develops electromagnetic field applications. In Section 6, the work is finally finished with a summary and some directions for further work.

2. Mathematical Preliminaries

A function f is meromorphic if it is analytic all around a domain D, except perhaps for poles in D (see [17]). Assign $\Sigma$ to the class of meromorphic functions of the following form:

$$f\left(z\right)={\displaystyle \frac{1}{z}}+\sum _{k=0}^{\infty }{a}_k{z}^k,$$

(1)

which are analytic in the open punctured unit disc ${\mathbb{U}}^{*}=\{z:z\in \mathbb{C}\mathrm{and}0<|z|<1\}=\mathbb{U}\setminus \left\{0\right\}$. Also, let ℘ be the class of analytic functions $\phi \left(z\right)$ with $\Re \left\{\phi \right(z\left)\right\}>0$ on $\mathbb{U}$, satisfying $\phi \left(0\right)=1$ and ${\phi }^{\prime }\left(0\right)>0$, which maps $\mathbb{U}$ onto a region starlike with respect to 1 and symmetric with respect to the real axis.

Definition 1.

A function $f\in \Sigma$ is meromorphic starlike of order β, indicated by ${\Sigma }^{*}\left(\beta \right)$, if

$$-\Re \left\{{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right\}>\beta (0\le \beta <1,z\in {\mathbb{U}}^{*}),$$

which was presented and examined by Pommerenke [1], Miller [2], and several others (see [3]).

Definition 2.

For two functions $f\left(z\right)$ and $g\left(z\right)$, analytic in $\mathbb{U}=\{z:z\in \mathbb{C}\mathrm{and}|z|<1\}$, $f\left(z\right)$ is subordinate to $g\left(z\right)$ ($f\left(z\right)\prec g\left(z\right)$) if there exists a function $\omega \left(z\right)$, analytic in $\mathbb{U}$ with $\omega \left(0\right)=0$ and $\left|\omega \right(z\left)\right|<1$ such that $f\left(z\right)=g\left(\omega \right(z\left)\right)$, and, if $g\left(z\right)$ is univalent in $\mathbb{U}$, then

$$f\left(z\right)\prec g\left(z\right)⟺f\left(0\right)=g\left(0\right)f\left(\mathbb{U}\right)\subset g\left(\mathbb{U}\right),$$

for details, see [5,18].

Definition 3.

A function $\omega \left(z\right)$, is called a Schwarz function if it is analytic in $\mathbb{U}$, with $\omega \left(0\right)=0$ and $\left|\omega \right(z\left)\right|<1$ for all $z\in \mathbb{U}$, introduced by Schwarz [19] and fundamental to subordination theory; see [5,18].

Definition 4.

Silverman et al. [20] presented and examined the class ${\Sigma }^{*}\left(\phi \right)$ of functions $f\in \Sigma$ for which

$$-{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \phi \left(z\right)(z\in {\mathbb{U}}^{*}).$$

Note that the class ${\Sigma }^{*}\left(\beta \right)$ is the special case of ${\Sigma }^{*}\left(\phi \right)$ when

$$\phi \left(z\right)={\displaystyle \frac{1+(1-2\beta )z}{1-z}}.$$

Definition 5.

For $f\in \Sigma$, Mohammed and Darus [21] presented and examined the class ${\Sigma }_b^{*}\left(\phi \right)$ by

$$1-{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}+1\right]\prec \phi \left(z\right),b\in {\mathbb{C}}^{*}=\mathbb{C}\setminus \left\{0\right\},$$

see also Reddy and Sharma [22], with $\gamma =1$. We observe that the following subclasses are obtained for appropriate values of b and $\phi \left(z\right)$:

1. 

${\Sigma }_1^{*}\left(\phi \right)={\Sigma }_1^{*}\left(\phi \right)$ (see [23] with $\alpha =1$ and [20]);

2. 

${\Sigma }_b^{*}\left({\displaystyle \frac{1+z}{1-z}}\right)=F^{*}\left(b\right)$ (see [24]);

3. 

${\Sigma }_1^{*}\left({\displaystyle \frac{1+(1-2\beta )z}{1-z}}\right)={\Sigma }_1^{*}\left(\beta \right)(0\le \beta <1)$ (see [1]);

4. 

${\Sigma }_1^{*}\left({\displaystyle \frac{1+Az}{1-Az}}\right)=K_1(A,B)(0\le B\le 1,-B\le A<B)$ (see [25]);

5. 

${\Sigma }_{(1-\rho )e^{-i\theta }cos\theta }^{*}\left({\displaystyle \frac{1+z}{1-z}}\right)={\Sigma }_{\theta }^{*}\left(\rho \right)(0\le \rho <1,|\theta |<{\displaystyle \frac{\pi }{2}})$ (see [26]).

Definition 6.

For $f\in \Sigma$, Aouf and Fatma [27] studied the class $M_b^{*}\left(\phi \right)$ by

$$1-{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}}+2\right]\prec \phi \left(z\right),b\in {\mathbb{C}}^{*}.$$

For appropriate values of b and $\phi \left(z\right)$, note that

1. 

$M_b^{*}\left({\displaystyle \frac{1+z}{1-z}}\right)=G^{*}\left(b\right)$ (see [24]);

2. 

$M_{(1-\rho )e^{-i\theta }cos\theta }^{*}\left(\phi \right)=M_{\rho ,\theta }^{*}(0\le \rho <1,|\theta |<{\displaystyle \frac{\pi }{2}})$ (see [27]).

The study of linear operators in geometric function theory has demonstrated its effectiveness in defining and evaluating new subclasses of analytic and meromorphic functions. Differential and integral operators, including fractional derivatives and integrals, which extend classical calculus to non-integer orders, have been presented by numerous authors (for instance, [28,29,30]). The Rafid operator, first presented by Atshan and Rafid in the context of analytic univalent functions [31], makes a significant contribution to this area. This operator has been successfully applied to study coefficient bounds, inclusion relations, and subordination qualities for a variety of function classes. Several researchers, including Abbas and Atshan [32], El-Emam [33], and many others [34,35], have expanded their applications to different subclasses and derived important geometric properties for analytic and meromorphic function classes. Collectively, these studies demonstrate the utility and versatility of the Rafid operator in modern function theory. However, no meromorphic univalent analogue of this operator has yet been identified or investigated. Motivated by this gap and the success of operator-based methods in analytic function analysis, we offer a novel generalized integral operator based on the Rafid operator structure, specifically tailored to act on the class of meromorphic univalent functions in the punctured unit disc.

Definition 7.

For $f\left(z\right)$ given by (1), $0\le \delta \le 1$ and $0\le \mu <1$, we define the operator $I_{\mu }^{\delta }:\Sigma \to \Sigma$ as

$$I_{\mu }^{\delta }f\left(z\right)={\displaystyle \frac{1}{{(1-\mu )}^{\delta +1}\mathrm{\Gamma }(\delta +1)}}{\int }_0^{\infty }{t}^{\delta +1}{e}^{-t/(1-\mu )}f\left(tz\right)dt$$

$$={\displaystyle \frac{1}{z}}+\sum _{k=0}^{\infty }{\displaystyle \frac{{(1-\mu )}^{k+1}\mathrm{\Gamma }(k+\delta +2)}{\mathrm{\Gamma }(\delta +1)}}{a}_k{z}^k={\displaystyle \frac{1}{z}}+\sum _{k=0}^{\infty }{\Delta }_{\delta ,\mu }\left(k\right)a_k{z}^k,$$

(2)

where

$${\Delta }_{\delta ,\mu }\left(k\right)={\displaystyle \frac{{(1-\mu )}^{k+1}\mathrm{\Gamma }(k+\delta +2)}{\mathrm{\Gamma }(\delta +1)}},$$

and satisfies the recurrence relation:

$$z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }=(\delta +1)I_{\mu }^{\delta +1}f\left(z\right)-(\delta +2)I_{\mu }^{\delta }f\left(z\right).$$

(3)

Remark 1.

For the series (2) to converge in ${\mathbb{U}}^{*}$, the coefficients $a_k$ must satisfy

$$|a_k|\le {\displaystyle \frac{C}{\mathrm{\Gamma }(k+\delta +2)}}forC>0.$$

This condition ensures that the terms $a_k{z}^k$ decay sufficiently fast for convergence in the punctured unit disk ${\mathbb{U}}^{*}$, as required for meromorphic functions.

We note that

1. 

$I_0^{\delta }f\left(z\right)=I^{\delta }f\left(z\right)={\displaystyle \frac{1}{z}}+{\sum }_{k=0}^{\infty }{\displaystyle \frac{\mathrm{\Gamma }(k+\delta +2)}{\mathrm{\Gamma }(\delta +1)}}{a}_k{z}^k$;

2. 

$I_{\mu }^{0}f\left(z\right)=I_{\mu }f\left(z\right)={\displaystyle \frac{1}{z}}+{\sum }_{k=0}^{\infty }{(1-\mu )}^{k+1}\mathrm{\Gamma }(k+2)a_k{z}^k$;

3. 

$I_0^{0}f\left(z\right)=If\left(z\right)={\displaystyle \frac{1}{z}}+{\sum }_{k=0}^{\infty }\mathrm{\Gamma }(k+2)a_k{z}^k$.

Based on the introduced operator $I_{\mu }^{\delta }$, we introduce a new subclass $M_b^{\lambda }(\delta ,\mu ,\phi )$ of meromorphic univalent functions, thereby contributing meaningful results to the theory of geometric function classes defined by integral operators.

Definition 8.

A function $f\left(z\right)\in \Sigma$ is in the class $M_b^{\lambda }(\delta ,\mu ,\phi )$ if and only if

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }f\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }}}-1\right]\prec \phi \left(z\right),$$

(4)

where $b\in {\mathbb{C}}^{*}=\mathbb{C}\setminus \left\{0\right\}$ and $\lambda \in \mathbb{C}\setminus (0,1]$.

We note that

1. 

$M_b^0(\delta ,\mu ,\phi )=S_b^{*}(\delta ,\mu ,\phi )=\left\{f\in \Sigma :1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }}{I_{\mu }^{\delta }f\left(z\right)}}-1\right]\prec \phi \left(z\right)\right\}$;

2. 

$M_1^0(\delta ,\mu ,\phi )={\Sigma }^{*}(\delta ,\mu ,\phi )$;

3. 

$M_b^0(\delta ,\mu ,{\displaystyle \frac{1+(1-2\beta )z}{1-z}})={\Sigma }_{\beta }^{*}(\delta ,\mu ,b)(0\le \beta <1)$;

4. 

$M_b^0(\delta ,\mu ,{\displaystyle \frac{1+z}{1-z}})={\Sigma }^{*}(\delta ,\mu ,b)$;

5. 

$M_{1-\beta }^0(\delta ,\mu ,{\displaystyle \frac{1+z}{1-z}})={\Sigma }_{\beta }^{*}(\delta ,\mu ,\beta )$.

Definition 9.

Pommerenke [7] introduced the Hankel determinant for $\varrho \ge 1$, $\mathit{\ell }\ge 0$ as

$$H_{\varrho }\left(\mathit{\ell }\right)=\left|\begin{array}{ccccc}{a}_{\mathit{\ell }}& a_{\mathit{\ell }+1}& a_{\mathit{\ell }+2}& \dots & a_{\mathit{\ell }+\varrho -1}\\ a_{\mathit{\ell }+1}& a_{\mathit{\ell }+2}& a_{\mathit{\ell }+3}& \dots & a_{\mathit{\ell }+\varrho }\\ ⋮& ⋮& ⋮& & ⋮\\ a_{\mathit{\ell }+\varrho -1}& a_{\mathit{\ell }+\varrho }& a_{\mathit{\ell }+\varrho +1}& \dots & a_{\mathit{\ell }+2\varrho -2}\end{array}\right|(a_1=1).$$

Note that, for $f\left(z\right)$ given by (1), the second Hankel determinant given by putting $\varrho =2$ and $\mathit{\ell }=0$ as $H_2\left(0\right)=\left|\begin{array}{cc}{a}_0& a_1\\ a_1& a_2\end{array}\right|=a_0{a}_2-a_1^2$.

The following lemmas are necessary for our investigation.

Lemma 1

(see [36]). Let

$$q\left(z\right)=1+c_{1}z+c_2{z}^2+\dots \in \wp ,$$

(5)

and $\eta \in \mathbb{C}$; then,

$$|c_2-\eta c_1^2|\le 2max\{1;|2\eta -1|\}.$$

The sharpness is given by the functions

$$q\left(z\right)={\displaystyle \frac{1+z^2}{1-z^2}}\mathrm{and}q\left(z\right)={\displaystyle \frac{1+z}{1-z}}.$$

Lemma 2

(see [36]). For $q\left(z\right)$ provided by (5), then

$$|c_2-v{c}_1^2|\le \left\{\begin{array}{cc}-4v+2\hfill & \mathit{if}v\le 0,\hfill \\ 2\hfill & \mathit{if}0\le v\le 1,\hfill \\ 4v-2\hfill & \mathit{if}v\ge 1.\hfill \end{array}\right.$$

When $v<0$ or $v>1$, the equality is valid if $q\left(z\right)={\displaystyle \frac{1+z}{1-z}}$ or a rotation of it. If $0<v<1$, then the equality is valid if $q\left(z\right)={\displaystyle \frac{1+z^2}{1-z^2}}$ or a rotation of it. If $v=0$, the equality is valid if

$$q\left(z\right)=\left({\displaystyle \frac{1+\alpha }{2}}\right){\displaystyle \frac{1+z}{1-z}}+\left({\displaystyle \frac{1-\alpha }{2}}\right){\displaystyle \frac{1-z}{1+z}}(0\le \alpha \le 1),$$

or a rotation of it. If $v=1$, the equality is valid if

$${\displaystyle \frac{1}{q\left(z\right)}}=\left({\displaystyle \frac{1+\alpha }{2}}\right){\displaystyle \frac{1+z}{1-z}}+\left({\displaystyle \frac{1-\alpha }{2}}\right){\displaystyle \frac{1-z}{1+z}}(0\le \alpha \le 1),$$

or a rotation of it. Additionally, the upper bound mentioned above is sharp and can be enhanced at $0<v<1$:

$$|c_2-v{c}_1^2|+v|c_1{|}^2\le 2\left(0<v\le {\displaystyle \frac{1}{2}}\right),$$

and

$$|c_2-v{c}_1^2|+(1-v)|c_1{|}^2\le 2\left({\displaystyle \frac{1}{2}}<v\le 1\right).$$

Lemma 3

(see [11]). Let $q\left(z\right)$ provided by (5) and we have $|c_k|\le 2$ ($k=1,2,\dots$), and the inequality is sharp; see also [7,37].

Lemma 4

(see [29]). Let $q\left(z\right)\in \wp$ provided by (5), and then

$$2c_2=c_1^2+x(4-c_1^2),4c_3=c_1^3+2x{c}_1(4-c_1^2)-x^2{c}_1(4-c_1^2){+2y(1-|x|}^2)(4-c_1^2),$$

(6)

for $\left|x\right|\le 1$, $\left|y\right|\le 1$.

3. Fekete–Szegö Problem

The Fekete–Szegö functional $|a_1-\eta a_0^2|$ is one of the most celebrated problems in geometric function theory, originating with the work of Fekete and Szegö [6] and extensively generalized in both analytic and meromorphic settings. Its significance lies in its ability to capture the interplay between the initial coefficients of univalent functions, providing sharp bounds that reveal extremal behavior and structural properties. The problem has been studied by several authors for various subclasses of analytic and meromorphic functions; see [22,38,39]. These developments highlight the ongoing relevance and vitality of the Fekete–Szegö problem. Motivated by this rich body of research, we derive a sharp estimate for this functional within our newly defined class $M_b^{\lambda }(\delta ,\mu ,\phi )$ of meromorphic functions associated with the Rafid operator, contributing a novel result to this active field.

Theorem 1.

Let $f\left(z\right)$ provided by (1) and

$$\phi \left(z\right)=1+B_{1}z+B_2{z}^2+\dots \mathit{with}{B}_1\ge 0.$$

(7)

If $f\left(z\right)\in M_b^{\lambda }(\delta ,\mu ,\phi )$, $\lambda \in \mathbb{C}\setminus (0,1]$ and $\eta \in \mathbb{C}$, then

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}\left|{\displaystyle \frac{b}{1-2\lambda }}\right|$$

$$max\left\{1;\left|{\displaystyle \frac{B_2}{B_1}}-B_{1}b\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right|\right\},B_1\ne 0,$$

(8)

$$|a_1|\le {\displaystyle \frac{1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}\left|{\displaystyle \frac{B_{2}b}{1-2\lambda }}\right|,B_1=0.$$

(9)

The result is sharp.

Proof. 

If $f\left(z\right)\in M_b^{\lambda }(\delta ,\mu ,\phi )$, then there is a Schwarz function $\omega \left(z\right)$, analytic in $\mathbb{U}$ with $\omega \left(0\right)=0$ and $\left|\omega \right(z\left)\right|<1$ in $\mathbb{U}$ such that

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{(I_{\mu }^{\delta }f(z))}^{\prime }+\lambda z{\left[z{(I_{\mu }^{\delta }f(z))}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }f(z)-\lambda z{(I_{\mu }^{\delta }f(z))}^{\prime }}}-1\right]=\phi (\omega (z)),$$

(10)

where $\omega \left(z\right)={\displaystyle \frac{q\left(z\right)-1}{q\left(z\right)+1}}$ and $q\left(z\right)\in \wp$ provided by (5), satisfying $\Re \left\{q\right(z\left)\right\}>0$, $q\left(0\right)=1$ and $q^{\prime }\left(0\right)>0$. Then, we have

$$\begin{array}{cc}\hfill \phi \left(\omega \right(z\left)\right)& =\phi \left({\displaystyle \frac{q\left(z\right)-1}{q\left(z\right)+1}}\right)=\phi \left({\displaystyle \frac{c_{1}z+c_2{z}^2+c_3{z}^3+\dots }{2+c_{1}z+c_2{z}^2+c_3{z}^3+\dots }}\right)\hfill \\ \hfill & =\phi \left\{{\displaystyle \frac{1}{2}}\left[c_{1}z+\left(c_2-{\displaystyle \frac{c_1^2}{2}}\right)z^2+\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)z^3+\dots \right]\right\}\hfill \\ \hfill & =1+{\displaystyle \frac{1}{2}}{c}_1{B}_{1}z+\left[{\displaystyle \frac{1}{2}}{B}_1\left(c_2-{\displaystyle \frac{c_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{c}_1^2{B}_2\right]z^2\hfill \end{array}$$

$$+\left[{\displaystyle \frac{1}{2}}{B}_1\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)+{\displaystyle \frac{1}{2}}{B}_2\left(c_1{c}_2-{\displaystyle \frac{c_1^3}{2}}\right)+{\displaystyle \frac{1}{8}}{B}_3{c}_1^3\right]z^3+\dots .$$

(11)

Let $h\left(z\right)$ denote the left-hand side of (10) so that

$$h\left(z\right)=1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }f\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }}}-1\right]$$

$$=1+{\displaystyle \frac{1}{b}}\left\{-(1-\lambda ){\Delta }_{\delta ,\mu }\left(0\right)a_0\right\}z+{\displaystyle \frac{1}{b}}\left\{-2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)a_1+{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)a_0^2\right\}{z}^2$$

$$+{\displaystyle \frac{1}{b}}\left\{-(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)a_2+(1-\lambda )(1-2\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(1\right)a_0{a}_1\right.$$

$$\left.-{(1-\lambda )}^3{\Delta }_{\delta ,\mu }^3\left(0\right)a_0^3\right\}{z}^3+\dots .$$

(12)

From (10)–(12), we have

$$1+{\displaystyle \frac{1}{b}}\left\{-(1-\lambda ){\Delta }_{\delta ,\mu }\left(0\right)a_0\right\}z+{\displaystyle \frac{1}{b}}\left\{-2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)a_1+{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)a_0^2\right\}{z}^2$$

$$+{\displaystyle \frac{1}{b}}\left\{-(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)a_2+(1-\lambda )(1-2\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(1\right)a_0{a}_1\right.$$

$$\left.-{(1-\lambda )}^3{\Delta }_{\delta ,\mu }^3\left(0\right)a_0^3\right\}{z}^3+\dots =1+{\displaystyle \frac{1}{2}}{c}_1{B}_{1}z+\left[{\displaystyle \frac{1}{2}}{B}_1\left(c_2-{\displaystyle \frac{c_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}{c}_1^2{B}_2\right]z^2$$

$$+\left[{\displaystyle \frac{1}{2}}{B}_1\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)+{\displaystyle \frac{1}{2}}{B}_2\left(c_1{c}_2-{\displaystyle \frac{c_1^3}{2}}\right)+{\displaystyle \frac{1}{8}}{B}_3{c}_1^3\right]z^3+\dots .$$

(13)

Comparing coefficients, we have

$$-(1-\lambda ){\Delta }_{\delta ,\mu }\left(0\right)a_0={\displaystyle \frac{B_1{c}_{1}b}{2}},$$

and

$${\displaystyle \frac{1}{2}}b{B}_1\left(c_2-{\displaystyle \frac{c_1^2}{2}}\right)+{\displaystyle \frac{1}{4}}b{B}_2{c}_1^2=-2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)a_1+{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)a_0^2,$$

or, equivalently,

$$a_0=-{\displaystyle \frac{B_1{c}_{1}b}{2(1-\lambda ){\Delta }_{\delta ,\mu }\left(0\right)}},$$

(14)

and

$$a_1=-{\displaystyle \frac{b{B}_1}{4(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{c_2-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right\}.$$

(15)

Therefore,

$$a_1-\eta a_0^2=-{\displaystyle \frac{b{B}_1}{4(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{c_2-v{c}_1^2\right\},$$

where

$$v={\displaystyle \frac{1}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\left\{1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right\}\right].$$

(16)

Using Lemma 1, we now obtain (8). Also, from (14) and (15), if $B_1=0$, we get

$$a_0=0,a_1=-{\displaystyle \frac{B_2{c}_1^{2}b}{8(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}.$$

(17)

Since $\Re \left\{q\right(z\left)\right\}>0$, then $|c_1|\le 2$ (see [40]); hence,

$$|a_1|\le {\displaystyle \frac{1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}\left|{\displaystyle \frac{B_{2}b}{1-2\lambda }}\right|,$$

which demonstrates (9). The functions

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }f\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }}}-1\right]=\phi \left(z^2\right),$$

and

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }f\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }f\left(z\right)\right)}^{\prime }}}-1\right]=\phi \left(z\right),$$

provide the sharpness.     □

Putting $\lambda =0$ in Theorem 1, we obtain the corollary that follows:

Corollary 1.

Let $f\left(z\right)$ provided by (1) and $\phi \left(z\right)$ provided by (7). If $f\left(z\right)\in M_b^0(\delta ,\mu ,\phi )=S_b^{*}(\delta ,\mu ,\phi )$ and $\eta \in \mathbb{C}$, then

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1\left|b\right|}{2{\Delta }_{\delta ,\mu }\left(1\right)}}max\left\{1;\left|{\displaystyle \frac{B_2}{B_1}}-B_{1}b\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right|\right\},B_1\ne 0,$$

$$|a_1|\le {\displaystyle \frac{|B_{2}b|}{2{\Delta }_{\delta ,\mu }\left(1\right)}},B_1=0.$$

Putting $\lambda =0$ and $b=1$ in Theorem 1, we have

Corollary 2.

Let $f\left(z\right)$ provided by (1) and $\phi \left(z\right)$ provided by (7). If $f\left(z\right)\in M_1^0(\delta ,\mu ,\phi )={\Sigma }^{*}(\delta ,\mu ,\phi )$ and $\eta \in \mathbb{C}$, then

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}max\left\{1;\left|{\displaystyle \frac{B_2}{B_1}}-B_1\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right|\right\},B_1\ne 0,$$

$$|a_1|\le {\displaystyle \frac{|B_2|}{2{\Delta }_{\delta ,\mu }\left(1\right)}},B_1=0.$$

Putting $\lambda =0$ and $b=(1-\rho )e^{-i\theta }cos\theta$ ($0\le \rho <1$, $\left|\theta \right|<{\displaystyle \frac{\pi }{2}}$) in Theorem 1, we get

Corollary 3.

Let $f\left(z\right)$ provided by (1) and $\phi \left(z\right)$ provided by (7). If $f\left(z\right)\in M_{(1-\rho )e^{-i\theta }cos\theta }^0(\delta ,\mu ,\phi )$ and $\eta \in \mathbb{C}$, then

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1(1-\rho )cos\theta }{2{\Delta }_{\delta ,\mu }\left(1\right)}}$$

$$max\left\{1;\left|{\displaystyle \frac{B_2}{B_1}}-B_1(1-\rho )e^{-i\theta }cos\theta \left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right|\right\},B_1\ne 0,$$

$$|a_1|\le {\displaystyle \frac{(1-\rho )cos\theta |B_2|}{2{\Delta }_{\delta ,\mu }\left(1\right)}},B_1=0.$$

Applying Lemma 2 yields the following theorem.

Theorem 2.

For real η, let $\phi \left(z\right)$ provided by (7) ($B_i>0$, $i=1,2$). If $f\left(z\right)\in M_1^{\lambda }(\delta ,\mu ,\phi )=M^{\lambda }(\delta ,\mu ,\phi )$ and $0\le \lambda <0.5$, then

$$|a_1-\eta a_0^2|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{-B_2+B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},\mathit{if}\eta \le {\sigma }_1,\hfill \\ {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}},\mathit{if}{\sigma }_1\le \eta \le {\sigma }_2,\hfill \\ {\displaystyle \frac{1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{B_2-B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},\mathit{if}\eta \ge {\sigma }_2,\hfill \end{array}\right.$$

(18)

where

$${\sigma }_1={\displaystyle \frac{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)\left[-B_1-B_2+B_1^2\right]}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)B_1^2}},$$

and

$${\sigma }_2={\displaystyle \frac{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)\left[B_1-B_2+B_1^2\right]}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}.$$

The result is sharp. Further, let

$${\sigma }_3={\displaystyle \frac{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)\left[-B_2+B_1^2\right]}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}.$$

1. 

If ${\sigma }_1\le \eta \le {\sigma }_3$, then

$$|a_1-\eta a_0^2|+{\displaystyle \frac{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}\left\{B_1+B_2-B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}{\left|a_0\right|}^2$$

$$\le {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}.$$

(19)

2. 

If ${\sigma }_3\le \eta \le {\sigma }_2$, then

$$|a_1-\eta a_0^2|+{\displaystyle \frac{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}\left\{B_1-B_2+B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}{\left|a_0\right|}^2$$

$$\le {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}.$$

(20)

Proof. 

For $f\left(z\right)\in M^{\lambda }(\delta ,\mu ,\phi )$, $q\left(z\right)$ provided by (5), $a_0$ and $a_1$ are provided by (14) and (15), and then

$$a_1-\eta a_0^2=-{\displaystyle \frac{B_1}{4(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{c_2-v{c}_1^2\right\},$$

(21)

where v is provided by (16). First, if $\eta \le {\sigma }_1$, then we have $v\le 0$. By applying Lemma 2 to (21), we have

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{{\displaystyle \frac{-B_2}{B_1}}+B_1\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}$$

$$={\displaystyle \frac{1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{-B_2+B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},$$

this clearly demonstrates inequality (18). Next, if ${\sigma }_1\le \mu \le {\sigma }_2$, then we have $0\le v\le 1$. Therefore, by applying Lemma 2 to (21), we have

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}},$$

this clearly demonstrates inequality (18). Finally, if $\eta \ge {\sigma }_2$, then we have $v\ge 1$; therefore, by applying Lemma 2 to (21), we have

$$|a_1-\eta a_0^2|\le {\displaystyle \frac{B_1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{{\displaystyle \frac{B_2}{B_1}}-B_1\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}$$

$$={\displaystyle \frac{1}{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}}\left\{B_2-B_1^2\left[1-{\displaystyle \frac{2(1-2\lambda ){\Delta }_{\delta ,\mu }\left(1\right)}{{(1-\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},$$

this clearly demonstrates inequality (18). In the same way, we establish (19) and (20). To demonstrate the sharpness of the bounds, we define the functions ${\chi }_{{\phi }_s}$ ($s=2,3,4,\dots$), $F_{\alpha }$, and ${\zeta }_{\alpha }$ ($0\le \alpha \le 1$), respectively, by

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }{\chi }_{{\phi }_s}\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }{\chi }_{{\phi }_s}\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }{\chi }_{{\phi }_s}\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }{\chi }_{{\phi }_s}\left(z\right)\right)}^{\prime }}}-1\right]=\phi \left(z^{s-1}\right),{\chi }_{{\phi }_s}\left(0\right)=0={\chi }_{{\phi }_s}^{\prime }\left(0\right)-1,$$

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }{F}_{\alpha }\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }{F}_{\alpha }\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }{F}_{\alpha }\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }{F}_{\alpha }\left(z\right)\right)}^{\prime }}}-1\right]=\phi \left({\displaystyle \frac{z(z+\alpha )}{1+\alpha z}}\right),F_{\alpha }\left(0\right)=0=F_{\alpha }^{\prime }\left(0\right)-1,$$

and

$$1+{\displaystyle \frac{1}{b}}\left[{\displaystyle \frac{-(1-\lambda )z{\left(I_{\mu }^{\delta }{\zeta }_{\alpha }\left(z\right)\right)}^{\prime }+\lambda z{\left[z{\left(I_{\mu }^{\delta }{\zeta }_{\alpha }\left(z\right)\right)}^{\prime }\right]}^{\prime }}{(1-\lambda )I_{\mu }^{\delta }{\zeta }_{\alpha }\left(z\right)-\lambda z{\left(I_{\mu }^{\delta }{\zeta }_{\alpha }\left(z\right)\right)}^{\prime }}}-1\right]=\phi \left(-{\displaystyle \frac{z(z+\alpha )}{1+\alpha z}}\right),{\zeta }_{\alpha }\left(0\right)=0={\zeta }_{\alpha }^{\prime }\left(0\right)-1.$$

Clearly, the functions ${\chi }_{{\phi }_s},F_{\alpha }$, and ${\zeta }_{\alpha }\in M_b^{\lambda }(\delta ,\mu ,\phi )$. If $\eta <{\sigma }_1$ or $\eta >{\sigma }_2$, then the equality is valid if $f\left(z\right)$ is ${\chi }_{{\phi }_2}$ or a rotation of it. When ${\sigma }_1<\mu <{\sigma }_2$, the equality is valid if $f\left(z\right)$ is ${\chi }_{{\phi }_2}$ or a rotation of it. If $\eta ={\sigma }_1$, the equality is valid if $f\left(z\right)$ is $F_{\alpha }$ or a rotation of it. If $\eta ={\sigma }_2$, the equality is valid if $f\left(z\right)$ is ${\zeta }_{\alpha }$ or a rotation of it.    □

Putting $\lambda =0$ in Theorem 2, we obtain

Corollary 4.

For real η, let $\phi \left(z\right)$ provided by (7) ($B_i>0$, $i=1,2$). If $f\left(z\right)\in S_b^{*}(\delta ,\mu ,\phi )$, then

$$|a_1-\eta a_0^2|\le \left\{\begin{array}{c}{\displaystyle \frac{1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}\left\{-B_2+B_1^2\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},\mathit{if}\eta \le {\sigma }_4,\hfill \\ {\displaystyle \frac{B_1}{2{\Delta }_{\delta ,\mu }\left(1\right)}},\mathit{if}{\sigma }_4\le \eta \le {\sigma }_5,\hfill \\ {\displaystyle \frac{1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}\left\{B_2-B_1^2\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\},\mathit{if}\eta \ge {\sigma }_5,\hfill \end{array}\right.$$

where

$${\sigma }_4={\displaystyle \frac{{\Delta }_{\delta ,\mu }^2\left(0\right)\left[-B_1-B_2+B_1^2\right]}{2{\Delta }_{\delta ,\mu }\left(1\right)B_1^2}},{\sigma }_5={\displaystyle \frac{{\Delta }_{\delta ,\mu }^2\left(0\right)\left[B_1-B_2+B_1^2\right]}{2{\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}.$$

The result is sharp. Further, let

$${\sigma }_6={\displaystyle \frac{{\Delta }_{\delta ,\mu }^2\left(0\right)\left[-B_2+B_1^2\right]}{2{\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}.$$

1. 

If ${\sigma }_4\le \eta \le {\sigma }_6$, then

$$|a_1-\eta a_0^2|+{\displaystyle \frac{{\Delta }_{\delta ,\mu }^2\left(0\right)}{2{\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}\left\{B_1+B_2-B_1^2\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}{\left|a_0\right|}^2\le {\displaystyle \frac{B_1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}.$$

2. 

If ${\sigma }_6\le \eta \le {\sigma }_5$, then

$$|a_1-\eta a_0^2|+{\displaystyle \frac{{\Delta }_{\delta ,\mu }^2\left(0\right)}{2{\Delta }_{\delta ,\mu }\left(1\right)B_1^2}}\left\{B_1-B_2+B_1^2\left[1-{\displaystyle \frac{2{\Delta }_{\delta ,\mu }\left(1\right)}{{\Delta }_{\delta ,\mu }^2\left(0\right)}}\eta \right]\right\}{\left|a_0\right|}^2\le {\displaystyle \frac{B_1}{2{\Delta }_{\delta ,\mu }\left(1\right)}}.$$

4. Second Hankel Problem

The second Hankel determinant $H_2\left(0\right)=a_0{a}_2-a_1^2$ is a fundamental tool in the study of coefficient problems for both analytic and meromorphic functions. It provides a powerful means of analyzing the interplay between the initial coefficients, revealing the extremal behavior and structural properties of the function classes. Its importance has been widely recognized, and numerous authors have extended its study to various subclasses; see [8,9,10,41,42]. These developments highlight the continued relevance of the Hankel determinant in geometric function theory. Motivated by this rich body of research, we derive a sharp bound for this determinant within our newly defined class of meromorphic functions associated with the Rafid operator, contributing a novel result to this well-established problem.

Theorem 3.

Let $f\left(z\right)$ given by (1) and $\phi \left(z\right)$ given by (7). If $f\left(z\right)\in M_b^{\lambda }(\delta ,\mu ,\phi )$ and $\lambda \in \mathbb{C}\setminus (0,1]$, then

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^2}{4{\Delta }_{\delta ,\mu }^2\left(1\right)}}{\left|{\displaystyle \frac{b}{1-2\lambda }}\right|}^2.$$

(22)

Proof. 

From (13), we have

$$\left[{\displaystyle \frac{1}{2}}b{B}_1\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)+{\displaystyle \frac{1}{2}}b{B}_2\left(c_1{c}_2-{\displaystyle \frac{c_1^3}{2}}\right)+{\displaystyle \frac{1}{8}}b{B}_3{c}_1^3\right]=-3(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)a_2$$

$$+(1-\lambda )(1-2\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(1\right)a_0{a}_1-{(1-\lambda )}^3{\Delta }_{\delta ,\mu }^3\left(0\right)a_0^3,$$

using (14) and (15), we get

$$a_2=-{\displaystyle \frac{b{B}_1}{6(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)}}\left\{\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)+{\displaystyle \frac{B_2}{B_1}}\left(c_1{c}_2-{\displaystyle \frac{c_1^3}{2}}\right)+{\displaystyle \frac{B_3}{4B_1}}{c}_1^3\right\}$$

$$+{\displaystyle \frac{b^2{B}_1^2{c}_1}{24(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)}}\left\{c_2-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right\}-{\displaystyle \frac{b^3{B}_1^3{c}_1^3}{24(1-3\lambda ){\Delta }_{\delta ,\mu }\left(2\right)}}.$$

(23)

Then, applying (14) and (15) to (23), we have

$$|a_0{a}_2-a_1^2|=\left|{\displaystyle \frac{b^2{B}_1^2{c}_1}{12(1-\lambda )(1-3\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left\{\left(c_3-c_1{c}_2+{\displaystyle \frac{c_1^3}{4}}\right)+{\displaystyle \frac{B_2}{B_1}}\left(c_1{c}_2-{\displaystyle \frac{c_1^3}{2}}\right)\right.\right.$$

$$+{\displaystyle \frac{B_3}{4B_1}}{c}_1^3\}-{\displaystyle \frac{b^3{B}_1^3{c}_1^2}{48(1-\lambda )(1-3\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left(c_2-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right)$$

$$+{\displaystyle \frac{b^4{B}_1^4{c}_1^4}{48(1-\lambda )\left(13\lambda \right){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}+{\displaystyle \frac{b^2{B}_1^2}{16{(1-2\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(1\right)}}$$

$$\left.{\left(c_2-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right)}^2\right|.$$

(24)

Substituting for $c_2$ and $c_3$ from (6), we get

$$|a_0{a}_2-a_1^2|=\left|{\displaystyle \frac{b^2{B}_1^2{c}_1}{12(1-\lambda )(1-3\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\right.$$

$$\left\{\left({\displaystyle \frac{c_1^3+2x{c}_1(4-c_1^2)-x^2{c}_1(4-c_1^2){+2y(1-|x|}^2)(4-c_1^2)}{4}}-{\displaystyle \frac{c_1^3+x{c}_1(4-c_1^2)}{2}}+{\displaystyle \frac{c_1^3}{4}}\right)\right.$$

$$+{\displaystyle \frac{B_2}{B_1}}\left({\displaystyle \frac{c_1^3+x{c}_1(4-c_1^2)}{2}}-{\displaystyle \frac{c_1^3}{2}}\right)+{\displaystyle \frac{B_3}{4B_1}}{c}_1^3\}-{\displaystyle \frac{b^3{B}_1^3{c}_1^2}{48(1-\lambda )(1-3\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}$$

$$\left\{{\displaystyle \frac{c_1^2+x(4-c_1^2)}{2}}-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right\}+{\displaystyle \frac{b^4{B}_1^4{c}_1^4}{48(1-\lambda )(1-3\lambda ){\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}$$

$$\left.-{\displaystyle \frac{b^2{B}_1^2}{16{(1-2\lambda )}^2{\Delta }_{\delta ,\mu }^2\left(1\right)}}{\left({\displaystyle \frac{c_1^2+x(4-c_1^2)}{2}}-{\displaystyle \frac{c_1^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right)}^2\right|.$$

Since $|c_1|\le 2$ by Lemma 1, let $c_1=c$ and freely assume that $c\in [0,2]$; we obtain

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^{2}c}{12{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^2}{(1-\lambda )(1-3\lambda )}}\right|·$$

$$\left|\left({\displaystyle \frac{c^3+2pc(4-c^2)-p^{2}c(4-c^2){+2y(1-|p|}^2)(4-c^2)}{4}}-{\displaystyle \frac{c^3+pc(4-c^2)}{2}}+{\displaystyle \frac{c^3}{4}}\right)\right.$$

$$\left.+{\displaystyle \frac{B_2}{B_1}}\left({\displaystyle \frac{c^3+pc(4-c^2)}{2}}-{\displaystyle \frac{c^3}{2}}\right)+{\displaystyle \frac{B_3}{4B_1}}{c}^3\right|+{\displaystyle \frac{B_1^3{c}^2}{48{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^2}{(1-\lambda )(1-3\lambda )}}\right|$$

$$\left|{\displaystyle \frac{c^2+p(4-c^2)}{2}}-{\displaystyle \frac{c^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right|+{\displaystyle \frac{B_1^4{c}^4}{48{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^4}{(1-\lambda )(1-3\lambda )}}\right|$$

$$+{\displaystyle \frac{B_1^2}{16{\Delta }_{\delta ,\mu }^2\left(1\right)}}{\left|{\displaystyle \frac{b}{1-2\lambda }}\right|}^2{\left|{\displaystyle \frac{c^2+p(4-c^2)}{2}}-{\displaystyle \frac{c^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right|}^2\le G\left(p\right),$$

with $p=\left|x\right|\le 1$. Additionally,

$$G^{\prime }\left(p\right)\le {\displaystyle \frac{B_1^{2}c}{12{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^2}{(1-\lambda )(1-3\lambda )}}\right|·$$

$$\left|\left({\displaystyle \frac{c^3}{4}}-c\right)+{\displaystyle \frac{B_2}{B_1}}\left(2c-{\displaystyle \frac{c^3}{2}}\right)+{\displaystyle \frac{B_3}{4B_1}}{c}^3\right|+{\displaystyle \frac{B_1^3{c}^2}{48{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^2}{(1-\lambda )(1-3\lambda )}}\right|$$

$$\left|2-{\displaystyle \frac{c^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right|+{\displaystyle \frac{B_1^4{c}^4}{48{\Delta }_{\delta ,\mu }\left(0\right){\Delta }_{\delta ,\mu }\left(2\right)}}\left|{\displaystyle \frac{b^4}{(1-\lambda )(1-3\lambda )}}\right|$$

$$+{\displaystyle \frac{B_1^2}{16{\Delta }_{\delta ,\mu }^2\left(1\right)}}{\left|{\displaystyle \frac{b}{1-2\lambda }}\right|}^2{\left|2-{\displaystyle \frac{c^2}{2}}\left[1-{\displaystyle \frac{B_2}{B_1}}+B_{1}b\right]\right|}^2.$$

Through simple computations, we can demonstrate that $G^{\prime }\left(p\right)>0$ for $p>0$, which implies that G is a function that increases. Hence, the upper bound for (24) corresponds to $p=1$ and $c=0$, obtaining (22).     □

Putting $\lambda =0$ in Theorem 3, we obtain

Corollary 5.

Let $f\left(z\right)$ given by (1) and $\phi \left(z\right)$ given by (7). If $f\left(z\right)\in S_b^{*}(\delta ,\mu ,\phi )$, then

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^2{\left|b\right|}^2}{4{\Delta }_{\delta ,\mu }^2\left(1\right)}}.$$

Putting $\lambda =0$ and $b=1$ in Theorem 3, we obtain

Corollary 6.

Let $f\left(z\right)$ given by (1) and $\phi \left(z\right)$ given by (7). If $f\left(z\right)\in {\Sigma }^{*}(\delta ,\mu ,\phi )$, then

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^2}{4{\Delta }_{\delta ,\mu }^2\left(1\right)}}.$$

Putting $b=(1-\rho )e^{-i\theta }cos\theta$ ($0\le \rho <1$, $\left|\theta \right|<{\displaystyle \frac{\pi }{2}}$) in Theorem 3, we obtain

Corollary 7.

Let $f\left(z\right)$ given by (1) and $\phi \left(z\right)$ given by (7). If $f\left(z\right)\in M_{(1-\rho )e^{-i\theta }cos\theta }^{\lambda }(\delta ,\mu ,\phi )$ and $\lambda \in \mathbb{C}\setminus (0,1]$, then

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^2(1-\rho )cos\theta }{{4|1-2\lambda |}^2{\Delta }_{\delta ,\mu }^2\left(1\right)}}.$$

Putting $\lambda =0$ and $b=(1-\rho )e^{-i\theta }cos\theta$ ($0\le \rho <1$, $\left|\theta \right|<{\displaystyle \frac{\pi }{2}}$) in Theorem 3, we obtain

Corollary 8.

Let $f\left(z\right)$ given by (1) and $\phi \left(z\right)$ given by (7). If $f\left(z\right)\in M_{(1-\rho )e^{-i\theta }cos\theta }^0(\delta ,\mu ,\phi )$, then

$$|a_0{a}_2-a_1^2|\le {\displaystyle \frac{B_1^2(1-\rho )cos\theta }{4{\Delta }_{\delta ,\mu }^2\left(1\right)}}.$$

In addition, we translate the theoretical framework of the previous results to electromagnetic field theory in the following section.

5. Applications in the Electromagnetic Field

In this section, we translate the theoretical framework into a versatile modeling tool for problems in $2D$ electromagnetic field theory. Our approach is to apply the operator $I_{\mu }^{\delta }$ to a known source potential, $f\left(z\right)$, to construct a new effective potential, $I_{\mu }^{\delta }f\left(z\right)$.

This transformed potential is mathematically designed to model the structural changes that a source field endures in a complicated setting. The operator’s parameters $\mu$ and $\delta$ model the effects of field regularization and spectral redistribution, which are common in wave–matter interactions. This method enables us to connect the rigorous results of our theoretical investigation to the geometric properties of physical fields, as we will demonstrate.

5.1. The Operator $I_{\mu }^{\delta }$ as a Field Transformation Kernel

The integral operator $I_{\mu }^{\delta }$ given in (2) serves as the core of our modeling framework. Its kernel ${\Delta }_{\delta ,\mu }\left(k\right)={\displaystyle \frac{{(1-\mu )}^{k+1}\mathrm{\Gamma }(k+\delta +2)}{\mathrm{\Gamma }(\delta +1)}}$ encapsulates the following physical phenomena through its parameters:

• Multipole Suppression and Field Regularization: We interpret the parameter $\mu$$(0\le \mu <1)$ as a regularization parameter. Its function is based on the operator’s kernel, which includes the damping factor ${(1-\mu )}^{k+1}$. This term has direct control over the amplitudes of the multipole coefficients $a_k$ in the transformed potential.
  The mechanism proceeds as follows: When $\mu$ is close to 0, the factor ${(1-\mu )}^{k+1}$ approaches 1 for all k, while the initial multipole moments remain basically unaltered. As $\mu$ approaches 1, the base $(1-\mu )$ becomes a small fraction. For higher-order moments (large k), raising this fractional base to a large power reduces the damping factor to an exceedingly small value, thereby suppressing these terms. As a result, geometric damping is most effective at attenuating the high-frequency (large k) components of the potential.
  This mathematical approach is similar to a low-pass spatial filter. It regularizes the singularity of the field by smoothing the potential, which is physically significant because real-world dispersive media frequently cannot tolerate arbitrarily high spatial frequency fields. We introduce this tunable process as a mathematical model for how environmental factors can limit the spatial complexity of the source field.
• Spectral Redistribution: We interpret the parameter $\delta$ ($0\le \delta \le 1$) as spectral order. It provides a technique for redistributing the transformed field’s energy among its multipole components by altering their relative weights. This is achieved by the Gamma function, $\mathrm{\Gamma }(k+\delta +2)$, in the operator’s kernel.
  The key characteristic of this term is its super-polynomial growth with k. This means it grows quicker than any simple power, such as $k^2$ and $k^3$. The value of $\delta$ within the prescribed range tunes this rapid growth. With an increase in $\delta$ from 0 to 1, $\mathrm{\Gamma }(k+\delta +2)$ grows faster with k, increasing the amplitudes of higher-order multipole moments (large k) compared to lower-order ones.
  Physically, this corresponds to broadening the spatial frequency spectrum of the potential. While the $\mu$ parameter acts as a low-pass filter, the $\delta$ parameter acts as a spectral shaping tool, enhancing the field with finer details and more complex spatial variations. This enables the operator to model phenomena in which an interaction with a medium or structure enhances the high-frequency components of a field.

For a meromorphic function $f\left(z\right)$ given by (1), we interpret it as a complex potential in 2D electrostatics as

• The function’s principal part at the origin, the $1/z$ term, represents the potential of a 2D line dipole source [43].
• The analytic part of the function $g\left(z\right)=a_0+a_{1}z+a_2{z}^2+...$ represents a superposed external potential that is regular at the origin.

The leading coefficients $a_k$ of this external field have the following physical meaning:

• $a_0$: Represents a constant potential offset. It contributes no electric field as $E=-\nabla a_0=0$.
• $a_1$: Represents the complex amplitude of a uniform external electric field. The field strength is proportional to $|a_1|$, and its direction is determined by $arg\left(a_1\right)$.
• $a_2$: Represents the strength of a quadrupole field, which generates an electric field that increases linearly with distance from the origin, as shown in a field gradient.

This framework allows us to study the interaction of a central dipole source with a complex background field. The following visualization in Figure 1 demonstrates the transformation induced by the operator $I_{\mu }^{\delta }$. We compare the original potential for $a_0=2$, $a_1=3$, and $a_k=0$ for $k\ge 2$:

$$f\left(z\right)={\displaystyle \frac{1}{z}}+2+3z,$$

with its transformed version $I_{\mu }^{\delta }f\left(z\right)$. For $\mu =0.3$ and $\delta =1$, the approximate potential is yielded as

$$I_{0.3}^{1}f\left(z\right)={\displaystyle \frac{1}{z}}+3+9z.$$

The plot shows field magnitude in the punctured unit disc ${\mathbb{U}}^{*}$, demonstrating how the operator alters the spatial distribution of field intensity while maintaining the essential singularity at $z=0$.

Figure 1 shows the effect of this transformation on the magnitude of the field. The original potential diagram on the left shows a strong field concentration at the singularity (yellow core). The plot on the right, which depicts the transformed potential, represents two important physical analogs of the operator’s parameters. First, the field regularization effect, dictated by $\mu =0.3$, is obvious in the reduced field intensity around the origin (blue core). This demonstrates the suppression of the source’s strength. Second, the spectral redistribution, governed by $\delta =1$, is seen as an increased field intensity in the outer regions of the figure (yellow arcs), demonstrating how the operator can transfer the field’s structure to higher spatial frequencies.

5.2. Subordination and Field Geometry Control

In this section, we will apply the theoretical concept of subordination to the practical design of efficient electromagnetic fields. The subordination condition provides a flexible framework for constraining function classes. For our application, we are interested in the property of starlikeness, which for a meromorphic potential $f\left(z\right)$ is defined by the specific subordination

$$-{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\prec \phi \left(z\right).$$

For this analysis, we choose the canonical univalent function:

$$\phi \left(z\right)={\displaystyle \frac{1+z}{1-z}}.$$

This specific choice corresponds to the classical condition for starlikeness

$$-\Re \left\{{\displaystyle \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}}\right\}>0.$$

Geometrically, functions obeying this subordination map the punctured unit disc to a starlike domain. A powerful correspondence can be drawn between this geometric property and the physics of power flow. According to this analogy, the radial non-looping streamlines of a vector field generated by a starlike function correspond to a desirable vortex-free unidirectional power flow. This interpretive framework, which links a purely geometric condition to a desirable physical outcome, is an effective method for modeling field behavior. The utility of applying subordination theory to constrain and guide solutions in complex electromagnetic problems has been demonstrated in numerous domains; see [14,15,16].

We now investigate how our operator $I_{\mu }^{\delta }$, as stated in Section 5.1, functions as a field transformation kernel, and how it interacts with this critical geometric constraint. We explore two distinct cases by applying the operator with parameters $\mu =0.3$ and $\delta =1$:

1. 

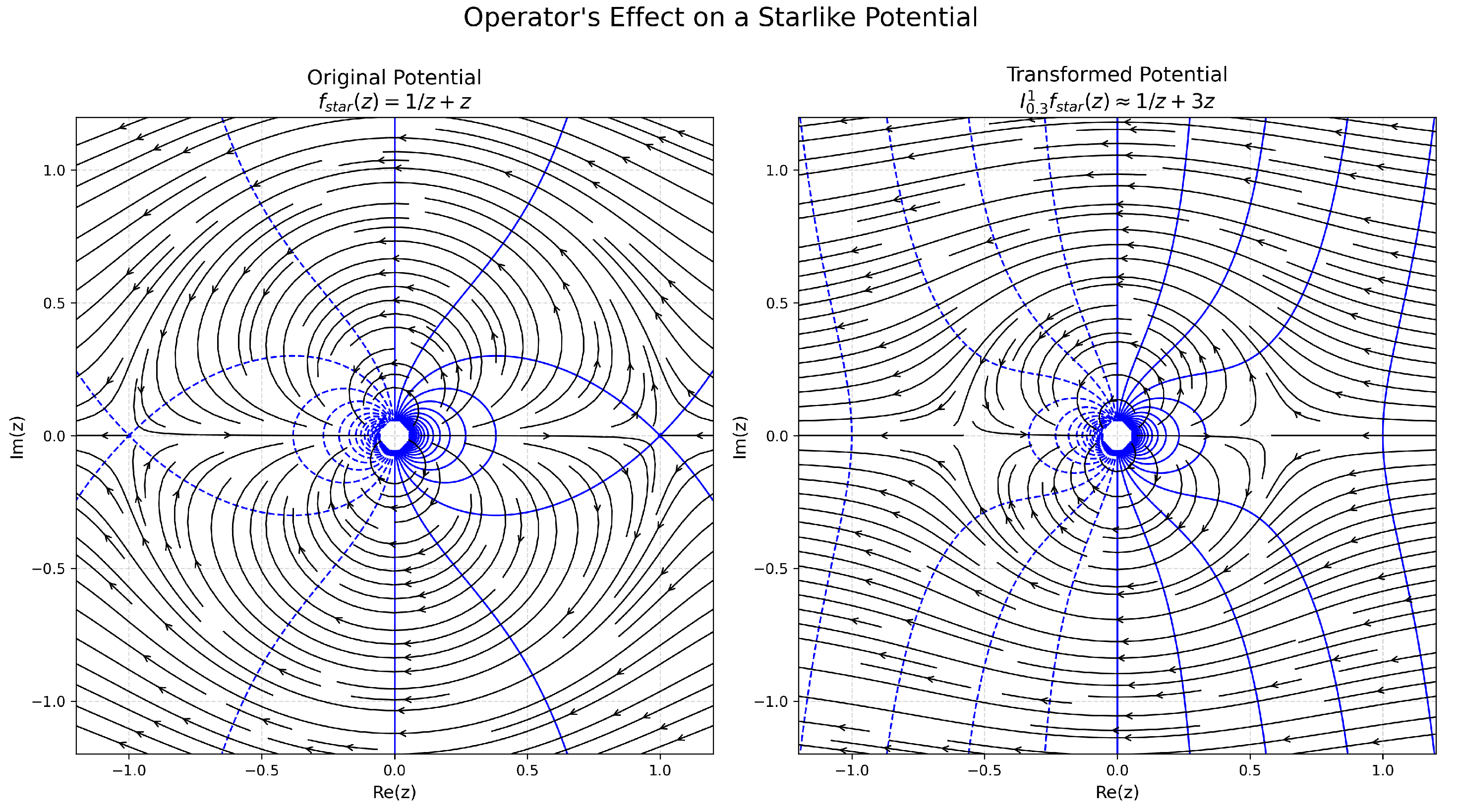
Starlike Potential: We begin with

$$f_{\mathrm{star}}\left(z\right)={\displaystyle \frac{1}{z}}+z(a_0=0,a_1=1\mathrm{and}{a}_k=0\mathrm{for}k\ge 2).$$

This function is starlike because the expression

$$-{\displaystyle \frac{z{f}_{\mathrm{star}}^{\prime }\left(z\right)}{f_{\mathrm{star}}\left(z\right)}}={\displaystyle \frac{1-z^2}{1+z^2}},$$

satisfying the subordination. Applying our operator yields the transformed potential

$$I_{0.3}^1{f}_{\mathrm{star}}\left(z\right)={\displaystyle \frac{1}{z}}+3z.$$

Figure 2 visualizes the field geometries.

The figure demonstrates how the operator acts on an established stable configuration. The original potential (left panel) demonstrates the ideal vortex-free field found in starlike functions. The transformed potential (right panel) is also starlike. The regularization ($\mu$) does not suppress lower-order multipoles, while the spectral redistribution ($\delta$) just rescales the uniform field component ($a_1$). As a result, the operator keeps the underlying vortex-free structure, demonstrating its stable behavior on functions that already satisfy the desired geometric restriction.

2. 

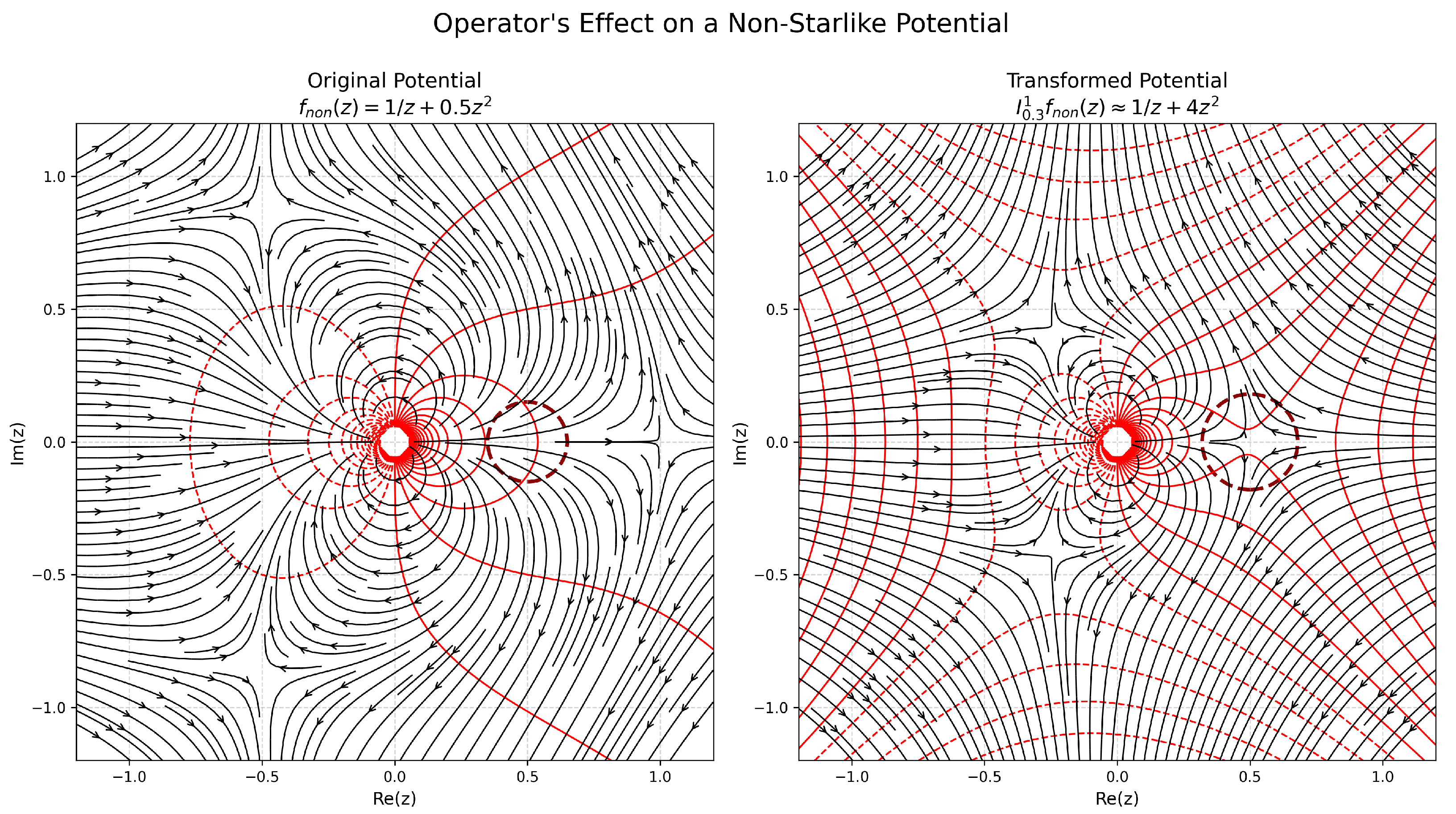
The Non-Starlike Potential: Next, we consider the potential

$$f_{\mathrm{non}}\left(z\right)={\displaystyle \frac{1}{z}}+0.5z^2(a_0,a_1=0,a_2=0.5\mathrm{and}{a}_k=0\mathrm{for}k\ge 2),$$

which violates the starlikeness subordination condition. Applying the operator yields the transformed effective potential

$$I_{0.3}^1{f}_{\mathrm{non}}\left(z\right)=1/z+4z^2.$$

Figure 3 illustrates the effect of this transformation.

The results visualized in Figure 3 are particularly revealing. The original potential field (left panel) shows a strong parasitic energy vortex as a direct result of breaking the starlikeness condition. The right panel depicts the transformed potential field. The operator’s action in this case is more pronounced: the spectral redistribution mechanism, driven by $\delta =1$, has amplified the $a_2$ coefficient by a factor of over 8 (${\Delta }_{1,0.3}\left(2\right)\approx 8$), whereas the regularization from $\mu =0.3$ provides only slight dampening. The net effect is a considerable augmentation of the $z^2$ term responsible for the non-starlike behavior, leading the energy vortex to be visually exacerbated. This example effectively demonstrates how the operator may be used to selectively boost specific multipole moments, modifying a field’s geometric features and managing its adherence to subordination constraints.

Taken together, the studies of the starlike and non-starlike cases in Figure 2 and Figure 3 illustrate the operator’s dual nature. Figure 2 shows the operator’s stability and preservation properties: when acting on a potential that already satisfies a desirable geometric constraint (starlikeness), the operator preserves that property by simply rescaling the field components. In contrast, Figure 3 demonstrates the operator’s transformative and amplifying properties: when acting on a potential with undesirable geometric features (a vortex), the operator’s spectral redistribution mechanism can selectively enhance such features. This demonstrates the operator’s utility not just in preserving ideal field structures but also in tweaking or aggravating specific geometric properties of a field, making it a versatile tool for simulating complex field transformations.

6. Conclusions

This paper established sharp coefficient bounds for meromorphic univalent functions in the class $M_b^{\lambda }(\delta ,\mu ,\phi )$, introducing a novel integral operator $I_{\mu }^{\delta }$ that generalizes existing transformations. We obtained the bounds for the Fekete–Szegö inequality and the second Hankel determinant bounds, constructing extremal functions to demonstrate sharpness. Also, we bridged geometric function theory with electromagnetic applications, presenting a framework where the operator acts as a transformation kernel to produce an effective potential. Our applications demonstrated that the operator’s parameters govern physical equivalents of field regularization and spectral redistribution. The major application demonstrated how subordination theory, when combined with our operator, may be utilized to study and control field geometric properties, such as vortex-free power flow conditions. Our findings demonstrate the usefulness of this new operator in both pure and applied contexts, providing an original instrument for investigating the link between geometric function theory and physical field modeling. The numerous linkages between the obtained coefficient inequalities and physical observables warrant a further in-depth analysis. As a result, a separate devoted study will be conducted to delve further into the physical interpretation of the Fekete–Szegö and Hankel determinant bounds, notably in terms of nano-antenna energy localization and scattering anisotropy.