On Structural Characterization and Computation of the Diameter and Girth of Bipartite Gap Poset Graphs with Python Application

Abstract

In this article, a correspondence between some important classes of numerical semigroups and well-known families of bipartite graphs has been established. Also, it has been demonstrated that, if $\mathrm{m}(\mathrm{S})$ is the multiplicity of a numerical semigroup $\mathrm{S}$, then the diameter and the girth of bipartite gap poset graphs are bounded by the numbers $2\mathrm{m}(\mathrm{S})-3$ and $\mathrm{m}(\mathrm{S})-1$, respectively. Moreover, the Python code to compute the diameter and girth of gap poset graphs has been implemented.

1. Introduction and Preliminaries

Algebraic graph theory is an interrelated research field that explores the fundamental relationships between algebra and graph theory [1,2]. It focuses on how algebraic structures such as groups, rings, and semigroups can be viewed and explored by using graphs, allowing graph-theoretic methods to expose algebraic aspects and vice versa. In 1878, Cayley [3] laid the foundation of this field by introducing Cayley graphs to represent groups graphically, offering visual and structural insight into group operations and symmetries. Later, in 1988, Beck [4] made a significant contribution to this field by introducing the concept of zero-divisor graphs for commutative rings. In this construction, the vertex set consists of non-zero zero-divisors of the ring, and two unique members are neighboring if their product is zero. This graphical form has been effective for understanding ring-theoretic characteristics like annihilators, ideals, and prime elements. Following Beck’s work, numerous authors expanded and generalized this concept. Anderson and Livingston [5] developed the zero-divisor graph by focusing primarily on non-zero zero-divisors, while Anderson and Badawi [6,7] investigated modifications such as entire graphs and ideal-based graphs, providing more information about the structure of commutative rings. Recently, different mathematicians [8,9,10,11,12] have assigned graphs to numerical semigroups and studied some properties of the graphs.

Graphs are widely used across numerous disciplines, including computer science, biology, communication networks, and operations research, due to their ability to abstractly represent complex systems, such as transportation routes, social interactions, molecular structures, and data networks [13,14]. In particular, bipartite graphs based on algebraic concepts are important for expressing interactions in chemical reaction networks and metabolic pathways [15]. This collaboration not only enriches the theoretical foundations of both fields but also helps to solve real-world problems using a combined algebraic-combinatorial perspective.

A graph $G=(V,E)$ consists of a finite set of vertices V and a set of edges E, where each edge connects a pair of vertices. The neighborhood of a vertex v in a simple undirected graph $G=(V,E)$, denoted by $N(v)$, is the set of all the vertices adjacent to v, and its cardinality is known as a degree of v, denoted by $deg(v)$. The diameter of a graph is the greatest distance between any pair of vertices in the graph, denoted by $diam(G)$. A cycle is a closed path with no repeated edges or internal vertices, and the girth of a graph is defined as the length of its shortest cycle, represented by $gr(G)$. A path graph $P_n$ is a simple linear graph where each internal vertex is adjacent to exactly two others, and the endpoints have a degree 1. A graph $K_n$ is said to be complete if every pair of distinct vertices is joined by an edge. A bipartite graph $B_G$ admits a vertex partition into two disjoint sets such that all the edges connect vertices across the sets, with no edges within a set. It is said to be balanced if both parts have equal cardinality. A regular graph is one in which all the vertices have the same degree, reflecting a uniform local structure.

In algebraic and applied contexts, graph invariants such as diameter and girth play pivotal roles in understanding both abstract structure and practical behavior. Within the algebraic framework of numerical semigroups, a small diameter in the associated gap poset graph reflects tightly interrelated gaps, often corresponding to semigroups with smaller multiplicity or denser Apéry sets. It is a property that directly relates to efficiency and robustness in real-world networks. For example, in communication networks, diameter is used to evaluate the Diameter-Constrained Reliability (DCR), which measures the probability that two nodes remain connected by a path not exceeding a prescribed length bound. This has practical implications in designing networks with bounded delays and fault tolerance, where minimizing diameter ensures faster data transmission and resilience to failures. Research such as [16,17,18,19,20,21] has highlighted that computing DCR is generally NP-hard, but exploiting diameter-based properties allows identification of specific topologies where reliability can be computed in polynomial time. Thus, the study of graph diameter not only advances algebraic graph theory but also plays a key role in optimizing communication systems, transportation routes, and distributed computing architectures. Girth reveals redundancy or minimal algebraic relations among gaps. A small girth may indicate fundamental additive relations in the gap structure. Beyond theory, these invariants are widely used in network reliability and optimization. Networks with low diameter ensure high communication efficiency and resilience, while high girth avoids short feedback loops that can destabilize systems [22].

A numerical semigroup is a subset $\mathrm{S}\subseteq N_0$ that is closed under addition, contains the zero element, and has a finite complement in $N_0$. The elements of $N_0\setminus \mathrm{S}$ are called gaps, and their total number is the genus $g(\mathrm{S})$ of the semigroup. The Frobenius number $F(\mathrm{S})$ is the largest integer not in $\mathrm{S}$, and the multiplicity is the smallest non-zero element of $\mathrm{S}$, denoted by $\mathrm{m}(\mathrm{S})$. Given a nonempty set $A\subseteq N_0$, the submonoid generated by A, denoted $\langle A\rangle$, is a numerical semigroup if and only if $gcd(A)=1$. Every numerical semigroup has a unique minimal system of generators, and the number of these generators defines the embedding dimension $e(\mathrm{S})$. The Frobenius problem [23,24] explores formulas for calculating the Frobenius number and genus of a numerical semigroup. Sylvester solved this problem in [25] for numerical semigroups with embedding dimension two. Because of their applications in coding theory, algebraic geometry, and factorization theory, numerical semigroups have received much attention in algebraic and combinatorial research over the last few decades. Several structural features have been investigated, including symmetric, pseudo-symmetric, and nearly symmetric semigroups [26]. The link between numerical semigroups and Apéry sets, Kunz coordinates, and their representation through combinatorial objects such as trees and posets has been widely studied in the literature [27,28], providing powerful tools for categorization and computing.

Partially ordered sets (posets) are mathematical structures composed of elements connected by a binary relation that is reflexive, antisymmetric, and transitive. This framework allows for the representation of relationships where not all the elements are comparable, making it useful in various fields, including computer science, combinatorics, and chemistry. Wachs [29] provided a comprehensive overview of poset theory and its connections with topology, particularly in understanding the structure of order complexes. Felsner et al. [30] proposed the concept of poset dimension, which has been further examined in following surveys, showing how posets can be represented as linear-order intersections and how this relates to computing complexity. De Loof et al. [31] demonstrated that posets may be utilized for multi-criteria ranking, which is useful in decision-making systems like chemical assessments and preference models. Posets also have a role in coding theory as they are utilized to define novel distance measures for error correction, as explained in Springer’s work on poset metrics. Additionally, posets have been extensively studied in the context of algebraic structures such as distributive lattices and Boolean algebras, leading to significant results in universal algebra and logic [32].

Posets are commonly formed in algebraic combinatorics from monomial ideals, numerical semigroups, and group actions, and they provide a convenient framework for defining simplicial complexes, resolving homological dimensions, and storing algebraic constraints in graphical form.

Several computational tools exist for the study of numerical semigroups, most notably the numericalsgps package in the GAP system, which provides a wide range of algebraic and combinatorial functionalities. While these packages are powerful, they often require familiarity with specialized algebraic software and may not provide immediate visualization features for graph structures. Our approach differs in that it leverages Python version 3.13.5, a widely accessible programming language, together with graph-theoretic libraries such as NetworkX and visualization packages like Matplotlib version 3.5. This makes it possible to construct, analyze, and visualize gap poset graphs in an integrated manner. Furthermore, our method is easily extensible to compute new invariants that are not yet implemented in standard packages. Thus, while the existing software emphasizes algebraic operations on semigroups, our contribution lies in providing a flexible user-friendly framework that directly bridges numerical semigroup theory with graph theory and visualization.

The remainder of this paper is organized as follows. In Section 2, we determine the conditions under which bipartite gap poset graphs are connected or disconnected. In Section 3, we characterize the bipartite gap poset graphs into different well-known families of graphs. In Section 4, we provide a bound on the diameter and a conjecture on the upper bound of the girth of a bipartite gap poset graph. In Section 5, we present the algorithms for constructing gap poset graphs, along with procedures to compute key graph invariants, such as diameter and girth. This paper concludes in Section 6.

2. Some Results on Connectedness of Bipartite Gap Poset Graphs

Let $x,y\in \mathrm{G}$, where $\mathrm{G}$ is the set of gaps of numerical semigroup $\mathrm{S}$, and then $y{\prec }_{\mathrm{S}}x$ if and only if $x-y\in \mathrm{S}$. Evidently, $(\mathrm{G},{\prec }_{\mathrm{S}})$ is a poset. An undirected simple graph $J_{\mathrm{G}}(\mathrm{S})$ is a graph such that

$$\mathrm{V}(J_{\mathrm{G}}(\mathrm{S}))=\{v_x:x\in \mathrm{G}\},$$

and

$$\mathrm{E}(J_{\mathrm{G}}(\mathrm{S}))=\{v_x{v}_y\iff x{\prec }_{\mathrm{S}}yory{\prec }_{\mathrm{S}}x\}.$$

A numerical semigroup $\mathrm{S}$ is elementry if and only if $F(\mathrm{S})<2\mathrm{m}(\mathrm{S})$. This implies that gap set $\mathrm{G}$ of $\mathrm{S}$ is of the form $\{1,2,\dots ,\mathrm{m}(\mathrm{S})-1\}\cup \mathcal{A}$, where $\mathcal{A}\subseteq \{\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+2,\dots ,2\mathrm{m}(\mathrm{S})-1\}$. It is demonstrated in [33] (see Theorem 2) that, if $\mathcal{A}$ is empty, then $J_{\mathrm{G}}(\mathrm{S})$ is an edgeless graph. In this paper, we consider $\mathcal{A}$ is always non-empty, and therefore $\mathrm{m}(\mathrm{S}) \le |J_{\mathrm{G}}(\mathrm{S})| \le 2\mathrm{m}(\mathrm{S})-2$. The following theorem demonstrates correspondence between the elementary numerical semigroups and the bipartite gap poset graphs.

Theorem 1. 

A numerical semigroup $\mathrm{S}$ is elementary if and only if the gap poset graph $J_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph.

Proof. 

$(\Rightarrow )$ This implication follows from Lemma $2.1$ of [33].

 $(\Leftarrow )$ Suppose $J_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph but $\mathrm{S}$ is not an elementary numerical semigroup. Then, from Theorem $2.4$ of [33], it follows that girth of $J_{\mathrm{G}}(\mathrm{S})$ is 3, which is not possible as $J_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph. Hence, $\mathrm{S}$ is an elementary numerical semigroup. □

In the rest of paper, we denote a bipartite gap poset graph by $B_{\mathrm{G}}(\mathrm{S})$. The following lemma provides us necessary and sufficient conditions for the connectedness of $B_{\mathrm{G}}(\mathrm{S})$ in terms of the Frobenius number of $\mathrm{S}$.

Lemma 1. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite gap poset graph and $V(B_{\mathrm{G}}(\mathrm{S}))=V_1\cup V_2$, where $V_1=\{v_1,v_2,\dots ,v_{\mathrm{m}(\mathrm{S})-1}\}$ and $V_2\subseteq \{v_{\mathrm{m}(\mathrm{S})+1},v_{\mathrm{m}(\mathrm{S})+2},\dots ,v_{2\mathrm{m}(\mathrm{S})-1}\}$. Then, the following statements hold:

(1) 

If $B_{\mathrm{G}}(\mathrm{S})$ is connected, then $F(\mathrm{S})=2\mathrm{m}(\mathrm{S})-1$.

(2) 

If $F(\mathrm{S})=2\mathrm{m}(\mathrm{S})-1$ and for every $i,j\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-1\}$, $N(v_i)\cap N(v_j)\ne \varnothing$, then $B_{\mathrm{G}}(\mathrm{S})$ is connected.

Proof. 

(1) If $F(\mathrm{S})\ne 2\mathrm{m}(\mathrm{S})-1$, then $F(\mathrm{S})=\mathrm{m}(\mathrm{S})+x$ for some $x\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-2\}$. Note that

$$(\mathrm{m}(\mathrm{S})+x)-(\mathrm{m}(\mathrm{S})-1)=x+1\notin \mathrm{S},$$

as min $(x+1)=2$ and max $(x+1)=\mathrm{m}(\mathrm{S})-1$. This implies $v_{\mathrm{m}(\mathrm{S})-1}$ has no edge with any vertex of $V_2$. This is a contradiction as $B_{\mathrm{G}}(\mathrm{S})$ is a connected graph; therefore, the Frobenius number of $\mathrm{S}$ must be $2\mathrm{m}(\mathrm{S})-1$.

(2) We need to show that there is path between every two distinct vertices $u,v\in \mathrm{V}(B_{\mathrm{G}}(\mathrm{S}))$. For this, we have the following cases:

• Case-1: If $u,v\in V_1$, then there exist some $w\in V_2$ such that $u-w-v$ is a path between u and v.
• Case-2: Let $u,v\in V_2$, and then we may assume that $u=v_{\mathrm{m}+x}$ and $v=v_{\mathrm{m}+y}$, where $x,y\in \{1,2,\dots ,\mathrm{m}-1\}$ with $x\ne y$. This implies there exist $v_x,v_y\in V_1$ such that $v_{\mathrm{m}+x}$ has an edge with $v_x$ and $v_{\mathrm{m}+y}$ has an edge with $v_y$ since $(\mathrm{m}(\mathrm{S})+x)-x=\mathrm{m}(\mathrm{S})=(\mathrm{m}(\mathrm{S})+y)-y$. Consider $v_{\mathrm{m}+z}\in N(v_x)\cap N(v_y)$ for some $z\in \{1,2,\dots ,\mathrm{m}-1\}$. This implies a path between u and v is $u-v_x-v_{\mathrm{m}+z}-v_y-v$.
• Case-3: Let $u\in V_1$ and $v\in V_2$. Assume that $v=v_{\mathrm{m}+x}$ for some $x\in \{1,2,\dots ,\mathrm{m}-1\}$. If $u=v_x$, then u and v are connected by an edge, so we have $u-v$. Now, if $u\ne v_x$, then there exist some $v_{\mathrm{m}+z}\in N(u)\cap N(v_x)$ for some $z\in \{1,2,\dots ,\mathrm{m}-1\}$ such that $u-v_{\mathrm{m}+z}-v_x-v$. □

If $F(\mathrm{S})=2\mathrm{m}(\mathrm{S})-1$, then $B_{\mathrm{G}}(\mathrm{S})$ may be disconnected (see the following example).

Example 1. 

Let $\mathrm{S}=\langle 5,7,8,11\rangle$, and then gap poset of $\mathrm{S}$ is $\mathrm{G}=\{1,2,3,4,6,9\}.$ The corresponding graph $B_{\mathrm{G}}(\mathrm{S})$ is given in Figure 1. Clearly, $F(\mathrm{S})=2(5)-1$, but $B_{\mathrm{G}}(\mathrm{S})$ is a disconnected graph.

3. Characterization of Bipartite Gap Poset Graphs of Minimum and Maximum Orders

We start this section by characterizing bipartite gap poset graphs of minimum order.

Proposition 1. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite gap poset graph of order $\mathrm{m}(\mathrm{S})$ and $F(\mathrm{S})=2\mathrm{m}(\mathrm{S})-1$, and then $B_{\mathrm{G}}(\mathrm{S})$ is connected.

Proof. 

We have $\frac{F(\mathrm{S})+1}{2}=\mathrm{m}(\mathrm{S})=\left|\mathrm{G}\right|$. This implies $\mathrm{S}$ is symmetric; then, from Proposition 2.2 of [33], it follows that $B_{\mathrm{G}}(\mathrm{S})$ is a connected graph. □

Proposition 2. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a disconnected bipartite gap poset graph of order $\mathrm{m}(\mathrm{S})$, and then $B_{\mathrm{G}}(\mathrm{S})$ has $2\mathrm{m}(\mathrm{S})-F(\mathrm{S})$ disconnected components.

Proof. 

Since $B_{\mathrm{G}}(\mathrm{S})$ is a disconnected bipartite poset graph of order $\mathrm{m}(\mathrm{S})$, therefore we have

$$V(B_{\mathrm{G}}(\mathrm{S}))=\{v_1,v_2,\dots ,v_{\mathrm{m}(\mathrm{S})-1}\}\cup \{v_{F(\mathrm{S})}\},$$

where $v_{F(\mathrm{S})}\in \{v_{\mathrm{m}(\mathrm{S})+1},v_{\mathrm{m}(\mathrm{S})+2},\dots ,v_{2\mathrm{m}(\mathrm{S})-2}\}$. We may assume that $F(\mathrm{S})=\mathrm{m}(\mathrm{S})+g$ for some $g\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-2\}$. Choose $x\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-1\}$ such that $1 \le g<x \le \mathrm{m}(\mathrm{S})-1$, and then $1<m-(x-g)<\mathrm{m}(\mathrm{S})-1$. This yields $\mathrm{m}(\mathrm{S})+g-x\notin \mathrm{S}$ for every value of x. So, number of vertices $v_i$ for $1 \le i \le \mathrm{m}(\mathrm{S})-1$ that are not connected with the vertex $v_{F(\mathrm{S})}$ is $\mathrm{m}(\mathrm{S})-g-1$. This implies total number of disconnected components of $B_{\mathrm{G}}(\mathrm{S})$ is $\mathrm{m}(\mathrm{S})-g=2\mathrm{m}(\mathrm{S})-F(\mathrm{S})$. □

Theorem 2. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite graph of order $\mathrm{m}(\mathrm{S})$. Then, the following statements are equivalent:

(1) 

$\mathrm{S}$ is an interval numerical semigroup of embedding dimension $\mathrm{m}(\mathrm{S})-1$.

(2) 

$\mathrm{S}$ is a symmetric numerical semigroup.

(3) 

The graph $B_{\mathrm{G}}(\mathrm{S})$ is isomorphic to the star graph $K_{1,\mathrm{m}(\mathrm{S})-1}$.

Proof. 

Since $B_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph of order $\mathrm{m}(\mathrm{S})$, therefore we have

$$V(B_{\mathrm{G}}(\mathrm{S}))=\{v_1,v_2,\dots ,v_{\mathrm{m}(\mathrm{S})-1}\}\cup \{v_x\},$$

where $v_x\in \{v_{\mathrm{m}(\mathrm{S})+1},v_{\mathrm{m}(\mathrm{S})+2},\dots ,v_{2\mathrm{m}(\mathrm{S})-1}\}$.

• $(1)\Rightarrow (2):$ This is obvious.
• $(2)\Rightarrow (3):$ If S is symmetric, then Proposition 1 provides $B_{\mathrm{G}}(\mathrm{S})$, a connected graph, and gr$(B_{\mathrm{G}}(\mathrm{S}))\in \{3,\infty \}$. This implies every vertex $v_i$ for $1 \le i \le \mathrm{m}(\mathrm{S})-1$ has an edge with the vertex $v_x$. As $B_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph, therefore gr$(B_{\mathrm{G}}(\mathrm{S}))$ cannot be 3, so $B_{\mathrm{G}}(\mathrm{S})\cong K_{1,\mathrm{m}(\mathrm{S})-1}$.
• $(3)\Rightarrow (1):$ This is straightforward. □

Theorem 3. 

The graph $B_{\mathrm{G}}(\mathrm{S})$ is a complete bipartite graph if and only if $B_{\mathrm{G}}(\mathrm{S})$ is a star graph.

Proof. 

If $B_{\mathrm{G}}(\mathrm{S})$ is a complete bipartite graph, then

$$V(B_{\mathrm{G}}(\mathrm{S}))=\{v_1,v_2,\dots ,v_{\mathrm{m}(\mathrm{S})-1}\}\cup \mathcal{B},$$

where $\mathcal{B}\subseteq \{v_{\mathrm{m}(\mathrm{S})+1},v_{\mathrm{m}(\mathrm{S})+2},\dots ,v_{2\mathrm{m}(\mathrm{S})-1}\}$. If possible, $\left|\mathcal{B}\right|>1$, and then there exist $\mathrm{m}(\mathrm{S})+x\in \mathcal{B}$ for some $x\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-2\}$. Note that

$$(\mathrm{m}(\mathrm{S})+x)-(\mathrm{m}(\mathrm{S})-1)=x+1\notin \mathrm{S}.$$

This is a contradiction, so $\left|\mathcal{B}\right|=1$ and therefore $B_{\mathrm{G}}(\mathrm{S})$ is a star graph. The converse implication is obvious. □

Theorem 4. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite graph of order $\mathrm{m}(\mathrm{S})$. Then, the following statements are equivalent:

(1) 

$\mathrm{S}$ is a numerical semigroup of the form $\langle \mathrm{m}(\mathrm{S}),\mathrm{m}(\mathrm{S})+1,\dots ,2\mathrm{m}(\mathrm{S})-3,2\mathrm{m}(\mathrm{S})-1\rangle$.

(2) 

$\mathrm{S}$ is a pseudo-symmetric numerical semigroup.

(3) 

The graph $B_{\mathrm{G}}(\mathrm{S})$ is isomorphic to the graph $K_{1,\mathrm{m}(\mathrm{S})-2}\cup \{v_{\mathrm{m}(\mathrm{S})-1}\}$.

Proof. 

Since $B_{\mathrm{G}}(\mathrm{S})$ is a bipartite graph of order $\mathrm{m}(\mathrm{S})$, therefore we have

$$V(B_{\mathrm{G}}(\mathrm{S}))=\{v_1,v_2,\dots ,v_{\mathrm{m}(\mathrm{S})-1}\}\cup \{v_x\},$$

where $v_x\in \{v_{\mathrm{m}(\mathrm{S})+1},v_{\mathrm{m}(\mathrm{S})+2},\dots ,v_{2\mathrm{m}(\mathrm{S})-1}\}$.

• $(1)\Rightarrow (2):$ This is obvious.
• $(2)\Rightarrow (3):$ If S is pseudo-symmetric, then

  $$\frac{F(\mathrm{S})+2}{2}=\left|B_{\mathrm{G}}(\mathrm{S})\right|=\mathrm{m}(\mathrm{S}).$$
• This implies $F(\mathrm{S})=2\mathrm{m}(\mathrm{S})-2$, and therefore $\frac{F(\mathrm{S})}{2}=\mathrm{m}(\mathrm{S})-1$. Theorem $2.5$ of [33] and Proposition 2 indicate that $B_{\mathrm{G}}(\mathrm{S})$ has two disconnected components and isomorphic to $K_{1,\mathrm{m}(\mathrm{S})-2}\cup \{v_{\mathrm{m}(\mathrm{S})-1}\}$.
• $(3)\Rightarrow (1):$ This is straightforward. □

Theorem 5. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite gap poset graph. Then, the following statements are equivalent:

(1) 

$|B_{\mathrm{G}}(\mathrm{S})|=2\mathrm{m}(\mathrm{S})-2$.

(2) 

$B_{\mathrm{G}}(\mathrm{S})$ is a graph isomorphic to $(\mathrm{m}(\mathrm{S})-1)P_2$.

(3) 

$B_{\mathrm{G}}(\mathrm{S})$ is a 1-degree regular bipartite graph.

(4) 

$B_{\mathrm{G}}(\mathrm{S})$ is a balanced graph.

Proof. 

$(1)\Rightarrow (2):$ We may assume that bipartition for $B_{\mathrm{G}}(\mathrm{S})$ is $V_1=\{v_x:1 \le x \le \mathrm{m}(\mathrm{S})-1\}$ and $V_2=\{v_{\mathrm{m}(\mathrm{S})+x}:1 \le x \le \mathrm{m}(\mathrm{S})-1\}$. Note that $\mathrm{m}(\mathrm{S})+x-x=\mathrm{m}(\mathrm{S})\in \mathrm{S}$. This implies, for every $1 \le x \le \mathrm{m}(\mathrm{S})-1$, there is an edge between $v_x$ and $v_{\mathrm{m}(\mathrm{S})+x}$. If $1 \le x<y \le \mathrm{m}(\mathrm{S})-1$, then $(\mathrm{m}+x)-y\in \{1,2,\dots ,\mathrm{m}(\mathrm{S})-1\}$. Also, if $1 \le y<x \le \mathrm{m}(\mathrm{S})-1$, then $(\mathrm{m}+x)-y\in \{\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+1,\dots ,2\mathrm{m}(\mathrm{S})-2\}$. Both cases imply there is no edge between $v_y$ and $v_{\mathrm{m}(\mathrm{S})+x}$. This provides deg$(v_{\mathrm{m}(\mathrm{S})+x})=1$ for every x, and therefore $B_{\mathrm{G}}(\mathrm{S})$ is isomorphic to $(\mathrm{m}(\mathrm{S})-1)$-copies of path graph $P_2$.

• The remaining implications are trivial. □

4. Diameter and Girth of Bipartite Gap Poset Graphs

In this section, we provide some bounds for the diameter and the girth of bipartite gap poset graphs $B_{\mathrm{G}}(\mathrm{S})$.

Lemma 2. 

Let order of $B_{\mathrm{G}}(\mathrm{S})$ be $2\mathrm{m}(\mathrm{S})-3$. If $\mathrm{m}(\mathrm{S})+1\notin \mathrm{S}$, then $B_{\mathrm{G}}(\mathrm{S})$ is disconnected.

Proof. 

Clearly, two vertices $v_x\in V_1$ and $v_y\in V_2$ have an edge only if $y-x\in \{\mathrm{m}(\mathrm{S}),\mathrm{m}(\mathrm{S})+r,$ for some $2 \le r \le \mathrm{m}(\mathrm{S})-2\}$. This implies deg$(v_y)\in \{1,2\}$, for every $v_y\in V_2$. Since $\mathrm{m}(\mathrm{S})+1,\dots ,\mathrm{m}(\mathrm{S})+r-1<\mathrm{m}(\mathrm{S})+r$, then

$$deg(v_p)=1,\mathrm{m}(\mathrm{S})+1 \le p \le \mathrm{m}(\mathrm{S})+r-1,$$

and

$$deg(v_q)=2,\mathrm{m}(\mathrm{S})+r+1 \le q \le 2\mathrm{m}(\mathrm{S})-1.$$

This provides

$$|\mathrm{E}(B_{\mathrm{G}}(\mathrm{S}))| \le 1(r-1)+2(\mathrm{m}(\mathrm{S})-r-1)=2\mathrm{m}(\mathrm{S})-r-3<(2\mathrm{m}(\mathrm{S})-3)-1=\left|B_{\mathrm{G}}(\mathrm{S})\right|-1.$$

This implies $B_{\mathrm{G}}(\mathrm{S})$ is disconnected. □

Theorem 6. 

Let order of $B_{\mathrm{G}}(\mathrm{S})$ be $2\mathrm{m}(\mathrm{S})-3$. Then, $\mathrm{m}(\mathrm{S})+1\in \mathrm{S}$ if and only if $B_{\mathrm{G}}(\mathrm{S})\cong P_{2\mathrm{m}(\mathrm{S})-3}$.

Proof. 

$(\Rightarrow )$ If $\mathrm{m}(\mathrm{S})+1\in \mathrm{S}$, then gap poset for $\mathrm{S}$ is

$$\mathrm{G}=\{1,2,\dots \mathrm{m}(\mathrm{S})-1\}\cup \{\mathrm{m}(\mathrm{S})+k:2 \le k \le \mathrm{m}(\mathrm{S})-1\}.$$

Note that $(\mathrm{m}(\mathrm{S})+2)-1=\mathrm{m}(\mathrm{S})+1\in S$ and $(2\mathrm{m}(\mathrm{S})-1)-(\mathrm{m}(\mathrm{S})-1)=\mathrm{m}(\mathrm{S})\in S$, while $(\mathrm{m}(\mathrm{S})+l)-1=\mathrm{m}(\mathrm{S})+(l-1)\notin S$, for $3 \le l \le \mathrm{m}-1$ and $(\mathrm{m}(\mathrm{S})+t)-(\mathrm{m}(\mathrm{S})-1)=t+1\notin S$, for $2 \le t \le \mathrm{m}-2$. This implies deg$(v_1)=1=$ deg$(v_{\mathrm{m}-1})$. Also, for each $2 \le x \le \mathrm{m}(\mathrm{S})-1$ and $1 \le y \le \mathrm{m}(\mathrm{S})-1$, $(\mathrm{m}(\mathrm{S})+x)-y\in \mathrm{S}$ if and only if either $y=x$ or $y=x-1$. This implies

$$v_1-v_{\mathrm{m}(\mathrm{S})+2}-v_2-v_{\mathrm{m}(\mathrm{S})+3}-v_3-\cdots -v_{\mathrm{m}(\mathrm{S})-2}-v_{2\mathrm{m}(\mathrm{S})-1}-v_{\mathrm{m}(\mathrm{S})-1}.$$

Consequently, we obtain the required result.

• $(\Leftarrow )$ This follows from Lemma 2. □

Conjecture 1. 

Let $B_{\mathrm{G}}(\mathrm{S})$ be a bipartite gap poset graph. If $\mathrm{m}(\mathrm{S})$ is the multiplicity of numerical semigroup $\mathrm{S}$, then diam$(B_{\mathrm{G}}(\mathrm{S})) \le 2\mathrm{m}(\mathrm{S})-4$.

Now, we propose the following conjecture for the girth of bipartite gap poset graphs.

Conjecture 2. 

Let $B_G(\mathrm{S})$ be a connected bipartite gap poset graph containing a finite cycle. If $\mathrm{m}(\mathrm{S})\ge 6$ is the multiplicity of numerical semigroup $\mathrm{S}$, then one of the following statements hold:

(1) 

If $\mathrm{m}(\mathrm{S})$ is odd, then $gr(B_G(\mathrm{S})) \le \mathrm{m}(\mathrm{S})-1$.

(2) 

If $\mathrm{m}(\mathrm{S})$ is even, then $gr(B_G(\mathrm{S}))\in \{4,6\}$.

In the following results, we prove this conjecture for connected bipartite gap poset graphs of order $2\mathrm{m}(\mathrm{S})-4$.

Proposition 3. 

Let $B_G(\mathrm{S})$ be a connected bipartite gap poset graph of order $2\mathrm{m}(\mathrm{S})-4$ containing a finite cycle, and then $gr(B_G(\mathrm{S})) \le \mathrm{m}(\mathrm{S})-1,$ where $\mathrm{m}(\mathrm{S})\ge 7$ is an odd number.

Proof. 

First of all, we show that there is some $\mathcal{A}\subseteq \{\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+2,\dots ,2\mathrm{m}(\mathrm{S})-1\}$ such that $B_G(\mathrm{S})$ contains a cycle of length $\mathrm{m}(\mathrm{S})-1$. For this, we consider

$$\mathcal{A}=\{\mathrm{m}(\mathrm{S})+1,\dots ,\frac{3\mathrm{m}(\mathrm{S})-5}{2},\frac{3\mathrm{m}(\mathrm{S})+1}{2},\dots ,2\mathrm{m}(\mathrm{S})-1\}.$$

Note that two vertices $v_i,v_j\in \mathrm{V}(B_G(\mathrm{S}))$ are connected if and only if $\mid i-j\mid \in \{\mathrm{m}(\mathrm{S}),\frac{3\mathrm{m}(\mathrm{S})-3}{2},\frac{3\mathrm{m}(\mathrm{S})-1}{2}\}.$ Since $\mathrm{m}(\mathrm{S})+1,\dots ,\frac{3\mathrm{m}(\mathrm{S})-5}{2}<\frac{3\mathrm{m}(\mathrm{S})-3}{2}$ and graph is connected, then

$$deg(v_i)=1,\mathrm{m}(\mathrm{S})+1 \le i \le \frac{3\mathrm{m}(\mathrm{S})-5}{2}.$$

For each $1 \le x \le \frac{\mathrm{m}(\mathrm{S})-1}{2}$, we have

$$\frac{3\mathrm{m}(\mathrm{S})-1}{2}+x-x=\frac{3\mathrm{m}(\mathrm{S})-1}{2},$$

$$\frac{3\mathrm{m}(\mathrm{S})-1}{2}+x-(x+1)=\frac{3\mathrm{m}(\mathrm{S})-3}{2},$$

$$\frac{3\mathrm{m}(\mathrm{S})-1}{2}+x-(\frac{\mathrm{m}(\mathrm{S})-1}{2}+x)=\mathrm{m}(\mathrm{S}).$$

This implies $deg(v_j)=3,\frac{3\mathrm{m}(\mathrm{S})+1}{2} \le j \le 2\mathrm{m}(\mathrm{S})-1$, and $deg(v_k)=1,\frac{\mathrm{m}(\mathrm{S})+3}{2}+1 \le k \le \mathrm{m}(\mathrm{S})-1.$ This implies the total number of pendent vertices of $B_G(\mathrm{S})$ is

$$(\frac{3\mathrm{m}(\mathrm{S})-5}{2}-\mathrm{m}(\mathrm{S})-1+1)+(\mathrm{m}(\mathrm{S})-1-\frac{\mathrm{m}(\mathrm{S})+3}{2}+1)=\mathrm{m}(\mathrm{S})-4.$$

Clearly, $deg(v_1)=2$, but it is not part of any cycle. Thus, only $\mathrm{m}(\mathrm{S})-1$ vertices are part of a cycle. The above discussion implies $B_G(\mathrm{S})$ is a graph as in the Figure 2.

Now, we have to show that, for any $\mathcal{A}\subseteq \{\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+2,\dots ,2\mathrm{m}(\mathrm{S})-1\}$, graph $B_G(\mathrm{S})$ does not contain a cycle of length greater than $\mathrm{m}(\mathrm{S})-1$. For this, we take $\mathrm{m}+x,\mathrm{m}+y\in \mathrm{S},$ where $\frac{\mathrm{m}(\mathrm{S})-1}{2} \le x \le \mathrm{m}(\mathrm{S})-2$ and $x+1 \le y \le \mathrm{m}(\mathrm{S})-1$. Since

$$\mathrm{m}(\mathrm{S})+1,\dots ,\mathrm{m}(\mathrm{S})+x-1<\mathrm{m}(\mathrm{S})+x,$$

therefore

$$deg(v_a)=1,\mathrm{m}(\mathrm{S})+1 \le a \le \mathrm{m}(\mathrm{S})+x-1.$$

Also, deg$(v_{\frac{\mathrm{m}(\mathrm{S})+1}{2}+u})=1,1 \le u \le \frac{\mathrm{m}(\mathrm{S})-3}{2}$ since an element $L\in B$ has an edge if it satisfies the following condition:

$$L-(\frac{\mathrm{m}(\mathrm{S})+1}{2}+u)=\mathrm{m}(\mathrm{S})or\mathrm{m}(\mathrm{S})+xor\mathrm{m}(\mathrm{S})+y.$$

Note that

$$L=\mathrm{m}(\mathrm{S})+(\frac{\mathrm{m}(\mathrm{S})+1}{2}+u)=\frac{3\mathrm{m}(\mathrm{S})+1}{2}+u\in B,$$

$$L=\mathrm{m}(\mathrm{S})+x+(\frac{\mathrm{m}(\mathrm{S})+1}{2}+u)=\frac{3\mathrm{m}(\mathrm{S})+1}{2}+u+x>F\notin B,$$

$$L=\mathrm{m}(\mathrm{S})+y+(\frac{\mathrm{m}(\mathrm{S})+1}{2}+u)=\frac{3\mathrm{m}(\mathrm{S})+1}{2}+y+u>F\notin B.$$

This implies the total number of pendent vertices of $B_G(\mathrm{S})$ is

$$(\mathrm{m}(\mathrm{S})+x-1-\mathrm{m}(\mathrm{S})-1+1)+(\frac{\mathrm{m}(\mathrm{S})-3}{2})=\frac{\mathrm{m}(\mathrm{S})-3}{2}+x-1,$$

and

$$2\mathrm{m}(\mathrm{S})-4-(\frac{\mathrm{m}(\mathrm{S})-3}{2}+x-1)=\frac{3\mathrm{m}(\mathrm{S})-3}{2}-2x<\mathrm{m}(\mathrm{S})-1.$$

This indicates that the number of vertices with degree greater than 1 is less than $\mathrm{m}(\mathrm{S})-1$. This implies $B_G(\mathrm{S})$ cannot contain a cycle of length greater than $\mathrm{m}(\mathrm{S})-1$.

• If $x=\frac{\mathrm{m}(\mathrm{S})-3}{2}$ and $\frac{\mathrm{m}(\mathrm{S})+1}{2} \le y \le \mathrm{m}(\mathrm{S})-2,$ then

  $$deg(v_a)=1,\mathrm{m}(\mathrm{S})+1 \le a \le \frac{3\mathrm{m}(\mathrm{S})-5}{2},$$

  $$deg(v_b)=2,\frac{3\mathrm{m}(\mathrm{S})-1}{2} \le b \le \mathrm{m}(\mathrm{S})+y-1,$$

  $$deg(v_c)=3,\mathrm{m}(\mathrm{S})+y+1 \le c \le 2\mathrm{m}(\mathrm{S})-1.$$
• So,

  $$|E(B_{\mathcal{G}}(\mathrm{S}))|=(\frac{2\mathrm{m}(\mathrm{S})-5}{2}-\mathrm{m}(\mathrm{S})-1+1)+2(\mathrm{m}(\mathrm{S})+y-1-\frac{3\mathrm{m}(\mathrm{S})-1}{2}+1)+$$

  $$3(2\mathrm{m}(\mathrm{S})-1-\mathrm{m}(\mathrm{S})-y-1+1)=2\mathrm{m}(\mathrm{S})-4+\frac{\mathrm{m}(\mathrm{S})-1}{2}-y \le \left|B_{\mathcal{G}}(\mathrm{S})\right|-1.$$
• This implies $B_{\mathcal{G}}(\mathrm{S})$ is either a path or disconnected graph, which is not possible.
• If $2 \le x \le \frac{\mathrm{m}(\mathrm{S})-1}{2},1 \le y \le x-1$ and $y\ne \frac{\mathrm{m}(\mathrm{S})-3}{2}$, then there exists a cycle

  $$v_{y+1}-v_{\mathrm{m}(\mathrm{S})+y+1}-v_1-v_{\mathrm{m}(\mathrm{S})+x+1}-v_{x+1}-v_{\mathrm{m}(\mathrm{S})+x+y+1}-v_{y+1}.$$
• Consequently, there is no cycle of length greater than $\mathrm{m}(\mathrm{S})-1$.
• If $1 \le x \le \frac{\mathrm{m}(\mathrm{S})-5}{2},\frac{\mathrm{m}(\mathrm{S})-1}{2} \le y \le 2\mathrm{m}(\mathrm{S})-1,$ then there exists a cycle

  $$v_{\mathrm{m}(\mathrm{S})+y+1}-v_{y+1}-v_{\mathrm{m}(\mathrm{S})+y+1+x}-v_{x+1}-v_{\mathrm{m}(\mathrm{S})+x+1}-v_1-v_{\mathrm{m}(\mathrm{S})+y+1}.$$
• This implies there is no cycle of length greater than $\mathrm{m}(\mathrm{S})-1$.
  □

Proposition 4. 

Let $B_G(\mathrm{S})$ be a connected bipartite gap poset graph of order $2\mathrm{m}(\mathrm{S})-4$ containing a finite cycle, and then $gr(B_G(\mathrm{S})) \le 6,$ where $\mathrm{m}(\mathrm{S})\ge 6$ is an even number.

Proof. 

Consider $\mathrm{m}(\mathrm{S})+1,\frac{3\mathrm{m}(\mathrm{S})}{2}\in \mathrm{S},$ and then for

$$\mathcal{A}=\{\mathrm{m}(\mathrm{S})+2,\dots ,\frac{3\mathrm{m}(\mathrm{S})}{2}-1,\frac{3\mathrm{m}(\mathrm{S})}{2}+1,\dots ,2\mathrm{m}(\mathrm{S})-1\},$$

the graph $B_G(\mathrm{S})$ contains a cycle of length 6 given as follows

$$v_{\frac{3\mathrm{m}(\mathrm{S})}{2}+1}-v_1-v_{\mathrm{m}(\mathrm{S})+2}-v_2-v_{\frac{3\mathrm{m}(\mathrm{S})}{2}+2}-v_{\frac{\mathrm{m}(\mathrm{S})}{2}+1}-v_{\frac{3\mathrm{m}(\mathrm{S})}{2}+1}.$$

Now, we have to show that, for any $\mathcal{A}\subseteq \{\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+2,\dots ,2\mathrm{m}(\mathrm{S})-1\}$, graph $B_G(\mathrm{S})$ does not contain a cycle of length greater than 6.

$(i)$

If $\mathrm{m}(\mathrm{S})+1,\mathrm{m}(\mathrm{S})+x\in \mathrm{S},2 \le x \le \frac{\mathrm{m}(\mathrm{S})-2}{2},or\frac{\mathrm{m}(\mathrm{S})+2}{2} \le x \le \mathrm{m}(\mathrm{S})-1$, then there is a cycle of length 6 in $B_G(\mathrm{S})$, given as follows

$$v_{\mathrm{m}(\mathrm{S})+2}-v_1-v_{\mathrm{m}(\mathrm{S})+x+1}-v_{x+1}-v_{\mathrm{m}(\mathrm{S})+x+2}-v_2-v_{\mathrm{m}(\mathrm{S})+2}.$$

$(ii)$

If $\frac{3\mathrm{m}(\mathrm{S})}{2}+r,\frac{3\mathrm{m}(\mathrm{S})}{2}+k+1\in \mathrm{S},0 \le r \le \frac{\mathrm{m}(\mathrm{S})-4}{2},r \le k \le \frac{\mathrm{m}(\mathrm{S})-4}{2},$ then

$$deg(v_p)=1,\mathrm{m}(\mathrm{S})+1 \le p \le \frac{3\mathrm{m}(\mathrm{S})-2}{2}+r,$$

$$deg(v_q)=2,\frac{3\mathrm{m}(\mathrm{S})+2}{2}+r \le q \le \frac{3\mathrm{m}(\mathrm{S})}{2}+k,$$

$$deg(v_s)=3,\frac{3\mathrm{m}(\mathrm{S})+4}{2}+k \le s \le 2\mathrm{m}(\mathrm{S})-1.$$

$$\mid E(B_G(\mathrm{S})\mid =(\frac{3\mathrm{m}(\mathrm{S})-2}{2}+r-\mathrm{m}(\mathrm{S})-1+1)+2(\frac{3\mathrm{m}(\mathrm{S})}{2}+k-\frac{3\mathrm{m}(\mathrm{S})+2}{2}-r)+$$

$$3(2\mathrm{m}(\mathrm{S})-1-\frac{3\mathrm{m}(\mathrm{S})+4}{2}-k)=2\mathrm{m}(\mathrm{S})-7-r-k<\mid B_G(\mathrm{S})\mid -1.$$

This implies the corresponding graph is disconnected.

$(iii)$

If $\frac{3\mathrm{m}(\mathrm{S})}{2}-u,\frac{3\mathrm{m}(\mathrm{S})}{2}-(l+1)\in \mathrm{S},0 \le u \le \frac{\mathrm{m}(\mathrm{S})-4}{2},u \le l \le \frac{\mathrm{m}(\mathrm{S})-4}{2},$ then the following cycle is contained in the graph $B_G(\mathrm{S})$:

$$v_{\frac{\mathrm{m}(\mathrm{S})}{2}-l}-v_{\frac{3\mathrm{m}(\mathrm{S})}{2}-l}-v_1-v_{\frac{3\mathrm{m}(\mathrm{S})+2}{2}-u}-v_{\frac{\mathrm{m}(\mathrm{S})+2}{2}-u}-v_{2\mathrm{m}(\mathrm{S})-1-u-l}-v_{\frac{\mathrm{m}(\mathrm{S})}{2}-l}.$$

$(iv)$

If $\frac{3\mathrm{m}(\mathrm{S})}{2}-x,\frac{3\mathrm{m}(\mathrm{S})}{2}+y\in \mathrm{S},1 \le x \le \frac{\mathrm{m}(\mathrm{S})-4}{2},1 \le y \le \frac{\mathrm{m}(\mathrm{S})-2}{2},$ then the graph $B_G(\mathrm{S})$ contains a cycle

$$v_{\frac{3\mathrm{m}(\mathrm{S})+2}{2}+y}-v_{\frac{\mathrm{m}(\mathrm{S})+2}{2}+y}-v_{2\mathrm{m}(\mathrm{S})+1+y-x}-v_{\frac{\mathrm{m}(\mathrm{S})+2}{2}-x}-v_{\frac{3\mathrm{m}(\mathrm{S})+2}{2}-x}-v_1-v_{\frac{3\mathrm{m}(\mathrm{S})+2}{2}+y}.$$

Consequently, we obtain gr($B_G(\mathrm{S})) \le 6.$ □

5. Algorithms and Python-Based Illustrations

In this section, we propose the algorithms and their Python implementations, followed by illustrative examples, as well as their application in chemical reaction networks.

Time complexity and space complexity of Algorithm 1 are quadratic and equal to $O(KM+M^2)$, $O(M^2)$, respectively, where K is the number of minimal generators of the numerical semigroup and M is computed upper bound. For two generators a and b, $M=max(2(ab-a-b),100)$, and for more than two generators $M=100\ast max(H)$.

Algorithm 1 Construction of Gap Poset Graph of a Numerical Semigroup

Input:  $H=\{h_1,h_2,\dots ,h_k\}$, the minimal system of generator of numerical semigroup $\mathrm{S}.$ Output:  Gap poset graph $B_G(\mathrm{S}).$   1: $\mathrm{S}\leftarrow \varnothing$   2: $\mathrm{frontier}\leftarrow \left[0\right]$   3: while $\mathrm{frontier}\ne \varnothing$ do   4:       $\mathrm{current}\leftarrow \mathrm{pop}(\mathrm{frontier})$   5:       if current > max_limit then   6:             continue   7:       end if   8:       if $\mathrm{current}\notin \mathrm{S}$ then   9:             add current to $\mathrm{S}$ 10:             for all $h\in H$ do 11:                    push $\mathrm{current}+h$ to frontier 12:             end for 13:       end if 14: end while 15: $\mathrm{Gaps}\leftarrow \{x\in N_0\mid 0 \le x<max(\mathrm{S})\wedge x\notin \mathrm{S}\}$ 16: if $\left|\mathrm{Gaps}\right|\ge 2$ then 17:     $\mathrm{max\_check}\leftarrow \mathrm{sum}\mathrm{of}\mathrm{two}\mathrm{largest}\mathrm{elements}\mathrm{of}\mathrm{gaps}$ 18: else 19:     $\mathrm{max\_check}\leftarrow 3·max(H)$ 20: end if 21: $\mathrm{S}\leftarrow \varnothing$, $\mathrm{frontier}\leftarrow \left[0\right]$ 22: Repeat step $3-14$ $\mathrm{with}\mathrm{max\_limit}\leftarrow \mathrm{max\_check}$ 23: $\mathrm{Gaps}\leftarrow \{x\in N_0\mid 0 \le x<\mathrm{max\_check}\wedge x\notin \mathrm{S}\}$ 24: Initialize empty gap poset graph $B_G(\mathrm{S})$ 25: for all $(a,b)\in \mathrm{Gaps}\mathrm{with}a<b$  do 26:     if $|a-b|\in \mathrm{S}$ then 27:         Add edge $(a,b)$ to gap poset graph $B_G(\mathrm{S})$ 28:     end if 29: end for 30: return $B_G(\mathrm{S}),\mathrm{Gaps},\mathrm{EdgeList}$

Time complexity is cubic $O(KM+M^3)$, and space complexity is quadratic $O(M^2)$ of Algorithm 2, where K is the number of minimal generators of numerical semigroups and M is computed upper bound. For two generators a and b, $M=max(2(ab-a-b),100)$, and for more than two generators $M=100\ast max(H)$. To assist researchers and support the validation and exploration of results in the study of numerical semigroups, we developed a Python-based tool that allows users to construct gap poset graphs derived from a given numerical semigroup $\mathrm{S}$. The tool provides functionality to compute important graph invariants, such as the diameter and girth of the resulting gap poset graphs. The tool can be accessed through the following link: https://gap-poset-graph-analyzer.onrender.com/ (accessed on 22 July 2025).

Algorithm 2 Compute the Diameter and the Girth of Gap Poset Graph

Input:  $H=\{h_1,h_2,\dots ,h_k\},$ the minimal system of generator of numerical semigroup $\mathrm{S}$ Output:  Diameter and the girth of gap poset graph $B_G(\mathrm{S})$   1: if length of generators is 2 then   2:     Let $a,b\leftarrow$ sorted generators   3:     $\mathtt{frobenius}\leftarrow ab-a-b$   4:     max_limit$\leftarrow max(2·\mathtt{frobenius},100)$   5: else   6:     max_limit$\leftarrow 100·max(\mathtt{generators})$   7: end if   8: Initialize numerical semigroup $\mathrm{S}\leftarrow \varnothing$ and frontier queue with 0   9: while frontier is not empty do 10:     Pop current element 11:     if current > max_limit then continue 12:     end if 13:     if current $\notin \mathrm{S}$ then 14:         Add current to $\mathrm{S}$ 15:         for all $h\in H$ do 16:            Append $current+h$ to frontier 17:         end for 18:     end if 19: end while 20: $gaps\leftarrow \{x\mid x\notin \mathrm{S},x<max(\mathrm{S})\}$ 21: Create empty graph $B_G(\mathrm{S})$ and add $gaps$ as nodes 22: for all pairs $(i,j)$ in $gaps$ do 23:     $diff\leftarrow |i-j|$ 24:     if $diff\in \mathrm{S}$ then 25:         Add edge $(i,j)$ to $B_G(\mathrm{S})$ 26:     end if 27: end for 28: if $B_G(\mathrm{S})$ is connected then 29:     Compute and return diameter$(B_G(\mathrm{S}))$ 30: else 31:     Report number of components; diameter not defined 32: end if 33: Compute girth via BFS: 34: for node in a subset of $B_G(\mathrm{S})$ do 35:     Perform BFS and track shortest cycles 36:     if cycle of length 3 found then 37:         return 3 as girth 38:     end if 39: end for 40: Return minimum cycle length as girth (or ∞ if none)

Example 2. 

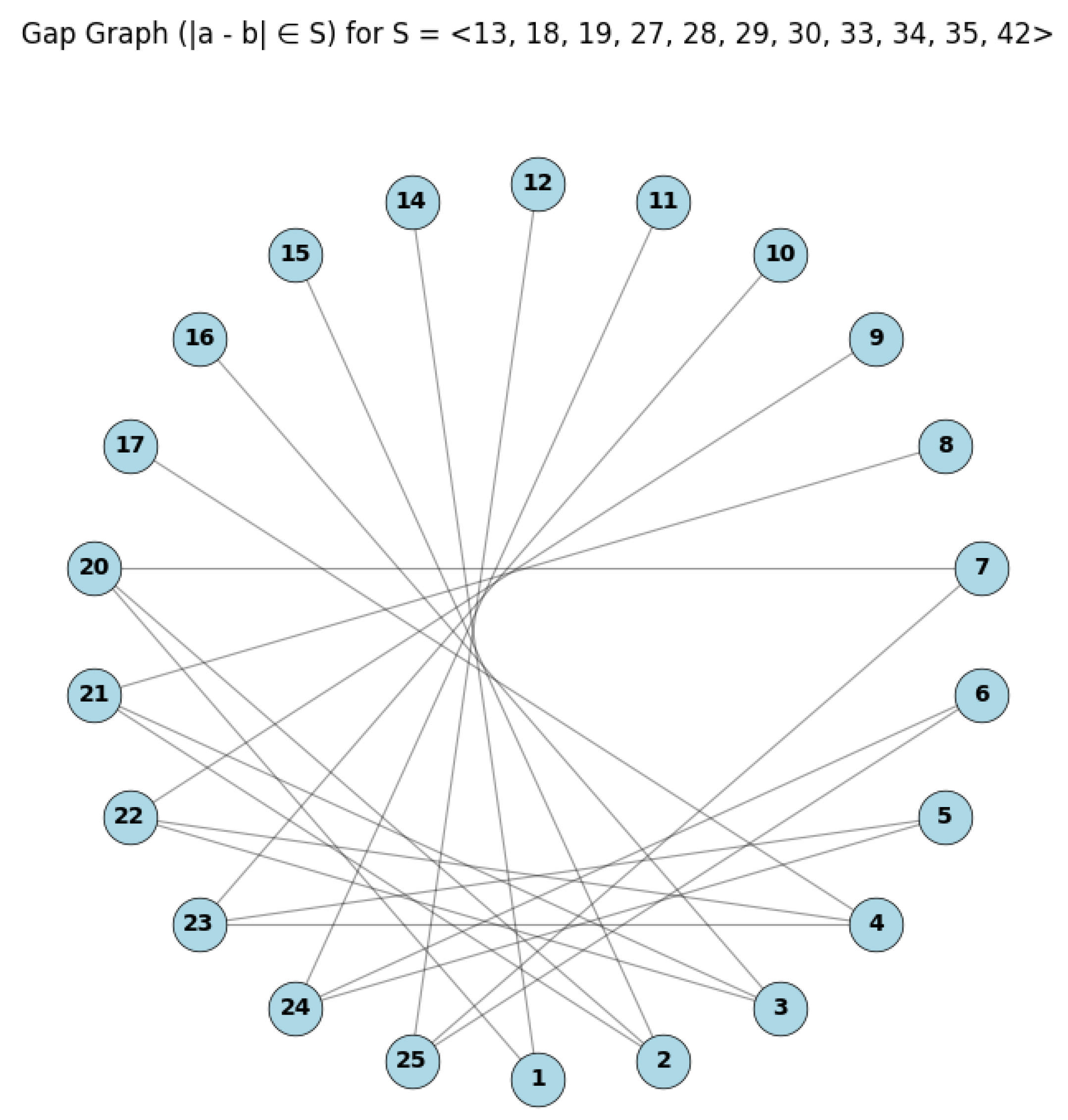
Let $\mathrm{S}=\langle 13,18,19,27,28,29,30,33,34,35,42\rangle$, and then we can use the following Python code to calculate the gap poset graph $B_G(\mathrm{S})$ and its diameter and girth (see Listing 1).

As illustrated in Figure 3, the ordered set of nodes $\{20,2,21,3,22,4,23,5,24,6,25,7\}$ forms the shortest cycle in the graph. Since each pair of consecutively listed nodes is connected by an edge, this implies shortest cycle has length 12, which establishes the girth of $B_G(\mathrm{S})$ as 12. Furthermore, the largest distance between any two vertices occurs between nodes 14 and 10, yielding graph of diameter 9.

Listing 1. Python console output.

Suppose a synthetic chemist needs to transform an initial molecular state (a short oligomer or intermediate) into a target state (a longer oligomer or final product) by a sequence of elementary reactions. Each elementary reaction can change molecular size by a quantity belonging to a fixed set of allowed step sizes (for instance, additions of building blocks of sizes given by available reagents). We model the allowed step sizes by gaps of numerical semigroup $\mathrm{S}=\langle 13,18,19,27,28,29,30,33,34,35,42\rangle$ such that nodes represent molecular species (substrates, intermediate, and product) and edges correspond to stoichiometrically possible reaction steps. The gap poset graph indicates hypothetically how many one-step reactions take place (i.e., direct edge between vertices) and two-step reactions (i.e., there is a vertex between two independent vertices that link with both of them) and so on. Diameter and girth of gap poset graphs provide information about how long any synthesis path can be and on the minimal length of possible cycles, which helps chemists and engineers to estimate worst-case synthesis depth and detect when a proposed reagent set is intrinsically inefficient. Also, it helps us in energy minimization, yield optimization, selection of catalyst, and alternative reagents.

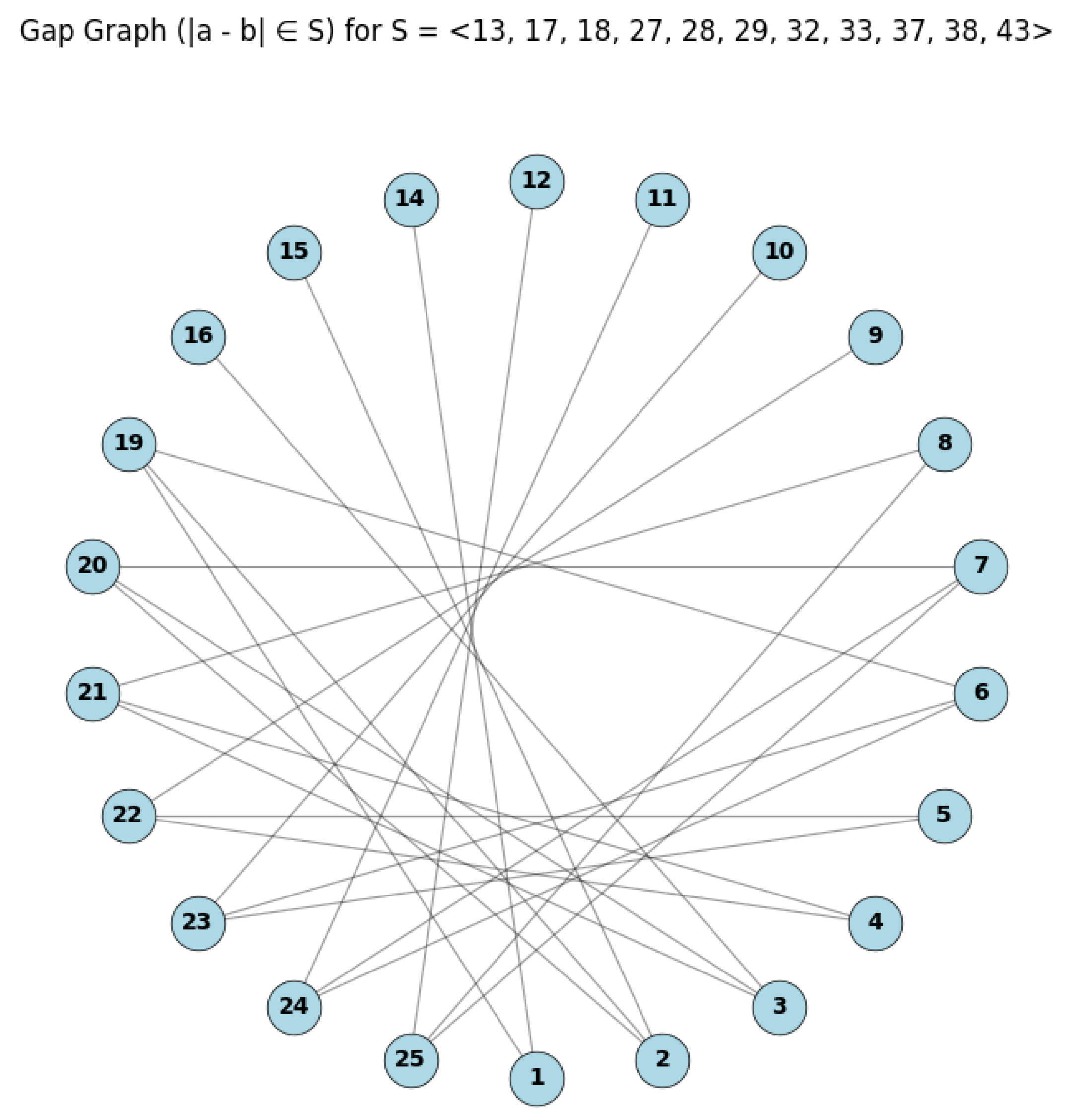
Example 3. 

Let $\mathrm{S}=\langle 8,10,11,12,17\rangle$, and then we can use the following Python code to compute the gap poset graph $B_G(\mathrm{S})$ and its diameter and girth (see Listing 2).

Listing 2. Python console output.

As illustrated in Figure 4, the ordered set of nodes $\{15,4,14,3,15\}$ forms the shortest cycle in the graph. Since each pair of consecutively listed nodes is connected by an edge, this implies shortest cycle has length 4, which establishes the girth of $B_G(\mathrm{S})$ as 4. Furthermore, the largest distance between any two vertices occurs between nodes 7 and 9, yielding graph has diameter $5.$

6. Conclusions

In this article, we investigated various structural properties of bipartite gap poset graphs associated with numerical semigroups. In Section 2, we determined the specific conditions under which they are connected or disconnected, providing insight into how the arrangement of gaps affects the overall structure. In Section 3, we concentrated on the characterization of bipartite gap poset graphs, in which we investigated how various configurations corresponded to different well-known graph types, such as balanced, path, and star. In Section 4, we provided a bound on the diameter of bipartite gap poset graphs. Additionally, we provided a conjecture on the upper bound of the girth of bipartite gap poset graphs. These findings help to deepen our understanding of the interaction between the additive structure of numerical semigroups and the combinatorial features of their related graphs, as well as open up new possibilities for research in algebraic graph theory. In Section 5, we presented the algorithms for constructing gap poset graphs, along with procedures to compute key graph invariants such as diameter and girth. Additionally, this section includes illustrative examples that demonstrate the practical application and effectiveness of the proposed methods.

The future extension is to investigate gap poset graphs beyond the bipartite case, exploring richer families of numerical semigroups and the new structural patterns they generate. Furthermore, studying additional graph invariants, including the chromatic number, domination number, and metric dimension of these graphs, would provide deeper insights into their structural and combinatorial properties.