Neighbor Full Sum Distinguishing Total Coloring of Planar Graphs with Girth at Least 5

Abstract

A neighbor full sum distinguishing total coloring of a graph G is a proper k-total coloring $\varphi$ such that no two adjacent vertices u and v satisfy $\omega \left(u\right)\ne \omega \left(v\right)$, where $\omega \left(v\right)=\varphi \left(v\right)+{\sum }_{e\ni v}\varphi \left(e\right)+{\sum }_{u\in N\left(v\right)}\varphi \left(u\right)$ and $N\left(v\right)=\left\{u\right|uv\in E\left(G\right)\}$. The minimum positive integer k is called the neighbor full sum distinguishing total coloring of G, or ${\mathrm{ftndi}}_{\Sigma }\left(G\right)$ for short. In this article, we verify that for a normal planar graph G, ${\mathrm{ftndi}}_{\Sigma }\left(G\right)\le \Delta \left(G\right)+3$ if $g\left(G\right)\ge 5$ and $\Delta \left(G\right)\ge 22$, which extends the result of Yue, et al. by reducing the girth condition from 6 to 5.

1. Introduction

In this paper, we consider that all graphs are simple, undirected and connected. A graph is said to be planar if it can be embedded in a plane such that its edges intersect only at their endpoints. Let G be a planar graph. We denote by $V\left(G\right)$, $E\left(G\right)$ and $F\left(G\right)$ the vertex set, the edge set and the face set, respectively. The degree of a vertex $v\in V\left(G\right)$ is the number of edges associated with v, and written as $d_G\left(v\right)$. A vertex with a degree of exactly k, at least k and at most k is referred to as a k-vertex, $k^{+}$-vertex and $k^{-}$-vertex, respectively. Specifically, if $d_G\left(v\right)=1$, then v is called a leaf. Moreover, the maximum degree of G, denoted by $\Delta \left(G\right)$, is defined as $\Delta \left(G\right)=max\left\{d\right(v)\mid v\in V(G\left)\right\}$. In turn, the minimum degree of G, denoted by $\delta \left(G\right)$, is defined as $\delta \left(G\right)=min\left\{d\right(v)\mid v\in V(G\left)\right\}$. The maximum average degree $mad\left(G\right)$ of a graph G is the maximum of the average degrees of its subgraphs. For a face $f\in F\left(G\right)$, the degree of f, denoted by $d_G\left(f\right)$, is defined as the number of edges on the boundary of f, and the definition of a k-, $k^{+}$-, or $k^{-}$-face is similar to that of the corresponding vertex. A cycle of length $k\ge 3$ in G is called a k-cycle, and the minimum length among all k-cycles is known as the girth of G, denoted by $g\left(G\right)$. Additionally, a graph G is normal if it has no isolated edges.

A proper k-total coloring of a graph is a mapping from k colors to its vertices and edges such that no two incident elements receive the same colors. In recent years, neighbor sum distinguishing total coloring of graphs as a constrained k-total coloring was first introduced by Pilśniak and Woźniak [1] in 2015, which has received much attention. A proper k-total coloring $\phi$ of a graph G is said to be a neighbor sum distinguishing total coloring if $\xi \left(u\right)\ne \xi \left(v\right)$ for any $uv\in E\left(G\right)$, where $\xi \left(x\right)=\phi \left(x\right)+{\sum }_{e\ni x}\phi \left(e\right)$ for each $x\in V\left(G\right)$, and the minimal number k of such coloring is called neighbor sum distinguishing total chromatic number, denoted by ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)$. Moreover, they also proposed the conjecture below.

Conjecture 1

([1]). Let G be a graph of order at least 2. Then, ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le \Delta \left(G\right)+3.$

Meanwhile, they showed that Conjecture 1 is valid for various classes of graphs, including complete graphs, cubic graphs, and so on. Subsequently, many results have been achieved in the study of neighbor sum distinguishing total coloring on planar graphs. In 2016, Qu et al. [2] obtained that ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le max\{\Delta \left(G\right)+3,14\}$ for a planar graph G. Later, Wang et al. [3] confirmed the validity of Conjecture 1 for planar graphs without containing 4-cycles, and then, Wang et al. [4] further proved that if planar graph G contains no adjacent triangles and $\Delta \left(G\right)\ge 8$, then ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le \Delta \left(G\right)+3$. In the same year, Ge et al. [5] showed that ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le max\{\Delta \left(G\right)+3,10\}$ if planar graph G does not contain 5-cycles. In 2022, Nakprasit et al. [6] proved that ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le \Delta \left(G\right)+3$ for a planar graph G without 4-cycles adjacent to 3-cycles and $\Delta \left(G\right)\ge 7$. In 2023, Huang et al. [7] verified that for any graph G with $mad\left(G\right)<4$, ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le max\{9,\Delta \left(G\right)+2\}$. Additionally, they provided a characterization of the neighbor sum distinguishing total chromatic number for graphs satisfying $mad\left(G\right)<4$ and $\Delta \left(G\right)\ge 8$. In 2024, Du et al. [8] presented two significant results regarding planar graph G. The first one is that if G has no 3-cycles adjacent to 4-cycles with $\Delta \left(G\right)\ge 8$ and without cut edges, then ${\chi }_{\Sigma }^{\prime \prime }\le \Delta \left(G\right)+2$. The second is that if G has no 4-cycles intersecting with 6-cycles and $\Delta \left(G\right)\ge 7$, then ${\chi }_{\Sigma }^{\prime \prime }\le \Delta \left(G\right)+3$. Just recently, Duan et al. [9] verified that ${\chi }_{\Sigma }^{\prime \prime }\left(G\right)\le max\{\Delta \left(G\right)+3,10\}$ for planar graph G without intersecting 4-cycles.

In 2017, Flandrin [10] extended the definition of neighbor sum distinguishing total coloring by incorporating the colors of adjacent vertices to form the notion of full sum, and introduced the concept of neighbor full sum distinguishing total coloring of graphs. For a graph G, suppose $\varphi :V\left(G\right)\cup E\left(G\right)\to \{1,2,\dots ,k\}$ is a proper k-total coloring of G. For each vertex $v\in V\left(G\right)$, let $N\left(v\right)=\{u\mid uv\in E(G\left)\right\}$ and $\omega \left(v\right)=\varphi \left(v\right)+{\sum }_{e\ni v}\varphi \left(e\right)+{\sum }_{u\in N\left(v\right)}\varphi \left(u\right)$. Furthermore, if $\omega \left(u\right)\ne \omega \left(v\right)$ for any $uv\in E\left(G\right)$, then $\varphi$ is termed a neighbor full sum distinguishing k-total coloring of G, abbreviated as k-NFSDTC of G. The smallest integer k for which a neighbor full sum distinguishing k-total coloring exists in G is referred to as the neighbor full sum distinguishing total chromatic number of G, simplified as ${\mathrm{ftndi}}_{\Sigma }\left(G\right)$. Cheng et al. [11] provided an insight for the neighbor full sum distinguishing total coloring through two specific types of Halin graphs. In 2023, Cui et al. [12] proposed Conjecture 2 and validated it for graphs such as paths, cycles, stars, wheels, complete bipartite graphs, complete graphs and trees.

Conjecture 2

([12]). If G is a normal graph, then ${\mathrm{ftndi}}_{\Sigma }\left(G\right)\le \Delta \left(G\right)+2$.

Recently, Yue et al. showed in [13] that ${\mathrm{ftndi}}_{\Sigma }\left(G\right)\le \Delta \left(G\right)+3$ if G is a normal planar graph with $g\left(G\right)\ge 6$ and $\Delta \left(G\right)\ge 10$. Inspired by Conjecture 2, we extend the result of [13] under the condition $g\left(G\right)\ge 5$ in some sense.

Theorem 1.

Let G be a normal planar graph with $g\left(G\right)\ge 5$ and $\Delta \left(G\right)\ge 22$. Then,

$${\mathrm{ftndi}}_{\Sigma }\left(G\right)\le \Delta \left(G\right)+3.$$

2. Demonstration of Main Result

At first, we present some lemmas to be utilized in the subsequent proof.

Lemma 1

([12]). For $n\ge 3$, suppose $S_n$ is a star of order $n+1$. Then, ${\mathrm{ftndi}}_{\Sigma }\left(S_n\right)=n+1$.

Lemma 2

([14]). Let $B_1$ and $B_2$ be the sets of integers, with $|B_1|=m\ge 2$ and $|B_2|=n\ge 2$. Let $B_3=\{x+y\mid x\in B_1,y\in B_2,x\ne y\}$. Then, $|B_3|\ge m+n-3$. Moreover, if $B_1\ne B_2$, then $|B_3|\ge m+n-2$.

By the definition of neighbor full sum distinguishing total coloring, it is evident that Lemma 3 always holds.

Lemma 3.

For a graph G, let u be a vertex of degree at least 2 in G. If v is a leaf neighbor of u, then $\omega \left(u\right)\ne \omega \left(v\right)$.

Proof of Theorem 1. 

Suppose that G is a normal planar graph. For a vertex v of G, we denote by $D_G\left(v\right)$ the number of neighbors of v that are not leaves, and $N_k^G\left(v\right)$ the quantity of neighbors of v with degree k in G. If $d_G\left(v\right)=2$, then v is called a good 2-vertex when $N_2^G\left(v\right)=0$, otherwise, it is called a bad 2-vertex (i.e., $N_2^G\left(v\right)\ne 0$). Let $N_{\tilde{2}}^G\left(v\right)$ be the quantity of bad 2-vertices neighboring v in G. For a face f of G, let $N_k^G\left(f\right)$ be the number of vertices with degree k that are incident to f. 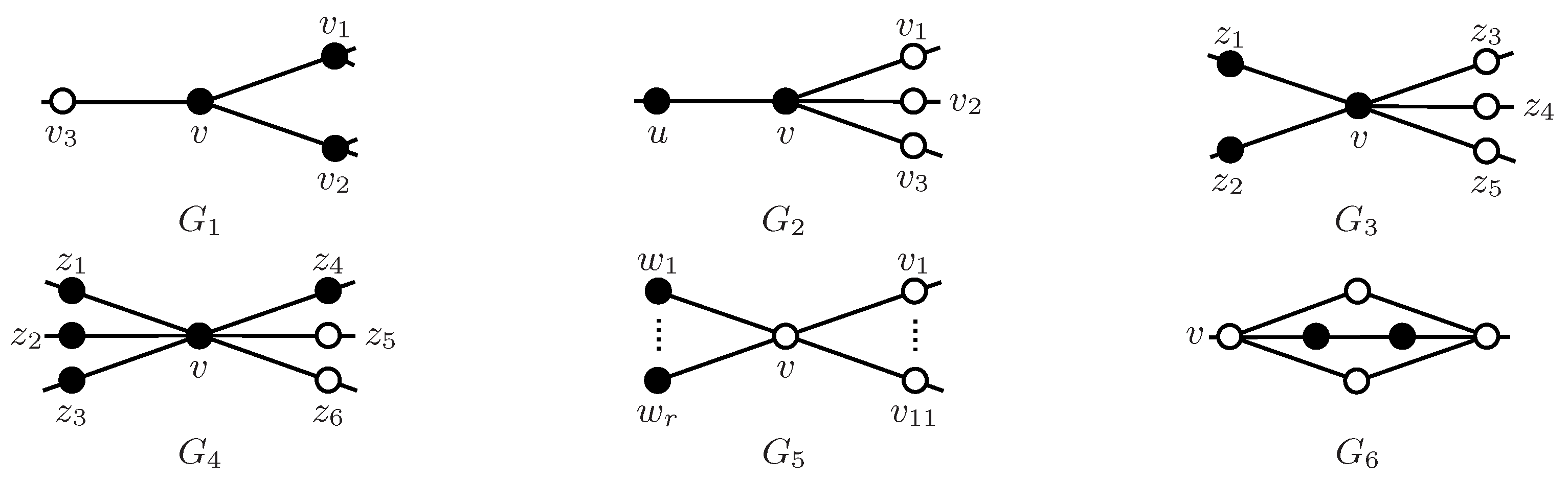In addition, Figure 1 illustrates a part of the reducible configurations of G originated from the proof. In these configurations, solid dots denote vertices with specified degrees, whereas hollow dots indicate vertices whose degrees remain unspecified.

To proceed a proof by contradiction, assume that G is a minimal counterexample to Theorem 1 with the minimal $\left|V\right|+\left|E\right|$. It is evident that G is connected due to the minimality. Let $G^{\prime }$ be a proper normal subgraph of G. Then, $G^{\prime }$ has a $(\Delta (G)+3)$-NFSDTC, denoted by ${\varphi }^{\prime }$. For each vertex $x\in V\left(G\right)$, let ${\omega }^{\prime }\left(x\right)$ denote the full sum of x under the coloring ${\varphi }^{\prime }$. In what follows, we drive some claims by extending ${\varphi }^{\prime }$ to be a $(\Delta (G)+3)$-NFSDTC $\varphi$ of G to contradict the minimality of G.

Claim 1.

No $4^{-}$-vertex is adjacent to a leaf in G.

Proof. 

Without loss of generality, assume that there exists a 4-vertex v adjacent to a leaf $v_1$. Let $v_2$, $v_3$ and $v_4$ be the neighbors of v other than $v_1$, and $G^{\prime }=G-v_1$. Then, from the minimality of G, $G^{\prime }$ has a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. From the principles of proper total coloring, we have $\varphi \left(v_{1}v\right)\notin \{{\varphi }^{\prime }\left(v\right),{\varphi }^{\prime }\left(v{v}_2\right),{\varphi }^{\prime }\left(v{v}_3\right),{\varphi }^{\prime }\left(v{v}_4\right)\}$, which means that there are 4 forbidden colors for $v_{1}v$ at most. Thus, $v_{1}v$ has at least $\Delta \left(G\right)+3-4=\Delta \left(G\right)-1\ge 21$ feasible colors. Likewise, $v_1$ has at least $\Delta \left(G\right)+3-2\ge 23$ feasible colors. By Lemma 2, it follows that there are at least 42 different values for $\varphi \left(v_1\right)+\varphi \left(v_{1}v\right)$. Hence, $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v_{1}v\right)$ also has at least 42 distinct values. Therefore, there must exist a value for $\omega \left(v\right)$ such that $\omega \left(v\right)\ne {\omega }^{\prime }\left(v_2\right)$, $\omega \left(v\right)\ne {\omega }^{\prime }\left(v_3\right)$ and $\omega \left(v\right)\ne {\omega }^{\prime }\left(v_4\right)$. In addition, by Lemma 3, we have $\omega \left(v\right)\ne \omega \left(v_1\right)$. Consequently, G has a $(\Delta (G)+3)$-NFSDTC $\varphi$, which contradicts the minimality of G. □

The following Claims 2 and 3 can be found in [13], so we omit their proof here.

Claim 2 ([13], Claim 2). There is no 2-vertex adjacent to two other 2-vertices in G.

Claim 3 ([13], Claim 3). There is no 2-vertex adjacent to a 3-vertex in G.

Claim 4.

3-vertex has at most one neighbor of degree 3 in G.

Proof. 

Assume that there exists a 3-vertex v adjacent to two 3-vertices in G. Let $v_i(i=1,2,3)$ be the neighbors of v with $d_G\left(v_1\right)=d_G\left(v_2\right)=3$, as shown in the structure $G_1$ in Figure 1. Let $v_4$ and $v_5$ be the neighbors of $v_1$ other than v, and $v_6$ and $v_7$ be the neighbors of $v_2$ other than v. The other neighbors of $v_3$ excluding v are denoted by $z_p$ for $1\le p\le k$, where $2\le k\le \Delta \left(G\right)-1$. Let $G^{\prime }=G-v$. Then, by the minimality of G, there exists a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ for $G^{\prime }$. We now color the vertex v and its incident edges.

Assume, without loss of generality, that $d_G\left(v_3\right)=\Delta \left(G\right)$. From the principles of proper total coloring, we have $\varphi \left(v_{3}v\right)\notin \{{\varphi }^{\prime }\left(z_p{v}_3\right)\mid 1\le p\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(v_3\right)\right\}$; this indicates that the edge $v_{3}v$ has $\Delta \left(G\right)$ forbidden colors and 3 feasible colors. Likewise, v has $\Delta \left(G\right)-1$ feasible colors since $\varphi \left(v\right)\notin \{{\varphi }^{\prime }\left(v_3\right),\varphi \left(v_{3}v\right),{\varphi }^{\prime }\left(v_1\right),{\varphi }^{\prime }\left(v_2\right)\}$. By Lemma 2, it follows that $\varphi \left(v_{3}v\right)+\varphi \left(v\right)$ has at least $\Delta \left(G\right)$ different values, and thus, $\omega \left(v_3\right)={\omega }^{\prime }\left(v_3\right)+\varphi \left(v_{3}v\right)+\varphi \left(v\right)$ also has at least $\Delta \left(G\right)$ different values. Therefore, there exists a value for $\omega \left(v_3\right)$ yielding $\omega \left(v_3\right)\ne \omega \left(z_p\right)$ with $1\le p\le \Delta \left(G\right)-1$.

Next, we consider the distinguishability of the full sums at $v_1$ and $v_2$ with their neighbors, as well as $v_3$ and v. Based on the previous discussion above, $\varphi \left(v_{3}v\right)$ and $\varphi \left(v\right)$ have already been determined. Then, by the principles of proper total coloring, $\varphi \left(v{v}_1\right)\notin \{\varphi \left(v_{3}v\right)$, $\varphi \left(v\right),{\varphi }^{\prime }\left(v_1\right),{\varphi }^{\prime }\left(v_1{v}_4\right),{\varphi }^{\prime }\left(v_1{v}_5\right)\}$, which means that the edge $v{v}_1$ has $\Delta \left(G\right)-2$ feasible colors. Similarly, $\varphi \left(v{v}_2\right)\notin \{\varphi \left(v_{3}v\right),\varphi \left(v\right),\varphi \left(v{v}_1\right),{\varphi }^{\prime }\left(v_2\right),{\varphi }^{\prime }\left(v_2{v}_6\right),{\varphi }^{\prime }\left(v_2{v}_7\right)\}$. This implies that the edge $v{v}_2$ has $\Delta \left(G\right)-3$ feasible colors. Furthermore, from the definition of neighbor full sum distinguishing total coloring, at most, one feasible color for $v{v}_2$ will cause $\omega \left(v\right)=\omega \left(v_1\right)$, leaving $\Delta \left(G\right)-4\ge 22-4=18>2$ feasible colors for $v{v}_2$. Thus, $\omega \left(v_2\right)={\omega }^{\prime }\left(v_2\right)+\varphi \left(v\right)+\varphi \left(v{v}_2\right)$ could take at least 18 different values, and so, there exists a value for $\omega \left(v_2\right)$ such that $\omega \left(v_2\right)\ne \omega \left(v_6\right)$ and $\omega \left(v_2\right)\ne \omega \left(v_7\right)$.

At this point, $\varphi \left(v{v}_2\right)$ has also been determined. From the definition of neighbor full sum distinguishing total coloring, there is at most one feasible color for $v{v}_1$ that leads to $\omega \left(v_3\right)=\omega \left(v\right)$, and at most one leading to $\omega \left(v\right)=\omega \left(v_2\right)$. So, this leaves $\Delta \left(G\right)-4\ge 18>2$ feasible colors for $v{v}_1$. Therefore, $\omega \left(v_1\right)={\omega }^{\prime }\left(v_1\right)+\varphi \left(v\right)+\varphi \left(v{v}_1\right)$ also has at least 18 distinct values, guaranteeing a choice that satisfies $\omega \left(v_1\right)\ne \omega \left(v_4\right)$ and $\omega \left(v_1\right)\ne \omega \left(v_5\right)$. Thus, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$, which contradicts the minimality of G. □

Claim 5.

There is no 2-vertex adjacent to a 4-vertex in G.

Proof. 

Assume that there exists a 2-vertex u adjacent to a 4-vertex v in G. Let $u_1$ be the neighbor of u distinct from v. Let $v_1$, $v_2$ and $v_3$ be the neighbors of v other than u, as shown in the reducible configuration $G_2$ depicted in Figure 1. Let $G^{\prime }=G-u$. Then, by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. Next, we will color the vertex u and its removal edges.

Assume, without loss of generality, that $d_G\left(u_1\right)=\Delta \left(G\right)$, and $z_p$ are the neighbors of $u_1$ distinct from v, where $1\le p\le \Delta \left(G\right)-1$. From the principles of proper total coloring, we have $\varphi \left(u_{1}u\right)\notin \{{\varphi }^{\prime }\left(u_1{z}_p\right)\mid 1\le p\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(u_1\right)\right\}$. Therefore, the edge $u_{1}u$ has $\Delta \left(G\right)$ forbidden colors and 3 feasible colors. Likewise, $\varphi \left(u\right)$∉$\{{\varphi }^{\prime }\left(u_1\right)$, $\varphi \left(u_{1}u\right),{\varphi }^{\prime }\left(v\right)\}$; this means that u has $\Delta \left(G\right)$ feasible colors. Meanwhile, $\varphi \left(uv\right)\notin \{\varphi \left(u_{1}u\right),\varphi \left(u\right),{\varphi }^{\prime }\left(v\right),$${\varphi }^{\prime }\left(v{v}_1\right),{\varphi }^{\prime }\left(v{v}_2\right),{\varphi }^{\prime }\left(v{v}_3\right)\}$, and thus, the edge $uv$ has $\Delta \left(G\right)-3$ feasible colors. From the definition of neighbor full sum distinguishing total coloring, there is at most one color from the feasible colors for $u_{1}u$ that results in $\omega \left(u\right)=\omega \left(v\right)$. Analogously, there exists at most one color among the feasible colors for $uv$ that results in $\omega \left(u_1\right)=\omega \left(u\right)$. Consequently, $u_{1}u$ possesses 2 remaining feasible colors, while $uv$ has $\Delta \left(G\right)-4$ remaining feasible colors. Note that u has at least $\Delta \left(G\right)$ feasible colors. Hence, it follows from Lemma 2 that $\varphi \left(u_{1}u\right)+\varphi \left(u\right)$ would obtain at least $\Delta \left(G\right)$ different values, and thus, $\omega \left(u_1\right)={\omega }^{\prime }\left(u_1\right)+\varphi \left(u_{1}u\right)+\varphi \left(u\right)$ also has $\Delta \left(G\right)$ different values at least. Therefore, there must exist a value for $\omega \left(u_1\right)$ such that $\omega \left(u_1\right)\ne \omega \left(z_p\right)$ with $1\le p\le \Delta \left(G\right)-1$ simultaneously.

Next, we consider the distinguishability of the full sum for v and its neighbors $v_1$, $v_2$ and $v_3$. Based on the previous analysis concerning $\omega \left(u_1\right)\ne \omega \left(z_p\right)$ for $1\le p\le \Delta \left(G\right)-1$, the color $\varphi \left(u\right)$ is now determined. Given that $\Delta \left(G\right)\ge 22$, there are at least $\Delta \left(G\right)-4\ge 18>3$ different values feasible for $\varphi \left(uv\right)$. Hence, $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(u\right)+\varphi \left(uv\right)$ also takes at least 18 different values; this means that there exists a value for $\omega \left(v\right)$ yielding $\omega \left(v\right)\ne \omega \left(v_i\right)$ with $1\le i\le 3$. Thus, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$, which contradicts the minimality of G. □

Claim 6.

A $5^{+}$-vertex is adjacent to at least 4 non-leaf neighbors. Moreover, if the $5^{+}$-vertex is adjacent to precisely 4 non-leaf neighbors, then it does not have a 2-vertex as its neighbor in G.

Proof. 

Firstly, we show that any $5^{+}$-vertex v is adjacent to at least 4 non-leaf neighbors in G. Assume by a contradiction that v has at most three non-leaf neighbors. For convenience, we write $v_1,\dots ,v_k$ as the leaf neighbors of v, and $z_1,\dots ,z_t$ as its non-leaf neighbors, where $k+t=d_G\left(v\right)$ and $0\le t\le 3$.

When $t=0$, v has no non-leaf neighbors, which implies that G is a star. Therefore, from Lemma 1, G admits a $(\Delta (G)+1)$-NFSDTC $\varphi$, which contradicts the minimality of G.

Without loss of generality, suppose that v has three non-leaf neighbors, $z_1$, $z_2$ and $z_3$. Then, $k=d_G\left(v\right)-3\ge 2$ at this moment. This means that v has at least two leaves. Let $G^{\prime }=G-v_1$. Then, by the minimality of G, there exists a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ for $G^{\prime }$. From the principles of proper total coloring, $v{v}_1$ has at least $\Delta \left(G\right)+3-d_G\left(v\right)\ge 3$ feasible colors since $\varphi \left(v{v}_1\right)\notin \{{\varphi }^{\prime }\left(v{v}_i\right)\mid 2\le i\le k\}\cup \{{\varphi }^{\prime }\left(v\right),{\varphi }^{\prime }\left(v{z}_1\right),{\varphi }^{\prime }\left(v{z}_2\right),{\varphi }^{\prime }\left(v{z}_3\right)\}$. Similarly, $v_1$ has at least $\Delta \left(G\right)+3-2\ge 23$ feasible colors. By Lemma 2, we have that $\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ owns at least 24 distinct values; this implies that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ also takes at least 24 distinct values. So, there must exist a value for $\omega \left(v\right)$ satisfying $\omega \left(v\right)\notin \{\omega \left(z_1\right),\omega \left(z_2\right),\omega \left(z_3\right)\}$. Furthermore, by Lemma 3, we have $\omega \left(v\right)\ne \omega \left(v_i\right)$ ($1\le i\le k$). Thus, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$ extended from ${\varphi }^{\prime }$, contradicting the minimality of G.

Next, we will prove that for any $5^{+}$-vertex v in G, if $D_G\left(v\right)=4$, then $N_2^G\left(v\right)=0$. Assume that there exists a $5^{+}$-vertex v (say, briefly) with $D_G\left(v\right)=4$ adjacent to a 2-vertex $z_1$. Let $v_1,\dots ,v_k$ for $k=d_G\left(v\right)-4$ denote the leaves of v, and $z_1,\dots ,z_4$ denote the non-leaf neighbors of v. Let $G^{\prime }=G-v_1$. Then, by the minimality of G, there exists a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ for $G^{\prime }$. From the principles of proper total coloring, $\varphi \left(v{v}_1\right)$∉$\{{\varphi }^{\prime }\left(v\right),{\varphi }^{\prime }\left(z_{1}v\right),{\varphi }^{\prime }\left(z_{2}v\right)$, ${\varphi }^{\prime }\left(z_{3}v\right),{\varphi }^{\prime }\left(z_{4}v\right)\}\cup \{{\varphi }^{\prime }\left(v{v}_i\right)\mid 2\le i\le k\}$. Thus, $v{v}_1$ should have at most $d_G\left(v\right)$ forbidden colors, leaving at least $\Delta \left(G\right)+3-d_G\left(v\right)\ge 3$ feasible colors. Likewise, $\varphi \left(v_1\right)$ obtains at least $\Delta \left(G\right)+3-2\ge 23$ feasible colors. Hence, by Lemma 2, we see that $\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ has at least 24 distinct values, which yields that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ also has at least 24 distinct values. Therefore, there must exist a value for $\omega \left(v\right)$ such that $\omega \left(v\right)\notin \{\omega \left(z_1\right),\omega \left(z_2\right),\omega \left(z_3\right)\}$. It further follows by Lemma 3 that $\omega \left(v\right)\ne \omega \left(v_i\right)$ with $1\le i\le k$. Consequently, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$ extended from ${\varphi }^{\prime }$, which contradicts the minimality of G. □

Claim 7.

No $5^{+}$-vertex v with $D_G\left(v\right)=5$ has at least two 2-vertices in G.

Proof. 

Suppose that G has a $5^{+}$-vertex v with $D_G\left(v\right)=5$ having two neighbors of degree 2, e.g., $z_1$ and $z_2$. Let $v_1,v_2,\dots ,v_k$ denote the leaves of v with $k=d_G\left(v\right)-5$. For convenience, we write $z_3$, $z_4$ and $z_5$ as the other three non-leaf neighbors of v.

Case 1.$d_G\left(v\right)=5$.

Here, $k=0$. This indicates that v is not a leaf, as depicted by the structure $G_3$ in Figure 1. Let $G^{\prime }=G-z_1$. Then, by the minimality of G, there exists a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ for $G^{\prime }$. Let $z_6$ be the other neighbor of $z_1$, differing from v. We now color the vertex $z_1$ and its incident edges.

Assume, without loss of generality, that $d_G\left(z_6\right)=\Delta \left(G\right)$. Let $z_{6,i}$ for $1\le i\le \Delta \left(G\right)-1$ be the neighbors of $z_6$ differ from $z_1$. From the principles of proper total coloring, $\varphi \left(z_6{z}_1\right)\notin \{{\varphi }^{\prime }\left(z_6{z}_{6,i}\right)\mid 1\le i\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(z_6\right)\right\}$. Therefore, $z_6{z}_1$ has $\Delta \left(G\right)$ forbidden colors and 3 feasible colors. Similarly, $\varphi \left(z_1\right)\notin \{{\varphi }^{\prime }\left(z_6\right),\varphi \left(z_6{z}_1\right),{\varphi }^{\prime }\left(v\right)\}$; thus, $z_1$ has $\Delta \left(G\right)$ feasible colors. Furthermore, $\varphi \left(z_{1}v\right)$∉$\{\varphi \left(z_6{z}_1\right)$, $\varphi \left(z_1\right)$, ${\varphi }^{\prime }\left(v\right)$, ${\varphi }^{\prime }\left(v{z}_2\right)$, ${\varphi }^{\prime }\left(v{z}_3\right)$, ${\varphi }^{\prime }\left(v{z}_4\right)$ and ${\varphi }^{\prime }\left(v{z}_5\right)\}$. Hence, $z_{1}v$ has $\Delta \left(G\right)-4$ feasible colors. According to the definition of neighbor full sum distinguishing total coloring, there is at most one feasible color for $z_6{z}_1$ such that $\omega \left(z_1\right)=\omega \left(v\right)$. Similarly $z_{1}v$ has at most one feasible color resulting in $\omega \left(z_6\right)=\omega \left(z_1\right)$. As a result, $z_6{z}_1$ has 2 remaining feasible colors, and $z_{1}v$ has $\Delta \left(G\right)-5$ remaining colors. Since $z_1$ has $\Delta \left(G\right)$ feasible colors, from Lemma 2, $\varphi \left(z_6{z}_1\right)+\varphi \left(z_1\right)$ would take at least $\Delta \left(G\right)$ distinct values. This implies that $\omega \left(z_6\right)={\omega }^{\prime }\left(z_6\right)+\varphi \left(z_6{z}_1\right)+\varphi \left(z_1\right)$ also takes at least $\Delta \left(G\right)$ different values. Thus, there exists a value for $\omega \left(z_6\right)$ satisfying $\omega \left(z_6\right)\ne \omega \left(z_{6,i}\right)$ with $1\le i\le \Delta \left(G\right)-1$.

We next consider the full sum distinguishability of vertex v with its neighbors $z_2$, $z_3$, $z_4$ and $z_5$. From the analysis of $\omega \left(z_6\right)\ne \omega \left(z_{6,i}\right)$ above, for $1\le i\le \Delta \left(G\right)-1$, $\varphi \left(z_1\right)$ is now defined. Since $\Delta \left(G\right)\ge 22$, $\varphi \left(z_{1}v\right)$ has at least $\Delta \left(G\right)-5\ge 17>4$ distinct values. This indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(z_1\right)+\varphi \left(z_{1}v\right)$ also takes at least 17 different values. Consequently, one can find a value for $\omega \left(v\right)$ yielding $\omega \left(v\right)\ne \omega \left(z_j\right)$ where $2\le j\le 5$. Consequently, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$ extended from ${\varphi }^{\prime }$, contradicting the minimality of G.

Case 2. $d_G\left(v\right)\ge 6$.

At this moment, $k\ge 1$. This indicates that v has at least one leaf. Let $G^{\prime }=G-v_1$. Then, by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. From the principles of proper total coloring, the edge $v{v}_1$ possesses $\Delta \left(G\right)+3-d_G\left(v\right)\ge 3$ feasible colors, and vertex $v_1$ possesses $\Delta \left(G\right)+3-2\ge 23$ feasible colors. Thus, $\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ would take at least 23 distinct values, which means that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ also takes at least 23 different values. Hence, there must exist a value for $\omega \left(v\right)$ satisfying $\omega \left(v\right)\ne \omega \left(z_j\right)$ for $1\le j\le 5$. Furthermore, by Lemma 3, we have $\omega \left(v\right)\ne \omega \left(v_i\right)$ for $1\le i\le k$. Therefore, one can obtain a $(\Delta (G)+3)$-NFSDTC $\varphi$ of G by extending ${\varphi }^{\prime }$, contradicting the minimality of G. □

Claim 8.

No $6^{+}$-vertex v with $D_G\left(v\right)=6$ is adjacent to at least four 2-vertices, in which at least one neighbor is a bad 2-vertex.

Proof. 

Suppose that G has a $6^{+}$-vertex v with $D_G\left(v\right)=6$ adjacent to at least four 2-vertices. Let $z_1,\dots ,z_6$ be the non-leaf neighbors of v, and let $v_j$ be the leaf neighbors of v, where $1\le j\le k$ and $k=d_G\left(v\right)-6$.

Firstly, we will show that $N_2^G\left(v\right)\le 3$. Suppose that $d_G\left(z_1\right)=\dots =d_G\left(z_4\right)=2$. The proof will proceed by concerning the value of $d_G\left(v\right)$.

Case 1. $d_G\left(v\right)=6$.

Here, $k=0$, this indicates that v is not adjacent to the leaf, as illustrated in the structure $G_4$ in Figure 1. Let $G^{\prime }=G-z_1$. Then, from the minimality of G, there is a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ in $G^{\prime }$. Let $z_7$ denote the other neighbors of $z_1$ differ from v. We now assign colors to the vertex $z_1$ and its incident edges.

Without loss of generality, assume that $d_G\left(z_7\right)=\Delta \left(G\right)$. Let $z_{7,i}$ be the neighbors of $z_7$ other than $z_1$, where $1\le i\le \Delta \left(G\right)-1$. From the principles of proper total coloring, $\varphi \left(z_7{z}_1\right)\notin \{{\varphi }^{\prime }\left(z_7{z}_{7,i}\right)\mid 1\le i\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(z_7\right)\right\}$. This implies that edge $z_7{z}_1$ has $\Delta \left(G\right)$ forbidden colors, and so, it leaves 3 feasible colors. Similarly, $\varphi \left(z_1\right)\notin \{{\varphi }^{\prime }\left(z_7\right),\varphi \left(z_7{z}_1\right),{\varphi }^{\prime }\left(v\right)\}$, and thus, $z_1$ has $\Delta \left(G\right)$ feasible colors. Additionally, since $\varphi \left(z_{1}v\right)\notin \{\varphi \left(z_7{z}_1\right),\varphi \left(z_1\right),{\varphi }^{\prime }\left(v\right)$, ${\varphi }^{\prime }\left(v{z}_2\right)$, ${\varphi }^{\prime }\left(v{z}_3\right),{\varphi }^{\prime }\left(v{z}_4\right),{\varphi }^{\prime }\left(v{z}_5\right),{\varphi }^{\prime }\left(v{z}_6\right)\}$, there are $\Delta \left(G\right)-5$ feasible colors for edge $z_{1}v$. According to the definition of neighbor full sum distinguishing total coloring, there is at most one feasible color for edge $z_7{z}_1$, causing $\omega \left(z_1\right)=\omega \left(v\right)$, and at most one feasible color for edge $z_{1}v$, leading to $\omega \left(z_7\right)=\omega \left(z_1\right)$. Thus, two feasible colors remain for edge $z_7{z}_1$, and $\Delta \left(G\right)-6$ colors for edge $z_{1}v$. Since $z_1$ has $\Delta \left(G\right)$ feasible colors, from Lemma 2, $\varphi \left(z_7{z}_1\right)+\varphi \left(z_1\right)$ would take at least $\Delta \left(G\right)$ different values. Consequently, $\omega \left(z_7\right)={\omega }^{\prime }\left(z_7\right)+\varphi \left(z_7{z}_1\right)+\varphi \left(z_1\right)$ also has at least $\Delta \left(G\right)$ different values, guaranteeing the existence of a value for $\omega \left(z_7\right)$ such that $\omega \left(z_7\right)\ne \omega \left(z_{7,i}\right)$, where $1\le i\le \Delta \left(G\right)-1$.

Now, we discuss the full sum distinguishability of v and its neighbors $z_2,\dots ,z_6$. Based on the previous analysis of $\omega \left(z_7\right)\ne \omega \left(z_{7,i}\right)$ for $1\le i\le \Delta \left(G\right)-1$, the color $\varphi \left(z_1\right)$ is now fixed. Since $\Delta \left(G\right)\ge 22$, there are at least $\Delta \left(G\right)-6\ge 16>5$ distinct values for $\varphi \left(z_{1}v\right)$. This indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(z_1\right)+\varphi \left(z_{1}v\right)$ also takes at least 16 distinct values. Accordingly, there exists a value for $\omega \left(v\right)$ yielding $\omega \left(v\right)\ne \omega \left(z_t\right)$ for $2\le t\le 6$. Thus, ${\varphi }^{\prime }$ can be extended to a $(\Delta (G)+3)$-NFSDTC of G, contradicting the minimality of G.

Case 2. $d_G\left(v\right)\ge 7$.

Here, $k\ge 1$, which means that v has a leaf neighbor. Let $G^{\prime }=G-v_1$. Then, by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. According to the definition of neighbor full sum distinguishing total coloring, $v{v}_1$ has at least $\Delta \left(G\right)+3-d_G\left(v\right)\ge 3$ feasible colors, and $v_1$ has $\Delta \left(G\right)+3-2\ge 23$ feasible colors. Hence, $\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ would take at least 23 distinct values; this indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v{v}_1\right)$ has at least 23 distinct values. Therefore, there is a value for $\omega \left(v\right)$ satisfying $\omega \left(v\right)\ne \omega \left(z_t\right)$ for $1\le t\le 6$. Moreover, by Lemma 3, it follows that $\omega \left(v\right)\ne \omega \left(v_j\right)$ for all $1\le j\le k$. Thus, one can obtain a $(\Delta (G)+3)$-NFSDTC $\varphi$ of G by extending ${\varphi }^{\prime }$, contradicting the minimality of G.

Secondly, we prove that $N_{\tilde{2}}^G\left(v\right)=0$. Suppose that v is adjacent to a bad 2-vertex $z_1$. Let $z_7$ be the other neighbor of $z_1$ besides v and $d_G\left(z_7\right)=2$. Let $z_8$ be the other neighbor of $z_7$ differing from $z_1$. Let $G^{\prime }=G-z_1$. Then, by the minimality of G, $G^{\prime }$ has a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$.

Without loss of generality, assume that $d_G\left(v\right)=\Delta \left(G\right)$. From the principles of proper total coloring, $\varphi \left(v{z}_1\right)\notin \{{\varphi }^{\prime }\left(v{v}_j\right)\mid 1\le j\le k\}\cup \{{\varphi }^{\prime }\left(v{z}_t\right)\mid 2\le t\le 6\}\cup \left\{{\varphi }^{\prime }\left(v\right)\right\}$. This means that $v{z}_1$ has $\Delta \left(G\right)$ forbidden colors and 3 feasible colors. Likewise, $\varphi \left(z_1\right)\notin \{{\varphi }^{\prime }\left(v\right),\varphi \left(v{z}_1\right)$, ${\varphi }^{\prime }\left(z_7\right)\}$, which follows that $z_1$ has $\Delta \left(G\right)$ feasible colors. Furthermore, $\varphi \left(z_1{z}_7\right)\notin \{\varphi \left(v{z}_1\right),\varphi \left(z_1\right)$, ${\varphi }^{\prime }\left(z_7\right),{\varphi }^{\prime }\left(z_7{z}_8\right)\}$; thus, $z_1{z}_7$ has $\Delta \left(G\right)-1$ feasible colors. From the definition of neighbor full sum distinguishing total coloring, there is at most one feasible color for edge $v{z}_1$ causing $\omega \left(z_1\right)=\omega \left(z_7\right)$, and at most one feasible color for $z_1{z}_7$, similarly causing $\omega \left(v\right)=\omega \left(z_1\right)$. Hence, 2 feasible colors remain for $v{z}_1$, and $\Delta \left(G\right)-2$ feasible colors for $z_1{z}_7$. Since $z_1$ has $\Delta \left(G\right)$ feasible colors, by Lemma 2, $\varphi \left(v{z}_1\right)+\varphi \left(z_1\right)$ has at least $\Delta \left(G\right)$ different values; this indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v{z}_1\right)+\varphi \left(z_1\right)$ takes at least $\Delta \left(G\right)$ distinct values. Thus, there is a value for $\omega \left(v\right)$ such that $\omega \left(v\right)\ne \omega \left(v_j\right)$ for $1\le j\le k$, as well as $\omega \left(v\right)\ne \omega \left(z_t\right)$ for $2\le t\le 6$.

Finally, we consider the full sum distinguishability of $z_7$ and its neighbor $z_8$. Based on the previous analysis of $\omega \left(v\right)\ne \omega \left(v_j\right)$ for $1\le j\le k$, and $\omega \left(v\right)\ne \omega \left(z_t\right)$ for $2\le t\le 6$, $\varphi \left(z_1\right)$ is already determined. Since $\Delta \left(G\right)\ge 22$, there are at least $\Delta \left(G\right)-2\ge 20$ distinct values for $\varphi \left(z_1{z}_7\right)$; as a result, $\omega \left(z_7\right)={\omega }^{\prime }\left(z_7\right)+\varphi \left(z_1\right)+\varphi \left(z_1{z}_7\right)$ possesses no fewer than 20 distinct values. Therefore, there is a value for $\omega \left(z_7\right)$ satisfying $\omega \left(z_7\right)\ne \omega \left(z_8\right)$, and thus, there exists a $(\Delta (G)+3)$-NFSDTC $\varphi$ in G extending from ${\varphi }^{\prime }$, contradicting the minimality of G. □

Claim 9.

No $7^{+}$-vertex v with $D_G\left(v\right)=k$ for $7\le k\le 11$ has at least $k-3$ neighbors of degree 2, in which at least $k-5$ neighbors are bad 2-vertices.

Proof. 

Without loss of generality, suppose that G contains a $7^{+}$-vertex v with $D_G\left(v\right)=11$. Let $w_i$ denote the leaf neighbors of v for $1\le i\le r$, and $v_j$ for $1\le j\le 11$ denote the neighbors of v with degree of at least 2, where $r=d_G\left(v\right)-11$, as in the structure $G_5$ depicted in Figure 1.

(1) We aim to show that $N_2^G\left(v\right)\le 7$. Assume by a contradiction that v has at least eight 2-vertices. Let $d_G\left(v_1\right)=\dots =d_G\left(v_8\right)=2$, and z denote the other neighbor of $v_1$ besides v. Two cases are considered depending on the degree of v.

Case 1. $d_G\left(v\right)\ge 12$.

In this case, $r\ge 1$, which implies that v has at least one leaf neighbor. Let $G^{\prime }=G-w_1$. Then, by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. From the principles of proper total coloring, $v{w}_1$ has at least $\Delta \left(G\right)+3-d_G\left(v\right)\ge 3$ feasible colors, and $w_1$ has $\Delta \left(G\right)+1\ge 23$ feasible colors. Thus, $\varphi \left(w_1\right)+\varphi \left(v{w}_1\right)$ takes no fewer than 23 distinct values. Furthermore, $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(w_1\right)+\varphi \left(v{w}_1\right)$ takes at least 23 different values. Therefore, there is a value for $\omega \left(v\right)$ satisfying $\omega \left(v\right)\ne \omega \left(v_j\right)$ where $1\le j\le 11$. Meanwhile, by Lemma 3, it follows that $\omega \left(v\right)\ne \omega \left(w_i\right)$ for $1\le i\le r$. Consequently, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$ extending ${\varphi }^{\prime }$, contradicting the minimality of G.

Case 2. $d_G\left(v\right)=11$.

Here, $r=0$, indicating that v has no leaf. Let $G^{\prime }=G-v_1$. Then, by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. Suppose without loss of generality that $d_G\left(z\right)=\Delta \left(G\right)$. Let $z_p$ be the neighbors of z other than $v_1$ for $1\le p\le \Delta \left(G\right)-1$. From the principles of proper total coloring, $\varphi \left(z{v}_1\right)\notin \{{\varphi }^{\prime }\left(z{z}_p\right)\mid 1\le p\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(z\right)\right\}$, which implies that there are 3 feasible colors for $z{v}_1$. Similarly, $\varphi \left(v_1\right)\notin \{{\varphi }^{\prime }\left(z\right),\varphi \left(z{v}_1\right),{\varphi }^{\prime }\left(v\right)\}$, which means that $v_1$ has $\Delta \left(G\right)$ feasible colors. Moreover, $\varphi \left(v_{1}v\right)$∉$\{\varphi \left(z{v}_1\right)$, $\varphi \left(v_1\right),{\varphi }^{\prime }\left(v\right)\}\cup \{{\varphi }^{\prime }\left(v{v}_j\right)\mid 2\le j\le 11\}$; hence, $v_{1}v$ has at least $\Delta \left(G\right)-10$ feasible colors. By the definition of neighbor full sum distinguishing total coloring, there is at most one color for $z{v}_1$ causing $\omega \left(v_1\right)=\omega \left(v\right)$, and at most one color for $v_{1}v$ similarly causing $\omega \left(z\right)=\omega \left(v_1\right)$. Thus, $z{v}_1$ has 2 remaining feasible colors and $v_{1}v$ has $\Delta \left(G\right)-11$ remaining feasible colors. Since $v_1$ has $\Delta \left(G\right)$ feasible colors, it follows from Lemma 2 that $\varphi \left(z{v}_1\right)+\varphi \left(v_1\right)$ has at least $\Delta \left(G\right)$ different values. This further implies that $\omega \left(z\right)={\omega }^{\prime }\left(z\right)+\varphi \left(z{v}_1\right)+\varphi \left(v_1\right)$ would take at least $\Delta \left(G\right)$ different values. Hence, $\omega \left(z\right)\ne \omega \left(z_p\right)$ for $1\le p\le \Delta \left(G\right)-1$.

Now, we consider the full sum distinguishability between v and its neighbors $v_j$ for $2\le j\le 11$. Based on the above analysis of $\omega \left(z\right)\ne \omega \left(z_p\right)$ for $1\le p\le \Delta \left(G\right)-1$, $\varphi \left(v_1\right)$ is now determined. Since $\Delta \left(G\right)\ge 22$, there are at least 11 feasible colors for $v_{1}v$. This indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v_{1}v\right)$ would take at least 11 different values. Thus, there is a value for $\omega \left(v\right)$ such that $\omega \left(v\right)\ne \omega \left(v_j\right)$ where $2\le j\le 11$, which contradicts the minimality of G.

(2) We here aim to prove that $N_{\tilde{2}}^G\left(v\right)\le 5$. Assume that v is adjacent to at least six bad 2-vertices. For convenience, we write $v_1,\dots ,v_6$ as these bad 2-vertices, and z is a neighbor of $v_1$ distinct from v with $d_G\left(z\right)=2$.

If $d_G\left(v\right)\ge 12$, then $r\ge 1$; this indicates that v has at least one leaf. This case can be proved using the same method as Case 1 in (1).

If $d_G\left(v\right)=11$, then $r=0$. In this case, it means that v has no leaf. Let $G^{\prime }=G-v_1$. Then by the minimality of G, $G^{\prime }$ admits a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$. Let $z_1$ be a neighbor of z distinct from $v_1$. We then assign colors to $v_1$ and its incident edges.

From the principles of proper total coloring, $z{v}_1$ has 2 forbidden colors and $\Delta \left(G\right)+1$ feasible colors since $\varphi \left(z{v}_1\right)\notin \{{\varphi }^{\prime }\left(z{z}_1\right),{\varphi }^{\prime }\left(z\right)\}$. Similarly, $\varphi \left(v_1\right)\notin \{{\varphi }^{\prime }\left(z\right),\varphi \left(z{v}_1\right)$, ${\varphi }^{\prime }\left(v\right)\}$, and thus, $v_1$ has $\Delta \left(G\right)$ feasible colors. Furthermore, $\varphi \left(v_{1}v\right)\notin \{\varphi \left(z{v}_1\right)$, $\varphi \left(v_1\right),{\varphi }^{\prime }\left(v\right)\}\cup \{{\varphi }^{\prime }\left(v{v}_j\right)\mid 2\le j\le 11\}$. Hence, $v_{1}v$ has $\Delta \left(G\right)-10$ feasible colors. By the definition of neighbor full sum distinguishing total coloring, there is at most one color for $z{v}_1$ causing $\omega \left(v_1\right)=\omega \left(v\right)$, and at most one color for $v_{1}v$ causing $\omega \left(z\right)=\omega \left(v_1\right)$. Therefore, $z{v}_1$ owns at least $\Delta \left(G\right)$ feasible colors, and $v_{1}v$ owns at least $\Delta \left(G\right)-11$ feasible colors. Note that $v_1$ has $\Delta \left(G\right)$ feasible colors. Hence, it follows from Lemma 2 that $\varphi \left(z{v}_1\right)+\varphi \left(v_1\right)$ would take at least $2\Delta \left(G\right)-3\ge 41$ different values. It induces that $\omega \left(z\right)={\omega }^{\prime }\left(z\right)+\varphi \left(z{v}_1\right)+\varphi \left(v_1\right)$ also has at least 41 different values. Hence, there is a value for $\omega \left(z\right)$ such that $\omega \left(z\right)\ne \omega \left(z_1\right)$.

We next consider the full sum distinguishability of v and its neighbors $v_j$ for $2\le j\le 11$. From the above analysis of $\omega \left(z\right)\ne \omega \left(z_1\right)$, the value $\varphi \left(z\right)$ is already determined. Since $\Delta \left(G\right)\ge 22$, $v_{1}v$ has at least $\Delta \left(G\right)-11\ge 11$ feasible colors. This indicates that $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(v_1\right)+\varphi \left(v_{1}v\right)$ also takes at least 11 different values. Accordingly, there is a value for $\omega \left(v\right)$ ensuring that $\omega \left(v\right)\ne \omega \left(v_j\right)$, where $2\le j\le 11$. Therefore, G admits a $(\Delta (G)+3)$-NFSDTC $\varphi$ by extending ${\varphi }^{\prime }$, which contradicts the minimality of G. □

From the statement of Claim 9, the following relationships can be derived, as shown in

Table 1. The relationships between $D_G\left(v\right)=k(7\le k\le 11)$, $N_2^G\left(v\right)$ and $N_{\tilde{2}}^G\left(v\right)$.

k	7	8	9	10	11
$max{N}_2^G\left(v\right)$	3	4	5	6	7
$max{N}_{\tilde{2}}^G\left(v\right)$	1	2	3	4	5

.

Claim 10.

No ${12}^{+}$-vertex v with $D_G\left(v\right)\ge 12$ has at least one neighbor that is a bad 2-vertex.

Proof. 

Suppose that G contains a ${12}^{+}$-vertex v such that $D_G\left(v\right)=12$. Let $v_i$ for $1\le i\le d_G\left(v\right)-1$ be the neighbors of v, and z be a bad 2-vertex adjacent to v, $z_1$ be the neighbor of z distinct from v with $d_G\left(z_1\right)=2$, and $z_2$ be the neighbor of $z_1$ distinct from z. Let $G^{\prime }=G-z$. Then, by the minimality of G, there is a $(\Delta (G)+3)$-NFSDTC ${\varphi }^{\prime }$ of $G^{\prime }$. We now color the vertex z and its incident edges.

Assume without loss of generality that $d_G\left(v\right)=\Delta \left(G\right)$. From the principles of proper total coloring, $\varphi \left(vz\right)\notin \{{\varphi }^{\prime }\left(v{v}_i\right)\mid 1\le i\le \Delta \left(G\right)-1\}\cup \left\{{\varphi }^{\prime }\left(v\right)\right\}$. Therefore, $vz$ has $\Delta \left(G\right)$ forbidden colors and 3 feasible colors. Similarly, we have that z has $\Delta \left(G\right)$ feasible colors due to $\varphi \left(z\right)\notin \{{\varphi }^{\prime }\left(v\right),\varphi \left(vz\right),{\varphi }^{\prime }\left(z_1\right)\}$, and $z{z}_1$ has at least $\Delta \left(G\right)-1$ feasible colors because $\varphi \left(z{z}_1\right)\notin \{\varphi \left(vz\right)$, $\varphi \left(z\right),{\varphi }^{\prime }\left(z_1\right),{\varphi }^{\prime }\left(z_1{z}_2\right)\}$. Furthermore, by the definition of neighbor full sum distinguishing total coloring, there is at most one feasible color for $vz$ such that $\omega \left(z\right)=\omega \left(z_1\right)$, and at most one feasible color for $z{z}_1$ such that $\omega \left(v\right)=\omega \left(z\right)$. Thus, $vz$ possesses at least 2 feasible colors, and $z{z}_1$ possesses at least $\Delta \left(G\right)-2$ feasible colors. Note that z has $\Delta \left(G\right)$ feasible colors. Hence, it follows from Lemma 2 that $\varphi \left(vz\right)+\varphi \left(z\right)$ would take at least $\Delta \left(G\right)$ different values. Therefore, $\omega \left(v\right)={\omega }^{\prime }\left(v\right)+\varphi \left(vz\right)+\varphi \left(z\right)$ also takes at least $\Delta \left(G\right)$ different values. So, there is a value for $\omega \left(v\right)$ such that $\omega \left(v\right)\ne \omega \left(v_i\right)$ for $1\le i\le \Delta \left(G\right)-1$.

Now, we consider the full sum distinguishability between $z_1$ and its neighbor $z_2$. By the analysis above concerning $\omega \left(v\right)\ne \omega \left(v_i\right)$ for $1\le i\le \Delta \left(G\right)-1$, the value $\varphi \left(z\right)$ is already determined. Since $\Delta \left(G\right)\ge 22$, there are at least $\Delta \left(G\right)-2\ge 20$ feasible colors for $z{z}_1$. Hence, $\omega \left(z_1\right)={\omega }^{\prime }\left(z_1\right)+\varphi \left(z\right)+\varphi \left(z{z}_1\right)$ would take at least 20 different values, and so, there is a value for $\omega \left(z_1\right)$ such that $\omega \left(z_1\right)\ne \omega \left(z_2\right)$. Consequently, one can obtain a $(\Delta (G)+3)$-NFSDTC $\varphi$ of G by extending ${\varphi }^{\prime }$, thus contradicting the minimality of G. □

Let H be the graph obtained from G by removing all leaves. Then, H is a connected subgraph of G with $g\left(H\right)\ge 5$ and $\Delta \left(H\right)\ge 22$. Furthermore, we have that Claims 1–10 also hold for H, and $\delta \left(H\right)\ge 2$. The additional properties of H are given as follows:

Fact 1.

 (1) 

For all $v\in V\left(G\right)$, $D_H\left(v\right)=D_G\left(v\right)$;

 (2) 

If $d_G\left(v\right)=k$ with $2\le k\le 4$, then $d_H\left(v\right)=k$;

 (3) 

For $f\in F\left(H\right)$ with $d_H\left(f\right)=5$, $N_{4^{+}}^H\left(f\right)\ge 2$.

Proof. 

Since H is a connected subgraph obtained from G by removing all leaves, the statements (1) and (2) follow from Claims 1–3 directly. Next, we need to prove statement (3). Let $f=v_1{v}_2{v}_3{v}_4{v}_5{v}_1$ be a 5-face in H. Then, the proof relies on analyzing $N_2^H\left(f\right)$.

• If $N_2^H\left(f\right)=0$, then by Claim 4, the face f is associated with at most three 3-vertices. Hence, $N_{4^{+}}^H\left(f\right)\ge 2$.
• If $N_2^H\left(f\right)=1$, we may suppose that $d_H\left(v_1\right)=2$, and then by Claims 2, 3, 5 and 6, it follows that $d_H\left(v_2\right)\ge 5$ and $d_H\left(v_5\right)\ge 5$.
• If $N_2^H\left(f\right)=2$, we consider two cases in the following:

  -

  When f is at least incident to a bad 2-vertex, we suppose $d_H\left(v_1\right)=d_H\left(v_2\right)=2$. From Claims 2, 3 and 5–10 we have either $5\le d_H\left(v_3\right)\le 11$ and $d_H\left(v_3\right)\ne 6$ or $5\le d_H\left(v_5\right)\le 11$ and $d_H\left(v_5\right)\ne 6$.

  -

  When f is not incident to any bad 2-vertex, we suppose that $d_H\left(v_1\right)=d_H\left(v_3\right)=2$. Then, from Claims 2, 3 and 5–9, we obtain $d_H\left(v_2\right)\ge 6$, $d_H\left(v_4\right)\ge 5$ and $d_H\left(v_5\right)\ge 5$.

• If $N_2^H\left(f\right)=3$, according to Claim 2, the only possible configuration is $d_H\left(v_1\right)=d_H\left(v_3\right)=d_H\left(v_4\right)=2$. Using Claims 2, 3 and 5–10, it follows that $7\le d_H\left(v_2\right)\le 11$ and $7\le d_H\left(v_5\right)\le 11$.
• If $N_2^H\left(f\right)\ge 4$, this contradicts the structural conditions described in Claim 2, and thus, such a case does not occur.

This completes the proof of $\left(3\right)$. □

For a $3^{+}$-vertex v in H with $N_{\tilde{2}}^H\left(v\right)\ne 0$, we conclude that each of its bad 2-vertex is only adjacent to at most one 5-face, which is formed together with v and its other neighbors (which may be some good 2-vertices). If not, a bad 2-vertex associated with two 5-faces would yield a 4-cycle, thereby contradicting the condition $g\left(H\right)\ge 5$, as illustrated by the configuration $G_6$ in Figure 1. Thus, each bad 2-vertex adjacent to v is incident with at most one 5-face. Furthermore, if any two bad 2-vertices adjacent to v are associated with the same $6^{+}$-face, then the number of 5-faces incident to v attains its maximum. In particular, if the number of bad 2-vertices adjacent to v is odd, and all bad 2-vertices are pairwise adjacent to a common $6^{+}$-face, then there must exist one bad 2-vertex that is associated with a $6^{+}$-face individually. Based on the above, we have the following fact.

Fact 2.  Every $3^{+}$-vertex v is associated with at most $d_H\left(v\right)-⌈{\displaystyle \frac{N_{\tilde{2}}^H\left(v\right)}{2}}⌉$ distinct 5-faces in G.

Subsequently, we carried out an analysis of charge transfer in the connected planar graph H. Applying Euler’s formula (i.e., $\left|V\right(H\left)\right|-\left|E\right(H\left)\right|+\left|F\right(H\left)\right|=2$) together with the Handshaking Lemma (i.e., ${\sum }_{v\in V\left(H\right)}{d}_H\left(v\right)={\sum }_{f\in F\left(H\right)}{d}_H\left(f\right)=2\left|E\left(H\right)\right|$), we derive the following equation:

$$\sum _{v\in V\left(H\right)}(2d_H\left(v\right)-6)+\sum _{v\in F\left(H\right)}(d_H\left(f\right)-6)=-12.$$

Thus, the initial charge function on H is defined as follows:

(a)

For every vertex $v\in V\left(H\right)$, let $ch\left(v\right)=2d_H\left(v\right)-6$.

(b)

For every face $f\in F\left(H\right)$, let $ch\left(f\right)=d_H\left(f\right)-6$.

A set of discharging rules are then applied to redistribute the charges among the vertices and faces. During the discharging process, the total sum of charges remains unchanged at $-12$. Upon completing the redistribution, we derive a new charge function $c{h}^{\prime }$ (say) such that $c{h}^{\prime }\left(x\right)\ge 0$ for every $x\in V\left(H\right)\cup F\left(H\right)$, leading to the following contradiction:

$$0\le \sum _{x\in V\left(H\right)\cup F\left(H\right)}c{h}^{\prime }\left(x\right)=\sum _{x\in V\left(H\right)\cup F\left(H\right)}ch\left(x\right)=-12.$$

The discharging rules are defined as follows:

 (R1) 

Each $4^{+}$-vertex gives ${\displaystyle \frac{1}{2}}$ to each incident 5-face.

 (R2) 

Each $5^{+}$-vertex gives 2 to each adjacent bad 2-vertex, and gives 1 to each adjacent good 2-vertex.

Now, we determine the new charge for all $x\in V\left(H\right)\cup F\left(H\right)$. First, we consider the new charge of each $v\in V\left(H\right)$.

 (1) 

$d_H\left(v\right)=2$. If v is a bad 2-vertex, then by Claims 2, 3, 5 and (R2), $c{h}^{\prime }\left(v\right)=ch\left(v\right)+2=-2+2=0$. If v is a good 2-vertex, then by Claims 2, 3, 5 and (R2), $c{h}^{\prime }\left(v\right)=ch\left(v\right)+1+1=-2+2=0$.

 (2) 

$d_H\left(v\right)=3$. One needs to set $c{h}^{\prime }\left(v\right)=ch\left(v\right)=0$.

 (3) 

$d_H\left(v\right)=4$. From Fact 2, we have that v is incident with at most four 5-faces. Then, by Claim 5 and (R1), we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-{\displaystyle \frac{1}{2}}\times 4=2-2=0$.

 (4) 

$d_H\left(v\right)=5$. Based on Claim 7, when v is adjacent to a good 2-vertex, it is incident with at most five 5-faces. Therefore, from (R1) and (R2), we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-1-{\displaystyle \frac{1}{2}}\times 5=4-1-{\displaystyle \frac{5}{2}}={\displaystyle \frac{1}{2}}>0$; when v is adjacent to bad 2-vertices, by Fact 2, it is incident with at most four 5-faces. Thus, by (R1) and (R2), we get $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-{\displaystyle \frac{1}{2}}\times 4=4-4=0$.

 (5) 

$d_H\left(v\right)=6$. By Claim 8, we know that v is incident with at most six 5-faces. Therefore, it follows from (R1) and (R2) that $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-{\displaystyle \frac{1}{2}}\times 6=6-6=0$.

 (6) 

$d_H\left(v\right)=7$. Together with Claim 9, Fact 2, (R1) and (R2), when v is not adjacent to any bad 2-vertex, is adjacent to at most three good 2-vertices and is incident with seven 5-faces, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-{\displaystyle \frac{1}{2}}\times 7={\displaystyle \frac{3}{2}}>0$; when v is adjacent to bad 2-vertices, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-2-{\displaystyle \frac{1}{2}}\times 6=8-7=1>0$.

 (7) 

$d_H\left(v\right)=8$. Based on Claim 9, Fact 2, (R1) and (R2), when v is not adjacent to any bad 2-vertex, is adjacent to at most four good 2-vertices and is incident with eight 5-faces, then $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-4-{\displaystyle \frac{1}{2}}\times 8=2>0$; when v is adjacent to one bad 2-vertex, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-2-{\displaystyle \frac{1}{2}}\times 7={\displaystyle \frac{3}{2}}>0$; when v is adjacent to two bad 2-vertices, it follows that $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-4-{\displaystyle \frac{1}{2}}\times 7={\displaystyle \frac{1}{2}}>0$.

 (8) 

$d_H\left(v\right)=9$. From Claim 9, Fact 2, (R1) and (R2), when v is not adjacent to any bad 2-vertex, it can be adjacent to at most five good 2-vertices and incident with nine 5-faces, and thus, $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-5-{\displaystyle \frac{1}{2}}\times 9={\displaystyle \frac{5}{2}}>0$; when v is adjacent to one bad 2-vertex, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-4-2-{\displaystyle \frac{1}{2}}\times 8=2>0$; when v is adjacent to two bad 2-vertices, it follows that $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-4-{\displaystyle \frac{1}{2}}\times 8=1>0$; when v is adjacent to three bad 2-vertices, we get $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-6-{\displaystyle \frac{1}{2}}\times 7={\displaystyle \frac{1}{2}}>0$.

 (9) 

$d_H\left(v\right)=10$. According to Claim 9, Fact 2, (R1) and (R2), when v is not adjacent to any bad 2-vertex, it can be adjacent to at most six good 2-vertices and incident with ten 5-faces, and thus, $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-6-{\displaystyle \frac{1}{2}}\times 10=3>0$; when v is adjacent to one bad 2-vertex, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-5-2-{\displaystyle \frac{1}{2}}\times 9={\displaystyle \frac{5}{2}}>0$; when v is adjacent to two bad 2-vertices, it follows that $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-4-4-{\displaystyle \frac{1}{2}}\times 9={\displaystyle \frac{3}{2}}>0$; when v is adjacent to three bad 2-vertices, we get $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-6-{\displaystyle \frac{1}{2}}\times 8=1>0$; when v is adjacent to four bad 2-vertices, we obtain $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-8-{\displaystyle \frac{1}{2}}\times 8=0$.

 (10) 

$d_H\left(v\right)=11$. From Claim 9, Fact 2, (R1) and (R2), when v is not adjacent to any bad 2-vertex, it can be adjacent to at most seven good 2-vertices and incident with eleven 5-faces, hence $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-7-{\displaystyle \frac{1}{2}}\times 11={\displaystyle \frac{7}{2}}>0$; when v is adjacent to one bad 2-vertex, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-6-2-{\displaystyle \frac{1}{2}}\times 10=3>0$; when v is adjacent to two bad 2-vertices, it follows that $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-5-4-{\displaystyle \frac{1}{2}}\times 10=2>0$; when v is adjacent to three bad 2-vertices, we obtain $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-4-6-{\displaystyle \frac{1}{2}}\times 9={\displaystyle \frac{3}{2}}>0$; when v is adjacent to four bad 2-vertices, we get $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-3-8-{\displaystyle \frac{1}{2}}\times 9={\displaystyle \frac{1}{2}}>0$; when v is adjacent to five bad 2-vertices, we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-2-10-{\displaystyle \frac{1}{2}}\times 8=0$.

 (11) 

$d_H\left(v\right)=k\ge 12$. By Claim 10, v is adjacent to at most k good 2-vertices and incident with k 5-faces. Therefore, according to (R1) and (R2), we have $c{h}^{\prime }\left(v\right)\ge ch\left(v\right)-k-{\displaystyle \frac{1}{2}}\times k=2k-6-k-{\displaystyle \frac{k}{2}}={\displaystyle \frac{k}{2}}-6\ge 0$.

Next, we will consider the new charge of every $f\in F\left(H\right)$.

 (a) 

When $d_H\left(f\right)=5$, from Fact 1 (3), f is incident with at least two $4^{+}$-vertices. Therefore, from (R1), we have $c{h}^{\prime }\left(f\right)\ge ch\left(f\right)+{\displaystyle \frac{1}{2}}\times 2=-1+1=0$.

 (b) 

When $d_H\left(f\right)=k\ge 6$, it follows that $c{h}^{\prime }\left(f\right)=ch\left(f\right)=k-6\ge 0$.

According to the process of the charge transfer described above, we present the following

Table 2. The initial charge, amount transfer, and final charge for $\forall x\in V\left(H\right)\cup F\left(H\right)$.

	2-vertex	3-vertex	4-vertex	5-vertex	6-vertex	7-vertex	8-vertex
initial charge	−2	0	2	4	6	8	10
amount transfer	2	0	≤2	≤4	≤6	≤7	≤${\displaystyle \frac{19}{2}}$
final charge	0	0	≥0	≥0	≥0	≥1	≥${\displaystyle \frac{1}{2}}$
	9-vertex	10-vertex	11-vertex	${12}^{+}$-vertex	5-face	$6^{+}$-face
initial charge	12	14	16	≥2k − 6	−1	≥0
amount transfer	≤${\displaystyle \frac{23}{2}}$	≤14	≤16	≤${\displaystyle \frac{3k}{2}}$	≥1	0
final charge	≥${\displaystyle \frac{1}{2}}$	≥0	≥0	≥0	≥0	≥0

In the table, only the final charge of 2-vertex and 5-face equals the initial charge plus the amount transferred, while that of other elements equal the initial charge minus the amount transferred. k refers to the degree of the ${12}^{+}$-vertex in the table.

to provide a clearer understanding and observation.

Consequently, the condition $c{h}^{\prime }\left(x\right)\ge 0$ holds for all $x\in V\left(H\right)\cup F\left(H\right)$, resulting in a contradiction. The proof is therefore completed. □

3. Conclusions and Future Work

In this paper, we prove by constructing a minimal counterexample and employing the discharging method that for a normal planar graph G, if $g\left(G\right)\ge 5$ and $\Delta \left(G\right)\ge 22$, then ${\mathrm{ftndi}}_{\Sigma }\left(G\right)\le \Delta \left(G\right)+3.$ This result extends our previous work [13] to some extent.

This result is derived under the condition of a large maximum degree and the restricted girth of a planar graph G; however, its neighbor full sum distinguishing total chromatic numbers has not yet achieved the bound $(\Delta (G)+2)$ described in Conjecture 2. Most notably, the proof process tells us that it is quite necessary to search for more detailed reducible configurations and to design more precise charge transfer rules.

In future research, one can consider the neighbor full sum distinguishing total coloring of normal planar graphs with $g\left(G\right)\le 4$, reduce the lower bound of the maximum degree currently presented in this result, and further attempt to answer Conjecture 2.