Relativistic Algebra over Finite Ring Continuum

Abstract

We present a formal reconstruction of the conventional number systems, including integers, rationals, reals, and complex numbers, based on the principle of relational finitude over a finite field ${\mathbb{F}}_{\mathsf{p}}$. Rather than assuming actual infinity, we define arithmetic and algebra as observer-dependent constructs grounded in finite field symmetries. Consequently, we formulate relational analogues of the conventional number classes, expressed relationally with respect to a chosen reference frame. We define explicit mappings for each number class, preserving their algebraic and computational properties while eliminating ontological dependence on infinite structures. For example, relationally framed rational numbers emerge from dense grids generated by primitive roots of a finite field, enabling proportional reasoning without infinity, while scale-periodicity ensures invariance under zoom operations, approximating continuity in a bounded structure. The resultant framework—that we denote as Finite Ring Continuum—aims to establish a coherent foundation for mathematics, physics and formal logic in an ontologically finite paradox-free informational universe.

1. Introduction

A growing body of work in mathematics and physics suggests that foundational structures are best understood through a relational or relativistic lens [1,2,3]. In such a paradigm, mathematical entities acquire meaning not as intrinsic absolutes but through their role within a system defined by internal symmetries and reference frames. Constants like 0, 1, or i are not metaphysical primitives but relational markers—origins, units, or axes—assigned by a chosen framing.

This perspective invites a re-evaluation of one of the most entrenched assumptions in mathematics: the acceptance of actual infinity. From real analysis to Hilbert spaces, infinity has been treated as foundational, despite its lack of empirical or computational realization. Under a relational view, such constructs may instead be interpreted as emergent limits or symbolic artifacts—arising when finite systems attempt to encode relationships that exceed their internal scope.

In our previous work [4], we argued that concepts like infinity, randomness, and undecidability are not ontological features of nature but epistemic placeholders—signals of representational saturation in finite informational systems. Here, we extend this view into a concrete formalism: a relativistic algebra constructed entirely over a finite field ${\mathbb{F}}_{\mathsf{p}}$, with observer-relative arithmetic and emergent relational numbers. It should be noted that the proposed framework does not imply the existence of any privileged or absolute value of the foundational parameter $\mathsf{p}$. The analysis of a specific order-$\mathsf{p}$ field ${\mathbb{F}}_{\mathsf{p}}$ is required for the systematic and incremental development of the underlying program. Particular values of the parameter $\mathsf{p}$ emerge as the constituent of the observer-dependent frame of reference in the proposed relational formalism.

To illustrate, consider an observer on the surface of planet Earth perceiving an infinite flat plane (as they indeed do) conveniently centered around their exact position. This is not just epistemic error, but an ontological misinterpretation of the true structure, that is, the large but finite, curved sphere. While the “flat Earth” paradigm may appear outdated to most modern audience, other egocentric models such as the geocentricity and heliocentricity are relatively recent, while the “infinite flat” ΛCDM universe model remains the prevailing cosmological framework despite the numerous evidence to the contrary. Similarly, classical infinite numbers with an absolutely defined origin 0 and scale 1 can be identified as an egocentric mathematical paradigm that extrapolates the apparently infinite axis of numbers beyond the horizon of its frame of reference and the respective information-processing capacity. The round Earth metaphor is a concrete example of how finiteness and infinity can be reconciled through relational, modular framing, as detailed in [5].

This relational paradigm finds a natural analogue in the development of modern physics. The transition from Newtonian mechanics to Einsteinian relativity redefined the very notions of space, time, and simultaneity—not as absolute quantities but as frame-dependent observations shaped by internal consistency and symmetry. Likewise, a relativistic mathematics replaces external absolutes with internal coherence, viewing all mathematical structures and operations as inherently contextual, subject to transformation, and defined through symmetry relations within finite systems. Such a shift—despite being initially counterintuitive—enables a more consistent and physically meaningful foundation for mathematics. It offers a unified perspective that bridges abstract algebra, geometry, and modern physical theory, and sets the stage for a reconstruction of mathematical reasoning grounded in self-contained, finite, and relational structures.

The present framework resonates with several contemporary perspectives that question the ontological status of the continuum and advocate for finitely constructed alternatives. In particular, Smolin has emphasized the need for a relational, observer-dependent formulation of physical laws, suggesting that the continuum is merely an idealization beyond the reach of internal observers [6,7]. Lev provided a comprehensive treatment of finite mathematics as a foundation for quantum theories [5] showing that the classical mathematics can be regarded as a special degenerate case of the finite mathematics, which is further advocated by Zeilberger [8]. Similarly, D’Ariano and collaborators have reconstructed quantum theory from finite, informationally grounded axioms, demonstrating that core features of quantum mechanics can emerge without invoking infinite-dimensional Hilbert spaces [9]. From a mathematical standpoint, the approach aligns with the ultrafinitist program developed by Benci and Di Nasso, which offers a rigorous alternative to classical cardinality through the theory of numerosities and bounded arithmetic [10,11].

Furthermore, the ultrafinitist school—pioneered by Yessenin-Volpin and Parikh—takes finitude even further by denying the meaningful existence of “too large” numbers and insisting on feasibility as a foundational constraint. Formalizations of ultrafinitism and feasibility arithmetic appear in works such as [12,13,14,15], which explore the proof-theoretic and computational consequences of enforcing strict constructive bounds on arithmetic.

Ultrafinitism enforces an a priori cutoff on numerical existence—only those magnitudes deemed “feasible” within a human or machine resource bound are admitted. By contrast, our relativistic framework treats finiteness not as a hard barrier but as a contextual framing condition: We allow arbitrarily large numbers, so “size” is always relative to the chosen frame. Infinite structures, such as integers and rationals emerge asymptotically or as coordinate projections, rather than being forbidden. Arithmetic operations become internal symmetries of a finite system, rather than operations constrained by external feasibility checks. This shift replaces the ultrafinitist’s absolute feasibility threshold with a relational notion of scope: any number “exists” within some finite frame, while “infinity” itself appears as a relative point beyond the horizon of observability and algebraic accessibility.

To support this framework, we further draw upon several key developments in mathematics and physics. The foundational critique of actual infinity has been explored in works such as [16,17], which emphasize the constructive and finitist approaches to mathematics. The relational perspective on mathematical objects aligns with category theory [1], where objects are defined by their morphisms and relationships rather than intrinsic properties. Additionally, the parallels between relativistic mathematics and modern physics are inspired by the symmetry principles in [2,3], which highlight the role of invariance and frame-dependence in physical laws. Finally, the informational limits of finite systems and their implications for mathematical representation are discussed in [18,19].

The present article forms the algebraic foundation of a three-part program designed to reconstruct the familiar continuous structures from finite arithmetic using the framework of Finite Ring Continuum (FRC) as depicted in Figure 1. The present work, Algebra, establishes a relational framing of the classical number hierarchy ($\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}$) as framed number classes (or f-numbers for short) within a single finite field, demonstrating that all constructions are covariant under a change of arithmetic frame. The subsequent article, Geometry, lifts this algebraic structure to a smooth two-sphere ${\mathcal{S}}_{\mathsf{p}}$ with constant internal curvature, from which canonical geometric constants are derived. The final manuscript, Composition, extends the framework from prime to composite moduli using the Chinese Remainder Theorem, yielding a bouquet of prime spheroids whose structure resembles a Seifert-fibred three-orbifold. This modular presentation ensures that each layer is developed with incremental and verifiable rigor.

2. Symmetry and Reference Frames in Finite Field

Consider a finite natural number $\mathsf{t}\in \mathbb{N}$ and let us define the following finite mathematical construct.

Definition 1

(Symmetry-Complete Field of radius $\mathsf{t}$). A finite field $\mathbb{F}$ is called Symmetrically Complete if it has the following exact structure. The field’s multiplicative group ${\mathbb{F}}_{\mathsf{p}}^{\times }$ is a disjoint union of exactly $\mathsf{t}$ distinct 4-element sets, including

(a) 

A structural set of 4th roots of unity $\{1,i,-1,-i\}=\{i^0,i^1,i^2,i^3\}$, generated by a unique element $i\in {\mathbb{F}}_{\mathsf{p}}^{\times }$ with $i^2=-1$; and

(b) 

Exactly $(\mathsf{t}-1)$ orbital classes of units of the form $(x,1/x,-x,-1/x)$, which correspond to the orbits under the action of the Klein four-group $G_K=\langle \sigma ,\tau \rangle$ generated by negation $\sigma \left(x\right)=-x$ and inversion $\tau \left(x\right)=x^{-1}$.

Theorem 1

(Symmetry Completeness). Any finite field ${\mathbb{F}}_{\mathsf{p}}$ of prime order $\mathsf{p}=4\mathsf{t}+1$, where $\mathsf{t}\in \mathbb{N}$ is Symmetry-Complete.

Proof. 

To prove that any finite field ${\mathbb{F}}_{\mathsf{p}}$ of radius $\mathsf{t}\in \mathbb{N}$ and prime order $\mathsf{p}=4\mathsf{t}+1$ is Symmetry-Complete, we verify the definition’s conditions step-by-step. Since $\mathsf{p}$ is prime, ${\mathbb{F}}_{\mathsf{p}}$ is a field, and its multiplicative group ${\mathbb{F}}_p^{\times }$ is cyclic of order $\mathsf{p}-1=4\mathsf{t}$.

Step 1: Existence and Structure of the Structural Set. Since $\mathsf{p}\equiv 1 (mod4)$, there exists $i\in {\mathbb{F}}_p^{\times }$ such that $i^2=-1$, e.g., constructible via the Tonelli–Shanks algorithm [22]. The elements $1,i,-1=i^2,-i=i^3$ are distinct: $i\ne \pm 1$ because $i^2=-1\ne 1={(\pm 1)}^2$. $i\ne -i$ because $i=-i$ implies $2i=0$, so $i=0$ (but $0^2=0\ne -1$). Similarly for other pairs. The set $C=\{1,i,-1,-i\}=\{i^k\mid k=0,1,2,3\}$ is the cyclic subgroup of order 4 in ${\mathbb{F}}_p^{\times }$ (unique, as ${\mathbb{F}}_p^{\times }$ is cyclic). It consists of the 4th roots of unity, solving $x^4-1=0$, and is closed under multiplication and inversion.

Step 2: Action of the Klein Four-Group and Orbits. Define the Klein four-group $G_K=\langle \sigma ,\tau \rangle$, where $\sigma :{\mathbb{F}}_{\mathsf{p}}^{\times }\to {\mathbb{F}}_{\mathsf{p}}^{\times }$ by $\sigma \left(x\right)=-x$ and $\tau :{\mathbb{F}}_p^{\times }\to {\mathbb{F}}_p^{\times }$ by $\tau \left(x\right)=x^{-1}$ (both involutions, commuting). $G_K$ acts on ${\mathbb{F}}_p^{\times }$. The structural class C is $G_K$-invariant: $\sigma \left(1\right)=-1$, $\sigma \left(i\right)=-i$, $\tau \left(1\right)=1$, $\tau \left(i\right)=-i$ (since $i^{-1}=i^3=-i$), etc., mapping C to itself. For $x\in {\mathbb{F}}_p^{\times }\setminus C$, the orbit is $G_K·x=\{x,-x,x^{-1},-x^{-1}\}$ and these four elements are distinct:

Suppose $x=-x$: then $2x=0$, so $x=0\notin {\mathbb{F}}_p^{\times }$.

$x=x^{-1}$: then $x^2=1$, so $x=\pm 1\in C$.

$x=-x^{-1}$: then $x^2=-1$, so $x=\pm i\in C$.

$-x=x^{-1}$: then $x^2=-1$, again $x=\pm i\in C$.

Similar contradictions for other pairs (e.g., $-x=-x^{-1}$ implies $x=x^{-1}$). Thus, each such orbit has exactly four elements.

Step 3: Disjoint Union and Count of Sets. The orbits are disjoint by the definition of group action orbits. The remaining elements after removing C (4 elements) are $4\mathsf{t}-4=4(\mathsf{t}-1)$, forming exactly $\mathsf{t}-1$ orbits of size 4. Including the structural set, ${\mathbb{F}}_{\mathsf{p}}^{\times }$ is the disjoint union of exactly $\mathsf{t}$ distinct 4-element sets. This satisfies the definition, so ${\mathbb{F}}_{\mathsf{p}}$ is Symmetry-Complete of radius $\mathsf{t}$. □

Interpretation 1.

We would like to argue that the rotational symmetry of the multiplicative group ${\mathbb{F}}_{\mathsf{p}}^{\times }$, and the emergence of dimensional geometry, which we henceforth discuss, are only possible in Symmetry-Complete Fields. A meaningful concept of rotation requires a transformation that is distinct from the one-dimensional act of scaling along a single axis. The existence of the structural class $\{1,i,-1,-i\}$ is the necessary and sufficient condition for such a transformation. It endows the system with two algebraically distinct transformative units, 1 and i, which can be interpreted as the basis vectors for a two-dimensional space, and allows for a quarter-turn transformation of multiplicative group $x\mapsto ix$.

Let ${\mathbb{F}}_{\mathsf{p}}=\{0,1,2,\dots ,\mathsf{p}-1\}$ be a Symmetrically Complete finite field of radius $\mathsf{t}\in \mathbb{N}$ and prime order $\mathsf{p}=4\mathsf{t}+1$. The elements of ${\mathbb{F}}_{\mathsf{p}}$ form a complete and closed set of relational representations of ${\mathbb{F}}_{\mathsf{p}}$ under modular addition, multiplication, and exponentiation. However, the specific numeric labels assigned to these elements—particularly the designation of 0 and 1 as the additive and multiplicative identities—are intrinsically relative and carry no absolute meaning within the field itself. The field ${\mathbb{F}}_{\mathsf{p}}$ is invariant under relabeling of its elements via any bijective affine transformation of the form

$$k\mapsto a+b·kmod\mathsf{p},$$

where $a\in {\mathbb{F}}_{\mathsf{p}}$ and $b\in {\mathbb{F}}_{\mathsf{p}}^{\times }$. Such transformations preserve the field structure and allow any element to be reinterpreted as an origin. In this sense, the element labeled 0 is not uniquely privileged; it simply represents the additive identity with respect to a chosen reference frame. The same applies to the label 1, which identifies the multiplicative unit only relative to a particular scaling.

Definition 2

(Affine Reference Frame). An affine reference frame $(a,b)$ in ${\mathbb{F}}_{\mathsf{p}}$ consists of picking two distinguished elements

$$0^{\prime }=a,1^{\prime }=b,a\ne b,$$

and then defining relabeled addition and multiplication by

$$\begin{array}{cc}\hfill x\oplus y& :=a+b\left((x-a)/b+(y-a)/b\right),\hfill \\ \hfill x\otimes y& :=a+b\left((x-a)/b·(y-a)/b\right),\hfill \end{array}$$

where divisions are in the original field ${\mathbb{F}}_{\mathsf{p}}$.

Lemma 1

(Affine Ring Isomorphism). Let ${\mathbb{F}}_{\mathsf{p}}$ be a finite field, and let two frames $(0,1)$ and $(a,b)$ be related by the affine bijection

$$\varphi :{\mathbb{F}}_{\mathsf{p}}⟶{\mathbb{F}}_{\mathsf{p}},\varphi \left(x\right)=a+bx,b\ne 0.$$

Then ϕ is a ring isomorphism between $\left({\mathbb{F}}_{\mathsf{p}},+,·\right)$ and $\left({\mathbb{F}}_{\mathsf{p}},\oplus ,\otimes \right)$. Consequently, any polynomial identity

$$P\left(x_1,\dots ,x_n\right)=0\mathit{holds}\mathit{in}\mathit{the}\mathit{standard}\mathit{frame}$$

if and only if the “relabeled” identity

$$P\left({\varphi }^{-1}\left(X_1\right),\dots ,{\varphi }^{-1}\left(X_n\right)\right)=0\mathit{holds}\mathit{in}\mathit{the}(a,b)\text{-}\mathit{frame},$$

where $X_i=\varphi \left(x_i\right)$.

Proof. 

Since $b\ne 0$, $\varphi$ is a bijection with inverse ${\varphi }^{-1}\left(X\right)=(X-a)/b$. For any $x,y\in {\mathbb{F}}_{\mathsf{p}}$,

$$\varphi (x+y)=a+b(x+y)=\left(a+bx\right)\oplus \left(a+by\right)=\varphi \left(x\right)\oplus \varphi \left(y\right),$$

and similarly

$$\varphi \left(xy\right)=a+b\left(xy\right)=\left(a+bx\right)\otimes \left(a+by\right)=\varphi \left(x\right)\otimes \varphi \left(y\right).$$

Thus, $\varphi$ preserves addition and multiplication, so it is a ring isomorphism. It follows immediately that any algebraic (polynomial) relation valid in one frame is carried over to the other by conjugation with $\varphi$, establishing frame-independence of all algebraic identities. □

Interpretation 2.

This formal result provides the basis for our conceptual model of an observer frame of reference. The algebraic fact that any element can be mapped to any other implies that the system has no intrinsic, privileged origin point. Therefore, physical concepts like “position”, “zero”, or “scale” are not properties of the system itself, but are relational constructs defined by the act of observation.

Therefore, in the absence of an externally imposed or contextually declared frame—such as one defined by a designated pair $(0,1)$—the labels in ${\mathbb{F}}_{\mathsf{p}}$ are relational rather than absolute. In other words, the roles of “zero” and “one” are a consequence of the system’s framing, making all representations in ${\mathbb{F}}_{\mathsf{p}}$ symmetric and interchangeable under coordinate transformation. To define our system unambiguously, we must specify a reference frame or coordinate system $(0,1)$ within the context of ${\mathbb{F}}_{\mathsf{p}}$, which then becomes a framed finite ring ${\mathbb{F}}_{\mathsf{p}}(0,1)$.

A typical diagram of a framed finite field ${\mathbb{F}}_{\mathsf{p}}(0,1)$, where $\mathsf{t}=3,\mathsf{q}=13$, is shown in Figure 2. We would like to specifically note that such a diagram is typically visualized as a circle on a 2D plane spanned by the radial axis $\mathsf{t}$ and rotational symmetry under the arithmetic operation of addition, thus assigning an intuitive geometric interpretation to the arithmetic structure of the additive group $({\mathbb{F}}_{\mathsf{p}},+)$.

We will henceforth assume all such systems to be framed systems ${\mathbb{F}}_{\mathsf{p}}(0,1)$ and will denote the corresponding finite ring as ${\mathbb{F}}_{\mathsf{p}}$ for simplicity, unless explicitly stated otherwise.

3. Finite Field as Discrete Geometric Structure

Let $\mathsf{p}=4\mathsf{t}+1$ be a prime and let ${\mathbb{F}}_{\mathsf{p}}$ denote the finite field with $\mathsf{p}$ elements [23]. The association between arithmetic operations and symbolic geometry detailed in Section 2 can be extended further. Specifically, in the finite field ${\mathbb{F}}_{\mathsf{p}}$, the basic arithmetic operations of counting, addition, multiplication, and exponentiation can all be understood as manifestations of the underlying symmetries of structural transformations of the field [24].

• Counting corresponds to the additive translation of the field, defined by the successor map:

  $$C_1:k\mapsto k+1mod\mathsf{p},\forall k\in {\mathbb{F}}_{\mathsf{p}}.$$

  (1)

  While typically taken for granted, the act of counting is an ontologically and informationally significant degree of freedom that both presupposes the existence of the field ${\mathbb{F}}_{\mathsf{p}}$ and determines the entirety of its structural properties. Furthermore, the counting operation establishes a translation symmetry that underpins all other arithmetic operations as its iterative applications.
• Addition (translation) corresponds to the iterative application of counting. The additive group $({\mathbb{F}}_{\mathsf{p}},+)$ forms a finite cyclic group of order $\mathsf{p}$, generated by the element 1. Translation symmetry is defined by additive shifts:

  $$T_a:k\mapsto k+amod\mathsf{p},\forall a\in {\mathbb{F}}_{\mathsf{p}}.$$

  (2)

  This operation reflects the periodic structure of the ring and can be viewed as a rotation by a steps around the absolute origin $⌀=\{\mathsf{t}=0\}$ (see Figure 2) and the corresponding circular configuration of the elements of ${\mathbb{F}}_{\mathsf{p}}$.
• Multiplication (scaling) corresponds to the iterative application of addition and furthermore reflects the scaling symmetry within the field. Scaling symmetry is defined by multiplicative operation

  $$S_m:k\mapsto m·kmod\mathsf{p},\forall m\in {\mathbb{F}}_{\mathsf{p}}^{\times },$$

  (3)

  and corresponds to a dilation or contraction of the additive structure, where the effect of multiplication is constrained by the modulus.
• Exponentiation (powering) is an iterative application of multiplication defined by the modular operation

  $$P_{ϵ}:k\mapsto k^{ϵ}mod\mathsf{p},\forall k\in {\mathbb{F}}_{\mathsf{p}}^{\times },ϵ\in {\mathbb{Z}}_{\mathsf{p}-1},$$

  (4)

  where ${\mathbb{Z}}_{\mathsf{p}-1}$ is a finite ring of the order $\mathsf{p}-1$, which is importantly no longer a field. This operation defines power maps and automorphisms that reveal the group-theoretic structure and internal symmetries of the field, and encodes deep number-theoretic properties such as primitive roots and residue classes [23].

Thus, the basic arithmetic operations in ${\mathbb{F}}_{\mathsf{p}}$ are not arbitrary—they are algebraic expressions of the field’s internal symmetries. They define how elements of the system transform under structured, invertible actions, and they reveal the harmonious regularity inherent in finite arithmetic.

Proposition 1

(3-Manifold Geometry of ${\mathbb{F}}_{\mathsf{p}}$). For a fixed value of the foundational parameter $\mathsf{t}$, the framed finite field ${\mathbb{F}}_{\mathsf{p}}$, together with its triplet of arithmetic symmetries, may be interpreted as a discrete symbolic three-dimensional manifold embedded in an abstract four-dimensional symmetry space $\left\{\right(\mathsf{t};a,m,ϵ\left)\right\}\subset \mathcal{U}$.

Consider a symbolic symmetry space $\mathcal{U}$, where all geometric objects, such as vertices, edges and faces, are defined relative to each other and the observer’s frame of reference, in the exact same way as the elements of the field ${\mathbb{F}}_{\mathsf{p}}$ in Figure 2 are defined by nothing else than their relation to each other and the observer’s frame of reference. Each vertex in $\mathcal{U}$ corresponds to a specific element in ${\mathbb{F}}_{\mathsf{p}}$, but the finite number of elements of the field ${\mathbb{F}}_{\mathsf{p}}$ can be repeated arbitrary many times in $\mathcal{U}$.

Interpretation 3

(Kaleidoscope Metaphor). Here, we would like to offer the metaphor of a kaleidoscope, where a relatively small set of physical elements generates an arbitrary large and seemingly-complex pattern via reflections and symmetries. The emergent patterns are dependent on the observer’s frame of reference, and the same set of elements can generate different patterns for different observers.

Definition 3

(Carrier hyper-cube). Define the carrier hyper-cube ${\mathcal{N}}_{\mathsf{p}}$ as a symbolic space defined by 4-tuples comprising a fixed value of $\mathsf{t}$ and all possible values of parameters $a,m,ϵ$ in ${\mathbb{F}}_{\mathsf{p}}$

$${\mathcal{N}}_{\mathsf{p}}:={\mathbb{F}}_{\mathsf{p}}^4=\{(\mathsf{t};a,m,ϵ)\mid \mathit{fixed}\mathsf{t}\in {\mathbb{F}}_{\mathsf{p}};a,m,ϵ\in {\mathbb{F}}_{\mathsf{p}}\}.$$

Definition 4

($(1,3)$-D Symmetry space). The 1-radial, 3-rotational dimension symmetry space $\mathcal{U}$ is defined as

$$\mathcal{U}=\bigcup _{\mathsf{t}}{\mathcal{U}}_{\mathsf{t}},$$

where each subspace ${\mathcal{U}}_{\mathsf{t}}$ is a radius-$\mathsf{t}$ quotient shell

$${\mathcal{U}}_{\mathsf{t}}:={\mathcal{N}}_{\mathsf{p}}/\mathcal{G}=\{\mathcal{G}·(\mathsf{t};a,m,ϵ)\mid a,m,ϵ\in {\mathbb{F}}_{\mathsf{p}}\},$$

with ${\mathcal{N}}_{\mathsf{p}}$ being the carrier hyper-cube; $\mathcal{G}:=\langle T_a,S_m,P_{ϵ}\rangle$ the symmetry group generated by the three arithmetic operations; and $(a,m,ϵ)$ are the rotational coordinates relative to the selected frame of reference $(0,1)$ associated with the additive, multiplicative, and exponentiation symmetries, respectively.

Interpretation 4

(Radius-$\mathsf{t}$ shells). Each subspace ${\mathcal{U}}_{\mathsf{t}}$ of the symmetry space $\mathcal{U}$ is a 3D shell of rotational symmetries and radius $\mathsf{t}$ that resides in the category of finite sets (or discrete spaces over the finite field ${\mathbb{F}}_{\mathsf{p}}$), where it is a finite discrete object with cardinality bounded by ${\mathsf{p}}^4/\left|\mathcal{G}\right|$, and its exact size is determined by the orbits under $\mathcal{G}$.

Interpretation 5

(Orbifold). Since ${\mathcal{N}}_{\mathsf{p}}$ is a four-dimensional vector space over ${\mathbb{F}}_{\mathsf{p}}$, and $\mathcal{G}$ acts on its points, $\mathcal{U}$ can be viewed as an orbifold -like structure in finite geometry, encoding equivalence classes of parameters $(\mathsf{t};a,m,ϵ)$ under the symmetry group $\mathcal{G}$.

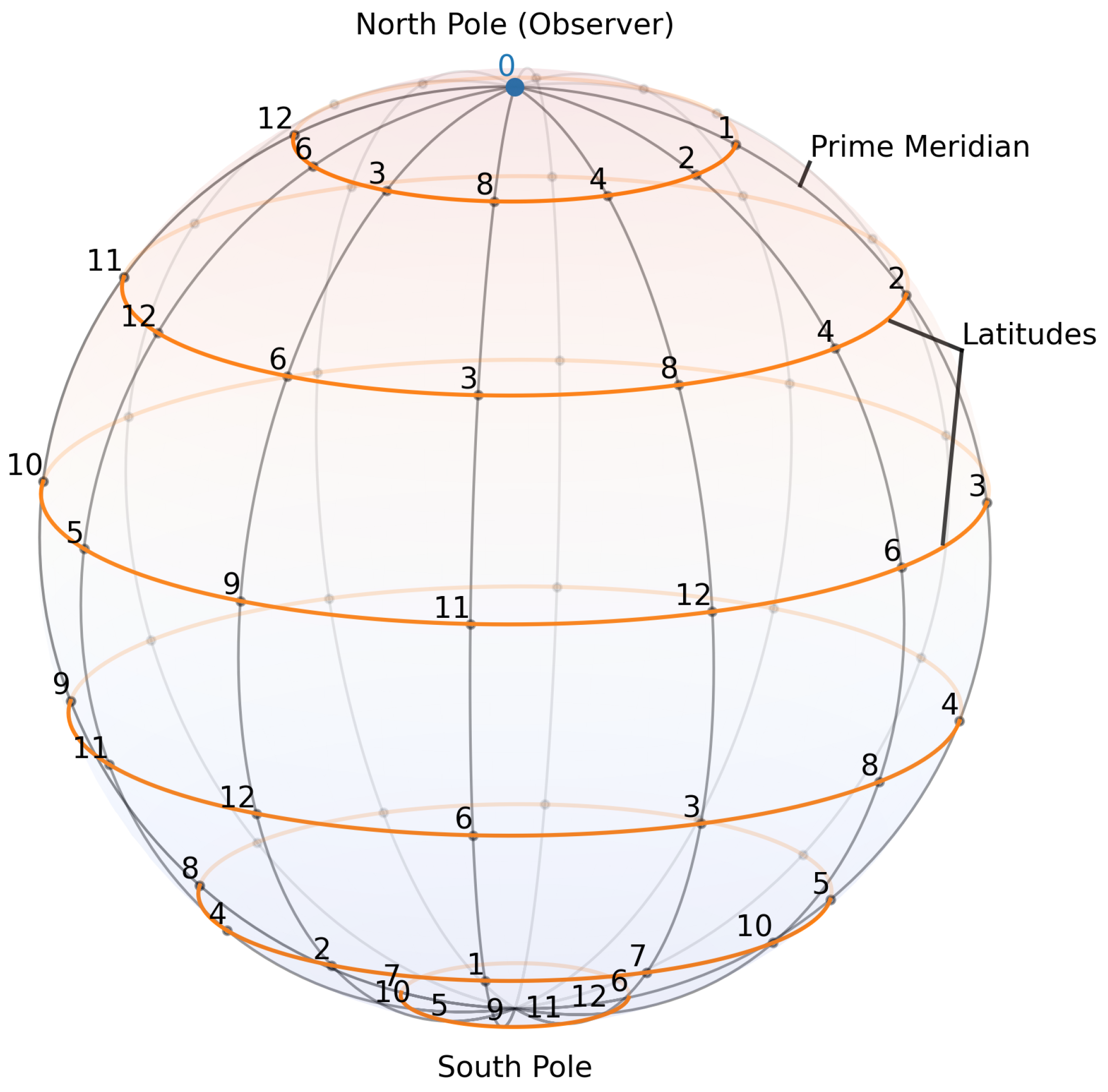
Definition 5

(Orbital complex ${\mathcal{S}}_{\mathsf{p}}$). Consider a framed finite field ${\mathbb{F}}_{\mathsf{p}}(0,1)$ and let us select an arbitrary primitive root $g\in {\mathbb{F}}_{\mathsf{p}}^{\times }$ as a fixed multiplicative generator of the field. Work inside the two-coordinate lattice

$$\left\{(\mathsf{t};a,n,ϵ=1)\mid a\in {\mathbb{F}}_{\mathsf{p}},n\in {\mathbb{Z}}_{\mathsf{p}-1}\right\}\subset {\mathcal{N}}_{\mathsf{p}}.$$

• (a) Meridians (longitudes) $M_n$: Let us first define the longitudinal great circle ${\overline{M}}_n\left(a\right)$ as

  $${\overline{M}}_n\left(a\right):=\{a{g}^n\mid a\in {\mathbb{F}}_{\mathsf{p}},\mathit{fixed}n\in {\mathbb{Z}}_{\mathsf{p}-1}\}={\mathbb{F}}_{\mathsf{p}},$$

  which is a cyclic ordering of all $\mathsf{p}$ field elements in which successive points differ by the addition of $g^n$. ${\overline{M}}_n$ is a great circle, comprised of a pair of meridians connected by an additive involution ${\overline{M}}_n\left(a\right)={\overline{M}}_{n^{\prime }}(-a)$, where $n^{\prime }=n+{\displaystyle \frac{\mathsf{p}-1}{2}}$. We therefore have exactly ${\displaystyle \frac{\mathsf{p}-1}{2}}$ distinct longitudinal great circles ${\overline{M}}_n$, or exactly $\mathsf{p}-1$ distinct meridians $M_n$.
• (b) Latitudes (parallels) $L_a$:

  $$L_a\left(m\right):=\{a{g}^m\mid \mathit{fixed}a\in {\mathbb{F}}_{\mathsf{p}},m\in {\mathbb{Z}}_{\mathsf{p}-1}\}={\mathbb{F}}_{\mathsf{p}}^{\times }.$$

  Here, exponent m varies while the additive factor a is fixed, resulting in cyclic orderings of the non-zero field elements in which successive points differ by the multiplicative factor g. Likewise, the pairs of duplicate latitudes are connected by the additive involution $L_a\left(m\right)=L_{-a}(m+{\displaystyle \frac{\mathsf{p}-1}{2}})$, and we have exactly ${\displaystyle \frac{\mathsf{p}-1}{2}}$ distinct latitudinal orbits.
• (c) Vertex set ${\mathcal{V}}_{\mathsf{p}}$: Although each non-zero field element lies on every meridian and latitude as sets, we define the set of distinct intersection between the meridians and latitudes as 

  $${\mathcal{V}}_{\mathsf{p}}:=\left\{M_n\right\}\times \left\{L_a\right\},\mathit{such}\mathit{that}\mathit{card}{\mathcal{V}}_{\mathsf{p}}={\displaystyle \frac{{(\mathsf{p}-1)}^2}{2}}+1.$$

  The resultant complex of orbits and vertices forms a combinatorial skeleton of a discrete 2-sphere ${\mathcal{S}}_{\mathsf{p}}$ in $\mathcal{U}$, as illustrated in Figure 3 for the framed finite field ${\mathbb{F}}_{13}(0,1)$, where the prime meridian $M_0\left(a\right)$ depicts the additive group $({\mathbb{F}}_{13},+)$ and the latitudes $L_a\left(m\right)$ comprise derangements of the multiplicative group $({\mathbb{F}}_{13}^{\times },·)$.

A more refined analysis of the structure, topology and properties of the orbital complex ${\mathcal{S}}_{\mathsf{p}}$ is presented in the companion article [20]. Here, we would like to summarize the obtained result, namely that the resultant discrete 2-sphere ${\mathcal{S}}_{\mathsf{p}}$ embedded in the 4D symmetry space $\mathcal{U}$ captures the essential symmetries and relationships of the finite field ${\mathbb{F}}_{\mathsf{p}}$ in a geometric form. The vertices of ${\mathcal{S}}_{\mathsf{p}}$ correspond to the elements of ${\mathbb{F}}_{\mathsf{p}}$, while the edges and faces represent the relationships between these elements under the operations of addition and multiplication.

4. Framed Numbers

4.1. Framed Integers

While the finite field ${\mathbb{F}}_{\mathsf{p}}$ provides a complete and closed algebraic structure, its inherently cyclic nature eliminates any meaningful notion of ordering or signed magnitude. In contrast, many physical and informational systems rely on the intuitive structure of the integers $\mathbb{Z}$, with concepts such as positive and negative values, proximity to an origin, and relational comparison. To bridge this conceptual gap, we would like to introduce a relativistic, context-dependent construction within ${\mathbb{F}}_{\mathsf{p}}$ that recovers the essential features of integer arithmetic in a familiar and logically consistent form.

In the conventional finite field ${\mathbb{F}}_{\mathsf{p}}$, we can define negative elements $-k\in {\mathbb{F}}_{\mathsf{p}}$ as the unique additive inverse of k, satisfying $k+(-k)\equiv 0mod\mathsf{p}$ [24]. This definition of negation is algebraically consistent but is purely modular and lacks any intrinsic ordering. For example, the element $-1$ in ${\mathbb{F}}_{\mathsf{p}}$ is not necessarily less than 0, as we can state $-1-0=-1=12$, or greater than 0, as we can also state $0-(-1)=1$, and the same applies to any other element in the field. The lack of a meaningful ordering relation in the finite field ${\mathbb{F}}_{\mathsf{p}}$ makes it impossible to define a signed magnitude or compare elements in a way that aligns with our intuitive understanding of integers.

Let us therefore consider the 3D representation of the finite field ${\mathbb{F}}_{\mathsf{p}}$ as depicted in Figure 3 by observing it from the top down. We would like to offer a metaphor of the “North Pole” frame of reference, but it is important to note that the surface of the manifold in Figure 3 does not have any real special points and the selection of such “North Pole” position and the corresponding frame of reference is purely arbitrary and subjective.

Correspondingly, the original additive sequence $0,1,\dots ,\mathsf{p}-1$ of the ring’s elements are represented as points located on the latitudinal axis—let us call it the prime meridian—of the 2-sphere ${\mathcal{S}}_{\mathsf{p}}$, while the multiplicative symmetry elements are now arranged in circular patterns along the longitudinal axes and around the origin.

Interpretation 6.

Let us imagine a naive local observer that is not aware of the spherical nature of the surface he is observing. We may need to hereby assume a sufficiently large cardinality $\mathsf{p}$ such that the local curvature is not apparent to such observer in the exact same way as the local curvature of the Earth is not apparent to a human observer. For such observer, the ${\mathbb{F}}_{\mathsf{p}}$ manifold surface would appear as flat, and with the sequence of elements $\dots ,-2,-1,0,1,2,\dots$ forming a horizontal axis around the observer’s position 0, as illustrated in Figure 4.

Definition 6

(Framed Integers). Define a mapping $k:\mathbb{Z}\to {\mathbb{F}}_{\mathsf{p}}$, with $k\left(z\right)=z(mod\mathsf{p})$. This wraps $\mathbb{Z}$ onto ${\mathbb{F}}_{\mathsf{p}}$, as depicted in Figure 4. The observer, located at 0 and bounded by horizon $H\ll \mathsf{p}$, perceives the prime meridian (signed integers) axis as infinite, extending in both directions toward their observation horizon. Thus, the apparent integer line emerges as a framed integer class ${}^{\mathsf{f}}\mathbb{Z}$, where negation, order, and comparison are reconstructed locally [25].

The resulting class of framed integers (or f-integers for short) ${}^{\mathsf{f}}\mathbb{Z}$ exhibits all the characteristic properties of the conventional integer set $\mathbb{Z}$, including sign, order, addition, subtraction and multiplication. This framework allows us to recover the intuitive and logical structure of integers—including signed quantities and magnitude comparison—entirely within the finite, self-contained system ${\mathbb{F}}_{\mathsf{p}}$, while preserving consistency with its modular arithmetic.

4.2. Framed Rationals

Having recovered the structure of signed integers $\mathbb{Z}$ over the finite field ${\mathbb{F}}_{\mathsf{p}}$, it is natural to ask whether further extensions of this framework can reproduce the next layer of classical number systems—namely, the rational numbers $\mathbb{Q}$. Rational numbers emerge from the pragmatic necessity to express and manipulate ratios of integers, and their introduction marks a critical step in the construction of continuous arithmetic, proportional reasoning, and linear structure.

The motivation for this extension is twofold. First, it allows us to reconstruct the essential properties of $\mathbb{Q}$ over ${\mathbb{F}}_{\mathsf{p}}$, making clear that rationality is not an intrinsic feature of infinite arithmetic but an emergent relational construct definable within finite algebra. Second, it enables a more expressive arithmetic language within the finite mathematical system, allowing for the representation of proportional relationships, scales, and geometric constructs entirely within the bounds of a finite and self-contained mathematical system.

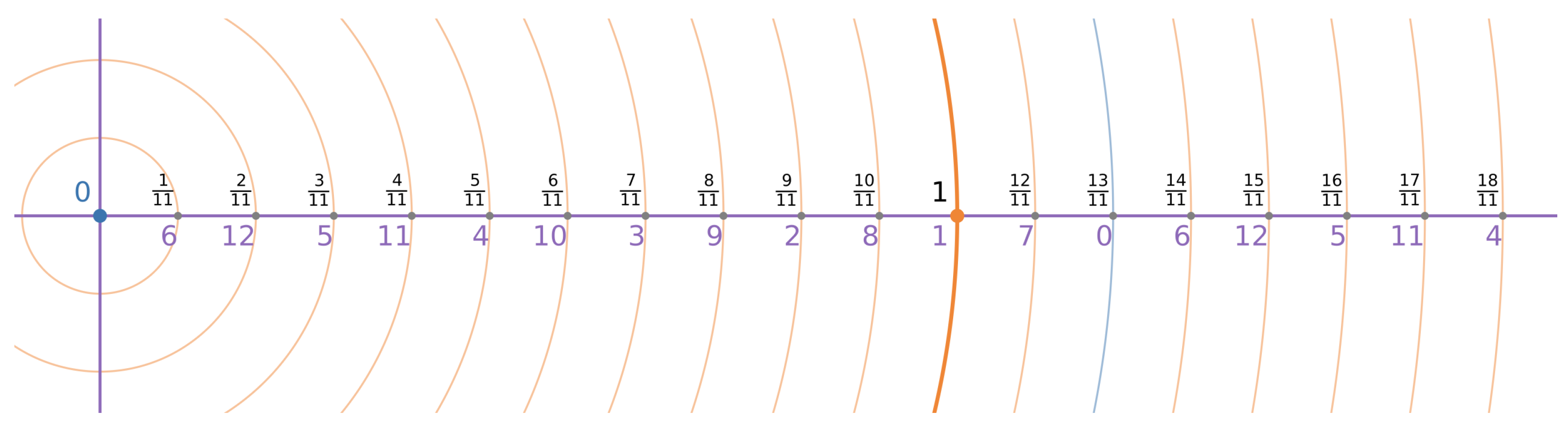
Definition 7

(Framed Rationals). Let ${\mathbb{F}}_{\mathsf{p}}$ be a finite field of prime order $\mathsf{p}=4\mathsf{t}+1$. We define the class of framed rational numbers (or f-rationals for short) ${}^{\mathsf{f}}\mathbb{Q}$ as follows:

$${}^{\mathsf{f}}\mathbb{Q}:=\left\{{\displaystyle \frac{a}{b}}\mid a\in \mathbb{Z},b=\prod _i{k}_i,k_i\in {\mathbb{F}}_{\mathsf{p}}^{\times }\right\}.$$

The corresponding value in the field is

$$k\left({\displaystyle \frac{a}{b}}\right):=a·b^{-1}mod\mathsf{p}.$$

Multiple representations can map to the same $k\in {\mathbb{F}}_{\mathsf{p}}$, forming equivalence classes as depicted in Figure 5, where we depict a selection of f-rations in a finite field ${\mathbb{F}}_{13}$. We furthermore show that ${}^{\mathsf{f}}\mathbb{Q}$ is dense in $\mathbb{Q}$ under a metric induced by bounded denominators $b=g^n$ [26], where g is some fixed primitive root of ${\mathbb{F}}_{\mathsf{p}}$ that forms a regular grid of rational points $a/g^n$ along the rational number axis, as illustrated in Figure 6, where we fix $q=13$ and $g=11$. For any $q\in \mathbb{Q}$ and $\epsilon >0$, there exists $q^{\prime }\in {}^{\mathsf{f}}\mathbb{Q}$ such that $|q-q^{\prime }|<\epsilon$.

The validity of such definition is ensured by the fact that all elements $k_i$ constituting the denominator product $b={\prod }_i{k}_i$ are invertible in ${\mathbb{F}}_{\mathsf{p}}^{\times }$. A selection of some simple examples of such framed rational numbers is depicted in Figure 5, where for each position along the prime meridian $q=a/b\in {}^{\mathsf{f}}\mathbb{Q}$, as indicated as a black label on top, and the corresponding finite field element $k\left(q\right)\in {\mathbb{F}}_{\mathsf{p}}$ is indicated as a purple label on the bottom.

Proposition 2.

Let ${\mathbb{F}}_{\mathsf{p}}(0,1)$ be a framed finite field, g is a fixed primitive root, and let $q=a/b\in \mathbb{Q}$ be any conventional rational number. Then for any $\epsilon >0$, there exists an integer $n\in \mathbb{N}$ and an integer $x\in \mathbb{Z}$ such that

$$\left|{\displaystyle \frac{a}{b}}-{\displaystyle \frac{x}{g^n}}\right|<\epsilon .$$

Proof. 

Let ${\displaystyle \frac{a}{b}}\in \mathbb{Q}$ be given, and let $\epsilon >0$ be an arbitrary small number.

Since $\mathsf{p}$ and g are fixed, the expression $g^n$ grows without bounds as $n\to \infty$. Therefore, there exists an integer $n\in \mathbb{N}$ such that

$${\displaystyle \frac{1}{g^n}}<\epsilon .$$

Now consider the set of rational points of the form

$$\left\{{\displaystyle \frac{k}{g^n}}|k\in \mathbb{Z}\right\},$$

as illustrated in Figure 6. This set is a uniform grid of rational numbers with step size ${\displaystyle \frac{1}{g^n}}$, which is less than $\epsilon$ by construction. There exists, therefore, an integer $x\in \mathbb{Z}$ such that

$$\left|{\displaystyle \frac{a}{b}}-{\displaystyle \frac{x}{g^n}}\right|<\epsilon ,$$

which completes the proof. □

Interpretation 7.

It is important to reiterate the meaning of this construct from an ontological viewpoint. More specifically, we stipulate that what actually “exists” are the $\mathsf{p}$ representations of the finite field ${\mathbb{F}}_{\mathsf{p}}$, while the derivative class of f-rationals $q\in {}^{\mathsf{f}}\mathbb{Q}$ constitutes an abstract mathematical construct derived from the inherent relational properties of the framed instance ${\mathbb{F}}_{\mathsf{p}}$.

In other words, the resultant field of framed rational numbers ${}^{\mathsf{f}}\mathbb{Q}$ will exhibit all the properties of the field of conventional numbers $\mathbb{Q}$ and can further approximate it with any arbitrary precision. Furthermore, for an observer with a limited observability horizon and sufficiently large values of cardinality $\mathsf{p}$, the framed rational field ${}^{\mathsf{f}}\mathbb{Q}$ becomes completely indistinguishable from its conventional counterpart, as all the desired rational numbers of the form $q=a/b$, where $b<\mathsf{p}$ are represented not approximately, but exactly within the scope of the f-rationals ${}^{\mathsf{f}}\mathbb{Q}$.

4.3. Scale-Periodicity of ${}^{\mathsf{f}}\mathbb{Q}$

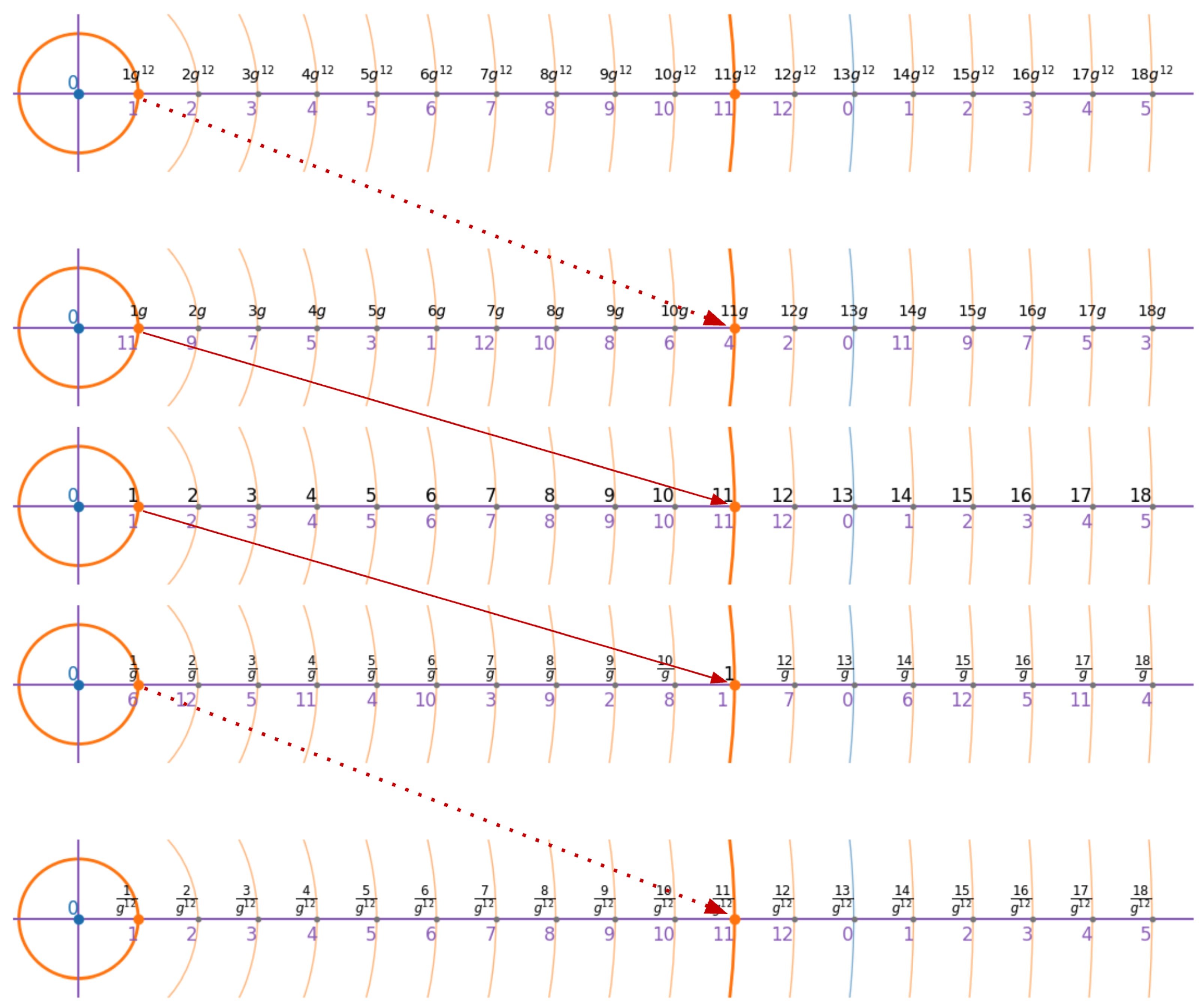
In the following section, we reiterate the key concept of scale invariance as a notable property of our finite relativistic algebra, where the selection of both the origin 0, and the scaling unit 1 are observer-dependent. This property is manifested through the periodicity of f-rationals under the operation of zooming—a process that shifts the scale of observation by a fixed factor. This periodicity is crucial for understanding how f-rationals behave under repeated scaling transformations, and it allows us to resolve any point on the framed real axis to arbitrary precision using only a finite set of data, making the framed real axis into a true continuum.

Recall that every f-rational number is represented in the framed field by a pair, as in Proposition 2:

$$[x,n]:={\displaystyle \frac{x}{g^n}},0\le x<\mathsf{p},n\in \mathbb{N},$$

where $g\in {\mathbb{F}}_{\mathsf{p}}^{\times }$ is a fixed generator of the multiplicative group. For each scale level n, the set

$${\mathcal{G}}_n:=\left\{[x,n]:0\le x<\mathsf{p}\right\}$$

forms a uniform grid of step $g^{-n}$ on the framed real axis, as depicted in Figure 7, where we depict a complete cycle $(-12,\dots ,-1,0,1,\dots ,12)$ of zoom scales for the prime $\mathsf{p}=13$ and generator $g=11$. The grid ${\mathcal{G}}_n$ is invariant under multiplication by $g^n$, which corresponds to a zoom operation that shifts the scale of observation by one unit.

Lemma 2

(Scale-periodicity). Let $\mathsf{p}$ be an odd prime and let g be any generator of ${\mathbb{F}}_{\mathsf{p}}^{\times }$. Then

$${\mathcal{G}}_{n+(\mathsf{p}-1)}={\mathcal{G}}_n\mathit{for}\mathit{every}n\ge 0.$$

Equivalently, multiplication of the denominator by $g^{\mathsf{p}-1}$ leaves the f-rational grid invariant. Hence, the zoom operation

$$Z:[x,n]⟼[x,n+1]$$

is $(\mathsf{p}-1)$-periodic.

Proof. 

Because g is a generator, Fermat’s little theorem gives $g^{\mathsf{p}-1}=1$ in ${\mathbb{F}}_{\mathsf{p}}^{\times }$. Hence,

$$[x,n+(\mathsf{p}-1)]={\displaystyle \frac{x}{g^n{g}^{\mathsf{p}-1}}}={\displaystyle \frac{x}{g^n}}=[x,n],$$

and the two grids coincide point-wise. □

4.4. Framed Reals

In classical mathematics, the field of real numbers $\mathbb{R}$ is introduced to enable the formulation of continuous functions, calculus, and metric spaces—tools indispensable for modeling physical phenomena and abstract structures alike. However, the real number line is defined as an uncountable, infinitary continuum, an ontological commitment that conflicts with the finite and relational framework we adopt in this study. Nonetheless, our need for continuous approximation and proportional reasoning persists, particularly in describing geometric constructs, dynamic systems, and analytic behaviours. Our approach is therefore pragmatic and epistemic rather than metaphysical. We seek to construct a class of framed real numbers (or f-reals) that fulfils the operational role of $\mathbb{R}$ without invoking actual infinity.

Definition 8

(Framed Reals ${}^{\mathsf{f}}\mathbb{R}$). Define truncated framed rationals:

$${}^{\mathsf{f}}\mathbb{Q}^{\le H}=\left\{[x,n]:0\le x<p,0\le n\le H\right\},[x,n]:={\displaystyle \frac{x}{g^n}},$$

where again g is a fixed primitive root of ${\mathbb{F}}_{\mathsf{p}}$. This set is finite and totally bounded under the metric:

$$d_H([x,n],[y,m]):=\left|{\displaystyle \frac{x}{g^n}}-{\displaystyle \frac{y}{g^m}}\right|.$$

Define ${}^{\mathsf{f}}\mathbb{R}$ as the closure of ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$. We show all computable real numbers can be approximated within $2^{-k}$ by some element $[x,n]\in {}^{\mathsf{f}}\mathbb{Q}^{\le H}$, where $H\ge \lceil k{log}_{2}p\rceil$ [27].

Proposition 3

(Finite Total Boundedness). For each fixed H, the metric space $\left({}^{\mathsf{f}}\mathbb{Q}^{\le H},d_H\right)$ is finite and thus totally bounded.

Proof. 

Since $0\le x<\mathsf{p}$ and $0\le n\le H$, there are $\left(P\right)\times (H+1)$ elements in ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$. Any finite metric space is trivially totally bounded. □

Theorem 2

(Approximation of Computable Reals). Let $r\in \mathbb{R}$ be a computable real number. For any integer $k\ge 1$ there exist integers $a_k,b_k$ with $b_k\ne 0$ such that

$$\left|r-\frac{a_k}{b_k}\right|<2^{-k}.$$

Moreover, if the observer’s horizon H satisfies

$$H\ge ⌈k{log}_2\mathsf{p}⌉,$$

then one can construct $[x_k,n_k]\in {}^{\mathsf{f}}\mathbb{Q}^{\le H}$ with

$$\left|r-[x_k,n_k]\right|<2^{-k-1}.$$

In order to prove Theorem 2 we first show that every Cauchy sequence $\left(x_n\right)\subseteq {}^{\mathsf{f}}\mathbb{Q}^{\le H}$ converges in ${}^{\mathsf{f}}\mathbb{R}$. The key step is a uniform bound on the number of steps in the Euclidean algorithm.

Lemma 3

(Euclidean-algorithm exponent bound). Let $\mathsf{p}$ be a prime and suppose $a,b\in \{1,2,\dots ,p-1\}$. If the Euclidean algorithm applied to $(a,b)$ produces k non-zero remainders before terminating, then

$$k\le ⌊{log}_2\left(p\right)⌋+1.$$

Proof. 

At each step of the Euclidean algorithm, if $\left(r_i\right)$ are the successive remainders with $r_0=a,r_1=b,r_{i+1}=r_{i-1}mod{r}_i$, then

$$r_{i-1}=q_i{r}_i+r_{i+1},0\le r_{i+1}<r_i,$$

and $q_i\ge 1$. It is known (Lamé’s theorem) that the worst-case sequence of quotients $\left(q_i\right)$ all equal 1, which yields the Fibonacci-type descent [28]. Let

$$r_{i+1}\le r_{i-1}-r_i,$$

so that

$$r_k\ge F_{k+1},$$

where $F_n$ is the n-th Fibonacci number. Since $r_k\ge 1$ and $F_n\ge 2^{(n-2)}$ for $n\ge 2$, termination after k steps implies

$$2^{k-1}\le F_{k+1}\le p-1⟹k-1\le {log}_2(p-1)<{log}_2\left(p\right),$$

hence $k\le \lfloor {log}_2\left(p\right)\rfloor +1$. □

Proof of Theorem 2. 

Let $\left(x_n\right)\subseteq {}^{\mathsf{f}}\mathbb{Q}^{\le H}$ be a Cauchy sequence with respect to the metric

$$d_H\left(a/b,c/d\right)=\left|ad-bc\right|/\left(bd\right),$$

where $|·|$ is taken in the integer sense and we require $a,b,c,d\le H$. By the Cauchy property, for any $ϵ>0$ there exists N such that for all $m,n\ge N$,

$$d_H(x_m,x_n)<ϵ.$$

Write $x_n=a_n/b_n$ in lowest terms. Apply the Euclidean algorithm to each pair $(a_n,b_n)$ to obtain the continued-fraction expansion

$${\displaystyle \frac{a_n}{b_n}}=q_{n,0}+{\displaystyle \frac{1}{q_{n,1}+\frac{1}{\ddots +\frac{1}{q_{n,k_n}}}}},$$

with $k_n\le \lfloor {log}_2\left(p\right)\rfloor +1$ by Lemma 3. Truncating at the J-th convergent yields a rational ${\displaystyle \frac{p_{n,J}}{q_{n,J}}}$ satisfying the standard bound

$$\left|{\displaystyle \frac{a_n}{b_n}}-{\displaystyle \frac{p_{n,J}}{q_{n,J}}}\right|<{\displaystyle \frac{1}{q_{n,J}^2}}.$$

Since $q_{n,J}\le b_n\le H$, for any chosen $J>{log}_2(H/ϵ)$ we get

$$\left|x_n-{\displaystyle \frac{p_{n,J}}{q_{n,J}}}\right|<{\displaystyle \frac{1}{H^2}}<ϵ.$$

Thus, $\left(x_n\right)$ is a Cauchy sequence in the complete metric space $\mathbb{R}$, hence converges to some real limit L. By construction of ${}^{\mathsf{f}}\mathbb{R}$ as the metric completion of ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$, this same limit L defines an element of ${}^{\mathsf{f}}\mathbb{R}$. Therefore, every Cauchy sequence in ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$ converges in ${}^{\mathsf{f}}\mathbb{R}$, proving completeness. □

Recall that ${}^{\mathsf{f}}\mathbb{R}$ is defined as the metric completion of the set

$${}^{\mathsf{f}}\mathbb{Q}^{\le H}=\left\{a/b|a,b\in \{1,2,\dots ,H\}\subset {\mathbb{F}}_{\mathsf{p}},gcd(a,b)=1\right\}$$

equipped with the metric

$$d_H\left(a/b,c/d\right)={\displaystyle \frac{|ad-bc|}{bd}}.$$

Proposition 4

(Compactness of ${}^{\mathsf{f}}\mathbb{R}$). ${}^{\mathsf{f}}\mathbb{R}$ is a compact metric space.

Proof. 

We invoke the standard characterization of compactness in metric spaces [29], namely that a metric space is compact if and only if it is complete and totally bounded.

• By Theorem 2, ${}^{\mathsf{f}}\mathbb{R}$ is complete: every Cauchy sequence in ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$ converges to a point of ${}^{\mathsf{f}}\mathbb{R}$.
• Proposition 3 establishes that ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$ is totally bounded. Since ${}^{\mathsf{f}}\mathbb{R}$ is the closure (completion) of ${}^{\mathsf{f}}\mathbb{Q}^{\le H}$, it too is totally bounded.

Therefore, ${}^{\mathsf{f}}\mathbb{R}$, being both complete and totally bounded, is compact. □

The resulting framed real field ${}^{\mathsf{f}}\mathbb{R}$ is thus defined as the topological closure of ${}^{\mathsf{f}}\mathbb{Q}$ under modular convergence. For any finite observer with bounded resolution and limited horizon of observability, ${}^{\mathsf{f}}\mathbb{R}$ is indistinguishable from the conventional real number continuum.

In conclusion, the field of f-reals ${}^{\mathsf{f}}\mathbb{R}$ is not a metaphysical continuum but a layered epistemic utilitarian construct. It combines:

(a)

Framed rationals that are finite rational numbers defined in Section 4.2,

(b)

Finite-algebraic numbers that satisfy algebraic equations within ${\mathbb{F}}_{\mathsf{p}}$, and

(c)

Structural invariants are framed real numbers identifiable by their respective structural roles in ${\mathbb{F}}_{\mathsf{p}}$, and can be associated with, or derived from, the classical transcendental constants $\pi$ and e. The detailed treatment of these constants will be provided in the companion paper [20].

This framework provides all the functional properties of the real numbers—continuity, density, and completeness—without invoking actual infinity. It affirms that, in a finite and informationally complete universe, continuum-like behavior is a pragmatic illusion emerging from local reasoning over a fundamentally finite arithmetic substrate.

Corollary 1

(Infinite knowability of ${}^{\mathsf{f}}\mathbb{R}$). The scale-periodicity principle provided by Theorem 2 implies that every point of the framed real axis ${}^{\mathsf{f}}\mathbb{R}$ can be resolved to arbitrary precision using only the finite data contained in a single period of scales $\{n,n+1,\dots ,n+\mathsf{p}-2\}$. Consequently, ${}^{\mathsf{f}}\mathbb{R}$ is a complete continuum despite arising from a finite field framework. We therefore refer to the resultant mathematical construct as the Finite Ring Continuum (FRC).

Interpretation 8.

Under the dictionary developed in Section 4.3, one step of the zoom map $\mathbb{Z}$ functions as a discrete renormalization-group (RG) transformation. Lemma 2 therefore realizes a closed RG flow: after $\mathsf{p}-1$ coarse-graining iterations all observables return to their original scale [30,31].

Interpretation 9.

It is important to distinguish the construction of f-reals ${}^{\mathsf{f}}\mathbb{R}$ from the field of p-adic numbers [32]. Both f-reals and p-adic numbers offer alternative completions of the rationals with hierarchical precision: p-adics use successive approximations via powers of p in an ultrametric topology, while f-reals employ powers of a primitive root g in finite fields to create dense grids for real-like approximations. However, p-adics rely on infinite series, yielding an uncountable, non-Archimedean field with local compactness, whereas f-reals are finite, periodic, and exhibit Archimedean properties without ontological infinity, prioritizing relational symmetries over infinite extensions.

4.5. Complex Plane over Finite Framed Field

Having established the construction of framed integers, rationals and reals over the finite field ${\mathbb{F}}_{\mathsf{p}}$ as relativistic, frame-dependent analogues of their classical counterparts, we seek to further extend this framework to encompass the algebraic closure of the framed real field. In conventional mathematics, the introduction of complex numbers $\mathbb{C}$ is necessitated by the absence of solutions to certain polynomial equations, such as $x^2+1=0$, within the real numbers. Analogously, in the finite framed context, we are motivated to introduce complex-like elements in order to achieve closure under operations that are otherwise impossible within the f-rational or f-reals alone.

Moreover, the construction of a framed complex plane enables the representation of rotations, oscillations, and other phenomena that are fundamental in both mathematics and physics, all within a finite and self-contained system. This approach not only mirrors the classical extension from $\mathbb{R}$ to $\mathbb{C}$, but also demonstrates that the essential properties and utility of complex numbers can be realized as emergent features of a finite, relational arithmetic—thereby reinforcing our framework’s central theme of relativistic, context-dependent number systems.

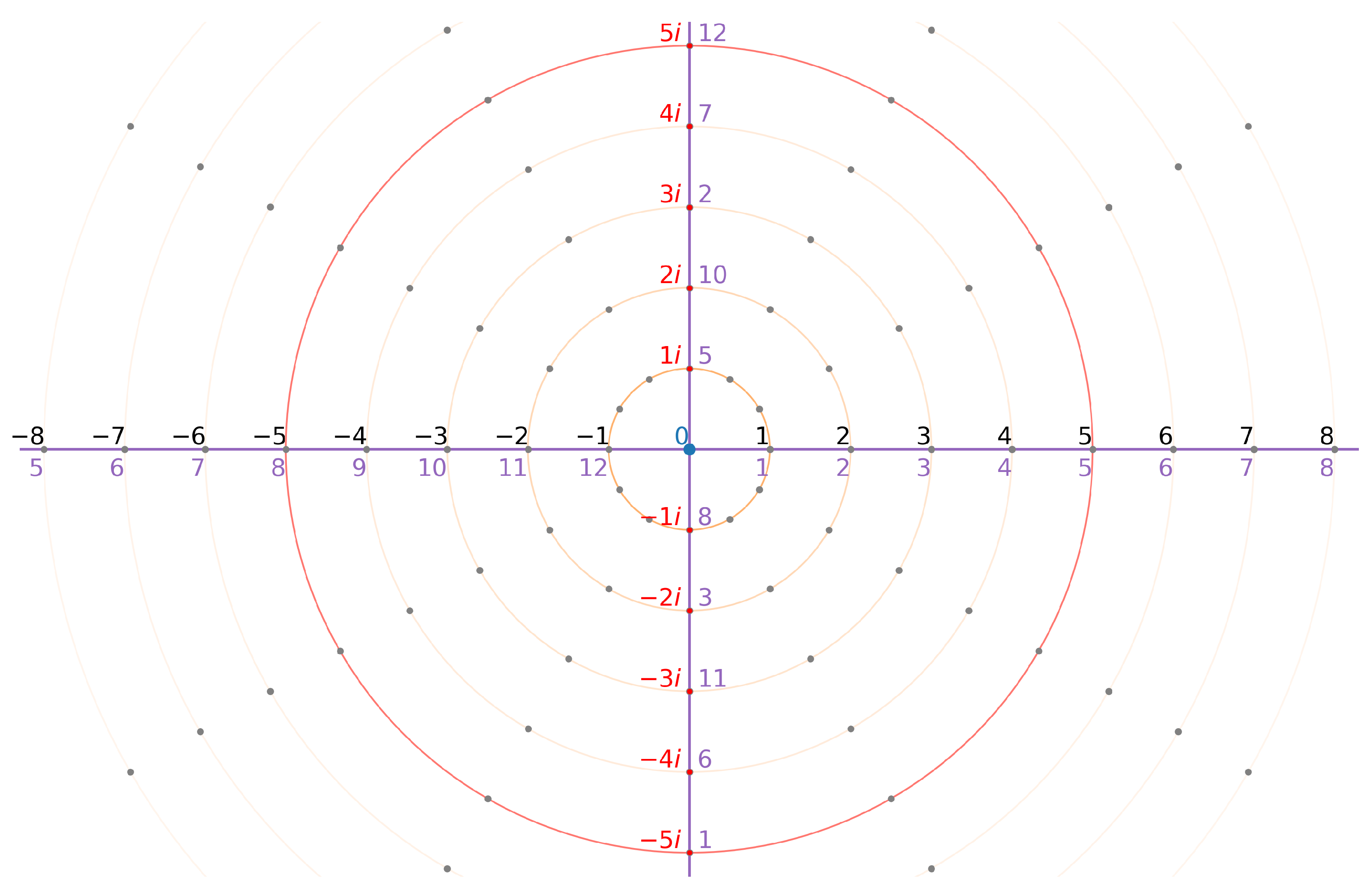
As is commonly known, the field of real numbers $\mathbb{R}$ does not contain any solutions of certain polynomial equations, such as the prominent equation $x^2+1=0$. But that is not the case for finite fields ${\mathbb{F}}_{\mathsf{p}}$ of prime order $\mathsf{p}=4\mathsf{t}+1$, where such solutions readily exist. For example, in the finite field ${\mathbb{F}}_5$, the equation $x^2+1=0$ has two solutions: $x=2$ and $x=3$. This is due to the fact that the multiplicative group of non-zero elements in such fields is cyclic and contains elements—and the corresponding rotational symmetry—of order 4, which allows for the existence of square roots of $-1$. In this case, we can define a special element $i_{\mathsf{t}}\in {\mathbb{F}}_{\mathsf{p}}$ that satisfies the equation $i_{\mathsf{t}}^2+1=0$. The element $i_{\mathsf{t}}$ is not unique, instead we have a pair of f-integer elements $i_{\mathsf{t}}$ and $-i_{\mathsf{t}}$ in ${\mathbb{F}}_{\mathsf{p}}$ that satisfy the equation, in the same way as we have pairs x and $-x$ of solutions for quadratic equations in the conventional complex plane $\mathbb{C}$.

Let us now observe the “North Pole” frame of reference of the spherical representation of the finite field ${\mathbb{F}}_{\mathsf{p}}$ illustrated in Figure 3 and Figure 5 with its prime meridian of f-reals ${}^{\mathsf{f}}\mathbb{R}$ forming the horizontal axis around the origin. The order-4 rotational symmetry of the finite field ${\mathbb{F}}_{\mathsf{p}}$ can be represented as a vertical axis of imaginary numbers $c=z·i_{\mathsf{t}}$, where $z\in \mathbb{Z}$, that are perpendicular to the prime meridian, as illustrated in Figure 8. The imaginary numbers c are represented by their respective red labels, while the corresponding elements $k\left(c\right)$ are depicted in purple.

Definition 9

(Framed complex class ${}^{\mathsf{f}}\mathbb{C}$). Consider a finite field ${\mathbb{F}}_{\mathsf{p}}$ of cardinality $\mathsf{p}=4\mathsf{t}+1$, fix a symbol $i_{\mathsf{t}}$ satisfying $i_{\mathsf{t}}^2=-1(mod\mathsf{p})$. We define the framed complex class ${}^{\mathsf{f}}\mathbb{C}$ as a quadratic extension of the framed real field ${}^{\mathsf{f}}\mathbb{R}$ such that

$${}^{\mathsf{f}}\mathbb{C}:={}^{\mathsf{f}}\mathbb{R}\left[i_{\mathsf{t}}\right]=\left\{a+b{i}_{\mathsf{t}}\mid a,b\in {}^{\mathsf{f}}\mathbb{R}\right\},$$

with the obvious component-wise addition and the usual complex-style multiplication $(a+b{i}_{\mathsf{t}})(c+d{i}_{\mathsf{t}})=(ac-bd)+(ad+bc)i_{\mathsf{t}}$. The map

$$\phi :{}^{\mathsf{f}}\mathbb{C}⟶{}^{\mathsf{f}}\mathbb{R}\times {}^{\mathsf{f}}\mathbb{R},a+b{i}_{\mathsf{t}}⟼(a,b)$$

is an isomorphism of ${}^{\mathsf{f}}\mathbb{R}$-modules, so ${}^{\mathsf{f}}\mathbb{C}\cong {}^{\mathsf{f}}\mathbb{R}\times {}^{\mathsf{f}}\mathbb{R}$ as additive groups.

Proposition 5.

The extension ${}^{\mathsf{f}}\mathbb{C}/{}^{\mathsf{f}}\mathbb{R}$ is a field exactly when $-1$ is a square in ${\mathbb{F}}_{\mathsf{p}}$, which is guaranteed by the construction condition $\mathsf{p}\equiv 1(mod4)$, then $i_{\mathsf{t}}\in {\mathbb{F}}_{\mathsf{p}}\subset {}^{\mathsf{f}}\mathbb{R}$ and ${}^{\mathsf{f}}\mathbb{C}={}^{\mathsf{f}}\mathbb{R}$.

Proof. 

When $\mathsf{p}\equiv 1(mod4)$ Hilbert’s theorem 90—or directly the cyclic structure of ${\mathbb{F}}_{\mathsf{p}}^{\times }$—provides an element $u\in {\mathbb{F}}_{\mathsf{p}}$ with $u^2\equiv -1$, so adjoining $i_{\mathsf{t}}$ does not enlarge ${}^{\mathsf{f}}\mathbb{R}$. □

Having completed the construction of the full hierarchy of relational number classes—framed integers, dense framed rationals, compact framed reals, and the algebraically closed framed complex plane—within a single finite field ${\mathbb{F}}_p$, we have in hand a self-contained algebra that faithfully mirrors the familiar $\mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$ tower up to any observer-chosen precision. The following section is intended as a brief preview of the practical utility and applications of the proposed Finite Ring Continuum framework and should not be regarded as a comprehensive treatment, which will be the subject of companion papers [20] and [21], as well as our future works.

5. Discussion and Ontological Perspective

We henceforth assert that only the $\mathsf{p}$ representations of ${\mathbb{F}}_{\mathsf{p}}$ truly exist. All framed number classes are epistemic constructs derived from relational symmetries and observer framing. The observer’s bounded horizon $H\ll i_{\mathsf{t}}=\sqrt{\mathsf{p}-1}$ induces the illusion of infinite domains [33].

Let us revisit the ontological concept of infinity as described in [4]. In the previous sections, we have established the finite framed field ${\mathbb{F}}_{\mathsf{p}}$ as an abstract relational sphere ${\mathbb{F}}_{\mathsf{p}}(0,1)$ with a limited-horizon observer at its origin 0. We would like now to consider the geometric point on our relational sphere that is the furthest away from the observer. This point is evidently the South Pole—the antipodal point to the North Pole $\mathsf{N}\equiv (\mathsf{t};0)$ on the prime meridian—of the relational sphere as depicted in Figure 3, which we will denote as $\mathsf{S}$ for now. We would like to emphasize the following important properties of $\mathsf{S}$.

• $\mathsf{S}$ is a unique point on the relational sphere that is the farthest away from the observer at 0.
• $\mathsf{S}$ is invisible to the observer at 0, that is to say it is located beyond any conceivable definition of the observer’s limited observability horizon.
• Finally, $\mathsf{S}$ is algebraically inaccessible to the observer at 0, in the sense that $\mathsf{S}\notin {\mathbb{F}}_{\mathsf{p}},{}^{\mathsf{f}}\mathbb{Q}$, and cannot be reached by any finite number of arithmetical steps along the surface of the relational sphere.

We would like to provide a formal proof of the less evident Property 3 as follows.

Theorem 3

(No South Pole in ${\mathbb{F}}_{\mathsf{p}}$). Let $\mathsf{p}>2$ be an odd prime. Then the only solution $s\in {\mathbb{F}}_{\mathsf{p}}$ to

$$2s\equiv 0(mod\mathsf{p})$$

is $s\equiv 0$. Equivalently, there is no nonzero framed rational $q\in {}^{\mathsf{f}}\mathbb{Q}$ whose image in ${}^{\mathsf{f}}\mathbb{Z}$ has additive order 2.

Proof. 

• Since $\mathsf{p}$ is prime, the additive group $({\mathbb{F}}_{\mathsf{p}},+)$ is cyclic of order $\mathsf{p}$. An element $s\in {\mathbb{F}}_{\mathsf{p}}$ has order 2 precisely if $2s\equiv 0(mod\mathsf{p}).$
• Because $gcd(2,\mathsf{p})=1$, multiplication by 2 is invertible in ${\mathbb{F}}_{\mathsf{p}}$. Hence, from $2s\equiv 0(mod\mathsf{p})$ it follows immediately that $s\equiv 0(mod\mathsf{p})$. There is no nontrivial order-2 element.
• By definition, each framed rational $q={\displaystyle \frac{a}{b}}\in {}^{\mathsf{f}}\mathbb{Q}$ is represented in the field by

  $$k\left(q\right)=a{b}^{-1}mod\mathsf{p}\in {\mathbb{F}}_{\mathsf{p}},$$

  so ${}^{\mathsf{f}}\mathbb{Q}\subseteq {\mathbb{F}}_{\mathsf{p}}$ under the embedding k. If some $q\in {}^{\mathsf{f}}\mathbb{Q}$ mapped to a non-zero order-2 element $s=k\left(q\right)\ne 0$, then $2s\equiv 0$ would force $s\equiv 0$, a contradiction.

Therefore, no “South Pole” antipodal point exists in ${}^{\mathsf{f}}\mathbb{Q}$ or ${}^{\mathsf{f}}\mathbb{Z}$, completing the proof. □

These properties of the geometrical point $\mathsf{S}$ are unmistakably consistent with the properties of the concept of infinity in its conventional sense. This gives us the justification to identify the relativistic antipodal point $\mathsf{S}$ with the concept of infinity in the context of ${\mathbb{F}}_{\mathsf{p}}$, and thus denote it as ∞. It should be noted that our interpretation is also consistent with the concept of an Extended real number line [34] and an extensive body of existing literature in conventional mathematics, where a compactification often involves adjoining infinities to a space to make it compact. Some such examples include the One-Point Compactification [35], Real Projective Line [36], and the Riemann Sphere [37].

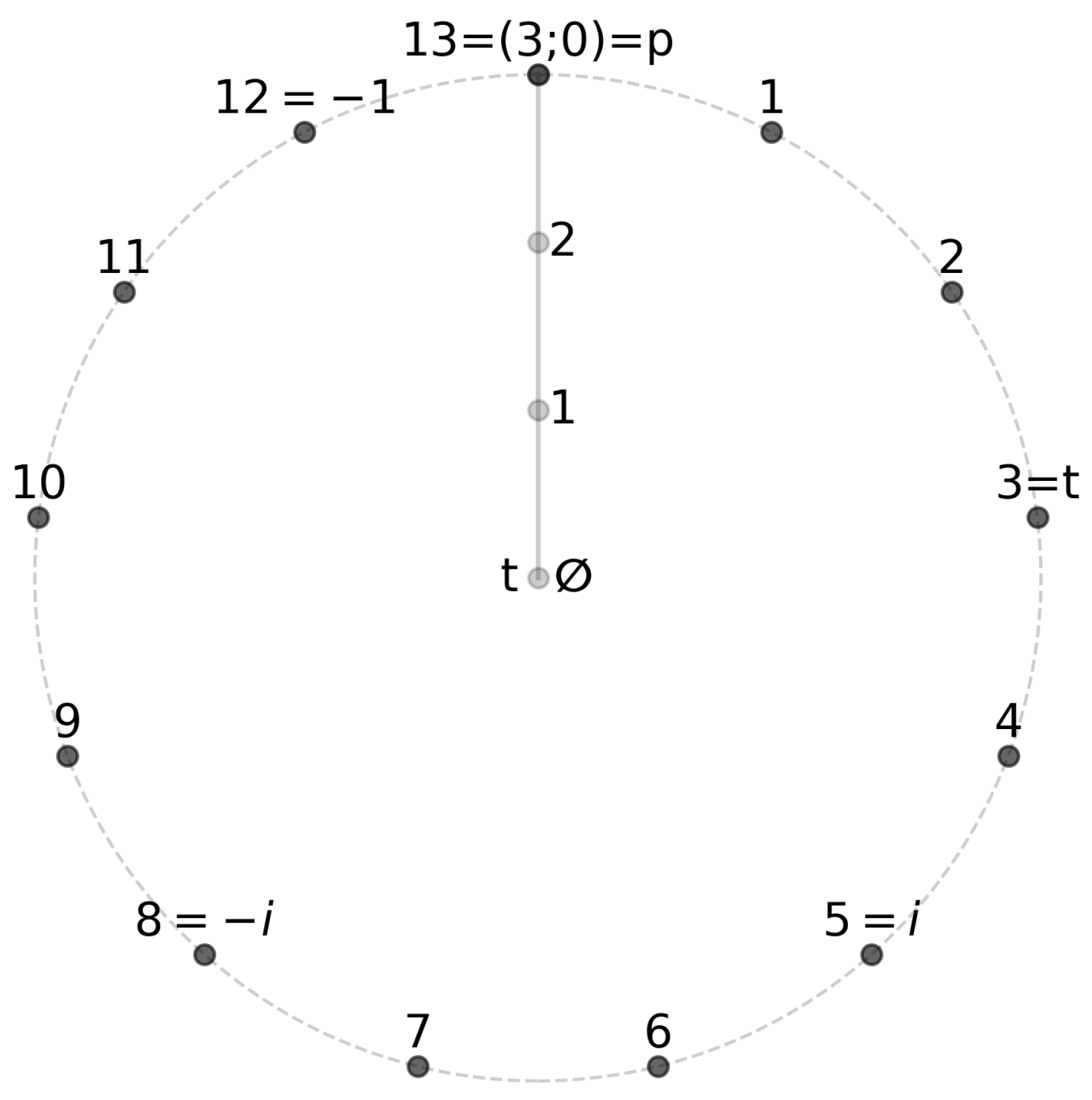
To exemplify, let us now consider the concrete example of $\mathsf{t}=3,\mathsf{p}=13$ and the corresponding finite framed field ${\mathbb{F}}_{13}(0,1)$. We can identify the value of the imaginary unit $i_3=5$. The corresponding visual representation of the finite field ${\mathbb{F}}_{13}$ is shown in Figure 9. The figure shows the state space of the finite field ${\mathbb{F}}_{13}$ as a circle on a 2D plane, with the major structural elements $-1,0,1,g=2,i_3$, as well as ∞ indicated. The antipodal point ∞ is located at the south pole of the relational sphere, which is the farthest point from the observer at 0.

6. Conclusions

This work reconstructs arithmetic over finite fields as a complete, self-consistent relativistic algebra. Number systems conventionally built on actual infinity are shown to emerge from finite, observer-relative structures in ${\mathbb{F}}_{\mathsf{p}}$. Specifically, we have shown that by interpreting addition, multiplication and exponentiation as internal symmetries of a finite framed field ${\mathbb{F}}_{\mathsf{p}}(0,1)$, one can reconstruct signed integers, rationals, reals and complex numbers in a way that matches classical behavior up to any desired precision, without ever invoking an infinite set. This construction preserves the familiar algebraic laws and analytic operations that underpin standard number systems, ensuring full compatibility with intuition and established mathematical practice.

We would like to conjecture, currently without a full proof, that the resultant FRC framework supports the full spectrum of modern mathematical techniques—solving polynomial equations, performing limit-like approximations via dense framed rationals, and modeling continuous symmetries through $\epsilon$-Lie-group approximations—while entirely replacing classical infinities with context-dependent finite representations. In doing so, it provides exact algebraic analogues for roots, exponentials and trigonometric relationships and offers a discrete yet arbitrarily precise scaffold for differential-geometric and analytic constructions. By eliminating any ontological reliance on actual infinity, this framework retains the power and flexibility of conventional mathematics in a fully finitary setting, while also offering an avenue towards the resolution of classical paradoxes of logic and set theory imposed by the prevalent infinitude conjecture.

The resulting structure is not merely a mathematical curiosity; it is a coherent and physically grounded alternative to standard formalism, suitable for the description of discrete, informationally finite physical systems. Ultimately, the proposed framework aims to substantiate the principle of ontological priority of the finite mathematics as the fundamental reality, while the conventional infinite structures emerge as utilitarian approximations, which are highly effective and accurate in many practical applications, but are structurally degenerate and logically incomplete, leading to numerous limitations and internal contradictions.

Looking forward, extending our framework to composite moduli, and exploring the implications for the analysis of dynamic physical systems, will further strengthen and broaden its applicability. We would like to propose that this relational, finite approach can potentially serve as a conceptually coherent foundation and, at least in some cases, a practical computational paradigm across mathematics, physics, formal logic and computer science.