Edgeworth Coefficients for Standard Multivariate Estimates

Abstract

I give for the first time explicit formulas for the coefficients needed for the fourth-order Edgeworth expansions of a multivariate standard estimate. I call these the Edgeworth coefficients. They are Bell polynomials in the cumulant coefficients. Standard estimates include most estimates of interest, including smooth functions of sample means and other empirical estimates. I also give applications to ellipsoidal and hyperrectangular sets.

1. Introduction and Summary

Suppose that $\widehat{w}$ is a standard estimate, as defined in Section 2, of an unknown parameter $w\in R^q$ of a statistical model, based on a sample of size n. For example, $\widehat{w}$ may be a smooth function of a sample mean, or a smooth functional of an empirical distribution. A smooth function of a standard estimate is also a standard estimate: see [1]. Section 2 summarises the multivariate Edgeworth expansions of Withers and Nadarajah (2010) [2] for the distribution and density of $X_n=n^{1/2}(\widehat{w}-w)$ in powers of $n^{-1/2}$ about the multivariate normal in terms of the Edgeworth coefficients, the $P_r$-coefficients of (18). For $r\ge 1$, these $P_r$ are needed for the $r+1$st term of the multivariate Edgeworth expansions. They are Bell polynomials in the cumulant coefficients of (9). They are given for $r=1$ by (19) and for $r=2,3$ by (19)–(21) in terms of the symmetrizing operator $\mathcal{S}$ and explicitly in Appendix A. Section 3 derives expansions on ellipsoidal and hyperrectangular sets.

When $q=2$, Section 4 simplifies these Edgeworth coefficients using an alternative notation. Examples include the distribution and density of a sample mean and of bivariate entangled gamma random variables.

Section 5 and Section 6 give conclusions and discussion and suggest some future directions. Appendix B explicitly gives the bivariate Hermite polynomials needed for bivariate Edgeworth expansions to $O\left(n^{-2}\right)$. The results of [3,4] could be considered heuristic. However, Section 5 of [5] showed that the Cornish–Fisher expansions (4) are valid under the usual conditions for validity of multivariate Edgeworth expansions. Their Section 5 appears to show that this is also true for the multivariate case. See also [6]. Appendix C gives for the first time a theorem for the validity of the Edgeworth expansions given here. Appendix D gives some corrigenda to the references. When q = 1, see also [7].

Univariate estimates. Suppose that $\widehat{w}$ is a standard estimate of $w\in R$ with respect to n, (typically the sample size). That is, $\widehat{w}$ is non-lattice, $E\widehat{w}\to w$ as $n\to \infty$, and its rth cumulant can be expanded as

$$\begin{array}{cc}& {\kappa }_r\left(\widehat{w}\right)\approx \sum _{j=r-1}^{\infty }{n}^{-j}{a}_{rj}\mathrm{for}r\ge 1,\hfill \end{array}$$

(1)

where the cumulant coefficients $a_{rj}$ may depend on n but are bounded as $n\to \infty$, and $a_{21}$ is bounded away from 0. Here and below, ≈ indicates an asymptotic expansion that need not converge. Thus, (1) holds in the sense that

$${\kappa }_r\left(\widehat{w}\right)=\sum _{j=r-1}^{I-1}{n}^{-j}{a}_{rj}+O\left(n^{-I}\right)\mathrm{for}I\ge r\ge 1,$$

where $y_n=O\left(x_n\right)$ means that $y_n/x_n$ is bounded in n. Ref. [4] replaced the artificial assumptions of [3,8] by (1) and gave the distribution, density and quantiles of

$$U_n={(n/a_{21})}^{1/2}(\widehat{w}-w)$$

as asymptotic expansions in powers of $n^{-1/2}$:

$$\begin{array}{cc}& P_n\left(u\right)=Prob.(U_n\le u)\approx \mathrm{\Phi }\left(u\right)-\varphi \left(u\right)\sum _{r=1}^{\infty }{n}^{-r/2}{h}_r\left(u\right),\hfill \end{array}$$

(2)

$$\begin{array}{c}\hfill p_n\left(u\right)=d{P}_n\left(u\right)/du\approx \varphi \left(u\right)[1+\sum _{r=1}^{\infty }{n}^{-r/2}{\overline{h}}_r\left(u\right)],\end{array}$$

(3)

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{-1}\left(P_n\left(u\right)\right)\approx u-\sum _{r=1}^{\infty }{n}^{-r/2}{f}_r\left(u\right),P_n^{-1}\left(\mathrm{\Phi }\left(u\right)\right)\approx u+\sum _{r=1}^{\infty }{n}^{-r/2}{g}_r\left(u\right),\end{array}$$

(4)

where $Prob.\left(A\right)$ is the probability that A is true,

$$\mathrm{\Phi }\left(u\right)=Prob.(N\le u)={\int }_{-\infty }^u\varphi \left(u\right)du,\varphi \left(u\right)={\left(2\pi \right)}^{-1/2}{e}^{-u^2/2},N\sim \mathcal{N}(0,1)$$

is a unit normal random variable with even moments $E{N}^{2k}=1.3\dots (2k-1)$, and $h_r\left(u\right),{\overline{h}}_r\left(u\right),f_r\left(u\right)$ and $g_r\left(u\right)$ are polynomials in u and also in the standardized cumulant coefficients $A_{ri}=a_{ri}/a_{21}^{r/2}$. For example,

$$\begin{array}{c}{h}_1\left(u\right)=f_1\left(u\right)=g_1\left(u\right)=A_{11}+A_{32}{H}_2/6,{\overline{h}}_1\left(u\right)=A_{11}{H}_1+A_{32}{H}_3/6,\hfill \\ h_2\left(u\right)=(A_{11}^2+A_{22})H_1/2+(A_{11}{A}_{32}+A_{43}/4)H_3/6+A_{32}^2{H}_5/72,\hfill \end{array}$$

(5)

where $H_k$ is the kth Hermite polynomial. By [9], for $I=\sqrt{-1}$,

$$\begin{array}{c}{H}_k=H_k\left(u\right)=\varphi {\left(u\right)}^{-1}{(-d/du)}^k\varphi \left(u\right)=E{(u+IN)}^k\mathrm{for}k\ge 0:\hfill \\ H_0=1,H_1=u,H_2=u^2-1,H_3=u^3-3u,H_4=u^4-6u^2+3.\hfill \end{array}$$

(6)

(A2) gives $H_k$ for $k\le 9$. Since $h_r\left(u\right)$ is even/odd for r odd/even,

$$\begin{array}{c}Prob.\left(\right|U_n|\le u)\approx \mathrm{\Phi }\left(u\right)-2\varphi \left(u\right)\sum _{r=1}^{\infty }{n}^{-r}{h}_{2r}\left(u\right)\mathrm{for}u>0.\hfill \end{array}$$

(7)

From (4), it follows that

$$\begin{array}{cc}& U_n\approx u+\sum _{r=1}^{\infty }{n}^{-r/2}{g}_r\left(N\right)\mathrm{where}N\sim \mathcal{N}(0,1).\hfill \end{array}$$

(8)

For a discussion of when to truncate (2)–(4), see [10].

Note 1.

Edgeworth’s expansion [11] was for $\widehat{w}$, the mean of n independent identically distributed random variables on R from a distribution with rth cumulant ${\kappa }_r$. Thus, (1) holds with $a_{r,r-1}={\kappa }_r$and $a_{ri}=0$. An explicit formula for its general term was given in [12].

For examples of the many applications of Cornish–Fisher expansions and the extensions of [13], see [14,15,16]. Applications in finance include [17,18]. For an application to Rayleigh fading amplitudes, see [19]. Ref. [20] used them for GPS accuracy. Refs. [21,22,23] successfully used them for system reliability, even though binomial random variables fall on a lattice. Ref. [24] used them for cosmology. Ref. [25] used them for optimal electric power flow.

Now suppose that ${\widehat{w}}_{*}$ is another standard estimate of w with the same asymptotic variance $a_{21}/n$. Denote its standardized cumulant coefficients by $A_{ri*}$. Suppose that

$$U_{n*}={(n/a_{21})}^{1/2}({\widehat{w}}_{*}-w)\sim {\mathrm{\Phi }}_n\left(u\right)={\int }_{-\infty }^u{\varphi }_n\left(u\right)du\to \mathrm{\Phi }\left(u\right)\mathrm{as}n\to \infty .$$

Then, one can expand $P_n\left(u\right)$ about ${\mathrm{\Phi }}_n\left(u\right)$ rather than $\mathrm{\Phi }\left(u\right)$. The above expressions for $P_n\left(u\right),h_k\left(u\right)$ become

$$\begin{array}{cc}& P_n\left(u\right)=Prob.(U_n\le u)\approx {\mathrm{\Phi }}_n\left(u\right)-{\varphi }_n\left(u\right)\sum _{r=1}^{\infty }{n}^{-r/2}{h}_{rn}\left(u\right),\mathrm{where}\hfill \\ & h_{1n}\left(u\right)=A_{110}+A_{320}{H}_{2n}/6,\hfill \\ & h_{2n}\left(u\right)=(A_{110}^2+A_{220})H_{1n}/2+(A_{110}{A}_{320}+A_{430}/4)H_{3n}/6+A_{320}^2{H}_{5n}/72,\hfill \\ & A_{rj0}=A_{rj}-A_{rj*},\mathrm{and}{H}_{kn}=H_{kn}\left(u\right)={\varphi }_n{\left(u\right)}^{-1}{(-d/du)}^k{\varphi }_n\left(u\right).\hfill \end{array}$$

Therefore, if, for example, we choose ${\widehat{w}}_{*}$ so that $A_{110}=A_{320}=0$, then

$$h_{1n}\left(u\right)=0,h_{2n}\left(u\right)=A_{220}{H}_{1n}/2+A_{430}{H}_{3n}/24,$$

and the number of terms in the analogues of $h_r,f_r,g_r$ are greatly reduced. The disadvantage is that $H_{kn}\left(u\right)$ is more complicated than $H_k\left(u\right)$. See [19]. For expansions about a matching Student’s, gamma, or F distribution, see [14,15,26].

Regularity conditions. The expansions of [27] and subsequent extensions by [1,3,4] all build on the fact that for $f\left(x\right)$ a density on R with finite cumulants, $exp\{A{(-d/dx)}^r/r!\}f\left(x\right)$ is a density with the same cumulants except that its rth cumulant has increased by A, and similarly for a density on $R^q$. For a sample mean, many authors have given precise conditions for the Edgeworth expansions. See, for example, p. 229 of [28] and (19.17), (20.48), (23.3) of [29]. The latter gives corrections for a lattice sample mean. Ref. [30] and its references also give conditions for their validity.

2. Multivariate Edgeworth Expansions

Suppose that $\widehat{w}$ is a standard estimate of $w\in R^q$ with respect to n. That is, $\widehat{w}$ is non-lattice, $E\widehat{w}\to w$ as $n\to \infty$, and for $r\ge 1$, $1\le i_1,\dots ,i_r\le q,$ the rth order cumulants of $\widehat{w}$ can be expanded as

$$\begin{array}{c}\hfill {\overline{k}}^{1-r}=k^{i_1\dots i_r}=\kappa ({\widehat{w}}^{i_1},\dots ,{\widehat{w}}^{i_r})\approx \sum _{d=r-1}^{\infty }{n}^{-d}{\overline{k}}_d^{1-r}\mathrm{where}{\overline{k}}_d^{1-r}=k_d^{i_1\dots i_r},\end{array}$$

(9)

and the cumulant coefficients ${\overline{k}}_d^{1-r}$ may depend on n but are bounded as $n\to \infty$. Thus, the bar replaces each $i_k$ by k. The use of $i_k$ is reserved for this purpose. For example, ${\overline{k}}_0^1=w^{i_1}$ and ${\overline{k}}_1^{12}=k_1^{i_1{i}_2}.$ I use this bar notation repeatedly to avoid double subscripts $i_k$. Therefore, I use I, not i, for $\sqrt{-1}$ below.

$$\begin{array}{c}\mathrm{As} n\to \infty ,X_n=n^{1/2}(\widehat{w}-w)\stackrel{\mathcal{L}}{\to }X={\mathcal{N}}_q(0,V)\mathrm{for}V=\left({\overline{k}}_1^{12}\right),q\times q,\hfill \end{array}$$

(10)

the multivariate normal on $R^q$, with density and distribution

$$\begin{array}{cc}& {\varphi }_V\left(x\right)={\left(2\pi \right)}^{-q/2}{\left(detV\right)}^{-1/2}exp(-x^{\prime }{V}^{-1}x/2),{\mathrm{\Phi }}_V\left(x\right)={\int }_{-\infty }^x{\varphi }_V\left(x\right)dx.\hfill \end{array}$$

(11)

V may depend on n, but I assume that $detV$ is bounded away from 0.

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{Set}Y=V^{-1}X\sim {\mathcal{N}}_q(0,V^{-1}),{\overline{Y}}_j=Y_{i_j},{\overline{\mu }}^{1-k}=E{\overline{Y}}_1\dots {\overline{Y}}_{k}of\left(A3\right),\hfill \\ \mathrm{So}E{\overline{Y}}_1{\overline{Y}}_2={\overline{V}}^{12}\mathrm{where}{\overline{V}}^{12}=V^{i_1{i}_2}\mathrm{is}\mathrm{the}(i_1,i_2)\mathrm{element}\mathrm{of}{V}^{-1}.\mathrm{Set}\hfill \end{array}\end{array}$$

(12)

$$\begin{array}{c}\hfill \begin{array}{c}{\overline{b}}_{2d}^{1-k}={\overline{k}}_d^{1-k},{\overline{b}}_{2d+1}^{1-k}=0,{\overline{t}}_k=t_{i_k},e_r\left(t\right)={\displaystyle \sum _{k=1}^{r+2}}{\overline{b}}_{k+r}^{1-k}{\overline{t}}_1\dots {\overline{t}}_k/k!,t\in R^q.\hfill \\ \mathrm{So},e_1\left(t\right)={\overline{k}}_1^1{\overline{t}}_1+{\overline{k}}_2^{1-3}{\overline{t}}_1{\overline{t}}_2{\overline{t}}_3/3!,e_2\left(t\right)={\overline{k}}_2^{12}{\overline{t}}_1{\overline{t}}_2/2+{\overline{k}}_3^{1-4}{\overline{t}}_1\dots {\overline{t}}_4/4!,\hfill \\ e_3\left(t\right)={\overline{k}}_2^1{\overline{t}}_1+{\overline{k}}_3^{1-3}{\overline{t}}_1\dots {\overline{t}}_3/3!+{\overline{k}}_4^{1-5}{\overline{t}}_1\dots {\overline{t}}_5/5!,\hfill \end{array}\end{array}$$

(13)

where here and below, I use the tensor summation convention of implicitly summing each $i_k$ over its range $1,\dots ,q$. For example,

$$\begin{array}{cc}& {\overline{b}}_2^1{\overline{t}}_1={\overline{k}}_1^1{\overline{t}}_1=\sum _{i_1=1}^q{k}_1^{i_1}{t}_{i_1}\mathrm{and}{\overline{b}}_2^{12}{\overline{t}}_1{\overline{t}}_2={\overline{k}}_1^{12}{\overline{t}}_1{\overline{t}}_2=\sum _{i_1,i_2=1}^q{k}_1^{i_1{i}_2}{t}_{i_1}{t}_{i_2}.\hfill \end{array}$$

Ordinary Bell polynomials. For a sequence $e=(e_1,e_2,\dots )$ from R, the partial ordinary Bell polynomial ${\tilde{B}}_{rs}={\tilde{B}}_{rs}\left(e\right)$ is defined by the identity

$$\begin{array}{cc}& \mathrm{for}s=0,1,2,\dots ,\mathrm{and}z\in R,S^s=\sum _{r=s}^{\infty }{z}^r{\tilde{B}}_{rs}\left(e\right)\mathrm{where}S=\sum _{r=1}^{\infty }{z}^r{e}_r.\hfill \end{array}$$

(14)

$$\begin{array}{c}\hfill \mathrm{So},{\tilde{B}}_{r0}={\delta }_{r0},{\tilde{B}}_{r1}=e_r,{\tilde{B}}_{rr}=e_1^r,{\tilde{B}}_{32}=2e_1{e}_2,\end{array}$$

(15)

where ${\delta }_{00}=1,{\delta }_{r0}=0$ for $r\ne 0.$ They are tabled on p. 309 of [31]. (The partial exponential Bell polynomials are not used in this paper.) The complete ordinary Bell polynomial, ${\tilde{B}}_r\left(e\right)$, is defined in terms of S of (14) by

$$\begin{array}{cc}& e^S=\sum _{r=0}^{\infty }{z}^r{\tilde{B}}_r\left(e\right).\mathrm{So}{\tilde{B}}_0\left(e\right)=1,\mathrm{and}\mathrm{for}r\ge 1,{\tilde{B}}_r\left(e\right)=\sum _{s=1}^r{\tilde{B}}_{rs}\left(e\right)/s!:\hfill \end{array}$$

(16)

$$\begin{array}{c}\hfill {\tilde{B}}_1\left(e\right)=e_1,{\tilde{B}}_2\left(e\right)=e_2+e_1^2/2,{\tilde{B}}_3\left(e\right)=e_3+e_1{e}_2+e_1^3/6.\end{array}$$

(17)

$$\begin{array}{c}\hfill \mathrm{Then},\mathrm{for}r\ge 1,{\tilde{B}}_r\left(e\left(t\right)\right)=\sum _{k=1}^{3r}[{\overline{P}}_r^{1-k}{\overline{t}}_1\dots {\overline{t}}_k:k-r\mathrm{even}],\end{array}$$

(18)

where the rth Edgeworth coefficient, ${\overline{P}}_r^{1-k}=P_r^{i_1\dots i_k}$, is a function of ${\overline{k}}_d^{1-r}$. One could use unsymmetrized ${\overline{P}}_r^{1-k}$. For example, by (17), ${\tilde{B}}_2\left(e\left(t\right)\right)$ needs the cross term in $e_1{\left(t\right)}^2/2,{\overline{k}}_1^4{\overline{k}}_2^{1-3}{\overline{t}}_1{\overline{t}}_2{\overline{t}}_3{\overline{t}}_4/6$. Thus, we could use ${\overline{k}}_1^4{\overline{k}}_2^{1-3}/6$ in ${\overline{P}}_2^{1-4}$. But as (68) below illustrates, there is a big advantage in making ${\overline{P}}_r^{1-k}$ symmetric in $i_1,\dots ,i_k$ using the operator $\mathcal{S}$ that symmetrizes over $i_1,\dots ,i_k$. Therefore, the ${\overline{P}}_r^{1-k}$ that we need for $r=1,2,3$ are

$$\begin{array}{cc}& {\overline{P}}_1^1={\overline{k}}_1^1,{\overline{P}}_1^{1-3}={\overline{k}}_2^{1-3}/3!,{\overline{P}}_2^{12}={\overline{k}}_2^{12}/2+k_1^1{\overline{k}}_1^2/2,\hfill \end{array}$$

(19)

$$\begin{array}{c}\hfill {\overline{P}}_2^{1-4}={\overline{k}}_3^{1-4}/4!+\mathcal{S}{\overline{k}}_1^4{\overline{k}}_2^{1-3}/6,{\overline{P}}_2^{1-6}=\mathcal{S}{\overline{k}}_2^{1-3}{\overline{k}}_2^{4-6}/72,\end{array}$$

(20)

$$\begin{array}{c}\hfill \begin{array}{c}{\overline{P}}_3^1={\overline{k}}_2^1,{\overline{P}}_3^{1-3}={\overline{k}}_3^{1-3}/6+\mathcal{S}{\overline{k}}_2^{12}{\overline{k}}_1^3/2+{\overline{k}}_1^1{\overline{k}}_1^2{\overline{k}}_1^3/6,\hfill \\ {\overline{P}}_3^{1-5}={\overline{k}}_4^{1-5}/5!+S_1/24+S_2/12+S_3/12\hfill \\ \mathrm{where}{S}_1=\mathcal{S}{\overline{k}}_3^{1-4}{\overline{k}}_1^5,S_2=\mathcal{S}{\overline{k}}_2^{12}{\overline{k}}_2^{345},S_3=\mathcal{S}{\overline{k}}_1^1{\overline{k}}_1^2{\overline{k}}_2^{345}/12,\hfill \\ {\overline{P}}_3^{1-7}=\mathcal{S}{\overline{k}}_2^{123}{\overline{k}}_3^{4-7}/144+\mathcal{S}{\overline{k}}_2^{123}{\overline{k}}_2^{4-6}{\overline{k}}_1^7/72,\hfill \\ {\overline{P}}_3^{1-9}=\mathcal{S}{\overline{k}}_2^{1-3}{\overline{k}}_2^{4-6}{\overline{k}}_2^{7-9}/6^4.\hfill \end{array}\end{array}$$

(21)

These formulas are mostly new. The terms involving $\mathcal{S}$ are given explicitly for the first time in Appendix A. By [2], the distribution and density of $X_n$ of (10) can be expanded as

$$\begin{array}{c}\hfill Prob.(X_n\le x)\approx \sum _{r=0}^{\infty }{n}^{-r/2}{P}_r\left(x\right),p_{X_n}\left(x\right)\approx \sum _{r=0}^{\infty }{n}^{-r/2}{p}_r\left(x\right),x\in R^q,\end{array}$$

(22)

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{where}{P}_0\left(x\right)={\mathrm{\Phi }}_V\left(x\right),p_0\left(x\right)={\varphi }_V\left(x\right),\mathrm{and}\hfill \\ P_r\left(x\right)={\tilde{B}}_r\left(e(-\partial /\partial x)\right){\mathrm{\Phi }}_V\left(x\right),p_r\left(x\right)={\tilde{B}}_r\left(e(-\partial /\partial x)\right){\varphi }_V\left(x\right)\mathrm{for}r\ge 1.\hfill \\ \mathrm{Set}{\mathsf{\partial }}_i=\partial /\partial x_i,{\overline{\partial }}_k={\partial }_{i_k}\mathrm{and}{\overline{O}}^{1-k}=O^{i_1\dots i_k}=(-{\overline{\partial }}_1)\dots (-{\overline{\partial }}_k).\hfill \\ \mathrm{Thus},\mathrm{by}\left(18\right),\mathrm{for}r\ge 1,P_r\left(x\right)={\displaystyle \sum _{k=1}^{3r}}[P_{rk}\left(x\right):k-r\mathrm{even}],\hfill \end{array}\end{array}$$

(23)

$$\begin{array}{c}\hfill \mathrm{and}{p}_r\left(x\right)/{\varphi }_V\left(x\right)=\sum _{k=1}^{3r}[{\tilde{p}}_{rk}:k-r\mathrm{even}]={\tilde{p}}_r\left(x\right),\end{array}$$

(24)

$$\begin{array}{c}\hfill \mathrm{where}{P}_{rk}\left(x\right)={\overline{P}}_r^{1-k}{\overline{H}}_{*}^{1-k},{\tilde{p}}_{rk}={\overline{P}}_r^{1-k}{\overline{H}}^{1-k},\end{array}$$

(25)

$$\begin{array}{c}\hfill {\overline{H}}_{*}^{1-k}={\overline{H}}_{*}^{1-k}(x,V)={\overline{O}}^{1-k}{\mathrm{\Phi }}_V\left(x\right)={\int }_{-\infty }^x{\overline{H}}^{1-k}{\varphi }_V\left(x\right)dx,\end{array}$$

(26)

$$\begin{array}{c}\hfill \mathrm{and}{\overline{H}}^{1-k}=H^{i_1\dots i_k}={\overline{H}}^{1-k}(x,V)={\varphi }_V{\left(x\right)}^{-1}{\overline{O}}^{1-k}{\varphi }_V\left(x\right)\end{array}$$

(27)

is the multivariate Hermite polynomial. By [9], for $I=\sqrt{-1}$,

$$\begin{array}{c}{\overline{H}}^{1-k}=E{\Pi }_{j=1}^k({\overline{y}}_j+I{\overline{Y}}_j)\mathrm{for}Y\mathrm{of}\left(12\right),\mathrm{where}{\overline{y}}_j=y_{i_j},y=V^{-1}x,\hfill \end{array}$$

(28)

$$\begin{array}{c}\hfill \mathrm{Thus},{\overline{H}}^1={\overline{y}}_1,{\overline{H}}^{12}={\overline{y}}_1{\overline{y}}_2-{\overline{V}}^{12},\end{array}$$

(29)

$$\begin{array}{c}\hfill {\overline{H}}^{1-3}={\overline{y}}_1{\overline{y}}_2{\overline{y}}_3-\sum ^3{\overline{y}}_1{\overline{V}}^{23},\sum ^3{\overline{y}}_1{\overline{V}}^{23}={\overline{y}}_1{\overline{V}}^{23}+{\overline{y}}_2{\overline{V}}^{13}+{\overline{y}}_3{\overline{V}}^{12},\end{array}$$

(30)

$$\begin{array}{c}\hfill H^{1-4}=y_1\dots y_4-\sum ^6{V}^{12}{y}_3{y}_4+{\mu }^{1-4},\end{array}$$

(31)

$$\begin{array}{c}\hfill H^{1-5}=y_1\dots y_5-\sum ^{10}{V}^{12}{y}_3\dots y_5+\sum ^5{y}_5{\mu }^{1-4},\end{array}$$

(32)

$$\begin{array}{c}\hfill H^{1-6}={\overline{y}}_1\dots {\overline{y}}_6-\sum ^{15}{\overline{y}}_1\dots {\overline{y}}_4{\overline{V}}^{56}+\sum ^{15}{\overline{y}}_1{\overline{y}}_2{\overline{\mu }}^{3-6}-{\overline{\mu }}^{1-6},\end{array}$$

(33)

for ${\overline{\mu }}^{1-2k}$ of (12). These give $p_1\left(x\right)$ and $p_2\left(x\right)$, and so $p_{X_n}\left(x\right)$ of (22) to $O\left(n^{-3/2}\right)$. For ${\overline{H}}^{1-k}$, for $7\le k\le 9$ needed for $p_3\left(x\right)$ when $q=2$, see Appendix B. $P_{rk}\left(x\right)$ is just ${\tilde{p}}_{rk}$ with ${\overline{H}}^{1-k}$ replaced by ${\overline{H}}_{*}^{1-k}$ of (26). For example,

$$\begin{array}{cc}& {\overline{H}}_{*}^1={\overline{J}}^1,{\overline{H}}_{*}^{12}={\overline{J}}^{12}-{\overline{V}}^{12}{\mathrm{\Phi }}_V\left(x\right),{\overline{H}}_{*}^{1-3}={\overline{J}}^{123}-\sum ^3{\overline{J}}^1{\overline{V}}^{23},where\hfill \\ & {\overline{J}}^{1-k}={\overline{J}}^{1-k}(x,V)=E{\overline{Y}}_1\dots {\overline{Y}}_{k}I(X\le x)={\overline{V}}^{1,k+1}\dots {\overline{V}}^{k,2k}{\overline{M}}^{k+1-2k},\hfill \\ & and{\overline{M}}^{a-b}={\overline{M}}^{a-b}(x,V)=E{\overline{X}}_a\dots {\overline{X}}_{b}I(X\le x)={\int }_{-\infty }^x{\overline{x}}_a\dots {\overline{x}}_b{\varphi }_V\left(x\right)dx.\hfill \end{array}$$

I call $\left\{{\overline{M}}^{a-b}(x,V)\right\}$the partial moments of${\mathrm{\Phi }}_V\left(x\right).$

By (22), the Edgeworth expansions to $O\left(n^{-2}\right)$ for the distribution and density of $X_n$ of (10) about those of $X={\mathcal{N}}_q(0,V)$ are given by

$$\begin{array}{c}\begin{array}{c}{P}_1\left(x\right)=e_1(-\partial /\partial x){\mathrm{\Phi }}_V\left(x\right)={\displaystyle \sum _{r=1}^3}{\overline{b}}_{r+1}^{1-r}{\overline{O}}^{1-r}{\mathrm{\Phi }}_V\left(x\right)/r!={\displaystyle \sum _{k=1,3}}{P}_{1k}\left(x\right),\hfill \\ \mathrm{where}{P}_{11}\left(x\right)={\overline{k}}_1^1(-{\overline{\partial }}_1){\mathrm{\Phi }}_V\left(x\right),P_{13}\left(x\right)={\overline{k}}_2^{1-3}{\overline{O}}^{1-3}{\mathrm{\Phi }}_V\left(x\right)/6,\hfill \\ p_1\left(x\right)={\overline{k}}_1^1(-{\overline{\partial }}_1){\varphi }_V\left(x\right)+{\overline{k}}_2^{1-3}{\overline{O}}^{1-3}{\varphi }_V\left(x\right)/6,\hfill \\ {\tilde{p}}_1\left(x\right)=p_1\left(x\right)/{\varphi }_V\left(x\right)={\displaystyle \sum _{k=1,3}}{\tilde{p}}_{1k},{\tilde{p}}_{11}={\overline{k}}_1^1{\overline{H}}^1,{\tilde{p}}_{13}={\overline{k}}_2^{1-3}{\overline{H}}^{1-3}/6,\hfill \end{array}\end{array}$$

(34)

$$\begin{array}{c}\hfill P_2\left(x\right)=\sum _{k=2,4,6}{P}_{2k}\left(x\right),{\tilde{p}}_2\left(x\right)=\sum _{k=2,4,6}{\tilde{p}}_{2k},\end{array}$$

(35)

$$\begin{array}{c}\hfill P_3\left(x\right)=\sum _{k=1,3,5,7,9}{P}_{3k}\left(x\right),{\tilde{p}}_3\left(x\right)=\sum _{k=1,3,5,7,9}{\tilde{p}}_{3k},\end{array}$$

(36)

for ${\tilde{p}}_{rk}$ and $P_{rk}$ of (25). Each has $q^k$ terms, but many are duplicates, as I make ${\overline{P}}_r^{1-k}$ symmetric in $i_1,\dots ,i_k$. Let us call (22) the basic Edgeworth expansions. Typically, $E\widehat{w}$ is a one-to-one function of w. In this case, an alternative is to use the zero-mean Edgeworth expansions, that is, the expansions for

$$\begin{array}{c}\begin{array}{c}{X}_{n0}=n^{1/2}(\widehat{w}-E\widehat{w})=X_n+{\delta }_n,\hfill \\ \mathrm{where}{\delta }_n=n^{1/2}(E\widehat{w}-w)\approx {\displaystyle \sum _{d=1}^{\infty }}{n}^{1/2-d}\left(k_d^i\right),\hfill \end{array}\end{array}$$

(37)

by (9) with $k=1$. That is,

$$\begin{array}{c}\hfill \begin{array}{c}Prob.(X_n\le x)=Prob.(X_{n0}\le x+{\delta }_n),p_{X_n}\left(x\right)=p_{X_{n0}}(x+{\delta }_n),\mathrm{where}\hfill \\ Prob.(X_{n0}\le x)\approx {\displaystyle \sum _{r=0}^{\infty }}{n}^{-r/2}{P}_{r0}\left(x\right),p_{X_{n0}}\left(x\right)\approx {\displaystyle \sum _{r=0}^{\infty }}{n}^{-r/2}{p}_{r0}\left(x\right),x\in R^q,\hfill \\ P_{00}\left(x\right)={\mathrm{\Phi }}_V\left(x\right),p_{00}\left(x\right)={\varphi }_V\left(x\right),\hfill \\ \mathrm{and}\mathrm{for}r\ge 1,P_{r0}\left(x\right)={\displaystyle \sum _{k=1}^{3r}}[P_{rk0}\left(x\right):k-r\mathrm{even}],\hfill \\ p_{r0}\left(x\right)/{\varphi }_V\left(x\right)={\displaystyle \sum _{k=1}^{3r}}[{\tilde{p}}_{rk0}:k-r\mathrm{even}]={\tilde{p}}_{r0}\left(x\right),\hfill \\ P_{rk0}\left(x\right)={\overline{P}}_{r0}^{1-k}{\overline{H}}_{*}^{1-k},{\tilde{p}}_{rk0}={\overline{P}}_{r0}^{1-k}{\overline{H}}^{1-k},\hfill \end{array}\end{array}$$

(38)

and ${\overline{P}}_{r0}^{1-k}$ is the zero-mean Edgeworth coefficient, that is, ${\overline{P}}_r^{1-k}$ with ${\overline{k}}_d^1\equiv 0.$ These are mostly simpler. By (19)–(21),

$$\begin{array}{cc}& {\overline{P}}_{10}^1=0,{\overline{P}}_{10}^{1-3}={\overline{k}}_2^{1-3}/3!,{\overline{P}}_{20}^{12}={\overline{k}}_2^{12}/2,{\overline{P}}_{20}^{1-4}={\overline{k}}_3^{1-4}/4!,\hfill \\ & {\overline{P}}_{20}^{1-6}=\mathcal{S}{\overline{k}}_2^{1-3}{\overline{k}}_2^{4-6}/72,{\overline{P}}_{30}^1=0,{\overline{P}}_{30}^{1-3}={\overline{k}}_3^{1-3}/6,\hfill \\ & {\overline{P}}_{30}^{1-5}={\overline{k}}_4^{1-5}/5!+\mathcal{S}{\overline{k}}_2^{12}{\overline{k}}_2^{3-5}/12,{\overline{P}}_{30}^{1-7}=\mathcal{S}{\overline{k}}_2^{123}{\overline{k}}_3^{4-7}/144,{\overline{P}}_{30}^{1-9}={\overline{P}}_3^{1-9}.\hfill \end{array}$$

The simplest example is when sampling from a distribution $F_0(x-w)$ where $F_0\left(x\right)$ is a known distribution with mean $0\in R^q$; then, the cumulant coefficients do not depend on w apart from the mean.

For the location-scale model when sampling from a distribution $F_0\left(V^{-1/2}(x-w)\right)$, where $F_0\left(x\right)$ is a known distribution with finite moments, mean $0\in R^q$ and covariance $I_q$, if $V=V\left(w\right)$ depends on w, then so do the cumulant coefficients. To make an inference on w, one needs to consider the Studentised statistic. For this and more general models, see [32,33].

Returning to the expansion for the density of $X_n$, the density of $X_n$ relative to its asymptotic value is

$$p_{X_n}\left(x\right)/{\varphi }_V\left(x\right)\approx 1+\sum _{r=1}^{\infty }{n}^{-r/2}{\tilde{p}}_r\left(x\right)=1+n^{-1/2}{\tilde{p}}_1\left(x\right)+O\left(n^{-1}\right)\mathrm{for}x\in R^q,$$

and ${\tilde{p}}_r\left(x\right)$ of (24). Thus, $n^{-1/2}{\tilde{p}}_1\left(x\right)$ is a simple measure of the inaccuracy of the Central Limit Theorem (CLT) approximation.

Example 1.

If the distribution of $\widehat{w}$ is symmetric about w, then, for r odd, $p_r\left(x\right)={\tilde{p}}_r\left(x\right)=P_r\left(x\right)=0$, and by (20), ${\tilde{p}}_{26}\left(x\right)=0$. Thus,

$$\begin{array}{c}\hfill p_{X_n}\left(x\right)/{\varphi }_V\left(x\right)=1+n^{-1}{\tilde{p}}_2\left(x\right)+O\left(n^{-2}\right),\end{array}$$

(39)

$$\begin{array}{c}\hfill \begin{array}{c}where{\tilde{p}}_2\left(x\right)={\tilde{p}}_{22}+{\tilde{p}}_{24},{\tilde{p}}_{22}={\overline{k}}_2^{12}{\overline{H}}^{12}/2,{\tilde{p}}_{24}={\overline{k}}_3^{1-4}{\overline{H}}^{1-4}/24.\hfill \\ Also,Prob.(X_n\le x)={\mathrm{\Phi }}_V\left(x\right)+n^{-1}{P}_2\left(x\right)+O\left(n^{-2}\right),where P_2=P_{22}+P_{24},\hfill \end{array}\end{array}$$

(40)

since ${\overline{P}}_2^{12}={\overline{k}}_2^{12}/2,{\overline{P}}_2^{1-4}={\overline{k}}_3^{1-4}/24.$ In this case, $n^{-1}{\tilde{p}}_2\left(x\right)$ is a measure of the inaccuracy of the CLT approximation. Also,

$$\begin{array}{c}\hfill Prob.(X_n\le x)={\mathrm{\Phi }}_V\left(x\right)+n^{-1}{P}_2\left(x\right)+O\left(n^{-2}\right),where{P}_2=P_{22}+P_{24}.\end{array}$$

(41)

Example 2.

Let $\widehat{w}$ be the sample mean from a distribution with finite cross cumulants ${\overline{\kappa }}^{1-r},r\ge 1$. Then, $E\widehat{w}=w$, and only the leading coefficient in (9) is non-zero. Thus,

$${\overline{k}}_1^1={\overline{k}}_2^{12}={\overline{k}}_2^1={\overline{k}}_3^{123}=0,\mathit{and}{\tilde{p}}_{11}={\tilde{p}}_{22}={\tilde{p}}_{31}={\tilde{p}}_{33}=0.$$

For $r=1,2,3$, the non-zero Edgeworth coefficients $P_r^{1-k}$ are

$$\begin{array}{cc}& {\overline{P}}_{10}^{1-3}={\overline{\kappa }}^{1-3}/3!,{\overline{P}}_{20}^{1-4}={\overline{\kappa }}^{1-4}/4!,{\overline{P}}_{20}^{1-6}=\mathcal{S}{\overline{\kappa }}^{1-3}{\overline{\kappa }}^{4-6}/72,,\hfill \\ & {\overline{P}}_{30}^{1-5}={\overline{\kappa }}^{1-5}/5!,{\overline{P}}_{30}^{1-7}=\mathcal{S}{\overline{\kappa }}^{123}{\overline{\kappa }}^{4-7}/144,{\overline{P}}_{30}^{1-9}=\mathcal{S}{\overline{\kappa }}^{1-3}{\overline{\kappa }}^{4-6}{\overline{\kappa }}^{7-9}/6^4.\hfill \end{array}$$

By (34)–(36), for $1\le r\le 3,P_{r0}\left(x\right)$ and ${\tilde{p}}_{r0}\left(x\right)$ have only r terms. Note that

$${\overline{P}}_{r0}^{1-k}=0\mathit{for}1\le k\le r+1,\mathit{and}{\overline{\kappa }}^{1-k}/k!fork=r+2.$$

Note 2.

For $H_k\left(x\right)$, the univariate Hermite polynomial of (6), and $1\le j\le q$, I define the jth marginal Hermite polynomial as

$$\begin{array}{c}\hfill H^{j^k}=E{(y_j+I{Y}_j)}^k={\tau }_j^k{H}_k\left({\tau }_j^{-1}{y}_j\right)\mathit{where}I=\sqrt{-1},{\tau }_j={\left(V^{jj}\right)}^{1/2}:\end{array}$$

(42)

$$\begin{array}{c}\hfill \begin{array}{c}{H}^j=y_j,H^{j^2}=y_j^2-V^{jj},H^{j^3}=y_j^3-3V^{jj}{y}_j,H^{j^4}=y_j^4-6V^{jj}{y}_j^2+3{\left(V^{jj}\right)}^2.\hfill \\ Thus,ifq=1,H^{1^k}(x,V)={\sigma }^{-k}{H}_k\left(\sigma x\right)=H_k(x,V),where{\sigma }^2=V.\hfill \end{array}\end{array}$$

(43)

Ref. [34] gave explicit expressions for a multivariate version of the Cornish–Fisher expansion when $q=2$. Ref. [35] showed how to extend (4) to the multivariate case by replacing (8) by

$$\begin{array}{cc}& X_n\approx X+\sum _{r=1}^{\infty }{n}^{-r/2}{g}_r\left(X\right).\hfill \end{array}$$

(44)

It would be very useful to obtain these multivariate $g_r\left(X\right)$ explicitly. How does one extend the univariate formula for $g_r\left(x\right)$ in terms of $h_r\left(x\right)$?

Note 3.

Standard estimates have a natural extension to Type b estimates. These are estimates for which the cumulant expansion (9) is replaced by

$${\overline{k}}^{1-r}=k^{i_1\dots i_r}=\kappa ({\widehat{w}}^{i_1},\dots ,{\widehat{w}}^{i_r})\approx \sum _{j=2r-2}^{\infty }{n}^{-j/2}{\overline{b}}_j^{1-r},where{\overline{b}}_j^{1-r}=b_j^{i_1\dots i_r}.$$

Examples are one-sided confidence interval limits. These have the form

$$\widehat{w}\approx \sum _{j=0}^{\infty }{n}^{-j/2}{t}_j\left(\widehat{\theta }\right),$$

where $\widehat{\theta }$is a standard estimate and $t_j$ are smooth functions. See [2] for more details.

3. Secondary or Derived Expansions

Let V have the Hermitian form $H^{\prime }\mathrm{\Lambda }H$, where $H^{\prime }H=I_q$.

$$\mathrm{Set}S=V^{-1/2}=H^{\prime }{\mathrm{\Lambda }}^{-1/2}H\mathrm{and}T=V^{1/2}=H^{\prime }{\mathrm{\Lambda }}^{1/2}H.$$

As in (25)–(27), I use tensor summation and the bar notation, and

$$\begin{array}{cc}& N\sim {\mathcal{N}}_q(0,I_q),X=TN\sim {\mathcal{N}}_q(0,V),Y=V^{-1}X=SN\sim {\mathcal{N}}_q(0,V^{-1}).\hfill \end{array}$$

From the second Edgeworth expansion in (22), it follows that for $C\subset R^q$,

$$\begin{array}{c}\hfill Prob.(X_n\in C)\approx \sum _{r=0}^{\infty }{n}^{-r/2}{P}_r\left(C\right),\mathrm{where}\end{array}$$

(45)

$$\begin{array}{c}\hfill \begin{array}{c}{P}_r\left(C\right)=E{p}_r\left(X\right)I(X\in C)={\int }_C{p}_r\left(x\right){\varphi }_V\left(x\right)dx.\hfill \\ \mathrm{Thus},P_0\left(C\right)=Prob.(X\in C)={\int }_{C}d{\mathrm{\Phi }}_V\left(x\right)={\mathrm{\Phi }}_V\left(C\right),\hfill \end{array}\end{array}$$

(46)

$$\begin{array}{c}\hfill \mathrm{and}\mathrm{for}r\ge 1,P_r\left(C\right)=\sum _{k=1}^{3r}[P_{rk}\left(C\right):k-r\mathrm{even}],\mathrm{where}\end{array}$$

(47)

$$\begin{array}{c}\hfill P_{rk}\left(C\right)=E{\tilde{p}}_{rk}\left(X\right)I(X\in C)={\int }_C{\tilde{p}}_{rk}\left(x\right){\varphi }_V\left(x\right)dx={\overline{P}}_r^{1-k}{\overline{H}}_{*}^{1-k}\left(C\right),\end{array}$$

(48)

$$\begin{array}{c}\hfill \mathrm{and}{\overline{H}}_{*}^{1-k}\left(C\right)=E{\overline{H}}^{1-k}(X,V)I(X\in C)={\int }_C{\overline{H}}^{1-k}{\varphi }_V\left(x\right)dx:\end{array}$$

(49)

$$\begin{array}{c}\hfill \begin{array}{c}{P}_1\left(C\right)=P_{11}\left(C\right)+P_{13}\left(C\right),P_{r1}\left(C\right)={\overline{P}}_r^1{\overline{H}}_{*}^1\left(C\right),P_{r3}\left(C\right)={\overline{P}}_r^{1-3}{\overline{H}}_{*}^{1-3}\left(C\right),\hfill \\ P_2\left(C\right)={\displaystyle \sum _{k=2,4,6}}{P}_{2k}\left(C\right),\mathrm{where}{P}_{r2}\left(C\right)={\overline{P}}_r^{12}{\overline{H}}_{*}^{12}\left(C\right),\hfill \\ P_{r4}\left(C\right)={\overline{P}}_r^{1-4}{\overline{H}}_{*}^{1-4}\left(C\right),P_{r6}\left(C\right)={\overline{P}}_r^{1-6}{\overline{H}}_{*}^{1-6}\left(C\right).\hfill \end{array}\end{array}$$

(50)

As ${\overline{H}}^{1-k}$ is a linear combination of ${\overline{y}}_1\dots {\overline{y}}_s$, we can write ${\overline{H}}_{*}^{1-k}\left(C\right)$ in terms of

$$\begin{array}{c}\hfill {\overline{m}}^{1-s}=E{\overline{Y}}_1\dots {\overline{Y}}_{s}I(VY\in C)={\int }_C{\overline{y}}_1\dots {\overline{y}}_s{\varphi }_V\left(x\right)dx:\end{array}$$

(51)

$$\begin{array}{c}\hfill \begin{array}{c}{\overline{H}}_{*}^1\left(C\right)={\overline{m}}^1,{\overline{H}}_{*}^{12}\left(C\right)={\overline{m}}^{12}-{\mathrm{\Phi }}_V\left(C\right){\overline{V}}^{12},{\overline{H}}_{*}^{1-3}\left(C\right)={\overline{m}}^{1-3}-{\displaystyle \sum ^3}{\overline{m}}^1{\overline{V}}^{23},\hfill \\ {\overline{H}}_{*}^{1-4}\left(C\right)={\overline{m}}^{1-4}-{\displaystyle \sum ^6}{\overline{m}}^{12}{\overline{V}}^{34}+{\mathrm{\Phi }}_V\left(C\right){\overline{\mu }}^{1-4},\hfill \\ {\overline{H}}_{*}^{1-6}\left(C\right)={\overline{m}}^{1-6}-{\displaystyle \sum ^{15}}{\overline{m}}^{1-4}{\overline{V}}^{56}+{\displaystyle \sum ^{15}}{\overline{m}}^{12}{\overline{\mu }}^{3-6}-{\mathrm{\Phi }}_V\left(C\right){\overline{\mu }}^{1-6}.\hfill \end{array}\end{array}$$

This gives $P_1\left(C\right)$ and $P_2\left(C\right)$ of (45). Therefore, it gives $Prob.(X_n\in C)$ to $O\left(n^{-3/2}\right)$. For $\widehat{w}$ a sample mean, $P_{22}\left(C\right)=0$, and for $k=4,6,$ the ${\overline{P}}_2^{1-k}$ needed for $P_{2k}\left(C\right)$ are given by Example 2.

If $-C=C$, then for r odd, ${\overline{m}}^{1-r}=P_{rk}\left(C\right)=P_r\left(C\right)=0,$ so that

$$\begin{array}{cc}& Prob.(X_n\in C)\approx \sum _{r=0}^{\infty }{n}^{-r}{P}_{2r}\left(C\right)={\mathrm{\Phi }}_V\left(C\right)+n^{-1}{P}_2\left(C\right)+O\left(n^{-2}\right).\hfill \end{array}$$

(52)

I now consider three such C’s.

Example 3.

Ellipsoidal C. Take $C=\{x:x^{\prime }{V}^{-1}x\le u\}$ for some $u>0$.

$$Then,-C=C,{\mathrm{\Phi }}_V\left(C\right)=Prob.(N^{\prime }N<u)=Prob.({\chi }_q^2<u).$$

(We might choose u such that ${\mathrm{\Phi }}_V\left(C\right)=0.5$ or $0.9$.) ${\overline{m}}^{1-s}$ of (51) is given by

$$\begin{array}{c}\hfill {\overline{m}}^{1-s}=E{\overline{Y}}_1\dots {\overline{Y}}_{s}I(N^{\prime }N<u)={\overline{S}}_{1,k+1}\dots {\overline{S}}_{k,2k}{\overline{R}}^{k+1-2k},\end{array}$$

(53)

$$\begin{array}{c}\hfill \mathit{where}{\overline{R}}^{1-k}=E{\overline{N}}_1\dots {\overline{N}}_{k}I(N^{\prime }N<u).\end{array}$$

(54)

$$\begin{array}{c}\hfill Thus,R^{12}=0,R^{11}=E{Z}_{1}I(Z_1+Z_2<u)=R_2,where\end{array}$$

(55)

$$\begin{array}{c}\hfill Z_1=N_1^2\sim {\chi }_1^2,Z_2=N^{\prime }N-N_1^2\sim {\chi }_{q-1}^{2}areindependent.Thus,\end{array}$$

(56)

$$\begin{array}{c}\hfill {\overline{m}}^{12}=R^{11}{\overline{S}}_1^{12},where{\overline{S}}_1^{12}=\sum _{i_3,i_4}{\overline{S}}_{13}{\overline{S}}_{24}I(i_3=i_4)=\sum _{i_3=1}^q{\overline{S}}_{13}{\overline{S}}_{23}={\overline{V}}^{12}.\end{array}$$

(57)

$$\begin{array}{c}\hfill Thus,by\left(50\right),P_{r2}\left(C\right)=(R_2-{\mathrm{\Phi }}_V\left(C\right)){\overline{P}}_r^{12}{\overline{V}}^{12}.\end{array}$$

(58)

Similarly, ${\overline{R}}^{1-k}=0$ unless k is even and $\{i_1,\dots ,i_k\}=\{1^{J_1},\dots ,q^{J_q}\}$, where $J_1,\dots ,J_q$ are even integers and $j^k$ is a string of j’s of length k.

• For $Z_1,Z_2$ of (56), set

$$\begin{array}{cc}& R_{2k}=E{N}_1^{2k}I(N^{\prime }N<u)=E{Z}_1^{k}I(Z_1+Z_2<u).\hfill \\ & \mathrm{Set}{R}_{2k_1,2k_2}=E{N}_1^{2k_1}{N}_2^{2k_2}I(N^{\prime }N<u)=E{Z}_1^{k_1}{Z}_2^{k_2}I(Z_1+Z_2+Z_3<u),\hfill \end{array}$$

where now, for $Z_1=N_1^2,Z_2=N_2^2$ and $Z_3=N^{\prime }N-Z_1-Z_2\sim {\chi }_{q-2}^2,$ so that $Z_1,Z_2,Z_3$ are independent. Set

$$\begin{array}{c}{I}_1=I(i_5=i_6\ne i_7=i_8)+I(i_5=i_7\ne i_6=i_8)+I(i_5=i_8\ne i_6=i_7).\mathit{Then},\hfill \\ {\overline{m}}^{1-4}=\sum _{i_5,\dots ,i_8}{\overline{S}}_{15}\dots {\overline{S}}_{48}[R_{4}I(i_5=\dots =i_8)+R_{22}{I}_1]=R_4{\overline{S}}_1^{1-4}+R_{22}{\overline{S}}_2^{1-4},\hfill \\ where{\overline{S}}_1^{1-k}=\sum _{j=1}^q{S}_{i_{1}j}\dots S_{i_{k}j},{\overline{S}}_2^{1-4}={\overline{S}}^{12:34}+{\overline{S}}^{13:24}+{\overline{S}}^{14:23},\hfill \\ and{\overline{S}}^{12:34}=\sum _{j\ne k}{S}_{i_{1}j}{S}_{i_{2}j}{S}_{i_{3}k}{S}_{i_{4}k}={\overline{V}}^{12}{\overline{V}}^{34}-{\overline{S}}_1^{1-4}by\left(57\right).\hfill \\ Thus,{\overline{S}}_2^{1-4}={\overline{\mu }}^{1-4}-3{\overline{S}}_1^{1-4},\hfill \\ {\overline{m}}^{1-4}={\overline{S}}_1^{1-4}{r}_4+{\overline{\mu }}^{1-4}{R}_{22},\mathit{where}{r}_4=R_4-3R_{22},\hfill \end{array}$$

(59)

$$\begin{array}{c}\hfill P_{r4}\left(C\right)={\overline{P}}_r^{1-4}[{\overline{S}}_1^{1-4}{r}_4+3{\overline{V}}^{12}{\overline{V}}^{34}{r}_5],where{r}_5=R_{22}-2R_2+{\mathrm{\Phi }}_V\left(C\right).\end{array}$$

(60)

Similarly, using ${\sum }_{j,k,l}^{\prime }$ to mean a sum over distinct $j,k,l$,

$$\begin{array}{c}\hfill \begin{array}{c}{\overline{m}}^{1-6}={\overline{S}}_{17}\dots {\overline{S}}_{6,12}[R_{6}I(i_7=\dots =i_{12})+R_{42}{I}_2+R_{222}{I}_3],\hfill \\ where{R}_{222}=E{N}_1^2{N}_2^2{N}_3^{2}I(N^{\prime }N<u),I_2={\displaystyle \sum ^{15}}{\overline{S}}^{1-4:56},I_3={\displaystyle \sum ^{90}}{\overline{S}}^{12:34:56},\hfill \\ {\overline{S}}^{1-4:56}={\displaystyle \sum _{j\ne k}}{S}_{i_{1}j}\dots S_{i_{4}j}{S}_{i_{5}k}{S}_{i_{6}k},{\overline{S}}^{12:34:56}={\displaystyle \sum _{j,k,l}^{\prime }}{S}_{i_{1}j}{S}_{i_{2}j}{S}_{i_{3}k}{S}_{i_{4}k}{S}_{i_{5}l}{S}_{i_{6}l}.\hfill \\ Thus,{\overline{P}}_r^{1-6}{\overline{m}}^{1-6}={\overline{P}}_r^{1-6}[{\overline{S}}_1^{1-6}{R}_6+15{\overline{S}}^{1-4:56}{R}_{42}+90{\overline{S}}^{12:34:56}{R}_{222}],\hfill \\ P_{r6}\left(C\right)={\overline{P}}_r^{1-6}[{\overline{m}}^{1-6}-15{\overline{m}}^{1-4}{\overline{V}}^{56}+15{\overline{m}}^{12}{\overline{\mu }}^{3-6}-{\mathrm{\Phi }}_V\left(C\right){\overline{\mu }}^{1-6}]\hfill \\ ={\overline{P}}_r^{1-6}[{\overline{S}}_1^{1-6}{R}_6+15{\overline{S}}^{1-4:56}{R}_{42}+90{\overline{S}}^{12:34:56}{R}_{222}-15{\overline{S}}_1^{1-4}{\overline{V}}^{56}{r}_4\hfill \\ +3{\overline{V}}^{12}{\overline{V}}^{34}{\overline{V}}^{56}{r}_6],where{r}_6=-15R_{42}+15R_2-{\mathrm{\Phi }}_V\left(C\right).\hfill \end{array}\end{array}$$

(61)

$P_2\left(C\right)$ of (52) is now given by (58), (60) and (61). Note that

$$\begin{array}{cc}& {\overline{V}}^{12}{\overline{V}}^{34}{\overline{V}}^{56}={\overline{S}}_1^{1-6}+\sum ^3{\overline{S}}_1^{1-4:56}+{\overline{S}}_1^{12:34:56}.\hfill \end{array}$$

We can write $R_{2k_1,\dots }$ in terms of $F_k\left(u\right)=Prob.({\chi }_k^2\le u):$

$$\begin{array}{cc}& R_{2k}=E{Z}_1^k{F}_{q-1}(u-Z_1)={\int }_0^u{z}_1^k{F}_{q-1}(u-z_1)d{F}_1\left(z_1\right)=G_{q-1}(u:k),\hfill \\ & R_{2k_1,2k_2}=E{Z}_2^{k_2}{G}_{q-2}(u-Z_2:k_1)={\int }_0^u{z}_2^{k_2}{G}_{q-2}(u-z_2:k_1)d{F}_1\left(z_2\right)\hfill \\ & =G_{q-2}(u:k_1{k}_2),\hfill \\ & R_{222}=E{Z}_3{G}_{q-3}(u-Z_3:11)={\int }_0^u{z}_3{G}_{q-3}(u-z_3:11)d{F}_1\left(z_3\right).\hfill \end{array}$$

For $X,X_n$ of (10), set

$$Q=X^{\prime }{V}^{-1}X\sim {\chi }_q^2,Q_n=X_n^{\prime }{V}^{-1}{X}_n,{\widehat{Q}}_n=X_n^{\prime }{\widehat{V}}^{-1}{X}_n=n{(\widehat{w}-w)}^{\prime }{\widehat{V}}^{-1}(\widehat{w}-w),$$

where $\widehat{V}$ is an estimate $\widehat{V}$ (empirical, semi-parametric, or parametric depending on the model used). Therefore,

$$Prob.(Q_n\le u)=Prob.({\chi }_q^2\le u)+n^{-1}{P}_2\left(C\right)+O\left(n^{-2}\right)=1-\alpha +O\left(n^{-1}\right)\mathrm{if}u={\chi }_{q,1-\alpha }^2,$$

the $1-\alpha$ quantile of ${\chi }_q^2$. It is often true that

$$Prob.({\widehat{Q}}_n\le u)=Prob.({\chi }_q^2\le u)+O\left(n^{-1}\right).$$

(An exact confidence region for w is only possible if $\widehat{w}$ is normal: see 5.3.2 of [36].) ${\chi }_q^2/q=G_{\gamma }/\gamma$, where $\gamma =q/2$, and $G_{\gamma }$ is a gamma random variable with mean γ. Thus, if $q=2$,

$${\mathrm{\Phi }}_V\left(C\right)=Prob.(G_1<u/2)=1-e^{-u/2}=1-\alpha \mathit{if}0<u=-2ln\alpha ,$$

$Q_n<-2ln\alpha$ with probability $1-\alpha +O\left(n^{-1}\right)$, and typically,

$${\widehat{Q}}_n\le -2ln\alpha withprobability1-\alpha +O\left(n^{-1}\right).$$

By way of illustration, Figure 1 plots the elliptical contours $x=X_n$ when $Q_n=-2ln\alpha$, for $1-\alpha =0.5,0.9,0.99,$ when

$$\begin{array}{cc}& V=\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right),V^{-1}=\left(\begin{array}{cc}2& -1\\ -1& 2\end{array}\right)/3.\hfill \end{array}$$

(62)

Therefore, the asymptotic correlation of ${\widehat{w}}_1$ and ${\widehat{w}}_2$ is 1/2.

One can do similarly for $q>2$, using ${\chi }_{q,1-\alpha }^2$ and two-dimensional slices of these ellipsoids. For related references on confidence regions, see [10].

The R functions. If$q=1,$then $R_{2k_1,2k_2}=R_{222}=0$ for $k_2>0$, and

$$R_{2k}=2g_{2k}\left(u^{1/2}\right),where{g}_k\left(u\right)=E{N}^{k}I(0<N<u)={\int }_0^u{n}^k\varphi \left(n\right)dn$$

is given in Example 4 using a recurrence formula. (A simpler way is to just use (7).)

Now take $q=2$.  Then,

$$\begin{array}{c}\hfill \begin{array}{c}{R}_{2k_1,2k_2}=4E{N}_1^{2k_1}{N}_2^{2k_2}I(N_1^2+N_2^2<u,N_1>0,N_2>0),\hfill \\ =4g_{2k_1,2k_2}\left(u^{1/2}\right)\mathit{where}{g}_{k_1{k}_2}\left(v\right)={\int }_0^{v}d{n}_1\varphi \left(n_1\right)n_1^{k_1}{g}_{k_2}\left({(v^2-n_1^2)}^{1/2}\right).\hfill \end{array}\end{array}$$

(63)

To obtain a recurrence formula for $g_{k_1{k}_2}=g_{k_1{k}_2}\left(v\right)$, set

$$\begin{array}{cc}& f_k\left(u\right)=g_k\left(u^{1/2}\right),A=\varphi \left(n_1\right)n_1^{k_1-1}{f}_{k_2}(v^2-n_1^2).\hfill \\ & Then,g_{k_1{k}_2}=-{\int }_0^{v}Ad\varphi \left(n_1\right)={\left[A\right]}_v^0+{\overline{g}}_{k_{1}2k_2},\mathit{where}\hfill \\ & {\overline{g}}_{k_{1}2k_2}={\int }_0^v\varphi \left(n_1\right)dA=(k_1-1)A_1+A_2,\hfill \\ & A_1={\int }_0^{v}d{n}_1\varphi \left(n_1\right)n_1^{k_1-2}{f}_{k_2}(v^2-n_1^2)=g_{k_1-2,k_2},\hfill \\ & A_2={\int }_0^{v}d{n}_1\varphi \left(n_1\right)n_1^{k_1-1}(-2n_1){\dot{f}}_{k_2}(v^2-n_1^2),{\dot{f}}_k\left(u\right)=d{f}_k\left(u\right)/du.\hfill \\ & f_k\left(v^2\right)=g_k\left(v\right)\Rightarrow 2v{\dot{f}}_{k_2}\left(v^2\right)={\dot{g}}_k\left(v\right)=v^k\varphi \left(v\right).\hfill \\ & Thus,{\dot{f}}_{k_2}(v^2-n_1^2)={\left[x^{k-1}\varphi \left(x\right)\right]}_{x=v^2-n_1^2}={(v^2-n_1^2)}^{(k-1)/2}\varphi \left(v\right)e^{n_1^2/2}.\hfill \\ & Thus,A_2=-\varphi \left(0\right)\varphi \left(v\right)A_3,wherefor{B}_{12}=B(k_1+1)/2,k_2+1)/2),\hfill \\ & A_3={\int }_0^{v}d{n}_1{n}_1^{k_1}{v^2-n_1^2}^{(k_2-1)/2}=v^{k_1+k_2}{B}_{12}/2.\hfill \\ & Thus,A_2=-\varphi \left(0\right)\varphi \left(v\right)v^{k_1+k_2}{B}_{12}/2=-A_{k_1{k}_2}.\hfill \\ & Thus,for{k}_1\ge 1,g_{k_1{k}_2}=(k_1-1)g_{k_1-2,k_2}+G_{k_1{k}_2},\hfill \\ & \mathit{where}{G}_{k_1{k}_2}=I(k_1=1)g_{k_2}\left(v\right)+A_{k_1{k}_2}.\hfill \end{array}$$

(64)

This recurrence formula for $g_{k_1{k}_2}$ of (63) gives

$$\begin{array}{cc}& R_{22}=4g_{22}\left(u^{1/2}\right)\mathit{where}{g}_{22}\left(v\right)=g_{22}=g_{02}+A_{22},\hfill \\ & and{A}_{22}=v^4{e}^{-v^2}/32\mathrm{as}{B}_{12}=\pi /8,\hfill \\ & R_{42}=4g_{42}\left(u^{1/2}\right)\mathit{where}{g}_{42}\left(v\right)=g_{42}=g_{02}+A_{42},\hfill \\ & and{A}_{42}=v^6{e}^{-v^2}/64\mathit{as}{B}_{12}=\pi /16.\hfill \end{array}$$

Therefore, we need $g_{02}$. By Example 4,

$$g_2\left(u\right)={\mathrm{\Phi }}_0\left(u\right)-u\varphi \left(u\right),where{\mathrm{\Phi }}_0\left(u\right)=\mathrm{\Phi }\left(u\right)-1/2.$$

Transforming to $u^2=v^2-n_1^2,$

$$\begin{array}{cc}& g_{02}={\int }_0^{v}d{n}_1\varphi \left(n_1\right)g_2\left(u\right)=e^{v^2/2}(A-B),\hfill \\ & \mathit{where}A={\int }_0^v{(v^2-u^2)}^{1/2}{\mathrm{\Phi }}_0\left(u\right)u\varphi \left(u\right)du,\hfill \end{array}$$

$$\begin{array}{cc}& B=\varphi \left(0\right){\int }_0^v{u}^2{(v^2-u^2)}^{1/2}\varphi \left(u\right)du={\left(2\pi \right)}^{-1}{v}^{2}I(-v^2),\hfill \\ & andI\left(t\right)={\int }_0^1{x}^{1/2}{(1-x)}^{-1/2}{e}^{tx}dx=\sum _{i=0}^{\infty }B(i+3/2,1/2)t^i/i!.\hfill \\ & B(i+3/2,1/2)={\pi }^{1/2}\mathrm{\Gamma }(i+3/2)/i!.\hfill \\ & \mathrm{\Gamma }(i+3/2)=\mathrm{\Gamma }(3/2){[3/2]}_i,where{\left[t\right]}_i=t(t+1)\dots (t+i-1).\hfill \\ & SoB={(v^2/8)}_1{F}_1(3/2,1:-v^2)\hfill \end{array}$$

where ${}_{1}F_1(3/2,1:t)$ is the confluent or degenerate hypergeometric function: see Section 9.21 of [37] and p. 504 of [38].

Now, suppose that $q>2$.Then,

$$\begin{array}{cc}& R_{2k_1,2k_2}=4E{N}_1^{2k_1}{N}_2^{2k_2}I(N_1^2+N_2^2<u-Z,N_1>0,N_2>0)\hfill \\ & =4E{g}_{2k_1,2k_2}\left({(u-Z)}^{1/2}\right),whereZ=\sum _{i=3}^q\sim {\chi }_{q-2}^2,\hfill \\ & and{R}_{222}=8E{N}_1^2{N}_2^2{N}_3^{2}I(N^{\prime }N<u,N_1>0,N_2>0,N_3>0)\hfill \\ & =8E{N}_3^2{R}_{22}(u-N_3^2-Z)I(N_3>0)\hfill \end{array}$$

where $R_{22}\left(u\right)=R_{22}$ of (63), and $Z={\sum }_{i=4}^q{N}_i^2\sim {\chi }_{q-3}^2$ is independent of $N_3$.

By Theorem 2.2 of [10], for $r\ge 1,$

$$\begin{array}{cc}& P_r\left(C\right)=\sum _{j=1}^{3r}{b}_{2r,j}{(U-1)}^j{F}_q\left(x\right),where{F}_q\left(x\right)=Prob.({\chi }_q^2<x),U^j{F}_q\left(x\right)=F_{q+2j}\left(x\right),\hfill \\ \hfill & b_{2r,j}={\overline{b}}_{2r}^{1-2j}{\overline{\mu }}^{1-2j},{\overline{\mu }}^{1-2j}=E{\overline{X}}_1\dots {\overline{X}}_{2j}.\hfill \\ & Forexample,P_r\left(C\right)isgivenby{b}_{21}=({\overline{k}}_2^{12}+{\overline{k}}_1^1{\overline{k}}_1^2){\overline{V}}^{12},\hfill \\ & b_{22}={\overline{k}}_3^{1-4}{\overline{V}}^{12}{\overline{V}}^{34}/4+{\overline{k}}_1^1{\overline{k}}_2^{34}{\overline{V}}^{12}{\overline{V}}^{34},\hfill \\ \hfill & b_{23}={\overline{k}}_2^{123}{\overline{k}}_2^{456}({\overline{V}}^{12}{\overline{V}}^{34}{\overline{V}}^{56}/4+{\overline{V}}^{14}{\overline{V}}^{25}{\overline{V}}^{36}/6).\hfill \end{array}$$

Its extension to ${\widehat{Q}}_n$ is given in Section 3 of [10] for parametric and non-parametric models.

Example 4.

Take $C=\{x:|{\left(V^{-1/2}x\right)}_j|\le u_j,j=1,\dots ,q\}$.

• Thus, $-C=C$. For $Y=V^{-1/2}N$ and $N\sim {\mathcal{N}}_q(0,I_q)$,

$${\mathrm{\Phi }}_V\left(C\right)={\Pi }_{j=1}^q{G}_0\left(u_j\right),where{G}_0\left(u\right)=Prob.\left(\right|N_1|<u)=2\mathrm{\Phi }\left(u\right)-1.$$

(We might choose $u_j\equiv u$ such that ${\mathrm{\Phi }}_V\left(C\right)=0.5$ or $0.9$.) For $S=V^{-1/2}$,

$$\begin{array}{cc}& {\overline{m}}^{1-k}=E{\overline{Y}}_1\dots {\overline{Y}}_k{I\left(\right|N|}_j<u_j,j=1,\dots ,q)={\overline{S}}_{1,k+1}\dots {\overline{S}}_{k,2k}{\overline{R}}^{k+1-2k},\hfill \\ & wherenow,{\overline{R}}^{1-k}=E{\overline{N}}_1\dots {\overline{N}}_k{I\left(\right|N|}_j<u_j,j=1,\dots ,q).\hfill \\ & \mathit{Set}{R}_{2k_1,\dots ,2k_s}=E{N}_1^{2k_1}\dots N_s^{2k_s}{I\left(\right|N|}_j<u_j,j=1,\dots ,q)\hfill \\ & =\left[{\Pi }_{j=1}^s{G}_{k_j}\left(u_j\right)\right]\left[{\Pi }_{j=s+1}^q{G}_0\left(u_j\right)\right],where\hfill \\ & G_k\left(u\right)=E{N}_1^{2k}I\left(\right|N_1|<u)=2g_{2k}\left(u\right),where\hfill \\ & g_k\left(u\right)=g_k={\int }_0^u{n}^k\varphi \left(n\right)dn=-{\int }_0^u{n}^{k-1}d\varphi \left(n\right)={\left[n^{k-1}\varphi \left(n\right)\right]}_u^0+(k-1)g_{k-2}:\hfill \\ & g_0=\mathrm{\Phi }\left(u\right)-1/2,g_1=\varphi \left(0\right)-\varphi \left(u\right),g_2=g_0-u\varphi \left(u\right),\hfill \\ & g_3=2\varphi \left(0\right)-(u^2+2)\varphi \left(u\right),g_4=3g_0-(u^3+3u)\varphi \left(u\right),\hfill \\ & g_5=2.4\varphi \left(0\right)-(u^4+4u^2+4.2)\varphi \left(u\right),g_6=3.5g_0-(u^5+5u^3+5.3u)\varphi \left(u\right),\hfill \\ & g_7=2.4.6\varphi \left(0\right)-(u^6+6u^4+66.4u^2+6.4.2)\varphi \left(u\right),\hfill \\ & g_8=3.5.7g_0-(u^7+7u^5+7.5u^3+7.5.3u)\varphi \left(u\right).\hfill \\ & As{R}^{12}=0,{\overline{m}}^{12}={\overline{V}}^{12}{R}_{2}by\left(\mathit{57}\right),where{R}_{2k}=2^q{g}_{2k}\left(u_1\right){\Pi }_{j=2}^q{g}_0\left(u_j\right).\hfill \\ & \mathit{Set}{R}_{2k_1,2k_2}=2^q\left[{\Pi }_{j=1}^2{g}_{2k_j}\left(u_j\right)\right]\left[{\Pi }_{j=3}^q{g}_0\left(u_j\right)\right],\hfill \\ & R_{2k_1,2k_2,2k_3}=2^q\left[{\Pi }_{j=1}^3{g}_{2k_j}\left(u_j\right)\right]\left[{\Pi }_{j=4}^q{g}_0\left(u_j\right)\right],\hfill \end{array}$$

Thus, now, ${\overline{m}}^{1-4}$ is given by (59) and (60) in terms of these new $R_{2k_1,\dots }$. Similarly, ${\overline{m}}^{1-6}$ and $P_{rk}\left(C\right)$ are given by Example 3 with these new $R_{2k_1,\dots }$. Therefore, we now have $P_2\left(C\right)$ of (52). If we choose $u_j\equiv u$, then

$$\begin{array}{cc}& R_{2k}=2^q{g}_{2k}{g}_0^{q-1},R_{2k_1,2k_2}=2^q\left[{\Pi }_{j=1}^2{g}_{2k_j}\right]g_0^{q-2},\hfill \\ & R_{2k_1,2k_2,2k_3}=2^q\left[{\Pi }_{j=1}^3{g}_{2k_j}\right]g_0^{q-3}.\hfill \end{array}$$

Example 5.

Take $C=\{x:|x_j|\le u_j,j=1,\dots ,q\}$. Thus, $-C=C$. This choice gives a set of q simultaneous intervals. For $Y=SN$ and $T=V^{1/2}$

$$\begin{array}{cc}& {\mathrm{\Phi }}_V\left(C\right)={Prob.\left(\right|\left(VY\right)}_j|<u_j{,j=1,\dots ,q)=Prob.(|\left(TN\right)}_j|<u_j,j=1,\dots ,q),\hfill \\ & {\overline{m}}^{1-k}=E{\overline{Y}}_1\dots {\overline{Y}}_k{I\left(\right|\left(VY\right)}_j|<u_j,j=1,\dots ,q)={\overline{S}}_{1,k+1}\dots {\overline{S}}_{k,2k}{\overline{R}}^{k+1-2k},\hfill \\ & wherenow,{\overline{R}}^{1-k}=E{\overline{N}}_1\dots {\overline{N}}_k{I\left(\right|\left(TN\right)}_j|<u_j,j=1,\dots ,q).\hfill \end{array}$$

Thus, ${\overline{R}}^{1\dots k}=0$ for k odd. ($R^{12}$ is no longer zero.) But each of those non-zero terms requires q numerical integrations. Consider the case $q=2$.

$$\begin{array}{cc}& I\left(\right|X_j|<u_j,j=1,2)=I(X_j<u_j,j=1,2)-I(X_1<-u_1,X_2<u_2)\hfill \\ & -I(X_1<u_1,X_2<-u_2)+I(X_1<-u_1,X_2<-u_2)\Rightarrow \hfill \\ & R^{jk}=F_{jk}(u_1,u_2)-F_{jk}(u_1,-u_2)-F_{jk}(-u_1,u_2)+F_{jk}(-u_1,-u_2),\hfill \\ & where{F}_{jk}(u_1,u_2)=E{N}_j{N}_{k}I(X_1<u_1,X_2<u_2)\hfill \\ & =\int d{n}_1\int d{n}_2\varphi \left(n_1\right)\varphi \left(n_2\right)I(\sum _{k=1}^2{T}_{jk}{n}_k<u_j,j=1,2).\hfill \end{array}$$

For more on these types of expansions and their inverses, see [13] and their simplifications given in Sections 4 and 5 of [16]. However, in these papers, the need to express results in terms of $S=V^{-1/2}$ did not arise. See also [39]. For the case of a sample mean with estimated covariance, it is possible to avoid the use of $S=V^{-1/2}$; see [40].

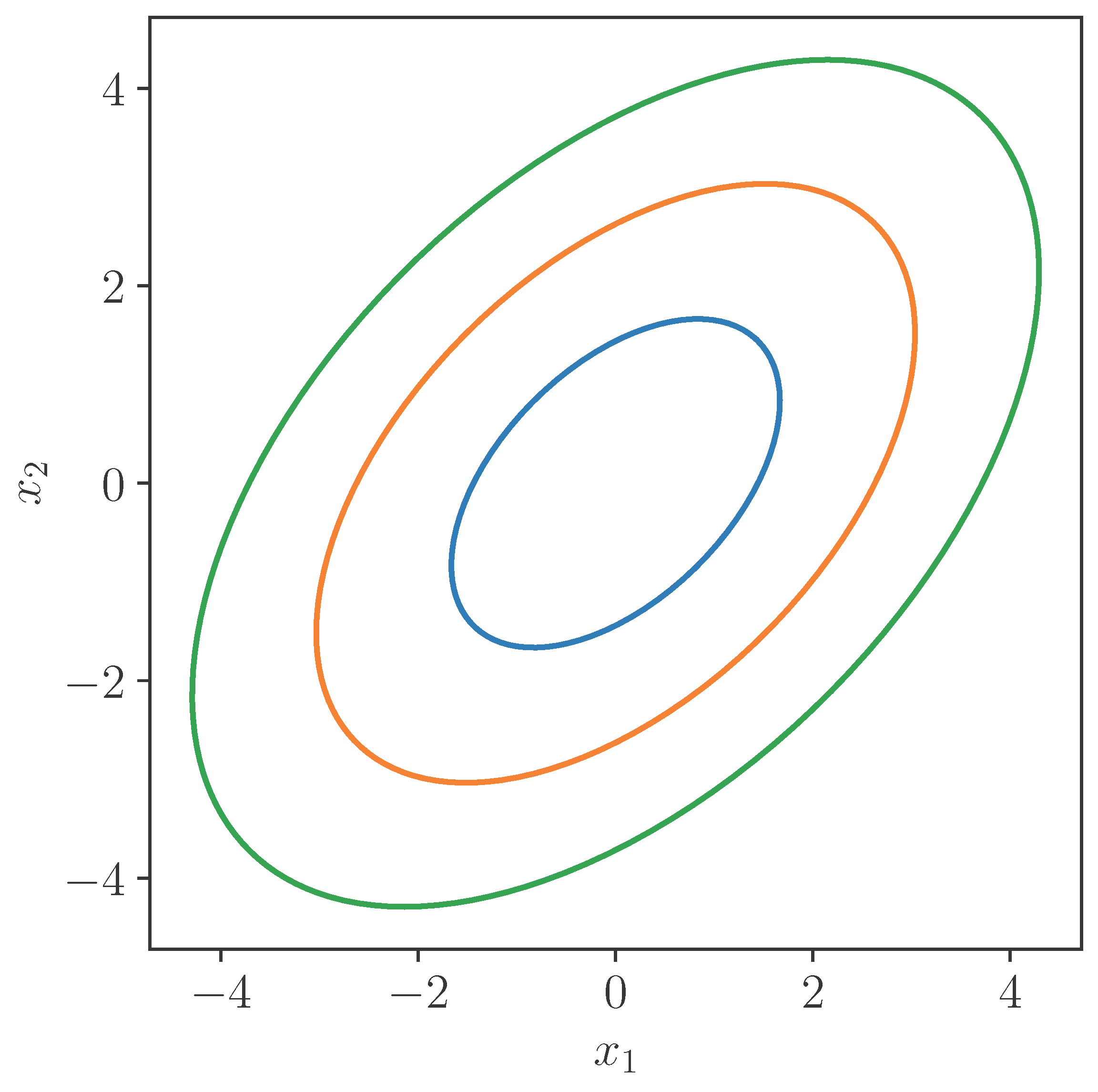
4. The Distribution of X_n = n^1/2($\widehat{\mathbf{w}}-\mathbf{w}$) for q = 2

As above, we set $y=V^{-1}x,Y=V^{-1}X\sim {\mathcal{N}}_q(0,V^{-1})$. Taking $q=2$, we switch notation to

$$\begin{array}{c}\hfill {\mu }_{ab}={\mu }^{1^a{2}^b}=E{Y}_1^a{Y}_2^b,\mathrm{so}\mathrm{that}{\mu }_{20}=V^{11},{\mu }_{11}=V^{12},\end{array}$$

(65)

$$\begin{array}{c}\hfill H_{ab}=H_{ab}\left(x\right)=H^{1^a{2}^b}=E{(y_1+I{Y}_1)}^a{(y_2+I{Y}_2)}^b\mathrm{for}I=\sqrt{-1}.\end{array}$$

(66)

Thus, $H_{k0}$ and $H_{0k}$ are given by (42) with $j=1$ and 2: $H_{10}=y_1,H_{01}=y_2,$

$$\begin{array}{cc}& H_{11}=y_1{y}_2-{\mu }_{11},H_{21}=y_1^2{y}_2-{\mu }_{20}{y}_2-2{\mu }_{11}{y}_1,H_{12}=y_1{y}_2^2-{\mu }_{02}{y}_1-2{\mu }_{11}{y}_2,\hfill \end{array}$$

and so on. The ${\mu }_{ab}$ and $H_{ab}$ needed here are given in Appendix B. Let us write the cumulant expansion (9) as

$$\begin{array}{cc}& {\kappa }_{ab}({\widehat{w}}_1,{\widehat{w}}_2)\approx \sum _{d=a+b-1}^{\infty }{n}^{-d}{k}_{abd}\mathrm{for}a+b\ge 1,\mathrm{where}{k}_{abd}=k_d^{1^a{2}^b}.\hfill \end{array}$$

(67)

Thus $k_{100}=w_1,k_{010}=w_2.$ The density of $X_n=n^{1/2}(\widehat{w}-w)$, $p_{X_n}\left(x\right)$, is given by (22) and (25) in terms of ${\tilde{p}}_r\left(x\right)$ and ${\tilde{p}}_{rk}$ of (25). As ${\overline{P}}_r^{1-k}$ is symmetric,

$$\begin{array}{cc}& {\tilde{p}}_{rk}=\sum _{b=0}^k{P}_r(k-b,b)H_{k-b,b},where{P}_r\left(ab\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{a+b}{a}}\right)P_r^{1^a{2}^b},\hfill \end{array}$$

(68)

for ${\overline{P}}_r^{1-k}$ of (19)–(21). Therefore, $P_r\left(ba\right)$ is just $P_r\left(ab\right)$ with 1 and 2 reversed.

$$\begin{array}{cc}& \mathrm{Set}\sum ^2{P}_r\left(ab\right)H_{ab}=P_r\left(ab\right)H_{ab}+P_r\left(ba\right)H_{ba}.\hfill \end{array}$$

Then, ${\tilde{p}}_r\left(x\right)$ is given for $r=1,2,3$ by (34)–(36) in terms of

$$\begin{array}{cc}& {\tilde{p}}_{r1}=\sum ^2{P}_r\left(10\right)H_{10},{\tilde{p}}_{r3}=\sum ^2[P_r\left(30\right)H_{30}+P_r\left(21\right)H_{21}],rodd,\hfill \\ & {\tilde{p}}_{22}=\sum ^2{P}_2\left(20\right)H_{20}+P_2\left(11\right)H_{11},\hfill \\ & {\tilde{p}}_{24}=\sum ^2[P_2\left(40\right)H_{40}+P_2\left(31\right)H_{31}]+P_2\left(22\right)H_{22},\hfill \\ & {\tilde{p}}_{26}=\sum ^2[P_2\left(60\right)H_{60}+P_2\left(51\right)H_{51}+P_2\left(42\right)H_{42}]+P_2\left(33\right)H_{33},\hfill \\ & {\tilde{p}}_{35}=\sum ^2[P_3\left(50\right)H_{50}+P_3\left(41\right)H_{41}+P_3\left(32\right)H_{32}],\hfill \\ & {\tilde{p}}_{37}=\sum ^2[P_3\left(70\right)H_{70}+P_3\left(61\right)H_{61}+P_3\left(52\right)H_{52}+P_3\left(43\right)H_{43}],\hfill \\ & {\tilde{p}}_{39}=\sum ^2[P_3\left(90\right)H_{90}+P_3\left(81\right)H_{81}+P_3\left(72\right)H_{72}+P_3\left(63\right)H_{63}+P_3\left(54\right)H_{54}].\hfill \end{array}$$

(69)

The $P_r\left(ab\right)$ needed in (68) for ${\tilde{p}}_{rk},r\le 3,$ are as follows, in terms of $k_{abd}$ of (67):

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{For}{\tilde{p}}_{11},P_1\left(10\right)=k_{101},(\mathrm{so}{P}_1\left(01\right)=k_{011}).\hfill \\ \mathrm{For}{\tilde{p}}_{13},P_1\left(30\right)=k_{302}/6,(\mathrm{so}{P}_1\left(03\right)=k_{032}/6,)P_1\left(21\right)=k_{212}/2.\hfill \\ \mathrm{For}{\tilde{p}}_{22},P_2\left(20\right)=k_{202}/2+k_{101}^2/2,P_2\left(11\right)=k_{112}+k_{101}{k}_{011}.\hfill \\ \mathrm{For}{\tilde{p}}_{24},P_2\left(40\right)=k_{403}/24+k_{101}{k}_{302}/6,P_2\left(31\right)=k_{313}/6+k_{101}{k}_{212}/2\hfill \\ +k_{011}{k}_{302}/6,P_2\left(22\right)=k_{223}/4+k_{011}{k}_{212}/2+k_{101}{k}_{122}/2.\hfill \\ \mathrm{For}{\tilde{p}}_{26},P_2\left(60\right)=k_{302}^2/72,P_2\left(51\right)=k_{302}{k}_{212}/12,\hfill \\ P_2\left(42\right)=k_{302}{k}_{122}/12+k_{212}^2/8,P_2\left(33\right)=k_{302}{k}_{032}/36+k_{212}{k}_{122}/4,\hfill \\ \mathrm{For}{\tilde{p}}_{31},P_3\left(10\right)=k_{102}.\mathrm{For}{\tilde{p}}_{33},P_3\left(30\right)=k_{303}/6+k_{202}{k}_{101}/2+k_{101}^3/6,\hfill \\ P_3\left(21\right)=k_{213}/2+k_{101}{k}_{112}+k_{011}{k}_{202}/2+k_{101}^2{k}_{011}/2.\hfill \\ \mathrm{For}{\tilde{p}}_{35},P_3\left(50\right)=k_{504}/120+k_{403}{k}_{101}/24+k_{302}[k_{202}+k_{101}^2]/12,\hfill \\ P_3\left(41\right)/5=P_3^{1^{4}2}=k_{414}/120+S_1/24+S_2/12+S_3/12,\mathrm{where}\hfill \\ S_1=(4k_{101}{k}_{313}+k_{011}{k}_{403})/5,S_2=(7k_{202}{k}_{212}+3k_{112}{k}_{302})/10,\hfill \\ S_3=(3k_{101}{k}_{011}{k}_{302}+7k_{101}^2{k}_{212})/10,\hfill \\ P_3\left(32\right)=10P_3^{11122}=k_{324}/12+S_1/24+S_2/12+S_3/12,\mathrm{where}\hfill \\ S_1=(3k_{101}{k}_{223}+2k_{011}{k}_{313})/5,S_2=(3k_{202}{k}_{122}+k_{022}{k}_{302}+6k_{112}{k}_{212})/10,\hfill \\ S_3=(3k_{101}^2{k}_{122}{k}_{302}+k_{011}^2{k}_{302}+6k_{101}{k}_{011}{k}_{212})/10.\hfill \\ \mathrm{For}{\tilde{p}}_{37},P_3\left(70\right)=k_{403}{k}_{302}/144+k_{302}^2{k}_{101}/72,\hfill \\ P_3\left(61\right)=k_{212}{k}_{403}/48+k_{302}{k}_{313}/36+k_{011}{k}_{302}^2/72+k_{101}{k}_{302}{k}_{212}/12.\hfill \\ P_3\left(52\right)=k_{403}{k}_{122}/48+k_{313}{k}_{212}/12+k_{223}{k}_{302}/24+k_{302}{k}_{212}{k}_{011}/12\hfill \\ +k_{101}(2k_{302}{k}_{122}+3k_{212}^2)/24,\hfill \\ P_3\left(43\right)=35P_3^{1^4{2}^3}=A/144+B/72\mathrm{for}A=k_{403}{k}_{032}+12k_{313}{k}_{122}+18k_{223}{k}_{212}\hfill \\ +4k_{133}{k}_{302},B=2k_{101}(k_{302}{k}_{032}+9k_{212}{k}_{122})+3k_{011}(2k_{302}{k}_{122}+3k_{212}^2).\hfill \\ \mathrm{For}{\tilde{p}}_{39},P_3\left(90\right)=k_{302}^3/6^4,P_3\left(81\right)=k_{302}^2{k}_{212}/144,\hfill \\ \mathrm{and}{P}_3\left(72\right)=k_{302}(k_{302}{k}_{122}+3k_{212}^2)/144,\hfill \\ P_3\left(63\right)=(3k_{302}^2{k}_{032}+16k_{302}{k}_{212}{k}_{122}+9k_{212}^3)/432,\hfill \\ P_3\left(54\right)=(2k_{212}{k}_{302}{k}_{032}+3k_{122}^2{k}_{302}+9k_{212}^2{k}_{122})/144.\hfill \end{array}\end{array}$$

(70)

Equations (22) and (25) now give the density of $X_n=n^{1/2}(\widehat{w}-w)$ to $O\left(n^{-2}\right)$.

$$\begin{array}{cc}& \mathrm{Set}{H}_{ab}^{*}={(-{\partial }_1)}^a{(-{\partial }_2)}^b{\mathrm{\Phi }}_V\left(x\right)={\int }_{-\infty }^x{H}_{ab}{\varphi }_V\left(x\right)dx.\hfill \\ & \mathrm{Thus},H_{ab}^{*}=H_{a-1,b-1}{\varphi }_V\left(x\right)\mathrm{if}a\ge 2,b\ge 1,\hfill \\ & H_{10}^{*}={\int }_{-\infty }^{x_2}{\varphi }_V\left(x\right)d{x}_2={\partial }_1{\mathrm{\Phi }}_V\left(x\right),H_{a0}^{*}={(-{\partial }_1)}^{a-1}{H}_{10}^{*}\mathrm{if}a\ge 2,\hfill \\ & H_{01}^{*}={\int }_{-\infty }^{x_1}{\varphi }_V\left(x\right)d{x}_1={\partial }_2{\mathrm{\Phi }}_V\left(x\right),H_{0b}^{*}={(-{\partial }_2)}^{b-1}{H}_{01}^{*}\mathrm{if}b\ge 1.\hfill \end{array}$$

(71)

The distribution of $X_n=n^{1/2}(\widehat{w}-w)$ is given by (22) and (26) in terms of $P_{rk}\left(x\right)$. $P_{rk}\left(x\right)$ is just the ${\tilde{p}}_{rk}$ above with $H_{ab}$ replaced by $H_{ab}^{*}$ of (71). That is,

$$\begin{array}{cc}& P_{rk}\left(x\right)=\sum _{b=0}^k{P}_r(k-b,b)H_{k-b,b}^{*}.\hfill \end{array}$$

(72)

Equations (22) and (26) now give $Prob.(X_n\le x)$ to $O\left(n^{-2}\right)$ for $X_n=n^{1/2}(\widehat{w}-w)$. For example, for $x={(1,1)}^{\prime }$ and $x={(2,2)}^{\prime }$, the values of $H_{ab}$ are given in Example A1.

By (45), $P(X_n\in C)$ is given to $O(n^{-2}$ by $P_r\left(C\right),r=1,2,3$, of (45) and (52). These are given by replacing ${\tilde{p}}_{rk},H_{ab}$ above by $P_{rk}\left(C\right)$ of (48) and the $H_{abC}=H^{1^a{2}^b}\left(C\right)$ of (49).

By Section 3, for $Y\sim {\mathcal{N}}_2(0,V^{-1}),$ and ${\mu }_{ab}=E{Y}_1^a{Y}_2^b$, $m_{ab}=E{Y}_1^a{Y}_2^{b}I(VY\in C)$ is given by

$$\begin{array}{cc}& H_{10C}=m_{10},H_{20C}=m_{20}-{\mathrm{\Phi }}_V\left(C\right){\mu }_{20},H_{11C}=m_{11}-{\mathrm{\Phi }}_V\left(C\right){\mu }_{11},\hfill \\ & H_{30C}=m_{30}-3m_{10}{\mu }_{20},H_{21C}=m_{21}-2m_{10}{\mu }_{11}-m_{01}{\mu }_{20},\hfill \\ & H_{40C}=m_{40}-6m_{20}{\mu }_{20}+{\mathrm{\Phi }}_V\left(C\right){\mu }_{40},\hfill \\ & H_{31C}=m_{31}-3m_{20}{\mu }_{11}-3m_{11}{\mu }_{20}+{\mathrm{\Phi }}_V\left(C\right){\mu }_{31},\hfill \\ & H_{22C}=m_{22}-m_{20}{\mu }_{02}-m_{02}{\mu }_{20}-4m_{11}{\mu }_{11}+{\mathrm{\Phi }}_V\left(C\right){\mu }_{22},\hfill \\ & H_{60C}=m_{60}-15m_{40}{\mu }_{20}+15m_{20}{\mu }_{40}-{\mathrm{\Phi }}_V\left(C\right){\mu }_{60},\hfill \\ & H_{51C}=m_{51}-10m_{31}{\mu }_{20}+5m_{11}{\mu }_{40}-5m_{40}{\mu }_{11}+10m_{20}{\mu }_{31}{\mathrm{\Phi }}_V\left(C\right){\mu }_{51},\hfill \\ & H_{42C}=m_{42}-6m_{22}{\mu }_{20}+m_{02}{\mu }_{40}-8m_{31}{\mu }_{11}+8m_{11}{\mu }_{31}-m_{40}{\mu }_{02}+6m_{20}{\mu }_{22}\hfill \\ & -{\mathrm{\Phi }}_V\left(C\right){\mu }_{42},\hfill \\ & H_{33C}=m_{33}+3\sum ^2(m_{20}{\mu }_{13}-m_{13}{\mu }_{20})-9m_{22}{\mu }_{11}+9m_{11}{\mu }_{22}-{\mathrm{\Phi }}_V\left(C\right){\mu }_{33}.\hfill \end{array}$$

These expressions can be read off those for $H_{ab}$ in Appendix B. If $-C=C$, then $0=m_{ab}=H_{abC}$ for $a+b$ odd. For Examples 3 and 4, $m_{11}={\mu }_{11}{R}_2,$ and $P_{r2}\left(C\right)$ of (48) is given by (58) in terms of ${\overline{P}}_r^{12}{\overline{V}}^{12}={\sum }^2{P}_r\left(20\right){\mu }_{20}+2P_r\left(11\right){\mu }_{11}$. For $r=2$, this is given by (70).

Example 6.

Let $\widehat{w}$ be a sample mean of a distribution with cumulants ${\kappa }_{ab}$. By Example 2, for $\left(rk\right)=\left(11\right),\left(22\right),\left(31\right),\left(33\right),$ $P_{rk}={\tilde{p}}_{rk}=0$, and we need the following Edgeworth coefficients.

$$\begin{array}{cc}& For{\tilde{p}}_{13}\mathit{and}{P}_{13}\left(x\right):P_1\left(30\right)={\kappa }_{30}/3!,P_1\left(21\right)={\kappa }_{21}/2,P_1\left(12\right)={\kappa }_{12}/2.\hfill \\ & For{\tilde{p}}_{24},P_{24}\left(x\right):P_2\left(40\right)={\kappa }_{40}/4!,P_2\left(31\right)={\kappa }_{31}/6,P_2\left(22\right)={\kappa }_{22}/4.\hfill \\ & For{\tilde{p}}_{26},P_{26}\left(x\right):P_2\left(60\right)={\kappa }_{30}^2/72,P_2\left(51\right)={\kappa }_{30}{\kappa }_{21}/12,\hfill \\ & P_2\left(42\right)=(2{\kappa }_{30}{\kappa }_{12}+3{\kappa }_{21}^2)/24,P_2\left(33\right)=({\kappa }_{30}{\kappa }_{03}+9{\kappa }_{21}{\kappa }_{12})/36.\hfill \\ & For{\tilde{p}}_{35},P_{35}\left(x\right):P_3\left(50\right)={\kappa }_{50}/5!,P_3\left(41\right)={\kappa }_{41}/4!,P_3\left(32\right)={\kappa }_{32}/12.\hfill \\ & For{\tilde{p}}_{37},P_{37}\left(x\right):P_3\left(70\right)={\kappa }_{40}{\kappa }_{30}/144,P_3\left(61\right)={\kappa }_{21}{\kappa }_{40}/48+{\kappa }_{30}{\kappa }_{31}/36,\hfill \\ & P_3\left(52\right)={\kappa }_{40}{\kappa }_{12}/48+{\kappa }_{31}{\kappa }_{21}/12+{\kappa }_{22}{\kappa }_{30}/24,\hfill \\ & P_3\left(43\right)=A/144\mathit{for}A={\kappa }_{40}{\kappa }_{03}+12{\kappa }_{31}{\kappa }_{12}+18{\kappa }_{22}{\kappa }_{21}+4{\kappa }_{13}{\kappa }_{30}.\hfill \end{array}$$

$$\begin{array}{cc}& For{\tilde{p}}_{39},P_{39}\left(x\right):P_3\left(90\right)={\kappa }_{30}^3/6^4,P_3\left(81\right)={\kappa }_{30}^2{\kappa }_{21}/144,\hfill \\ & P_3\left(72\right)={\kappa }_{30}({\kappa }_{30}{\kappa }_{12}+3{\kappa }_{21}^2)/144,P_3\left(63\right)=(3{\kappa }_{30}^2{\kappa }_{03}+16{\kappa }_{30}{\kappa }_{21}{\kappa }_{12}\hfill \\ & +9{\kappa }_{21}^3)/432,P_3\left(54\right)=(2{\kappa }_{21}{\kappa }_{30}{\kappa }_{03}+3{\kappa }_{12}^2{\kappa }_{30}+9{\kappa }_{21}^2{\kappa }_{12})/144.\hfill \end{array}$$

For $a<b,P_r\left(ab\right)$ is $P_r\left(ba\right)$ with superscripts one and two reversed. The $P_2\left(ab\right)$ needed for $P_2\left(C\right)$ of (45) and (52) are those given above for ${\tilde{p}}_{24},{\tilde{p}}_{26}$.

For a specific case of a bivariate sample mean, consider the following.

Example 7.

An  entangled gamma  model. Let $G_0,G_1,G_2$ be independent gamma random variables with means $\gamma ={\gamma }_0,{\gamma }_1,{\gamma }_2$. For $i=1,2$, set $X_i=G_0+G_i,w_i=E{X}_i={\gamma }_0+{\gamma }_i$, and let $\widehat{w}$ be the mean of a random sample of size n distributed as $X={(X_1,X_2)}^{\prime }$. Thus, $E\widehat{w}=w,$ and $n\widehat{w}\stackrel{\mathcal{L}}{=}{(G_{n0}+G_{n1},G_{n0}+G_{n2})}^{\prime }$, where $G_{n0},G_{n1},G_{n2}$ are independent gamma random variables with means $n{\gamma }_0,n{\gamma }_1,n{\gamma }_2$. The rth order cumulants of X are ${\kappa }^{i^r}=(r-1)!w_i,$ and otherwise, $(r-1)!{\gamma }_0$. For example, ${\kappa }_{20}={\kappa }^{11}=w_1,{\kappa }_{02}={\kappa }^{22}=w_2,{\kappa }_{11}={\kappa }^{12}={\gamma }_0,{\kappa }_{30}=2w_1,{\kappa }_{03}=2w_2,{\kappa }_{21}={\kappa }^{112}={\kappa }_{12}={\kappa }^{122}=2!{\gamma }_0$, and

$$\begin{array}{cc}& V=\left(\begin{array}{cc}{w}_1& {\gamma }_0\\ {\gamma }_0& w_2\end{array}\right),V^{-1}=\left(\begin{array}{cc}{w}_2& -{\gamma }_0\\ -{\gamma }_0& w_1\end{array}\right)/D\mathit{where}D=detV=w_1{w}_2-{\gamma }_0^2.\hfill \end{array}$$

Thus, $y=V^{-1}x={(w_2{x}_1-{\gamma }_0{x}_2,-{\gamma }_0{x}_1+w_1{x}_2)}^{\prime }/D.$ Set ${\nu }_i=w_i/{\gamma }_0.$ Then, V has correlation ${\left({\nu }_1{\nu }_2\right)}^{-1/2}$. This ranges from 0 at ${\gamma }_0=0$ to 1 at ${\gamma }_0=\infty .$ Thus, ${\widehat{w}}_1$ and ${\widehat{w}}_2$ are positively entangled. (For a negatively entangled example, replace $G_{n0}+G_{n2}$ by $-G_{n0}+G_{n2}$: the correlation is then $-{\left({\nu }_1{\nu }_2\right)}^{-1/2}$. An extension to $R^q$ is $n{\widehat{w}}_i={\lambda }_i{G}_{n0}+G_{ni},i=1,\dots q.$) For $c=0,1,\dots ,$ set

$$\sum ^2{w}_1^c{H}_{ab}=w_1^c{H}_{ab}+w_2^c{H}_{ba}.$$

By Example 6, for $r\le 3,\left\{{\tilde{p}}_{rk}\right\}$ are given by the equations following (69) in terms of

$$\begin{array}{cc}& P_1\left(10\right)=0,P_1\left(30\right)=w_1/3,(so{P}_1\left(01\right)=0,P_1\left(03\right)=w_2/3,)P_1\left(21\right)={\gamma }_0,\hfill \\ & P_2\left(20\right)=P_2\left(11\right)=0,P_2\left(40\right)=w_1/4,P_2\left(31\right)={\gamma }_0,P_2\left(22\right)=3{\gamma }_0/2,\hfill \\ & P_2\left(60\right)=w_1^2/18,P_2\left(51\right)=w_1{\gamma }_0/3,P_2\left(42\right)=w_1{\gamma }_0/3+{\gamma }_0^2/2,\hfill \\ & P_2\left(33\right)=w_1{w}_2/9+{\gamma }_0^2,P_3\left(10\right)=P_3\left(30\right)=P_3\left(21\right)=0,P_3\left(50\right)=w_1/5,\hfill \\ & P_3\left(41\right)={\gamma }_0,P_3\left(32\right)=2{\gamma }_0,P_3\left(70\right)=w_1^2/12,P_3\left(61\right)=7{\gamma }_0{w}_1/12,\hfill \\ & P_3\left(52\right)=(3{\gamma }_0{w}_1+4{\gamma }_0^2)/4,P_3\left(43\right)=(w_1{w}_2+4{\gamma }_0{w}_1+30{\gamma }_0^2)/12,\hfill \\ & P_3\left(90\right)=w_1^3/162,P_3\left(81\right)=w_1^2{\gamma }_0/18,P_3\left(72\right)={\gamma }_0{w}_1(w_1+3{\gamma }_0)/18,\hfill \\ & P_3\left(63\right)=(3w_1^2{w}_2+16w_1{\gamma }_0^2+9{\gamma }_0^3)/54,P_3\left(54\right)=(2{\gamma }_0{w}_1{w}_2+3{\gamma }_0^2{w}_1+9{\gamma }_0^3)/18.\hfill \end{array}$$

Now, consider the  entangled exponential  case ${\gamma }_i\equiv 1$. Thus, $w_i\equiv 2,$ V and $V^{-1}$ are given by (62),

$$\begin{array}{cc}& P_1\left(30\right)=2/3,P_1\left(21\right)=1,P_2\left(40\right)=1/2,P_2\left(31\right)=1,P_2\left(22\right)=3/2,\hfill \\ & P_2\left(60\right)=2/9,P_2\left(51\right)=2/3,P_2\left(42\right)=7/6,P_2\left(33\right)=13/9,P_3\left(50\right)=2/5,\hfill \\ & P_3\left(41\right)=1,P_3\left(32\right)=2,P_3\left(70\right)=1/3,P_3\left(61\right)=7/6,P_3\left(52\right)=5/2,\hfill \\ & P_3\left(43\right)=13/3,P_3\left(90\right)=4/81,P_3\left(81\right)=2/9,P_3\left(72\right)=5/9,P_3\left(63\right)=54/54,\hfill \\ & P_3\left(54\right)=23/18.\hfill \end{array}$$

For $x={(1,1)}^{\prime }$ and $x={(2,2)}^{\prime }$, the values of $H_{ab}$ are given in Example A1, and by symmetry, ${\sum }^2$ can be replaced by 2 in (69) and the other equations for ${\tilde{p}}_{rk}$.

Thus, if $x={(1,1)}^{\prime }$, then $y={(1,1)}^{\prime }/3,{\tilde{p}}_1\left(x\right)=-62/81\approx -0.7654,$ so that our measure of the inaccuracy of the CLT is $n^{-1/2}{\tilde{p}}_1\left(x\right)=-31/81\approx -0.3827$ for $n=4$ and $-62/3^5\approx -0.2551$

$$\begin{array}{cc}& For x={(1,1)}^{\prime },{\tilde{p}}_{24}=7/18\approx 0.3889,{\tilde{p}}_{26}=-697/3^8\approx -0.1062,\hfill \\ & {\tilde{p}}_2\left(x\right)=3709/\left(23^8\right)\approx 0.2827,{\tilde{p}}_{35}=1594/\left(53^5\right)\approx 1.3119,\hfill \\ & {\tilde{p}}_{37}=16330/3^7\approx 7.4669,{\tilde{p}}_{39}=-3508524/3^{12}\approx -6.6019,\hfill \\ & {\tilde{p}}_3\left(x\right)=5784408/\left(53^{12}\right)\approx 2.1769,\hfill \\ & so{p}_{X_n}\left(x\right)/{\varphi }_V\left(x\right)\approx 1-0.7654n^{-1/2}+0.2827n^{-1}+2.1769n^{-3/2}+O\left(n^{-2}\right)\hfill \\ & \approx 1-0.1914+0.0177+0.0340ifn=16 sothat only three terms can be used,\hfill \\ & \approx 1-0.0957+0.0044+0.0043 ifn=64.\hfill \end{array}$$

If $x={(2,2)}^{\prime }$, then $y={(2,2)}^{\prime }/3,{\tilde{p}}_1\left(x\right)=-64/81\approx -0.7901$, and our measure of the inaccuracy of the CLT is $n^{-1/2}{\tilde{p}}_1\left(x\right)=-32/81\approx -0.395$ for $n=4$, and $-16/81\approx -0.197$ for $n=16$.

$$\begin{array}{cc}& \mathit{For}x={(2,2)}^{\prime },{\tilde{p}}_{24}=-7/9\approx -0.7778,{\tilde{p}}_{26}=9380/3^8\approx 1.4251,\hfill \\ & {\tilde{p}}_2\left(x\right)=4247/3^8\approx ,0.6473\hfill \\ & {\tilde{p}}_{35}=608/\left(53^7\right)\approx 0.05560,{\tilde{p}}_{37}=22096/3^8\approx 3.3678,\hfill \\ & {\tilde{p}}_{39}=-12331328/3^{13}\approx -7.7345,{\tilde{p}}_3\left(x\right)\approx -4.3111,\hfill \\ & so{p}_{X_n}\left(x\right)/{\varphi }_V\left(x\right)\approx 1-0.7901n^{-1/2}+0.6473n^{-1}-4.3111n^{-3/2}+O\left(n^{-2}\right)\hfill \\ & \approx 1-0.1975+0.0040-0.0067ifn=16.\hfill \end{array}$$

Example 8.

As in Example 1, suppose that the distribution of $\widehat{w}$ is symmetric about w. By (40),

$$\begin{array}{cc}& 2{\tilde{p}}_{22}=k_2^{11}{H}_{20}+2k_2^{12}{H}_{11}+k_2^{22}{H}_{02},\hfill \\ & 24{\tilde{p}}_{24}=k_3^{1111}{H}_{40}+4k_3^{1112}{H}_{31}+6k_3^{1122}{H}_{22}+4k_3^{1222}{H}_{13}+k_3^{2222}{H}_{04},\hfill \end{array}$$

and $P_{2k}\left(x\right)$ needed for (41) is ${\tilde{p}}_{2k}$ with $H_{ab}$ replaced by $H_{ab}^{*}$ of (71). Now, suppose that $\widehat{w}={\widehat{W}}_1-{\widehat{W}}_2$, where ${\widehat{W}}_1$ and ${\widehat{W}}_2$ are independent copies of a random vector $\widehat{W}.$ Then, the cumulants of $\widehat{w}$ of odd order are zero, and the cumulants of even order are twice those of $\widehat{W}.$

Consider the case $\widehat{W}=\widehat{w}$, the bivariate entangled gamma of Example 7. Thus, $w={(0,0)}^{\prime }$, the odd cumulants of $\widehat{w}$ are zero, and the odd ${\tilde{p}}_r\left(x\right),P_r\left(x\right)$ are zero. Denote $V,x,y,X,Y$ of Example 4 as $V_0,x_0,y_0,X_0,Y_0$. Then,

$$\begin{array}{cc}& V=2V_0,X=2^{1/2}{X}_0,Y=2^{-1/2}{Y}_0,\hfill \\ & H_{ab}=2^{-(a+b)/2}{H}_{ab}(x_0,V_0)\mathit{where}x=2^{1/2}{x}_0,y=2^{-1/2}{y}_0.\hfill \end{array}$$

By Example 2, ${\tilde{p}}_{22}=0,P_2\left(40\right)=k_3^{1^4}/24,P_2\left(31\right)={\kappa }_{40}/6,P_2\left(22\right)={\kappa }_{22}/4$, where ${\kappa }_{40}=12({\gamma }_1+{\gamma }_3),{\kappa }_{31}={\kappa }_{22}=12{\gamma }_3.$

$$\begin{array}{cc}& So,{\tilde{p}}_2\left(x\right)=\sum ^2[({\gamma }_1+{\gamma }_3)H_{40}+4{\gamma }_3{H}_{31}]+6{\gamma }_3{H}_{22}.\hfill \end{array}$$

Now, consider the exponential case ${\gamma }_i\equiv 1$. Thus,

$$\begin{array}{cc}& {\tilde{p}}_2\left(x\right)={\tilde{p}}_{24}=\sum ^2[H_{40}+2H_{31}]+2H_{22}\hfill \\ & =7/9\approx 0.778\mathrm{if}x=(1,1)or-14/9\approx -1.556\mathrm{if}x=(2,2).\hfill \end{array}$$

Thus, for $n=16,n^{-1}{\tilde{p}}_2\left(x\right)\approx 0.049\mathrm{if}x=(1,1),or-0.194\mathrm{if}x=(2,2).$ Here, I used the values of $H_{ab}$ given in the example of [41].

5. Conclusions

Most estimates of interest are standard estimates, including functions of sample moments, like the sample correlation, and any smooth multivariate function of Fisher’s k-statistics; see [5] for these. In Section 2, I gave the density and distribution of $X_n=n^{1/2}(\widehat{w}-w)$ to $O\left(n^{-2}\right)$, for $\widehat{w}$ any standard estimate, in terms of functions of the cumulants coefficients ${\overline{k}}_j^{1-r}$ of (9), the coefficients ${\overline{P}}_r^{1-k}$ of (18)–(21). Section 3 gave explicit detail when $q=2$ using the alternative notation $P_r\left(ab\right)$. Section 3 gave as examples Edgeworth expansions for the probability of $X_n$ lying in an ellipsoidal or hyperrectangular set.

6. Discussion

A good approximation for the distribution of an estimate is vital for accurate inference. It enables one to explore the distribution’s dependence on underlying parameters. Equation (22) gives expansions in powers of $n^{-1/2}$, for the distribution and density of a multivariate standard estimate, in terms of the Edgeworth coefficients ${\overline{P}}_r^{1-k}$ of (18). As noted at the end of Sections 1 and 5 of [35], the Cornish–Fisher expansions (4) are valid under the usual conditions for validity of the Edgeworth expansion (2), and their Section 5 appears to show that this is also true for the multivariate case. Appendix C shows for the first time how to find the extended Edgeworth expansions of (22) on a rigorous basis. Examples of standard estimates are moment estimates and maximum likelihood estimates. The underlying cumulant coefficients will be functions of the parameters of the model on which $\widehat{w}$ is based. For $\widehat{w}$ a k-statistic or a polynomial in k-statistics, the cumulant coefficients are polynomials in the cumulants of the sample.

The analytic results given here avoid the need for simulation, jack-knife or bootstrap methods while providing greater accuracy than them. Ref. [42] used the Edgeworth expansion to show that the bootstrap gives accuracy to $O\left(n^{-1}\right)$. Ref. [43] said that “2nd order correctness usually cannot be bettered”. But this is not true using these analytic results. Simulation, while popular, can at best shine a light on behaviour when there is only a small number of parameters.

Estimates based on a sample of independent but not identically distributed random vectors, are also generally standard estimates. For example, for a univariate sample mean $\overline{w}=n^{-1}{\sum }_{j=1}^n{X}_{jn}$, where $X_{jn}$ has an rth cumulant ${\kappa }_{rjn}$, ${\kappa }_r\left(\overline{w}\right)=n^{1-r}{\kappa }_r$, where ${\kappa }_r=n^{-1}{\sum }_{j=1}^n{\kappa }_{rjn}$ is the average rth cumulant. For some examples, see [2,44,45,46]. The latter is for a function of a weighted mean of complex random matrices. It gives an application in electrical engineering of channel capacity for multiple arrays.

Estimates based on a stationary sample can also be standard estimates. See [47].

For conditions for the validity of multivariate Edgeworth expansions, see [30] and its references.

Refs. [3,8] did not deal with the question of when these expansions diverged. I showed how to confront this in the numerical examples in Example 7 and [4].

Lastly, I discuss numerical computation. I have used [41] for the numerical calculations in Example 7. One could also download R-4.4.1 for Windows and google the routines needed. dmvnorm computes the density function of the multivariate normal specified by the mean and co-variance matrix. Use mvtnorm for the multivariate normal. See also qmvnorm for quantiles. rmvnorm generates multivariate normal variables. Googling “bivariate hermite polynomials r” gives https://cran.r-project.org/web/packages/calculus/vignettes/hermite.html (accessed on 25 June 2025). One can then use install.packages(“calculus”). However, I have not used this route.

Some future directions.

• Ref. [13] showed how to generalise the expansions of Cornish and Fisher about $N(0,1)$ to expansions about an arbitrary continuous distribution. Their results are cumbersome as they involve partition theory. In [16], I overcame this using Bell polynomials. It would be straightforward to apply these to expansions about ${\chi }_q^2$ in Example 3 to obtain the percentiles of $n{(\widehat{w}-w)}^{\prime }{V}^{-1}(\widehat{w}-w)$ and $n{(\widehat{w}-w)}^{\prime }{\widehat{V}}^{-1}(\widehat{w}-w)$. However, in the latter case, we first need to derive the cumulant coefficients of ${\widehat{V}}^{-1/2}(\widehat{w}-w)$ from those of $\widehat{w}$. This can be done by applying [1].
• It would very useful to obtain the multivariate $g_r\left(X\right)$ of (44) explicitly.
• The multivariate expansions considered here have been about the multivariate normal. However, as noted at the end of Section 1, expansions about other distributions can greatly reduce the number of terms in each $P_r\left(x\right),{\tilde{p}}_r\left(x\right)$ and $P_r\left(C\right)$ by matching bias and/or skewness. While this was derived for $q=1$ by Withers and [10,14,15] about Student’s distribution, the F-distribution and the gamma distribution, to date, this has yet to be derived for multivariate expansions about, for example, a multivariate gamma distribution.
• The results given here are the first step for constructing confidence intervals and confidence regions. To do this one estimates the cumulant coefficients. See [32,33,48] for the case $q=1$.
• The results here can be extended to tilted (saddle-point) expansions by applying the results of [2]. These are very useful where convergence fails, that is, where the CLT cannot be improved upon, typically due to $\widehat{w}$ being in a tail. The tilted version of the multivariate distribution and density of a standard estimate are given by Corollaries 3 and 4 there. Tilting was first used in statistics by [27]. He gave an approximation to the density of a sample mean. See also [49]. Ref. [7] gave a univariate extension to $S_N$ where $S_N$ was the sum of N independent and identically distributed observations, and N was Poisson. The extension of the present results from ${\widehat{w}}_n=\widehat{w}$ to ${\widehat{w}}_N$ would be useful for both univariate and multivariate observations. For a review of references on tilting, see [2].
• Ref. [41] wrote a python program to obtain both analytic and numerical values of multivariate normal moments and multivariate Hermite polynomials when $q=2$. It would be useful to have these extended to $q=3$ and 4. (The alternative notation for ${\overline{\mu }}^{1-k}$ and ${\overline{H}}^{1-k}$ when $q=3$ or 4 is straightforward.)
• The end of Appendix C suggests a way of giving more theorems for Edgeworth expansions.