Fixed-Point Theorems in Branciari Distance Spaces

Abstract

In this study, the concepts of $\sigma$-Caristi maps and generalized $\sigma$-contraction maps are introduced, and fixed-point theorems for such maps are established. A generalization of Caristi’s fixed-point theorem and Banach’s contraction principle is proved. The relationships among the various contraction conditions introduced in this paper are examined. Examples are provided to elucidate the main theorem, and applications to integral and differential equations are also discussed.

1. Introduction

In 1922, Banach [1] proved a famous fixed-point theorem, which is called the Banach contraction principle. Since then, this contraction principle has played an important role in mathematical analysis and applied mathematical analysis, and many authors have proposed generalizations and extensions of the Banach contraction principle. Many authors, such as [2,3,4,5,6] and those that are referenced in their studies, investigated various forms of contractive conditions and proved related fixed-point results.

On the one hand, many authors studied fixed-point theory in various spaces. Several authors generalized metric spaces and extended Banach’s contraction principle. For example, Huang and Zhang [7], Matthews [8], Amini-Harandi [9], and Branciari [10] introduced the concepts of cone metric spaces, partial distance spaces, metric-like spaces, and Branciari distance spaces, respectively.

Guo and Lakshmikantham [11] investigated some coupled fixed-point results by introducing the concept of coupled fixed points, and an application to coupled quasisolutions of the initial value problems for ordinary differential equations. Samet and Vetro [12] introduced the notion of n-tuple fixed points as a generalization of coupled fixed points and established related fixed-point results. Rad, Shukla, and Rahimi [13] proved that the results of n-tuple fixed points in cone metric spaces and metric-like spaces can be obtained from fixed-point theorems; the converse is also true.

Antón-Sancho [14] also studied fixed-point theory in the field of Higgs bundles, pursuing another direction of research. He proved the existence of fixed points for automorphisms of the moduli spaces of principal bundles over a compact algebraic curve, and he [15,16] obtained fixed-point results for automorphisms of the vector bundle moduli spaces and involutions of G-Higgs bundle moduli spaces.

Caristi [17] proved the fixed-point theorem in the so-called Caristi fixed-point theorem, which states that a map $S:X\to X$, where $(X,d)$ is a complete metric space, has a fixed point provided that it satisfies the following condition:

$$d(x,Sx)\le \varphi \left(x\right)-\varphi \left(Sx\right),\forall x\in X$$

where $\varphi :X\to [0,\infty )$ is a lower-semicontinuous function.

After that, it was shown that this theorem is equivalent to Ekeland’s variational principle and the Bishop–Phelps theorem, which have a great number of applications in many branches of mathematics and applied mathematics and are crucial tools in many fields, including nonlinear analysis, dynamic systems, optimization theory, game theory, economics modeling, equilibrium theory, optimization problems, computational methods, variational inequalities, differential equations, integral equations and control theory, population dynamics, and epidemiological methods. It is also known as the most beautiful and useful extension of Banach’s contraction principle, and due to its importance, many authors, such as [18,19,20,21] and those that they reference in their studies, obtained generalizations and extensions of Caristi’s theorem; in addition, some authors [22,23,24,25,26] presented new proofs of Caristi’s theorem.

Very recently, Isik et al. [27] presented a generalization of Caristi’s fixed-point theorem in complete metric spaces by using the concept of the control function.

In this study, we give the concept of $\sigma$-Caristi maps and prove the existence of fixed points for such $\sigma$-Caristi maps in Branciari distance spaces. We generalize the notion of $\sigma$-contractions and obtain related fixed-point results in Branciari distance spaces. We examined the interrelations among the various contraction conditions presented in this paper. In addition, we present examples to analyze the main theorems, and we give applications to integral equations and differential equations.

2. Preliminaries

Jleli and Samet [28] gave the concept of $\sigma$-contractions and used this notion to generalize Banach’s contraction principle. Whenever $\sigma :(0,\infty )\to (1,\infty )$ is non-decreasing and satisfies (${\sigma }_1$) and (${\sigma }_2$),

(${\sigma }_1$)

For any sequence $\left\{u_n\right\}\subset (0,\infty )$,

$$u_n\to 0(\mathrm{as}n\to \infty )\iff \sigma \left(u_n\right)\to 1(\mathrm{as}n\to \infty );$$

(${\sigma }_2$)

There are $\varkappa \in (0,1)$ and $\aleph \in (0,\infty ]$:

$${\displaystyle \frac{\sigma \left(u\right)-1}{u^{\varkappa }}}\to \aleph (\mathrm{as}u\to 0^{+}).$$

Ahmad et al. [29] obtained an extension of the result of [28] to metric spaces by replacing (${\sigma }_2$) with the condition that

(${\sigma }_3$)

$\sigma$ is continuous on $(0,\infty ).$

Very recently, Işik et al. [27] generalized Caristi’s result in metric spaces with (${\sigma }_2$), (${\sigma }_3$), (${\sigma }_4$) and (${\sigma }_5$), where

(${\sigma }_4$)

For any $\mu ,\nu >0$,

$$\sigma (\mu +\nu )\le \sigma \left(\mu \right)\sigma \left(\nu \right);$$

(${\sigma }_4$)’

For any $\mu ,\nu >0$,

$$\sigma (\mu +\nu )=\sigma \left(\mu \right)\sigma \left(\nu \right);$$

(${\sigma }_5$)

$\sigma$ is strictly increasing;

(${\sigma }_6$)

For any $\mu ,\nu >0$,

$$\sigma (\mu -\nu )\le {\displaystyle \frac{\sigma \left(\mu \right)}{\sigma \left(\nu \right)}};$$

(${\sigma }_7$)

For any $\mu >0$ and $r>0$,

$${\left[\sigma \left(\mu \right)\right]}^r\le \sigma \left(r\mu \right).$$

In 2000, Branciari [10] introduced the notion of Branciari distance spaces and extended the Banach contraction principle to Branciari distance spaces with two conditions:

($c_1$)

The topology generated by the Branciari distance is a Hausdorff space;

($c_2$)

Any Branciari distance is continuous in each coordinate.

Since then, the authors of [30,31] investigated the characteristics of Branciari distance spaces. They obtained the following characteristics.

$\left(b_1\right)$

A Branciari distance does not have to be continuous at each coordinate;

$\left(b_2\right)$

A convergent sequence does not have to be a Cauchy sequence;

$\left(b_3\right)$

The limit of a convergent sequence is not guaranteed to be unique;

$\left(b_4\right)$

An open ball does not necessarily need to be an open set. Hence, the existence of a topology compatible with the Branchiari distance is not guaranteed.

However, many researchers have realized that, despite the aforementioned topological disadvantages, Brancian distance spaces are attractive spaces for studying and developing fixed-point theory without additional conditions. It is for this reason that a considerable number of researchers ([30,31,32,33,34,35,36,37,38,39] and the references therein) have expressed interest in the Branciari distance spaces; consequently, they have undertaken studies of fixed-point theory in these spaces.

Recall the definition of Branciari distance spaces in [10].

Let $B(\ne \varnothing )$ be a given set. A map $\rho :B\times B\to [0,\infty )$ is called a Branciari distance, provided that for all $\upsilon ,\zeta \in E$ and for all $\varsigma ,\iota \in B\setminus \{\upsilon ,\zeta \}$ with $\varsigma \ne \iota$,

($\rho$1)

$\rho (\upsilon ,\zeta )=0⟺\upsilon =\zeta$;

($\rho$2)

$\rho (\upsilon ,\zeta )=\rho (\zeta ,\upsilon )$;

($\rho$3)

$\rho (\upsilon ,\zeta )\le \rho (\upsilon ,\varsigma )+\rho (\varsigma ,\iota )+\rho (\iota ,\zeta )$ (trapezoidal inequality).

Here, $(B,\rho )$ is called a Branciari distance space.

Remark 1

([40]). For a Branciari distance space $(B,\rho )$, the following holds:

(i) 

$(B,\rho )$ is not reducible to a metric space;

(ii) 

In general, the topology on B generated by ρ does not exist.

Remark 2.

A trapezoidal inequality holds whenever a triangular inequality is satisfied. However, the converse is not true. Metric spaces are included in the family of Branciari distance spaces.

The concept of convergence in Branciari distance spaces is defined similarly to that of metric spaces.

Let $(B,\rho )$ be a Branciari distance space and let $\left\{{\xi }_n\right\}\subset B$ be a sequence. Then, we say that

(i)

$\left\{{\xi }_n\right\}$ converges to $\xi$ if it satisfies

$$\underset{n\to \infty }{lim}\rho ({\xi }_n,\xi )=0;$$

(ii)

$\left\{{\xi }_n\right\}$ is Cauchy whenever the condition

$$\underset{n,m\to \infty }{lim}\rho ({\xi }_n,{\xi }_m)=0\mathrm{holds};$$

(iii)

$(B,\rho )$ is complete when every Cauchy sequence in B converges to a point in B.

Let $(B,\rho )$ be a Branciari distance space, and let ${⊺}_{\rho }$ be a topology on B such that, for any $E\subset B$ and any sequence $\left\{c_m\right\}\subset E,$

$$B-E\in {⊺}_{\rho }⟺[\underset{m\to \infty }{lim}\rho (c_m,c)=0\Rightarrow c\in E].$$

(1)

Here, $(B,{⊺}_{\rho })$ is called a sequential topological space (see [34]).

A map $T:B\to B$ is continuous [34] whenever the following condition holds.

For any sequence $\left\{c_m\right\}\subset B$,

$$\underset{m\to \infty }{lim}\rho (c_m,c)=0\Rightarrow \underset{m\to \infty }{lim}\rho (T{c}_m,Tc)=0.$$

In Example 1.1 ([31]) and Example 3 ([34]), we can see the properties $\left(b_1\right)\sim \left(b_4\right)$ of Branciari distance spaces.

In the following example, we can see some characteristics of sequential topology on Branciari distance spaces.

Example 1.

Let $B=\{1,2\}\cup \{1-{\displaystyle \frac{1}{n}}:n=1,2,3,···\}$. Suppose that $\rho :B\times B\to [0,\infty )$ is a map defined by

$$\rho (\xi ,\zeta )=\left\{\begin{array}{c}0,(\xi =\zeta ),\hfill \\ 1,(\xi ,\zeta \in \{1,2\left\}\right),\hfill \\ 1,(\xi ,\zeta \in \{1-{\displaystyle \frac{1}{n}}:n\in \mathbb{N}\}),\hfill \\ {\displaystyle \frac{1}{n}},(\xi \in \{1,2\}and\zeta \in \{1-{\displaystyle \frac{1}{n}}:n\in \mathbb{N}\}).\hfill \end{array}\right.$$

Then, $(B,\rho )$ is a complete Branciari distance space.

It follows from (1) that the sequential topology ${⊺}_{\rho }$ on B generated by the Branciari distance space given in Example 1 is

$${⊺}_{\rho }=\{\varnothing ,B,\{1-{\displaystyle \frac{1}{n}}:n\in \mathbb{N}\},\left\{1\right\}\cup \{1-{\displaystyle \frac{1}{n}}:n\in \mathbb{N}\},\left\{2\right\}\cup \{1-{\displaystyle \frac{1}{n}}:n\in \mathbb{N}\}\}.$$

(2)

Remark 3.

We have some properties of sequential topology and sequential continuity on Branciari distance spaces.

(i) 

From (2), we have that the sequential topological space $(B,{⊺}_{\rho })$ generated by the Branciari distance space given in Example 1 is not a Hausdorff space.

(ii) 

ρ is not continuous with respect to $(B,{⊺}_{\rho })$ because

$$\underset{k\to \infty }{lim}\rho (1-{\displaystyle \frac{1}{k}},2)=0implies\underset{n\to \infty }{lim}\rho (1-{\displaystyle \frac{1}{k}},{\displaystyle \frac{1}{2}})\ne \rho (2,{\displaystyle \frac{1}{2}}).$$

(3)

Throughout this paper, unless otherwise stated, we let B denote a Branciari distance space with Branciari distance $\rho$. In addition, we represent by $\mathcal{CM}(B,B)$ the class of all self maps defined on a complete Branciari distance space B.

Lemma 1

([41]). Let $(B,\rho )$ be a complete Branciari distance space. Assume that $\left\{{\xi }_n\right\}\subset B$ is a Cauchy sequence and $\xi ,\zeta \in B$. If there exists $k_0\in N$ such that

(i) 

${\xi }_n\ne {\xi }_m\forall n,m>k_0$;

(ii) 

${\xi }_n\ne \xi \forall n>k_0$;

(iii) 

${\xi }_n\ne \zeta \forall n>k_0$;

(iv) 

${lim}_{n\to \infty }\rho ({\xi }_n,\xi )={lim}_{n\to \infty }\rho ({\xi }_n,\zeta )$,

then $\xi =\zeta$.

Lemma 2

([37]). Let $\left\{{\xi }_m\right\}\subset B$ be a Cauchy sequence such that

$$\underset{m\to \infty }{lim}\rho ({\xi }_m,\xi )=0.$$

Then,

$$\underset{m\to \infty }{lim}\rho (\zeta ,{\xi }_m)=\rho (\zeta ,\xi ),\forall \zeta \in B.$$

3. Fixed Points

We introduce the notion of the $\sigma$-Caristi map on Branciari distance space; it is the motivation from the paper by Isik et al.

Let $\sigma :(0,\infty )\to (1,\infty )$ be a function.

Then, we say that $C\in \mathcal{CM}(B,B)$ is a $\sigma$-Caristi map if there exists an lsc function $\varphi :B\to [a,\infty )$, where $a>0$, such that

$$\sigma \left(\rho (\xi ,C\xi )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(C\xi \left)\right)}},\forall \xi \in B(\xi \ne C\xi ).$$

(4)

Proposition 1.

Let $C\in \mathcal{CM}(B,B)$ be a σ-Caristi map with an lsc function $\varphi :B\to [a,\infty )$, where $a>0$.

For each $\xi \in B$, let

$$R\left(\xi \right)=\{\zeta \in B:\zeta \ne \xi ,\sigma \left(\rho (\xi ,\zeta )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(\zeta \left)\right)}}\}.$$

If σ is non-decreasing and satisfies the condition ($\sigma 4$), then the following hold:

(i) 

$R\left(\xi \right)\ne \varnothing ,\forall \xi \in B$;

(ii) 

$\varphi \left(\zeta \right)<\varphi \left(\xi \right),\forall \zeta \in R\left(\xi \right)$;

(iii) 

$R\left(\zeta \right)\subset R\left(\xi \right),\forall \zeta \in R\left(\iota \right),\forall \iota \in R\left(\xi \right)$.

Proof. 

Since C is a $\sigma$-Caristi map, it satisfies that for all $\xi \in B$ with $\xi \ne C\xi$,

$$\sigma \left(\rho (\xi ,C\xi )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(C\xi \left)\right)}}.$$

Hence, $C\xi \in R\left(\xi \right)$, and so $R\left(\xi \right)\ne \varnothing$. Thus, (i) is proved.

Let $\zeta \in R\left(\xi \right)$. Then, we have

$$\zeta \ne \xi \mathrm{and}\sigma \left(\rho (\xi ,\zeta )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(\zeta \left)\right)}},$$

which implies

$$\sigma \left(\varphi \right(\zeta \left)\right)<\sigma \left(\varphi \right(\xi \left)\right),$$

and so

$$\varphi \left(\zeta \right)<\varphi \left(\xi \right).$$

Hence, (ii) is satisfied.

Let $\iota \in R\left(\xi \right)$, and let $\zeta \in R\left(\iota \right)$.

Then, we have that

$$\iota \ne \xi \mathrm{and}\sigma \left(\rho (\xi ,\iota )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(\iota \left)\right)}},$$

$$\zeta \ne \iota \mathrm{and}\sigma \left(\rho (\iota ,\zeta )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\iota \left)\right)}{\sigma \left(\varphi \right(\zeta \left)\right)}}.$$

Assume that $\varsigma \in R\left(\zeta \right)$.

Then, we obtain that

$$\varsigma \ne \zeta \mathrm{and}\sigma \left(\rho (\zeta ,\varsigma )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\zeta \left)\right)}{\sigma \left(\varphi \right(\varsigma \left)\right)}}.$$

Hence,

$$\sigma \left(\varphi \right(\varsigma \left)\right)<\sigma \left(\varphi \right(\zeta \left)\right)<\sigma \left(\varphi \right(\iota \left)\right)<\sigma \left(\varphi \right(\xi \left)\right).$$

(5)

If $\varsigma =\xi$, then from (5), we have

$$\sigma \left(\varphi \right(\xi \left)\right)<\sigma \left(\varphi \right(\xi \left)\right),$$

which is a contradiction. Thus,

$$\varsigma \ne \xi .$$

(6)

Applying (${\rho }_3$) and (${\sigma }_4$), we infer that

$$\begin{array}{cc}\hfill & \sigma \left(\rho \right(\varsigma ,\xi \left)\right)\hfill \\ \hfill =& \sigma \left(\rho \right(\xi ,\varsigma \left)\right)\hfill \\ \hfill \le & \sigma \left(\rho \right(\xi ,\iota \left)\right)\sigma \left(\rho \right(\iota ,\zeta \left)\right)\sigma \left(\rho \right(\zeta ,\varsigma \left)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(\iota \left)\right)}}{\displaystyle \frac{\sigma \left(\varphi \right(\iota \left)\right)}{\sigma \left(\varphi \right(\zeta \left)\right)}}{\displaystyle \frac{\sigma \left(\varphi \right(\zeta \left)\right)}{\sigma \left(\varphi \right(\varsigma \left)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(\varsigma \left)\right)}}.\hfill \end{array}$$

(7)

It follows from (6) and (7) that

$$\varsigma \in R\left(\xi \right).$$

Thus, (iii) is proved.    □

Remark 4.

Proposition 1 holds whenever (${\sigma }_4$) and (${\sigma }_5$) are satisfied.

Theorem 1.

Let $C\in \mathcal{CM}(B,B)$ be a σ-Caristi map with an lsc function $\varphi :B\to [a,\infty )$, where $a>0$. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$) and (${\sigma }_5$), then C possesses a fixed point.

Proof. 

Assume that

$$\xi \ne C\xi ,\forall \xi \in B.$$

Let ${\xi }_1\in B$ be given.

Since $R\left({\xi }_1\right)\ne \varnothing$, we can choose a point ${\xi }_2\in R\left({\xi }_1\right)$ such that

$$\varphi \left({\xi }_2\right)\le \underset{\iota \in R\left({\xi }_1\right)}{inf}\varphi \left(\iota \right)+1.$$

Inductively, we can construct a sequence $\left\{{\xi }_n\right\}\subset B$ such that

$${\xi }_{n+1}\in R\left({\xi }_n\right)\mathrm{and}\varphi \left({\xi }_{n+1}\right)\le \underset{\iota \in R\left({\xi }_n\right)}{inf}\varphi \left(\iota \right)+{\displaystyle \frac{1}{n}},\forall n\in \mathbb{N}.$$

(8)

Since ${\xi }_{n+1}\in R\left({\xi }_n\right)$,

$${\xi }_{n+1}\ne {\xi }_n\mathrm{and}\sigma \left(\rho ({\xi }_n,{\xi }_{n+1})\right)\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_{n+1}\right)\right)}}$$

(9)

which implies

$$\sigma \left(\varphi \left({\xi }_{n+1}\right)\right)<\sigma \left(\varphi \left({\xi }_n\right)\right)\forall n\in \mathbb{N}.$$

Thus, the sequence $\left\{\varphi \left({\xi }_n\right)\right)\}$ is decreasing.

We now show that $\left\{{\xi }_n\right\}$ is Cauchy.

Using (9) and (${\sigma }_4$), we find that

$$\begin{array}{cc}\hfill & \sigma \left(\varphi \left({\xi }_1\right)\right)>{\displaystyle \frac{\sigma (\varphi \left({\xi }_1\right)}{\sigma (\varphi \left({\xi }_n\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_1\right)\right)}{\sigma \left(\varphi \left({\xi }_2\right)\right)}}{\displaystyle \frac{\sigma \left(\varphi \left({\xi }_2\right)\right)}{\sigma \left(\varphi \left({\xi }_3\right)\right)}}···{\displaystyle \frac{\sigma \left(\varphi \left({\xi }_{n-1}\right)\right)}{\sigma \left(\varphi \left({\xi }_n\right)\right)}}\hfill \\ \hfill \ge & \sigma \left(\rho ({\xi }_1,{\xi }_2)\right)\sigma \left(\rho ({\xi }_2,{\xi }_3)\right)···\sigma \left(\rho ({\xi }_{n-1},{\xi }_n)\right)\hfill \\ \hfill =& \sigma (\sum _{k=1}^{n-1}\rho ({\xi }_k,{\xi }_{k+1})),\hfill \end{array}$$

which implies

$$\sum _{k=1}^{n-1}\rho ({\xi }_k,{\xi }_{k+1})<\varphi \left({\xi }_1\right).$$

Hence,

$$\sum _{n=1}^{\infty }\rho ({\xi }_n,{\xi }_{n+1})<\infty .$$

(10)

Let $ϵ>0$ be given.

From (10), there exists a positive integer N such that

$$\sum _{n=N}^{\infty }\rho ({\xi }_n,{\xi }_{n+1})<ϵ.$$

Thus, we have that for all $n,m>N$,

$$\rho ({\xi }_n,{\xi }_m)<\sum _{n=N}^{\infty }\rho ({\xi }_n,{\xi }_{n+1})<ϵ.$$

Hence, $\left\{{\xi }_n\right\}$ is a Cauchy sequence.

By the completeness of B, there is ${\xi }_{*}\in B$ with

$$\underset{k\to \infty }{lim}\rho ({\xi }_{*},{\xi }_k)=0.$$

(11)

Since $\varphi$ is an lsc function and $\left\{\varphi \left({\xi }_n\right)\right\}$ is a decreasing sequence,

$$\varphi \left({\xi }_{*}\right)\le \underset{n\to \infty }{lim}inf\varphi \left({\xi }_n\right)\le \underset{n\in \mathbb{N}}{inf}\varphi \left({\xi }_n\right)\le \varphi \left({\xi }_n\right),\forall n\in \mathbb{N}.$$

(12)

We show that

$${\xi }_{*}\ne {\xi }_n,\forall n\in \mathbb{N}.$$

(13)

If ${\xi }_{*}={\xi }_l$ for some $l\in \mathbb{N}$, then it follows from (9) and (12) that

$$1<\sigma \left(\rho ({\xi }_l,{\xi }_{l+1})\right)\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_l\right)\right)}{\sigma \left(\varphi \left({\xi }_{l+1}\right)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_l\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}}=1,$$

which is a contradiction.

Thus, (13) holds.

Next, we assert that

$$\bigcap _{m\in \mathbb{N}}R\left({\xi }_m\right)=\left\{{\xi }_{*}\right\}.$$

By (${\sigma }_4$) and (9), we find that

$$\begin{array}{cc}\hfill & \sigma \left(\rho ({\xi }_n,{\xi }_m)\right)\hfill \\ \hfill \le & \sigma \left(\rho ({\xi }_n,{\xi }_{n+1})\right)\sigma \left(\rho ({\xi }_{n+1},{\xi }_{n+2})\right)\dots \sigma \left(\rho ({\xi }_{m-1},{\xi }_m)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_m\right)\right)}},\forall m,n\in \mathbb{N},m>n.\hfill \end{array}$$

Thus, from (12), we infer that

$$\sigma \left(\rho ({\xi }_n,{\xi }_m)\right)\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_m\right)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}}.$$

(14)

Since (${\sigma }_5$) is satisfied, (14) yields the following inequality:

$$\rho ({\xi }_n,{\xi }_m)\le {\sigma }^{-1}\left({\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}}\right).$$

(15)

By applying Lemma 2 to (11) to (15), we find that

$$\rho ({\xi }_n,{\xi }_{*})\le {\sigma }^{-1}\left({\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}}\right),$$

which yields

$$\sigma \left(\rho ({\xi }_n,{\xi }_{*})\right)\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \left({\xi }_{*}\right)\right)}},\forall n\in \mathbb{N}.$$

Hence,

$${\xi }_{*}\in R\left({\xi }_n\right),\forall n\in \mathbb{N},$$

and thus,

$${\xi }_{*}\in \bigcap _{n\in \in \mathbb{N}}R\left({\xi }_n\right).$$

Applying Proposition 1(iii) to ${\xi }_n\in R\left({\xi }_{n-1}\right)$, we find that

$$R\left({\xi }_{*}\right)\subset R\left({\xi }_{n-1}\right)\forall n=2,3,···,$$

which implies that

$$R\left({\xi }_{*}\right)\subset \bigcap _{n\in \mathbb{N}}R\left({\xi }_n\right).$$

(16)

Let

$$\iota \in \bigcap _{n\in \mathbb{N}}R\left({\xi }_n\right).$$

Then, we infer that

$$\iota \in R\left({\xi }_{n+1}\right)\mathrm{and}{\xi }_{n+1}\in R\left({\xi }_n\right)\forall n\in \mathbb{N}.$$

By applying Proposition 1(iii),

$$R\left(\iota \right)\subset R\left({\xi }_n\right),\forall n\in \mathbb{N}.$$

From (8), we infer that $\forall n\in \mathbb{N}$,

$$\sigma \left(\rho ({\xi }_n,\iota )\right)\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left(\varphi \right(\iota \left)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma \left({inf}_{\iota \in R\left({\xi }_n\right)}\varphi \left(\iota \right)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \left({\xi }_n\right)\right)}{\sigma (\varphi \left({\xi }_{n+1}\right)-\frac{1}{n})}}.$$

(17)

Since $\{\varphi \left({\xi }_n\right\}$ is decreasing and $\varphi$ is bounded below by a, there exists $L\ge a$ such that

$$\underset{n\to \infty }{lim}\varphi \left({\xi }_n\right)=L.$$

(18)

By letting $n\to \infty$ in Equation (17) and using (${\sigma }_3$),

$$\underset{n\to \infty }{lim}\sigma \left(\rho ({\xi }_n,\iota )\right)=1.$$

(19)

It follows from (${\sigma }_1$) that

$$\underset{n\to \infty }{lim}\rho ({\xi }_n,\iota )=0.$$

(20)

Applying Lemma 1,

$${\xi }_{*}=\iota ,$$

and hence,

$$\bigcap _{n\in \mathbb{N}}R\left({\xi }_n\right)=\left\{{\xi }_{*}\right\}.$$

From (16), we find that

$$R\left({\xi }_{*}\right)\subset \left\{{\xi }_{*}\right\}.$$

Because ${\xi }_{*}\ne C{\xi }_{*}$, it follows from (4) that

$$C{\xi }_{*}\in R\left({\xi }_{*}\right),$$

and so

$${\xi }_{*}=C{\xi }_{*},$$

which leads to a contradiction.

Hence, C possesses a fixed point.    □

Remark 5.  (i)   If σ is a non-decreasing function in Theorem 1, then C possesses a fixed point. 

(ii) 

Theorem 1 extends Theorem 2 of [27] to Branciari distance spaces.

We now present an example to analyze Theorem 1.

Example 2.

Let $B=\{1,2,3,4\}$, and let $\rho :B\times B\to [0,\infty )$ be a map defined as follows:

$$\begin{array}{cc}\hfill & \rho (1,2)=\rho (2,1)=3,\hfill \\ \hfill & \rho (2,3)=\rho (3,2)=\rho (1,3)=\rho (3,1)=1,\hfill \\ \hfill & \rho (1,4)=\rho (4,1)=\rho (2,4)=\rho (4,2)=\rho (3,4)=\rho (4,3)=4,\hfill \\ \hfill & \rho (z,z)=0,\forall z\in B.\hfill \end{array}$$

Then, $(B,\rho )$ is a complete Branciari distance space (see [32]).

Let $C:B\to B$ be a map defined by

$$C\xi =\left\{\begin{array}{cc}1\hfill & (\xi =1,2),\hfill \\ 3\hfill & (\xi =3,4).\hfill \end{array}\right.$$

Suppose that $\varphi :B\to [a,\infty )$, where $a>0$, is a map defined by $\varphi \left(x\right)=5x$, and let $\sigma (ı)=e^{ı},\forall ı>0$.

Then, (${\sigma }_4$) and (${\sigma }_5$) hold, and ϕ is an lsc function.

We now show that C is a σ-Caristi map with lsc $\varphi \left(x\right)=5x.$

We infer that

$$\rho (\xi ,C\xi )=\left\{\begin{array}{cc}\rho (1,1)=0\hfill & (\xi =1),\hfill \\ \rho (2,1)=3\hfill & (\xi =2),\hfill \\ \rho (3,3)=0\hfill & (\xi =3),\hfill \\ \rho (4,3)=4\hfill & (\xi =4).\hfill \end{array}\right.$$

Hence,

$$\rho (\xi ,C\xi )>0⟺\xi =2,4.$$

Consider the following two cases.

First case: Let $\xi =2$.

Then, we have that

$${\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(S\xi \left)\right)}}={\displaystyle \frac{\sigma \left(10\right)}{\sigma \left(5\right)}}=e^5>e^3=\sigma \left(\rho (\xi ,S\xi )\right).$$

Second case: Let $\xi =4$.

Then, we find that

$${\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(S\xi \left)\right)}}={\displaystyle \frac{\sigma \left(20\right)}{\sigma \left(15\right)}}=e^5>e^4=\sigma \left(\rho (\xi ,S\xi )\right).$$

Hence, C is a σ-Caristi map with $\varphi \left(x\right)=5x.$ The suppositions of Theorem 1 hold, and there are fixed points 1 and 3 on the map C.

Corollary 1.

Let $C\in \mathcal{CM}(B,B)$ be such that

$$\sigma \left(\rho (\xi ,\zeta )\right)\le {\displaystyle \frac{\sigma \left(\phi \right(\xi ,\zeta \left)\right)}{\sigma \left(\phi \right(C\xi ,C\zeta \left)\right)}},\forall \xi ,\zeta \in B(\xi \ne \zeta ),$$

(21)

where $\phi :B\times B\to [a,\infty )$, where $a>0$, is lsc with respect to the first variable. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), and (${\sigma }_5$), then C possesses only one fixed point.

Proof. 

For each $\xi \in B$, let $\zeta =C\xi$ and $\varphi \left(\xi \right)=\phi (\xi ,C\xi )$.

Then, $\varphi :B\to [a,\infty )$ is an lsc function. It follows from (21) that for all $\xi \in B$ with $\xi \ne C\xi$,

$$\sigma \left(\rho (\xi ,C\xi )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(C\xi \left)\right)}}.$$

By Theorem 1, C possesses a fixed point.

We now show that C possesses only one fixed point.

Let $u=Cu$ and $v=Cv$ be such that $u\ne v$.

From (21), we acquire that

$$1<\sigma \left(\rho (u,v)\right)\le {\displaystyle \frac{\sigma \left(\phi \right(u,v\left)\right)}{\sigma \left(\phi \right(Cu,Cv\left)\right)}}={\displaystyle \frac{\sigma \left(\phi \right(u,v\left)\right)}{\sigma \left(\phi \right(u,v\left)\right)}}=1,$$

which leads to a contradiction.

Hence, C possesses only one fixed point.    □

Corollary 2.

Let $C\in \mathcal{CM}(B,B)$ be such that

$$\sigma \left(\rho \right(C\xi ,C\zeta \left)\right)<\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right),\forall \xi ,\zeta \in E(C\xi \ne C\zeta ),$$

(22)

where $\varphi :[0,\infty )\to [0,\infty )$ is an lsc function with $\varphi \left(t\right)<t,\forall t>0$, and ${\displaystyle \frac{\varphi \left(t\right)}{t}}$ is a non-decreasing function. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), (${\sigma }_5$), (${\sigma }_6$), and (${\sigma }_7$), where

(${\sigma }_6$)

$\forall \mu ,\nu >0$ with $\mu -\nu >0$,

$$\sigma (\mu -\nu )\le {\displaystyle \frac{\sigma \left(\mu \right)}{\sigma \left(\nu \right)}};$$

(${\sigma }_7$)

$\forall \mu ,r>0$,

$${\left[\sigma \left(\mu \right)\right]}^r=\sigma \left(\mu r\right),$$

then C possesses only one fixed point.

Proof. 

As (${\sigma }_5$) holds, it follows from (22) that

$$\rho (C\xi ,C\zeta )<\varphi \left(\rho \right(\xi ,\zeta \left)\right),$$

which implies

$$0<\rho (\xi ,\zeta )-\varphi \left(\rho \right(\xi ,\zeta \left)\right)\le \rho (\xi ,\zeta )-\rho (C\xi ,C\zeta ).$$

Hence, we find that

$$\begin{array}{cc}\hfill & \sigma \left(\left(1-{\displaystyle \frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}\right)\rho (\xi ,\zeta )\right)\hfill \\ \hfill =& \sigma \left(\rho (\xi ,\zeta )-\varphi \left(\rho \right(\xi ,\zeta \left)\right)\right)\hfill \\ \hfill \le & \sigma \left(\rho (\xi ,\zeta )-\rho (C\xi ,C\zeta )\right).\hfill \end{array}$$

Let $\phi (\xi ,\zeta )=a+{\displaystyle \frac{\rho (\xi ,\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}}$ for all $\xi ,\zeta \in B$ with $\xi \ne \zeta$, where $a>0$.

Then, $\phi :B\times B\to [a,\infty )$ is an lsc function with respect to the first variable. Since $\rho (C\xi ,C\zeta )<\rho (\xi ,\zeta )$ and ${\displaystyle \frac{\varphi \left(t\right)}{t}}$ is non-decreasing, it follows from $\left(\sigma 5\right)$ and $\left(\sigma 6\right)$ that

$$\begin{array}{cc}\hfill & \sigma \left(\rho \right(\xi ,\zeta \left)\right)\hfill \\ \hfill =& {\left[\sigma \left(\left(1-{\displaystyle \frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}\right)\rho (\xi ,\zeta )\right)\right]}^{{\displaystyle \frac{1}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (x,y)}}}}\hfill \\ \hfill \le & {\left[\sigma (\rho (\xi ,\zeta )-\rho (C\xi ,C\zeta ))\right]}^{{\displaystyle \frac{1}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}}}\hfill \\ \hfill =& \sigma \left(\left(a+{\displaystyle \frac{\rho (\xi ,\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}}\right)-\left(a+{\displaystyle \frac{\rho (C\xi ,C\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}}\right)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(a+\frac{\rho (\xi ,\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}}\right)}{\sigma \left(a+\frac{\rho (C\xi ,C\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta \left)\right)}{\rho (\xi ,\zeta )}})\right)}}\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(a+\frac{\rho (\xi ,\zeta )}{1-\frac{\varphi \left(\rho \right(\xi ,\zeta )}{\rho (\xi ,\zeta )}}\right)}{\sigma \left(a+\frac{\rho (C\xi ,C\zeta )}{1-\frac{\varphi \left(\rho \right(C\xi ,C\zeta \left)\right)}{\rho (C\xi ,C\zeta )}}\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\sigma \left(\phi \right(\xi ,\zeta \left)\right)}{\sigma \left(\phi \right(C\xi ,C\zeta \left)\right)}}.\hfill \end{array}$$

By applying Corollary 1, C possesses only one fixed point.    □

Remark 6.

Taking $\sigma \left(u\right)=e^u,\forall u>0$ in Corollary 1 (or Corollary 2), we have Corollary 2.1 (or Corollary 2.3) of [20].

A map $C\in \mathcal{CM}(B,B)$ is called a generalized $\sigma$-contraction if it satisfies the following condition.

There exists a function $\sigma :(0,\infty )\to (1,\infty )$ such that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta ))}{\sigma \left(\varphi \right(\rho (C\xi ,C\zeta ))}},\forall \xi ,\zeta \in B(C\xi \ne C\zeta ),$$

(23)

where $\varphi :(0,\infty )\to (0,\infty )$ satisfies

$$\underset{t\to 0^{+}}{lim}\varphi \left(t\right)=0.$$

(24)

Theorem 2.

Let $C\in \mathcal{CM}(B,B)$ be a generalized σ-contraction. If σ satisfies (${\sigma }_1$), (${\sigma }_4$), and (${\sigma }_5$), then C possesses only one fixed point.

Proof. 

Let ${\xi }_0\in B$, and let ${\xi }_n=C{\xi }_{n-1},\forall n\in \mathbb{N}.$

Then, we infer that ${\xi }_{n-1}\ne {\xi }_n,\forall n\in \mathbb{N}.$ Otherwise, C possesses a fixed point. So, the proof is finished.

From (23), we find that $\forall n\in \mathbb{N}$,

$$1<\sigma \left(\rho ({\xi }_n,{\xi }_{n+1})\right)\le {\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_{n-1},{\xi }_n)\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_n,{\xi }_{n+1})\right)\right)}}.$$

(25)

We now show that $\left\{{\xi }_n\right\}$ is Cauchy.

From (25) and (${\sigma }_4$), we find that

$$\begin{array}{cc}\hfill & \sigma \left(\sum _{k=1}^{n-1}\rho ({\xi }_k,{\xi }_{k+1})\right)\hfill \\ \hfill \le & \sigma \left(\rho ({\xi }_1,{\xi }_2)\right)\sigma \left(\rho ({\xi }_2,{\xi }_3)\right)······\sigma \left(\rho ({\xi }_{n-1},{\xi }_n)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_0,{\xi }_1)\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_1,{\xi }_2)\right)\right)}}{\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_1,{\xi }_2)\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_2,{\xi }_3)\right)\right)}}······{\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_{n-2},{\xi }_{n-1})\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_{n-1},{\xi }_n)\right)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_0,{\xi }_1)\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_{n-1},{\xi }_n)\right)\right)}}\hfill \\ \hfill <& \sigma \left(\varphi \left(\rho ({\xi }_0,{\xi }_1)\right)\right).\hfill \end{array}$$

Hence, we acquire

$$\sum _{k=1}^{n-1}\rho ({\xi }_k,{\xi }_{k+1})<\varphi \left(\rho ({\xi }_0,{\xi }_1)\right),$$

which yields

$$\sum _{n=1}^{\infty }\rho ({\xi }_n,{\xi }_{n+1})<\infty .$$

Thus, $\left\{{\xi }_n\right\}$ is Cauchy. Because B is complete, there is ${\xi }_{*}\in B$ such that

$$\underset{n\to \infty }{lim}\rho ({\xi }_{*},{\xi }_n)=0.$$

By ($\rho 3$), (${\sigma }_4$), and (23), we infer the following inequality,

$$\begin{array}{cc}\hfill & \sigma (\rho ({\xi }_n,C{\xi }_{*})\hfill \\ \hfill \le & \sigma \left(\rho ({\xi }_n,{\xi }_{*})\right)\sigma \left(\rho ({\xi }_{*},{\xi }_{n+1})\right)\sigma \left(\rho ({\xi }_{n+1},C{\xi }_{*})\right)\hfill \\ \hfill \le & \sigma \left(\rho ({\xi }_n,{\xi }_{*})\right)\sigma \left(\rho ({\xi }_{*},{\xi }_{n+1})\right){\displaystyle \frac{\sigma \left(\varphi \left(\rho ({\xi }_n,{\xi }_{*})\right)\right)}{\sigma \left(\varphi \left(\rho ({\xi }_{n+1},C{\xi }_{*})\right)\right)}}\hfill \\ \hfill <& \sigma \left(\rho ({\xi }_n,{\xi }_{*})\right)\sigma \left(\rho ({\xi }_{*},{\xi }_{n+1})\right)\sigma \left(\varphi \left(\rho ({\xi }_n,{\xi }_{*})\right)\right).\hfill \end{array}$$

(26)

Applying (24) to the term $\varphi \left(\rho ({\xi }_n,{\xi }_{*})\right)$ in (26), we find that

$$\underset{n\to \infty }{lim}\varphi \left(\rho ({\xi }_n,{\xi }_{*})\right)=0,$$

because

$$\underset{n\to \infty }{lim}\rho ({\xi }_n,{\xi }_{*})=0.$$

Hence, we infer that

$$\underset{n\to \infty }{lim}\sigma \left(\varphi \left(\rho ({\xi }_n,{\xi }_{*})\right)\right)=1.$$

(27)

By letting $n\to \infty$ in (26) and applying (27),

$$\underset{n\to \infty }{lim}\sigma \left(\rho ({\xi }_n,C{\xi }_{*})\right)=1,$$

which yields

$$\underset{n\to \infty }{lim}\rho ({\xi }_n,C{\xi }_{*})=0.$$

Applying Lemma 1, we find that ${\xi }_{*}=C{\xi }_{*}$, and C possesses a fixed point.

We now show that C possesses only one fixed point.

Let $\mu =C\mu$ and $\nu =C\nu$ be such that $\mu \ne \nu$.

Then, it follows from (23) that

$$1<\sigma \left(\rho (\mu ,\nu )\right)=\sigma \left(\rho (C\mu ,C\nu )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\mu ,\nu ))}{\sigma \left(\varphi \right(\rho (C\mu ,C\nu ))}}=1,$$

which leads to a contradiction.

Hence, C possesses only one fixed point.    □

Applying Theorem 2 to Newton’s method, we can find the roots of equations.

We recall Newton’s iterative scheme:

$${\xi }_{n+1}={\xi }_n-{\displaystyle \frac{f\left({\xi }_n\right)}{f^{\prime }\left({\xi }_n\right)}},n=0,1,2,···$$

where $f:X\to \mathbb{R},X\subset \mathbb{R}$, is a differentiable function, and ${\xi }_0$ is an initial point for finding the root of the equation $f\left(\xi \right)=0$.

Example 3.

Let $f\left(\xi \right)={\xi }^2-4$, and let us apply Theorem 2 to determine the roots of the equation $f\left(\xi \right)=0$.

We define a map $C:[2,\infty )\to [2,\infty )$ using

$$C\xi =\xi -{\displaystyle \frac{f\left(\xi \right)}{f^{\prime }\left(\xi \right)}}={\displaystyle \frac{1}{2}}(\xi +{\displaystyle \frac{4}{\xi }}).$$

Then, we have that for $\xi \in [2,\infty ),C\xi =\xi$ if and only if $f\left(\xi \right)=0$.

Let $\sigma \left(u\right)=e^u\forall u>0$ and $\varphi \left(t\right)=2t\forall t>0$.

We find that for all $\xi ,\zeta \in [2,\infty )$ with $\rho (C\xi ,C\zeta )>0$,

$$\begin{array}{cc}\hfill & \sigma \left(\rho (C\xi ,C\zeta )\right)=\sigma (\mid C\xi -C\zeta \mid )=\sigma ({\displaystyle \frac{1}{2}}\mid (\xi +{\displaystyle \frac{4}{\xi }})-(\zeta +{\displaystyle \frac{4}{\zeta }})\mid )\hfill \\ \hfill =& \sigma ({\displaystyle \frac{1}{2}}\mid \xi -\zeta \mid \mid 1-{\displaystyle \frac{4}{\xi \zeta }}\mid )\le \sigma ({\displaystyle \frac{1}{2}}\mid \xi -\zeta \mid )\hfill \\ \hfill \le & \sigma (2\mid \xi -\zeta \mid -\mid \xi -\zeta \mid )\le \sigma (2\mid \xi -\zeta \mid -2\mid C\xi -C\zeta \mid )\hfill \\ \hfill =& \sigma (\varphi \left(\rho (\xi ,\zeta )\right)-\varphi \left(\rho (C\xi ,C\zeta )\right))={\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\varphi \right(\rho (C\xi ,C\zeta )\left)\right)}}\hfill \end{array}$$

By Theorem 2, C has a fixed point ${\xi }_{*}\in [2,\infty )$. In fact, ${\xi }_{*}=2$. Thus, the equation $f\left(\xi \right)=0$ has a solution ${\xi }_{*}=2$.

Corollary 3 is obtained by taking $\sigma (ı)=e^{ı}\forall ı>0$ in Theorem 2.

Corollary 3.

Let $C\in \mathcal{CM}(B,B)$ be such that

$$\rho (C\xi ,C\zeta )\le \varphi \left(\rho \right(\xi ,\zeta \left)\right)-\varphi \left(\rho \right(C\xi ,C\zeta \left)\right),\forall \xi ,\zeta \in B(C\xi \ne C\zeta ),$$

where $\varphi :(0,\infty )\to (0,\infty )$ satisfies (24).

Then, C possesses only one fixed point.

Remark 7.

Corollary 3 generalizes and extends Theorem 4 [27] to Branciari distance spaces without the continuity of map C and $\varphi \left(0\right)=0$.

Remark 8.

It follows from Remark 2 that our main theorems also hold in complete metric spaces.

4. Corollaries

In this section, we give several fixed-point results and coupled fixed-point results that are obtained by applying the main theorem.

Corollary 4

(Caristi). Let $C\in \mathcal{CM}(B,B)$ be such that

$$\rho (\xi ,C\xi )\le f\left(\xi \right)-f\left(C\xi \right),\forall \xi \in B(\xi \ne C\xi ),$$

(28)

where $f:B\to [0,\infty )$ is an lsc function.

Then, C possesses a fixed point.

Proof. 

Let $\sigma \left(\nu \right)=e^{\nu },\forall \nu >0$.

It follows from (28) that for all $\xi \in B$ with $\xi \ne C\xi ,$

$$\sigma \left(\rho (\xi ,C\xi )\right)=e^{\rho (\xi ,C\xi )}\le e^{f\left(\xi \right)-f\left(C\xi \right)}={\displaystyle \frac{e^{f\left(\xi \right)}}{e^{f\left(C\xi \right)}}}.$$

(29)

We define $f:B\to [0,\infty )$ by

$$f\left(\xi \right)=-a+ln\left(\sigma \right(\varphi \left(\xi \right)\left)\right)),$$

where $\varphi :B\to [a,\infty )$, $a>0$, is an lsc function.

Then, f is an lsc function. From (29), we acquire that for all $\xi \in B$ with $\xi \ne C\xi$,

$$\sigma \left(\rho (\xi ,C\xi )\right)\le {\displaystyle \frac{e^{f\left(\xi \right)}}{e^{f\left(C\xi \right)}}}={\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(C\xi \left)\right)}}.$$

By Theorem 1, C possesses a fixed point.    □

Recall that a map $C\in \mathcal{CM}(B,B)$ is called $\sigma$-contraction [28] if it satisfies

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k,\forall \xi ,\zeta \in B(C\xi \ne C\zeta ),$$

(30)

where $k\in (0,1)$, and $\sigma :(0,\infty )\to (1,\infty )$ is a function.

Jleli and Samet [28] proved that every $\sigma$-contraction $C\in \mathcal{CM}(B,B)$ possesses only one fixed point whenever $\sigma$ is non-decreasing and satisfies (${\sigma }_1$) and (${\sigma }_2$).

By applying Corollary 2, we have Theorem 2.1 of [28].

Corollary 5

(Jleli and Samet). Let $C\in \mathcal{CM}(B,B)$ be a σ-contraction. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$),(${\sigma }_5$), (${\sigma }_6$), and (${\sigma }_7$), then C possesses only one fixed point.

Proof. 

We define $\varphi :[0,\infty )\to [0,\infty )$ by $\varphi \left(s\right)=ks,\forall s>0$, where $k\in (0,1)$.

Then, $\varphi$ is an lsc function. By applying (30) and (${\sigma }_7$), we have that for all $\xi ,\zeta \in B$ with $C\xi \ne C\zeta$,

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k=\sigma \left(k\rho (\xi ,\zeta )\right)=\sigma (\varphi \left(\rho (\xi ,\zeta )\right).$$

By Corollary 2, C possesses only one fixed point.    □

Corollary 6.

Let $C\in \mathcal{CM}(B,B)$ be such that

$$\sigma \left(\rho (C\xi ,CC\xi )\right)\le {\left[\sigma \left(\rho (\xi ,C\xi )\right)\right]}^k,\forall \xi \in B(C\xi \ne CC\xi ),$$

where $k\in (0,1)$. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), (${\sigma }_5$), (${\sigma }_6$), and (${\sigma }_7$), then C possesses only one fixed point.

Remark 9.

Let $(B,\rho )$ be a Branciari distance space such that ρ is an lsc function with respect to the first variable. If (${\sigma }_7$) is satisfied, then the σ-Caristi map is a generalization of a σ-contraction. In fact, if $C:B\to B$ is a σ-contraction, then there is $k\in (0,1)$ such that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k,\forall \xi ,\zeta \in B(C\xi \ne C\zeta ).$$

Let $k=1-r,r\in (0,1)$.

We find that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k={\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^{1-r}={\displaystyle \frac{\sigma \left(\rho \right(\xi ,\zeta \left)\right)}{{\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^r}},$$

which implies

$$\sigma \left(\rho (\xi ,\zeta )\right)\le {\displaystyle \frac{{\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^{\frac{1}{r}}}{{\left[\sigma \left(\rho (C\xi ,C\zeta )\right)\right]}^{\frac{1}{r}}}}={\displaystyle \frac{\sigma \left(\frac{1}{r}\rho (\xi ,\zeta )\right)}{\sigma \left(\frac{1}{r}\rho (C\xi ,C\zeta )\right)}}.$$

Let $\zeta =C\xi$ and $\varphi \left(\xi \right)={\displaystyle \frac{1}{r}}\rho (\xi ,C\xi )$.

Then, we infer that

$$\sigma \left(\rho (\xi ,C\xi )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\xi \left)\right)}{\sigma \left(\varphi \right(C\xi \left)\right)}}.$$

Hence, C is a σ-Caristi map.

Remark 10.

Inequality (23) of Theorem 2 is a generalization of a σ-contraction whenever (${\sigma }_7$) is satisfied. In fact, if C is a σ-contraction, then

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k,\forall \xi ,\zeta \in B(C\xi \ne C\zeta )wherek\in (0,1).$$

Then, we have that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^{{\displaystyle \frac{k}{1+k-\sqrt{k}}}},$$

which implies that

$${\left[\sigma \left(\rho (C\xi ,C\zeta )\right)\right]}^{1-\sqrt{k}}\le {\displaystyle \frac{{\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k}{{\left[\sigma \left(\rho (C\xi ,C\zeta )\right)\right]}^k}}.$$

Hence, we infer that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\displaystyle \frac{{\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^{\frac{k}{1-\sqrt{k}}}}{{\left[\sigma \left(\rho (C\xi ,C\zeta )\right)\right]}^{\frac{k}{1-\sqrt{k}}}}}={\displaystyle \frac{\sigma \left(\frac{k}{1-\sqrt{k}}\rho (\xi ,\zeta )\right)}{\sigma \left(\frac{k}{1-\sqrt{k}}\rho (C\xi ,C\zeta )\right)}}.$$

Let $\varphi \left(s\right)={\displaystyle \frac{k}{1-\sqrt{k}}}s,\forall s>0$.

Then, we find that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\varphi \right(\rho (C\xi ,C\zeta )\left)\right)}}.$$

A map $C\in \mathcal{CM}(B,B)$ is called a $\sigma$-($\varphi ,\phi$)-contraction if it satisfies the following condition.

There exists a function $\sigma :(0,\infty )\to (0,\infty )$ such that

$$\sigma \left(\varphi \left(\rho (C\xi ,C\zeta )\right)\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}}\forall \xi ,\zeta \in B(\xi \ne \zeta )$$

(31)

where $\varphi :[0,\infty )\to [0,\infty )$ is a continuous and strictly increasing function and $\phi :[0,\infty )\to [0,\infty )$ is a continuous and non-decreasing function such that $\varphi \left(t\right)=\phi \left(t\right)=0$ if and only if $t=0$ and

$$0<\varphi \left(t\right)\le t,\phi \left(t\right)\ge t,\forall t>0$$

(32)

Note that $\varphi :(0,\infty )\to (0,\infty )$ is a continuous and strictly increasing function and $\phi :(0,\infty )\to (0,\infty )$ is a continuous and non-decreasing function such that (32) is satisfied.

Remark 11.

A generalized σ-contraction is a generalization of a σ-($\varphi ,\phi$)-contraction, where σ is satisfied (${\sigma }_5$). Actually, if $C\in \mathcal{CM}(B,B)$ is a σ-($\varphi ,\phi$)-contraction, then from (31), we have that

$$\varphi \left(\rho (C\xi ,C\zeta )\right)<\varphi \left(\rho (\xi ,\zeta )\right)because\left({\sigma }_5\right)holds.$$

Hence, $\rho (C\xi ,C\zeta )<\rho (\xi ,\zeta )$ and, thus, $\phi (C\xi ,C\zeta )\le \rho (\xi ,\zeta )$. It follows from (31) that

$$\begin{array}{cc}\hfill & \sigma \left(\varphi \left(\rho (C\xi ,C\zeta )\right)\right)\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}}\le {\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (C\xi ,C\zeta )\left)\right)}}\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\rho \right(\xi ,\zeta \left)\right)}{\sigma \left(\phi \right(\rho (C\xi ,C\zeta )\left)\right)}}\le {\displaystyle \frac{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (C\xi ,C\zeta )\left)\right)}},\forall \xi ,\zeta \in B(C\xi \ne C\zeta ).\hfill \end{array}$$

Hence, we infer that

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\displaystyle \frac{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (C\xi ,C\zeta )\left)\right)}},\forall \xi ,\zeta \in B(C\xi \ne C\zeta ).$$

Remark 12.

A σ-contraction map is σ-($\varphi ,\phi$)-contraction, where σ is satisfied (${\sigma }_5$), (${\sigma }_6$) and (${\sigma }_7$).

Let $C:B\to B$ be σ-contraction. Then there exists $0<k<1$ such that, for all $\xi ,\zeta \in B,$

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k.$$

Let $\varphi \left(t\right)=t,\phi \left(t\right)=rt,r=1-k$ and let $\sigma \left(t\right)=e^t,\forall t>0$.

Then, we have that

$$\begin{array}{cc}\hfill & \sigma \left(\varphi \left(\rho (C\xi ,C\zeta )\right)\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^{1-r}={\displaystyle \frac{\sigma \left(\rho \right(\xi ,\zeta \left)\right)}{{\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^r}}\hfill \\ \hfill =& {\displaystyle \frac{\sigma \left(\rho \right(\xi ,\zeta \left)\right)}{\left[\sigma \right(r\rho (\xi ,\zeta )\left)\right]}}={\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}},\forall \xi \ne \zeta .\hfill \end{array}$$

Hence, C is a σ-($\varphi ,\phi$)-contraction map.

The following example shows that $\sigma$-Caristi map is not a $\sigma$-contraction map, and it is not a generalized $\sigma$-contraction.

Example 4.

Let $B=[0,\infty )$ and $\rho (\xi ,\zeta ))=\mid \xi -\zeta \mid ,\forall \xi ,\zeta \in B$.

Let us define a map $C:B\to B$ by $C\xi =\sqrt{\xi }$, and let $\varphi \left(t\right)=\phi \left(t\right)=t,\sigma \left(t\right)=e^t,\forall t>0$.

Then, we infer that, for all $\xi \in B$,

$${\displaystyle \frac{\sigma \left(\phi \right(\xi \left)\right)}{\sigma \left(\phi \right(C\xi \left)\right)}}=\sigma (\phi \left(\xi \right)-\phi \left(C\xi \right))=\sigma (\xi -\sqrt{\xi })=\sigma \left(\rho (\xi ,C\xi )\right).$$

Hence, C is a σ-Caristi map.

We now show that C is not a generalized σ-contraction map.

Suppose that C is a generalized σ-contraction map.

Then, for all $\xi ,\zeta \in B$ with $\xi >\zeta$,

$$\begin{array}{cc}\hfill & e^{\sqrt{\xi }-\sqrt{\zeta }}=\sigma \left(\rho (C\xi ,C\zeta )\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\phi \right(\rho (\xi ,\zeta )\left)\right)}{\sigma \left(\phi \right(\rho (C\xi ,C\zeta )\left)\right)}}={\displaystyle \frac{\sigma \left(\rho \right(\xi ,\zeta \left)\right)}{\sigma \left(\rho \right(C\xi ,C\zeta \left)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{e^{\xi -\zeta }}{e^{\sqrt{\xi }-\sqrt{\zeta }}}}=e^{(\sqrt{\xi }-\sqrt{\zeta })(\sqrt{\xi }+\sqrt{\zeta }-1)}.\hfill \end{array}$$

Hence,

$$\sqrt{\xi }+\sqrt{\zeta }-1\ge 1$$

which leads to a contradiction, for $\xi ={\displaystyle \frac{1}{4}},\zeta ={\displaystyle \frac{1}{16}}$.

Hence, C is not a generalized σ-contraction.

Example 5.

Let $B=[5,\infty )$ and $\rho (\xi ,y)=\mid \xi -y\mid ,\forall \xi ,y\in B$.

Define a map $C:B\to B$ by $C\xi ={\displaystyle \frac{1}{5}}\xi +4$, and let $\varphi \left(t\right)=t,\phi \left(t\right)={\displaystyle \frac{1}{2}}t,\sigma \left(t\right)=e^t\forall t>0$.

$$\begin{array}{cc}\hfill & \sigma \left(\rho (C\xi ,C\zeta )\right)=\sigma ({\displaystyle \frac{1}{5}}\mid \xi -\zeta \mid )\hfill \\ \hfill \le & \sigma ({\displaystyle \frac{4}{5}}\mid \xi -\zeta \mid )=\sigma (\varphi (\mid \xi -\zeta \mid )-\varphi (\mid C\xi -C\zeta \mid ))\hfill \\ \hfill =& \sigma (\varphi \left(\rho (\xi ,\zeta )\right)-\varphi \left(\rho (C\xi ,C\zeta )\right))={\displaystyle \frac{\sigma \left(\varphi \right(\rho (\xi ,\zeta ))}{\varphi \left(\rho \right(C\xi ,C\zeta \left)\right)}}.\hfill \end{array}$$

Thus, C is a generalized σ-contraction map.

We now show that C is not a σ-Caristi map.

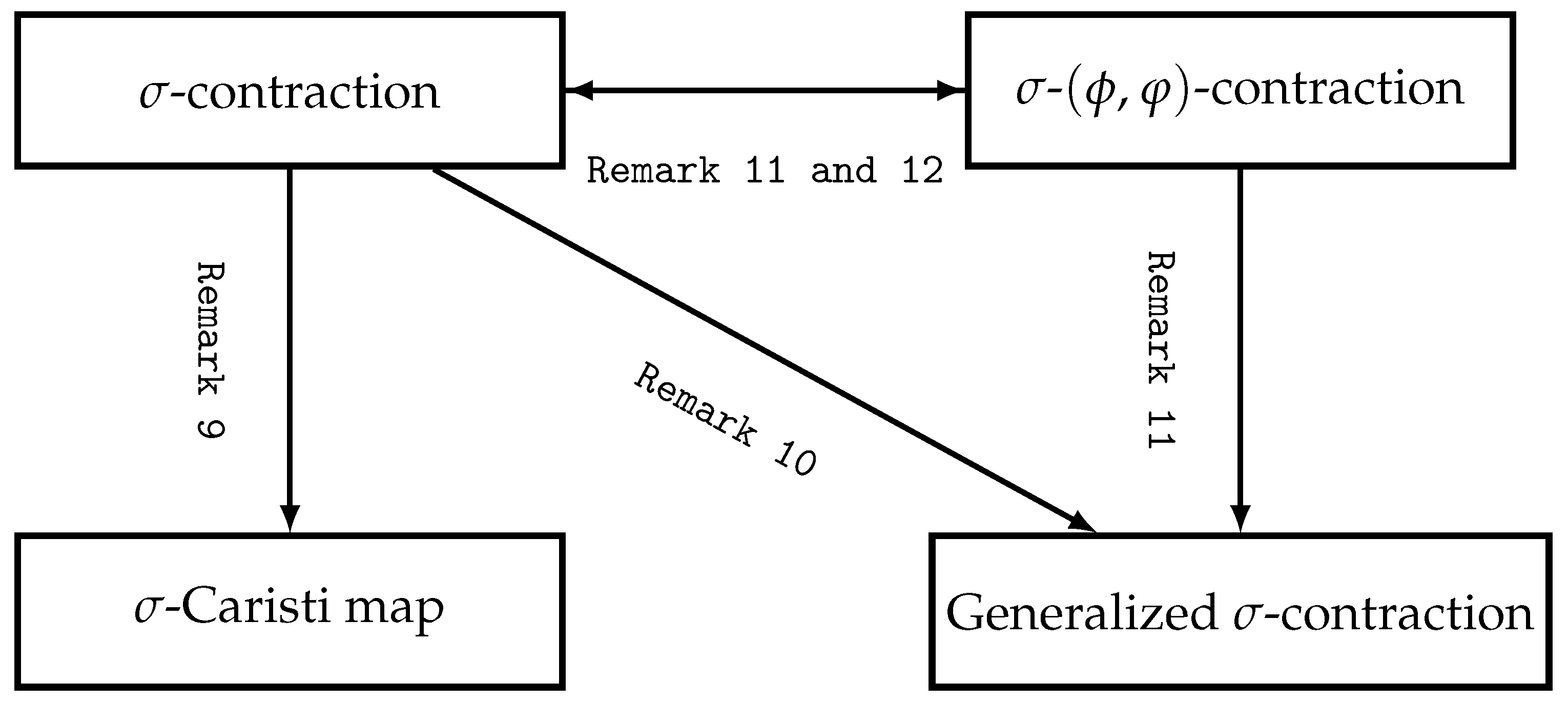
We infer that, for all $\xi ,\zeta \in B$,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\sigma \left(\varphi \right(\xi )}{\sigma \left(\varphi \right(C\xi \left)\right)}}=\sigma (\varphi \left(\xi \right)-\varphi \left(C\xi \right))=\sigma ({\displaystyle \frac{2}{5}}\xi -2)\hfill \\ \hfill <& \sigma ({\displaystyle \frac{4}{5}}\xi -4)=\sigma \left(\rho (\xi ,C\xi )\right)\hfill \end{array}$$

This implies that C is not a σ-Caristi map.

The following figure is derived from the previously mentioned remarks and the above examples. Here, the conditions of $\sigma$ applied in each remark are also applied.

The following Figure 1 was created with reference to [42].

From the above figure, it can be seen that a $\sigma$-contraction implies a $\sigma$-Caristi mapping, a generalized $\sigma$-contraction, and a $\sigma$-($\varphi ,\phi$)-contraction. Moreover, a $\sigma$-($\varphi ,\phi$)-contraction also implies a $\sigma$-contraction. On the other hand, there is no implication relationship between the generalized $\sigma$-contraction and the $\sigma$-Caristi mapping.

By taking $\sigma \left(u\right)=1+ln(1+u),u>0$ in Theorem 1, we acquire Corollary 7.

Corollary 7.

Let $C\in \mathcal{CM}(B,B)$ be such that

$$1+ln(1+\rho (\xi ,C\xi ))\le {\displaystyle \frac{1+ln(1+\varphi (\xi \left)\right)}{1+ln(1+\varphi (C\xi \left)\right)}},\forall \xi \in B(\xi \ne C\xi ),$$

where $\varphi :B\to [a,\infty )$ is an lsc function, $a>0$.

Then, C possesses a fixed point.

We apply Theorem 1 to prove the existence of coupled fixed points.

Let B be a nonempty set, and let $P:B\times B\to B$ be a map. A point $(\xi ,\zeta )\in B\times B$ is said to be a coupled fixed point of P if it satisfies

$$P(\xi ,\zeta )=\xi \mathrm{and}P(\zeta ,\xi )=\zeta .$$

Lemma 3

([43]). Let B be a nonempty set, $(\xi ,\zeta )\in B\times B$, and let $P:B\times B\to B$ be a map. We assume that $Q:B\times B\to B\times B$ is a map defined by

$$Q(\xi ,\zeta )=\left(P\right(\xi ,\zeta ),P(\zeta ,\xi \left)\right).$$

(33)

Then, we find that

$$P(\xi ,\zeta )=\xi \mathit{and}P(\zeta ,\xi )=\zeta ⟺Q(\xi ,\zeta )=(\xi ,\zeta ).$$

Lemma 4.

Let $(B,\rho )$ be a complete Branciari distance space. We define $\widehat{\rho }:B^2\times B^2\to [0,\infty )$ by

$$\widehat{\rho }((\xi ,\zeta ),(\varsigma ,\iota ))=\rho (\xi ,\varsigma )+\rho (\zeta ,\iota ).$$

(34)

Then, $(B\times B,\widehat{\rho })$ is a complete Branciari distance space.

Proof. 

Let $(\xi ,\zeta ),(\varsigma ,\iota )\in B\times B$. Then, we have that

$$\widehat{\rho }((\xi ,\zeta ),(\varsigma ,\iota ))=0\iff \rho (\xi ,\varsigma )+\rho (\zeta ,\iota )=0\iff (\xi ,\zeta )=(\varsigma ,\iota ).$$

Thus, ($\rho 1$) is satisfied. Obviously, ($\rho 2$) holds.

We infer that for all $(\xi ,\zeta ),(\varsigma ,\iota )\in B\times B$ and for all distinct points $(\mu ,\nu ),(\kappa ,\omega )\in B\times B\setminus \left\{\right(\xi ,\zeta ),(\varsigma ,\iota \left)\right\}$,

$$\begin{array}{cc}\hfill & \widehat{\rho }((\xi ,\zeta ),(\varsigma ,\iota ))=\rho (\xi ,\varsigma )+\rho (\zeta ,\iota )\hfill \\ \hfill \le & \rho (\xi ,\mu )+\rho (\mu ,\kappa )+\rho (\kappa ,\varsigma )+\rho (\zeta ,\nu )+\rho (\nu ,\omega )+\rho (\omega ,\iota )\}\hfill \\ \hfill \le & \rho (\xi ,\mu )+\rho (\zeta ,\nu )+\rho (\mu ,\kappa )+\rho (\nu ,\omega )+\rho (\kappa ,\varsigma ),\rho (\omega ,\iota )\hfill \\ \hfill =& \widehat{\rho }((\xi ,\zeta ),(\mu ,\nu ))+\widehat{\rho }((\mu ,\nu ),(\kappa ,\omega ))+\widehat{\rho }((\kappa ,\omega ),(\varsigma ,\iota )).\hfill \end{array}$$

Thus, ($\rho 3$) holds. Hence, $(B\times B,\widehat{\rho })$ is a Branciari distance space.

We now show that $(B\times B,\widehat{\rho })$ is complete.

Let $\{{\varpi }_n=({\xi }_n,{\zeta }_n)\}\subset B\times B$ be a Cauchy sequence, and let $ϵ>0$ be given.

Then, there exists $n_0\in \mathbb{N}$ such that for all $m>n>n_0$,

$$\widehat{\rho }({\varpi }_n,{\varpi }_m)<ϵ,$$

which implies that

$$\rho ({\xi }_n,{\xi }_m)<{\displaystyle \frac{1}{2}}ϵ\mathrm{and}\rho ({\zeta }_n,{\zeta }_m)<{\displaystyle \frac{1}{2}}ϵ\mathrm{for}\mathrm{all}m>n>n_0.$$

Hence, $\left\{{\xi }_n\right\}$ and $\left\{{\zeta }_n\right\}$ are Cauchy sequences in B. From the completeness of B, there exist $\xi ,\zeta \in B$ such that

$$\underset{n\to \infty }{lim}\rho (\xi ,{\xi }_n)=0\mathrm{and}\underset{n\to \infty }{lim}\rho (\zeta ,{\zeta }_n)=0.$$

Hence, there exists $n_1\in \mathbb{N}$ such that for all $n>n_1$,

$$\rho ({\xi }_n,\xi )<{\displaystyle \frac{1}{2}}ϵ\mathrm{and}\rho ({\zeta }_n,\zeta )<{\displaystyle \frac{1}{2}}ϵ.$$

Thus, we have that for all $n>n_1,$

$$\widehat{\rho }({\varpi }_n,(\xi ,\zeta ))=\widehat{\rho }(({\xi }_n,{\zeta }_n),(\xi ,\zeta ))=\rho ({\xi }_n,\xi )+\rho ({\zeta }_n,\zeta )<ϵ.$$

Hence, we have the desired result. □

Corollary 8.

Let $(B,\rho )$ be a complete Branciari distance space. We assume that $P:B\times B\to B$ is a map such that for all $(\xi ,\zeta )\in B\times B$ with $(\xi ,\zeta )\ne \left(P\right(\xi ,\zeta ),P(\zeta ,\xi \left)\right)$,

$$\sigma (max\{\rho (\xi ,P(\xi ,\zeta )),\rho (\zeta ,P(\zeta ,\xi ))\})\le {\displaystyle \frac{\sigma \left(\widehat{\varphi }(\xi ,\zeta )\right))}{\sigma \left(\widehat{\varphi }(P(\xi ,\zeta ),P(\zeta ,\xi ))\right)}}$$

(35)

where $\widehat{\varphi }:B\times B\to [a,\infty )$ is an lsc function, $a>0$. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), and (${\sigma }_5$), then P possesses a coupled fixed point.

Proof. 

Let Q and $\widehat{\rho }$ be defined as in (31) and (32), respectively.

Then, from (33), we find that for all $(\xi ,\zeta )\in B\times B$ with $(\xi ,\zeta )\ne Q(\xi ,\zeta )$,

$$\begin{array}{cc}\hfill & \sigma (\widehat{\rho }((\xi ,\zeta ),Q(\xi ,\zeta ))=\sigma (max\{\rho (\xi ,P(\xi ,\zeta )),\rho (y,P(\zeta ,\xi ))\})\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\widehat{\varphi }(\xi ,\zeta )\right)}{\sigma \left(\widehat{\varphi }(P(\xi ,\zeta ),P(\zeta ,\xi ))\right)}}={\displaystyle \frac{\sigma \left(\widehat{\varphi }(\xi ,\zeta )\right)}{\sigma \left(\widehat{\varphi }\left(Q(\xi ,\zeta )\right)\right)}}.\hfill \end{array}$$

By Theorem 1, Q possesses a fixed point. Thus, P possesses a coupled fixed point. □

The following result is obtained using Remark 2.

Corollary 9.

Let $(B,\rho )$ be a complete metric space. We assume that $P:B\times B\to B$ is a map such that for all $(\xi ,\zeta )\in B\times B$ with $(\xi ,\zeta )\ne \left(P\right(\xi ,\zeta ),P(\zeta ,\xi \left)\right)$,

$$\sigma (max\{\rho (\xi ,P(\xi ,\zeta )),\rho (\zeta ,P(\zeta ,\xi ))\})\le {\displaystyle \frac{\sigma \left(\widehat{\varphi }(\xi ,\zeta )\right))}{\sigma \left(\widehat{\varphi }(P(\xi ,\zeta ),P(\zeta ,\xi ))\right)}}$$

(36)

where $\widehat{\varphi }:B\times B\to [a,\infty )$ is an lsc function, $a>0$. If σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), and (${\sigma }_5$), then P possesses a coupled fixed point.

Lemma 5.

Let $(B,\rho )$ be a complete Branciari distance space. Suppose that σ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), and (${\sigma }_5$).

Then, the following assertions are equivalent.

(i) 

We assume that $P:B\times B\to B$ satisfies the condition

$$\sigma (\rho (P(\xi ,\zeta ),P({\xi }_{*},{\zeta }_{*}))\le {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^{\alpha }{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^{\beta }$$

(37)

for all $\xi ,\zeta ,{\xi }_{*},{\zeta }_{*}\in B$, where $0<\alpha +\beta <1$.

Then, P possesses a unique coupled fixed point.

(ii) 

We assume that $C:B\to B$ satisfies the condition

$$\sigma \left(\rho (C\xi ,C\zeta )\right)\le {\left[\sigma \left(\rho (\xi ,\zeta )\right)\right]}^k$$

(38)

for all $\xi ,\zeta \in B$, where $0<k<1$.

Then, C possesses a unique fixed point.

Proof. 

Firstly, we show that (i) implies (ii).

Let $k=\alpha +\beta$. Then, for all $\xi ,y,{\xi }_{*},y_{*}\in B$, it follows from (i) that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \sigma (\widehat{\rho }(Q(\xi ,\zeta ),Q({\xi }_{*},{\zeta }_{*})\hfill \\ \hfill =& \sigma (\widehat{\rho }((P(\xi ,\zeta ),P(\zeta ,\xi )),(P({\xi }_{*},{\zeta }_{*}),P({\zeta }_{*},{\xi }_{*})))\hfill \\ \hfill =& \sigma (\rho (P(\xi ,\zeta ),P({\xi }_{*},{\zeta }_{*}))+\rho (P(\zeta ,\xi ),P({\zeta }_{*},{\xi }_{*})))\hfill \\ \hfill \le & \sigma \left(\rho (P(\xi ,\zeta ),P({\xi }_{*},{\zeta }_{*}))\right)\sigma \left(\rho (P(\zeta ,\xi ),P({\zeta }_{*},{\xi }_{*}))\right)\hfill \\ \hfill \le & {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^{\alpha }{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^{\beta }{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^{\alpha }{\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^{\beta }\hfill \\ \hfill =& {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^{\alpha +\beta }{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^{\alpha +\beta }\hfill \\ \hfill =& {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^k{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^k\hfill \\ \hfill =& {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^k\hfill \\ \hfill =& {\left[\sigma (\rho (\xi ,{\xi }_{*})+\rho (\zeta ,{\zeta }_{*}))\right]}^k\hfill \\ \hfill =& {\left[\sigma \left(\widehat{\rho }((\xi ,\zeta ),({\xi }_{*},{\zeta }_{*}))\right)\right]}^k.\hfill \end{array}\end{array}$$

Hence, the proof follows from (ii).

Let us define a map $P:B\times B\to B$ using

$$P(\xi ,\zeta )=C\xi .$$

It follows from (34) that for all $\xi ,\zeta ,{\xi }_{*},{\zeta }_{*}\in B$,

$$\sigma \left(\rho (P(\xi ,\zeta ),P({\xi }_{*},{\zeta }_{*}))\right)\le {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^k,$$

which corresponds to (35) with $\alpha =k$ and $\beta =0$.

Thus, by (i), P has a unique coupled fixed point $(\xi ,\zeta )\in B\times B$. Hence,

$$x=P(\xi ,\zeta )=C\xi \mathrm{and}\zeta =P(\xi ,\zeta )=C\zeta .$$

From (26), we have

$$\rho (\xi ,\zeta )=\rho \left(P\right(\xi ,\zeta ),P(\zeta ,\xi \left)\right)\le k\rho (\xi ,\zeta ),$$

which implies that $\xi =\zeta$.

Thus, C has a unique fixed point. □

Corollary 10.

Let $(B,\rho )$ be a complete Branciari distance space. Suppose that ρ satisfies (${\rho }_1$), (${\rho }_3$), (${\rho }_4$), and (${\rho }_5$). We assume that $P:B\times B\to B$ satisfies the condition

$$\sigma (\rho (P(\xi ,\zeta ),P({\xi }_{*},{\zeta }_{*}))\le {\left[\sigma \left(\rho (\xi ,{\xi }_{*})\right)\right]}^{\alpha }{\left[\sigma \left(\rho (\zeta ,{\zeta }_{*})\right)\right]}^{\beta }$$

(39)

for all $\xi ,\zeta ,{\xi }_{*},{\zeta }_{*}\in B$, where $0<\alpha +\beta <1$.

Then, P possesses a unique coupled fixed point.

Proof. 

By Remark 9 and Theorem 1, C has a fixed point whenever the contractive condition in (36) is satisfied. Obviously, the contractive condition in (36) guarantees the uniqueness of the fixed point. From Lemma 5, we have the desired result. □

Remark 13.

The above result is an extension of Theorem 2.2 from [13], and Lemma 5 and Corollary 10 hold for n-tuple fixed points (see [13]).

5. Applications

The most interesting application of fixed-point theory is its application to function spaces. In this section, we show the existence and uniqueness of solutions to integral equations and differential equations in function spaces.

Let $C\left(\right[0,T],\mathbb{R})=\{f\mid f:[0,T]\to \mathbb{R}\mathrm{be}\mathrm{continuous}\}$, and let $\rho (f,g)=sup\{\mid f(t)-g(t)\mid :t\in [0,T\left]\right\}$, where $T>0$. Obviously, $\left(C\right([0,T],\mathbb{R}),\rho )$ is a complete metric space, and hence, it is a complete Branciari distance space.

5.1. Integral Equations

We consider an integral equation of the form

$$f\left(t\right)=p\left(t\right)+{\int }_0^{T}H(t,s)K(s,f\left(s\right))ds,t\in [0,T]$$

(40)

where $p:[0,T]\to \mathbb{R},K:[0,T]\times \mathbb{R}\to \mathbb{R}$ and $H:[0,T]\times [0,T]\to \mathbb{R}$ are continuous, and $H(t,·):[0,T]\to \mathbb{R}$ is measurable.

Theorem 3.

We assume that $H(t,s)\ge 0$ for all $t,s\in [0.T]$, and ${\int }_0^{T}H(t,s)ds\le 1$ for all $t\in [0,T]$, and we suppose that for each $t\in [0,T]$ and for all $f,g\in C\left(\right[0,T],\mathbb{R})$,

$$\mid K(t,f\left(t\right))-K(t,g\left(t\right))\mid \le -1+\sqrt{1+{(f\left(t\right)-g\left(t\right))}^2}.$$

Then, the integral Equation (31) has a solution in $C\left(\right[0,T],\mathbb{R})$.

Proof. 

We define a map $Sf\left(t\right)=p\left(t\right)+{\int }_0^{T}H(t,s)K(s,f\left(s\right))ds,t\in [0,T]$, and suppose that $\sigma$ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), (${\sigma }_5$), and (${\sigma }_6$).

We infer that for all $t\in [0,T]$,

$$\begin{array}{cc}\hfill & \mid Sf\left(t\right)-Sg\left(t\right)\mid =\mid {\int }_0^{T}H(t,s)\left(K\right(s,f\left(s\right)-K(s,g\left(s\right))ds\mid \hfill \\ \hfill \le & {\int }_0^{T}H(t,s)\mid K(s,f\left(s\right)-K(s,g\left(s\right)\mid ds\hfill \\ \hfill \le & {\int }_0^{T}H(t,s)(-1+\sqrt{1+{(f\left(s\right)-g\left(s\right))}^2})ds\hfill \\ \hfill \le & {\int }_0^{T}H(t,s)(-1+\sqrt{1+{\left(\rho (f,g)\right)}^2})ds\hfill \\ \hfill \le & -1+\sqrt{1+{\left(\rho (f,g)\right)}^2}.\hfill \end{array}$$

By taking the supremum and applying (${\sigma }_6$), we find that

$$\sigma \left(\rho (Sf,Sg)\right)\le \sigma (-1+\sqrt{1+{\left(\rho (f,g)\right)}^2}),$$

which implies that

$$\begin{array}{cc}\hfill & \sigma \left(\rho (Sf,Sg)\right)\le \sigma {\left(\rho (f,g)\right)}^2-{\left(\rho (Sf,Sg)\right)}^2)\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill =& \sigma \left(\varphi \right(\rho (f,g))-\varphi (\rho (Sf,Sg)\left)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\left(\varphi \right(\rho (f,g))}{\varphi \left(\rho \right(Sf,Sg\left)\right)}}\forall f,g\in [0,T]\hfill \end{array}$$

(42)

where $\varphi \left(t\right)=t^2$.

By Theorem 2, S has a fixed point. Thus, Equation (31) has a solution. □

5.2. Differential Equations

Our objective is to apply Theorem 2 to show the existence of a solution for the following first-order periodic boundary value problem:

$$\left\{\begin{array}{cc}& f^{\prime }\left(t\right)=\theta (t,f\left(t\right)),t\in [0,T],\hfill \\ \hfill & f\left(0\right)=f\left(T\right)\hfill \end{array}\right.$$

(43)

where $f\in C\left(\right[0,T],\mathbb{R})$, and $\theta :[0,T]\times \mathbb{R}\to \mathbb{R}$ is a continuous function.

Let $G(t,s)$ be a Green function defined by

$$G(t,s)=\left\{\begin{array}{cc}& {\displaystyle \frac{e^{\eta (T+s-t)}}{e^{\eta T}-1}},0\le s\le t\le T,\hfill \\ & {\displaystyle \frac{e^{\eta (s-t})}{e^{\eta T}-1}},0\le t\le s\le T\hfill \end{array}\right.$$

for any positive real number $\eta$ with $\eta >T$.

Note that

$$\underset{t\in [0,T]}{sup}{\int }_0^{T}G(t,s)ds=1.$$

The preceding problem (34) is equivalent to the integral equation

$$f\left(t\right)={\int }_0^{T}G(t,s)[\theta (s,f\left(s\right))+\eta f\left(s\right)]ds.$$

(44)

We define the map $S:C\left(\right[0,T],\mathbb{R})\to C\left(\right[0,T],\mathbb{R})$ by

$$S\left(f\left(t\right)\right)={\int }_0^{T}G(t,s)[\theta (s,f\left(s\right))+\eta f\left(s\right)]ds,t\in [0,T].$$

Then, f is a solution of (34) if and only if it is a fixed point of S. q

Theorem 4.

We assume that for any $f\left(t\right),g\left(t\right)\in C\left(\right[0,T],\mathbb{R})$,

$$\mid \theta (t,f\left(t\right))+\eta f\left(t\right)-[\theta (t,g\left(t\right))+\eta g\left(t\right)]\mid \le {\displaystyle \frac{-1+\sqrt{1+4{[f\left(t\right)-g\left(t\right)]}^2}}{2}}$$

(45)

where $t\in [0,T],\eta >T>0$.

Then, Equation (34) has a solution.

Proof. 

Suppose that $\sigma$ satisfies (${\sigma }_1$), (${\sigma }_3$), (${\sigma }_4$), (${\sigma }_5$), and (${\sigma }_6$).

Applying (36), we infer that for any $f\left(t\right),g\left(t\right)\in C\left(\right[0,T],\mathbb{R})$,

$$\begin{array}{cc}\hfill & \mid S\left(f\right(t\left)\right)-S\left(g\right(t\left)\right)\mid \hfill \\ \hfill =& \mid {\int }_0^{T}G(t,s)[\theta (s,f\left(s\right))+\eta f\left(s\right)]ds-{\int }_0^{T}G(t,s)[\theta (s,g\left(s\right))+\eta g\left(s\right)]ds\mid \hfill \\ \hfill \le & {\int }_0^{T}G(t,s)\mid \theta (s,f\left(s\right))+\eta f\left(s\right)-\theta (s,g\left(s\right))-\eta g\left(s\right)\mid ds\hfill \\ \hfill \le & \underset{t\in [0,T]}{sup}\mid \theta (s,f\left(s\right))+\eta f\left(s\right)-\theta (s,g\left(s\right))-\eta g\left(s\right)\mid {\int }_0^{T}G(t,s)ds\hfill \\ \hfill \le & {\displaystyle \frac{-1+\sqrt{1+4{[f\left(s\right)-g\left(s\right)]}^2}}{2}}\hfill \\ \hfill \le & {\displaystyle \frac{-1+\sqrt{1+4{\left[\rho (f,g)\right]}^2}}{2}}.\hfill \end{array}$$

We take the supremum to find that

$$\rho (S\left(f\right),S\left(g\right))\le {\displaystyle \frac{-1+\sqrt{1+4{\left[\rho (f,g)\right]}^2}}{2}},$$

which implies that

$$\begin{array}{cc}\hfill & \sigma \left(\rho \right(S\left(f\right),S\left(g\right)\left)\right)\hfill \\ \hfill \le & \sigma ({\left[\rho (f,g)\right]}^2-{\left[\rho (S\left(f\right),S\left(g\right))\right]}^2)\hfill \\ \hfill =& \sigma \left(\varphi \right(\rho (f,g))-\varphi (S\left(f\right),S\left(g\right)\left)\right)\hfill \\ \hfill \le & {\displaystyle \frac{\sigma \left(\varphi \right(\rho (f,g))}{\varphi \left(S\right(f),S(g\left)\right)}},\mathrm{where}\varphi \left(t\right)=t^2\forall t>0.\hfill \end{array}$$

(46)

By Theorem 2, S has a fixed point. Hence, Equation (34) has a solution. □

6. Conclusions

In this study, we give the concepts of $\sigma$-Caristi maps and generalized $\sigma$-contraction maps and have related fixed-point results in the setting of complete Branciari distances. By applying the main theorem, we have several corollaries, including Caristi’s fixed-point theorem, Jleli and Samet’s fixed-point theorem, and coupled fixed-point theorem. We give examples to illustrate the sequential topology and the main theorem. In particular, we provide an example of applying the main theorem to Newton’s method to find the roots of an equation. We investigated the relationships among various contraction conditions introduced in this paper. As applications, we solve an integral equation and an ordinary differential equation with the help of our main result.

In the future, based on our main theorem, we will investigate the $\sigma$-Ekland variational principle and the $\sigma$-Takahashi minimization principle, and we will discuss their equivalence with our main theorem.