The Complexity of Classes of Pyramid Graphs Based on the Fritsch Graph and Its Related Graphs

Abstract

A quantitative study of the complicated three-dimensional structures of artificial atoms in the field of intense matter physics requires a collaborative method that combines a statistical analysis of unusual graph features related to atom topology. Simplified circuits can also be produced by using similar transformations to streamline complex circuits that need laborious mathematical calculations during analysis. These modifications can also be used to determine the number of spanning trees required for specific graph families. The explicit derivation of formulas to determine the number of spanning trees for novel pyramid graph types based on the Fritsch graph, which is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle, is the focus of our study. We conduct this by utilizing our understanding of difference equations, weighted generating function rules, and the strength of analogous transformations found in electrical circuits.

1. Introduction

A spanning tree is a subgraph of an undirected, connected graph that contains every vertex in the original graph but only utilizes the fewest edges required to join them, creating a tree structure (i.e., no cycles). It basically connects every node in a network without forming unnecessary loops.

The complexity $\tau \left(G\right)$ of $G$ is another name for the number of spanning trees $\tau \left(G\right)$, which is equal to the total number of different spanning subgraphs of $G$ that are trees.

Determining closed-form expressions for the complexity (number of spanning trees) in various graph types has garnered significant interest. Eulerian circuit counting [1], network analysis techniques in psychological networks [2], chemical isomer enumeration [3,4], and solving intractable issues like the traveling salesman and Steiner tree problems [5] are some of the important applications of this field of study. It is also possible to identify the most complex graphs by examining various graph types, which have applications in network resilience [6,7].

A graph must have a spanning tree since every node in the network it represents needs to be able to communicate with every other node. Dependability can be raised by increasing the number of spanning trees.

A Kirchhoff classical result [8] from 1847 can be used to determine the number of spanning trees for a connected graph $G=(V,E)$ with $n$ vertices. With $A$ representing the adjacency matrix of $G$ and $D$ representing the diagonal matrix of its degrees, the Kirchhoff matrix is a characteristic matrix $L=D-A$, where $L=\left[a_{ij}\right]$ is defined as follows:

$$L=[a_{ij}]=\left\{\begin{array}{l}\mathit{deg}(v_i) \mathrm{i}\mathrm{f} i=j\\ -1 \mathrm{i}\mathrm{f} (v_i,v_j)\in E\left(G\right)\\ 0 \mathrm{i}\mathrm{f} (v_i,v_j)\notin E\left(G\right)\end{array}\right.$$

All co-factors of $L$ are equal to the number of spanning trees in the graph $G$.

Another technique to calculate the complexity of a graph $G \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} n \mathrm{v}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{e}\mathrm{s}$ is as follows: Let ${\mu }_1\ge {\mu }_2\ge \dots \ge {\mu }_n(=0)$ represent the $L$ matrix’s eigenvalues. Kelmans and Chelnokov [9] demonstrated the following in 1974:

$$\tau (G)={\displaystyle \frac{1}{n}}\prod _{i=1}^{n-1}{\mu }_i$$

(1)

One common method for counting the number of spanning trees is the deletion–contraction strategy. This method is dependable for determining the number of spanning trees $\tau \left(G\right)$ in a multigraph $G$. This technique makes use of the fact that

$$\tau \left(G\right)=\tau (G-e)+\tau (G/e)$$

(2)

where $G-e$ indicates the graph that is produced by deleting an arbitrary edge $e$, and $G/e$ indicates the graph that is produced by contracting an arbitrary edge e [10,11]. Numerous works have focused on counting and maximizing the number of spanning trees for various graph families [12,13,14].

Kirchhoff’s interest in electrical networks stemmed from the possibility that an edge-weighted graph, whose weights represent the conductance of the associated edges, may be thought of as an electrical network. It is possible to express the effect conductance between two vertices $u,v$ as the quotient of the (weighted) number of spanning trees and the (weighted) number of so-called thickets, which are spanning forests that have exactly two components and the characteristic that each component contains exactly one of the vertices $u,v$ [15,16]. Below are the effects of several simple changes on the number of spanning trees. $\tau \left(G\right)$ is the weighted number of spanning trees. Let $G$ be an edge weighted graph and $H$ be its electrically equivalent graph.

• Parallel edges: The count of spanning trees, $\tau \left(H\right)$, stays the same when two parallel edges in $G$ with conductances of $x$ and $y$ are combined to form a single edge in $H$ with a conductance of $x+y$.
• Serial edges: $\tau \left(H\right)$ is equal to $(1/(x+y)$ times $\tau \left(G\right)$ if two serial edges in $G$ with conductances $x$ and $y$ are linked to generate a single edge in $H$ with a conductance $xy/(x+y)$.
• Δ-Y transformation: The number of spanning trees in $H$, $\tau \left(H\right)$, can be computed as ${\left(\mathit{xy}+\mathit{yz}+zx\right)}^2/xyz$ times $\tau \left(G\right)$ once a triangle in $G$ with conductances $x,y$, and $z$ is transformed into an electrically equivalent star graph in $H$ with conductances $u=\left(\mathit{xy}+\mathit{yz}+zx\right)/x$, $v=\left(\mathit{xy}+\mathit{yz}+zx\right)/y$, and $w=\left(\mathit{xy}+\mathit{yz}+zx\right)/z.$
• Y-Δ transformation is the process of converting a star graph in $G$ with conductances $x$, $y$, and $z$ into an electrically equivalent triangle in H with conductances $u=yz/\left(x+y+z\right)$, $v=xz/\left(\right(x+y+z)$, and $w=xy/\left(\right(x+y+z)$. The result $\tau \left(H\right)$ is given by $1/\left(\right(x+y+z)$ multiplied by $\tau \left(G\right)$.

2. Main Results

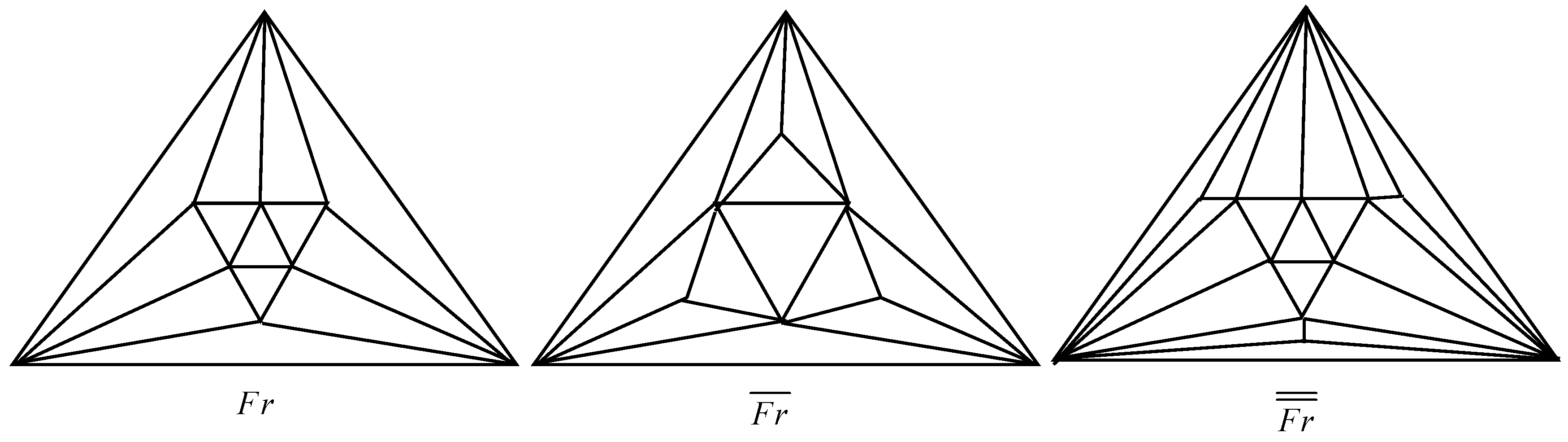
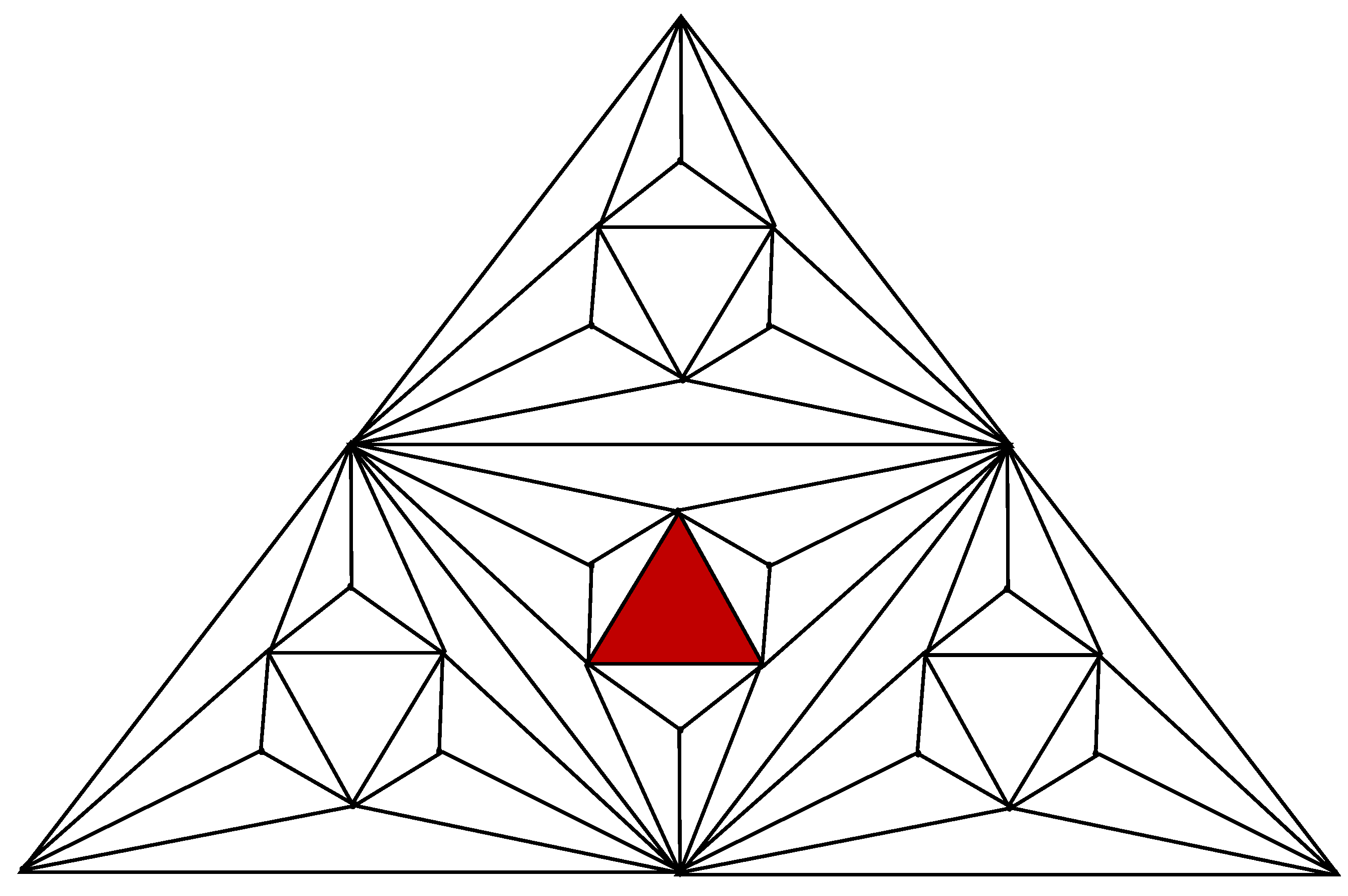
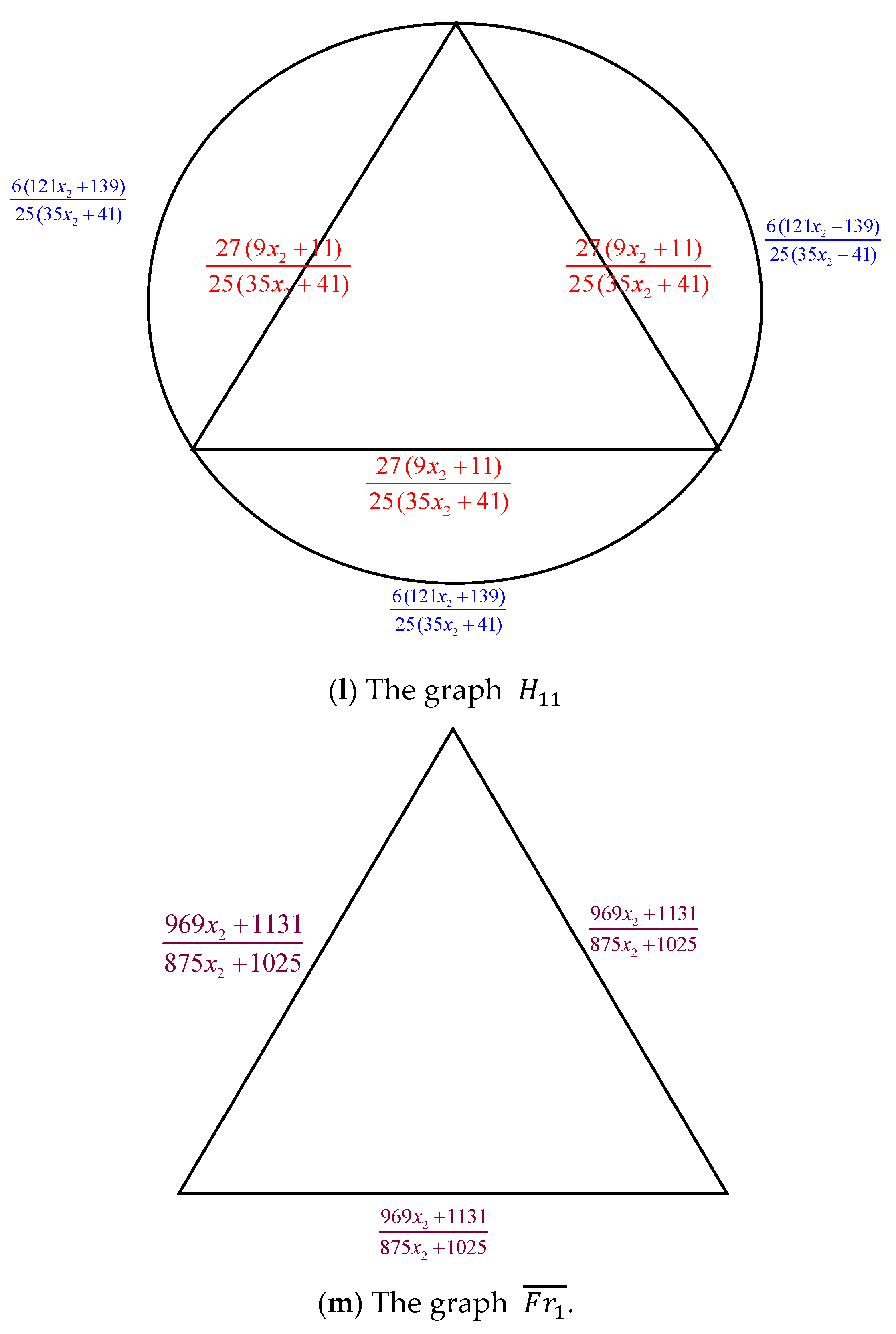
The Fritsch graph has nine vertices and twenty-one edges, making it a maximum planar graph. It is isomorphic to the triaugmented triangular prism’s skeleton. The Fritsch graph plays a crucial role in demonstrating flaws in Kempe’s attempted proof of the four-color theorem. The graph is notable because it highlights how Kempe chains, used in the flawed proof, can interact in a way that invalidates the color swapping strategy.

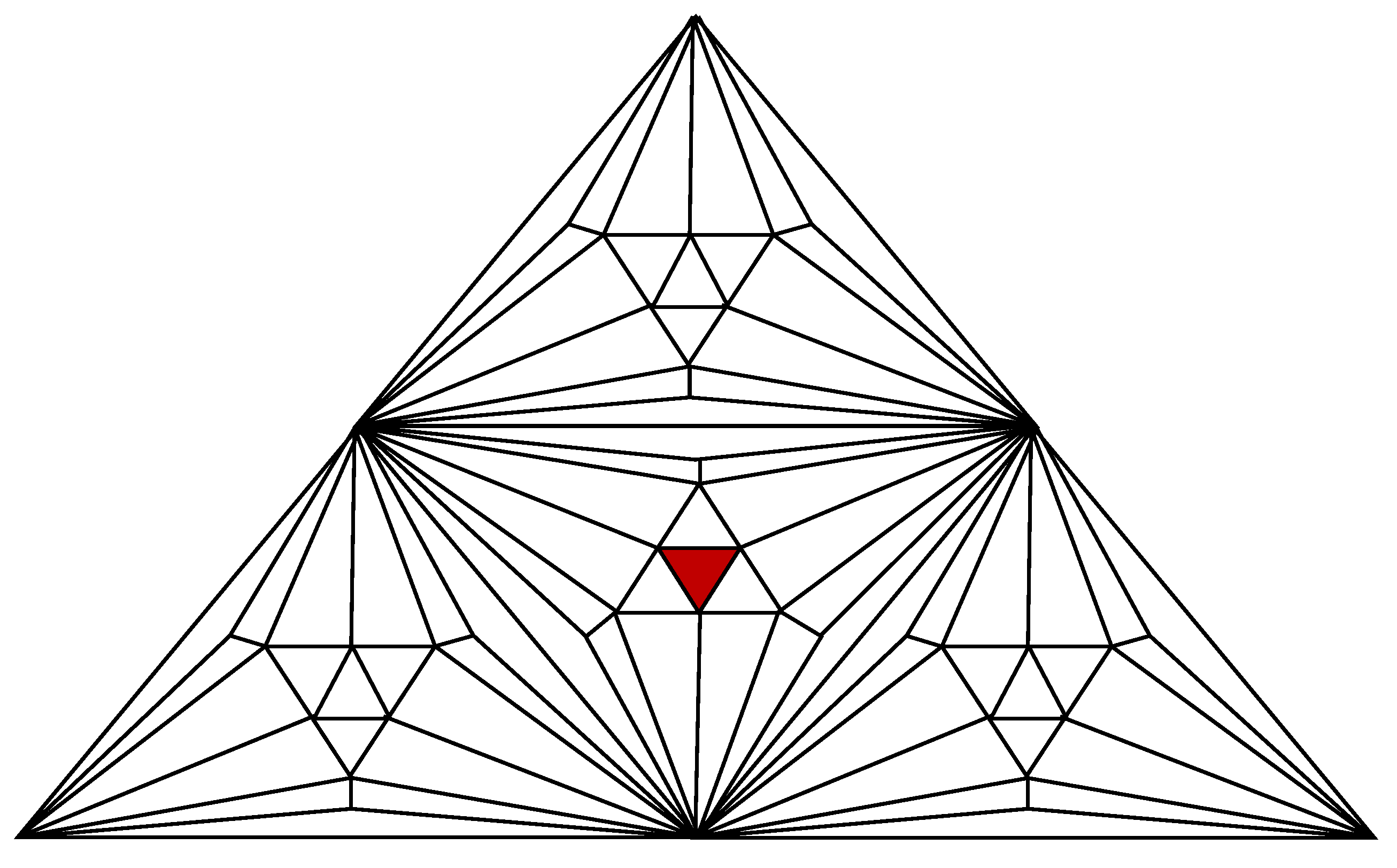
Creating a new structure from an old one is always the aim in mathematics. Graphs are another area where this is true, as a given set of graphs can be used to create many new graphs. The number of spanning trees of three new forms of pyramidal graphs made from the Fritsch graph and two of their related graphs, represented by $Fr,\overline{Fr}$ and $\overline{\overline{Fr}}$ respectively, will be precisely determined in this work, as illustrated in Figure 1.

2.1. Number of Spanning Trees of Pyramid Graph $F{r}_n$ Created by Fritsch $Fr$

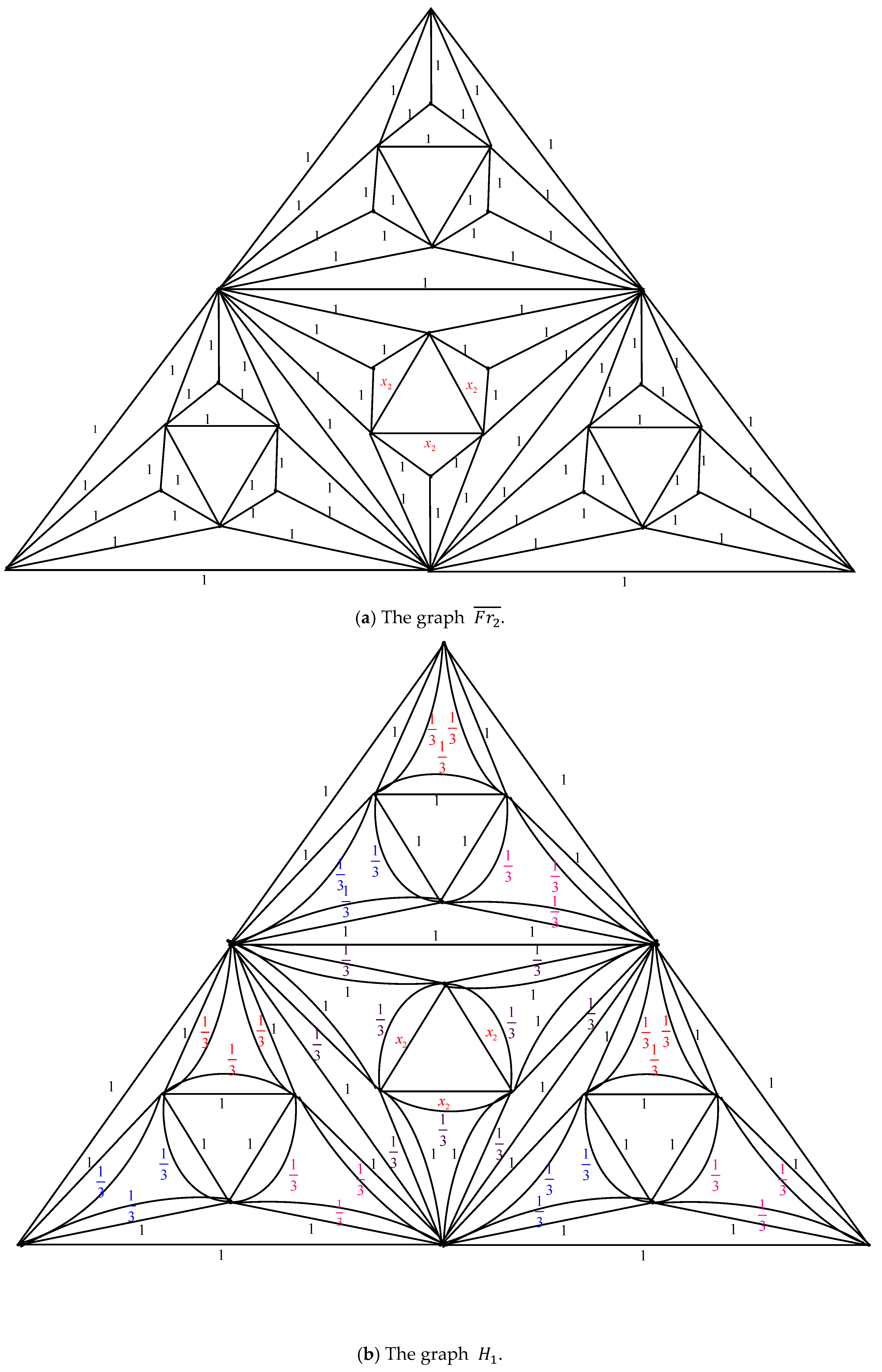
The pyramid graph $F{r}_n$ is defined recursively using the graph $F{r}_2$ and the graph $F{r}_1$ (triangle or $K_3$) as follows: $F{r}_n(n\ge 3)$ is created by replacing the center triangle in $F{r}_{n-1}$ with $F{r}_2$. See Figure 2. According to this construction, the total vertices $\left|V\left(F{r}_n\right)\right|$ and edges $\left|E(F{r}_n)\right|$ are $\left|V\left(F{r}_n\right)\right|=27n-24$ and $\left|E(F{r}_n)\right|=78n-75$, $n=\mathrm{1,2},\dots$. The average degree of $F{r}_n$ is in the large $n$ limit which is $5.8$.

Theorem 1.

The number of spanning trees in a pyramid graph, $F{r}_n$, created by the Fritsch graph series for $n\ge 1$, is determined by

$$\begin{gathered} 3\times {\left(71221248\right)}^{n-1}\times \\ {\left( {\displaystyle \frac{\left({\left( \frac{628563359+25097\sqrt{627267309} }{1296050}\right)}^{n-1 } \left( 412155311+16565\sqrt{627267309} \right)+1909 \left( 3155-\sqrt{627267309 }\right)\right)}{\left({\left( \frac{628563359+25097\sqrt{627267309}}{1296050} \right)}^{n-1} \left( 370187855+14656\sqrt{627267309 }\right)+47990351\right)}} \right)}^2 \\ {\times ( \left({\displaystyle \frac{47081}{2}}+{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}}\right){\left(25097+\sqrt{627267309 }\right)}^{n-2} \\ +\left( {\displaystyle \frac{47081}{2}}-{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}} \right){\left( 25097-\sqrt{627267309}\right)}^{n-2})}^2 \end{gathered}$$

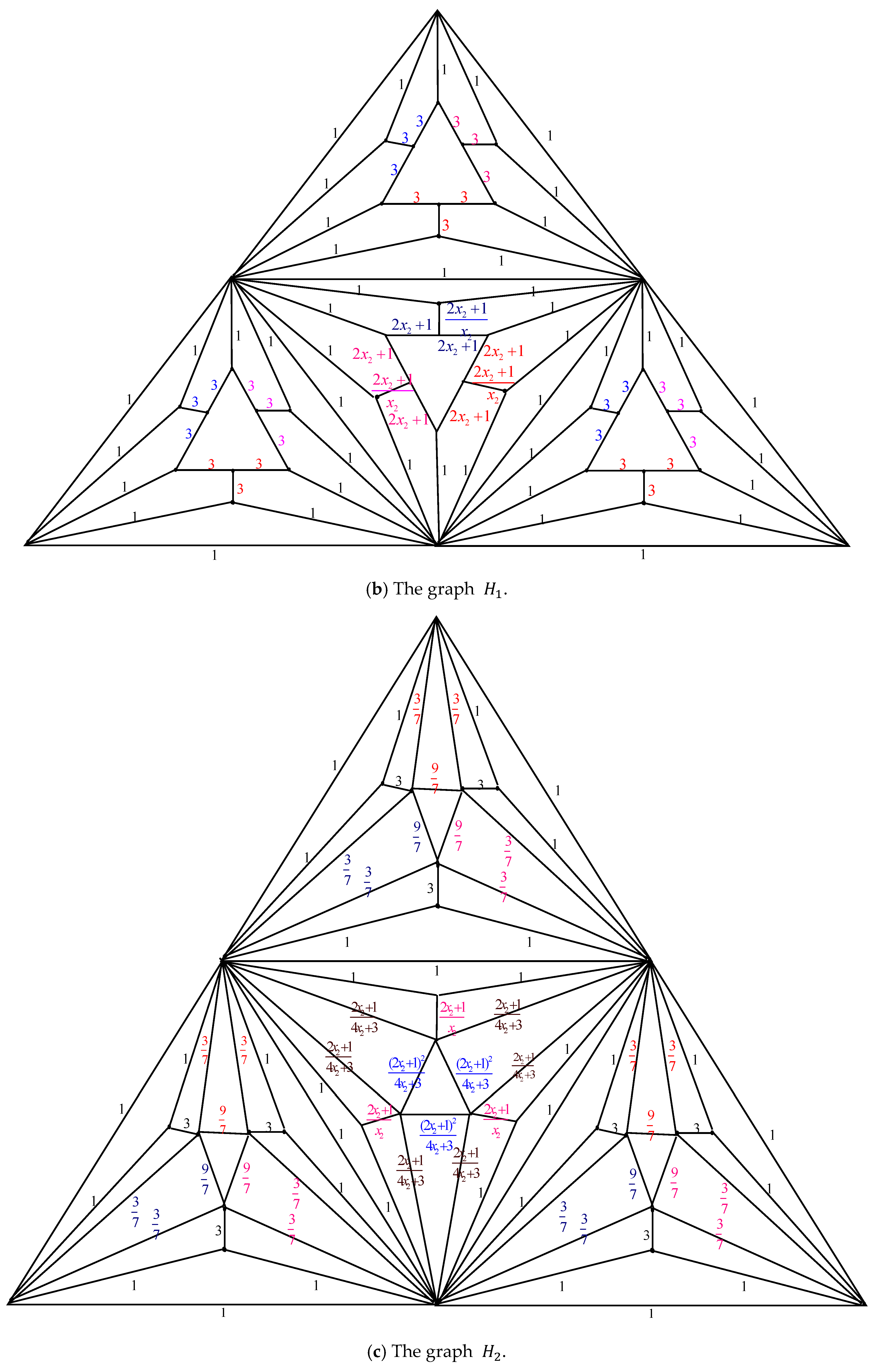
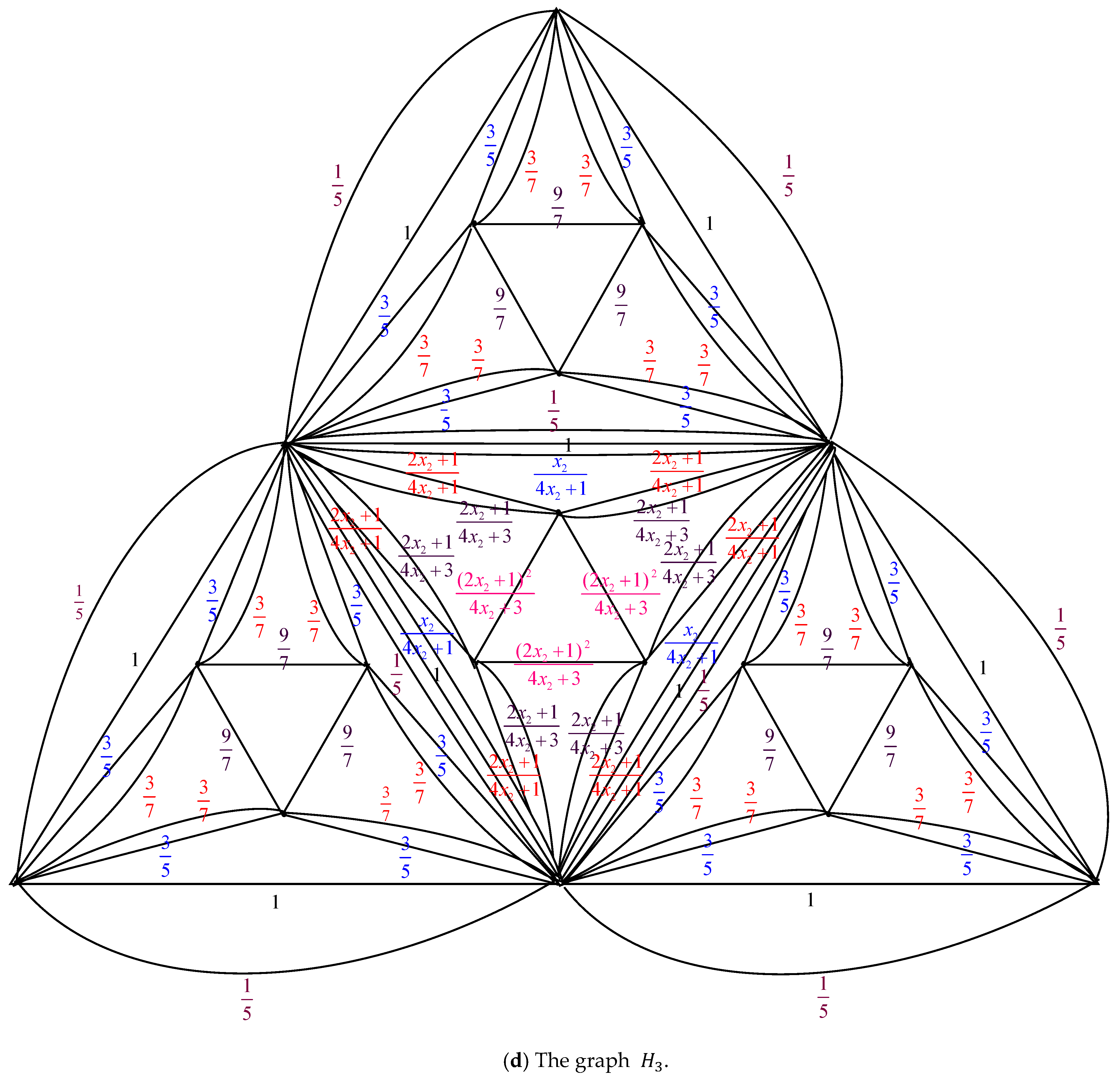
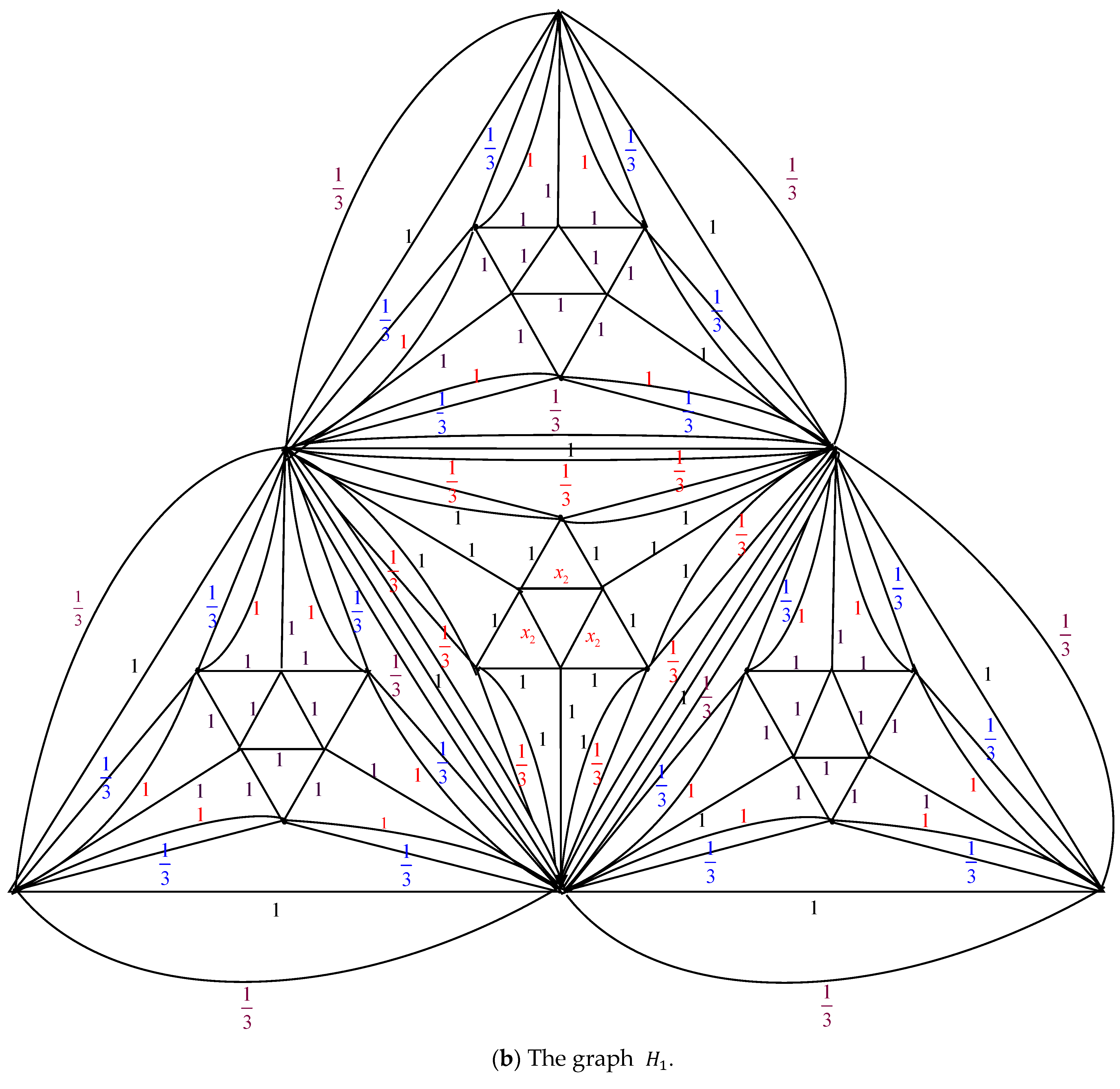
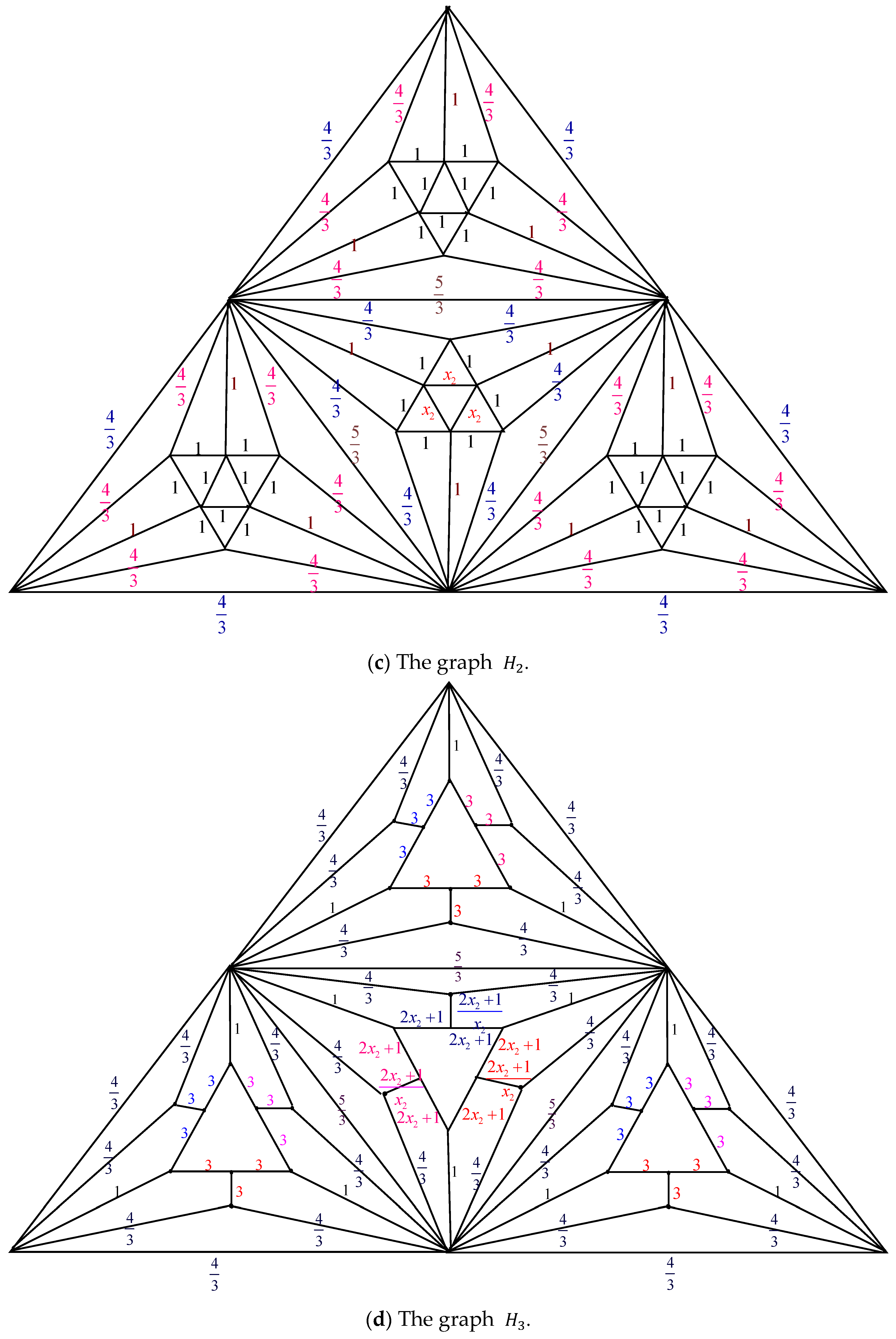
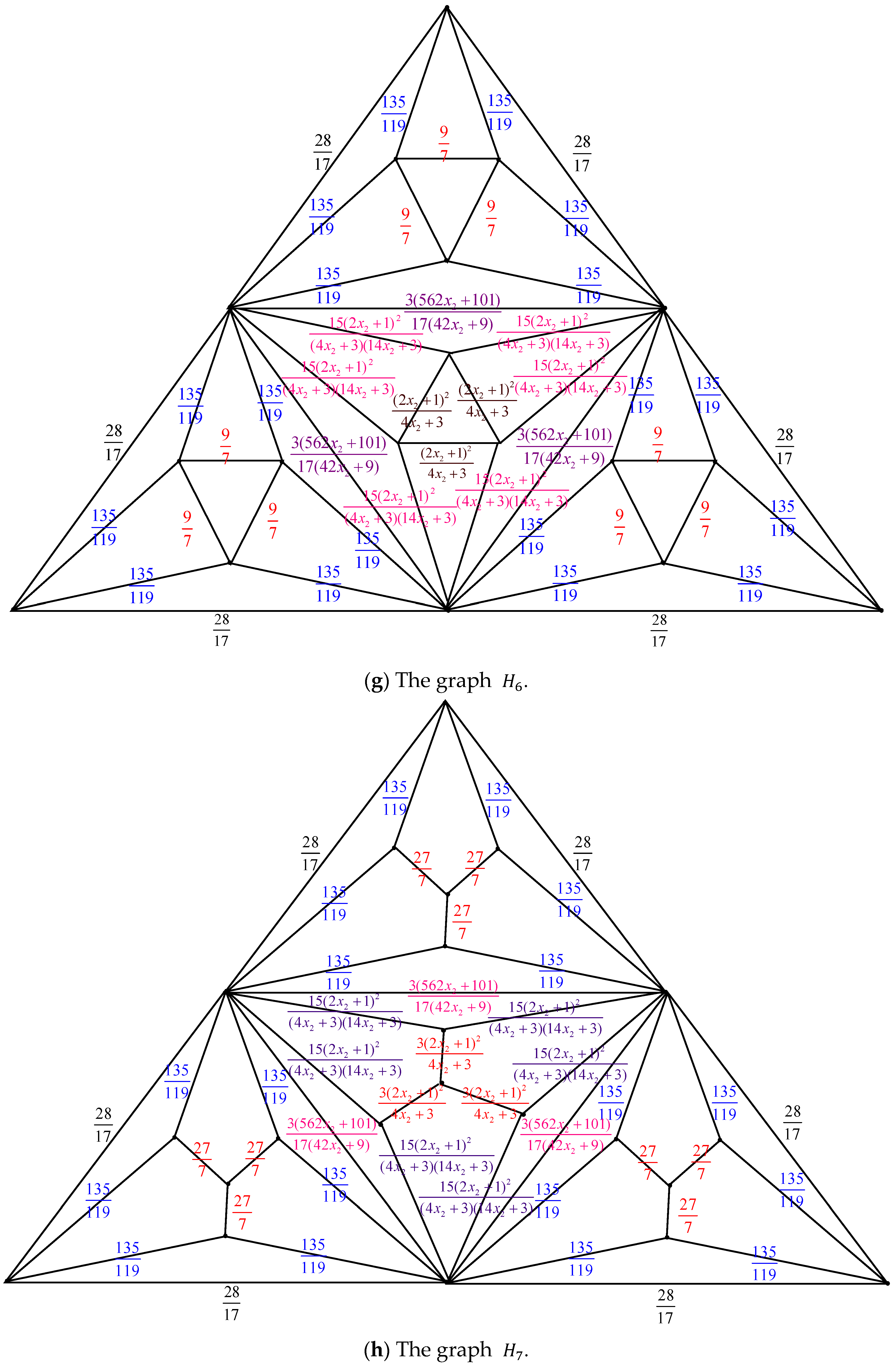
Proof. 

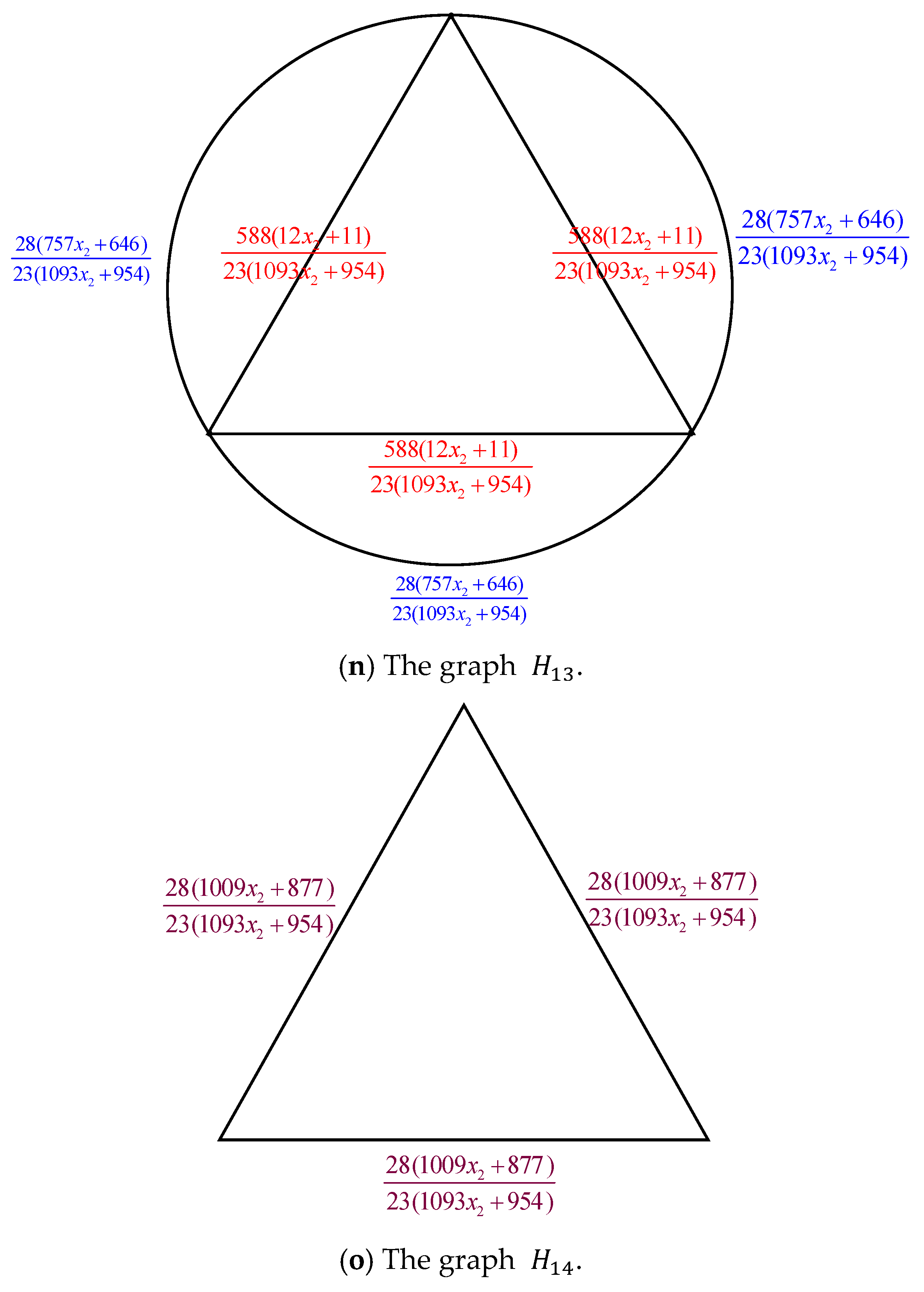
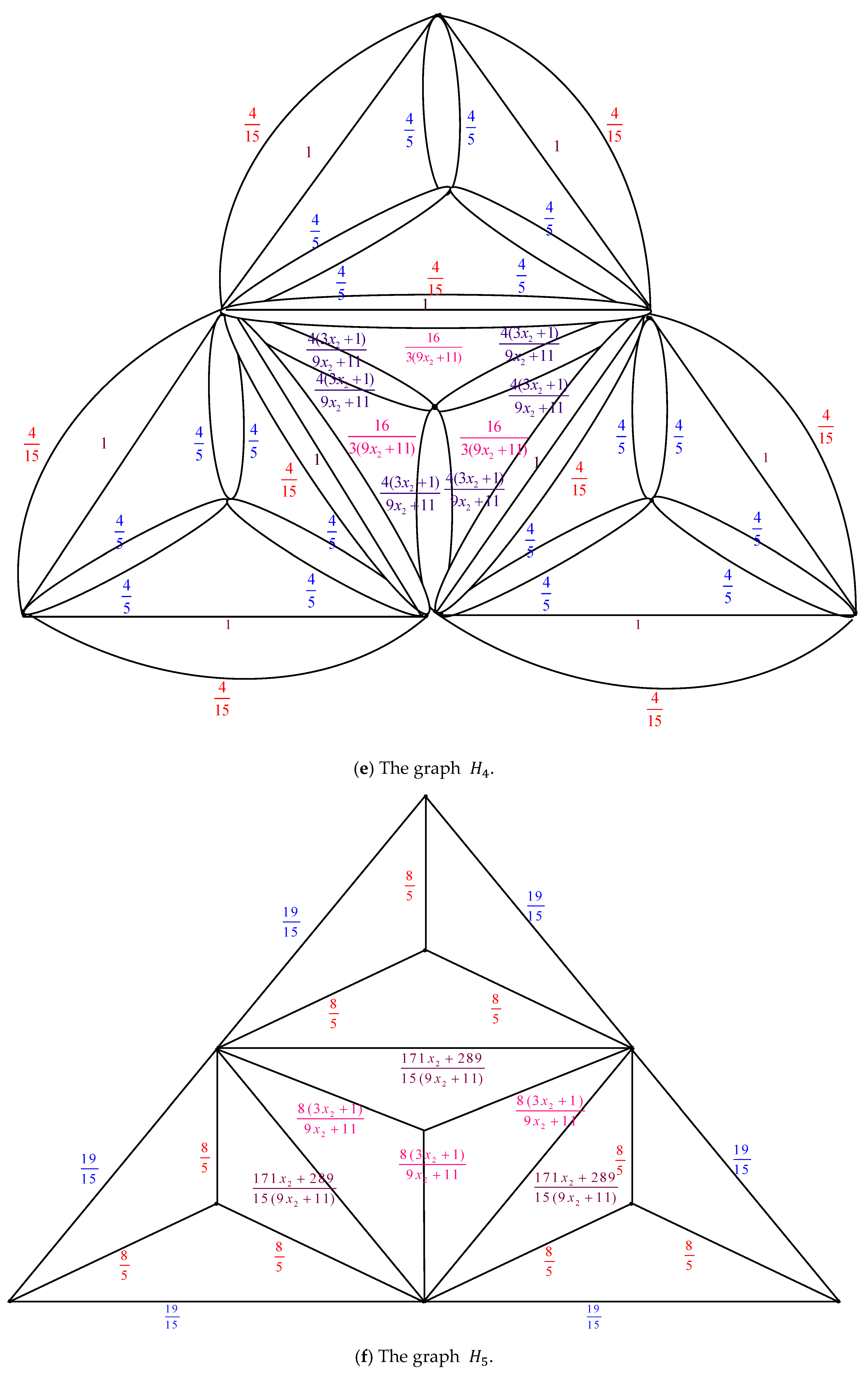
By applying the electrically equivalent transformation, $F{r}_i$ is converted to $F{r}_{i-1}$. Figure 3 illustrates the process of converting $F{r}_2$ to $F{r}_1$.

The result of combining these thirteen transformations is

$$\begin{gathered} \tau \left(F{r}_2\right)=\left[{\displaystyle \frac{{x_2}^3}{9^9{\left(2x_2+1\right)}^6}}\times 7^9\times {\left(4x_2+3\right)}^3\times {\left(5\right)}^9\times {\left({\displaystyle \frac{4x_2+1}{x_2}}\right)}^3\times \left({\displaystyle \frac{7^3}{9^7}}\right)\times {\displaystyle \frac{\left(4x_2+3\right)}{{\left(2x_2+1\right)}^2}}\times {\left({\displaystyle \frac{207}{35}}\right)}^9 \\ \times {\left({\displaystyle \frac{{\left(2x_2+1\right)}^2\left(12x_2+11\right)}{\left(4x_2+1\right)\left(4x_2+3\right)}}\right)}^3\times {\left({\displaystyle \frac{648}{161}}\right)}^3\times \left({\displaystyle \frac{72{\left(2x_2+1\right)}^2}{\left(4x_2+3\right)\left(12x_2+11\right)}}\right)\times {\displaystyle \frac{\left(276x_2+253\right)}{9\left(757x_2+646\right)}} \\ \times {\left({\displaystyle \frac{3279x_2+2862}{276x_2+253}}\right)}^3\times {\displaystyle \frac{252\left(757x_2+646\right)}{23\left(1093x_2+954\right)}}\right]\tau \left(F{r}_1\right). \end{gathered}$$

Thus

$$\tau \left(F{r}_2\right)=71221248(25139x_2+21942{)}^2\tau (F{r}_1).$$

(3)

Additionally

$$\tau (F{r}_n)=\prod _{i=2}^{n}71221248(25139x_i+21942{)}^2\tau (F{r}_1)=3\times 71221248^{n-1}{x}_1^2[ \prod _{i=2}^n(25139x_i+21942){]}^2$$

(4)

where $x_{i-1}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}},i=\mathrm{2,3},...,n.$

The equation for its characteristic is $25139{\lambda }^2-6310\lambda -24556=0$ with roots ${\lambda }_1={\displaystyle \frac{3155-\sqrt{627267309}}{25139}}$ and ${\lambda }_2={\displaystyle \frac{3155+\sqrt{627267309}}{25139}}$. These two roots can be subtracted from both sides of $x_{i-1}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}}$, to obtain

$$\begin{gathered} x_{i-1}-{\displaystyle \frac{3155-\sqrt{627267309}}{25139}}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}}-{\displaystyle \frac{3155-\sqrt{627267309}}{25139}} \\ ={\displaystyle \frac{(25097+\sqrt{627267309})[x_i-\frac{3155-\sqrt{627267309}}{25139}]}{(25139x_i+21942)}} \end{gathered}$$

(5)

$$\begin{gathered} x_{i-1}-{\displaystyle \frac{3155+\sqrt{627267309}}{25139}}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}}-{\displaystyle \frac{3155+\sqrt{627267309}}{25139}} \\ ={\displaystyle \frac{(25097-\sqrt{627267309})[x_i-\frac{3155+\sqrt{627267309}}{25139}]}{(25139x_i+21942)}} \end{gathered}$$

(6)

Let $y_i={\displaystyle \frac{x_i-\frac{3155-\sqrt{627267309}}{25139}}{x_i-\frac{3155+\sqrt{627267309}}{25139}}}$. Then by Equations (5) and (6), we get the following:

$$y_{i-1}=({\displaystyle \frac{628563359+25097\sqrt{627267309}}{1296050}})y_i \mathrm{and} y_i=({\displaystyle \frac{628563359+25097\sqrt{627267309}}{1296050}}{)}^{n-i}{y}_n.$$

Therefore

$$x_i={\displaystyle \frac{(\frac{628563359+25097\sqrt{627267309}}{1296050}{)}^{n-i}(\frac{3155+\sqrt{627267309}}{25139})y_n-\frac{3155-\sqrt{627267309}}{25139}}{(\frac{628563359+25097\sqrt{627267309}}{1296050}{)}^{n-i}{y}_n-1}}.$$

Thus

$$x_1={\displaystyle \frac{(\frac{628563359+25097\sqrt{627267309}}{1296050}{)}^{n-1}(\frac{3155+\sqrt{627267309}}{25139})y_n-\frac{3155-\sqrt{627267309}}{25139}}{(\frac{628563359+25097\sqrt{627267309}}{1296050}{)}^{n-1}{y}_n-1}}$$

(7)

With the coefficients of $28252x_n+24556$ and $25139x_n+21942$, represented by the symbols ${\alpha }_n$ and ${\beta }_n$, respectively, and using the formula $x_{i-1}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}}$, we have

$$25139x_n+21942={\alpha }_0(28252x_n+24556)+{\beta }_0(25139x_n+21942),$$

$$25139x_{n-1}+21942={\displaystyle \frac{{\alpha }_1(28252x_n+24556)+{\beta }_1(25139x_n+21942)}{{\alpha }_0(28252x_n+24556)+{\beta }_0(25139x_n+21942)}},$$

$$25139x_{n-2}+21942={\displaystyle \frac{{\alpha }_2(28252x_n+24556)+{\beta }_2(25139x_n+21942)}{{\alpha }_1(28252x_n+24556)+{\beta }_1(25139x_n+21942)}},$$

$$⋮$$

$$25139x_{n-i}+21942={\displaystyle \frac{{\alpha }_i(28252x_n+24556)+{\beta }_i(25139x_n+21942)}{{\alpha }_{i-1}(28252x_n+24556)+{\beta }_{i-1}(25139x_n+21942)}},$$

(8)

$$25139x_{n-(i+1)}+21942={\displaystyle \frac{{\alpha }_{i+1}(28252x_n+24556)+{\beta }_{i+1}(25139x_n+21942)}{{\alpha }_i(28252x_n+24556)+{\beta }_i(25139x_n+21942)}},$$

(9)

$$⋮$$

$$25139x_2+21942={\displaystyle \frac{{\alpha }_{n-2}(28252x_n+24556)+{\beta }_{n-2}(25139x_n+21942)}{{\alpha }_{n-3}(28252x_n+24556)+{\beta }_{n-3}(25139x_n+21942)}}$$

(10)

When Equation (10) is substituted into Equation (4), we get

$$\tau \left(F{r}_n\right)=3\times 71221248^{n-1}{x}_1^2\left[{\alpha }_{n-2}\right(28252x_n+24556)+{\beta }_{n-2}(25139x_n+21942){]}^2$$

(11)

where ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=25139,{\beta }_1=21942$. By the expression $x_{i-1}={\displaystyle \frac{28252x_i+24556}{25139x_i+21942}}$ and using Equations (8) and (9), we have

$${\alpha }_{i+1}=50194{\alpha }_i-2592100{\alpha }_{i-1};{\beta }_{i+1}=50194{\beta }_i-2592100{\beta }_{i-1}$$

(12)

Equation (12) has the characteristic equation ${\mu }^2-50194\mu +2592100=0$. Its roots are ${\mu }_1=25097+\sqrt{627267309}$ and ${\mu }_2=25097-\sqrt{627267309}$.

The general solutions of Equation (12) are ${\alpha }_i=h_1{\mu }_1^i+h_2{\mu }_2^i;{\beta }_i=k_1{\mu }_1^i+k_2{\mu }_2^i$.

Given the initial conditions ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=25139,{\beta }_1=21942,$ we obtain

$$\begin{gathered} {\alpha }_i={\displaystyle \frac{25139\sqrt{627267309}}{125454618}}[(25097+\sqrt{627267309}{)}^i-(25097-\sqrt{627267309}{)}^i]; \\ {\beta }_i=({\displaystyle \frac{627267309-3155\sqrt{627267309}}{125454618}})(25097+\sqrt{627267309}{)}^i+ \\ ({\displaystyle \frac{627267309+3155\sqrt{627267309}}{125454618}})(25097-\sqrt{627267309}{)}^i \end{gathered}$$

(13)

If $x_n=1$, this means that $F{r}_n$ is without any electrically equivalent transformation.

When Equation (13) is inserted into Equation (11), we obtain

$$\begin{gathered} \tau \left(F{r}_n\right)=3\times x_1^2\times {\left(71221248\right)}^{n-1}{[ \left({\displaystyle \frac{47081}{2}}+{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}}\right){\left(25097+\sqrt{627267309}\right)}^{n-2} \\ +\left({\displaystyle \frac{47081}{2}}-{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}}\right){\left(25097-\sqrt{627267309}\right)}^{n-2}]}^2,n\ge 2. \end{gathered}$$

(14)

Equation (14) is satisfied for $n=1$ and $\tau \left(F{r}_1\right)=3$. Thus, the number of spanning trees in the pyramid graph $F{r}_n$ is determined by

$$\begin{gathered} \tau \left(F{r}_n\right)=3\times x_1^2\times {\left(71221248\right)}^{n-1}{[ \left({\displaystyle \frac{47081}{2}}+{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}}\right){\left(25097+\sqrt{627267309}\right)}^{n-2} \\ +\left({\displaystyle \frac{47081}{2}}-{\displaystyle \frac{392999919\sqrt{\frac{3}{209089103}}}{2}}\right){\left(25097-\sqrt{627267309}\right)}^{n-2}]}^2,n\ge 1. \end{gathered}$$

(15)

where

$$\begin{gathered} x_1={\displaystyle \frac{{\left(\frac{628563359+25097\sqrt{627267309}}{1296050}\right)}^{n-1 } \left( 412155311+16565\sqrt{627267309} \right)+1909 \left( 3155-\sqrt{627267309 } \right)}{\left({\left( \frac{628563359+25097\sqrt{627267309}}{1296050} \right)}^{n-1} \left( 370187855+14656\sqrt{627267309}\right)+47990351\right)}}, \\ n\ge 1 \end{gathered}$$

(16)

The result is obtained by inserting Equation (16) into Equation (15). □

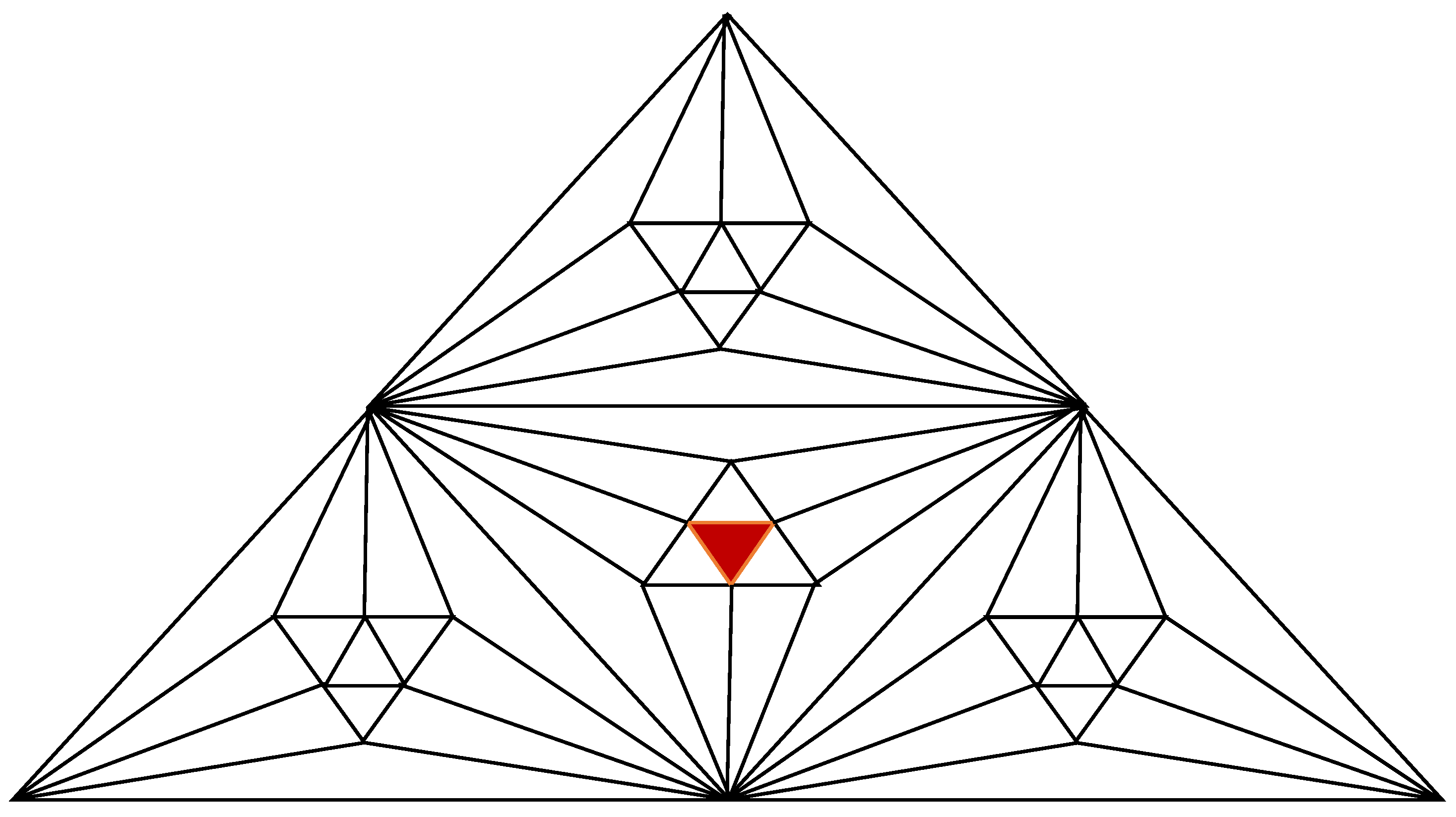
2.2. Number of Spanning Trees of Pyramid Graph $\overline{F{r}_n}$ Created by Related Fritsch Graph $\overline{Fr}$

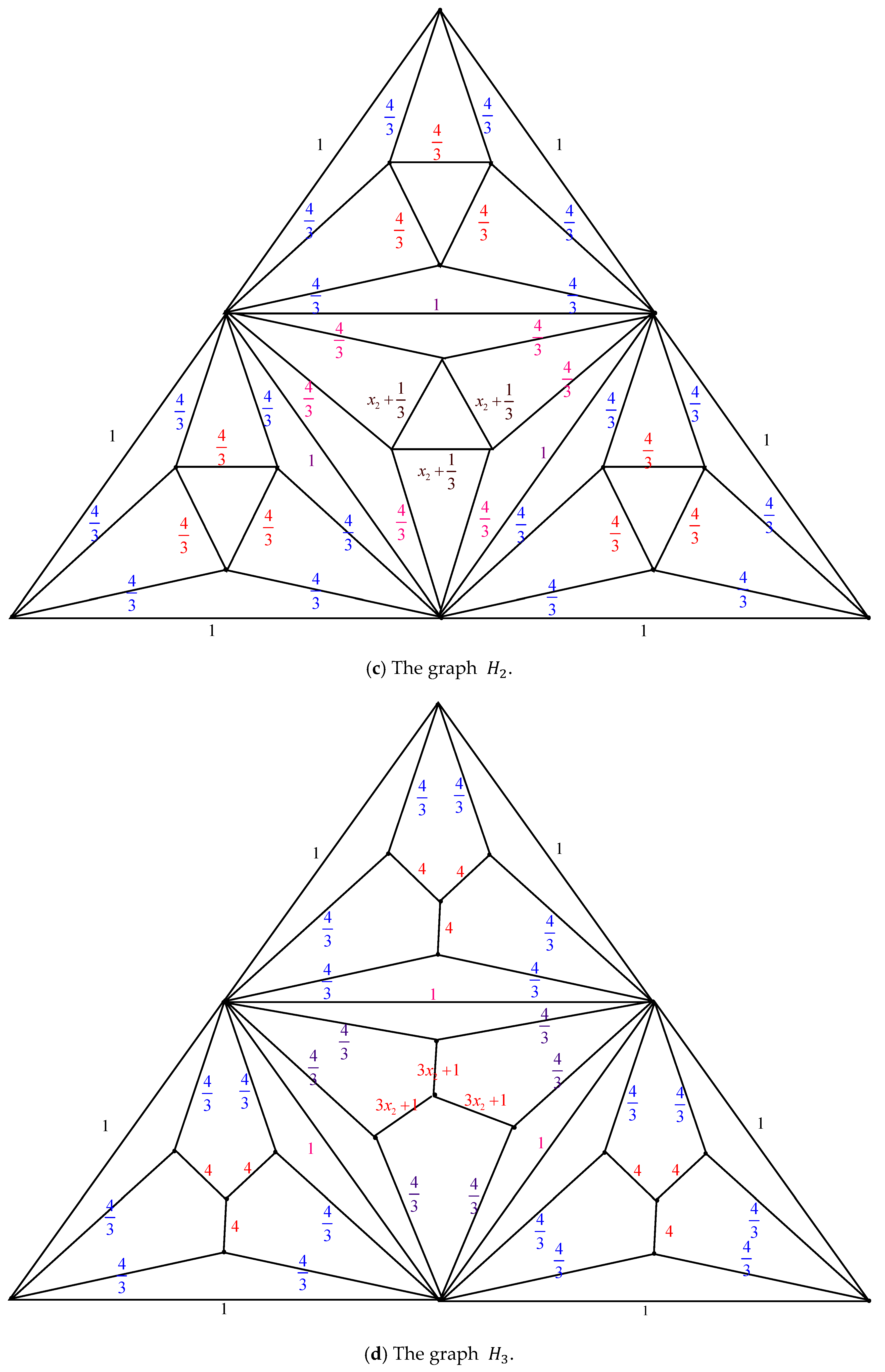
The pyramid graph $\overline{F{r}_n}$ is defined recursively using the graph $\overline{F{r}_2}$ and the graph $\overline{F{r}_1}$ (triangle or $K_3$) as follows: $\overline{F{r}_n}$ $(n\ge 3)$ is created by replacing the center triangle in $\overline{F{r}_{n-1}}$ with $\overline{F{r}_2}$. See Figure 4. According to this construction, the total vertices $\left|V( \overline{F{r}_n})\right|$ and edges $\left|E( \overline{F{r}_n})\right|$ are $\left|V( \overline{F{r}_n})\right|=30n-27$ and $\left|E( \overline{F{r}_n})\right|=78n-75$, $n=\mathrm{1,2},....$ The average degree of $\overline{F{r}_n}$ is in the large n limit which is 5.2.

Theorem 2.

The number of spanning trees in a pyramid graph, $\overline{F{r}_n}$, created by the related Fritsch graph series $\overline{Fr}$ for $n\ge 1$, is determined by

$$\begin{gathered} 3\times {(13589544960)}^{n-1}{({\displaystyle \frac{{(\frac{992209+997\sqrt{990409}}{1800})}^{n-1}(993209+1003\sqrt{990409})-100(28+\sqrt{990409})}{7{(\frac{992209+997\sqrt{990409}}{1800})}^{n-1}(128987+129\sqrt{990409})+87500}})}^2{((950 \\ +135050\sqrt{{\displaystyle \frac{7}{141487}}}){(997+\sqrt{990409})}^{n-2}+(950-135050\sqrt{{\displaystyle \frac{7}{141487}}}){(997-\sqrt{990409})}^{n-2})}^2 \end{gathered}$$

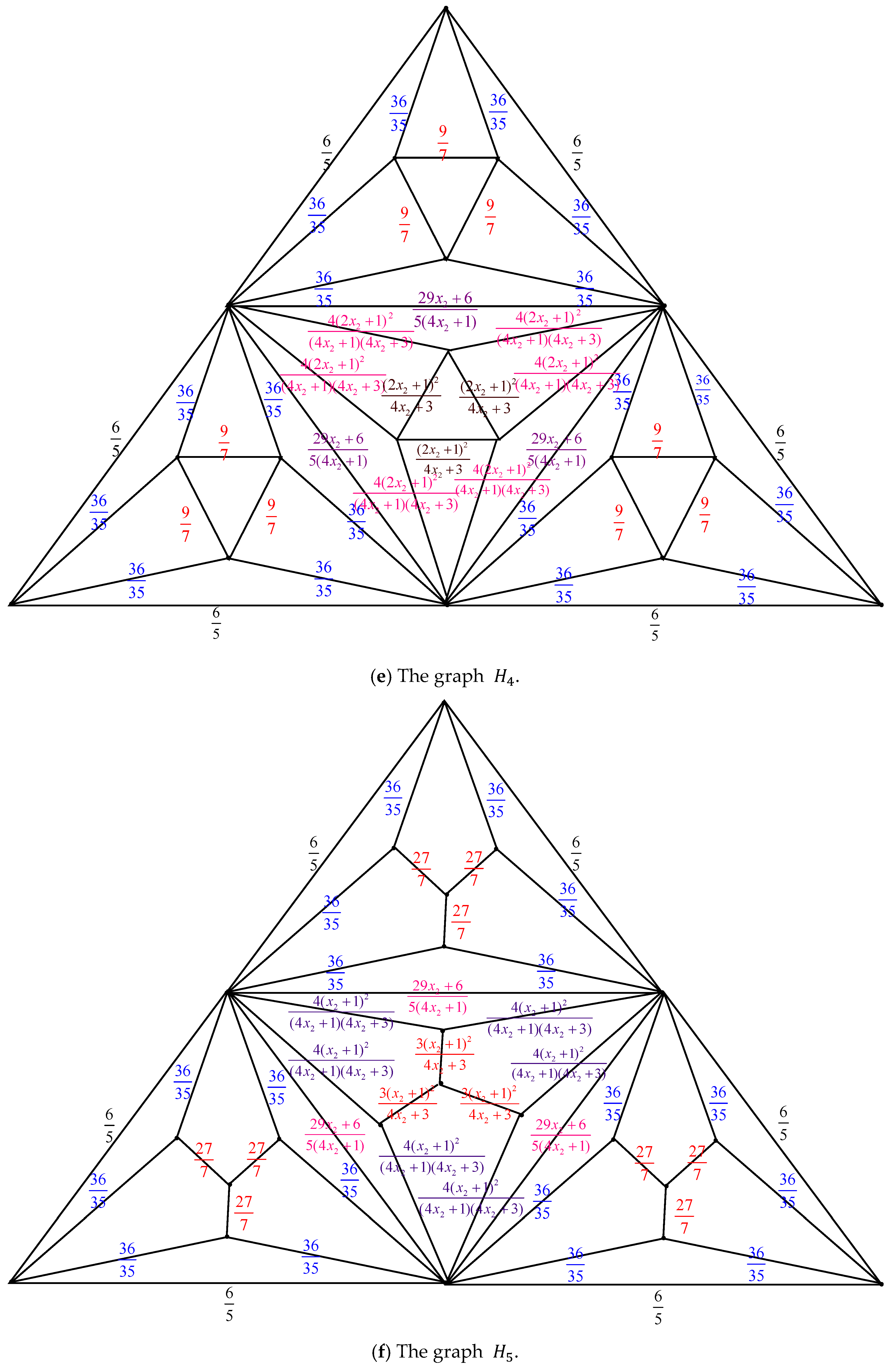
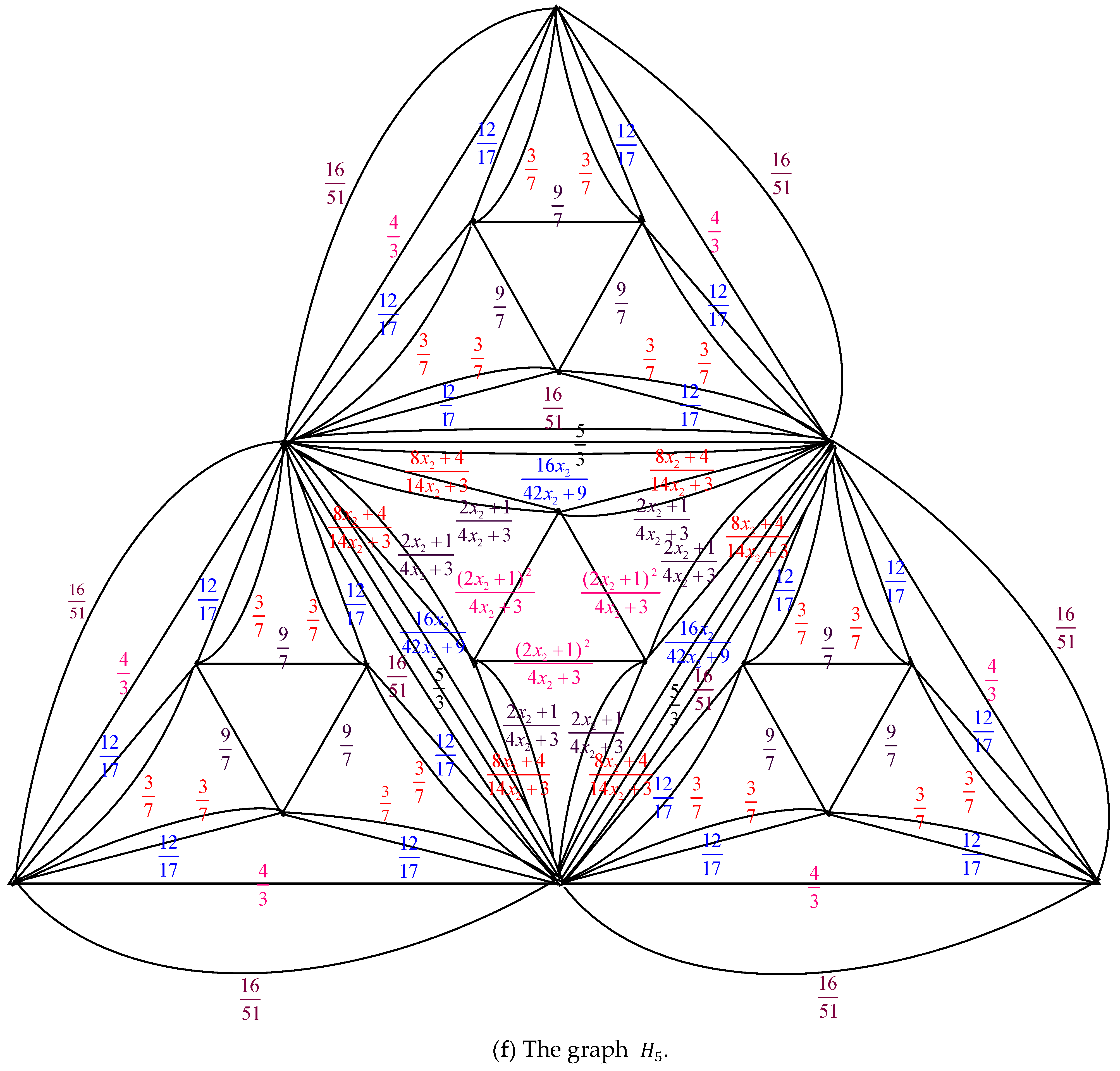
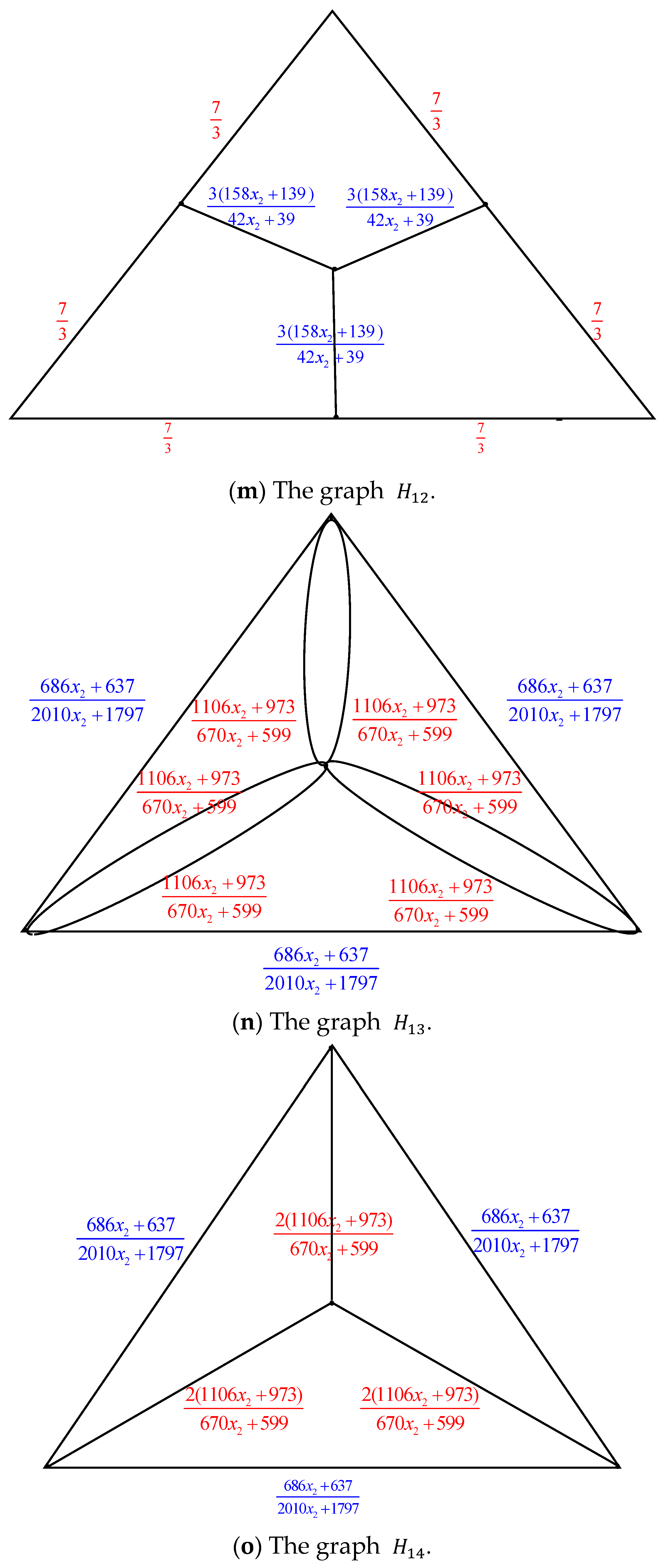
Proof. 

By applying the electrically equivalent transformation, $\overline{F{r}_i}$ is converted to $\overline{F{r}_{i-1}}$. Figure 5 illustrates the process of converting $\overline{F{r}_2}$ to $\overline{F{r}_1}$.

The result of combining these ten transformations is

$$\begin{gathered} \tau \left( \overline{F{r}_2}\right)=\left[3^{12}\times {\displaystyle \frac{1}{{12}^3}}\times {\displaystyle \frac{1}{9x_2+3}}\times {\left({\displaystyle \frac{20}{3}}\right)}^9\times {\left({\displaystyle \frac{9x_2+11}{3}}\right)}^3\times {\left({\displaystyle \frac{24}{5}}\right)}^3\times {\displaystyle \frac{24\left(3x_2+1\right)}{\left(9x_2+11\right)}}\times {\displaystyle \frac{1}{9}}\times \left({\displaystyle \frac{45x_2+55}{121x_2+139}}\right) \\ \times {\left({\displaystyle \frac{105x_2+123}{9x_2+11}}\right)}^3\times \left({\displaystyle \frac{54\left(121x_2+139\right)}{25\left(35x_2+41\right)}}\right)\right]\tau \left( \overline{F{r}_1}\right). \end{gathered}$$

Thus

$$\tau \left(\overline{F{r}_2}\right)=13589544960(875x_2+1025{)}^2\tau (\overline{F{r}_1}).$$

(17)

Additionally

$$\tau (\overline{F{r}_n})=\prod _{i=2}^{n}13589544960(875x_i+1025{)}^2\tau (\overline{F{r}_1})=3\times 13589544960^{n-1}{x}_1^2[\prod _{i=2}^n(875x_i+1025){]}^2$$

(18)

where $x_{i-1}={\displaystyle \frac{969x_i+1131}{875x_i+1025}},i=\mathrm{2,3},...,n.$

This has a characteristic equation $875{\lambda }^2+56\lambda -1131=0$ with the roots ${\lambda }_1={\displaystyle \frac{-28-\sqrt{990409}}{875}}$ and ${\lambda }_2={\displaystyle \frac{-28+\sqrt{990409}}{875}}$. These two roots can be subtracted from both sides of $x_{i-1}={\displaystyle \frac{969x_i+1131}{875x_i+1025}}$, to obtain

$$x_{i-1}+{\displaystyle \frac{28+\sqrt{990409}}{875}}={\displaystyle \frac{969x_i+1131}{875x_i+1025}}+{\displaystyle \frac{28+\sqrt{990409}}{875}}={\displaystyle \frac{(997+\sqrt{990409})[x_i+\frac{28+\sqrt{990409}}{875}]}{(875x_i+1025)}}$$

(19)

$$x_{i-1}+{\displaystyle \frac{28-\sqrt{990409}}{875}}={\displaystyle \frac{969x_i+1131}{875x_i+1025}}+{\displaystyle \frac{28-\sqrt{990409}}{875}}={\displaystyle \frac{(997-\sqrt{990409})[x_i+\frac{28-\sqrt{990409}}{875}]}{(875x_i+1025)}}$$

(20)

Let $y_i={\displaystyle \frac{x_i+\frac{28+\sqrt{990409}}{875}}{x_i-\frac{28-\sqrt{990409}}{875}}}$. Then by Equations (19) and (20), we get $y_{i-1}=({\displaystyle \frac{992209+997\sqrt{990409}}{1800}})y_i$ and $y_i=({\displaystyle \frac{992209+997\sqrt{990409}}{1800}}{)}^{n-i}{y}_n.$

Therefore

$$x_i={\displaystyle \frac{( \frac{992209+997\sqrt{990409}}{1800}{ )}^{n-i} ( \frac{-28+\sqrt{990409}}{875} ){ y}_n+\frac{28+\sqrt{990409}}{875}}{( \frac{992209+997\sqrt{990409}}{1800}{ )}^{n-i}{y}_n-1}}$$

Thus

$$x_1={\displaystyle \frac{( \frac{992209+997\sqrt{990409 }}{1800} {)}^{n-1} \left(\frac{-28+\sqrt{990409}}{875}\right){ y}_n+\frac{28+\sqrt{990409}}{875}}{( \frac{992209+997\sqrt{990409}}{1800} {)}^{n-1}{ y}_n-1}}$$

(21)

Using the formula $x_{i-1}={\displaystyle \frac{969x_i+1131}{875x_i+1025}}$ and designating the coefficients of $969x_n+1131 \mathrm{a}\mathrm{n}\mathrm{d} 875x_n+1025$ as ${\alpha }_n$ and ${\beta }_n$, we have

$$875x_n+1025={\alpha }_0(969x_n+1131)+{\beta }_0(875x_n+1025),$$

$$875x_{n-1}+1025={\displaystyle \frac{{\alpha }_1(969x_n+1131)+{\beta }_1(875x_n+1025)}{{\alpha }_0(969x_n+1131)+{\beta }_0(875x_n+1025)}},$$

$$875x_{n-2}+1025={\displaystyle \frac{{\alpha }_2(969x_n+1131)+{\beta }_2(875x_n+1025)}{{\alpha }_1(969x_n+1131)+{\beta }_1(875x_n+1025)}},$$

$$⋮$$

$$875x_{n-i}+1025={\displaystyle \frac{{\alpha }_i(969x_n+1131)+{\beta }_i(875x_n+1025)}{{\alpha }_{i-1}(969x_n+1131)+{\beta }_{i-1}(875x_n+1025)}},$$

(22)

$$875x_{n-(i+1)}+1025={\displaystyle \frac{{\alpha }_{i+1}(969x_n+1131)+{\beta }_{i+1}(875x_n+1025)}{{\alpha }_i(969x_n+1131)+{\beta }_i(875x_n+1025)}}$$

(23)

$$⋮$$

$$875x_2+1025={\displaystyle \frac{{\alpha }_{n-2}(969x_n+1131)+{\beta }_{n-2}(875x_n+1025)}{{\alpha }_{n-3}(969x_n+1131)+{\beta }_{n-3}(875x_n+1025)}}.$$

(24)

When Equation (24) is substituted into Equation (18), we get

$$\tau \left(\overline{F{r}_n}\right)=3\times 13589544960^{n-1}{x}_1^2\left[{\alpha }_{n-2}\right(969x_n+1131)+{\beta }_{n-2}(875x_n+1025){]}^2$$

(25)

where ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=875,{\beta }_1=1025$. By the expression $x_{n-1}={\displaystyle \frac{969x_n+1131}{875x_n+1025}}$ and Equations (23) and (24), we have

$${\alpha }_{i+1}=1994{\alpha }_i-3600{\alpha }_{i-1};{\beta }_{i+1}=1994{\beta }_i-3600{\beta }_{i-1}$$

(26)

Equation (26) has the characteristic equation ${\mu }^2-1994\mu +3600=0.$ Its roots are ${\mu }_1=997+\sqrt{990409}$ and ${\mu }_1=997-\sqrt{990409}$.

The general solutions of Equation (26) are ${\alpha }_i=h_1{\mu }_1^i+h_2{\mu }_2^i;{\beta }_i=k_1{\mu }_1^i+k_2{\mu }_2^i$.

Given the initial conditions ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=875, {\beta }_1=1025$, we have

$$\begin{gathered} {\alpha }_i={\displaystyle \frac{875\sqrt{990409}}{1980818}}[(997+\sqrt{990409}{)}^i-(997-\sqrt{990409}{)}^i]; \\ {\beta }_i=({\displaystyle \frac{990409+28\sqrt{990409}}{1980818}})(997+\sqrt{990409}{)}^i+({\displaystyle \frac{990409-28\sqrt{990409}}{1980818}})(997-\sqrt{990409}{)}^i \end{gathered}$$

(27)

If $x_n=1$, this means that $\overline{F{r}_n}$ is without any electrically equivalent transformation.

When Equation (27) is inserted into Equation (25), we obtain the following:

$$\begin{gathered} \tau \left(\overline{F{r}_n}\right)=3\times x_1^2\times {(13589544960 )}^{n-1}{ ( \left(950+135050\sqrt{{\displaystyle \frac{7}{141487}}} \right){\left( 997+\sqrt{990409} \right)}^{n-2}+( 950 \\ -135050\sqrt{{\displaystyle \frac{7}{141487}}} ){ ( 997-\sqrt{990409} )}^{n-2})}^2,n\ge 2 \end{gathered}$$

(28)

Equation (28) is satisfied for $n=1$ and $\tau \overline{(F{r}_1})=3$. Thus, the number of spanning trees in the pyramid graph $\overline{F{r}_n}$ is determined by

$$\begin{gathered} \tau \left(\overline{F{r}_n}\right)=3\times x_1^2\times {(13589544960)}^{n-1}{((950+135050\sqrt{{\displaystyle \frac{7}{141487}}}){ \left(997+\sqrt{990409}\right)}^{n-2} \\ +\left(950-135050\sqrt{{\displaystyle \frac{7}{141487}}}\right){(997-\sqrt{990409})}^{n-2})}^2,n\ge 1 \end{gathered}$$

(29)

where

$$x_1=\frac{{\left( \frac{992209+997\sqrt{990409}}{1800} \right)}^{n-1}\left(993209+1003 \sqrt{990409} \right)-100 ( 28+\sqrt{990409} )}{7{\left( \frac{992209+997\sqrt{990409}}{1800} \right)}^{n-1}( 128987+129\sqrt{990409} )+87500},n\ge 1$$

(30)

The result is obtained by inserting Equation (30) into Equation (29). □

2.3. Number of Spanning Trees of Pyramid Graph $\overline{\overline{F{r}_n}}$ Created by Graph $\overline{\overline{Fr}}$

The pyramid graph $\overline{\overline{F{r}_n}}$ is defined recursively using the graph $\overline{\overline{F{r}_2}}$ and the graph $\overline{\overline{F{r}_1}}$ (triangle or $K_3$) as follows: $\overline{\overline{F{r}_n}}$$(n\ge 3)$ is created by replacing the center triangle in $\overline{\overline{F{r}_{n-1}}}$ with $\overline{\overline{F{r}_2}}$. See Figure 6. According to this construction, the total vertices $\left|V(\overline{\overline{F{r}_n}})\right|$ and edges $\left|E(\overline{\overline{F{r}_n}})\right|$ are $\left|V(\overline{\overline{F{r}_n}})\right|=39n-36$ and $\left|E(\overline{\overline{F{r}_n}})\right|=114n-111$, $n=\mathrm{1,2},\dots$. The average degree of $\overline{\overline{F{r}_n}}$ is in the large $n$ limit which is $5.85$.

Theorem 3.

The number of spanning trees in a pyramid graph $\overline{\overline{F{r}_n}}$, created by the related Fritsch graph series $\overline{\overline{Fr}}$ for $n\ge 1$, is determined by

$$\begin{gathered} 3\times {\left(106758347898180000\right)}^{n-1} (({\left({\displaystyle \frac{2445697+1565\sqrt{2442169}}{3528}}\right)}^{n-1}(2237383+1531\sqrt{2442169})+ \\ 558(367-\sqrt{2442169}))/{({\left({\displaystyle \frac{2445697+1565\sqrt{2442169}}{3528}}\right)}^{n-1}(1694449+973\sqrt{2442169})+747720))}^2 \\ {(({\displaystyle \frac{1269}{2}}+{\displaystyle \frac{1982457}{2\sqrt{2442169}}}){({\displaystyle \frac{1565+\sqrt{2442169}}{2}})}^{n-2}+({\displaystyle \frac{1269}{2}}-{\displaystyle \frac{1982457}{2\sqrt{2442169}}}){({\displaystyle \frac{1565-\sqrt{2442169}}{2}})}^{n-2})}^2 \end{gathered}$$

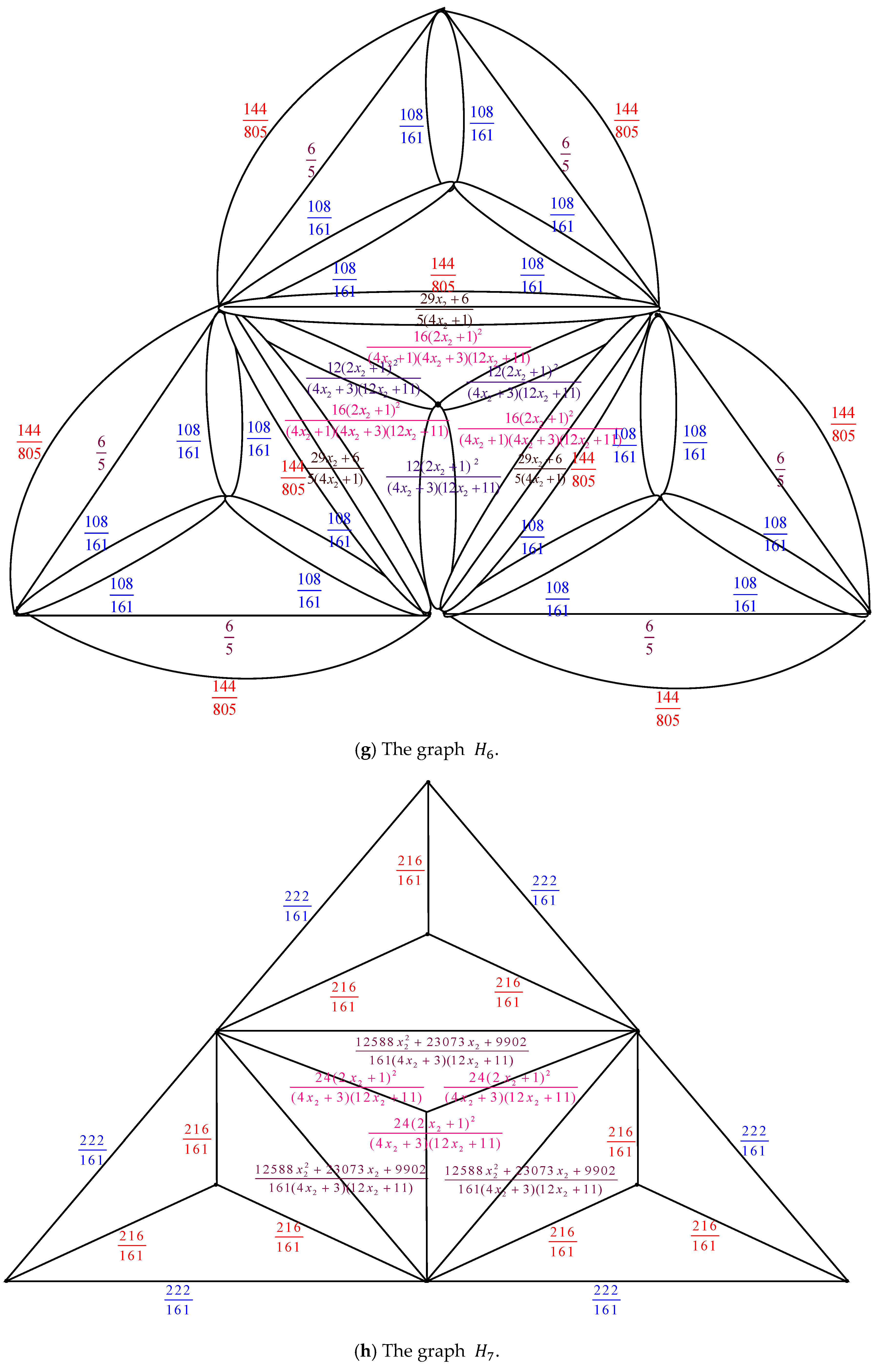
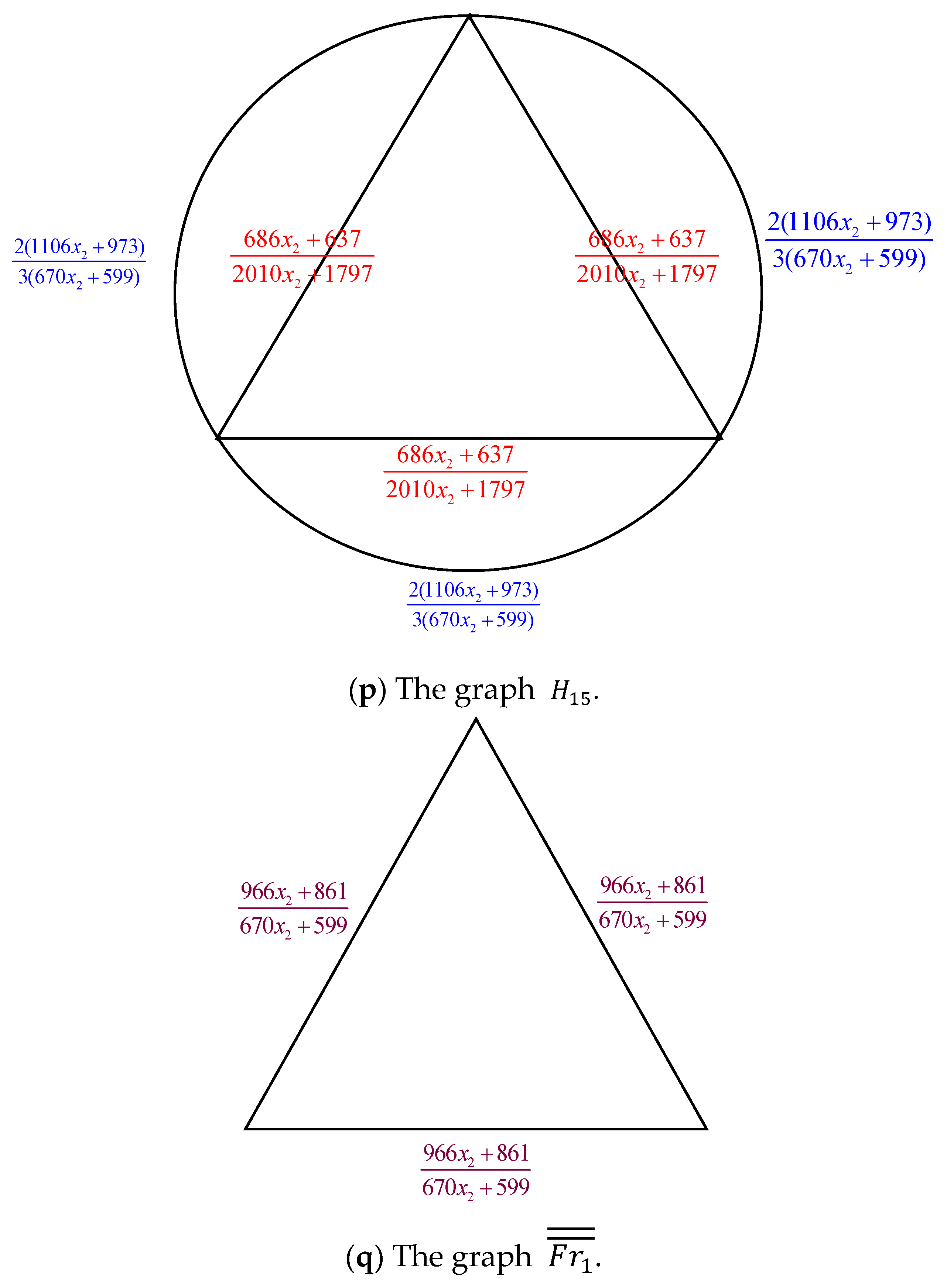
Proof. 

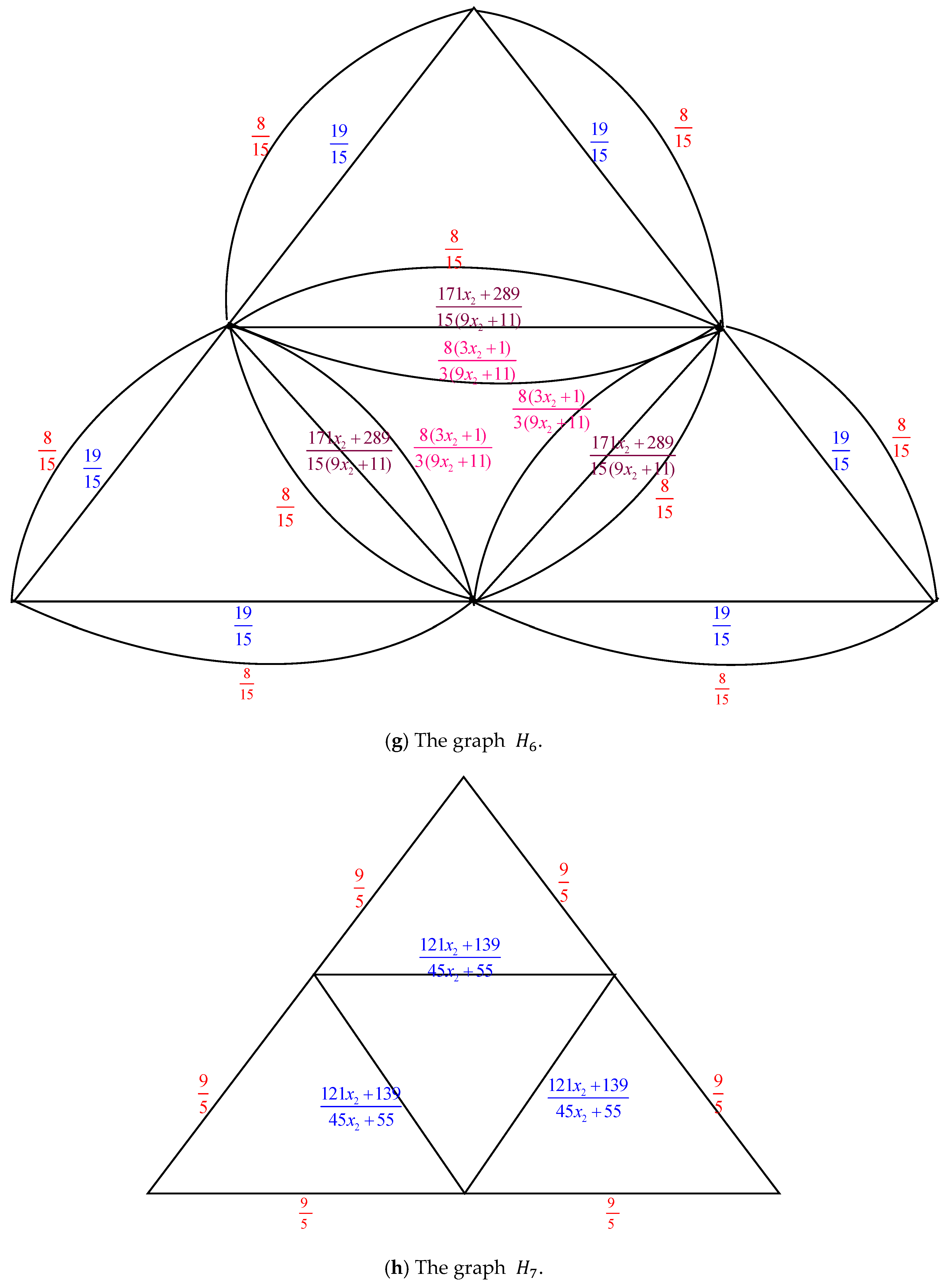
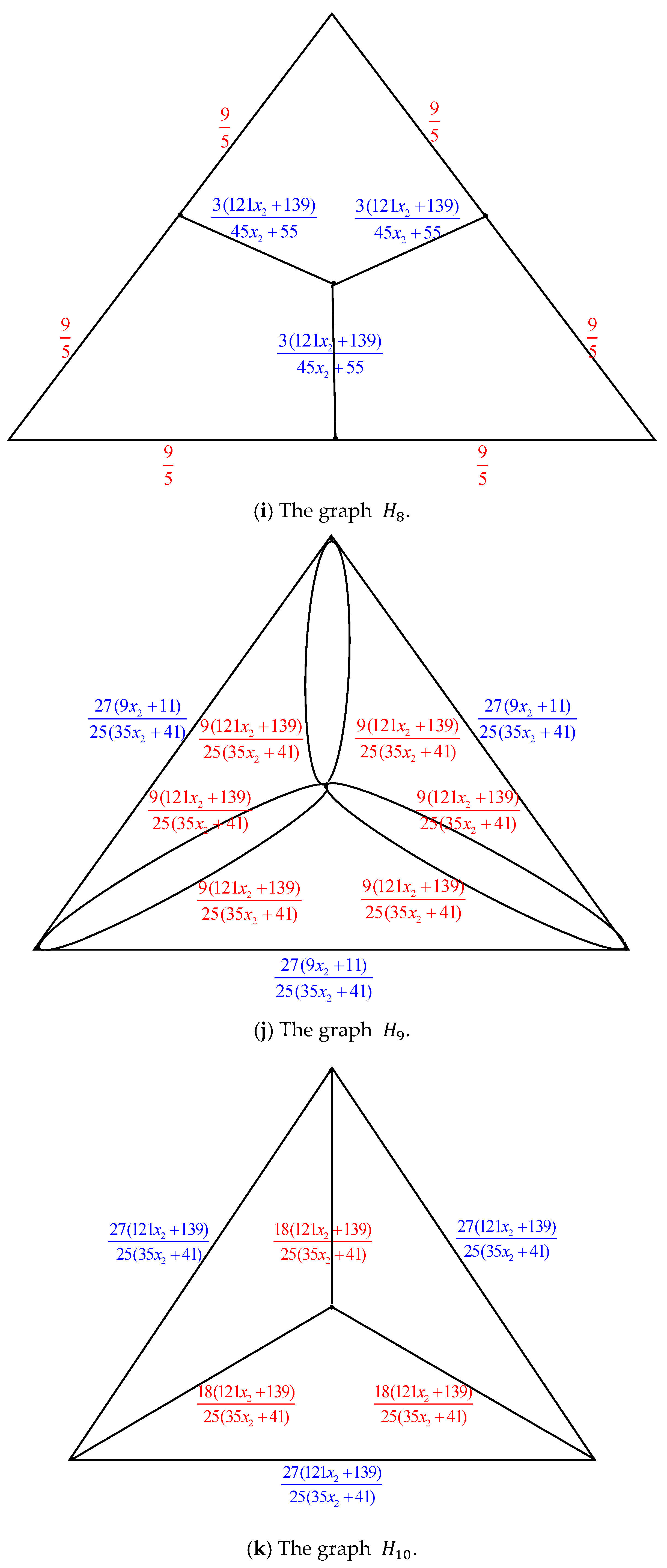
By applying the electrically equivalent transformation, $\overline{\overline{F{r}_i}}$ is converted to $\overline{\overline{F{r}_{i-1}}}$. Figure 7 illustrates the process of converting $\overline{\overline{F{r}_2}}$ to $\overline{\overline{F{r}_1}}$.

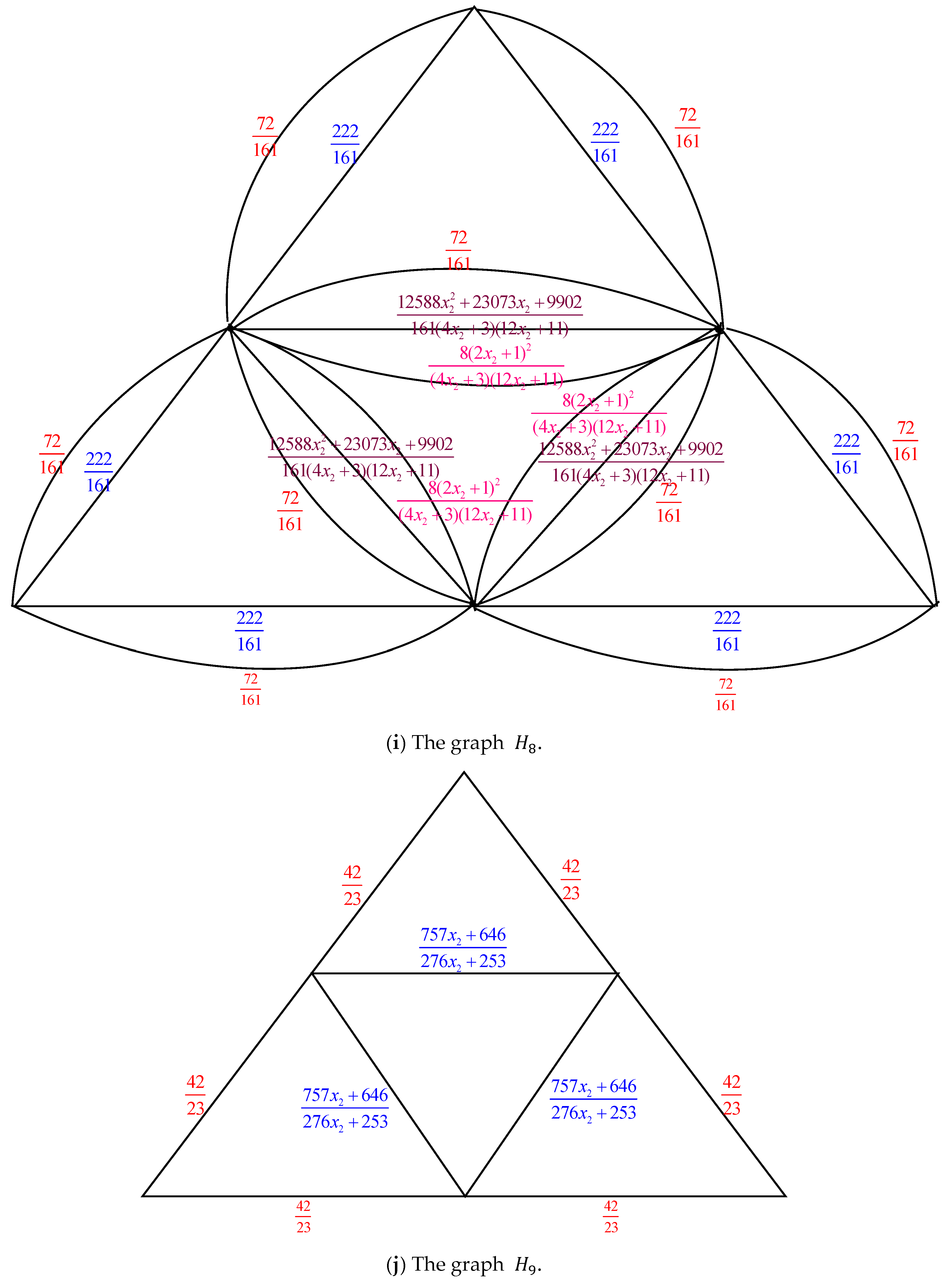
The result of combining these fifteen transformations is

$$\begin{gathered} \tau (\overline{\overline{F{r}_2}})=3^{12}\times {\displaystyle \frac{1}{9^9}}\times {\displaystyle \frac{{x_2}^3}{{(2x_2+1)}^6}}\times 7^9\times {(4x_2+3)}^3\times {({\displaystyle \frac{17}{3}})}^9\times {({\displaystyle \frac{14{ x}_2+3}{3 x_2}})}^3\times ({\displaystyle \frac{7^3}{9^7}})\times {\displaystyle \frac{(4 x_2+3)}{{(2{ x}_2+1)}^2}}\times {({\displaystyle \frac{729}{119}})}^9 \\ \times {({\displaystyle \frac{3{(2x_2+1)}^2(14x_2+13)}{(4x_2+3)(14 x_2+3)}})}^3\times {({\displaystyle \frac{30}{7}})}^3\times ({\displaystyle \frac{90{(2x_2+1)}^2}{(4{ x}_2+3)(14 x_2+13)}})\times {\displaystyle \frac{(42x_2+39)}{9(158 x_2+139)}} \\ \times {({\displaystyle \frac{670x_2+599}{42 x_2+39}})}^3\times {\displaystyle \frac{6(1106 x_2+973)}{(670 x_2+599)}}\tau (). \end{gathered}$$

Thus

$$\tau (\overline{\overline{F{r}_2}})=1067583647898180000(670x_2+599{)}^2\tau (\overline{\overline{F{r}_2}}).$$

(31)

Additionally

$$\begin{gathered} \tau \left(\overline{\overline{F{r}_n}}\right)=\prod _{i=2}^{n}1067583647898180000(670x_i+599{)}^2\tau (\overline{\overline{F{r}_1}}) \\ =3\times 1067583647898180000^{n-1}{x}_1^2[{\prod }_{i=2}^n(670x_i+599){]}^2 \end{gathered}$$

(32)

where $x_{i-1}={\displaystyle \frac{966x_i+861}{670x_i+599}},i=\mathrm{2,3},\dots ,n.$ Its characteristic equation is $670{\lambda }^2-367\lambda -861=0$, with roots ${\lambda }_1={\displaystyle \frac{367-\sqrt{2442169}}{1340}}$ and ${\lambda }_2={\displaystyle \frac{367+\sqrt{2442169}}{1340}}$. Subtracting these two roots on both sides of $x_{i-1}={\displaystyle \frac{966x_i+861}{670x_i+599}}$, we get

$$\begin{gathered} x_{i-1}-{\displaystyle \frac{367-\sqrt{2442169}}{1340}}={\displaystyle \frac{966x_i+861}{670x_i+599}}-{\displaystyle \frac{367-\sqrt{2442169}}{1340}} \\ ={\displaystyle \frac{\left(1565+\sqrt{2442169} \right) [ x_i-\frac{367-\sqrt{2442169}}{1340} ]}{2( 670x_i+599 )}} \end{gathered}$$

(33)

$$\begin{gathered} x_{i-1}-{\displaystyle \frac{367+\sqrt{2442169}}{1340}}={\displaystyle \frac{966x_i+861}{670x_i+599}}-{\displaystyle \frac{367+\sqrt{2442169}}{1340}} \\ ={\displaystyle \frac{\left( 1565-\sqrt{2442169} \right) [ x_i-\frac{367+\sqrt{2442169}}{1340} ]}{2(670x_i+599 )}} \end{gathered}$$

(34)

Let $y_i={\displaystyle \frac{x_i-\frac{367-\sqrt{2442169}}{1340}}{x_i-\frac{367+\sqrt{2442169}}{1340}}}$.

Then by Equations (33) and (34), we get $y_{i-1}=\left({\displaystyle \frac{2445697+1565\sqrt{2442169}}{3528}}\right)y_i$ and

$$y_i=( \frac{2445697+1565\sqrt{2442169}}{3528} {)}^{n-i}{y}_n.$$

Therefore

$$x_i={\displaystyle \frac{( \frac{2445697+1565\sqrt{2442169}}{3528} {)}^{n-i}\left( \frac{367+\sqrt{2442169}}{1340} \right){ y}_n-\frac{367-\sqrt{2442169}}{1340}}{( \frac{2445697+1565\sqrt{2442169}}{3528} {)}^{n-i} y_n-1}}.$$

Thus

$$x_1={\displaystyle \frac{( \frac{2445697+1565\sqrt{2442169}}{3528}{ )}^{n-1}( \frac{367+\sqrt{2442169}}{1340} )y_n-\frac{367-\sqrt{2442169}}{1340}}{( \frac{2445697+1565\sqrt{2442169}}{3528} {)}^{n-1}{y}_n-1}}$$

(35)

Using the formula $x_{i-1}={\displaystyle \frac{966x_i+861}{670x_i+599}}$ and designating the coefficients of $966x_n+861$ and $670x_n+599$ as ${\alpha }_n$ and ${\beta }_n$, we have

$$670x_n+599={\alpha }_0(966x_n+861)+{\beta }_0(670x_n+599),$$

$$670x_{n-1}+599={\displaystyle \frac{{\alpha }_1(966x_n+861)+{\beta }_1(670x_n+599)}{{\alpha }_0(966x_n+861)+{\beta }_0(670x_n+599)}},$$

$$670x_{n-2}+599={\displaystyle \frac{{\alpha }_2(966x_n+861)+{\beta }_2(670x_n+599)}{{\alpha }_1(966x_n+861)+{\beta }_1(670x_n+599)}},$$

$$⋮$$

$$670x_{n-i}+599={\displaystyle \frac{{\alpha }_i(966x_n+861)+{\beta }_i(670x_n+599)}{{\alpha }_{i-1}(966x_n+861)+{\beta }_{i-1}(670x_n+599)}},$$

(36)

$$670x_{n-(i+1)}+599={\displaystyle \frac{{\alpha }_{i+1}(966x_n+861)+{\beta }_{i+1}(670x_n+599)}{{\alpha }_i(966x_n+861)+{\beta }_i(670x_n+599)}},$$

(37)

$$⋮$$

$$670x_2+599={\displaystyle \frac{{\alpha }_{n-2}(966x_n+861)+{\beta }_{n-2}(670x_n+599)}{{\alpha }_{n-3}(966x_n+861)+{\beta }_{n-3}(670x_n+599)}}.$$

(38)

When Equation (38) is substituted into Equation (32), we get

$$\tau (\overline{\overline{F{r}_2}})=3\times 1067583647898180000^{n-1}{x}_1^2[{\alpha }_{n-2}(966x_n+861)+{\beta }_{n-2}(670x_n+599){]}^2$$

(39)

where ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=670,{\beta }_1=599$. By the expression $x_{i-1}={\displaystyle \frac{966x_i+861}{670x_i+599}}$ and Equations (36) and (37), we have

$${\alpha }_{i+1}=1565{\alpha }_i-1764{\alpha }_{i-1};{ \beta }_{i+1}=1565{\beta }_i-1764{\beta }_{i-1}$$

(40)

Equation (40) has the characteristic equation ${\mu }^2-1565\mu +1764=0.$ Its roots are ${\mu }_1={\displaystyle \frac{1565+\sqrt{2442169}}{2}}$ and ${\mu }_2={\displaystyle \frac{1565-\sqrt{2442169}}{2}}$.

The general solutions of Equation (40) are ${\alpha }_i=h_1{\mu }_1^i+h_2{\mu }_2^i;{\beta }_i=k_1{\mu }_1^i+k_2{\mu }_2^i$.

Given the initial conditions ${\alpha }_0=0,{\beta }_0=1$ and ${\alpha }_1=670,{\beta }_1=599$, we have

$$\begin{gathered} {\alpha }_i={\displaystyle \frac{670\sqrt{2442169}}{2442169}}[({\displaystyle \frac{1565+\sqrt{2442169}}{2}}{)}^i-({\displaystyle \frac{1565+\sqrt{2442169}}{2}}{)}^i]; \\ {\beta }_i=({\displaystyle \frac{2442169-367\sqrt{2442169}}{4884338}})({\displaystyle \frac{1565+\sqrt{2442169}}{2}}{)}^i \\ +( {\displaystyle \frac{2442169+367\sqrt{2442169}}{4884338}})({\displaystyle \frac{1565-\sqrt{2442169}}{2}} {)}^i \end{gathered}$$

(41)

If $x_n=1$, this means that $\overline{\overline{F{r}_n}}$ is without any electrically equivalent transformation.

When Equation (41) is inserted into Equation (39), we obtain

$$\begin{gathered} \tau \left(\overline{\overline{F{r}_n}}\right)=3\times x_1^2\times {\left(106758347898180000\right)}^{n-1}{\left(\left({\displaystyle \frac{1269}{2}}+{\displaystyle \frac{1982457}{2\sqrt{2442169}}}\right){\left({\displaystyle \frac{1565+\sqrt{2442169}}{2}}\right)}^{n-2}+ \\ \left({\displaystyle \frac{1269}{2}}-{\displaystyle \frac{1982457}{2\sqrt{2442169}}}\right){\left({\displaystyle \frac{1565-\sqrt{2442169}}{2}}\right)}^{n-2}\right)}^2,n\ge 2. \end{gathered}$$

(42)

Equation (42) is satisfied for $n=1$ and $\tau \left(\overline{\overline{F{r}_n}}\right)=3$. Thus, the number of spanning trees in the sequence of the graph $\overline{\overline{F{r}_n}}$ is determined by

$$\begin{array}{ll}\tau (\overline{\overline{F{r}_n}})=3\times x_1^2& \\ & \times {\left(106758347898180000\right)}^{n-1}(\left({\displaystyle \frac{1269}{2}}+{\displaystyle \frac{1982457}{2\sqrt{2442169}}}\right){\left({\displaystyle \frac{1565+\sqrt{2442169}}{2}}\right)}^{n-2}\\ & +\left({\displaystyle \frac{1269}{2}}-{\displaystyle \frac{1982457}{2\sqrt{2442169}}}\right){{\left({\displaystyle \frac{1565-\sqrt{2442169}}{2}}\right)}^{n-2})}^2,n\ge 1\end{array}$$

(43)

where

$$x_1={\displaystyle \frac{{\left(\frac{ 2445697+1565\sqrt{2442169}}{3528} \right)}^{n-1}\left( 2237383+1531\sqrt{2442169} \right)+558\left( 367-\sqrt{2442169 }\right)}{{\left( \frac{2445697+1565\sqrt{2442169} }{3528}\right)}^{n-1}( 1694449+973\sqrt{2442169} )+747720}}$$

(44)

The result is obtained by inserting Equation (44) into Equation (43). □

3. Numerical Results

The values of the number of spanning trees in the graphs $\tau (F{r}_n),\tau (\overline{F{r}_n})$, and $\tau (\overline{\overline{F{r}_n}})$ are shown in the following

Table 1. This table shows some of the numbers for the pyramid graph $F{r}_n$ spanning tree count.

$\mathit{n}$	$\mathit{\tau }\left(\mathit{F}{\mathit{r}}_{\mathit{n}}\right)$
1	3
2	595840848878370816
3	106707180749521149279206454746677248
4	19107851727493992841163289907951233946454397491871744
5	3421606268097367048895726265969595422130168100899195236894586523615232

,

Table 2. This table shows some of the numbers for the pyramid graph $\overline{F{r}_{n }}$ spanning tree count.

$\mathit{n}$	$\mathit{\tau }(\overline{\mathit{F}{\mathit{r}}_{\mathit{n}}})$
1	3
2	179789679820800000
3	9697793127051120495361523712000000
4	523046936889575576192567454766298592675102720000000
5	28210343478816088618974934925711446742498999448683259573043200000000

and

Table 3. This table shows some of the numbers for the pyramid graph $\overline{\overline{F{r}_n}}$ spanning tree count.

$\mathit{n}$	$\mathit{\tau }(\overline{\overline{\mathit{F}{\mathit{r}}_{\mathit{n}}}})$
1	3
2	1069055356324272207660000
3	279186674647567005563231690975473914913200000000
4	72895214842904525037897880850154069102870750125233146218424000000000000
5	19032826541987370547012520501914939903996473462422852589142424061545049132730080000000000000000

:

4. Spanning Tree Entropy

Once we have exact formulas for the number of spanning trees of the three pyramid graphs, $F{r}_n$, $\overline{F{r}_{n }}$, and $\overline{\overline{F{r}_n}}$, we can compute the spanning tree entropy Z, a finite number and an interesting metric defining the network topology. In [17,18], this is explained as follows: With reference to graph $G$,

$$Z(G)=\underset{n\to \infty }{lim}{\displaystyle \frac{\mathit{ln}\tau (G)}{\left|V(G)\right|}}.$$

(45)

$$Z(F{r}_n)={\displaystyle \frac{1}{27}}\left(\mathit{ln}\left[71221248\right]+2\mathit{ln}\left[25097+\sqrt{627267309}\right]\right)=1.47,$$

$$Z(\overline{F{r}_{n }})={\displaystyle \frac{1}{27}}\left(25\mathit{ln}\left[2\right]+\mathit{ln}\left[405\right]+2\mathit{ln}\left[997+\sqrt{990409}\right]\right)=1.43,$$

$$Z(\overline{\overline{F{r}_n}})={\displaystyle \frac{1}{39}} (ln[26689586974545000]+2 ln[1565+\sqrt{2442169}])=1.38.$$

Despite having the same number of vertices, edges, and average degree, the pyramid graph $F{r}_n$ has a higher entropy than the pyramid graph $\overline{F{r}_{n }}$. Similarly, even though the pyramid graph $\overline{\overline{F{r}_n}}$ has more vertices, edges, and average degrees than the pyramid graphs $F{r}_n$ and $\overline{F{r}_{n }}$, its entropy is lower. Additionally, the apollonian graph [19], which has an average degree of 5 (entropy 1.354), has a lower entropy than all pyramid graphs $F{r}_n$, $\overline{F{r}_{n }}$, and $\overline{\overline{F{r}_n}}$.

The entropy of the graphs under investigation is also higher than that of the square grid graph, which has an average degree of 4 and an entropy of 1.166, and lower than that of the triangle grid graph, which has an average degree of 6 and an entropy of 1.62 [20].

5. Conclusions

In this study, we use electrically equivalent transformations to determine the number of spanning trees of particular pyramid graphs produced from the Fritsch graph and other related graphs. This technique’s strength is its ability to avoid the laborious computation of Laplacian spectra, which is a requirement for a general approach to spanning tree determination. Furthermore, our findings indicate a relationship between entropy and the graph’s average degree.