Abstract
The n-dimensional enhanced hypercube is a well-known variation of hypercube networks. Its structure can be obtained from the hypercube by adding complementary edges. We denote a network G to be a conditionally faulty model if every fault-free vertex of G connects at least two fault-free edges. Let and be the set of faulty vertices and faulty edges in , respectively. In this paper, for the conditionally faulty with , where and k have different parity, I prove that contains a fault-free cycle with every odd length l, where .
MSC:
05C38; 05C82; 94C15
1. Introduction
Interconnection networks are significant for designing massive parallel or distributed systems, and they have attracted more and more research interest [1]. Hypercubes, as a kind of interconnection network topology, have many positive characteristics, such as regularity, a recursive structure, symmetry, and a logarithmic diameter [1]. Numerous variants of the hypercube have been proposed in the literature [2,3,4,5,6,7,8]. One variant that has attracted a great deal of research interest is the enhanced hypercube [9], since it possesses many properties superior to the standard hypercube [9,10,11,12,13,14,15]. Specifically, when , we call the folded hypercube [16,17,18,19] in the case where .
A variety of network topologies have been investigated and constructed by researchers. However, failures may occur when a network is put to use. Latifi [1] introduced the conditionally faulty model. A network is a g-conditionally faulty model if each vertex of the network is incident to at least g fault-free neighbors, where . Many fault-tolerant embeddings in conditionally faulty networks are being investigated. We will use and to denote the set of faulty vertices and faulty edges in . Hsieh and Kuo [3] proved that a fault-free cycle of length can be embedded in when and . Hsieh and Chang [4] showed that contains a fault-free cycle of length at least with , and , in which each node is incident to at least two critical edges. We define and as the set of faulty vertices and faulty edges in . Kuo [17] studied , indicating that when , has a fault-free even cycle with length from 4 to , where , while also having a fault-free odd cycle with length from to , where is even. Kuo and Hsieh [19] studied the conditionally faulty with , and proved that has a fault-free even cycle with length from 4 to and also has a fault-free odd cycle with length from to when is even. Kuo et al. [18] proved that under the condition that each vertex connects at least four fault-free neighbors, for , has a fault-free even cycle with length from 4 to , where ; for even , it has a fault-free odd cycle with length from to , where . We represent with the set of a pair of adjacent faulty vertices in . Kuo et al. [20] showed that in , every fault-free edge lies on an even cycle with length from 4 to for ; it also lies on an odd cycle with length from to for even . We will use and to represent the set of faulty vertices and faulty edges in . Liu et al. [13] considered with under the conditionally faulty model and proved that contains a fault-free cycle of every even length from 4 to when and k have the same parity; also, contains a fault-free cycle of every odd length from to when and k have different parity. Liu et al. [14] also considered with , , and , showing that there is a cycle with length in . Due to the above motivation, in this paper, I completely improve [19] and partially improve [11] odd cycle embedding and consider the cycle-embedding properties in the conditionally faulty enhanced hypercube. For and k having different parity, if , then it is proved that contains a fault-free cycle of every odd length from to .
This paper is composed of four sections: In Section 2, I present and explore some basic terminology and lemmas related to hypercubes, i-partitions, and automorphism. The construction of the desired odd cycles is proposed in Section 3. Particularly, Section 3 focuses on the odd cycle embedding in the conditionally faulty , with and k having different parity, when , , or . Finally, Section 4 presents some conclusions and future work.
2. Preliminaries
For graph definitions and terminology not mentioned here, see [21]. A connected graph can be used to model a network, where V denotes the vertex set of the graph G, and E is called the edge set of the graph G. Let the graph be a subgraph of if and . If and , then we that say the graph is a subgraph of induced by . We represent a mapping f from to such that if and only if ; then, we call the two graphs and isomorphic, denoted by . We call x and y adjacent if . We use a sequence of adjacent vertices, , to represent a path with the original vertex and end vertex . The path is a cycle when .
The n-dimensional hypercube can be denoted by , with or and . Clearly, , . We denote the ith dimensional edge set by . We use to denote the distance between u and v, which corresponds to the shortest path between u and v in G.
Tzeng and Wei [9] proposed the enhanced hypercube , which can be constructed from by adding complementary edges. Let be the complementary edge set, given as , where is the complement of —i.e., iff for . Clearly, and .
An automorphism of a graph G is a permutation on such that if and only if for . For an undirected graph G, if for every pair of vertices , there exists an automorphism of G that maps u to v, we say that the graph G is vertex-transitive, also known as vertex-symmetric. A graph G is edge-transitive if for any , there exists an automorphism such that . It is well known that hypercubes are vertex-transitive and edge-transitive. However, enhanced hypercubes are vertex-transitive but not edge-transitive [22].
Definition 1
([13]). For , an i-partition on , partitions along dimension i to form two -dimensional cubes, where :
- (i)
- For , , we partition into two -dimensional hypercubes and , where (respectively, ) is the subgraph of induced by , (respectively, ). Thus, .
- (ii)
- For , , we partition into two -dimensional enhanced hypercubes and , where (respectively, ) is the subgraph of induced by , (respectively, ). Thus, .
Lemma 1
([14]). For , let σ be an automorphism of such that for any . If , then is disconnected. If , then .
Lemma 2
([5]). Let u and v be any two different vertices in , where . There exists a path of length l joining u and v with and .
Lemma 3
([6]). For and , let u and v be any two distinct fault-free vertices in . Then, contains a fault-free path with length l, and .
Lemma 4
([7,23]). For and , every fault-free edge of lies on a fault-free even cycle with length l, .
Lemma 5.
If , and , then every fault-free edge of lies on a fault-free even cycle with length l, .
Proof.
Definition 1 indicates that . We give e as a fault-free edge in :
- (i)
- . Lemma 4 ensures that the result is true.
- (ii)
- . By Lemma 1, for any arbitrary edge , we have an automorphism such that . Since and is isomorphic to , . Lemma 4 indicates that lies on a fault-free cycle of every even length from 4 to .
By the above cases, the lemma holds. □
Lemma 6
([24]). For and , every fault-free edge of the conditionally faulty lies on a even cycle with length l, .
Lemma 7
([7]). For , , and , contains a fault-free even cycle with length from 4 to .
Lemma 8
([17]). If and is even, then contains a fault-free odd cycle with length l, .
3. Odd Cycle Embedding in Conditionally Faulty
Firstly, we show two basic lemmas for and , , which will be used as the basic cases of the proof of Theorem 1.
Lemma 9.
In conditionally faulty , if , then we will find the fault-free odd cycles with length .
Proof.
In conditionally faulty , if , the odd cycle with length can be easily found.
If and , by the vertex-transitivity of , we can assume that the vertex 000 is faulty. Let 000 be a faulty vertex. Thus, (010, 011, 001, 010), (001, 011, 111, 110, 010, 001), and (001, 011, 111, 101, 100, 110, 010, 001) form the desired cycles of lengths 3, 5, and 7 respectively.
If and , by the edge-transitivity of , we hypothesize that the faulty edge is the 1-dimensional edge , the 2-dimensional edge (000, 010), the 3-dimensional edge (000, 001), or the complementary edge (000, 011). We can construct the odd cycle with lengths 3, 5, and 7, respectively, the same as above. □
Lemma 10.
In conditionally faulty , , contains fault-free odd cycles with length l, .
Proof.
By Lemma 8, has a fault-free odd cycle with length when . Now, we consider . If , it is easy to construct the fault-free cycle of every odd length from 3 to . We suppose that in the following. Definition 1 indicates that we can partition along an i-dimensional faulty edge, ; then, it forms two subcubes satisfying that is conditionally faulty.
Case 1. .
Case 1.1. , .
Let , , , , and , for , where denotes the set of hypercube edges between and . Since is conditionally faulty, it follows that every vertex in (resp. ) connects at least two fault-free edges of (resp. ). It follows that , , and . Let us suppose that ; then, , and .
Case 1.1.1. .
Note that and . Since and every vertex is incident to at least two fault-free vertices, by Lemma 9, there exists a fault-free cycle of every odd length from 3 to in . Since , we can always find an edge on cycle such that the edges in are all fault-free. Since , , and , by Lemma 3, there exists a fault-free path of length from 3 to in , where is the set of complementary edges in . Note that the edge is fault-free. We have . forms the desired cycle of every odd length with length .
Case 1.1.2. , i.e., and .
If and , we find an edge in satisfying that . Let us say that the edge is fault-free temporarily. Thus, the number of faulty elements is 1. Similarly to Case 1.1.1, we take instead of the edge in Case 1.1.1. If and there exists the faulty edge in such that the edges in are all fault-free, the rest of the proof of this case is similar to Case 1.1.1. If either and the edges in are not all fault-free when is a faulty edge in or and , we will find the desired odd fault-free cycle as follows: Since , by Lemma 9, we hypothesize that a vertex is fault-free temporarily such that is a fault-free odd cycle with length from 3 to containing the vertex x and , where z and w are two adjacent vertices on the cycle in . Since and , by Lemma 2, is a path with length in . is an odd cycle with length , in .
Case 1.2. , .
Let , , , , and , for , where denotes the set of hypercube edges between and . Then, we have , and . Without loss of generality, we hypothesize that . Then, we have and .
Case 1.2.1. .
Since , by Lemma 4, is a fault-free even cycle with length in . Let us recall that and ; we will select an edge on cycle satisfying that (resp. ) and (resp. ) and choose an edge on cycle satisfying that (resp. and . can form the desired cycle with lengths 3 and 5. Since and , by Lemma 3, there exists a fault-free path with length in . is an odd cycle with length in . Thus, .
Case 1.2.2. , i.e., and .
If , we find a faulty edge and assume that is fault-free temporarily. Thus, . Since and , the edges in or are all fault-free. Similarly to Case 1.2.1, we take instead of the edges and in Case 1.2.1. If , then . We find a vertex x in and say that it is a fault-free vertex temporarily such that is an even cycle with length from 4 to containing the vertex x and (resp. ), where z and w are two adjacent vertices of x on cycle in . Since and in , by Lemma 2, is a path with length in . Hence, forms the cycle with length in . Note that the fault-free cycle of length 3 in is easy to find. Finally, .
Case 2. . i.e., .
We choose two arbitrary faulty vertices which differ at the j-th position, where . We partition along dimension j such that every 3-dimensional cube has at least one faulty vertex. If , the rest of the proof of this case is similar to that of the last part of Case 1.1.2. Similarly to Case 1.2.2, we can also find the odd cycles in .
In summary, the lemma is true. □
Now, we consider the embedding of odd cycles in conditionally faulty when and k have different parity, , and . We first give a proof of the odd cycles in , , as follows.
Corollary 1.
In the conditionally faulty , , if and , then there exists a fault-free odd cycle with length from to .
Proof.

Since for and , we find two faulty vertices and which are different exactly ar the jth position, that is, , where , . Now, we can partition along dimension j into two subcubes such that each subcube has at least one faulty vertex and , where is the number of faulty edges between the two subcubes (see Table 1).

Table 1.
Cycle construction in the proof of Corollary 1 when and in , .
- , , .Let , (resp. , and ). We hypothesize that . Thus, and . Since , by Lemma 10, is a fault-free odd cycle with length in . Since every subcube has at least one faulty vertex and , there exist at most three faulty vertices in when . Note that every vertex in (resp. ) connects at least two fault-free edges of (resp. ).
- (i)
- If , , and , we will find an odd cycle with length from to . The following apply: On one hand, if and , let us say that the edge is fault-free temporarily. Thus, . By Lemma 10, there exists a fault-free cycle containing the edge with odd length in . Note that . As and , Lemma 3 indicates that is a path with odd length from 3 to . Hence, is an odd cycle with length . Since and , it follows that . Therefore, . On the other hand, if and , we choose a vertex and say that it is fault-free temporarily such that when there exists a cycle with length containing the vertex x by Lemma 10, and the vertices z and w are adjacent to x on cycle in . Note that . Since , by Lemma 3, is a path with odd length , . Thus, is an odd cycle with length . Since and , it follows that . Therefore, .
- (ii)
- If and , we can use a similar method to the above to construct an odd cycle with length from to .
- , , .Let and (resp. and ) denote the set of faulty vertices and faulty edges in (resp. ), respectively. We hypothesize that . Thus, , and . Note that there exists only one faulty edge in under the above condition. Hence, every vertex in (resp. ) connects at least two fault-free edges of (resp. ). The following apply:
- (i)
- If , , and , we will find an odd cycle with length from to . Let . Let us say that the edge is fault-free temporarily. Since , either , or . We hypothesize the former to be true. Now, the number of faulty elements in is three, and by Lemma 7, there exists a fault-free even cycle containing the faulty edge whose length is from 4 to . Note that or . Since , by Lemma 3, is a path with length in . Thus, is an odd cycle with length . In addition, since , we find a fault-free vertex such that the vertices in are both fault-free. Since , by Lemma 3, is a fault-free path with length and in . Hence, is an odd cycle with length and . Thus, .
- (ii)
- If and , we can use a similar method to the above to find odd cycles with length from to .
□
Lemma 11.
In a conditionally faulty , if and have different parity, , and , then it contains a fault-free odd cycle with length l, .
Proof.



Since , contains at most one vertex which is incident to exactly two fault-free edges. If not, , a contradiction.
Case 1. , . By Definition 1, we partition along dimension of some faulty edge into two subcubes and .
The proof of this case is by induction on n. By Lemma 10, the lemma is true if . We hypothesize that the result is true for . We now consider that .
Let , , , , and , for , where denotes the set of hypercube edges between and . Then, we have , and . Let us assume . It implies that and . Since every vertex in is incident to at least two fault-free edges, every vertex in (respectively, ) is incident to at least two fault-free edges of (respectively, ) (see Table 2).

Table 2.
Cycle construction in the proof of Lemma 11 when , .
Case 1.1. .
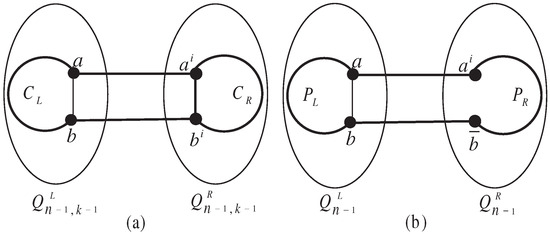
As , it implies that the conditionally faulty has a fault-free odd cycle with length from to . Let be a fault-free cycle with length in . Since when , obviously, one can choose an edge in such that the edges in are all fault-free. Lemma 5 ensures that the edge lies on a fault-free cycle of every even length from 4 to in . Thus, forms a cycle with length . forms a cycle whose length is from to (see Figure 1a). (In this paper, in the figures, we use the straight full line, the dotted line, and the curved line to denote the fault-free edge, the faulty edge, and the path, respectively. We use the bold lines to denote the selected desired fault-free cycle).

Figure 1.
Illustrations of Case 1.1 and Case 2.1.2 in the proof of Lemma 11. (a) is the desired fault-free cycle in ; (b) is the desired fault-free cycle in .
Case 1.2. .
Note that . has a fault-free odd cycle with length . The following apply:
- If , we can select a faulty edge and suppose that it is fault-free temporarily such that the edges in are all fault-free. Thus, contains a cycle with length containing the edge . We take instead of in Case 1.1. The rest of the construction of this case is similar to that of Case 1.1. Thus, we can construct the desired cycle as and , and the length is from to . Since , there exists the desired odd cycle with length l, .
- If when for , we find a faulty vertex , and there exists a fault-free cycle with odd length containing the vertex x in by the induction hypothesis, and the elements in are all fault-free, where z and w are two adjacent vertices of x on the cycle . Since and , Lemma 2 ensures that there exists a path whose length is every even integer from 2 to in . Thus, forms the desired cycle of length from to in . Since , we have . Thus, .
Case 2. , . Definition 1 ensures that we can partition along dimension of some faulty edge into two subcubes and .
For , let , , , , , and . Then, we have , and . We hypothesize that . Then, we have and . Since every vertex of connects edges and , it follows that is conditionally faulty. Since every vertex in connects at least two fault-free edges, and , we can obtain that there exists at most one vertex in which connects exactly only one fault-free edge in . If not, then , a contradiction.
Case 2.1. .
Case 2.1.1. .
Since there exist distinct vertices in and for , we choose a fault-free vertex satisfying that the elements in are all fault-free. Note that . Since , by Lemma 3, there exists a fault-free path with odd length in . Hence, is a path with length (see Table 3).

Table 3.
Cycle construction in the proof of Lemma 11 when , and .
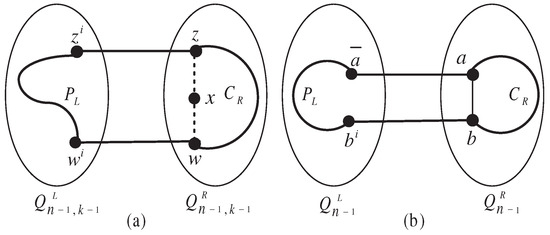
Case 2.1.2. .
Let us recall that has vertex-disjoint edges and when ; we find a fault-free edge such that the edges in or are all fault-free edges. Let us say that the former is true. Note that or . As , Lemma 3 implies that is fault-free and its length is every even integer , or . Thus, the cycle has length l, . That is, or . The following apply:
- If each vertex in connects at least two fault-free edges, since , by Lemma 6, lies on a fault-free cycle of every even length from 6 to in . Thus, we have with length from to . Since , and , we can conclude that . Thus, we have (see Figure 1b).
- If there is a vertex, say , that connects exactly one fault-free edge, say , as the vertex x connects faulty edges in , it implies that . Let us suppose that . Since x is incident to faulty edges of and , there exists at least one faulty edge incident to the vertex x, say , such that . Let us say that the edge is fault-free temporarily. Then, we can use t to replace t as in the above subcase. Similarly, we construct the path , whose length is .
Case 2.2. .
Case 2.2.1. If , then we have , and (see Table 4).

Table 4.
Cycle construction in the proof of Lemma 11 when or , and .
If , then Corollary 1 indicates that it holds. Now, we consider . For , , and , 7 helps to find an even cycle with length from 4 to in . Clearly, we find an edge such that or . We hypothesize the former to be true. As , Lemma 2 implies that is an even path with length in , where or . Finally, is an odd cycle with length l, where or .
Case 2.2.2. If , then , , and .
We select an edge in satisfying that . Lemma 2 indicates that is the desired path with length . In the following, we choose a faulty edge in such that the edges in are fault-free and say that the edge is a fault-free edge temporarily. If every vertex in is incident to at least two fault-free edges, Lemma 6 implies that is the desired cycle with length . If there exists a vertex which connects exactly one edge in , we can take s as the vertex and find an adjacent faulty edge satisfying when is fault-free. Finally, we find the odd cycle as with length from .
In summary, the lemma is true. □
Lastly, we consider the embedding of odd cycles in conditionally faulty where and k have different parity, , and .
Lemma 12.
In conditionally faulty , if and have different parity and , then contains a fault-free odd cycle with l, where .
Proof.
Since , there exists at most one vertex which is adjacent to exactly two fault-free vertices. If not, we hypothesize that there exist two such vertices, and we have , a contradiction. If every vertex in is adjacent to at least two fault-free vertices, we choose two vertices and in to find an integer i satisfying that , . If there is a vertex in adjacent to exactly two fault-free vertices, we find a faulty vertex adjacent to the vertex a. Definition 1 indicates that can be partitioned along dimension i into two -dimensional cubes such that every cube has exactly one faulty vertex and every vertex connects at least two fault-free edges in .
Case 1. , .
The proof of this case is by induction on n. By Lemma 10, the lemma holds when . We hypothesize that the result is true for . We now consider that . We can denote and . Let us suppose that . We can conclude that and .
Case 1.1. and .
As and every vertex in is adjacent to at least two fault-free edges, is a cycle with length in .
Let be a fault-free cycle with length in . As for , we choose an edge in cycle such that . Since , Lemma 5 indicates that the edge lies on a fault-free cycle with every even length from 4 to in . Therefore, forms the desired cycle with length from to .
Case 1.2. and .
On one hand, since for , is a cycle with every odd length in . On the other hand, let . Let us say that the vertex x is fault-free temporarily. There exists a cycle containing the vertex x with length in , and the vertices z and w are adjacent to the vertex x on the cycle such that the vertices in are both fault-free. Note that . Since , by Lemma 3, is a path with length in . Obviously, forms the desired cycle with length l, . Since , , and , . Hence, (see Figure 2a).

Figure 2.
Illustrations of Case 1.2 and Case 2.2.2 in the proof of Lemma 12. (a) is the desired fault-free cycle in ; (b) is the desired fault-free cycle in .
Case 2. , .
We denote and . Let us suppose that . Thus, , and .
Case 2.1. .
Let us recall that and for ; we will find a vertex satisfying that . Note that . Since , by Lemma 3, there exists a fault-free path with length in . Thus, is an odd cycle with length in .
Case 2.2. .
Case 2.2.1. .
Since for , by Lemma 7, is a fault-free even cycle with length in . Since for and the smallest length of cycle is 4, we choose an edge on the cycle such that the edges in or are both fault-free. We hypothesize that the former is true. Thus, the path is of length . Since , and or , by Lemma 3, there exists a fault-free path with length in . forms the desired cycle with length in .
Case 2.2.2. .
Since , , and for , by Lemma 7, there exists a fault-free cycle of every even length from 4 to in . Since and , we find an edge in the cycle such that the vertices in or are fault-free. If not, we have for , which contradicts the fact that . We can assume that the former is true. Since , we can obtain that . Note that or . Since , Lemma 3 implies that is a path with length or . Hence, is an odd cycle with length or (see Figure 2b).
By combining the above cases, the lemma holds. □
Theorem 1.
In conditionally faulty , if and have different parity and , then contains a fault-free odd cycle with length l, .
Proof.
By Lemma 9 and Lemma 10, the theorem holds in and , , respectively. Lemma 11 indicates that the theorem holds in when and k have different parity, , and . In addition, by Lemma 12, the theorem holds in when and k have different parity and . In summary, Theorem 1 is true. □
4. Concluding Remarks
Network topology is an important issue in the design of computer networks since it is crucial to many key properties, such as symmetry and fault tolerance. In this article, we focus on the conditionally faulty enhanced hypercube , where and k have different parity. We prove that contains a fault-free odd cycle with length from to when . We believe that the structure constructed in this paper will be helpful in future research.
We will continue to investigate the fault tolerance of different networks under different faulty structures, such as the faulty structure, the faulty structure, and so on. To improve the efficiency of hypercube networks in structural fault-tolerant models, this seems to be a good direction for future research.
Funding
This research was supported by Ningbo Natural Science Foundation (No. 2023J186), General Scientific Research Foundation of Zhejiang Province Education Department (No. Y202351606), and Ph.D Research Foundation of Ningbo University of Technology (No. 2090011540015).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Leighton, F.T. Introduction to Parallel Algorithms and Architecture: Arrays · Trees · Hypercubes; Morgan Kaufmann: San Mateo, CA, USA, 1992. [Google Scholar]
- Chen, M.R.; Habib, M.; Lin, C.K. A novel edge connectivity based on edge partition for hypercube and folded hypercube. Appl. Math. Comput. 2024, 470, 128558. [Google Scholar] [CrossRef]
- Hsieh, S.Y. Fault-tolerant cycles embedding in the hypercube with more both faulty vertices and faulty edges. Parallel Comput. 2006, 32, 84–91. [Google Scholar] [CrossRef]
- Hsieh, S.Y.; Chang, N.W. Extended fault-tolerant cycle embedding in faulty hypercubes. IEEE Trans. Reliab. 2009, 58, 702–710. [Google Scholar] [CrossRef]
- Li, T.K.; Tsai, C.H.; Tan, J.J.M.; Hsu, L.H. Bipanconnectivity and edge-fault-tolerant bipancyclicity of hypercubes. Inf. Process. Lett. 2003, 87, 107–110. [Google Scholar] [CrossRef]
- Ma, M.J.; Liu, G.Z.; Pan, X.F. Path embedding in faulty hypercubes. Appl. Math. Comput. 2007, 192, 233–238. [Google Scholar] [CrossRef]
- Tsai, C.H. Fault-tolerant cycles embedded in hypercubes with mixed link and node failures. Appl. Math. Comput. 2008, 21, 855–860. [Google Scholar] [CrossRef]
- Zhuo, N.J.; Zhang, S.M.; Chang, J.M.; Ye, C.F. Non-inclusive diagnosability of folded hypercube-like networks. Discret. Appl. Math. 2025, 364, 237–246. [Google Scholar] [CrossRef]
- Tzeng, N.F.; Wei, S. Enhanced hypercube. IEEE Trans. Comput. 1991, 40, 284–294. [Google Scholar] [CrossRef]
- Cheng, E.; Qiu, K.; Shen, Z.Z. On the g-extra diagnosability of enhanced hypercubes. Theor. Comput. Sci. 2022, 921, 6–19. [Google Scholar] [CrossRef]
- Liu, M. Cycles embedding in enhanced hypercubes with faulty vertices. Symmetry 2024, 16, 44. [Google Scholar] [CrossRef]
- Liu, M. Vertex-fault-tolerant cycles embedding in four-conditionally faulty enhanced hypercube networks. IEEE Access 2024, 12, 80062–80070. [Google Scholar] [CrossRef]
- Liu, M.; Liu, H.M. Cycles in conditional faulty enhanced hypercube networks. J. Commun. Netw. 2012, 14, 213–221. [Google Scholar] [CrossRef]
- Liu, M.; Liu, H.M. Paths and cycles embedding on faulty enhanced hypercube networks. Acta Math. Sci. 2013, 32B, 227–246. [Google Scholar] [CrossRef]
- Xu, L.Q. Symmetric property and the bijection between perfect matchings and sub-hypercubes of enhanced hypercubes. Discret. Appl. Math. 2023, 324, 41–45. [Google Scholar] [CrossRef]
- Hsieh, S.Y.; Kuo, C.N.; Chou, H.H. A further result on fault-free cycles in faulty folded hypercubes. Inf. Process. Lett. 2009, 110, 41–43. [Google Scholar] [CrossRef]
- Kuo, C.N. Pancyclicity and bipancyclicity of folded hypercubes with both vertex and edge faults. Theor. Comput. Sci. 2015, 602, 125–131. [Google Scholar] [CrossRef]
- Kuo, C.N.; Cheng, Y.H. Cycles embedding in folded hypercubes with conditionally faulty vertices. Discret. Appl. Math. 2017, 220, 55–59. [Google Scholar] [CrossRef]
- Kuo, C.N.; Hsieh, S.Y. Pancyclicity and bipancyclicity of conditional faulty folded hypercubes. Inf. Sci. 2010, 180, 2904–2914. [Google Scholar] [CrossRef]
- Kuo, C.N.; Cheng, Y.H. Every edge lies on cycles of folded hypercubes with a pair of faulty adjacent vertices. Discret. Appl. Math. 2021, 294, 1–9. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Zuse Institute Berlin: Berlin, Germany, 1980. [Google Scholar]
- Imrich, W.; Klavžar, S. Product Graphs: Structure and Recognition; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Hsieh, S.Y.; Shen, T.H. Edge-bipancyclicity of a hypercube with faulty vertices and edges. Discret. Appl. Math. 2008, 156, 1802–1808. [Google Scholar] [CrossRef]
- Yang, D.W.; Gu, M.M. Conditional fault-tolerant edge-bipancyclicity of hypercubes with faulty vertices and edges. Theor. Comput. Sci. 2016, 627, 82–89. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).