Full Automorphism Group of (m, 2)-Graph in Finite Classical Polar Spaces
Abstract
1. Introduction
2. Preliminaries on the Symplectic Polar Space
3. Properties of -Graph in the Symplectic Polar Space

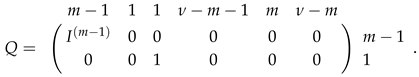

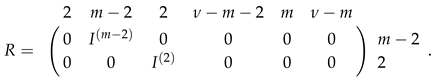
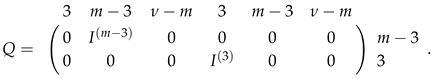


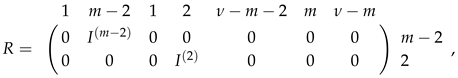

4. Automorphisms of -Graph in the Symplectic Polar Space
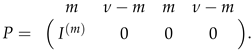



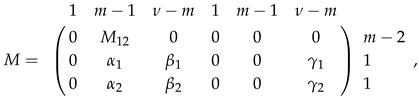
5. Conclusions and Further Study
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beule, J.D.; Klein, A.; Metsch, K. Substructures of finite classical polar spaces. In Current Research Topics in Galois Geometry; Storme, L., De Beule, J., Eds.; Mathematics Research Developments, Nova Science: Hauppauge, NY, USA, 2012; pp. 35–61. [Google Scholar]
- Ball, S. Finite Geometry and Combinatorial Applications, Number 82 in London Mathematical Society Student Texts; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Brouwer, A.E.; Maldeghem, H.V. Strongly Regular Graphs, Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2022; p. 182. [Google Scholar]
- Wan, Z.X.; Tang, Z.M. Symplectic graphs and their automorphisms. Eur. J. Combin. 2006, 27, 38–50. [Google Scholar][Green Version]
- Tits, J. Buildings of Spherical Type and Finite BN-Pairs; Lecture Notes in Math; Springer: Berlin/Heidelberg, Germany, 1974; p. 386. [Google Scholar]
- Zeng, L.W.; Chai, Z.; Feng, R.Q.; Ma, C.L. Full autommrphism group of generalized symplectic group. Sci. China Math. 2013, 56, 1509–1520. [Google Scholar] [CrossRef]
- Wan, Z.X.; Zhou, K. Unitary graphs and their automorphisms. Ann. Comb. 2010, 14, 367–395. [Google Scholar] [CrossRef]
- Liu, W.; Ma, C.L.; Wang, K.S. Full automorphism group of generalized unitary graphs. Linear Algebra Appl. 2012, 437, 684–691. [Google Scholar] [CrossRef]
- Gu, Z.H.; Wan, Z.X. Orthogonal graphs of odd characteristic and their automorphisms. Finite Fields Appl. 2008, 14, 291–313. [Google Scholar] [CrossRef]
- Wan, Z.X.; Zhou, K. Orthogonal graphs of characteristic 2 and their automorphisms. Sci. China Ser. A 2009, 52, 361–380. [Google Scholar] [CrossRef]
- Li, F.G.; Wang, Y.X. Subconstituents of dual polar graph in finite classical space III. Linear Algebra Appl. 2002, 349, 105–123. [Google Scholar] [CrossRef]
- Huo, L.J.; Guo, W.N.; Ma, C.L. Automorphisms of generalized orthogonal graphs with odd characteristic. Acta Math. Sin. Chin. Ser. 2014, 57, 71–88. [Google Scholar][Green Version]
- Huo, L.J.; Guo, W.N.; Zhang, G.S. Automorphisms of generalized orthogonal graphs of characteristic 2. Front. Math. China 2014, 9, 303–319. [Google Scholar] [CrossRef]
- Wan, Z.X. Geometry of Classical Groups over Finite Fields; Science Press: Beijing, China; New York, NY, USA, 2002. [Google Scholar]
- Wei, H.Z.; Wang, Y.X. Suborbits of the transitive set of subspaces of type (m, 0) under finite classical groups. Algebra Colloq. 1996, 3, 73–84. [Google Scholar]
| Name | Symbol | n | G | |
|---|---|---|---|---|
| symplectic | 0 | |||
| Hermitian | ||||
| Hermitian | ||||
| hyperbolic | ||||
| parabolic | 0 | |||
| elliptic | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, S.; Zeng, L. Full Automorphism Group of (m, 2)-Graph in Finite Classical Polar Spaces. Axioms 2025, 14, 614. https://doi.org/10.3390/axioms14080614
Zhang Y, Liu S, Zeng L. Full Automorphism Group of (m, 2)-Graph in Finite Classical Polar Spaces. Axioms. 2025; 14(8):614. https://doi.org/10.3390/axioms14080614
Chicago/Turabian StyleZhang, Yang, Shuxia Liu, and Liwei Zeng. 2025. "Full Automorphism Group of (m, 2)-Graph in Finite Classical Polar Spaces" Axioms 14, no. 8: 614. https://doi.org/10.3390/axioms14080614
APA StyleZhang, Y., Liu, S., & Zeng, L. (2025). Full Automorphism Group of (m, 2)-Graph in Finite Classical Polar Spaces. Axioms, 14(8), 614. https://doi.org/10.3390/axioms14080614





