Mathematical Modeling, Bifurcation Theory, and Chaos in a Dusty Plasma System with Generalized (r⋆, q⋆) Distributions
Abstract
1. Introduction
1.1. Research Foundation
1.2. Insights from Prior Studies
1.3. Identified Research Gaps
1.4. Core Contributions
- Basin of attraction.
- Lyapunov exponents.
- Fractal Dimension.
- Bifurcation diagram.
- Poincaré map.
- Time analysis.
- Multi-stability analysis.
- Chaotic attractor.
- Return map.
- Power spectrum.
- Three-dimensional (3D) phase portrait.
- Two-dimensional (2D) phase portrait.
1.5. Research Structure
2. Mathematical Framework
Mathematical Modeling of the Governing System
3. Construction of the Autonomous Dynamic System
Bifurcation Analysis
- 1.
- If , the point is locally stable and corresponds to a center.
- 2.
- If , the point is unstable and corresponds to a saddle.
- 3.
- If , the point is non-hyperbolic.
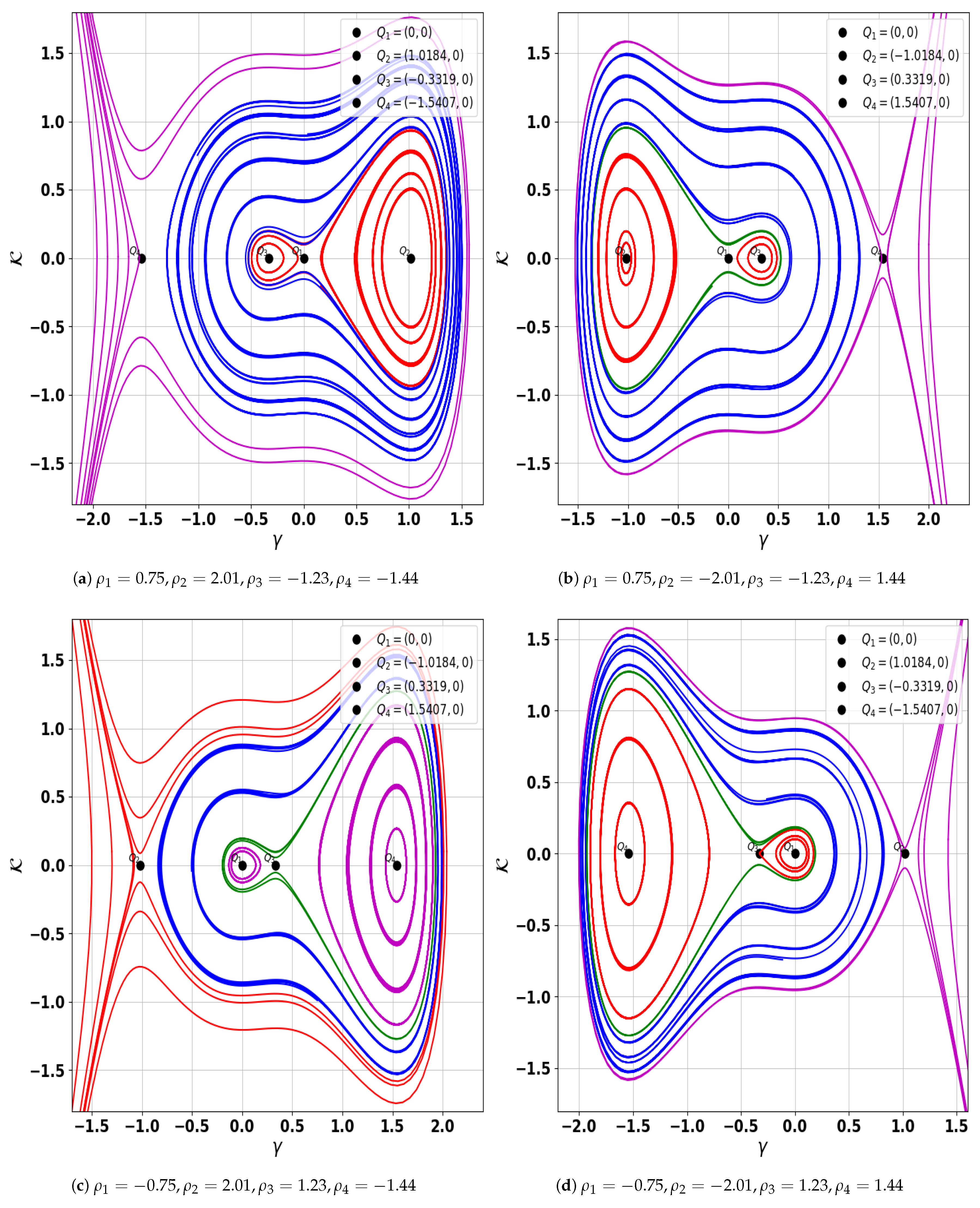
| Sub-Figure | Conditions | Equilibrium Point |
|---|---|---|
| Figure 1a | Center: (1.0184, 0), (−0.3319, 0), Saddle: (0, 0), (−1.5407, 0) | |
| Figure 1b | Center: (−1.0184, 0), (0.3319, 0), Saddle: (0, 0), (1.5407, 0) | |
| Figure 1c | Center: (0, 0), (1.5407, 0), Saddle: (−1.0184, 0), (0.3319, 0) | |
| Figure 1d | Center: (−0.42922, 0), Saddle: (0, 0) | |
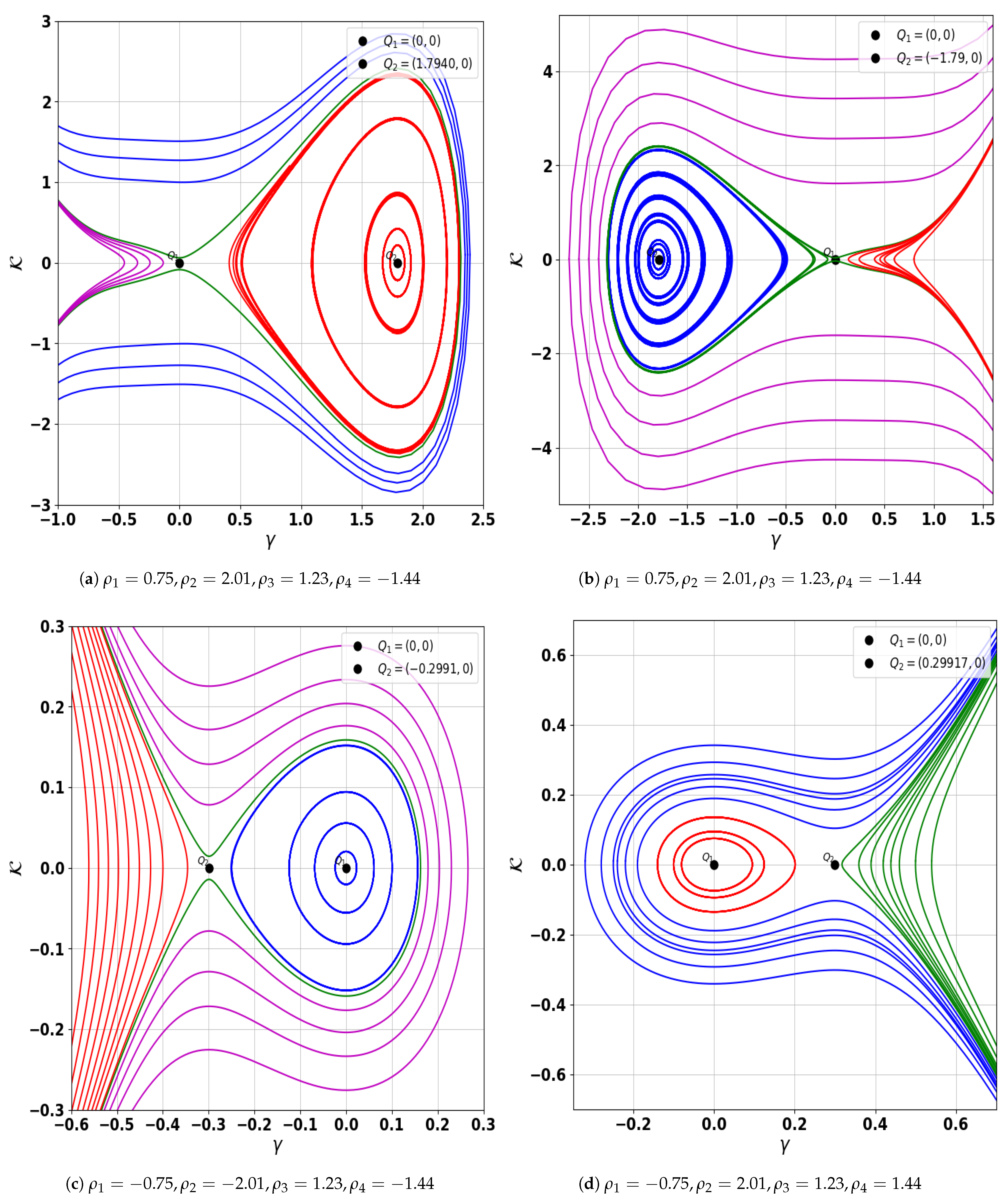
| Figure 2a | Center: (1.7940, 0), Saddle: (0, 0) | |
| Figure 2b | Center: (−1.7940, 0), Saddle: (0, 0) | |
| Figure 2c | Center: (0, 0), Saddle: (−0.29917, 0) | |
| Figure 2d | Center: (0, 0), Saddle: (0.29917, 0) | |
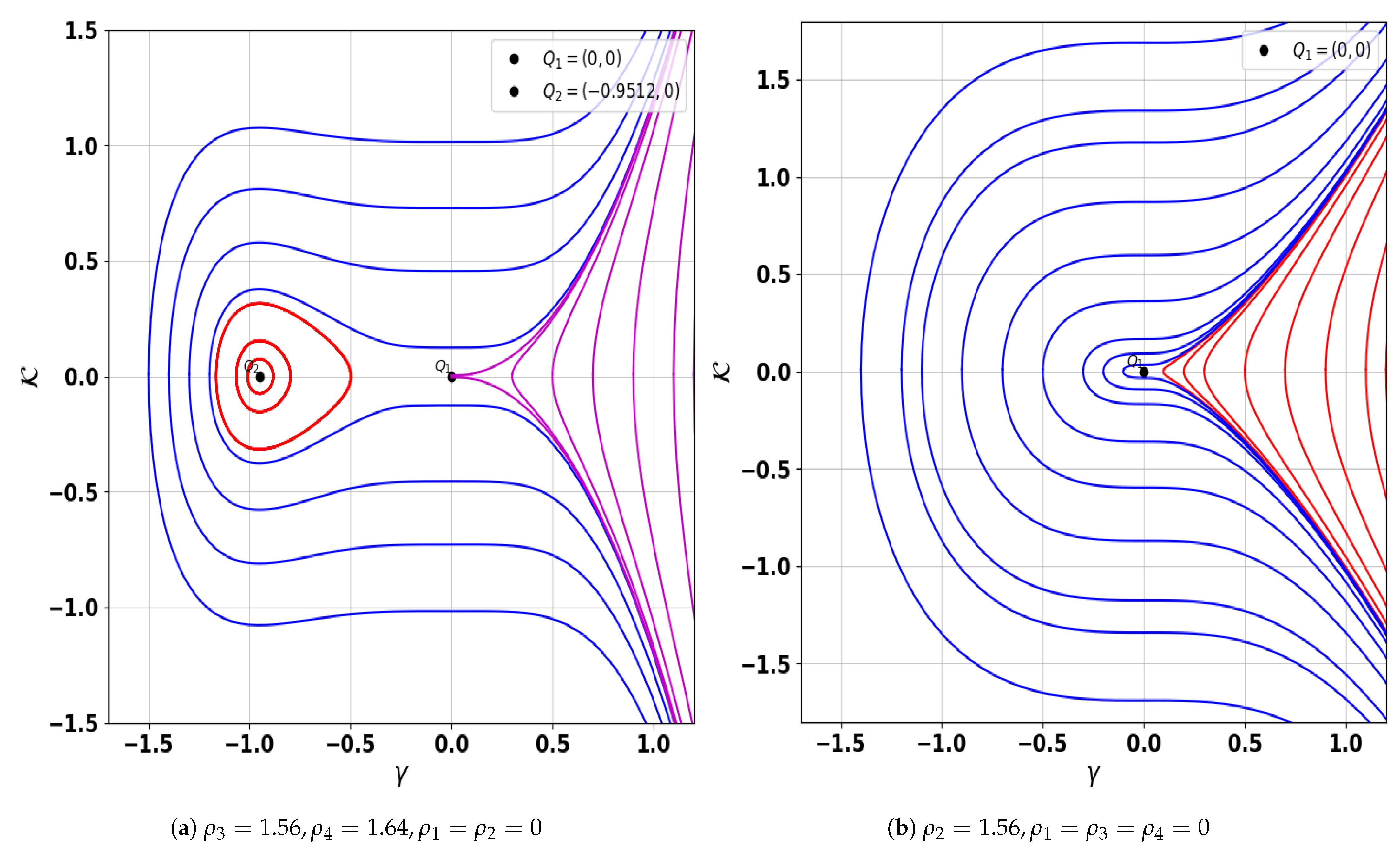
| Figure 3a | Saddle: (0, 0), Center: (−0.9512, 0) | |
| Figure 3b | Cusp: (0, 0) |
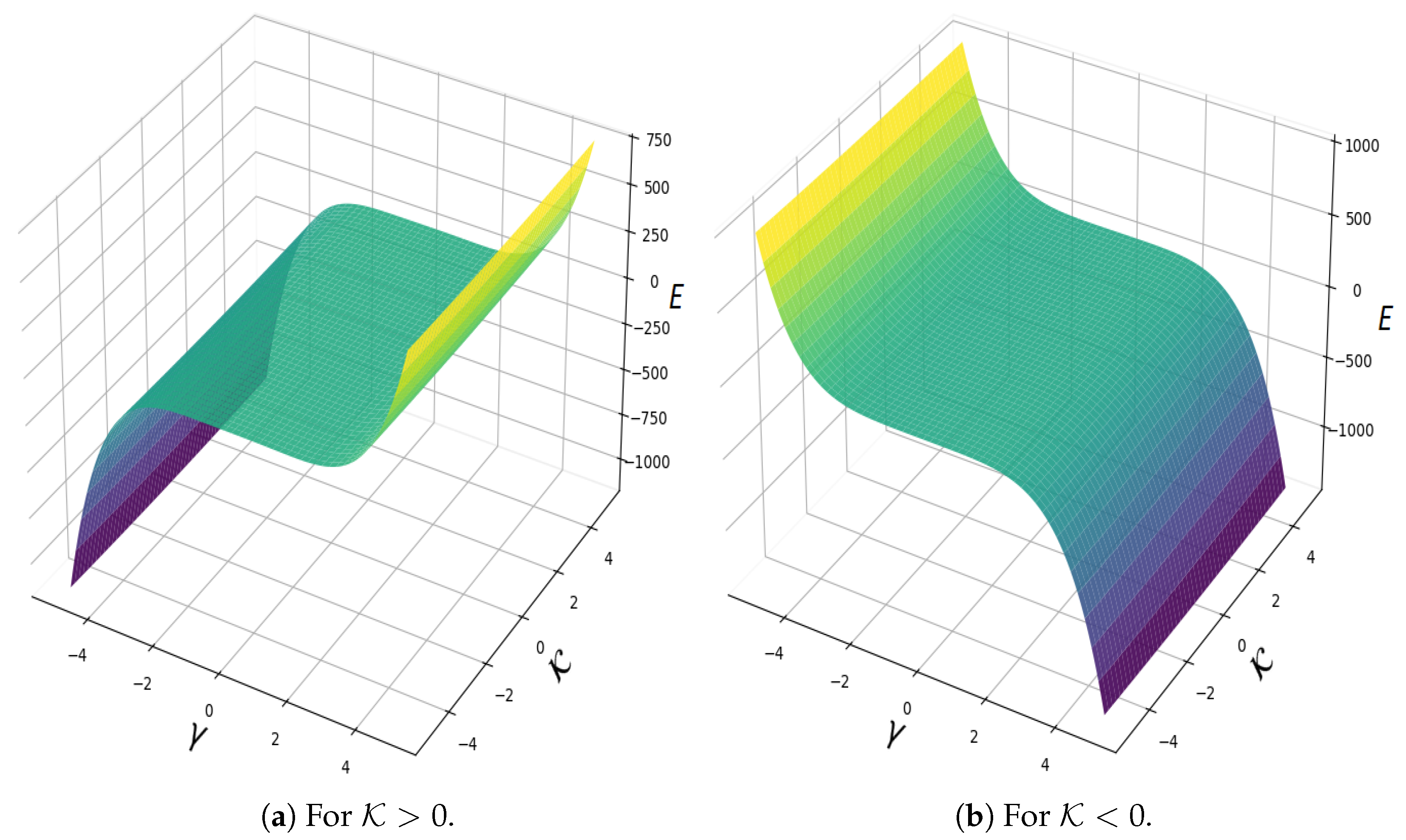
4. Hamiltonian Approach to Dynamical Systems
- 1.
- The function attains a maximum or minimum at the pointif .
- 2.
- has a saddle point at if .
- 3.
- If , further analysis is required to classify the nature of the stationary point.
5. Chaos Analysis
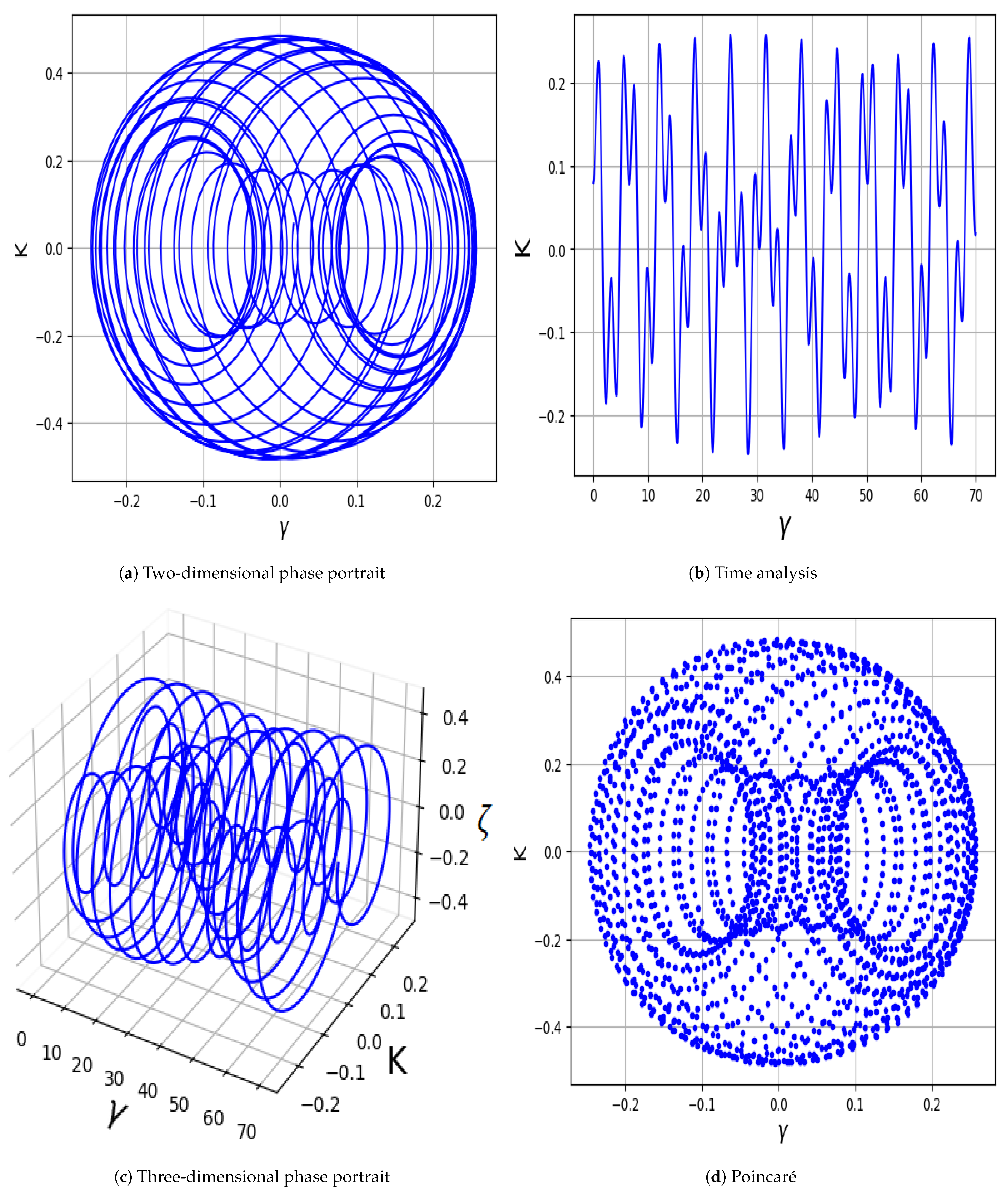
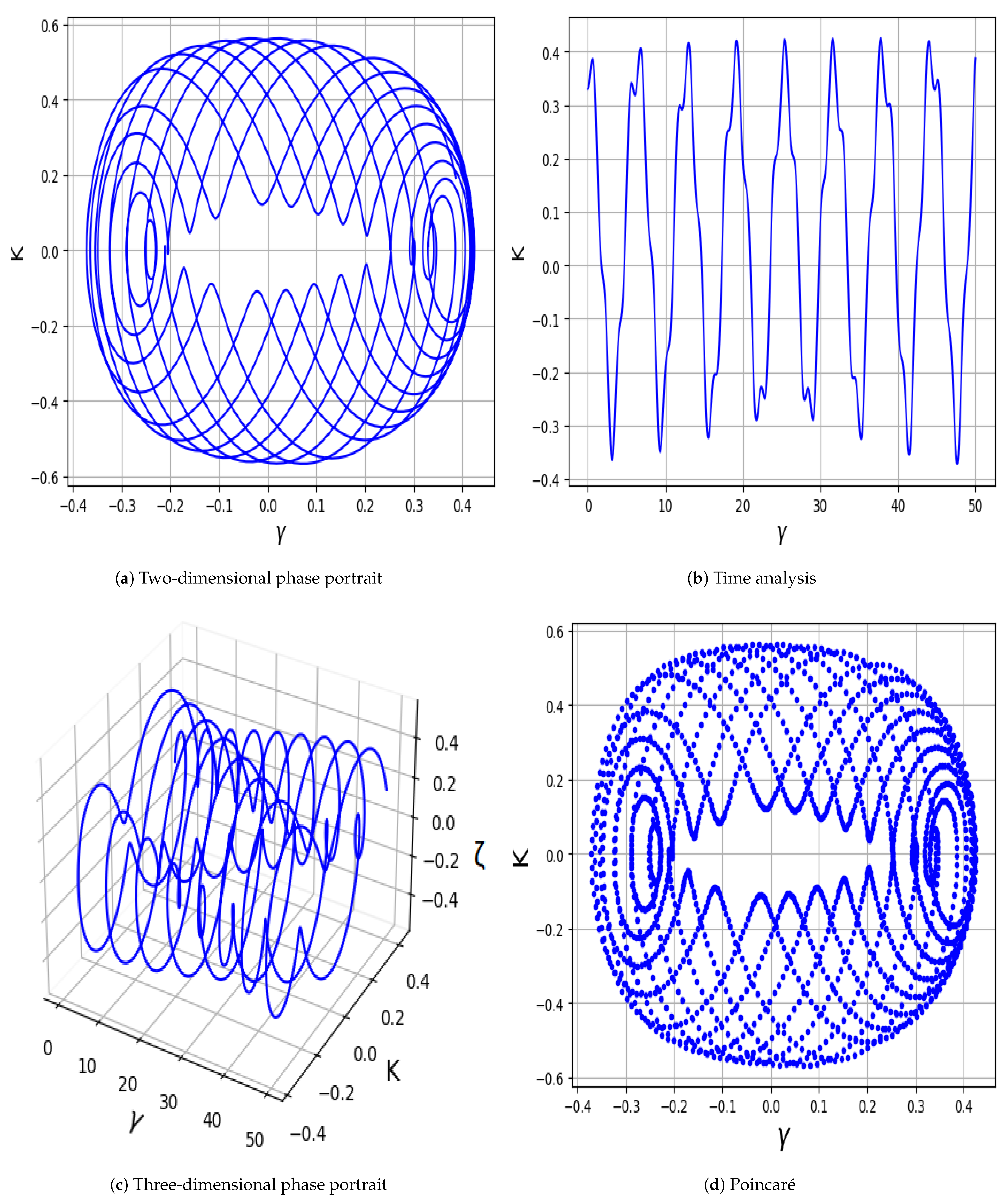
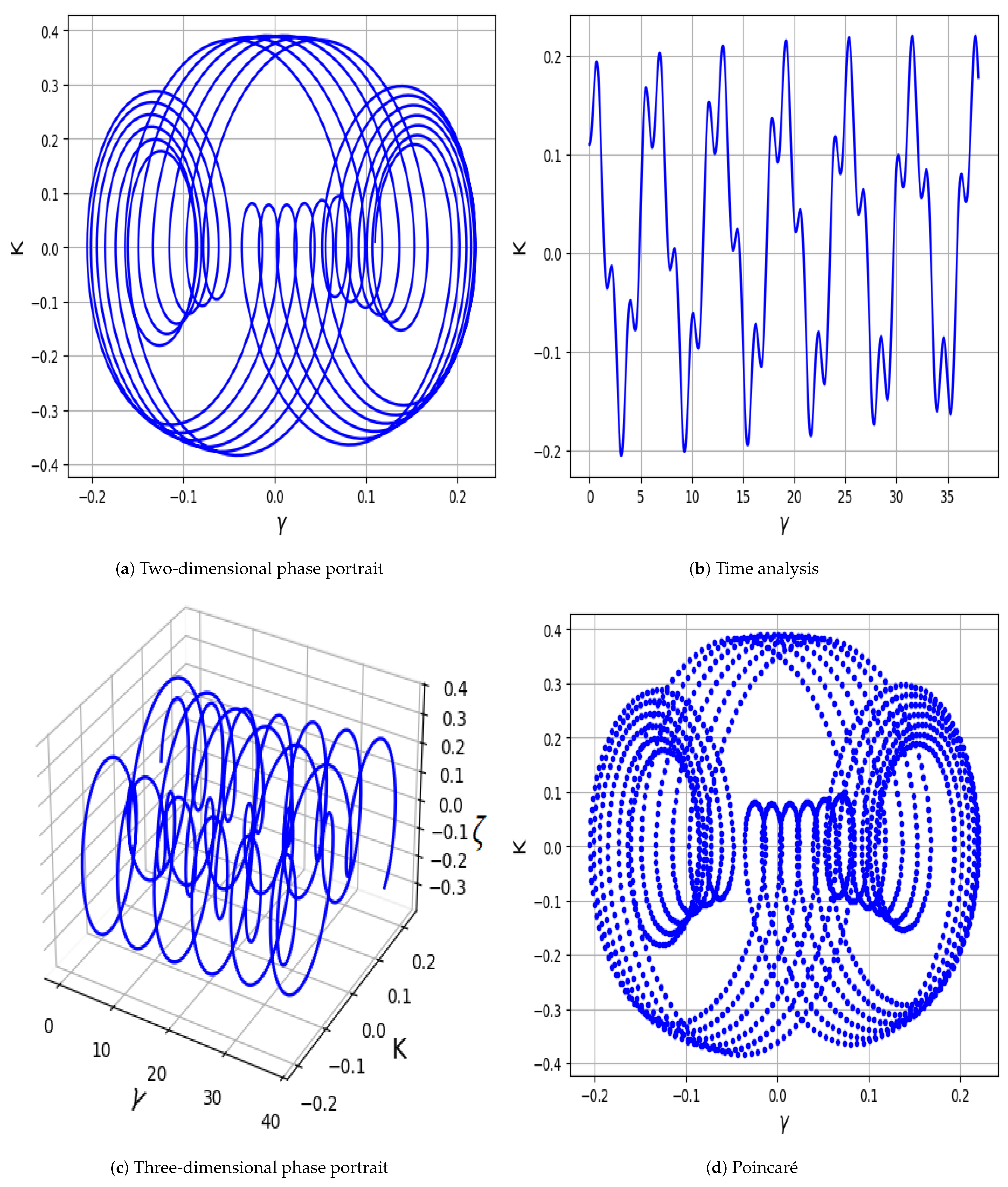
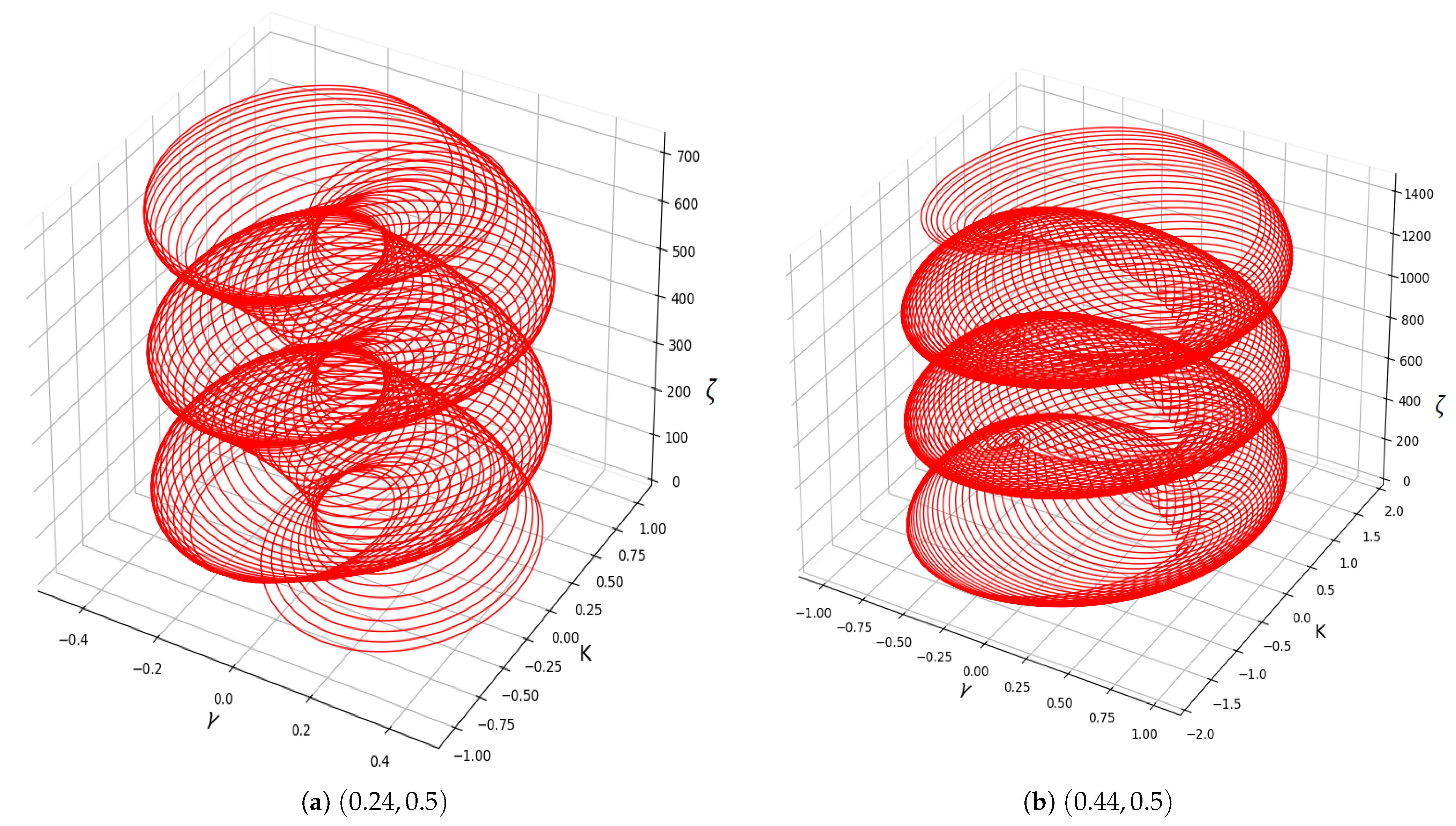
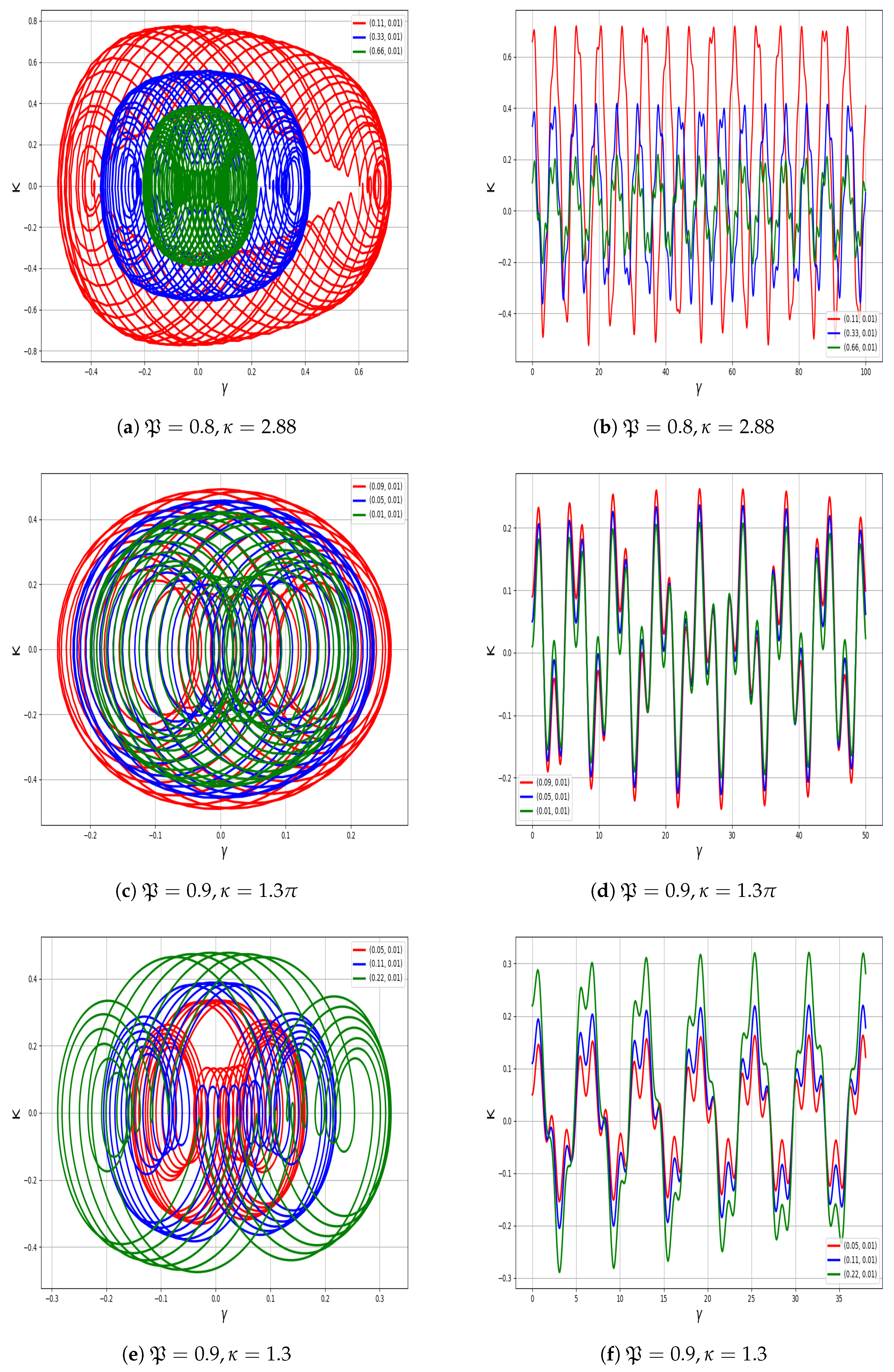
- In Figure 5a–d, the parameter values are set as , , , , , and , with demonstrating the influence of positive electrons. The system exhibits strongly chaotic behavior, characterized by densely intertwined and irregular trajectories that do not settle into any repeating pattern.
- In Figure 6a–d, the system is analyzed using , , , , , and , with indicating the role of positive electrons. The trajectories show partially organized loops with irregularities, indicating quasi-periodic or weakly chaotic dynamics with signs of sensitivity to initial conditions.
- In Figure 7a–d, we set , , , , , and , with reflecting the contribution of positive electrons The orbits form smooth, layered loops with structured repetition, reflecting quasi-periodic behavior without evident irregular transitions.
6. Techniques for Identifying Chaos
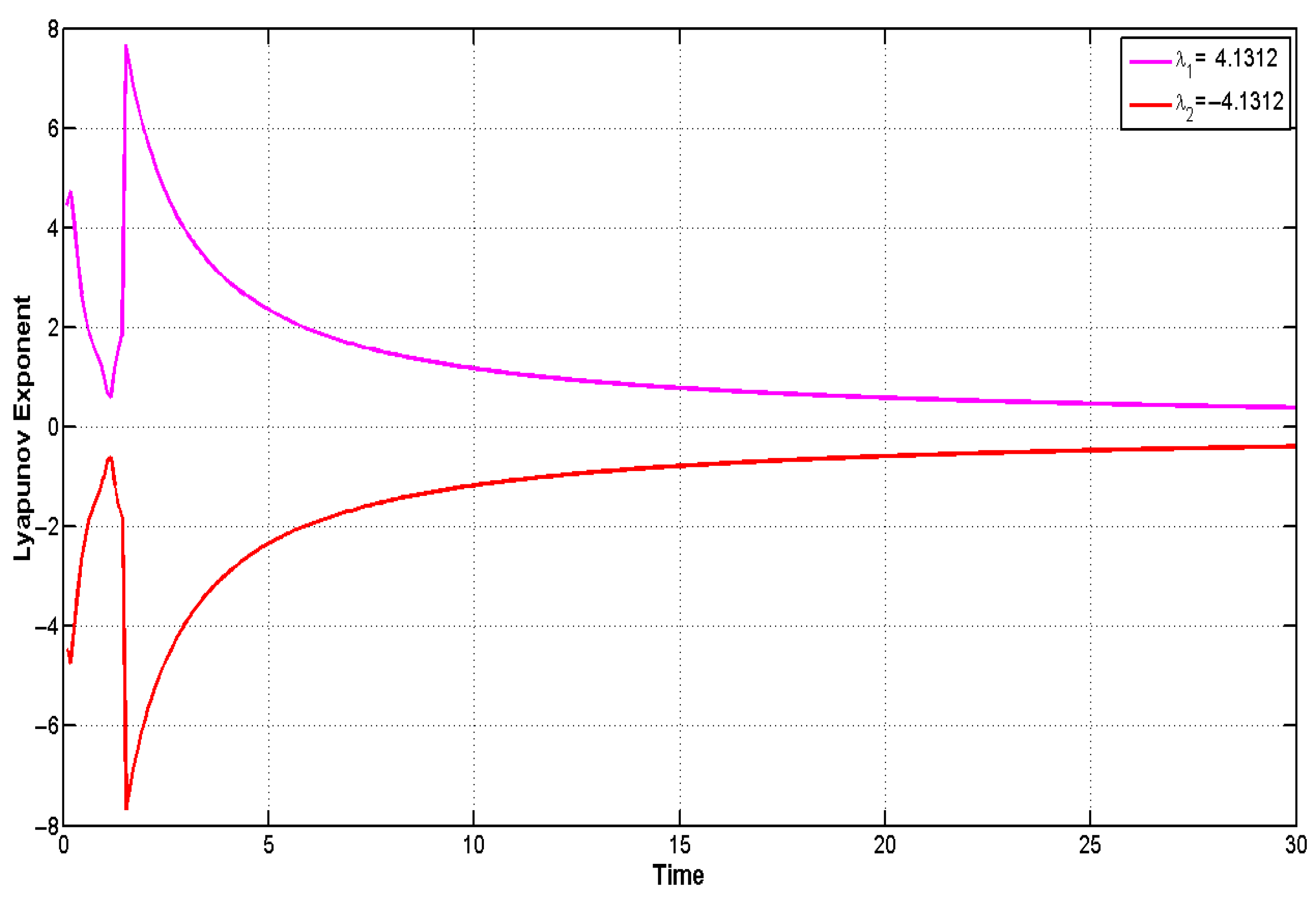
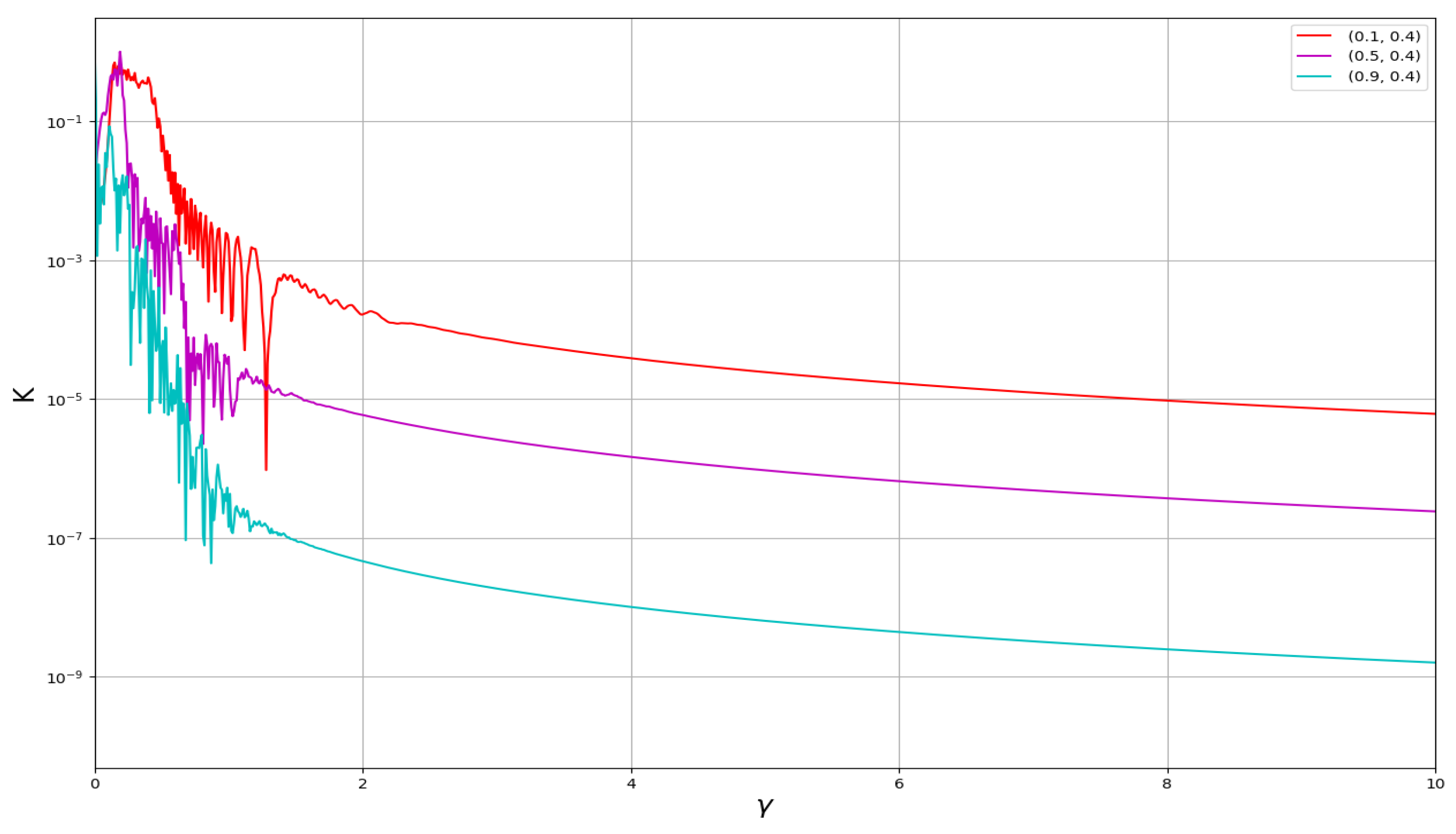
6.1. Lyapunov Exponents Technique
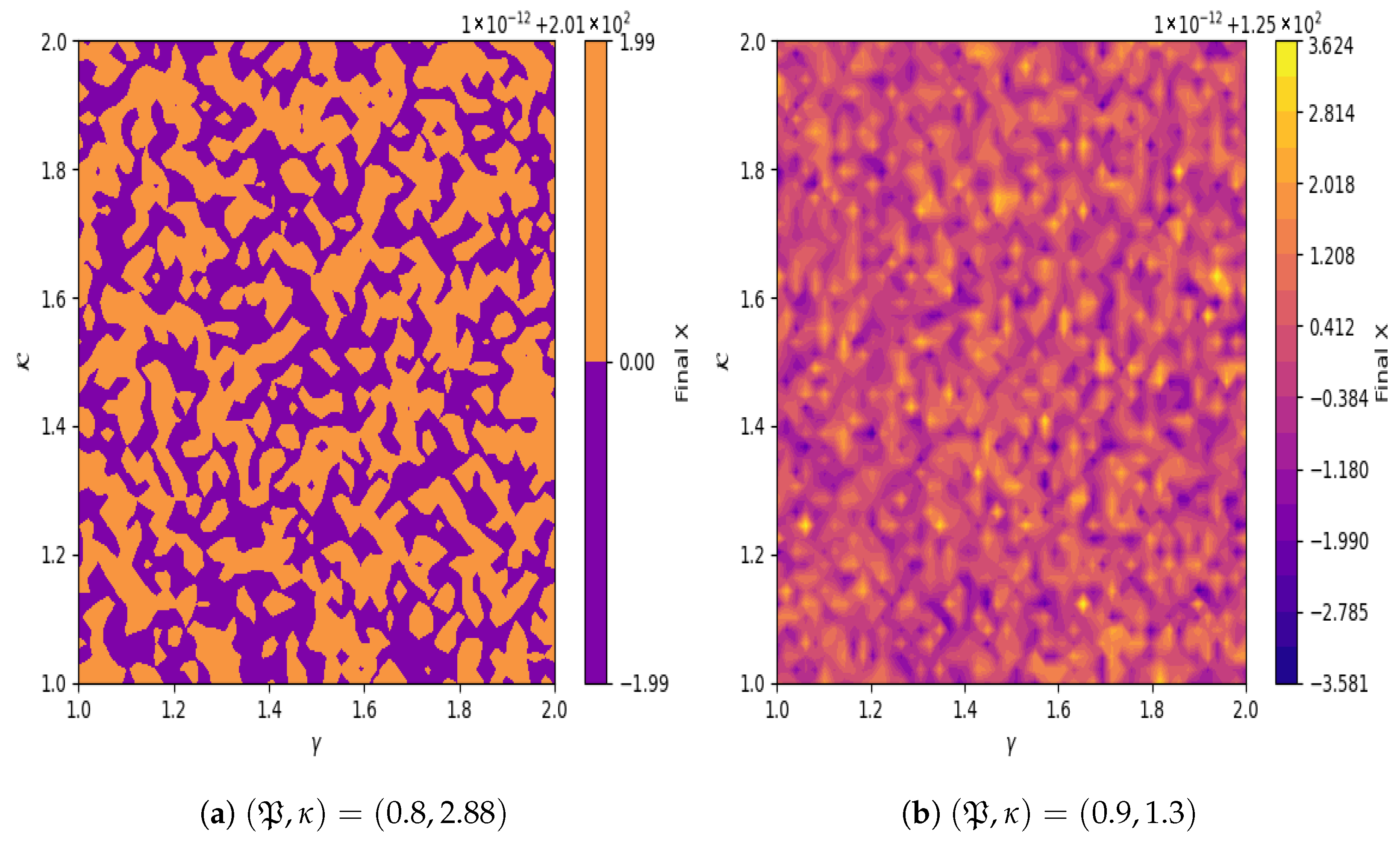
6.2. Basin of Attraction Technique
6.3. Chaotic Attractor Technique
6.4. Power Spectrum Technique
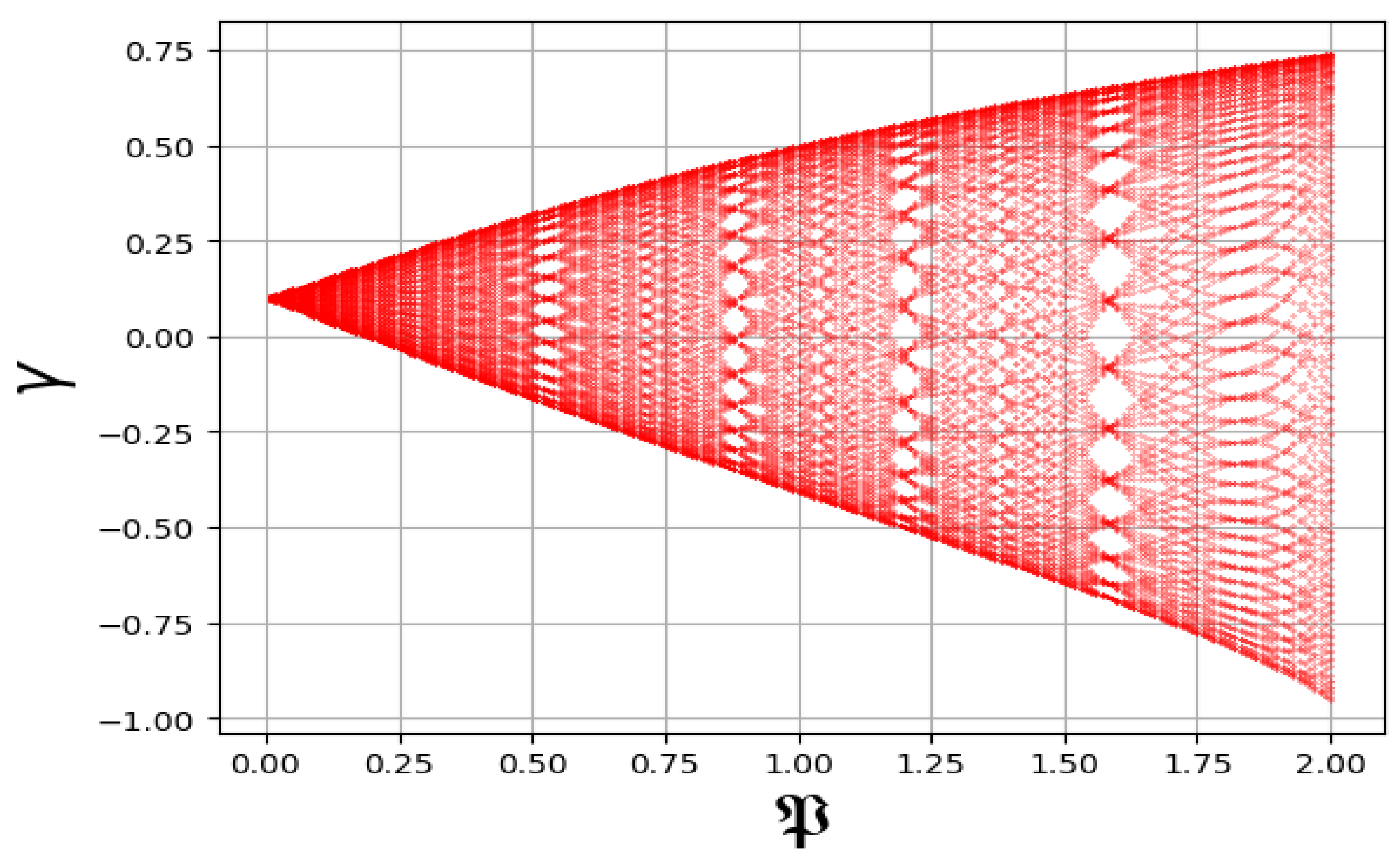
6.5. Bifurcation Diagram Technique
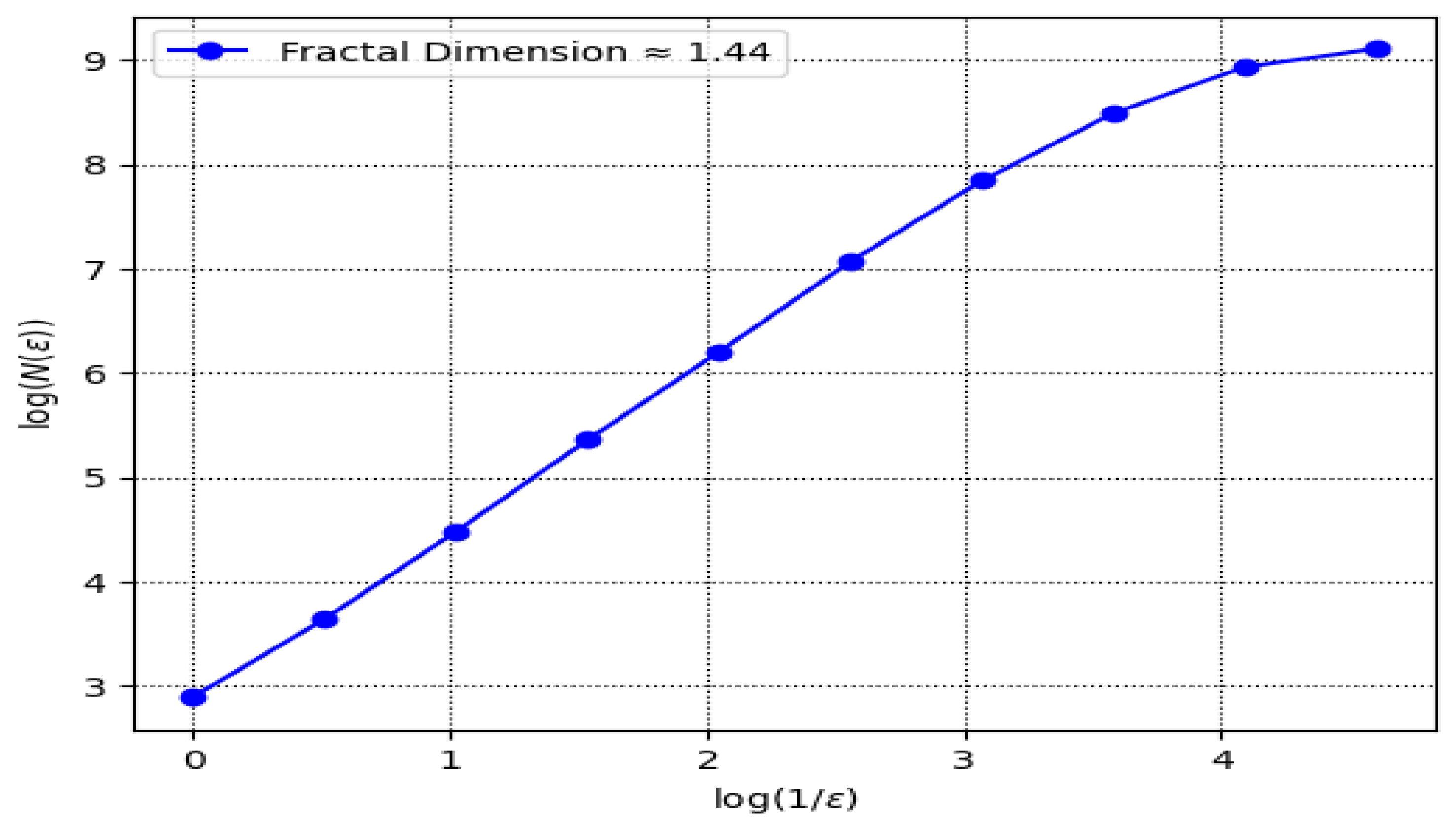
6.6. Fractal Dimension Technique
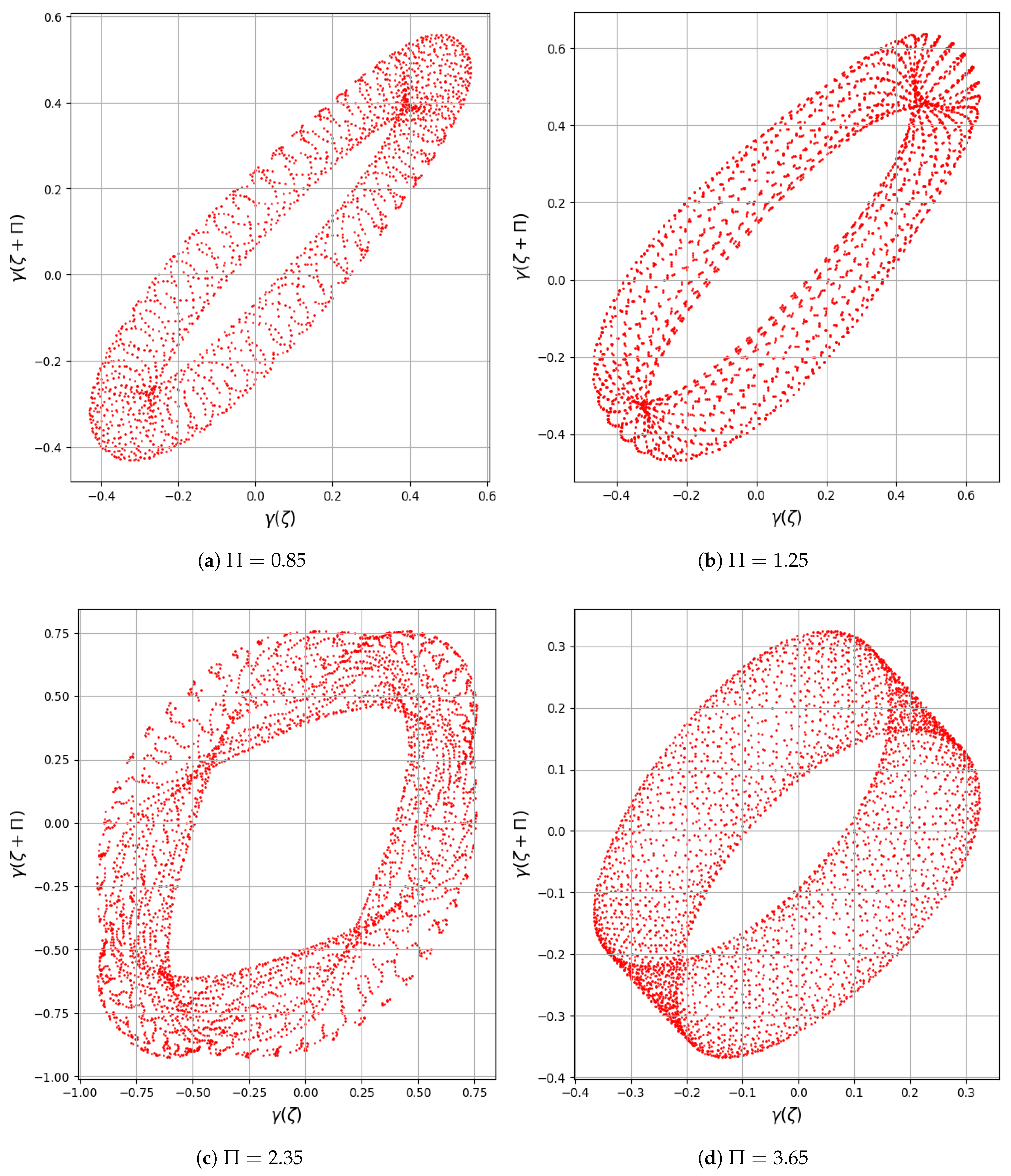
6.7. Return Map Technique
- In Figure 14a for , the points form a nearly closed loop with mild dispersion, indicating quasi-periodic behavior with slight sensitivity.
- In Figure 14b for , the loop becomes more stretched and irregular, showing an onset of chaotic motion.
- In Figure 14c for , the map appears highly scattered and densely filled, reflecting a strongly chaotic regime.
- In Figure 14d for , the Return map shows a tighter, more organized structure, suggesting a possible return to quasi-periodicity.
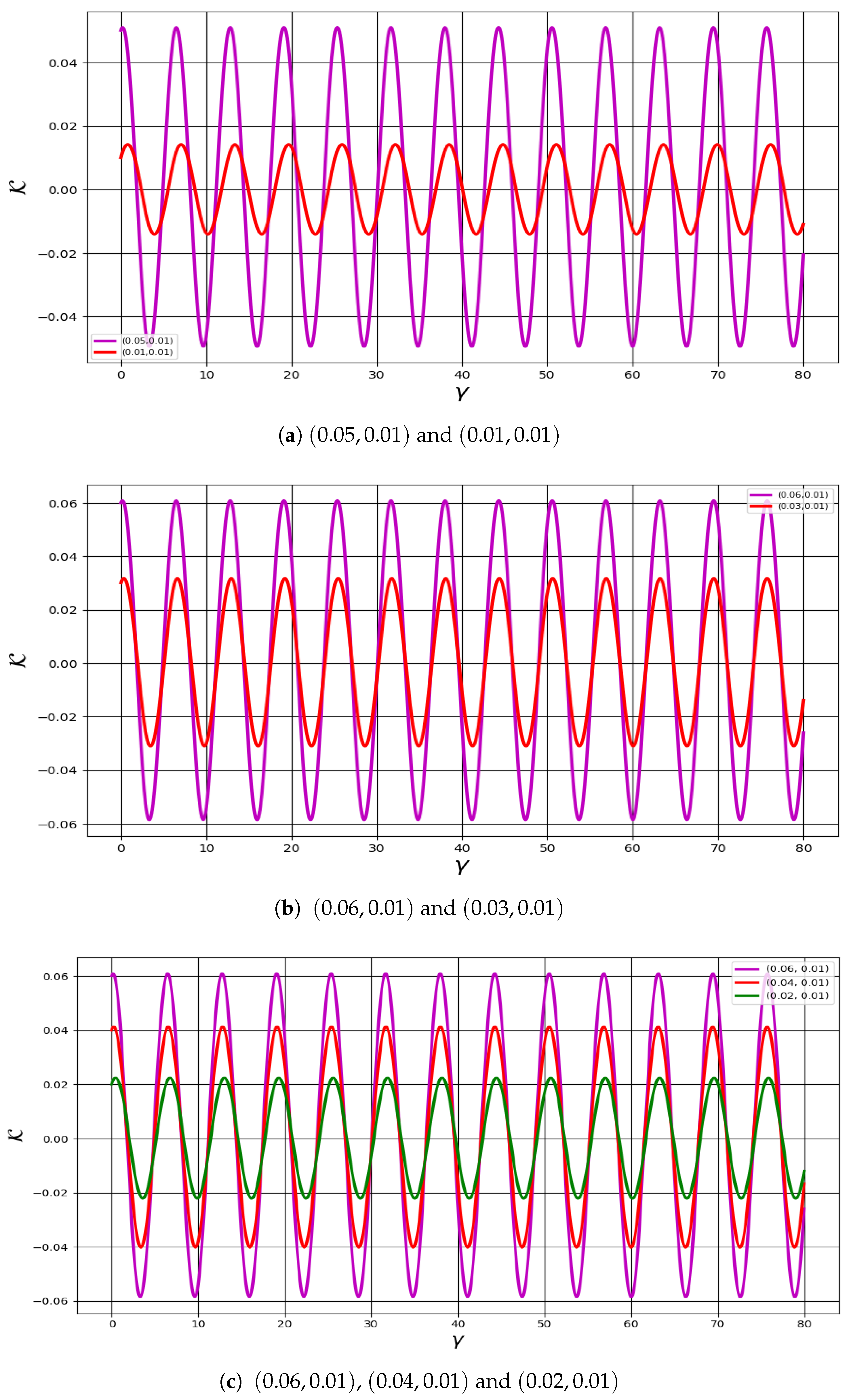
6.8. Multi-Stability Analysis Technique
7. Sensitivity Analysis
8. Conclusions
- Firstly, the Galilean transformation is applied to convert the model into an autonomous dynamical system. Using bifurcation theory, we construct all corresponding phase portrait plots, which are displayed in Figure 1, Figure 2 and Figure 3 for possible cases of discriminant. The parameter values for all phase portraits are described in Table 1. The understanding of these phase portraits and their dependence on key plasma parameters offers valuable insights into the onset of bifurcations, periodicities, and possible chaotic regimes in realistic dusty plasma conditions.
- Additionally, an external driving force is introduced into the planar system, and several analytical techniques are employed to identify chaotic and quasi-periodic behaviors; while various forms can be considered for the perturbation term—such as , , ,, and —the present study adopts the form for further analysis [26]. Using phase portraits, Bifurcation diagrams, Poincaré maps, Lyapunov exponents, Fractal Dimensions, Return maps, Power spectra, time series analyses, Basins of attraction, and Multi-stability analysis, quasi-periodic and chaotic features are successfully revealed in the modified system, as illustrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. In the chaotic and quasi-periodic behaviors analysis, we fix the values of positive electrons, ions, and parameters , while varying the frequency and amplitude of the external force under different initial conditions. The complex behaviors observed, such as chaos, quasi-periodicity, and Multi-stability, are highly relevant to various space and laboratory plasma environments. In particular, external perturbations similar to those modeled here can arise in regions like Saturn’s rings, cometary tails, and plasma boundaries, where charged dust particles interact with fluctuating fields. Understanding the response of dust-ion acoustic waves to such perturbations helps explain energy transport, localization, and the development of instabilities in both natural and experimental plasma systems.
- Finally, sensitivity analysis is conducted to investigate the influence of negative and positive electrons under varying initial conditions of the autonomous dynamical system, as illustrated in Figure 16a–c. All values of negative and positive electrons, as well as with initial conditions, are described in Table 3. As an overall observation, the system is sensitive to variations in initial conditions and particle concentrations.
- Future Research Directions: Future research could be directed toward investigating higher-dimensional dust plasma models, incorporating magnetic field effects to analyze the modified characteristics of dust acoustic wave propagation. Extending the current study to account for non-Maxwellian distributions beyond the framework, such as Cairns or Tsallis distributions, could offer deeper insights into particle trapping and nonthermal effects. Moreover, allowing for spatial and temporal variations in dust charge may reveal richer nonlinear behaviors. The emergence of localized structures such as lumps, breathers, and rogue waves in such generalized plasma environments presents a promising direction for analytical and numerical exploration. Recent advances in PINN and deep learning techniques could also be leveraged for solving governing equations and predicting complex plasma behaviors with high precision. Furthermore, experimental validation using laboratory dusty plasma setups would be essential to verify the theoretical predictions and enhance their applicability to space and astrophysical scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Velocity | |
| Frequency | |
| Amplitude | |
| Ion densities | |
| Dust density | |
| Electron densities | |
| Ion temperatures | |
| Electrostatic potential | |
| Effective temperature | |
| Electron temperatures | |
| Effective Debye length | |
| Normalization constant | |
| Equilibrium value of | |
| Equilibrium value of | |
| Equilibrium value of | |
| Effective dust acoustic speed | |
| g | Velocity of the traveling wave |
| Inverse dusty plasma frequency | |
| Number densities of cold electron | |
| Number densities of hot electron | |
| Spectral indices in the generalized distribution function | |
| Number of elementary charges on the dust grain surface |
References
- Shukla, P.K.; Mamun, A.A. Introduction to Dusty Plasma Physics; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Abid, A.A.; Khan, M.Z.; Lu, Q.; Yap, S.L. A generalized AZ-non-Maxwellian velocity distribution function for space plasmas. Phys. Plasmas 2017, 24, 033702. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Cairns, R.A.; Bingham, R.; Dendy, R.O.; Nairn, C.M.; Shukla, P.K.; Mamun, A.A. Ion sounds like solitary waves with density depressions. J. Phys. IV 1995, 5, C6–C43. [Google Scholar]
- Zaheer, S.; Murtaza, G.; Shah, H.A. Some electrostatic modes are based on non-Maxwellian distribution functions. Phys. Plasmas 2004, 11, 2246–2255. [Google Scholar] [CrossRef]
- Qureshi, M.N.; Shi, J.K.; Ma, S.Z. Landau damping in space plasmas with generalized (r, q) distribution function. Phys. Plasmas 2005, 12, 122902. [Google Scholar] [CrossRef]
- Rubab, N.; Murtaza, G. Dust-charge fluctuations with non-Maxwellian distribution functions. Phys. Scr. 2006, 73, 178. [Google Scholar] [CrossRef]
- Rubab, N.; Murtaza, G.; Mushtaq, A. Effect of non-Maxwellian particle trapping and dust grain charging on dust acoustic solitary waves. Phys. Plasmas 2006, 13, 112104. [Google Scholar] [CrossRef]
- Lee, M.J.; Jung, Y.D. Propagation of symmetric and anti-symmetric surface waves in a self-gravitating magnetized dusty plasma layer with generalized (r, q) distribution. Phys. Plasmas 2018, 25, 053704. [Google Scholar] [CrossRef]
- Ullah, S.; Masood, W.; Siddiq, M.; Rizvi, H. Oblique modulation and envelope excitations of nonlinear ion sound waves with cubic nonlinearity and generalized (r, q) distribution. Phys. Scr. 2019, 94, 125604. [Google Scholar] [CrossRef]
- Xu, C.; Ur Rahman, M.; Emadifar, H. Bifurcations, chaotic behavior, sensitivity analysis and soliton solutions of the extended Kadometsev–Petviashvili equation. Opt. Quantum Electron. 2024, 56, 405. [Google Scholar] [CrossRef]
- San, S.; Beenish; Alshammari, F.S. Analytical and Dynamical Study of Solitary Waves in a Fractional Magneto-Electro-Elastic System. Fractal Fract. 2025, 9, 309. [Google Scholar] [CrossRef]
- Jhangeer, A.; Talafha, A.M.; Ansari, A.R. Analytical solutions and dynamical behaviors of the extended Bogoyavlensky-Konopelchenko equation in deep water dynamics. Phys. Scr. 2024, 100, 015279. [Google Scholar] [CrossRef]
- El-Wakil, S.A.; Abulwafa, E.M.; Elhanbaly, A.A. Super-soliton dust-acoustic waves in four-component dusty plasma using non-extensive electron and ion distributions. Phys. Plasmas 2017, 24, 073705. [Google Scholar] [CrossRef]
- Kanti Das, T.; Ali, R.; Chatterjee, P. Effect of dust ion collision on dust ion acoustic waves in the framework of the damped Zakharov-Kuznetsov equation in the presence of external periodic force. Phys. Plasmas 2017, 24, 103703. [Google Scholar] [CrossRef]
- Taha, R.M.; El-Taibany, W.F. Bifurcation analysis of nonlinear and supernonlinear dust–acoustic waves in a dusty plasma using the generalized (r, q) distribution function for ions and electrons. Contrib. Plasma Phys. 2020, 60, e202000022. [Google Scholar] [CrossRef]
- Kopçasız, B.; Yaşar, E. Novel exact solutions and bifurcation analysis to the dual-mode nonlinear Schrödinger equation. J. Ocean. Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Jhangeer, A.; Beenish; Riha, L. Symmetry analysis, dynamical behavior, and conservation laws of the dual-mode nonlinear fluid model. Ain Shams Eng. J. 2025, 16, 103178. [Google Scholar] [CrossRef]
- Sidorov, N.; Loginov, B.; Sinitsyn, A.V.; Falaleev, M.V. Lyapunov–Schmidt Methods in Nonlinear Analysis and Applications; Springer Science Business Media: Dordrecht, The Netherlands, 2013; Volume 550. [Google Scholar]
- Zhu, X.; Xia, P.; He, Q.; Ni, Z.; Ni, L. Ensemble Classifier Design Based on Perturbation Binary Salp Swarm Algorithm for Classification. CMES-Comput. Model. Eng. Sci. 2023, 135, 653–671. [Google Scholar] [CrossRef]
- Sidorov, N.; Sidorov, D.; Li, Y. Basins of attraction and stability of nonlinear systems’ equilibrium points. Differ. Equ. Dyn. Syst. 2023, 31, 289–300. [Google Scholar] [CrossRef]
- Li, B.; Liang, H.; He, Q. Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos Solitons Fractals 2021, 146, 110856. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; He, Q. Multi-scale systemic risk and spillover networks of commodity markets in the bullish and bearish regimes. N. Am. J. Econ. Financ. 2022, 62, 101766. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Li, X.; Eskandari, Z.; He, Q. Bifurcation analysis and complex dynamics of a Kopel triopoly model. J. Comput. Appl. Math. 2023, 426, 115089. [Google Scholar] [CrossRef]
- Beenish; Samreen, M. Qualitative Behavior and Travelling Wave Solutions of the (n+1)-Dimensional Camassa-Holm Kadomtsev-Petviashvili Equation. Int. J. Geom. Methods Mod. Phys. 2025, 2550275. [Google Scholar] [CrossRef]
- Li, Z.; Lyu, J.; Hussain, E. Bifurcation, chaotic behaviors, and solitary wave solutions for the fractional Twin-Core couplers with Kerr law non-linearity. Sci. Rep. 2024, 14, 22616. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beenish; Samreen, M.; Alshammari, F.S. Mathematical Modeling, Bifurcation Theory, and Chaos in a Dusty Plasma System with Generalized (r⋆, q⋆) Distributions. Axioms 2025, 14, 610. https://doi.org/10.3390/axioms14080610
Beenish, Samreen M, Alshammari FS. Mathematical Modeling, Bifurcation Theory, and Chaos in a Dusty Plasma System with Generalized (r⋆, q⋆) Distributions. Axioms. 2025; 14(8):610. https://doi.org/10.3390/axioms14080610
Chicago/Turabian StyleBeenish, Maria Samreen, and Fehaid Salem Alshammari. 2025. "Mathematical Modeling, Bifurcation Theory, and Chaos in a Dusty Plasma System with Generalized (r⋆, q⋆) Distributions" Axioms 14, no. 8: 610. https://doi.org/10.3390/axioms14080610
APA StyleBeenish, Samreen, M., & Alshammari, F. S. (2025). Mathematical Modeling, Bifurcation Theory, and Chaos in a Dusty Plasma System with Generalized (r⋆, q⋆) Distributions. Axioms, 14(8), 610. https://doi.org/10.3390/axioms14080610







