Existence and Uniqueness of Solutions for Impulsive Stochastic Differential Variational Inequalities with Applications
Abstract
1. Introduction
- (i)
- If in (1), then it transforms into the following problem: find and , such thatwhich is still a new problem.
- (ii)
2. Preliminaries
3. Existence and Uniqueness of ISDVI
- H()
- The function satisfies the following conditions:
- (i)
- Boundedness: .
- (ii)
- Lipschitz continuity: .
- H()
- The function adheres to the subsequent conditions:
- (i)
- Boundedness: .
- (ii)
- Lipschitz continuity: .
- H()
- The function meets the ensuing requirements:
- (i)
- .
- (ii)
- .
- H()
- The function : meets the subsequent criteria:
- (i)
- For each index , there exists a constant , such that for every , we have .
- (ii)
- Lipschitz continuity: .
- H()
- The function ϑ: satisfies the following conditions:
- (i)
- Growth condition: .
- (ii)
- Lipschitz continuity: .
4. Application
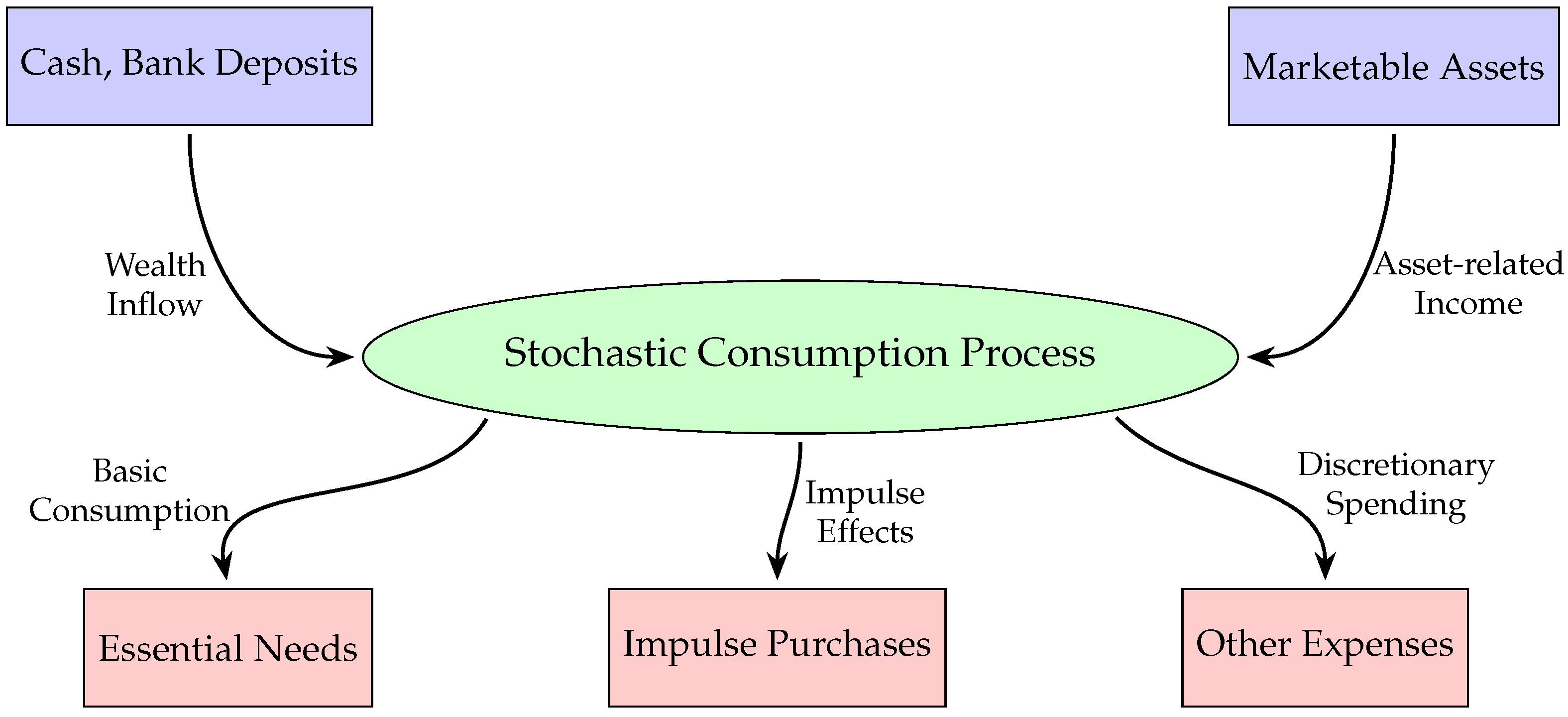
4.1. Stochastic Consumption Process
4.2. An Example from an Electrical Circuit Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drissi-Kaitouni, O. A variational inequality formulation of the dynamic traffic assignment problem. Eur. J. Oper. Res. 1993, 71, 188–204. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer: New York, NY, USA, 2003. [Google Scholar]
- Neittaanmäki, P.; Tiba, D. A variational inequality approach to constrained control problems for parabolic equations. Appl. Math. Optim. 1988, 17, 185–201. [Google Scholar] [CrossRef]
- Aubin, J.P.; Cellina, A. Differential Inclusions: Set-Valued Maps and Viability Theory; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Pang, J.S.; Stewart, D.E. Differential variational inequalities. Math. Program. 2008, 113, 345–424. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z. Differential variational inequality approach to dynamic games with shared constraints. Math. Program. 2014, 146, 379–408. [Google Scholar] [CrossRef]
- Gwinner, J. On a new class of differential variational inequalities and a stability result. Math. Program. 2013, 139, 205–221. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zeng, S.D. Differential variational inequalities in infinite Banach spaces. Acta Math. Sci. 2017, 37, 26–32. [Google Scholar] [CrossRef]
- Zeng, S.; Liu, Z.; Migorski, S. A class of fractional differential hemivariational inequalities with application to contact problem. Z. Angew. Math. Phys. 2018, 69, 36. [Google Scholar] [CrossRef]
- Cen, J.; Khan, A.A.; Motreanu, D.; Zeng, S. Inverse problems for generalized quasi-variational inequalities with application to elliptic mixed boundary value systems. Inverse Probl. 2022, 38, 065006. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, S.; Motreanu, D. Evolutionary problems driven by variational inequalities. J. Differ. Equ. 2016, 260, 6787–6799. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lu, L. Coupled system of fractional hemivariational inequalities with applications. Optimization 2024, 73, 969–994. [Google Scholar] [CrossRef]
- Hao, J.; Li, M. A new class of fractional Navier–Stokes system coupled with multivalued boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2024, 136, 108098. [Google Scholar] [CrossRef]
- Hao, J.; Han, J.; Liu, Q. Existence and convergence analysis of second-order delay differential variational–hemivariational inequalities with memory terms. Nonlinear Anal. Real World Appl. 2025, 85, 104373. [Google Scholar] [CrossRef]
- Han, J.; Lu, L.; Zeng, S. Evolutionary variational–hemivariational inequalities with applications to dynamic viscoelastic contact mechanics. Z. Angew. Math. Phys. 2020, 71, 32. [Google Scholar] [CrossRef]
- Han, J.; Li, C.; Zeng, S. Applications of generalized fractional hemivariational inequalities in solid viscoelastic contact mechanics. Commun. Nonlinear Sci. Numer. Simul. 2022, 115, 106718. [Google Scholar] [CrossRef]
- Vetro, C.; Zeng, S. Regularity and Dirichlet problem for double-phase energy functionals of different power growth. J. Geom. Anal. 2024, 34, 105. [Google Scholar] [CrossRef]
- Zeng, S.; Bouach, A.; Haddad, T. On nonconvex perturbed fractional sweeping processes. Appl. Math. Optim. 2024, 89, 73. [Google Scholar] [CrossRef]
- Hao, X.; Liu, L.; Wu, Y. Mild solutions of impulsive semilinear neutral evolution equations in Banach spaces. J. Nonlinear Sci. Appl. 2016, 9, 6183–6194. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Arjunan, M.M.; Vijayakumar, V. Existence of global solutions for second order impulsive abstract partial differential equations. Nonlinear Anal. Theory Methods Appl. 2011, 74, 6747–6757. [Google Scholar] [CrossRef]
- Nisar, K.S.; Vijayakumar, V. An analysis concerning approximate controllability results for second-order Sobolev-type delay differential systems with impulses. J. Inequalities Appl. 2022, 2022, 53. [Google Scholar] [CrossRef]
- Valliammal, N.; Jothimani, K.; Johnson, M.; Panda, S.K.; Vijayakumar, V. Approximate controllability analysis of impulsive neutral functional hemivariational inequalities. Commun. Nonlinear Sci. Numer. Simul. 2023, 127, 107560. [Google Scholar] [CrossRef]
- Liu, K.; Fečkan, M.; O’Regan, D.; Wang, J. (omega, c)-periodic solutions for time-varying non-instantaneous impulsive differential systems. Appl. Anal. 2022, 101, 5469–5489. [Google Scholar] [CrossRef]
- Liu, K.; Fečkan, M.; Wang, J.R. A class of (omega, T)-periodic solutions for impulsive evolution equations of Sobolev type. Bull. Iran. Math. Soc. 2022, 48, 2743–2763. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, K. Periodic Solutions for Conformable Non-autonomous Non-instantaneous Impulsive Differential Equations. Math. Slovaca 2024, 74, 1489–1506. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, K. Properties of the solutions to periodic conformable non-autonomous non-instantaneous impulsive differential equations. Electron. J. Differ. Equ. 2024, 2024, 1–22. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J.B. Stochastic variational inequalities: Single-stage to multistage. Math. Program. 2017, 165, 331–360. [Google Scholar] [CrossRef]
- Wang, R.; Kinra, K.; Mohan, M.T. Asymptotically autonomous robustness in probability of random attractors for stochastic Navier-Stokes equations on unbounded Poincaré domains. SIAM J. Math. Anal. 2023, 55, 2644–2676. [Google Scholar] [CrossRef]
- Wang, R.; Chen, P. Enhanced Mean Random Attractors for Nonautonomous Mean Random Dynamical Systems in Product Bochner Spaces. Commun. Math. Stat. 2024, 1–30. [Google Scholar] [CrossRef]
- Yang, M.; Lv, T.; Wang, Q. The averaging principle for Hilfer fractional stochastic evolution equations with Lévy noise. Fractal Fract. 2023, 7, 701. [Google Scholar] [CrossRef]
- Yang, M.; Huan, Q.; Cui, H.; Wang, Q. Hilfer fractional stochastic evolution equations on the positive semi-axis. Alex. Eng. J. 2024, 104, 386–395. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Huang, N.; Li, X. Euler scheme for solving a class of stochastic differential variational inequalities with some applications. Commun. Nonlinear Sci. Numer. Simul. 2023, 127, 107577. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, Y.; Huang, N. A stochastic fractional differential variational inequality with Lévy jump and its application. Chaos Solitons Fractals 2024, 178, 114372. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Huang, N.; Li, X. Penalty method for solving a class of stochastic differential variational inequalities with an application. Nonlinear Anal. Real World Appl. 2023, 73, 103889. [Google Scholar] [CrossRef]
- Weng, H.Y.; Chen, T.; Huang, J.N.; O’Regan, D. A new class of fractional impulsive differential hemivariational inequalities with an application. Nonlinear Anal. Model. Control 2022, 27, 199–220. [Google Scholar] [CrossRef]
- Han, L.; Tiwari, A.; Camlibel, M.K.; Pang, J.S. Convergence of time-stepping schemes for passive and extended linear complementarity systems. SIAM J. Numer. Anal. 2009, 47, 3768–3796. [Google Scholar] [CrossRef]
- Haase, H.; Garbe, H.; Gerth, H. Grundlagen der Elektrotechnik; Schöneworth: Hannover, Germany, 2009. [Google Scholar]
- Ahmadian, D.; Ballestra, L.V.; Shokrollahi, F. A Monte-Carlo approach for pricing arithmetic Asian rainbow options under the mixed fractional Brownian motion. Chaos Solitons Fractals 2022, 158, 112023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, K. Existence and Uniqueness of Solutions for Impulsive Stochastic Differential Variational Inequalities with Applications. Axioms 2025, 14, 603. https://doi.org/10.3390/axioms14080603
Liu W, Liu K. Existence and Uniqueness of Solutions for Impulsive Stochastic Differential Variational Inequalities with Applications. Axioms. 2025; 14(8):603. https://doi.org/10.3390/axioms14080603
Chicago/Turabian StyleLiu, Wei, and Kui Liu. 2025. "Existence and Uniqueness of Solutions for Impulsive Stochastic Differential Variational Inequalities with Applications" Axioms 14, no. 8: 603. https://doi.org/10.3390/axioms14080603
APA StyleLiu, W., & Liu, K. (2025). Existence and Uniqueness of Solutions for Impulsive Stochastic Differential Variational Inequalities with Applications. Axioms, 14(8), 603. https://doi.org/10.3390/axioms14080603




