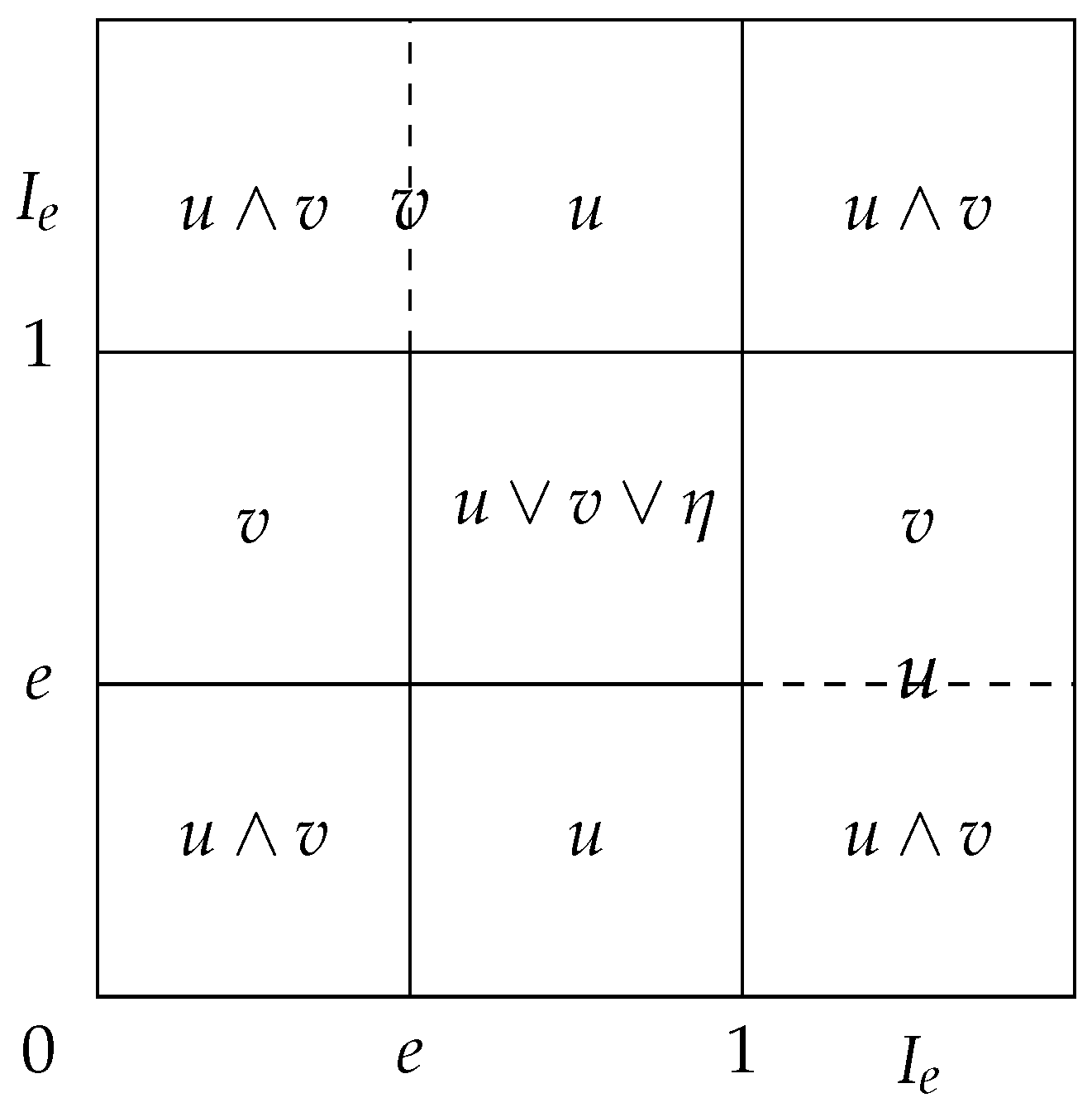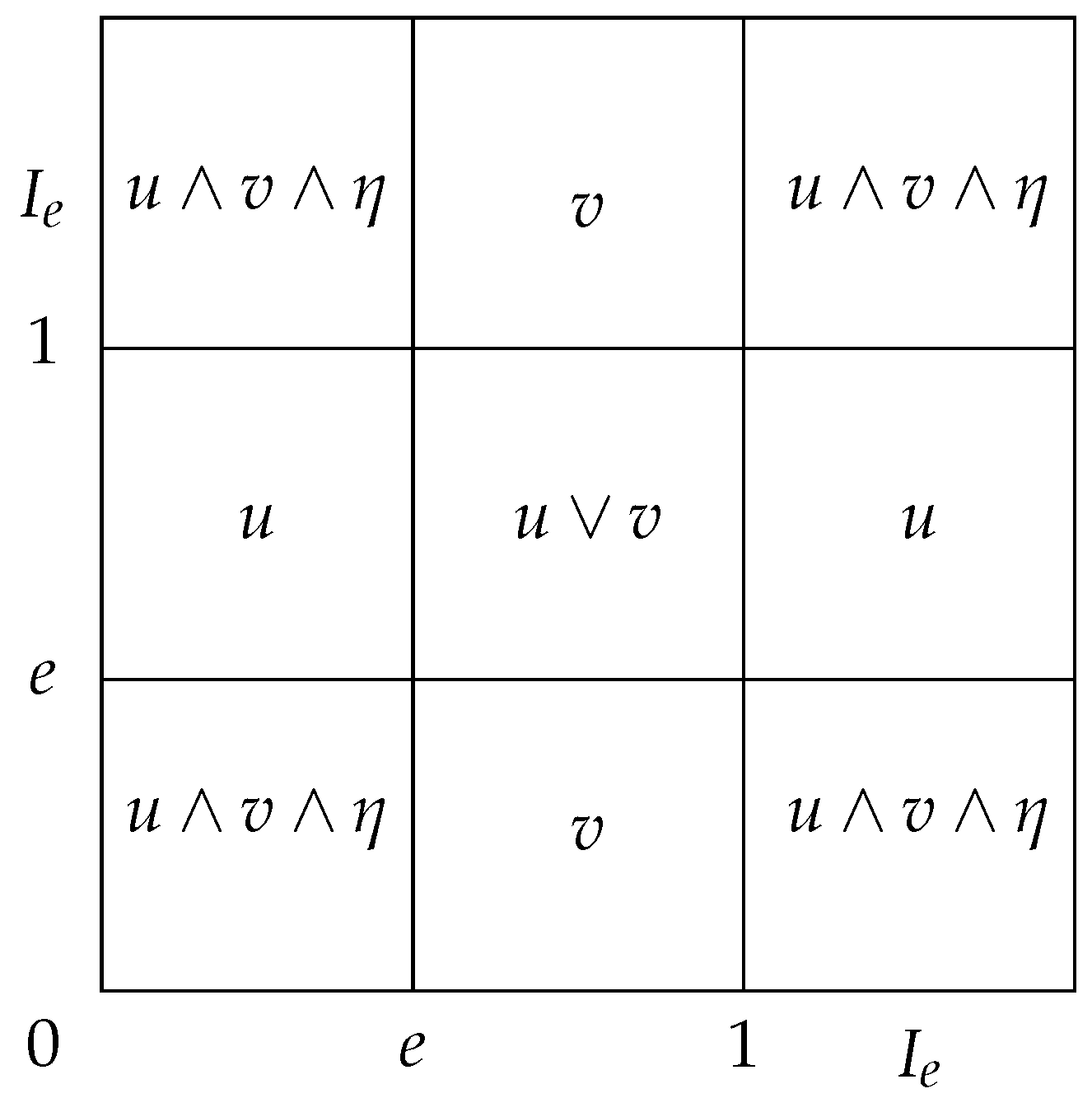Element-Based Construction Methods for Uninorms on Bounded Lattices

Abstract

Uninorms are aggregation operators that generalize the t-norms (t-conorms), which are extensions of the logical connectives $\wedge (\vee )$ to the fuzzy set theory. The methods of constructing uninorms on more general algebraic structures (such as bounded posets, lattices, etc.) are an important subject of study, including an extensive work concerning these operations on the unit real interval $[0, 1]$. The construction of uninorms on bounded lattices has been extensively studied using various aggregation functions, such as t-norms, t-conorms, and t-subnorms. In this paper, we present construction methods for uninorms, based on the elements of a lattice, without using the existence of the mentioned operators. We determine the necessary and sufficient conditions for the introduced construction methods to result in the uninorms. Then, we show the differences between our methods and several methods known from the literature, including some illustrative examples.

1. Introduction

Aggregation functions are basic functions that combine several inputs into a single output. They satisfy the monotonicity and boundary conditions. Triangular norms, triangular conorms, uninorms, nullnorms, etc., are among the well-known aggregation functions. A uninorm becomes a t-norm when the neutral element is 1, and a t-conorm when it is 0.

Uninorms are a special type of associative aggregation operator having a neutral element in $[0, 1]$, introduced by Yager and Rybalov in [1], the Tivity property, and they have a neutral element e in $[0, 1]$. In addition, they are frequently studied in pure mathematics, expert systems, economics and finance, computer and engineering sciences, and social sciences, and some of the applied sciences where they have an application [1,2,3,4].

The journey of uninorms on bounded lattices commenced with Karaçal and Mesiar’s seminal work, where they conclusively established the presence of these operators on any given bounded lattice, as detailed in [5]. Then, uninorms were studied from many different perspectives [2,6,7,8,9,10]. Researchers working with uninorms on bounded lattices have been heavily focused on figuring out constructing methods of uninorms on bounded lattices [1,5,11,12,13,14,15,16,17], in which the authors utilized some aggregation operators on subintervals. According to our best knowledge, there is no element-based construction method for uninorms on a bounded lattice. In this paper, we investigate element-based construction methods for uninorms by elaborating on different cases of an element $\eta$ of a bounded lattice L and establishing the necessary and sufficient conditions required for these construction methods to produce a uninorm on L. Also, we give explanatory examples as well as comparative examples with the existing methods.

The paper is organized as follows: Section 2 provides a brief overview of bounded lattices, t-norms, t-conorms, and uninorms on bounded lattices. Section 3 contains the main results: new element $\eta \notin \{0,e,1\}$ based construction methods for uninorms on a bounded lattice L when $\eta \in I_e$ or $\eta \in (e,1)$ or $\eta \in (0,e)$. We determine the necessary and sufficient conditions for each position of the element $\eta$ to obtain uninorms and put the necessary and sufficient conditions on the bounded lattice L. Moreover, the dual forms are also provided. Meanwhile, we provide some examples to illustrate the construction methods. Furthermore, we show that our new construction methods are different from the existing methods in the literature.

2. Notations, Definitions and a Review of Previous Results

In this section, we revisit some fundamental concepts.

Definition 1

([18]). Let $(L,\le ,0,1)$ be a bounded lattice. If $u\le v$ or $v\le u$, then the elements u and v are called comparable; otherwise, they are called incomparable, and in this case, the notation $u\left|\right|v$ is used.

Hereafter, we define $I_e$ as the set of all elements $u\in L$ such that u is incomparable with e; formally, $I_e=\{u\in L:u|\left|e\right\}$, it has all elements of the lattice L which are incomparable with the element e. Let $A\left(e\right)$ be the set defined by $A\left(e\right)=[0,e]\times [e,1]\cup [e,1]\times [0,e]$.

Definition 2

([18]). Let $(L,\le ,0,1)$ be a bounded lattice and $j,g\in L$ with $j\le g$. The interval $[j,g]$ is a subset of L given by

$$[j,g]=\{f\in L|j\le f\le g\}.$$

Similarly, $(j,g],[j,g)$ and $(j,g)$ can be defined.

Definition 3

([19]). Let $(L,\le ,0,1)$ be a bounded lattice. An operation $T\left(S\right):L\times L\to L$ is called a triangular norm, t-norm in short (triangular conorm, t-conorm in short) if it exhibits the following properties: it is increasing, Abelian, associative, and possesses 1 (0) as its neutral element.

Example 1.

Let $(L,\le ,0,1)$ be a bounded lattice. The minimal t-norm $T_W$ and the maximal t-norm $T_{\wedge }$ on a bounded lattice L are given, respectively, as follows:

$$T_W\left(u,v\right)=\left\{\begin{array}{ccc}u\wedge v\hfill & & \mathrm{if}1\in \{u,v\}\hfill \\ 0\hfill & & otherwise\hfill \end{array}\right.$$

$$T_{\wedge }(u,v)=u\wedge v.$$

The minimal t-conorm $S_{\vee }$ and the maximal t-conorm $S_W$ on a bounded lattice L are given, respectively, as follows:

$$S_{\vee }(u,v)=u\vee v$$

$$S_W\left(u,v\right)=\left\{\begin{array}{ccc}u\vee v\hfill & & \mathrm{if}0\in \{u,v\}\hfill \\ 1\hfill & & otherwise.\hfill \end{array}\right.$$

Definition 4

([16]). Let $(L,\le ,0,1)$ be a bounded lattice. An Abelian semigroup operation $U:L^2\to L$ is called a uninorm if it has a neutral element $e\in L$ and it is increasing.

Note that a uninorm is a t-norm (t-conorm) when $e=1$ ($e=0$).

Proposition 1

([5]). Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and U be a uninorm on L with the neutral element e. Then the following properties hold:

• (i) $u\wedge v\le U(u,v)\le u\vee v$ for $(u,v)\in A\left(e\right)$.
• (ii) $U(u,v)\le u$ for $(u,v)\in L\times [0,e]$.
• (iii) $U(u,v)\le v$ for $(u,v)\in [0,e]\times L$.
• (iv) $u\le U(u,v)$ for $(u,v)\in L\times [e,1]$.
• (v) $v\le U(u,v)$ for $(u,v)\in [e,1]\times L$.

Proposition 2

([5]). Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L$ and U a uninorm with the neutral element e on L. Then

• $\left(i\right)$$T^{\ast }{=U|}_{{[0,e]}^2}:{[0,e]}^2\to [0,e]$ is a t-norm on $[0,e]$.
• $\left(ii\right)$$S^{\ast }{=U|}_{{[e,1]}^2}:{[e,1]}^2\to [e,1]$ is a t-conorm on $[e,1]$.

Definition 5

([2]). Let L be a bounded lattice and A and B be two aggregation functions on L. A is called smaller than B if for any elements $u,v\in L$, $A(u,v)\le B(u,v)$.

We recommend [5,6,11,12,13,14,15,16,20,21,22,23,24,25] for more details about uninorms on bounded lattices.

3. Element-Based Construction Methods of Uninorms on Bounded Lattices

In this section, Theorems 1, 3 and 5 propose three construction methods for uninorms on a bounded lattice L, determined by an arbitrary fixed point $\eta \notin \{0,e,1\}$, under which additional constraints are introduced. Our construction methods are compared with some construction methods known from the related literature. Also, the differences between our construction methods and those in the literature are emphasized. Some illustrative examples for our construction methods for uninorms on a bounded lattice are provided.

In the following theorem, a method to produce uninorms by means of an arbitrary element $\eta \in I_e$ is given.

Theorem 1.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in I_e$. Then the function $U^{\ast 1}:L^2\to L$ defined by

$$U^{\ast 1}(u,v)=\left\{\begin{array}{cc}u\wedge v\wedge \eta \hfill & (u,v)\in {[0,e)}^2\cup [0,e)\times I_e\cup I_e\times [0,e)\cup I_e\times I_e,\hfill \\ u\hfill & (u,v)\in (e,1]\times ([0,e)\cup I_e)\cup L\times \left\{e\right\},\hfill \\ v\hfill & (u,v)\in ([0,e)\cup I_e)\times (e,1]\cup \left\{e\right\}\times L,\hfill \\ u\vee v\hfill & otherwise,\hfill \end{array}\right.$$

(1)

is a uninorm on L with the neutral element e if and only if $v<u$ for all $u\in (e,1),v\in I_e$.

Proof. 

Necessity. Since $U^{\ast 1}$ is monotone, $v=U^{\ast 1}(e,v)\le U^{\ast 1}(u,v)=u$ when $u\in (e,1)$ and $v\in I_e$. Therefore, it is obtained that $v<u$.

Sufficiency. (i) Monotonicity: Let us show that for every element $u,v\in L$ with $u\le v$, $U^{\ast 1}(u,w)\le U^{\ast 1}(v,w)$ for all $w\in L$. If u and v are both elements of $[0,e)$ or $\left\{e\right\}$ or $(e, 1]$ or $I_e$, $U^{\ast 1}(u,w)\le U^{\ast 1}(v,w)$ is always satisfied for all $w\in L$ since $u\le v$. If $u=0$ or $u=1$, the inequality is satisfied; therefore, they are omitted. The proof is then split into all the remaining possible cases as follows:

1.

 Let $u\in (0,e)$.

1.1.

 $v=e$,

1.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 1}(u,w)=u\wedge w\wedge \eta \le w=U^{\ast 1}(v,w).$

1.1.2

 If $w=e$, then $U^{\ast 1}(u,w)=u\le e=U^{\ast 1}(v,w).$

1.1.3.

 If $w\in (e,1)$, then $U^{\ast 1}(u,w)=w=U^{\ast 1}(v,w).$

1.2.

 $v\in (e,1)$,

1.2.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 1}(u,w)=u\wedge w\wedge \eta \le v=U^{\ast 1}(v,w).$

1.2.2.

 If $w=e$, then $U^{\ast 1}(u,w)=u\le v=U^{\ast 1}(v,w).$

1.2.3.

 If $w\in (e,1)$, then $U^{\ast 1}(u,w)=w\le v\vee w=U^{\ast 1}(v,w).$

1.3.

 $v\in I_e$,

1.3.1.

 If $w\in (0,e)\cup I_e, \mathrm{then}{U}^{\ast 1}(u,w)=u\wedge w\wedge \eta \le v\wedge w\wedge \eta =U^{\ast 1}(v,w).$

1.3.2.

 If $w=e$, then $U^{\ast 1}(u,w)=u\le v=U^{\ast 1}(v,w).$

1.3.3.

 If $w\in (e,1)$, then $U^{\ast 1}(u,w)=w=U^{\ast 1}(v,w).$

2.

 $u=e$,

2.1.

 $v\in (e,1)$,

2.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 1}(u,w)=w<v=U^{\ast 1}(v,w).$

2.1.2.

 If $w=e$, then $U^{\ast 1}(u,w)=e\le v=U^{\ast 1}(v,w).$

2.1.3.

 If $w\in (e,1)$, then $U^{\ast 1}(u,w)=w\le v\vee w=U^{\ast 1}(v,w).$

3.

 $u\in I_e$,

3.1.

 $v\in (e,1)$,

3.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 1}(u,w)=u\wedge w\wedge \eta \le v=U^{\ast 1}(v,w).$

3.1.2.

 If $w=e$, then $U^{\ast 1}(u,w)=u\le v=U^{\ast 1}(v,w).$

3.1.3.

 If $w\in (e,1)$, then $U^{\ast 1}(u,w)=w\le v\vee w=U^{\ast 1}(v,w).$

• (ii) Associativity: We demonstrate that $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(U^{\ast 1}(u,v),w)$ for all $u,v,w\in L$. If $u=e$, the equality is satisfied; therefore, they are omitted. Again, the proof is split into all the remaining possible cases by considering the relationships between the elements $u,v,w$ and e as follows.

1.

 Let $u\in [0,e)\cup I_e$.

1.1.

 $v\in [0,e)\cup I_e$,

1.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v\wedge w\wedge \eta )=u\wedge v\wedge w\wedge \eta =U^{\ast 1}(u\wedge v\wedge \eta ,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

1.1.2. If $w\in (e,1]$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,w)=w=U^{\ast 1}(u\wedge v\wedge \eta ,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

1.2.

 $v\in (e,1]$,

1.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v)=v=U^{\ast 1}(v,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

1.2.2. If $w\in (e,1]$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v\vee w)=v\vee w=U^{\ast 1}(v,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

2.

 $u\in (e,1]$.

2.1.

 $v\in [0,e)\cup I_e$,

2.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v\wedge w\wedge \eta )=u=U^{\ast 1}(u,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

2.1.2. If $w\in (e,1]$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,w)=u\vee w=U^{\ast 1}(u,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

2.2.

 $v\in (e,1]$,

2.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v)=u\vee v=U^{\ast 1}(u\vee v,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

2.2.2. If $w\in (e,1]$, then $U^{\ast 1}(u,U^{\ast 1}(v,w))=U^{\ast 1}(u,v\vee w)=u\vee v\vee w=U^{\ast 1}(u\vee v,w)=U^{\ast 1}(U^{\ast 1}(u,v),w).$

It is easy to observe the commutativity of $U^{\ast 1}$ and the fact that e is a neutral element of $U^{\ast 1}$.

Therefore, $U^{\ast 1}$ is a uninorm on L with the neutral element e. □

The structure of the uninorm $U^{\ast 1}$ given in the Formula (1) is summarized in Figure 1.

In the following example, an illustration of how Theorem 1 is applied is provided.

Example 2.

Consider the bounded lattice $L_1=(\{0,a,b,c,d,e,\eta ,1\},\le ,0,1)$ characterized by the Hasse diagram in Figure 2. If we apply the formula (1) in Theorem 1, the uninorm $U^{\ast 1}$ on $L_1$ is obtained as in

Table 1. The uninorm $U^{\ast 1}$ induced by the Formula (1) in Theorem 1.

${\mathit{U}}^{\ast 1}$	0	a	b	c	d	e	$\mathit{\eta }$	1
0	0	a	0	0	0	0	0	1
a	a	a	a	a	a	a	a	1
b	0	a	$\eta$	d	d	b	$\eta$	1
c	0	a	d	d	d	c	d	1
d	0	a	d	d	d	d	d	1
e	0	a	b	c	d	e	$\eta$	1
$\eta$	0	a	$\eta$	d	d	$\eta$	$\eta$	1
1	1	1	1	1	1	1	1	1

.

Remark 1.

In general, the uninorm $U^{\ast 1}$ defined in Theorem 1 is different from the uninorms obtained by the construction methods of uninorms in the literature. Considering Example 2, it is easily seen that $U^{\ast 1}\ne U_{t_1},U_e^T,U_{(T,e)}$ and $U_t$, regardless of the choice of the corresponding t-norms on $[0, e]$ in [5,11,13,15], since

$$\begin{array}{l}{U}^{\ast 1}(d,c)=d\wedge c\wedge \eta =d\ne c=U_{t_1}(d,c),\\ U^{\ast 1}(0,c)=0\wedge c\wedge \eta =0\ne c=U_e^T(0,c),\\ U^{\ast 1}(d,c)=d\wedge c\wedge \eta =d\ne c=U_{(T,e)}(d,c),\\ U^{\ast 1}(0,c)=0\wedge c\wedge \eta =0\ne c=U_t(0,c),\end{array}$$

respectively. Also, it is clear that the lattice $L_1$ satisfies the constraints of Theorem 3.1 in [12] and Theorem 3.1 in [14]. We obtain $U^{\ast 1}\ne U_{t_e}$ since $U^{\ast 1}(d,c)=d\wedge c\wedge \eta =d\ne c=U_{t_e}(d,c)$ regardless of the choice of the t-norm $T_e$ on $[0, e]$ in [12]. In addition, $U^{\ast 1}\ne U^{\prime },$ since $U^{\ast 1}(c,b)=c\wedge b\wedge \eta =d\ne b=c\vee b=U^{\prime }(c,b)$ regardless of the choice of the t-norm $T_e$ on $[0, e]$ and the t-conorm $S_e$ on $[e,1]$ in [14]. Moreover, regardless of the choice of the t-conorm S on $[e,1]$ in [22], $U^{\ast 1}\ne U_{S_1}$ since $U^{\ast 1}(a,c)=a\ne c=U_{S_1}(a,c)$. Besides all this, since $U^{\ast 1}(0,1)=1$ and $U_{s_1}(0,1)=U_e^S(0,1)=U_{(S,e)}(0,1)=U_s(0,1)=U_{s_e}(0,1)=U_{T_1}(0,1)=U^{″}(0,1)=0$ on any lattice regardless of the choice of the corresponding t-norms on $[0, e]$ and/or t-conorms on $[e,1]$ in [5,11,12,13,14,15,22].

Based on the duality principle, another construction method for uninorms on the bounded lattice L is introduced.

Theorem 2.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in I_e$. Then the function $U_{\ast 1}:L^2\to L$ defined by

$$U_{\ast 1}(u,v)=\left\{\begin{array}{ll}u\wedge v\hfill & (u,v)\in {[0,e)}^2,\hfill \\ u& (u,v)\in [0,e)\times ((e,1]\cup I_e)\cup L\times \left\{e\right\},\\ v& (u,v)\in ((e,1]\cup I_e)\times [0,e)\cup \left\{e\right\}\times L,\\ u\vee v\vee \eta & otherwise,\end{array}\right.$$

(2)

is a uninorm on L with the neutral element e if and only if $u<v$ for all $u\in (0,e),v\in I_e$.

Proof. 

The proof follows easily from Theorem 1, and therefore, it is omitted. □

The structure of the uninorm $U_{\ast 1}$ given in the Formula (2) is summarized in Figure 3.

With the following theorem, another method to produce a uninorm by means of an arbitrary element $\eta \in (e,1)$ is given.

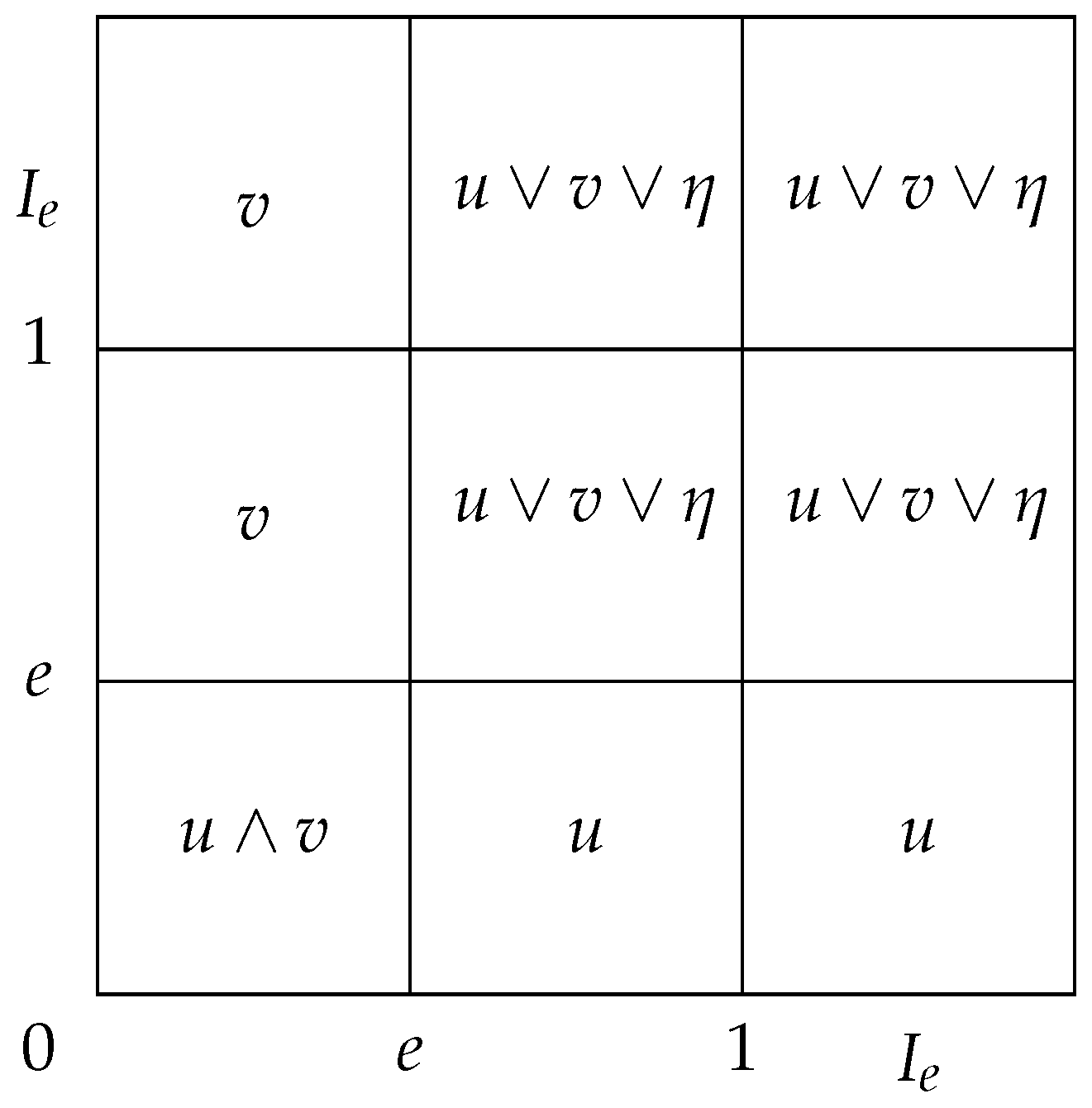
Theorem 3.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in (e,1)$. Then the function $U^{\ast 2}:L^2\to L$ defined by

$$U^{\ast 2}(u,v)=\left\{\begin{array}{ll}u\wedge v\hfill & (u,v)\in {[0,e)}^2\cup [0,e)\times I_e\cup I_e\times [0,e)\cup I_e\times I_e,\hfill \\ u\hfill & (u,v)\in (e,1]\times ([0,e)\cup I_e)\cup L\times \left\{e\right\},\hfill \\ v& (u,v)\in ([0,e)\cup I_e)\times (e,1]\cup \left\{e\right\}\times L,\\ u\vee v\vee \eta & otherwise,\end{array}\right.$$

(3)

is a uninorm on L with the neutral element e if and only if $u<v$ for all $u\in I_e,v\in (e,1)$.

Proof. 

Necessity. Since $U^{\ast 2}$ is monotone, $u=U^{\ast 2}(e,u)\le U^{\ast 2}(u,v)=v$ when $u\in I_e$ and $v\in (e,1)$; therefore, it is obtained that $u<v$.

Sufficiency. (i) Monotonicity: Let us show that for every element $u,v\in L$ with $u\le v$, $U^{\ast 2}(u,w)\le U^{\ast 2}(v,w)$ for all $w\in L$. If u and v are both elements of $[0,e)$ or $\left\{e\right\}$ or $(e, 1]$ or $I_e$, $U^{\ast 2}(u,w)\le U^{\ast 2}(v,w)$ is always satisfied for all $w\in L$ since $u\le v$. If $u=0$ or $u=1$, the inequality is satisfied; therefore, they are omitted. The proof is then split into all the remaining possible cases as follows:

1.

 Let $u\in (0,e)$.

1.1.

 $v=e$,

1.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 2}(u,w)=u\wedge w\le w=U^{\ast 2}(v,w).$

1.1.2.

 If $w\in [e,1)$, then $U^{\ast 2}(u,w)=w=U^{\ast 2}(v,w).$

1.2.

 $v\in (e,1)$,

1.2.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 2}(u,w)=u\wedge w\le v=U^{\ast 2}(v,w).$

1.2.2.

 If $w=e$, then $U^{\ast 2}(u,w)=u\le v=U^{\ast 2}(v,w).$

1.2.3.

 If $w\in (e,1)$, then $U^{\ast 2}(u,w)=w\le v\vee w\vee \eta =U^{\ast 2}(v,w).$

1.3.

 $v\in I_e$,

1.3.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 2}(u,w)=u\wedge w\le v\wedge w=U^{\ast 2}(v,w).$

1.3.2.

 If $w=e$, then $U^{\ast 2}(u,w)=u\le v=U^{\ast 2}(v,w).$

1.3.3.

 If $w\in (e,1)$, then $U^{\ast 2}(u,w)=w=U^{\ast 2}(v,w).$

2.

 $u=e$,

2.1

 $v\in (e,1)$,

2.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 2}(u,w)=w<v=U^{\ast 2}(v,w).$

2.1.2.

 If $w=e$, then $U^{\ast 2}(u,w)=e\le v=U^{\ast 2}(v,w).$

2.1.3.

 If $w\in (e,1)$, then $U^{\ast 2}(u,w)=w\le v\vee w\vee \eta =U^{\ast 2}(v,w).$

3.

 $u\in I_e$,

3.1.

 $v\in (e,1)$,

3.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 2}(u,w)=u\wedge w\le v=U^{\ast 2}(v,w).$

3.1.2.

 If $w=e$, then $U^{\ast 2}(u,w)=u\le v=U^{\ast 2}(v,w).$

3.1.3.

 If $w\in (e,1)$, then $U^{\ast 2}(u,w)=w\le v\vee w\vee \eta =U^{\ast 2}(v,w).$

• (ii) Associativity: We demonstrate that $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(U^{\ast 2}(u,v),w)$ for all $u,v,w\in L$. If $u=e$, the equality is satisfied; therefore, they are omitted. Again, the proof is split into all the remaining possible cases by considering the relationships between the elements $u,v,w$ and e as follows.

1.

 Let $u\in [0,e)\cup I_e$.

1.1.

 $v\in [0,e)\cup I_e$,

1.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v\wedge w)=u\wedge v\wedge w=U^{\ast 2}(u\wedge v,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

1.1.2. If $w\in (e,1]$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,w)=w=U^{\ast 2}(u\wedge v,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

1.2.

 $v\in (e,1]$,

1.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v)=v=U^{\ast 2}(v,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

1.2.2. If $w\in (e,1]$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v\vee w\vee \eta )=v\vee w\vee \eta =U^{\ast 2}(v,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

2.

 $u\in (e,1]$.

2.1.

 $v\in [0,e)\cup I_e$,

2.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v\wedge w)=u=U^{\ast 2}(u,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

2.1.2. If $w\in (e,1]$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

2.2.

 $v\in (e,1]$,

2.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v)=u\vee v\vee \eta =U^{\ast 2}(u\vee v\vee \eta ,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

2.2.2. If $w\in (e,1]$, then $U^{\ast 2}(u,U^{\ast 2}(v,w))=U^{\ast 2}(u,v\vee w\vee \eta )=u\vee v\vee w\vee \eta =U^{\ast 2}(u\vee v\vee \eta ,w)=U^{\ast 2}(U^{\ast 2}(u,v),w).$

It is easy to observe the commutativity of $U^{\ast 2}$ and the fact that e is a neutral element of $U^{\ast 2}$.

Therefore, $U^{\ast 2}$ is a uninorm on L with the neutral element e. □

The structure of the uninorm $U^{\ast 2}$ given in the Formula (3) is summarized in Figure 4.

In the following example, a uninorm on the bounded lattice $L_2$ with the element $\eta \in (e,1)$ is constructed by means of Theorem 3.

Example 3.

Consider the bounded lattice $L_2=(\{0,a,b,c,d,e,f,\eta ,1\},\le ,0,1)$ characterized by the Hasse diagram in Figure 5. If we apply the formula (3) in Theorem 3, the uninorm $U^{\ast 2}$ on $L_2$ is obtained as in

Table 2. The uninorm $U^{\ast 2}$ induced by the Formula (3) in Theorem 3.

${\mathit{U}}^{\ast 2}$	0	a	b	c	d	e	f	$\mathit{\eta }$	1
0	0	a	0	0	0	0	0	$\eta$	1
a	a	a	a	a	a	a	a	a	1
b	0	a	b	c	d	b	f	$\eta$	1
c	0	a	c	c	f	c	f	$\eta$	1
d	0	a	d	f	d	d	f	$\eta$	1
e	0	a	b	c	d	e	f	$\eta$	1
f	0	a	f	f	f	f	f	$\eta$	1
$\eta$	$\eta$	a	$\eta$	$\eta$	$\eta$	$\eta$	$\eta$	$\eta$	1
1	1	1	1	1	1	1	1	1	1

.

Remark 2.

It is worth noting that the uninorm $U^{\ast 2}$ is not equal, up to our best knowledge, to the uninorms obtained by the construction methods of uninorms in the literature. Considering Example 3, it is easily seen that $U^{\ast 2}\ne U_{t_1},U_e^T,U_{(T,e)}$ and $U_t$ regardless of the choice of the corresponding t-norms on $[0, e]$ in [5,11,13,15], since

$$\begin{array}{l}{U}^{\ast 2}(d,c)=d\wedge c=f\ne b=d\vee c=U_{t_1}(d,c),\hfill \\ U^{\ast 2}(a,c)=a\ne 1=U_e^T(a,c),U^{\ast 2}(d,c)=d\wedge c=f\ne \eta =d\vee c\vee e=U_{(T,e)}(d,c),\\ U^{\ast 2}(d,c)=d\wedge c=f\ne 1=U_t(d,c),\hfill \end{array}$$

respectively. Also, it is clear that the lattice $L_2$ satisfies the constraints of Theorem 3.1 in [12] and Theorem 3.1 in [14]. We obtain $U^{\ast 2}\ne U_{t_e}$ since $U^{\ast 2}(d,c)=d\wedge c=f\ne b=d\vee c=U_{t_e}(d,c)$ regardless of the choice of the t-norm $T_e$ on $[0, e]$ in [12]. In addition, $U^{\ast 2}\ne U^{\prime }$ since $U^{\ast 2}(c,d)=c\wedge d=f\ne b=c\vee d=U^{\prime }(c,d)$ regardless of the choice of the t-norm $T_e$ on $[0, e]$ and t-conorm $S_e$ on $[e,1]$ in [14]. Moreover, regardless of the choice of the t-conorm $S_e$ on $[e,1]$ in [22], $U^{\ast 2}\ne U_{S_1}$ since $U^{\ast 2}(a,c)=a\ne c=U_{S_1}(a,c)$. Furthermore, since $U^{\ast 2}(0,1)=1$ and $U_{s_1}(0,1)=U_e^S(0,1)=U_{(S,e)}(0,1)=U_s(0,1)=U_{s_e}(0,1)=U_{T_1}(0,1)=U^{″}(0,1)=0$ on any lattice regardless of the choice of the corresponding t-norms on $[0, e]$ and/or t-conorms on $[e,1]$ in [5,11,12,13,14,15,22].

Another construction method is introduced in Theorem 4 without proof, as it is dual to Theorem 3.

Theorem 4.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in (0,e)$. Then the function $U_{\ast 2}:L^2\to L$ defined by

$$U_{\ast 2}(u,v)=\left\{\begin{array}{cc}u\wedge v\wedge \eta \hfill & (u,v)\in {[0,e)}^2,\hfill \\ u\hfill & (u,v)\in [0,e)\times ((e,1]\cup I_e)\cup L\times \left\{e\right\},\hfill \\ v\hfill & (u,v)\in ((e,1]\cup I_e)\times [0,e)\cup \left\{e\right\}\times L,\hfill \\ u\vee v\hfill & otherwise,\hfill \end{array}\right.$$

(4)

is a uninorm on L with the neutral element e if and only if $u<v$ for all $u\in (0,e)$, $v\in I_e$.

The structure of the uninorm $U_{\ast 2}$ given in the Formula (4) is summarized in Figure 6.

In the following theorem, a method to produce uninorm by means of a fixed element $\eta \in (0,e)$ is given.

Theorem 5.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in (0,e)$. Then the function $U^{\ast 3}:L^2\to L$ defined by

$$U^{\ast 3}(u,v)=\left\{\begin{array}{cc}u\wedge v\wedge \eta \hfill & (u,v)\in ([0,e)\cup I_e)\times ([0,e)\cup I_e),\hfill \\ u\hfill & (u,v)\in ([0,e)\cup I_e)\times (e,1]\cup L\times \left\{e\right\},\hfill \\ v\hfill & (u,v)\in (e,1]\times ([0,e)\cup I_e)\cup \left\{e\right\}\times L,\hfill \\ u\vee v\hfill & otherwise,\hfill \end{array}\right.$$

(5)

is a uninorm on L with the neutral element e.

Proof. 

 (i) Monotonicity: Let us show that for every element $u,v\in L$ with $u\le v$, $U^{\ast 3}(u,w)\le U^{\ast 3}(v,w)$ for all $w\in L$. If u and v are both elements of $[0,e)$ or $\left\{e\right\}$ or $(e, 1]$ or $I_e$, $U^{\ast 3}(u,w)\le U^{\ast 3}(v,w)$ is always satisfied for all $w\in L$ since $u\le v$. If $u=0$ or $u=1$, the inequality is satisfied; therefore, they are omitted. The proof is then split into all the remaining possible cases as follows.

1.

 Let $u\in (0,e)$.

1.1.

 $v=e$,

1.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 3}(u,w)=u\wedge w\wedge \eta \le w=U^{\ast 3}(v,w).$

1.1.2.

 If $w\in [e,1)$, then $U^{\ast 3}(u,w)=u\le w=U^{\ast 3}(v,w).$

1.2.

 $v\in (e,1)$,

1.2.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 3}(u,w)=u\wedge w\wedge \eta \le w=U^{\ast 3}(v,w).$

1.2.2.

  If $w=e$, then $U^{\ast 3}(u,w)=u\le v=U^{\ast 3}(v,w).$

1.2.3.

 If $w\in (e,1)$, then $U^{\ast 3}(u,w)=u\le v\vee w=U^{\ast 3}(v,w).$

1.3.

 $v\in I_e$,

1.3.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 3}(u,w)=u\wedge w\wedge \eta \le v\wedge w\wedge \eta =U^{\ast 3}(v,w).$

1.3.2.

 If $w\in [e,1)$, then $U^{\ast 3}(u,w)=u\le v=U^{\ast 3}(v,w).$

2.

 $u=e$,

2.1.

 $v\in (e,1)$,

2.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 3}(u,w)=w=U^{\ast 3}(v,w).$

2.1.2.

 If $w=e$, then $U^{\ast 3}(u,w)=u\le v=U^{\ast 3}(v,w).$

2.1.3.

 If $w\in (e,1)$, then $U^{\ast 3}(u,w)=w\le v\vee w=U^{\ast 3}(v,w).$

3.

 $u\in I_e$,

3.1.

 $v\in (e,1)$,

3.1.1.

 If $w\in (0,e)\cup I_e$, then $U^{\ast 3}(u,w)=u\wedge w\wedge \eta \le w=U^{\ast 3}(v,w).$

3.1.2.

 If $w=e$, then $U^{\ast 3}(u,w)=u\le v=U^{\ast 3}(v,w).$

3.1.3.

 If $w\in (e,1)$, then $U^{\ast }(u,w)=u\le v\vee w=U^{\ast 3}(v,w).$

• (ii) Associativity: We demonstrate that $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(U^{\ast 3}(u,v),w)$ for all $u,v,w\in L$. If $u=e$, the equality is satisfied; therefore, they are omitted. Again, the proof is split into all the remaining possible cases by considering the relationships between the elements $u,v,w$ and e as follows.

1.

 Let $u\in [0,e)\cup I_e$.

1.1.

 $v\in [0,e)\cup I_e$,

1.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v\wedge w\wedge \eta )=u\wedge v\wedge w\wedge \eta =U^{\ast 3}(u\wedge v\wedge \eta ,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

1.1.2. If $w\in (e,1]$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v)=u\wedge v\wedge \eta =U^{\ast 3}(u\wedge v\wedge \eta ,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

1.2.

 $v\in (e,1]$,

1.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

1.2.2. If $w\in (e,1]$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v\vee w)=u=U^{\ast 3}(u,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

2.

 $u\in (e,1]$.

2.1.

 $v\in [0,e)\cup I_e$,

2.1.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v\wedge w\wedge \eta )=v\wedge w\wedge \eta =U^{\ast 3}(v,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

2.1.2. If $w\in (e,1]$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v)=v=U^{\ast 3}(v,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

2.2.

 $v\in (e,1]$,

2.2.1. If $w\in [0,e)\cup I_e$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,w)=w=U^{\ast 3}(u\vee v,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

2.2.2. If $w\in (e,1]$, then $U^{\ast 3}(u,U^{\ast 3}(v,w))=U^{\ast 3}(u,v\vee w)=u\vee v\vee w=U^{\ast 3}(u\vee v,w)=U^{\ast 3}(U^{\ast 3}(u,v),w).$

It is easy to observe the commutativity of $U^{\ast 3}$ and the fact that e is a neutral element of $U^{\ast 3}$.

Therefore, $U^{\ast 3}$ is a uninorm on L with the neutral element e. □

The structure of the uninorm $U^{\ast 3}$ given in the Formula (5) is summarized in Figure 7.

Example 4.

Consider the bounded lattice $L_3=(\{0,a,b,c,d,e,f,k,m,\eta ,1\},\le ,0,1)$ characterized by the Hasse diagram in Figure 8. If we apply the formula (5) in Theorem 5, the uninorm $U^{\ast 3}$ on $L_3$ is obtained as in

Table 3. The uninorm $U^{\ast 3}$ induced by the Formula (5) in Theorem 5.

${\mathit{U}}^{\ast 3}$	0	a	b	c	d	e	f	k	m	$\mathit{\eta }$	1
0	0	0	0	0	0	0	0	0	0	0	0
a	0	m	m	m	m	a	a	m	m	m	a
b	0	m	$\eta$	$\eta$	$\eta$	b	b	$\eta$	m	$\eta$	b
c	0	m	$\eta$	$\eta$	$\eta$	c	c	$\eta$	m	$\eta$	c
d	0	m	$\eta$	$\eta$	$\eta$	d	d	$\eta$	m	$\eta$	d
e	0	a	b	c	d	e	f	k	m	$\eta$	1
f	0	a	b	c	d	f	f	k	m	$\eta$	1
k	0	m	$\eta$	$\eta$	$\eta$	k	k	$\eta$	m	$\eta$	k
m	0	m	m	m	m	m	m	m	m	m	m
$\eta$	0	m	$\eta$	$\eta$	$\eta$	$\eta$	$\eta$	$\eta$	m	$\eta$	$\eta$
1	0	a	b	c	d	1	1	k	m	$\eta$	1

.

Remark 3.

 In general, the construction method given by Theorem 5 produces a different uninorm from the uninorms obtained by the construction methods of uninorms in the literature. Regardless of the choice of the lattice L and the corresponding t-norms on $[0, e]$ and/or t-conorms on $[e,1]$ in [5,11,12,13,14,15,22], $U^{\ast 3}\ne U_{t_1},U_e^T,U_{(T,e)},U_t,U_{t_e},U_{S_1}$ and $U^{\prime }$ since $U^{\ast 3}(0,1)=0\ne 1=U_{t_1}(0,1)=U_e^T(0,1)=U_{(T,e)}(0,1)=U_t(0,1)=U_{t_e}(0,1)=U_{S_1}(0,1)=U^{\prime }(0,1).$ Also, considering Example 4, $U^{\ast 3}\ne U_{s_1},U_e^S,U_{(S,e)}$ and $U_s$ since

$$\begin{array}{l}{U}^{\ast 3}(c,d)=c\wedge d\wedge \eta =\eta \ne b=c\wedge d=U_{s_1}(c,d),\\ U^{\ast 3}(a,b)=a\wedge b\wedge \eta =m\ne 0=U_e^S(a,b),\\ U^{\ast 3}(a,b)=a\wedge b\wedge \eta =m\ne a=a\wedge b\wedge e=U_{(S,e)}(a,b),\\ U^{\ast 3}(c,d)=c\wedge d\wedge \eta =\eta \ne 0=U_s(c,d),\end{array}$$

respectively. Furthermore, one can easily check that the lattice $L_2$ satisfies the constraints of Theorem 3.12 in [12] and Theorem 3.8 in [14]. We obtain $U^{\ast 3}\ne U_{s_e}$ since $U^{\ast 3}(b,c)=b\wedge c\wedge \eta =\eta \ne 0=U_{s_e}(b,c)$ regardless of the choice of the t-conorm $S_e$ on $[e,1]$ in [12]. In addition, $U^{\ast 3}\ne U^{″},$ since $U^{\ast 3}(c,d)=c\wedge d\wedge \eta =\eta \ne b=c\wedge d=U^{″}(c,d)$ regardless of the choice of the t-norm $T_e$ on $[0, e]$ and the t-conorm $S_e$ on $[e,1]$ in [14]. Moreover, regardless of the choice of the t-norm $T_e$ on $[0, e]$ in [5,11,12,13,14,15,22].

Based on the duality principle, another construction method for uninorms on the bounded lattice L is introduced.

Theorem 6.

Let $(L,\le ,0,1)$ be a bounded lattice, $e\in L\setminus \{0,1\}$ and $\eta \in (e,1)$. Then the function $U_{\ast 3}:L^2\to L$ defined by

$$U_{\ast 3}(u,v)=\left\{\begin{array}{cc}u\wedge v\hfill & (u,v)\in {[0,e)}^2,\hfill \\ u\hfill & (u,v)\in ([e,1)\cup I_e)\times [0,e)\cup L\times \left\{e\right\},\hfill \\ v\hfill & (u,v)\in [0,e)\times ([e,1)\cup I_e)\cup \left\{e\right\}\times L,\hfill \\ u\vee v\vee \eta \hfill & otherwise,\hfill \end{array}\right.$$

(6)

is a uninorm on L with the neutral element e.

Proof. 

The proof follows easily from Theorem 5, and therefore, it is omitted. □

The structure of the uninorm $U_{\ast 3}$ given in the Formula (6) is summarized in Figure 9.

4. Conclusions

In this article, we have developed new methods for constructing uninorms with a neutral element e on a bounded lattice L using an arbitrary fixed $\eta \in L$ that is not $0,e$ or 1. We thoroughly explored all possible cases of the element $\eta$ of the lattice L, i.e., $\eta \in I_e$ or $\eta \in (e,1)$ or $\eta \in (0,e)$. For each construction method, we established necessary and sufficient conditions to ensure the resulting operation is indeed a uninorm on L. To clarify our methods, we have provided numerous examples and compared our techniques with existing ones in the literature. Looking ahead, we will continue studying element-based construction methods for nullnorms and some other aggregation functions on bounded lattices.