Two-Party Quantum Private Comparison with Pauli Operators

Abstract

Quantum private comparison (QPC) is a quantum cryptographic protocol designed to enable two mutually distrustful parties to securely compare sensitive data without disclosing their private information to each other or any external entities. This study proposes a novel QPC protocol that leverages Bell states to ensure data privacy, utilizing the fundamental principles of quantum mechanics. Within this framework, two participants, each possessing a secret integer, encode the binary representation of their values using Pauli-X and Pauli-Z operators applied to quantum states transmitted from a semi-honest third party (TP). The TP, which is bound to protocol compliance and prohibited from colluding with either participant, measures the received sequences to determine the comparison result without accessing the participants’ original inputs. Theoretical analyses and simulations validate the protocol’s strong security, high efficiency, and practical feasibility in quantum computing environments. An advantage of the proposed protocol lies in its optimized utilization of Bell states, which enhances qubit efficiency and experimental practicality. Moreover, the proposed protocol outperforms several existing Bell-state-based QPC schemes in terms of efficiency.

1. Introduction

Secure multiparty computation (MPC) is a cryptographic technique, enabling multiple mutually distrustful parties to collaboratively compute a function over their private inputs while ensuring that no party accesses the confidential data of others [1]. Private comparison, an important branch of MPC, originated from Yao’s millionaire problem [2], in which two millionaires meeting on the street desire to ascertain who has greater wealth without revealing their actual financial status to one another. Inspired by the millionaire problem, Boudot et al. [3] introduced a variation called the socialist millionaire problem, where two millionaires determine whether their wealth is equal without disclosing the exact amounts. Thus, solving the millionaire problem (designing privacy comparison protocols) has become a focal point in both classical and quantum cryptography fields.

Lo [4] pointed out that the inherent impossibility of securely evaluating a two-party function without compromising privacy in a purely bilateral framework is a critical challenge when designing privacy comparison protocols. To address this challenge, researchers have proposed incorporating a semi-honest third party (TP). Acting as a semi-trusted intermediary, the TP facilitates the secure comparison of private inputs but cannot collude with any participating parties.

The security of classical cryptographic protocols, regardless of those for privacy comparison and others, primarily rely on computationally hard mathematical problems such as integer factorization and discrete logarithms, which cannot be efficiently solved using classical computational resources under current conditions. Unfortunately, the emergence of quantum algorithms implemented on quantum computing platforms presents a substantial challenge to the security of classical cryptographic protocols. For example, Shor algorithm [5] leverages the parallelism of quantum computing and the superposition property of quantum states to reduce the complexity of solving these hard mathematical problems from exponential scale in classical computers to polynomial time. Consequently, once quantum computing matures sufficiently, existing cryptographic systems may become vulnerable. It is imperative to develop quantum-resistance protocols that are resilient to threats posed by quantum algorithms.

In response, researchers have investigated quantum-resistance protocols that integrate classical and quantum mechanics. These include quantum secret sharing [6,7,8], quantum key agreement [9,10,11], quantum secure direct communication [12,13,14,15], quantum private set intersection [16,17] and quantum secure multiparty computation (QMPC) [18]. The security of these quantum-resistance protocols is based on the principles of quantum mechanics, thereby resisting threats from quantum algorithms.

Quantum private comparison (QPC), a crucial branch of QMPC, enables parties to compare their confidential inputs without revealing each other’s confidential data. In 2009, Yang and Wen [19] proposed the first QPC protocol, which utilized decoy photons and a one-way hash function to ensure security and confidentiality during the comparison process. Subsequent advancements by Tseng et al. [20] introduced a Bell-state-based QPC protocol that achieves a qubit efficiency of 50% by utilizing the two-particle entanglement correlation of Bell states. However, this protocol is vulnerable to attacks from the TP attempting to steal participants’ private inputs by exploiting fake Bell states. To enhance its security, two feasible solutions are proposed in Ref. [21]. Lang [22] designed the QPC protocol that utilizes the quantum CNOT gate instead of classical exclusive-OR operations to facilitate comparison, but it cannot prevent the disturbance attack implemented by an outsider eavesdropper and the TP’s measuring attack [23]. Huang et al. [24] designed the protocol by utilizing the entanglement swapping among three Bell states. Although it can compare three bits in each round, it is difficult to implement with the current technologies due to the effects of decoherence and environmental noise. Lang et al. [25] developed the protocol using a single Bell state, reducing the states generation switching costs but lowering qubit efficiency to 16.67%. Hou et al. [26] developed a protocol that encodes private inputs into Bell states using rotation operations, achieving a qubit efficiency of 25%. Similarly, Hou and Wu [27] employed a comparable method to encode private inputs into Bell states using unitary operations.

Additionally, various quantum states have been explored as carriers of quantum information for transmitting private data. These states include single photons [28,29,30,31,32,33], multi-qubit entangled states [34,35,36,37,38,39], cluster states [40,41], and d-level quantum states [42,43,44,45]. Among these, protocols that utilize simplified quantum resources (e.g., single photons and Bell states) are more feasible and practical than those relying on multi-qubit and d-level quantum states, due to the ease of operation and manipulation of single photons and Bell states. Despite the advantages of Bell states, many existing Bell-state-based QPC protocols face challenges in achieving high qubit efficiency, with many achieving less than 50%.

Inspired by the aforementioned Bell-state-based QPC protocols and with the aim of enhancing their efficiency, we propose a novel approach that utilizes Bell states and Pauli operators to design a QPC protocol. The primary contributions of this work are as follows.

(1)

By transmitting private information as Pauli operators applied to Bell states, the proposed protocol is more practical and efficient than those that rely on multi-qubit and d-level quantum states.

(2)

The protocol achieves a qubit efficiency of 50%, requiring one Bell state and a bit of pre-shared key for each bit compared. This efficiency surpasses that of many existing Bell-state-based QPC protocols.

(3)

By simulating a concrete example using IBM Quantum Qiskit simulator with a designed quantum circuit, the feasibility of the protocol has been validated.

(4)

Security analyses confirm the protocol’s resilience against both external attacks and insider threats.

The remainder of this paper is organized as follows: Section 2 introduces the Pauli operators and Bell states used in the protocol. Section 3 and Section 4 detail the implementation steps of the proposed protocol and the simulations conducted via IBM Quantum Qiskit simulator, respectively. Section 5 presents a security analysis of the protocol. Section 6 discusses the findings, and Section 7 concludes the paper by summarizing the contributions and exploring potential future directions.

2. Pauli Operators and Bell States

The Pauli-X and Pauli-Z operators [46] are single-qubit gates that are mathematically defined as

$$X=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),Z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

(1)

Four Bell states are given by

$$\left|{\phi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|0\right.〉+\left|1\right.〉\left|1\right.〉\right)$$

(2)

$$\left|{\phi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|0\right.〉-\left|1\right.〉\left|1\right.〉\right)$$

(3)

$$\left|{\psi }^{+}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|1\right.〉+\left|1\right.〉\left|0\right.〉\right)$$

(4)

$$\left|{\psi }^{-}\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|1\right.〉-\left|1\right.〉\left|0\right.〉\right)$$

(5)

When applying the operations $X^{a_1}{Z}^{a_2}$ and $X^{b_1}{Z}^{b_2}$ (where $a_1,a_2,b_1,b_2\in \left\{\mathrm{0,1}\right\}$) to four Bell states, the resulting states are shown in

Table 1. The resulting states.

Operations	$\left|{\mathit{\phi }}^{+}\right.⟩$	$\left|{\mathit{\phi }}^{-}\right.⟩$	$\left|{\mathit{\psi }}^{+}\right.⟩$	$\left|{\mathit{\psi }}^{-}\right.⟩$
$X^0{Z}^0\otimes X^0{Z}^0$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$
$X^0{Z}^0\otimes X^0{Z}^1$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$
$X^0{Z}^0\otimes X^1{Z}^0$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$
$X^0{Z}^0\otimes X^1{Z}^1$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$
$X^0{Z}^1\otimes X^0{Z}^0$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$
$X^0{Z}^1\otimes X^0{Z}^1$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$
$X^0{Z}^1\otimes X^1{Z}^0$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$
$X^0{Z}^1\otimes X^1{Z}^1$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$
$X^1{Z}^0\otimes X^0{Z}^0$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$
$X^1{Z}^0\otimes X^0{Z}^1$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$
$X^1{Z}^0\otimes X^1{Z}^0$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$
$X^1{Z}^0\otimes X^1{Z}^1$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$
$X^1{Z}^1\otimes X^0{Z}^0$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$
$X^1{Z}^1\otimes X^0{Z}^1$	$\left|{\psi }^{+}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$
$X^1{Z}^1\otimes X^1{Z}^0$	$\left|{\phi }^{-}\right.⟩$	$\left|{\phi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$
$X^1{Z}^1\otimes X^1{Z}^1$	$\left|{\phi }^{+}\right.⟩$	$\left|{\phi }^{-}\right.⟩$	$\left|{\psi }^{+}\right.⟩$	$\left|{\psi }^{-}\right.⟩$

.

According to Table 1, we find that the Bell states remain unchanged if and only if the same operations are performed on both the first and second particles of the Bell states. This property is crucial for the design of the proposed protocol that follows.

3. The Implementation Steps of the Proposed Protocol

The primary objective of the quantum private comparison (QPC) protocol is to determine whether the confidential inputs X and Y, held by Alice and Bob respectively, are equivalent. This comparison is facilitated by a semi-honest third party (TP), which complies with the protocol but is restricted from colluding with either participant. Crucially, the protocol ensures that neither Alice nor Bob leaks any information about their private inputs to each other or external adversaries.

The protocol assumes a noiseless and lossless quantum channel to guarantee the integrity of quantum state transmissions. Prior to execution, Alice and Bob convert their secrets into n-bit binary strings, denoted as $X=\left(x_{n-1}, x_{n-2},\cdots ,x_0\right)$ and $Y=\left(y_{n-1}, y_{n-2},\cdots {,y}_0\right)$, where $x_i,y_i\in \left\{\mathrm{0,1}\right\}$ for $i=\mathrm{0,1},\cdots ,n-1$. If the length of X or Y is shorter than n, zeros are appended to the higher-order bits. The parameter n, determined by security requirements, is publicly disclosed to the TP. Subsequently, Alice and Bob employ a quantum key distribution (QKD) protocol (e.g., BB84 [47]) to establish a shared secret key $K_{AB}=\left(k_n{k}_{n-1}\cdots k_0\right)$, restructured as $K_{AB}=\left(k_{⌈n/2⌉-1}^{\prime },k_{⌈n/2⌉-2}^{\prime },\cdots ,k_0^{\prime }\right)$, where $k_j^{\prime }=k_{2j+1}{k}_{2j}$ for $j=\mathrm{0,1},\cdots ,⌈n/2⌉-2,⌈n/2⌉-1.$

Protocol Execution:

Step 1. Alice and Bob partition X and Y into $⌈n/2⌉$ groups, where ⌈·⌉ is the ceiling function. If n is odd, a padding bit (0) is added to the final group to ensure uniform group sizes of two bits.

Step 2. The TP prepares $⌈n/2⌉$ Bell states, randomly selected from the set defined in Equations (2)–(5). These states are divided into two sequences: $S_A$ (first particles) and $S_B$ (second particles). For security validation, the TP generates decoy-photon sequences $D_A$ and $D_B$, composed of randomly chosen states from $\left\{\left|0\right.⟩,\left|1\right.⟩,\left|+\right.⟩,\left|-\right.⟩\right\}$. All decoy photons in $D_A$ and $D_B$ are inserted into $S_A$ and $S_B$, forming modified sequences $S_A^{\prime }$ and $S_B^{\prime }$, which are transmitted to Alice and Bob, respectively.

Step 3. Upon receiving $S_A^{\prime }(S_B^{\prime }$), Alice (Bob) acknowledges receipt. The TP then discloses the positions and measurement bases (Z-basis for $\left|0\right.⟩ \mathrm{o}\mathrm{r} \left|1\right.⟩$; X-basis for $\left|+\right.⟩ \mathrm{o}\mathrm{r} \left|-\right.⟩$) of the decoy photons. Alice (Bob) measures the decoy photons in $D_A\left(D_B\right)$, obtaining results $R_A\left(R_B\right)$, which are returned to the TP for error rate calculation. If the error rate exceeds a predefined threshold $\left(\tau =2\sim 8.9\%\right)$ depending on the channel situation (e.g., the distance, etc.) [48,49], the protocol is terminated and restarted; otherwise, it proceeds to the next step.

Step 4. After removing decoy photons $D_A$ ($D_B)$ from $S_A^{\prime }(S_B^{\prime }$), Alice (Bob) applies operations $X^{a_{2j+1}}{Z}^{a_{2j}}$ ($X^{b_{2j+1}}{Z}^{b_{2j}}$) to $S_A(S_B$), where $a_{2j+1}=x_{2j+1}\oplus k_{2j+1}$ and $a_{2j}=x_{2j}\oplus k_{2j}$ (similar for $b_{2j+1}, b_{2j}$). The resulting sequences $U_A(U_B$) are embedded with new decoy-photon sequence $D_A^{\prime }\left(D_B^{\prime }\right)$, forming $G_A\left(G_B\right)$, which are sent to the TP.

Step 5. The TP verifies eavesdropping using the aforementioned decoy-photon method in Step 2. If secure, the TP removes $D_A^{\prime }\left(D_B^{\prime }\right)$ from $G_A\left(G_B\right)$ and performs Bell-state measurements on $U_A$ and $U_B$. A match between the measurement results $R_T$ and the initially prepared Bell states confirms $X=Y$; otherwise, $X\ne Y$.

4. Simulations for Two Concrete Examples

Example 1.

Comparison of the equality of the secret integers $X_0=54$ and $Y_0=22$.

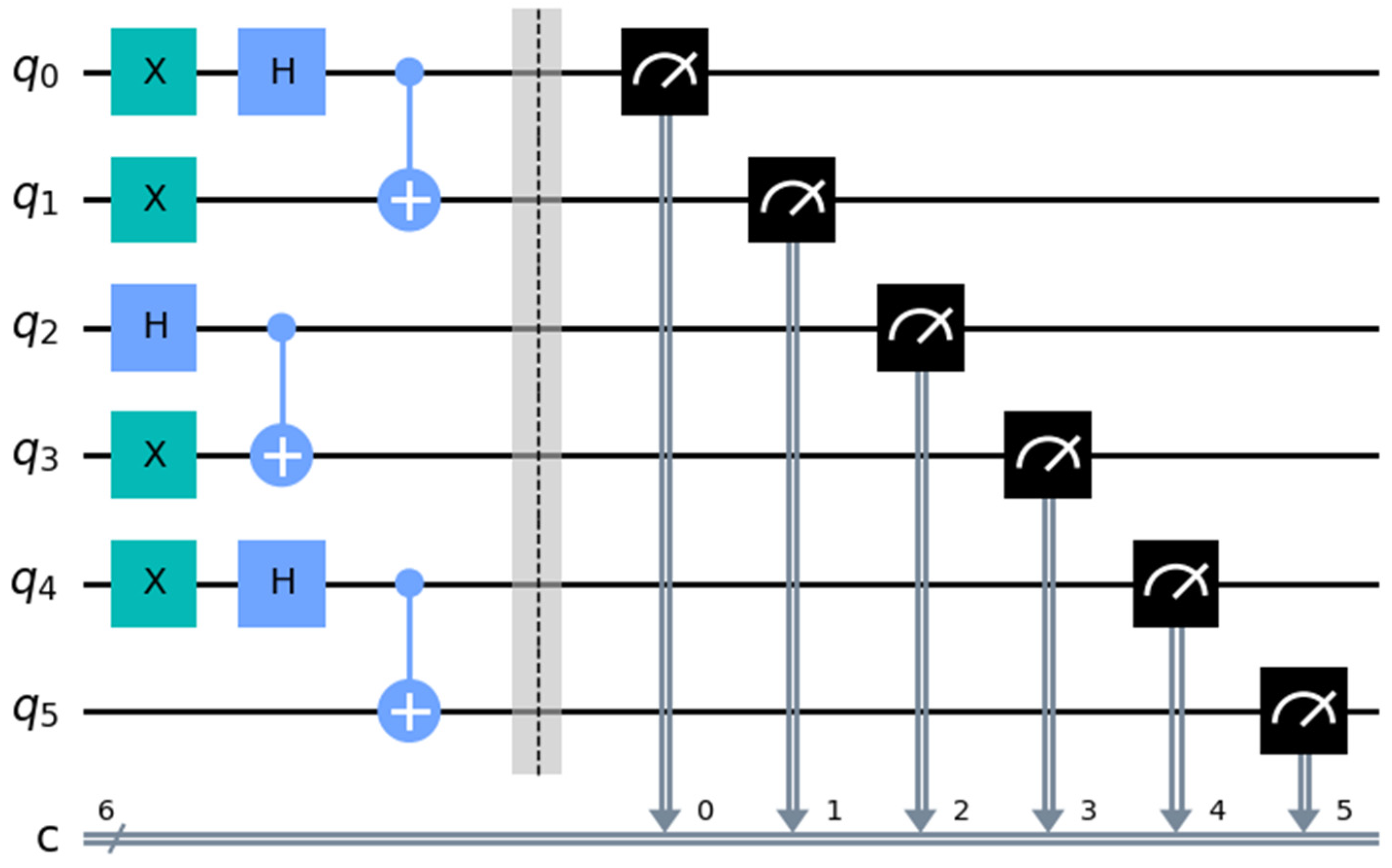
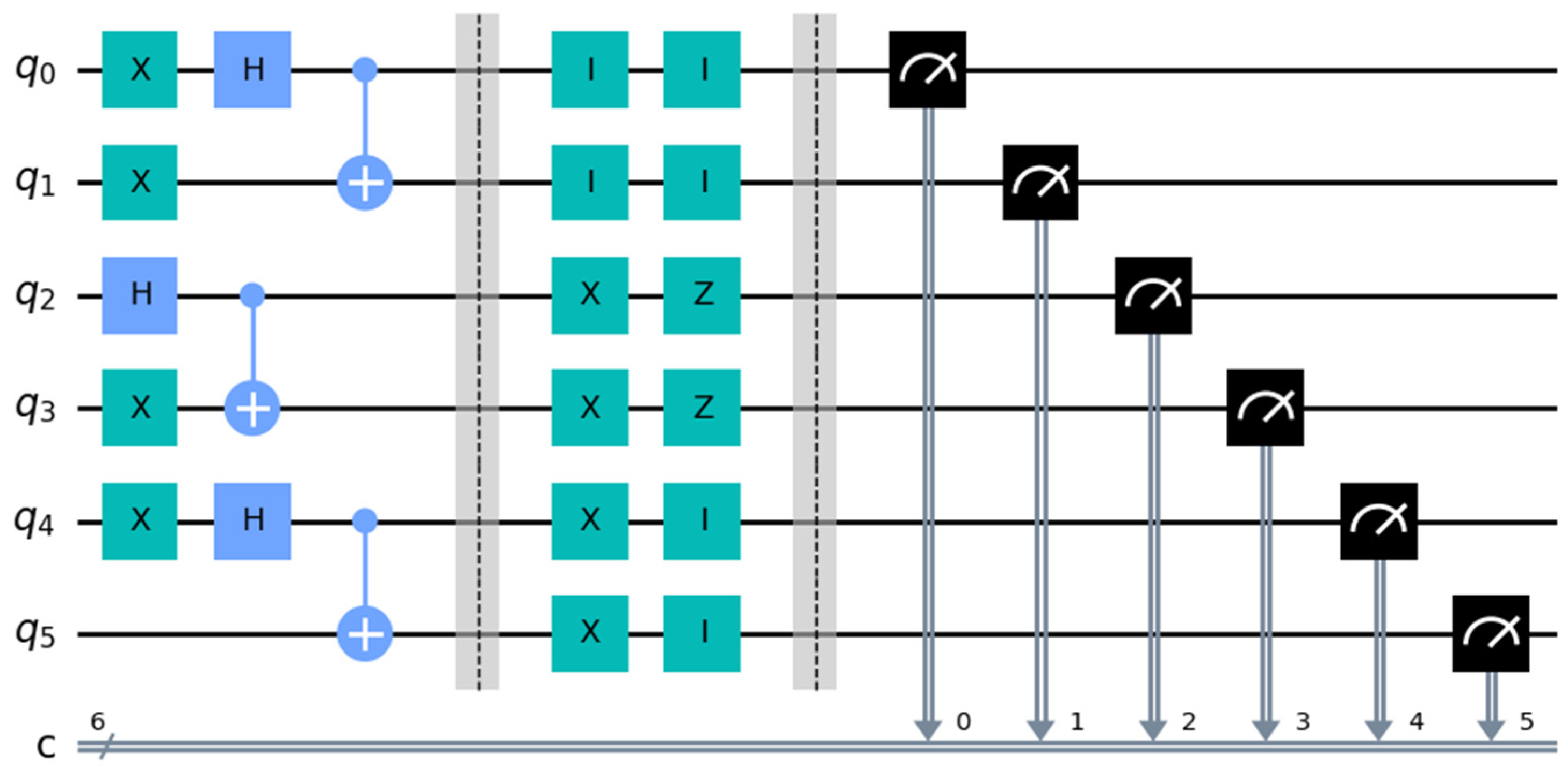
The binary representations of $X_0$ and $Y_0$ are $X_0=(\mathrm{1,1},\mathrm{0,1},\mathrm{1,0})$ and $Y_0=(\mathrm{1,0},\mathrm{1,1},0)$, respectively. The length of the strings is set to 6. Since the length of $Y_0$ is shorter than 6, zeros are appended to the higher-order bits, resulting in the restructured binary representation of $Y_0$ as $Y_0=(0, \mathrm{1,0},\mathrm{1,1},0)$. Alice and Bob partition them into three 2-bit groups: $X_0=\left(\mathrm{11,01,10}\right)$ and $Y_0=\left(\mathrm{01,01,10}\right)$. Let the shared secret key $K_{AB}=\left(\mathrm{1,1},\mathrm{0,0},\mathrm{0,1}\right)=\left(\mathrm{11,00,01}\right)$. The initial preparation includes three Bell states: $\left\{\left|{\psi }^{-}\right.⟩,\left|{\psi }^{+}\right.⟩,\left|{\phi }^{-}\right.⟩\right\}$.

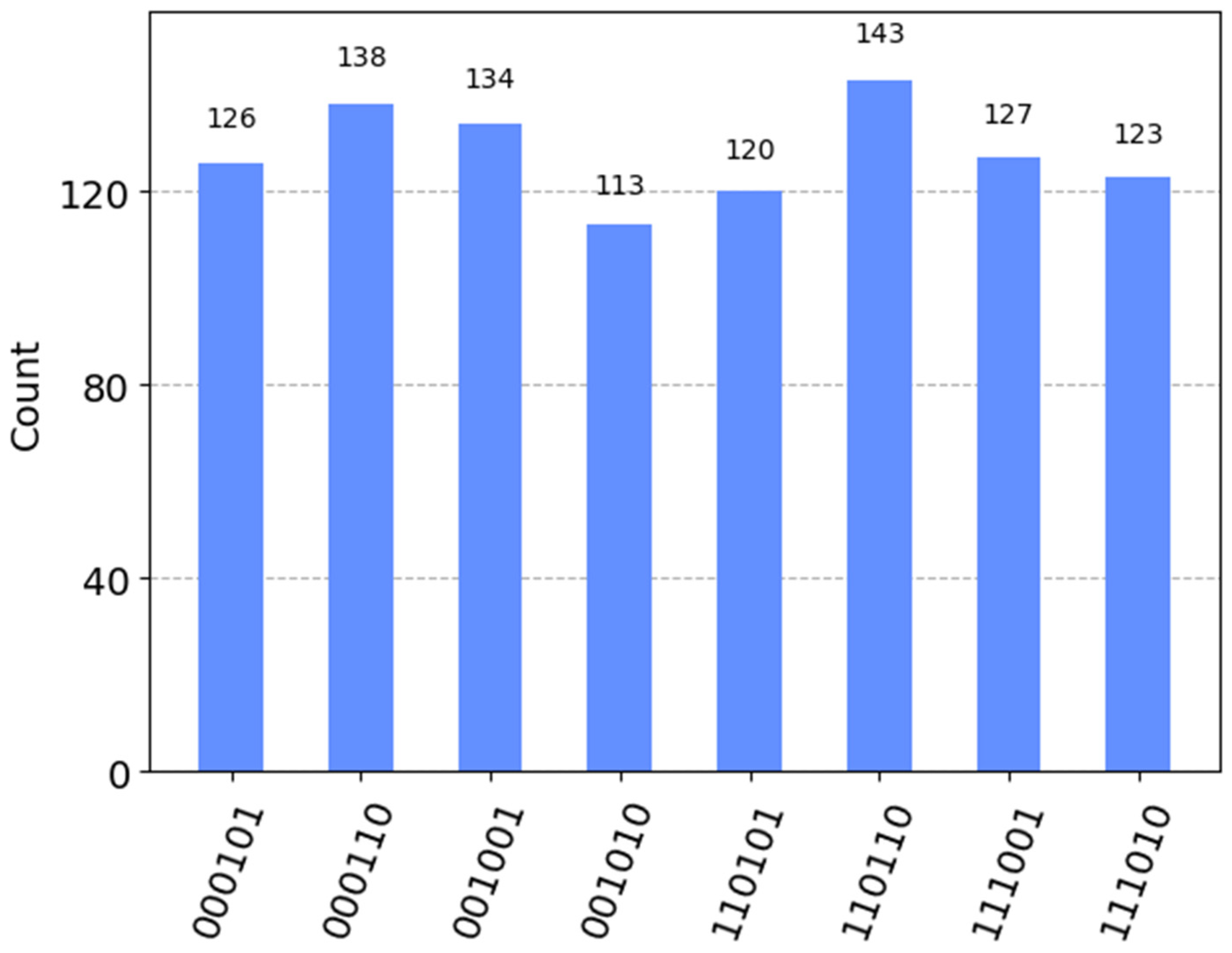
The quantum circuit implementation of these three Bell states $\left\{\left|{\psi }^{-}\right.⟩,\left|{\psi }^{+}\right.⟩,\left|{\phi }^{-}\right.⟩\right\}$ is composed of Hadamard and CNOT gates, as shown in Figure 1. The left half of Figure 1 separated by barrier lines is for preparing Bell states, while the right half is for measuring Bell states using Z basis. The measurement results of the three Bell states, obtained using the IBM Quantum Qiskit simulator (Qiskit: 0.44.1; Python: 3.11.4; OS: Windows) with 1024 shots, are displayed in Figure 2.

Based on $X_0$, $Y_0$ and $K_{AB}$, the corresponding operations on the three Bell states $\left\{\left|{\psi }^{-}\right.⟩,\left|{\psi }^{+}\right.⟩,\left|{\phi }^{-}\right.⟩\right\}$ are {$II\otimes$X$I$, $I$Z$\otimes I$Z, XZ$\otimes$XZ}. The quantum circuit implementation for comparing the equality of the secret integers $X_0=54$ and $Y_0=22$ is shown in Figure 3, and the results of its probability measurements are presented in Figure 4.

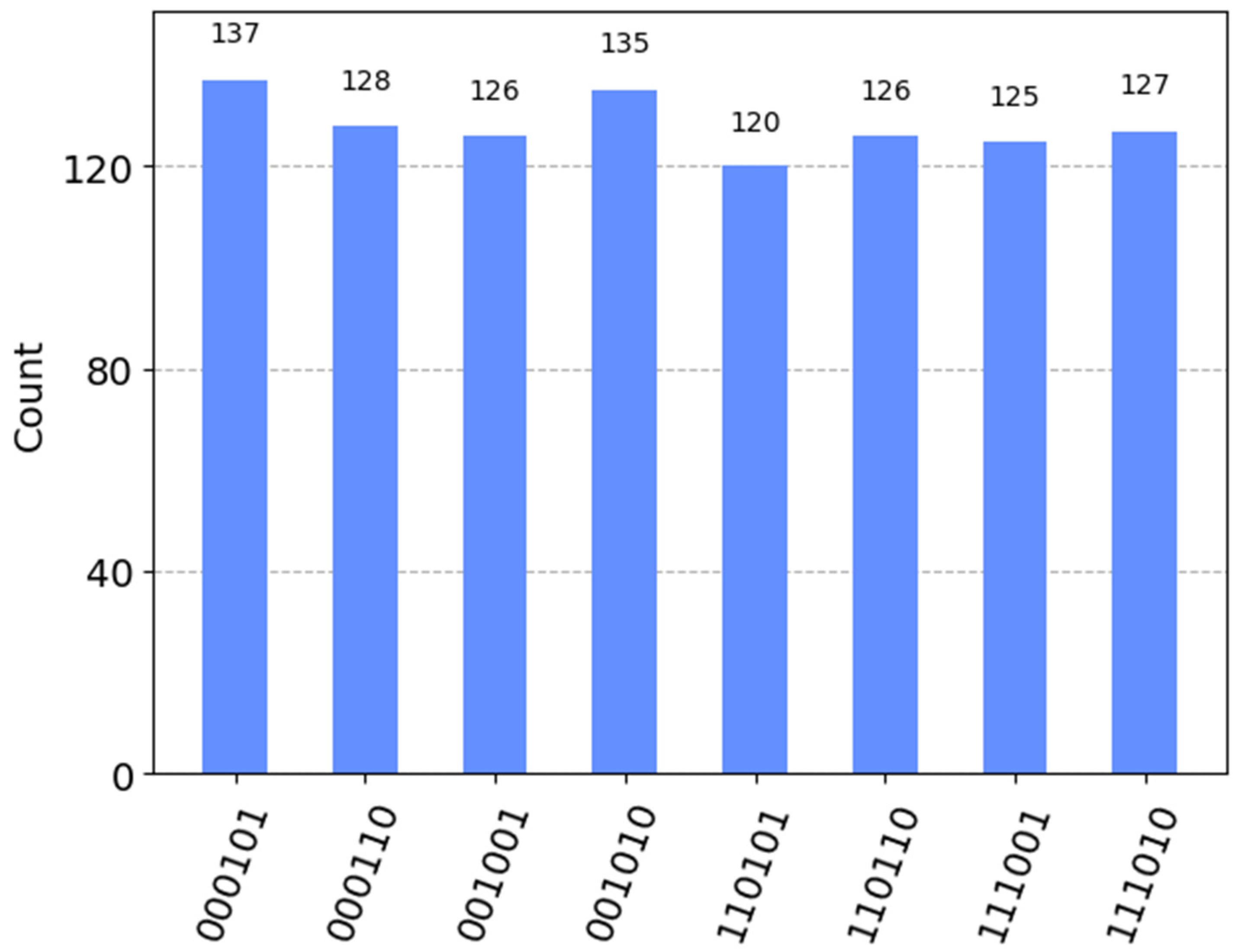
According to the bar chart in Figure 4, the measurement results of the computational basis states do not match those in Figure 2. This indicates that the measurement outcomes do not align with the initially prepared Bell states. Consequently, we can conclude that $X_0\ne Y_0$.

Example 2.

Comparison of the equality of the secret integers $X_1=63$ and $Y_1=63$.

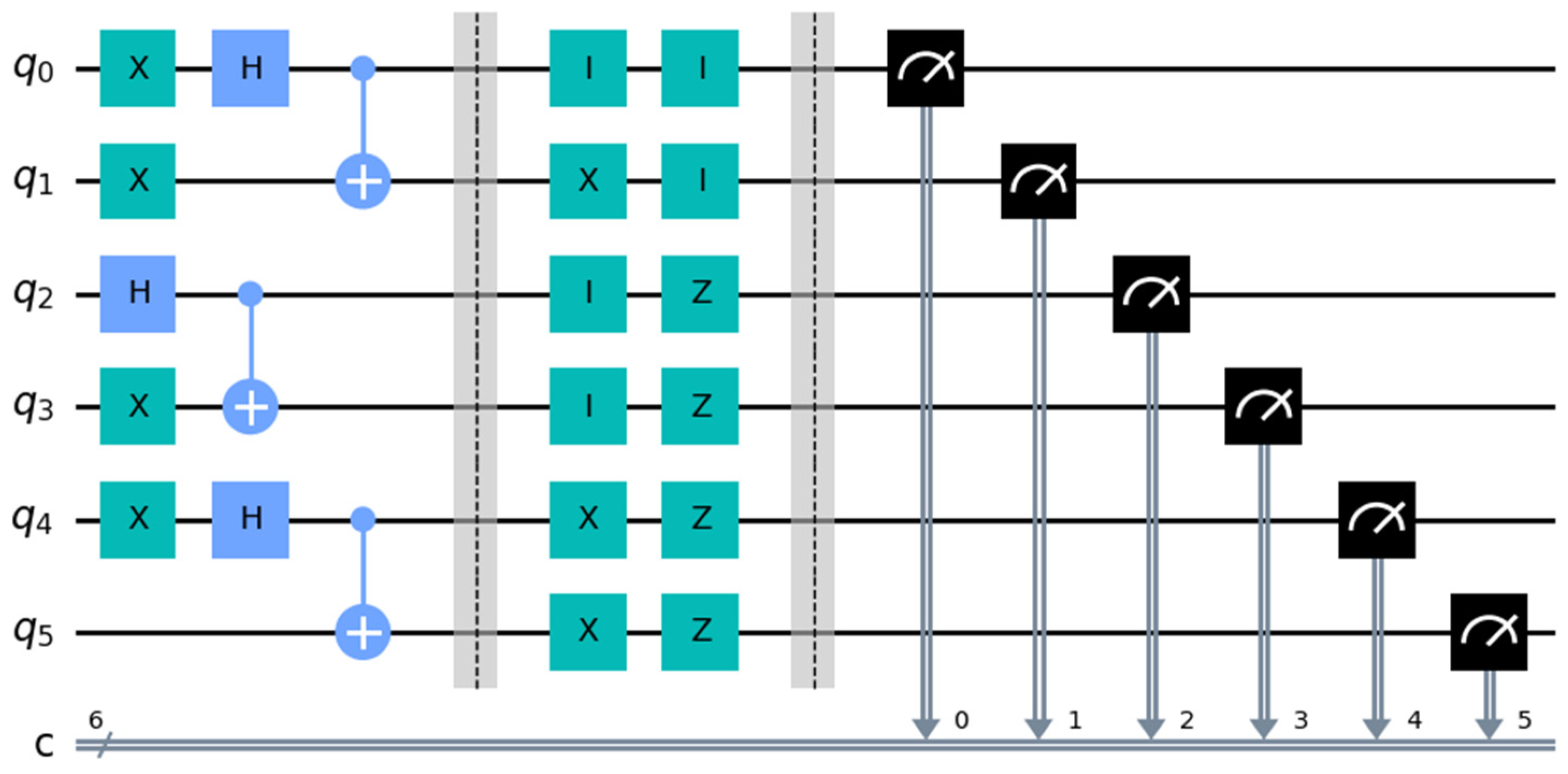
The binary representations of $X_1$ and $Y_1$ are $X_1=(\mathrm{1,1},\mathrm{1,1},\mathrm{1,1})$ and $Y_1=(\mathrm{1,1},\mathrm{1,1},\mathrm{1,1})$, respectively. Alice and Bob partition them into three 2-bit groups: $X_1=\left(\mathrm{11,11,11}\right)$ and $Y_1=\left(\mathrm{11,11,11}\right)$. Let the shared secret key $K_{AB}=\left(\mathrm{1,1},\mathrm{0,0},\mathrm{0,1}\right)=\left(\mathrm{11,00,01}\right).$ The initial preparation includes three Bell states: $\left\{\left|{\psi }^{-}\right.⟩,\left|{\psi }^{+}\right.⟩,\left|{\phi }^{-}\right.⟩\right\}$.

Based on $X_1$, $Y_1$ and $K_{AB}$, the corresponding operations on three Bell states $\left\{\left|{\psi }^{-}\right.⟩,\left|{\psi }^{+}\right.⟩,\left|{\phi }^{-}\right.⟩\right\}$ are {$II\otimes I$I, XZ$\otimes$XZ, X$I\otimes$X$I$}. 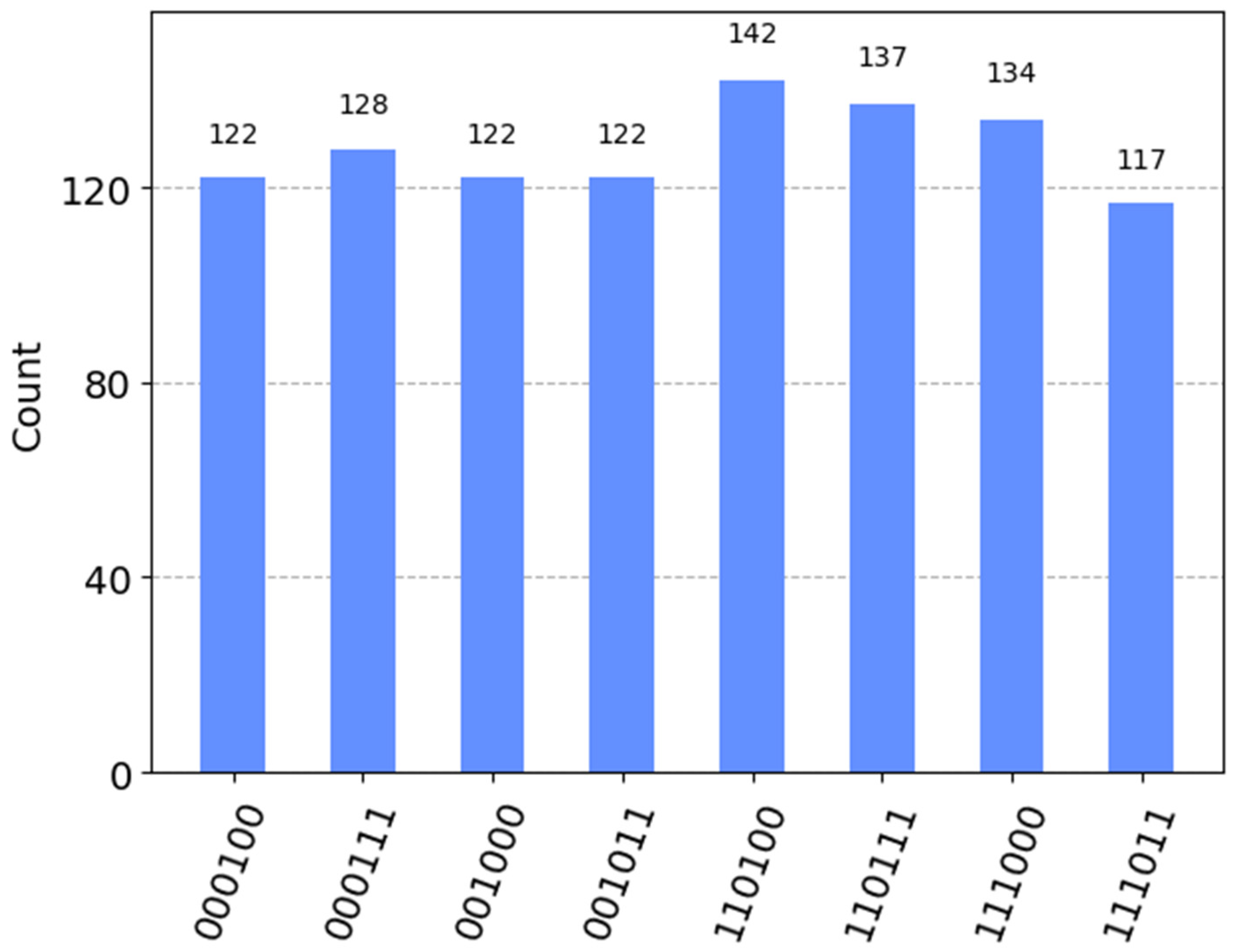The quantum circuit implementation for comparing the equality of the secret integers $X_1=63$ and $Y_1=63$ is shown in Figure 5, and the results of its probability measurements are presented in Figure 6.

According to the bar chart in Figure 6, the measurement results of the computational basis states are identical to those in Figure 2, although the counts of each computational basis state may differ due to the influence of noise and decoherence. This result indicates that the measurement results align with the initially prepared Bell states. Consequently, we can conclude that $X_1=Y_1$.

Although we utilize two example simulation experiments to demonstrate the feasibility of the proposed protocol, its scalability when comparing multiple bits remains unaffected. It has been reported that Zuchongzhi 3.0 [50], a superconducting quantum computer prototype comprising 105 qubits and achieving high operational fidelities, was constructed in 2025. As the number of available qubits increases, our protocol can further demonstrate its scalability on actual quantum hardware.

5. Security Analysis

In the execution of the protocol, the entanglement correlation between particles in Bell states is utilized to ensure the security of the particle distribution phase. The insertion of decoy photons into the particles, along with the implementation of quantum key distribution for sharing a pre-shared key, enhances security during the information transfer phase. In this section, we demonstrate that the proposed protocol is resilient against both external and participant attacks.

5.1. External Attacks

When quantum sequences are transmitted through a quantum channel, an external eavesdropper, often referred to as Eve, may employ quantum-attack strategies to compromise the private inputs. The primary quantum attack strategies include intercept-measure-resend [51], entangle-measure [52], man-in-the-middle [53], and quantum Trojan-Horse attacks [54]. We will analyze whether the proposed protocol is secure against these quantum attack strategies as follows.

5.1.1. Intercept-Measure-Resend Attack

In the proposed QPC protocol, the intercept-measure-resend attack refers to Eve intercepting the quantum sequences $G_A$ and $G_B$, measuring them with Z-basis or X-basis, and resending the modified sequences to the TP. Unfortunately, this attack faces significant challenges due to the lack of information regarding the inserted positions and measurement bases of the decoy photons. These specific details will be disclosed when the TP receives the sequences.

As an example, consider a decoy photon prepared in the state $\left|1\right.⟩$. When Eve measures this decoy photon using the Z basis ($\left|0\right.⟩,\left|1\right.⟩$), she successfully passes the eavesdropping detection. Conversely, when she measures the decoy photon using the X basis ($\left|+\right.⟩,\left|-\right.⟩$), she passes the eavesdropping detection with a probability of 50%, since $\left|0\right.⟩$ and $\left|1\right.⟩$ are equal superpositions of $\left|+\right.⟩$ and $\left|-\right.⟩$. The choice between the Z basis and the X basis occurs with equal probability, each having a 50% chance. Thus, the probability of choosing the X basis and passing the eavesdropping detection is ${\displaystyle \frac{1}{2}}\times 1+{\displaystyle \frac{1}{2}}\times {\displaystyle \frac{1}{2}}={\displaystyle \frac{3}{4}}$. 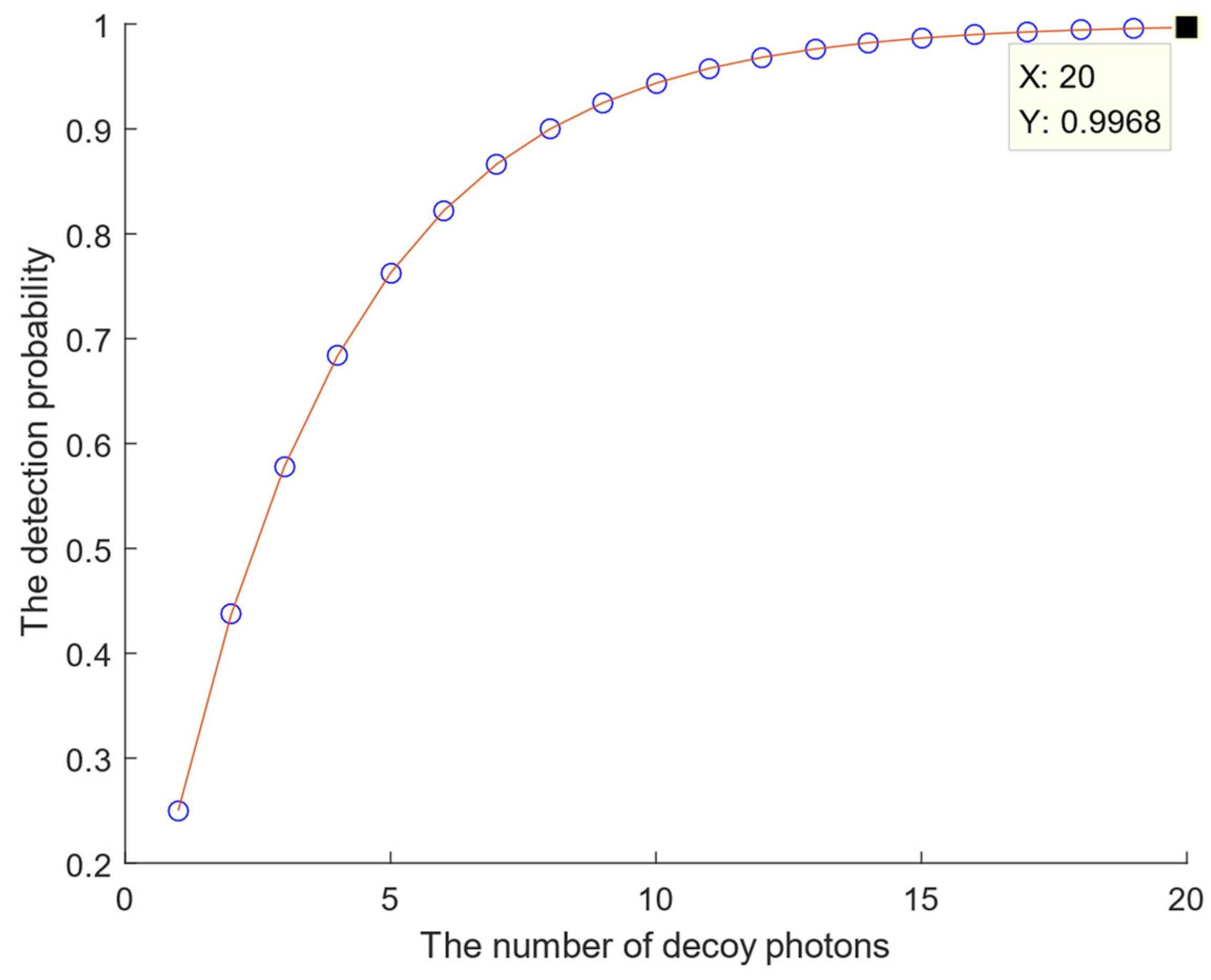Consequently, for each decoy photon, Eve has a 3/4 probability of successfully performing the intercept-measure-resend attack. However, for d decoy photons, the detection probability becomes $1-{\left({\displaystyle \frac{3}{4}}\right)}^d$. The relationship between the number of decoy photons and the detection probability is illustrated in Figure 7.

According to the results presented in Figure 7, when d = 20, the detection probability reaches 0.9968. However, as the number of decoy photons increases, the detection probability approaches 1. Consequently, Eve will not succeed in executing the intercept-measure-resend attack.

5.1.2. Entangle-Measure Attack

This attack involves Eve intercepting the quantum sequences $S_A^{\prime }$ and $S_B^{\prime }$, and entangling them with the prepared auxiliary state $\left|u_1\right.⟩$ through a specific unitary operation $U_1$ during the first quantum sequence transmission. During the second quantum sequence transmission, Eve intercepts the quantum sequences $G_A$ and $G_B$, and performs the specific unitary operation $U_2$ to entangle them with the prepared auxiliary state $\left|u_2\right.⟩$. Eve can then measure the prepared auxiliary states $\left|e_1\right.⟩$ and $\left|e_2\right.⟩$ to extract private information about the confidential inputs.

During the first quantum sequence transmission, performing $U_1$ on $\left|e_1\right.⟩$ and states $\left|0\right.⟩$ and $\left|1\right.⟩$ proceeds as follows:

$$U_1\left|0\right.〉\left|u_1\right.〉=\left|0\right.〉\left|u_{00}\right.〉+\left|1\right.〉\left|u_{01}\right.〉=\sqrt{A}\left|0\right.〉\left|{\widehat{u}}_{00}\right.〉+\sqrt{B}\left|1\right.〉\left|{\widehat{u}}_{01}\right.〉$$

(6)

$$U_1\left|1\right.〉\left|u_1\right.〉=\left|0\right.〉\left|u_{10}\right.〉+\left|1\right.〉\left|u_{11}\right.〉=\sqrt{B}\left|0\right.〉\left|{\widehat{u}}_{10}\right.〉+\sqrt{A}\left|1\right.〉\left|{\widehat{u}}_{11}\right.〉$$

(7)

$$\begin{array}{ll}{U}_1\left|+\right.〉\left|u_1\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|u_{00}\right.〉+\left|1\right.〉\left|u_{01}\right.〉+\left|0\right.〉\left|u_{10}\right.〉+\left|1\right.〉\left|u_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(\left|u_{00}\right.〉+\left|u_{01}\right.〉+\left|u_{10}\right.〉+\left|u_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(\left|u_{00}\right.〉-\left|u_{01}\right.〉+\left|u_{10}\right.〉-\left|u_{11}\right.〉\right)\\ & =\left|+\right.〉\left|u_{++}\right.〉+\left|-\right.〉\left|u_{+-}\right.〉\end{array}$$

(8)

$$\begin{array}{ll}{U}_1\left|-\right.〉\left|u_1\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|u_{00}\right.〉+\left|1\right.〉\left|u_{01}\right.〉+\left|0\right.〉\left|u_{10}\right.〉-\left|1\right.〉\left|u_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(\left|u_{00}\right.〉+\left|u_{01}\right.〉-\left|u_{10}\right.〉-\left|u_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(\left|u_{00}\right.〉-\left|u_{01}\right.〉-\left|u_{10}\right.〉+\left|u_{11}\right.〉\right)\\ & =\left|+\right.〉\left|u_{-+}\right.〉+\left|-\right.〉\left|u_{--}\right.〉\end{array}$$

(9)

The states $\left\{\left|u_{00}\right.⟩,\left|u_{01}\right.⟩,\left|u_{10}\right.⟩,\left|u_{11}\right.⟩\right\}$ are four pure states determined by unitary operation $U_1$ and satisfy the following conditions.

$$〈u_{00}|u_{00}〉=〈u_{01}|u_{01}〉=A+B=1$$

(10)

$$〈u_{10}|u_{10}〉=〈u_{11}|u_{11}〉=B+A=1$$

(11)

$$〈u_{00}|u_{10}〉=〈u_{01}|u_{11}〉=0$$

(12)

Without loss of generality, we can set

$$〈u_{00}|u_{01}〉=〈u_{10}|u_{11}〉=〈u_{00}|u_{10}〉=〈u_{01}|u_{11}〉=0$$

(13)

We specify the angles between nonorthogonal vectors as

$$〈{\widehat{u}}_{00}|{\widehat{u}}_{11}〉=\cos x,〈{\widehat{u}}_{01}|{\widehat{u}}_{10}〉=\cos y,0\le x,y\le {\displaystyle \frac{\pi }{2}}$$

(14)

Furthermore, the probability of Eve not being detected is given as

$$P\left(\left|0\right.〉\right)=〈u_{00}|u_{00}〉=P\left(\left|1\right.〉\right)=〈u_{11}|u_{11}〉=A$$

(15)

$$P\left(\left|+\right.〉\right)=P\left(\left|-\right.〉\right)={\displaystyle \frac{1}{2}}\left(1+A\cos x+B\cos y\right)$$

(16)

Therefore, the average detection probability during the first quantum sequence transmission is given by

$$P_d^1={\displaystyle \frac{A}{2}}+{\displaystyle \frac{\left(1-A\cos x-B\cos y\right)}{4}}$$

(17)

When $A=0,B=1$, $P_d^1$ comes to the minimum.

$$d_1=\min \left(P_d^1\right)={\displaystyle \frac{1}{4}}-{\displaystyle \frac{\cos x}{4}},0\le d_1\le {\displaystyle \frac{1}{4}}$$

(18)

During the second quantum sequence transmission, performing $U_2$ on $\left|e_2\right.⟩$ and states $\left|0\right.⟩$ and $\left|1\right.⟩$ proceeds as follows:

$$U_2\left|0\right.〉\left|u_2\right.〉=\left|0\right.〉\left|{u^{\prime }}_{00}\right.〉+\left|1\right.〉\left|{u^{\prime }}_{01}\right.〉=\sqrt{A^{\prime }}\left|0\right.〉\left|{{\widehat{u}}^{\prime }}_{00}\right.〉+\sqrt{B^{\prime }}\left|1\right.〉\left|{{\widehat{u}}^{\prime }}_{01}\right.〉$$

(19)

$$U_2\left|1\right.〉\left|u_2\right.〉=\left|0\right.〉\left|{u^{\prime }}_{10}\right.〉+\left|1\right.〉\left|{u^{\prime }}_{11}\right.〉=\sqrt{B^{\prime }}\left|0\right.〉\left|{{\widehat{u}}^{\prime }}_{10}\right.〉+\sqrt{A^{\prime }}\left|1\right.〉\left|{{\widehat{u}}^{\prime }}_{11}\right.〉$$

(20)

$$\begin{array}{ll}{U}_2\left|+\right.〉\left|u_2\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|{u^{\prime }}_{00}\right.〉+\left|1\right.〉\left|{u^{\prime }}_{01}\right.〉+\left|0\right.〉\left|{u^{\prime }}_{10}\right.〉+\left|1\right.〉\left|{u^{\prime }}_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(\left|{u^{\prime }}_{00}\right.〉+\left|{u^{\prime }}_{01}\right.〉+\left|{u^{\prime }}_{10}\right.〉+\left|{u^{\prime }}_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(\left|{u^{\prime }}_{00}\right.〉-\left|{u^{\prime }}_{01}\right.〉+\left|{u^{\prime }}_{10}\right.〉-\left|{u^{\prime }}_{11}\right.〉\right)\\ & =\left|+\right.〉\left|{u^{\prime }}_{++}\right.〉+\left|-\right.〉\left|{u^{\prime }}_{+-}\right.〉\end{array}$$

(21)

$$\begin{array}{ll}{U}_2\left|-\right.〉\left|u_2\right.〉& ={\displaystyle \frac{1}{\sqrt{2}}}\left(\left|0\right.〉\left|{u^{\prime }}_{00}\right.〉+\left|1\right.〉\left|{u^{\prime }}_{01}\right.〉+\left|0\right.〉\left|{u^{\prime }}_{10}\right.〉-\left|1\right.〉\left|{u^{\prime }}_{11}\right.〉\right)\\ & ={\displaystyle \frac{1}{2}}\left|+\right.〉\left(\left|{u^{\prime }}_{00}\right.〉+\left|{u^{\prime }}_{01}\right.〉-\left|{u^{\prime }}_{10}\right.〉-\left|{u^{\prime }}_{11}\right.〉\right)\\ & +{\displaystyle \frac{1}{2}}\left|-\right.〉\left(\left|{u^{\prime }}_{00}\right.〉-\left|{u^{\prime }}_{01}\right.〉-\left|{u^{\prime }}_{10}\right.〉+\left|{u^{\prime }}_{11}\right.〉\right)\\ & =\left|+\right.〉\left|{u^{\prime }}_{-+}\right.〉+\left|-\right.〉\left|{u^{\prime }}_{--}\right.〉\end{array}$$

(22)

The states $\left\{\left|{u\prime }_{00}\right.⟩,\left|{u\prime }_{01}\right.⟩,\left|{u\prime }_{10}\right.⟩,\left|{u\prime }_{11}\right.⟩\right\}$ are four pure states determined by unitary operation $U_2$ and satisfy the following conditions.

$$〈{u^{\prime }}_{00}|{u^{\prime }}_{00}〉=〈{u^{\prime }}_{01}|{u^{\prime }}_{01}〉=A^{\prime }+B^{\prime }=1$$

(23)

$$〈{u^{\prime }}_{10}|{u^{\prime }}_{10}〉=〈{u^{\prime }}_{11}|{u^{\prime }}_{11}〉=B^{\prime }+A^{\prime }=1$$

(24)

$$〈{u^{\prime }}_{00}|{u^{\prime }}_{10}〉=〈{u^{\prime }}_{01}|{u^{\prime }}_{11}〉=0$$

(25)

Without loss of generality, we can set

$$〈{u^{\prime }}_{00}|{u^{\prime }}_{01}〉=〈{u^{\prime }}_{10}|{u^{\prime }}_{11}〉=〈{u^{\prime }}_{00}|{u^{\prime }}_{10}〉=〈{u^{\prime }}_{01}|{u^{\prime }}_{11}〉=0$$

(26)

We specify the angles between nonorthogonal vectors as

$$〈{{\widehat{u}}^{\prime }}_{00}|{{\widehat{u}}^{\prime }}_{11}〉=\cos x^{\prime },〈{{\widehat{u}}^{\prime }}_{01}|{{\widehat{u}}^{\prime }}_{10}〉=\cos y^{\prime },0\le x^{\prime },y^{\prime }\le {\displaystyle \frac{\pi }{2}}$$

(27)

In the same way, the average detection probability during the second quantum sequence transmission is given by

$$d_2={\displaystyle \frac{1}{4}}-{\displaystyle \frac{\cos x^{\prime }}{4}},0\le d_2\le {\displaystyle \frac{1}{4}}$$

(28)

Reference [55] pointed out that the optimal incoherent attack by Eve consists of a balanced strategy, where $x=x^{\prime }$. Therefore, we have

$$d=d_1=d_2={\displaystyle \frac{1}{4}}-{\displaystyle \frac{\cos x}{4}},0\le d\le {\displaystyle \frac{1}{4}}$$

(29)

The mutual information between the participants and Eve is written as

$$I\left(A:E\right)=1-h\left({\displaystyle \frac{1+{\sin }^{2}x}{2}}\right)=1-h\left(1-{\displaystyle \frac{{\left(1-4d\right)}^2}{2}}\right)$$

(30)

where h denotes the Shannon binary entropy. From Equation (30), we can infer that $I\left(A:E\right)$ is a monotonic increasing function. The more information Eve seeks to obtain, the greater the detection probability she will induce. Therefore, Eve will not succeed in executing the entangle-measure attack.

5.1.3. Man-in-the-Middle Attack

This attack involves Eve intercepting the sequences containing the encoded private inputs and preparing fake sequences in place of the intercepted sequence. We take intercepting the sequence $G_A$ and preparing ${G\prime }_A$ as an example. The same method can be applied to analyze the interception of sequence $G_B$. For security validation, Eve prepares guessed states as decoy photons, denoting the i-th decoy photon as $D_i$, which corresponds to the j-th qubit in $G_A$. The j-th qubit of ${G\prime }_A$ is denoted as ${D\prime }_i$. Both $D_i$ and ${D\prime }_i$ are prepared using basis $B=\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ and $B^{\prime }=\left\{\left|+\right.⟩,\left|-\right.⟩\right\}$. When Alice discloses the measurement basis of $D_i$, Eve measures ${D\prime }_i$ using the basis B′ and obtains the results ${D″}_i$. The probability that ${D″}_i=D_i$ is as follows.

(1)

If $B^{\prime }=B$ and ${D\prime }_i=D_i$, the probability that ${D″}_i={D\prime }_i$ is 1.

(2)

If $B^{\prime }=B$ and ${D\prime }_i\ne D_i$, the probability that ${D″}_i=D_i$ is 0.

(3)

If $B^{\prime }\ne B$ and ${D\prime }_i=D_i$, the probability that ${D″}_i=D_i$ is 1/2.

The detection probability for a decoy photon is

$$\begin{array}{l}P\left(D_i^{″}=D_i\right)=P\left(D_i^{″}=D_i|B^{\prime }=B\right)P\left(B^{\prime }=B\right)+P\left(D_i^{″}=D_i|B^{\prime }\ne B\right)P\left(B^{\prime }\ne B\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{2}}\left(P\left(D_i^{″}=D_i|B^{\prime }=B\right)+P\left(\left(D_i^{″}=D_i|B^{\prime }\ne B\right)\right)\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{2}}\left(\begin{array}{l}P\left(D_i^{″}=D_i|B^{\prime }=B,D_i^{\prime }=D_i\right)P\left(D_i^{\prime }=D_i\right)+\\ P\left(D_i^{″}=D_i|B^{\prime }=B, D_i^{\prime }\ne D_i\right)P\left(D_i^{\prime }\ne D_i\right)+{\displaystyle \frac{1}{2}}\end{array}\right)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}={\displaystyle \frac{1}{2}}\left(1\times {\displaystyle \frac{1}{2}}+0\times {\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\right)={\displaystyle \frac{1}{2}}\end{array}$$

(31)

For d decoy photons, the detection probability becomes $1-{\left({\displaystyle \frac{1}{2}}\right)}^d$. When $d=10$, the detection probability reaches 0.999. However, as the number of decoy photons increases, the detection probability approaches 1. Consequently, Eve will not succeed in executing the man-in-the-middle attack.

5.1.4. Quantum Trojan-Horse Attacks

Quantum Trojan horse attacks are broadly classified into two categories: (1) invisible photon attacks [36], where an eavesdropper injects undetectable photons into the quantum channel to probe transmitted states, and (2) delayed photon attacks [38], where photons are strategically delayed to intercept or alter communication. These attacks represent critical vulnerabilities in bidirectional quantum communication systems. The round-trip transmission mechanism inherent to the proposed protocol is particularly susceptible to such threats. To counter these risks, the protocol integrates wavelength filters to eliminate extraneous photon wavelengths and photon-number splitters to detect anomalous photon counts, thereby neutralizing covert eavesdropping attempts.

5.2. Participant Attacks

Participants may maliciously attempt to deduce or alter each other’s private inputs, thereby compromising data confidentiality. A detailed security analysis of insider threats is provided below.

5.2.1. Security Against Attacks from Alice or Bob

In this protocol, Alice and Bob assume symmetrical roles. For generality, we analyze the scenario where Bob acts maliciously to deduce Alice’s secret. Alice encodes her secrets through quantum operations (Pauli-X and Pauli-Z gates) on sequence S_A. To reconstruct Alice’s secrets, Bob would require both S_A and the transformed sequence U_A. However, since no direct quantum channel exists between Alice and Bob, Bob’s only opportunity to obtain S_A and U_A lies in intercepting transmissions between the TP and Alice. Such interception falls under external eavesdropping, which the protocol neutralizes via the decoy-state method described in Steps 3 and 5. An analogous analysis applies if Alice attempts to compromise Bob’s secrets. Therefore, the protocol’s design inherently safeguards both parties’ secrets against collusion and insider attacks.

5.2.2. Security Against Attacks from TP

While the semi-honest TP might attempt to extract additional information by analyzing intermediate results or deviating from the protocol, its capabilities are limited by the protocol’s architectural constraints. The TP is solely responsible for the initial preparation and distribution of Bell states and subsequent Bell-basis measurements. Although the TP possesses knowledge of the initially prepared and post-transformation Bell states, it cannot reverse-engineer the participants’ secrets (X or Y) from these correlations. Even if the TP hypothetically substitutes Bell states with single photons and measures the returned particles, it lacks knowledge of the shared secret key K_AB, which is exclusively held by Alice and Bob. Without K_AB, the TP cannot resolve the encoded values X and Y. As a result, the protocol ensures that the TP gains no information about the participants’ secrets beyond the final comparison outcome.

6. Discussion

Qubit efficiency [29], a critical metric for evaluating quantum resource utilization, quantifies the ratio of classical bits securely compared to the total quantum resources consumed excluding those used for eavesdropping detection. Given that ${\eta }_c$ denotes the number of classical bits compared, ${\eta }_t$ denotes the qubits used for encoding private inputs, and ${\eta }_k$ denotes the bits allocated for pre-shared key, the qubit efficiency is defined as:

$${\eta }_e={\displaystyle \frac{{\eta }_c}{{\eta }_t+{\eta }_k}}$$

(32)

In our protocol, ⌈n/2⌉ Bell states (two-qubit systems) and an n-bit pre-shared key enable the comparison of n classical bits, yielding ${\eta }_c=n$, ${\eta }_t=n$, and ${\eta }_k=n$. This results in a qubit efficiency of 50%. A comparative analysis with existing protocols is detailed in

Table 2. A comparison with other Bell-state-based QPC protocols.

Protocol	Quantum Resource	Usage of Unitary Operation	Usage of Quantum Entanglement Swapping	Usage of Pre-Shared Key	Quantum Measurement	Privacy Disclosure	Bit Number Compared Each Round	Compare Rounds	Qubit Efficiency
Ref. [20]	Bell states	No	No	No	Single particle	Yes	1	n	50%
Ref. [22]	Bell states	Yes	No	No	$\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ basis	Yes	1	n	50%
Ref. [24]	Bell states	No	Yes	Yes	GHZ-basis	No	3	$⌈n/3⌉$	20%
Ref. [25]	Bell states	No	No	No	$\left\{\left|0\right.⟩,\left|1\right.⟩\right\}$ basis	No	1	n	16.67%
Ref. [26]	Bell states	Yes	No	Yes	Bell-basis	No	1	n	25%
Ref. [27]	Bell states	Yes	No	Yes	Bell-basis	No	1	n	25%
Ours	Bell states	Yes	No	Yes	Bell-basis	No	2	$⌈n/2⌉$	50%

.

Ref. [20] utilizes Bell states and XOR operations with single-particle measurements, achieving 50% efficiency. However, it is vulnerable to semi-honest TP attacks via fake Bell states. Ref. [22] employs Bell states and CNOT gates with Z-basis measurements, attaining 50% efficiency but is susceptible to outsider disturbance attacks and TP measuring attacks. Ref. [24] relies on entanglement swapping and GHZ-basis measurements, requiring three Bell states and nine pre-shared key bits to compare three classical bits, yielding 20% efficiency. Ref. [25] uses single Bell states $\left|{\phi }^{+}\right.⟩$ and XOR operations, achieving only 16.67% efficiency (three Bell states per compared bit). Refs. [26,27] incorporate rotation/unitary operations and Bell measurements, achieving 25% efficiency (one Bell state and one pre-shared key bit per compared bit).

Compared with existing Bell-state-based QPC protocols, our protocol offers the following improvements.

(1)

Our protocol employs Bell states, Pauli-X and Pauli-Z encoding, and Bell measurements without entanglement swapping [24], further enhancing its feasible implementation.

(2)

By leveraging a single Bell state and two pre-shared key bits to compare two classical bits, it achieves 50% qubit efficiency—double that of Refs. [26,27] and higher than Refs. [24,25].

(3)

Although the proposed protocol has equal qubit efficiency with Refs. [20,22], it provides security against the TP’s attack and external eavesdropping through decoy-state validation and the QKD-secured key, while the schemes in Refs. [20,22] are not secure and may result in privacy disclosure.

7. Conclusions

In this study, we propose an efficient quantum private comparison (QPC) protocol that harnesses the entanglement properties of Bell states to enable secure and privacy-preserving comparisons of confidential data. Participants encode their private inputs using Pauli-X and Pauli-Z operators on quantum sequences distributed by a semi-honest third party (TP). This design achieves 50% qubit efficiency—a significant improvement over existing Bell-state-based protocols—by utilizing a single Bell state and two pre-shared key bits to compare two classical bits. The protocol’s practicality is validated through experimental simulations on the IBM Quantum Qiskit simulator, confirming its operational feasibility in real-world quantum environments. A comprehensive security analysis demonstrates the protocol’s robustness against both external attacks and insider threats. By integrating Bell-state encoding, QKD-secured keys, and decoy-state validation, our protocol addresses vulnerabilities in prior works, such as susceptibility to fake Bell states and disturbance attacks. Compared to existing QPC schemes, our protocol offers superior efficiency and experimental viability, achieved through minimal quantum resource requirements and simplified operations (no entanglement swapping or GHZ-basis measurements). Future work will extend this framework to noisy intermediate-scale quantum (NISQ) environments, incorporating error mitigation techniques for real-world deployment. Additionally, we aim to design semi-quantum private comparison protocols to reduce reliance on quantum devices, further alleviating resource constraints in practical applications.