1. Introduction of and Rationale for Proposed Experiment
It is an experimental fact that there does not exist a ground triplet state of the natural
He atom. The
absence of the triplet state associated with the singlet ground state in the
He atom spectrum led Pauli to the discovery of the Pauli exclusion principle (PEP) [
1]. According to the PEP, no two electrons in a many-electron system can occupy the same quantum state. The PEP is a description of the
individual electron, with the quantum numbers specifying the occupation of
one-particle states. With the advent of the papers by Schrödinger [
2] the following year, Dirac [
3] and Heisenberg [
4], to account for the indistinguishability of electrons, postulated that the
many-interacting-electron wave function solutions to the Schrödinger equation must be antisymmetric in an interchange of the coordinates of any two electrons (including the spin coordinate)—the eponymous Pauli principle (PP). Orbital-based theories obeying the PEP confirm that such a ground triplet state for the
He atom cannot exist. There is also no analytical or numerical correlated wave function solution to the Schrödinger equation for this state.
In this paper, we present rigorous theoretical proof of the existence of a ground triplet state of a two-dimensional two-electron ‘artificial atom’ or semiconductor quantum dot [
5,
6,
7] in a magnetic field. We derive an exact analytical correlated wave function for this state. The quantum dot additionally possesses the property of being in the low-electron-density high-electron-correlation Wigner regime [
8,
9]. Based on our understanding of the natural
atom, one would expect that there exists
solely a ground singlet state for any two-electron system. However, that is theoretically not the case. We therefore propose the creation of a Wigner-regime two-electron quantum dot and, subsequently, a search for the spectral line of the ground triplet state. A more detailed rationale, experimental and theoretical, for the proposed experiment follows.
(A) As a result of the development of semiconductor technology, it has been possible to create ‘artificial atoms’ or quantum dots [
5,
6,
7] that possess properties similar to those of natural atoms. The motion of the electrons is confined to two dimensions within a quantum well in a thin layer of a semiconductor, such as GaAs sandwiched between two layers of another AlGaAs semiconductor. The motion can be further restricted by electric and magnetic fields. The charge of the electron is modified by the dielectric constant of the semiconductor, and its mass is the band effective mass. For GaAs, the dielectric constant
, and the band effective mass
, where
m is the free electron mass. But the most significant difference between artificial and natural atoms is that the binding potential of the electrons in the former is harmonic and not Coulombic. This has been confirmed both theoretically [
10] as well as by an experiment [
5,
6,
7]. As a consequence, the parameters of the ‘artificial atom’ differ from those of a natural atom, e.g., the size is about an order of magnitude greater. As the proposed experiment involves a quantum dot in the Wigner regime, we note that there exists work on the creation of magnetically induced Wigner crystals [
11,
12,
13,
14]. Hence, such a Wigner-regime two-electron quantum dot can be physically created. When this is achieved, we suggest employing the single-electron-capacitance spectroscopy method of Ashoori et al. [
5] for the experimental search for the ground triplet-state spectral line.
(B) The equation describing the quantum dot in a magnetic field is the Schrödinger–Pauli [
15] equation, for which the Hamiltonian explicitly accounts for the electron spin moment and its interaction with the external magnetic field. Therefore, in addition to the paramagnetic and diamagnetic components, there is a magnetization (spin) component to the current density. There has been considerable theoretical work [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30] on the two-electron quantum dot in a magnetic field for both ground and excited states, principally in the high-electron-density low-electron-correlation regime. The present work shows that there exists an exact analytical solution for a ground triplet state in the Wigner low-electron-density regime [
8,
9] characterized by an electron interaction energy much greater than the kinetic energy. Further, this expression is valid for an
arbitrary value of the magnetic field, weak or strong. Thus, the ground triplet state is
theoretically predicted by an
exact solution to the Schrödinger–Pauli equation. We note that in prior work [
31], we derived the analytical solution for the ground singlet state in the Wigner regime together with many of its properties, including the energy. This provides additional information for experimentalists. Hence, from a theoretical perspective, for the two-electron Wigner-regime quantum dot in a magnetic field, both a ground triplet and singlet state exist
simultaneously.
To put this work in context, there are two other relevant points of interest:
(a) The spin moments of any bound two-electron system can be polarized to create a triplet state by applying a high magnetic field. There has been earlier theoretical work [
6,
7,
32,
33,
34] on such spin polarization in the case of the two-electron quantum dot. In such work, the solutions of the interacting Schrödinger–Pauli equation are treated, for example, as finite configuration-interaction functions of single-particle orbitals or via perturbation theory. The energy is studied as a
function of the magnetic field. It is observed that there is a flip of the ground singlet state to a triplet state at a specific value of the magnetic field: spin polarization occurs due to a high magnetic field, known as the Zeeman effect. These calculations are numerical, and not exact in a rigorous mathematical sense. We refer the reader to the review articles [
6,
7] and other similar work for a summary of this.
The present work, however, is distinct in the following ways:
(i) The ground triplet state obtained in our work is an
exact, closed-form analytical and correlated wave function solution of the Schrödinger–Pauli equation;
(ii) we show that the
solution exists solely in the high-electron-correlation Wigner regime;
(iii) being an exact solution, it satisfies all requisite symmetry properties and electron coalescence constraints of a triplet-state wave function
exactly;
(iv) as noted above, in [
31], we derived an
analytical correlated wave function for the ground singlet state in the Wigner regime. It can be shown analytically that it is possible for both the ground triplet and singlet states to exist in the
same magnetic field. In fact it can be shown that the singlet state can exist for a magnetic field that is greater than that of the triplet state. This proves that the expression derived for the ground triplet state does not represent a high-magnetic-field spin-polarized state.
(b) Another two-electron system is the three-dimensional Hooke’s atom [
35,
36,
37], in which the electrons are also bound by a harmonic potential. In this case, there is no magnetic field present. For this system, we also derived an
exact closed-form analytical correlated wave function solution for the
ground triplet state of the corresponding Schrödinger equation. This solution also exists in the high-electron correlation Wigner regime. Thus,
there exists a ground triplet state for such an atom even in the absence of a magnetic field. We further note that it is also possible to derive [
38,
39], for Hooke’s atom, an exact analytical correlated wave function for the ground singlet state in the Wigner regime of this atom. The existence of such a ground triplet state of a 3D ‘artificial atom’ contrasts with that of the natural
He atom.
In
Section 2, we present the general analytical form of a Wigner regime ground state wave function solution to the two-dimensional Schrödinger–Pauli equation for a two-electron quantum dot in a magnetic field in which the two electrons have the
same spin moment. For a particular choice of solution, in
Section 3, we explain that this wave function satisfies all established and recently derived [
40] requisite symmetry properties and coalescence constraints of a ground triplet state. These properties are the following: the PP of antisymmetry; the Wave Function Identity; odd parity; odd parity about each point of electron–electron coalescence; the node electron–electron coalescence constraint [
41,
42,
43,
44]; and the zero-node structure. To prove the simultaneous existence of a Wigner-regime ground singlet state at the same value of the magnetic field, we provide in
Appendix A an example of such an exact analytical solution. In our concluding remarks of
Section 4, we discuss the significance to quantum mechanics of the probable experimental observation of the triplet-state spectral line.
2. Ground-State Triplet Wave Function of the Two-Electron Quantum Dot in a Magnetic Field: General Form
In this section, we present the expression derived by us of the general form of the
exact solution to the
ground state of a two-electron quantum dot in a magnetic field in a
triplet state. (For the procedure for obtaining a general solution to the corresponding Schrödinger–Pauli equation, we refer the reader to [
16,
17,
18,
19].) Consider a two-electron semiconductor (of dielectric constant
) quantum dot in a magnetic field (
, with
representing the vector potential). The electrons, of charge
and spin angular momentum vector
, are bound by a harmonic field
such that
, where the scalar potential
, with (
) representing the harmonic binding force constant and frequency, and
the band effective mass. The corresponding Schrödinger–Pauli equation is
where
represents the canonical momentum operator, and the effective (starred) properties are as follows:
is the gyromagnetic ratio,
is the Bohr magneton, and
is the screened charge. There exist
exact closed-form analytical solutions to this differential equation for an infinite set of values of an effective force constant. Because the solutions are exact, they inherently account for the electron correlations due to both the Pauli principle and Coulomb repulsion. The solutions to the equation are of the form
with
representing the correlated spatial and
the spin components, and
and
being the spatial and spin coordinates. The reason for the existence of such correlated analytical solutions is that the Schrödinger–Pauli differential equation is separable into a center of mass and a relative coordinate component. The center-of-mass differential equation is the harmonic oscillator equation. The differential equation for the relative coordinate, which explicitly accounts for the Coulomb electron–electron interaction, can be solved in closed analytical form.
We consider the two electrons to have the
same spin moment. In the symmetric gauge
with
, there exist an
infinite number of closed-form analytical solutions of the Schrödinger–Pauli equation with
zero and a
finite number of nodes [
16,
17]. The number of nodes is associated with the solution to the relative coordinate differential equation. The angular momentum quantum number,
, … Each solution corresponds to a number
p of terms in a polynomial. For each value of
and
terms, there are at least two solutions with different numbers of nodes, different values of an effective force constant
, and different energies. The higher the value of
p, the more solutions are obtained. For example, for
and
terms, there are five solutions with a variety numbers of nodes,
values, and energies. In the present work, we are concerned
solely with the
zero-node solutions to the relative coordinate differential equation, which, for each value of
m, lead to the lowest value of
and to the lowest value of the energy corresponding to a ground state. Thus, for these exact correlated solutions, a state is defined by the number of nodes
n, the angular momentum quantum number
m, and the value
p of terms in a polynomial involving the relative coordinate.
In effective atomic units
, the general form of the spatial component function
of the zero-node solutions are of the analytical form
where the subscript
n corresponds to the number of nodes of the solution to the relative coordinate differential equation, which, in this case, is zero;
N is the normalization constant;
is the angular momentum quantum number;
is the angle of the relative coordinate vector
;
;
is the
lowest value of the effective force constant, with
representing the Larmor frequency;
is a finite polynomial, with
p representing the number of terms; and
represents the coefficients. Such solutions exist for all
. For the component of the wave function which arises from the center-of-mass differential equation, we employ the solution corresponding to the ground state of the harmonic oscillator. Finally, the corresponding spin functions
are always such that
, i.e., the spin moments of the electrons are the same. The corresponding solutions to Equation (
1) for zero nodes are designated as
. The Pauli principle
antisymmetry of the solutions
is due to the phase factor
, and this is explained below.
3. Particular Wigner-Regime Ground-State Triplet Wave Function
In this section, we consider a particular ground-state triplet wave function of the form of Equations (2)–(4), and note its well-behavedness and exact satisfaction of all requisite ground triplet-state properties. Such an analysis confirms that the expression derived does in fact correspond to a ground triplet-state wave function. The specific solution considered is characterized by the finite polynomial , where ; the angular momentum quantum number , which corresponds to electrons of the same spin moment; , for which the normalization constant ; the coefficients ; ; ; and the phase factor is .
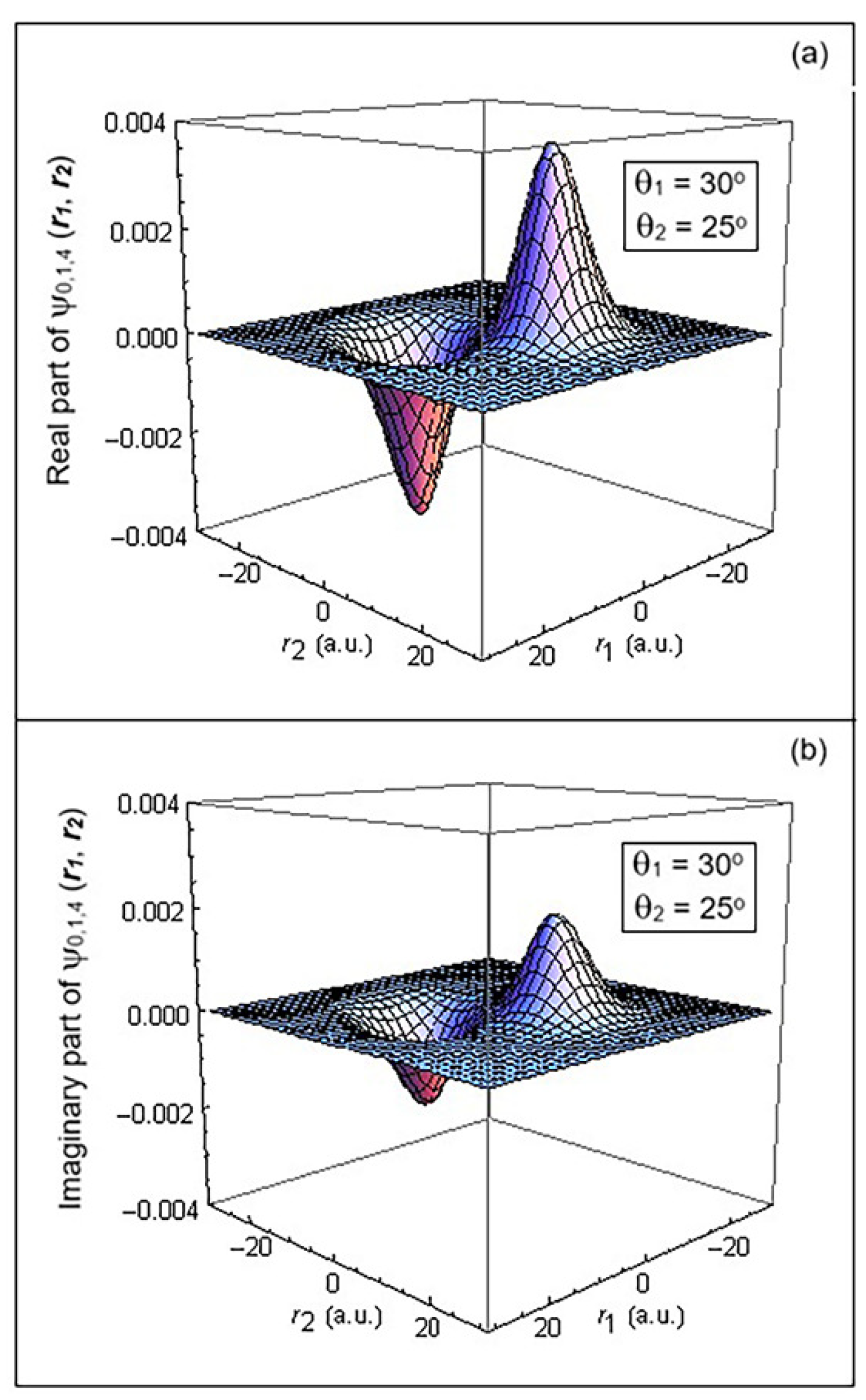
(i) Figure 1 is a plot of the Real and Imaginary parts of
as a function of the electron coordinates
and
. It is evident that the function
is single-valued, smooth, and bounded (the function
is also plotted for the negative values
to demonstrate its parity (see
(iv) below)).
(ii) The function satisfies the Pauli principle (PP): . Since , the spin component is symmetric in an interchange of the coordinates . The spatial component is antisymmetric in an interchange of , i.e., . This is due to the phase factor . The magnitude of the relative vector does not change, so the polynomial remains unchanged, but its angle (angle of vector that points from the tip of to the tip of changes to when the electrons interchange their positions, thus changing the sign of the phase factor.
(iii) The function
satisfies the Wave Function Identity:
. This symmetry operation involves an interchange of the spatial coordinates of the electrons whilst keeping their spin moments unchanged, followed by an inversion. When
is changed to
, and
is changed to
, the center-of-mass coordinate
becomes
, but its magnitude is unchanged, as is the magnitude of the relative coordinate
. It is
that contributes to the function
(note that
in the exponent in Equation (
3) is equivalent to
). (In [
16,
40], the discovery of a new symmetry property of two-electron systems referred to as the
Wave Function Identity is described. This property then leads to the understanding that the
parity of all singlet states is even, and that of all triplet states is odd. This identity also shows that the parity of singlet states
about each point of electron–electron coalescence is even, and that of triplet states is odd).
(iv) The
parity of the function
is odd for electrons of parallel spin, as must be the case, i.e.,
(this follows from the Wave Function Identity). This may also be seen from the phase factor
. When
are inverted to
, the magnitude of the relative vector
remains unchanged so that the polynomial
is unchanged, but the relative vector angle
changes to
, thus changing the sign of the function
(See
Figure 1).
(v) The function
satisfies the node electron–electron coalescence condition. The integral form of the electron–electron and electron–nucleus coalescence constraints in dimensions
is derived in [
16,
41,
42,
43,
44]. For
, the electron–electron coalescence constraint is
where
is an unknown vector. As the spins of the electrons are the same, the probability of two electrons being at the same physical position is zero, and thus, in Equation (
5),
, and the spatial component function
vanishes.
(vi) The parity of about each point of electron–electron coalescence is odd because this is a triplet state.
(vii) The function is square integrable, as all properties of the system are determinable.
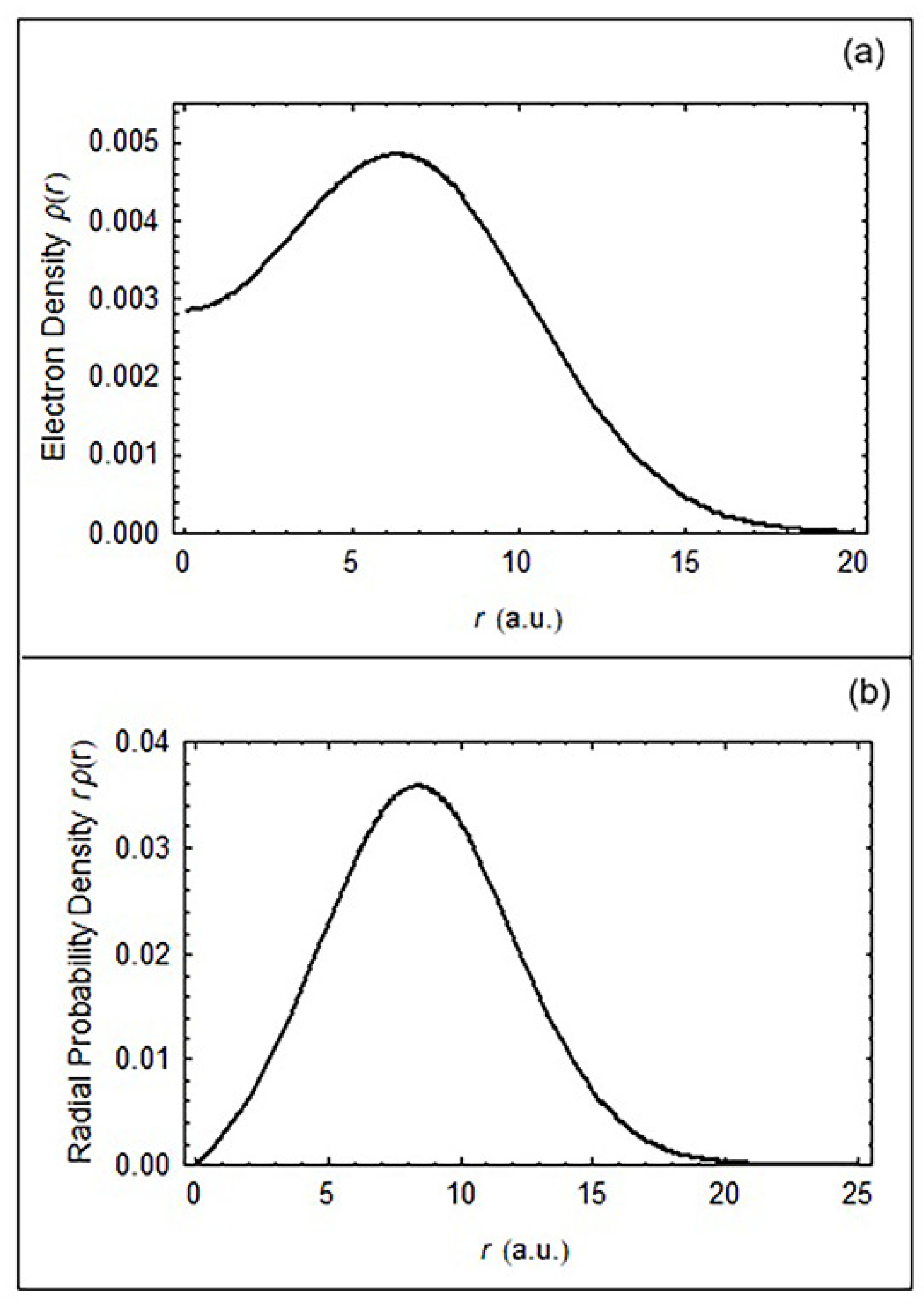
In
Figure 2a, we plot the density
, where
.
Figure 2b is a plot of the radial probability density
.
Figure 3a is a plot of the physical current density
, where the operator
is a sum of its paramagnetic
, diamagnetic
, and magnetization
components, where
,
,
, where the magnetization density operator
. The flow line contours of the current density
are plotted in
Figure 3b. The white regions in the contour plots indicate the low- and high-current-density zones.
The canonical kinetic energy ; the electron interaction energy ; the electromagnetic energy ; the total energy .
(viii) Observe that both the radial probability density in
Figure 2b and the physical current density in
Figure 3a, representing the ground triplet state of interest, exhibit a
single shell, as they must.
(ix) The function
corresponds to the Wigner low-electron-density high-electron-correlation regime. This is evident from the structure of the density
in
Figure 2a, typical of this regime: there is a local minimum at the origin, and the maximum occurs well away from it. That the function
corresponds to this regime is further confirmed by the ratio
, a key characteristic of the Wigner system.
(x) Here are a few general remarks with regard to the nodal structure of the exact correlated solutions of the Schrödinger–Pauli equation for the two-electron quantum dot in a magnetic field. The nodal structure of the wave function solutions is governed by the solutions to the relative coordinate differential equation. The state of the system is defined by these nodes. As expected, the ground triplet state has zero nodes.
The phase factor provides a finite value (0) for the total wave function at any position, because when the Real part of the wave function vanishes, the Imaginary part is finite, and vice versa. For example, the Real part of the wave function is zero when the projections of the vectors and on the x-axis are the same. The total wave function is then Imaginary (finite). On the other hand, the Imaginary part of the wave function is zero when the projection of the vectors and on the y-axis are the same. The total wave function is then Real (finite). Thus, there are no nodes in the triplet ground-state wave function due to the phase factor.
The only positions at which the total wave function vanishes (other than at infinity) are when the radial and angular coordinates of the individual electrons are the same, i.e., when both the projections on the x-axis are the same and the projections on the y-axis are the same. This corresponds to the case of electron–electron coalescence discussed in (v) above. The ground triplet-state wave function satisfies the node electron–electron coalescence constraint. Thus, there are an infinite number of such coalescence nodes. These nodes differ from the nodes representing the state of the system (this indicates whether the state is ground or excited) which exist in the solutions of the relative coordinate differential equation.