Hexic-Chebyshev Collocation Method for Solving Distributed-Order Time-Space Fractional Diffusion Equations
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Calculus
2.2. Hexic-Kind Chebyshev Polynomials
3. Hexic Chebyshev Collocation for Distributed-Order Fractional Diffusion
4. Convergence Analysis
- □
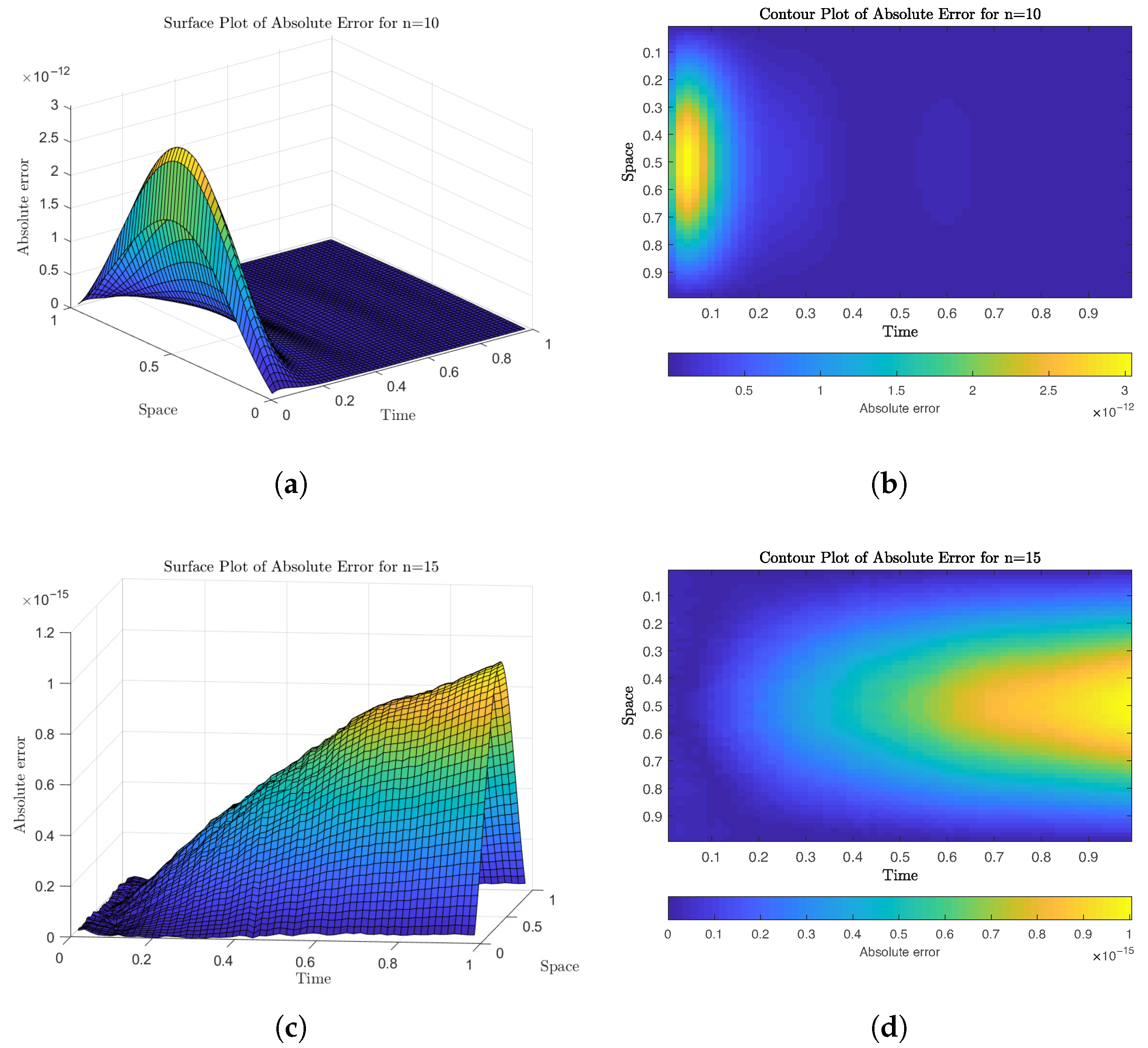
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Metzler, R.; Krafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamic approach. Phys. Rep. 2000, 339, 1–72. [Google Scholar] [CrossRef]
- Mathieu, B.; Melchior, P.; Oustaloup, A.; Ceyral, C. Fractional differentiation for edge detection. Signal Process. 2003, 83, 2421–2432. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; World Scientific: Singapore, 2017. [Google Scholar]
- Ionescu, C.; Lopes, A. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Amin, A.; Lopes, A.M. Fractional-order shifted Legendre collocation method for solving non-linear variable-order fractional Fredholm integro-differential equations. Comput. Appl. Math. 2022, 41, 2. [Google Scholar]
- Owolabi, K.; Atangana, A. Numerical approximation of nonlinear fractional parabolic differential equations with Caputo–Fabrizio derivative in Riemann-Liouville sense. Chaos Soliton. Fract. 2017, 99, 171–179. [Google Scholar] [CrossRef]
- Babaei, A.; Banihashemi, S. A stable numerical approach to solve a time-fractional inverse heat conduction problem. Iran. J. Sci. Technol. Trans. A. 2017, 42, 2225–2236. [Google Scholar] [CrossRef]
- Babaei, A.; Banihashemi, S. Reconstructing unknown nonlinear boundary conditions in a time-fractional inverse reaction-diffusion-convection problem. Numer. Methods Part. Differ. Equ. 2018, 35, 976–992. [Google Scholar] [CrossRef]
- Babaei, A.; Jafari, H.; Banihashemi, S. A collocation approach for solving time-fractional stochastic heat equation driven by an additive noise. Symmetry 2020, 12, 904. [Google Scholar] [CrossRef]
- El-Ajou, A.; Moa’ath, N.; Al-Zhour, Z.; Momani, S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique. Fract. Calc. Appl. Anal. 2020, 23, 356–377. [Google Scholar] [CrossRef]
- Bologna, M.; Tsallis, C.; Grigolini, P. Anomalous diffusion associated with nonlinear fractional derivative Fokker-Planck-like equation: Exact time-dependent solutions. Phys. Rev. E 2000, 62, 2213. [Google Scholar] [CrossRef]
- Pramukkul, P.; Svenkeson, A.; Grigolini, P.; Bologna, M.; West, B. Complexity and the fractional calculus. Adv. Math. Phys. 2013, 2013, 498789. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Zaky, M.A.; Lopes, A.M.; Galhano, A. A Fractional Time-Space Stochastic Advection-Diffusion Equation for Modeling Atmospheric Moisture Transport at Ocean-Atmosphere Interfaces. Fractal Fract. 2025, 9, 211. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Tavares, D.; Almeida, R.; Torres, D.F.M. Caputo derivatives of fractional variable order: Numerical approximations. Commun. Nonlinear Sci. Numer. Simul. 2016, 35, 69–87. [Google Scholar] [CrossRef]
- Sweilam, N.; AL-Mekhlafi, S.; Shatta, S.; Baleanu, D. Numerical Study for a Novel Variable-Order Multiple Time Delay Awareness Programs Mathematical Model. Appl. Numer. Math. 2020, 158, 212–235. [Google Scholar] [CrossRef]
- Babaei, A.; Jafari, H.; Banihashemi, S. Numerical solution of variable order fractional nonlinear quadratic integro-differential equations based on the sixth-kind Chebyshev collocation method. J. Comput. Appl. Math. 2020, 377, 112908. [Google Scholar] [CrossRef]
- Moniri, Z.; Babaei, A.; Moghaddam, B.P. Robust numerical framework for simulating 2D fractional time-space stochastic diffusion equation driven by spatio-temporal noise: L1-FFT hybrid approach. Commun. Nonlinear Sci. Numer. Simul. 2025, 146, 108791. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Machado, J.A.T. Application of variable-order fractional calculus in solid mechanics. Appl. Eng. Life Soc. Sci. Part A 2019, 7, 207–224. [Google Scholar]
- Moghaddam, B.P.; Babaei, A.; Dabiri, A.; Galhano, A. Fractional Stochastic Partial Differential Equations: Numerical Advances and Practical Applications—A State of the Art Review. Symmetry 2024, 16, 563. [Google Scholar] [CrossRef]
- Machado, J.T. Optimal variable-order fractional PID controllers for dynamical systems. J. Comput. Appl. Math. 2018, 339, 40–48. [Google Scholar]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of distributed-order fractional operators: A review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.J.; Machado, J.A.T.; Srivastava, H.M. A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput. 2016, 274, 143–151. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Chen, Y. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat. Mech. Its Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Obembe, A.D.; Hossain, M.E.; Abu-Khamsin, S.A. Variable-order derivative time fractional diffusion model for heterogeneous porous media. J. Pet. Sci. Eng. 2017, 152, 391–405. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Caputo, M. Distributed order differential equations modelling dielectric induction and diffusion. Fract. Calc. Appl. Anal. 2001, 4, 421–442. [Google Scholar]
- Caputo, M. Diffusion with space memory modelled with distributed order space fractional differential equations. Ann. Geophys. 2003, 46. [Google Scholar] [CrossRef]
- Chechkin, A.; Gorenflo, R.; Sokolov, I.M. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef]
- Duan, J.; Baleanu, D. Steady periodic response for a vibration system with distributed order derivatives to periodic excitation. J. Vib. Control. 2018, 24, 3124–3131. [Google Scholar] [CrossRef]
- Srokowski, T. Levy flights in nonhomogeneous media: Distributed-order fractional equation approach. Phys. Rev. E 2008, 78, 031135. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Pilipovic, S.; Zorica, D. Time distributed-order diffusion-wave equation. I. Volterra-type equation. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2009, 465, 1869–1891. [Google Scholar] [CrossRef]
- Solís-Pérez, J.; Gómez-Aguilar, J.; Atangana, A. Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 2018, 114, 175–185. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Numerical solution methods for distributed order differential equations. Fract. Calc. Appl. Anal. 2001, 4, 531–542. [Google Scholar]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Appl. Math. Comput. 2007, 187, 295–305. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Numerical analysis for distributed-order differential equations. J. Comput. Appl. Math. 2009, 225, 96–104. [Google Scholar] [CrossRef]
- Luchko, Y. Boundary value problems for the generalized time-fractional diffusion equation of distributed order. Fract. Calc. Appl. Anal. 2009, 12, 409–422. [Google Scholar]
- Gorenflo, R.; Luchko, Y.; Stojanovic, M. Fundamental solution of a distributed order time-fractional diffusion-wave equation as probability density. Fract. Calc. Appl. Anal. 2013, 16, 297–316. [Google Scholar] [CrossRef]
- Duong, P.L.T.; Kwok, E.; Lee, M. Deterministic analysis of distributed order systems using operational matrix. Appl. Math. Model. 2016, 40, 1929–1940. [Google Scholar] [CrossRef]
- Naber, M. Distributed order fractional sub-diffusion. Fractals 2004, 12, 23–32. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, Y.; Rahimkhani, P. Application of generalized Lucas wavelet method for solving nonlinear fractal-fractional optimal control problems. Chaos Solitons Fractals 2023, 170, 113348. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zayernouri, M.; Karniadakis, G.E. Petrov–Galerkin and spectral collocation methods for distributed order differential equations. SIAM J. Sci. Comput. 2017, 39, 1003–1037. [Google Scholar] [CrossRef]
- Zaky, M.A. A Legendre collocation method for distributed-order fractional optimal control problems. Nonlinear Dyn. 2018, 91, 2667–2681. [Google Scholar] [CrossRef]
- Li, X.; Rui, H. A block-centered finite difference method for the distributed-order time-fractional diffusion-wave equation. Appl. Numer. Math. 2018, 131, 123–139. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Lima, P.M. An improved composite collocation method for distributed-order fractional differential equations based on fractional Chelyshkov wavelets. Appl. Numer. Math. 2019, 145, 1–27. [Google Scholar] [CrossRef]
- Pourbabaee, M.; Saadatmandi, A. A novel Legendre operational matrix for distributed order fractional differential equations. Appl. Math. Comput. 2019, 361, 215–231. [Google Scholar] [CrossRef]
- Arianfar, M.; Moghaddam, B.P.; Babaei, A. Computational technique for a class of nonlinear distributed-order fractional boundary value problems with singular coefficients. Comput. Appl. Math. 2021, 40, 190. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Tenreiro Machado, J.A.; Morgado, M.L. Numerical approach for a class of distributed order time fractional partial differential equations. Appl. Numer. Math. 2019, 136, 152–162. [Google Scholar] [CrossRef]
- Bu, W.; Ji, L.; Tang, Y.; Zhou, J. Space-time finite element method for the distributed-order time fractional reaction diffusion equations. Appl. Numer. Math. 2020, 152, 446–465. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. A POD-based reduced-order Crank-Nicolson/fourth-order alternating direction implicit (ADI) finite difference scheme for solving the two-dimensional distributed-order Riesz space-fractional diffusion equation. Appl. Numer. Math. 2020, 158, 271–291. [Google Scholar] [CrossRef]
- Kazmi, K.; Khaliq, A.Q. An efficient split-step method for distributed-order space-fractional reaction-diffusion equations with time-dependent boundary conditions. Appl. Numer. Math. 2020, 147, 142–160. [Google Scholar] [CrossRef]
- A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 2011, 62, 2364–2373. [CrossRef]
- Dabiri, A.; Butcher, E.A.; Nazari, M. Coefficient of restitution in fractional viscoelastic compliant impacts using fractional Chebyshev collocation. J. Sound Vib. 2017, 388, 230–244. [Google Scholar] [CrossRef]
- Khader, M.; Saad, K. A numerical approach for solving the fractional Fisher equation using Chebyshev spectral collocation method. Chaos Solitons Fractals 2018, 110, 169–177. [Google Scholar] [CrossRef]
- Srivastava, H.; Saad, K.M.; Khader, M. An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 2020, 140, 110174. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Efficient modified Chebyshev differentiation matrices for fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 284–310. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Stable fractional Chebyshev differentiation matrix for the numerical solution of multi-order fractional differential equations. Nonlinear Dyn. 2017, 90, 185–201. [Google Scholar] [CrossRef]
- Ezz-Eldien, S. Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35, 5662–5672. [Google Scholar]
- Babaei, A.; Banihashemi, S.; Parsa Moghaddam, B.; Dabiri, A. An algorithmic exploration of variable order fractional partial integro-differential equations via hexic shifted Chebyshev polynomials. Comput. Appl. Math. 2024, 43, 1–18. [Google Scholar] [CrossRef]
- Masjed-Jamei, M. A basic class of symmetric orthogonal polynomials using the extended Sturm–Liouville theorem for symmetric functions. J. Math. Anal. Appl. 2007, 325, 753–775. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Youssri, Y.H. Sixth-kind Chebyshev spectral approach for solving fractional differential equations. J. Nonlinear Sci. Numer. Simul. 2019, 20, 191–203. [Google Scholar] [CrossRef]
- Kahaner, D.; Moler, C.; Nash, S. Numerical Methods and Software; Prentice-Hall Series in Computational Mathematics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Jian, H.Y.; Huang, T.Z.; Zhao, X.L.; Zhao, Y.L. A fast implicit difference scheme for a new class of time distributed-order and space fractional diffusion equations with variable coefficients. Adv. Differ. Equ. 2018, 2018, 205. [Google Scholar] [CrossRef]
- Hu, X.; Liu, F.; Turner, I.; Anh, V. An implicit numerical method of a new time distributed-order and two-sided space-fractional advection-dispersion equation. Numer. Algorithms 2016, 72, 393–407. [Google Scholar] [CrossRef]



| FID Method [64] with | Proposed method with | |||||
| N | n | CPU-time | ||||
| 5 | − | 6 | − | |||
| 10 | 9 | |||||
| 20 | 12 | |||||
| 40 | 15 | |||||
| FID Method [64] with | Proposed method with | |||||
| N | n | CPU-time | ||||
| 5 | − | 6 | − | |||
| 10 | 9 | |||||
| 20 | 12 | |||||
| 40 | 15 | |||||
| n | CPU-time | CPU-time | ||||
| 3 | − | − | ||||
| 6 | ||||||
| 9 | ||||||
| 12 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babaei, A.; Banihashemi, S.; Moghaddam, B.P.; Dabiri, A. Hexic-Chebyshev Collocation Method for Solving Distributed-Order Time-Space Fractional Diffusion Equations. Axioms 2025, 14, 515. https://doi.org/10.3390/axioms14070515
Babaei A, Banihashemi S, Moghaddam BP, Dabiri A. Hexic-Chebyshev Collocation Method for Solving Distributed-Order Time-Space Fractional Diffusion Equations. Axioms. 2025; 14(7):515. https://doi.org/10.3390/axioms14070515
Chicago/Turabian StyleBabaei, Afshin, Sedigheh Banihashemi, Behrouz Parsa Moghaddam, and Arman Dabiri. 2025. "Hexic-Chebyshev Collocation Method for Solving Distributed-Order Time-Space Fractional Diffusion Equations" Axioms 14, no. 7: 515. https://doi.org/10.3390/axioms14070515
APA StyleBabaei, A., Banihashemi, S., Moghaddam, B. P., & Dabiri, A. (2025). Hexic-Chebyshev Collocation Method for Solving Distributed-Order Time-Space Fractional Diffusion Equations. Axioms, 14(7), 515. https://doi.org/10.3390/axioms14070515










