1. Introduction
In the field of automatic control, the adoption of appropriate control strategies not only improves system safety and reliability but also enhances production efficiency. Unlike conventional tracking control methods that only utilize the current and past values of the reference signal in the design of controller, preview tracking control is an approach that not only considers these values, but also fully incorporates the available future values of the reference signal into the design of controller to enhance system tracking accuracy and performance [
1]. In the past 60 years, numerous scholars have conducted research on preview tracking control, achieving substantial progress in both theoretical development and engineering applications. In theoretical aspects, novel preview tracking control theories have been developed through integration with various types of control systems. For example, reference [
2] proposes an LMI-based reliable preview tracking control design method for a class of discrete-time Lipschitz nonlinear systems with actuator failures. Reference [
3] investigates the preview tracking control problem for a class of continuous-time interconnected systems with uncertainties. In [
4], the design of preview tracking controllers is proposed for linear stochastic systems subject to multiplicative noise. Moreover, by combining preview tracking control with other control methodologies, novel preview tracking control approaches have been derived. For example, reference [
5] proposes a preview repetitive control scheme by integrating preview tracking control with repetitive control for continuous linear systems subject to equivalent input disturbances. Reference [
6] proposes fault-tolerant preview control through the integration of preview and fault-tolerant techniques for discrete-time linear systems. Reference [
7] explores preview-saturation control for a class of uncertain periodic discrete-time systems with input saturation by integrating preview control with saturation control techniques. In practical applications, the exploration of suitable implementation fields for preview tracking control has been ongoing since its theoretical inception [
8]. Early applications included X-Y planar workstations [
9] and robotic arm control [
10]. As the theory developed, its applications expanded to diverse engineering domains such as automotive suspension devices [
11,
12], wind turbine systems [
13,
14], and self-driving vehicle technologies [
15,
16,
17]. However, its potential in nuclear reactors remains underexplored despite recent technological advancements.
The nuclear reactor, also termed atomic reactor, is a facility designed to harness nuclear energy through controlled chain fission reactions and enable its effective utilization [
18]. Its primary advantages lie in delivering substantial, low-cost energy. For nuclear reactors, maintaining safe and stable operation is crucial to ensuring energy supply security, safeguarding environmental safety, and protecting public health [
19]. The pressurizer, a critical safety component in nuclear reactors, maintains stable internal pressure under operational conditions. The pressurizer control system effectively regulates the reaction rate, prevents reactor overheating or power excursions, and maintains the pressurizer’s water level and pressure at predetermined setpoints [
20,
21]. Researchers have conducted extensive studies on pressurizer control mechanisms. Reference [
22] proposes an intelligent fuzzy neural network PID-based control for pressurizer pressure regulation, demonstrating enhanced disturbance rejection and transient suppression compared with traditional PID methods. Reference [
23] applies an Active Disturbance Rejection Control for pressurizer water-level dynamics, achieving lower overshoot and stronger robustness in simulation. Furthermore, optimal tracking control methods have been applied to discrete-time nonlinear nuclear systems, showing improved tracking accuracy in load-following regimes in [
24]. Reference [
25] developed a nonlinear MPC strategy to track power level changes in nuclear reactors under constraints, improving both steady-state accuracy and transient response. Reference [
26] proposes a fuzzy logic-based controller for an advanced pressurizer. This controller employs integrated level sensing and valve actuation to maintain optimal pressurizer volume, thereby providing adequate margin for the primary coolant’s expansion and contraction dynamics. A fuzzy PI controller for power rod position control of nuclear reactors was proposed in [
27]. Under this controller, the optimal pressure in the reactor can be maintained at 100% or deviate from this pressure level only for a short period of time. Based on [
27], reference [
28] verifies that the fuzzy control methods applied to the voltage regulator system of nuclear power plants show robustness and can tolerate different types of faults, such as sensor, equipment, and actuator failures.
It is worth noting that the above studies mainly focus on traditional PID, fuzzy control, or ADRC-based strategies, all of which fail to fully utilize the future information of reference signals, and there is still a lack of systematic research on applying preview control to pressure and water level regulation in nuclear systems. Preview tracking control has proven benefits in other safety-critical systems by enabling anticipatory action that reduces overshoot, improves settling time, and enhances robustness. Motivated by the above analysis, this paper aims to study the application of preview tracking control in nuclear reactor control. According to references [
27,
28], the simplified mathematical model of the pressurizer control system is
where
is the pressure of the regulator;
represents the speed of the control rod movement;
indicates the pressure of the regulator when the control rod is fully inserted into the reactor;
is the reverse pressure on the regulator generated when the reactor is discharged;
indicates the pressure lost by the regulator due to the external environment. From the point of view of control theory,
,
, and
represent the external disturbances. Since the control input
appears in the integrand, Equation (1) is a continuous-time integral equation. For practical implementation, the system and signals need to be processed and analyzed in discrete form. A zero-order hold can be used to discretize Equation (1). Let the sampling interval be
, and set
and
, which leads to
namely,
By defining the system output
as the pressure
of the regulator, the corresponding discretized system of (1) is derived as
The structure of Equation (2) clearly indicates that it falls into the category of discrete-time systems with state delays. In this paper, we first investigate the general form of such systems, design a preview tracking controller accordingly, and subsequently apply the obtained results to (2).
Notations: and denote the sets of -dimensional real vector and real matrix, respectively; () means that the matrix is positive definite (positive semi-definite); () shows that the matrix is negative definite (negative semi-definite); denotes the space of square-summable sequences. The vectors mean , where denotes the Euclidean norm.
2. Problem Description
Consider the general form of the control system (2):
where
,
and
represent the state vector, input vector, and output vector of the system, respectively;
is the positive integer that represents the state delay of the system;
,
,
, and
are all constant matrices;
is the external disturbance vector. The initial conditional function of the system is
,
.
Remark 1. Equation (3) originates from the simplified mathematical model of the voltage regulator system (Equation (1)). Discretizing Equation (1) yields Equation (2), and Equation (3) generalizes Equation (2) to accommodate a broader class of control systems. Unlike conventional control systems, Equation (3) features control inputs that consist of the cumulative sum of historical inputs, i.e., “discrete integral” of . Therefore, (3) is a completely new type of discrete-time control system.
For system (3), the following basic assumption is given:
Assumption. Let the reference signal of system (3) be , and is previewable; that is, at each time , the value of reference signal are known, where is the preview step. The value of the reference signal does not change after steps, namely, Remark 2. This assumption implies that the future values of the reference signal are known in advance (i.e., previewable), which is the basic assumption of the preview control problem [1,29]. In practical scenarios (e.g., robotic motion or voltage regulation), the reference signal is often generated by a planner or an external system, making its future values accessible over a finite horizon . The difference between the reference signal and the output signal is defined as the error signal , i.e., The purpose of this study is to design a tracking controller with preview compensation for system (3), such that the output signal can asymptotically track the reference signal , that is, the error signal asymptotically converges to the zero vector.
In order to evaluate the tracking performance of the system (3), the following performance index function is introduced for the system:
where
and
are given positive definite weight matrices. In the performance index (5), the first term optimizes the tracking error, while the second term optimizes the control energy. Therefore, the physical interpretation of (5) lies in achieving rapid asymptotic regulation of the tracking error with relatively low control input magnitude.
3. Construction of the Augmented Error System
We use the commonly used augmented error system method in preview control theory to transform the tracking problem of system (3) into a regulation problem.
First, from the state equation of (3), we can get
Subtracting (6) from the state equation (3) yields
where
is a first-order difference operator, which is defined as
By acting
to both sides of
, we obtain
Noting that
and
, we apply Equations (7) and (8) to derive
Subsequently, based on the assumptions specifying the prescribed conditions for the reference signal, the following identity can be obtained:
where
Introducing a new state vector
Combining (7), (9), and (10) yields a dynamic equation:
where
It is noted that Equation (11) contains no difference term of the control input
. Consequently, the control input derived for system (11) does not incorporate a discrete integral of the error signal
, resulting in the absence of an integrator in the closed-loop system. This structural deficiency inherently impedes the elimination of steady-state errors [
29]. To eliminate steady-state errors, we introduce a discrete integrator, which is defined by the following formula:
Combining Equations (11) and (12) yields the following:
where
We refer to (13) as the augmented error system of system (3). Note that is the part of the vector of , and if the state vector of the system (13) asymptotically approaches the zero vector, then will also asymptotically approach the zero vector. This ensures that the output of system (3) asymptotically tracks the reference signal . This indicates that the controller designed for system (13) can serve as a tracking controller for system (3).
4. The Design of Preview Controller
Noting that the system (13) is subject to external disturbance
, we introduce the following
performance index for system (3) to evaluate the impact of disturbance signals on system performance.
where the constant
indicates the level of disturbance attenuation.
According to the performance index function (5) and index (14), it is known that the weights are selected based on the relative importance assigned to different control objectives. emphasizes tracking error reduction. provides moderate control effort. balances the performance index function with external disturbance. Therefore, engineers can choose weight matrices based on different requirements.
By introducing the performance signal,
where
for system (13), Equation (14) can be rewritten equivalently as
and the performance index function (5) can be written as follows:
For system (13), we design a memory-based state feedback controller:
where
and
are the feedback gain matrices to be determined, such that the resulting closed-loop system,
Satisfies the following:
- (a)
When the system is asymptotically stable;
- (b)
Under the zero initial condition, for a given interference rejection level and an arbitrary non-zero , (16) holds.
According to
control theory, the closed-loop system satisfying conditions (a) and (b) is said to be asymptotically stable with an
disturbance attenuation level
, and the corresponding controller is termed an
controller with disturbance attenuation level
[
30]. From (17), it follows that the numerator term on the left side of (16) corresponds exactly to the tracking performance index function (5). Since (16) holds for any non-zero
, a smaller
implies a smaller value
of the tracking performance function.
We now determine the feedback gain matrices and using Lyapunov stability theory and the LMI method, which yields the preview tracking controller for system (3). The first key theorem of this paper is given as follows.
Theorem 1. Suppose that Assumption holds. For a given constant , if there exist matrices , , and satisfyingthen the closed-loop system (19) is asymptotically stable with the disturbance attenuation level . Proof of Theorem 1. First, select positive definite matrices
and
satisfying the conditions of this theorem, and construct the following quadratic form:
This quadratic form is then employed as a Lyapunov function for system (19).
Differentiating the Lyapunov function (21) along the trajectories of the closed-loop system (19) yields the following:
Letting
, (22) can be equivalently rewritten as
where
The conclusion of this theorem is proved through two steps.
Step 1: We prove that, when the external interference signal , the closed-loop system (19) is asymptotically stable.
From (23), it follows that when
, the difference of the Lyapunov function (21) along the trajectories of the closed-loop system (19) is given by
where
Based on Lyapunov stability theory, the closed-loop system (19) is asymptotically stable in (24) if . Thus, we only need to prove that holds under the conditions of this theorem.
By performing a congruence transformation on the left-hand side of inequality (20) (pre-multiplying by
and post-multiplying by
, and noting that such a transformation does not affect the negative definiteness of a matrix, we conclude that the matrix inequality,
holds.
From the properties of negative definite matrices, the validity of the matrix inequality (25) implies that
holds. Since
and
, it follows that
. Consequently, by the Schur complement lemma, (26) holds if and only if
holds. By direct computation, it can be shown that the left side of Equation (27) is the matrix
. Hence, under the conditions of the theorem, we obtain
. As a result, the first step is proven.
Step 2: We prove that, under zero initial conditions, inequality (16) holds for a given disturbance attenuation level and an arbitrary non-zero .
Since
, the Schur complement lemma implies that (20) holds if and only if
which means
Noting
, the sufficient and necessary condition for (28) is
namely,
On the other hand, from (15), (18), and (23), we can obtain
In summary, when (20) holds, we have
On both sides of (31), summing
from 0 to
yields
Under the zero initial condition,
can be known based on the properties of the Lyapunov function (21). Thus,
namely, under the zero initial condition, for a given disturbance attenuation level
and arbitrary non-zero
, (16) holds. This completes the proof of Theorem 1. □
Remark 3. Based on the Bounded Real Lemma [31], the matrix inequality (20) implicitly characterizes the norm bound through the inequality (31). Summing over yields the standard norm condition , with being the -to- transfer function. Therefore, satisfying condition (20) implies that the designed controller achieves the desired performance constraint on the -to- transfer function . Based on Theorem 1, we present a method for determining the feedback gain matrices and , which leads to the following theorem.
Theorem 2. Suppose that Assumption holds. For a given constant , if there exist matrices , , and such thatholds, then the controller of the system (13) with disturbance attenuation level is (18), and , . Proof of Theorem 2. We only need to show that when the conditions of this theorem hold, the conditions of Theorem 1 also hold. A congruence transformation is applied to the left side of LMI (33) by pre-multiplication with matrix
and post-multiplication with matrix
. As congruence transformations preserve negative definiteness, (33) holds if and only if
In (34), let , , , and , and we obtain (20). Thus, the condition of Theorem 1 is satisfied, and then Theorem 2 is proven. □
Remark 2. In Theorem 2, the disturbance attenuation level is specified in advance. According to the previous analysis, a smaller ccorresponds to a smaller value of the tracking performance function , indicating better tracking performance. Therefore, to improve tracking performance, should be chosen as small as possible. However, an excessively small may render LMI (33) infeasible. In fact, the minimal disturbance attenuation level that ensures the feasibility of LMI (33) can be obtained by solving the following optimization problem:
Finally, based on Theorem 2, we derive the explicit form of the preview tracking controller for system (3), leading to Theorem 3.
Theorem 3. Under the Assumption, if there exist matrices , , , and such that (33) has feasible solutions or the optimization problem (35) has solutions, then the controller of (3) is given bywhere Proof of Theorem 3. From the analysis in
Section 3, it is known that the controller designed for system (13) can ensure the output
of system (3) asymptotically tracks the reference signal
. Thus, according to Theorem 2 and Remark 2, when the conditions of Theorem 3 are satisfied, (18) is the tracking controller of system (3).
We decompose the gain matrices and of Equation (18) as follows
From the discrete integrator (12), it is derived that , .
It is noted that , and . Thus, we can obtain
This completes the proof of the theorem. □
Remark 4. In the controller (36),
and
are the preview terms of the reference signal. The preview terms rely on known future values of the reference signal
(e.g., from a pre-defined trajectory or real-time sensor measurements), but they do not require continuous differentiability. Instead, the derivatives and are calculated via finite differences (e.g., ), which is feasible for discrete-time implementations. This approach is standard in preview control and path-following applications.
5. Numerical Simulation
This section gives two examples to illustrate the applicability and effectiveness of the proposed controller. Example 1 is the pressurizer control system model, where the level of disturbance attenuation is given in advance. Example 2 is a numerical example, where the minimum level of disturbance attenuation needs to be determined.
Example 1. As mentioned in the introduction, the discrete-time system corresponding to the pressurizer control system model is given by Equation (2). By setting the sampling interval as , it follows from (2) and that the time delay . The performance index function (5) is specified with weighting matrices and , while the disturbance attenuation level is set to . In system (2), the parameter is chosen as . The initial condition is , . We perform numerical simulations for two distinct reference signals.
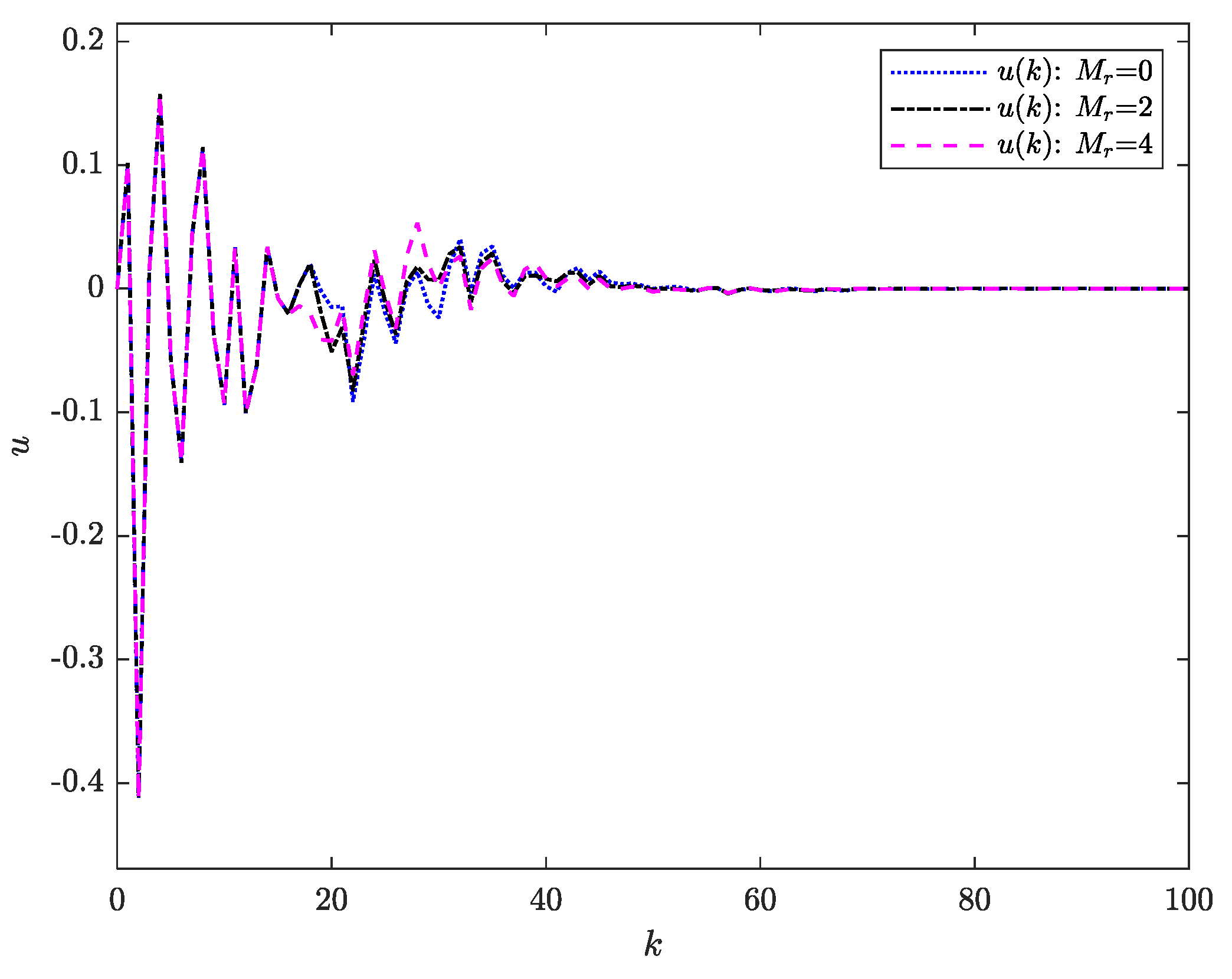
To investigate the effect of preview information on system performance, comparative simulations are performed for different preview lengths (, and ). When , the matrices , . When , the matrices , . When , the matrices , .
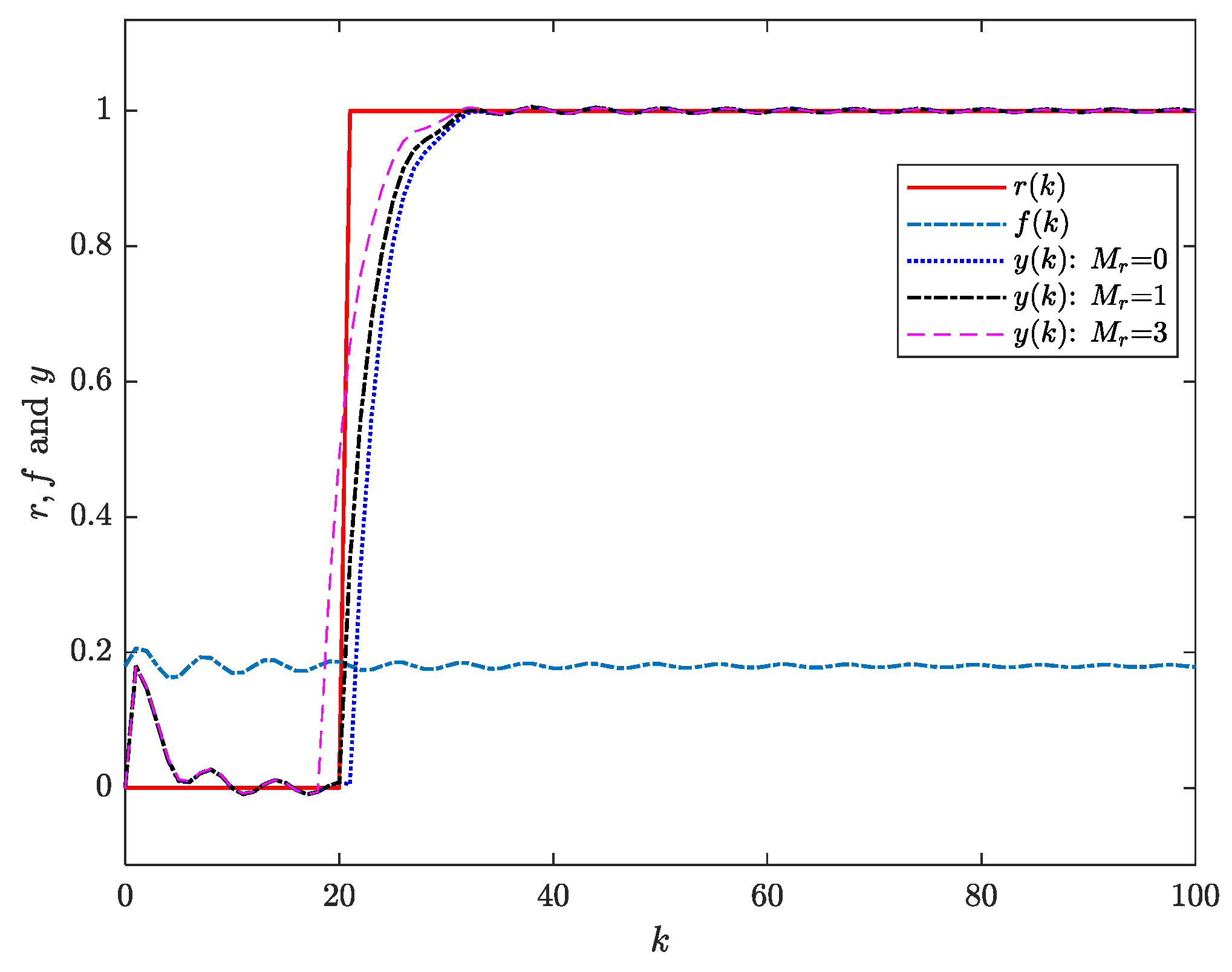
The closed-loop output responses to the step reference signal (37) are shown in
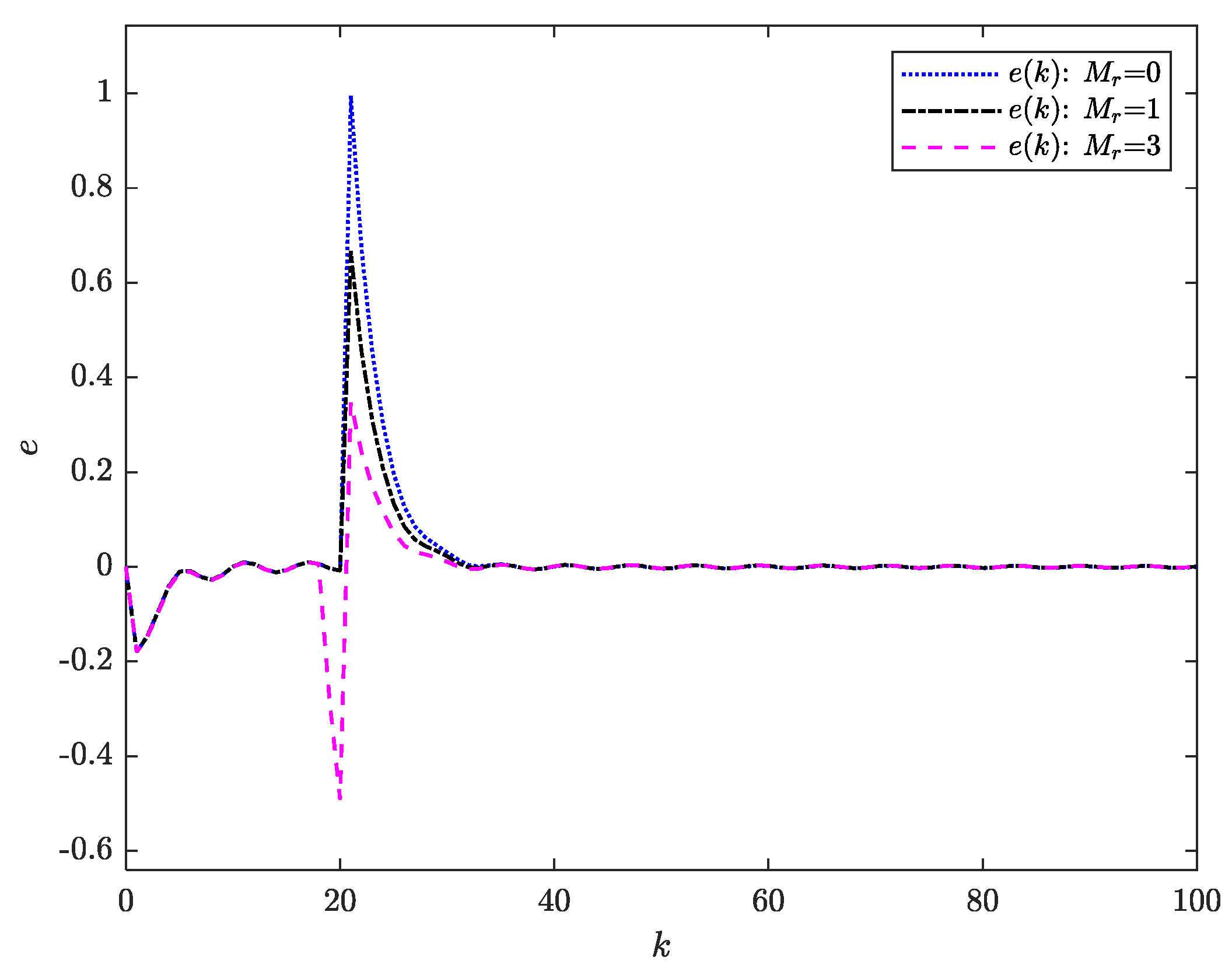
Figure 1. The corresponding tracking errors and control inputs are depicted in
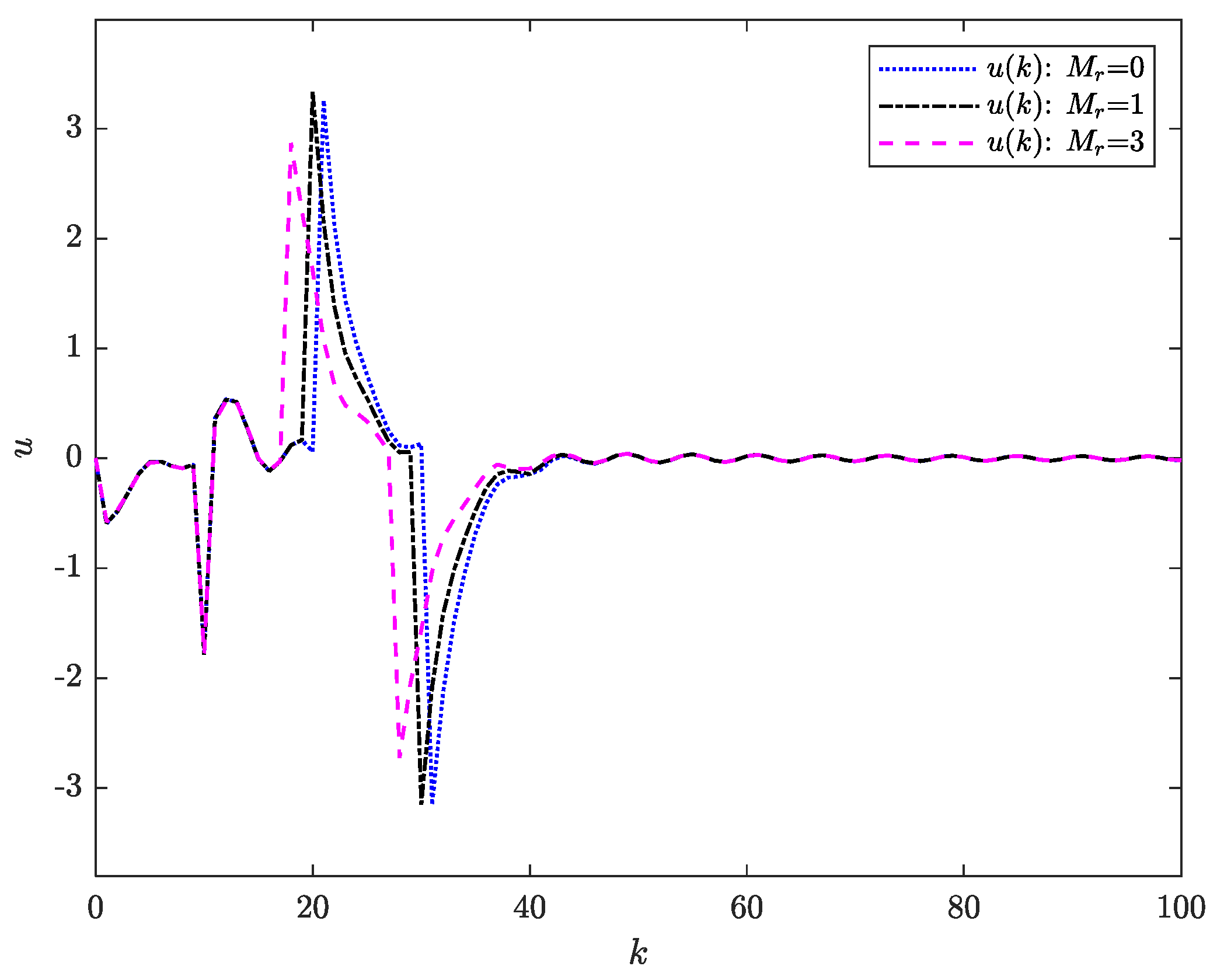
Figure 2 and
Figure 3, respectively.
From
Figure 1, it can be observed that the system output successfully tracks the reference signal under the three preview conditions (
,
and
). Moreover, the preview-based controller enhances transient performance by accelerating the tracking speed.
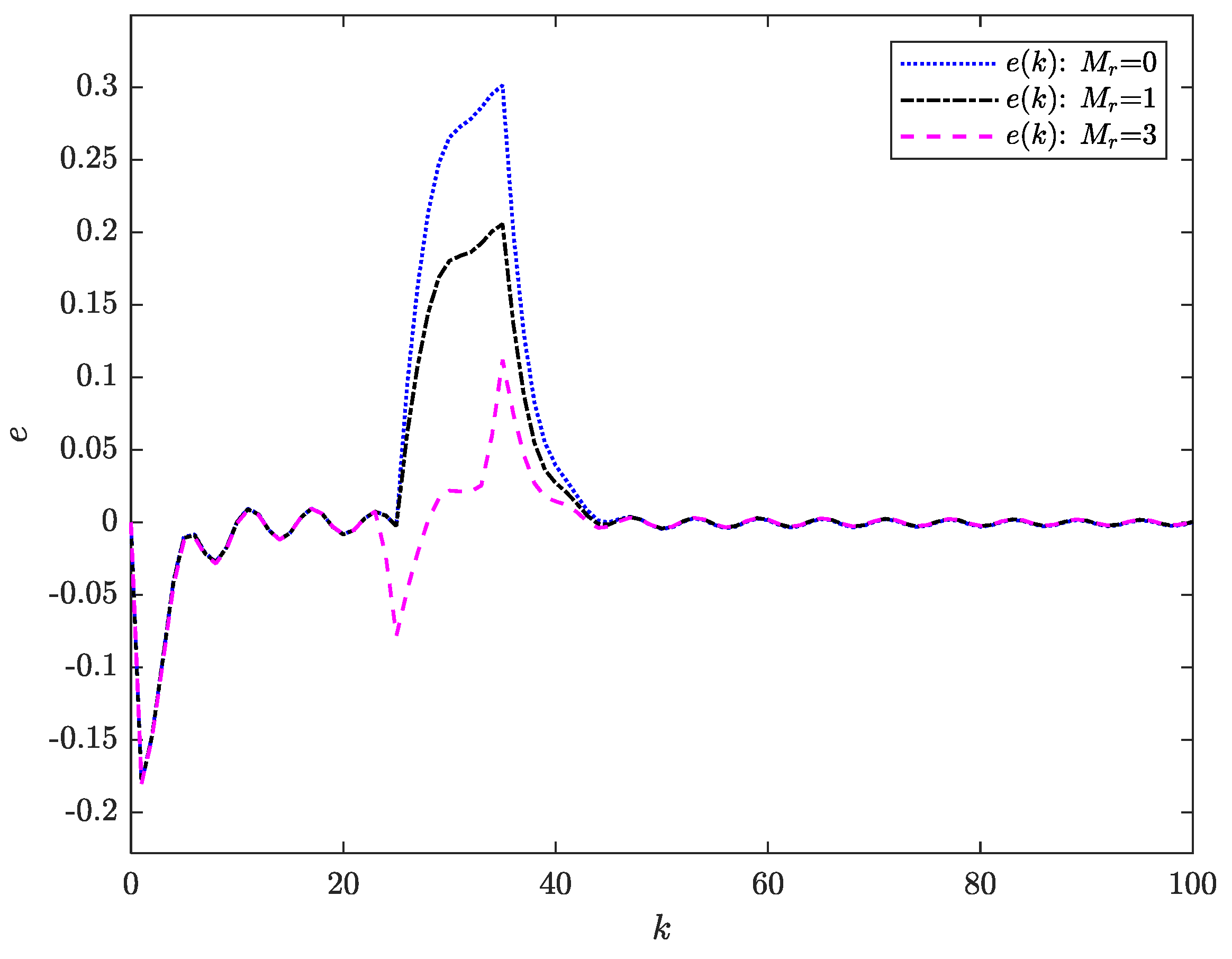
Figure 2 further reveals that the preview action contributes to a reduction in tracking error. As evidenced in
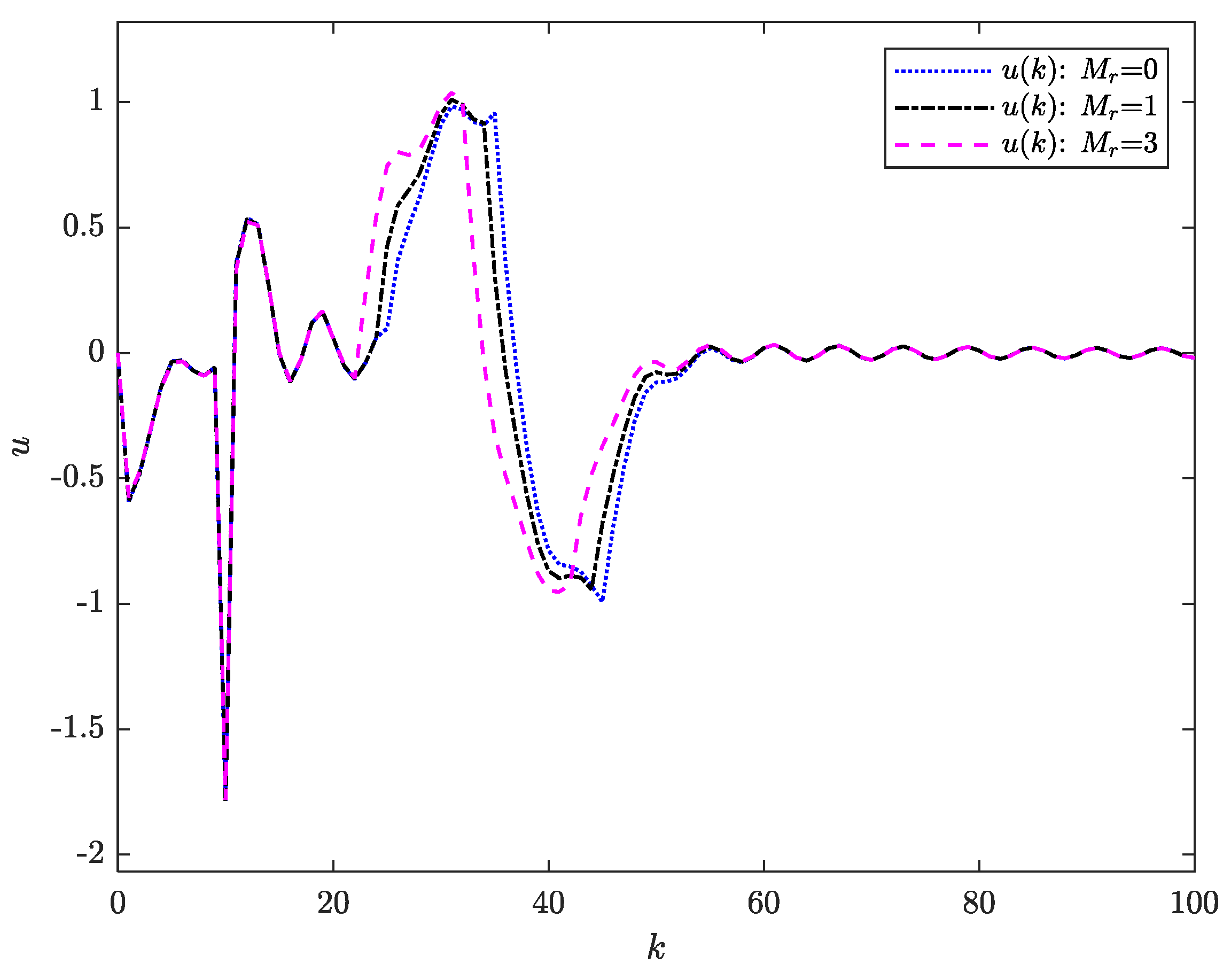
Figure 3, the control input remains bounded across all preview horizons.
Similarly, in order to illustrate the influence of preview information on the closed-loop system, three cases of , and are simulated, respectively.
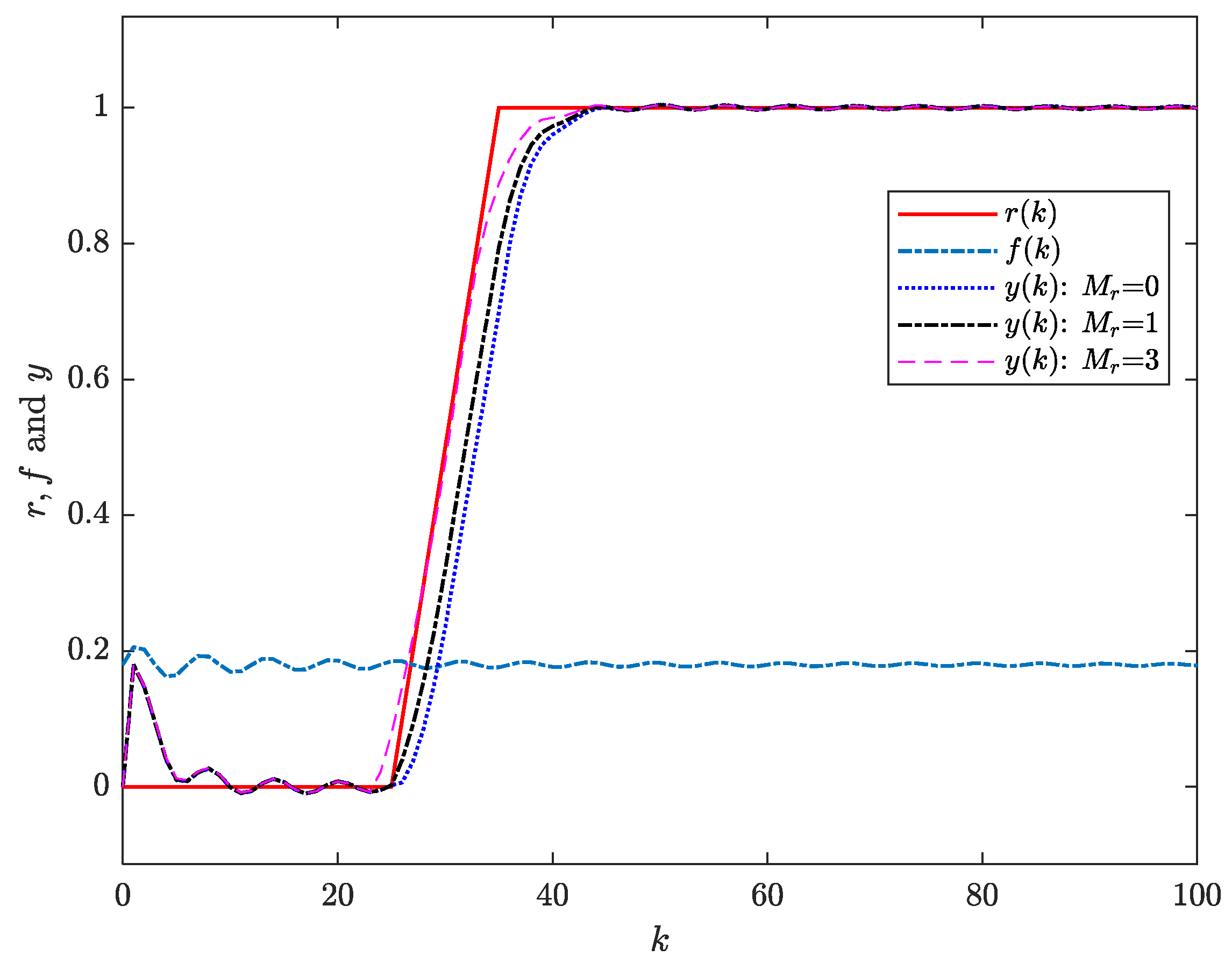
Figure 4,
Figure 5 and
Figure 6 show the output response, tracking error, and control input of the closed-loop system, respectively. Similarly, it can be observed from
Figure 4 and
Figure 5 that as the preview horizon of the reference signal increases, the tracking error decreases, and the output of the closed-loop system follows the reference signal more quickly.
Figure 6 demonstrates that the control input remains bounded.
Through numerical computation, we obtained the Integral of Absolute Error (IAE) and Integral of Time-weighted Absolute Error (ITAE) values for three preview step configurations: When
,
,
; When
,
,
; When
,
,
. Moreover, to illustrate the impact of different weight matrix selections on the tracking performance of the system, we conducted simulations using various weight matrices and levels of disturbance attenuation. The corresponding IAE and ITAE values are calculated, and the results are summarized in
Table 1.
In practical applications, these weights are typically chosen by control engineers based on specific performance requirements, such as prioritizing tracking accuracy, reducing control energy, or enhancing disturbance rejection.
Example 2. Consider the following discrete-time delay systemand the external disturbance signal is The reference signal is set as
Let the initial state function be constant zero, and the weight matrix in the performance index function be , . Numerical simulations were conducted for three cases: no preview (), and preview steps and . Using MATLAB’s LMI toolbox, we obtain the following results:
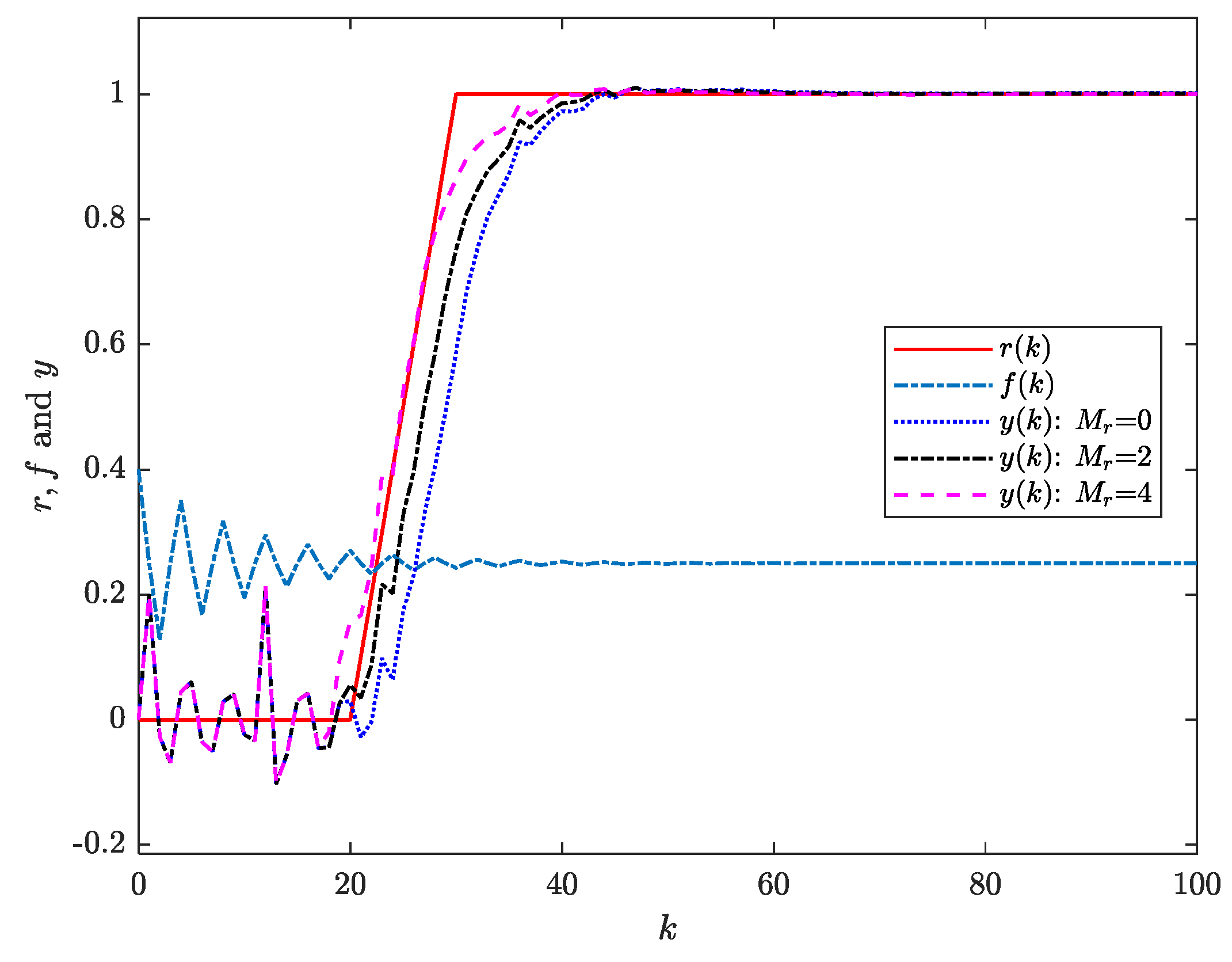
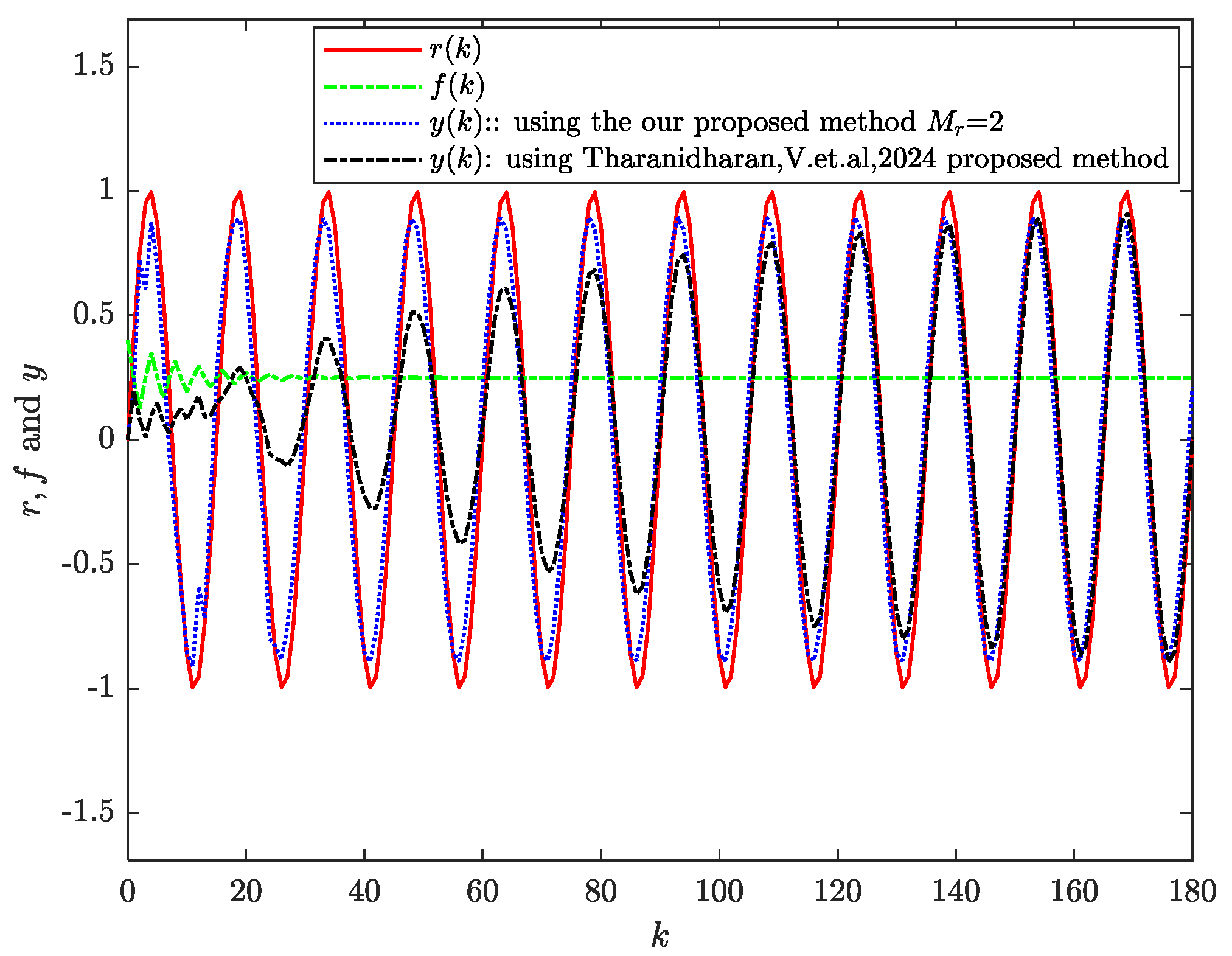
The tracking performance of system (39) is shown in
Figure 7. From the figure, it can be observed that as time increases, the output signal of system (39) asymptotically tracks the reference signal, regardless of whether preview action is employed. By comparing the system responses under controllers with preview (i.e.,
or
) and without preview (i.e.,
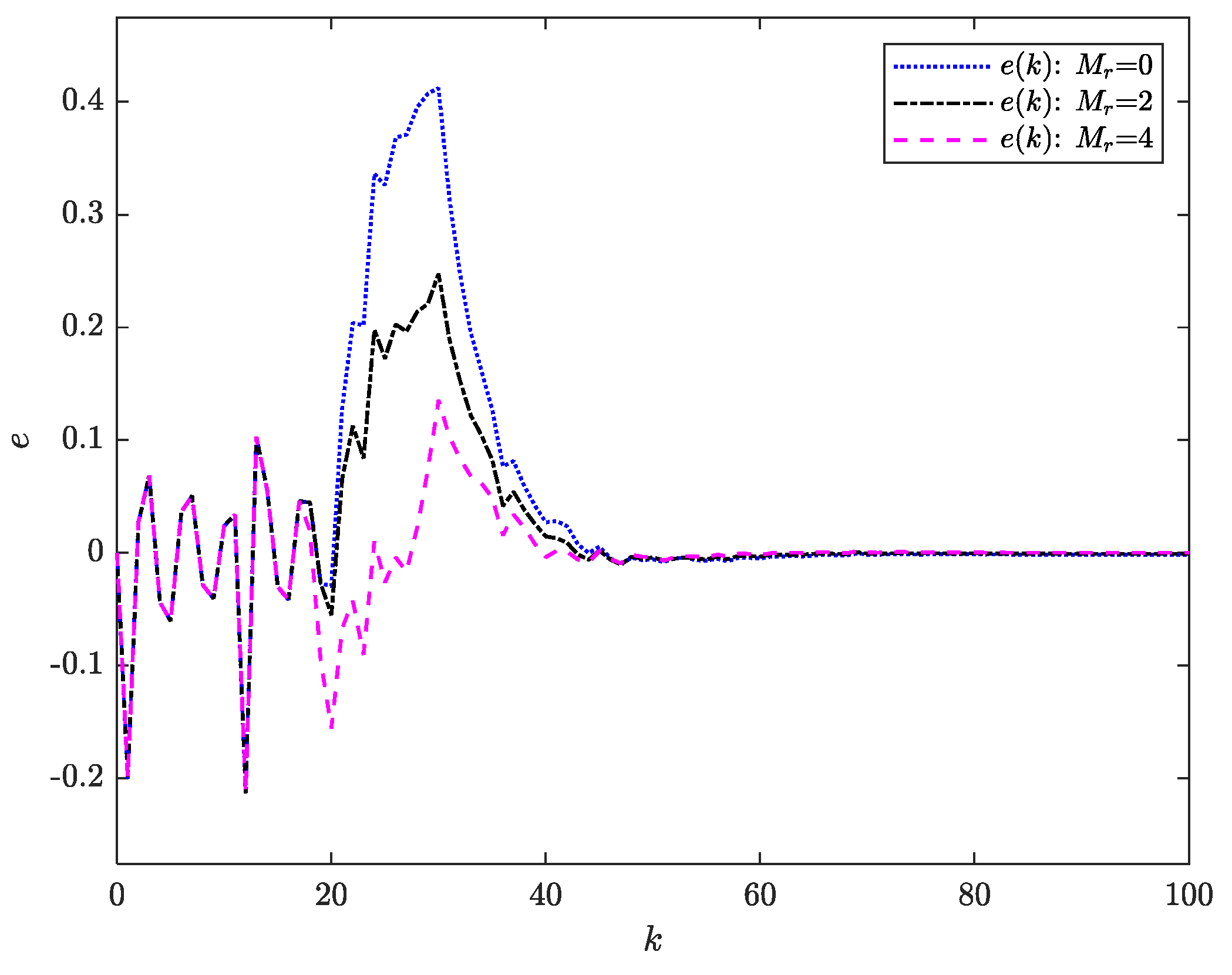
), it can be observed that the preview-based controllers enable the output vector to respond in advance and allow the system output to track the reference signal more rapidly. The tracking error of the system is shown in
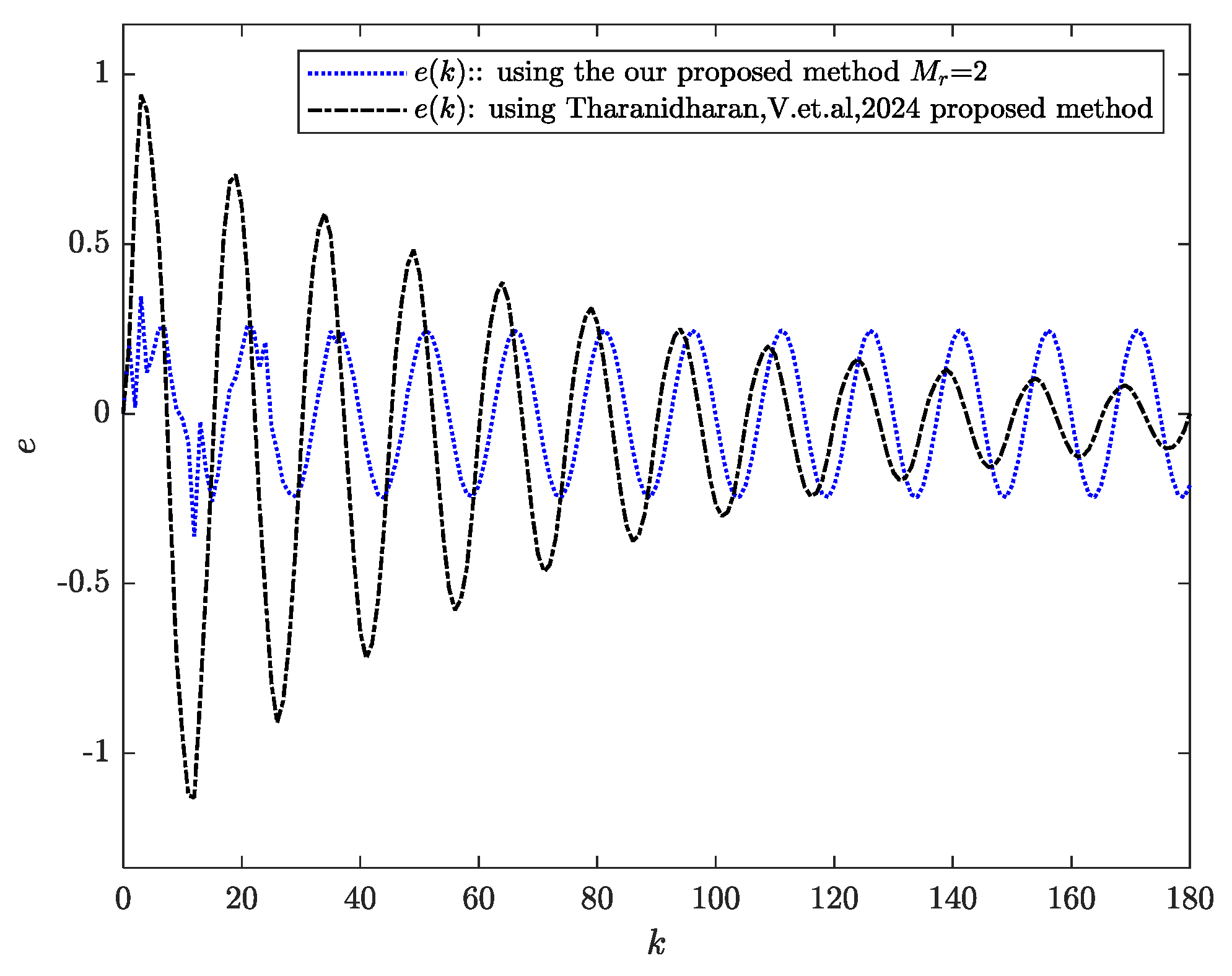
Figure 8. By examining
Figure 7 and
Figure 8 together, it can be observed that increasing the preview horizon improves the tracking accuracy, and the overall system error decreases as the preview horizon lengthens.
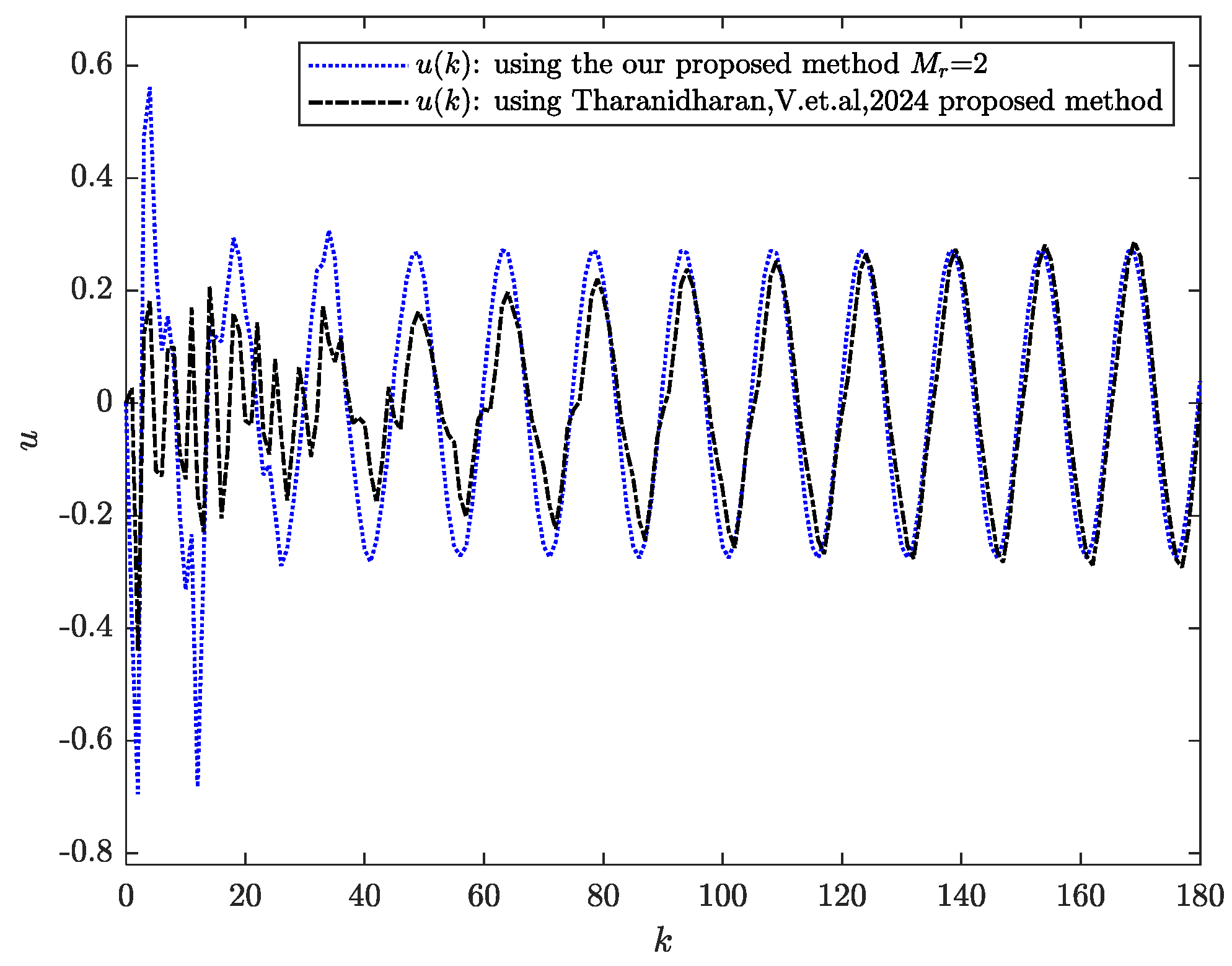
Figure 9 shows the control input of the system. It can be seen from
Figure 9 that the control input remains bounded. These findings verify the effectiveness of preview control in enhancing the system’s tracking performance.
To enable a direct comparison between the proposed preview tracking control method and the repetitive tracking control method based on reference [
32], we applied both approaches to simulate Example 2. Since repetitive tracking control is designed for periodic signal tracking, the reference signal was selected as:
. In addition, we set
,
,
, while keeping all other parameters the same as those in Example 2. The simulation results are shown in
Figure 10,
Figure 11 and
Figure 12, where the black line represents the control method from reference [
32], and the blue line corresponds to the proposed control method.
Through this comparison, we observed that for periodic signal tracking, the proposed preview-based method demonstrates significantly better performance during the initial tracking stage. However, as time progresses, the tracking error of the repetitive control method gradually becomes smaller than that of the preview-based approach. This indicates that both methods have their respective advantages: the preview control strategy offers a faster initial response, while the repetitive control method achieves better long-term steady-state accuracy.