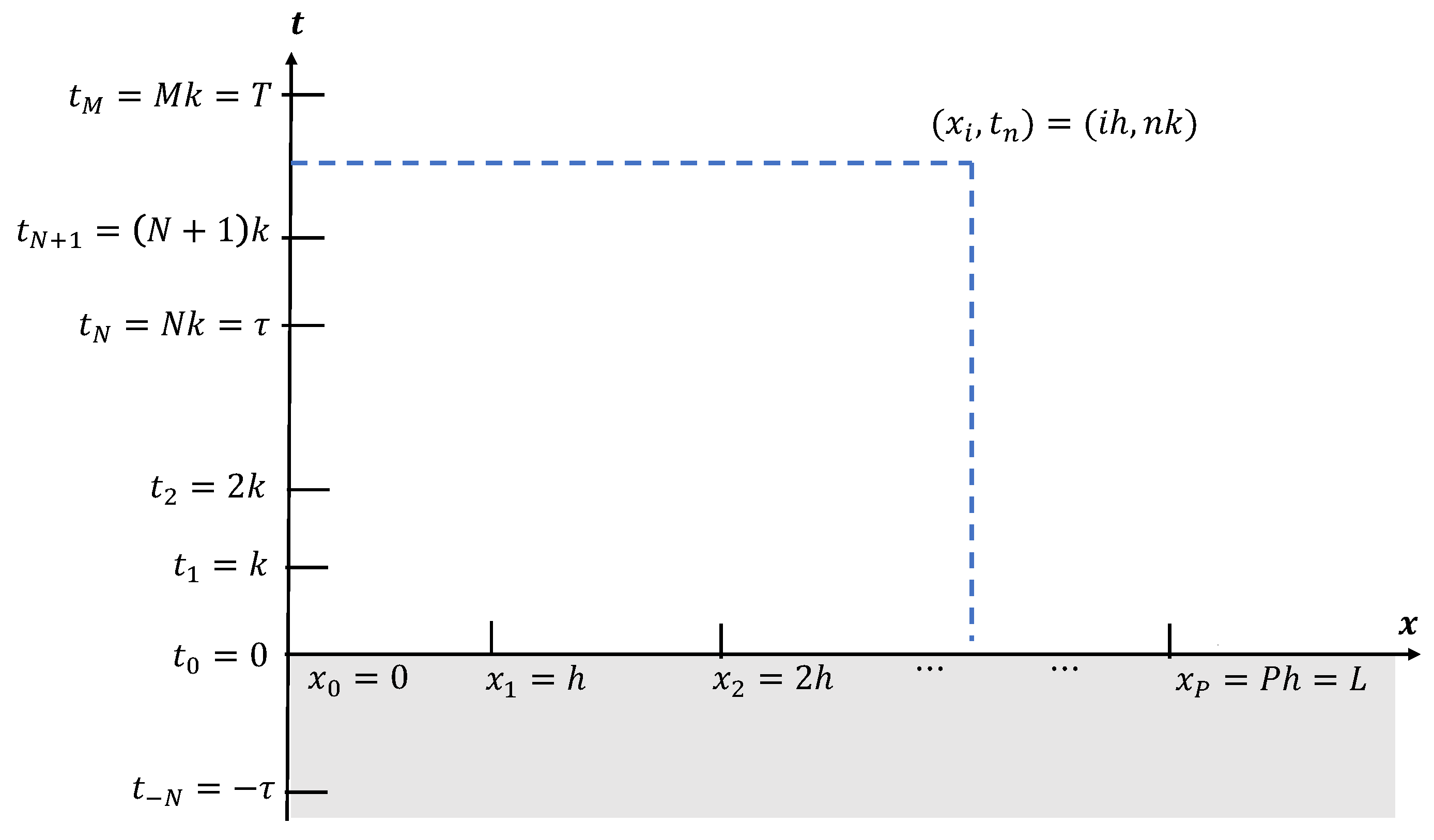Asymptotic Stability of a Finite Difference Scheme for a Wave Equation with Delayed Damping

Abstract

In this paper, we propose an implicit finite difference scheme for a wave equation with strong damping and a discrete delay term. Although the scheme is implicit, the use of second-order finite difference approximations for the strong damping term in both space and time prevents it from being unconditionally stable. A sufficient condition for the asymptotic stability of the scheme is established by applying the Jury stability criterion to show that all roots of the characteristic polynomial associated with the resulting linear recurrence lie strictly inside the unit disk. This stability condition is derived under an appropriate constraint that links the time and space discretization steps with the damping and delay parameters. A numerical example is provided to illustrate the decay behavior of the scheme and confirm the theoretical findings.

1. Introduction

Delays are ubiquitous in many physical and engineering systems, and experimental evidence suggests that they cannot be ignored. They naturally arise in the study of wave propagation, structural vibrations, and signal processing, where time delays play a critical role in transmission and filtering. Moreover, delays are prevalent in diverse scientific disciplines such as control theory and heat transfer in materials with thermal memory (see [1,2,3] and references therein).

The well-posedness and stability of delayed evolution equations have attracted considerable attention from researchers; see, for example, [4,5,6,7,8]. Likewise, the numerical solution and stabilization of schemes for both ordinary and partial differential equations with delay have been active areas of research for decades. We refer the reader to [9,10,11,12] for ODEs, and to [13,14,15,16] for PDEs and references therein.

In [13], Garcia et al. considered the diffusion equation with delay

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }t}}(t,x)=a^2{\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}}(t,x)+a^2{c}^2{\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}}(t-\tau ,x),\hfill & t>\tau ,0\le x\le l,\hfill \\ u(t,x)=\varphi (t,x),\hfill & 0\le t\le \tau ,0\le x\le l,\hfill \\ u(t,0)=u(t,l)=0,\hfill & t\ge 0,\hfill \end{array}\right.\end{array}$$

(1)

where $\tau >0$, $a\ne 0$, and $0<c<1$ are real constants. They proved the convergence and asymptotic stability of an explicit finite difference scheme for this problem. In [14], the same authors analyzed the convergence of an implicit finite difference scheme applied to the same model.

In [16], Zhang et al. established asymptotic stability results for a compact $\theta$-method applied to a generalized delay diffusion equation. In another related work, Lekomtsev and Pimenov [15] developed a weighted numerical scheme for parabolic equations with delay, specifically addressing the case of variable heat conductivity. They investigated the accuracy, stability, and convergence order of the proposed method.

While the above studies focus primarily on parabolic problems with delay, related efforts have also been directed toward wave equations exhibiting damping and memory behaviors. Several other articles have proposed and analyzed finite difference schemes for wave equations with various damping and memory effects, notably those in [17,18,19,20].

In this paper, we consider a system of wave equations with strong damping and a delayed damping term, given by

$$\begin{array}{cccc}\hfill & u_{tt}(x,t)=u_{xx}(x,t)+{\mu }_1{u}_{txx}(x,t)-{\mu }_2{u}_t(x,t-\tau ),\hfill & \hfill & \mathrm{in}[0,L]\times (0,\infty ),\hfill \end{array}$$

(2a)

$$\begin{array}{cccc}\hfill & u(0,t)=u(L,t)=0,\hfill & \hfill & \hfill \end{array}$$

(2b)

$$\begin{array}{cccc}\hfill & u(x,0)=u_0\left(x\right),u_t(x,0)=u_1\left(x\right),\hfill & \hfill & \mathrm{in}[0,L],\hfill \end{array}$$

(2c)

$$\begin{array}{cccc}\hfill & u_t(x,t-\tau )=f_0(x,t-\tau ),\hfill & \hfill & \mathrm{in}[0,L]\times (0,\tau ),\hfill \end{array}$$

(2d)

where $\tau >0$, and ${\mu }_1,{\mu }_2$ are positive constants. The system (2a)–(2d) features a time-delay term appearing in the first time derivative$u_t$, rather than in the state variable itself—a configuration that introduces significant analytical and numerical challenges. The implicit finite difference scheme constructed to approximate the solution of Problem (2) is based on classical second-order Taylor expansions for the derivatives of $u(x,t)$ (see [21]). These approximations are applied in both space and time and are paired with a consistent initialization of the delay term over the interval $[-\tau ,0]$, as discussed in Section 3.

While delay differential equations and PDEs with delay in the state variable u have been extensively studied, and some works have addressed delays in spatial derivatives such as $u_x$ or $u_{xx}$ in diffusion-type models, the presence of a delay in $u_t$ directly affects the system’s temporal dynamics and has received comparatively less attention. This type of delay introduces implicit memory effects and complicates both the discretization process and stability analysis, particularly within finite difference frameworks.

To the best of our knowledge, this specific configuration has not been thoroughly addressed in the literature. In this work, we construct a fully discrete, second-order accurate (in both time and space) implicit finite difference scheme tailored to this structure. Despite the presence of a strong damping term, our stability analysis—based on the Jury criterion—reveals that the scheme is conditionally stable, depending on the time step, delay, and damping parameters. These results highlight the subtle interplay between the delay structure and numerical stability, underscoring the need for careful analysis when extending finite difference methods to non-standard delayed PDEs.

In this paper, we focus on constructing a second-order finite difference scheme to approximate the solution of the system (2a)–(2d), building on the work presented in [13,14]. Following the introduction, Section 2 provides essential theoretical results on the continuous system and introduces key definitions that underpin the stability analysis of the discretized model. The finite difference scheme itself is presented in Section 3, with a rigorous stability analysis given in Section 4. Finally, Section 5 illustrates the performance of the proposed scheme through numerical experiments that confirm the theoretical findings. The paper concludes in Section 6.

2. Preliminaries

This section provides the theoretical background necessary for the stability analysis of the proposed finite difference scheme. We begin by recalling an exponential stability result for the continuous Problem (2a)–(2d), which ensures that the system’s energy decays under appropriate parameter conditions. We then review the Jury stability criterion, which is instrumental in analyzing the stability of the fully discretized system.

2.1. Exponential Stability of the Continuous System

Before presenting the numerical approximation and its stability analysis, we recall a theoretical result that establishes exponential stability for wave equations with time-delay feedback. In [6], the authors consider a wave equation with frictional (weak) damping and delayed feedback and prove exponential stability under the condition ${\mu }_2<{\mu }_1$. Although their analysis focuses on weak damping, a similar stabilization mechanism applies in the presence of strong damping (i.e., ${\mu }_1\Delta u_t$), where the analogous condition becomes

$$\begin{array}{c}\hfill {\mu }_2<{\displaystyle \frac{{\mu }_1}{C_p}},\end{array}$$

(3)

with $C_p$ denoting the Poincaré constant arising from the use of the Poincaré inequality.

To ensure that the continuous system exhibits exponential stability, we assume throughout our stability analysis of the discrete scheme that the parameters ${\mu }_1$ and ${\mu }_2$ satisfy Condition (3).

2.2. Review of the Jury Stability Criterion

Jury’s criterion is a classical method used to assess the stability of linear time-invariant discrete-time systems by analyzing their characteristic polynomials in the z-domain. It serves as the discrete-time counterpart to the Routh–Hurwitz criterion used in continuous-time analysis. The method determines whether all roots of the characteristic polynomial lie strictly inside the unit circle in the complex plane. This is achieved by applying a sequence of algebraic tests to the coefficients of the polynomial. For a detailed treatment of the Jury stability criterion and its application to discrete-time systems, we refer the reader to [22,23].

We let $D\left(z\right)$ be the characteristic polynomial of the system, given by

$$D\left(z\right)=a_0{z}^n+a_1{z}^{n-1}+\cdots +a_{n-1}z+a_n,\mathrm{with}{a}_0>0.$$

To determine the system’s stability, the Jury table is constructed using the coefficients of $D\left(z\right)$. The first two rows contain the coefficients in forward and reverse order, respectively. Each subsequent row is computed recursively.

The structure of the Jury table is as follows:

$$\begin{array}{ccccccc}{a}_0& a_1& a_2& \cdots & a_{n-2}& a_{n-1}& a_n\\ a_n& a_{n-1}& a_{n-2}& \cdots & a_2& a_1& a_0\\ b_0& b_1& b_2& \cdots & b_{n-2}& b_{n-1}\\ b_{n-1}& b_{n-2}& \cdots & b_2& b_1& b_0\\ ⋮& ⋮& & \ddots & & ⋮& ⋮\end{array}$$

The entries of the third and subsequent rows are computed using the following determinant-based formulas:

$$b_i=\left|\begin{array}{cc}{a}_n& a_{n-1-i}\\ a_0& a_{i+1}\end{array}\right|,c_j=\left|\begin{array}{cc}{b}_{n-1}& b_{n-2-j}\\ b_0& b_{j+1}\end{array}\right|,i=0,\cdots ,n-1,j=0,\cdots ,n-2.$$

For the polynomial $D\left(z\right)$ to be stable (i.e., all of its roots lie within the unit circle), it must satisfy the following necessary conditions:

$$D\left(1\right)>0,{(-1)}^{n}D(-1)>0.$$

Additionally, the sufficient conditions provided by the Jury test include

$$a_0>|a_n|,|b_{n-1}|>|b_0|,|c_{n-2}|>|c_0|,\cdots$$

These conditions are applied iteratively through each row of the table. Violation of any one of them indicates that the system is unstable.

2.3. Well-Posedness of the Continuous Problem

Before proceeding with the discretization, we briefly state a standard existence and uniqueness result for the continuous System (2a)–(2d). The well-posedness can be established using semigroup theory combined with energy estimates.

Theorem 1

(Well-posedness of the continuous problem). We let ${\mu }_1,{\mu }_2>0$, and assume that the initial data satisfy $u_0,u_1\in H_0^1\left(\mathsf{\Omega }\right)$ and $f_0\in L^2((0,\tau );H_0^1\left(\mathsf{\Omega }\right))$. Then System (2a)–(2d) admits a unique weak solution

$$u\in C^1([0,T];H_0^1\left(\mathsf{\Omega }\right)).$$

For further details and related proofs, we refer the reader to [24,25].

3. Finite Difference Scheme

Building on the foundational work in [13], we begin by discretizing the spatial domain and time interval to construct a finite difference scheme that approximates the solution of System (2a)–(2d). The resulting scheme is then reformulated as a two-level scheme (see [26]), which facilitates the stability analysis presented in the following section.

Spatial discretization: We let $L>0$ and define $h={\displaystyle \frac{L}{P}}$ for some integer P. Then we can divide the interval $[0,L]$ into P intervals of equal size h. We denote by $x_i=ih$ for $i=0,1,\cdots ,P$ the partition nodes (see Figure 1).

Time discretization: We can truncate the time interval $(0,\infty )$ to $(0,T]$ for sufficiently large integer $T>\tau$. Then we divide the interval $[0,T]$ into M equal sub-intervals using the time step-size $k={\displaystyle \frac{T}{M}}$. We denote by $t_n=nk$, for $n=0,1,\cdots ,M$ the nodes of the time partitioning. Furthermore, we let $\tau =Nk$, where $N<M$ (see Figure 1).

The discrete solution: Next, we approximate the solution $u(x,t)$ with the discrete solution $u(x_i,t_n)=u(ih,nk)$ for $i=0,\cdots ,P$ and $n=0,\cdots ,M$ and we write $u(x,t)\approx u_i^n=u(ih,nk)$. Similarly, we approximate $u(x,t-\tau )\approx u_i^{n-N}=u(ih,(n-N)k)$.

Remark 1.

The discrete-time domain shown in Figure 1 covers the main computational interval $[0,T]$, while the delayed term $u_t(x,t-\tau )$ requires initialization on the separate interval $[-\tau ,0]$. This distinction is visualized by shading the region $t<0$. All delay values are initialized via the given function $f_0(x,t-\tau )$ as defined in Equation (2d).

Finite difference approximations. The partial derivatives in (2) are approximated using second-order central differences as follows:

$$\begin{array}{cc}\hfill u_{tt}{|}_{(x_i,t_n)}& \approx {\displaystyle \frac{u_i^{n-1}-2u_i^n+u_i^{n+1}}{k^2}},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill u_{xx}{|}_{(x_i,t_n)}& \approx {\displaystyle \frac{u_{i-1}^n-2u_i^n+u_{i+1}^n}{h^2}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill u_{txx}{|}_{(x_i,t_n)}& \approx {\displaystyle \frac{1}{2k{h}^2}}\left[(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1})-(u_{i-1}^{n-1}-2u_i^{n-1}+u_{i+1}^{n-1})\right],\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill u_t{|}_{(x_i,t_n-\tau )}& \approx {\displaystyle \frac{u_i^{n-N+1}-u_i^{n-N-1}}{2k}},\hfill \end{array}$$

(7)

where k and h are the time and space steps, respectively, and $N\in \mathbb{N}$ satisfies $\tau =Nk$.

Substituting the above approximations into the PDE (2), sampled at the grid point $(x_i,t_n)$, yields the discrete equation:

$$\begin{array}{cc}\hfill 2h^2{u}_i^{n-1}-4h^2{u}_i^n+2h^2{u}_i^{n+1}& =2k^2(u_{i-1}^n-2u_i^n+u_{i+1}^n)\hfill \\ \hfill & +{\mu }_{1}k(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1})\hfill \\ \hfill & -{\mu }_{1}k(u_{i-1}^{n-1}-2u_i^{n-1}+u_{i+1}^{n-1})\hfill \\ \hfill & -{\mu }_{2}k{h}^2{u}_i^{n-N+1}+{\mu }_{2}k{h}^2{u}_i^{n-N-1}.\hfill \end{array}$$

Rearranging terms, we obtain an update formula for $u_i^{n+1}$:

$$\begin{array}{cc}\hfill -{\mu }_{1}k{u}_{i-1}^{n+1}+2({\mu }_{1}k+h^2)u_i^{n+1}-{\mu }_{1}k{u}_{i+1}^{n+1}& =-{\mu }_{1}k{u}_{i-1}^{n-1}+2({\mu }_{1}k-h^2)u_i^{n-1}-{\mu }_{1}k{u}_{i+1}^{n-1}\hfill \\ \hfill & +2k^2(u_{i-1}^n+u_{i+1}^n)+4(h^2-k^2)u_i^n\hfill \\ \hfill & -\alpha (u_i^{n-N+1}-u_i^{n-N-1}),\hfill \end{array}$$

(8)

where $\alpha ={\mu }_{2}k{h}^2$.

We define $U^n={[u_1^n,u_2^n,\cdots ,u_{P-1}^n]}^T\in {\mathbb{R}}^{P-1}$. Recurrence (8) can be written in compact matrix form as

$$\begin{array}{c}\hfill A{U}^{n+1}=C{U}^n+B{U}^{n-1}-\alpha (U^{n-N+1}-U^{n-N-1}),n\ge 0,\end{array}$$

(9)

where A, B, and C are tridiagonal matrices.

For completeness, their entries are defined as follows:

$$\begin{array}{cc}\hfill A& =\mathrm{tridiag}(-{\mu }_{1}k,2({\mu }_{1}k+h^2),-{\mu }_{1}k),\hfill \\ \hfill B& =\mathrm{tridiag}(-{\mu }_{1}k,2({\mu }_{1}k-h^2),-{\mu }_{1}k),\hfill \\ \hfill C& =\mathrm{tridiag}(2k^2,4(h^2-k^2),2k^2).\hfill \end{array}$$

Since Scheme (9) is a three-level recurrence, the initial vectors $U^0$ and $U^1$ must be computed using the initial and delay data provided in (2c)–(2d).

The finite difference approximations of the initial and boundary conditions:

The initial and boundary conditions in (2) are also approximated by the finite difference approximations as follows:

$$\begin{array}{cc}\hfill u_0^n=u_P^n=0,& n=0,\cdots ,M\mathrm{boundary}\mathrm{condition}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill u_i^0=u_0\left(x_i\right),& i=1,\cdots ,P-1\mathrm{initial}\mathrm{condition}\mathrm{for}u\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill u_i^1-u_i^{-1}=2k{u}_1\left(x_i\right),& i=1,\cdots ,P-1\mathrm{initial}\mathrm{condition}\mathrm{for}{u}_t\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill u_i^{n-N+1}-u_i^{n-N-1}=2k{f}_0(x_i,t_n-\tau ),& i=1,\cdots ,P-1\mathrm{and}n=0,\cdots ,N-1\hfill \end{array}$$

(13)

Using (11), we define $U^0={[u_1^0,u_2^0,\cdots ,u_{P-1}^0]}^T$. To define the vector $U^1$, we first rewrite the initial Condition (12) as $u_i^{-1}=u_i^1-2k{u}_1\left(x_i\right)$, or in a vector notation as

$$\begin{array}{c}\hfill U^{-1}=U^1+V,\end{array}$$

(14)

where $V=-2k{[u_1\left(x_1\right),u_1\left(x_2\right),\cdots ,u_1\left(x_{P-1}\right)]}^T\in {\mathbb{R}}^{P-1}$.

Next, we write the matrix Equation (9) at $n=0$ as follows:

$$\begin{array}{c}\hfill A{U}^1=B{U}^{-1}+C{U}^0-\alpha \left(U^{-N+1}-U^{-N-1}\right).\end{array}$$

After substituting $U^{-1}$ from (14), we can solve for $U^1$ the following equation:

$$\begin{array}{c}\hfill (A-B)U^1=BV+C{U}^0-\alpha \left(U^{-N+1}-U^{-N-1}\right).\end{array}$$

(15)

Once the solution of (15) is obtained, we can compute $U^{-1}$ from (14). However, solving (15) requires evaluating $U^{-N+1}-U^{-N-1}$ that can be obtained from (13) with $n=0$ as follows:

$$\begin{array}{c}\hfill U^{-N+1}-U^{-N-1}=F^0,\end{array}$$

where $F^n$ is a $P-1$ vector defined as

$$\begin{array}{c}\hfill F^n=2k{[f_0(x_1,t_n-\tau ),f_0(x_2,t_n-\tau ),\cdots ,f_0(x_{P-1},t_n-\tau )]}^T,\mathrm{for}n\ge 0\end{array}$$

(16)

Note that for $n=1,\cdots ,N-1$, the conditions in (13) can be written in vector notation as

For $n=N-1\Rightarrow$	$U^0-U^{-2}=F^{N-1}$
For $n=N-2\Rightarrow$	$U^{-1}-U^{-3}=F^{N-2}$
For $n=N-3\Rightarrow$	$U^{-2}-U^{-4}=F^{N-3}$
⋮	⋮
For $n=3\Rightarrow$	$U^{4-N}-U^{2-N}=F^3$
For $n=2\Rightarrow$	$U^{3-N}-U^{1-N}=F^2$
For $n=1\Rightarrow$	$U^{2-N}-U^{-N}=F^1$

Given $U^0$ and $U^{-1}$ (from (14)), we can solve the first two equations to obtain $U^{-2}$ and $U^{-3}$, respectively. Subsequently, we can compute $U^{-4},\dots ,U^{-N}$ in a step-by-step manner.

We let $A_{*}$ denote the block diagonal matrix $diag(A,I,I,\cdots ,I)$, where I is the identity matrix of size $(P-1)\times (P-1)$, ${\displaystyle U_{*}^n={[U^n,U^{n-1},\cdots ,U^{n-N+1},U^{n-N},U^{n-N-1}]}^T}$ and

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_{*}=\left[\begin{array}{cccccccc}C& B& 0& \cdots & 0& -\alpha I& 0& \alpha I\\ I& 0& 0& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0& 0\\ 0& 0& 0& \cdots & 0& 0& I& 0\end{array}\right].\end{array}$$

(17)

Then, Equation (9) can be rewritten in an equivalent compact form

$$\begin{array}{c}\hfill A_{*}{U}_{*}^{n+1}={\mathsf{\Phi }}_{*}{U}_{*}^n,n\ge 0.\end{array}$$

(18)

Since ${\mu }_1,k,h>0$, the matrix A is symmetric and positive definite and therefore nonsingular (invertible). The invertibility of the matrix A implies that the block diagonal matrix $A_{*}$ is also invertible. We let ${\mathsf{\Psi }}_{*}:=A_{*}^{-1}{\mathsf{\Phi }}_{*}$. Equation (18) has a unique solution given by

$$\begin{array}{c}\hfill U_{*}^{n+1}={\mathsf{\Psi }}_{*}{U}_{*}^n,n\ge 0.\end{array}$$

(19)

4. Asymptotic Stability of the Fully Discrete Scheme

In this section, we establish conditions on the mesh parameters that ensure the asymptotic stability of the fully discretized System (19). Specifically, we determine sufficient criteria under which all eigenvalues of the associated amplification matrix ${\mathsf{\Psi }}_{*}$ lie strictly inside the unit disk. This guarantees that the discrete solution decays asymptotically as time progresses, in accordance with the Jury stability criterion.

Given the matrix

$$\begin{array}{c}\hfill \mathcal{M}=\left[\begin{array}{cccccc}-2& 1& 0& \cdots & 0& 0\\ 1& -2& 1& \cdots & 0& 0\\ 0& 1& -2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & -2& 1\\ 0& 0& 0& \cdots & 1& -2\end{array}\right],\end{array}$$

we can define the matrices $A,B$ and C in terms of the matrix $\mathcal{M}$ as follows:

$$\begin{array}{cc}\hfill A& =2h^{2}I-{\mu }_{1}k\mathcal{M},\hfill \\ \hfill B& =-2h^{2}I-{\mu }_{1}k\mathcal{M},\hfill \\ \hfill C& =4h^{2}I+2k^2\mathcal{M}.\hfill \end{array}$$

(20)

The eigenvalues of the matrix $\mathcal{M}$ (see, for example, [21]) are given by

$$\begin{array}{c}\hfill {\lambda }_m=-4{sin}^2\left({\displaystyle \frac{\pi m}{2P}}\right),m=1,\dots ,P-1,\end{array}$$

(21)

and decrease strictly as m increases. Moreover, the matrix $\mathcal{M}$ is diagonalizable and can be written as $\mathcal{M}=Q\mathsf{\Lambda }{Q}^{-1}$, where Q is the matrix of eigenvectors and $\mathsf{\Lambda }$ is the diagonal matrix of eigenvalues. Having that the identity matrix can be written as $I=Q{Q}^{-1}$, we reformulate the block matrices ${\mathsf{\Phi }}_{*}$ and $A_{*}$ as follows:

$$\begin{array}{cc}\hfill A_{*}& =Q_{*}{\tilde{A}}_{*}{Q}_{*}^{-1},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathsf{\Phi }}_{*}& =Q_{*}{\tilde{\mathsf{\Phi }}}_{*}{Q}_{*}^{-1},\hfill \end{array}$$

(23)

where ${\tilde{A}}_{*}=diag(2h^{2}I-{\mu }_{1}k\mathsf{\Lambda },I,\cdots ,I)$, $Q_{*}=diag(Q,Q,\cdots ,Q)$ and

$$\begin{array}{cc}\hfill {\tilde{\mathsf{\Phi }}}_{*}=& \left[\begin{array}{cccccccc}4h^{2}I+2k^2\mathsf{\Lambda }& -2h^{2}I-{\mu }_{1}k\mathsf{\Lambda }& 0& \cdots & 0& -\alpha I& 0& \alpha I\\ I& 0& 0& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & I& 0& 0& 0\\ 0& 0& 0& \cdots & 0& I& 0& 0\\ 0& 0& 0& \cdots & 0& 0& I& 0\end{array}\right].\hfill \end{array}$$

(24)

Substituting (22) and (23) into (18), we obtain

$$\begin{array}{c}\hfill Q_{*}{\tilde{A}}_{*}\left(Q_{*}^{-1}{U}_{*}^{n+1}\right)=Q_{*}{\tilde{\mathsf{\Phi }}}_{*}\left(Q_{*}^{-1}{U}_{*}^n\right),n\ge 0.\end{array}$$

(25)

We let ${\mathcal{U}}^n:=Q^{-1}{U}^n={[{\phi }_1^n,{\phi }_2^n,\cdots ,{\phi }_{P-1}^n]}^{\top }\in {\mathbb{R}}^{P-1}$, and define the block vector

$${\mathcal{U}}_{*}^n:={[{\mathcal{U}}^n,{\mathcal{U}}^{n-1},\dots ,{\mathcal{U}}^{n-N+1},{\mathcal{U}}^{n-N},{\mathcal{U}}^{n-N-1}]}^{\top }=Q_{*}^{-1}{U}_{*}^n,$$

so that ${\mathcal{U}}_{*}^n\in {\mathbb{R}}^{(P-1)(N+2)}$. Then, the difference Equation (25) simplifies to

$$\begin{array}{c}\hfill {\mathcal{U}}_{*}^{n+1}={\tilde{\mathsf{\Psi }}}_{*}{\mathcal{U}}_{*}^n,n\ge 0,\end{array}$$

(26)

where ${\tilde{\mathsf{\Psi }}}_{*}:={\tilde{A}}_{*}^{-1}{\tilde{\mathsf{\Phi }}}_{*}$. It follows that ${\mathsf{\Psi }}_{*}$ (from (19)) and ${\tilde{\mathsf{\Psi }}}_{*}$ (from (26)) are similar matrices and therefore share the same set of eigenvalues.

Equation (26) may be reformulated into an equivalent expression by reordering its components. For $m=1,\dots ,P-1$, we define

$$H_m^n:={[{\phi }_m^n,{\phi }_m^{n-1},\dots ,{\phi }_m^{n-N+1},{\phi }_m^{n-N},{\phi }_m^{n-N-1}]}^{\top },$$

and assemble them into a block vector

$$H_{*}^n:={[H_1^n,H_2^n,\dots ,H_{P-1}^n]}^{\top }.$$

In a similar manner, for $m=1,\dots ,P-1$, we define the diagonal matrix

$$D_m:=diag\left(2h^2-{\mu }_{1}k{\lambda }_m,1,\dots ,1\right),$$

and the matrix $G_m$ as

$$\begin{array}{c}\hfill G_m:=\left[\begin{array}{cccccccc}4h^2+2k^2{\lambda }_m& -(2h^2+{\mu }_{1}k{\lambda }_m)& 0& \cdots & 0& -\alpha & 0& \alpha \\ 1& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0& 0\\ 0& 0& 0& \cdots & 0& 0& 1& 0\end{array}\right],\end{array}$$

We then define $D_{*}:=diag(D_1,\dots ,D_{P-1})$ and $G_{*}:=diag(G_1,\dots ,G_{P-1})$. The matrix $D_{*}$ is invertible, since each $D_m$ is invertible for $m=1,\dots ,P-1$. This allows us to introduce the block matrix

$${\widetilde{\tilde{\mathsf{\Psi }}}}_{*}:=D_{*}^{-1}{G}_{*}=diag(D_1^{-1}{G}_1,\cdots ,D_{P-1}^{-1}{G}_{P-1}),$$

and to rewrite the difference Equation (26) in the equivalent form:

$$\begin{array}{c}\hfill H_{*}^{n+1}={\widetilde{\tilde{\mathsf{\Psi }}}}_{*}{H}_{*}^n,n\ge 0.\end{array}$$

(27)

The matrices ${\tilde{\mathsf{\Psi }}}_{*}$ and ${\widetilde{\tilde{\mathsf{\Psi }}}}_{*}$ are similar and therefore have the same set of eigenvalues.

The matrices

$$\begin{array}{c}\hfill D_m^{-1}{G}_m=\left[\begin{array}{cccccccc}{\displaystyle \frac{4h^2+2k^2{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}}& {\displaystyle \frac{-(2h^2+{\mu }_{1}k{\lambda }_m)}{2h^2-{\mu }_{1}k{\lambda }_m}}& 0& \cdots & 0& {\displaystyle \frac{-\alpha }{2h^2-{\mu }_{1}k{\lambda }_m}}& 0& {\displaystyle \frac{\alpha }{2h^2-{\mu }_{1}k{\lambda }_m}}\\ 1& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 1& 0& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & 1& 0& 0& 0\\ 0& 0& 0& \cdots & 0& 1& 0& 0\\ 0& 0& 0& \cdots & 0& 0& 1& 0\end{array}\right],\end{array}$$

for $m=1,\dots ,P-1$, are companion matrices (see [27]) corresponding to the $P-1$ polynomials

$$\begin{array}{c}\hfill {\pi }_m\left(z\right)=z^{N+2}-{\displaystyle \frac{4h^2+2k^2{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}}{z}^{N+1}+{\displaystyle \frac{2h^2+{\mu }_{1}k{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}}{z}^N+{\displaystyle \frac{\alpha }{2h^2-{\mu }_{1}k{\lambda }_m}}{z}^2-{\displaystyle \frac{\alpha }{2h^2-{\mu }_{1}k{\lambda }_m}}.\end{array}$$

(28)

The $N+2$ roots of each polynomial ${\pi }_m\left(z\right)$ are precisely the eigenvalues of the matrix $D_m^{-1}{G}_m$. Therefore, verifying that all eigenvalues of the block matrix ${\mathsf{\Psi }}_{*}$ in (19) lie strictly within the unit disk reduces to showing that all roots of ${\pi }_m\left(z\right)$, for $m=1,\dots ,P-1$, lie inside the unit disk.

Remark 2.

The index m corresponds to the spectral modes associated with the diagonalization of the spatial discretization matrix $\mathcal{M}$, whose eigenvalues ${\lambda }_m<0$ define the modal structure of the semi-discrete system. This decoupling enables mode-by-mode stability analysis via the characteristic polynomials ${\pi }_m\left(z\right)$. Consequently, verifying that all such polynomials have roots strictly inside the unit disk ensures the asymptotic stability of the fully discrete scheme.

To analyze the stability of discrete dynamical systems or difference schemes—particularly when explicit root-finding is impractical—we often turn to root location criteria tailored to the unit disk. One such result is the Jury stability criterion, a discrete analogue of the Routh–Hurwitz test for continuous systems. It provides a systematic, algebraic procedure to determine whether all the roots of a characteristic polynomial lie strictly inside the unit circle. This criterion is especially well suited for analyzing the stability of linear recurrence relations and finite difference schemes, making it a natural tool in our context. In this work, we apply the Jury test to assess the stability of the proposed second-order scheme by verifying the root conditions of the associated characteristic equation.

To assess the stability of the proposed finite difference scheme, we analyze the location of the roots of its characteristic equation. For this purpose, we employ the Jury stability criterion, presented in Section 2, which is well suited for evaluating whether all roots of ${\pi }_m\left(z\right)$ lie within the unit circle.

Proposition 1.

We let $N>0$ and let ${\lambda }_m$ denote the mth eigenvalue of the matrix $\mathcal{M}$ defined in (21). Suppose the parameters ${\mu }_1,{\mu }_2,k$, and h are positive and satisfy the following Courant–Friedrichs–Lewy (CFL) time-step restriction involving the spectral radius $\rho \left(\mathcal{M}\right):={max}_m\left|{\lambda }_m\right|$:

$$\begin{array}{c}\hfill 0<k<k_{CFL}:=min\left\{{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+({\mu }_1+4{\mu }_2)\rho \left(\mathcal{M}\right)}},{\displaystyle \frac{\sqrt{2}h}{\sqrt{\rho \left(\mathcal{M}\right)}}}\right\}.\end{array}$$

(29)

Then all roots of the polynomial ${\pi }_m\left(z\right)$ defined in (28) lie strictly inside the unit disk.

Proof. 

We analyze the asymptotic stability of the fully discrete scheme by applying the Jury stability criterion to the mode-wise characteristic polynomial

$$\begin{array}{c}\hfill {\pi }_m\left(z\right)=z^{N+2}-A_m{z}^{N+1}+B_m{z}^N+C_m{z}^2-C_m=\sum _{j=0}^n{a}_j{z}^{n-j},n=N+2.\end{array}$$

(30)

The coefficients $A_m,B_m,C_m$ are given by

$$A_m={\displaystyle \frac{4h^2+2k^2{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}},B_m={\displaystyle \frac{2h^2+{\mu }_{1}k{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}},C_m={\displaystyle \frac{{\mu }_{2}k{h}^2}{2h^2-{\mu }_{1}k{\lambda }_m}},$$

where ${\lambda }_m<0$ is the mth eigenvalue of $\mathcal{M}$. The coefficients $a_j$ in (A1) are

$$\begin{array}{cc}\hfill a_0=1,a_1=-A_m,& a_2=B_m,a_{n-2}=C_m,a_{n-1}=0,a_n=-C_m,\hfill \\ \hfill & a_j=0\mathrm{for}3\le j\le n-3.\hfill \end{array}$$

Before proceeding, we note that the coefficients $A_m,B_m$, and $C_m$ share the same denominator $2h^2-{\mu }_{1}k{\lambda }_m$, which is positive since ${\lambda }_m<0$. Therefore, $C_m>0$ immediately. The coefficients $A_m$ and $B_m$ are also positive provided that

$$k^2<{\displaystyle \frac{2h^2}{|{\lambda }_m|}}\mathrm{and}k<{\displaystyle \frac{2h^2}{{\mu }_1\left|{\lambda }_m\right|}}.$$

These inequalities are both implied by the CFL condition (29). Hence, we conclude that all three coefficients $A_m,B_m$, and $C_m$ are positive under the CFL restriction.

• Step 1: Necessary conditions. We first verify the necessary Jury conditions:

  $$\begin{array}{cc}\hfill & \mathrm{NC}1:{\pi }_m\left(1\right)=1-A_m+B_m={\displaystyle \frac{-2k^2{\lambda }_m}{2h^2-{\mu }_{1}k{\lambda }_m}}>0,\sin \mathrm{ce}{\lambda }_m<0.\hfill \\ \hfill & \mathrm{NC}2:{(-1)}^n{\pi }_m(-1)=1+A_m+B_m>0,\sin \mathrm{ce}{A}_m,B_m>0.\hfill \end{array}$$
• Step 2: First sufficient condition. The condition $|a_0|>|a_n|$ becomes

  $$\mathrm{SC}1:1>|-C_m|=C_m,$$

  which leads to

  $$\begin{array}{c}\hfill C_m<1\iff {\displaystyle \frac{{\mu }_{2}k{h}^2}{2h^2-{\mu }_{1}k{\lambda }_m}}<1.\end{array}$$

  (31)

  Since ${\lambda }_m<0$, the denominator is positive. Multiplying both sides and solving gives

  $$\begin{array}{c}\hfill k<{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+{\mu }_1{\lambda }_m}}.\end{array}$$

  (32)

  Although ${\lambda }_m<0$, the right-hand side remains positive because

  $${\mu }_2{h}^2+{\mu }_1{\lambda }_m<{\mu }_2{h}^2+{\mu }_1\left|{\lambda }_m\right|<{\mu }_2{h}^2+{\mu }_1\rho \left(\mathcal{M}\right),$$

  which implies

  $${\displaystyle \frac{2h^2}{{\mu }_2{h}^2+{\mu }_1{\lambda }_m}}>{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+{\mu }_1\rho \left(\mathcal{M}\right)}}.$$

  Under the CFL condition (29), we have

  $$k<{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+({\mu }_1+4{\mu }_2)\rho \left(\mathcal{M}\right)}}<{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+{\mu }_1\rho \left(\mathcal{M}\right)}},$$

  which ensures Inequality (32) holds. Hence, $C_m<1$ and the first necessary condition (SC1) is satisfied.
• Step 3: Second sufficient condition. The next Jury condition involves

  $$b_0=a_n{a}_1-a_0{a}_{n-1}=(-C_m)(-A_m)=A_m{C}_m,b_{n-1}=a_n^2-a_0^2=C_m^2-1.$$

  Note. The quantity $b_0=A_m{C}_m$ is positive under the CFL condition (29). Also, Step 2 guarantees that $b_{n-1}=C_m^2-1<0$. The Jury condition reads

  $$\mathrm{SC}2:|b_{n-1}|>|b_0|\Rightarrow 1-C_m^2>A_m{C}_m.$$

  To verify this inequality rigorously, we consider the difference

  $$1-C_m^2-A_m{C}_m={\displaystyle \frac{{(2h^2-{\mu }_{1}k{\lambda }_m)}^2-\left[h^4{k}^2{\mu }_2^2+2h^{2}k{\mu }_2(2h^2+k^2{\lambda }_m)\right]}{{(2h^2-{\mu }_{1}k{\lambda }_m)}^2}}.$$

  We let $D\left(k\right):=2h^2-{\mu }_{1}k{\lambda }_m$ and define the polynomial

  $$\chi \left(k\right):=D{\left(k\right)}^2-h^4{k}^2{\mu }_2^2-2h^{2}k{\mu }_2(2h^2+k^2{\lambda }_m).$$

  Thus, Condition $1-C_m^2>A_m{C}_m$ is equivalent to $\chi \left(k\right)>0$.
  Since $\chi \left(0\right)=D{\left(0\right)}^2=4h^4>0$, it suffices to show $\chi \left(k\right)$ is non-decreasing. Direct differentiating gives

  $${\chi }^{\prime }\left(k\right)=-4{\mu }_2{h}^4-2{\mu }_2^{2}k{h}^4+4{\mu }_1|{\lambda }_m|h^2+6{\mu }_2\left|{\lambda }_m\right|k^2{h}^2+2{\mu }_1{\lambda }_m^{2}k.$$

  Each term in ${\chi }^{\prime }\left(k\right)$ is nonnegative except the first two, which are of size $O\left(h^4\right)$. The positive terms scale like $O\left(h^2\right)$ or $O\left(k\right)$. Then, under the CFL restriction (29), we have

  $$k<min\left\{{\displaystyle \frac{2h^2}{({\mu }_1+4{\mu }_2)\left|{\lambda }_m\right|}},{\displaystyle \frac{\sqrt{2}h}{\sqrt{|{\lambda }_m|}}}\right\}.$$

  This ensures the positive terms dominate. Hence, ${\chi }^{\prime }\left(k\right)\ge 0$, and $\chi \left(k\right)\ge \chi \left(0\right)>0$ for all $0\le k\le k_{\mathrm{CFL}}$. We conclude that SC2 is satisfied.
• Step 4: Higher-order conditions. Due to the sparsity of ${\pi }_m\left(z\right)$, all higher-order determinants in the Jury table involve only the nonzero coefficients $a_0,a_1,a_2,a_{n-2},a_n$. This structure allows the higher-order Jury inequalities to be expressed in a simplified form:

  $$(1-{\theta }_1{C}_m)(1-{\theta }_2{C}_m)>{\theta }_3{C}_m,\mathrm{with}{\theta }_i>0.$$

  A detailed verification of this form and the derivation of representative cases, including the third sufficient condition SC3, is provided in Appendix A. That appendix shows how these inequalities follow from the previously established conditions SC1 and SC2, and are thus guaranteed by the CFL restriction (29).

Therefore, under the CFL condition (29), all Jury conditions are satisfied for each mode m, and all roots of ${\pi }_m\left(z\right)$ lie strictly inside the unit disk.  □

Remark 3.

If the damping and delay parameters ${\mu }_1$ and ${\mu }_2$ are sufficiently large, then the first term in the CFL condition (29) becomes more restrictive than the second, and the condition simplifies to

$$k<{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+({\mu }_1+4{\mu }_2)\rho \left(\mathcal{M}\right)}}.$$

However, for generality and mathematical precision, we retain the full minimum expression in (29).

Remark 4.

While the proposed scheme discretizes a wave equation with delay, the Jury criterion is not applied to the PDE directly but to the characteristic polynomial ${\pi }_m\left(z\right)$ derived from the recurrence relation (A1). The coefficients depend on delay parameters (e.g., ${\mu }_2$) but remain constant for each mode. Thus, the standard Jury test is applicable. See [28] for more general validation.

Since the roots of ${\pi }_m\left(z\right)$ are the eigenvalues of the matrix ${\widetilde{\tilde{\mathsf{\Psi }}}}_{*}$, and hence are also eigenvalues of ${\mathsf{\Psi }}_{*}$, we arrive at the following result.

Proposition 2.

We let $k,h>0$. If the CFL-type condition (29) is satisfied, then all eigenvalues of the matrix ${\mathsf{\Psi }}_{*}$ in (19) lie strictly inside the unit disk.

The following theorem then follows immediately from Proposition 2 and ([29] Theorem 4.13).

Theorem 2

(Stability of the Discrete Scheme). We let $k,h>0$. If Inequality (29) is satisfied, then the finite difference scheme (19) is asymptotically stable.

Remark 5.

In [13], the authors consider the delayed diffusion equation stated in our Introduction as Equation (1). Their stability condition for the explicit scheme is given in Theorem 5 (page 863) and reads

$$\Delta t<{\displaystyle \frac{\Delta x^2}{2a^2(1+c^2)}},$$

where a is the diffusion coefficient and c is the delay strength. The condition reflects a CFL-type restriction that involves the time step $\Delta t$, space step $\Delta x$, and delay-related constant.

In [14], the same delay model is treated using implicit schemes, and unconditional stability is shown in Proposition 4 (page 1284) through spectral norm estimates of a block companion matrix.

In contrast, the present work considers a delayed wave equation with strong damping and delay in the derivative $u_t(t-\tau )$. The resulting discrete scheme leads to a higher-order recurrence relation, and the stability condition derived in Proposition 1 implies

$$0<k<{\displaystyle \frac{2h^2}{{\mu }_2{h}^2+({\mu }_1+4{\mu }_2)\rho \left(\mathcal{M}\right)}},$$

where ${\mu }_1$ and ${\mu }_2$ are the damping and the delay parameters, respectively, and $\rho \left(\mathcal{M}\right)$ is the spectral radius of the spatial discretization matrix.

This condition shares the CFL-type structure with [13], but reflects the more complex dynamics introduced by the wave operator and delay in the derivative term. As the associated characteristic polynomial has higher degree and five nonzero terms, we apply the Jury stability criterion rather than relying on spectral radius estimates or root formulas. This approach offers a general framework to verify asymptotic stability in delayed wave systems.

Remark 6.

The exponential stability of the continuous system is ensured under certain assumptions on the delay and damping parameters presented in Condition (3). In contrast, the CFL-type condition (29) arises purely from the discrete stability analysis and is not inherited from the continuous model. This condition ensures that the roots of the characteristic polynomial lie strictly inside the unit disk, thereby guaranteeing asymptotic stability of the numerical scheme.

5. Numerical Examples

We now illustrate the performance of the proposed finite difference scheme by solving System (2a)–(2d) in a one-dimensional spatial domain. The domain is discretized uniformly with spatial step size h, and time integration is carried out using the second-order implicit scheme derived in Section 3.

To investigate the stability of the numerical scheme, we consider parameter values ${\mu }_1$ and ${\mu }_2$ that satisfy the exponential stability Condition (3) of the continuous system. This ensures that any observed instability is due to the discretization and not the underlying PDE. We also examine the role of the CFL-type restriction (29), which governs the asymptotic stability of the discrete scheme. As ${\mu }_2$ increases, both conditions become more restrictive, emphasizing the need for careful parameter selection.

The initial data for all test cases are given by

$$\begin{array}{c}\hfill u_0\left(x\right)=2x(x-L),u_1\left(x\right)=0,f_0(x,t-\tau )=sin\left(x\right).\end{array}$$

(33)

We compare two test cases where the continuous system is exponentially stable, but the numerical scheme may or may not be stable depending on whether the CFL condition is satisfied. These cases are summarized in

Table 1. Satisfaction of stability conditions in each test case.

Case	Condition I:	Condition II:
	${\displaystyle {\mathit{\mu }}_{\mathit{2}}<\frac{{\mathit{\mu }}_{\mathit{1}}}{{\mathit{C}}_{\mathit{p}}},{\mathit{C}}_{\mathit{p}}=\frac{\mathit{L}}{\mathit{\pi }}}$	${\displaystyle \mathit{k}<{\mathit{k}}_{\mathit{CFL}}}$
1	Satisfied	Satisfied
2	Satisfied	Not satisfied

, where we denote the continuous stability Condition (3) as Condition I and the CFL-type condition (29) as Condition II.

We fix the spatial domain to the interval $[0,5]$ and the time interval to $[0,200]$. The scheme parameters $h,k,\tau ,{\mu }_1,{\mu }_2$ are listed in

Table 2. Parameter values used for each test case.

Case	h	k	$\mathit{\tau }$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{k}}_{\mathit{CFL}}$
1	0.5	0.01036	1.03	3.0	1.69646	0.01295
2	0.5	0.01554	1.55	3.0	1.69646	0.01295

.

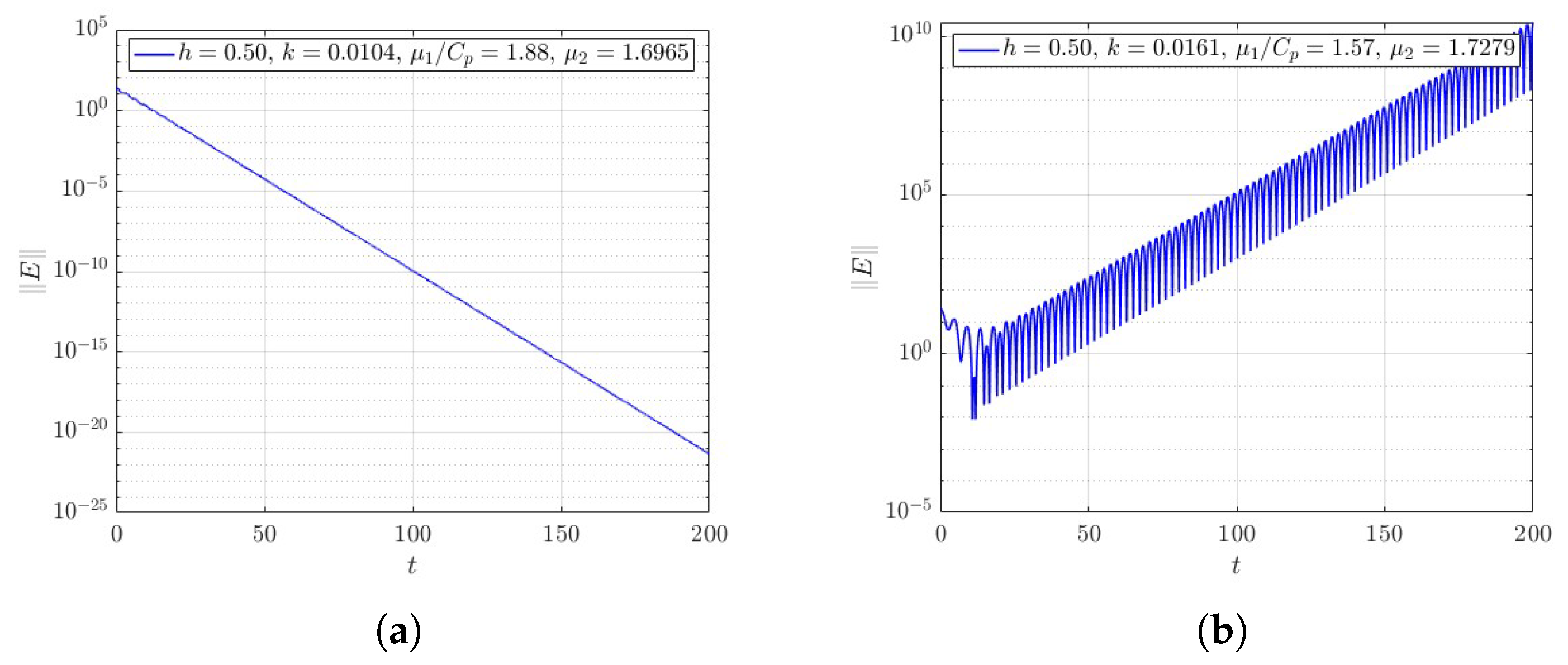
Figure 2 shows the evolution of the energy norm

$$\begin{array}{c}\hfill \parallel E\parallel ={\displaystyle \frac{1}{2}}\left[\parallel u_t{\parallel }^2+{\parallel \nabla u\parallel }^2\right]\end{array}$$

(34)

over time on a logarithmic scale. In Case 1, where both stability conditions are satisfied, the energy decays exponentially, indicating that the discrete scheme faithfully reproduces the decay behavior of the continuous system. In Case 2, although the continuous system is exponentially stable, the CFL condition is violated. As a result, the numerical solution becomes unstable over time. These results highlight the necessity of the discrete stability condition for maintaining asymptotic stability in practice, even when the continuous model is well behaved.

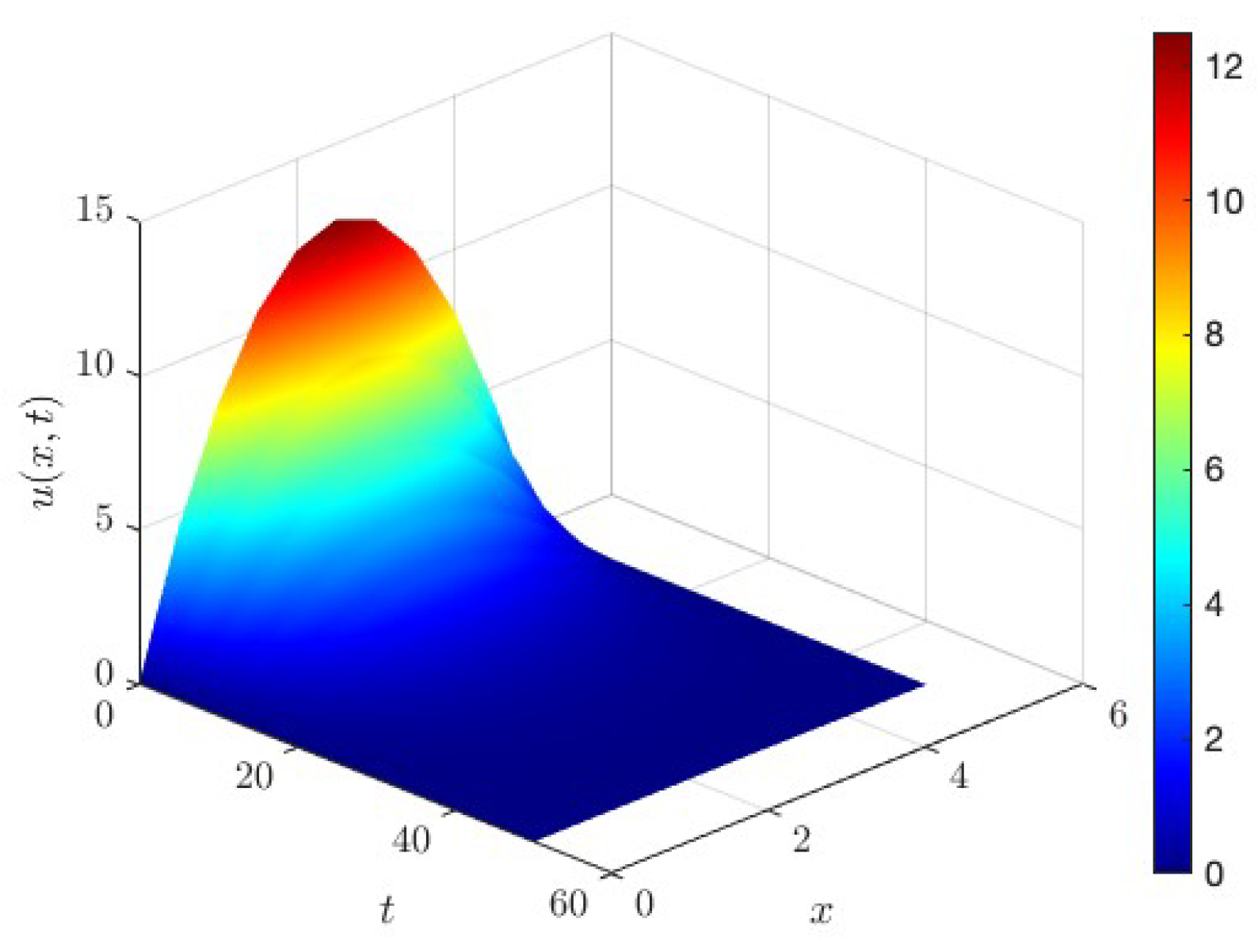
To complement the energy norm analysis, we present the numerical solution $u(x,t)$ under the parameter values used in Case 1. As shown in Figure 3, the solution profiles at selected time levels exhibit a clear decrease in amplitude over time. This indicates that the solution decays across the spatial domain. Figure 4 provides a 3D surface plot of $u(x,t)$, highlighting the smooth decay of the solution. These plots visually confirm the behavior predicted by the theoretical analysis: the solution vanishes gradually as time progresses, in accordance with the exponential decay of the energy norm.

Remark 7.

The parameter sets in Table 2 and

Table 3. Parameter values for the simulations in Figure 5. All configurations satisfy the CFL-type stability condition.

h	k	$\mathit{\tau }$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{k}}_{\mathit{CFL}}$
0.50	0.0155	0.1554	1.1310	3.9021	0.019425
0.50	0.0052	0.0518	3.3929	3.9021	0.006475
0.50	0.0031	0.0311	5.6549	3.9021	0.003885

are designed to test the stability of the scheme under different theoretical scenarios. Specifically, we vary ${\mu }_1$, ${\mu }_2$, τ, and k to create cases that either satisfy or violate the derived stability conditions (Condition I and Condition II). These parameters are not chosen to reflect a specific physical application, but rather to support a structured numerical investigation of the proposed scheme’s stability behavior.

5.1. Effect of Damping Strength and CFL Restriction on Decay Rate

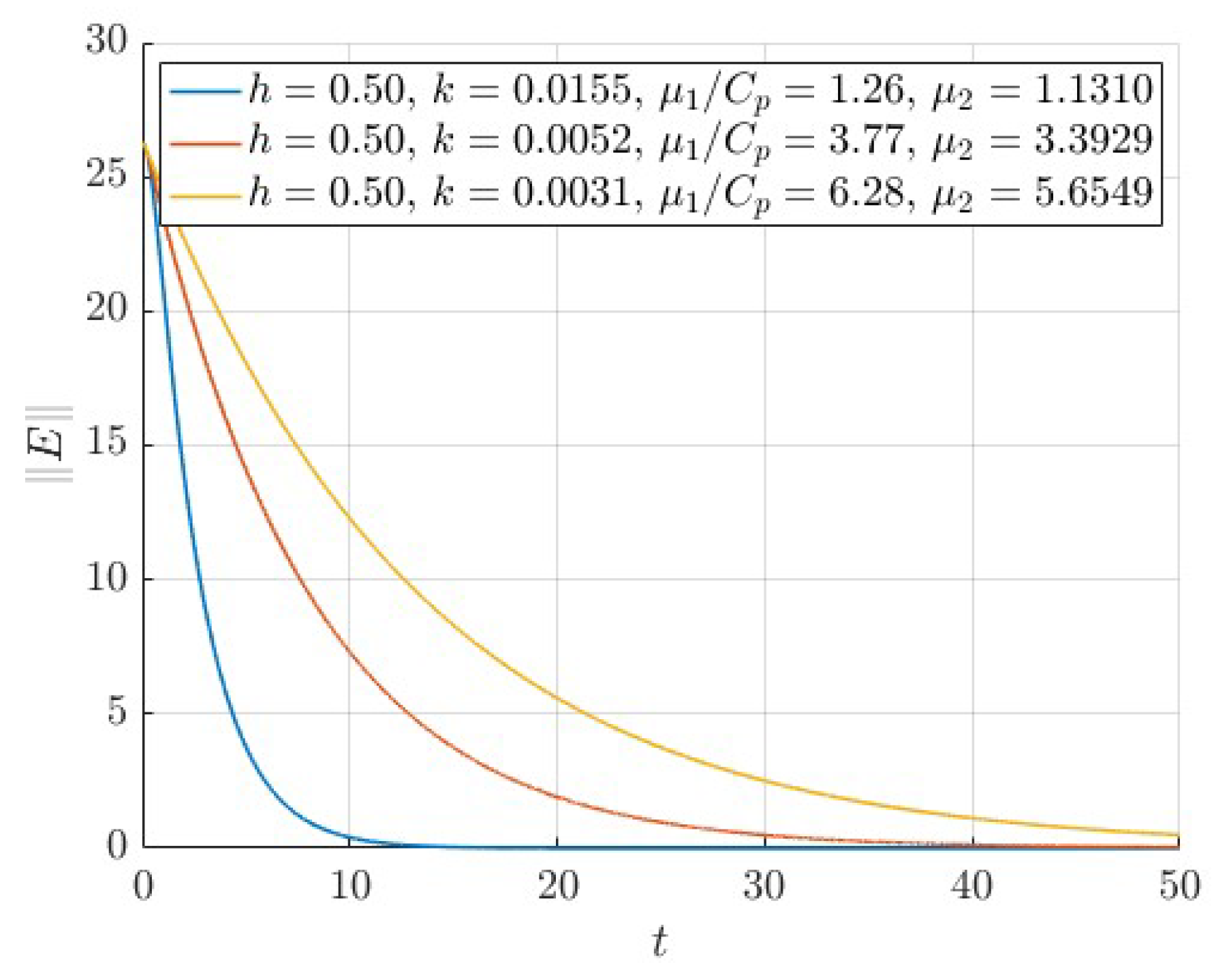
To explore the effect of increasing the damping parameter ${\mu }_1$ on the energy decay rate, we simulate three configurations of Case 1, keeping ${\mu }_2$ fixed and adjusting k to satisfy the CFL-type stability condition (29) in each case. The corresponding parameter values are listed in Table 3. The results are presented in Figure 5, plotted on a linear scale, with time restricted to the interval $[0,30]$ to highlight differences in the early-stage decay behavior.

All three simulations satisfy both stability conditions, yet the observed decay rate varies. The case with the smallest ${\mu }_1$ exhibits the fastest decay. As ${\mu }_1$ increases, the CFL restriction imposes a smaller time step k, which leads to slower decay. This observation illustrates the practical trade-off: stronger damping does not necessarily accelerate decay in simulations due to the more restrictive CFL condition it entails.

5.2. Effect of the CFL Condition When Continuous Stability Fails

We also consider a case where the exponential stability condition for the continuous system is not satisfied (i.e., ${\mu }_2\ge {\mu }_1/C_p$), while the CFL-type condition remains enforced. As illustrated in Figure 6a, the numerical solution in this case still exhibits asymptotic decay, confirming the stabilizing influence of the CFL condition on the discrete scheme. This result suggests that the CFL restriction plays a central role in maintaining numerical stability, even when the continuous system lies near or beyond the exponential stability threshold.

By contrast, when both the continuous and discrete stability conditions are violated, as shown in Figure 6b, the solution becomes numerically unstable. This reinforces the necessity of satisfying at least the CFL condition for obtaining stable numerical results.

6. Conclusions and Future Work

In this paper, we analyzed a wave equation with strong damping and a delay term. We developed a fully discrete second-order finite difference scheme for the spatial and temporal discretization of the problem. The stability of the discrete scheme was rigorously analyzed using the Jury stability criterion. A CFL-type condition on the time step was derived to guarantee that the roots of the characteristic polynomials associated with each mode lie strictly within the unit disk, ensuring asymptotic stability of the scheme.

Numerical experiments confirmed the theoretical results and demonstrated that the discrete solution exhibits exponential-like decay in practice, consistent with the behavior of the continuous system. These results highlight the effectiveness of the proposed method and emphasize the importance of careful parameter selection in the presence of time delay.

The proposed scheme can in principle be extended to higher spatial dimensions such as (1 + 2)D or (1 + 3)D. The finite difference formulation and stability framework are generalizable, but such an extension would lead to significantly larger discrete systems, increasing both computational cost and implementation complexity. Efficient implementation in higher dimensions remains an open direction for future study.

Beyond dimensionality, extending the scheme to non-uniform grids in space or time is another important challenge. Non-uniform discretization would require the reformulation of the stability analysis, likely leading to mesh-dependent conditions. This direction is particularly relevant for adaptive methods or problems with localized features.

Another promising direction for future work is the development of higher-order accurate difference schemes for delayed wave equations. While standard finite difference techniques can be extended to achieve greater accuracy, doing so may significantly increase the complexity of both implementation and stability analysis. Extending the Jury-based framework to handle such cases remains an open challenge.

Finally, incorporating nonlinearities—such as a nonlinear source term—into the delayed wave model is a natural next step. While the finite difference scheme could be modified to handle such terms, the linear stability tools used in this paper would not directly apply. A new analysis framework would be needed, possibly based on energy methods or nonlinear stability theory.